MODEL VERHULST DETERMINISTIK DAN STOKASTIK

(1)

i

MODEL VERHULST DETERMINISTIK DAN STOKASTIK

Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Oleh : Happy Christanti

NIM: 123114001

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

(2)

ii

DETERMINISTIC AND STOCHASTIC VERHULST MODEL

Thesis

Presented as a Partial Fulfillment of the Requirement to Obtain the Sarjana Sains Degree

in Mathematics

By :

Happy Christanti Student Number: 123114001

MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY YOGYAKARTA

(3)

(4)

(5)

v

PERNYATAAN KEASLIAN KARYA

Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini tidak memuat karya atau bagian orang lain, kecuali yang telah disebutkan dalam kutipan atau daftar pustaka, sebagaimana layaknya karya ilmiah.

Yogyakarta, 31 Maret 2016 Penulis,

(6)

vi

HALAMAN PERSEMBAHAN

“Bersukacitalah dalam pengharapan, sabarlah

dalam kesesakan, dan bertekunlah dalam doa!”

(Roma 12:12)

Karya ini kupersembahkan untuk: Tuhan Yesus Kristus yang senantiasa menyertaiku Mama, Papa dan Kakak tercinta yang selalu mendukungku

(7)

vii

ABSTRAK

Dinamika populasi merupakan salah satu penelitian di bidang matematika biologi yang paling aktif. Pada skripsi ini akan dibahas model Verhulst dan beberapa pengembangannya, seperti model Verhulst dengan batas bawah, model pemanenan Schaefer, model penyebaran teknologi, dan model Verhulst dengan laju pertumbuhan tidak konstan. Model Verhulst dan beberapa pengembangannya tersebut akan diselesaikan secara analitik. Kita juga akan memeriksa kestabilan titik ekuilibrium dan menyajikan grafik dengan menggunakan Matlab atau Maple. Lebih lanjut lagi, kita akan mengkonstruksi model stokastik Verhulst dengan mempertimbangkan derau putih yang berasal dari gerak Brown ke dalam model deterministik yang bersesuaian. Kita selesaikan model stokastik tersebut menggu-nakan kalkulus stokastik Ito.

(8)

viii

ABSTRACT

Population dynamic is one of the most active research areas in mathema-tical biology. In this thesis we will discuss the Verhulst model and some of its modifications, such as Verhulst model with lower threshold, harvesting model of Schaefer, spreading-technology model, and Verhulst model with time dependent growth rate. Some of these models will be solved analytically. We also investigate the stability of the equilibrium solutions and present some simulations by using Matlab or Maple. Furthermore, we will construct a stochastic Verhulst model by incorporating a white noise coming from Brownian motion to the corresponding deterministic model. We solve the stochastic model by using Ito’s stochastic calculus.

(9)

ix

KATA PENGANTAR

Puji dan syukur penulis panjatkan kepada Tuhan Yesus Kristus yang selalu menyertai dan membimbing penulis sehingga penulis mampu menyelesaikan skripsi ini dengan baik. Skripsi ini dibuat sebagai salah satu syarat dalam menye-lesaikan studi Strata satu (S1) dan memperoleh gelar Sarjana Sains (S.Si.) pada Program Studi Matematika, Fakultas Sains dan Teknologi, Universitas Sanata Dharma Yogyakarta.

Penulis menyadari bahwa proses penulisan skripsi ini melibatkan banyak pihak yang membantu penulis dalam menghadapi berbagai macam kesulitan dan hambatan selama proses penulisan skripsi. Oleh karena itu pada kesempatan ini penulis mengucapkan terima kasih kepada:

1. Bapak Hartono, Ph.D selaku Kaprodi Matematika dan Dosen Pembimbing Akademik.

2. Bapak Dr. rer. nat. Herry P. Suryawan, S.Si., M.Si. selaku Dosen Pembimbing Skripsi.

3. Romo Prof. Dr. Frans Susilo, SJ., Ibu M. V. Any Herawati, S.Si., M.Si., Bapak Ir. Ig. Aris Dwiatmoko, M.Sc., Bapak Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D., dan Ibu Lusia Krismiyati Budiasih, S.Si., M.Si. selaku dosen-dosen prodi matematika yang telah memberikan banyak pengetahuan kepada penulis selama proses perkuliahan.

4. Bapak/Ibu dosen/karyawan Fakultas Sains dan Teknologi yang telah berdinamika bersama selama penulis berkuliah.

(10)

x

5. Teman-teman Matematika 2012: Boby, Ajeng, Tika, Oxi, Putri, Juli, Ferni, Risma, Ega, Rian, Budi, Lia, Anggun, Sila, Noni, Arum, Dewi, Ilga, Amanda, terimakasih untuk kebersamaan, keceriaan, semangat dan bantu-an selama proses perkuliahbantu-an. Bbantu-anyak suka dbantu-an duka, namun tidak ada kata menyerah.

6. Kakak-kakak dan adik-adik tingkat: Kak Indra, Kak Ensi, Kak Ochi, Kak Jojo, Kak Ayu, Kak Tika, Kak Pandu, Kak Ratri, Kak Astri, Ambar, Bintang, Inge, Dion, Rey, Agung, Bella, Monik dan yang lainnya, terima-kasih untuk semangat dan dukungannya.

7. Semua pihak yang tidak dapat disebutkan satu per satu dalam proses penulisan skripsi ini.

Semoga segala perhatian, dukungan, bantuan dan cinta yang telah diberikan mendapatkan balasan dari Tuhan Yesus Kristus. Penulis menyadari bahwa masih banyak kekurangan dalam penulisan skripsi ini. Oleh karena itu, penulis mengha-rapkan kritik dan saran demi penyempurnaan skripsi ini. Harapan penulis, semoga skripsi ini bermanfaat bagi pembaca dan menjadi referensi belajar yang baik.

Yogyakarta, 31 Maret 2016 Penulis,

(11)

xi

LEMBAR PERNYATAAN PERSETUJUAN

PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS

Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma:

Nama : Happy Christanti

Nomor Mahasiswa : 123114001

Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan Universitas Sanata Dharma karya ilmiah saya yang berjudul:

MODEL VERHULST DETERMINISTIK DAN STOKASTIK

beserta perangkat yang diperlukan (bila ada). Dengan demikian saya memberikan kepada Perpustakaan Universitas Sanata Dharma hak untuk menyimpan, mengalihkan dalam bentuk media lain, mengelolanya dalam bentuk pangkalan data, mendistribusikan secara terbatas, dan mempublikasikannya di Internet atau media lain untuk kepentingan akademis tanpa perlu meminta izin dari saya maupun memberikan royalti kepada saya selama tetap mencatumkan nama saya sebagai penulis.

Demikian pernyataan ini yang saya buat dengan sebenarnya. Dibuat di Yogyakarta

Pada tanggal: 31 Maret 2016 Yang menyatakan

(12)

xii

DAFTAR ISI

HALAMAN JUDUL ...i

HALAMAN PERSETUJUAN PEMBIMBING ...iii

HALAMAN PENGESAHAN ...iv

HALAMAN KEASLIAN KARYA ...v

HALAMAN PERSEMBAHAN ...vi

ABSTRAK ...vii

ABSTRACT ...viii

KATA PENGANTAR ...ix

LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI...xi

DAFTAR ISI ...xii

DAFTAR GAMBAR ...xv BAB I PENDAHULUAN ...1 A. Latar Belakang ...1 B. Rumusan Masalah ...7 C. Batasan Masalah ...7 D. Tujuan Penulisan ...8 E. Manfaat Penulisan ...8 F. Metode Penulisan ...8 G. Sistematika Penulisan ...9

(13)

xiii

BAB II PERSAMAAN DIFERENSIAL ...11

A. Persamaan Diferensial Biasa ...11

1. Persamaan Diferensial ...11

2. Persamaan Diferensial Linier ...12

3. Persamaan Diferensial Variabel Terpisah ...14

B. Persamaan Diferensial Stokastik ...16

1. Teori Peluang...17

2. Integral Ito ...32

3. Persamaan Diferensial Stokastik ...54

BAB III MODEL VERHULST DETERMINISTIK...58

A. Model Pertumbuhan Populasi Verhulst ...64

1. Penyelesaian Model Verhulst ...65

2. Analisa Kualitatif Model Verhulst ...69

B. Beberapa Pengembangan Model Pertumbuhan Populasi Verhulst ....74

1. Model Verhulst dengan Batas Bawah (Threshold) ...74

2. Model Pemanenan Schaefer ...88

3. Model Penyebaran Teknologi...96

4. Model Verhulst dengan Laju Pertumbuhan tidak Konstan ...101

BAB IV MODEL VERHULST STOKASTIK ...113

A. Model Pertumbuhan Stokastik yang Memuat Derau yang Berasal dari Gerak Brown ...113

(14)

xiv BAB V PENUTUP ...125 A. Kesimpulan ...125 B. Saran ...127 DAFTAR PUSTAKA ...129 LAMPIRAN ...131

(15)

xv

DAFTAR GAMBAR

Gambar 2.1 Ilustrasi Grafik Fungsi Densitas Peluang ...23

Gambar 2.2 Contoh Lintasan Sampel Gerak Brown dengan ...31

Gambar 2.3 Ilustrasi geometri integral Riemann ...33

Gambar 2.4 Ilustrasi Jumlahan Riemann-Stieltjes ...39

Gambar 2.5 Ilustrasi Jumlahan Riemann-Stieltjes ...40

Gambar 3.1 Grafik Penyelesaian Model Malthus saat ...59

Gambar 3.2 Grafik Penyelesaian Model Gompertz dengan dan ...62

Gambar 3.5 Grafik Penyelesaian Model Verhulst dengan ...73

Gambar 3.6 Grafik Penyelesaian Model Verhulst dengan Batas Bawah dengan , , dan ...87

Gambar 3.7 Grafik Penyelesaian Model Schaefer saat dan ...93

Gambar 3.8 Grafik Penyelesaian Model Schaefer saat , , dan ...94

Gambar 3.9 Grafik Penyelesaian Model Schaefer saat , , dan ...95

(16)

xvi

Gambar 3.10 Grafik Penyelesaian Model Penyebaran Teknologi saat ,

, dan ...100

Gambar 3.11 Grafik Penyelesaian Model Verhulst Laju tak Konstan dengan

( ) ...110

( ) ( ) ...111

( ) ...112

Gambar 4.1 Contoh Lintasan Sampel Penyelesaian Model Verhulst Stokastik saat

, , , dan . ...123

(17)

1

BAB I PENDAHULUAN

A. Latar Belakang

Banyak matematikawan yang sudah mengembangkan model matematika untuk pertumbuhan populasi. Thomas Robert Malthus (1798), seorang ahli ekonomi asal Inggris, menjadi salah satu tokoh yang berpengaruh dalam pe-ngembangan model pertumbuhan populasi. Model Malthus atau disebut juga model eksponensial, yaitu:

, ( )

( ) ( )

dengan t adalah variabel waktu, r adalah konstanta laju pertumbuhan intrinsik yang besarnya adalah , dan ( ) ada-lah banyaknya individu di dalam populasi pada waktu t. Dengan metode pe-misahan variabel masalah nilai awal tersebut mempunyai penyelesaian:

( )

Hal ini berarti bahwa pertumbuhan populasi bertumbuh secara eksponensial dan besarnya bergantung pada kondisi awal , konstanta laju pertumbuhan r dan waktu t. Hal tersebut tidak realistis untuk , sebab tidak mungkin suatu populasi bertumbuh secara eksponensial tanpa batas. Sebagai ilustrasi, jika diambil t menuju tak hingga, maka diperoleh ( ) juga menuju tak hingga.

(18)

Model Gompertz merupakan salah satu pengembangan model Malthus yang cukup terkenal. Biasanya model Gompertz digunakan untuk memodel-kan pertumbuhan tumor maupun dinamika populasi. Dalam skripsi ini amemodel-kan dibahas model Gompertz yaitu:

, ( )

_{( )} ( )

dengan adalah variabel waktu, ( ) adalah banyaknya individu di dalam populasi pada waktu t, adalah konstanta positif yang menyatakan laju pertumbuhan populasi, dan adalah konstanta positif yang menunjukkan seberapa cepat penyelesaian model Gompertz menuju ke kestabilan asimtotik. Kita juga dapat menyatakan sebagai laju perubahan besarnya populasi. Dengan menggunakan metode pemisahan variabel masalah nilai awal tersebut memiliki penyelesaian

( ) ( )

Jika diambil nilai limitnya, maka kita memperoleh:

( )

Hal tersebut menunjukkan bahwa dalam jangka waktu yang lama penyelesai-annya bergerak menuju ke suatu nilai yang bergantung pada dan .

Meskipun ada beberapa kekurangan pada model Malthus, misalnya tidak dipertimbangkannya aspek logistik yaitu keterbatasan kapasitas alam untuk mengadopsi atau menghidupi populasi, namun model tersebut digunakan sampai awal abad ke-XIX. Pada tahun 1838, seorang matematikawan asal

(19)

Belgia bernama Pierre-François Verhulst, memperbaiki model Malthus yang dianggap tidak realistis. Model Verhulst tersebut kemudian berkembang dan menjadi salah satu model sederhana terbaik untuk memodelkan pertumbuhan populasi. Model Verhulst juga disebut sebagai model logistik, yaitu:

, ( ) ( ) 4 ( ) 5 ( )

dengan t adalah variabel waktu, r adalah konstanta laju pertumbuhan, ( )

adalah banyaknya individu dalam populasi pada waktu t, dan K adalah kapa-sitas ambang atau kemampuan maksimum alam untuk menghidupi populasi. Dengan metode pemisahan variabel masalah nilai awal tersebut tersebut mempunyai penyelesaian:

( )

. /

Model ini lebih realistis, sebab jika diambil nilai t menuju tak hingga, maka diperoleh:

. /

Hal ini berarti populasi akan bertumbuh secara asimtotik ke K untuk t menuju tak hingga.

Konstanta laju pertumbuhan r menandakan bahwa laju pertumbuhan suatu populasi bersifat konstan terhadap waktu. Dengan kata lain, waktu tidak mempengaruhi konstanta laju pertumbuhan populasi. Hal tersebut bisa saja terjadi, namun secara umum tidak mungkin bahwa laju pertumbuhan populasi

(20)

konstan terhadap waktu. Pada skripsi ini model Verhulst akan dikembangkan lagi menjadi model Verhulst dengan laju pertumbuhan tidak konstan atau laju pertumbuhannya merupakan fungsi dari waktu, yaitu:

, ( ) ( ) ( ) 4 ( ) 5 ( )

dengan ( ) suatu fungsi terhadap t yang menyatakan bahwa laju pertumbu-han populasi besarnya bergantung pada waktu. Populasi yang berbeda mem-punyai laju pertumbuhan yang berbeda-beda pula terhadap waktu. Beberapa populasi memiliki periode reproduksi yang berbeda-beda, bergantung pada waktu. Misalnya pada beberapa mamalia memiliki waktu reproduksi yang berbeda. Mamalia seperti anjing, serigala, dan beruang hanya bereproduksi sekali dalam setahun, sedangkan mamalia seperti kuda dan domba memiliki siklus reproduksi yang pendek, sehingga dalam setahun bisa bereproduksi lebih dari satu kali.

Selain model Verhulst dengan laju pertumbuhan tidak konstan, model Verhulst juga dapat dikembangkan lagi menjadi model Verhulst dengan batas bawah dan model Schaefer (model pemanenan). Model Verhulst dengan batas bawah pada dasarnya menyatakan bahwa terdapat konstanta T yang merepre-sentasikan batas bawah banyaknya individu dalam suatu populasi yang menyebabkan populasi tersebut tidak punah. Dengan kata lain, jika banyak-nya individu dalam populasi kurang dari T, maka populasi tersebut menuju kepunahan. Model Verhulst dengan batas bawah yaitu:

(21)

, ( ) ( ) 4 ( ) 5 ( ( )* ( )

dengan t adalah variabel waktu, r adalah konstanta laju pertumbuhan, ( )

adalah banyaknya individu dalam populasi pada waktu t, K adalah kapasitas ambang atau kemampuan maksimum alam untuk menghidupi populasi, dan T adalah batas bawah banyaknya individu agar populasi tidak punah.

Model Schaefer atau model pemanenan berbentuk:

, ( ) ( ) 4 ( ) 5 ( ) ( )

dengan t adalah variabel waktu, r adalah konstanta laju pertumbuhan populasi normal, ( ) adalah banyaknya individu dalam populasi pada waktu t, K adalah kapasitas ambang atau kemampuan maksimum alam untuk menghidu-pi populasi, dan E adalah konstanta positif yang menyatakan laju pemanenan.

Selain untuk memodelkan dinamika populasi, model Verhulst juga dapat dimodifikasi untuk memodelkan penyebaran teknologi. Model penyebaran teknologi serupa dengan model pertumbuhan populasi Verhulst, yaitu:

, ( ) ( ) ( ( ) * ( )

dengan adalah variabel waktu, adalah banyaknya individu yang berpotensi menggunakan teknologi, adalah konstanta positif yang menyatakan laju penyebaran teknologi, menyatakan limit asimtotik, dengan adalah konstanta positif yang menyatakan seberapa besar penurunan limit asimtotik.

(22)

Kita dapat menginterpretasikan sebagai laju penurunan minat pengguna teknologi yang berkaitan.

Pada kenyataannya, sering kali pertumbuhan populasi “diganggu” oleh hal-hal yang tidak direncanakan (tidak terduga), misalnya: bencana alam, penyakit, predator alami, perburuan dan lain sebagainya. Hal tersebut menye-babkan model deterministik menjadi tidak relevan lagi untuk digunakan. Oleh karena itu kita perlu memperbaiki model deterministik menjadi model stokastik. Model stokastik memuat unsur acak atau ketidakpastian. Model Verhulst stokastik dirumuskan seperti model Verhulst deterministik dengan menambahkan faktor derau pada fungsi laju pertumbuhan, yakni ( ) ( ) . Model Verhulst deterministik sekarang menjadi:

( )

, ( ) - ( ) 4 ( )

5

( ) ( ) ( ) 4 ( )5 ( ) 4 ( )5

Derau di dalam kalkulus stokastik dipandang sebagai derau putih Gaussian, yaitu turunan terhadap waktu dari gerak Brown. Jadi model Verhulst stokastik diberikan oleh:

( ) ( ) ( ) 4 ( )5 ( ) ( ) 4 ( )5 ( )

dengan ( ) adalah fungsi laju pertumbuhan berkaitan dengan model deterministik, ( ) koefisien difusi yang menyatakan seberapa besar derau atau gangguan yang mempengaruhi laju pertumbuhan populasi dan ( )

(23)

adalah proses Wiener atau gerak Brown. Namun dalam skripsi ini akan dicari penyelesaian model Verhulst stokastik yang lebih sederhana, yaitu

( ) ( ) 4 ( )5 ( ) ( )

dengan berturut-turut adalah konstanta laju pertumbuhan populasi ber-kaitan dengan suku deterministik dan stokastik.

Dalam skripsi ini juga akan disajikan grafik penyelesaian model Ver-hulst deterministik dan stokastik dengan menggunakan Matlab atau Maple.

B. Rumusan Masalah

Perumusan masalah yang akan dibicarakan pada skripsi ini adalah:

1. Bagaimana model Verhulst deterministik untuk pertumbuhan populasi dan beberapa pengembangannya dirumuskan, diselesaikan, dan dianalisa? 2. Bagaimana model Verhulst stokastik untuk pertumbuhan populasi

dirumuskan dan diselesaikan?

C. Batasan Masalah

Skripsi ini dibatasi pada masalah-masalah sebagai berikut.

1. Model deterministik yang dibahas ialah model Verhulst serta beberapa pe-ngembangannya, seperti model Verhulst dengan batas bawah, model Verhulst dengan laju pertumbuhan tidak konstan, model Schaefer (model pemanenan), dan model penyebaran teknologi.

2. Model stokastik yang dibahas ialah model Verhulst yang memuat derau yang berasal dari gerak Brown.

3. Baik model deterministik dan stokastik dibatasi pada populasi homogen, yakni populasi yang terdiri dari satu jenis spesies saja.

(24)

4. Model yang dibicarakan ialah model kontinu, yaitu menggunakan persamaan diferensial biasa tingkat satu.

5. Populasi pada model yang dibicarakan hanya menempati satu daerah yang tetap.

D. Tujuan Penulisan

Tujuan dari penulisan tugas akhir ini adalah untuk menyelesaikan dan menganalisa model pertumbuhan populasi Verhulst, baik yang bersifat deter-ministik maupun stokastik.

E. Manfaat penulisan

Manfaat yang dapat diperoleh dari penulisan skripsi ini adalah kita dapat memahami dan menganalisa pertumbuhan populasi satu spesies dengan model matematika, khususnya dengan model Verhulst deterministik dan stokastik. Selain itu juga kita dapat memperkirakan besarnya populasi satu spesies di masa yang akan datang.

F. Metode Penulisan

Metode yang digunakan penulis dalam penulisan skripsi ini adalah metode studi pustaka, yaitu dengan membaca dan mempelajari buku-buku atau jurnal-jurnal yang berkaitan dengan model pertumbuhan populasi Verhulst, baik deterministik maupun stokastik.

(25)

G. Sistematika Penulisan BAB I PENDAHULUAN A. Latar Belakang B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penulisan G. Sistematika Penulisan

BAB II PERSAMAAN DIFERENSIAL A. Persamaan Diferensial Biasa

1. Persamaan Diferensial 2. Persamaan Diferensial Linier

3. Persamaan Diferensial Variabel Terpisah B. Persamaan Diferensial Stokastik

1. Teori Peluang 2. Integral Ito

3. Persamaan Diferensial Stokastik BAB III MODEL VERHULST DETERMINISTIK

A. Model Pertumbuhan Populasi Verhulst 1. Penyelesaian Model Verhulst 2. Analisa Kualitatif Model Verhulst

(26)

B. Beberapa Pengembangan Model Pertumbuhan Populasi Verhulst 1. Model Verhulst dengan Batas Bawah (Threshold) (Efek Allee) 2. Model Pemanenan Schaefer

3. Model Penyebaran Teknologi

4. Model Verhulst dengan Laju Pertumbuhan tidak Konstan BAB IV MODEL VERHULST STOKASTIK

A. Model Pertumbuhan Stokastik yang Memuat Derau yang Berasal dari Gerak Brown

B. Penyelesaian Model Verhulst Stokastik BAB V PENUTUP

A. Kesimpulan B. Saran

(27)

11

BAB II

PERSAMAAN DIFERENSIAL

A. Persamaan Diferensial Biasa 1. Persamaan Diferensial

Persamaan diferensial adalah persamaan yang memuat variabel-variabel tak bebas dan turunan-turunannya terhadap variabel-variabel bebas.

Secara umum, persamaan diferensial dikategorikan dalam dua ke-las yaitu biasa dan parsial. Persamaan diferensial biasa adalah persamaan diferensial yang hanya melibatkan satu variabel bebas. Misal ( ) adalah fungsi satu variabel, dengan adalah variabel bebas dan adalah variabel tak bebas, maka suatu persamaan diferensial biasa dapat dinyatakan dalam bentuk:

( ( )) ( )

Jika ( ) maka persamaan diferensial di atas dinamakan persamaan diferensial homogen.

Sementara itu, persamaan diferensial parsial adalah suatu persamaan diferensial yang melibatkan dua atau lebih variabel bebas.

Definisi 2.1 Tingkat Persamaan Diferensial

Tingkat atau order dari persamaan diferensial didefinisikan sebagai tingkat dari turunan tertinggi yang muncul dalam persamaan diferensial.

(28)

Contoh 2.1

1.

merupakan persamaan diferensial biasa tingkat satu.

2. merupakan persamaan diferensial biasa tingkat dua. 3.

merupakan persamaan diferensial parsial tingkat satu.

4.

merupakan persamaan diferensial parsial

tingkat dua.

2. Persamaan Diferensial Linier

Persamaan diferensial dikatakan linier jika:

a) tidak ada perkalian antara variabel-variabel tak bebas dengan dirinya sendiri atau dengan turunan-turunannya,

b) tidak ada fungsi transendental (trigonometri, logaritma, eksponensial, siklometri, hiperbolik) yang terlibat dari fungsi dalam variabel-variabel tak bebas.

Persamaan diferensial yang tidak linier disebut persamaan diferensial tak linier. Sebagai contoh:

- merupakan persamaan diferensial yang linier dalam .

- merupakan persamaan diferensial yang tak linier dalam karena terdapat perkalian antara variabel tak bebas dengan turunannya, yaitu .

-

merupakan persamaan diferensial yang tidak linier

(29)

-

merupakan persamaan diferensial yang tak

linier karena terdapat perkalian antara variabel-variabel tak bebasnya, yaitu .

Secara umum, persamaan diferensial linier tingkat satu dapat ditulis sebagai berikut:

( ) (2.1)

dengan ( ) ( ) adalah fungsi yang kontinu, merupakan interval untuk dan merupakan interval untuk .

Definisi 2.2 Penyelesaian Persamaan Diferensial

Fungsi terdiferensial dikatakan penyelesaian persamaan diferensial (2.1) pada sebuah interval ( ) dengan syarat ( ) untuk , apabila adalah fungsi yang terdiferensial kontinu pada , dan ( ) ( ( )), untuk .

Definisi 2.3 Masalah Nilai Awal (Intial Value Problem)

Masalah nilai awal adalah persamaan diferensial yang dilengkapi dengan data pada satu titik awal domain.

Definisi 2.4 Penyelesaian Masalah Nilai Awal

Misal ( ) ( ) ( ) dan diasumsikan kontinu pada ( ) ( ). Kita katakan fungsi adalah penyelesaian masalah nilai awal:

{ ( ) ( )

(30)

pada interval ( ) dengan syarat , apabila adalah penyele-saian dari persamaan (2.1) pada , dan ( ) .

Titik dinamakan titik awal untuk masalah nilai awal (2.2) dan dikatakan nilai awal untuk masalah nilai awal (2.2).

3. Persamaan Diferensial Variabel Terpisah

Untuk mengidentifikasi persamaan diferensial variabel terpisah, pertama kita tulis persamaan diferensial tingkat satu (2.1) dalam bentuk:

( ) ( ) ( ) ( ) ( ) ( ) (2.3) dengan dan merupakan fungsi yang bergantung pada dan . Jika kita ambil adalah suatu fungsi yang hanya bergantung dan adalah sebuah fungsi yang hanya bergantung , maka persamaan (2.3) menjadi:

( ) ( )

(2.4) Persamaan (2.4) disebut persamaan diferensial variabel terpisah.

Metode yang dipakai untuk menyelesaikan persamaan diferensial variabel terpisah dinamakan metode pemisahan variabel. Penyelesaian persamaan diferensial (2.4) dapat dicari dengan terlebih dahulu menulis-kan dalam bentuk diferensial

(31)

Selanjutnya, integralkan masing-masing sukunya

∫ ( ) ∫ ( )

untuk suatu .

Contoh 2.2

Temukan solusi persamaan diferensial :

( ) ( )

Jawab:

Persamaan diferensial tersebut merupakan persamaan diferensial variabel terpisah. Misalkan ( ) ( ) ( ) dan ( )

.

Langkah 1: bagi kedua ruas dengan ( ) ( ) , diperoleh:

Langkah 2: Integralkan masing-masing suku, diperoleh:

∫ ∫ ∫

∫( ) ∫( ₎ ₍ ₎

Definisi 2.5 Titik Ekuilibrium dari Persamaan Diferensial Diberikan persamaan diferensial sebagai berikut

(32)

Titik dimana disebut titik ekuilibrium jika ( ) untuk seti-ap . Dengan kata lain titik ekuilibrium terjadi saat

Contoh 2.3

Diberikan persamaan diferensial sebagai berikut

( )

Syarat ekuilibrium yaitu

Sehingga, titik ekuilibrium persamaan diferensial di atas yaitu dan .

B. Persamaan Diferensial Stokastik

Alasan munculnya kalkulus stokastik yaitu karena seringkali kita menjumpai situasi yang tidak dapat diprediksi sebelumnya atau disebut unsur acak, sehingga metode-metode pada kalkulus deterministik tidak mampu menyelesaikan masalah tersebut. Persamaan diferensial stokastik adalah persamaan diferensial yang memuat unsur acak yang biasa disebut derau (noise), yaitu:

( ) ( )

dengan merupakan sebuah proses stokastik, dan adalah fungsi-fungsi dua variabel, dan menyatakan gangguan atau unsur acak dari masalah yang bersangkutan. Pada skripsi ini akan dibahas yang

(33)

berasal dari gerak Brown, yaitu unsur acak atau gangguan yang memiliki variansi yang tak terbatas.

1. Teori Peluang

Untuk menyelesaikan persamaan diferensial stokastik kita perlu mem-pelajari kalkulus Itô. Pertama, kita harus mengingat konsep dasar teori peluang.

Definisi 2.6 Percobaan Acak (Random Experiment)

Sebuah percobaan dikatakan acak apabila hasil dari percobaan tidak dapat diprediksi sebelumnya.

Definisi 2.7 Ruang Sampel (Sample Space) dan Titik Sampel (Sample Point) Himpunan , yaitu semua kemungkinan hasil dari percobaan acak dinamakan

ruang sampel. Suatu anggota dinamakan titik sampel.

Contoh 2.4

Pada sebuah percobaan pelemparan koin, kemungkinan hasil yang muncul adalah “angka” dan “gambar" . Jadi * +. dan disebut titik sampel.

Definisi 2.8 Kejadian (Event)

Sebuah kejadian adalah suatu koleksi dari hasil percobaan yang merupakan himpunan bagian dari ruang sampel.

Definisi 2.9

Jika dan adalah kejadian dari ruang sampel , maka i. Gabungan dari dua kejadian dapat ditulis sebagai berikut

(34)

ii. Irisan dari dua kejadian dapat ditulis sebagai berikut

* +

iii. Komplemen suatu kejadian dapat ditulis sebagai berikut

* +

iv. Selisih suatu kejadian dapat ditulis sebagai berikut

Definisi 2.10 Kejadian Saling Asing (Disjoint)

Sepasang kejadian dan dikatakan saling asing jika

Definisi 2.11 Peluang (Probability)

Misal adalah kejadian pada ruang sampel berhingga, notasi peluang

( ) menyatakan peluang kejadian akan terjadi dan diberikan oleh:

( )

( ) ( )

Definisi 2.12 Aljabar- ( -Algebra)

Misal himpunan tak kosong. Aljabar- pada adalah koleksi himpunan bagian dari yang memenuhi:

i.

ii. jika , maka

iii. jika , maka ⋃ .

Contoh 2.5

Koleksi berikut merupakan aljabar- dari himpunan bagian : 1. * +

(35)

2. * + untuk suatu dan

3. ( ) * +

merupakan aljabar- terkecil pada , dan (himpunan kuasa dari ) merupakan aljabar- terbesar yang memuat semua himpunan bagian yang mungkin dari .

Sedangkan * + untuk suatu dan bukan merupakan aljabar- , karena .

Definisi 2.13 Ukuran Peluang (Probability Measure)

M aljabar- pada himpunan tak kosong . Fungsi , ) disebut ukuran peluang jika memenuhi:

i. Untuk sebarang kejadian , ( ) . ii. ( ) .

iii. Jika , maka

(⋃

+ ∑ ( )

Kesamaan berlaku jika adalah barisan himpunan yang saling asing.

Definisi 2.14

Misal adalah aljabar- pada himpunan tak kosong dan ukuran peluang pada .

i. ( ) disebut ruang terukur (measurable space)

(36)

Teorema 2.1

Jika dan adalah kejadian dan adalah ruang sampel, maka i. ( ) .

ii. ( ) ( ).

iii. Jika , maka ( ) ( ).

iv. ( ) ( ) ( ) ( ). Lebih lanjut, jika dan saling asing maka

( ) ( ) ( ) Bukti: i. Karena ( ) ( ) ( ) ( ) maka ( ) . ii. Karena ( ) ( ) ( ) ( ) maka ( ) ( ). iii. Karena ( ) dan ( ) , maka ( ) , ( ( ) , (

)-dan karena , ( )- , maka diperoleh ( ) ( ). iv. Kita punya

( ) ( ) ( )

(37)

( ) ( ) ( ) ( )

Maka

( ) ( ) , ( ) ( , ( ) ( ( ) ( )

Jadi ( ) ( ) ( ) ( ).

Jika dan saling asing, maka . Kita memperoleh

( ) ( ) ( ) ( ) ( ) ( ) ( )

( ) ( ) ■

Contoh 2.6

Dari 52 kartu remi diambil sebuah kartu secara acak. Berapa peluang teram-bilnya sebuah kartu berbentuk hati atau As.

Jawab:

Misal adalah ruang sampel dengan ( ) , adalah kejadian terambil-nya kartu hati dengan ( ) , dan adalah kejadian terambilnya kartu As dengan ( ) . Kejadian menyatakan kejadian kartu As berben-tuk hati. Karena hanya ada satu kartu As yang berbenberben-tuk hati, maka ( ) . Kita akan mencari peluang terambilnya sebuah kartu berbentuk hati atau As yaitu ( ). Kita tahu bahwa satu dari kartu As berbentuk hati, maka . Dari teorema 2.1 (iv), kita dapatkan

( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )

(38)

Definisi 2.15 Kejadian Saling Bebas (Independent) Dua kejadian dan dikatakan saling bebas jika

( ) ( ) ( )

Definisi 2.16 Variabel Acak (Random Variable)

Misal adalah ruang sampel, fungsi disebut variabel acak. Sebuah variabel acak dikatakan diskrit apabila atau terhitung (artinya terdapat fungsi bijektif ). Sedangkan jika tidak terhitung maka variabel acak dikatakan kontinu.

Contoh 2.7

Pada sebuah percobaan pelemparan koin, kita tulis “1” untuk “angka” dan “0” untuk “gambar". Jadi kita peroleh variabel acak ( ) * + untuk

* +. Dengan kata lain * + adalah sebuah variabel acak diskrit.

Definisi 2.17 Variabel Acak Saling Bebas (Independent) Dua variabel acak dan dikatakan saling bebas jika

( ) ( ) ( )

untuk setiap himpunan bagian yang mungkin dan dari . Hal ini berarti kejadian * + dan * + saling bebas. Dalam hal ini * + adalah notasi singkat untuk * ( ) +.

(39)

Definisi 2.18 Fungsi Densitas Peluang (Probability Density Function)

Fungsi disebut fungsi densitas peluang dari variabel acak pada ruang peluang ( ) jika

i. ( ) , ( );

ii. ( ) ∫ ( ) untuk sebarang sedemikian sehingga

; iii. ∫ ( ) .

Berikut adalah ilustrasi grafik dari fungsi densitas peluang ( ). (i) ditunjukkan dengan kurva yang selalu berada di atas sumbu horizontal, (ii) dtunjukkan oleh daerah yang diarsir dan (iii) merupakan luas total area di bawah kurva.

Gambar 2.1 Ilustrasi Grafik Fungsi Densitas Peluang.

Definisi 2.19 Nilai Harapan (Expectation/ Mean/ Expectation Value)

Nilai harapan dari sebuah variabel acak kontinu diberikan oleh:

( ) ∫ ( )

(40)

Nilai harapan dapat diintepretasikan sebagai rata-rata berbobot (weighted average) dari nilai pada ruang sampelnya.

Teorema 2.2 Nilai Harapan Perkalian Dua Variabel Acak yang Saling Bebas Misal adalah dua variabel acak yang saling bebas, maka

( ) ( ) ( )

Bukti:

Menurut definisi nilai harapan.

( ) ∫ ∫ ( )

Karena dan saling bebas maka ( ) dapat ditulis

( ) ∫ ( ) ∫ ( ) ( ) ( ) ■

Definisi 2.20 Variansi (Variance)

Misalkan adalah variabel acak kontinu, variansi dinotasikan dengan ( )

atau menyatakan ukuran dari variasi atau penyebaran distribusi peluang dari variabel acak dan didefinisikan oleh

( ) 0( ( )) 1 ,( ) - ∫ ( ) ( )

Akar dari variansi disebut standar deviasi dari , yaitu

(41)

Definisi 2.21 Fungsi Distribusi (Distribution Function)

Didefinisikan fungsi distribusi ( ) sebagai peluang variabel acak berni-lai kurang dari atau sama dengan , yaitu

( ) ( ) ∫ ( )

Persamaan di atas mengakibatkan ( ) saat dan

( ) ∫ ( ) ( ) ( )

Definisi 2.22 Momen

ke-Momen ke- suatu variabel acak yaitu ( ).

Definisi 2.23 Fungsi Pembangkit Momen (Moment-Generating Function)

Fungsi pembangkit momen ( ) untuk suatu variabel acak didefinisikan sebagai berikut

( ) ( ₎

Fungsi pembangkit momen dikatakan ada jika terdapat konstanta positif sedemikian sehingga ( ) hingga untuk .

Teorema 2.3

Jika ( ) ada, maka untuk sebarang bilangan bulat positif

( )

|

( )_{( ) (} ₎

Bukti Teorema 2.2 dapat dilihat pada buku “Mathematical Statistics with Applications” karangan Dennis D. Wackerly, dkk, tahun 2008 halaman 139 (Teorema 3.12).

(42)

Definisi 2.24 Distribusi Normal (Normal Distribution)

Suatu variabel acak dikatakan berdistribusi normal dengan rata-rata dan variansi (notasi: ( )) jika memiliki fungsi densitas peluang berbentuk ( ) √ ( ) Teorema 2.4

Misal adalah variabel acak berdistribusi normal, maka

( ) ∫ ( ) dan ( ) ∫ ( ) ( ) Bukti:

Pertama kita cari fungsi pembangkit momen dari variabel acak yang berdistribusi normal, yaitu

( ) ( ₎ ∫ √ ( ) √ ∫ ( ) √ ∫ ( ) √ ∫ [( ) ] √ ∫ [ ] √ ∫ [ ( ) ]

(43)

√ ∫ 0 . ( ) / 1 √ ∫ 0 ( ) ( ) 1 √ ∫ [. ( )/ ] √ ∫ . ( )/ ( ) ∫ √ . ( )/ Fungsi √ . ( )/

_{merupakan fungsi densitas peluang distribusi} nor-mal dengan rata-rata dan variansi , dan menurut definisi fungsi densitas peluang, maka

∫ √ . ( )/

Sehingga kita peroleh fungsi pembangkit momen distribusi normal yaitu

( )

Dengan menggunakan teorema 2.3, kita memperoleh

( ) ( ) | ( ) | ( )

(44)

dan ( ) ( ) | ( ) | ( )

Selanjutnya akan ditunjukkan ( ) .

( ) 0( ( )) 1 , ( ) ( ) ( ) ( ( )) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ■ Catatan:

Jika suatu variabel acak berdistribusi normal memiliki rata-rata dan variansi maka variabel acak dikatakan berdistribusi normal standar dan dinotasikan oleh ( ).

Definisi 2.25 Proses Stokastik (Stochastic Process)

Proses stokastik * +, dengan adalah koleksi dari variabel acak yang terdefinisi pada ruang peluang ( ) yang terindeks dengan parameter .

(45)

Definisi 2.26 Lintasan Sampel (Sample Path)

Untuk suatu , koleksi * ( ) + dinamakan lintasan sampel dari pada .

Definisi 2.27 Aljabar- yang dibangkitkan oleh proses stokastik

Untuk sebuah proses stokastik * +, aljabar- ( ) adalah aljabar- terkecil yang memuat semua himpunan yang berbentuk

* ( ( ) ) +

untuk setiap himpunan yang mungkin dari fungsi pada . Maka ( )

disebut aljabar- yang dibangkitkan oleh .

Definisi 2.28

Proses stokastik * + dan * + pada ruang peluang

( ) dikatakan ekuivalen jika:

* +

untuk setiap . Kita katakan adalah versi dari , dan sebaliknya.

Definisi 2.29 Filtrasi (Filtration)

Filtrasi pada ruang terukur ( ) adalah koleksi aljabar- ( ) pada yang memenuhi:

untuk setiap .

Definisi 2.30

Proses stokastik ( ) dikatakan teradaptasi terhadap filtrasi

(adapted to the filtration) ( ) jika:

(46)

untuk setiap . Fungsi disebut -terukur.

Proses stokastik selalu teradaptasi terhadap filtrasi natural yang dibangkit-kan oleh :

( )

Definisi 2.31 Gerak Brown (Brownian Motion)

Proses stokastik ( ) dinamakan gerak Brown atau proses Wiener jika memenuhi kondisi-kondisi berikut:

i. .

ii. berdistribusi normal dengan rata-rata dan variansi untuk

, artinya untuk setiap , dengan berlaku

( )

√ ( )∫

( )

iii. adalah variabel acak-variabel acak yang saling bebas untuk . Dengan kata lain, mempu-nyai kenaikan yang saling bebas (independent increments) atau

( ) ( ) ( )

untuk setiap , dengan .

iv. Mempunyai lintasan sampel yang kontinu, yakni untuk setiap

fungsi ( ) , ) adalah fungsi kontinu. Berikut adalah contoh lintasan sampel gerak Brown.

(47)

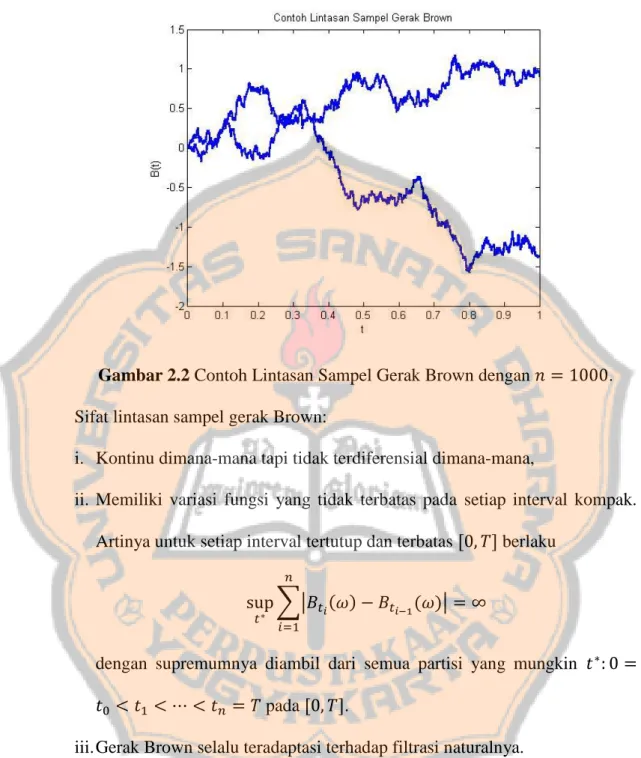
Gambar 2.2 Contoh Lintasan Sampel Gerak Brown dengan . Sifatlintasan sampel gerak Brown:

i. Kontinu dimana-mana tapi tidak terdiferensial dimana-mana,

ii. Memiliki variasi fungsi yang tidak terbatas pada setiap interval kompak. Artinya untuk setiap interval tertutup dan terbatas , - berlaku

∑| ( ) ( )|

dengan supremumnya diambil dari semua partisi yang mungkin pada , -.

iii. Gerak Brown selalu teradaptasi terhadap filtrasi naturalnya.

Bukti dapat dilihat pada buku “Elementary Stochastic Calculus with Finance in View” karangan Thomas Mikosch tahun 1998 halaman 36.

Derau putih (white noise) didefinisikan sebagai turunan distribusi dari gerak Brown terhadap waktu, yakni

(48)

Pengertian derau putih sebagai turunan distribusi ini akan kita gunakan secara informal. Dari sini diperoleh bahwa derau putih adalah sebuah proses Gauss (berdistri-busi normal) dengan rata-rata dan variansi . Derau putih sering digunakan sebagai model matematika untuk gangguan acak yang bersifat sa-ling bebas untuk tiap waktu yang berbeda dan memiliki fluktuasi yang besar.

2. Integral Itô

Kita telah mengetahui bahwa lintasan sampel gerak Brown tidak terdiferensial dimana-mana dan memiliki variasi yang tak terbatas pada suatu interval kompak. Pada bagian ini akan ditunjukkan bahwa integral yang telah kita kenal yaitu integral Riemann ataupun integral Riemann-Stietjes tidak dapat digunakan untuk mengintegralkan fungsi dengan inte-gratornya merupakan lintasan gerak Brown. Selanjutnya akan didefinisi-kan integral stokastik Itô sebagai alat untuk mengintegraldidefinisi-kan fungsi yang memuat lintasan sampel gerak Brown.

a. Integral Riemann

Integral Riemann tentunya sudah tidak asing lagi bagi kita, karena sudah pernah kita pelajari pada kalkulus dasar. Pada bagian ini akan dijelaskan integral Riemann secara sederhana.

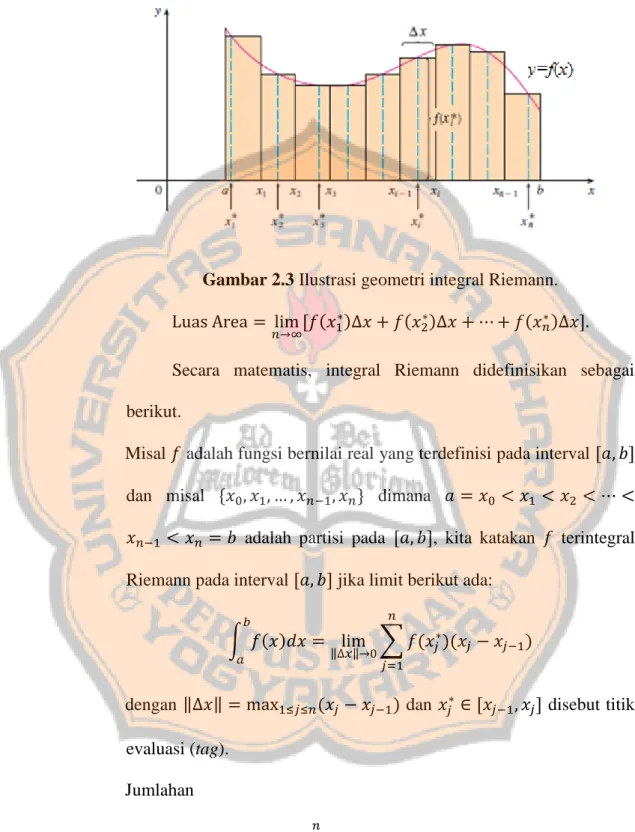
Secara geometri, integral Riemann sering diintepretasikan sebagai jumlahan luas area yang dibentuk untuk mencari luas daerah yang dibatasi oleh suatu kurva. Berikut ini adalah ilustrasi secara geometri integral Riemann:

(49)

Gambar 2.3 Ilustrasi geometri integral Riemann.

, ( ) ( ) ( ) -

Secara matematis, integral Riemann didefinisikan sebagai berikut.

Misal adalah fungsi bernilai real yang terdefinisi pada interval ,

-dan misal * + dimana adalah partisi pada , -, kita katakan terintegral

Riemann pada interval , - jika limit berikut ada:

∫ ( )

‖ ‖ ∑ ( )( )

dengan ‖ ‖ ( ) dan , - disebut titik evaluasi (tag).

Jumlahan

∑ ( )( )

(50)

Catatan:

1. Untuk menentukan jumlah partisi pada interval , - menjadi subinterval yang sama panjang, gunakan rumus

2. Jika terbatas pada , - atau berarti , - ( ) dan kontinu di sana kecuali pada sejumlah titik yang berhingga, maka terintegral Riemann pada , -. Lebih lanjut, jika kontinu pada seluruh interval , -, maka terintegral Riemann pada , -.

Contoh 2.8

Hitung ∫ ( ) ! Jawab:

Bagi , - dalam buah subinterval yang sama panjang, yaitu ma-sing-masing intervalnya memiliki panjang

( )

Kita peroleh

(51)

Jadi, ( ) . / , sehingga untuk se-tiap , - ∑ ( )( ) ∑ ( ) ∑ ( * ∑ ( *

Berdasarkan kelinieran notasi sigma, kita peroleh

∑ ( )( ) ∑ ∑ ∑ ∑

Berdasarkan rumus jumlah khusus (lihat lampiran 2), kita peroleh

∑ ( )( )

(52)

( *

Karena merupakan suatu partisi yang tetap, maka ‖ ‖ setara dengan . Sehingga dapat disimpulkan bahwa

∫ ( ) ‖ ‖ ∑ ( )( ) [ ( *]

Ada dua teorema penting penting dalam teori integral Riemann.

Teorema 2.5 Teorema Dasar Kalkulus I

Jika kontinu pada interval tertutup , - dan misal adalah sebuah titik pada ( ), maka

∫ ( ) ( )

Teorema 2.6 Teorema Dasar Kalkulus II

Jika kontinu (dan terintegral Riemann) pada interval , - dan misal sebarang antiturunan pada pada , -, maka

∫ ( ) ( ) ( )

Bukti teorema dasar kalkulus pertama dan kedua dapat dilihat pada buku “Calculus (9th Edition)” karangan Dale Varberg, dkk tahun 2007 halaman 235 (Teorema A) dan 243 (Teorema A) berturut-urut.

(53)

Contoh 2.9

Gunakan teorema dasar kalkulus kedua untuk menghitung integral yang diberikan pada contoh sebelumnya!

Jawab:

Pada ∫ ( ) kita punya , , ( ) dan

( ) . Kita hitung ( ) dan ( ) sebagai berikut:

( ) ( ) ( ) ( )

( ) ( )

Dengan teorema dasar kalkulus kedua, kita peroleh

∫ ( )

( ) ( ) ( )

b. Integral Riemann-Stieltjes

Integral Remann-Stieltjes merupakan integral Riemann yang diperumum. Integral ini melibatkan dua fungsi ( ) dan ( ) yang terdefinisi pada interval , -, dinotasikan ∫ ( ) ( ). Jika kita ambil ( ) , maka kita peroleh integral Riemann ∫ ( ) . Definisi integral Riemann-Stieltjes dari ( ) terhadap ( ) serupa dengan integral Riemann.

Misal adalah fungsi kontinu bernilai real yang terdefinisi pada inter-val , - dan adalah fungsi naik monoton yang terdefinisi pada in-terval , -. Misal * + dimana adalah partisi pada , -, kita katakan

(54)

dikata-kan terintegral Rieman-Stieltjes pada , - terhadap fungsi jika limit berikut ada

∫ ( ) ( )

‖ ‖ ∑ ( )( ( ) ( ))

dengan ‖ ‖ ( ) dan , - disebut titik evaluasi (tag).

Contoh 2.10

Bagaimana jika kontinu dan naik monoton dengan kontinu, apa-kah ∫ ( ) ( ) ada?

Jawab:

Dengan menggunakan integral parsial, kita misalkan

( ) ( ) dan ( ) ( ) Kita peroleh: ∫ ( ) ( ) ( ) ( ) | ∫ ( ) ( )

Karena kontinu dan kontinu dan naik monoton, maka

∫ ( ) ( )

terintegral Riemann-Stieltjes.

Contoh 2.11

Jika dan keduanya kontinu pada , -, apakah ∫ ( ) ( )

(55)

Jawab:

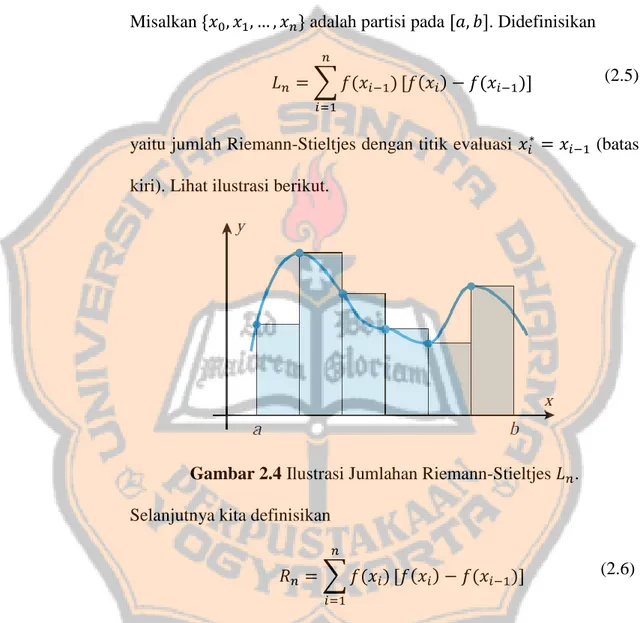
Belum tentu. Untuk menunjukkan hal ini, kita selidiki kasus , yakni apakah ∫ ( ) ( ) ada?

Misalkan * + adalah partisi pada , -. Didefinisikan

∑ ( )

, ( ) ( )- (2.5)

yaitu jumlah Riemann-Stieltjes dengan titik evaluasi (batas

kiri). Lihat ilustrasi berikut.

Gambar 2.4 Ilustrasi Jumlahan Riemann-Stieltjes . Selanjutnya kita definisikan

∑ ( )

, ( ) ( )- (2.6)

yaitu jumlah Riemann-Stieltjes dengan titik evaluasi (batas kanan). Lihat ilustrasi berikut.

(56)

Gambar 2.5 Ilustrasi Jumlahan Riemann-Stieltjes . Misal , cek apakah ‖ ‖ ‖ ‖ ?

Dari (2.5) dan (2.6) kita peroleh

∑ ( ) , ( ) ( )- ∑ ( ) , ( ) ( ∑* ( ), ( ) ( )- ( ), ( ) ( )-+ ∑, ( ) ( , ( ) ( )- ∑, ( ) ( (2.7) dan ∑ ( ) , ( ) ( )- ∑ ( ) , ( ) ( ∑* ( ), ( ) ( )- ( ), ( ) ( )-+ ∑, ( ) ( , ( ) ( )-

(57)

∑ ( ) ( )

( ) ( ) (2.8)

Dari persamaan (2.7) dan (2.8), kita memperoleh

( ) ( ) ∑, ( ) ( [ ( ) ( ) ∑, ( ) ( ] (2.9) dan ( ) ( ) ∑, ( ) ( [ ( ) ( ) ∑, ( ) ( ] (2.10)

Perhatikan persamaan (2.7). Nilai

‖ ‖ ∑, ( ) (

disebut variasi kuadratik fungsi pada , -. Jadi jelas bahwa

‖ ‖ ‖ ‖

jika variasi kuadratik fungsi pada , - tidak sama dengan nol. Dengan kata lain, integral Riemann-Stieltjes berlaku jika variasi kuadratik fungsi pada , - sama dengan nol.

(58)

Bagaimana jika yaitu gerak Brown ( ), apakah inte-gral Riemann-Stieltjes memungkinkan untuk mencari ∫ ( ) ? Berikut adalah sifat-sifat dasar dari gerak Brown.

1. Kontinu dimana-mana tetapi tidak terdiferensial dimana-mana. 2. Untuk sebarang , berdistribusi normal dengan rata-rata

dan variansi . Untuk sebarang , ( ) * +. Bukti:

Asumsikan , karena berdistribusi normal dan memiliki kenaikan yang saling bebas, maka

( ) ( )

( ( ) ) Sifat distributif

( ( )) Kelinieran nilai harapan

( ) Definisi gerak Brown

Definisi gerak Brown

yang berarti sama dengan * +.

3. Untuk yang tetap, proses stokastik ̃ juga

merupakan gerak Brown.

4. Untuk sebarang bilangan real , proses stokastik ̃ ( ) √ juga merupakan gerak Brown.

5. Variasi kuadratik pada setiap interval , - adalah . Untuk melihat hal ini, perhatikan teorema berikut:

(59)

Teorema 2.7

Misal * + adalah partisi dari interval kompak

, -. Maka:

∑( )

(2.11)

pada ( ) dengan ‖ ‖ ( ) . Dengan

( ) * ( ) +

Bukti:

Ingat bahwa ∑( ) dan misalkan

∑ 0( ) ( )1 ∑ (2.12) dengan ( ) ( ). Maka: ∑ (2.13)

untuk , dan ( ) karena mempunyai kenaikan yang saling bebas dan ( ) . Di sisi lain, ( ) ( ) (lihat lampiran 3) dan untuk pada persamaan (2.13), diperoleh

( ) 2( ) ( )( ) ( ) 3

( ) ( ) ( ) ( )

(60)

Sehingga, dari persamaan (2.13) kita memperoleh ∑ ( ) ‖ ‖ ∑( ) ( )‖ ‖

saat ‖ ‖ . Hal ini menunjukkan bahwa konvergen ke 0 di ( ). Dan dari persamaan (2.12), mengakibatkan persamaan (2.11) terpenuhi. ■

Pada gerak Brown, kita mempunyai

∑ ( )

dan

∑ ( )

dengan titik evaluasi untuk yaitu pada dan pada . Kita mempunyai ∑ ( ) ∑ ( ) ∑( ) dan ∑ ( ) ∑ ( )

(61)

∑( ) Kita memperoleh [ ∑( ) ] dan [ ∑( ) ]

Menggunakan teorema 2.7, kita peroleh

‖ ‖ [ ( ) ]

dan

‖ ‖ [ ( ) ]

Sehingga kita dapatkan variasi kuadratik dari gerak Brown yaitu

‖ ‖ ( ) [ ( )] [ ( ) ]

Jadi integral Riemann-Stieltjes tidak bisa dipakai untuk mendefinsi-kan integral fungsi terhadap gerak Brown ∫ ( ) . Oleh karena itu muncullah teori integral stokastik yang pertama kali diperkenalkan oleh matematikawan Jepang Kiyoshi Itô pada tahun 1946. Tujuannya ialah jika diberikan sebarang proses stokastik ( ) dengan

(62)

sifat-sifat tertentu dan diberikan gerak Brown ( ), kita ingin mendefinisikan integral stokastik

∫ ( ) ( )

dengan , - . Integral tersebut selanjutnya dikenal de-ngan nama integral Itô.

c. Integral Itô

Persamaan diferensial yang memuat derau:

( ) ( )

dengan ( ) ( ) merupakan suatu fungsi dan diinte-pretasikan sebagai turunan dari gerak Brown yaitu . Persamaan tersebut dapat kita tulis

( ) ( )

atau jika ditulis dalam bentuk diferensial kita peroleh persamaan dife-rensial stokastik:

( ) ( )

Persamaan di atas dapat ditulis dalam bentuk persamaan integral sebagai berikut:

∫ ∫ ( ) ∫ ( )

∫ ( ) ∫ ( )

(63)

Disini

∫ ( )

merupakan bentuk integral Riemann, sedangkan

∫ ( )

merupakan bentuk integral Itô yang didefinisikan sebagai integral se-buah fungsi dari proses stokastik terhadap gerak Brown. Selanjutnya, akan dikonstruksikan integral Itô.

Definisi 2.32

Misal ( ) merupakan aljabar- yang dibangkitkan oleh variabel acak . Untuk

, didefinisikan kelas dari fungsi ( ) , ) yang memenuhi

i. teradaptasi- ( ). ii. 0∫ ( ) 1 .

Misal menotasikan semua himpunan dari fungsi tangga di , yaitu fungsi yang berbentuk

( ) ( )

dengan , untuk partisi . Didefinisikan integral Itô untuk fungsi tangga sebagai berikut

, - ∫ ( ) ∑ ( )

(64)

Lemma 2.1 Sifat-Sifat Integral Itô

Untuk sebarang dan , integral Itô memenuhi i. , - bersifat terukur- ( ), ii. ( , -) iii. ,( , -) - ∫ , ( ) - , iv. , - , - , -. Lemma 2.2 Ruang padat di . Artinya yaitu

untuk setiap terdapat barisan * + di dalam sehingga ( ).

Bukti Lemma 2.1 dan 2.2 dapat dilihat di Lecture Notes “Stochastic Diffe-rential Equations” karangan Thomas Önskog tahun 2009 pada halaman 21 (Lemma 3.4) dan 22 (Lemma 3.5) berturut-urut.

Definisi 2.33

Itô integral dari didefinisikan oleh

∫ ( )

dengan limitnya berada di ( ) dan * + adalah barisan dari fung-si di sedemikian sehingga

∫ , ( ) ( ) -

(65)

Contoh 2.12

Hitung integral ∫ . Jawab:

Misal adalah partisi dari interval , -. Pilih ( ) ∑ ( ) dengan . Maka

6∫ ( ) 7 *∑ ∫ ( ) + ∑ ∫ [. / ] ∑ ∫ ( ) ∑ [ | ∑ [( * ( *] ∑ ( * ∑ ( ) ∑ ( ) _jika _.

(66)

Sehingga kita tahu bahwa ∫ ∫ ( ) ∑ . / ∑ dengan . Sekarang perhatikan ( ) ( ) ( )

Dari persamaan di atas, kita memperoleh

∑ ∑ 0( ) 1

∑( ) ∑( ) ∑

Menurut teorema 2.7 ∑ ( ) , sehingga ∑

∑

Sehingga kita peroleh

∫

(67)

Teorema 2.8 Rumus Itô

Misal adalah proses Itô yang diberikan oleh:

dan ( ) (, ) ) yaitu fungsi yang terdiferensial kontinu dua kali pada , ) . Maka,

( )

juga merupakan proses Itô, dan berlaku

( )

( ) ( ) ( )

dengan ( ) ( ) ( ) dihitung berdasarkan aturan:

Bukti teorema Rumus Itô dapat dilihat pada buku “Stochastic Differential Equations. An Introduction with Applications” karangan Bernt Øksendal tahun 2003 halaman 44 (Teorema 4.1.2).

Bentuk Integral dari Rumus Itô

Dengan mengintegralkan rumus Itô terhadap variabel waktu dari sampai kita memperoleh ( ) ( ) ∫ ( ) ∫ 6 ( ) ( )7 Contoh 2.13 Hitung: a. ∫

(68)

b. ∫

Jawab:

a. Pilih ( ) , maka ( ) dan dari rumus Itô kita memperoleh

( ) ( ) ∫ ( ) ∫ 6 ( ) ( )7 ∫ ∫ ( * ∫ ∫ Sehingga diperoleh ∫ ∫ ∫ ∫

b. Pilih ( ) , maka ( ) dan dari rumus Itô diperoleh

( ) ( ) ∫ ( ) ∫ 6 ( ) ( )7 ∫ ∫ ( * ∫ ∫

Sehingga kita memperoleh

(69)

Teorema 2.9 Teorema Fundamental Kalkulus Itô

Misal ( ) adalah antiderivatif atau integral tak tentu dalam variabel dari fungsi kontinu ( ) dengan dan kontinu, maka berlaku:

∫ ( ) ( ) | ∫ [

( )

( )]

Khususnya, jika tidak bergantung waktu, yakni ( ) ( ), maka

∫ ( ) ( ) | ∫ ( )

Teorema di atas merupakan bentuk lain dari Rumus Itô jika mempunyai antiturunan .

Contoh 2.14

Hitung ∫ ! Jawab:

Jika ( ) maka ( ) dan

( ) ∫ ( ) ∫

Dengan menggunakan metode integral parsial, kita misalkan

dan maka ( ) ∫

(70)

untuk .

Jadi menurut Teorema Fundamental Kalkulus Itô kita memperoleh

∫ ( ) ( ) | ∫ ( )

∫ ( ) | ∫ ( )

( ) ( ) ∫ ( )

∫ ∫

Berdasarkan contoh 2.12 (b), kita memperoleh

∫ 4 ∫ 5 ∫ ∫ Sehingga diperoleh ∫ ∫ ( * ∫

3. Persamaan Diferensial Stokastik

Persamaan diferensial stokastik ialah persamaan diferensial yang berbentuk:

(71)

( ) ( ) (2.14)

dengan ( ) adalah variabel acak yang merupakan penyelesaian dari persamaan tersebut, adalah gerak Brown, ( ) adalah koefisien bagian deterministik dan ( ) adalah koefisien bagian stokastik. Fungsi-fungsi ( ) dan ( ) selalu diasumsikan memenuhi sifat-sifat terbatas dan kontinu agar teorema eksistensi dan ketunggalan penyelesai-an berlaku. (Lihat buku “Stochastic Differential Equations An Introduc-tion with ApplicaIntroduc-tions” karangan Bernt Øksendal halaman 66 (Teorema 5.2.1)).

Proposisi 2.1 Persamaan Diferensial Stokastik Linier Persamaan diferensial stokastik linier:

( ( ) ( )) ( ( ) ( )) (2.15)

dengan nilai awal mempunyai penyelesaian umum:

4 ∫ ( ( ) ( ) ( )) ∫ ( ) 5

dengan

4∫ ( ( ) ( ( )) * ∫ ( ) 5

Lihat Lecture Notes “Stochastic Differential Equations” karangan Thomas Önskog tahun 2009 halaman 36 (Proposisi 4.2).

(72)

Kita juga bisa meyelesaikan persamaan diferensial stokastik tak linier:

( ) ( ) (2.16)

dengan mengambil transformasi ( ), dimana adalah fungsi yang memiliki invers (paling tidak pada interval tertutup , - ) dan linier. Sekarang, kita evaluasi nilai dengan menggunakan rumus Itô:

( ) ( ) ( )( ) ( ) ( ), ( ) ( ) ( ), ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ), ( ) ( ) ( ) ( )

-karena dan , maka

( ) ( ) ( ) ( ) ( ) ( )( ( )) 6 ( ) ( ) ( ) ( )( ( )) 7 ( ) ( ) (2.17) Misal , maka:

(73)

( ) ( ) ( ) ( )( ( )) ( ) ( ) ( ) (2.18) dan ( ) ( ) ( ) ( ) ( ) (2.19)

(74)

58

BAB III

MODEL VERHULST DETERMINISTIK

Model populasi untuk satu spesies dikemukakan pertama kali oleh Malthus. Modelnya diberikan oleh masalah nilai awal:

, ( )

( ) ( )

(3.1)

dengan t adalah variabel waktu, r adalah konstanta laju pertumbuhan yang besarnya adalah , dan ( ) banyaknya individu di dalam populasi pada waktu t. Dengan metode pemisahan variabel model pertumbuhan populasi (3.1) dapat diselesaikan sebagai berikut:

( )

( ) (3.2)

Integralkan kedua ruas persamaan (3.2):

∫ ( ) ( ) ∫ ( ( )) dengan . Jadi, ( ) Misal , maka: ( ) (3.3) Subtitusikan nilai awal ( ) ke persamaan (3.3) untuk mendapatkan nilai yang memenuhi:

(75)

( )

(3.4)

Substitusikan persamaan (3.4) ke (3.3), diperoleh:

( )

yang menandakan bahwa pertumbuhan populasi bertumbuh secara eksponen-sial dan besarnya bergantung pada kondisi awal , konstanta laju pertumbu-han r dan waktu t. Oleh karena itu model Malthus disebut juga model eksponensial. Model eksponensial tidak realistis, sebab untuk , tidak mungkin suatu populasi bertumbuh secara eksponensial tanpa batas. Sebagai ilustrasi, jika diambil t menuju tak hingga, maka diperoleh ( ) juga menuju tak hingga.

Grafik model Malthus ditunjukan oleh Gambar 3.1, sebagai berikut:

(76)

Terdapat pengembangan model Malthus yang cukup terkenal, yaitu model Gompertz yang biasanya digunakan untuk memodelkan pertumbuhan tanaman, penyebaran penyakit tumor, dan lain sebagainya. Berikut akan dibahas penyelesaian dan analisa kestabilan titik ekuilibrium model Gom-pertz. Model Gompertz berbentuk masalah nilai awal sebagai berikut:

, ( ) _{( )} ( ) (3.5)

dengan t adalah variabel waktu, adalah konstanta laju pertumbuhan, ( )

adalah banyaknya individu di dalam populasi pada waktu t, dan adalah konstanta positif yang menunjukkan seberapa cepat penyelesaian model Gompertz menuju ke kestabilan asimtotik. Kita juga dapat menyatakan sebagai laju perubahan besarnya populasi.

a. Penyelesaian

Dengan metode pemisahan variabel model Gompertz (3.5) dapat ditulis:

( ) ( )

_(3.6)

Integralkan kedua ruas persamaan (3.6):

∫ ( ) ( ) ∫ ( ( ))

untuk suatu . Jadi,

(77)

( )

Misal , maka:

( ) (3.7)

Subtitusikan nilai awal ( ) ke persamaan (3.7) untuk mendapatkan nilai yang memenuhi: