ANALISIS PROFIL DAN APLIKASINYA SKRIPSI. Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains Program Studi Matematika

i

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Oleh :

Anindita Kusumastuti NIM : 033114009

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

ii

Presented As Partial Fulfillment of The Requirenets To Obtain The Sarjana Sains Degree

In Mathematics

By :

Anindita Kusumastuti Student Number : 033114009

STUDY PROGRAM OF MATHEMATICS SCIENCE DEPARTEMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY YOGYAKARTA

iii

ANALISIS PROFIL DAN APLIKASINYA

Oleh:

Anindita Kusumastuti NIM: 033114009

Telah disetujui oleh :

Pembimbing

iv

Dipersiapkan dan ditulis oleh: Anindita Kusumastuti

NIM: 033114009

Telah dipertahankan di hadapan Panitia Penguji Skripsi Pada tanggal 29 Oktober 2007

dan dinyatakan memenuhi syarat

Susunan Panitia Penguji:

Nama Lengkap Tanda tangan

Ketua : Ir. Greg. Heliarko, S.J., S.S., B.S.T., M.Sc., M.A Sekretaris : Lusia Krismiyati Budiasih, S.Si., M.Si.

Anggota : Ir. Ig. Aris Dwiatmoko, M.Sc.

Anggota : Ch. Enny Murwaningtyas, S.Si, M.Si . Anggota : Lusia Krismiyati Budiasih, S.Si., M.Si.

Yogyakarta, November 2007

Fakultas Sains dan Teknologi

Universitas Sanata Dharma Dekan.

v

dalam kutipan dan daftar pustaka, sebagaimana layaknya karya ilmiah.

Yogyakarta, November 2007 Penulis

vi

Tidak ada usaha yang gagal, kegagalan adalah usaha untuk mencapai kemenangan.

( Krisna )

Semoga semua pikiran yang baik datang dari segala arah. Karena kasih sayangku,

Aku sendiri yang menghancurkan kegelapan yang timbul dari kebodohan dengan Sinar Cahaya Ilmu Pengetahuan

( Dr. dr. I Dewa Gede Sukardja )

Skripsi ini kupersembahkan kepada :

Bapak Ibuku dan adikku tersayang,

Untuk semua keluarga besarku, sahabat, dosen, teman, murid-muridku tercinta,

vii

bersama-sama. Analisis profil bertujuan untuk mengetahui ciri dari suatu populasi. Dalam skripsi ini, analisis profil yang akan dibahas dikhususkan untuk dua populasi yang saling independen. Salah satu bagian yang paling penting dalam analisis profil adalah uji hipotesis, yang terdiri atas tiga tahap yaitu uji hipotesis keparalelan, kesamaan level, dan pengaruh utama p – variabel. Ketiga tahap tersebut menjawab tiga tujuan analisis profil.

Dalam tahap uji hipotesis, data yang diperlukan adalah vektor rata-rata dan matriks dispersi untuk masing-masing populasi. Vektor rata-rata tersebut merupakan ciri bagi masing-masing populasi. Selanjutnya kedua vektor rata-rata akan diuji mengggunakan uji hipotesis. Hasil pengujian hipotesis berupa suatu kesimpulan yang dapat memberi ciri bagi masing-masing populasi, dilihat dari tiga hal yaitu keparalelan, level, dan pengaruh utama p – variabel.

Pada skripsi ini akan disajikan aplikasi analisis profil untuk data mahasiswa Universitas Sanata Dharma Yogyakarta tahun angkatan 1998-2004.

viii

simultaneously. The purpose of profile analysis is to identify a population characteristic. In this thesis, the domain of the profile analysis are two independent population. One of importance in profile analysis is hypothesis testing, which are consist of three steps. Those are parallelism, level equality, and main effects of p – variables. Those three steps answer three objectives of profile analysis.

The data needed in the hypothesis testing are mean vectors and dispersion matrices from each population. Each of mean vectors is a characteristic popula-tion. Both mean vectors will be test by hypothesis testing. The result of the hy-pothesis testing is a conclusion which gives characteristic to every population, viewed from three things those are parallelism, level, and main effects of p – vari-ables.

In this thesis, the application of profile analysis will be assigned for Sanata Dharma University data in academic year 1998-2004.

ix

ini. Salam serta Shalawat tak lupa selalu tercurah kepada Nabi Muhammad SAW atas keteladanan-Nya hingga akhir zaman.

Penulis menyadari bahwa dalam menyelesaikan skripsi ini banyak ditemukan hambatan dan kesulitan. Namun, berkat dukungan yang luar biasa dari banyak pihak, akhirnya skripsi ini dapat terselesaikan. Oleh karena itu dengan segala kerendahan hati, penulis ingin mengucapkan terima kasih kepada :

1. Bapak Ir. Ig. Aris Dwiatmoko, M.Sc, selaku dosen pembimbing skripsi yang telah meluangkan waktu, pikiran, dan dengan sangat sabar membimbing penulis dalam menyusun skripsi ini.

2. Ibu Lusia Krismiyati Budiasih, S.Si, M.Si, selaku Ketua Program Studi Matematika FST USD Yogyakarta dan dosen penguji, yang dengan sabar telah membimbing serta memberikan kesempatan bagi penulis untuk mengikuti Program PK 7.

3. Bapak Y.G. Hartono, M.Sc, yang telah memberikan banyak saran dan dorongan semangat kepada penulis dengan pengalamannya yang luar biasa. 4. Ibu Enny Murwaningtyas, S.Si, M.Si, selaku dosen pembimbing akademik

dan dosen penguji, yang dengan sabar mendampingi penulis selama kuliah di USD Yogyakarta.

5. Bapak dan Ibu Dosen Matematika, Fisika, dan Komputer FST yang telah memberikan ilmu yang sangat berguna bagi penulis.

6. Ibu Ch. Suwarni, Bapak Z. Tukidjo, dan Ibu Linda yang dengan sabar telah memberikan pelayanan administrasi dan urusan-urusan perkuliahan kepada penulis.

7. Mas Susilo dan Mas Widodo selaku laboran lab komputer dasar yang selalu memberikan bantuan kepada penulis.

8. Perpustakaan USD dan staf yang telah memberikan fasilitas dan kemudahan kepada penulis.

x

oom-tante) atas doa dan dukungannya selama ini.

11. Teman-teman Matematika angkatan 2003 (Eko bin Sipit, Septi “Kicrit...”, Dewi “Cempluk”, Ridwan bin Jegul, Ankgie binti Sumi, Valent yang lembut, Merry yang apa aja dech, Mekar binti Oneng, Kamsi, dan Itha) yang selalu kompak dan ceria, serta selalu memberiku semangat. Terimakasih teman, takkan kulupakan kegilaan-kegilaan kita. Ku tunggu sepak terjang kalian!

12. Teman-teman Ikom, Fisika, dan TI 2003 : Iyus, Pakdhe Galih, Danang, Embek, Ima, Gurit, Adeth dan masih banyak lagi yang telah berjuang bersama dalam PS “Sopo Selo”.

13. Teman-teman di Sanggar Tari Bagong Kussudiarjo, Sriwijaya Musik, dan Assyifa yang selalu memberi doa, dukungan, dan suasana kerja yang menyenangkan : Ibu (Almh). Ida Manutrenggana, Pakdhe Topo, Mbak Wuri, Ibu Feli, Ibu Ari Kun, Nanil, Mas Wawan, dan teristimewa untuk Mas Agung tersayang yang selalu memberi keceriaan dan semangat dikala suka dan duka.

14. Teman-teman KKN kelompok 25 : Nanang, Iyas, Yabes, Hana “Ma’e Telo”, Ria binti Dodot, Tirza binti Kuntilanak, dan Djati bin robot gedhek, atas kenangan yang tak terlupakan.

15. Murid-muridku di SMAN 2 Yogyakarta, SMAN 11 Yogyakarta, di Sriwijaya Musik, dan dimanapun kalian berada, yang selalu memberiku semangat. Terimakasih atas pengertian kalian, walaupun kadang harus ditinggal-tinggal. Kalianlah sumber semangat dan gembiraku. Karena kalianlah “Mbak Anin alias Bu Anin” bisa seperti sekarang. I love You All... 16. Seluruh Kakak-kakak dan adik-adik angkatanku. Terimakasih atas

xi

dan semuanya aja. Terimakasih atas kerja samanya selama ini.

18. Teman-teman yang luar biasa : Handirofa Agustaf dan Nanda Rigih Djatmiko, terimakasih atas kebersamaan yang telah dilalui bersamaku. 19. Teman-teman seluruh peserta Pelayaran Kebangsaan VII (Ruth, Harisma,

Mei, Wati, dan masih banyak lagi) yang telah memberikan kenangan yang luar biasa kepada penulis. Tak lupa terimakasih yang spesial untuk dr. Dhanny Primantara, J.S, dokternya anak-anak PK 7, yang telah membuka mata hatiku dan membuatku kembali bangkit menatap masa depan.

Penulis menyadari bahwa dalam penulisan skripsi ini masih terdapat beberapa kekurangan, oleh karena itu kritik dan saran yang membangun akan diterima dengan segala keterbukaan hati. Akhirnya penulis berharap semoga skripsi ini dapat berguna bagi semua pihak yang membutuhkan dan dapat menjadi bahan kajian selanjutnya.

Yogyakarta, November 2007

xii

HALAMAN JUDUL... i

HALAMAN JUDUL (INGGRIS)... ii

HALAMAN PERSETUJUAN PEMBIMBING... iii

HALAMAN PENGESAHAN... iv

PERNYATAAN KEASLIAN KARYA... v

HALAMAN PERSEMBAHAN... vi

ABSTRAK... vii

ABSTRACT... viii

KATA PENGANTAR... ix

DAFTAR ISI... xii

DAFTAR TABEL... xv

DAFTAR GAMBAR... xvi

DAFTAR LAMPIRAN... xvii

BAB I PENDAHULUAN A. Latar Belakang... 1 B. Rumusan Masalah... 5 C. Pembatasan Masalah... 6 D. Tujuan Penulisan... 7 E. Metode Penulisan... 7 F. Manfaat Penulisan... 7

xiii

B. Beberapa Distribusi yang Penting... 21

1. Distribusi χ2_{... 22}

2. Distribusi t ... 25

3. Distribusi F... 29

C. Distribusi Normal Multivariat... 33

D. Distribusi Wishart... 52

E. Distribusi Hotelling _T2_{... 55}

BAB III ANALISIS PROFIL A. Konsep Dasar Analisis Profil... 65

B. Uji Hipotesis... 73

1. Kondisi Keparalelan... 74

2. Kondisi Kesamaan Level... 76

3. Kondisi Pengaruh Utama p – Variabel... 80

C. Statistik Uji... 82

1. Kondisi Keparalelan... 82

2. Kondisi Kesamaan Level... 84

3. Kondisi Pengaruh Utama p – Variabel... 86

D. Tahap-Tahap Uji Hipotesis Dalam Analisis Profil... 87

1. Kondisi Keparalelan... 87

xiv A. Sumber Data... 113 B. Kasus I... 113 1. Analisis Data... 114 2. Kesimpulan... 117 C. Kasus II... 118 1. Analisis Data... 120 2. Kesimpulan... 124 BAB V KESIMPULAN... 127 DAFTAR PUSTAKA... 129 LAMPIRAN... 131

xv Tabel 1... 71 Tabel 2 ... 85 Tabel 3... 89 Tabel 4 ... 97 Tabel 5... 104 Tabel 6 ... 108 Tabel 7... 126

xvi Gambar 3.1 ... 68 Gambar 3.2 ... 75 Gambar 3.3 ... 78 Gambar 3.4 ... 78 Gambar 3.5 ... 79 Gambar 3.6 ... 81 Gambar 3.7 ... 90 Gambar 3.8 ... 96 Gambar 3.9 ... 102 Gambar 3.10 ... 107 Gambar 3.11 ... 111 Gambar 4.1 ... 117 Gambar 4.2 ... 123 Gambar 4.3 ... 124

xvii

Lampiran 1 ... 132 Lampiran 2 ... 135

BAB I PENDAHULUAN

A. Latar Belakang

Dalam kehidupan sehari-hari, pengamatan sering dilakukan dalam berbagai hal. Misalnya mengamati bentuk suatu barang, fungsi barang itu, bentuk wajah seseorang, tingkah laku seseorang, dan masih banyak lagi. Biasanya pengamatan tersebut didasarkan pada pemikiran subyektifitas belaka, sehingga pengamatan yang dilakukan hanya sepintas dan tidak rinci. Pengamatan suatu objek yang tidak rinci terkadang menimbulkan kebingungan bahkan ketidaktahuan saat harus menjelaskan lebih jauh tentang ciri objek itu. Hal ini dapat terjadi akibat pengamatan hanya dilakukan pada kulit terluar dari suatu objek, tanpa melihat objek itu lebih dalam. Apalagi jika yang diamati adalah dua objek yang hampir sama, baik segi bentuk, sifat ataupun karakteristik lainnya. Kesulitan yang biasanya timbul adalah saat harus menemukan pembeda yang paling signifikan di antara keduanya. Oleh karena itu pengamatan harus dilakukan secara rinci dengan cara melihat objek dari berbagai sisi. Mengapa hal itu harus dilakukan ? Karena di kehidupan nyata, objek sesungguhnya multidimensional. Jika ciri-ciri dari objek yang akan diamati sudah dikenal dengan baik dan mendalam, maka objek tersebut akan mudah dikenal, sehingga kesulitan-kesulitan dalam pengamatan suatu objek dapat diminimalkan.

Di zaman yang serba maju seperti sekarang ini, nampaknya sudah tidak tepat lagi jika pengamatan hanya dilakukan atas perkiraan belaka tanpa dasar yang kuat.

Oleh karena itu, munculah suatu metode yang dapat digunakan untuk mengatasi masalah dalam pengamatan ciri suatu objek, yaitu analisis profil. Dalam skripsi ini analisis profil yang akan dibahas adalah analisis profil untuk dua populasi yang saling independen

Analisis profil adalah salah satu analisis multivariat yang merupakan metode statistika untuk menganalisis data dengan lebih dari dua variabel tak bebas secara bersama-sama. Analisis multivariat adalah perluasan dari analisis univariat. Dalam analisis univariat, analisis hanya dilakukan untuk satu variabel tak bebas saja. Oleh karena itu dalam analisis profil akan dilakukan analisis terhadap lebih dari dua variabel tak bebas dengan tujuan untuk mengetahui ciri-ciri populasi yang diteliti.

Analisis profil dimulai dengan asumsi bahwa profil dideskripsikan multidimensional. Karena multidimensional, maka ia tersusun dari beberapa komponen, misalkan p - komponen. Komponen-komponen itulah yang memberi ciri bagi suatu profil, sehingga akan membedakan profil objek itu dibanding profil objek lain. Dalam bahasa statistika, komponen-komponen penyusun itu disebut variabel. Variabel-variabel penyusun profil dapat dinyatakan dalam bentuk vektor yang dinamai vektor ciri. Vektor ciri tersebut tidak lain adalah vektor rata-rata, yang diperoleh dengan cara mencari rata-rata setiap variabel pengamatan untuk seluruh responden. Selanjutnya vektor cirilah yang akan mewakili profil suatu populasi.

Misalkan profil dideskripsikan sebagai p – dimensi multinormal variabel random X. Karena melibatkan p variabel random, maka ada X₁, X₂, K , X_P

variabel pengamatan, sehingga vektor X adalah matriks dengan baris atau kolom tunggal yang dapat ditulis menjadi X' =

[

X1 X2 K X_p

]

. Jika ada dua populasi yang diteliti, maka x = 1'

[

x11 x12 K x1p

]

dan

' 2

x =

[

x21 x22 K x2p

]

adalah rata-rata sampel masing-masing variabel untuk setiap populasi.

Sebagai contoh, suatu lembaga psikologi akan melakukan tes terhadap dua kelompok sampel anak yang diambil dari dua populasi. Populasi pertama adalah anak-anak dengan kelainan sejak lahir yang dalam bahasa kedokteran disebut Transient Neonatal Tyrosinemia (TNT) sedangkan populasi kedua adalah anak-anak normal. Masing-masing kelompok sampel berjumlah 27 orang anak-anak dengan usia 8 sampai 9 tahun. Kelompok sampel pertama diambil dari populasi pertama, sedangkan kelompok sampel kedua diambil dari populasi kedua. Dalam tes tersebut ada10 variabel psikologis yang akan diteliti, yaitu :

1

X = kemampuan menerima informasi melalui indera pendengaran

2

X = kemampuan menerima informasi melalui indera penglihatan

3

X = kemampuan memori pendengaran

4

X = kemampuan memori penglihatan

5

X = kemampuan mengumpulkan memori pendengaran

6

X = kemampuan mengumpulkan memori penglihatan

7

X = kemampuan melengkapi memori penglihatan

8

X = kemampuan melengkapi memori dalam hal tata bahasa

9

10

X = kemampuan mengekspresikan memori yang ada dengan bahasa tubuh Dalam contoh di atas, profil populasi yang akan diteliti, dideskripsikan menjadi 10 variabel psikologis. Kesepuluh variabel di atas akan disusun menjadi suatu vektor ciri yang akan mewakili profil kedua populasi yang diteliti.

Setelah vektor ciri atau vektor rata-rata dari masing-masing populasi diketahui, maka keduanya akan dibandingkan menggunakan uji hipotesis. Uji hipotesis dalam analisis profil tentunya mengikuti asumsi-asumsi dalam pengujian vektor rata-rata untuk kasus multivariat. Asumsi-asumsi tersebut adalah populasi-populasi yang diteliti berdistribusi normal multivariat dan kesamaan matriks varian-kovarian (matriks dispersi) untuk semua variabel tak bebas.

Contoh kasus lain misalnya, sebuah lembaga yang membawahi seluruh perusahaan makanan di Indonesia ingin mengetahui tingkat kepuasaan pelanggan produk mie Sedap dan Indomie. Lembaga tersebut mengambil 5 variabel penelitian yaitu :

1

X = persepsi tentang rasa

2

X = persepsi tentang banyaknya pilihan rasa

3

X = persepsi tentang harga

4

X = persepsi tentang iklan yang lebih menarik

5

X = persepsi tentang kemudahan dalam mendapatkannya di toko-toko Dalam contoh tersebut, profil 2 produk mie dideskripsikam menjadi 5 variabel. Seperti pada contoh sebelumnya, 5 variabel di atas akan diteliti menggunakan uji hipotesis. Setelah dilakukan pengujian hipotesis, maka dapat disimpulkan alasan

konsumen kedua produk mie tersebut mengapa lebih memilih salah satu dari kedua produk mie yang diteliti.

Dalam analisis profil ada 3 hal penting yang harus terjawab. Ketiga hal tersebut adalah :

1. Apakah profil kedua populasi sama, dalam hal ini apakah grafik profilnya paralel ?

2. Bila kedua profil populasi paralel, apakah keduanya juga terletak pada level yang sama ?

3. Kembali asumsikan bahwa kedua profil populasi paralel, maka apakah rata-rata kedua populasi tersebut berbeda secara simultan ? Dalam hal ini, adakah pengaruh utama akibat adanya p – variabel ?

Ketiga pertanyaan tersebut akan disusun menjadi hipotesis-hipotesis yang berbeda sesuai dengan kondisi masing-masing pertanyaan. Dalam skripsi ini ketiga pertanyaan tersebut akan dijawab untuk masing-masing kondisi, yaitu kondisi keparalelan, kondisi kesamaan level, serta kondisi pengaruh utama p – variabel.

B. Rumusan Masalah

Permasalahan yang akan dibahas dalam skripsi ini dapat dirumuskan sebagai berikut :

1. Bagaimana landasan teori analisis profil ?

2. Bagaimana mengetahui ciri-ciri dua populasi yang saling independen menggunakan analisis profil ?

C. Pembatasan Masalah

Dalam skripsi ini, penulis membahas tentang analisis profil dan aplikasinya dalam analisis data. Penulisan skripsi ini dibatasi pada beberapa hal karena sudah diperoleh dalam perkuliahan atau di luar jangkauan skripsi ini. Hal-hal yang tidak dibahas adalah sebagai berikut :

1. Asumsi normalitas yang menjadi landasan dalam analisis profil tidak diuji, karena fokus dari skripsi ini adalah pada metode.

2. Beberapa konsep dan teorema dalam aljabar matriks tidak dibuktikan, contohnya tentang matriks idempoten dan akar karakteristik, rank dari suatu matriks, dan beberapa sifat determinan .

3. Hal-hal yang berkaitan dengan penurunan distribusi Wishart. Tetapi sifat-sifat distribusi Wishart digunakan untuk membuktikan beberapa teorema.

4. Beberapa teorema tidak dibuktikan karena diluar jangkauan skripsi ini, misalnya Teorema Ketunggalan. Namun Teorema Ketunggalaan langsung diaplikasikan untuk membuktikan beberapa teorema.

5. Konsep tentang Integral Aitken. Namun bentuk integral aitken digunakan untuk membuktikan beberapa teorema.

6. Analisis profil yang dibahas dalam skripsi ini dibatasi hanya untuk dua sampel yang saling independen.

7. Seluruh data yang dijadikan contoh dalam skripsi ini diasumsikan berdistribusi Normal Multivariat tanpa dilakukan pengujian.

D. Tujuan Penulisan

Tujuan penulisan skripsi ini adalah mengenalkan salah satu teknik analisis data multivariat, yaitu analisis profil untuk dua populasi sehingga dapat mengetahui landasan teori analisis profil serta dapat menerapkannya untuk menganalisis data.

E. Metode Penulisan

Penulisan skripsi ini menggunakan metode studi pustaka, yaitu dengan menggunakan buku-buku, jurnal-jurnal, dan makalah-makalah yang telah dipublikasikan, sehingga tidak ditemukan hal baru.

F. Manfaat Penulisan

Manfaat yang diharapkan dari penulisan skripsi ini adalah : 1. Mengetahui landasan teori analisis profil.

2. Dapat mengggunakan distribusi normal multivariat dalam analisis profil.

G. Sistematika Penulisan

BAB I : PENDAHULUAN

Bab ini berisi gambaran umum tentang isi skripsi ini yang meliputi latar belakang masalah, perumusan masalah, pembatasan masalah, tujuan penulisan, manfaat penulisan, metode penulisan, dan sistematika penulisan.

BAB II : ALJABAR MATRIKS DAN DISTRIBUSI MULTIVARIAT Bab ini berisi beberapa teori yang melandasi pembahasan bab selanjutnya, yaitu beberapa konsep dalam aljabar matriks dan sifat-sifatnya, beberapa distribusi penting lainnya yang merupakan analogi dari kasus univariat, distribusi normal multivariat, distribusi Wishart, dan distribusi Hotelling T2. BAB III : ANALISIS PROFIL

Bab ini membahas tentang konsep dasar analisis profil, uji hipotesis untuk tiga kondisi dalam analisis profil, yaitu kondisi keparalelan, kondisi kesamaan level, dan kondisi pengaruh utama p - variabel. Kemudian akan dibahas juga tentang statistik uji yang digunakan, tahap-tahap analisis profil, serta contoh aplikasi analisis profil dengan data sekunder.

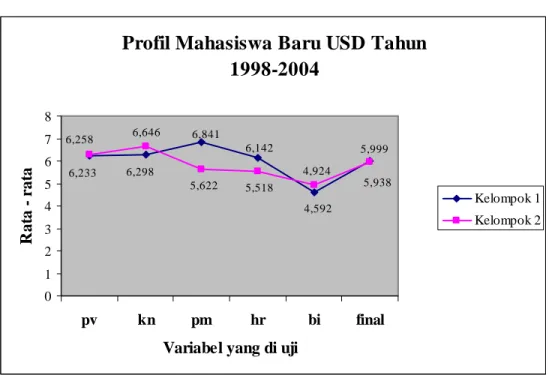
BAB IV : APLIKASI ANALISIS PROFIL DALAM ANALISIS DATA Bab ini berisi tentang kasus pengamatan ciri dua profil yang akan diselesaikan mengunakan analisis profil dengan SPSS 12.0 dan Matlab 6.5.1.

BAB V : KESIMPULAN

Bab ini berisi kesimpulan dari keseluruhan materi yang telah dipaparkan.

BAB II

ALJABAR MATRIKS DAN DISTRIBUSI MULTIVARIAT

Pada bab ini akan dibahas mengenai dasar-dasar teori yang akan dipergunakan pada bab III. Dasar-dasar teori itu meliputi beberapa konsep dan teorema yang berhubungan dengan aljabar matriks, distribusi multivariat dan sifat-sifatnya, distribusi Wishart, serta distribusi Hotelling T . 2

A. Beberapa Konsep dalam Aljabar Matriks Definisi 2.1.1

Jika A adalah suatu matriks n × n, maka skalar λ disebut eigennilai dari A jika dan hanya jika Ax=λx, untuk suatu vektor taknol x∈ℜn. Vektor x itu disebut eigenvektor yang bersesuain dengan λ.

Definisi 2.1.2

Suatu matriks bujur sangkar A disebut Simetrik jika A=At.

Definisi 2.1.3

Jika A adalah matriks simetrik n × n dan x'Ax ≥ _{0 untuk setiap vektor} taknol x ∈ℜn, maka A disebut matriks semidefinit positif, dan ditulis A ≥ O. Jika A adalah matriks simetrik n × n dan x'Ax > 0 untuk setiap vektor taknol x

n

ℜ

∈ , maka A disebut matriks definit positif, dan ditulis A > O.

Teorema 2.1.1

Matriks A adalah definit positif jika dan hanya jika semua eigennilai dari A adalah positif.

Bukti :

( )

⇒ Andaikan bahwa A definit positif dan λ adalah sebarang eigennilai dari A. Jika x adalah eigenvektor yang bersesuain dengan λ, maka x ≠ 0, sehingga 0<x'Ax = x'λx = λ x 2 dimana x adalah panjang baku dari x. Karena

2

x >0, maka haruslah λ>0.

( )

⇐ Andaikan semua eigennilai dari A bernilai positif. Harus ditunjukkan bahwa x'Ax > 0 untuk setiap x≠0. Andaikan

x x

y= , sehingga y =1. Menurut

teorema dalam aljabar matriks, jika A adalah matriks simetrik n×n dengan nilaieigen λ₁≥λ₂≥K≥λ_n dan x adalah vektor di ℜn _{sedemikian hingga x =1,} maka λ₁≥x'Ax≥λ_n. Karena y =1, maka y'Ay≥λ_n>0 , di mana λ_n adalah nilaieigen terkecil dari A. Jadi,

0 1 2 > =                 = x Ax x x x A x x Ay y ' ' '

Definisi 2.1.4

Jika A adalah matriks bujur sangkar dan A≠0, maka A disebut sebagai matriks non-singular dan mempunyai invers, dinotasikan dengan A−1 dan

I A A

AA−1= −1 = . Jika A=0, maka matriks A disebut sebagai matriks singular.

Teorema 2.1.2

Misalkan A suatu matriks n×n, maka determinan matriks A dapat dihitung dengan mengalikan anggota-anggota pada sembarang baris (kolom) dengan kofaktornya dan menjumlahkan hasil kali yang didapatkan, untuk setiap 1≤ i ≤ n dan 1≤ j ≤ n, nj nj j j j jC a C a C a + + + = _{1 1 2 2} K ) det(A

( perluasan kofaktor di sepanjang kolom ke – j ) dan in in i i i i C a C a C a + + + = _{1 1 2 2} K ) det(A

( perluasan kofaktor di sepanjang baris ke – i ) ٱ

Sifat-sifat Determinan

1. Jika A adalah suatu matriks n×n, maka det(At)=det(A).

2. Jika A dan B adalah matriks-matriks bujur sangkar yang berukuran sama dan A dapat dibalik, maka

) det( ) det( ) det(AB = A B

Contoh 2.1.1 Misalkan A =           − − − 2 4 5 3 4 2 0 1 3

. Akan dihitung det(A dengan perluasan )

kofaktor disepanjang baris pertama. Maka,

) det(A = 2 4 5 3 4 2 0 1 3 − − − = 2 4 3 4 3 − − - (1) 2 5 3 2 − − + 0 4 5 4 2 − − = 3 (-4) – (1)(-11) + 0 = -1. Diketahui pula At =           − − − 2 3 0 4 4 1 5 2 3

Akan dihitung pula det(At) dengan perluasan disepanjang kolom pertama. Maka,

) det(At = 2 3 0 4 4 1 5 2 3 − − − = 2 4 3 4 3 − − - (1) 2 5 3 2 − − + 0 4 5 4 2 − − = 3 (-4) – (1)(-11) + 0 = -1. Jadi det(At)=det(A)= -1

Definisi 2.1.5

Misalkan P adalah matriks bujur sangkar berorde n. P disebut matriks orthogonal jika dan hanya jika invers P adalah tranpos dari P sendiri, sehingga dapat ditulis P−1=Pt.

Teorema 2.1.3

Sebuah matriks orthogonal adalah non-singular.

Bukti :

Misalkan P adalah matriks bujur sangkar n×n. Menurut definisi 2.1.5, P dikatakan orthogonal jika dan hanya jika invers matriks P sama dengan tranpos P sendiri, sehingga ditulis P−1=Pt. Sedangkan menurut definisi 2.1.4, matriks P dikatakan non-singular jika P dapat dibalik atau mempunyai invers. Dari dua definisi di atas dapat disimpulkan bahwa jika P orthogonal maka P mempunyai invers atau dapat dibalik, sehingga P non-singular. Jadi terbukti bahwa sebuah

matriks orthogonal adalah non-singular. ٱ

Teorema 2.1.4

Determinan dari matriks orthogonal adalah sama dengan 1.

Bukti :

Misalkan P adalah matriks orthogonal dengan ukuran n×n, sedangkan _Pt adalah transpos dari P dengan ukuran n×n. Menurut definisi 2.1.5,

t P P−1=

Kalikan masing-masing ruas dengan P sehingga, PP−1 = PPt

t P P

Andaikan bahwa det(P)≠1, maka dengan memperhatikan definisi 2.1.5, sifat determinan (2) dan persamaan (2.1.1), maka harus dicari det(_Pt) _{yang memenuhi}

) det( ) det( )

det(P Pt = I . Menurut sifat determinan (1) diketahui bahwa )

det( )

det(Pt = P , maka tidak ada det(Pt) yang memenuhi det(P)det(Pt)=det(I) kecuali det(P)= det(Pt)=1. Jadi, jika P adalah matriks orthogonal dengan ukuran

n

n× maka det(P)=1. ٱ

Definisi 2.1.6

Sebuah matriks A =

( )

a_ij dapat dipartisi dalam beberapa bentuk. Misalnya di bawah ini adalah 3 partisi yang mungkin dari sebuah matriks umum A berukuran

4

3× . Pertama, matriks A dapat dipartisi dengan mengelompokkan baris-baris dalam kesatuan vertikal, seperti berikut :

A =           34 33 32 31 24 23 22 21 14 13 12 11 a a a a a a a a a a a a = _      2 1 A A .

Kedua, matriks A dapat juga dipartisi dengan mengelompokkan kolom-kolom dalam kesatuan horisontal, seperti berikut :

[

1 2 3

]

34 33 32 31 24 23 22 21 14 13 12 11 A A A A =           = a a a a a a a a a a a a .

Ketiga, matriks A dapat juga dipartisi dengan mengelompokkan baris-baris dan kolom-kolom menjadi kelompok-kelompok kecil seperti contoh di bawah ini :

      =           = 22 21 12 11 34 33 32 31 24 23 22 21 14 13 12 11 A A A A A a a a a a a a a a a a a .

Misalkan A sebuah matriks m×n dan B sebuah matriks n×p. Andaikan A dan B dipartisi dengan sesuai. Jika submatriks dari A dan B dinotasikan berturut-turut sebagai A_ij dan B_ij, di mana i adalah kelompok-kelompok baris dan j adalah kelompok-kelompok kolom, maka AB = C, di mana C adalah matriks

p

m× yang dinotasikan sebagai C =

( )

C_ij dan

∑

= = 1 k kj ik ij A B C adalah submatriks ke - ij dari matriks C. Contoh 2.1.2 Misalkan           = × × × 3 1 2 3 3 1 3 4 _A A A dan _      = × × × _{3 3}2 2 3 1 5 3B B B Maka 5 4× AB =       2 2 1 2 2 1 1 1 B A B A B A B A Teorema 2.1.5

Misalkan A adalah matriks non-singular yang dipartisi dengan ukuran n×n mengikuti bentuk berikut :

      = 22 21 12 11 A A A A A

di mana A mempunyai ukuran _ij

(

n_i×n_j

)

untuk i, j = 1, 2 dan n=n₁+n₂, n

n <

< 1

0 .

Misalkan pula A−1=B dan B dipartisi sebagai :

      = 22 21 12 11 B B B B B

di mana B mempunyai ukuran _ij

(

n_i×n_j

)

untuk i, j = 1, 2. Jika A₁₁ ≠0 dan

0 22 ≠

A , maka pernyataan-pernyataan berikut ini berlaku : 1. 111 − B dan 221 − B ada 2.

[

1 ₂₁

]

1 22 12 11 − − −A A A A dan

[

1 ₁₂

]

1 11 21 22 − − −A A A A ada 3.         − − − − − − = = ₋ − ₋ − ₋ − ₋ − ₋ − − 1 12 1 11 21 22 1 11 21 1 12 1 11 21 22 1 22 12 1 21 1 22 12 11 1 21 1 22 12 11 1 ) ( ) ( ) ( ) ( A A A A A A A A A A A A A A A A A A A A B A Bukti :

Untuk membuktikan pernyataan pertama, dibutuhkan bukti pernyataan kedua dan ketiga. Oleh karena itu dari tiga pernyataan di atas, yang akan dibuktikan terlebih dahulu adalah pernyataan kedua, kemudian pernyataan ketiga, dan yang terakhir pernyataan pertama.

a) Bukti pernyataan kedua (2)

Misalkan         − = − ₋ I A A Α A 1 11 21 1 11 0 0 (2.1.2)

A A0 =         − − − I A A Α 1 11 21 1 11 0       22 21 12 11 A A A A =         − − − 12 1 11 21 22 12 1 11 0 A A A A A A I A A0 = I(A₂₂−A₂₁A₁₁−1A₁₂) = I A₂₂−A₂₁A₁₁−1A₁₂ = A₂₂−A₂₁A₁₁−1A₁₂

Dengan memperhatikan sifat determinan (2) maka : 0

0

0_A= _{A A}≠

A (2.1.3)

Oleh karena itu A₂₂ −A₂₁A₁₁−1A₁₂ ≠0, maka (A₂₂ −A₂₁A₁₁−1A₁₂) non-singular, sehingga [A₂₂ −A₂₁A₁₁−1A₁₂]−1 ada. Misalkan         ₋ = ₋₁− 22 1 22 12 00 0 A A A I A (2.1.4)

Kalikan A dengan A00, sehingga :

A A00 =         ₋ − − 1 22 1 22 12 0 A A A I       22 21 12 11 A A A A =         ₋ − − I A A A A A A 21 1 22 21 1 22 12 11 0 A A00 = I(A₁₁−A₁₂A₂₂−1A₂₁) = 1 ₂₁ 22 12 11 A A A A I − − = A₁₁−A₁₂A₂₂−1A₂₁

Dengan memperhatikan sifat determinan (2) maka : 0 00 00 _{= ≠} A A A A (2.1.5)

Oleh karena itu 1 ₂₁ 0 22 12 11− ≠ − _A A A A , maka ( 1 ₂₁) 22 12 11 A A A A − − non-singular, sehingga 1 21 1 22 12 11 ] [A −A A− A − ada.

Jadi pernyataan kedua terbukti. ٱ

b) Bukti pernyataan ketiga (3)

Dengan hipotesis A−1=B ⇔ BA = I, maka :

      22 21 12 11 B B B B       22 21 12 11 A A A A = _      I I 0 0 (2.1.6)

Dari persamaan (2.1.6) didapatkan persamaan : I A B A B_{11 11}+ _{12 21}= (2.1.7) 0 22 12 12 11A +B A = B (2.1.8) 0 21 22 11 21A +B A = B (2.1.9) I A B A B_{21 12}+ _{22 22}= (2.1.10)

Telah diketahui sebelumnya bahwa A₁₁ ≠0 dan A₂₂ ≠0. Oleh karena itu 1 11 −

A dan A ada. Karena ₂₂−1 A ada, maka dari persamaan (2.1.8) didapatkan : ₂₂−1

0 22 12 12 11A +B A = B B₁₂ =−B₁₁A₁₂A₂₂−1 (2.1.11) Dengan mensubstitusikan persamaan (2.1.11) ke dalam persamaan (2.1.7), maka diperoleh : I A A A B A B − − 21= 1 22 12 11 11 11 atau B₁₁[A₁₁−A₁₂A₂₂−1A₂₁]=I.

Menurut pembuktian sebelumnya, karena [A₁₁−A₁₂A₂₂−1A₂₁]−1 ada, maka : 1 21 1 22 12 11 11 [ ] − − − = A A A A B (2.1.12) Karena 1 11 −

A ada, maka dari persamaan (2.1.9) diperoleh : 0 21 22 11 21A +B A = B B₂₁ =−B₂₂A₂₁A₁₁−1 (2.1.13) Dengan mensubstitusikan persamaan (2.1.13) ke persamaaan (2.1.10), maka diperoleh : I A B A A A B + = − − 22 22 12 1 11 21 22 atau I A A A A B₂₂[ ₂₂− _{21 11}−1 ₁₂]=

Menurut pembuktian sebelumnya, karena [A₂₂−A₂₁A₁₁−1A₁₂]−1 ada, maka :

1 12 1 11 21 22 22 [ ] − − − = A A A A B (2.1.14)

Oleh karena itu, matriks B dapat ditulis sebagai :

        − − − − − − = _{− − − − −} − − − − − 1 12 1 11 21 22 1 11 21 1 12 1 11 21 22 1 22 12 1 21 1 22 12 11 1 21 1 22 12 11 ) ( ) ( ) ( ) ( A A A A A A A A A A A A A A A A A A A A B (2.1.15)

Di mana matriks B adalah invers dari matriks A seperti pada asumsi awal, sehingga dapat ditulis :

B = _Α −1

Jadi pernyataan ketiga terbukti. ٱ

c) Bukti pernyataan pertama (1) Dari persamaan (2.1.15), didapatkan :

1 21 1 22 12 11 11 ( ) − − − = A A A A B

1 12 1 11 21 22 22 ( ) − − − = A A A A B

Karena (A₁₁−A₁₂A₂₂−1A₂₁)−1 dan (A₂₂−A₂₁A₁₁−1A₁₂)−1 ada, maka dijamin bahwa

1 11 −

B dan B ada. Jadi, pernyataan pertama terbukti. ₂₂−1 ٱ Oleh karena itu, seluruh pernyataan dalam teorema 2.1.5 telah terbukti.

Teorema 2.1.6

Jika A di dalam matriks partisi A pada teorema 2.1.5 non-singular, maka ₁₁

12 1 11 21 22 11 A A A A A A= − − .

Jika A₂₂ non-singular, maka A =A₂₂ A₁₁−A₁₂A₂₂−1A₂₁ .

Bukti : Kembali gunakan         − = − ₋ I A A Α A 1 11 21 1 11 0 0 dan asumsikan A₁₁ ≠0. Dengan mengalikan A dengan _{A , maka :} 0

A A0 ₌         − − − I A A Α 1 11 21 1 11 0       22 21 12 11 A A A A =         − − − 12 1 11 21 22 12 1 11 0 A A A A A A I A0A ₌ 12 1 11 21 22 A A A A − − = A0 A_. Diketahui pula A0 =A₁₁−1 = A₁₁ −1. Jadi, A₁₁−1A= A₂₂ −A₂₁A₁₁−1A₁₂ 1 ₁₂ 11 21 22 11 A A A A A A= − − . (2.1.16)

Misalkan         ₋ = ₋₁− 22 1 22 12 00 0 A A A I

A dan asumsikan bahwa A₂₂ ≠0

Kalikan A dengan A00_{, sehingga :}

A A00 ₌         ₋ − − 1 22 1 22 12 0 A A A I       22 21 12 11 A A A A =         ₋ − − I A A A A A A 21 1 22 21 1 22 12 11 0 A A00 ₌ 21 1 22 12 11 A A A A − − = A00 A _. Diketahui pula A00 =A₂₂−1 =A₂₂ −1. Jadi, A₂₂ −1A= A₁₁−A₁₂A₂₂−1A₂₁ 1 ₂₁ 22 12 11 22 A A A A A A= − − . (2.1.17)

Oleh karena itu teorema 2.1.6 terbukti ٱ

Definisi 2.1.7

Misalkan A adalah matriks bujur sangkar, maka A idempoten bila A2=A.

B. Beberapa Distribusi yang Penting

Kebanyakan metode-metode untuk pengujian hipotesis didasarkan pada anggapan bahwa bentuk distribusi populasinya diketahui. Tetapi dalam statistika inferensia (yang dikembangkan atas dasar sampel), sampel dianggap diambil dari populasi yang mempunyai distribusi binomial, distribusi normal, atau bentuk distribusi tertentu lainnya. Uji F dan uji t didasarkan atas anggapan semacam itu yakni bahwa distribusi populasinya normal dan variansinya homogen. Sedangkan uji chi-kuadrat (χ2_{) yang lebih dikenal dengan sebutan uji goodness of fit tidak}

memerlukan anggapan tertentu tentang bentuk distribusi populasi dari mana sampel diambil. Berikut ini akan dijelaskan lebih lanjut beberapa distribusi penting yang akan digunakan dalam pembahasan dalam bab III tentang statistik uji.

1. Distribusi χ2

Definisi 2.2.1

Misalkan X₁,X₂,K,X_n adalah variabel normal yang saling bebas dan masing-masing variabel tersebut berdistribusi normal dengan rata-rata nol dan variansi 1. Maka,

∑

= = + + + = n i i n X X X X 1 2 2 2 2 2 1 2 _K χ

adalah variabel random χ2 dengan derajat bebas n, bila fungsi densitasnya adalah

( )

_{( )}

( )

      − Γ = 2 /2−1 2 2 / 2 2 1 exp 2 / 2 1 _{χ χ} χ n n n f (2.2.1) di mana ≤ 2<∞ 0 χ dan n = 1, 2, K

Fungsi pembangkit momen untuk distribusi χ2 _{dengan derajat bebas n adalah :}

( ) (

)

/2 2 1 2 n t t M_χ = − − , 2 1 < t . Teorema 2.2.1

Bila S adalah variansi sampel random yang berukuran n yang diambil dari 2 suatu populasi berdistribusi normal dengan variansi σ2, maka

(

)

2 2 2 1 σ χ = n− S (2.2.2)

adalah sebuah nilai variabel random χ2 yang mempunyai distribusi chi-kuadrat dengan derajat bebas n – 1.

Bukti :

Akan dibuktikan dengan induksi matematika.

Sebelum memasuki pembuktian dengan induksi matematika, perlu diingat bahwa :

n X n X X X X n i i n n

∑

= = + + + = 1 2 K 1 _(2.2.3)

∑

(

)

= − − = n i n i n X X n S 1 2 2 1 1 (2.2.4)

( )

∑

(

)

= − = − n i n i n X X S n 1 2 2 1 .

Pertama, pandang kasus n = 2 maka :

2 2 1 2 X X X = + ,

(

)

(

)

2 1 2 2 2 1 2 1 2 2 2 2 X X X X S i i = − − − =

∑

= .

Selain itu X dan 2 S saling bebas. Maka ₂2

(

)

(

)

~

( )

0

2 1 2 1 2 2 2 1 2 2 χ σ σ X X S n− n = − _{, karena}

( )

0,1 ~ 2 2 1 X _N X σ −

. Jadi untuk n = 2, teorema 2.2.1 bernilai benar.

Dimisalkan bahwa teorema 2.2.1 berlaku untuk suatu n tertentu dan akan ditunjukkan berlaku pula untuk n+1, sehingga menurut induksi matematika juga berlaku untuk semua nilai n. Pertama,

1 1 1 ₊ + = + + n X X n X n n n (2.2.5) dan

(

)

∑

+ = + + = − 1 1 2 1 2 1 n i n i n X X nS =

∑

(

)

+ = + − + − 1 1 2 1 n i n n n i X X X X =

(

) (

) (

)

(

)

(

1

)

2 1 1 1 1 1 2 1 2 + + = + + = − + + − − + −

∑

∑

n n n i n i n n n i n i X X X X X n X X X =

∑

(

−

)

+ = n i n i X X 1 2

[

(

) (

1

)(

₁

)

(

)

(

1

)

2

]

2 1 2 + + 1 + + − n + n − n _n − n + + n− n n X X X X X n X X X (2.2.6)

Dengan mensubstitusikan persamaan (2.2.5) ke persamaan (2.2.6), maka diperoleh : 2 1 + n nS =

(

)

2

(

₁

)

2 1 1 _n X_n Xn n n S n − + + − ₊ . Karena n/(n+1)

(

X_n+1−Xn

)

~N

( )

0,σ2 , maka

(

)

~

( )

0 1 2 1 2 2 1 χ σ n n X X n n − + + .

Selain itu, menurut hipotesis induksi

(

n−1

)

S_n2 σ2 ~χ_n2₋₁

( )

0 dan X bebas dari n

2

n

S . Karena X_n+1 bebas dari X dan n S , maka terbukti bahwa : _n2

2 2 1 σn+ S n ~χ_n2

( )

0 .

2. Distribusi t

Distribusi t biasanya digunakan untuk sampel yang kecil (n<30). Distribusi ini lebih dikenal dengan sebutan distribusi t-Student. Statistik T didefinisikan sebagai perbandingan variabel random normal standard X dan variabel random Y yang berdistribusi chi-kuadrat (χ2) dengan derajat bebas r, di mana keduanya saling bebas. Maka nilai satistik T dapat ditulis menjadi :

r Y X T / = (2.2.7) Teorem 2.2.2

Variabel random T berdistribusi t-student dengan derajat bebas r dan fungsi densitasnya adalah :

( )

( )

r

(

t r

)

t R r r t f_{T r} ∈ +       Γ       ₊ Γ = ₊ ,untuk / 1 1 2 2 1 2 / ) 1 ( 2 2 / 1 π Bukti :

Akan dibuktikan dengan metode transformasi variabel :

( )

, 0 2 1 2/2 > = _e− _x x f x X π

( )

( ) _{, 0} 2 2 1 1 /2 1 /2 2 / >       Γ = _y − _e− _y r y f r y r Y Maka :

( )

( /2) 1 /2 2 / 2 / 2 2 1 1 2 1 , 2 r y r x XY y e r e y x f − − −       Γ = π

( )

,untuk dan 0 2 2 1 2 1 , /2 ( /2) 1 /2 2 / 2 > ∈       Γ = _e− _y −_e− _{x R y} r y x f x r y r XY π . Pandang transformasi : r y x r y x t / ) / ( 1/2 = =

( )

y r t y r t x= / 1/2= /

dan elemen matriks Jacobiannya adalah :

( )

(

t y r

)

( )

y r y r t g₁₁= / 1/2 = / 1/2= / δδ , sehingga :

( )

1/2 / r y J =

( )

1/2 / r y J = .

Maka untuk x∈R dan y>0 didapatkan :

( )

t y f

( )

x y J f_TY , = _XY ,

( )

(

( )

1/2

)

( )

1/2 / , / ,y f t y r y y r t f_TY = _XY =

(

)

( /2)1

( )

1/2 2 2 / 1 2 / / 2 exp 2 ) / ( exp 2 2 1 1 2 1 r y y y r y t r r r       − −       Γ − π = ( /2)1

( )

1/2 2 2 / / 1 2 exp 2 2 1 1 2 1 r y y r t y r r r −               + −       Γ π

= 2( )1 1/2 1 2 2 / 1 2 exp 2 2 1 1 2 1 − ₋               + −       Γ r y r t y r r r π .

Oleh karena itu :

( )

=

∫

∞

( )

0 f t,y dy t f_{T TY} = y ( )r dy r t y r r r 2 / 1 1 2 1 2 2 / 0 exp ₂ 1 2 2 1 1 2 1 − ₋ ∞               + −       Γ

∫

_π = y ( )dy r t y r r r r 1 2 1 0 2 2 / 2 / 1 1 2 exp 2 2 1 1 2 1 ∞ − −

_∫

              + −       Γ π . Misalkan : 2 1 2       + = r t y w       + = r t w y 2 1 2       + = r t dw dy 2 1 2 dw r t dy       + = ₂ 1 2 Maka :

( )

( ) dw r t r t w e r r t f r w r T ) / 1 ( 2 ) / 1 ( 2 2 2 1 1 2 1 2 1 2 1 2 0 2 / 2 / 1 +       +       Γ = − ∞ − −

_∫

π

= ( )

( )

(

)

( )

(

_{t r}

)

e w( ) dw r t r r w r r r r 2 / 1 0 2 2 / 1 2 2 / 2 / 1 2 / 1 / 1 2 / 1 2 2 / 2 2 1 ∞ − − − − −

_∫

+ + Γ π =

( )

( )

r

(

t r

)

e w(( ) ) dw r w r r r r 1 2 / 1 0 2 / ) 1 ( 2 2 / 2 / ) 1 ( 2 / 1 2 / 1 / 1 2 2 / 2 2 1 ∞ − + − + + −

_∫

+ Γ π . nilai (( ) )       ₊ Γ = − + ∞ −

∫

1/2 1 ₂1 0 r dw w e w r . sehingga,

( )

t f_T =

(

₂

)

( 1)/2 2 / 1 / 1 ) ( 1 2 2 1 + +       Γ       + Γ r r t r r r π ٱ

Jadi terbukti bahwa :

( )

( )

r

(

t r

)

t R r r t f_{T r} ∈ +       Γ       + Γ = ₊ ,untuk / 1 1 2 2 1 2 / ) 1 ( 2 2 / 1 π .

Probabilitas P

(

T ≤t

)

untuk nilai-nilai terpilih dari t dan r diberikan dalam tabel pada lampiran tabel t.

Teorema 2.2.3

Bila X dan S masing-masing adalah rata-rata dan variansi dari suatu 2 variabel random berukuran n yang diambil dari suatu populasi normal dengan rata-rata µ dan variansi σ2_{, maka :}

n S X T / µ − = (2.2.8)

v = n-1.

Bukti :

Karena

(

n−1

)

S2/σ2~χ_n2₋₁ dan X ~N

(

µ,σ2/n

)

serta kedua variabel random saling bebas, maka :

2 2 2 /n S X T σ σ µ − = 1 − = n Y V T ) 1 /( − = n Y V T ٱ

dimana V ~N

( )

0,1 dan Y ~χ_n2₋₁. Teorema ini mengikuti definisi distribusi t yang telah dijelaskan sebelumnya.

3. Distribusi F

Statistik F didefinisikan sebagai perbandingan dua variabel random chi-kuadrat yang saling bebas, dimana masing-masing variabel random tersebut dibagi dengan derajat bebasnya, sehingga nilai statistik F dapat ditulis menjadi

2 1 / / v Y v X F=

di mana X dan Y adalah variabel random yang berdistribusi chi-kuadrat dengan derajat bebas v dan ₁ v , dan keduanya saling bebas. ₂

Teorema 2.2.4 Misalkan X berdistribusi 2 1 v χ , Y berdistribusi 2 2 v

χ yang saling bebas, dan

2 1 / / v Y v X

F= . Variabel random F dikatakan memiliki distribusi F dengan derajat

bebas v dan ₁ v bila fungsi densitasnya : ₂

( )

[

]

        ≤ > + + − ⋅ Γ Γ + Γ =                                        0 , 0 0 , ) ) / ( 1 ) ( 2 1 2 1 / 2 1 2 1 2 1 1 2 1 2 1 2 1 2 1 ( 2 / 1 1 2 / / f f f v v f v v v v v v f f v v v v F Bukti :

Akan dibuktikan dengan metode transformasi variabel :

( )

         > Γ ≤ = − −         0 2 1 1 0 , 0 , 2 / 1 ) 2 / 1 ( 2 1 ₁/2 x e x v x x f x v v X

( )

         > Γ ≤ = − −         0 2 1 0 , 0 , 2 / 1 ) 2 / ( 2 2 1 2 2 2 / y e y v y y f y v v Y

      = = = 2 1 / / v y v x f y z h y v v x y v v x v y v x f 1 2 2 1 2 1 / / = ⋅ = = x y f v v = 2 1 f z v v x 2 1 = karena y=z

maka transformasinya menjadi :

     ₌ = = z f v v x z y h 2 1

dan elemen matriks Jacobian yang relevan adalah :

z v v z f v v f g 2 1 2 1 11 =      ∂ ∂ = f v v z f v v z g 2 1 2 1 12 =      ∂ ∂ =

( )

0 21 _∂ = ∂ = y f g ₂₂

( )

=1 ∂ ∂ = z z g

Jadi matriks Jacobiannya menjadi :

z v v f v v z v v J 2 1 2 1 2 1 1 0 = = sehingga z v v J 2 1 = Untuk f, z >0, didapatkan :

( )

x e y e J v y f f v y v x v v Y F 2 / 1 ) 2 / ( 2 / 2 / 1 ) 2 / ( 2 / 1 , 2 2 1 1 ₂ 2 1 1 2 2 1 1 , − − − −       Γ       Γ =

( )

, 2 2 1 1 2 2 1 1 , ( /2) 1 /2 2 / 2 / 1 ) 2 / ( 2 / 1 , 2 2 1 1 J e z e x v z f f v z v x v v Z F − − − −       Γ       Γ = karena Z = Y Dengan fz v v x 2 1 = maka :

( )

x e z e J v z f f v z v x v v Z F 2 / 1 ) 2 / ( 2 / 2 / 1 ) 2 / ( 2 / 1 , 2 2 1 1 ₂ 2 1 1 2 2 1 1 , − − − −       Γ       Γ = = ( /2) 1 ( /2) 1 ( /2)1 1 ) 2 / ( 2 1 ) ( 2 1 2 1 2 1 1 1 2 1 2 2 1 2 1 1 − − − − + _           Γ       Γ v v v v v v z z f v v v v z v v e fz v v z 2 1 2 / 2 1 2 exp _ −      − × =

(

)

( ) ⋅            + −       Γ       Γ − + + − 1 2 exp 2 2 1 2 1 / 2 1 1 2 1 ) ( 2 1 2 1 1 ) 2 / ( 2 / 2 1 1 2 2 1 1 1 f v v z z v v f v v v v v v v v Maka :

( )

f f

( )

f z dz f_{F FZ} , 0 ,

∫

∞ = =

(

)

( ) 1 . 2 exp 2 2 1 2 1 / 2 1 0 1 2 1 ) ( 2 1 2 1 1 ) 2 / ( 2 / 2 1 1 2 2 1 1 1 dz f v v z z v v f v v v v v v v v             + −       Γ       Γ

∫

∞ + − + −

Untuk menentukan f_F

( )

f dimisalkan : , 1 2 ₂ 1 _{f t} v v z =       + sehingga 1 2 1 ₁ 2 −       + = f v v t z

dz = _ ∈

[

∞

)

     + − , 0 , 1 2 1 2 1 _{f dt t} v v Maka :

( )

f f

( )

f z dz f_F =

∫

∞ _FZ 0 , , =

(

)

( ) 2( )1 1 2 1 1 2 1 ) ( 2 1 2 1 1 ) 2 / ( 2 / 2 1 1 2 1 2 2 1 1 1 . 1 2 2 2 1 2 1 / + − − + + + −       +       Γ       Γ v v v v v v v v f v v v v f v v f t ( ) dt v v v v

∫

∞ + − −       + × 0 1 2 1 1 2 1 1 2 1 2 =

(

) (

)

_{( )}

(

)

[

]

(1 2) 1 1 2 1 2 1 1 2 / 2 1 2 / 2 1 2 1 / 1 2 1 2 1 / 2 1 v v v v f v v f v v v v v v + − + ⋅       Γ       Γ     + Γ ٱ Jadi terbukti :

( )

[

]

        ≤ > + + − ⋅ Γ Γ + Γ =                                        0 , 0 0 , ) ( 2 / 1 ) / ( 1 1 ) 2 / ( 2 1 2 1 / 2 1 2 1 2 1 1 2 1 2 1 2 1 2 1 / f f v v f v v v f v v v v v v f f v F

Probabilitas P

(

F ≤ f

)

untuk nilai-nilai terpilih dari f dan v₁, v₂ diberikan dalam tabel pada lampiran tabel F.

C. Distribusi Normal Multivariat

Definisi distribusi normal multivariat dapat dilihat dari dua hal. Yang pertama, definisi sederhana distribusi normal multivariat dalam fungsi densitas dan yang kedua adalah definisi yang berdasar pada keunikan distribusi multivariat

normal yang dinamakan kombinasi linear. Beberapa pembuktian teorema yang berkaitan dengan distribusi normal multivariat, menggunakan pembahasan tentang fungsi pembangkit momen dari vektor variabel random. Oleh sebab itu akan dikemukakan juga tentang teorema ketunggalan yang menjadi dasar dalam pembahasan fungsi pembangkit momen. Namun dalam skripsi ini, teorema ketunggalan tidak dibuktikan karena diluar jangkauan pembahasan skripsi.

Definisi 2.3.1

Fungsi densitas normal multivariat dalam p – dimensi untuk vektor random X =

[

X₁ X₂ K X_p

]

'

, adalah fungsi f di mana

f

( )

x =

( )

∑ −

(

−

)

∑

(

−

)

 − _{x µ} µ x 1 2 / 1 2 / ₂ 1 exp 2 1 t p π (2.3.1)

dengan µ = vektor mean p×1 ∑ = matriks dispersi X p× p

∑ = determinan matriks ∑

1 −

∑ = invers matriks ∑

Selain itu diketahui pula ∑ adalah matriks definit positif dan −∞ < X < _i ∞ untuk i = 1, 2,K , p.

Definisi 2.3.2

Jika X =

[

X1 X2 K X_p

]

'

adalah vektor variabel random yang mempunyai fungsi densitas (2.3.1) maka X dikatakan berdistribusi normal multivariat dan ditulis X ~ N_p

( )

µ,∑ .

Pada situasi univariat, jika X₁,X₂,K,X_N adalah nilai-nilai variabel random X yang menyatakan sebuah populasi berhingga dengan ukuran N, maka

rata-ratanya adalah N X N X X X N i i N

∑

= = + + + = 1 2 K 1 µ ,

dan variansinya adalah

(

)

N X N i i

∑

= − = 1 2 2 µ σ .

Jika hanya tersedia satu sampel random saja, misalnya X₁,X₂,K,X_n, maka dapat dihitung rata dan variansi sampel yang merupakan penduga bagi rata-rata dan variansi populasi.

n X n X X X X n i i n n

∑

= = + + + = 1 2 K 1 _,

(

)

∑

= − − = n i n i n X X n S 1 2 2 1 1 .

Pada situasi univariat, nilai harapan bagi variabel random X dilambangkan dengan E

( )

X . Dengan kata lain, nilai harapan suatu variabel random dapat ditafsirkan sebagai nilai tengah atau rata-rata dari populasi tersebut yang ditulis dengan notasi : µ=E

( )

X . Pada situasi multivariat yang melibatkan vektor

random X berdimensi p, nilai harapan juga disajikan dalam bentuk vektor. Untuk lebih jelasnya perhatikan definisi berikut ini.

Definisi 2.3.3

Nilai harapan suatu vektor random didefinisikan sebagai vektor yang komponen-komponennya adalah nilai harapan dari komponen-komponen asal. Jadi, jika f

( )

x berdimensi n adalah fungsi nilai vektor dari vektor random X berdimensi p,

( )

( )

( )

( )

            = x x x x f n f f f M 2 1

maka nilai harapan dari f didefinisikan oleh

[ ]

( )

[

]

( )

[

]

( )

[

]

_       ∑ ∫ =             = ∞ ∞ − xf(x) x x x f(x) x x x f diskret kasus ) ( kontinu kasus , ) ( , 2 1 P d p f E f E f E E n M Definisi 2.3.4

Vektor mean µ berdimensi p didefinisikan sebagai berikut

[ ]

       ∑ ∫ =               =               = = ∞ ∞ − xx x x x x X µ diskret kasus , ) ( kontinu kasus , ) ( ] [ ] [ ] [ 2 1 2 1 P d p X E X E X E E p p µ µ µ M M