Proceedings of the 3rd IMT-GT Regional Conference on Mathematics, Statistics and Applications
Universiti Sains Malaysia
THE MAXIMUM RUN UP PROPAGATION OF WAVE
ON A SLOPING BEACH
1
Said Munzir,
2Ichsan Setiawan,
1Marwan,
1Rasudin
1Jurusan Matematika 2Jurusan Ilmu Kelautan
FMIPA, Universitas Syiah Kuala, Banda Aceh, Indonesia Contact person : [email protected]
Abstract. An integrated code for wave propagation (tsunami) caused by bottom motion such as underwater land slides or tectonic earth quakes toward the beach should contain three essential elements. The first element is the code that can represent the dynamic motion of the bottom in the source region, the code for the free flow region, and the run-up code suitable in the coastal and inland region. Most of existing codes can predict well the arrival time of the waves from the source region to the coast but are not very reliable for predicting wave height near the coastal region. This is because such codes do not take the effect of dispersion into account; such effect is not negligible in the generation region, with consequences for the free flow region and for the arrival wave near the coast. For given bathymetry and topography, the wave height near the coast is important information to further predict the run-up height and so to compute the flooded area inland. The objective of this paper is to present the essential third element to a currently developed code for water wave propagation caused by moving bottoms. The code is based on shallow water equation (SWE model) to include dynamic bottom variations suitable for computation in the source region that are significant in the deep water of the free flow region. The additional element to the code is the run-up code. The existing 1-D SWE code will be connected to a run-up code for which the SWE code will provide influx to the last one. Extension to 2-D code will be considered and executed rudimentarily giving direction to further in depth investigation
Keywords : Tsunami waves , shallow water equation , run-up waves, sloping beach.
1
Introduction
The general characteristic of water wave is mainly influenced by the nonlinear behavior of the water medium. This characteristic causes the changes of water wave form as a function of position and time. In the wave travel, due to this characteristic, the wave amplitude is increasing as reported by [1,2,3,5,6,10]. This surely causes certain consequences over the beach condition if the wave travels toward the coastal area [7,8,9].
The damage caused by water wave is related to how far, big, and quick the wave motion when it reach the coast area. Abbrasion problem and coastal damage triggered by water wave, which is an integrated part of this research, has been studied by many experts. This problem is a complex problem as it involve many parameters, both hydrodynamic parameters from fluid motion as well as parameters related to material transport in the sea bottom [9,13,14]. However, the study of maximum run-up of a water wave traveled on a sloping beach has not been discussed. It should be emphasized that the abrasion and desedimentasion of beaches is strongly related to the wave run up.
In this paper, the wave maximum run up when it travels to the coastal area will be presented. The relation between this run up and the beach slope will also be shown. Understanding this formula is important, to give development direction and model application in the specific study which connect the real condition of abrasion and desedimentation in the coastal area.
This paper is organized in the following order. In the section 2, the mathematical model describing the wave evolution near the beach is presented. The model solution followed by the maximum run-up is presented in the section 3. Finally, this paper will be ended with concluding remarks.
2
Mathematical Model
boundary condition on the moving plate. The mathematical model describing the wave evolution on a shallow water surface can be written as [12]
(
)
Where b denote dynamical sea bottom and φ is fluid velocity potential, while h is the water depth. The equation can also be written as
0
This equation is known as shallow water equation (SWE). This equation is a simple form of the complete equation. Here x represent the spatial variable in the horizontal direction and z represent the spatial variable in vertical direction. h(x,t) is the water depth and η(x,t) is the wave elevation at the position x and the time t. Mean while, u(x,t) denote the water particle flow velocity component in the horizontal direction and g is the gravitation.
Here, the SWE is solved using the condition occurred in the Burger equation. This is done to explain the problem of wave breaking phenomena. The solution of the equation (1) is obtained by initially transforming the equation into Burger equation which can be written as
0
One of the solutions of the equation (3) can be written as
)
With the boundary condition
)
This solution represents the event of the wave breaking due to nonlinearity effect. The breaking of the wave is an important information for the wave run up.
3
The solution of the model and run up wave
when u c
. For the positive sign (+), equation (7) can also be written as
0
which is a Burger equation. The solution of this equation is
For b(x)=x, the corresponding form of equation (1) is
It can be simplified using the transformations h=H, 2
2
Using the transformations, the equation (18) is transformed into the new shallow water equation which is written
as
It can be observed that the structure of the equation (19) is similar to that of the equation (6). Then, it can be
further transformed using q(ξ,τ)=k−3A, A= H , U(ξ,τ)=K−2A and K =U+2A=2Al together with
Consequently, it yields
x
0x
smaxh
maxθ
Figure 2. Topography for the case of b(x)=αxwhere α =tanθ.
For this case, the equation (1) which correspond to the case is
α
g x h g x u u t u
x hu t h
− = ∂ ∂ + ∂ ∂ + ∂ ∂
= ∂ ∂ + ∂ ∂
0 ) (
. (24)
Then, the transformations that can be used are defined as h=αL0h', u=u0u', x=L0x', t=T0t',
α
g L T0 = 0
and u0 = gL0α . Using these transformations, the equation (24) can also be written as
1 ' ' ' ' ' '
'
0 '
) ' ' ( ' '
− = ∂ ∂ + ∂ ∂ + ∂ ∂
= ∂ ∂ + ∂ ∂
x h x u u t u
x u h t h
. (25)
It can be observed that the equation (25) is similar to the equation (18). Using the same method as was used the equation (18), it gives
( )
(
)
22 9
1
, x x
gt t x
h = s− , (26)
with
2 0
2 1 2 gh t g t x
xs = + l − α . (27)
This equation represent the distance reached by the wave on the beach having the slope of α. Here, x0 represent the coastal line and hl is the wave amplitude before reaching the coastal line. Form the equation (27), the formula for maximum to reach maximum run up of the wave is obtained. This formula can be written as
g h
t l
α 2
max = . (28)
Hence, the maximum run up of the wave coming to the beach having the slope αcan also be found. This maximum run up formula is written as
αl
h x
xmax = 0+2 . (29)
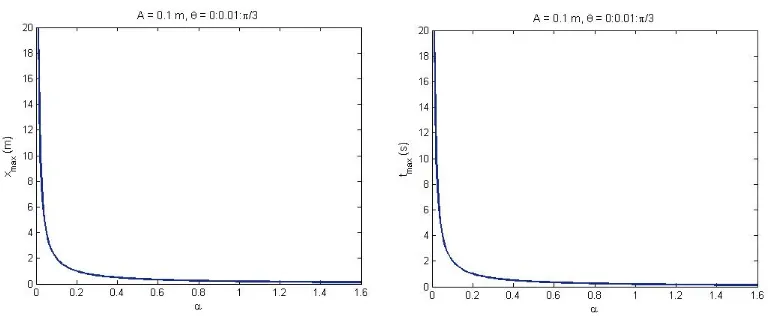
Figure 3. Graph describing the relation between
x
max(left) andt
max (right) with α4
Concluding Remarks
The maximum wave run up was studied using the shallow water equation (SWE). Based on the computation conducted, a formula is obtained which relates the maximum wave run up with the slope of the beach and the incoming wave amplitude. It concludes that the maximum run up is proportional to the incoming wave amplitude and reverse proportional to the beach slope. In addition, it is also obtained that the maximum time to reach the maximum run up is proportional to with the square root of the incoming wave amplitude and reverse proportional to the square root of the beach slope.
Acknowledgments
The authors would like to express their grattitude to Dr. Andonowati for her collaboration and cooperation on conducting this research. We would also like to thank Mathematics Department, Syiah Kuala University for the facilities we used in the Modeling and Simulation Lab. Finally, special honour for BRR NAD-Nias for financing this research in the financial year 2007.
References
1. C.T. Stanberg (1998), “On the non--linear behaviour of ocean wave gorups”, In: B.L. Edge and J.M. Hemsley (eds), Ocean Wave Measurement and Analysis, Reston, VA, USA : American Society of Civil Engineers (ASCE) 2, 1227-1241
2. E. van Groesen, Andonowati, E. Soewono (1999), “Non-linear effects in bi-chromatic surface waves”,
Proc. Estonian Acad. Sci., Mathematics and Physics 48, 206-229
3. Marwan dan Andonowati (2003), “Perubahan bentuk pada perambatan signal bikromatik dan pengaruhnya terhadap amplitudo maksimum”, JMS FMIPA ITB, Vol. 8 No. 2, 81-87
4. J.J. Wijetunge (2006), “Field in measurements in Sri Langka of maximum water levels due to Sumatera Tsunami of December 2004 and strategies for mitigating the risk from coastal hazards”, Proceedings of the Eleventh Asian Congress of Fluid Mechanics, Kuala Lumpur, Malaysia, 109-114.
5. J. Westhuis, E. van Groesen,R.H.M. Huijsmans (2001), “Experiments and numerics of bichromatic wave groups”, J. Waterway, Port, Coastal and Ocean Engineering 127, 334-342
6. Andonowati, E. van Groesen, “Optical pulse deformation in second order non-linear media”, Journal of Non-linear Optics Physics and Materials, 12, 221-234.
7. G. Klopman, M. W. Dingemans and E. van Groesen (2005), “ A variational model for fully non-linear water waves of Boussinesq type”, Proceedings 20th International Workshop on Water Waves and Floating Bodies, ed. J. Grue, Spitsbergen, pg 129-132.
8. E. van Groesen & G. Klopman (2005), “Dispersive effects in tsunami generation”, Proceedings of The Indonesian Ocean Forum 2005, 13-15 July, Bali Indonesia.
10. E. Cahyono (2002), “Analytical wave codes for predicting surface waves in a laboratory basin”, Ph.D Thesis, Fac. of Mathematical Sciences Univ. of Twente, The Netherlands
11. E. van Groesen (1998), “Wave groups ini uni-directional surface wave models”, Journal of Engineering Mathematics 34 : 215-226
12. G.B. Whitham (1974), “Linear and non-linear waves”, John Wiley and Sons, New York
13. O. Bokhove, (2005) : Hamiltonian restriction of Vlasov equations into two-layer isopycnic and isentropic equations. Applied Math. Lett. 18, 1418-1425.