UKBM XII 3.4 4.4 aplikasi turunan fungsi

(1)

APLIKASI TURUNAN FUNGSI TRIGONOMETRI

1. Identitas

a. Nama Mata Pelajaran : Matematika Peminatan

b. Semester : 5

c. Materi Pokok : Aplikasi turunan fungsi trigonometri d. Alokasi Waktu : 8 x 2 jam pelajaran

e. Kompetensi Dasar :

f. Tujuan Pembelajaran:

g. Materi Pembelajaran

Matematika untuk SMA/MA Kelas XII Kelopok Peminatan Matematika dan Ilmu-Ilmu Alam. 2017. Sukino. Jakarta: Erlangga.

UKBM MTK P/3.4/4.4/5/6-6

3.4. Menjelaskan Keberkaitan turunan pertama dan kedua fungsi dengan nilai maksimum, nilai minimum, selang kemonotonan fungsi serta titik belok dan selang kecekungan kurva fungsi trigonometri.

4.4. Menyelesaikan masalah yang berkaitan dengan nilai maksimum, nilai minimum, selang kemonotonan fungsi, kemiringan garis singgung serta titik belok dan selang kecekungan kurva fungsi trigonometri.

Melalui pendekatan saintifik dengan menggunakan model pembelajaran

Problem Based Learning, peserta didik dapat menjelaskan dan menentukan aplikasi turunan fungsi trigonometri yang meliputi kemiringan garis singgung dan persamaan garis singgung kurva, nilai maksimum dan minimum, serta kenomotonan dan kecekungan kurva sebuah fungsi trigonometri, dengan mengembangkan sikap religius, penuh tanggung jawab, bekerja keras, serta dapat mengembangkan kemampuan berpikir

(2)

1. Pastikan dan fokuskan apa yang akan anda pelajari hari ini.

2. Baca dan pahami Pendahuluan (Apersepsi) untuk membantu anda memfokuskan permasalahan yang akan dipelajari.

3. Cari referensi/buku-buku teks yang terkait dengan topik/permasalahan yang anda hadapi.

4. Jangan lupa browsing internet untuk menda-patkan pengetahuan yang up to date.

5. Selalu diskusikan setiap persoalan yang ada dengan teman-teman dan atau guru.

6. Presentasikan hasil pemahaman anda agar bermanfaat bagi orang lain.

Jika tahapan-tahapan telah kalian lewati, kalian boleh meminta tes formatif kepada Bp/Ibu guru sebagai prasyarat untuk melanjutkan ke UKBM berikutnya. Oke.?!

h. Kegiatan Pembelajaran

a) Pendahuluan

Sebelum belajar pada materi ini silahkan kalian amati narasi di bawah ini.

Apersepsi : Jika kita mengunjung orang sakit di kamar ICU, kita akan melihat alat pemacu jantung yang disambungkan ke pasien. Layar pada monitor menggambarkan grafik sebuah fungsi kurva lengkung turun, naik serta mendatar. Keadaan grafik kurva lengkung yang terletak pada monitor tersebut merupakan salah satu aplikasi turunan fungsi yang akan kita pelajari dalam bab berikut. Keadaan naik turun menandakan kecekungan kurva pada sebuah selang atau interval. Keadaan yang stabil menandakan kemonotonan suatu kurva tersebut.

Nah sekarang kalian perlu menggunakan pengetahuan tersebut dan menggabungkannya dengan pengetahuan mengenai turunan fungsi trigonometri.

(3)

b) Peta Konsep

2. Kegiatan Inti

Kegiatan Belajar 1

Sebelumnya telah kalian ketahui bahwa kemiringan garis singgung kurva

y=f(x) di titik

₍

x1, f

(

x1

)

adalah m=f '(x1)

Penyelesaian

Persamaan kurva y=sin3x−3 sinx

Gradien garis singgung adalah turunan pertama dari persamaan kurva

m=y'=3(sinx)3−1d(sinx)

Sebuah kurva memliki persamaan . Tentukan kemiringan garis singgung kurva tersebut pada titik di mana dan tentukan persamaan garis singgung tersebut

(4)

Gradien untuk x=π

Selanjutnya kita cari titk singgungnya

x1=π

Kalikan kedua ruas dengan 8 diperoleh

8y+9

_√

3=−3x+π

⟺8y=−3x+π−9

_√

3

⟺3x+8y−π+9

√

3=0

Persamaan Garis Singgung dan Garis Normal Sebuah Kurva y=f(x)di titik A (x1, y1).

Persamaan garis normal kurva adalah persamaan garis yang tegak lurus terhadap garis singgung suatu kurva.

Persamaan garis normal ditentukan oleh :

y−y₁= 1

f'(x)(x−x1)

(5)

1. Nilai kemiringan garis singgung pada kurva y = sin x di absis π

3 adalah ….

2. Persamaan garis singgung pada kurva f(x)=sinx+2pada

titik

(

π₆,5

2

)

adalah ….

3. Persamaan garis normal pada kurva f(x)= cosx

1+sinxpada

titik yang berabsis π

2 adalah ….

Apabila kalian telah mampu menyelesaikan persoalan di atas, maka kalian bisa melanjutkan pada kegiatan belajar 2 berikut.

Telah dibahas pada buku matematika wajib kelas XI bahwa turunan pertama f'₍_x

)<0 menyatakan fungsi turun dan f'₍_x

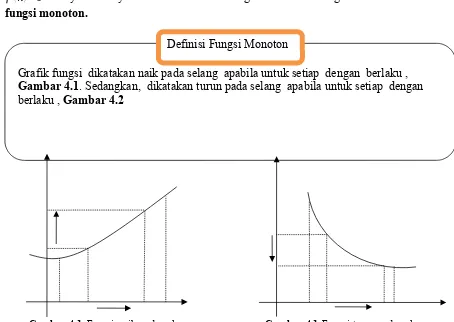
)>0 menyatakan fungsi naik. Sedangkan, f'(x)=0 menyatakan syarat titik stasioner. Fungsi naik atau fungsi turun disebut fungsi monoton.

Grafik fungsi dikatakan naik pada selang apabila untuk setiap dengan berlaku , Gambar 4.1. Sedangkan, dikatakan turun pada selang apabila untuk setiap dengan berlaku , Gambar 4.2

Definisi Fungsi Monoton

Gambar 4.1 Fungsi naik pada selang

(6)

Tentukan selang dimana fungsi naik, fungsi turun dari f(x)=2cosx−cos 2x dalam

selang (0,2π)

Penyelesaian

(1) Tentukan dahulu turunan pertama, f '(x) f(x)=2cosx−cos 2x

f'

(x)=…+… f'(x)=…+…(…) f'₍_x

)=…(…−…)

(2) Tentukan titik-titik stasioner dengan syarat f'₍_x

)=0

Jadi, …(…−…)=0, 0<x<2π

…=0 atau (…−…)=0

⟺…=0 ⟺cosx=cos…

⟺sinx=sin… x=… (*memenuhi/tidak memenuhi)

x=… (*memenuhi/tidak memenuhi) atau

atau x=(2π−…)

x=π−…=… (*memenuhi/tidak memenuhi) ¿… (*memenuhi/tidak memenuhi)

Jadi, dalam interval 0<x<2π ada tiga absis yang memenuhi yaitu … , … , dan ….

Mari menetukan ordinat titik stasioner dengan menyubstitusikan nilai-nilai x ini ke f(x)=2cosx−cos 2x .

Untuk x=…

f(x)=2cos…−cos…

¿2(…)−(…)=…

Untuk x=…

f(x)=2cos…−cos…

¿2(…)−(…)=…

Untuk x=…

x=2 cos…−cos…

¿2(…)−(…)=…

Masalah

(7)

Jadi titik-titik stasioner f(x) adalah (… , …),(… , …),(… , …).

(3) Menentukan tanda f'(x) di sisi kiri dan sisi kanan titik stasioner dalam suatu

daerah untuk selang yang diberikan (0<x<2π).

Ketiga titik stasioner akan membagi interval (0<x<2π) menjadi 4 daerah.

Daerah I untuk 0<x<…; daerah II untuk …<x<…; daerah III untuk …<x<…

dan daerah IV untuk …<x<2π .

Untuk menentukan tanda setiap selang kita perlu memilih salahsatu absis x yang ,udah dihitung (sudut-sudut istimewa). Misalnya, dalam daerah I: 0<x<…

kita memilih x=…; daerah II: …<x<… kita memilih x=…; daerah III: …<x<…

kita memilih x=… ; dan daerah IV: …<x<2π kita memilih x=…. Proses ini

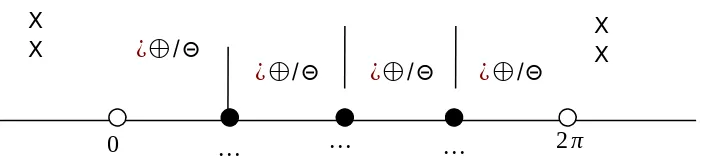
ditunukkan pada gambar Gambar 4.2

Mari kita tentukan tanda (positif atau negatif) dari f'(x)=−2 sinx(1−2 cosx)

pada setiap daerah untuk absis x yang telah dipilih. Daerah I (0<x<…) untuk x=…

Tanda-tanda f '(x) untuk setiap daerah yang telah diuji di atas ditunjukkkan pada

Gambar 4.3

Gambar 4.2 Titik-titik stasioner yang membagi selang atas empat daerah

(8)

(4) Menentukan selang di mana fungsi naik atau turun

Daerah di mana tanda f'(x)>0 menyatakan selang fungsi naik dan tanda f'(x)<0

menyatakan selang fungsi turun. Dengan memerhatikan secara saksama Gambar 4.3, jelas bahwa:

fungsi naik dalam daerah … : …<x<… dan

daerah … : …<x<…

fungsi turun dalam daerah … : …<x<… dan

daerah IV : …<x<…

AYO BELATIH !!

Diberikan f(x)=2sinx−cos 2x dalam selang 0≤ x ≤2π. Tentukan selang

kemonotonan fungsi tersebut menggunakan turunan pertama.

Titik stasioner terjadi jika dipenuhi f ’(x)=0, yaitu titik di mana gradien

kurva sama dengan nol. Untuk menentukan jenis titik stasioner dapat menggunakan dua metode yaitu metode pertama dengan menggunakan uji turunan pertama dan metode kedua menggunakan tanda uji turunan kedua di titik stasioner.

1. Metode Pertama : Uji turunan pertama pada kedua sisi di sebelah titik stasioner.

Ayo Menyimpulkan

Langkah-langkah menentukan selang kemonotonan Kurva Fungsi Trigonometri ……….. ……….. ……….. ………..

¿⨁/⊝

X X X

X

¿⨁/⊝

2π

… _…

…

0

Gambar 4.3 Titik-titik stasioner (bulatan hitam) berikut tanda-tanda f '(x) dalam tiap

(9)

a. Jika dari sisi sebelah kiri titik stasioner menuju ke sisi sebelah kanannya terjadi perubahan tanda gradient :

 dari f ’(x)>0 menjadi f ’(x)<0, maka jenis titik stasioner adalah titik balik

maksimum.

 dari f ’(x)<0 menjadi f ’(x)>0, maka jenis titik stasioner adalah titik balik

minimum.

b. Jika dari sisi sebelah kiri titik stasioner menuju ke sisi sebelah kanannya tidak terjadi perubahan tanda gradien, keduanya f ’(x)>0 (titik belok naik)

atau keduanya f ’(0)<0 (titik belok turun), maka jenis titik stasioner adalah

titik belok.

(10)

x=… . Atau x=… . 2. Jika cosx=cosa maka

x=… . Atau x=… .

3. Jika tanx=tana maka x=… .

4. Titik stasioner terjadi apabila dipenuhi f'(x)=… .

Contoh soal :

Diberikan f(x)=sinx+cosx, dengan 0≤ x ≤2π.

a.Tentukan semua titik stasioner berikut jenisnya. b. Tentukan titik-titik ujung interval.

Penyelesaian :

a. Langkah – langkah penyelesaian :

1) Menentukan koordinat titik stasioner, gradient kurva adalah nol (f ‘(x)=0). f(x)=sinx+cosx, dengan 0≤ x ≤2π

f ‘(x)=¿

cosx=sinx ↔cosx=cos(π

2−x)

x=

(

π

2−x

)

+n.2π atau x= −

(

π

2−x

)

+n.2π

x+x= π

2+n.2π atau x=

−π

2 +x+n.2π

2x= π₂+n.2π atau x−x= −π

2 +n.2π

x= π

4+n . π atau 0=

−π

2 +n.2π( tidak memenuhi)

n=0 x= π₄+0=π

4

n=1  x=¿= π

4+1.π= 5π

4

n=2 x= π₄+2π>2π (tidak memenuhi)

Jadi, ada dua absis yang memenuhi titik stasioner yaitu ¿ π

4 dan x= 5π

(11)

untuk x=¿ π

Jadi, ada dua titik stasioner yaitu (π

4 ,

√

2) dan ( 5π

4 ,−

√

2).

2) Gambar absis stasioner pada garis bilangan dalam selang yang diberikan.

3) Tentukan dua titik Uji, satu di kiri dan satu lagi di kanan titik stasioner. Substitusikan absis titik uji pada f ‘(x), yang diambil hanyalah tanda dari f ‘(x), positif atau negative.

(12)

Dengan memperhatikan tabel dapat disimpulkan bahwa x=π

4 adalah absis

titik balik maksimum dan x=5π

4 adalah absis titik balik minimum.

Jadi, jenis titik balik (π

4 ,

√

2¿ adalah titik balik maksimum dan ( 5π

4 ,−

√

2¿

adalah titik balik minimum.

b. Titik maksimun atau titik minimum yang kita peroleh dari f ’(x)=0

sesungguhnya adalah titik maksimum lokal atau titik minimum lokal dalam selang yang diberikan. Supaya menjadi titik maksimum mutlak atau titik minimum mutlak, maka nilai dari titik-titik stasioner ini harus dibandingkan dengan nilai-nilai fungsi pada titik-titik ujung interval. Jika nilai maksimum lebih besar dari nilai terbesar ordinat titik ujung interval, maka titik ini adalah titik maksimum mutlak. sedangkan jika nilai minimum lebih kecil dari nilai terkecil ordinat titik ujung, maka titik ini adalah titik minimum mutlak.

Absis tiitk-titik ujung interval adalah x=0dan x=2π.

f(x)=sinx+cosx

untuk x=0→ f (0)=sin 0+cos 0=0+1=1.

untuk x=2π → f(2π)=sin 0+cos 0=0+1=1.

Jadi, titik-titik ujung interval adalah (0,1) dan (2π ,1¿

2. Metode Kedua : Menggunakan tanda uji turunan kedua di titik stasioner. Contoh soal :

Tentukan nilai minimum mutlak dari y=2sinx+cos 2x dalam selang

0≤ x ≤2π. Penyeleaaian :

Pertama kita tentukan dahulu absis titik stasioner, yaitu saat gradient kurva sama dengan nol (f ‘(x)=0).

f(x)=2sinx+cos 2x ,0≤ x ≤2π

f '(x)=2cosx+(−2 sin 2x)2 cosx−2 sin 2x

f '(x)=0

2 cosx−2 sin 2x= 0

(13)

cosx=sin2x

Jadi, ada empat absis titik stasioner yang diperoleh, yaitu x = (π₆ ,π

2, 5π

6 , 3π

2 ¿

Selanjutnya kita akan menentukan mana dari keempat absis titik stasioner ini yang termasuk titik balik minimum(sesuai yang diminta dalam soal). Kaitan antara tanda dari turunan kedua fungsi pada titik stasioner ( ”(c), dengan x=c

adalah absis titik stasioner) dengan jenis titik stasionernya. Ini dinyatakan dalam teorema berikut.

Mari kita terapkan teorema metode 2 ini untuk menentukan mana dari keempat absis stasioner yang telah kita hitung sebelumnya, yang merupakan absis titik minimum. Karena metode 2 adalah metode uji tanda turunan kedua, maka kita perlu menentukan dahulu turunan kedua, f ”(x), sebelum mengujinya.

f(x)=2sinx+cos 2x

Teorema Nilai Balik

Misalkan y=f(x) terdefinisi pada selang a<x<b. Misalkan juga f ‘(c)=0, yang berarti x=cadalah absis titik stasioner.

1) Jika f “(c)<0 atau negative, maka f(c) adalah nilai balik maksimum.

2) Jika f ”(c)>0 atau positif, maka f(c) adalah nilai balik minimum.

(14)

f '(x)=2cosx−2sin 2x

2 . untuk menentukan nilai

minimum mutlak, mka kita harus membandingkan kedua nilai minimum ini dengan nilai-nilai fungsi pada ujung-ujung selang ¿ dan x=2π)

Nilai minimum f(x) = 2 sin x + cos 2x untuk kedua tiitik balik minimum,

x=π

untuk kedua titik di ujung-ujung selang x=0f (0)=2 sin 0+cos 0=0+1=1 x=2π f (2π)=2sinπ+cos 2π=0+1=1

Jika keempat nilai ini kita bandingkan, maka nilai yang paling kecil adlah -3. Jadi nilai minimum mutlak dari y=2sinx+cos 2x adalah -3, yang terjadi

ketika x=3π

2

AYO BERLATIH

1. Diberikan f(x)=2cosx –cos 2x, dengan 0<x<2π. Tentukan semua titik

(15)

2. Tentukan nilai minimum mutlak dari f(x)=2sinx+cos 2x, dengan 0≤ x ≤2π

dengan menggunakan uji turunan kedua.

Menentukan rumus nilai ekstrem dari y=Asinx+Bcosx yaitu :

syarat kurva y=Asinx+Bcosx mencapai ekstrem adalah y ’=0. y=Asinx+Bcosx

y ’=0

… … – … …=0

……=… …

 sinx

cosx= … …

… …=… …

Kemungkinan 1

tanx=−A −B

Hipotenusa =

_√

(…)2+(…)2=

√

…2+…2

Sin x = …

√

…2+…2

Cos x = …

√

…2

+…2

Nilai ekstrem fungsi y=Asinx+Bcosx

y=…

(

…

√

…2+…2

)

+…( …

√

…2+…2

)=−(…

2

+…2)

√

…2+…2

=−

√

…2+…2

Kemungkinan 2

tanx=A B

Hipotenusa =

_√

…2+…2

sinx = …

√

…2

+…2

cosx= …

√

…2

+…2

(16)

y=…

(

…

√

…2+…2

)

+…(

…

√

…2+…2)=

…2

+…2

√

…2+…2=

√

…

2

+…2

KESIMPULAN

AYO BERLATIH

1. Tentukan nilai maksimum dan minimum dari f(x)=sinx –cosx !

2. Tentukan nilai maksimum dari f(x)=4 cos2x+14 sin2x+24sinxcosx+10!

Turunan kedua f ' '(x) dapat digunakan untuk menentukan jenis dari titik stasioner,

apakah merupakan untuk merupakan titik minimum, titik maksimum, ataukah titik belok. Suatu kurva memiliki titik stasioner minimum pada selang I jika dalam selang I kurva cekung ke atas. Sedangkan suatu kurva memiliki titik stasioner minimum pada selang I jika dalam selang I kurva cekung ke bawah.

f '(x) naik berarti f''(x)>0 dan f '(x) turun berarti f''(x)<0. Oleh karena itu, bisa disimpulkan :

a. Bila f''(x)>0, x∈I , maka f(x) cekung ke atas pada I.

b. Bila f''₍_x

)<0, x∈I , maka f(x) cekung ke bawah pada I.

1. Jika sinx=sina maka,

x=… . Atau x=… .

Nilai Ekstrem y = A sin x + B cos x

untuk kurva y = A sin x + B cos x, dengan A dan B adalah konstanta, maka. Nilai minimum :

Nilai maksimum :

Grafik fungsi dikatakan cekung ke atas pada selang bila naik pada selang . Sedangkan, dikatakan cekung ke bawah pada selang bila turun pada selang .

(17)

2. Jika cosx=cosa maka

x=… . Atau x=… .

3. Jika tanx=tana maka x=… .

4. Titik stasioner terjadi apabila dipenuhi f'₍_x

)=… .

… +n∙ …(*memenuhi/tidak memenuhi)

n=0⟹x=…

… (*memenuhi/ tidak memenuhi)

n=2⟹x=…

…+… ∙ …= …

… (*memenuhi/tidak memenuhi)

Jadi ada dua absis yang memenuhi titik stasioner yaitu … . Untuk x=…⟹f(…)=sin…+cos…=…+…=…

Untuk x=…⟹f(…)=sin…+cos…=…+…=…

Jadi, ada dua titik stasioner yaitu (… , …) dan (…, …)

(18)

Diberikan (x)=20x−10 sin 4x ,0≤ x ≤ π. Tentukan selang kecekungan kurva.

Penyelesaian

(1) Tentukan dahulu turunan kedua fungsi. f(x)=20x−10 sin 4x

f'₍_x

)=…−…

f''(x)=…+…⟺f''(x)=…

(2) Tentukan absis titik-titik yang diperoleh dari syarat kecekungan kurva. Syarat cekungan ke atas f''(x)>…

…>…

⟺…>0

Titik-titik krtis yang diperoleh untuk: …=0

x=…(*memenuhi/tidak memenuhi)  Untuk n=2

x=…(*memenuhi/tidak memenuhi)

Jadi ada 5 nilai absis titik kritis, yaitu: ……….. (3) Kelima x ini membagi selang [0, π] menjadi 4 daerah, daerah I: 0<x<… ; daerah

II; …<x<… ; daerah III: …<x<… ; daerah IV: …<x<π, seperti ditunjukkan

pada Gambar 4.4. Kita akana menentukan tanda f ' '(x) untuk setiap daerah.

Untuk itu, kita perlu memilih salah satu nilai absis x dalam setiap daerah sebagai wakil untuk penentuan tanda f ' '(x). Kita memilih x=… , x=… , x=… , x=…

berturut-turut dalam daerah I,II, III, dan IV

Mari kita menentukan tanda (positif atau negatif) dari f''₍_x

)=160 sin 4x pada setiap daerah dengan meyubstitusi absis x sebagai wakil daerah.

Daerah I (0<x<…) dengan wakilx=…

f''(…)=160 sin…=160 sin… (¿⨁/⊝)

Daerah II (…<x<…) dengan wakil x=…

Ayo Menalar

Gambar 4.4 Menentukan tanda kecekungan grafik dengan menggunakan tanda turunan

(19)

f''₍_…

)=160 sin…=… (¿⨁/⊝)

Daerah III (…<x<…) dengan wakil x=…

f''(…)=160 sin…=160 sin…

¿160 sin…=…>0 (¿⨁/⊝)

Daerah IV (…<x<π) dengan wakil x=…

f''(…)=160 sin…=160 sin…

¿160 sin(2π+…)=…(¿⨁/⊝)

Tanda-tanda f ' '(x) untuk setiap daerah yang telah diuji di atas ditunjukkan pada

Gambar 4.5

(4) Dengan menggunakan Gambar 4.5 sekarang kita bisa menentukan selang kecekungan kurva.

 Kurva cekung ke atas untuk f''₍_x

)>0, x∈I, yaitu pada daerah …: …<x<… dan

daerah …: …<x<…

 Kurva cekung ke bawah untuk f''(x)<0, x∈I, yaitu pada daerah II : …<x<… dan

daerah IV : …<x<…

AYO BERLATIH

1. Diberikan f(x)=2sinx dalam selang [0,2π].

a. Tentukan selang kecekungan kurva fungsi tersebut.

Ayo Menyimpulkan

Langkah-langkah menentukan selang kecekungan kurva fungsi trigonometri ……….. ……….. ……….. ………..

Gambar 4.5 Tanda-tanda dalam setiap daerah untuk menentukan kecekungan grafik

X X X X

I II II

I

(20)

2. Diberikan f(x)=2sinx dalam selang [0, π].

a. Tentukan persamaan garis singgung kurva pada

titik dimana x=π.

3. Penutup

Setelah kalian belajar bertahap dan berlanjut melalui kegiatan belajar 1, 2, 3 dan 4 berikut untuk mengukur diri kalian terhadap materi yang sudah kalian pelajari. Jawablah sejujurnya terkait dengan penguasaan materi pada UKBM ini di Tabel berikut.

Tabel Refleksi Diri Pemahaman Materi

No Pertanyaan Ya Tidak

1. Apakah Anda dapat menyelesaikan masalah yang berkaitan dengan gradient garis singgung dan persamaan garis singgung suatu kurva fungsi trigonometri?

2. Apakah Anda dapat menyelesaikan masalah yang berkaitan dengan nilai maksimum dan nilai minimum fungsi trigonometri?

3. Apakah Anda dapat menyelesaikan masalah yang selang kemonotonan dan kecekungan kurva sebuah fungsi trigonometri?

Jika menjawab “TIDAK” pada salah satu pertanyaan di atas, maka pelajarilah kembali materi tersebut dalam Buku Teks Pelajaran (BTP) dan pelajari ulang UKBM ini dengan bimbingan Guru atau teman sejawat. Jangan putus asa untuk mengulang lagi!. Dan apabila kalian menjawab “YA” pada semua pertanyaan, maka kalian boleh sendiri atau mengajak teman lain yang sudah siap untuk mengikuti tes formatif agar kalian dapat belajar ke UKBM berikutnya... Oke.?