PENINGKATAN KEMAMPUAN ABSTRAKSI DAN GENERALISASI MATEMATIS SISWA SEKOLAH MENENGAH PERTAMA
MELALUI PEMBELAJARAN DENGAN PENDEKATAN
METAPHORICAL THINKING
Diajukan untuk Memenuhi Sebagian dari Syarat untuk Memperoleh Gelar Magister Pendidikan
Program Studi Pendidikan Matematika
Mukhtar
1103434
PROGRAM STUDI PENDIDIKAN MATEMATIKA SEKOLAH PASCA SARJANA
UNIVERSITAS PENDIDIKAN INDONESIA BANDUNG
PENINGKATAN KEMAMPUAN ABSTRAKSI DAN GENERALISASI MATEMATIS SISWA SEKOLAH MENENGAH PERTAMA
MELALUI PEMBELAJARAN DENGAN PENDEKATAN
METAPHORICAL THINKING
Oleh Mukhtar S.Si IPB Bogor, 2010
Sebuah Tesis yang diajukan untuk memenuhi salah satu syarat memperoleh gelar Magister Pendidikan (M.Pd.) pada Fakultas Pasca Sarjana
© Mukhtar 2013
Universitas Pendidikan Indonesia Juli 2013
Hak Cipta dilindungi undang-undang.
Skripsi ini tidak boleh diperbanyak seluruhya atau sebagian, dengan dicetak ulang, difoto kopi, atau cara lainnya tanpa ijin dari penulis.
LEMBAR PENGESAHAN
PENINGKATAN KEMAMPUAN ABSTRAKSI DAN GENERALISASI MATEMATIS SISWA SEKOLAH MENENGAH PERTAMA MELALUI PEMBELAJARAN
ABSTRAK
Penelitian ini didasarkan pada permasalahan rendahnya kemampuan abstraksi dan generalisasi matematis. Kemudian sangat sedikit pembahasan yang membahas abstraksi dan generalisasi matematis. Pada penelitian ini akan diungkap perbedaan peningkatan kemampuan abstraksi dan generalisasi matematis antara siswa yang memperoleh pembelajaran matematika dengan pendekatan metaphorical thinking dan pembelajaran konvensional. Jenis penelitian ini adalah kuasi eksperimen. Sampel dalam penelitian ini adalah siswa kelas IX yang berasal dari dua kelas pada salah satu SMP di Kota Serang. Instrument penelitian ini terdiri atas seperangkat tes kemampuan abstraksi dan generalisasi matematis, LKS, Modul Pembelajaran, serta angket Skala Sikap. Desain penelitian yang digunakan adalah Nonequivalent Control Group Design. Kedua kelas diberikan pretes dan postes mengenai kemampuan abstraksi dan generalisasi matematis. Kelas eksperimen diberikan angket berupa skala sikap. Hipotesis penelitian diuji melalui uji parametric (Uji-t dan Uji Anova Dua Jalur) dan uji non-parametrik (Uji Mann-Whitney). Hasil penelitian menunjukkan bahwa peningkatan kemampuan abstraksi dan generalisasi siswa yang memperoleh pembelajaran matematika dengan pendekatan metaphorical thinking lebih baik daripada siswa yang memperoleh pembelajaran matematika dengan pendekatan konvensional. Factor pendekatan pembelajaran dan kategori kemampuan awal matematis terhadap peningkatan kemampuan abstraksi dan generalisasi matematis tidak terdapat interaksi. Selain itu, hasil penelitian ini diketahui bahwa siswa memiliki sikap positif terhadap matematika, pembelajaran dengan pendekatan
metaphorical thinking, serta kemampuan abstraksi dan generalisasi matematis.
DAFTAR ISI
LEMBAR JUDUL ... i
LEMBAR PENGESAHAN ... ii
LEMBAR PERNYATAAN ... iii
ABSTRAK ... iv
KATA PENGANTAR ... v
UCAPAN TERIMAKASIH ... vi
DAFTAR ISI ... viii
DAFTAR TABEL ... ix
DAFTAR GAMBAR ... xiii
DAFTAR LAMPIRAN ... xvi
BAB I PENDAHULUAN ... 1
A. Latar Belakang Masalah... 1
B. Rumusan Masalah ... 9
C. Tujuan Penelitian ... 10
D. Manfaat Penelitian ... 11
E. Variabel Penelitian ... 12
BAB II LANDASAN TEORITIS ... 15
A. Abstraksi ... 15
B. Generalisasi ... 19
C. Metaphorical Thinking ... 23
D. Penelitian Relevan ... 27
E. Hipotesis Penelitian ... 30
BAB III METODE PENELITIAN ... 31
A. Desain Penelitian ... 31
B. Populasi dan Sampel Penelitian ... 32
C. Instrumen Penelitian ... 33
D. Teknik Pengumpulan Data ... 45
E. Teknik Analisis Data ... 45
F. Tahap Penelitian ... 49
BAB IV HASIL PENELITIAN DAN PEMBAHASAN ... 50
A. Hasil Penelitian ... 50
B. Pembahasan Hasil Penelitian ... 99
BAB V KESIMPULAN DAN SARAN ... 107
A. Kesimpulan ... 107
B. Implikasi ... 109
C. Rekomendasi ... 110
BAB I
PENDAHULUAN
A. Latar Belakang Masalah
Mengutip dari Abraham S Lunchin dan N Lunchin (1973) yang menyatakan: “Apakah matematika itu?” yang dapat dijawab secara berbeda-beda tergantung bilamana pertanyaan itu dijawab, di mana dijawab, siapa yang menjawab, dan apa sajakah yang dipandang termasuk dalam matematika.”
Menjawab pertanyaan “Apakah matematika itu?” tidaklah dapat dengan mudah untuk dijawab dengan satu atau dua kalimat begitu saja, oleh karena itu kita harus berhati-hati. Berbagai pendapat muncul tentang pengertian matematika tersebut, dipandang dari pengetahuan dan pengalaman masing-masing yang berbeda, antara lain mengatakan bahwa matematika itu bahasa simbol; matematika bahasa numerik; matematika adalah bahasa yang menghilangkan sifat kabur, majemuk, dan emosional; matematika adalah metode berpikir logis; matematika adalah sarana berpikir; matematika adalah logika pada masa dewasa; matematika adalah ratunya ilmu dan sekaligus pelayannya; matematika adalah sains mengenai kuantitas dan besaran; matematika adalah suatu sains yang bekerja menarik kesimpulan-kesimpulan yang perlu; matematika adalah sains formal yang murni; matematika adalah sains yang memanipulasi simbol; matematika adalah ilmu tentang bilangan dan ruang; matematika adalah ilmu yang mempelajari hubungan pola, bentuk, dan struktur; matematika adalah ilmu yang abstrak dan deduktif; matematika adalah aktivitas manusia (Suherman, 2004).
menentukan prinsip-prinsip keteraturan dari suatu sistem, mendefinisikan secara aksiomatik, teoritik, atau mengabstraksi dunia nyata ke dalam model sebuah sistem. Alat-alat matematika adalah abtraksi, representasi simbolik, dan manipulasi secara simbolik.
Dari definisi di atas yang disampaikan oleh para ahli matematika mengenai definisi matematika, abstraksi dan generalisasi merupakan hal yang penting untuk dikaji secara lebih lanjut.
KTSP (2006:2) juga menyatakan bahwa melatih kemampuan abstraksi dan generalisasi merupakan bagian dari lima tujuan umum mempelajari matematika, yaitu:
1) Memahami konsep matematika, menjelaskan keterkaitan antar konsep dan mengaplikasikan konsep atau logaritma, secara luwes, akurat, efisien, dan tepat dalam pemecahan masalah;
2) Menggunakan penalaran pada pola dan sifat, melakukan manipulasi matematika dalam membuat „generalisasi‟ menyusun bukti, atau menjelaskan gagasan dan pernyataan matematika;
3) Memecahkan masalah yang meliputi kemampuan memahami masalah, merancang model matematika, menyelesaikan model dan menafsirkan solusi yang diperoleh; 4) Mengkomunikasikan gagasan dengan simbol, tabel, diagram, atau media lain
untuk memperjelas keadaan atau masalah;
Istilah abstraksi dan generalisasi harus mendapatkan perhatian yang berarti oleh para matematikawan dan pendidik matematika, dan abstraksi dan generalisasi masing-masing dapat disebut sebagai proses dan hasil dari proses tersebut (Harel & Tall, 1989). Carolyn dan Jonathan (2010) menyatakan bahwa seorang siswa yang mahir dalam matematika harus mempunyai kemampuan abstraksi dan generalisasi.
Abstraksi pada matematika telah berkembang sangat pesat pada pertengahan abad XX. Seiring dengan perkembangan abstraksi pada matematika adalah generalisasi matematika [Kappel, 2001:3]. Dengan abstraksi dan generalisasi, formalisme matematika menjadi semacam kebutuhan (keharusan) dalam setiap perkembangan
matematika(Murtiyasa, 2012).
Berdasarkan pengertian matematika yang disampaikan oleh para ahli matematika, dapat disimpulkan bahwa abstraksi yang terdapat dalam materi pelajaran matematika dapat dikembangkan dari situasi serta mengenali ide-ide matematika yang ada pada
situasi tersebut. Termasuk dalam kemampuan abstraksi ini adalah kemampuan untuk
membawa persoalan-persoalan yang ada ke dalam model-model matematika.
Kemampuan generalisasi yang dipahami secara umum dapat diartikan sebagai penarikan kesimpulan umum atas sejumlah contoh atau data khusus yang diberikan.
Selama beberapa tahun terakhir para peneliti telah mengembangkan teori untuk menganalisis proses-proses abstraksi. Para penulis menganggap abstraksi sebagai aktivitas budaya yang mengarah kepada pembentukan makna baru ketika mengorganisasikan dan merestrukturisasi kembali pengetahuan matematika ke dalam struktur baru. Proses abstraksi terjadi karena kebutuhan atau motif (Hershkowitz, Schwarz, dan Dreyfus 2001).
Hal yang sama juga diutarakan oleh Monaghan dan Ozmantar (2004) yang menyatakan bahwa abstraksi adalah isu-isu penting dalam matematika pendidikan. Kemudian Diena (1963), Piaget (1970) dan Skemp (1986) menyatakan bahwa masalah abstraksi telah menarik perhatian banyak pendidik. Masih banyak lagi pernyataan dari para matematikawan dan pendidik matematika yang menyatakan bahwa inti dari matematika adalah abstraksi. Pengertian generalisasi digunakan baik di dalam matematika maupun di luar matematika, artinya pengertian generalisasi dipakai dalam konteks yang lebih luas (Harel, & Tall, 1989). Kajian terhadap generalisasi pada kurikulum matematika di sekolah-sekolah telah menjadikan perhatian dari peneliti yang dilakukan selama bertahun-tahun. Mereka telah membuat beberapa upaya untuk menyelidiki tahap atau tingkat dalam pengembangan yang difokuskan pada kemampuan siswa untuk menggeneralisasi (Juan Antonio García-Cruz & Antonio Martinón, 1998). Menurut (Zazkis, Liljedahl, dan Chernoff, 2008) menyatakan bahwa pembelajaran mengenai generalisasi sudah dianggap penting sejak masa lalu. Hal yang sama disampaikan oleh Davidov (1972/1990 : 10) menyatakan bahwa generalisasi dapat mengembangkan kemampuan anak dan itu harus dianggap sebagai salah satu satu tujuan utama dari pembelajaran sekolah''. Selanjutnya, Mason ( 1996 : 65 ) menyatakan bahwa generalisasi adalah detak jantung atau napas dari matematika. Jika guru tidak menyadari pentingnya dari generalisasi, dan tidak membiasakan siswa untuk belajar dan berlatih terhadap generalisasi, proses berpikir matematika tidak akan pernah terjadi''. Kalaupun generalisasi itu penting dan merupakan pusat dalam melakukan matematika (doing math), bahwa generalisasi matematika kenyataan merupakan tugas yang menantang (sulit) bagi banyak pelajar (Bills, Ainley & Wilson, 2006 ; Lee, 1996 , Stacey, 1989 ; Stacey & Mc Gregor, 2001 ; Becker & Rivera, 2005 ).
aktivitas matematika maka para ahli membagi ke dalam berbagai jenis generalisasi (Zazkis & Liljedahl, 2002) yang akan dikaji pada sub bab selanjutnya.
Generalisasi menurut Shurter dan Pierce dalam (Sumarmo, 1987) adalah proses penalaran berdasarkan pemeriksaan hal secukupnya, kemudian memperoleh kesimpulan untuk semuanya atau sebagian besar hal-hal tadi. Hal itu sejalan dengan pendapat Mundiri (2010) yang menyatakan bahwa generalisasi sebagai proses penalaran yang bertolak dari sejumlah fenomena individu menuju kesimpulan umum yang mengikat seluruh fenomena sejenis dengan fenomena individual yang diselidiki. Dengan begitu hukum yang disimpulkan dari fenomena yang diselidiki berlaku bagi fenomena sejenis yang belum diselidiki (Yuni, 2010).
Pernyataan yang sama disampaikan oleh Hudoyo (1988: 76) menyatakan bahwa, berpikir matematika merupakan kegiatan mental, yang dalam prosesnya menggunakan generalisasi. Lebih jauh Hudoyo (2001: 82) menjelaskan bahwa proses generalisasi juga merupakan aspek atau bagian esensial dari berpikir matematika. Berkaitan dengan pentingnya generalisasi dalam matematika, NCTM (2000: 262) merekomendasikan bahwa tujuan pembelajaran penalaran pada kelas 6 sampai kelas 8 adalah agar siswa: 1) Menguji pola dan struktur untuk mendeteksi keteraturan; 2) Merumuskan generalisasi dan konjektur; dan 3) Membuat dan mengevaluasi argumen matematika (Dahiana, 2010).
Studi TIMSS yang diselenggarakan oleh International Association for the Evaluation of Educational Achievement (IEA), merupakan sebuah asosiasi internasional untuk menilai prestasi dalam pendidikan, diketahui bahwa data hasil survei TIMSS tahun 2007, peringkat belajar matematika siswa kelas VIII Indonesia pada urutan ke-36 dari 49 negara yang turut berpartisipasi. Nilai rerata siswa Indonesia berada di bawah rerata internasional. Indonesia hanya memperoleh nilai rerata 397, sedangkan nilai rerata skala internasional adalah 500 (Balitbang, 2011). Selama keikutsertaan Indonesia dalam TIMSS, peringkat belajar matematika siswa Indonesia tidak ada perubahan yang berarti dan selalu menduduki urutan 10 besar terbawah di antara negara-negara peserta lainnya (Rahman, 2012).
Laporan analisis studi PISA tidak jauh berbeda dengan hasil TIMSS. PISA yang diselenggarakan oleh Organisation for Economic Cooperation and Development
(OECD), pada tahun 2009 menyimpulkan bahwa literasi matematis siswa di Indonesia pada peringkat ke-61 dari 65 negara yang turut berpartisipasi. Skor rerata literasi matematis internasional adalah 500, sedangkan Indonesia hanya memperoleh skor rerata 371 (Balitbang, 2011). Bila dibandingkan dengan hasil laporan PISA selama keikutsertaan Indonesia, skor rerata yang diperoleh siswa Indonesia pada tahun 2009 merupakan skor yang paling rendah (Rahman, 2012).
Laporan TIMSS dan PISA di atas merupakan salah satu indikator yang menunjukkan bahwa hasil pembelajaran kemampuan abstraksi dan generalisasi matematis siswa Indonesia masih rendah. Menurut Anggraini (2010) rendahnya hasil pembelajaran matematika di Indonesia disebabkan oleh beberapa faktor. Salah satu faktor penyebabnya, berkaitan dengan pembelajaran yang diselenggarakan guru di sekolah. Menurut Widdiharto (2004) dan Tahmir (2007) dalam Anggraini (2010) menyatakan bahwa pembelajaran di Sekolah Menengah Pertama (SMP) cenderung
Banyak alternatif yang bisa dilakukan agar penyajian materi pelajaran dapat lebih menarik. Salah satu alternatif tersebut adalah dengan menggunakan metafora. Dengan metafora siswa dapat lebih memahami dan memaknai matematika tidak sekadar menghapal rumus. Metafora yang diberikan dapat berupa cerita-cerita sukses, perumpamaan-perumpamaan atau stimulasi. Setelah pembelajaran siswa diharapkan memiliki wawasan yang lebih baik tentang kehidupan nyata yang akan dilaluinya kelak, sehingga motivasi mereka untuk lebih sungguh-sungguh dalam memahami pelajaran matematika dapat ditingkatkan (Neni, 2010).
Menurut (Mish, 1991) dalam (Groth & Bergner, 2005) metafora dapat didefinisikan sebagai, "Sebuah kiasan terhadap kata atau frase yang menunjukkan satu jenis obyek atau ide yang digunakan di tempat lain untuk menunjukkan rupa atau analogi antara keduanya.
Menurut Andrade (2004) bahwa selama dekade terakhir kegiatan penelitian terhadap metafora telah dilakukan secara progresif, terlihat dari Araya, 2000; Bills, 2003; Edward, 2005; English, 1997; Ferrara, 2003; Johnson & Lakoff, 2003; Lakoff & Núñez, 2000; Parzysz et al, 2003;. Pouilloux, 2004; Presmeg, 1997; Seitz, 2001;Sfard, 1994, 1997, dan banyak lainnya.
Pernyataan di atas juga sejalan dengan apa yang diungkapkan oleh Lakoff dan Johnson (1980) bahwa sejak awal tahun delapan puluhan penelitian terhadap metafora telah dipertimbangkan kembali sebagai pentingnya komponen berpikir.
pernyataan Presmeg (1992) dapat mempengaruhi perilaku pemecahan masalah menuju ke arah yang lebih baik.
Dalam beberapa tahun terakhir, beberapa penulis (Font & Acevedo 2003; Johnson,1987; Lakoff & Núñez, 2000; Leino & Drakenberg, 1993; Núñez, 2000, Presmeg, 1992, 1997; Sfard, 1994, 1997) telah menunjukkan bahwa metafora mempunyai peranan penting dalam pembelajaran dan pengajaran matematika. Menurut Lakoff dan Núñez (2000), metafora menghasilkan konsep yang berhubungan antara sumber domain dan domain target dengan memetakan dan menarik kesimpulan dari sumber ke target domain. Karena metafora menyatukan berbagai indra, indera tersebut sangat penting bagi manusia dalam membangun pengertian untuk entitas matematika"... sebagian besar yang paling dasar, serta yang paling canggih pada ide matematika adalah metafora di alam "(Lakoff dan Núñez, hal 364).
Meskipun konsep metafora dapat secara langsung disampaikan, tetapi pada ruang kelas guru yang menggunakan metafora, sengaja atau tidak, harus berusaha menjelaskan terlebih dahulu mengenai subjek matematika kepada siswa supaya menjadi lebih jelas dengan bertujuan untuk memberikan pemahaman terhadap siswa (Frant, Acevedo, dan Font, 2004).
Carreira (dalam Hendriana, 2010) memberikan gambaran bahwa menemukan hubungan antara matematika dan fenomena nyata adalah sebuah proses dan usaha memainkan model yang penting. Model matematika merupakan rangkuman sejumlah konsep matematika dan rangkuman sejumlah interpretasi yang memerlukan interpretasi kuat. Diperlukan proses integratif antara model dan aplikasi matematika dalam pembelajaran di kelas dan seluruh aktivitas diharapkan mempunyai pengaruh positif pada belajar matematika sehingga belajar matematika menjadi bermakna.
Carreira (dalam Hendriana, 2010) konsep berpikir yang menekankan pada kemampuan menghubungkan ide matematika dan fenomena yang ada adalah
dan sejumlah asumsi yang dinyatakan dalam model. Setiap deskripsi dari matematika membawa sebuah perubahan dan sejumlah asumsi yang dinyatakan dalam model. Model ini akan berceritera banyak jika didukung oleh kemampuan interpretasi pembacanya.
Berdasarkan latar belakang di atas, penulis terdorong untuk melaksanakan penelitian dalam upaya untuk meningkatkan kemampuan abstraksi dan generalisasi matematis siswa SMP melalui pembelajaran dengan pendekatan metaphorical thinking.
B. Rumusan Masalah
Berdasarkan latar belakang masalah yang telah diuraikan, maka permasalahannya:
1. Apakah peningkatan kemampuan abstraksi matematis siswa yang mengikuti pembelajaran dengan pendekatan metaphorical thinking berbeda dengan kemampuan abstraksi matematis siswa dengan pembelajaran konvensional? 2. Apakah peningkatan kemampuan abstraksi matematis siswa yang mengikuti
pembelajaran dengan pendekatan metaphorical thinking lebih baik daripada siswa yang memperoleh pembelajaran konvensional ditinjau dari kategori KAM siswa (tinggi, sedang, dan rendah)?
3. Apakah peningkatan kemampuan abstraksi matematis siswa berbeda antar kategori KAM dengan pendekatan pembelajaran metaphorical thinking?
4. Apakah peningkatan kemampuan abstraksi matematis siswa berbeda antar kategori KAM dengan pendekatan pembelajaran konvensional?
5. Apakah terdapat interaksi antara faktor pendektakan pembelajaran dan kategori KAM terhadap kemampuan abstraksi matematis siswa?
yang memperoleh pembelajaran secara konvensional ditinjau dari keseluruhan siswa?
7. Apakah peningkatan kemampuan generalisasi matematis siswa yang mengikuti pembelajaran dengan pendekatan metaphorical thinking lebih baik daripada siswa yang memperoleh pembelajaran geometri secara konvensional ditinjau dari kategori KAM siswa (tinggi, sedang, dan rendah)?
8. Apakah peningkatan kemampuan generalisasi matematis siswa berbeda antar kategori KAM dengan pendekatan pembelajaran metaphorical thinking?
9. Apakah peningkatan kemampuan generalisasi matematis siswa berbeda antar kategori KAM dengan pendekatan pembelajaran konvensional?
10.Apakah terdapat interaksi antara faktor pendekatan pembelajaran dan KAM terhadap kemampuan generalisasi matematis siswa?
11.Bagaimana tanggapan siswa terhadap pelajaran matematika, terhadap pembealajaran matematika dengan pendekatan metaphorical thinking, terhadap abstraksi, dan generalisasi matematis?
C. Tujuan Penelitian
Pada dasarnya, tujuan penelitian ini adalah untuk mendapatkan jawaban dari rumusan masalah di atas. Secara rinci, tujuan penelitiannya adalah sebagai berikut: 1. Mengetahui apakah peningkatan kemampuan abstraksi matematis siswa yang
mengikuti pembelajaran dengan pendekatan metaphorical thinking berbeda dengan kemampuan abstraksi matematis siswa dengan pembelajaran konvensional
3. Mengetahui apakah peningkatan kemampuan abstraksi matematis siswa berbeda antar kategori KAM dengan pendekatan pembelajaran metaphorical thinking. 4. Mengetahui apakah peningkatan kemampuan abstraksi matematis siswa berbeda
antar kategori KAM dengan pendekatan pembelajaran konvensional.
5. Mengetahui apakah terdapat interaksi antara faktor pendektakan pembelajaran dan kategori KAM terhadap kemampuan abstraksi matematis siswa.
6. Mengetahui apakah peningkatan kemampuan generalisasi matematis siswa yang mengikuti pembelajaran dengan pendekatan metaphorical thinking berbeda daripada siswa yang memperoleh pembelajaran secara konvensional ditinjau dari keseluruhan siswa.
7. Mengetahui apakah peningkatan kemampuan generalisasi matematis siswa yang mengikuti pembelajaran dengan pendekatan metaphorical thinking lebih baik daripada siswa yang memperoleh pembelajaran geometri secara konvensional ditinjau dari kategori KAM siswa (tinggi, sedang, dan rendah).
8. Mengetahui apakah peningkatan kemampuan generalisasi matematis siswa berbeda antar kategori KAM dengan pendekatan pembelajaran metaphorical thinking.
9. Mengetahui apakah peningkatan kemampuan generalisasi matematis siswa berbeda antar kategori KAM dengan pendekatan pembelajaran konvensional. 10.Mengetahui apakah terdapat interaksi antara faktor pendekatan pembelajaran dan
KAM terhadap kemampuan generalisasi matematis siswa.
11.Menelaah tanggapan siswa terhadap pelajaran matematika, terhadap pembealajaran matematika dengan pendekatan metaphorical thinking, terhadap abstraksi, dan generalisasi matematis.
D. Manfaat Penelitian
matematis siswa, kemudian lebih memahami model pendekatan pembelajaran
metaphorical thinking. Adapun manfaat dari penelitian ini dapat dirinci sebagai berikut:
1. Manfaat Teoritis
Hasil penelitian ini diharapkan dapat menambah khasanah ilmu, khususnya dalam bidang pendidikan mengenai kemampuan abstraksi dan generalisasi matematis, dan model pembelajaran metaphorical thinking pada siswa.
2. Manfaat Praktis
Adapun manfaat praktis dari penelitian ini adalah:
1. Pihak sekolah dapat mengetahui kemampuan abstraksi dan generalisasi matematis pada siswa. Hal ini berguna dalam memberikan pembinaan pada siswa dalam mengembangkan kemampuan abstraksi dan generalisasi matematis siswa lebih baik.
2. Penelitian ini berguna sebagai input bagi siswa tentang kemampuan abstraksi dan generalisasi matematis, sehingga diharapkan dapat dimanfaatkan dalam pengembangan diri siswa terutama dalam meningkatkan kemampuan abstraksi dan generalisasi matematis siswa lebih baik.
E. Variabel Penelitian
F. Definisi Operasional
Agar tidak terjadi perbedaan pendapat mengenai hal-hal yang dimaksudkan dalam penelitian ini, diperlukan definisi operasional sebagai berikut:
1. Kemampuan abstraksi matematika adalah suatu proses pembentukan konsep berupa objek-objek matematika yang bersifat abstrak melalui serangkaian aktivitas pengorganisasian ulang pengetahuan-pengetahuan matematis yang sudah dikonstruksi sebelumnya menjadi suatu struktur yang baru, aktivitas-aktivitas ini adalah:
a. Mengidentifikasi karakteristik objek melalui pengalaman langsung.
b. Mengidentifikasi karakteristik objek yang dimanipulasi atau diimajinasikan c. Merepresentasikan gagasan matematika dalam bahasa dan simbol-simbol
matematika
d. Melepaskan sifat-sifat kebendaan dari sebuah objek atau dekontekstualisasi dengan kata lain idealisasi
e. Membuat hubungan antarproses atau konsep untuk membentuk suatu pengertian baru
f. Mengaplikasikan konsep pada konteks yang sesuai g. Melakukan manipulasi objek matematis yang abstrak
2. Kemampuan generalisasi matematika yaitu kemampuan proses penarikan kesimpulan dengan memeriksa keadaan khusus menuju kesimpulan umum. Penalaran tersebut mencakup pengamatan contoh-contoh khusus dan menemukan sebuah pola. Adapun indikator kemampuan generalisasi dalam penelitian ini adalah:
a. Perception of generality, atau dapat mengenal sebuah pola;
b. Expresion of generality, atau mampu menguraikan sebuah aturan/pola, baik secara numerik maupun verbal;
d. Manipulation of generality, atau mampu menerapkan aturan/pola dari berbagai persoalan.
3. Pendekatan Metaphorical thinking adalah pendekatan pembelajaran untuk memahami, menjelaskan dan mengkomunikasikan konsep-konsep abstrak menjadi hal yang lebih konkrit dengan membandingkan dua hal atau lebih yang berbeda makna baik yang berhubungan maupun tidak berhubungan
4. Pendapat (respon) siswa adalah tanggapan siswa yang menunjukkan kecenderungan siswa untuk merespon positif atau negatif tentang pelajaran matematika.
BAB III
METODE PENELITIAN
A. Desain Penelitian
Penelitian ini merupakan penelitian kuasi eksperimen dengan desain kelompok kontrol non-ekivalen. Ruseffendi (2010) mengungkapkan bahwa desain kelompok kontrol non-ekivalen tidak berbeda dengan desain penelitian kelompok kontrol pretes-postes, kecuali dalam pengelompokkan subjek. Pada desain kelompok kontrol non-ekivalen, subjek tidak dikelompokkan secara acak. Alasan pemilihan desain ini dikarenakan di lapangan sering tidak memungkinkan untuk mengelompokkan subjek secara acak. Diagram desain penelitian ini adalah sebagai berikut:
Kelas Eksperimen : O X O
Kelas Kontrol : O O
dimana : X : Pendekatan pembelajaran metaphorical thinking
O : Pemberian Pretes dan Postes
: Subjek tidak dikelompokan secara acak
Penelitian ini bertujuan untuk menelaah dan menyelidiki pengaruh pembelajaran matematika dengan pendekatan metaphorical thinking dalam peningkatan kemampuan abstraksi dan generalisasi matematis siswa. Pengaruh pembelajaran tersebut dilihat dengan cara membandingkan kemampuan abstraki dan generalisasi matematis siswa pada kelas eksperimen dan kelas konvensional. Pembelajaran matematika di kelas eksperimen menggunakan pendekatan metaphorical thinking, sedangkan pembelajaran yang lainnya yaitu secara konvensional.
kemampuan awal matematis diperoleh dari data hasil raport siswa. Data tersebut diranking dan dikelompokkan berdasarkan kategori KAM (tinggi, sedang, dan rendah) dengan menggunakan kriteria 25% masing-masing untuk kategori kemampuan awal tinggi dan rendah (Sudjana, 2010). Adapun keterkaitan antara variabel bebas dan variabel terikat disajikan pada tabel berikut.
Tabel 3.1
Keterkaitan antara Variabel Bebas dan Variabel Terikat
Kemampuan yang Diukur Abstraksi (Abs) Generalisasi (Gen)
Pembelajaran (PK) (PM) (PK) (PM)
PK : Pembelajaran matematika secara konvensional
PM : Pembelajaran matematika dengan pendekatanMethaporical Thinking
B. Populasi dan Sampel Penelitian
Penelitian ini dilaksanakan di SMPN 13 Kota Serang. Populasinya adalah seluruh siswa kelas IX Tahun Ajaran 2012/2013 semester ganjil yang terdiri dari 6 kelas. Pendekatan methaporical thinking dalam penelitian ini khusus untuk materi barisan dan deret, sehingga alasan pemilihan kelas IX sebagai populasi karena materi barisan dan deret merupakan materi pokok pada kelas IX.
dapat dijadikan sampel memiliki karakteristik dan kemampuan akademik yang relatif setara.
C. Instrumen Penelitian
Dalam penelitian ini, instrumen penelitian yang digunakan berupa tes dan non-tes. Instrumen dalam bentuk tes terdiri dari tes kemampuan abstraksi dan generalisasi matematis dalam bentuk jawaban singkat dan uraian, sedangkan instrumen dalam bentuk non-tes yaitu skala sikap siswa. Masing-masing instrumen tersebut selengkapnya diuraikan sebagai berikut.
1. Tes Kemampuan Abstraksi dan Generalisasi Matematis
Tes diberikan kepada siswa untuk mengukur kemampuan abstraksi dan generalisasi matematis siswa sebelum dan sesudah proses pembelajaran pada kelas eksperimen dan kelas konvensional. Materi yang diujikan adalah materi barisan dan bilangan. Instrumen tes kemampuan abstraksi matematis terdiri dari enam soal berbentuk essay dengan jawaban singkat, sedangkan instrumen tes generalisasi matematis terdiri dari empat soal uraian. Indikator masing-masing kemampuan dapat dilihat pada Lampiran B.
Penyusunan tes instrumen di awali dengan pembuatan kisi-kisi soal, kemudian dilanjutkan dengan penyusunan soal, membuat alternatif jawaban dan aturan skor untuk masing-masing butir soal. Sebelum digunakan, instrument diuji cobakan terlebih dahulu untuk memeriksa validitas, reliabilitas, daya pembeda dan tingkat kesukaran soal. Instrumen tes diuji cobakan kepada siswa kelas X SMA N 3 Kota Serang sebanyak 30 orang siswa. Perhitungan hasil uji coba tersebut adalah sebagai berikut.
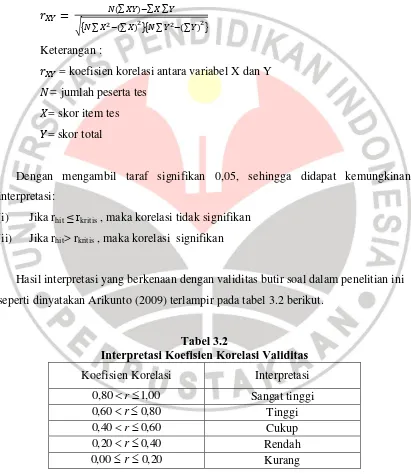
Dalam mengukur validitas tiap butir tes, digunakan koefisien korelasi Pearson r.
Dengan mengambil taraf signifikan 0,05, sehingga didapat kemungkinan interpretasi:
(i) Jika rhit≤ rkritis , maka korelasi tidak signifikan
(ii) Jika rhit> rkritis , maka korelasi signifikan
Hasil interpretasi yang berkenaan dengan validitas butir soal dalam penelitian ini seperti dinyatakan Arikunto (2009) terlampir pada tabel 3.2 berikut.
Data uji coba diolah dengan perhitungan secara statistic. Rangkuman uji validitas tes kemampuan abstraksi matematis disajikan pada tabel berikut.
Tabel 3.3
Uji Validitas Soal Tes Kemampuan Abstraksi Matematis No Koefisien Korelasi Interpretasi
1 0.64 Tinggi
2 0.856 Sangat tinggi
3 0.792 Tinggi
4 0.588 Cukup
5 0.83 Sangat tinggi
6 0.836 Sangat tinggi
Dari Tabel 3.3, tampak bahwa soal-soal tes kemampuan abstraksi matematis sudah valid. Artinya, ketujuh soal tersebut dapat dikatakan layak untuk mengukur kemampuan abstraksi matematis siswa.Soal nomor 1, 2, 3, 5, dan 6 validitasnya termasuk kategori cukup, tinggi, sangat tinggi. Soal nomor 2,5, dan 6 validitasnya termasuk kategori sangat tinggi, selengkapnya ada pada Lampiran B.
Tabel 3.4
Uji Validitas Soal Tes Kemampuan Generalisasi Matematis No Koefisien Korelasi Interpretasi
7 0.83 Sangat Tinggi
8 0.663 Tinggi
9 0.643 Tinggi
10 0.88 Sangat Tinggi
2. Reliabilitas Butir Soal
Penentuan keandalan butir tes berkenaan dengan masalah dari pengaruh error yang tidak sistematik dalam suatu pengukuran. Keandalan suatu tes dinyatakan sebagai derajat atau tingkat suatu tes dan skornya dipengaruhi faktor non-sistematik. Makin sedikit faktor yang non-sistematik, makin tinggi keandalannya (Dewanto, 2004). Untuk mengukur reliabilitas soal menggunakan Cronbach’s Alpha (Suherman, 2003: 154) yaitu:
∑
dengan:
: koefisien reliabilitas soal : banyak butir soal
: variansi item : variansi total
Tingkat reliabilitas dari soal uji coba komunikasi matematis masalah sebagai berikut.
Tabel 3.5
Klasifikasi Tingkat Reliabilitas Besarnya r Tingkat Reliabilitas
r11 < 0,20 Kecil
0,20 ≤ r11 < 0,40 Rendah
0,40 ≤ r11 < 0,70 Sedang
0,70 ≤ r11 < 0,90 Tinggi
0,90 ≤ r11 < 1,00 Sangat tinggi
matematisdapat dilihat pada tabel dibawah ini, sedangkan untuk perhitungan realibilitas dengan program Anates versi 4.0 dapat dilihat pada Lampiran B.
Tabel 3.6
Uji Reliabilitas Soal Tes Kemampuan Abstraksi dan Generalisasi Matematis
Kemampuan Reliabilitas Interpretasi
Abstraksi 0,88 Tinggi
Generalisasi 0,80 Tinggi
Berdasarkan tabel 3.6, tampak bahwa reliabilitas hasil uji coba tes kemampuan abstraksi termasuk kategori sedang, sedangkan untuk tes kemampuan generalisasi termasuk kategori tinggi. Artinya, tingkat ketepatan dan konsistensi soal-soal tes yang digunakan dalam instrumen sudah layak untuk mengukur kemampuan abstraksi dan generalisasi matematis siswa. Hal ini sesuai dengan yang diungkapkan Arikunto (2009) bahwa suatu tes dapat dikatakan mempunyai taraf kepercayaan yang tinggi jika tes tes tersebut dapat memberikan hasil yang tetap.
3. Reliabilitas Butir Soal
Menurut (Suparlan, 2005: 36) dalam (Edi, 2012) tingkat kesukaran digunakan untuk mengklasifikasikan setiap item instrumen tes kedalam tiga kelompok tingkat kesukaran untuk mengetahui apakah sebuah instrumen tergolong mudah, sedang atau sukar. Tingkat kesukaran tes dihitung dengan rumus:
̅ , Keterangan:
Tabel 3.7 kemampuan abstraksi matematis dapat dilihat pada tabel berikut.
Tabel 3.8 merupakan butir soal kemampuan abstraksi kategori sedang, sedangkan satu soal lainnya yaitu no 3 merupakan kategori mudah. Hal ini menunjukkan bahwa soal nomor 3 yang daya pembedanya tidak baik, erat kaitannya dengan kesulitan soal tersebut, selengkapnya ada pada Lampiran B.
Tabel 3.9
9 37.86 Sedang
10 65.00 Sedang
Dapat dilihat di Tabel 3.9 bahwa butir soal kemampuan generalisasi matematis tidak ada yang terlalu mudah maupun terlalu sukar. Sebanyak 3 soal yang termasuk kategori sedang dan 1 soal yang termasuk kategori sukar, selengkapnya ada pada Lampiran B.
4. Daya pembeda
Menurut Suherman (2003: 161) dalam (Edi, 2012) daya pembeda butir soal adalah kemampuan butir soal tersebut untuk membedakan antara siswa yang pandai dengan siswa yang tidak pandai atau antara siswa yang berkemampuan tinggi dengan siswa yang berkemampuan rendah. Daya pembeda tes dihitung dengan rumus:
Keterangan :
DP = Daya pembeda
JBA = Jumlah skor dari kelompok atas (unggul)
JBB = Jumlah skor siswa dari kelompok bawah (asor)
JSA = Jumlah siswa dari kelompok atas
Daya pembeda instrumen tes kemampuan abstraksi dan generalisasi matematis menggunakan interpretasi sebagai berikut.
Tabel 3.10
Koefisien Daya Pembeda
Koefisien Daya
Pembeda Interpretasi
DP ≥0,40 Sangat baik
0,30 ≤DP < 0,40 Baik
DP < 0,20 Tidak baik Sumber: Depdiknas (2006)
Untuk data dalam jumlah yang banyak (kelas besar), maka sebanyak 25% siswa yang memperoleh skor tertinggi dikategorikan kedalam kelompok atas (higher group) dan sebanyak 25% siswa yang memperoleh skor terendah dikategorikan kelompok bawah (lower group).
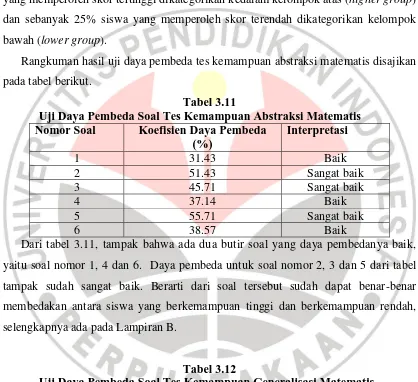
Rangkuman hasil uji daya pembeda tes kemampuan abstraksi matematis disajikan pada tabel berikut.
Tabel 3.11
Uji Daya Pembeda Soal Tes Kemampuan Abstraksi Matematis Nomor Soal Koefisien Daya Pembeda
Soal tes kemampuan generalisasi matematis, dari Tabel 3.12 dapat dilihat bahwa daya pembeda sebagian besar dari soal-soalnya termasuk kategori cukup dan sangat baik yaitu sebanyak 4 soal. Selanjutnya, soal-soal tersebut direvisi atau diperbaiki agar dapat digunakan dalam penelitian. Selengkapnya ada pada Lampiran B.
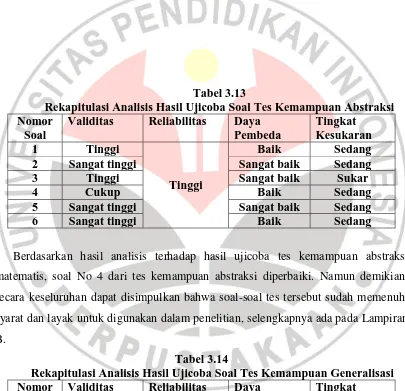
Tabel 3.13
Rekapitulasi Analisis Hasil Ujicoba Soal Tes Kemampuan Abstraksi Nomor
Berdasarkan hasil analisis terhadap hasil ujicoba tes kemampuan abstraksi matematis, soal No 4 dari tes kemampuan abstraksi diperbaiki. Namun demikian, secara keseluruhan dapat disimpulkan bahwa soal-soal tes tersebut sudah memenuhi syarat dan layak untuk digunakan dalam penelitian, selengkapnya ada pada Lampiran B.
Tabel 3.14
Berdasarkan hasil analisis terhadap hasil ujicoba tes kemampuan generalisasi matematis, soal No 7 dari tes kemampuan gneralisasi diperbaiki. Namun demikian, secara keseluruhan dapat disimpulkan bahwa soal-soal tes tersebut sudah memenuhi syarat dan layak untuk digunakan dalam penelitian, selengkapnya ada pada Lampiran B.
5. Skala Sikap
Untuk melihat sikap siswa kelas eksperimen harus dilakukan uji statistik yaitu uji perbedaan rerata. Karena data sikap merupakan data ordinal, maka harus dikonversi terlebih dahulu menjadi data interval. Al-rasyid (1994) menyatakan bahwa mengubah data dari skala ordinal menjadi skala interval dinamakan transfomasi data.
Transformasi data dilakukan dengan salah satu metode yaitu metode Successive Interval. Biasanya jawaban responden diukur dengan menggunakan skala likert (Likert scale) yakni pemberian nilai numerikal dengan skor 1,2,3,4, setiap skor yang diperoleh akan memiliki tingkat pengukuran ordinal. Nilai numerikal tersebut dianggap sebagai objek dan selanjutnya melalui proses transformasi ditempatkan ke dalam interval. Langkah-langkahnya sebagai berikut:
a. Untuk setiap pertanyaan, hitung frekuensi jawaban setiap pilihan jawaban b. Berdasarkan frekuensi setiap pilihan jawaban dihitung proporsinya
c. Dari proporsi yang diperoleh, hitung proporsi kumulatif untuk setiap pilihan jawaban
d. Tentukan nilai batas z untuk setiap pilihan jawaban
Scale
Score = scale value + | | + 1 (Sundayana, 2010)
Setelah kedua data menjadi data interval maka diuji rerata, dengan terlebih dahulu melakukan uji normalitas, homogenitas dan kemudian uji-t.
Setelah instrumen skala sikap matematis dinyatakan layak digunakan,. Kisi-kisi dan instrumen sikap matematis disajikan pada Lampiran A. Tujuan uji coba untuk mengetahui validitas setiap item pernyataan dan sekaligus untuk menghitung bobot setiap pilihan (SS, S, N, TS, STS) dari setiap pernyataan. Dengan demikian, pemberian skor setiap pilihan dari pernyataan skala sikapmatematis siswa ditentukan secara a posteriori yaitu berdasarkan distribusi jawaban responden dengan metode MSI (Methode of Succesive Interval).
Dengan menggunakan metode ini bobot setiap pilihan (SS, S, N, TS, STS) dari setiap pernyataan dapat berbeda-beda tergantung pada sebaran respon siswa. Dari hasil uji coba, proses perhitungan validitas butir pernyataan dan skor masing-masing pilihan skala sikapmatematis secara lengkap terdapat pada Lampiran B.
a. Analisis Validitas Skala Matematis
Perhitungan validitas butir item pernyataan menggunakan software SPSS 20.0 For Windows. Berikut hasil validitas butir item pernyataan skala sikap matematis disajikan pada Tabel 3.15 berikut
Tabel 3.15
Hasil Uji Validitas Butir Item Pernyataan Pernyataan Koefisien Korelasi
(Pearson Correlation)
Signifikansi
Korelasi Kategori Keputusan
P1 0,501 0,004 Valid Dipakai
P2 0,259 0,159 Tidak Valid Direvisi
P5 0,281 0,125 Tidak Valid Direvisi
Perhitungan validitas butir item pernyataan menggunakan perhitungan secara statistik. Untuk validitas butir item pernyataan digunakan korelasi product moment
dari Karl Pearson, yaitu korelasi setiap butir item pernyataan dengan skor total. Apabila rhitung ≥ rtabel maka item pernyataan dikatakan valid atau nilai Signifikansi Korelasi kurang dari α (0,05), dengan rtabel sebesar 0,339.
Berdasarkan tabel hasil uji validitas di atas, dapat dilihat bahwa sebanyak 15 item pernyataan valid, dan 9 item pernyataan tidak valid. Untuk pernyataan yang tidak valid akan direvisi untuk selanjutnya digunakan kembali untuk mengukur skala sikap matematis, selengkapnya ada pada Lampiran D.
b. Analisis Reliabilitas Skala Sikap Matematis
adalah dengan membandingkan rhitung dan rtabel. Jika rhitung > rtabel maka soal reliabel,
sedangkan jika rhitung≤ rtabel maka soal tidak reliabel.
Hasil perhitungan selengkapnya ada pada Lampiran B. Berikut ini merupakan rekapitulasi hasil perhitungan reliabilitas.
Tabel 3.16
Reliabilitas Skala Sikap Matematis rhitung rtabel Kriteria Kategori
0,741 0,339 Reliabel Sangat Tinggi
Maka untuk α = 5% dengan derajat kebebasan dk = 31 diperoleh harga rtabel
0,339. Hasil perhitungan reliabilitas berdasarkan tabel 3.13 di atas diperoleh rhitung
sebesar 0,715. Artinya soal tersebut reliabel karena 0,741 > 0,304 dan termasuk kedalam kategori sangat tinggi. Hasil analisis tersebut menunjukkan bahwa skala sikap matematis telah memenuhi karakteristik yang memadai untuk digunakan dalam penelitian, selengkapnya ada pada Lampiran D.
6. Pengembangan Bahan Ajar
Bahan ajar dalam penelitian ini adalah bahan ajar yang digunakan dalam pembelajaran matematika dengan aktivitas metaphorical thinking untuk kelompok-kelompok eksperimen. Bahan ajar disusun berdasarkan kurikulum yang berlaku di lapangan yaitu Kurikulum Tingkat Satuan Pendidikan. Isi bahan ajar memuat materi-materi matematika untuk kelas IX semester II dengan langkah-langkah pembelajaran
D. Teknik Pengumpulan Data
Data dalam penelitian ini dikumpulkan melalui tes pengetahuan awal matematika, tes kemampuan abstraksi dan generalisasi matematis dan skala sikap. Data yang berkaitan dengan kemampuan awal matematis dikumpulkan melalui nilai raport, untuk data kemampuan abstraksi dan generalisasi matematis siswa dikumpulkan melalui pre-test dan post-test, data yang berkaitan dengan skala sikap siswa dikumpulkan melalui penyebaran skala sikap siswa.
E. Teknik Analisis Data
Data yang diperoleh dari penelitian ini adalah data kuantitatif dan data kualitatif. Untuk itu pengolahan terhadap data yang telah dikumpulkan, dilakukan secara kualitatif dan kuantitatif.
1. Analisis Data Kuantitatif
Data-data kuantitatif diperoleh dalam bentuk hasil uji instrumen, data pre-test,
post-test, N-gain serta skala sikap siswa. Data hasil uji instrumen diolah dengan perhitungan untuk memperoleh validitas, reliabilitas, daya pembeda serta derajat kesukaran soal. Sedangkan data hasil pre-test, post-test, N-gain dan skala sikap siswa diolah dengan bantuan program software SPSS Versi 20.0 for Windows.
a. Data Hasil Tes Kemampuan Abstraksi dan Generalisasi Matematis
Data yang diperoleh dari hasil tes abstraksi dan generalisasi matematis diolah melalui tahapan sebagai berikut:
1) Memberikan skor jawaban siswa sesuai dengan kriteria penskoran yang digunakan.
2) Membuat skor pre-test dan post-test siswa kelas eksperimen dan kelas konvensional.
3) Menentukan skor peningkatan abstraksi dan generalisasi matematis dengan rumus N-gain ternormalisasi (Meltzer, 2002) yaitu:
Hasil perhitungan N-gain kemudian diinterpretasikan dengan menggunakan klasifikasi sebagai berikut:
Tabel 3.18
Klasifikasi Gain Ternormalisasi Besarnya N-gain (g) Klasifikasi
g ≥ 0,70 Tinggi
0,30 ≤ g < 0,70 Sedang
g < 0,30 Rendah
4) Melakukan uji normalitas untuk mengetahui kenormalan data skor pre-test,
post-test dan N-gain kemampuan berpikir logis matematis menggunakan uji statistik Shapiro-Wilk.
Dengan kriteria uji sebagai berikut:
Jika nilai Sig. (p-value) < α (α =0,05), maka H0 ditolak
Jika nilai Sig. (p-value) ≥ α (α =0,05), maka H0 diterima.
Adapun rumusan hipotesisnya adalah: H0: Data berdistribusi normal
5) Menguji homogenitas varians skor pre-test, post-test dan N-gain kemampuan berpikir logis matematis menggunakan uji Levene.
Dengan kriteria uji sebagai berikut:
Jika nilai Sig. (p-value) < α (α =0,05), maka H0 ditolak
Jika nilai Sig. (p-value) ≥ α (α =0,05), maka H0 diterima.
Adapun hipotesis yang akan diuji adalah: H0: Kedua data bervariansi homogen
H1: Kedua data tidak bervariansi homogen
6) Setelah data memenuhi syarat normal dan homogen, selanjutnya dilakukan uji kesamaan rataan skor pre-test dan uji perbedaan rataan skor post-test dan N-gain menggunakan uji-t yaitu Independent Sample T-Test.
7) Melakukan uji perbedaan rataan skor N-gain kemampuan abstraksi dan generalisasi matematis siswa yang mendapat pembelajaran metaphorical thinking dan pembelajaran konvensional berdasarkan kategori pengetahuan awal matematis siswa (tinggi, sedang, dan rendah). Uji statistik yang digunakan adalah uji-t yaitu Independent Sample T-Test untuk masing-masing kategori kemampuan awal matematis pada kelas eksperimen dan kelas konvensional.
8) Melakukan uji perbedaan interaksi antara pembelajaran (metaphorical thinking
dan konvensional) dan kemampuan awal matematis siswa (tinggi, sedang, dan rendah) terhadap peningkatan kemampuan abstraksi dan generalisasi matematis dengan uji analysis of variance (ANOVA) dua jalur dilanjutkan dengan uji
Scheffe (varians homogen) untuk melihat letak perbedaanya.
Penentuan skor skala sikap matematis menggunakan MSI (Methode of Succesive Interval) untuk mengubah data ordinal menjadi data interval. Data skor skala sikap yang diperoleh diolah melalui tahap-tahap berikut:
1) Hasil jawaban untuk setiap pertanyaan dihitung frekuensi setiap pilihan jawaban.
2) Frekuensi yang diperoleh setiap pertanyaan dihitung proporsi setiap pilihan jawaban.
3) Berdasarkan proporsi untuk setiap pertanyaan tersebut, dihitung proporsi kumulatif untuk setiap pertanyaan.
4) Kemudian ditentukan nilai batas untuk Z bagi setiap pilihan jawaban dan setiap pertanyaan.
5) Berdasarkan nilai Z, tentukan nilai densitas (kepadatan). Nilai densitas dapat dilihat pada tabel ordinat Y untuk lengkungan normal standar.
6) Hitung nilai skala/ scale value/ SV untuk setiap pilihan jawaban dengan persamaan sebagai berikut:
7) Langkah selanjutnya yaitu tentukan nilai k, dengan rumus: k= 1 +| � � |.
8) Langkah terakhir yaitu transformasikan masing-masing nilai pada SV dengan rumus: SV + k.
9) Selanjutnya dilakukan Uji-t dengan one sample t-test untuk melihat apakah ada perbedaan signifikan sikap matematis siswa yang mendapat pembelajaran
metaphorical thinking. Kriteria pengujian adalah terima H0 apabila Asymp. Sig.
F. Tahap Penelitian
Penelitian ini akan dilaksanakan mulai bulan Februari 2013 tahun ajaran 2012/2013. Penelitian dibagi ke dalam beberapa tahapan sebagai berikut.
1. Tahap Persiapan
Tahap persiapan penelitian meliputi tahap-tahap penyusunan proposal, seminar proposal, studi pendahuluan, penyusunan instrumen penelitian, pengujian instrumen dan perbaikan instrumen.
2. Tahap Pelaksanaan Penelitian
Tahap pelaksanaan penelitian meliputi tahap implementasi instrumen, implementasi pembelajaran dengan pembelajaran metaphorical thinking, serta tahap pengumpulan data.
3. Tahap Penulisan Laporan
BAB V
KESIMPULAN DAN SARAN
A. Kesimpulan
Berdasarkan analisis data yang telah disajikan dan pembahasan hasil penelitian yang telah diuraikan, dapat diambil kesimpulan sebagai berikut:
1. Secara keseluruhan peningkatan kemampuan abstraksi matematis siswa yang memperoleh pembelajaran matematika dengan pendekatan methaporical thinking
lebih baik daripada pembelajaran konvensional. Bila memperhatikan kemampuan awal matematis, pada kemampuan awal matematis kategori tinggi dan sedang peningkatan kemampuan abstraksi matematis siswa yang memperoleh pembelajaran matematika dengan pendekatan methaporical thinking dan siswa yang memperoleh pembelajaran matematika dengan konvensional tidak berbeda signifikan. Namun, untuk kemampuan awal matematis kategori rendah, peningkatan kemampuan abstraksi matematis siswa yang memperoleh pembelajaran matematika dengan pendekatan metaphorical thinking lebih baik daripada pembelajaran konvensional.
2. Perbedaan kemampuan awal matematis memberikan pengaruh signifikan terhadap peningkatan kemampuan abstraksi matematis siswa.
3. Ditinjau berdasarkan kemampuan awal, tidak terdapat perbedaan peningkatan kemampuan abstraksi matematis siswa yang dalam pembelajarannya menggunakan pendekatan pembelajaran konvensional. Namun terdapat perbedaan peningkatan kemampuan abstraksi matematis siswa yang dalam pembelajarannya menggunakan pendekatan pembelajaran MT.
matematis tidak secara bersama-sama memberikan pengaruh terhadap peningkatan kemampuan abstraksi matematis.
5. Secara keseluruhan peningkatan kemampuan generalisasi matematis siswa yang memperoleh pembelajaran matematika dengan pendekatan Methaporical Thinking lebih baik dari pada pembelajaran konvensional. Bila memperhatikan kemampuan awal matematis, untuk kemampuan awal matematis kategori tinggi dan rendah, peningkatan kemampuan generalisasi matematis siswa yang memperoleh pembelajaran matematika dengan pendekatan Methaporical Thinking lebih baik daripada pembelajaran konvensional. Namun, untuk kemampuan awal matematis kategori sedang, peningkatan kemampuan generalisasi matematis siswa yang memperoleh pembelajaran matematika dengan pendekatan Methaporical Thinking tidak berbeda secara signifikan dengan pembelajaran konvensional.
6. Perbedaan kemampuan awal matematis tidak memberikan pengaruh signifikan terhadap peningkatan kemampuan generalisasi matematis siswa.
7. Ditinjau berdasarkan kemampuan awal, tidak terdapat perbedaan peningkatan kemampuan generalisasi matematis siswa yang dalam pembelajarannya menggunakan pendekatan pembelajaran konvensional. Namun terdapat perbedaan peningkatan kemampuan generalisasi matematis siswa yang dalam pembelajarannya menggunakan pendekatan pembelajaran MT
8. Terdapat interaksi yang signifikan antara faktor pendekatan pembelajaran dan kategori kemampuan awal matematis terhadap peningkatan kemampuan generalisasi matematis. Artinya, faktor pembelajaran dan kategori kemampuan awal matematis secara bersama-sama memberikan pengaruh terhadap peningkatan kemampuan generalisasi matematis.
B. Implikasi
Berdasarkan hasil penelitian, ada beberapa hal saran berhubungan dengan penelitian ini, antara lain:
1. Penelitian ini hanya terbatas pada materi deret dan barisan. Diharapkan pada peneliti lainnya untuk mengembangkan pembelajaran matematika dengan pendekatan methaporical thinking pada materi matematika lainnya di sekolah menengah.
2. Penerapan pendekatan pembelajaran methaporical thinking direspon dengan baik, oleh sebab itu pendekatan pembelajaran ini dapat dijadikan sebagai salah satu upaya dalam mereformasi pengelolaan pembelajaran yang lebih berkualitas. 3. Lembar Kerja Siswa (LKS) maupun modul pembelajaran sangat membantu siswa
mengikuti pelajaran. Namun peran aktif guru atau pengajar sangat penting dibutuhkan dalam membimbing dan mengarahkan siswa mencapai tujuan pembelajaran.
4. Pada penelitian ini hanya dikaji kemampuan abstraksi dan generalisasi matematis saja, untuk itu diharapkan pada penelitian lainnya untuk mengkaji pembelajaran matematika dengan pendekatan Methaporical Thinking dalam meningkatan kemampuan berpikir matematis lainnya.
C. Rekomendasi
Berdasarkan kesimpulan dan implikasi penelitian di atas, diajukan beberapa saran sebagai berikut.
1. Pendekatan pembelajaran metaphorical thinking hendaknya menjadi alternatif pendekatan pembelajaran bagi guru SMP khususnya dalam meningkatkan kemampuan abstraksi dan generalisasi matematis siswa.
2. Penerapan pembelajaran dengan pendekatan pembelajaran metaphorical thinking, sebaiknya guru membuat sebuah skenario dan perencanaan yang matang, sehingga pembelajaran metaphorical thinking dapat diterapkan pada semua kategori pengetahuan awal matematis siswa.
3. Perlu dilakukan penelitian lanjutan, untuk melihat keefektivan penerapan pendekatan pembelajaran metaphorical thinking pada semua kategori pengetahuan awal matematis siswa pada sekolah dengan peringkat sedang dan baik.
4. Pembelajaran metaphorical thinking supaya tidak asing bagi siswa dan mudah diterapkan, sebaiknya dari mulai tingkat sekolah dasar sudah mulai diperkenalkan dengan memilih materi yang sesuai dengan karakteristik strategi pembelajaran
DAFTAR PUSTAKA
Ainley, J., Bills, L., & Wilson, K. (2005). Designing spreadsheetbased tasks for purposeful algebra. International Journal of Computers for Mathematical Learning, 10(3), 191–215.
Andrade, J. S. (2007). “Metaphors And Cognitive Modes In The Teaching-Learning Of Mathematics” Working Group 1. CERME 5 (2007).
Anggraeni, Y (2010). “Peningkatan Kemampuan Penalaran dan Komunikasi
Matematis Siswa SMP Melalui Reciprocal Tecahing”. Thesis PPs UPI. Bandung;
tidak diterbitkan.
Araya, R.: 2000, La Inteligencia Matemática, Ed. Universitaria, Santiago, Chile. Arikunto, S., (2002). Prosedur Penelitian. Jakarta: Rineka Cipta.
Badan Standar Nasional Pendidikan (BSNP, 2006). Panduan Penyusunan Kurikulum Tingkat Satuan Pendidikan Jenjang Pendidikan Dasar dan Menengah. Jakarta: Badan Standar Nasional Pendidikan.
Badudu, J. S (2009). “Kamus Ungkapan Bahasa Indonesia”. Jakarta: Kompas.
Becker, J. R., & Rivera, F. (2005). Generalization strategies of beginning high school algebra students. In H. L. Chick, & J. L. Vincent (Eds.). Proceedings of the 29th Conference of the International Group for the Psychology of Mathematics Education (Vol. 4, pp. 121–128). Melbourne: PME.
Bills, C.: 2003, Metaphor In Young Children's Mental Calculation, Proc. CERME 3, http://www.dm.unipi.it/~didattica/CERME3/proceedings/Groups/TG1/TG1_bills _c erme3.pdf [ 29 Juli 2012]
Bishop (ed.), Mathematical Knowledge: Its Growth Through Teaching, Kluwer Academic Publishers, Dordrecht, pp. 63–85.
Bolite Frant, J. et al. (2004). Reclaiming Visualization: When Seeing Does Not Imply Looking. TSG 28, ICME 10, Denmark [http://www.icme-organisers.dk/tsg28/] [3 Agustus 2012]
Carolyn, C dan Pluker, J (2010). Critical Issues And Practices In Gifted Education. By Nationtal Association For Gifted Children.
Carreira, S. (2001). Where There’s a Model, There’s a Methaphor: Metaphorical
Thinking in Students’ Understanding of a Mathematical Model. An International
Journal Mathematical Thinking and Learning. 3 (4), 261-287
Cox, Bill (2003). Researching the Teaching and Learning of Mathematics:
Proceedings of MATHED Intensive Programme 2003 How can we inspire our mathematics students?. Aston University and MSOR Subject Centre of the Higher Education Academy
Dahiana, W O (2010). Peningkatan Kemampuan Pemahaman dan Generalisasi Matematis siswa dengan pembelajaran dengan pendekatan induktif-deduktif berbasis konstruktivisme. Tesis PPs UPI. Bandung; tidak diterbitkan.
Dahlan, J. A., (2004). Meningkatkan Kemampuan Penalaran dan Pemahaman Matematika Siswa Sekolah Menengah Lanjutan Tingkat Pertama Melalui Pendekatan Pembelajaran Open-Ended. Disertasi pada PPs UPIBandung: Tidak dipublikasikan.
Davydov, V. (1972/1990). Type Of Generalization In Instruction: Logical And Psychological Problems In The Structuring Of School Curricula. In J. Kilpatrick (Ed.), Soviet studies in mathematics education (Vol. 2). Reston, VA: National Council of Teachers of Mathematics.
Departemen Pendidikan Nasional, Direktorat Jenderal Pendidikan Dasar dan Menenngah, Direktorat Pendidikan Lanjutan Pertama (2002). Materi Pembelajaran Terintegrasi Matematika Tahun 2004 MTK 26, Jakarta Depdiknas. DePorter, B., dan Hernacki, M. (1999). Quantum Learning: Membiasakan Belajar
Dewanto, S.P. (2003). Upaya Meningkatkan Kemampuan Berpikir Tingkat Tinggi melalui Pembelajaran dengan Menggunakan Pendekatan Induktif-Deduktif.
Tesis PPs UPI. Bandung; tidak diterbitkan.
Dorfler, W.: 1991, „Forms and means of generalization in mathematics’, in A.J. ________. (1991). Forms And Means Of Generalization In Mathe-Matics. In A. J.
Bishop (Ed.), Mathematical knowledge: Its growth through teaching (pp. 63–85). Dordrecht, Netherlands: Kluwer.
Dreyfus, T. (2001). The Construction of Abstract Knowledge in Interaction.
Proceeding of the 25th Conference of the International Group for the Psychology of Mathematics Education. (Vol.2, pp.377-384). Utrecht, The Netherland: PME. _________. (2002). Advanced Mathematical Thinking Process. Mathematics
Education Library (Vol. 11. Pp 25-41). New York: Kluwer Academic Publisher. Dubinsky, Ed. (2002). A Radical Conrstructivist does CL. [Online] [4 Agustus 2012] Dubinsky, Ed
Edi (2012). Pengaruh penggunaan model pembelajaran anchored instruction terhadap kemampuan komunikasi matematis dan self-concept siswa. Tesis PPs UPI. Bandung; tidak diterbitkan
Endarmoko, E. (2006). Tesaurus Bahasa Indonesia. Jakarta Gramedia Pustaka Utama Edwards, L.: 2005, Metaphors and Gestures in Fraction Talk, Proc. CERME 4,
http://ermeweb.free.fr/CERME4/CERME4_WG1.pdf [8 Agustus 2012] English, L. (ed.): 1997, Mathematical Reasoning: Analogies, Metaphors, And Images
Lawrence Erlbaum Associates, London.
____________: Mathematical reasoning: Analogies, metaphors, and images (pp. 339-371). Mahwah, New Jersey: Lawrence Erlbaum Associates.
Ferrari, P. (2003). Abstraction in Mathemathics. Departimento di Science e Technologie Avanzate, Unviversita delp Piemonte Oreintale, corso T. Borsalino 54, 15100 alesandria AL. Italy: The Royal Society.
Font, V. (2000). Procediments Per Obtenir Expressions Simbòliques a Partir de Gràfiques. Aplicacions a Les Derivades. Tesis doctoral no publicada. Universitat de Barcelona.
Font, V. & Acevedo, J. I. (2003). Fenómenos Relacionados Con el uso de Metáforas en el Discurso del Profesor. El caso de las Gráficas de Funciones. Enseñanza de las Ciencias, 21, 3, 405-418.
Groth, R. E & Bergner, J. A (2005). “Pre-Service Elementary School Teachers’
Metaphors For The Concept Of Statistical Sample” Statistics Education
Research Journal, 4(2), 27-42, http://www.stat.auckland.ac.nz/serj © International Association for Statistical Education (IASE/ISI), Nov, 2005 [7 Agustus 2012]
García C, J. A & Martinón, A (1998). level of generalization in linear pattern. Universidad de La Laguna : Proceeding of the 22nd Conference of the International Group for the Psychology of Mathematics Education, Vol 2, pp 329-336. University of Stellenbosch, South Africa (1998).
Harel, G & Tall, D (1989). “The General, the Abstract, and the Generic
in Advanced Mathematics” For the Learning of Mathematics, 11 1, 38–42 (1989.
Harel, G., & Tall, D. (1991). The General, The Abstract And The Generic In Advanced Mathematics. For the Learning of Mathematics, 11(1), 38–42.
Hilman, M (2010). Meningkatkan Kemampuan Generalisasi Matematis Siswa SMA melalui Pembelajaran dengan Model Investigasi Kelompok.
Heris, Hendriana (2010). Peningkatan kemampuan pemahaman dan komunikasi matematis siswa Sekolah Menengah Pertama melalui pembelajaran dengan menggunakan pendekatan Methaporical Thinking. Disertasi PPs UPI. Bandung; tidak diterbitkan.
Johnson, M. & Lakoff, G.: 2003, Metaphors We Live. The University of Chicago Press, N.Y.
Kamus Besar Bahasa Indonesia (2005). Departemen Pendidikan Nasional Jakarta: Balai Pustaka
Kappel, F., 2001, “The Role of Mathematics in the 21st Century” Makalah
dalamSeminar Nasional Matematika di Universitas Brawijaya pada tanggal 6 Agustus2001, Malang : Universitas Brawijaya.
Lakatos, I.: Proofs and refutations: The logic of mathematical discovery. Cambridge University Press, Cambridge (1976)
Lakoff, G. & Núñez, R. (2000). Where Mathematics Comes From: How The Embodied Mind Brings Mathematics Into Being. New York: Basic Books. Lee, L.: 1996, „An initiation into algebraic culture through generalization activities‟,
in N.Bednarz, C. Kieran and Lee, L. (eds.), Approaches to Algebra: Perspectives for Research and Teaching, Kluwer Academic Publishers, Dordrecht, pp. 87– 106.
Leino, A.L. & Drakenberg, M. (1993). Metaphor: An Educational Perspective. Research Bulletin 84, Department of Education, University of Helsinki.
Michelmore, M & White, P. (2004). Abstraction in Mathematics and Mathematics Learning. Proceedding of the 28th Conference of the International Group for the Psychology of Mathematics Education. Vol 3 hal 329-336
Mason, J. (1999). Learning And Doing Mathematics. (2nd revised edition). York, UK: QED.
Maulana (2010). Alternatif pembelajaran matematika dengan pendekatan metakognitif untukmeningkatkan kemampuan berpikir kritis mahasiswa PGSD. Tesis SPS UPI Bandung: Tidak diterbitkan.
Mason, J. (2001). Tunja Sequences As Example Of Employing Students; Power To Generalize. Mathematics Teacher, 94(3), 164–169.
Mason, J. (2006). What Makes And Example Exemplary: Pedagogical and didactical issues in appreciating multiplicative structures. In
______________. Structured Variation Grids. Available:
http://msc.open.ac.uk/jhm3/. [3 Agustus 2012]
Mason, J., Burton, L., & Stacey, K. (1985). Thinking mathematically. Reading, massachusetts: Addison-Wesley Publishing Company.
Mason, J., & Pimm, D. (1984). Generic Examples: Seeing The General In The Particular. Educational Studies in Mathematics, 15, 277– 289.
Monaghan, J. & Ozmantar, M.F. (2004). Abstraction and consolidation. In M. J. Høines & A. B. Fuglestad (Eds.), Proceedings of the 28th International Conference for the Psychology of Mathematics Education, Vol. 3 (pp. 353-360).
Bergen, Norway: Bergen University College.
Murtiyasa, Budi (2010). Strategi pengembangan pembelajaran matematika pada abad XX. Universitas Muhammaddiyah Surakarta.
NCTM, (2000). Princip And Standars For School Mathematics. Reston: Virginia. Neni, (2010). Peningkatan Pemahaman dan disposisi matematis siswa denga
pembelajaran melalui pendekatan Methaporical Thinking. Tesis SPS UPI Bandung: Tidak diterbitkan.
Núñez, R. (2000). Mathematical Idea Analysis: What Embodied Cognitive Science Can Say About The Human Nature Of Mathematics, en Nakaora T. y Koyama M. (eds.).
Nurhasanah, F. (2010). Abstraksi Siswa SMP Dalam Belajar Geometri Melalui
Penerapan Model Van Hiele Dan Geometers’ Sketchpad. Tesis SPS UPI
Bandung: Tidak diterbitkan.
Orton, A., & Orton, J. (1999). Pattern And The Approach To Algebra. In A. Orton (Ed.), Pattern in the teaching and learning of mathematics (pp. 104–120). London, UK: Cassell.
3,http://www.dm.unipi.it/~didattica/CERME3/proceedings/Groups/TG1/TG1_int roduction_cerme3.pdf [ 5 Agustus 2012]
Pesci, Angela. (2004). Mediation Of Metaphorical Discourse In The Reflection On
One’s Own Individual Relationship With The Taught Discipline: an
experience with mathematics teachers Department of Mathematics, University of Pavia.
Pouilloux J.-Y.: 2004, Article Sur La Métaphore, Encyclopædia Universalis, Paris. Presmeg, N. C.: 1997, Reasoning With Metaphors And Metonymies In Mathematics
Learning, in English (ed.), Mathematical reasoning: Analogies, metaphors, and images, Lawrence Erlbaum Associates, London, pp. 267-279. Proceedings of PME24 (vol.1, pp. 3-22). Hiroshima: Hiroshima University.
Radford, L. (2003). Gestures, Speech, And The Sprouting Of Signs: A
Semiotic-Cultural Approach To Students’ Types Of Generalization. Mathematical
Thinking and Learning, 5(1), 37–70.
___________________.Prototypes, Metaphors, Metonymies, And Imaginative Rationality In High School Mathematics. Educational Studies in Mathematics, 23 (6), 595-610.
___________________. Reasoning With Metaphors And Metonymies In Mathematics Learning. In L. D. English (Ed.), Mathematical reasoning: Analogies, metaphors, and images (pp. 267-279). Mahwah, New Jersey: Lawrence Erlbaum Associates. Rahman, B (2012). “pembelajaran matematika, khususnya materi geometri dengan
Wingeom untuk meningkatkan kemampuan spasial dan penalaran matematis siswa”. Thesis PPs UPI. Bandung; tidak diterbitkan.
Risna (2011). Pembelajaran Geometri dengan Wingeom untuk Meningkatkan Kemampuan Penalaran dan Spasial Matematis Siswa. Tesis SPS UPI Bandung: Tidak diterbitkan.
R. Zazkis and S.R. Campbell (Eds.), Number Theory In Mathematics Education: Perspectives And Prospects (pp. 41– 68). Lawrence Erlbaum Press.
Rosita, I. (2007). Strategi Heuristik Untuk Meningkatkan Kemampuan Generalisasi Matematis Siswa kelas X SMA. Tesis pada SPS. Bandung: Tidak dipublikasikan. Ruseffendi, E. T. (1988). Pengantar Kepada Membantu Guru Mengembangkan
Kompetensinya Dalam Pengajaran Untuk Meningkatkan CBSA. Bandung: Tarsito.
R. Zazkis et al. (2008). The role of examples in forming and refuting generalizations. ZDM Mathematics Education (2008) 40:131–141
Seitz, J.: 2001, The Biological And Bodily Basis Of Metaphor, http://philosophy.uoregon.edu/metaphor/neurophl.htm
Sfard, A.: 1994, Reification As The Birth Of Metaphor, For the Learning of Mathematics 141, 44-54.
Sfard, A.: 1997, Commentary: On metaphorical roots of conceptual growth, in L. English (ed.), Mathematical reasoning: Analogies, metaphors, and images, Lawrence Erlbaum Associates, London, pp. 339-371.
Sriraman, B. (2004). Reflective Abstraction, Uniframes and the Formulation of
Generalizations. Journal of Mathematical Behav-ior, 23, 205–222.
Stacey, K. (1989). Finding And Using Patterns In Linear Generalizing Problems. Educational Studies in Mathematics, 20, 147–164.
Stacey, K., & Mac Gregor, M. (2001). Curriculum Reform And Approaches To Algebra. In R. Sutherland, T. Rojano, A. Bell, &R. Lins (Eds.), Perspectives on school algebra (pp. 141–154). Dordrecht, Netherlands: Kluwer.
Sugiyono. (2009). Statistik Untuk Penelitian. Bandung: CV. Alfabeta. Suherman, E. (2003). Evaluasi Pembelajaran Matematika. Bandung: JICA
Sujono. (1998). Pengajaran Matematika untuk Sekolah Menengah. Jakarta: Depdikbud. P2LPTK.