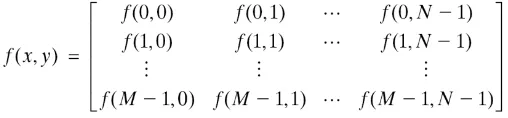BAB 2
LANDASAN TEORI
Pada bab ini membahas landasan atas teori-teori yang bersifat ilmiah untuk mendukung penulisan tugas akhir ini, beserta dengan penelitian sebelumnya. Teori-teori yang dibahas dalam bab ini mengenai pengertian citra, algoritma corner detection, Harris Corner Detection, backpropagation dan beberapa subpokok pembahasan lain.
2.1 Pengertian Citra
Citra merupakan sebuah representasi yang mirip dengan sebuah objek dan terdiri dari sebuah array dua dimensi (Phillips, 2000). dapat dibentuk oleh variasi yang menerus dalam shading, warna, bentuk dan tekstur, yang dapat didefinisikan secara geometris dan kompleks (Simarmata, 2006). Citra sebagai output sistem perekam data dapat bersifat optik berupa foto, bersifat analog yang berupa sinyal video seperti layar televisi, dan juga bersifat digital yang dapat langsung disimpan pada suatu media penyimpanan atau pita magnetik (Sutoyo et al. 2009).
2.1.1 Citra Analog
Gambar 2.1 Contoh Citra Analog pada Televisi
Gambar 2.2 Contoh Citra Analog hasil Scanner
2.1.2 Citra Digital
Citra yang akan digunakan pada penelitian ini menggunakan format citra digital. Proses digitalisasi pada citra juga merupakan proses pengubahan bentuk citra analog menjadi citra digital, sehingga dapat diolah menggunakan komputer. Pada Gambar 2.3 merupakan gambar elemen sistem pemrosesan citra digital.
Gambar 2.3 Elemen Pemrosesan Citra Digital
Media Penyimpanan
Komputer
Piranti Tampilan Digitizer
Operasi dari sistem pemrosesan citra tersebut dibagi menjadi empat kategori prinsip: digitalisasi, pemrosesan, penayangan dan penyimpanan. Digitizer (digital image acquistition system) digunakan untuk menangkap citra digital yang melakukan penjelajahan citra dan mengonversi ke representasi numerik sebagai input bagi komputer digital. Digitizer terdiri dari tiga komponen dasar, iatu sensor citra yang bekerja sebagai pengukur intensitas cahaya, perangkat penjelajah yang berfungsi merekam hasil pengukuran intensitas pada seluruh bagian citra dan pengubah analog-ke-digital yang berfungsi melakukan pengubahan dak kuantitasi.
Hasil dari digitizer adalah matriks yang elemen-elemennya menyatakan nilai intensitas cahaya pada suatu titik. Contoh digitizer adalah kamera digital dan scanner. Komputer lalu digunakan untuk sistem permorsesan citra dan bervariasi dari komputer mikro sampai kamputer besar yang mampu melakukan bermacam fungsi digital dengan resolusi tinggi. Hasil pengolahan ini kemudian direpresentasikan kepada piranti tampilan yang dapat dilihat oleh manusia, sedangkan media penyimpanan berfungsi untuk menyimpan hasil konversi citra menjadi citra digital sehingga dapat disimpan secara permanen sehingga dapat diproses lagi.
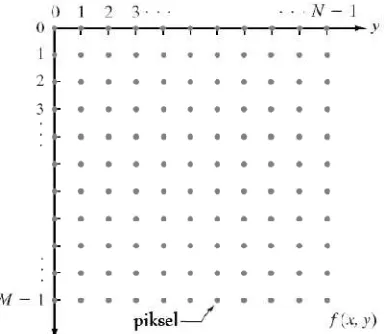
Citra digital tersusun dalam bentuk kisi yang berisi nilai yang dipresentasikan dengan deretan bit. Sebuah citra dapat didefinisikan sebagai fungsi f(x,y), yang menyatakan derajat keabuan (gray level) pada koordinat x dan y. Koordinat x dinyatakan sebagai kolom dan y dinyatakan sebagai baris. Perpotongan antara baris dan kolom disebut dengan piksel (picture element), yaitu elemen terkecil dalam sebuah citra. Gambar 2.4 menunjukan posisi koordinat citra digital.
Citra digital berbentuk empat persegi panjang dan ukurannya dinyatakan sebagai tinggi x lebar (baris x kolom). Citra digital dengan tinggi N, lebar M dan memiliki derajat keabuan (grey level) L dapat disusun dengan fungsi sebagai berikut:
( , ) = yang dinyatakan dengan f(x,y). Oleh karena itu, sebuah citra digital dapat dilihat pada Gambar 2.5 berikut:
Gambar 2.5 Fungsi Matriks pada Citra
Dicontohkan sebuah citra memiliki ukuran sebesar 100 x 100 piksel dengan nilai yang beragam pada setiap pikselnya. Maka matriks yang terdiri dari 100 baris dan 100 kolom dapat dipresentasikan pada Gambar 2.6.
⎣
Gambar 2.6 Presentasi Matriks pada Citra
Piksel pertama pada koordinat (0,0) memiliki nilai sebesar 0, yang berarti berwarna hitam. Sedangkan piksel yang berada pada koordinat (0,1) memiliki nilai 255, yang berarti berwarna putih, dan koordinat (0,3) memiliki nilai 143 yang artinya warna piksel berada diantara hitam dan putih, begitulah membaca piksel seterusnya.
Nilai piksel pada sebuah citra memiliki nilai rentang tertentu yang terdiri dari rentang minimum dan maksimum. Jangkauannya juga berbeda berdasarkan jenis warnanya. Berikut adalah jenis-jenis citra berdasarkan nilai pikselnya (Putra, 2010; Gonzales et al. 2009; Burger & Burge, 2008; Jähne, 2005; Phillips, 2000):
1. Citra biner (binary image) atau juga dapat disebut citra monokrom adalah citra digital yang hanya terdiri dari dua warna, yaitu hitam dan putih pada tiap piksel. Warna hitam diwakili dengan 0 dan warna putih diwakili dengan 1. Contoh citra biner dapat dilihat pada Gambar 2.7 di bawah ini.
Gambar 2.7 Contoh Binary Image
2. Citra grayscale (grayscale image) merupakan citra yang memiliki warna hitam, keabuan dan putih dalam setiap pikselnya. Citra ini memiliki kedalaman piksel 8 bit, dengan rentang sebanyak 256 warna (28 = 256). Contoh citra grayscale dapat dilihat pada Gambar 2.8.
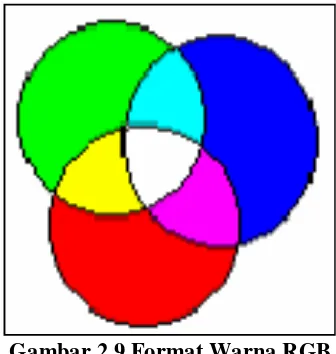
3. Citra warna (true color) merupakan citra yang menggunakan kombinasi dari tiga warna, yaitu: Red, Green dan Blue, sehingga disebut sebagai citra RGB. Setiap komponen warna yang terdapat pada piksel dapat mencapai 8 bit (28 = 256 warna) dengan format warna dapat dilihat pada Gambar 2.9.
Gambar 2.9 Format Warna RGB
Hal ini menyebabkan setiap piksel pada citra RGB membutuhkan media penyimpanan 3 byte. Jumlah kemungkinan kombinasi warna pada citra RGB adalah 224 atau lebih dari 16 juta warna. Contoh citra warna dapat dilihat pada Gambar 2.10.
2.2 Corner Detection
Banyak sekali informasi dalam sebuah citra yang dapat digunakan sebagai sebuah representasi sebuah citra. Informasi ini dapat berupa tepi, sudut, warna, garis dan masih banyak yang lainnya.
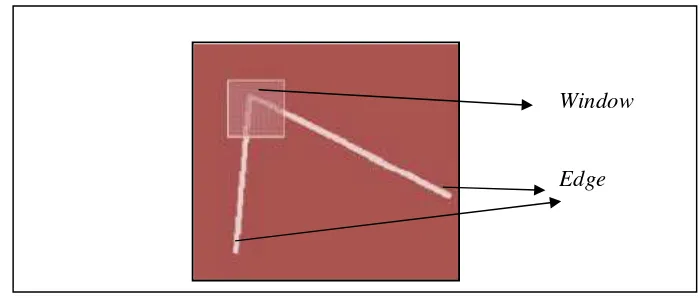
Corner detection adalah pendekatan yang digunakan dalam computer vision untuk mengekstrak beberapa jenis feature, mengetahui karakteristik dari sebuah citra, lalu menyimpulkan isi suatu citra (Bhatia & Chabbra, 2011). Corner dapat didefinisikan sebagai perpotongan dari dua buah edge atau titik yang menghasilkan dua arah edge dominan yang berbeda pada sebuah local neighbor (Burger, 2008). Untuk mengenali corner dapat dilakukan dengan menggeser window ke segala arah sehingga pada satu waktu tertentu didapatlah sebuah perbedaan yang besar yang kemudian diindentifikasikan sebagai corner, seperti yang dapat dilihat pada Gambar 2.11.
Gambar 2.11 Cuplikan Windowing
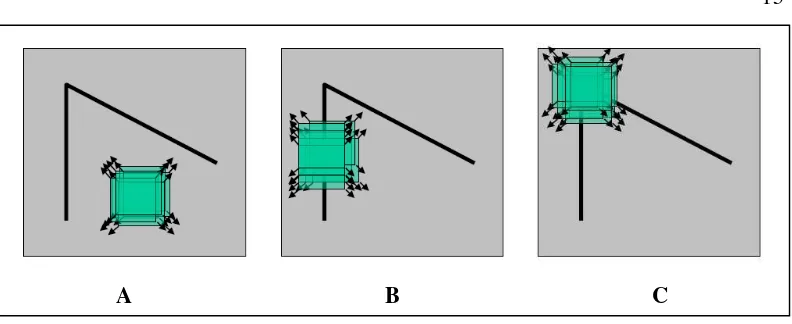
Apabila window digeser ke segala arah tetapi menghasilkan simpulan bagian flat dari objek dan tidak mendapat nilai apapun, maka hasilnya akan menjadi Gambar 2.12 bagian A, karena tidak terjadi perubahan dalam arah manapun. Pada Gambar 2.12 bagian B terjadi bila window digeser ke segala arah dan menghasilkan simpulan yang menyatakan bagian tepi dari objek yang disebut edge. Bila terjadi perubahan intensitas yang tertumpu pada satu sudut dari berbagai arah atau edge ketika window digeser maka akan dihasilkan sudut dari objek yang disebut sebagai corner, seperti yang ditujukan pada Gambar 2.12 bagian C.
Window
A B C Gambar 2.12 Ide Dasar Corner Detection
Corner detection banyak digunakan dalam motion detection (pendeteksi gerak), image registration (pendaftaran citra), video tracking (pelacakan video), image mosaicing, panoroma stitching, 3D modeling dan pengenalan objek. Corner detector yang baik harus memenuhi sejumlah kriteria, termasuk membedakan antara sudut-sudut yang benar dan salah, yang memiliki noise cukup besar, dan secara akurat dapat menentukan lokasi sudut.
Ketentuan dasar yang digunakan dalam menentukan sudut, yaitu: ketika sebuah edge didefiniskan dalam sebuah citra, maka sebuah corner point didefinisikan sebagai sebuah area yang menunjukan nilai gradien dalam arah yang sama. Sebuah detektor akan dapat mendeteksi titik sudut (corner) yang terdapat pada sebuah citra walau citra tersebut berubah arah.
Fungsi corner detector dapat dilihat pada Gambar 2.13. Di bawah terdapat sebuah segitiga yang berdiri tegak. Detektor akan mendeteksi sudut yang terdapat pada segitiga tersebut. Jika posisi segitiga diubah sedikit, maka detektor masih dapat mendeteksi sudut yang terdapat pada segitiga walau ada perubahan baik secara rotasi maupun tidak secara akurat.
2.2.1 Harris Corner Detection (HCD)
Operator ini dibangun oleh Harris dan Stephens didasarkan pada operator Moravec (Harris & Stephens, 1988) dan merupakan salah satu interest point detector yang cukup populer karena dapat mendeteksi sudut dengan stabil secara rotasi, skala, pencahayaan (Schmid et al. 2000). Interest point detection merupakan salah satu terminologi computer vision yang mengacu pada pendeteksian titik yang kemudian akan diproses. Secara umum fungsi detektor memiliki ciri umum yang terdiri dari fungsi matematika yang dapat ditemukan pada sebuah citra serta dapat ditekesi maupun terjadi perbedaan rotasi. Operator Harris juga sangat sensitif terhadap noise dalam sebuah citra (Guelzim et al. 2011).
Operator ini banyak digunakan sebagai salah satu proses dalam pengembangan robot vision. Kumpulan citra yang diambil menggunakan operator ini akan digunakan dalam proses interpretasi robot. Sehingga robot dapat mengambil kesimpulan dalam perubahan citra. Harris corner detector didasarkan pada fungsi perubahan autorkorelasi, dimana perubahan sinyalnya dapat diukur dalam arah yang berbeda. Autokorelasi ini memiliki rumus matematis sebagai berikut:
( , ) = [ ( , ) − ( + ∆ + ∆ ) ] (2.2)
dimana:
1. (xi,yi) = titik pada jendela W (fungsi Gaussian) yang berpusat di (x,y)
2. I(.,.) = fungsi citra. 3. (∆ ,∆ ) = pergeseran W
Sementara itu, citra yang digeser dirumuskan dengan ekspansi Taylor, yakni:
+ ∆ + ∆ ≅ ( , ) + [ ( , ) ( , ) ] ∆
∆ (2.3)
( , ) = [ ( , ) − ( + ∆ + ∆ ) ]
dimana C(x,y) merupakan matriks auto correlation yang menangkap nilai intensitas dari struktur local neighbour.
Harris Corner Detection (HCD) menghitung nilai rata-rata matriks yang diambil dari perubahan gradien citra, lalu mengombinasikan dengan nilai eigenvalues untuk mendapatkan nilai corner, yang diambil dari nilai maksimum posisi corner yang teridentifikasi. Ada beberapa tahap dalam mencari corner menggunakan operator ini, yaitu dengan mencari nilai local structure matrix, nilai corner response function (CRF), lalu menentukan nilai corner points (Burger & Burge, 2008).
2.2.1.1 Local Structure Matrix (LSM)
Perhitungan dimulai dari turunan parsial pertama (first partial derivative) fungsi citra I(u,v) dalam arah vertikal dan horisontal. Dimana persamaannya dapat dinyatakan sebagai berikut:
Ix(u,v) = ( , ) dan Iy(u,v) = ( , ). (2.5)
A(u,v) = (u,v) (2.6)
B(u,v) = (u,v) (2.7)
C(u,v) = (u,v) . (u,v) (2.8)
yang ditafsirkan sebagai elemen dari local structure matrix M(u,v):
M = = . (2.9)
Selanjutnya, tiap-tiap ketiga fungsi A(u,v), B(u,v), dan C(u,v) dihaluskan dari kekusutan (convolution) menggunakan nilai Gaussian filter , . Dimana nilai Gaussian filternya menggunakan fungsi:
,
=
( )(2.10)
untuk adalah standard derivation (simpangan baku) dari fungsi dan r adalah radius dari nilai tengah citra. Nilai piksel yang terletak pada tengah citra menerima nilai maksimum, sehingga dari nilai Gaussian filter , dapat menghasilkan nilai fungsi matriks sebagai berikut:
= ∗ , ∗ ,
∗ , ∗ , =
̅
̅
̅
(2.11)
Karena matriks simetris, matriks dapat didefinisikan sebagai:
′ = 0
0
(2.12)
dimana dan adalah eigenvalues dari matriks yang didefinisikan sebagai:
, =
( )
= ̅+ ± ̅ − 2 ̅ + + 4 ̅ (2.13) Untuk
trace = ̅+ dan det( ) = ̅ - ̅ (2.14)
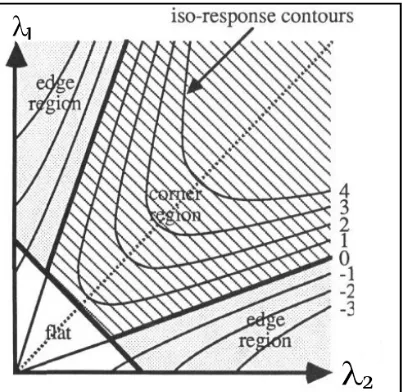
Eigenvalues yang bernilai positif dan bilangan ril, memuat informasi penting mengenai local image structure. Nilai hasil dari local image structure akan dipengaruhi oleh eigenvalues. Untuk menyeleksi corner yang baik harus melihat nilai eigenvalues, seperti yang ditunjukkan pada Gambar 2.14 berikut ini.
Gambar 2.14 Kurva Klasifikasi Corner, Flat, dan Edge (Harris-Stephens, 1988)
Dari Gambar 2.14 di atas, dapat kita lihat bahwa pengklasifikasian auto correlation sudah terlihat dengan jelas. Seperti yang sudah dibahas sebelumnya, ada tiga hal yang mempengaruhi nilai eigenvalues dari operator ini, yaitu sebagai berikut:
Gambar 2.15 Representasi Eigenvalues Flat
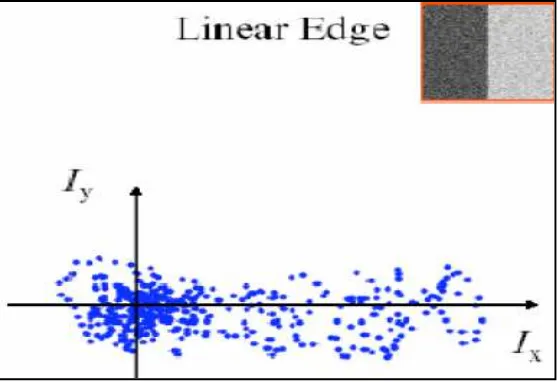
2. Jika > 0 atau memiliki nilai positif yang besar dan = 0, atau sebaliknya nilai = 0 dan > 0, maka wilayah autokorelasi itu disebut sebagai edge, yang menyebabkan perubahan cukup besar dalam arah tegak lurus. Bentuk ilustrasinya dapat dilihat pada Gambar 2.16 di bawah ini.
Gambar 2.16 Representasi Eigenvalues Edge
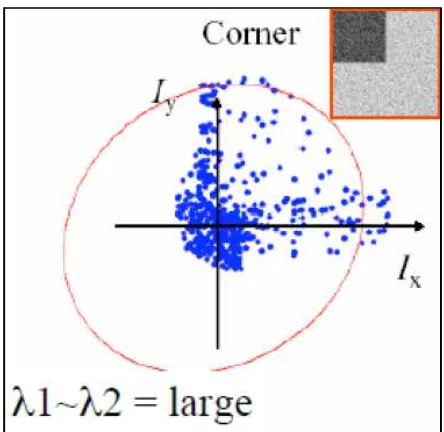
Gambar 2.17 Representasi Eigenvalues Corner
2.2.1.2 Corner Response Function (FCR)
Dari persamaan (2.12) di atas, maka nilai selisih dari dua eigenvalues adalah
- = 2 . . ( ( ) ) − det ( ) (2.15)
dimana nilai (0,25 . ( ( ) ) ) > det ( ) dalam setiap kasus. Dalam sebuah corner nilai persamaan tersebut harus sekecil mungkin, yang kemudian di definiskan dengan fungsi:
Q(u,v) = ( ) – α . ( ( ) ) = ( ̅ - ̅ ) – α . ̅+
(2.16)
sebagai sebuah nilai ukur dari kekuatan corner (corner strength). Q(u,v) disebut sebagai fungsi corner response (corner response function) dan mengembalikan nilai
maksimum. Dalam prakteknya, nilai α berada di antara 0,04 sampai 0,06 dengan nilai
maksimal 0,25. Semakin besar nilai α, maka semakin kecil sensitifitas dari detector
2.2.1.3 Menentukan Nilai Corner Points
Sebuah citra yang berlokasi pada (u,v) diseleksi sebagai sebuah kandidat corner points ketika:
Q(u,v) > tH (2.17)
dimana threshold (nilai ambang) tH diambil berdasarkan konten yang dan secara
tipikal terletak di antara range 10.000 sampai 1.000.000 dalam sebuah citra. Jika nilai corner ci = (ui, vi, qi) yang sudah didapatkan akan diinput ke dalam:
Corners = [c1, c2, … cN] (2.18)
yang kemudian akan diurutkan secara descending (menurun) (qi ≥qi+1) berdasarkan
corner strength qi = Q(ui, vi) seperti yang sudah didefenisikan pada Pers. (2.17).
Untuk menekan nilai false corner yang berada di sekitar area true corner maka harus dibuat nilai spesifik untuk mengeliminasi nilai false corner. Memenuhi hal ini maka list Corners diletakan dimulai dari depan sampai belakang (front to back), dan nilai corner yang lemah akan terletak di bagian akhir list dimana bagian ini terdapat dalam daerah corner yang kuat, kemudian dihapus. Proses pengolahan corner detector dapat dilihat pada Gambar 2.18.
Gambar 2.18 Flowchart Corner Detector (Harris-Stephens, 1988)
2.2.2 Algoritma Harris Corner Detection
Berikut ini adalah algoritma Harris Corner Detection yang digunakan untuk mendeteksi corner (Harris-Stephens, 1988):
1. Melakukan perhitungan x dan y dari citra.
3. Mencari jumlah nilai produk dari tiap piksel yang kemudian dikalikan dengan fungsi Gaussian.
4. Mendefinisikan tiap piksel (x,y) ke dalam matriks M. 5. Menghitung nilai corner response R tiap piksel. 6. Menghitung nilai ambang R.
7. Menghitung nilai nonmax titik yang telah ditentukan. 8. Memasukkan nilai corner yang ditemukan.
2.3 Jaringan Saraf Tiruan (Neural Network)
Ketika manusia berpikir, aktivitas yang terjadi adalah aktivitas untuk mengingat, memahami, menyimpan, dan memanggil kembali apa yang pernah dipelajari oleh otak. Jaringan saraf tiruan hanya menirukan aktivitas tersebut. Hanya saja, manusia memiliki cara kerja yang lebih kompleks dan lebih rumit daripada yang diperkirakan (Pustpitaningrum, 2006).
Jaringan saraf tiruan (JSS) atau Neural Network (NN) merupakan salah satu bidang komputer yang menirukan aktivitas otak manusia, dimana komputer diusahakan agar berpikir seperti manusia. Jaringan Saraf Tiruan direpresentasikan sebagai toplogi graf yang terhubung antara yang satu dengan yang lain. Dimana dalam tiap garis (edge) memiliki titik (node) yang saling menghubungkan antara yang satu dengan yang lain. Titik-titik tersebutlah yang akan memasukkan sekaligus mengeluarkan informasi.
Gambar 2.19 Struktur Jaringan Saraf Tiruan (Muis, 2009)
2.3.1 Aristektur
Pembagian arsitektur jaringan saraf tiruan bisa dilihat dari kerangka kerja dan skema interkoneksi, yang dapat dilihat dari jumlah lapisan (layer) dan jumlah node pada setiap lapisan. Lapisan-lapisan penyusunnya dapat dibagi menjadi tiga, yaitu:
1. Lapisan input (input layer), yang menerima input dari dari luar dan merupakan penggambaran dari sebuah masalah.
2. Lapisan tersembunyi (hidden layer), yang tidak dapat secara langsung diamatai, di sini dilakukan proses pengolahan informasi.
3. Lapisan keluaran (output layer), yang merupakan hasil dari informasi terhadap sebuah permasalahan.
Berdasarkan lapisan ini, maka Jaringan Saraf Tiruan dapat dibagi ke dalam tiga macam arsitektur, yaitu:
1. Jaringan kompetitif (competitive layer), pada jaringan ini, sekumpulan neuron bersaing untuk mendapatkan hak aktif. Pada lapisan ini terdapat jaringan dengan lapisan kompetitif yang memiliki bobot -ε seperti yang ditunjukkan pada Gambar 2.20.
2. Jaringan lapisan tunggal (single layer net), dimana aristekturnya hanya memiliki satu buah lapisan. Jaringan ini hanya menerima input, kemudian langsung mengolahnya menjadi output tanpa harus melalui lapisan tersembunyi. Seperti yang ditunjukkan pada Gambar 2.21 terlihat lapisan input memiliki 3 neuron, yaitu X1, X2, dan X3. Lapisan output terdiri dari 2 neuron, yaitu Y1 dan Y2. Dimana kedua neuron tersebut saling berhubungan, yang thubungan masing-masing neuron memiliki bobot yang bersesuaian. Semua input akan berhubungan dengan setiap unit output.
Gambar 2.21 Jaringan Lapisan Tunggal (Single Layer Net) (Hermawan, 2006)
Gambar 2.22 Jaringan Saraf Multilapis (Multilayer Net) (Hermawan, 2006)
2.3.2 Paradigma Pembelajaran
2.3.2.1 Pembelajaran Tak Terawasi (Unsupervised Learning)
Pada pembelajaran ini, tidak terjadi proses penglasifikasian pola, sehingga sistem akan melakukan proses dengan sendirinya. Algoritma ini sehing kali memiliki perhitungan yang kompleks dan akurasinya lebih rendah dibandingkan dengan pembelajaran terawasi. Algoritma ini dirancang untuk belajar dengan cepat dan lebih praktis dalam hal kecepatan.
2.3.2.2 Pembelajaran Terawasi (Supervised Learning)
Pada pembelajaran ini mengasumsikan ketersediaan contoh-contoh penglasifikasian kelas-kelas pembelajaran, yang memanfaatkan keanggotan kelas dari setiap contoh pelatihan. Dengan informasi ini, sistem dapat mendeteksi kesalahan klasifikasi pola sebagai umpan balik ke dalam jaringan, sehingga mampu menghasilkan jawaban yang semirip mungkin dengan jawaban benar yang telah diketahui oleh jaringan.
Pembelajaran ini mengacu pada pencarian kemungkinan kombinasi bobot yang naik ataupun turun derajat kesalahannya. Sistem akan memanfaatkan informasi tersebut untuk mendefinisikan kesalahan numerik yang mencari penurunan kesalahan.
2.3.3 Backpropagation
Backpropagation (BP) merupakan salah satu algoritma yang sering digunakan untuk menyelesaikan masalah-masalah yang rumit. Hal ini disebabkan karena jaringan dengan algoritma ini dilatih dengan menggunakan metode pembelajaran terbimbing. Pada jaringan diberikan pola masukan dan pola keluaran yang diinginkan.
Ketika suatu pola diberikan kepada jaringan, bobot-bobot diubah untuk memperkecil perbedaan pola keluaran dan pola yang diinginkan. Latihan ini dilakukan sehingga semua pola yang dikeluarkan jaringan dapat memenuhi pola yang diinginkan, seperti yang terlihat di arsitektur backpropagation pada Gambar 2.23.
Gambar 2.23 Arsitektur Jaringan Backpropagation (Muis, 2009)
Algoritma backpropagation dimulai dengan memberikan pola masukan ke dalam lapisan. Setiap pola merupakan nilai aktivasi unit-unit masukan, yang memiliki bobot dan dihitung jumlahnya dengan menggunakan:
=
(2.19)
dimana: Xj = jumlah bobot unit masukan j
Yi = nilai masukan yang berasal dari unit i
Wij = bobot dari unit i sampai ke j
Setelah jumlah bobot dari Xj dihitung dan ditemukan hasilnya, maka diterapkankanlah
fungsi sigmoid yang akan menghasilkan nilai antara 0 dan 1. Pada algoritma backpropagation, fungsi sigmod yang dipakai memiliki persamaan:
( ) = 1 1 +
(2.20)
Hasil perhitungan Yj merupakan nilai aktivasi pada unit pengolah j. Nilai ini
Di sini eror dihitung pada semua unit pengolah dan bobotpun diubah pada semua sambungan. Perhitungan dimulai dari lapisan keluaran dan mundur sampai lapisan masukan. Hasil keluaran dari umpan maju dibandingkan dengan hasil keluaran yang diinginkan. Berdasarkan perbedaan ini kemudian dihitung eror untuk tiap-tiap lapisan pada jaringan.
Pertama-tama, dihitung eror untuk lapisan keluaran, kemudian disesuaikan dengan setiap sambungan bobot-bobot yang menuju ke lapisan keluaran. Setelah itu dihitung nilai eror pada lapisan tersembunyi dan dihitung perubahan bobot yang menuju lapisan tersembunyi. Demikian proses dilakukan mundur sampai ke lapisan masukan secara iteratif. Jika j adalah salah satu unit pada lapisan keluaran, maka eror lapisan keluaran dapat ditentukan dengan persamaan:
= ( − ) ′( ) (2.21)
dimana: tj = keluaran yang diinginkan dari unit j
aj = keluaran dari unit j
′( ) = turunan dari fungsi sigmoid Xj = hasil penjumlahan berbobot
Jika j adalah suatu lapisan tersembunyi, maka eror lapisan tersembunyi dapat ditentukan dengan menggunakan persamaan:
= ′( )
(2.22)
∆ = ŋ (2.23)
dimana: ∆ = perubahan bobot dari unit i ke unit j ŋ = laju belajar (konvergensi)
δj = eror lapisan tersembunyi
Variabel ŋ menyatakan suatu konstanta belajar yang berharga antara 0,25 sampai 0,75. Nilai ini menunjukkan kecepatan belajar dari jaringan. Nilai yang terlalu tinggi dapat menyebabkan jaringan menjadi tidak stabil, sedangkan nilai yang terlalu kecil dapat menjadikan waktu belajar yang lama. Oleh karena ini pemilihan nilai ŋ harus seoptimal mungkin agar didapatkan proses belajar yangc cepat.
Begitu nilai keluaran dihitung, nilai tersebut akan dibandingkan dengan nilai keluaran yang dibutuhkan dengan nilai eror minumum E. Permukaan eror kadang-kadang mengalami penurunan sampai mencapai suatu kondisi minimum, yang kadang-kadang bisa naik kembali. Eror yang paling mimum, merupakan eror yang diinginkan. Eror minimum E dapat dipakai menggunakan persamaan:
= 1
Dalam backpropagation satu buah lapisan tersembunyi bisa dikatakan cukup memandai untuk menyelesaikan masalah sembarang fungsi sigmoid. Dengan menggunakan lebih dari satu buah lapisan tersembunyi, satu masalah lebih mudah untuk diselesaikan. Meskipun begitu, tidak ada ketentuan khusus mengenai banyaknya jumlah lapisan tersembunyi yang dibutuhkan (Ganatra et al. 2011). Dalam penelitian ini, penulis menggunakan 4 (empat) buah lapisan tersembunyi.
∆ = (2.25)
∆ = (2.26)
Jika eror tidak terjadi, maka menjadi 0 (nol) dan hal ini akan menyebabkan koreksi ∆ = 0, dengan kata lain pembaharuan bobot berlanjut dalam arah yang sama seperti yang sebelumnya. Jika parameter momentum digunakan, maka persamaan pembaharuan bobot dengan pelatihan t, dan t+1 untuk pelatihan selanjutnya, mengalami modifikasi sebagai berikut:
( + 1) = ( ) + + [ ( ) − ( −1) ] (2.27)
atau
( + 1) = + ∆ ( ) (2.28)
dan,
( + 1) = ( ) + + [ ( )− ( −1) ] (2.29)
atau
( + 1) = + ∆ ( ) (2.30)
dimana: Z1 … Zn = nilai lapisan tersembunyi
Vij = bobot dari lapisan masukan dan lapisan tersembunyi
Wij = bobot dari lapisan tersembunyi dan lapisan keluaran
δ = eror informasi
α = konstanta berkelanjutan
µ = momentum
2.3.4 Algoritma Backpropagation
Algoritma backpropagation dapat dibagi ke dalam dua bagian, yaitu: algoritma pelatihan dan algoritma aplikasi. Pada algoritma pelatihan terdapat 3 (tiga) tahap, yaitu: tahap umpan maju, tahap backpropagation error dan pembaharuan bobot. Sedangkan pada algoritma aplikasi hanya menggunakan tahap umpan maju. Berikut adalah algoritma backpropagation:
0. Inisialisasi bobot.
Tentukan angka pembelajaran (α).
Tentukan nilai ambang atau set siklus pelatihan (epoch) sebagai kondisi berhenti. 1. While kondisi berhenti tidak terpenuhi.
Do langkah ke-2 (dua) sampai ke-9 (sembilan).
2. Untuk setiap pasangan pelatihan, kerjakan langkah 3 (tiga) sampai langkah ke-8 (delapan).
Tahap umpan maju (feedforward)
3. Tiap unit masukan (xi, i = 1, …, n) menerima masukan xi dan diteruskan ke lapisan tersembunyi.
4. Tiap unit tersembunyi (zj, j = 1, …, p) menjumlahkan nilai masukan terbobot
_ = +
(2.31)
dengan menerapkan fungsi aktivasi hitung:
= ( _ ) (2.32)
dan dikirim ke unit-unit keluaran.
5. Tiap unit keluaran (yk, k = 1, …, m) menjumlahkan nilai masukan terbobot
_ = +
dengan menerapkan fungsi aktivasi hitung:
= ( _ ) (2.34)
Tahap backpropagation error
6. Tiap unit keluaran (yk, k = 1, …, m) menerima target pola yang berkaitan dengan
pola input pembelajaran, yang kemudian dihitung nilai erornya menggunakan persamaan (2.19) dan dimodifikasi menjadi:
= ( − ) ′( _ ) (2.35)
gunakan koreksi bobot untuk memperbaiki nilai wjk pada persamaan (2.25) dan
koreksi bias untuk memperbaiki nilai w0k menggunakan:
∆
= (2.36)lalu kirim ke lapisan tersembunyi di bawahnya.
7. Tiap unit tersembunyi (zj, j = 1, …, p) menjumlahkan delta inputnya dari unit-unit
yang berada di atasnya.
_ =
(2.37)
Nilai ini dikalikan dengan turunan dari fungsi aktivasinya untuk mendapatkan nilai eror, seperti pada persamaan (2.24), sehingga menghasilkan:
= _ ′( _ ) (2.38)
gunakan koreksi eror pada persamaan (2.26) untuk memperbaiki nilai vij dan
koreksi bias untuk memperbaiki nilai v0j menggunakan:
Tahap update bobot, bias dan indeks.
8. Tiap unit keluaran (yk, k = 1, …, m) memperbaharui bobot-bobot dan indeksnya (j
= 0, 1, …, p) menggunakan persamaan (2.28), yang dapat disederhanakan sebagai:
( ) = ( ) + ∆ (2.40)
Tiap nilai unit tersembunyi (zj, j = 1, …, p) memperbaharui bobot dan indeksnya (i
= 0, 1, …, n) menggunakan persamaan (2.30), yang dapat disederhanakan sebagai:
( ) = ( ) + ∆ (2.41)
9. Tes kondisi berhenti.
2.4 Format File JPEG
Pada penelitian ini, citra yang digunakan adalah citra berformat JPEG (Joint Photographic Expert Group) atau JPG. JPEG menggunakan teknik kompresi yang menyebabkan kualitas citra turun (lossy compression). Setiap kali menyimpan file ke tipe JPG dari tipe lain, ukuran gambar akan mengecil, kualitas citra turun dan tidak dapat dikembalikan lagi. Pada gambar-gambar tertentu, penurunan kualitas citra hampir tidak terlihat oleh mata.
File JPEG digunakan untuk citra yang memiliki banyak warna karena format ini memiliki kedalaman warna 24 bit atau sekitar 16 juta warna dan umumnya digunakan untuk menyimpan citra hasil foto. Format file ini mampu menyimpan citra dengan mode warna RGB, CMYK dan grayscale. Karakteristik JPEG memiliki ekstensi .jpg atau .jpeg.
2.5 Penelitian Terdahulu
Pada tahun 2005, Devireddy dan Rao menggunakan metode BP untuk mendeteksi tulisan tangan. Pada penelitian tersebut dibuktikan bahwa sistem memiliki kemampuan untuk mengenali pola tanpa harus terpengaruh dari perubahan posisi dari sebuah nilai input. Citra juga dapat digunakan dalam pengenalan wajah menggunakan algoritma genetic dan BP untuk meningkatkan efisiensi kecocokan wajah (Anam et al. 2009). Selain itu, pendeteksian juga dapat dilakukan dengan mencari perbedaan rotasi perubahan sebuah cita menggunakan LED Angle (light-emitting diode deflection angle) sehingga dapat mengenali objek dari sudut berbeda (Li, 2011). Peneletian juga dapat digunakan dengan menggabungkan beberapa metode untuk meningkatkan hasil pendeteksian yang lebih akurat, dengan menggunakan dua metode pendekatan (Bhatia, 2011).
Adapun beberapa penelitian sebelumnya yang telah dilakukan untuk mendeteksi cita berdasarkan masa lalunya, dapat dilihat pada Tabel 2.1.
Tabel 2.1 Penelitian Sebelumnya
No Judul Pengarang Tahun Kelebihan Kekurangan