Bab 5 Sinyal dan Sistem Waktu Diskrit - Sinyal sistem bab5 rev 03

Bab 5

Sinyal dan Sistem Waktu Diskrit

Oleh:

Tri Budi Santoso

Laboratorium Sinyal, EEPIS-ITS

Edited by Foxit Reader

Copyright(C) by Foxit Corporation,2005-2009

Materi:

Tujuan:

• Siswa mampu menyelesaikan konsep dasar

transformasi Fourier Waktu Diskrit

Sub Bab:

5.1. Transformasi Fourier Waktu Kontinyu

5.2. Discrete-Time Fourier Series (DTFT)

5.3. Discrete-Fourier Transform (DFT)

5.4. Komputasi DFT

5.5. Komputasi Inverse DFT

5.6. Interpretasi Hasil DFT

5.1. Continues Time Fourier Transform

• Sinyal periodik waktu kontinyu f(t) dengan periode T dinyatakan sebagai bentuk weighted sum pada complex exponential:

dimana:

F_k = koefisien-koefisien ekspansi

Ω₀ = frekuensi fundamental Î Ω₀ =π/T

t

e

F

t

f

k

jk k

∑

∞

−∞ =

Ω

=

0

)

(

Î untuk semua nilai t (1)

∫

− Ω

= T jk

k f t e tdt

T F

0

0

Lanjutan….

• Persamaan (1) dikenal sebagai deret Fourier eksponensial komplek • Dalam terminologi deret geometri seringkali dinyatakan sebagai

(

)

∑

∞ =

Ω

+

Ω

+

=

1 0 0

0

cos

sin

)

(

k

k

k

k

t

b

k

t

a

a

t

f

∫

=

=

T

F

dt

t

f

T

a

0 0 0

(

)

1

(2)

(3)

∫

Ω

=

+

−

=

T k k

k

f

t

k

dt

F

F

T

a

0 0

cos

)

(

2

(

)

∫

Ω

=

−

=

₋ T k k

k

f

t

k

dt

F

F

j

5.2. Discrete-Time Fourier Series (DTFT)

• Untuk sinyal periodik waktu diskrit x(n) dengan periode N. Kita kenal frekuensi digital 0 ~ 2π. Ekspansinya dinyatakan dalam:

∑

−

=

=

1

0

0

)

(

1

)

(

N

k

n jk

e

k

X

N

n

x

ω ₍₆₎

(7)

∑

−

=

−

=

1

0

0

)

(

)

(

N

k

n jk

e

n

x

k

X

ω

Persamaan (6) dan (7) dikenal sebagai pasangan Discrete Fourier Series (DFS)

Dalam hal ini

ω₀ = frekuensi fundamental = 2π/sampling rate

Lanjutan….

• Untuk N genap:

• Untuk N ganjil:

n

N

A

n

N

k

k

B

n

N

k

k

A

A

n

x

N k N k

π

π

π

cos

2

2

sin

)

(

2

cos

)

(

)

0

(

)

(

1 ) 2 / ( 1 1 ) 2 / ( 1

⎟

⎠

⎞

⎜

⎝

⎛

+

⎟

⎠

⎞

⎜

⎝

⎛

+

⎟

⎠

⎞

⎜

⎝

⎛

+

=

∑

∑

− = − =

∑

∑

− = − =

⎟

⎠

⎞

⎜

⎝

⎛

+

⎟

⎠

⎞

⎜

⎝

⎛

+

=

( 1)/2

1 2 / ) 1 ( 1

2

sin

)

(

2

cos

)

(

)

0

(

)

(

N k N k

n

N

k

k

B

n

N

k

k

A

A

n

x

π

π

……….(8a)

Lanjutan

Untuk N Genap:

5.3. Disc re te -Fo urie r Tra nsfo rm (DFT)

• Bisa digunakan untuk sinyal periodik dan non periodik

• Dimana ω₀=2π/N • Bentuk Inversnya:

• Dalam terminologi (W_N=e-j2π/N_{) dinyatakan:}

1

0

)

(

)

(

1 0

0

≤

≤

−

=

∑

− = −

N

k

e

n

x

k

X

N n n

jkω

(10)

1

0

)

(

1

)

(

1 0

0

≤

≤

−

=

∑

− =

N

n

e

k

X

N

n

x

N n n

jkω

(11)

Sifat-Sifat DFT

• Secara umum sama dengan sifat Transformasi Fourier waktu kontinyu.

• Tetapi durasi untuk n dibatasi 0 s/d N-1. Maka setelah n = N-1, akan berputar kembali pada nilai n = 0.

• Dari beberapa sifat tsb, kita bahas 4 saja, yaitu: - Sifat Linearitas

- Sifat Circular Translation

a. Sifat Linearitas

DFT[a

₁

x

₁

(n)] = a

₁

X

₁

(k) , DFT[a

₂

x

₂

(n)] = a

₂

X

₂

(k)

Maka:

DFT[a

₁

x

₁

(n) + a

₂

x

₂

(n)] = a

₁

DFT[x

₁

(n)] + a

₂

DFT[x

₂

(n)]

b. Sifat Circular Translation

• Pada kasus translasi linearÆx(n-n₀) merupakan

bentuk pergeseran ke kanan.

• Tetapi pada kasus sinyal non-periodik (n = 0 s/d N-1), maka pergeseran terbatas sampai dengan N-1.

Setelah itu kembali ke n=0Î Modulo N, maka

bentuknya menjadi

N=8 0

1

2

3 4 5

6 7

x(n) = [x(0), x(1),……, x(N-2), x(N-1)]

x((n-1)mod N) = [x(N-1), x(0),……, x(N-3), x(N-2)] ……

x((n-n₀)mod N) = [x(N-n₀), x(N-n₀+1),……., x(N- n₀ -1)] ……

x((n-N)mod N) = [x(0), x(1),……, x(N-2), x(N-1)]

DFT[(n-N)mod N]=W_Nkm_X(k)

c. Sifat Perkalian dengan Eksponensial

Jika

DFT[x(n)] = X(k)

Maka DFT[W

_N-ln

x(n)] =X((k-l) mod N)

d. Sifat Circular Convolution

• Konvolusi Linear:

• Konvolusi Circular:

)

(

)

(

)

(

)

(

)

(

)

(

_{2 1 2 1 2}

1

n

x

n

x

n

k

x

k

atau

x

k

x

n

k

x

k k

−

−

=

∗

∑

∑

∞ −∞ = ∞ −∞ =

[

]

( ) ( )

[

] [

]

{

(

)

(

)

}

)

(

)

(

)

(

)

(

2 1 1 2 1 2 1 2 1

n

x

F

n

x

F

F

n

x

n

x

e

X

e

X

n

x

n

x

F

j j

⋅

=

∗

=

∗

− ω ω

(

)

(

)

∑

∑

− = − =

−

=

−

∆

⊗

1 0 2 1 1 0 2 1 2 1

mod

)

(

)

(

)

(

mod

)

(

)

(

)

(

N k N k

N

k

n

x

k

x

k

x

N

k

n

x

n

x

n

x

Dimana x

₁

(n-k)mod N) merupakan versi ter-refleksi dan

ter-translasi (geser) pada x

₁

(n)

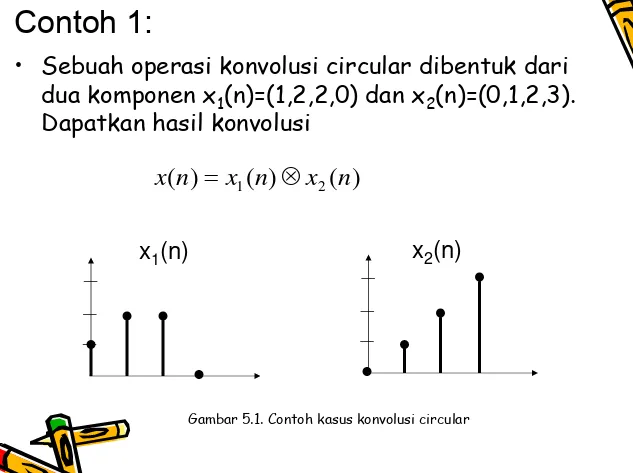
Contoh 1:

• Sebuah operasi konvolusi circular dibentuk dari

dua komponen x

₁

(n)=(1,2,2,0) dan x

₂

(n)=(0,1,2,3).

Dapatkan hasil konvolusi

)

(

)

(

)

(

n

x

₁

n

x

₂

n

x

=

⊗

x

₁

(n)

x

₂

(n)

Penyelesaian:

Step 2: x₁(k) = (1, 2, 2, 0) x₂((1-k)mod 4)= (1, 0, 3, 2)

--- + y(0) = 1 0 6 0

= 7 Step 1: x₁(k) = (1, 2, 2, 0)

x₂((0-k)mod 4)= (0, 3, 2, 1) --- + y(0) = 0 6 4 0

= 10

Step 3: x₁(k) = (1, 2, 2, 0) x₂((2-k)mod 4)= (2, 1, 0, 3)

--- + y(0) = 1 2 0 0

= 4

Step 4: x₁(k) = (1, 2, 2, 0) x₂((3-k)mod 4)= (3, 2, 1, 0)

--- + y(0) = 3 4 2 0

= 9

Step 5: x₁(k) = (1, 2, 2, 0) x₂((0-k)mod 4)= (0, 3, 2, 1)

--- + y(5) = 0 6 4 0

= 10

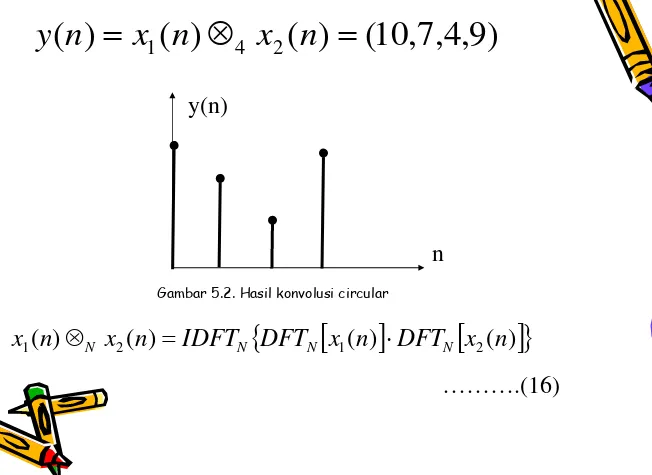
Hasilnya:

)

9

,

4

,

7

,

10

(

)

(

)

(

)

(

n

=

x

₁

n

⊗

₄

x

₂

n

=

y

n

y(n)

[

]

[

]

{

(

)

(

)

}

)

(

)

(

_{2 1 2}

1

n

x

n

IDFT

DFT

x

n

DFT

x

n

x

⊗

_N

=

_{N N}

⋅

_N

……….(16)

5.5. Computation of Inverse DFT

( )

∑

−

=

−

=

−

⎟

⎠

⎞

⎜

⎝

⎛

=

1

0

1

,....,

1

,

0

;

1

)

(

N

k

kn

N

n

N

W

k

X

N

n

x

5.6. Interpretation of DFT Result

x(n)

Î

versi diskrit (tersampel) pad asinyal analog x

_a

(t)

Frekuensi indek

(tanpa satuan)

k

Frekuensi digital

(radiant)

ω

_k

= k2

π

/N

Frekuensi indek

(tanpa satuan)

Ω

_k

= k2

π

/NT

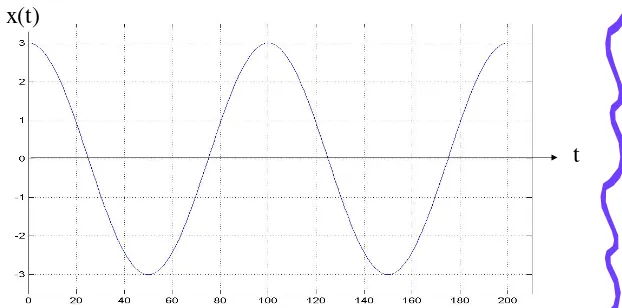
Contoh 2

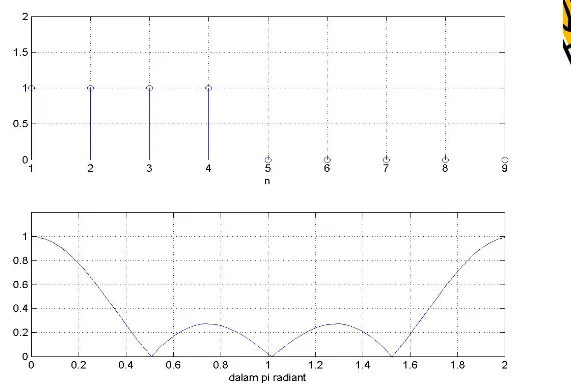
• Dapatkan transformasi Fourier dari sinyal cosinus yang

memiliki periode eksak di dalam window yang terdapat pada sampel. Tetapkan x(n) seperti pada Gambar dibawah yang direpresentasikan sebagai x(t) = 3cos(2πt), pada t=nT. Untuk suatu n = 0~ 99, dan T=0,01.

t

x(t)

Penyelesaian

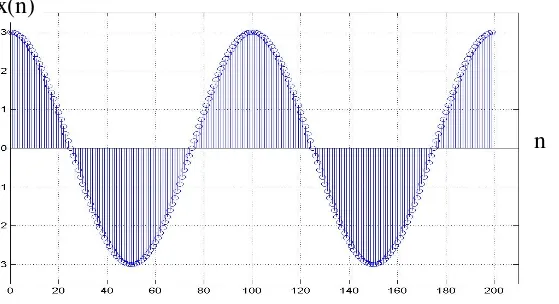
• Didapatkan sekuen diskrit sebagai

x(n) = 3cos(2πnT) = 3cos(0.02πn) untuk

n =0,1,….,199. Perlu dicatat bahwa x(n) merupakan sinyal cosinus sepanjang dua periode.

n

x(n)

• Bagian real X

_R

(k) dan imajiner X

_I

(k) dapat

dihitung dari persamaan (11).

1

0

)

(

)

(

1

0

0

≤

≤

−

=

∑

−

=

−

N

k

e

n

x

k

X

N

n

n jkω

(

)

(

) (

(

)

(

)

)

∑

−

=

−

=

1

0

0 0

sin

cos

02

,

0

cos

3

)

(

N

n

n

k

j

n

k

n

k

X

π

ω

ω

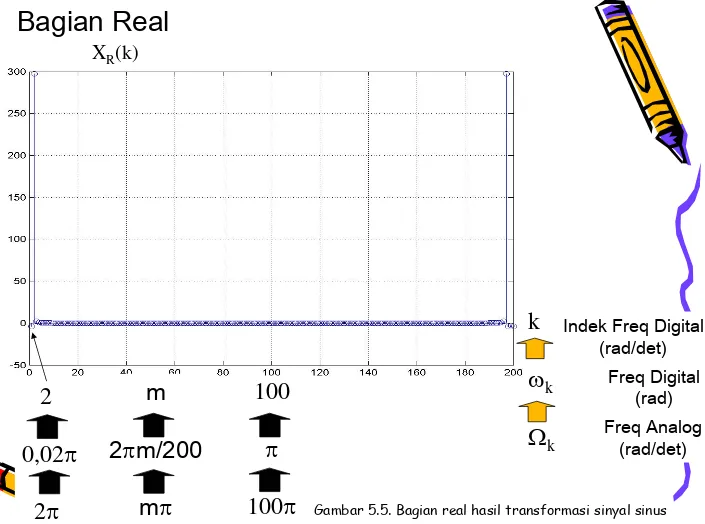
Bagian Real

X_R(k)

2

0,02

π

2

π

Freq Analog (rad/det) Freq Digital

(rad) Indek Freq Digital

(rad/det)

k

ω

_k

Ω

_k

m

2

π

m/200

m

π

100

π

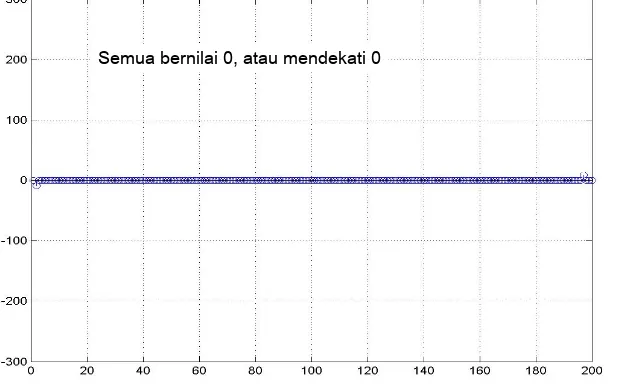
Bagian Imaginer

Semua bernilai 0, atau mendekati 0

Perhatikan pada bagian Real, ada dua nilai muncul

yaitu pada indek frekuensi (2) dan (N-2 =198).

Masing-masing dengan nilai 300. Ini

merepresentasikan (AN/2), dimana:

- A=3

Î

amplitudo

- N = 300

Î

jumlah sampel yang digunakan

Karena struktur sampling, frekuensi indek 2 berkaitan

secara tepat dengan penuh pada gelombang cosinus.

Contoh 3

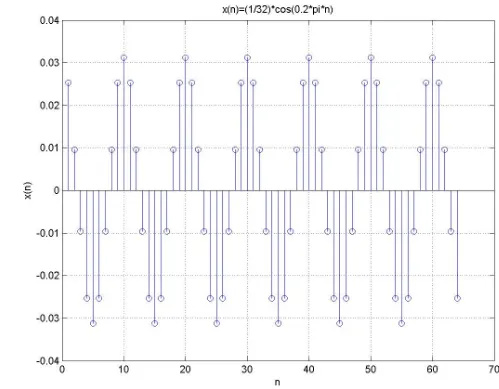
• Gambarkan magnitudo pada DFT 64 titik pada x(n) = (1/32) sin (0,2πn). Dengan nilai n=0,1,…,63

Penyelesaian

X(k) = X

_R

(k) + X

_I

(k)

Magnitudonya:

( ) ( )

k

X

k

X

( ) ( )

k

X

k

X

k

X

(

)

=

_{R R}

+

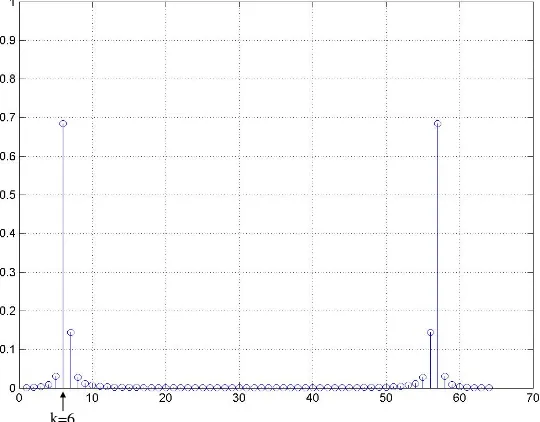
_{I I}

Seperti terlihat pada gambar sebelumnya, dengan persamaan tersebut terjadi 6,4 gelombang sinus.

Jika gelombang sinus tepat pada 1 periode penuh, |X(k)| akan memiliki nilai (AN/2), sehingga:

1

2

64

32

1

2

⎟

⎠

=

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

=

AN

k=6

5.7. Hubungan DFT-Fourier Transform

• Transformasi Fourier

• Discrete Fourier Transform

( )

∑

( )

∑

−

( )

=

− ∞

−∞ =

−

=

=

1

0

N

n

n j n

n j j

e

n

x

e

n

x

e

X

ω ω ω

( )

( )

(

)

1

,...,

1

,

0

1

0

/

2

=

−

=

∑

−

=

−

N

k

e

n

x

k

X

N

n

Sinyal Tersampel dan Transformasi Fouriernya

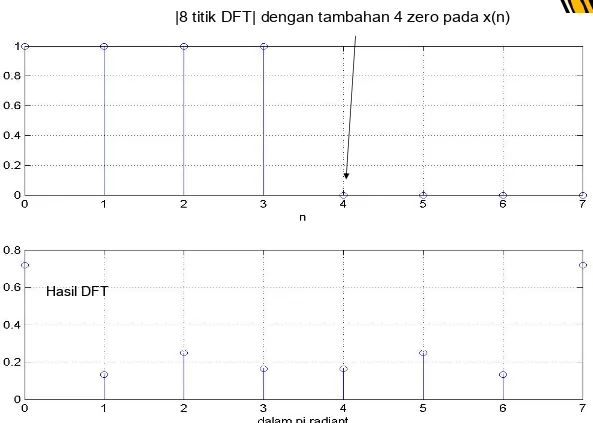
Zero Padding

|8 titik DFT| dengan tambahan 4 zero pada x(n)

Hasil DFT

|16 titik DFT| dengan tambahan 12 zero pada x(n)

Hasil DFT

|64 titik DFT| dengan tambahan 60 zero pada x(n)

Hasil DFT

Contoh Lain DFT pada Sinyal Sinus

x(n) = (1/64)*(sin(2*pi*n/64) + (1/3)*sin(2*pi*15*n/64))

Soal Latihan

[ ]

⎩ ⎨ ⎧ = = = 9 ,..., 2 , 1 ; 0 0 ; 1 ) n n n x a

[ ]

; 0,1,2,...,9 )x n = e 2 5 n =

d j πn

[ ]

⎩ ⎨ ⎧ = = = 9 ,... 2 , 1 ; 0 0 ; 1 ) k k k X a _a

1. Dapatkan bentuk transformasi Fourier (DFT)10-point untuk sinyal waktu diskrit berikut ini:

2. Dapatkan bentuk invers Transformasi Fourier (IDFT) 10-point untuk sinyal berikut ini:

[ ]

1 ; 0,1,2,...,9 ) X k = k =

b _b

[ ]

1 ; 1,2,...,9 )x n = n =

b

[ ]

⎩ ⎨ ⎧ ≠ = = 4 ; 0 4 ; 1 ) n n n x c

[ ]

⎩

⎨

⎧

=

=

=

9

,

8

,

6

,

5

,

4

,

2

,

1

,

0

;

0

7

,

3

;

1

)

k

k

k

X

c

_c

[ ]

cos

(

2

/

5

)

;

0

,

1

,

2

,...,

9

)

X

k

=

k

k

=

3. Sebuah sinyal waktu diskrit dinyatakan dalam bentuk komplek berikut ini

[ ]

( )

1

,...

2

,

1

,

0

;

/ 2

1

n

=

e

n

=

N

−

x

j πk N n

Dapatkan bentuk transformasi Fourier waktu diskrit (DFT) dari x[n] sebanyak N-titik

4. Sebuah sinyal waktu diskrit tersusun dari fungsi sinusioda: x₂[n]=cos(2π_kn/N)

Dapatkan bentuknya dalam domain frekuensi N-titik

5. Buatlah sebuah program visualisasi dengan Matlab untuk domain waktu dan domain frekuensi untuk sinyal berikut ini:

6. Buat visualisasi sinyal domain waktu & frekuensi sinyal ini:

a). 1,1,1,1,0,0,0,……0,0 b). 1,1,1,1,0,0,0,……….0,0

c). 1,1,1,1,0,0,0,………0,0 d). 1,1,1,1,0,0,0,……….0,0 16 titik _{32 titik}

64 titik _{128 titik} 7. Buat visualisasi domain waktu dan domain frekuensi untuk sinyal: a) x[n] = sinc(2π_{n/10) ; n = -30,-29,…..-1,0,1,……..,29,30}

b)

⎪

⎩

⎪

⎨

⎧

=

=

−

−

−

−

=

=

30

,

29

...,

,...

2

,

1

;

0

0

;

1

1

,

2

,....,

29

,

30

;

0

]

[

n

n

n

n