1
Pengantar Penerjemah
Saya awali tulisan ini dengan Nama Alloh Sang Maha Pengasih Sang Maha Penyayang. Segala Puji bagi-Nya yang telah mengajarkan ilmu kepada siapa saja yang dikehendaki-Nya.
Sungguh, saya merasa terbantu dengan dokumen “Introduction to Kalman Filter” oleh Greg Welch & Gary Bishop, 2012, dalam memahami esensi kalman filter diskrit. Saya coba terjemahkan, mungkin dapat membantu pembaca yang enggan berlama-lama dengan bahasa Inggris namun tertarik memahami konsep kalman filter diskrit. Bagian tentang Extended Kalman Filter belum sempat saya terjemahkan, semoga bisa dilanjutkan di lain waktu. Semoga bermanfaat.
Surabaya, 4 Maret 2014 / 2 Jumadil ula 1435H
Penerjemah: mochamad nur qomarudin, alfiyahibnumalik@gmail.com Dokumen ini saya publish di: mnurqomarudin.blogspot.com
Daftar Istilah
Beberapa istilah yang banyak disebut dalam dokumen iniEstimasi: pencarian nilai sebenarnya dari nilai yang sudah tercampur dengan noise Filter: alat/algoritma untuk estimasi
Step: waktu diskrit, bilangan bulat, disimbolkan dengan k
Diskrit: sinyal yang hanya memiliki nilai pada saat-saat tertentu, dengan interval waktu yang konstan, cth. memiliki nilai setiap 5 detik
Noise: gangguan yang menimpa sinyal
Kovarian: yg dimaksud dalam dokumen ini adalah Varian, yaitu besaran statistik yang menyatakan kuadrat dari standar deviasi
Momen: istilah lain dari fungsi ekspektasi, cth. ekspektasi orde satu disebut momen pertama White noise: noise yang memiliki magnitude yang tetap untuk semua frekuensi
2
[TERJEMAHAN]
Pengenalan Kalman Filter
Greg Welch1 Gary Bishop219 Juni 2012 TR 95-041
Department of Computer Science University of North Carolina Chapel Hill
Chapel Hill, NC 27599-3175 Diperbarui: Senin, 24 Juli 2006 Abstrak
Di tahun 1960, R. E. Kalman mempublikasikan makalahnya yang menjelaskan sebuah solusi rekursif terhadap persoalan filter linier untuk data diskrit. Sejak saat itu, Kalman Filter menjadi topik penelitian dan terapan yang luas, terutama di bidang navigasi otomatis atau terpandu. Kalman Filter merupakan sekumpulan persamaan matematik yang menawarkan cara komputasi rekursif dan efisien untuk mengestimasi state dari sebuah proses, sedemikian rupa sehingga meminimumkan rata-rata dari kuadrat error. Filter ini sangat berguna dalam beberapa aspek: mendukung estimasi state yang telah lalu, saat ini, dan juga state masa depan, dan mampu bekerja meskipun sifat-sifat model sistem tidak diketahui.
Tujuan dari makalah ini adalah untuk memberi pengenalan praktis tentang Kalman Filter diskrit. Pengenalan ini meliputi deskripsi dan beberapa diskusi tentang dasar Kalman Filter diskrit, penurunan, deskripsi dan beberapa diskusi tentang Extended Kalman Filter, dan contoh sederhana dengan bilangan nyata beserta hasilnya.
Kalman Filter Diskrit
Di tahun 1960, Kalman mempublikasikan makalahnya yang menjelaskan sebuah persoalan penyaringan linier data diskrit [Kalman, 60]. Sejak saat itu, Kalman Filter menjadi topik penelitian dan terapan yang luas, terutama di bidang navigasi otomatis atau terpandu. Pengenalan tentang gagasan umum Kalman Filter yang paling mudah dipahami dapat disimak dalam Bab 1 dari [Maybeck79], sedangkan pengenalan yang lebih kompleks dapat dibaca di dalam [Sorenson70], yang juga memuat beberapa cerita sejarah yang menarik. Pustaka lain untuk lebih lanjut meliputi [Gelb74; Grewal93; Maybeck79; Lewis86; Brown92; Jacobs93].
1 welch@cs.unc.edu, http://www.cs.unc.edu/welch 2 gb@cs.unc.edu, http://www.cs.unc.edu/gb
3
Proses yang Diestimasi
Persoalan umum untuk Kalman Filter diskrit adalah mencoba untuk mengestimasi state 𝑥 ∈ ℜ𝑛 dari sebuah proses waktu diskrit yang dinyatakan oleh persamaan beda stokastik linier
1 1 1 k k k k Ax Bu w x (1.1)
dengan pengukuran 𝑧 ∈ ℜ𝑚 yang dinyatakan k k k Hx v
z (1.2)
wk dan vk adalah variabel acak yang mewakili noise proses dan noise pengukuran, keduanya independen, jenis white noise, dengan probabilitas berdistribusi normal.
) , 0 ( ~ ) (w N Q p (1.3) ) , 0 ( ~ ) (v N R p (1.4)
Dalam praktik, kovarian noise proses Q dan kovarian noise pengukuran R bisa berubah dalam tiap waktu atau pengukuran, namun di sini keduanya diasumsikan konstan.
Matriks A (nxn) dalam persamaan beda (1.1) menghubungkan state pada waktu diskrit sebelumnya, yaitu k-1, dengan state pada waktu diskrit sekarang, yaitu k, tanpa pengaruh fungsi pemicu u atau noise proses w. Dalam praktik, A bisa berubah dalam tiap waktu, tapi di sini kita asumsikan konstan. Matriks B (nxl) menghubungkan input kontrol u ϵ Rl dengan state x, u bersifat opsional (bisa ada / tidak). Matriks H (mxn) dalam persamaan pengukuran (1.2) menghubungkan state dengan pengukuran 𝑧𝑘. Dalam praktik, H bisa berubah dalam tiap waktu atau pengukuran, tapi di sini kita asumsikan konstan.
Komputasi Filter
Kita definisikan 𝑥̂𝑘− ∈ ℜ𝑛 (perhatikan notasi “minus” di atas) sebagai pra-estimasi state pada step k berdasarkan data dari proses (1.1) sebelum step k, dan 𝑥̂𝑘 ∈ ℜ𝑛 sebagai pasca estimasi state pada step k berdasarkan nilai 𝑧𝑘. Lalu, kita definisikan pra dan pasca estimasi untuk error sebagai k k k x x e , dan k k k x x e
Kovarian pra-estimasi error adalah
] E[ k kT
k e e
P
(1.5) dan kovarian pasca-estimasi error adalah
4
] E[ k kT k e e
P (1.6)
Dalam menurunkan persamaan untuk kalman filter, kita mulai dengan persamaan yang menghitung pasca-estimasi state 𝑥̂𝑘 yang dibangun dari kombinasi pra-estimasi 𝑥̂𝑘− dan selisih antara nilai ukur aktual 𝑧𝑘 dan prediksi nilai ukur 𝐻𝑥̂𝑘− sebagai berikut (1.7). Beberapa pertimbangan untuk (1.7) dapat dibaca dalam buku “The Probabilistic Origins of the Filter” kami sertakan di bawah
𝑥̂𝑘 = 𝑥̂𝑘−+K(𝑧𝑘− 𝐻𝑥̂𝑘−) (1.7) selisih (𝑧𝑘− 𝐻𝑥̂𝑘−) di (1.7) disebut perbaikan atau selisih pengukuran. Selisih ini mewakili ketidaksesuaian antara nilai ukur yang diprediksi 𝐻𝑥̂𝑘− dan nilai ukur sebenarnya 𝑧𝑘. Selisih nol berarti nilai keduanya sama persis.
Matrix K (nxm) di (1.7) dipilih sebagai faktor penguat (gain) yang meminimumkan kovarian pasca-estimasi error (1.6). Untuk penjelasan detil, lihat [Maybeck79; Brown92; Jacobs93]. Salah satu formulasi K yang meminimumkan (1.6) adalah3
𝐾𝑘 = 𝑃𝑘−𝐻𝑇(𝐻𝑃
𝑘−𝐻𝑇+ 𝑅)−1 (1.8)
𝐾𝑘 =
𝑃𝑘−𝐻𝑇
𝐻𝑃𝑘−𝐻𝑇+ 𝑅
Pada (1.8) kita lihat bahwa kovarian error pengukuran R mendekati nol, sehingga gain K membuat selisih pengukuran berpengaruh lebih besar. Secara matematis,
lim
𝑅𝑘→0
𝐾𝑘 = 𝐻−1
Di sisi lain, bila kovarian pra-estimasi error 𝑃𝑘− mendekati nol, maka gain K membuat selisih pengukuran berpengaruh lebih kecil. Secara matematis,
lim
𝑃𝑘−→0𝐾𝑘 = 0
Cara lain untuk memahami peran gain K adalah: bila kovarian error pengukuranR mendekati nol, nilai ukur aktual 𝑧𝑘 jauh lebih dipercaya kebenarannya, sedangkan prediksi nilai ukur
𝐻𝑥̂𝑘− semakin tidak dapat dipercaya kebenarannya. Bila kovarian pra-estimasi error 𝑃𝑘−
mendekati nol, nilai ukur aktual 𝑧𝑘 semakin tidak dapat dipercaya, sedangkan prediksi nilai ukur 𝐻𝑥̂𝑘− semakin dapat dipercaya kebenarannya.
3 Semua persamaan Kalman filter dapat direkayasa menjadi beberapa bentuk. Persamaan (1.8) mewakili salah
5
Konsep Probabilitas dalam Filter
Pertimbangan dalam penentuan (1.7) berakar pada probabilitas pra-estimasi 𝑥̂𝑘− yang bersyarat pada semua nilai ukur 𝑧𝑘 sebelumnya (aturan Bayes). Kalman filter melibatkan dua momen pertama dari distribusi variabel state,
𝐸[𝑥𝑘] = 𝑥̂𝑘
𝐸[(𝑥𝑘− 𝑥̂𝑘)(𝑥𝑘− 𝑥̂𝑘)𝑇] = 𝑃𝑘
Nilai pasca-estimasi state (1.7) mewakili rata-rata / mean (momen pertama) dari distribusi state – nilai ini berdistribusi normal bila kondisi (1.3) dan (1.4) dipenuhi. Kovarian pasca-estimasi error (1.6) mewakili varian dari distribusi state (momen ke dua non-sentral). Dengan kalimat lain,
𝑝(𝑥𝑘|𝑧𝑘)~𝑁(𝐸[𝑥𝑘], 𝐸[(𝑥𝑘− 𝑥̂𝑘)(𝑥𝑘− 𝑥̂𝑘)𝑇])
𝑝(𝑥𝑘|𝑧𝑘) = 𝑁(𝑥̂𝑘, 𝑃𝑘) Penjelasan lebih lanjut, baca [Maybeck79; Brown92; Jacobs93].
Algoritma Kalman Filter Diskrit
Kita awali bagian ini dengan pengantar ringkas, memuat konsep operasional umum dari salah satu tipe Kalman filter diskrit (lihat catatan kaki sebelumnya). Selanjutnya, kita akan fokus pada persamaan-persamaan spesifik dan kegunaannya untuk tipe ini.
Kalman filter mengestimasi satu proses melalui mekanisme kontrol umpan-balik: Filter mengestimasi state dari proses kemudian mendapat umpan balik berupa nilai hasil pengukuran yang bercampur noise. Persamaan untuk Kalman filter dikelompokkan dalam dua bagian: persamaan update waktu dan persamaan update pengukuran. Persamaan update waktu bertugas untuk mendapatkan nilai pra-estimasi untuk waktu step selanjutnya. Persamaan update pengukuran bertugas untuk keperluan umpan balik, seperti memadukan hasil pengukuran terbaru dengan nilai pra-estimasi untuk mendapatkan nilai pasca-estimasi yang lebih baik.
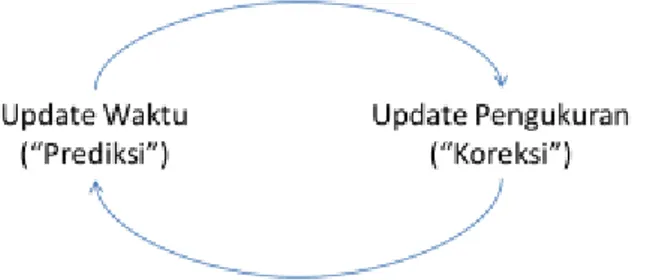
Persamaan update waktu disebut juga persamaan prediksi, sedangkan persamaan update pengukuran disebut persamaan koreksi. Algoritma estimasi Kalman filter menyerupai algoritma prediksi-koreksi untuk menyelesaikan masalah numerik sebagaimana pada Gambar 1-1.
6
Gambar 1-1. Siklus kerja Kalman filter diskrit. Update waktu membuat prediksi nilai state. Update pengukuran, menyesuaikan nilai prediksi dengan nilai ukur aktual.
Persamaan spesifik untuk update waktu dan pengukuran disertakan dalam Tabel 1-1 dan Tabel 1-2.
Tabel 1-1: Persamaan update waktu untuk Kalman filter diskrit
𝑥̂𝑘− = 𝐴𝑥̂𝑘−1+ 𝐵𝑢𝑘−1 (1.9)
𝑃𝑘− = 𝐴𝑃𝑘−1𝐴𝑇+ 𝑄 (1.10) Perhatikan, persamaan update waktu memproyeksikan (memprediksi) nilai state dan estimasi kovarian dari waktu step k-1 menuju step k. A dan B dari (1.1), dan Q dari (1.3). Kondisi awal untuk filter telah dibahas pada referensi terdahulu.
Tabel 1-2: Persamaan update pengukuran untuk Kalman filter diskrit
𝐾𝑘 = 𝑃𝑘−𝐻𝑇(𝐻𝑃𝑘−𝐻𝑇+ 𝑅)−1 (1.11)
𝑥̂𝑘 = 𝑥̂𝑘−+K(𝑧𝑘− 𝐻𝑥̂𝑘−) (1.12)
𝑃𝑘 = (1 − 𝐾𝑘𝐻)𝑃𝑘− (1.13) Tugas pertama dalam Update pengukuran adalah menghitung Kalman Gain, Kk. Persamaan Kalman gain di sini (1.11) sama dengan (1.8). Selanjutnya mengukur nilai proses aktual 𝑧𝑘, kemudian menghitung pasca-estimasi state dengan melibatkan nilai hasil pengukuran sebagaimana (1.12). Persamaan (1.12) sama dengan (1.7). Tugas terakhir adalah mendapatkan nilai pasca-estimasi kovarian error melalui (1.13).
Setelah menjalani satu siklus update waktu dan pengukuran, siklus ini diulang yang mana nilai pasca-estimasi sebelumnya digunakan untuk memprediksi nilai pra-estimasi yang baru. Sifat rekursif ini adalah satu sifat penting dari Kalman filter – membuat implementasi praktis jauh lebih sederhana daripada implementasi Wiener filter [Brown92] yang dirancang untuk beroperasi dengan melibatkan semua data secara langsung dalam setiap kali estimasi. Gambar 1-2 menampilkan operasi Kalman filter secara menyeluruh.
Parameter Filter dan Penyesuaiannya
Dalam implementasi filter, kovarian noise pengukuran R biasanya diukur sebelum filter dioperasikan. Pengukuran koverian error pengukuran R umumnya dapat dilakukan karena
7
kita dapat mengambil sampel pengukuran secara offline untuk menentukan varian dari noise pengukuran.
Penentuan kovarian noise proses Q umumnya lebih sulit, karena kita tidak dapat mengamati proses secara langsung. Terkadang satu model proses yang sederhana dapat menghasilkan estimasi yang baik dengan pemilihan Q yang tepat, bila pengukuran terhadap proses dapat diandalkan.
Pada keadaan yang lain, seringkali penyesuaian (tuning) parameter filter Q dan R dapat menghasilkan performansi filter yang “superior” (secara statistik). Mekanisme penyesuaian ini biasanya dijalankan secara offline, terkadang dengan bantuan Kalman filter tipe yang lain. Proses penyesuaian ini disebut identifikasi sistem.
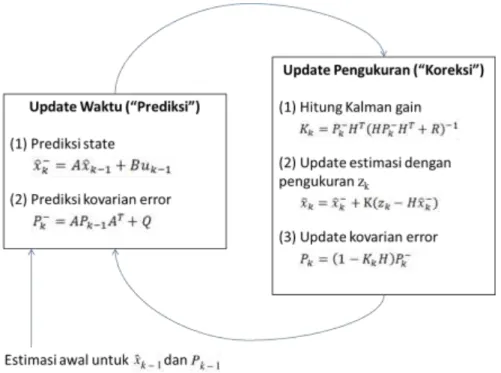
Gambar 1-2: Skema lengkap Operasi Kalman filter, menggabungkan diagram pada Gambar 1-1 dan persamaan pada Tabel 1-1 dan Tabel 1-2.
Karena Q dan R adalah konstan, kovarian error estimasi Pk dan Kalman gain Kk akan stabil dengan cepat kemudian bernilai konstan (lihat persamaan update filter di Gambar 1-2). Jika demikian, kedua parameter ini dapat dihitung dulu dengan menjalankan filter secara offline, atau (misal) dengan menentukan nilai steady-state dari Pk sebagaimana pada [Grewal93]. Seringkali, error pengukuran tidak bernilai konstan, demikian juga noise proses, ada kala tidak bernilai konstan atau berubah secara dinamis selama filter sedang bekerja – menjadi Qk – untuk menyesuaikan dengan dinamika proses yang berbeda. Contoh, dalam pelacakan posisi kepala seorang user di lingkungan virtual 3D, kita perlu mengurangi magnitud Qk bila user bergerak lambat, dan menignkatkan magnitudnya bila bergerak cepat. Pada kasus ini, Qk
8
dipilih dengan mempertimbangkan ketidakpastian pada kehendak user dan ketidakpastian pada model.
Aplikasi Kalman Filter: Estimasi Nilai Konstan
Kita akan coba untuk mengestimasi satu nilai konstan acak skalar, misalnya nilai tegangan. Anggaplah kita mampu mengukur nilai konstan tersebut, tetapi pengukuran yang dilakukan terganggu dengan noise pengukuran sebesar 0,1 volt RMS dengan tipe white noise (misal, konverter analog ke digital yang digunakan tidak cukup akurat). Dalam contoh ini, proses dinyatakan dengan persamaan beda linier
𝑥𝑘= 𝐴𝑥𝑘−1+ 𝐵𝑢𝑘−1+ 𝑤𝑘
𝑥𝑘 = 𝑥𝑘−1+ 𝑤𝑘
dengan pengukuran 𝑧 ∈ ℜ1, yaitu
𝑧𝑘= 𝐻𝑥𝑘+ 𝑣𝑘
𝑧𝑘= 𝑥𝑘+ 𝑣𝑘
State x tidak berubah dari step ke step, jadi A=1. Tidak ada input kontrol, jadi u=0. Pengukuran yang bercampur noise langsung didapatkan dari state x, jadi H=1.
Parameter dan Persamaan Filter
Persamaan update waktu adalah
𝑥̂𝑘− = 𝑥̂𝑘−1 𝑃𝑘− = 𝑃𝑘−1+ 𝑄 dan persamaan update pengukuran adalah
𝐾𝑘 = 𝑃𝑘−(𝑃𝑘−+ 𝑅)−1 (3.1) 𝐾𝑘 = 𝑃𝑘 − 𝑃𝑘−+ 𝑅 𝑥̂𝑘= 𝑥̂𝑘−+ 𝐾(𝑧𝑘− 𝑥̂𝑘−) 𝑃𝑘 = (1 − 𝐾𝑘)𝑃𝑘−
Anggaplah varian noise proses sangat kecil, Q = 1x105. (Kita bisa saja menetapkan Q = 0, tapi menetapkan Q yang kecil namun tidak nol akan memberikan fleksibilas dalam “tuning” atau penyesuaian parameter filter, akan kita contohkan di bawah). Anggaplah, berdasarkan pengalaman yang kami tahu, nilai sebenarnya dari nilai konstan acak tersebut berdistribusi probabilitas normal, jadi kita beri filter kita dengan nilai tebakan nol. Dengan kata lain, sebelum menjalankan filter, kita tetapkan 𝑥̂𝑘−1 = 0
9
Kita juga perlu menetapkan nilai awal untuk Pk-1, sebut saja P0. Bila kita yakin bahwa nilai awal estimasi state 𝑥̂0 = 0 adalah benar, kita boleh menetapkan P0 = 0. Tetapi bila ada ketidakpastian pada nilai awal estimasi 𝑥̂0 yang kita tetapkan, maka memilih P0 = 0 mengakibatkan filter percaya sejak awal bahwa 𝑥̂𝑘 = 0. Dengan demikian, kita perlu menetapkan P0 dengan nilai yang lain. Kita bisa menetapkan sembaran nilai 𝑃0 ≠ 0 dan filter pada akhirnya akan konvergen. Kita mulai dengan menetapkan P0 = 1.
Simulasi
Untuk permulaan, kita tetapkan secara acak satu nilai konstan x = -0,37727 (tidak ada “topi” di atas x karena ini mewakili “nilai sebenarnya”). Lalu kita simulasikan 50 pengukuran 𝑧𝑘 yang memiliki error berdistribusi normal di sekitar nol dengan standar deviasi 0.1 (ingat, kita anggap pengukuran terganggu dengan white noise pengukuran sebesar 0.1 volt rms). Sebenarnya, kami bisa saja melakukan pengukuran ketika filter sedang bekerja, tapi dengan melakukan pengukuran 50 data sebelum filter dijalankan, kami dapat menjalankan beberapa macam simulasi dengan data pengukuran yang sama persis (maksudnya, dengan noise pengukuran yang sama) sehingga perbandingan antara beberapa simulasi dengan parameter yang berbeda akan lebih bermakna.
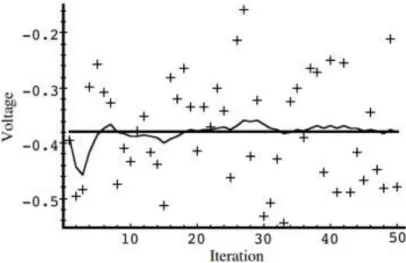
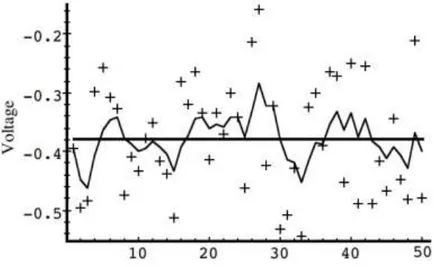
Dalam simulasi pertama, kami tetapkan varian error pengukuran R=(0,1)2=0,01. Karena ini adalah nilai varian error pengukuran sebenarnya, maka kami berharap mendapat performansi filter “terbaik” dalam arti keseimbangan antara kecepatan respon filter dan varian estimasi. Hal ini akan nampak jelas pada simulasi ke dua dan ke tiga. Gambar 3-1 menampilkan hasil simulasi pertama. Nilai konstan acak yang sebenarnya x = -0,37727, ditampilkan dalam garis lurus tebal, pengukuran yang bercampur noise diwakili tanda plus, dan estimasi filter diwakili dengan kurva.
Gambar 3-1. Simulasi pertama: R=(0,1)2=0,01. Nilai konstan acak yang sebenarnya x=-0,37727 dinyatakan dengan garis lurus tebal, pengukuran yang bercampur noise diwakili tanda plus, dan estimasi filter diwakili kurva.
10
Ketika pemilihan P0, kami nyatakan bahwa pemilihan ini tidak terlalu penting selama 𝑃0 ≠ 0, karena pada akhirnya estimasi filter akan konvergen (menuju pada satu nilai). Gambar 3-2 di bawah, kami telah plot nilai Pk terhadap iterasi. Pada iterasi ke-50, nilai Pk, yang semula ditetapkan 1 (volt2), bergerak konvergen dan menetap di sekitar 0,0002 (volt2).
Gambar 3-2. Setelah 50 iterasi, nilai awal kovarian error Pk=1 bergerak konvergen dan
menetap di sekitar 0,0002 (volt2).
Dalam bagian 1, topik “Parameter Filter dan Penyesuaiannya” kami paparkan secara singkat tentang pengubahan dan “penyesuaian” parameter Q dan R untuk mendapatkan performansi filter yang berbeda. Dalam Gambar 3-3 dan Gambar 3-4 di bawah, kita dapat amati apa yang terjadi ketika R diperbesar atau diperkecil dengan faktor 100. Di Gambar 3-3, filter diberi tahu bahwa varian error pengukuran adalah 100 kali lebih besar (maksudnya R=1) jadi filter “lebih lambat” dalam mempercayai data pengukuran.
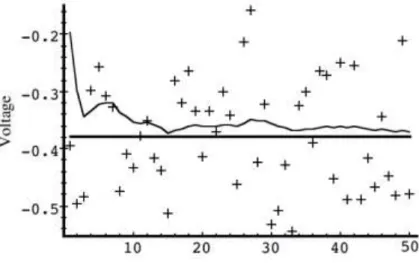
Gambar 3-3. Simulasi ke dua: R=1. Filter lebih lambat dalam merespon data pengukuran, akibatnya varian estimasi filter berkurang.
11
Pada Gambar 3-4, Filter diberi tahu bahwa varian error pengukuran adalah 100 kali lebih kecil (maksudnya R=0,0001), jadi filter “sangat cepat” mempercayai data pengukuran yang bercampur noise.
Gambar 3-4. Simulasi ke empat: R=0,0001. Filter merespon data pengukuran dengan cepat sekali, akibatnya varian estimasi filter meningkat.
Meskipun estimasi satu nilai konstan adalah topik yang relatif sederhana, namun mampu mendemonstrasikan unjuk kerja Kalman filter dengan jelas. Pada Gambar 3-3 nampak jelas bahwa estimasi Kalman filter lebih halus daripada data pengukuran yang bercampur noise.
12
Daftar Pustaka
[Brown92] Brown, R. G. and P. Y. C. Hwang. 1992. Introduction to Random Signals and Applied Kalman Filtering, Second Edition, John Wiley & Sons, Inc.
[Gelb74] Gelb, A. 1974. Applied Optimal Estimation, MIT Press, Cambridge, MA.
[Grewal93] Grewal, Mohinder S., and Angus P. Andrews (1993). Kalman Filtering Theory and Practice. Upper Saddle River, NJ USA, Prentice Hall.
[Jacobs93] Jacobs, O. L. R. 1993. Introduction to Control Theory, 2nd Edition. Oxford University Press.
[Julier96] Julier, Simon and Jeffrey Uhlman. “A General Method of Approximating Nonlinear Transformations of Probability Distributions,” Robotics Research Group, Department of Engineering Science, University of Oxford [cited 14 November 1995]. Available from http://www.robots.ox.ac.uk/~siju/work/publications/Unscented.zip. Also see: “A New Approach for Filtering Nonlinear Systems” by S. J. Julier, J. K. Uhlmann, and H. F. Durrant-Whyte, Proceedings of the 1995 American Control Conference, Seattle, Washington, Pages:1628-1632.
Available from http://www.robots.ox.ac.uk/~siju/work/publications/ACC95_pr.zip. Also see Simon Julier's home page at http://www.robots.ox.ac.uk/~siju/.
[Kalman60] Kalman, R. E. 1960. “A New Approach to Linear Filtering and Prediction Problems,” Transaction of the ASME—Journal of Basic Engineering, pp. 35-45 (March 1960). [Lewis86] Lewis, Richard. 1986. Optimal Estimation with an Introduction to Stochastic Control Theory, John Wiley & Sons, Inc.
[Maybeck79] Maybeck, Peter S. 1979. Stochastic Models, Estimation, and Control, Volume 1, Academic Press, Inc.
[Sorenson70] Sorenson, H. W. 1970. “Least-Squares estimation: from Gauss to Kalman,” IEEE Spectrum, vol. 7, pp. 63-68, July 1970