KONVERGENSI MODIFIKASI VARIAN METODE CHEBYSHEV-HALLEY MENGGUNAKAN INTERPOLASI KUADRATIK TUGAS AKHIR

KONVERGENSI MODIFIKASI VARIAN METODE

CHEBYSHEV-HALLEY MENGGUNAKAN INTERPOLASI

KUADRATIK

TUGAS AKHIR

Diajukan sebagai Salah Satu Syarat untuk Memperoleh Gelar Sarjana Sains

pada Jurusan Matematika

Oleh:

SILVIA YUTIKA

10854002885

FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS ISLAM NEGERI SULTAN SYARIF KASIM RIAU

PEKANBARU

KONVERGENSI MODIFIKASI VARIAN METODE

CHEBYSHEV-HALLEY MENGGUNAKAN INTERPOLASI

KUADRATIK

SILVIA YUTIKA

10854002885

Tanggal Sidang : 23 Mei 2013

Tanggal Wisuda : 2013

Jurusan Matematika Fakultas Sains dan Teknologi

Universitas Islam Negeri Sultan Syarif Kasim Riau Jl. HR. Soebrantas No.155 Pekanbaru

ABSTRAK

Varian metode Chebyshev-Halley merupakan salah satu metode iterasi dengan orde konvergensi empat untuk menentukan akar-akar persamaan nonlinier. Kecepatan sebuah metode iterasi bergantung kepada orde konvergensinya. Pada tugas akhir ini penulis memodifikasi varian metode Chebyshev-Halley menggunakan interpolasi kuadratik guna meningkatkan orde konvergensi. Berdasarkan hasil penelitian, diperoleh bahwa modifikasi Varian metode Chebyshev-Halley menghasilkan orde konvergensi tujuh yang melibatkan 3 evaluasi fungsi yaitu f(zn),f(yn),

) (x_n

f dan 2 evaluasi fungsi turunan f'(y_n), f'(x_n) dengan indeks Efficiency sebeszar 1.475

KATA PENGANTAR

Alhamdulillahirabbil’alamin, puji syukur penulis ucapkan kehadirat Allah

SWT atas segala limpahan rahmat dan hidayah-Nya sehingga penulis dapat

menyelesaikan tugas akhir dengan judul “KONVERGENSI MODIFIKASI

VARIANT METODE CHEBYSHEV-HALLEY MENGGUNAKAN INTERPOLASI KUADRATIK”. Penulisan tugas akhir ini dimaksudkan untuk memenuhi salah satu syarat dalam rangka menyelesaikan studi Strata 1 (S1) di UIN Suska Riau. Shalawat beserta salam selalu tercurahkan kepada Nabi

Muhammad SAW, mudah-mudahan kita semua selalu mendapat syafa’at dan

dalam lindungan Allah SWT amin.

Dalam penyusunan dan penyelesaian tugas akhir ini, penulis tidak terlepas dari bantuan berbagai pihak, baik langsung maupun tidak langsung. Untuk itu, penulis mengucapkan terimakasih yang tak terhingga kepada kedua orang tua tercinta ayahanda dan ibunda yang tidak pernah lelah dalam mencurahkan kasih sayang, perhatian, do’a, dan dukungan untuk menyelesaikan tugas akhir ini. Selanjutnya ucapan terimakasih kepada :

1. Bapak Prof. Dr. H. M. Nazir Karim, M.A selaku Rektor Universitas Islam Negeri Sultan Syarif Kasim Riau.

2. Ibu Dra. Hj. Yenita Morena, M.Si selaku Dekan Fakultas Sains dan

Teknologi Universitas Islam Negeri Sultan Syarif Kasim Riau.

3. Ibu Sri Basriati, M.Sc selaku Ketua Jurusan Matematika Fakultas Sains dan

Teknologi Universitas Islam Negeri Sultan Syarif Kasim Riau.

4. Bapak Wartono, M.Sc, selaku pembimbing yang telah banyak membantu,

mengarahkan, mendukung, dan membimbing penulis dengan penuh kesabarannya dalam penulisan tugas akhir ini.

5. Bapak Mohammad Soleh, M.Sc selaku penguji I yang telah banyak

membantu, memberikan kritikan dan saran serta dukungan dalam penulisan tugas akhir ini.

6. Bapak M.Nizam Muhaijir,S.Si selaku penguji II yang telah banyak membantu, mendukung dan memberikan saran dalam penulisan tugas akhir ini.

7. Semua dosen-dosen Jurusan Matematika yang telah memberikan dukungan

serta saran dalam menyelesaikan tugas akhir ini.

8. Teman-teman seperjuangan angkatan 2008 di Jurusan Matematika Fakultas

Sains dan Teknologi Universitas Islam Negeri Sultan Syarif Kasim.

9. Semua pihak yang telah memberikan dukungan kepada penulis terutama

kepada kak Hari Saputra dalam proses penulisan tugas akhir ini hingga selesai yang tidak dapat penulis sebutkan namanya satu persatu.

Dalam penyusunan tugas akhir ini penulis telah berusaha semaksimal mungkin. Walaupun demikian tidak tertutup kemungkinan adanya kesalahan dan kekurangan baik dalam penulisan maupun dalam penyajian materi. Untuk itu penulis mengharapkan kritik dan saran dari berbagai pihak demi kesempurnaan tugas akhir ini.

Pekanbaru, 23 Mei 2013

DAFTAR ISI

Halaman

LEMBAR PERSETUJUAN... ii

LEMBAR PENGESAHAAN ... iii

LEMBAR HAK ATAS KEKAYAAN INTELEKTUAL... iv

LEMBAR PERNYATAAN ... v LEMBAR PERSEMBAHAN ... vi ABSTRAK ... vii ABSTRACT... viii KATA PENGANTAR ... ix DAFTAR ISI... xi

DAFTAR TABEL... xiii

DAFTAR SIMBOL... xiv

DAFTAR SINGKATAN ... xv

DAFTAR LAMPIRAN ... xvi

BAB I PENDAHULUAN

1.1 Latar Belakang Masalah... I-1 1.2 Rumusan Masalah ... I-3 1.3 Batasan Masalah ... I-3 1.4 Tujuan Penelitian ... I-3 1.5 Manfaat Penelitian ... I-4 1.6 Sistematika Penulisan ... I-4 BAB II LANDASAN TEORI

2.1 Orde Konvergensi ... II-1 2.2 Deret Taylor ... II-5 2.3 Metode Newton dan Konvergensinya ... II-8 2.4 Metode Halley dan Konvergensinya ... II-11 2.4.1 Metode Chebyshev-Halley ... II-11 2.4.2 Varian Metode Chebyshev-Halley ... II-16

2.5 Interpolasi ... II-21 2.5.1 Interpolasi Linier ... II-21 2.5.2 Interpolasi Kuadratik ... II-22 BAB III METODOLOGI PENELITIAN

BAB IV PEMBAHASAN

4.1. Modifikasi Varian Metode Chebyshev-Halley

Menggunakan Interpolasi Linier ... IV-1 4.2 Interpolasi Kuadratik ... IV-7

4.2.1 Modifikasi Varian Metode Chebyshev-Halley

Menggunakan Interpolasi Kuadratik ... IV-7

4.2.2 Analisa Kekonvergenan ... IV-9 4.3 Simulasi Numerik ... IV-13 BAB V PENUTUP

5.1 Kesimpulan ... V-1 5.2 Saran... V-2 DAFTAR PUSTAKA

LAMPIRAN

BAB I

PENDAHULUAN

1.1 Latar Belakang

Para Ilmuwan dibidang sains dan teknik sering dihadapkan dengan sebuah persoalan matematis yang rumit berbentuk persamaan nonlinear. Metode numerik

adalah teknik untuk menyelesaikan permasalahan-permasalahan yang

diformulasikan secara matematis dengan operasi hitungan atau aritmatika biasa. Salah satu penerapan metode numerik dalam perhitungan aritmatika adalah mencari akar-akar persamaan nonlinier. Salah satu metode pencarian akar-akar persamaan yang sering dingunakan adalah Metode Newton dengan orde konvergensi berbentuk kuadratik. Oleh karena itu, metode Newton cukup cepat menghampiri akar-akar persamaan nonlinier. Bentuk umum metode newton adalah,     n x f x f x x n n n n , ) ( ' ) ( 1 0, 1, 2, 3 . . . (1.1)

Untuk memulai iterasi pada metode Newton diperlukan sebuah tebakan awal

0

x Apabila tebakan awalnya diambil cukup dekat ke akar , maka metode

Newton akan konvergen secara kuadratik.

Peneliti telah banyak melakukan berbagai macam metode pendekatan dengan memodifikasi berbagai metode iterasi untuk meningkatkan orde konvergensi. Kecepatan konvergensi sebuah metode bergantung pada orde konvergensinya dalam meminimalkan jumlah iterasi, maka dikembangkan suatu metode numerik dengan konvergensi kubik yang dikenal metode Halley, dengan bentuk umumnya adalah :

, ) ( ' ) ( 1 1 n n f f n n x f x f L L x x _           _ (1.2) dengan . ) ( ' ) ( ) ( " 2 1 2 n n n f x f x f x f L 

Yaotang Li, Peiyuan Zhang dan Yanyan Li (2009) telah mengembangkan metode Newton dengan memodifikasi menggunakan turunan kedua yang menghasilkan orde konvergensi kubik yang dikenal metode Chebyshev-Halley dengan bentuk : , ) ( ' ) ( )) ( 1 ( ) ( 2 1 1 1 n n n f n f n n x f x f x L x L x x _            _ (1.3) dengan 2 ) ( ' ) ( ' ) ( " n n n f x f x f x f L  (1.4)

Kemudian Yaotang Li, Peiyuan Zhang dan Yanyan Li (2009) telah melakukan pendekatan dengan memodifikasi persamaan (1.3). Tujuan nya untuk mengaproksimasi turunan ke dua, yang disebut varian Metode Chebyshev-Halley. Hasil dari modifikasi yang telah di aprokmasikan diperoleh orde Konvergensi keempat.

Rumus varian Metode Chebyshev-Halley,

) ( ' ) ( ) ( 2 ) ( ) ( 1 1 n n n n n n n x f x f y f x f y f x x _           _ (1.5) dengan ) ( ' ) ( n n n n x f x f x y  

Kou Jisheng, Li Yitian dan Wang Xiuhua (2006) telah mengembangkan metode Newton dengan memodifikasi menggunakan turunan kedua yang menghasilkan orde konvergensi empat.

Wartono dan Fitriyah Rita (2012), telah mengembangan Metode King dan

memodifikasinya dengan interpolasi kuadratik. Hasil modifikasi tersebut

diperoleh orde konvergensi ketujuh.

Changbum Chun (2007) telah mengembangkan metode Jarrat dengan memodifikasi menggunakan interpolasi kuadratik yang menghasilkan orde konvergensi enam.

Metode Halley merupakan metode yang konvergen secara kubik atau memiliki orde konvergensi tingkat tiga dan Varian Metode Chebyshev-Halley yang memiliki orde konvergensi tingkat empat yang artinya secara teori metode Halley dan Varian Metode Chebyshev-Halley lebih cepat konvergen ke akarnya bila dibandingkan dengan metode Newton.

Oleh karena itu, pada tugas akhir ini penulis tertarik untuk melakukan penelitian dengan memodifikasi Varian Metode Chebyshev-Halley menggunakan Interpolasi Kuadratik untuk menghasilkan tingkat orde konvergensi yang tinggi.

1.2 Rumusan Masalah

Rumusan masalah pada tugas akhir ini adalah bagaimana menentukan orde konvergensi dari modifikasi persamaan (1.5) menggunakan Interpolasi Kuadratik.

1.3 Batasan Masalah

Batasan masalah pada tugas akhir ini yaitu :

1. Fungsi f adalah suatu fungsi nonlinear dengan satu variabel dan fungsinya

bernilai riil.

2. Metode iterasi yang akan dimodifikasi adalah Varian Metode

Chebyshev-Halley yang diberikan pada persamaan (1.5).

3. Simulasi numerik dilakukan dengan menggunakan perangkat lunak Matlab.

1.4 Tujuan Penelitian

Tujuan penelitian ini adalah sebagai berikut :

1. Untuk memperoleh persamaan modifikasi Varian Metode

Chebyshev-Halley.

2. Untuk memperoleh orde konvergensi modifikasi Varian Metode

Chebyshev-Halley menggunakan Interpolasi Kuadratik.

3. Mensimulasikan secara numerik persamaan iterasi modifikasi Varian

1.5 Manfaat Penelitian

Manfaat penelitian dari tugas akhir ini adalah sebagai berikut :

1. Diperoleh metode baru setelah memodifikasi Varian Metode

Chebyshev-Halley dengan menggunakan Interpolasi Kuadratik.

2. Dapat dingunakan untuk menentukan akar-akar persamaan non-linear

dengan tingkat kekonvergenan lebih tinggi.

1.6 Sistematika Penulisan

Sistematika penulisan skripsi ini mencakup lima bab yaitu :

BAB I Pendahuluan

Bab ini berisi tentang latar belakang, perumusan masalah, batasan masalah, tujuan dan manfaat penelitian.

BAB II Landasan Teori

Bab ini berisi tentang teori-teori dasar yang digunakan dalam Tugas Akhir.

BAB III Metodologi Penelitian

Bab ini berisi tentang metodologi penelitian yang digunakan dalam Tugas Akhir.

BAB IV Modifikasi Persamaan (1.5) menggunakan Interpolasi Kuadratik

Bab ini berisi tentang pembahasan bagaimana bentuk rumusan baru dari persamaan (1.5) setelah dimodifikasi menggunakan Interpolasi Kuadratik, serta bagaimana bentuk orde konvergensinya. Selain itu dilengkapi dengan simulasi numerik.

BAB V Kesimpulan dan Saran

BAB II

LANDASAN TEORI

Beberapa teori yang dingunakan dalam penyusunan tugas akhir ini adalah :

2.1 Orde Konvergensi

Kecepatan suatu metode konvergensi merupakan suatu ukuran keefektifan suatu metode numerik. Konvergensi adalah kecenderungan untuk memiliki galat (kesalahan), yang diakibatkan oleh pemenggalan, yang mendekati nilai nol. Orde konvergensi juga merupakan suatu tingkat percepatan dalam penyelesaian persamaan nonlinear f(x)0, yang merupakan gambaran dari kekonvergenan

metode iterasi tersebut. Apabila suatu metode iterasi berorde dua maka metode iterasi ini akan konvergen secara kuadratik, dan apabila metode iterasi berorde tiga maka metode iterasi ini akan konvergen secara kubik, dan seterusnya. Untuk lebih jelas yang menerangkan tentang orde konvergensi adalah sebagai berikut:

Definisi 2.1 : (John H Mathews, 1992). Misalkan {x_n}_n0 adalah barisan yang konvergen ke , dan diberikan e_n x_n  untuk n0. Jika terdapat M 0

dan p0 sedemikian hingga

M e e x x n n n p n n n     _      1 1 lim lim   (2.1)

Persamaan (2.1) dapat dikatakan{xn}konvergen  dengan orde konvergensi p. Jika p1 maka {x_n} memiliki orde konvergensi linier, jika p1, maka }

{xn memiliki orde konvergensi kuadratik, dan seterusnya. Untuk nilai n yang

besar maka persamaan (2.1) menjadi

M x x p n n _      1 sehingga, p n n M x x _1   

Apabila notasi e_n x_n  merupakan notasi untuk nilai tingkat kesalahan pada iterasi ke- n , pada suatu metode yang menghasilkan suatu barisan

 

xn ,

maka suatu persamaan

) ( 1 1     np p n n Ce O e e , (2.2)

dapat disebut sebagai persamaan tingkat kesalahan, sedangkan nilai p pada persamaan (2.2) menunjukkan orde konvergensinya.

Contoh 2.1 : (John H Mathews, 1992). Tunjukkan bahwa fungsi 2

3 )

(x  x3  x

f dengan nilai awalp₀ 2,4, dan akar  2 memiliki orde

konvergensi kuadratik jika dengan menggunakan metode Newton.

Jawab:

Diketahui metode Newton memiliki bentuk umum sebagai berikut:

) ( ' ) ( 1 n n n n x f x f x x _  

Untuk itu, dengan mengambil p2 yang menunjukkan bahwa orde

konvergensi pada

 

xn adalah kuadratik, sehingga diperoleh:

Tabel 2.1. Konvergensi Kuadratik Metode Newton pada Akar Sederhana

K xn xn1 xn en  xn  2 1 n n e e _ 0 -2,400000000 0,323809524 0,400000000 0,476190475 1 -2,076190476 0,072594465 0,076190476 0,619469086 2 -2,003596011 0,003587422 0,003596011 0,664202613 3 -2,000008589 0,000008589 0,000008589 4 -2,000000000 0,000000000 0,000000000 kemudian p n n M x x _1   

Berdasarkan Teorema Convergence Rate for Newton-Raphson Iteration

(Mathews, John. H, 1992) bahwa:

2 1 ) ( ' ) ( " n n e f f e    

sehingga 3 2 9 12 2 1 ) 2 ( ' ) 2 ( " 2 1       f f M kemudian diperoleh: 000008589 , 0 3  x dan x₂   0,0035960112 0,0000012931 maka, 2 3 3 2 3 000008589 , 0       x x

Maka terbukti bahwa fungsi ( ) 3 3 2

x x x

f memiliki orde konvergensi

kuadratik.

Berikut definisi 2.1 dan 2.2 yang menjelaskan tentang keefektifan persamaan orde konvergensi dalam menyelesaikan persamaan nonlinear untuk menghampiri akar-akar persamaannya.

Definisi 2.2 Efficiency Index (Manoj Kumar Singh, 2009). Index efisiensi

merupakan definisi yang sederhana, yaitu

m P I

1

 (2.3)

Dimana P adalah banyaknya orde dari sebuah metode, sedangkan m merupakan

jumlah dari evaluasi fungsi dari metode tersbut termasuk juga fungsi turunannya. Semakin besar nilai indexnya maka metode itu semakin efektif dalam menyelesaikan persamaan nonlinier.

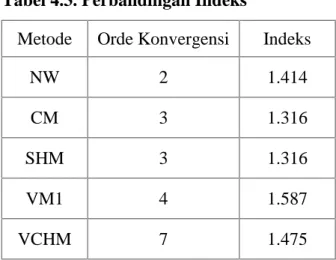
Contoh 2.2. Tentukanlah nilai indeks dari metode Newton dan Varian metode

Chebyshev-Halley?

Jawab:

Oleh karena metode Newton hanya mempunyai dua fungsi f(x_n) dan f'(x_n), sedangkan orde konvergensinya dua, yaitu

) ( 3 2 2 1 n n n C e O e e _  

maka nilai indeksnya adalah:

2 1 1 2  _Pm I

2  414 , 1 

Sedangkan varian Metode Chebyshev-halley mempunyai tiga fungsi yaitu ) (xn f ,f'(xn),f(yn) ) ( ) 2 ( 3 4 5 2 3 2 1 n n n c c c e O e e _   

maka nilai indexnya adalah:

3 1 1 4  _Pm I 3 4  5874 , 1 

Oleh karena nilai indeks Varian Metode Chebyshev-Halley lebih besar dibandingkan dengan metode Newton, maka Varian Metode Chebyshev-Halley lebih efektif dalam menyelesaikan persamaan nonlinear.

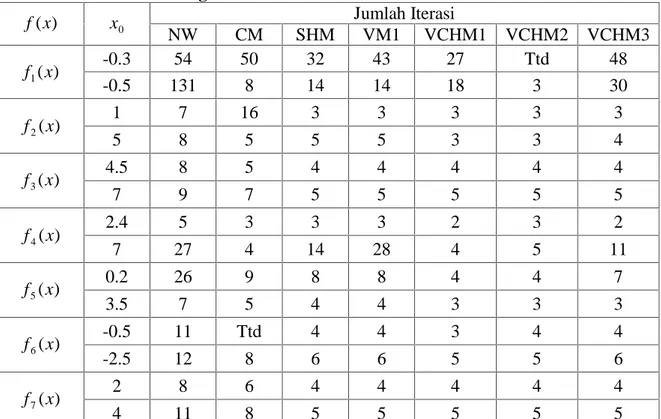
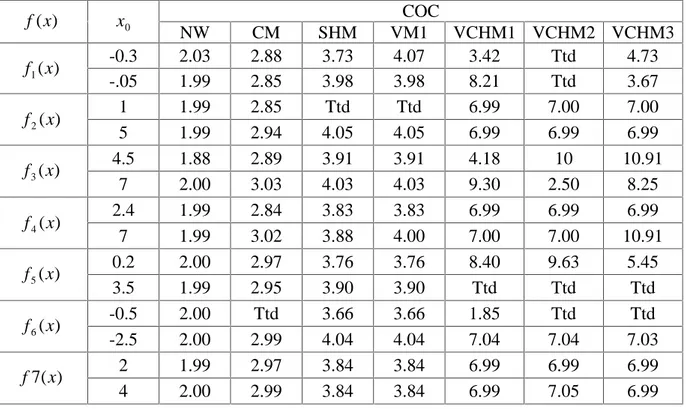
Selanjutnya untuk menegaskan tingkat orde konvergensi suatu metode iterasi, perlu dilakukan perbandingan terhadap hampiran akar-akar dari sebuah fungsi f. Salah satu metode yang digunakan untuk penegasan itu dikenal dengan istilah Computational Order of Convergence (COC). Berikut ini diberikan definisi tentang COC.

Definisi 2.3 Computational Order of Convergence (Weerakoon, 2000).

Diberikan  adalah akar dari f(x), dan andaikan xn1, xn dan xn1

berturut-turut alalah iterasi yang dekat dengan , maka, Computational Order of

Convergence (COC) yang dinotasikann dengan  dapat diaproksimasikan dengan menggunakan rumus ) /( ) ( ln ) /( ) ( ln 1 1             n n n n x x x x (2.4) Oleh karena x_n1 e_n1, maka persamaan (2.3) dapat ditulis kembali menjadi

) /( ) ( ln ) /( ) ( ln 1 1    n n n n e e e e  (2.5)

2.2 Deret Taylor

Deret Taylor merupakan deret berbentuk polinomial. Koefisien polinomial tersebut tergantung pada turunan fungsi pada titik yang bersangkutan. Teorema ini juga memberikan estimasi besarnya galat dari pendekatan itu. Berikut ini diberikan teorema tentang Deret Taylor.

Teorema 2.1 : (Edwin J. Purcell, 2004) Diberikan f fungsi yang di mana turunan

ke-(n1)-nya ada untuk setiap x pada selang terbuka I yang mengandung a . Jadi untuk setiap x di dalam I ,

          (3) ) 3 ( ) 2 ( ) 2 ( ) ( ! 3 ) ( ) ( ! 2 ) ( ) )( ( ' ) ( ) (x f a f a x a f a x a f a x a f ) ( ) ( ! ) ( ) ( ) ( ) ( x R a x n a f n n n    (2.6) dengan 1 ) 1 ( ) ( )! 1 ( ) ( ) (      n n n x a n c f x R (2.7)

adalah suku sisa dalam rumus Taylor dan c adalah titik di antara x dan a .

Persamaan (2.7) merupakan galat dari persamaan Taylor. Oleh karena itu, jika P_n(x)adalah persamaan Taylor, maka

         3 '' ' 2 '' ' ) ( ! 3 ) ( ) ( ! 2 ) ( ) )( ( ) ( ) (x f a f a x a f a x a f a x a P ) ( ) ( ! ) ( ) ( x R a x n a f n n    (2.8)

dan persamaan (2.6) dapat ditulis lagi dalam bentuk

) ( ) ( ) (x P x R x f  _n  _n (2.9)

Bukti: Misalkan sebuah polinomial berderajat n dengan fungsi f pada selang

terbuka I. Maka untuk setiap xIberlaku

n n x a b a x b a x b a x b b x f( ) ( ) ( ) 3( )3 ( ) 2 2 1 0           



   n n n x a b x f( ) ( ) (2.10)

Jika persamaan (2.10) diturunkan secara berurutan mulai dari f ' x( )sampai ) ( ) ( x f n maka 1 3 4 2 3 2 1 ' ) ( ) ( 4 ) ( 3 ) ( 2 ) (x b  b xa  b xa  b xa  b_nn xa n f  2 2 3 3 2 '' ) )( 1 ( ) ( 4 3 2 ) ( 3 2 2 ) (x  b   b xa    b xa  b_nn n xa n f  3 4 3 '' ' ) )( 2 )( 1 ( ) ( 4 3 2 3 2 ) (x   b    b xa  b_nn n n xa n f   ! ) ( ) ( n b x f n  _{n (2.11)}

Subtitusikan xa ke persamaan (2.11) maka

0 ) (a b f  1 '

)

(

a

b

f



2 ''

2

)

(

a

b

f



3 '' '

3

2

)

(

a

b

f





4 ) 4 ( 4 . 3 . 2 ) (a b f   ! ) ( ) ( n b a f n  _n Sehingga ! ) ( ) ( n a f b n n  (2.12)

Oleh karena itu, jika persamaan (2.12) disubtitusikan ke dalam persamaan (2.10) maka n n n a x n a f x f ( ) ! ) ( ) ( 0 ) (  



 

Selanjutnya dapat dapat diurai menjadi persamaan (2.8) yang disebut dengan

Deret Taylor. Kemudian untuk membuktikan galatnya, definisikan fungsi

)

(x

R

_n dihimpunan terbuka I dengan

n n n x a n a f a x a f a x a f a f x f x R ( ) ! ) ( ) ( ! 2 ) ( ) )( ( ' ) ( ) ( ) ( (2) ) 2 ( ) (         

Kemudian misalkan x dan a konstanta, dan definisikan fungsi baru g pada himpunan terbuka I dengan

           (3) ) 3 ( ) 2 ( ) 2 ( ) ( ! 3 ) ( ! 2 ) )( ( ) )( ( ' ) ( ) ( ) (t f x f t f t x t f t x t f t x t g n n n n n a x t x x R n t x t f ) ( ) ( ) ( ! ) )( (     

Jika disubtitusikan t x jelaslah bahwa g(x)0, dan

! ) )( ( ! 2 ) )( ( ) )( ( ' ) ( ) ( ) ( ) ( ) 2 ( ) 2 ( n a x a f a x a f a x a f a f x f a g n n            n n n a x a x x R ) ( ) ( ) (    ) ( ) (x R x R_n  _n  0 

Karena x dan a adalah titik pada himpunan terbuka I yang menyebabkan

0 ) ( )

(x g a 

g maka kita dapat menerapkan Teorema Nilai Rata-rata untuk

Turunan. Untuk itu, terdapat sebuah bilangan real c di antara x dan a sedemikian rupa sehinggag'(c)0. Selanjutnya dengan menerapkan aturan perkalian dengan berulang kali, diperoleh turunang(t) dengan bentuk:

2 '' ' ' ) ( ) 1 )( ( 2 ) ( [ ! 2 1 )] ( " ) ( ) 1 )( ( ' [ ) ( 0 ) (t f t f t x t f t f t x t x t g            )] ( ) ( ) 1 ( ) )( ( [ ! 1 )] ( '' ' f t x t 1 x t f ( 1) t n t f   n  n    n n 1 ) ( ) 1 )( ) )( 1 ( ) ( _      n _nn a x t x n x R 1 1 ) ( ) ( ) ( ) 1 ( )] ( ) [( ! 2 1          n n _{n n}n a x t x x R n t f t x (2.13)

Jadi, berdasarkan teorema nilai rata-rata untuk turunan, terdapat suatu nilai c di antara x dan a sedemikian sehingga,

1 1 ) ( ) ( ) ( ) 1 ( )] ( ) [( ! 1 ) ( ' 0  _         n _nn n n a x c x x R n c f c x n c g

Kemudian diperoleh 1 1 ) ( ) ( ) ( ) 1 ( )] ( ) [( ! 1        n _nn n n a x c x x R n c f c x n 1 1 ) ( )! 1 ( ) ( ) (      n n n x a n c f x R

Sehingga, persamaan (2.7) terbukti.

Contoh 2.3 : Ubahlah f(x)2x36x211x6 menurut deret Taylor kedalam pangkat x₀ 1 Jawab : n n a x n a f a x a f a x a f a f x f ( ) ! ) ( ... ) ( ! 2 ) ( ) )( ( ' ) ( ) ( ) ( ) 2 ( ) 2 (         6 11 6 2 ) (x  x3 x2  x f f(1)2x3 6x₂ 11x61 11 12 6 ) ( 2 ' _{  } x x x f f '(1)6x2 12x115 12 12 ) ( ''   x x f f ''(1)12x120 12 ) ( '' '  x f f'''(1)12 Jadi ( )2 36 2 11 6 x x x x f 3 ) 1 ( 12 ) 1 ( 5 1     x x

2.3 Metode Newton dan Orde Konvergensinya

Metode Newton berasal dari turunan deret Taylor Orde 1. Metode ini merupakan salah satu metode klasik yang sering digunakan untuk mencari akar-akar persamaan nonlinier. Misalkan fungsi f dapat diekspansi di sekitar xx_n

menggunakan deret Taylor dengan x pendekatan_n f(x)0, jika f(x) diekspansi di sekitar x xn sampai orde pertama, maka diperoleh

) ( ' ) ( ) ( ) (x f xn x xn f xn f    (2.14)

Karena f(x)0, selanjutnya distribusikan ke persamaan (2.14) dengan mengambil x xn1 sehingga

) ( ' ) ( ) ( 0 f x_n  x_n1x_n f x_n ) ( ) ( ' ) (xn1xn f xn f xn ) ( ' ) ( 1 n n n n x f x f x x _   ,... 3 , 2 , 1 , 0 , ) ( ' ) ( 1     n x f x f x x n n n n (2.15)

Persamaan (2.15) merupakan persamaan metode Newton.

Teorema 2.2 : Misalkan f(x) adalah fungsi bernilai riil yang mempunyai turunan pertama, kedua dan ketiga pada interval (a,b). Jika f(x) mempunyai akar

 pada interval (a,b) dan x adalah nilai tebakan awal yang mendekati akar₀ , maka persamaan (2.15) memiliki orde konvergensi tingkat dua dengan persamaan error    n n x e dengan ) ( ' ) ( ! 1 ( )   f f j C j j  j 1,2,3,

Bukti: Misalkan  adalah akar dari f(x), maka f()0. Asumsikan

0 ) ( ' x 

f dan x_n  e_n. Selanjutnya dengan menggunkan rumus ekspansi

Taylor untuk mengaproksimasi fungsi f di sekitar  , diperoleh ) ( ) (x_n f e_n f   ) ( ) ( ! 3 ) ( '' ) ( ! 2 ) ( '' ) )( ( ' ) ( ) (x_n f f x_n f x_n 2 f x_n 3 O e_n4 f            

Oleh karena x_n  e, maka diperoleh

) ( ) ( '' ' ! 3 1 ) ( '' ! 2 1 ) ( ' ) ( ) (x_n f f e_n f e_n2 f e3_n O e_n4 f          (2.16)

Karena f()0, maka dengan melakukan manipulasi aljabar pada persamaan

(2.16) diperoleh           ) ( ' ) ( ) ( ' ) ( '' ' ! 3 1 ) ( ' ) ( " ! 2 1 ) ( ' ) ( 4 3 2       f e O f e f f e f e f x f n n n n n



( )



) ( ' e_n C₂e_n2 C₃e3_n O e_n4 f      (2.17)

Jika untuk f'(x_n)dilakukan ekspansi Taylor di sekitar  maka ) ( ) ( ' xn f en f    ) ( ) ( ! 3 ) ) ( ! 2 ) ( '' ' ) )( ( '' ) ( ' 3 4 ) 4 ( 2 n n n n x O e f x f x f f               

Oleh karena x_n  e, maka diperoleh

) ( ) ( ! 3 1 ) ( '' ' ! 2 1 ) ( '' ) ( ' f en f en2 f (4) en3 O en4 f                     ) ( ' ) ( ) ( ' ) ( ! 3 1 ) ( ' ) ( '' ' ! 2 1 ) ( ' ) ( " 1 ) ( ' 4 3 ) 4 ( 2         f e O f e f f e f f e f f n n n n



1 2 3 ( )



) ( ' C2en C3en2 O en3 f      (2.18)

Selanjutnya dilakukan pembagian persamaan (2.17) oleh persamaan (2.18)







1 2 3 ( )



) ( ' ) ( ) ( ' ) ( ' ) ( 3 2 3 2 4 3 3 2 2 n n n n n n n n n e O e C e C f e O e C e C e f x f x f         







1 2 3 ( )



) ( 3 2 3 2 4 3 3 2 2 n n n n n n n e O e C e C e O e C e C e       



( )

 

(1 2 2 3 3 2 ( 3)



4 3 3 2 2 n n n n n n n Ce Ce Oe Ce Ce Oe e        



2 ₂ 3 ₃ 2 ( 3)



2...  C e_n Ce_n O e_n



( )

 



1 2 3 ( )

 

4 22 2 ...





3 2 3 2 4 3 3 2 2          en Cen Cen Oen Cen Cen Oen Cen ) ( 3 2 2 n n n Ce Oe e    (2.19)

Kemudian dengan mensubtitusikan persamaan (2.19) ke persamaan Newton

) ( ' ) ( 1 n n n n x f x f x x _   )) ( ( _{n 2 n}2 _n3 n e C e O e x   

Oleh karena x_n e_n  maka x_n1 e_n1 , sehingga diperoleh,

)) ( ( ₂ 2 3 1 n n n n n e e C e O e e _      ) ( 3 2 2 1 n n n C e O e e _   (2.20)

Berdasarkan Teorema 2.2, metode Newton memiliki orde konvergensi kuadratik.

2.4 Metode Halley dan Orde Konvergensinya 2.4.1 Metode Chebyshev-Halley

Definisi 2.3 : (Yaotang Li, Peiyuan Zhang, 2009) Metode Chebyshev-Halley

menghasilkan orde konvergensi tingkat tiga.

Pandang persamaan metode Chebyshev-Halley sebagai berikut :

, ) ( ' ) ( ) ( 1 ( ) ( 2 1 1 1 n n n f n f n n x f x f x L x L x x _            _ (1.3)

Metode Chebyshev-Halley mempunyai dua fungsi yaitu f(x_n) dan f'(x_n) untuk persamaan (1.3). dengan . ) ( ' ) ( ) ( " 2 n n n f x f x f x f L  (1.4)

Dan untuk persamaan (1.4) mempunyai tiga fungsi yaitu f"(x_n), f(x_n)dan

2 ) ( ' x_n

f .

Berikut ini akan membahas mengenai error metode Chebyshev-Halley yang menunjukkan orde konvergensinya.

Teorema 2.3: Misalkan f(x) adalah fungsi yang berniali riil yang memiliki turunan pertama, kedua dan ketiga pada interval (a,b). Jika f(x)memiliki akar  pada (a,b) dan x adalah nilai tebakan awal yang cukup dekat dengan₀  , maka metode iterasi pada persamaan (2.1) memenuhi persamaan error dengan

   _n n x e

Misalkan  adalah akar dari f(x), maka f()0. Asumsikan bahwa

0 ) ( ' x 

f dan x_n  e_n. Seterusnya dengan menggunakan ekspansi Taylor

diperoleh ) ( ) (xn f en f    ) ( ) ( ! 3 ) ( ' ' ) ( ! 2 ) ( ' ' ) )( ( ' ) ( ) ( 2 3 4 n n n n n x O e f x f x f f x f            

Oleh karena x_n  e, maka diperoleh ) ( ) ( '' ' ! 3 1 ) ( '' ! 2 1 ) ( ' ) ( ) (x_n f f e_n f e_n2 f e_n3 O e_n4 f          (2.21)

Karena f()0, maka dengan melekukan manipulasi aljabar pada persamaan (2.21) diperoleh           ( ) ) ( ' ) ( '' ' ! 3 1 ) ( ' ) ( '' ! 2 1 ) ( ' ) ( 4 3 2 n n n n n O e f e f f e f e f x f      (2.22) dengan ) ( ' ) ( ! 1 ( )   f f j C j

j  , dengan j 1,2,3,, maka persamaan (2.22)

menjadi



( )



) ( ' ) (x_n f e_n C₂e_n2 C₃e_n3 O e_n4 f      (2.23)

Jika untuk f'(x_n) dilakukan ekspansi Taylor di sekitar  maka ) ( ) ( ' xn f en f    ) ( ) ( ! 3 ) ) ( ! 2 ) ( '' ' ) )( ( '' ) ( ' 3 4 ) 4 ( 2 n n n n x O e f x f x f f               

Oleh karena xn  e, maka diperoleh

) ( ) ( ! 3 1 ) ( '' ' ! 2 1 ) ( '' ) ( ' f en f en2 f (4) en3 O en4 f                     ) ( ' ) ( ) ( ' ) ( ! 3 1 ) ( ' ) ( '' ' ! 2 1 ) ( ' ) ( " 1 ) ( ' 4 3 ) 4 ( 2         f e O f e f f e f f e f f n n n n



1 2 3 ( )



) ( ' C₂e_n C₃e_n2 O e_n3 f      (2.24)

Jika untuk f ''(x_n) dilakukan ekspansi Taylor di sekitar maka ) ( '' ) ( '' xn f en f    ) ( ) ( ! 2 1 ) ( '' ' ) ( '' f en f (4) en2 O e3n f                  ) ( ' ) ( ) ( ' ) ( ! 2 1 ) ( ' ) ( '' ' ) ( ' ) ( '' ) ( ' 3 2 ) 4 (         f e O f e f f e f f f f n n n           ( ) ) ( ' ) ( ! 4 1 12 ) ( ' ) ( '' ' ! 3 1 6 ) ( ' ) ( '' ! 2 1 2 ) ( ' 3 2 ) 4 ( n n n e O f e f f e f f f f       



2 3



4 3 2 6 12 ( 2 ) ( ' C C en C en O en f      (2.25)

Jika persamaan (2.23) dibagi dengan persamaan (2.24) diperoleh

)) ( 3 2 1 )( ( ' )) ( )( ( ' ) ( ' ) ( 3 2 3 2 4 3 3 2 2 n n n n n n n n n e O e C e C f e O e C e C e f x f x f          ) ( 3 2 1 ) ( 3 2 3 2 4 3 3 2 2 n n n n n n n e O e C e C e O e C e C e       



e_n C₂e_n2 C₃e_n3 O(e_n4)

 

 12C₂e_n 3C₃e_n2 O(e_n3)







  



  e_n C₂e_n2 C₃e_n3 O(e_n4)



 





     2  3 2 



3 2 3 2 3 2 3 ( ) (2 3 ( ) 2 1 C en C en O en C en C en O en



  



  e_n C₂e_n2 C₃e_n3 O(e_n4)



 





    2 2 



2 3 2 3 2 3 ( ) 4 2 1 C e_n C e_n O e_n C e_n



( )

 

1 2 (4 3 3) 2 ( 3)



2 2 2 4 3 3 2 2 n n n n n n n C e Ce Oe C e C C e Oe e          ) ( ) 2 2 ( ₂2 ₃ 3 4 2 2 n n n n C e C C e O e e      (2.26)

Kemudian jika pada persamaan (2.25) dikali dengan persamaan (2.23) diperoleh







'( )2 6 (





'( )



( )





) ( ) ( '' x_n f x_n f C₂ C₃e_n Oe_n2 f e_n C₂e_n2 C₃e_n3 O e_n4 f         



2 (2 6 ) 8 ( )



) ( ' 2 3 3 4 2 3 2 2 2 2 n n n n C C e C C e O e e C f       (2.27)

Jika persamaan (2.24) dikuadratkan maka diperoleh







_{2 3}



2 3 2 2 ) ( 3 2 1 ) ( ' ) ( ' x_n f C e_n C e_n O e_n f     



1 4 (6 4 ) 12C ( )



) ( ' 2 C₂e_n C₃ C₂2 e_n2 ₂C₃e_n3 O e_n4 f        (2.28)

Jika persamaan (2.27) dibagi dengan persamaan (2.28) diperoleh







1 4 (6 4 ) 12C ( )



) ( ' ) ( 8 ) 6 2 ( 2 ) ( ' ) ( ' ) ( ) ( '' 4 3 3 2 2 2 2 3 2 2 4 3 3 2 2 3 2 2 2 2 2 n n n n n n n n n n n e O e C e C C e C f e O e C C e C C e C f x f x f x f             =

_





_

) ( 12C ) 4 6 ( 4 1 ) ( 8 ) 6 2 ( 2 4 3 3 2 2 2 2 3 2 4 3 3 2 2 3 2 2 2 n n n n n n n n e O e C e C C e C e O e C C e C C e C          =



2C₂e_n (2C₂2 6C₃)e_n2 8C₂C₃e_n3O(e_n4)



X



_{3 4}



1 3 2 2 2 2 3 2 (6 4 ) 12C ( ) 4 1 C en  C  C en  C en O en 

=



2 (2 6 ) 8 2 3 3 ( 4)



2 3 2 2 2en C C en C C en O en C     X







1 4 (6 4 ) 12C2 3 3  ( 4)  2 2 2 3 2en C C en C en O en C



4C₂e_n (6C₃ 4C₂2)e_n2 12C₂C₃e_n3 O(e_n4)



2 ...



=2 (6 6 ) ( 28 2 3 16 23) 3 ( 4) 2 2 2 3 2en C C en C C C en O en C       (2.29) Jadi ) ( ) 16 28 ( ) 6 6 ( 2 2 3 23 3 4 2 2 2 3 2 n n n n f C e C C e C C C e O e L        kemudian, )) ( ) 16 28 ( ) 6 6 ( 2 ( 1 1L_f   C₂e_n  C₃  C₂2 e_n2   C₂C₃ C₂3 e_n3 O e_n4 )) ( ) 16 28 ( ) 6 6 ( 2 ( C₂e_n  C₃  C₂2 e_n2   C₂C₃  C₂3 e3_n O e_n4    maka diperoleh, )) ( ) 16 28 ( ) 6 6 ( 2 ( ) ( ) 16 28 ( ) 6 6 ( 2 1 3 3 4 2 3 2 2 2 2 3 2 4 3 3 2 3 2 2 2 2 3 2 n n n n n n n n f f e O e C C C e C C e C e O e C C C e C C e C L L                         1 (2C₂e_n (6C₃ 6C₂2)e_n2 ( 28C₂C₃ 16C₂3)e_n3 O(e_n4)) ) ( )) ( ) 16 28 ( ) 6 6 ( 2 ( 2 3 23 3 4 2 4 2 2 2 3 2 2 n n n n n C C e CC C e Oe Oe e C                 2 3 2 2 2 3 3 2 3 2 2 2 4 2 ) 12 12 ( ) 32 5 ( ( ) (e_n C C C e_n C C e_n O    6 2 3 2 3 2 2 4 2 2 ) 16 28 ( 1 ) ( ) 1 4 C e_n   O e_n    C C  C e_n ) 16 28 ( 4 ( ) 16 28 )( 6 6 ( 2 2 2 3 23 2 5 3 2 3 2 3 2 2 2 C C C C e C C C C C    n       3 3 2 2 2 2 3 2 3 2 4 2 3 2 2 6 ) ) ( ( 28 16 ) 4 ( 6 6 )) 6 ( C  C e_n   C C  C  C  C  C e_n    n n C e e C C C₂2 6 ₃) 4 2 ₂2) 2 2 ₂ 6 ( (               2 2 2 2 3 2 2 2 ( ( 6 6 ) 4 ) 2 1 C e_n  C C  C e_n ) ( ) 6 6 ( 4 3 3 4 2 2 2 2 n n O e e C C C     (2.30)

jika persamaan (2.29) 4dikalikan dengan persamaan (2.30), maka

          (2 (6 6 ) ( 28 16 ) ( )) 1 ) ( ' ) ( ) ( '' 3 3 4 2 3 2 2 2 2 3 2 2 n n n n f f n n n e O e C C C e C C e C L L x f x f x f        2 2 2 2 3 2 2 2 ( ( 6 6 ) 4 ) 2 1 ( C en  C C  C en )) ( ) 6 6 ( 4 3 3 4 2 2 2 2 n n O e e C C C    

3 3 2 2 2 2 2 2 2 2 3 2 2 2 ( ( 6 6 ) 4 ) 4 ( 6 6 ) 2 1 (  Cen  C  C  C en  C  C  C en              2 3 2 2 3 3 2 3 2 4 4 ) 6 6 ( ) 16 28 (( ) ( ) ) (e_n O e_n C C C e_n C C e_n O       6 3 2 2 2 2 3 2 3 2 4 2 ) ( ) 4( 28 16 ) ( 6 6 ) 2C en O en C C C  C C C en ) 16 28 ( ) 6 6 ( ) 6 6 ( 4 (  C₂2  C₃ 2C₂  C₂2  C₃   C₂C₃  C₂3        3 2 2 2 2 2 5 2 2 2 3 2 2 6 ) 4 )) (8 ( 6 6 ) 6 ( ( C C  C e_n  C C C C ) 16 28 ( 2 ) 4 ) 6 6 ( )( 6 6 ( 2 3 23 2 2 2 3 2 2 3 2 2 C C C C C C C C           ) 6 6 ( 2 ) 4 ) 6 6 ( ( 2 ( ) 4 ₂2 ₃ 2 ₂2 _{2 2}2 ₃ 2 e C C C C C C C _n           2 2 2 3 2 2 2 2 3 3 2 3 2 2 28C C 16C )e (4 C 6C 6C )e 2C e C   n     n   2 3 2 2 2 3 2 2 2 2 2 (4 6 6 ) (2( ( 6 6 ) 4 2            C e_n C C C e_n C C ) ( ) 16 28 ) 6 6 ( 2 ) 3 2 2 3 23 3 4 2 2 2 2 2 C C C C C C C en O en C        (2.31) ) 4 ) 6 6 ( ( 2 1 ( 2 1 1 ( 1 2 1 1 _   ₂   ₂2  ₃  2 ₂2 2          _{n n} f f e C C C e C L L     ) ( ) 6 6 ( 42C₂  C₂2  C₃ e_n3 O e_n4 ) 6 6 ( ) 4 ) 6 6 ( (( 1 ) ( 2 1 3 2 2 2 2 2 2 3 2 2 4 C C C C C C e O _n            n n n C C C e C e e C C C C 2 2 3 2 2 2 2 3 3 2 3 2 2 14 8 ) (2 3 3 )   (2.32) ) 6 6 ( ) 4 ) 6 6 ( (( 1 ) ( 2 1 ( ) ( ' ) ( 1 2 1 1 Oe4 C₂2 C₃ 2C₂2 C₂ C₂2 C₃ x f x f L L n n n f f                       ) ) 3 3 2 ( ) 8 14 2 2 3 2 2 2 2 3 3 2 3 2 2 C C C en C C C en C en C         X ( (2 2 3) 3 ( 4)) 2 2 2 2 n n n n C e C C e O e e     ) ( ) 2 2 2 3 4 2 2 2 3 n n n C C C e O e e       (2.33) sehingga,                    ) ( ' ) ( 1 2 1 1 1 n n f f n n x f x f L L x x 



2 2 22) 3 ( 4)



2 2 3 n n n n e C C C e O e x        )) ( ) 2 2 ( 22 3 4 2 2 3 1 n n n n n e e C C C e O e e _         ) ( ) 2 2 2 3 4 2 2 2 3 1 n n n n n e e C C C e O e e _         ) ( ) 2 2 ( _{3 2}2 ₂2 3 4 1 n n n C C C e O e e _        (2.34)

jika ruas kiri dan ruas kanan pada persamaan (2.34) di kurangkan dengan , diperoleh, ) ( ) 2 2 ( _{3 2}2 ₂2 3 4 1 n n n C C C e O e e _      ) ( ) 2 2 ( 22 3 4 2 2 3 1 n n n C C C e O e e _       (2.35)

2.4.2 Varian Metode Chebyshev-Halley

Pada persamaan (1.3) dapat dibentuk menjadi lebih sederhana dengan mengekspansi turunan kedua. Hal ini dilakukan oleh Yaotang Li, Peiyuan Zhang (2009) dengan bentuk awalnya adalah :

, ) ( ' ) ( 1 2 1 1 1 n n f f n n x f x f L L x x _            _ dengan . ) ( ' ) ( ) ( " 2 n n n f x f x f x f L  Misalkan ) ( ' ) ( n n n n x f x f x y   (2.36)

Exspansi f(y_n)di sekitar x x_ndengan menggunakan teorema Taylor, diperoleh

2 ) )( ( " ) )( ( ' ) ( ) ( 2 n n n n n n n n x y x f x y x f x f y f      (2.37)

substitusikan persamaan (2.36) ke persamaan (2.37), sehingga diperoleh,

               2 ) ( ' ) ( ) ( " ) ( ) ( ) ( 2 2 n n n n n n x f x f x f x f x f y f 2 2 ) ( ' 2 ) ( ) ( " ) ( n n n n x f x f x f y f  (2.38)

kemudian kalikan kedua ruas persamaan (2.38) dengan 2f'(x_n)2, maka

2 2 ) ( ) ( " ) ( ) ( ' 2f xn f yn  f xn f xn (2.39)

selanjutnya, kedua ruas pada persamaan (2.39) dikalikan dengan ₂ ) ( 1 n x f diperoleh 2 2 ) ( ) ( ) ( ' 2 ) ( " n n n n x f y f x f x f  (2.40)

substitussikan persamaan (2.40) ke persamaan (1.4), sehingga diperoleh

2 2 2 ) ( ' ) ( ) ( ) ( ) ( ' 2 n n n n n f x f x f x f y f x f L  ) ( ) ( 2 n n x f y f  (2.41)

Substitusikan persamaan (2.41) ke persamaan (1.3) dan diperoleh

) ( ' ) ( )) ( 1 ( ) ( 2 1 1 1 n n n f n f n n x f x f x L x L x x _            _ ) ( ' ) ( ) ( ) ( 2 1 ) ( ) ( 2 2 1 1 1 n n n n n n n n x f x f x f y f x f y f x x                           (2.42)

Dengan menggunakan aljabar, persasamaa (2.42) dapat disederhanakn menjadi

) ( ' ) ( ) ( 2 ) ( ) ( 1 1 n n n n n n n x f x f y f x f y f x x _           _ (2.43)

Persamaan (2.43) merupakan persamaan modifikasi varian metode Chebyshev-Halley.

Berikut ini juga akan dibahas mengenai error dari modifikasi Varian Metode Chebyshev-Halley yang menunjukkan orde konvergensinya.

Teorema 2.4 : (Yaotang Li, Peiyuan Zang, 2009) Misalkan f(x) adalah fungsi bernilai rill yang mempunyai turunan di f :I R, untuk I interval terbuka. Jika

0

x menghampiri  maka persamaan di atas mempunyai orde konvergensi tingkat empat dengan persamaan error

) ( ) 2 ( ₂3 _{2 3} 4 5 1 n n n c c c e O e e _   

Misalkan 2 , 1 , 1 , 0     B C D A dimana en  xn  dan ) ( ' ) ( ! 1 ( )   f f j c j j 

Bukti: Misalkan  adalah akar dari f(x), maka f()0. Asumsikan

0 ) ( ' x 

f dan xn  en. Selanjutnya dengan menggunakan rumus ekspansi

Taylor untuk mengaproksimasi fungsi f di sekitarx , diperolehn

 

[ ( )] ) (x_n f' e_n C₂e_n2 C₃e3_n C₄e_n4 O e5_n f       (2.44)

 

[1 2 3 4 ( )] ) ( 3 4 4 2 3 2 ' ' n n n n n f C e C e C e O e x f       (2.45) dengan ) ( ' ) ( ! 1 ( )   f f j C j

j  dan j  1,2,3, dan en xn . Selanjutnya, dari

persamaan (2.44) dan (2.45) diperoleh:

 

 





3

 

 

4





4 2 3 2 5 4 4 3 3 2 2 4 3 2 1 ) ( ' ) ( ' ' _{n n n n} n n n n n n n e O e c e c e c f e O e c e c e c e f x f x f           

 





 



3 4



4 2 3 2 5 4 4 3 3 2 2 4 3 2 1 n n n n n n n n n e O e c e c e c e O e c e c e c e         

 







₃

 

₄



1 4 2 3 2 5 4 4 3 3 2 2 1 2 3 4            e_n c e_n c e_n c e_n Oe_n c e_n c e_n c e_n Oe_n

 









3

 

4



4 2 3 2 5 4 4 3 3 2 2 n n n n 1 2 n 3 n 4 n n n c e c e c e Oe c e c e c e Oe e          

 



3 4



...



2 4 3 3 2 2 3 2      c en c en c en Oen ) ( ) 10 3 ) 4 3 ( ( ) 2 2 ( (e_n c₂e_n2   c₃ c₂2 e_n3 c₂  c₃ c₂2  c₄ c₂c₃ e_n4 O e5_n  sehingga diperoleh,

 

 

( ( 2 2 ) (7 4 3 ) ( ) ' 5 4 4 3 2 3 2 3 2 2 3 2 2 n n n n n n n e O e c c c c e c c e c e x f x f          (2.46)

Selanjutnya, substitusikan persamaan (2.46) ke persamaan

) ( ' ) ( n n n n x f x f x y   )) ( ) 2 2 ( ( 3 22 3 4 2 2 n n n n n e c e c c e O e x       





 



2 3 4



2 3 2 2 n 2 2 n n n n e c e c c e Oe e        



2



3

 

4 2 3 2 2en 2c c en Oen c      (2.47)

Dengan demikian, maka ) ( ) (y_n f e_n f    ) ( ) ( ! 2 ) ( '' ) )( ( ' ) ( f y_n f y_n 2 O e_n3 f            (2.48)

Karena f()0maka dengan melakukan manipulasi aljabar pada persamaan (2.48) diperoleh

 

''( )

 

( ) ! 2 1 ) ( ' 2 2 2 3 2 2en f c en O en c f     

 

 

_          ) ( ' ) ( ) ( ' ) ( " ! 2 1 ) ( ' 3 2 2 2 2 2 _{ }   f e O f e c f e c f n n n





 



2 3 4



2 3 2 2 2 2 ) ( ' c e_n c c e_n O e_n f       (2.49) Untuk persamaan         2 2 2 3 3 2 2 ) ( (2 2 )) ( ) ( ) (xn Bf yn A Ac Bc en Ac B c c en Af ) ( )) 10 3 ) 4 3 ( ( ( 4 2 3 3 4 2 2 3 2 4 B c c c c c c en O en Ac        (2.50) dan untuk         2 3 2 3 3 2 2 2 ) ( (2 2 )) ( ) ( ) (xn Df yn Cen Cc Dc en Cc D c c en Cf ) ( )) 10 3 ) 4 3 ( ( (Cc₄ D c₂  c₂  c₂2  c₄  c₂c₃ e_n4 O e_n5 (2.51) Sehingga          C e c c D Cc C e Dc Cc y Df x Cf y Bf x Af _{n n} n n n n 2 3 2 3 3 2 2 ) ( (2 2 )) ( 1 ) ( ) ( ) ( ) ( ) ( )) 10 3 ) 4 3 ( ( ( 4 3 3 2 4 2 2 3 2 4 n n e O C e c c c c c c D Cc              C e c c D Cc C e Dc Cc_{2 2}) _n ( ₃ (2 ₃ 2 ₂3)) _n2 ( ) ( )) 10 3 ) 4 3 ( ( ( 4 3 3 2 4 2 2 3 2 4 n n e O C e c c c c c c D Cc       

Maka, dengan menggunakan ekspansi deret sehingga bentuk                  _{ }      C c c D Cc A C C e Bc Ac C Dc Cc A C A y Df x Cf y Bf x Af n n n n n 2 2 3 3 2 2 2 2 2 2 ( ( ( 1 ) ( ) ( ) ( ) ( ) ( ) )) 2 2 ( ) )( ( ) ) ( 2 2 2 3 3 2 2 2 2 2 2 2 2 n e c c B Ac C Dc Cc Bc Ac C Dc Cc         ) ( ) ))( 2 2 ( ( ) 10 3 ) 4 3 ( ( ) )) 2 2 ( )( ( 2 ) 10 3 ) 4 3 ( ( ( ) ( ) 2 2 ( ) ( 1 3 4 2 2 2 2 3 3 3 2 4 2 2 3 4 4 2 2 2 3 3 2 2 3 2 4 2 2 3 2 4 2 2 2 2 2 2 3 3 2 2 n n Oe e C Dc Cc c c B Ac c c c c c c B Ac C c c D Cc Dc Cc C c c c c c c D Cc A C Dc Cc C c c D Cc Bc Ac C                                                                                                    

Selanjutnya kita masukan nilai A, B, C dan D maka didapat

) 4 3 ( ) 3 3 ( ( ) 2 ( ) ( ) ( ) ( ) ( ₂ 2 3 2 2 2 3 2 2 3 2 2 2e c c e c c c c c c c y Df x Cf y Bf x Af n n n n n n            ) ( ) ) 2 2 ( 10 3c₄  c₂c₃  c₃  c₂2 c₂ e_n3 O e_n4  (2.52)

Kemudian ditambahkan 1 setelah itu subtitusikan persamann (2.52) dan (2.46) sehingga diperoleh ) ( ) 2 ( ₂3 _{2 3} 4 5 1 n n n c c c e O e x _     (2.53)

Karena xn_1 en_1 , maka persamaan (2.53)

menjadi e_n1   (2c₂3 c₂c₃)e_n4 O(e_n5) ) ( ) 2 ( 2 3 4 5 3 2 1 n n n c c c e O e e _    (2.54)