commit to user
30 BAB III
METODE PENELITIAN
A. Subyek Penelitian
Penelitian ini merupakan penelitian mengenai pengaruh variabel moneter dan ketidakpastian inflasi terhadap tingkat inflasi. Penelitian ini dilakukan pada negara anggota ASEAN berpenghasilan menengah, yaitu; Indonesia, Filipina, Malaysia dan Thailand dalam periode 1998 - 2015.
B. Jenis dan Sumber Data
Data yang digunakan dalam penelitian ini merupakan data sekunder yang bersifat runtut waktu (time series) dalam satuan triwulan dari 1998-2015 dan
cross section yang meliputi empat negara anggota ASEAN berpendapatan menengah meliputi Indonesia, Filipina, Malaysia, dan Thailand. Variabel yang digunakan yaitu inflasi yang diperoleh dari persentase perubahan nilai Indeks Harga Konsumen (IHK) / CPI (Consumer Price Index), jumlah uang beredar (JUB), dan tingkat suku bunga berdasarkan tingkat suku bunga deposito berjangka periode 1998 – 2015.
Data dalam penelitian ini adalah data sekunder yang diperoleh dari data IFS (International Financial Statistik) yang diterbitkan oleh IMF (International Monetary Fund). Penelitian ini menggunakan negara Indonesia, Filipina, Malaysia, dan Thailand sebagai sampel negara anggota ASEAN berpendapatan menengah.
commit to user
31 C. Definisi Operasional Variabel
1. Inflasi
Inflasi adalah meningkatnya harga komoditas secara umum dan terus menerus dalam periode tertentu. Inflasi di suatu negara dapat terlihat dari perubahan atau selisih antara Indeks Harga Konsumen (CPI/Consumer Price Index) tahun berjalan dengan Indeks Harga Konsumen tahun sebelumnya dengan melakukan perhitungan sebagai berikut (Case dan Fair, 2006:58):
Data tingkat inflasi dalam penelitian ini diperoleh dari perhitungan selisih IHK yang bersumber dari data triwulan International Financial Statistic yang dikeluarkan oleh IMF dalam satuan persen (Lampiran I). 2. Ketidakpastian Inflasi
Ketidakpastian inflasi adalah ketidakjelasan mengenai tingkat inflasi dimasa depan (Bussiness Dictionary, 2016). Data ketidakpastian inflasi ini akan diperoleh dengan melihat tingkat volatilitas tingkat inflasi yang terjadi pada periode tahun 1998-2015 pada masing-masing negara dalam satuan persen, dengan menggunakan metode ARMA (2,2) untuk Indonesia, metode AR(1) untuk Filipina, metode AR(2) – EGARCH (1,2) untuk Malaysia, dan metode ARMA(1,(1)(3))-TARCH (2) untuk Thailand. Hasil estimasi inilah yang digunakan sebagai nilai ketidakpastian inflasi dalam penelitian (Lampiran I).
commit to user
32 3. Jumlah Uang beredar
Penelitian ini menggunakan pertumbuhan jumlah uang beredar dalam arti luas (Broad Money). Jumlah uang beredar dalam arti luas adalah jumlah uang kartal, giro selain dari pemerintah pusat, tabungan dan deposito mata uang asing milik masyarakat selain pemerintah pusat, cek dan surat berharga. Pertumbuhan jumlah uang beredar dihitung menggunakan rumus umum persentase pertumbuhan sebagai berikut:
Penelitianini menggunakan nilai pertumbuhan jumlah uang beredar dalam satuan persen. Data jumlah uang beredar diperoleh dari
International Financial Statistic yang dikeluarkan oleh IMF yang dinyatakan dalam data triwulan dengan satuan juta per mata uang nasional masing-masing negara.
4. Tingkat Suku Bunga
Tingkat suku bunga adalah tingkat keuntungan minimum yang diharapkan pemodal dari investasi dalam bentuk simpanan. Tingkat suku bunga dalam penelitian ini adalah tingkat suku bunga deposito perbankan rata-rata dalam satuan persen dengan periode triwulanan. Suku bunga deposito adalah tingkat bunga yang dibayarkan bank atau lembaga serupa untuk permintaan, waktu dan simpanan (The World Bank, 2016). Data diperoleh dari International Financial Statistic yang dikeluarkan oleh IMF yang dinyatakan dalam persen.
commit to user
33 D. Metode Analisis Time Series
Penelitian ini menggunakan metode penelitian analisis runtut waktu dan data panel. Metode runtut waktu digunakan dalam estimasi ketidakpastian dengan metode estimasi AR(p), ARMA(p,q), AR(p)–EGARCH (m,n), dan ARMA(p,q)-TARCH (m) dan uji kausalitas dengan Granger Causality test. Sebelum melakukan estimasi perlu dilakukan uji stasioneritas data. Pengujian stasioneritas data dilakukan dengan menggunakan uji ADF (The Augmented Dickey-Fuller). Analisis dilakukan dengan menggunakan software pengolah data e-views 8.
1. Uji Stasioneritas
Salah satu asumsi penting yang harus dipenuhi dalam analisis time series adalah asumsi data bersifat stasioner. Rosadi (2012) menjelaskan bahwa pada model stasioner, sifat-sifat statistik dimasa yang akan datang dapat diramalkan berdasarkan data historis yang telah terjadi di masa lalu. Beberapa uji stasioneritas yang dapat dilakukan antara lain (Rosadi, 2012: 38):
a) Untuk mendeteksi ketidak-stasioneran data dalam mean (rata-rata) dapat digunakan plot dari data dalam urutan waktu, plot fungsi autokorelasi (Autocorrelation function/ACF) dan plot fungsi autokorelasi parsial (Partial ACF/PACF). Jika data mengandung komponen trend maka plot ACF/PACF akan meluruh secara perlahan dan data non-stasioner dalam mean.
b) Untuk mendeteksi ketidak-stasioneran dalam varians dapat digunakan plot ACF/PACF dari residual kuadrat.
commit to user
34
c) Stasioneritas juga dapat diperiksa dengna mengamati apakah data runtut waktu mengandung akar unit (unit root), yakni apakah terdapat komponen trend yang berupa random walk dalam data. Terdapat berbagai metode untuk melakukan uji akar unit, diantaranya Dickey Fuller, Augmented Dickey-Fuller, dan lain-lain.
Dalam penelitian ini uji stasioneritas akan dilakukan dengan menggunakan uji akar unit (Unit root test) berdasarkan metode uji akar unit ADF (The Augmented Dickey-Fuller). Model umum ADF yang dijelaskan oleh Rosadi (2012) adalah:
∑
H0 : δ = 0 (Data tidak stasioner)
Ha : H0 : δ < 0 (Data stasioner)
Keterangan :
: first different variabel yang diteliti α : konstanta
: komponen trend : Variabel penelitian
: panjang lag yang digunakan : error term
commit to user
35
2. ARMA (Autoregressive and Moving Average)
ARMA disebut juga sebagai metode Box-Jenkins. Widarjono (2013) menjelaskan bahwa model Box-Jenkins merupakan salah satu teknik peramalan data time series yang hanya berdasarkan perilaku data variabel yang diamati. ARMA menggunakan nilai masa lalu dan sekarang dari variabel dependen itu sendiri untuk menghasilkan sebuah peramalan jangka pendek. Model ARMA dapat dituliskan sebagai berikut (Ajija et al., 2011: 75):
a) Autoregressive (AR(p))
( ) ( ) ( ) ( ) b) Moving Average (MA(q))
c) Autoregressive Moving Average (ARMA (p,q))
Keterangan:
α , μ ,θ : konstanta δ : nilai rataan Y μt : random term
u : white noise stochastic error term
Model ARIMA digunakan apabila data terintegrasi pada orde d
(data stasioner pada d difference). Widarjono (2013) menjelaskan model ARIMA dapat ditulis ARIMA (p,d,q) dimana p menjelaskan orde
commit to user
36
diselisihkan sebelum menjadi stasioner, dan q menjelaskan orde Moving Average.
Berapa tahap yang dilakukan dalam metode ARMA menurut Rosadi (2012) antara lain:
1. Identifikasi model ARMA
Identifikasi model dapat dilakukan setelah data yang diperoleh bersifat stasioner dalam rata-rata dan varian. Stasioneritas dapat diketahui dengan melihat plot ACF dan PACF atau dengan melakukan uji akar unit. Penentuan model ARIMA dilakukan dengan membandingkan plot sampel ACF/PACF dengan sifat-sifat fungsi ACF/PACF teoritis dari model ARMA. Rosadi (2012) merangkum sifat dari plot sampel ACF/PACF dari model ARIMA sebagaimana tertera pada Tabel 3.1.
Tabel 3.1 Sifat-sifat ACF/PACF dari Model ARMA
Proses Sampel ACF Sampel PACF
White noise
(random walk)
Tidak terdapat plot yang melewati batas interval pada lag >0
Tidak terdapat plot yang melewati batas interval pada lag >0
AR (p) Meluruh menuju nol secara eksponensial
Di atas batas interval maksimum sampai lag ke p dan di bawah batas pada lag > p
MA (q) Di atas batas interval maksimum sampai lag ke q dan di bawah batas pada lag > q
Meluruh menuju nol secara eksponensial
ARMA (p,q) Meluruh menuju nol secara eksponensial
Meluruh menuju nol secara eksponensial
commit to user
37 2. Estimasi Parameter Model ARMA
Rosadi (2012) menjelaskan setelah mendapatkan nilai orde p
dan q, maka dapat dilakukan estimasi parameter model dengan menggunakan metode Maximum Likelihood, Least Square (kuadrat terkecil), Hanan Rissanen, metode Whittle, dan lain-lain.
3. Uji Diagnostik dan pemilihan model terbaik
Uji diagnostik dilakukan pada model estimasi dengan melakukan verifikasi kesesuaian model dengan sifat-sifat data. Model yang tepat akan memiliki sifat-sifat yang sesuai dengan data asli, seperti sifat white noise. Untuk melihat sifat white noise dapat dilakukan dengan cara melihat sifat plot ACF/PACF atau dengan melalui uji korelasi serial dengan menggunakan uji Box-Pierce atau Ljung Box. Apabila hipotesis diagnostic check ditolak maka model yang telah diidentifikasi tidak dapat digunakan. Perlu dilakukan identifikasi kembali pada model yang mungkin sesuai untuk data (Rosadi, 2012).
Pemilihan model terbaik pada model-model yang telah memenuhi uji diagnostik dapat dilakukan dengan memilih model yang memiliki ukuran kriteria infromasi Akaike Information Criteria (AIC) atau Schwartz Bayesian Information Criteria (SIC).
4. Aplikasi model
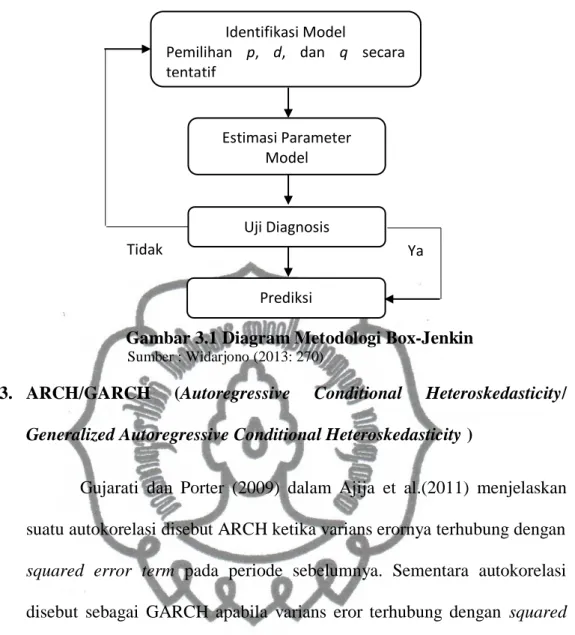
Setelah model terbaik diperoleh, model tersebut dapat digunakan. Widarjono (2013) menggambarkan tahap-tahap ARMA ini dalam sebuah skema berikut.
commit to user
38
Gambar 3.1 Diagram Metodologi Box-Jenkin
Sumber : Widarjono (2013: 270)
3. ARCH/GARCH (Autoregressive Conditional Heteroskedasticity/
Generalized Autoregressive Conditional Heteroskedasticity )
Gujarati dan Porter (2009) dalam Ajija et al.(2011) menjelaskan suatu autokorelasi disebut ARCH ketika varians erornya terhubung dengan
squared error term pada periode sebelumnya. Sementara autokorelasi disebut sebagai GARCH apabila varians eror terhubung dengan squared error term pada beberapa periode sebelumnya. GARCH merupakan bentuk perluasan dari model ARCH (Autoregressive Conditional Heteroskedasticity) yang dikembangkan oleh Bollerslev tahun 1986. ARCH /GARCH dapat digunakan untuk menganalisis estimasi OLS yang memiliki masalah heterokedastisitas (variance error yang tidak konstan). ARCH/GARCH digunakan sebagai modeling dan peramalan dengan mengabaikan sifat heteroskedastisitas pada model. Rosadi (2012) menjelaskan bahwa metode GARCH adalah salah satu model runtut waktu
Identifikasi Model
Pemilihan p, d, dan q secara tentatif Estimasi Parameter Model Uji Diagnosis Prediksi Ya Tidak
commit to user
39
yang dapat digunakan untuk menggambarkan sifat dinamik fungsi volatilitas (standar deviasi) dari data (Rosadi, 2012).
Dalam membentuk model ARCH dan GARCH secara umum terdapat dua persamaan yang berbeda, yaitu persamaan rataan bersyarat (conditional mean) dan persamaan untuk ragam bersyarat (conditional variance). Model tersebut dapat dituliskan sebagai berikut (Rosadi,2012):
a) Conditional Mean
b) Conditional Variance (ARCH/GARCH)
∑ ∑ ∑ Keterangan : : Variabel dependen : Variabel independen : residual : conditional variance 0 : konstanta : komponen ARCH
: ramalan varians dari periode sebelumnya (komponen GARCH) Berbeda dengan ARCH, pada model GARCH varian residual tidak hanya dipengaruhi oleh residual periode lalu, tetapi juga oleh varians
commit to user
40
residual periode lalu . GARCH juga mengharuskan nilai parameter dalam model bernilai positif atau non-negativity constraint berlaku,
dimana .
4. Model Asymmetric Autoregressive Conditional Heteroskedasticity
Model GARCH yang telah dijelaskan memiliki karakteristik respons volatilitas yang simetris (symmetric shocks to volatility) atau sama terhadap guncangan baik guncangan positif (good news) maupun negatif (bad news). Pengembangan model GARCH mengakomodasi kemungkinan adanya respon volatilitas yang asimetris. Dimana respon (gejolak pasar) lebih besar ketika bad news datang dibandingkan dengan good news.
Dalam Susanti (2015) dijelaskan bahwa adanya efek asimetris (leverage effect) dapat diketahui dengan melakukan pemodelan GARCH pada data runtut waktu. Berdasakan pada model tersebut kemudian dilakukan uji korelasi antara (residual kuadrat) dengan (lag residual) dengan menggunakan korelasi silang (cross-correlation) pada model. Adanya efek asimetris ditandai dengan korelasi yang tidak sama dengan nol.
Salah satu teknik pemodelan respon ARCH/GARCH asimetris yaitu model Threshold ARCH (TARCH) dan Exponential GARCH (EGARCH).
a. TARCH
Model ARCH (p) dalam bentuk TARCH dapat dituliskan dalam formula (Widarjono, 2013:299):
commit to user
41
Dimana d adalah variabel dummy, =1 jika , dan
=0 untuk .
Dalam model TARCH good news pada periode t–1
( ) dan bad news pada periode t–1 ( )
mempunyai efek yang berbeda terhadap conditional variance.
Good news berdampak pada α dan bad news berdampak pada α+ϕ. Jika ϕ ≠0 maka terdapat efek asimetris.
b. EGARCH
Model standar GARCH (p,q) dalam bentuk EGARCH dituliskan sebagai berikut (Susanti, 2015):
∑ { (| | √ ) } ∑ ( )
Jika hipotesis respon asimetris berlaku, maka diharapkan nilai γ < 0 dan signifikan. Penggunaan ln pada persamaan ini menunjukkan bahwa varian bersifat eksponensial bukan dalam bentuk kuadratik layaknya ARCH, GARCH atau TARCH. Penggunaan ln menjamin bahwa varian bersyarat akan selalu bernilai positif, meskipun nilai parameternya negatif. Hal ini menghilangkan asumsi non-negativity constraint.
Widarjono (2013) menjelaskan bahwa persamaan EGARCH
terdiri dari dua unsur. Unsur pertama adalah magnitude effect |
|
commit to user
42
terhadap varian saat ini. Unsur kedua adalah sign effect ( )
yang menunjukkan perbedaan pengaruh shock positif dan negatif
pada periode t terhadap varian saat ini. 5. Kriteria Pemilihan Model
Penelitian ini menggunakan metode Akaike’s Information Criterion (AIC) dan Schwarz Information Criterion (SIC). Fathurahman (2009) menjelaskan kedua metode tersebut memiliki kelebihan dibandingkan menggunakan metode koefisien determinasi (R2) yang banyak digunakan. AIC dan SIC memiliki kelebihan pada pemilihan model regresi terbaik untuk tujuan peramalan (forecasting). Metode ini dapat menjelaskan kecocokan model dengan data yang ada dan nilai yang terjadi di masa mendatang.
Widarjono (2007 dalam Fathurahman, 2009) menyebutkan beberapa kelemahan koefisien determinasi (R2), salah satunya adalah metode R2 hanya digunakan untuk peramalan in sample yaitu apakah prediksi model bisa sedekat mungkin dengan data yang ada, tidak ada jaminan bahwa metode R2 mampu meramalkan nilai di masa mendatang, dan nilai R2 tidak pernah menurun jika terus ditambahkan variabel prediktor di dalam model walaupun variabel prediktor tersebut kurang atau tidak relevan.
(∑ )
commit to user 43 Keterangan : k = jumlah parameter n = jumlah observasi e = 2,718 ε = residual
Pada penggunaannnya AIC dan SIC memiliki kegunaan yang tidak berbeda. Semakin kecil nilai AIC dan SIC maka semakin baik sebuah model.
6. Akurasi Estimasi
Baik tidaknya hasil estimasi suatu model sangat menentukan dalam pemilihan model. Model terbaik adalah model dengan nilai akurasi tertinggi, atau nilai kesalahan estimasi terkecil. Woschnagg dan Cipan (2004) menjelaskan beberapa metode pengukuran akurasi peramalan, salah satunya adalah RMSE, MAE, dan MAPE.
1) RMSE (Root Mean Squared Error)
Nilai RMSE tergantung pada skala variabel dependen. Pengukuran ini sering digunakan sebagai ukuran relatif untuk membandingkan peramalan untuk series yang sama dengan model yang berbeda. Semakin kecil nilai error, maka semakin baik kemampuan permalan dari model berdasarkan kriteria RMSE (Woschnagg dan Cipan, 2004:13).
√
∑( ̂ ( ) )
commit to user
44
Satu masalah yang terkait dengan penggunaan tindakan RMSE atau serupa adalah kenyataan bahwa varians kesalahan perkiraan bervariasi di seluruh waktu. Fair (1986 dalam Woschnagg dan Cipan, 2004) mengatakan bahwa tidak ada interpretasi statistik yang benar-benar tepat yang dapat diletakkan pada RMSE karena mereka bukan perkiraan parameter dalam model.
2) MAE (Mean Absolute Error)
∑| ̂ ( ) |
Mean absolute error juga tergantung pada skala variabel dependen, namun ukuran ini lebih kurang sensitif pada nilai deviasi yang besar daripada kuadrat yang hilang biasanya (Woschnagg dan Cipan, 2004:14).
3) MAPE (Mean Absolute Percentage Error)
Menurut Woschnagg dan Cipan (2004) pengukuran akurasi popular lainnya adalah Mean Absolute Percentage Error. MAPE adalah sebuah skala independen. Namun, MAPE dikritik karena masalah asimetri dan ketidakstabilannya ketika nilai asli bernilai kecil. MAPE sebagai ukuran akurasi dipengaruhi oleh empat permasalahan yaitu (Woschnagg dan Cipan, 2004:14):
a. Kesalahan yang besarnya menyamai nilai aktual menghasilkan nilai MAPE yang lebih besar.
b. Nilai MAPE yang besar terjadi saat data nilai aktual bernilai kecil c. Outlier dapat mendistorsi perbandingan dalam studi empiris.
commit to user
45
d. MAPE tidak dapat dibandingkan secara langsung dengan model yang naif seperti random walk.
∑ |
̂ ( ) |
7. Pemilihan Lag Optimum
Salah satu hal penting sebelum melakukan uji kausalitas Granger adalah menentukan lag optimum. Uji kausalitas Granger sangat sensitif terhadap nilai lag yang digunakan. Thornton dan Batten (1984) menjelaskan bagaimana sensitifnya nilai lag yang digunakan terhadap hasil uji kausalitas yang diperoleh dari uji kausalitas granger antara tingkat pendapatan nasional dan jumlah uang beredar dengan nilai lag 4 dan 8 yang dipilih secara acak. Hasil kausalitas dengan lag 4 menunjukkan bahwa pendapatan nasional tidak mempengaruhi jumlah uang beredar, sedangkan lag 8 menunjukkan hasil kebalikannya.
Berdasarkan penjelasan Thornton dan Batten (1984) pemilihan lag secara acak dapat menyebabkan munculnya hasil yang salah. Oleh karena itu pemilihan lag optimum dapat dilakukan berdasarkan pada kriteria tertentu. Beberapa kriteria yang sering digunakan dalam pemilihan lag optimum adalah Akaike information Criterion (AIC), Schwarz Information Criterion (SC) dan Hannan-Quinn Criterion (HQ). Lag optimum berdasarkan kriteria informasi tersebut dipilih dengan melihat nilai final prediction error correction (FPE) atau jumlah AIC, SIC, dan HQ terkecil.
commit to user
46 8. Uji Kausalitas Granger
Uji Kausalitas ini dimaksudkan untuk mengetahui bahwa dari dua variabel yang berhubungan, variabel mana yang menyebabkan variabel lain berubah. Seperti, apakah variabel A menyebabkan variabel B, atau sebaliknya variabel B menyebabkan variabel A. Gujarati (2004 dalam Prakoso, 2009: 61) menjelaskan beberapa kemungkinan hasil yang dapat diperoleh dari hasil uji Granger ini antara lain:
a. Hubungan kausalitas satu arah dari Bt ke At , yang disebut sebagai
unidirectional causality from Bt ke At
b. Hubungan kausalitas satu arah dari At ke Bt , yang disebut sebagai
unidirectional causality from At to Bt
c. Kausalitas dua arah atau saling mempengaruh (bidirectional causality)
d. Tidak terdapat hubungan saling ketergantungan (no causality) Hipotesis dalam uji Kausalitas Granger antara lain :
H0 : Suatu variabel tidak menyebabkan suatu variabel lainnya
Ha : Suatu variabel menyebabkan satu variabel lainnya.
Berikut ini model yang digunakan oleh Jiranyakul dan Opiela (2010) untuk menguji hubungan kausalitas antara inflasi dan ketidakpastian inflasi: ∑ ∑ ∑ ∑
commit to user
47
Kedua model tersebut masing-masing digunakan utnuk menguji apakah inflasi (πt) menyebabkan ketidakpastian inflasi (ht) dan apakah ketidakpastian inflasi (ht) menyebabkan inflasi (πt).
Keterangan :
ht : ketidakpastian inflasi (inflation uncertainty)
πt : inflasi α , γ : konstanta
β : koefisien pengaruh inflasi
δ : koefisien pengaruh ketidakpastian inflasi , : error term
E. Analisis Data Panel
Analisis data panel yaitu ganbungan dari data runtut waktu (time series) selama tahun 1998-2015 dan deret lintang (cross section) yang meliputi empat negara. Menurut Baltagi dalam Gujarati dan Porter (2012:237) keunggulan penggunaan analisis data panel adalah sebagai berikut:
1. Teknis estimasi data panel dapat mengatasi heterogenitas secara tegas dalam perhitungan dengan melibatkan variabel-variabel individual secara spesifik.
2. Analisis data panel memberikan informasi yang lebih banyak, variabilitas yang lebih baik mengurangi hubungan antara variabel bebas, memberikan lebih banyak derajat kebebasan, dan lebih efisien.
commit to user
48
3. Dengan mempelajari observasi cross-section yang berulang-ulang, data panel lebih baik digunakan untuk melakukan studi mengenai dinamika perubahan.
4. Data panel mampu mendeteksi dan mengukur dampak yang secara sederhana tidak bisa dilihat pada data time-series murni dan cross-section
murni.
5. Data panel memungkinkan peneliti untuk mempelajari model perilaku yang lebih kompleks dibandingkan data time-series dan cross-section. 6. Data panel dapat meminimalkan bias dengan membuat data yang tersedia
untuk beberapa ribu unit.
Terdapat tiga metode pendekatan dalam data panel, yaitu common effect model, fixed effect model dan random effect model. Gujarati dan Porter (2012) menjelaskan ketiga model tersebut adalah sebagai berikut:
1. Common effect : Pooled Least Square (PLS)
Metode Pooled Least Square (PLS) merupakan metode yang digunakan untuk menegstimasi data panel dengan menggabungkan seluruh observasi pada masing-masing variabel. Sehingga intersep dari semua objek cross-section sama, dengan kata lain metode ini mengasumsikan tidak ada perbedaan setiap individu dalam berbagai kurun waktu ( time-invariant).
2. Fixed Effect Model (FEM)
Fixed effect model mengasumsikan bahwa terdapat perbedaan intersep antar individu. Akan tetapi, koefisien (slope) dari variabel independen tetap sama antar individu atau antar waktu.
commit to user
49
Fixed effect model dapat dibedakan menjadi dua, yaitu : a. Model Fixed Effect Satu Arah
Setiap individu memiliki intersep yang berbeda-beda, tetapi tidak berubah dengan seiring berjalannya waktu.
b. Model Fixed Effect Dua Arah
Dengan menambahkan efek waktu pada setiap intersep dan efek waktu tersebut dapat dihitung dengan menggunakan dummy waktu.
3. Random Effect Model (REM)
Jika pendekatan dengan menggunakan variabel dummy justru mencerminkan keterbatasan pengetahuan mengenai model yang sebenarnya, maka lebih baik mencoba untuk mengabaikan melalui
disturbance term. Pendekatan ini yang disebut pendekatan Random Effect Model (REM) atau Error Components Model (ECM) yang menggunakan asumsi bahwa β1i merupakan variabel random dengan nilai rata-rata dari
β1. Selanjutnya nilai intersep untuk tiap individu dimodelkan sebagai
berikut :
β1i = β1 + εi i = 1, 2, …, N
dimana εi adalah random error term dengan nilai rata-rata nol dan
variance ζε2.
Perbedaan antara FEM dan ECM antara lain setiap individu cross-section pada FEM memiliki nilai intersep masing-masing. Sedangkan pada ECM memiliki intersep bersama yang mewakili nilai rata-rata dari semua
commit to user
50
intersep (cross-section) dan komponen eror εi mewakili deviasi dari
intersep individual terhadap nilai rata-rata tersebut.
F. Pemilihan Teknik Estimasi
Pemilihan teknik estimasi regresi dapat dilakukan dengan melakukan beberapa uji untuk mengetahui metode estimasi terbaik. Salah satu uji yang dapat dilakukan antara lain sebagai berikut.
1. Uji Chow (Likelihood Ratio)
Uji Chow dilakukan untuk memilih apakah pendekatan Common Effect atau Fixed Effect yang lebih baik digunakan untuk regresi data panel. Hipotesis yang digunakan dalam uji Chow adalah :
H0 : Common Effect Model (restricted)
H1 : Fixed Effect Model (unrestricted)
Jika hasil uji Chow menunjukkan nilai F-statistik lebih besar dari F-tabel (F-stat > F-tabel) atau probabilitasnya lebih kecil dari nilai taraf signifikansi (prob < α), maka H0 ditolak dan model Fixed Effect yang lebih
baik digunakan. Sedangkan, jika uji Chow menunjukkan nilai F-statistik lebih kecil dari nilai F-tabel (F-stat < F-tabel) dan nilai probabilitas lebih besar dari nilai taraf signifikansi (prob > α), maka model Common Effect
yang lebih baik digunakan. F-statistik dapat dihitung dengan rumus (Gujarati dan Porter, 2013 : 321)
( ) ( ) ( ) Keterangan :
commit to user
51
R2R = Residual Sum of Squares (model Common Effect)
m = Jumlah restriksi linear n = Jumlah observasi k = Jumlah Parameter 2. Uji Hausman
Uji Hausman dilakukan untuk menentukan model estimasi data panel terbaik antara Fixed Effect Model atau Random Effect Model. Terdapat beberapa hal penting yang perlu diperhatikan untuk menentukan pendekatan mana yang dipilih (FEM atau ECM) dalam estimasi data panel, antarai lain (Judge dalam Gujarati dan Porter, 2012):
a. Jika T (jumlah data time series) besar dan N (jumlah unit cross-section) kecil, kemungkinan akan ada sedikit perbedaan parameter yang diestimasi oleh FEM dan ECM. Dalam hal ini, FEM lebih disukai.
b. Ketika N besar dan T kecil, hasil estimasi yang didapatkan dari kedua metode dapat berbeda secara signifikan. Jika unit atau cross-section diambil tidak random dari sampel yang besar maka FEM pantas untuk digunakan. Jika unit cross-section dianggap diambil secara acak maka ECM dapat digunakan.
c. Jika komponen error individual (εi) dan satu atau lebih variabel
independen saling berkorelasi lebih baik menggunakan FEM, sedangkan jika εi dan satu atau lebih variabel independen tidak
commit to user
52
d. Jika N besar dan T kecil, dan jika asumsi yang melandasi ECM terpenuhi, maka estimator ECM lebih efisien dibandingkan FEM. e. Tidak seperti FEM, ECM dapat mengestimasi koefisien dari
variabel yang tidak dipengaruhi waktu seperti gender dan etnisitas. Hipotesis yang digunakan adalah sebagai berikut:
H0 = model yang dipilih Random Effect Model
H1 = model yang dipilih Fixed Effect Model
Widarjono (2013) menjelaskan uji Hausman dilakukan dengan membandingkan nilai statistik Husman dengan nilai tabel distribusi Chi-square dengan degree of freedom sejumlah variabel independen. Bila nilai statistik Hausman lebih besar dari nilai Chi-square dan nilai probabilitasnya lebih kecil dari nilai signifikansi (prob < α) maka H0
ditolak dan pendekatan Fixed Effect Model yang terbaik. Sedangkan, bila nilai statistik Hausman lebih kecil dari nilai Chi-square dan nilai probabilitas lebih besar dari nilai signifikansi (prob > α) maka H0 diterima
dan pendekatan Random Effect Model yang terbaik.
G. Uji Asumsi Klasik
Sebelum dilakukan analisis pada data, terlebih dahulu dilakukan uji asumsi klasik. Jika terdapat penyimpangan pada salah satu asumsi klasik, maka dapat digunakan pengujian statistik non parametrik untuk mengatasinya. Sementara itu, statistik parametrik digunakan untuk mengujian data apabila data variabel terbebas dari multikolinearitas, autokorelasi, dan heteroskedastisitas. Berikut ini penjelasan mengenai uji asumsi klasik.
commit to user
53 1. Uji Multikolinearitas
Dalam model regresi diasumsikan tidak memuat hubungan dependensi linear antarvariabel independen. Jika terjadi hubungan dependensi linear yang kuat diantara variabel independen maka dinamakan terjadi problem multikolinearitas. Jika terjadi multikolinearitas maka nilai
standar error dari koefisien menjadi tidak valid sehingga hasil uji signifikansi koefisien dengan uji t tidak valid. (Rosadi, 2012 : 52).
Gujarati dan Porter (2012) menjelaskan bahwa multikolinearitas sebagai kondisi dimana adanya suatu hubungan linear yang sempurna diantara sebagian atau seluruh variabel penjelas dalam sebuah model regresi. Konsekuensi dari adanya multikolinearitas tidak menyebabkan estimator menjadi bias, menurut Christopher Achen multikolinearitas hanya mempersulit seseorang mendapatkan koefisien estimasi dengan
standard error kecil (Gujarati dan Porter, 2012 : 414).
Uji multikolinearitas dapat dilakukan dengan metode Klien, yaitu membandingkan nilai koefisien determinasi (R2) dengan nilai regresi dari masing-masing variabel independen (r2). Apabila nilai R2 > r2 maka model tidak mengandung gejala multikolinearitas. Sedangkan, apabila R2 < r2 maka model mengandung gejala multikolinearitas (Widarjono, 2013 : 107).
2. Uji Autokorelasi
Autokorelasi dapat diartikan sebagai korelasi diantara anggota seri dari beberapa observasi-observasi yang diurutkan berdasarkan waktu (time series) atau tempat (cross-section). Salah satu uji autokorelasi yang umum
commit to user
54
digunakan adalah uji Durbin Watson. Beberapa asumsi yang mendasari pengujian antara lain (Gujarati dan Porter, 2012:37):
a. Lakukan regresi OLS dan dapatkan residual-residual b. Hitung nilai d (Durbin Watson)
c. Untuk ukuran sampel tertentu dan jumlah variabel penjelas tertentu, tentukan kritieria dL dan dU.
d. Pengambilan keputusan pada hasil uji diterangkan sebagai berikut: Tabel 3.2 Aturan Pengambilan Keputusan Uji Durbin-Watson
Hipotesis Nol Keputusan Jika
Tidak ada autokorelasi positif Tolak 0 < d < dL
Tidak ada autokorelasi positif Tidak ada keputusan dL ≤ d ≤ dU
Tidak ada autokorelasi negatif Tolak 4-dL < d < 4
Tidak ada autokorelasi negatif Tidak ada keputusan 4-dU ≤ d ≤ 4-dU
Tidak ada korelasi, baik positif
maupun negatif Terima dU ≤ d ≤ 4-dU
Sumber : Gujarati dan Porter (2012 :37)
3. Uji Heteroskedastisitas
Uji heteroskedastisitas salah satunya dapat dilakukan dengan uji Park. Uji Park pada prinsipnya meregresi residual yang dikuadratkan dengan variabel bebas pada model. Langkah-langkah uji park antara lain:
a. Melakukan regresi terhadap model dengan metode Ordinary Least Squares (OLS) dan diperoleh nilai residualnya.
b. Melakukan regresi terhadap residual kuadrat.
c. Jika nilai t statistik lebih kecil dari nilai t tabel atau probabilitas t statistik lebih besar dari derajat signifikansi (prob>α), maka tidak terdapat gejala heteroskedastisitas dan jika nilai t statistik lebih besar dari t tabel atau probabilitas t statistik kurang dari nilai
commit to user
55
derajat signifikansi (prob<α), maka terdapat gejala heteroskedastisitas.
H. Uji Statistik
Uji statistik dilakukan untuk melihat bagaimana variabel mempengaruhi variabel independen dengan beberapa uji tertentu, seperti uji t-statistik, uji F-statistik dan uji koefisien determinasi.
1. Uji t-statistik
Gujarati dan Porter (2013:149-152) berpendapat bahwa secara umum uji signifikansi merupakan sebuah prosedur, dimana hasil sampel digunakan untuk membuktikan kebenaran atau kesalahan dari hipotesis nol. Ide dasar pengujian signifikansi dilatar belakangi oleh uji statistik (estimator) dari distribusi sampel dari suatu statistik yang dinyatakan oleh hipotesis nol. Keputusan untuk menerima atau menolak H0 dibuat
berdasarkan nilai uji statistik yang diperoleh dari data yang telah ada. Sebuah statistik dikatakan signifikan secara statistik apabila nilai uji statistik berada pada daerah tolak atau daerah kritis. Sebaliknya, sebuah pengujian statistik dikatakan tidak signifikan apabila nilai uji statistiknya berada pada daerah penerimaan.
Beberapa langkah dalam uji t statistik antara lain : a. Hipotesis :
1) H0 : Variabel independen tidak berpengaruh signifikan
commit to user
56
2) H1 : Variabel independen berpengaruh signifikan terhadap
variabel dependen.
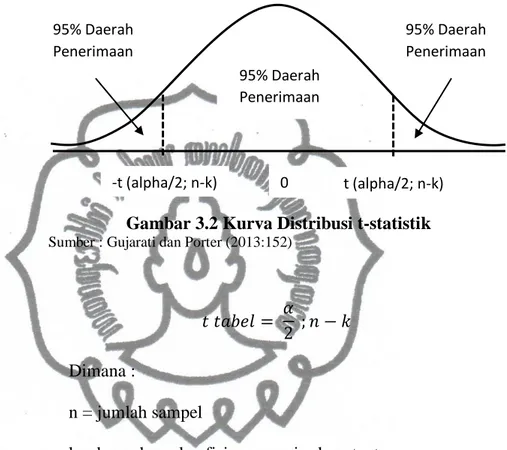
b. Menentukan daerah tolak dan daerah penerimaan pada kurva distribusi
Gambar 3.2 Kurva Distribusi t-statistik
Sumber : Gujarati dan Porter (2013:152)
Dimana :
n = jumlah sampel
k = banyaknya koefisien regresi + konstanta c. Hitung nilai t dengan rumus berikut
̂ ( ̂ ) Dimana :
t = Uji signifikansi
̂ = estimator nilai yang dinyatakan dalam hipotesis nol
= parameter dinyatakan dalam hipotesis nol se( ̂ ) = standard error estimator yang telah ditentukan
95% Daerah Penerimaan 95% Daerah Penerimaan 95% Daerah Penerimaan -t (alpha/2; n-k) 0 t (alpha/2; n-k)
commit to user
57
d. Berdasarkan hasil t hitung diperoleh kemudian dibandingkan dengan t-tabel. Kesimpulan hasil uji t dapat diambil berdasarkan ketentuan berikut:
1) H0 diterima jika t hitung lebih kecil dari nilai t tabel (t hitung <
t tabel), artinya tidak ada pengaruh signifikan antara variabel independen terhadap variabel dependen.
2) H1 diterima apabila t hitung lebih besar dati nilai t tabel (t
hitung > t tabel), artinya ada pengaruh signifikan antara variabel independen terhadap variabel dependen.
2. Uji F-statistik
Uji F dilakukan untuk mengetahui pengaruh variabel independen secara simultan (bersama-sama) terhadap variabel dependen. Penggunaan derajat signifikansi tergantung pada keputusan peneliti yaitu 0,01 (1%); 0,05 (5%) dan 0,1 (10%). Beberapa langkah yang perlu dilakukan dalam uji F antara lain (Gujarati, 2013):
a. Hipotesis :
1) H0 : β1 = β2 = β3 = 0, artinya secara simultan tidak ada
pengaruh antara variabel independen terhadap variabel dependen
2) H1 : β1 ≠ β2 ≠ β3 ≠ 0, artinya secara simultan terdapat
pengaruh variabel independen terhadap variabel dependen b. Menentukan derajat signifikansi (α), yaitu 0,05 (5%)
c. Menentukan daerah toak dan terima.
commit to user
58
d. Menghitung nilai F hitung dengan rumus sebagai berikut ( )
( ) ( ) e. Hasil uji F dapat diketehui dengan ketentuan berikut:
1) Jika F hitung > F tabel, maka H0 ditolak dan H1 diterima.
Semua variabel independen secara simultan merupakan penjelas yang signifikan terhadap variabel dependen.
2) Jika F hitung < F tabel maka H0 diterima dan H1 ditolak.
Semua variabel independen secara simultan bukan merupakan penjelas yang signifikan terhadap variabel dependen.
3. Uji R2 (Koefisien Determinasi)
Besarnya R2 disebut juga sebagai koefisien determinasi dan merupakan ukuran yang umum digunakan untuk mengukur goodness of fit
dari sebuah regresi. Secara verbal R2 mengukur proporsi atau persentasi dari variasi total pada variabel dependen yang dijelaskan oleh model regresi. Terdapat dua sifat dari R2 yang perlu diperhatikan, yaitu (Gujarati dan Porter, 2013: 97):
1. Besarnya tidak pernah negatif.
2. Batasannya adalah 0 ≤ R2 ≤ 1. Jika R2 bernilai 1 (satu), artinya kesesuaian garisnya tepat. Di sisi lain, jika R2 bernilai 0 (nol), artinya tidak terdapat hubungan antara regresan dan regresor. Semakin nilai R2 mendekati nilai 1 (satu), artinya semakin baik kemampuan variabel independen dapat menjelaskan pengaruh terhadap variabel dependen. Koefisien determinasi dapat dihitung dengan rumus:
commit to user 59 ∑( ̂ ̅) ∑( ̅) atau ∑ ̂ ∑( ̅)
Keterangan :
ESS = Jumlah kuadrat (explained sum of squares) TSS = Total jumlah kuadrat (total sum of squares) RSS = Jumlah sisa (residual sum of squares)