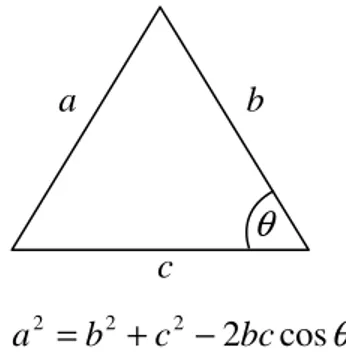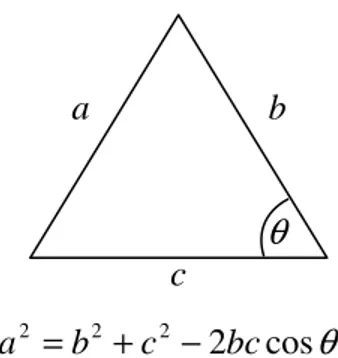Generalisasi beberapa aturan dalam geometri dengan menggunakan darab eksterior - USD Repository

Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Oleh: Albertus Dedi NIM: 053114015

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

ii Final Project

Presented as Partial Fulfillment of the Requirements To Obtain the SARJANA SAINS Degree

In Mathematics

By: Albertus Dedi

Student Number: 053114015

MATHEMATICS STUDY PROGRAM MATHEMATICS DEPARTMENT SCIENCE AND TECHNOLOGY FACULTY

SANATA DHARMA UNIVERSITY YOGYAKARTA

v

vi

memuat karya orang lain, kecuali yang telah disebutkan dalam kutipan dan daftar pustaka, sebagaimana layaknya karya ilmiah.

Yogyakarta, Januari 2010 Penulis

vii

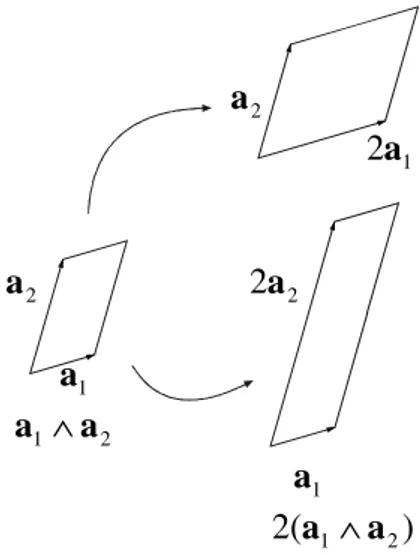
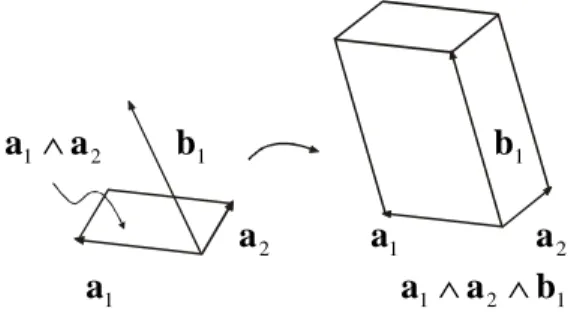
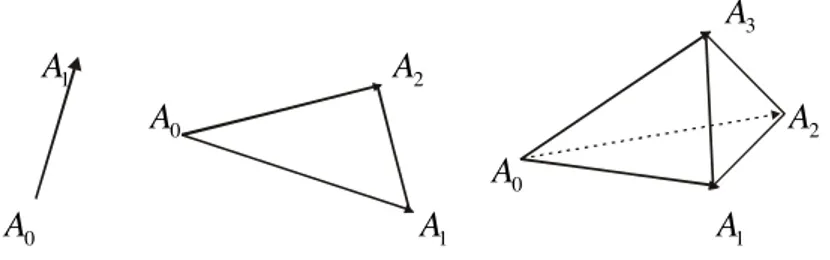
(k+m) sederhana. Simpleks-k dan balokgenjang berdimensi-k dapat dinyatakan sebagai darab eksterior dari k buah vektor di n

viii

(k+m)-vectors. The oriented k-simplexes and k-dimensional oriented parallelepipeds can be represented as exterior product of k vector in n

ix

Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma: Nama : Albertus Dedi

Nomor Mahasiswa : 053114015

Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan Universitas Sanata Dharma karya ilmiah yang berjudul:

GENERALISASI BEBERAPA ATURAN DALAM GEOMETRI DENGAN MENGGUNAKAN DARAB EKSTERIOR

Beserta perangkat yang diperlukan (bila ada). Dengan demikian saya memberikan kepada Perpustakaan Universitas Sanata Dharma hak untuk menyimpan, mengalihkan dalam bentuk media lain, mengelolanya dalam bentuk pangkalan data, mendistribusikan secara terbatas, dan mempublikasikan di Internet atau media lain untuk kepentingan akademis tanpa meminta ijin dari saya maupun memberikan royalty kepada saya selama tetap mencantumkan nama saya sebagai penulis.

Demikian pernyataan ini saya buat dengan sebenarnya. Dibuat di Yogyakarta.

Pada Tanggal: 15 Januari 2010 Yang menyatakan,

x

dan rahmat-Nya sehingga penulis dapat menyelesaikan skripsi ini.

Berkat dukungan dan bantuan dari banyak pihak, akhirnya skripsi ini dapat terselesaikan. Oleh karena itu, penulis mengucapkan terima kasih kepada:

1. Ibu Maria Vianney Any Herawati S.Si., M.Si. selaku dosen pembimbing yang telah memberikan pengarahan dan bimbingan selama penyusunan skripsi ini. 2. Bapak Yosef Agung Cahyanta S.T., M.T. selaku Dekan Fakultas Sains dan

Teknologi yang telah mendukung penulis selama penyusunan skripsi ini.

3. Ibu Lusia Krismiyati Budiasih S.Si., M.Si. selaku Kaprodi Matematika yang telah memberikan nasehat, saran dan dukungan kepada penulis.

4. Romo Prof. Dr. Frans Susilo S.J. selaku Dosen Pembimbing Akademik angkatan 2005 yang telah memberikan nasehat, saran dan dukungan kepada penulis.

5. Bapak dan Ibu dosen yang telah memberikan bekal ilmu kepada penulis.

6. Sekretariat Fakultas Sains dan Teknologi beserta staf yang telah memberikan pelayanan administrasi kepada penulis selama masa perkuliahan.

7. Perpustakaan Universitas Sanata Dharma dan staf yang telah menyediakan fasilitas dan memberikan kemudahan kepada penulis selama masa perkuliahan. 8. Kedua orang tuaku tercinta: Bapak Paulus Kasno dan Ibu Lucia Sri Amaliyah

xi

10. Teman-teman Matematika 2005 yang telah memberikan saran dan nasehat kepada penulis.

Penulis juga mengucapkan terima kasih kepada semua pihak yang telah membantu penulis dalam penyusunan skripsi ini yang tidak dapat saya sebutkan satu-persatu di sini.

Yogyakarta, Januari 2010

xii

HALAMAN JUDUL DALAM BAHASA INGGRIS... ii

HALAMAN PERSETUJUAN PEMBIMBING... iii

HALAMAN PENGESAHAN... iv

HALAMAN PERSEMBAHAN... v

HALAMAN PERNYATAAN KEASLIAN KARYA... vi

HALAMAN ABSTRAK... vii

HALAMAN ABSTRACT... viii

LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS... ix

KATA PENGANTAR... x

DAFTAR ISI... xii

BAB I PENDAHULUAN... 1

A. Latar Belakang... 1

B. Perumusan Masalah... 3

C. Pembatasan Masalah... 3

D. Tujuan Penulisan... 3

E. Metode Penulisan... 4

F. Manfaat Penulisan... 4

xiii

C. Ruang Vektor... 37

BAB III DARAB EKSTERIOR... 54

A. Hubungan Matriks dengan Vektor... 54

B. Vektor-k Sederhana... 61

C. Operasi pada Vektor-k Sederhana... 78

D. Vektor-k... 93

BAB IV APLIKASI DARAB EKSTERIOR... 100

A. Simpleks-k... 100

B. Aturan Kosinus pada Simpleks-k... 114

C. Aturan Pythagoras pada Simpleks-k Ortogonal... 123

D. Aturan Jajargenjang pada Balokgenjang Berdimensi-k... 128

BAB V PENUTUP... 140

A. Kesimpulan... 140

B. Saran... 141

xiv

Gambar 2... 2

Gambar 3... 62

Gambar 4... 63

Gambar 5... 64

Gambar 6... 72

Gambar 7... 75

Gambar 8... 79

Gambar 9... 88

Gambar 10... 91

Gambar 11... 101

Gambar 12... 113

Gambar 13... 114

Gambar 14... 115

Gambar 15... 116

Gambar 16... 117

Gambar 17... 118

Gambar 18... 123

Gambar 19... 128

Gambar 20... 130

B. Latar Belakang Masalah

Dalam matematika, khususnya geometri sering dijumpai suatu aturan yang dinamakan aturan kosinus dan aturan jajargenjang. Aturan kosinus diterapkan dalam suatu segitiga. Aturan kosinus dalam segitiga digunakan untuk mencari sudut antara sisi-sisi segitiga dan panjang sisi-sisi segitiga. Sedangkan, aturan jajargenjang diterapkan pada jajargenjang. Aturan jajargenjang digunakan untuk mencari panjang sisi-sisi jajargenjang dan panjang diagonal jajargenjang.

Aturan kosinus untuk sebarang segitiga dengan panjang sisi-sisinya a,b,c dan salah satu sudutnya θ seperti yang tampak pada gambar 1 adalah sebagai berikut:

a b

θ c

θ

cos 2

2 2 2

bc c

b

a = + −

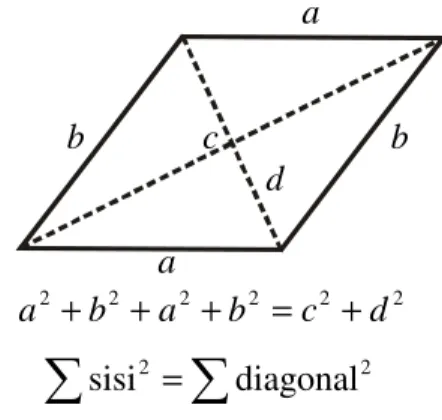
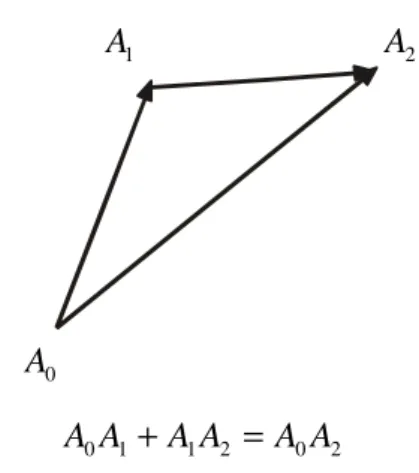
Aturan jajargenjang untuk sebarang jajargenjang dengan panjang sisi-sisinya a,b dan panjang diagonalnya c,d seperti yang tampak pada Gambar 2 adalah sebagai berikut:

a

b c b d

a

2 2 2 2 2 2

d c b a b

a + + + = +

∑

∑

2 = 2

diagonal sisi

Gambar 2. Aturan jajargenjang

Selain dalam segitiga dan jajargenjang, aturan kosinus dan aturan jajargenjang dapat diperumum. Generalisasi dari suatu segitiga disebut simpleks berorientasi berdimensi-k atau simpleks-k berorientasi. Sedangkan, generalisasi dari suatu jajargenjang disebut balokgenjang berorientasi berdimensi-k.

Untuk menggeneralisasikan aturan kosinus dan aturan jajargenjang pada simpleks-k berorientasi dan balokgenjang berorientasi berdimensi-k, dibutuhkan suatu operasi yang disebut darab eksterior. Darab eksterior dilambangkan dengan tanda ∧.

Misalkan k

i

Λ ∈

=

∑

=1

i ia

a λ n adalah vektor-k dan m j

j j ∈Λ

=

∑

=1 b

b β n adalah

vektor-m, maka darab eksterior dari a dan b didefinisikan sebagai berikut:

∑

∑

∑

_= ∧

  

  

∧

   

 

= ∧

=

= ij

j i j i j

j j i

i

i ( )

1 1

b a b

a b

C. Perumusan Masalah

Permasalahan yang dibahas dalam skripsi ini dapat dirumuskan sebagai berikut: 1. Apa yang dimaksud darab eksterior?

2. Bagaimana cara memperoleh generalisasi aturan kosinus pada simpleks-k menggunakan darab eksterior?

3. Bagaimana cara memperoleh generalisasi aturan jajargenjang pada balokgenjang berdimensi-k menggunakan darab eksterior?

D. Pembatasan Masalah

Pembahasan masalah dalam skripsi ini dimulai dari dasar teori mengenai aljabar linear yang hanya dikhususkan pada pembahasan mengenai matriks, vektor dan ruang vektor. Selain itu, penulis hanya membahas mengenai kegunaan darab eksterior pada aturan kosinus dan aturan jajargenjang dan tidak membahasnya pada permasalahan goemetri yang lain.

E. Tujuan Penulisan

Penulisan skripsi ini bertujuan untuk

1. Mempelajari dan memahami mengenai darab eksterior.

2. Memperoleh generalisasi aturan kosinus pada simpleks-k dengan menggunakan darab eksterior.

F. Metode Penulisan

Metode yang digunakan dalam penulisan karya ilmiah ini adalah metode studi pustaka, yaitu dengan menggunakan buku-buku, jurnal-jurnal dan karangan ilmiah yang telah dipublikasikan, sehingga belum ditemukan hal baru.

G. Manfaat Penulisan

Manfaat yang diharapkan dari penulisan skripsi ini adalah:

1. Membahas mengenai darab ekterior agar dapat diteliti lebih lanjut demi perkembangan ilmu Matematika.

2. Mengembangkan pengaplikasian darab eksterior pada geometri, antara lain untuk memperoleh generalisasi aturan kosinus dan aturan jajargenjang.

H. Sistematika Penulisan BAB I PENDAHULUAN

BAB II ALJABAR LINEAR A. Matriks

B. Vektor

C. Ruang Vektor

BAB III DARAB EKSTERIOR A. Hubungan Matriks dengan Vektor B. Vektor-k Sederhana

C. Operasi pada Vektor-k Sederhana D. Vektor-k

BAB IV APLIKASI DARAB EKSTERIOR A. Simpleks-k

B. Aturan Kosinus pada Simpleks-k

C. Aturan Pythagoras pada Simpleks-k Ortogonal

D. Aturan Jajargenjang pada Balokgenjang Berdimensi-k

Dalam bab ini dibahas dasar-dasar aljabar linear mengenai matriks, vektor dan ruang vektor yang akan dipakai sebagai landasan untuk pokok bahasan pada bab-bab berikutnya.

A. Matriks

Definisi 2.1

Secara singkat, matriks adalah jajaran bilangan berbentuk empat persegi panjang. Bilangan-bilangan dalam jajaran tersebut disebut entri dari matriks. Untuk menuliskan matriks tanpa secara khusus menulis entri-entrinya dapat dipergunakan huruf kapital A, B, C dan sebagainya. Ukuran suatu matriks dinyatakan dalam jumlah baris (arah horizontal) dan kolom (arah vertikal) yang dimilikinya. Orde dari matriks adalah ukuran dari matriks yang memiliki jumlah baris dan jumlah kolom yang sama. Pada umumnya, aij akan menyatakan entri matriks A yang berada pada baris ke-i dan kolom ke- j.

Definisi 2.2

Definisi 2.3

Jika A dan B keduanya adalah matriks berukuran m×n, maka jumlah A+B adalah matriks berukuran m×n yang entri ke-ijnya adalah aij +bij untuk setiap pasang (i, j).

Definisi 2.4

Jika A adalah matriks berukuran m×n dan B adalah matriks berukuran n×r, maka hasil kali AB adalah matriks C berukuran m×r yang entri-entrinya didefinisikan sebagai berikut:

∑

=

= n

k kj ik ij a b c

1

.

Definisi 2.5

Matriks satuan adalah matriks I=[αij] berorde n di mana

  

≠ = =

. jika 0

jika 1

j i

j i ij

α

Contoh 2.1

Contoh dari matriks satuan berorde 5 adalah

     

 

     

 

=

1 0 0 0 0

0 1 0 0 0

0 0 1 0 0

0 0 0 1 0

0 0 0 0 1

Definisi 2.6

Invers perkalian dari suatu matriks A berorde n adalah matriks B sedemikian se-hingga AB=BA=I.

Contoh 2.2

Misalkan terdapat sebuah matriks

     

= 1 3

4 2

A ,

maka matriks

   

 

= − ₋

5 1 10

3 5 2 10

1 B

adalah invers dari matriks A, karena

     

=

   

       

= − ₋

1 0

0 1 1

3 4 2

5 1 10

3 5 2 10

1 AB

dan

     

=

         

 

= − ₋

1 0

0 1 1 3

4 2 51 10

3 5 2 10

1

BA .

Teorema 2.1

Invers dari suatu matriks A adalah tunggal.

Bukti

C IC C BA AC

B BI

B= = ( )=( ) = = .

Jadi, terbukti bahwa invers dari suatu matriks A adalah tunggal. ■

Selanjutnya, untuk menyebut invers perkalian dari suatu matriks A cukup dengan mengatakan invers dari A dan ditulis sebagai −1

A .

Definisi 2.7

Suatu matriks A berorde n dikatakan singular jika matriks A tersebut tidak memiliki invers.

Teorema 2.2

Jika A dan B adalah matriks-matriks yang tak singular dengan ukuran yang sama, maka AB tak singular dan

1 1 1 )

(AB − =B−A− .

Bukti

Perhatikan kesamaan berikut:

I AA AIA

A BB A A

B

AB)( −1 −1)= ( −1) −1 = −1 = −1 = (

dan

I BB BIB

B AA B AB A

B−1 −1)( )= ( −1) −1 = −1 = −1 =

( .

Dengan demikian, terbukti bahwa matriks −1 −1 A

Definisi 2.8

Transpos dari suatu matriks A berukuran m×n adalah matriks B berukuran n×m yang didefinisikan sebagai berikut:

ji ij a b =

untuk i=1,2, ,m dan j=1,2, ,n. Transpos dari matriks A dinyatakan oleh T

A .

Contoh 2.3 Jika

   

 

=

10 8 6

2 8 4

A ,

maka

  

 

  

 

=

10 2

8 8

6 4 T

A .

Definisi 2.9

Operasi baris elementer pada matriks A berukuran m×n ada tiga macam, yaitu: I. Mempertukarkan dua baris atau kolom dari matriks A.

II. Mengalikan suatu baris atau kolom dari matriks A dengan konstanta bukan nol.

Definisi 2.10

Matriks elementer adalah suatu matriks yang diperoleh dari matriks satuan I dengan melakukan satu operasi baris elementer.

Terdapat tiga jenis matriks-matriks elementer yang berkorespondensi dengan ketiga jenis operasi baris elementer, yaitu:

1. Matriks elementer jenis I adalah matriks yang diperoleh dengan mempertukarkan dua baris atau kolom dari matriks I.

2. Matriks elementer jenis II adalah matriks yang diperoleh dengan mengalikan satu baris atau kolom dari matriks I dengan konstanta bukan nol.

3. Matriks elementer jenis III adalah matriks yang diperoleh dengan menjumlahkan kelipatan dari satu baris atau kolom pada baris atau kolom yang lain dari matriks

I.

Contoh 2.4

1. Contoh dari matriks elementer jenis I adalah matriks

  

 

  

 

=

1 0 0

0 0 1

0 1 0 1

E .

Matriks E₁ adalah matriks elementer jenis I karena diperoleh dengan mempertukarkan kolom pertama dengan kolom kedua dari matriks I.

2. Contoh dari matriks elementer jenis II adalah matriks

  

 

  

 

=

3 0 0

0 1 0

0 0 1 2

Matriks E₂ adalah matriks elementer jenis II karena diperoleh dengan mengalikan baris ketiga dari matriks I dengan konstanta tiga.

3. Contoh dari matriks elementer jenis III adalah

  

 

  

 

=

1 0 0

0 1 0

3 0 1 3

E .

Matriks E3 adalah matriks elementer jenis III karena diperoleh dengan menjumlahkan 3 kali baris ketiga pada baris pertama dari matriks I.

Definisi 2.11

Determinan dari suatu matriks A berorde n, dinyatakan sebagai det(A), adalah suatu skalar yang diasosiasikan dengan matriks A dan didefinisikan sebagai berikut:

  

> +

+ +

= +

+ +

= =

1 jika

1 jika )

det(

2 2 1 1 2

2 1 1

11

n a

a a

a a

a

n a

nj nj j

j j j in in i

i i

i A A A A A A

A

untuk i=1,2, ,n dan j=1,2, ,n. Di mana

) det( ) 1

( ij

j i

ij M

A = − +

adalah kofaktor-kofaktor yang diasosiasikan dengan entri-entri dalam baris ke-i atau kolom ke- j dalam matriks A. Sedangkan, det(Mij) adalah minor dari aij di mana

ij

Contoh 2.5

Misalkan terdapat sebuah matriks A berukuran 3×3

  

 

  

 

=

6 4 5

2 1 3

4 5 2

A ,

maka dengan mengekspansikan det(A) sepanjang baris pertama diperoleh

13 13 12 12 11 11 )

det(A =a A +a A +a A

) det( )

1 ( ) det( )

1 ( ) det( )

1

( 4 _{13 13}

12 12

3 11

11 2

M M

M a a

a + − + −

− =

4 5

1 3 4 6 5

2 3 5 6 4

2 1

2 − +

=

) 5 12 ( 4 ) 10 18 ( 5 ) 8 6 (

2 − − − + −

=

16

− = .

Teorema 2.3

Jika matriks B adalah matriks berukuran n×n yang diperoleh dari matriks A dengan cara mengalikan sebuah baris ke-i atau kolom ke-j dari matriks A dengan suatu skalar α , maka

) det( )

det(B =α A .

Bukti

Jika det(B) diekspansikan dengan kofaktor-kofaktor sepanjang baris ke-i, maka

in in i

i i

i a a

a A A A

B)=α 1 1+α 2 2 + +α det(

) (ai1Ai1+ai2Ai2 + +ainAin

) det(A α

= .

Jika det(B) diekspansikan dengan kofaktor-kofaktor sepanjang kolom ke-j, maka

nj nj j

j j

j a a

a A A A

B)=α _{1 1} +α _{2 2} + +α det(

) (a1jA1j +a2jA2j + +anjAnj

=α

) det(A α

= .

Dengan demikian, terbukti bahwa jika matriks B berukuran n×n yang diperoleh dari matriks A dengan cara mengalikan sebuah baris atau kolom matriks A dengan suatu skalar α , maka

) det( )

det(B =α A ■

Teorema 2.4

Misalkan matriks A adalah suatu matriks berukuran n×n.

1. Jika matriks A memiliki baris atau kolom yang semua elemennya adalah nol, maka det(A)=0.

2. Jika matriks A memiliki dua baris atau kolom yang sama, maka det(A)=0.

Bukti

                = nn n n n a a a a a a 2 1 1 12 11 0 0 0 A                 = nn n n in i i n a a a a a a a a a 2 1 2 1 1 12 11 . 0 . 0 . 0 . Misalkan                 = nn n n in i i n a a a a a a a a a 2 1 2 1 1 12 11 ) 1 ( A .

Karena matriks A diperoleh dari matriks (1)

A dengan cara mengalikan baris ke-i dengan suatu skalar α =0, maka berdasarkan Teorema 2.3 diperoleh

0 ) det( . 0 ) det( )

det(A =α A(1) = A(1) = .

    

 

    

 

=

nn nj

n

n j

n j

a a

a

a a

a

a a

a

. 0

. 0

. 0

1

2 2

21

1 1

11

.

Misalkan

    

 

    

 

=

nn nj

n

n j

n j

a a

a

a a

a

a a

a

1

2 2

21

1 1

11

) 2 (

A .

Karena matriks A diperoleh dari matriks (2)

A dengan cara mengalikan kolom ke- j dengan suatu skalar α =0, maka berdasarkan Teorema 2.3 diperoleh

0 ) det( . 0 ) det( )

det( = (2) = (2) = A A

A α .

Dengan demikian, terbukti bahwa jika matriks A memiliki baris atau kolom yang semua elemennya adalah nol, maka

0 )

det(A = . ■

2. Teorema 2.4 bagian 2 akan dibuktikan dengan menggunakan induksi matematika. a. Teorema 2.4 bagian 2 akan dibuktikan untuk n=2.

Misalkan matriks A adalah matriks berukuran 2×2 yang mempunyai dua baris yang sama, yaitu:

     

= b a

b a

A ,

maka

0 )

Misalkan matriks A adalah matriks berukuran 2×2 yang mempunyai dua kolom yang sama, yaitu:

     

= d c

d c

A ,

maka

0 )

det(A =cd −cd = . Jadi, Teorema 2.4 bagian 2 terbukti untuk n=2.

b. Diasumsikan Teorema 2.4 bagian 2 benar untuk n=k, sehingga Teorema 2.4 bagian 2 berlaku untuk semua matriks A berukuran k×k.

c. Teorema 2.4 bagian 2 akan dibuktikan berlaku untuk semua matriks A berukuran (k+1)×(k+1).

Dengan mengekspansikan det(A) sepanjang baris ke-i dari matriks A di mana baris ke-i tidak sama dengan baris yang lain, maka diperoleh

) det( )

det( )

det( )

det(A =±ai1 Mi1 ±ai2 Mi2 ± ±ai,k+1 Mi,k+1 .

Karena semua Mij adalah matriks-matriks berukuran k×k di mana dua barisnya sama, maka det(Mij)=0 (berdasarkan Teorema 2.4 bagian 2b).

Akibatnya

0 0 . 0

. 0 . )

det(A =±ai1 ±ai2 ± ±ai,k+1 = .

Dengan mengekspansikan det(A) sepanjang kolom ke- j dari matriks A di mana kolom ke- j tidak sama dengan kolom yang lain, maka diperoleh

) det(

) det( )

det( )

Karena semua Mij adalah matriks-matriks berukuran k×k di mana dua kolomnya sama, maka det(Mij)=0 (berdasarkan Teorema 2.4 bagian 2b).

Akibatnya

0 0 . 0

. 0 . )

det(A =±a1j ±a2j ± ±ak+1,j = .

Dengan demikian, terbukti bahwa jika matriks A adalah matriks yang memiliki dua baris atau kolom yang sama, maka

det(A)=0. ■

Teorema 2.5

Misalkan matriks A adalah suatu matriks berukuran n×n. Jika Ajk menyatakan kofaktor dari ajk dan Aki menyatakan kofaktor dari aki untuk k =1,2. ,n, maka

ni nj i

j i j jn in j

i j

i a a a a a

a₁A ₁+ ₂A ₂ + + A = ₁ A₁ + ₂ A₂ + + A

  

≠ = =

j i

j i jika 0

jika )

det(A

...(1)

Bukti

Jika i= j, maka persamaan (1) taklain adalah ekspansi kofaktor dari det(A)

sepanjang baris ke-i atau kolom ke- j dari matriks A. Jadi, berdasarkan Definisi 2.11 terbukti bahwa

) det(

2 2 1 1 2

2 1

1Aj + i Aj + + inAjn = jAi + jA i + + njAni = A

i a a a a a

a .

Selanjutnya, persamaan (1) akan dibuktikan dalam kasus i≠ j.

        

 

        

 

=

nn n

n

in i

i

in i

i

n

a a

a

a a

a

a a

a

a a

a

2 1

2 1

2 1

1 12

11

) 3 (

A .

Karena dua baris dari matriks (3)

A adalah sama, maka berdasarkan Teorema 2.4 bagian 2 determinan dari matriks A(3) sama dengan nol.

Jika det( (3))

A diekspansikan oleh kofaktor-kofaktor sepanjang baris ke-j, maka

jn in j

i j

i a a

a₁ (3) 1 ₂ (3) 2 (3) )

3 (

) det(

0= A = A + A + + A

=ai1Aj1+ai2Aj2 + +ainAjn.

Misalkan matriks A(4) adalah matriks yang diperoleh dengan mengganti kolom ke-i dari matriks A dengan kolom ke-j dari matriks A, yaitu:

    

 

    

 

=

nn nj

nj n

n j

j

n j

j

a a

a a

a a

a a

a a

a a

1

2 2

2 21

1 1

1 11

) 4 (

A .

Karena dua kolom dari matriks (4)

A adalah sama, maka berdasarkan Teorema 2.4 bagian 2 determinan dari matriks (4)

A sama dengan nol. Jika det( (4))

A diekspansikan oleh kofaktor-kofaktor sepanjang kolom ke-i, maka ni

nj i

j i

j a a

a₁ (4)1 ₂ (4)2 (4) )

4 (

) det(

0= A = A + A + + A

Dengan demikian, terbukti bahwa jika Ajk menyatakan kofaktor dari ajk dan Aki menyatakan kofaktor dari aki untuk k =1,2. ,n, maka

ni nj i

j i j jn in j

i j

i a a a a a

a₁A ₁+ ₂A ₂ + + A = ₁ A₁ + ₂ A₂ + + A

  

≠ = =

j i

j i jika 0

jika )

det(A

■

Teorema 2.6

Jika matriks B berukuran n×n diperoleh dari matriks A dengan cara menambahkan c kali baris ke-i pada baris ke-j atau menambahkan c kali kolom ke-i pada kolom ke-j, maka

) det( )

det(B = A .

Bukti

Jika det(B) diekspansikan oleh kofaktor-kofaktor sepanjang baris ke-j, maka

jn in jn j

i j j i

j ca a ca a ca

a A A A

B) ( ) ( ) ( )

det( = 1+ 1 1+ 2 + 2 2 + + +

) (

)

(aj1Aj1+ +ajnAjn +c ai1Aj1 + +ainAjn

= .

Berdasarkan Teorema 2.5, maka diperoleh

0 . ) (

)

det(B = aj₁Aj₁+ +ajnAjn +c

jn jn j

j a

a A + + A

= 1 1

) det(A

= .

nj ni nj j

i j j i

j ca a ca a ca

a A A A

B) ( ) ( ) ( )

det( = 1 + 1 1 + 2 + 2 2 + + +

) (

)

(a1jA1j+ +anjAnj +c a1iA1j + +aniAnj

= .

Berdasarkan Teorema 2.5, maka diperoleh

0 . ) (

)

det(B = a1jA1j + +anjAnj +c

nj nj j

j a

a A + + A

= 1 1

) det(A

= .

Dengan demikian, terbukti bahwa jika matriks B berukuran n×n diperoleh dari matriks A dengan cara menambahkan c kali baris ke-i pada baris ke-j atau menambahkan c kali kolom ke-i pada kolom ke-j, maka

det(B)=det(A). ■

Teorema 2.7

Jika matriks B berukuran n×n diperoleh dengan cara menukar baris atau kolom dari matriks A, maka

) det( )

det(B =− A .

Bukti

                      = nn n n jn j j in i i n a a a a a a a a a a a a 2 1 2 1 2 1 1 12 11 A .

Apabila baris ke-i dikurangi baris ke- j, maka akan menghasilkan

                      − − − = nn n n jn j j jn in j i j i n a a a a a a a a a a a a a a a 2 1 2 1 2 2 1 1 1 12 11 ) 5 ( A .

Selanjutnya, baris ke-i dari matriks (5)

A ditambahkan pada baris ke- j, diperoleh

                      − − − = nn n n in i i jn in j i j i n a a a a a a a a a a a a a a a 2 1 2 1 2 2 1 1 1 12 11 ) 6 ( A .

Apabila baris ke-i dari matriks (6)

        

 

        

 

− −

− =

nn n

n

in i

i

jn j

j

n

a a

a

a a

a

a a

a

a a

a

2 1

2 1

2 1

1 12

11

) 7 (

A .

Karena matriks-matriks (5) (6) ,A

A dan (7)

A dibentuk dari matriks A dengan cara menambahkan c kali baris ke-j pada baris ke-i, maka berdasarkan Teorema 2.6 diperoleh

) det( ) det( ) det( )

det( (5) (6) (7) A A

A

A = = = .

Akhirnya, jika baris ke-i dari matriks A(7) dikalikan dengan konstanta c=−1, maka diperoleh

        

 

        

 

=

nn n

n

in i

i

jn j

j

n

a a

a

a a

a

a a

a

a a

a

2 1

2 1

2 1

1 12

11

) 8 (

A .

Di mana (8)

A taklain adalah matriks yang diperoleh dengan mempertukarkan baris ke-i dengan baris ke- j dari matriks A.

Karena matriks A(8) diperoleh dengan cara mengalikan baris ke-i dari matriks A(7) dengan konstanta c=−1, maka berdasarkan Teorema 2.3 diperoleh

) det( )

det( . 1 )

det( (8) (7)

A A

A =− =− .

              = nn nj ni n n j i n j i a a a a a a a a a a a a 1 2 2 2 21 1 1 1 11 A .

Apabila kolom ke-i dikurangi kolom ke- j, maka akan menghasilkan

              − − − = nn nj nj ni n n j j i n j j i a a a a a a a a a a a a a a a 1 2 2 2 2 21 1 1 1 1 11 ) 9 ( A .

Selanjutnya, kolom ke-i dari matriks (9)

A ditambahkan pada kolom ke-j, sehingga diperoleh               − − − = nn ni nj ni n n i j i n i j i a a a a a a a a a a a a a a a 1 2 2 2 2 21 1 1 1 1 11 ) 10 ( A .

Apabila kolom ke-i dari matriks (10)

A dikurangi kolom ke- j, maka akan menghasilkan               − − − = nn ni nj n n i j n i j a a a a a a a a a a a a 1 2 2 2 21 1 1 1 11 ) 11 ( A .

Karena matriks-matriks (9) (10) ,A

A dan (11)

A dibentuk dari matriks A dengan cara menambahkan c kali kolom ke-j pada kolom ke-i, maka berdasarkan Teorema 2.6 diperoleh ) det( ) det( ) det( )

det( (9) (10) (11) A A

A

Akhirnya, jika kolom ke-i dari matriks (11)

A dikalikan dengan konstanta c=−1, maka diperoleh

    

 

    

 

=

nn ni

nj n

n i

j

n i

j

a a

a a

a a

a a

a a

a a

1

2 2

2 21

1 1

1 11

) 12 (

A .

Di mana (12)

A taklain adalah matriks yang diperoleh dengan mempertukarkan kolom ke-i dengan kolom ke- j dari matriks A.

Karena matriks (12)

A diperoleh dengan cara mengalikan kolom ke-i dari matriks )

11 (

A dengan konstanta c=−1, maka berdasarkan Teorema 2.3 diperoleh )

det( )

det( . 1 )

det( (12) (11)

A A

A =− =− .

Dengan demikian, terbukti bahwa jika matriks B berukuran n×n diperoleh dari matriks A dengan cara menukar baris atau kolom, maka

) det( )

det(B =− A . ■

Teorema 2.8

Jika matriks A adalah suatu matriks berukuran n×n dan matriks E adalah matriks elementer berukuran n×n, maka

) det( ) det( )

det(EA = E A .

Bukti

Karena matriks A adalah matriks berukuran n×n dan E adalah matriks elementer berukuran n×n yang diperoleh dengan mempertukarkan baris atau kolom ke-i dengan baris atau kolom ke- j dari matriks I, maka berdasarkan Teorema 2.7 diperoleh

) det( )

det(EA =− A . Khususnya,

1 ) det( )

det( )

det(E = EI =− I =− . Jadi, untuk sebarang matriks elementer E jenis I, akan berlaku

) det( ) det( ) det( )

det(EA =− A = E A .

2. Teorema 2.8 akan dibuktikan untuk matriks E adalah matriks elementer jenis II. Karena matriks A adalah matriks berukuran n×n dan matriks E adalah matriks elementer berukuran n×n yang diperoleh dengan mengalikan suatu baris atau kolom dari matriks I dengan suatu skalar α, maka berdasarkan Teorema 2.3 diperoleh

( )

det( )

det EA =α A . Khususnya,

( )

=det

( )

=αdet( )=α

det E EI I ,

sehingga

( )

det( ) det( )det( ) det EA =α A = E A .

Karena matriks A adalah matriks berukuran n×n dan matriks E adalah matriks elementer berukuran n×n yang diperoleh dengan menambahkan c kali baris ke-i pada baris ke-j atau menambahkan c kali kolom ke-i pada kolom ke-j dari matriks I, maka berdasarkan Teorema 2.6 diperoleh

( )

det( ) det EA = A

Karena matriks E adalah matriks elementer jenis III berukuran n×n, maka elemen-elemen diagonalnya 1. Akibatnya

( )

1 det E = . Dengan demikian,

( )

det( ) 1.det( ) det( )det( )

det EA = A = A = E A .

Jadi, terbukti bahwa jika matriks A adalah suatu matriks berukuran n×n dan matriks E adalah matriks elementer berukuran n×n, maka

) det( ) det( )

det(EA = E A ■

Teorema 2.9

Jika matriks A adalah suatu matriks berukuran n×n, maka )

det( )

det(AT = A .

Bukti

Teorema 2.9 akan dibuktikan dengan menggunakan induksi matematika.

2. Diasumsikan Teorema 2.9 benar untuk n=k, sehingga Teorema 2.9 berlaku untuk semua matriks A berukuran k×k.

3. Teorema 2.9 akan dibuktikan berlaku untuk semua matriks A berukuran

) 1 ( ) 1

(k+ × k+ .

Dengan mengekspansikan det(A) sepanjang baris pertama dari A diperoleh

) det( )

det( )

det( )

det(A =a11 M11 −a12 M12 ± ±a1,k+1 M1,k+1 .

Karena semua Mij adalah matriks-matriks berukuran k×k, maka

) det( )

det(Mij = MijT . Akibatnya

) det(

) det( )

det( )

det( 11 11 12 12 1, 1 1, 1

T k k

T T

a a

a − ± ± _{+ +}

= M M M

A ...(2)

Ruas kanan dari persamaan (2) taklain adalah ekspansi minor dari det( T) A dengan menggunakan baris pertama dari T

A , sehingga ) det( )

det( T

A

A = .

Dengan demikian, terbukti bahwa jika matriks A adalah suatu matriks berukuran n

n× , maka

) det( )

det( T

A

A = . ■

Definisi 2.12

Matriks U dikatakan ekivalen baris dengan matriks A jika terdapat baris matriks-matriks elementer E1,E2, ,Ek, sehingga

A E E E

Dengan kata lain, matriks U ekivalen baris dengan matriks A jika matriks U dapat diperoleh dari matriks A dengan operasi-operasi baris yang berhingga banyaknya.

Teorema 2.10

Matriks A berukuran n×n mempunyai invers jika dan hanya jika det(A)≠0.

Bukti

Misalkan matriks U adalah matriks ekselon baris tereduksi yang diperoleh dari matriks A. Maka,

A E E E

U= k k−1 1 . Akibatnya

) det( ) det( ) det( ) det( )

det(U = Ek Ek₋₁ E₁ A .

Karena determinan dari semua matriks elementer taknol, maka mengakibatkan

)

det(U dan det(A) keduanya nol atau keduanya taknol. Jika A mempunyai invers, maka diperoleh U=I. Akibatnya det(U)=1≠0 dan sebagai konsekuensinya

0 )

det(A ≠ . Sebaliknya, jika det(A)≠0, maka det(U)≠0, sehingga U tidak memiliki satu baris bilangan nol. Akibatnya matriks U=I, sehingga A mempunyai invers.

Teorema 2.11

Jika matriks A dan B adalah matriks n×n, maka

) det( ) det( )

Bukti

Misalkan matriks U adalah matriks ekselon baris tereduksi yang diperoleh dari matriks A, maka

U E E E

A= _{k k−1 1} . Dengan demikian,

UB E E E

AB= _{k k−1 1} , sehingga

) det( ) det(

)

det(AB = EkEk−1 E1 UB .

Jika A mempunyai invers, maka matriks U adalah matriks identitas, sehingga

1 1 1

1 EI E E E

E E

A= _{k k−} = _{k k−}

dan

B IB

UB= = .

Akibatnya

) det( ) det( ) det( ) det(

)

det(AB = EkEk−1 E1 UB = A B .

Jika A tidak mempunyai invers, maka matriks U mempunyai baris yang semua elemennya sama dengan nol. Dengan demikian, matriks UB mempunyai baris yang semua elemennya sama dengan nol atau det(UB)=0. Akibatnya

0 0 ). det(

) det( ) det(

)

det(AB = EkEk−1 E1 UB = EkEk−1 E1 = . Karena matriks A tidak memiliki invers, maka det(A)=0. Dengan demikian,

0 ) det(AB =

=0.det(B)

B. Vektor

Definisi 2.13 Ruang n

merupakan himpunan semua tupel-n yang terdiri dari bilangan-bilangan real. Bentuk umum dari n

adalah

n =

{

∈

i n u u u

u , , , )|

( _{1 2} ,i=1,2, ,n

}

.

Definisi 2.14 Vektor u di n

adalah pasangan terurut (u1,u2, ,un) dengan u1,u2, ,un merupakan bilangan real. Nilai dari u1,u2, ,un disebut komponen atau koordinat dari vektor. Untuk menuliskan vektor adalah sebagai berikut:

) , , ,

(u1 u2 un =

u .

Definisi 2.15

Jumlah u+v dari dua vektor u=(u1,u2, ,un) dan v=(v1,v2, ,vn) adalah vektor )

, , ,

(u₁+v₁ u₂ +v₂ un +vn =

+v

u .

Sedangkan, perkalian skalar dari vektor u=(u1,u2, ,un) dengan skalar (bilangan real) s, adalah vektor

) , , ,

(su1 su2 sun

su= .

Definisi 2.16

2 2

2 2

1) ( ) ( )

( |

|u = u + u + + un .

Definisi 2.17

Vektor satuan adalah vektor yang panjangnya satu.

Misalkan u=(u1,u2, ,un) dan u≠0, maka vektor

      = = | | , , | | , | | | | 2 1 u u u u u

v u u un

merupakan vektor satuan yang mempunyai arah sama dengan vektor u. Hal ini dapat dilihat karena 2 2 2 2 1 | | | | | | | | _      + +       +       = u u u

v u u un

| | ) ( ) ( )

( 2 2 2

2 1 u n u u

u + + +

= | | | | u u = 1 = . Pada ruang n

terdapat terdapat n buah vektor satuan standar yaitu:

) 1 , , 0 , 0 , 0 ( , ), 0 , , 1 , 0 , 0 ( ), 0 , , 0 , 1 , 0 ( ), 0 , , 0 , 0 , 1

( _{2 3}

1 = e = e = en =

e .

Contoh 2.6 Pada 2

dan 3

vektor satuan biasanya dinotasikan dengan i,j, dan k, yaitu:

) 0 , 0 , 1 ( =

Ketiga vektor ini memegang peranan penting, karena untuk setiap vektor )

, , (u1 u2 u3 =

u dapat ditulis sebagai kombinasi ketiga vektor tersebut, yaitu: )

, , (u1 u2 u3 =

u

) , 0 , 0 ( ) 0 , , 0 ( ) 0 , 0 ,

(u₁ + u₂ + u₃ =

) 1 , 0 , 0 ( ) 0 , 1 , 0 ( ) 0 , 0 , 1

( 2 3

1 u u

u + +

=

k j

i _{2 3}

1 u u

u + +

= .

Definisi 2.18

Perkalian titik dari dua vektor u=(u1,u2, ,un) dan v=(v1,v2, ,vn) di n

didefinisikan sebagai berikut:

n nv u v

u + +

= 1 1

.v

u .

Perhatikan bahwa perkalian titik dari suatu vektor dengan dirinya sendiri sama halnya dengan kuadrat panjang vektor tersebut. Hal ini terlihat sebagai berikut:

2 2 2

1 1

1 | |

.u u

u =uu + +unun =u + +un = .

Teorema 2.12

Misalkan ada vektor u=(u1,u2, ,un), v=(v1,v2, ,vn), dan w=(w1,w2, ,wn) di n

dan ada suatu skalar s, maka perkalian titik memenuhi sifat berikut: 1. u.v= v.u (Komutatif).

5. u.u=0 jika dan hanya jika u=0.

6. u.v≤|u||v| (Ketaksamaan Cauchy-Schwarz).

Bukti

1. u.v=u1v1 + +unvn

n nu v u

v + +

= 1 1

=v.u.

2. u.(v+w)=u1(v1+w1)+ +un(vn +wn)

=(u1v1+u1w1)+(u2v2 +u2w2)+ +(unvn +unwn) ) (

)

(u1v1+u2v2 + +unvn + u1w1+u2w2 + +unwn =

w u v u. + .

= .

3. (su).v=(su1)v1+ +(sun)vn =s(u1v1)+ +s(unvn)

) (u1v1 unvn

s + +

=

) . (uv s

= . 4. u.u=u1u1+ +unun.

Karena u1,u2, ,un∈ , maka

0 ≥ i iu u

di mana i=1,2, ,n. Akibatnya

0 .u=u1u1+ +unun ≥

5. (⇒)

Diketahui bahwa

0 .u= u

0 1

1u + +unun =

u .

Karena uiui ≥0 di mana i=1,2, ,n, maka u1u1+ +unun =0 hanya bila

n u u

u1, 2, , semuanya sama dengan 0. Akibatnya ) , , ,

(u1 u2 un =

u

) 0 , , 0 , 0 (

=

0

= .

) (⇐

Diketahui bahwa

0 u=

=(0,0, ,0),

maka

n nu u u

u + +

= 1 1

.u u

0 . 0 0

.

0 + +

=

0

= .

6. Jika u=0 atau v=0, maka kedua ruas pada ketaksamaan Cauchy-Schwarz sama dengan nol. Oleh karena itu, ketaksamaan tersebut berlaku.

Jika u≠0 dan v ≠0, maka untuk setiap bilangan real x nilai

0 ) ).(

(xu+v xu+v ≥

0 ) . ( ) . ( 2 ) .

( 2 + + ≥

v v v u u

merupakan fungsi kuadrat dalam x yang harus selalu taknegatif. Ini berarti fungsi kuadrat tersebut tidak mempunyai akar real yang berbeda. Oleh karena itu, diskriminannya tidak mungkin positif atau

0 ) . )( . ( 4 ) . (

4 2 _{− ≤}

v v u u v

u ,

sehingga

2 2 2

| | | | ) .

(uv ≤ u v . Akibatnya

| || | .v u v

u ≤ ■

Definisi 2.19

Dua buah vektor u=(u1,u2, ,un) dan v=(v1,v2, ,vn) di n

saling ortogonal (tegak lurus) apabila

0 .v=

u .

Contoh 2.7

Diketahui u=(2,−1,3,4) dan v=(1,2,4,−3). Selidiki apakah u dan v merupakan vektor ortogonal.

Jawab:

0 ) 3 .( 4 4 . 3 2 ). 1 ( 1 . 2

.v= + − + + − =

u

Definisi 2.20

Dua buah vektor u=(u1,u2, ,un) dan v=(v1,v2, ,vn) di n

saling ortonormal apabila vektor u dan v saling ortogonal dan masing-masing vektor mempunyai panjang satu.

Contoh 2.8

Vektor-vektor standar di n

, yaitu:

) 1 , , 0 , 0 , 0 ( , ), 0 , , 1 , 0 , 0 ( ), 0 , , 0 , 1 , 0 ( ), 0 , , 0 , 0 , 1

( 2 3

1 = e = e = en =

e

merupakan vektor-vektor yang saling ortonormal satu sama lain karena mereka saling ortogonal dan panjang dari vektor-vektor standar di n

sama dengan satu.

Definisi 2.21

Apabila u=(u₁,u₂, ,un) dan v=(v1,v2, ,vn) adalah vektor taknol, maka sudut antara vektor u=(u1,u2, ,un) dan v=(v1,v2, ,vn) di

n

didefinisikan sebagai berikut:

| || |

. cos

v u

v u =

θ .

C. Ruang Vektor

Definisi 2.22

berada di V. Himpunan V disebut ruang vektor apabila memenuhi aksioma-aksioma berikut:

1. Tertutup terhadap penjumlahan V

v u V v

u ∈ + ∈

∀ , , .

2. Komutatif terhadap penjumlahan u

v v

u+ = + untuk setiap u,v∈V. 3. Asosiatif terhadap penjumlahan

w v u w v

u+( + )=( + )+ untuk setiap u,v,w∈V. 4. Elemen identitas terhadap penjumlahan

u 0 u V

0∈ + =

∃ , untuk setiap u∈V. 5. Elemen invers terhadap penjumlahan

0 u u V u V

u∈ ∃− ∈ + − =

∀ , , ( ) .

6. Tertutup terhadap perkalian dengan skalar real

∈

∀α ,∀u∈V,αu∈V.

7. α(u+v)=αu+αv untuk setiap skalar real α dan u,v∈V. 8. (α +β)u=αu+βu untuk setiap skalar real α,β dan u∈V. 9. (αβ)u=α(βu) untuk setiap skalar real α,β dan u∈V. 10. Identitas perkalian dengan skalar

u u=

.

1 untuk setiap u∈V dan 1 adalah identitas perkalian.

Contoh 2.9

Perlihatkanlah bahwa ruang n

Jawab

Untuk memperlihatkan bahwa ruang n

merupakan ruang vektor, maka akan diperlihatkan ruang n

memenuhi aksioma-aksioma pada Definisi 2.22.

Misalkan ada vektor u=(u1,u2, ,un), v=(v1,v2, ,vn) dan w=(w1,w2, ,wn) berada di n

. Misalkan juga ada skalar α , β∈ , maka 1. u+v=(u1+v1,u2 +v2, ,un +vn)∈

n . 2. u+v=(u1+v1,u2 +v2, ,un +vn)

=(v1+u1,v2 +u2, ,vn +un) = v+u.

3. u+(v+w)=(u1 +(v1+w1),u2 +(v2+w2), ,un +(vn +wn)) ) ) (

, , ) (

, )

((u1+v1 +w1 u2 +v2 +w2 un +vn +wn =

w v

u+ +

=( ) .

4. Ada vektor 0=(0,0, ,0)∈ n yang mengakibatkan ) 0 , , 0 , 0

( +u1 +u2 +un =

+u 0

) , , ,

(u1 u2 un =

u

= ,

sehingga vektor 0∈ n

adalah elemen identitas terhadap penjumlahan di ruang n

.

5. Untuk setiap u=(u1,u2, ,un)∈ n

, ada −u=(−u1,−u2, ,−un)∈ n

yang mengakibatkan

)) ( , ), ( ), ( ( )

(− = u1 + −u1 u2 + −u2 un + −un

+ u

) 0 , , 0 , 0 (

=

0

= ,

sehingga invers terhadap penjumlahan untuk setiap vektor u∈ n adalah vektor ∈

−u n.

6. αu=(αu1,αu2, ,αun)∈ n

.

7. α(u+v)=(α(u1+v1),α(u2 +v2), ,α(un +vn)) ) ,

, ,

(αu1+αv1 αu2 +αv2 αun +αvn =

v

u α

α +

= .

8. (α +β)u=((α +β)u1,(α +β)u2, ,(α +β)un) ) ,

, ,

(αu1+βu1 αu2 +βu2 αun +βun =

u

u β

α +

= .

9. (αβ)u=((αβ)u1,(αβ)u2, ,(αβ)un) )) ( , ), ( ), (

(α βu₁ α βu₂ α βun =

) (βu α

= .

10. 1.u=(1.u1,1.u2, ,1.un) ) , , ,

(u1 u2 un

= =u.

Dengan demikian, terlihat bahwa ruang n

merupakan ruang vektor.

Teorema 2.13

2. Invers penjumlahan dari vektor u adalah tunggal. 3. (−1)(u)=−u.

Bukti

Perhatikan bahwa 1. 0u=(0+0)u =0u+0u

) 0 ( 0 0 ) 0 (

0u+ − u = u+ u+ − u

0=0u+0 0=0u.

Jadi, terbukti bahwa 0u=0.

2. Misalkan u+v=0, maka 0

u u=− +

−

=−u+(u+v)

=(−u+u)+v =0+v

v

= .

Jadi, terbukti bahwa invers dari u adalah tunggal.

=0u =0.

Karena invers penjumlahan dari vektor u adalah tunggal (berdasarkan Teorema 2.13 bagian 2), maka

u u =−

−1)( )

( .

Jadi, terbukti bahwa (−1)(u)=−u. ■

Definisi 2.23

Suatu himpunan bagian W disebut ruang bagian dari suatu ruang vektor V jika W itu sendiri merupakan suatu ruang vektor dibawah penjumlahan dan perkalian skalar yang didefinisikan pada V.

Teorema 2.14

Himpunan bagian takkosong W merupakan suatu ruang bagian dari ruang vektor V, jika dan hanya jika syarat-syarat berikut terpenuhi.

1. Jika u dan v adalah vektor-vektor pada W, maka u+v berada pada W.

2. Jika s adalah skalar sebarang dan u adalah vektor sebarang pada W, maka su berada pada W.

Bukti

) (⇒

) (⇐

Diasumsikan syarat 1 dan 2 berlaku. Karena syarat-syarat ini merupakan aksioma 1 dan aksioma 6 pada ruang vektor, maka kita hanya perlu menunjukkan bahwa W memenuhi kedelapan aksioma lainnya. Aksioma 2, 3, 7, 8, 9, dan 10 secara otomatis terpenuhi oleh vektor pada W karena aksioma tersebut terpenuhi oleh vektor-vektor pada V. Oleh karena itu, untuk melengkapi bukti, kita hanya perlu membuktikan bahwa aksioma 4 dan 5 terpenuhi oleh vektor-vektor pada W.

Misalkan u adalah vektor sebarang pada W. Menurut syarat 2, su berada pada W untuk setiap skalar s. Dengan mengatur s=0, sesuai dengan Teorema 2.13 bagian 1 diperoleh 0u=0 berada pada W, dan dengan mengatur s=−1, maka berdasarkan Teorema 2.13 bagian 3 diperoleh (−1)u=−u berada pada W. _■

Definisi 2.24

Misalkan u1,u2, ,un adalah vektor-vektor dalam suatu ruang vektor V. Jumlahan vektor-vektor berbentuk

n n c c

c1u1 + 2u2 + + u

di mana c1,c2, ,cn adalah skalar-skalar disebut kombinasi linear dari u1,u2, ,un.

Definisi 2.25

Misalkan u1,u2, ,un adalah vektor-vektor dalam suatu ruang vektor V, maka himpunan semua kombinasi linear dari u1,u2, ,un disebut rentang dari

n u u

Contoh 2.10 Dalam 3

, rentang(e₁,e₂) adalah himpunan semua vektor berbentuk )

0 , , ( ) 0 , 1 , 0 ( ) 0 , 0 , 1 ( 2

1 β α β α β

αe + e = + =

untuk setiap skalar α dan β.

Sedangkan, rentang(e₁,e₂,e₃) adalah himpunan semua vektor berbentuk ) , , ( ) 1 , 0 , 0 ( ) 0 , 1 , 0 ( ) 0 , 0 , 1 ( 3 2

1 β γ α β γ α β γ

αe + e + e = + + =

untuk setiap skalar α , β dan γ . Jadi, rentang(e₁,e₂,e₃)= 3.

Definisi 2.26

Jika U=

{

u1,u2, ,un

}

adalah himpunan tak kosong yang terdiri dari vektor-vektor, maka persamaan

0 u u

u +c + +cn n = c_{1 1 2 2}

memiliki paling tidak satu solusi, yaitu

0 , , 0 , 0 ₂

1 = c = cn =

c .

Jika ini satu-satunya solusi, maka U disebut sebagai himpunan bebas linear. Jika terdapat solusi-solusi yang lain, maka U disebut himpunan bergantung linear.

Contoh 2.11

Perhatikan vektor-vektor satuan standar

) 1 , , 0 , 0 , 0 ( , ), 0 , , 0 , 1 , 0 ( ), 0 , , 0 , 0 , 1

( ₂

1 = e = en =

e pada n

0 e e

e +c + +cn n = c_{1 1 2 2}

) 0 , , 0 , 0 , 0 ( ) 1 , , 0 , 0 , 0 ( )

0 , , 0 , 1 , 0 ( ) 0 , , 0 , 0 , 1

( 2

1 +c + +cn =

c

atau secara ekivalen,

) 0 , , 0 , 0 ( ) , , ,

(c₁ c₂ cn = .

Ini mengakibatkan bahwa c1 =0,c2 =0, ,cn =0, sehingga U=

{

e1,e2, ,en

}

adalah himpunan yang bebas linear.

Contoh 2.12 Misalkan

) 3 , 2 , 1 (

=

x ,

maka himpunan

{

e₁,e₂,e₃,x

}

adalah bergantung linear. Hal ini terlihat sebagai berikut:

c1e1+c2e2 +c3e3+c4x=0 c1(1,0,0)+c2(0,1,0)+c3(0,0,1)+c4(1,2,3)=0

(c1,0,0)+(0,c2,0)+(0,0,c3)+(c4,2c4,3c4)=0...(3) Persamaan (3) menghasilkan

0 4 1+c = c

c₂ +2c₄ =0 c₃+3c₄ =0 Misalkan

1 4 =− c

2 2 = c

3 3 = c

mengakibatkan

0 3

2 _{2 3} 1+ e + e −x=

e .

Jadi, himpunan

{

e1,e2,e3,x

}

adalah bergantung linear.

Teorema 2.15

Suatu himpunan U dengan dua atau lebih vektor adalah bergantung linear jika dan hanya jika paling tidak salah satu dari vektor pada U dapat dinyatakan sebagai suatu kombinasi linear dari vektor-vektor lain pada U.

Bukti

) (⇒

Misalkan U=

{

u1,u2, ,un

}

adalah suatu himpunan dengan dua atau lebih vektor. Jika U bergantung linear, maka terdapat skalar c1,c2, ,cn yang tidak semuanya nol, sedemikian sehingga

0 u u

u

u +c + +c_{i i} + +c_{n n} =

c_{1 1 2 2} ...(4) Misalkan ci ≠0 untuk suatu i, maka (4) dapat ditulis kembali sebagai

n i n

i i

i

c c c

c c

c

u u

u

u _

    

− + +

     

− +

     

−

= 2

2 1

n n k k

ku + u + + u

= 1 1 2 2

yang menyatakan vektor ui sebagai suatu kombinasi linear dari vektor-vektor lain pada U.

) (⇐

Misalkan U=

{

u1,u2, ,un

}

adalah suatu himpunan dengan dua atau lebih vektor. Misalkan vektor ui untuk suatu i dapat dinyatakan sebagai kombinasi vektor-vektor lain pada U, yaitu:

n n i ku k u k u u = _{1 1} + _{2 2} + + , sehingga

0 u u

u

u_i −k_{1 1}−k_{2 2} − −k_{n n} = . Akibatnya U bergantung linear karena persamaan

0 u u

u

u +c + +c_{i i} + +c_{n n} = c_{1 1 2 2}

dipenuhi oleh

n n

i c k

c k c k

c1 =− 1, 2 =− 2, , =1, =− yang tidak semuanya nol.

Dengan demikian, terbukti bahwa suatu himpunan U dengan dua atau lebih vektor adalah bergantung linear jika dan hanya jika paling tidak salah satu dari vektor pada U dapat dinyatakan sebagai suatu kombinasi linear dari vektor-vektor

Teorema 2.16

Misalkan U=

{

u1,u2, ,un

}

adalah himpunan tak kosong yang terdiri dari vektor-vektor, maka teorema berikut berlaku.

1. Jika U mengandung suatu vektor nol, maka U bergantung linear.

2. Jika U mengandung suatu vektor yang merupakan kelipatan skalar dari vektor lainnya, maka U bergantung linear.

Bukti

1. Misalkan himpunan U mengandung suatu vektor nol pada vektor ke-i, maka U dapat dituliskan

{

u u ui un

}

U= 1, 2, , , ,

=

{

u1,u2, ,0, ,un

}

untuk suatu i.

Misalkan ci =1 dan cj =0 untuk