PROGRAM LINEAR BILANGAN BULAT UNTUK
MENYELESAIKAN MASALAH PENJADWALAN PENERBANGAN
PADA BANDAR UDARA SUPADIO
MAKALAH
Diajukan untuk Memenuhi Salah Satu Syarat
Memperoleh Gelar Sarjana Sains
Program Studi Matematika
Disusun Oleh :
Margaretha Agnes Oktaviani
103114008
PROGRAM STUDI MATEMATIKA
JURUSAN MATEMATIKA
FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA
YOGYAKARTA
INTEGER LINEAR PROGRAMMING
TO SOLVE AIRCRAFT SCHEDULING PROBLEM
IN SUPADIO AIRPORT
PAPER
Presented as Partial Fulfillment of the Requirements
To Obtain the Degree of Sarjana Sains
Mathematics Study Program
By :
Margaretha Agnes Oktaviani
103114008
MATHEMATICS STUDY PROGRAM
DEPARTMENT OF MATHEMATICS
FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY
YOGYAKARTA
MOTTO DAN PERSEMBAHAN
If God had wanted us to fly,
wouldn't He have given us wings ?
Ku persembahkan tugas akhir ku ini untuk :
ABSTRAK
Peran utama Air Traffic Controller ialah menjaga kelancaran lalu lintas udara. Salah satu cara untuk menjaga kelancaran lalu lintas udara ialah dengan mengatur pendaratan atau lepas landas suatu pesawat.
Pada tugas akhir ini akan digunakan program linear bilangan bulat dan program linear bilangan bulat campuran untuk menyelesaikan masalah pendaratan. Untuk masalah pendaratan yang melibatkan lebih dari satu landasan pacu, perhitungan dilanjutkan dengan menggunakan model partisi himpunan. Pada bagian akhir tugas akhir ini, akan dilakukan penerapan dari program linear bilangan bulat pada data real, yakni data penerbangan Bandar Udara Supadio Pontianak dari tanggal 20 Januri 2014 – 26 Januari 2014.
ABSTRACT
The main role of Air Traffic Controller is to maintain air traffic running smooth. One way to control air traffic running smooth is done by regulate the landing or taking off an aircraft.
In this paper, it will be used an integer linear programming and a mixed integer linear programming to solve the aircraft scheduling problem. For aircraft scheduling problem involving more than one runway, the aircraft scheduling problem is formulated as a set partitioning problem. In this paper also present the implementation of integer linear programming in Supadio Airport. The data used are data in Supadio Airport Pontianak, from January 20, 2014 until January 26, 2014.
KATA PENGANTAR
Puji dan syukur penulis haturkan kepada Yesus Kristus dan Bunda Maria
atas berkatNya yang selalu menyertai penulis dalam menyelesaikan tugas akhir ini
tepat waktu. Kesulitan dan hambatan yang penulis alami selama penulisan tugas
akhir ini, penulis percayai sebagai suatu proses untuk membuat penulis menjadi
lebih kuat, tidak gampang menyerah dan selalu berserah kepadaNya dalam
menjalani hidup ini.
Dalam kesempatan ini, penulis ingin mengucapkan terima atas segala
bimbingan, dorongan, semangat, sehingga tugas akhir ini terselesaikan dengan
baik, kepada :
1. Bapak Johanes Eka Priyatma, M.Sc., Ph.D., selaku Rektor Universitas
Sanata Dharma.
2. Ibu Paulina Heruningsih Prima Rosa, S.Si., M.Sc., selaku Dekan Fakultas
Sains dan Teknologi Universitas Sanata Dharma.
3. Ibu Lusia Krismiyati Budiasih, S.Si., M.Si., selaku Ketua Program Studi
Matematika Universitas Sanata Dharma, sekaligus menjadi dosen
pembimbing yang dengan penuh kesabaran, kesungguhan hati serta
memberikan banyak ide serta masukan kepada penulis dalam menyelesaikan
tugas akhir ini.
4. Bapak Y. G . Hartono Ph.D., yang telah memberikan ide dan masukan untuk
5. Seluruh Dosen Program Studi Matematika serta karyawan Fakultas Sains
dan Teknologi. Terima kasih atas bimbingan, doa dan pelajaran yang
diberikan selama berkuliah di Universitas Sanata Dharma.
6. Bapak Fajar selaku Distrik Manager PPNPI Distrik Pontianak yang telah
mengizinkan penulis untuk mengambil data mengenai proses pendaratan
dan lepas landas suatu pesawat pada Bandar Udara Supadio.
7. Om Yasid dan Mas Rahmat yang telah membantu penulis dalam
menyelesaikan tugas akhir ini.
8. Keluargaku yang tercinta, my big boss, Yohanes Untung Sadjoko dan Ibu
Murwani Sulistiati yang senantiasa memberi dukungan, semangat dan
mendoakan anaknya yang selalu bikin panik ini. Terima kasih atas
kesabaran dan kasih sayang dalam mendidik anak-anaknya. Kakak penulis,
Bertha Ajeng Aryati dan adik penulis Albertus Anggito Pramudito, terima
kasih atas doa dan dukungannya selama ini.
9. Keluarga Besar Mbah Citro (kakung dan putri) dan Mbah Prapto (kakung
dan putri) dan keluarga-keluarga yang lain, terima kasih atas doa dan
dukungannya.
10. Sahabat-sahabat penulis di Program Studi Matematika, Dini, Leny, Sari,
Marsel, Yosi, Selly, Astri, Ayu, Arga, Tika, Ratri, Pandu, Roy, Yohan, yang
selalu setia mendengar keluh kesah, menemani dan memberi semangat
untuk penulis yang sangat berarti.
11. Keluarga Besar Program Studi Matematika, terima kasih atas segala
12. Sahabat terbaik, Ellies yang setia mendengar keluh kesah dan selalu
membantu penulis dalam menyelesaikan tugas akhir ini,
13. Teman-teman sekaligus keluarga penulis, Keluarga Besar Bu Marno
Gerbang Tengah : Mbak Niken, Dea, Mela, terima kasih atas semangat,
dukungan, doa, serta kebersamaannya. Banyak suka dan duka telah kita
lewati bersama selama ini.
14. Semua pihak yang telah mendukung dan membantu penulis dalam
menyelesaikan tugas akhir ini yang tidak dapat disebutkan satu per satu.
Terima kasih banyak atas semua bantuannya.
Akhirnya penulis menyadari bahwa tugas akhir ini memiliki berbagai
kekurangan. Oleh karena itu penulis mengharapkan kritik dan saran dari pembaca.
Semoga tugas akhir ini dapat menjadi referensi bagi rekan-rekan dalam
mengembangkan ilmu pengetahuan.
Yogyakarta, 19 Juli 2014
DAFTAR ISI
COVER ... i
HALAMAN PERSETUJUAN PEMBIMBING ... iii
HALAMAN PENGESAHAN ... iv
PERNYATAAN KEASLIAN KARYA ... iv
LEMBAR PERSETUJUAN PUBLIKASI KARYA ILMIAH………v
MOTTO DAN PERSEMBAHAN ... vi
G. Sistematika Penulisan ... 5
BAB II : PROGRAM LINEAR ... 7
A. Matriks dan Operasi Baris Elementer ... 7
B. Program Linear... 12
C. Metode Simpleks ... 18
D. Metode Pencabangan dan Pembatasan... 29
BAB III : MASALAH PENDARATAN PESAWAT ... 41
A. Perumusan Masalah Pendaratan Pesawat Dengan Program Linear ... 44
B. Model Partisi himpunan ... 62
BAB IV : APLIKASI PROGRAM LINEAR BILANGAN BULAT DALAM PENJADWALAN PENERBANGAN PADA BANDAR UDARA
SUPADIO ... 81
BAB V : PENUTUP ... 107
A. KESIMPULAN ... 107
B. SARAN ... 108
BAB I
PENDAHULUAN
A. Latar Belakang
Pemandu lalu lintas udara atau yang lebih dikenal dengan Air Traffic
Controller adalah suatu lembaga yang berjasa dalam menyediakan layanan
pengatur lalu–lintas udara. Air Traffic Controller (ATC) bertugas untuk mencegah pesawat terlalu berdekatan satu sama lain dan menghindarkan pesawat dari
tabrakan. Tugas lain dari ATC ialah mengatur kelancaran lalu lintas udara,
membantu pilot dalam menangani keadaan darurat, dan memberikan informasi
yang dibutuhkan pilot, seperti informasi cuaca, informasi lalu lintas udara,
navigasi dan sebagainya.
ATC adalah rekan terdekat pilot dalam menerbangkan pesawat. Ini
dikarenakan segala aktivitas yang akan dilakukan oleh pilot harus mendapat
persetujuan dari ATC, yang nantinya ATC akan memberikan informasi, instruksi
dan izin kepada pilot sehingga tercapai tujuan keselamatan penerbangan. Semua
komunikasi yang dilakukan oleh ATC dan pilot haruslah menggunakan peralatan
yang sesuai dan memenuhi aturan. Adapun aturan-aturan yang terkait dengan
keselamatan penerbangan diatur pada dokumen Peraturan Keselamatan
Peraturan Keselamatan Penerbangan Sipil juga mengatur tentang layanan
lalu lintas udara yang diberikan oleh ATC. Adapun pelayanan lalu lintas udara
yang diberikan oleh ATC sesuai dengan PKPS terdiri dari 3 layanan, yakni
aerodrome control service, approach control service, dan area control service.
Aerodrome control service memberikan layanan lalu lintas kepada pilot yang
sedang berada di area bandar udara dan sekitarnya, seperti layanan lepas landas
(take off), pendaratan (landing), perjalanan pesawat dari/menuju apron (taxiing).
Approach control service adalah layanan yang diberikan saat pesawat berada di
udara, baik yang baru saja melakukan penerbangan atau yang akan melakukan
pendaratan. Area control services adalah layanan yang diberikan saat penerbangan melakukan penjelajahan, teruma penjelajahan yang terkontrol.
Pada tulisan ini akan dipaparkan mengenai masalah terkait aerodrome
control service, khususnya mengenai pendaratan pesawat. Pendaratan dilakukan
pada waktu yang ditentukan, dibatasi oleh waktu terawal dan waktu paling lambat
untuk mendarat. Waktu terawal menunjukkan waktu tercepat suau pesawat dapat
melakukan pendaratan, yakni jika pesawat melakukan penerbangan dengan
kecepatan penuh. Begitupula dengan waktu terlama menunjukkan waktu paling
lambat suatu pesawat diperbolehkan melakukan pendaratan, jika pesawat terbang
dengan kecepatan standar.
Hal lain yang harus diperhatikan adalah mengenai waktu yang dibutuhkan
pesawat-pesawat dan petugas-petugas untuk mempersiapkan proses pendaratan
dalam satu waktu. Perlu diketahui bahwa setiap pesawat membutuhkan waktu
sesuai, akan mempengaruhi penjadwalan pendaratan pesawat berikutnya, karena
penjadwalan ini sangat mempengaruhi satu sama lain. Terlebih jika pada bandar
udara tersebut memiliki tingkat kesibukan yang sangat tinggi.
Pada tugas akhir ini, akan dibahas mengenai layanan ATC tentang
aerodrom control service di Bandar Udara Supadio Pontianak yang dikhususkan
pada penjadwalan waktu pendaratan suatu pesawat agar tidak terjadi ‘tabrakan’
waktu. Penjadwalan waktu pendaratan pesawat ini harus diperhatikan dengan
baik, karena proses pendaratan tidak dapat dilakukan pada satu waktu yang
bersamaan, mengingat Bandar Udara Supadio hanya memiliki satu landasan pacu.
Konsep yang digunakan dalam melakukan penjadwalan ini adalah
meminimumkan total deviasi waktu dari waktu mendarat yang ditargetkan untuk
setiap pesawat. Adapun deviasi waktu disini ialah penyimpangan waktu
pendaratan pesawat dari target waktu yang telah ditentukan. Dimisalkan suatu
pesawat A memiliki target waktu pendaratan pada pukul 12.00, namun pada
kenyataannya pesawat mendarat pada pukul 12.15. ini berarti deviasi waktu
pendaratan pesawat terhadap taget waktunya ialah 15 menit.
Berdasarkan kendala-kendala umum yang terdapat pada suatu proses
penjadwalan penerbangan, maka dalam tugas akhir ini akan dilakukan
penjadwalan penerbangan pada Bandar Udara Supadio Pontianak sebagai masalah
B. Rumusan Masalah
a. Bagaimana merumuskan masalah pendaratan pesawat dengan program
linear bilangan bulat ?
b. Bagaimana menyelesaikan masalah pendaratan pesawat dengan
menggunakan model partisi himpunan ?
c. Bagaimana merumuskan masalah pendaratan pesawat dengan program
linear bilangan bulat campuran ?
d. Bagaimana menentukan penjadwalan dalam proses pendaratan dan
lepas landas pada Bandar Udara Supadio Pontianak dengan metode
program linear bilangan bulat?
C. Batasan Masalah
a. Model yang digunakan adalah model statis, yakni tidak adanya
tambahan pesawat dalam keadaan darurat (penjadwalan khusus untuk
penerbangan yang sudah terjadwal).
b. Keterlambatan pesawat (delay) yang terjadi masih dalam interval waktu yang diperbolehkan.
D. Tujuan Penulisan
a. Memahami bagaimana mencari penyelesaian dari permasalahan
penjadwalan penerbangan dengan menggunakan program linear
b. Menentukan penjadwalan penerbangan dengan menggunakan program
linear bilangan bulat.
E. Metode Penulisan
Metode penulisan dilakukan dengan studi pustaka dan studi kasus, dengan
mengambil data waktu penerbangan pada Bandar Udara Supadio Pontianak.
F. Manfaat penulisan
a. Dapat mengaplikasikan program linear bilangan bulat untuk masalah
penjadwalan penerbangan.
b. Membantu berbagai pihak dalam menentukan penjadwalan yang salah
satunya menggunakan program linear bilangan bulat.
G. Sistematika Penulisan
I. Bab 1 : Pendahuluan
a. Latar Belakang
b. Batasan Masalah
c. Rumusan Masalah
d. Tujuan Penulisan
e. Metode Penulisan
f. Manfaat Penulisan
II. Bab II : Dasar Teori
a. Matriks dan Operasi Baris Elementer
b. Program Linear
c. Metode Simpleks
d. Metode Pencabangan dan pembatasan
III. Bab III : Masalah Pendaratan
IV. Bab IV : Aplikasi Program Linear Bilangan Bulat Dalam
Penjadwalan Penerbangan Pada Bandar Udara Supadio
BAB II
Program Linear
A. Matriks dan Operasi Baris Elementer
Matriks merupakan suatu susunan bilangan-bilangan (real maupun
kompleks) yang berbentuk segi empat dan ditulis diantara tanda kurung. Tanda
kurung yang biasa digunakan ialah ( ) ataupun , -. Ukuran matriks ditentukan oleh jumlah baris dan kolom yang terdapat pada matriks tersebut. Misalkan
jumlah baris pada matriks tersebut adalah m dan jumlah kolom pada matriks tersebut adalah n, maka matriks tersebut berukuran . Ukuran matriks ini untuk seterusnya disebut sebagai ordo matriks. Penamaan matriks ditulis dengan
menggunakan huruf kapital, sedangkan elemen-elemen di dalam matriks ditulis
dengan huruf kecil. Bila A merupakan suatu matriks dan merupakan
elemen-elemen dalam matriks, maka secara umum matriks A dapat dituliskan sebagai
Matriks dapat digunakan untuk menyelesaikan masalah program linear.
Dalam menyelesaikan program linear, suatu matriks haruslah diubah bentuknya
menjadi matriks eselon ataupun menjadi bentuk matriks eselon tereduksi dengan
Definisi 2.1.1
Suatu matriks A dikatakan dalam bentuk eselon jika :
1. Elemen tak nol pertama pada sembarang baris taknol harus diletakkan
disebelah kanan entri yang pertama di baris di atasnya. Elemen tak nol
pertama dalam setiap baris disebut sebagai elemen kunci.
2. Baris yang semua elemennya nol dikelompokkan di baris akhir pada
matriks.
Definisi 2.1.2
Suatu matriks A dikatakan dalam bentuk eselon baris tereduksi jika semua
kondisi di bawah dipenuhi :
1. Matriks A berbentuk matriks eselon
2. Semua elemen kunci dari A adalah 1.
3. Semua elemen di atas elemen kunci adalah 0.
Definisi 2.1.3
Matriks yang diperluas (augmented matrix)pada suatu sistem persamaan linear
adalah matriks yang dibentuk dari matriks koefisien dan diberikan kolom
Definisi 2.1.4
Misalkan * + merupakan himpunan vektor dari matriks . Suatu vektor dari disebut bergantung linear pada S jika terdapat skalar
sedemikian sehingga :
Vektor inilah yang disebut sebagai kombinasi linear.
Contoh 1.1 :
Misalkan . / .
/adalah vektor-vektor di . wmerupakan
kombinasi linear dari v, jika w dapat dinyatakan sebagai kelipatan dari v
. / . /
Karena w dapat dinyatakan sebagai kelipatan dari v maka w merupakan kombinasi
linear dari v
Definisi 2.15
Matriks A dan B dikatakan ekivalen baris jika matriks B dapat diperoleh dengan
Definisi 2.1.6
Operasi baris elementer merupakan operasi yang dilakukan untuk mengubah
matriks biasa menjadi matriks eselon ataupun matriks eselon baris tereduksi,
dengan langkah-langkah :
1. Menukar baris i dengan baris j
2. Mengalikan setiap elemen pada baris i dengan suatu skalar k
3. Mengubah baris i dengan cara menjumlahkan elemen-elemen pada baris i
dengan perkalian baris j dengan skalar k.
Operasi baris elementer ini tidak mengubah sistem persamaan linear itu
sendiri. Artinya, penyelesaian yang dihasilkan oleh operasi baris elementer akan
sama hasilnya dengan penyelesaian sistem persamaan linear sebelumnya. Hal ini
dijamin oleh teorema berikut ini :
Teorema 2.1 :
Andaikan matriks A dan B merupakan matriks ekuivalen baris. Maka sistem yang dimiliki oleh matriks A sebagai matriks yang diperluas memiliki himpunan penyelesaian yang sama seperti sistem yang dimiliki matriks B sebagai matriks yang diperluas.
Bukti :
Jika dikenakan sebuah operasi baris elementer pada matriks A, maka diperoleh matriks A1, dimana matriks tersebut merupakan suatu matriks yang diperluas untuk sistem yang baru. Asumsikan bahwa sistem yang baru memiliki
himpunan penyelesaian yang sama seperti sistem asli dengan matriks yang
penyelesaian yang sama seperti sistem aslinya, catat bahwa setiap baris dari A1
adalah kombinasi linear baris dari matriks asli. Maka untuk setiap persamaan
pada sistem yang baru merupakan kombinasi linear dari persamaan pada sistem
asli, dimana persamaan pada sistem baru menunjukkan bahwa setiap penyelesaian
dari sistem asli juga merupakan suatu penyelesaian lainnya.
Sebaliknya, setiap penyelesaian dari sistem yang baru juga merupakan
penyelesaian asli. Hal ini dikarenakan dapat dibaliknya operasi baris elementer.
Dampak yang ditimbulkan dari penjumlahan perkalian dari baris yang diberikan
ke baris lainnya dapat dibatalkan dengan mengurangkan perkalian yang sama
pada baris yang diberikan. Pembagian dengan bilangan tak nol dapat
membatalkan dampak yang ditimbulkan dari perkalian konstanta tak nol pada
suatu baris. Maka dari matriks A1 dapat ditransformasikan kembali pada matriks A
menggunakan operasi baris elementer. Uraian yang sama pada sebelumnya
sekarang menunjukkan bahwa setiap penyelesaian dari sistem yang baru juga
merupakan suatu penyelesaian dari sistem asli. Sehingga dari uraian membuktikan
bahwa sistem yang baru memiliki himpunan penyelesaiana yang sama seperti
sistem asli dengan matriks yang diperluas A adalah benar.
Sekarang karena B ekuivalen baris dengan A, maka terdapat urutan
dari suatu matriks, dimana , dan untuk setiap i ,
dihasilkan dengan mengenakan operasi baris elementer pada . Sistem
sistem 0 memiliki himpunan penyelesaian yang sama dengan sistem 1, himpunan
penyelesaian untuk sistem 2 sampai himpunan penyelesaian sistem n juga memiliki himpunan penyelesaian yang sama. Sehingga uraian ini membuktikan
teorema 2.1.
B. Program Linear
Program Linear (Linear Programming) merupakan salah satu teknik analisis dari kelompok teknik riset operasi yang menggunakan model matematika.
Program Linear (PL) bertujuan untuk mencari, memilih, dan menentukan
alternatif yang terbaik diantara sekian alternatif layak yang tersedia. Pada tahun
1947, Dr. George Dantzig, matematikawan Amerika Serikat mengembangkan
suatu metode yang efisien, yaitu metode simpleks untuk menyelesaikan program
linear. Sejak pengembangan metode simpleks oleh Dr. George Dantzig, program
linear sering digunakan untuk menyelesaikan permasalahan yang ada di
kehidupan sehari-hari, baik di bidang ekonomi, industri, militer, maupun sosial.
Salah satu ciri khas dari program linear ialah masalah yang hendak
diselesaikan dengan program linear harus memenuhi lima macam asumsi dasar,
yakni :
1. Linearitas
Yakni fungsi tujuan dari kendala haruslah berbentuk linear
2. Proporsionalitas
Perubahan nilai pada fungsi objektif akan sebanding dengan perubahan
3. Aditivitas
Asumsi ini menganggap nilai tujuan dari masing-masing kegiatan tidak
saling mempengaruhi
4. Divisibilitas
Nilai pada variabel keputusan dapat berupa pecahan maupun berupa
bilangan bulat.
5. Deterministik
Asumsi ini menyatakan bahwa semua parameter yang terdapat pada
program linear dapat diperkirakan dengan pasti, meskipun jarang dipenuhi
secara tepat
Dalam program linear akan ditemukan beberapa istilah yang akan
mendukung penyelesaian dari program linear, yakni:
Definisi 2.2.1
Variabel keputusan (decision variable) merupakan suatu unsur yang perubahannya berdampak pada pengambilan keputusan penyelesaian masalah.
Variabel keputusan biasanya dinotasikan sebagai dengan Definisi 2.2.2
Variabel pengetat (slack variable) merupakan variabel tambahan yang mengubah suatu sistem pertidaksamaan menjadi sistem persamaan, dengan cara
menambahkan variabel pengetat tersebut pada ruas kiri suatu pertidaksamaan.
Variabel pengetat ini digunakan pada pertidaksamaan yang berbentuk
Definisi 2.2.3
Variabel Surplus merupakan variabel tambahan yang menjadikan suatu sistem
pertidaksamaan menjadi sistem persamaan, dengan cara mengurangkan variabel
pengetat tersebut pada ruas kiri suatu pertidaksamaan. Variabel surplus ini
digunakan pada pertidaksamaan yang berbentuk ( ) . Definisi 2.2.4
Fungsi objektif adalah fungsi dari variabel keputusan yang dibuat dengan tujuan
memaksimalkan keuntungan atau meminimumkan kerugian.
Definisi 2.2.5
Batasan-batasan yang dikenakan pada variabel keputusan yang dapat berupa
persamaan atau pertidaksamaan disebut kendala. Kendala inilah yang akan
mempengaruhi pengambilah keputusan.
Definisi 2.2.6
Koefisien teknis (technological coefficient) adalah koefisien yang dimiliki oleh variabel keputusan. Disebut koefisien teknis karena koefisien ini mempengaruhi
teknologi yang akan digunakan dalam penyelesaian program linear.
Definisi 2.2.7
Sebuah fungsi ( ) disebut fungsi linear jika dan hanya jika untuk sembarang konstanta , dapat ditulis sebagai :
Definisi 2.2.8
Jika suatu fungsi linear pada sisi kiri bernilai sama atau melebihi fungsi atau
konstanta pada sisi kanan, maka kondisi ini disebut pertidaksamaan linear dan
direpresentasikan dalam bentuk:
( )
dengan ( ) merupakan fungsi linear.
Sama halnya, jika fungsi pada sisi kirinya bernilai kurang dari atau sama dengan
fungsi atau konstanta pada sisi kanan. Kondisi ini direpresentasikan dalam bentuk:
( )
dengan ( ) merupakan fungsi linear.
Definisi 2.2.9
Konstanta yang berada pada sisi kanan suatu persamaan pada kendala
menunjukkan sumber daya yang tersedia. Sisi sebelah kanan ini biasa dinotasikan
dengan RHS (Right Hand Side).
Program linear adalah suatu masalah optimasi yang mana fungsi objektif
dari permasalahan ini berbentuk linear, serta variabel dan kendala yang terdapat
pada program linear terdiri dari persamaan dan pertidaksamaan linear. Adapun
Minimumkan/maksimumkan
Yang memenuhi kendala sebagai berikut :
dengan ,
dimana z adalah fungsi objektif, merupakan variabel keputusan, adalah koefisien teknis, adalah RHS.
Secara umum bentuk di atas dapat dituliskan sebagai :
Minimumkan/maksimumkan
∑
yang memenuhi kendala sebagai berikut :
∑
Bila semua kendala pada masalah memaksimumkan berbentuk ∑ maka bentuk program linear tersebut dikatakan bentuk maksimum baku.
Definisi 2.2.10
Penyelesaian dalam program linear berarti himpunan nilai variabel-variabel
keputusan yang memenuhi kendala-kendala.
Definisi 2.2.11
Penyelesaian optimal merupakan penyelesaian yang memaksimumkan/
meminimumkan fungsi objektif .
Adapun dalam penyelesaian program linear, terdapat tiga kemungkinan
penyelesaian, yakni :
1. Program linear tidak memiliki penyelesaian
2. Program linear memiliki penyelesaian tunggal
3. Program linear memiliki penyelesaian tak hingga banyak
Dalam menyelesaikan program linear banyak metode yang dapat
digunakan, diantaranya metode grafik dan metode simpleks. Pada tugas akhir ini
akan dibahas mengenai metode simpleks untuk menyelesaikan permasalahan
C. Metode Simpleks
Metode simpleks dikembangkan oleh George Dantzing pada tahun 1947.
Metode simpleks merupakan suatu metode yang digunakan untuk mencari
penyelesaian program linear dengan didasari teknik eliminasi eselon baris
tereduksi dalam penentuan penyelesaian optimalnya dan memerlukan perhitungan
yang berulang-ulang. Metode simpleks ini memiliki keunggulan dibandingkan
dengan metode grafik, yakni masalah program linear yang dapat diselesaikan
tidak hanya terbatas pada dua variabel keputusan saja, melainkan dapat mencakup
lebih dari dua variabel keputusan.
Pada tugas akhir ini, masalah program linear yang akan dibahas memiliki
kendala berbentuk campuran. Kendala berbentuk campuran yang dimaksud adalah
pada kendala memiliki beberapa bentuk pertidaksamaan maupun berbentuk
persamaan, yakni ( ) , ( ) , dan
( ) . Oleh karena itu, metode simpleks yang akan dibahas pada tugas akhir ini menggunakan kendala campuran. Adapun untuk memudahkan
pembaca dalam memahami metode simpleks, maka digunakanlah prinsip
memaksimumkan, karena prinsip memaksimumkan dalam metode simpleks lebih
mudah dipahami daripada prinsip meminimumkan.
Tahapan-tahapan yang harus dilakukan dalam menyelesaikan permasalahan
program linear dengan metode simpleks yakni :
1. Mengubah masalah program linear bentuk umum menjadi bentuk kanonik,
dengan cara mengubah kendala berbentuk pertidaksamaan menjadi bentuk
Beberapa hal yang harus dilakukan pada tahapan ini ialah :
a. untuk kendala yang berbentuk pertidaksamaan linear ( )
sisi kiri pertidaksamaan dijumlahkan dengan variabel pengetat sehingga pertidaksamaan berubah menjadi persamaan
( )
b. untuk setiap kendala yang berbentuk ( ) , sisi kiri pertidaksamaan dikurangi dengan suatu variabel surplus dan
ditambah dengan variabel semu sehingga pertidaksamaan berubah
menjadi ( )
c. jika RHS suatu masalah program linear bernilai negatif ( ), maka setiap suku pada kendala terkait haruslah dikali -1 agar diperoleh
.
2. Membuat tabel awal simpleks
Tabel awal simpleks ini berisi koefisien-koefisien fungsi objektif dan
kendala pada masalah program linear kanonik. Misalkan bentuk kanonik
dari masalah program linear dengan kendala campuran dituliskan sebagai :
( ) ( ) ( ) ( )
dengan :
:koefisien variabel keputusan,
: variabel keputusan,
: koefisien fungsi objektif,
: RHS,
: variabel pengetat, : variabel surplus,
: variabel semu, ( ) Maka tabel awal metode simpleks ini ialah :
Tabel 2.3.1. Tabel awal simpleks
… 0 … 0 0 … 0 -M … -M
… … … …
0 1 … 0 0 … 0 0 … 0
0 … 0 .. 1 0 … 0 0 … 0
-M ( ) … ( ) 0 … 0 -1 … 0 1 … 0
-M … 0 … 0 0 … -1 0 … 1
0 … 0 0 … 0 0 … 0 -M … -M Z
… 0 … 0 0 … 0 0 … 0
Definisi 2.2.11
Variabel dasar (VD) merupakan variabel yang nilainya positif dan hanya
muncul satu kali pada tabel simpleks dan nilainya ialah +1. Banyaknya
variabel dasar akan sama dengan banyaknya kendala. Pada penyelesaian
awal variabel pengetat merupakan variabel dasar. Sedangkan variabel non dasar (VND) merupakan variabel yang nilainya nol pada sembarang iterasi.
3. Melakukan uji optimalitas
Setelah dilakukan pengubahan bentuk program linear menjadi bentuk
kanonik, maka yang dilakukan selanjutnya ialah uji optimalitas. Uji
optimalitas ini bertujuan untuk menentukan apakah variabel dasar sudah
mengoptimalkan nilai fungsi objektif atau belum. Pada tahapan ini nilai
dilakukan dalam melakukan uji optimalitas adalah menyelidiki semua nilai
, kemudian perhatikan tiga hal berikut ini :
a. Nilai menunjukkan masih dimungkinkan untuk terjadi penambahan nilai z pada perhitungan selanjutnya.
b. Apabila semua maka penyelesaian yang ada sudah bernilai optimal, maka pencarian dihentikan. Hal ini dikarenakan sudah tidak
ada penambahan nilai yang dapat terjadi.
4. Mencari variabel dasar yang akan keluar dan variabel non dasar yang akan
masuk ke dalam tabel simpleks.
Langkah-langkah yang dilakukan pada tahapan ini ialah :
a. Menentukan kolom kunci
Kolom kunci diperoleh dengan menentukan maksimum dari . Hal ini dipilih karena tujuan utama dari masalah program linear
adalah memaksimumkan nilai , maka untuk mencari kolom kunci
dicari penambahan nilai yang terbesar.
b. Menyelidiki kolom kunci
Hal yang perlu diperhatikan pada tahapan ini ialah :
i) Jika pada semua elemen pada kolom kunci bernilai negatif, maka
perhitungan dihentikan, karena pada masalah program ini tidak
memiliki penyelesaian.
ii) Namun apabila tidak semua elemen kunci bernilai negatif, maka
c. Menentukan baris kunci
Baris kunci diperoleh dengan uji rasio, yakni dengan menentukan
(
* .
d. Menentukan elemen kunci
Elemen kunci adalah perpotongan antara baris kunci dan kolom kunci.
Elemen kunci inilah yang menjadi variabel dasar yang baru.
e. Mengubah elemen pada pivot menjadi +1 dan mengubah
elemen-elemen terkait menggunakan operasi baris elemen-elementer. Hal ini
dilakukan karena elemen-elemen dari kolom variabel dasar selalu
direpresentasikan dengan vektor dasar standar.
5. Setelah nilai pada baris bernilai tak positif, maka penyelesaian telah optimal. Perhitungan dihentikan. Hasil akhir dilihat dari nilai yang
terdapat pada perhitungan, dalam hal ini . Namun, jika nilai pada baris masih ada yang bernilai positif, maka perhitungan dilanjutkan pada langkah ke-4.
Dari langkah-langkah di atas didapatkan algoritma untuk metode simpleks
yakni :
1. Ubah pertidaksamaan pada fungsi objektif dan kendala ke dalam
kanonik
2. Membuat tabel simpleks awal
4. Tentukan :
a. kolom kunci dengan menentukan ( ), jika :
i) semua elemen kolom kunci bernilai negatif, perhitungan
dihentikan
5. Lakukan operasi baris elementer pada elemen yang terkait elemen kunci
dan kembali ke langkah 4
Berikut akan diberikan contoh penyelesaian program linear dengan metode
simpleks:
Maksimalkan
Kendala :
Tahap ke-2 : membuat tabel awal simpleks
3 2 0 0
Peubah
bebas
0 2 5 1 0 9 9/2
0 4 2 0 1 9 9/4
0 0 0 0 0
3 2 0 0
Tahap ke-3 : uji optimalitas
Menyelidiki nilai , karena nilai maka perhitungan dilanjutkan
Tahap ke-4 : menentukan variabel dasar mana yang akan keluar
b. Menyelidiki kolom kunci dengan melihat nilai pada kolom kunci.
Karena pada kolom kunci nilai pada elemen-elemennya bernilai positif,
maka perhitungan dilanjutkan.
c. Menentukan baris kunci dengan mencari minimum dari
(
* , yakni .
d. Elemen kunci pada masalah ini adalah perpotongan antara kolom
dan baris .
e. Mengubah elemen kunci menjadi +1 dan mengubah elemen-elemen
terkait menggunakan operasi baris elementer. Sehingga didaptkan tabel
seperti di bawah ini:
3 2 0 0
Peubah
bebas
0 0 4 1 -1/2 9 9/8
3 1 0.5 0 1/4 9/4 9/2
3 3/2 0 3/4 -27/4
0 1/2 0 -3/4
Karena pada tabel masih terdapat nilai , maka perhitungan dilanjutkan kembali pada langkah 4.
Iterasi 2 :
a. Menentukan kolom kunci, yakni kolom
b. Karena nilai pada elemen-elemen kolom kunci bernilai positif, maka
perhitungan dilanjutkan.
c. Menentukan baris kunci, yakni baris
d. Pivot pada masalah ini adalah perpotongan antara kolom dan baris .
e. Mengubah elemen pada pivot menjadi +1 dan mengubah elemen-elemen
terkait manggunakan operasi baris elementer. Sehingga didapatkan tabel
seperti di bawah ini :
3 2 0 0
Peubah bebas
2 0 1 1/4 -1/8 9/8
3 1 0 -1/8 5/16 27/16
3 2 1/8 11/16 117/16
0 0 -1/8 -11/16
Karena nilai maka perhitungan dihentikan, karena telah diperoleh peyelesaian optimal. Berdasarkan tabel, diperoleh
,
dan
.
Penyelesaian yang didapatkan dengan metode simpleks ini sama dengan
Dari keluaran tersebut didapatkan penyelesaian untuk masalah program linear
adalah dan dengan nilai z = 7.3125.
Metode simpleks yang telah dipaparkan di muka merupakan metode
simpleks yang digunakan untuk menyelesaikan masalah program linear
maksimisasi. Untuk menyelesaikan program linear minimisasi, langkah yang
digunakan sama dengan langkah masalah program linear maksimisasi, hanya
saja koefisien pada fungsi objektif dikali dengan -1. Penyelesaian yang
diperoleh dengan masalah maksimisasi ini akan sama dengan penyelesaian
masalah minimumnya. Hanya saja nilai dari fungsi objektif dari masalah
program linear minimum ini merupakan negatif dari nilai fungsi objektif
masalah program linear maksimum.
Berikut akan diberikan contoh untuk masalah minimisasi :
Contoh 2.3.2 :
minimumkan
kendala :
Pertama, langkah yang harus dilakukan adalah mengalikan fungsi
objektif dengan -1:
Kemudian ubah kendala berbentuk pertidaksamaan ke dalam bentuk kanonik:
Dengan cara yang sama seperti masalah maksimisasi menggunakan
metode simpleks didapatkan dengan z = -100. Sehingga penyelesaian dari masalah program linear minimisasi di atas yakni
, dengan nilai dari fungsi objektif masalah minimisasi adalah ( ) .
D. Metode Pencabangan dan Pembatasan (Branch and Bound)
Pada masalah program linear, penyelesaian yang didapatkan dapat berupa
bilangan pecahan maupun bilangan bulat. Namun pada kasus-kasus tertentu
dibutuhkan penyelesaian yang berupa bilangan bulat. Sebagai contoh, dalam
penentuan jumlah mobil yang akan dijual pada suatu perusahaan otomotif agar
penjualan menghasilkan keuntungan yang maksimal, tidak mungkin jumlah mobil
berupa bilangan bulat. Maka dari itu penyelesaian program linear bilangan bulat
dibutuhkan pada kasus-kasus tertentu.
Program linear yang penyelesaiannya berupa bilangan bulat inilah yang
untuk seterusnya disebut sebagai program linear bilangan bulat (Integer
Programming). Banyak metode yang dapat digunakan untuk menyelesaikan
program linear bilangan bulat, diantaranya metode pencabangan dan pembatasan,
metode pemotongan bidang (cutting plane), dan metode heuristic. Pada subbab selanjutnya akan dibahas mengenai metode pencabangan dan pembatasan.
Metode pencabangan dan pembatasan diusulkan pertama kali oleh A. H.
Land dan A. G. Doig pada tahun 1960. Metode pencabangan dan pembatasan
merupakan salah satu metode untuk menyelesaikan masalah program linear
bilangan bulat. Ide dasar dari metode pencabangan dan pembatasan ini ialah
membagi penyelesaian dari masalah program linear menjadi beberapa
submasalah. Proses pembagian penyelesaian ini biasa disebut dengan
pencabangan (branching). Tujuan dari pencabangan ini sendiri ialah untuk memudahkan dalam menyelesaikan masalah program linear.
Prinsip kerja dari metode ini ialah mencabangkan penyelesaian dari soal
program linear yang tidak memiliki penyelesaian bilangan bulat. Percabangan
dilakukan sampai ditemukan penyelesaian yang berbentuk bilangan bulat. Dalam
menyelesaikan masalah program linear dengan metode pencabangan dan
a. Pencabangan(Branching)
Pada langkah ini, pencabangan dilakukan pada penyelesaian yang belum
berbentuk bilangan bulat. Pencabangan dilakukan dengan memecah masalah
program linear awal menjadi dua bagian, kemudian menambahkan kendala
baru. Dalam pencabangan, kendala yang ditambahkan merupakan
pembulatan ke atas dan pembulatan ke bawah dari penyelesaian yang masih
berbentuk pecahan. Sehingga dari pencabangan tersebut menghasilkan
kendala baru untuk masing-masing pencabangannya, yakni :
i. ⌈ ⌉, dimana ⌈ ⌉ merupakan pembulatan ke atas dari penyelesaian program linear yang berbentuk pecahan, dan
ii. ⌊ ⌋, dimana ⌊ ⌋ merupakan pembulatan ke bawah dari penyelesaian program linear yang berbentuk pecahan.
Proses pencabangan ini terus dilakukan hingga diperoleh penyelesaian
bilangan bulat yang pertama.
b. Penetapan Batas(Bounding)
Langkah penetapan batas ini dilakukan setelah diselesaikannya proses
pencabangan. Penetapan batas ini merupakan langkah untuk membatasi
penyelesaian, agar didapatkan penyelesaian yang optimal. Pada metode
pencabangan dan pembatasan ini terdapat dua batas yaitu:
i. Batas Atas (upper bound)
Batas atas ini digunakan dalam menyelesaikan masalah program linear
objektif pertama yang berbentuk bilangan bulat. Sehingga apabila
dalam pencabangan diperoleh penyelesaian optimal dengan nilai lebih
besar dari batas atas ini, maka penyelesaian tersebut diabaikan.
Namun apabila dalam pencabangan selanjutnya diperoleh
penyelesaian yang lebih kecil dari batas atas, maka penyelesaian
tersebut dijadikan batas atas yang baru, dan batas lama diabaikan.
Pembatasan dilakukan terus hingga tidak dimungkinkan untuk
dilakukan pencabangan lagi. Sehingga penyelesaian optimal yang
diperoleh dari masalah program linear adalah penyelesaian bilangan
bulat yang menjadi batas terkahir.
ii. Batas bawah (lower bound)
Batas bawah ini digunakan dalam menyelesaikan masalah program
linear yang berbentuk maksimum. Batas bawah merupakan
penyelesaian fungsi objektif pertama yang berbentuk bilangan bulat.
Apabla dalam pencabangan selanjutnya diperoleh penyelesaian
bilangan bulat yang lebih kecil dari batas bawah, maka penyelesaian
diabaikan. Namun apabila dari pencabangan selanjutnya diperoleh
penyelesaian bilangan bulat yang lebih besar dari batas bawah, maka
penyelesaian yang baru ini dijadikan batas bawah yang baru, dan batas
bawah lama diabaikan. Pembatasan ini dilakukan terus menerus
hingga tidak dimungkinkan lagi dilakukan pencabangan. Sehingga
secara umum, penyelesaian optimal dari masalah program linear yang
c. Penghentian pencabangan (Fathoming)
Pencabangan atau pencarian penyelesaian pada suatu sub masalah
dihentikan jika :
1. Infeasible atau tidak memiliki daerah layak
2. Semua variabel keputusan yang harus bernilai bilangan bulat sudah
bernilai bilangan bulat.
3. Pada masalah maksimisasi, penghentian pencabangan pada suatu sub
masalah dilakukan jika fungsi objektif dari sub masalah tersebut tidak
lebih besar atau sama dengan nilai batas bawah. Sedangkan pada
masalah minimisasi penghentian pencabangan sub masalah dilakukan
jika fungsi objektif tidak lebih kecil atau sama dengan nilai batas atas.
Adapun cara langkah-langkah yang dilakukan dalam menyelesaikan
program linear menggunakan metode pencabangan dan pembatasan adalah :
1. Menyelesaikan masalah program linear awal ( ), kemudian lihat penyelesaiannya. Apabila penyelesaian berbentuk bilangan bulat,
perhitungan dihentikan. Namun, jika penyelesaian berupa bilangan pecahan
maka perhitungan dilanjutkan pada langkah selanjutnya.
3. Lakukan penetapan batas dengan cara mengambil salah satu penyelesaian
yang berbentuk bilangan bulat pertama yang dihasilkan dari penyelesaian.
4. Setelah didapatkan batas atas dan bawah, dan dapat dilengkapi menjadi ⌈ ⌉ dan ⌊ ⌋
5. Kemudian selesaikan masalah program linear baru tersebut. Apabila dalam
penyelesaian masih berupa bilangan pecahan, lakukan perhitungan yang
sama untuk setiap cabang dan kembali pada langkah 2.
Kondisi optimal dalam penyelesaian program linear bilangan bulat
menggunakan metode pencabangan dan pembatasan ini tercapai, jika :
1. Tidak ada ada lagi submasalah yang perlu dicabangkan lagi
2. Pada masalah maksimisasi penyelesaian optimal merupakan penyelesaian
submasalah yang saat ini menjadi batas bawah
3. Pada masalah minimisasi penyelesaian optimal merupakan penyelsaian
submasalah yang saat ini menjadi batas atas.
Berikut akan diberikan contoh penyelesaian proglam linear dengan metode
pencabangan dan pembatasan :
Contoh 2.4.1
Maksimumkan
Kendala :
Penyelesaian :
Iterasi 1:
Langkah 1 : menyelesaikan
Dengan bantuan software QM for windows 2 diperoleh penyelesaian :
Langkah ke-2 : melakukan pencabangan :
Untuk didapatkan 2 pencabangan, yakni dan . Dimana kendala baru adalah dan .
Langkah ke-3 : melakukan penetapan batas
Karena belum diperoleh penyelesaian bilangan bulat, maka batas bawah belum
bisa ditetapkan.
Masalah program linear baru dapat dituliskan dengan :
Maksimumkan
Kendala :
dan
Maksimumkan
Kendala :
Langkah ke-5 : mencari penyelesaian dan .
Setelah dilakukan perhitungan dengan bantuan software QM for windows 2, didapatkan penyelesaian sebagai berikut :
Untuk diperoleh :
𝐿𝑃
Untuk diperoleh :
Dapat dilihat, pada pnyelesaian penyelesaian sudah optimal, karena semua nilai dari variabel keputusan sudah berbentuk bilangan bulat. Namun,
untuk , masih ada variabel keputusan yang berbentuk desimal, maka untuk dilakukan perhitungan kembali untuk . Maka perhitungan kembali pada langkah 2.
Iterasi ke-2 :
Langkah ke-2 : melakukan pencabangan
Untuk didapatkan 2 pencabangan, yakni dan . Dimana kendala baru adalah dan .
Karena pada diperoleh penyelesaian bilangan bulat, maka ditetapkan sebagai batas bawah.
Langkah ke-4 : melengkapi masalah program linear baru
Sehingga masalah program linear baru dapat dituliskan dengan :
Maksimumkan
Kendala :
Maksimumkan
Kendala :
𝐿𝑃
Langkah ke-5 : mencari penyelesaian dan .
Setelah dilakukan perhitungan dengan bantuan software QM for windows 2, didapatkan penyelesaian sebagai berikut :
Untuk tidak diperoleh penyelesaian
Untuk diperoleh :
Dapat dilihat, pada tidak memiliki penyelesaian, sehingga tidak dapat digunakan sebagai penentu nilai optimal dari . Namun, untuk , masih terdapat variabel keputusan yang berbentuk desimal, maka untuk dilakukan
perhitungan kembali untuk . Maka perhitungan kembali pada langkah 2. Dengan cara yang sama dengan iterasi-iterasi sebelumnya, maka akan
diperoleh penyelesaian optimal dari masing-masing submasalah yakni :
Untuk diperoleh :
Untuk diperoleh :
dari penyelesaian tersebut, didapatkan penyelesaian optimal adalah
. Nilai ini dipilih karena nilai yang didapatkan merupakan batas bawah terakhir dalam penyelesaian program linear ini. Sehingga tidak ada
BAB III
MASALAH PENDARATAN PESAWAT
Perkembangan teknologi pada masa kini, menyebabkan peningkatan
produksi di berbagai sektor kehidupan. Begitu pula halnya dengan sektor
penerbangan. Pada sektor ini, terjadi peningkatan dalam produksi pesawat
terbang. Tentu saja hal ini sangat membantu masyarakat untuk melakukan
mobilitas dengan mudah. Namun peningkatan jumlah pesawat terbang ini juga
mengakibatkan permasalahan baru, yakni terbatasnya penggunaan landasan pacu
yang tidak sepadan dengan jumlah pesawat terbang yang ada. Hal ini merupakan
masalah yang sangat besar dalam lalu lintas udara, karena landasan pacu memiliki
peran yang sangat penting dalam proses pendaratan maupun lepas landas.
Saat jumlah pesawat terbang yang akan menggunakan landasan pacu
melebihi kapasitas penggunaan landasan pacu, maka akan ada sejumlah pesawat
terbang yang tidak dapat mendarat pada waktu pendaratan yang telah ditentukan.
Jika ini terjadi, tentu saja akan ada nilai pinalti yang diterima maskapai tersebut,
terutama penggunaan bahan bakar yang berlebihan jika melakukan penerbangan
dengan kecepatan tinggi. Maskapai juga akan mempertimbangkan nilai pinalti
yang berbeda untuk setiap penundaan penerbangan. Bergantung pada jumlah
penundaan yang terjadi, mungkin akan ada penumpang yang memilih untuk
pesawat tentunya akan dibutuhkan untuk penerbangan selanjutnya, sehingga
penjadwalan ulang penugasan sangat diperlukan dan tentunya akan menyebabkan
penundaan penerbangan kembali.
Terdapat banyak nilai pinalti yang akan diakibatkan oleh masalah ini,
diantaranya nilai pinalti yang dihasilkan dari penundaan penerbangan,
pembayaran lembur para awak pesawat dan lainnya (Min, 2005). Tentu saja
masalah pendaratan pesawat ini harus diselesaikan, karena ini merupakan hal yang
sangat penting dalam kegiatan lalu lintas udara. Penyelesaian permasalahan ini
dilakukan dengan meminimumkan total nilai pinalti yang terjadi, sehingga
menghasilkan penjadwalan yang efektif.
Diberikan sebuah himpunan pesawat dengan waktu mendarat yang telah
ditargetkan dan selang waktu pesawat untuk mendarat. Fungsi objektif dari
Masalah Pendaratan Pesawat (MPP) ini ialah meminimumkan total deviasi waktu
dari waktu mendarat yang ditargetkan untuk setiap pesawat. Terdapat biaya yang
dikenakan untuk setiap pesawat jika mendarat sebelum atau sesudah waktu yang
telah ditargetkan. Setiap pesawat yang akan melakukan pendaratan haruslah
memenuhi kriteria-kriteria pendaratan yang diberikan, yakni selang waktu
pendaratan dan jeda waktu antar pesawat saat melakukan pendaratan.
Saat memasuki jangkauan radar Air Traffic Control (ATC), suatu pesawat membutuhkan penugasan tentang waktu yang diberikan untuk melakukan
pendaratan. Waktu pendaratan haruslah sesuai dengan selang waktu yang
terlambat suatu pesawat diperbolehkan mendarat. Selang waktu ini akan berbeda
untuk setiap pesawatnya. Waktu tercepat menunjukkan waktu yang ditempuh
suatu pesawat jika terbang dengan kecepatan maksimum. Kemudian, untuk waktu
terlambat menunjukkan waktu yang ditempuh suatu pesawat jika melakukan
penerbangan dengan bahan-bakar yang efisien.
Setiap pesawat juga akan memiliki kecepatan paling ekonomis, yaitu
kecepatan standar. Kecepatan ekonomis disini merupakan kecepatan yang
mengeluarkan biaya minimal untuk penggunaan bahan bakarnya. Kecepatan
ekonomis (standar) inilah yang nantinya akan menjadi ‘patokan’ dalam penentuan
waktu pendaratan pesawat atau yang disebut waktu yang ditergetkan. Jika ATC
meminta suatu pesawat untuk terbang dalam kecepatan lambat, sedang atau cepat,
maka akan ada suatu nilai pinalti yang dikenakan. Gambar 3.1 menggambarkan
variasi nilai pada suatu selang waktu pendaratan suatu pesawat.
Gambar 3.1: variasi nilai pinalti pada suatu selang waktu pendaratan pesawat
(Min, 2005)
Pada gambar dijelaskan bahwa nilai pinalti dari suatu pesawat akan nol jika
waktu mendarat dari pesawat tersebut sesuai dengan waktu yang ditargetkan.
Nilai Pinalti
Sedangkan untuk waktu yang mendarat selain waktu yang ditargetkanakan
dikenakan nilai pinalti.
A. Perumusan Masalah Pendaratan Pesawat Dengan Program
Linear
Pada paparan sebelumnya, dijelaskan bahwa saat suatu pesawat hendak
melakukan pendaratan, pesawat membutuhkan informasi mengenai waktu yang
diijinkan untuk melakukan pendaratan. Waktu pendaratan haruslah sesuai dengan
selang waktu yang diberikan, dimana selang waktu tersebut dibatasi oleh waktu
terawal dan waktu terlambat suatu pesawat diperbolehkan mendarat. Setiap selang
waktu akan berbeda antara suatu pesawat dengan pesawat lainnya. Dengan kata
Dimisalkan P merupakan himpunan urutan pendaratan pesawat-pesawat dengan
P={{1},{2},{3},{1,2},{1,3},{3,1},{2,3},{3,2},{1,2,3},{1,3,2}}, dan dimisalkan :
: waktu pendaratan tercepat pesawat
ke-: waktu pendaratan yang ditargetkan pesawat ke- : waktu pendaratan terlambat pesawat ke-
Maka pertidaksamaan (3.1) dapat ditulis secara sistematis sebagai berikut :
Pada kenyataan di lapangan, terkadang waktu yang ditargetkan suatu
pesawat untuk melakukan pendaratan tidak selalu terpenuhi. Sehingga muncullah
istilah waktu pendaratan, yakni waktu pendaratan pesawat pada keadaan real.
Waktu pendaratan ini juga dibatasi oleh waktu pendaratan terawal ( ) dan waktu pendaratan terlambat ( ). Jika dinotasikan dalam bentuk yang lebih sederhana, Waktu pendaratan antar pesawat tidak diperbolehkan saling berdekatan.
Waktu pendaratan tersebut haruslah diberi jeda waktu tertentu. Jeda waktu
tersebut ditentukan oleh kebutuhan masing-masing pesawat. Dimisalkan adalah
pesawat yang melakukan pendaratan sebelumnya, dan adalah pesawat yang
melakukan pendaratan setelahnya, maka jeda waktu antara waktu pendaratan
pesawat dan dapat dinotasikan dengan . Di muka telah dijelaskan bahwa permasalahan yang dibahas dalam tugas akhir ini ialah permasalahan satu
landasan pacu, maka tidak diperbolehkan sama dengan 0. Kemudian, karena
merupakan jeda waktu, maka haruslah lebih besar dari nol atau dapat ditulis
secara matematis menjadi 0. Dengan demikian, estimasi waktu pendaratan
pesawat ( ) dengan jeda waktu pendaratan antar pesawat. Sehingga dapat
Pada penjabaran di muka telah dijelaskan bahwa pada kenyataannya,
tidak selalu terpenuhi. Sehingga suatu pesawat terkadang mendarat sebelum atau
sesudah , namun tetap dalam selang waktu yang ditentukan. Dalam
permasalahan ini, yang akan diminimumkan ialah beda waktu antara dan .
Karena dapat terjadi sebelum atau sesudah , maka di sini dapat didefinisikan
dua kendala baru, yakni jika terjadi sebelum maka beda waktu tersebut disimbolkan dengan . Kemudian jika terjadi sesudah maka beda waktu tersebut disimbolkan dengan . Beda waktu ini menunjukkan seberapa cepat
pesawat akan mendarat sebelum atau sesudah , sehingga dapat dituliskan :
[
Secara matematis, persamaan (3.7) dan (3.8) dapat ditulis :
(3.9)
(3.10) Dalam hal ini, dan berada pada suatu interval waktu tertentu, yakni
interval yang dibatasi oleh atau , dan . Beda waktu ini harus lebih dari nol.
Sehingga, jika ditulis dalam bentuk interval menjadi :
0 (3.11) 0 (3.12) Kendala-kendala ini tentu saja menjamin ataupun akan selalu lebih besar
dari nol.
Jika dilihat secara keseluruhan kendala-kendala yang ada, dan cukup
memberikan pengaruh penting dalam penentuan penjadwalan. Rentang minimum
nilai-nilai inilah yang akan ditentukan agar memberikan hasil penjadwalan.
Fungsi objektif untuk Masalah Pendaratan Pesawat ini ialah meminimumkan
deviasi waktu dari . Karena nilai yang yang menunjukkan deviasi waktu dari
ialah dan , maka dapat dituliskan rumusan untuk fungsi objektifnya adalah :
∑
dimana dan merupakan nilai pinalti untuk setiap pesawat jika melakukan
pendaratan sebelum atau sesudah waktu yang ditentukan.
Berdasarkan pemaparan di muka, dapat dilihat bahwa pada kasus ini
memiliki kendala-kendala yang harus dipenuhi, yang merupakan pertidaksamaan
linear. Pada kasus ini juga terdapat suatu fungsi yang akan dioptimalkan dengan
cara diminimumkan. Dengan demikian kasus ini dapat dirumuskan sebagai
masalah program linear. Karena variabel dan menunjukkan beda waktu yang
berbentuk bilangan bulat, maka masalah pendaratan pesawat ini dapat
diselesaikan dengan program linear bilangan bulat dimana salah satu metode
untuk menyelesaikannya ialah metode pencabangan dan pembatasan. Pada tugas
akhir ini, akan diberikan contoh soal penjadwalan dengan 1 landasan pacu dan
dengan 2 landasan pacu.
Contoh 3.1 :
Diberikan sebuah contoh dari masalah pendaratan, dimana terdiri dari 3
pesawat dan 1 landasan pacu. Selang waktu dan nilai pinalti pendaratan
masing-masing pesawat diberikan pada Tabel 3.1.1. Jeda waktu antar pesawat juga telah
ditetapkan, yakni menit.
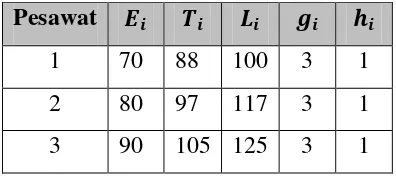
Tabel 3.1.1 : Data pendaratan 3 pesawat (dalam menit)
Pesawat
1 70 88 100 3 1
2 80 97 117 3 1
Berdasarkan data di atas, dapat dicari seluruh kemungkinan urutan. Karena
pada contoh ini, data yang ada merupakan data pendaratan 3 pesawat pada bandar
udara yang memiliki 1 landasan pacu, maka keseluruhan kemungkinan urutan
dapat dicari dengan rumus :
dengan n merupakan jumlah pesawat yang ada, dimana merupakan permutasi i dari n. Jadi berdasar rumusan tersebut, maka dari ke tiga pesawat ini akan menghasilakan :
( )
Namun dari ke enam urutan tersebut tidak semua dapat digunakan untuk
menentukan urutan yang optimum. Hal ini dikarenakan ada beberapa urutan yang
tidak memenuhi kendala pada masalah mendaratan pesawat ini. Sebagai contoh,
untuk pendaratan yang dimulai dari pesawat 3 kemudian dilanjutkan dengan
pendaratan pesawat 2, dan dilanjutkan lagi dengan pendaratan pesawat 1 yang
disimbolkan dengan {3 → 2 → 1), tidak dapat digunakan. Ini karena berdasarkan
data pada Tabel 3.1.1, diketahui bahwa waktu terawal untuk pesawat 3 adalah
pesawat 3 mendarat pada waktu terawal, yakni pada menit ke 90, maka paling
cepat pesawat 2 dapat mendarat pada menit ke 100 ( ). Waktu pendaratan pesawat 2 masih dipenuhi dalam selang waktu yang ditentukan.
Kemudian, jika dilanjutkan, maka pesawat 1 minimal dapat mendarat pada menit
ke 110 ( ), Padahal diketahui pada Tabel 3.1.1 pesawat 1 hanya dapat mendarat pada selang waktu [70,100]. Tentu saja waktu pendaratan untuk pesawat
1 ini tidak memenuhi kendala pada masalah pendaratan pesawat, maka untuk
urutan {3 2 1} tidak dapat digunakan. Sehingga dari hasil perhitungan yang
sama didapatkanlah urutan penerbangan yang memungkinkan adalah sebagai
berikut :
Tabel 3.1.2 : Data urutan pendaratan pesawat yang memungkinkan
Urutan Pendaratan
Urutan 1 {1 → 2 → 3}
Urutan 2 {2 → 1 → 3 }
Urutan 3 {2 → 3 → 1 }
Urutan 4 {3 → 1 → 2 }
Pada urutan 1 ditulis {1 → 2 → 3}, yang menandakan bahwa pesawat
pertama yang melakukan pendaratan adalah pesawat 1, kemudian disusul oleh
juga untuk urutan-urutan selanjutnya. Berdasarkan urutan-urutan pendaratan
pesawat yang memungkinkan tersebut, setiap urutan memiliki nilai pinalti yang
berbeda. Sebagai contoh, untuk mengetahui nilai pinalti dari urutan 1 maka kita
menggunakan metode Pencabangan dan pembatasan dan diselesaikan dengan
bantuan Software QM for Windows 2, dengan kendala-kendala sebagai berikut:
1) 13)
2) 14)
3) 15)
4) 10 16)
5) 10 17)
6) 18)
7) 19)
8) 20)
9) 21)
10) 22)
11)
12)
dari keluaran tersebut diketahui bahwa untuk urutan 1 → 2 → 3 memiliki
. dengan demikian sebaiknya pesawat mendarat pada menit ke 88, 98 dan 108 dengan nilai pinalti sebesar 4.
Dengan cara yang sama dilakukan perhitungan untuk mencari nilai pinalti
untuk setiap urutan, dan dituliskan pada tabel di bawah ini :
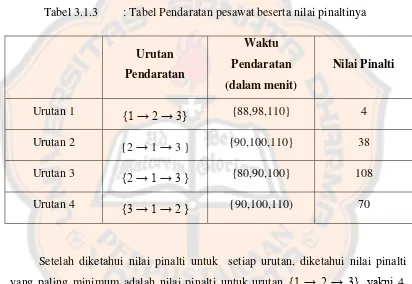
Tabel 3.1.3 : Tabel Pendaratan pesawat beserta nilai pinaltinya
Urutan
Setelah diketahui nilai pinalti untuk setiap urutan, diketahui nilai pinalti
yang paling minimum adalah nilai pinalti untuk urutan {1 → 2 → 3}, yakni 4.
Sehingga penjadwalan yang dianjurkan adalah {1 → 2 → 3}, yakni pendaratan
dimulai dari pesawat 1, dilanjutkan pesawat 2, kemudian dilanjutkan kembali
dengan pesawat 3.
Contoh 3.2 :
Diberikan sebuah contoh dari masalah pendaratan, dimana terdiri dari 3
pesawat dan 2 landasan pacu. Selang waktu dan nilai pinalti pendaratan
asing-masing pesawat diberikan pada Tabel 3.1.1. Jeda waktu antar pesawat juga telah
Tabel 3.2.1 : Data pendaratan 3 pesawat (dalam menit)
kemungkinan urutan yang dapat digunakan untuk pendaratan pesawat. Adapun
banyaknya urutan pendaratan pesawat yang mungkin terjadi dapat dicari dengan
Namun dari ke-15 urutan tersebut, tidak semua dapat digunakan untuk
menentukan urutan pendaratan yang paling optimum. Hal ini dikarenakan ada
beberapa urutan yang tidak memenuhi kendala pada masalah pendaratan pesawat
ini. Sebagai contoh untuk urutan pendaratan pesawat 2 kemudian dilanjutkan
pendaratan pesawat 1, yang disimbolkan dengan {2 1}, tidak dapat digunakan.
Ini karena berdasarkan data pada Tabel 3.1.1, diketahui bahwa waktu terawal
untuk pesawat 2 adalah pada menit ke 88 dengan jeda waktu antar pesawat =10
menit. Dimisalkan pesawat 2 mendarat pada waktu terawal, yakni pada menit ke
88, maka paling cepat pesawat 1 dapat mendarat pada menit ke 98( ). Padahal diketahui pada Tabel 3.1.1 pesawat 1 hanya dapat mendarat pada selang
waktu [50,95]. Tentu saja waktu pendaratan untuk pesawat 1 ini tidak memenuhi
kendala pada masalah pendaratan pesawat, maka untuk urutan {2 1} tidak dapat
digunakan. Sehingga urutan pendaratan {2 1} tidak termasuk dalam ruang solusi
S, dimana S merupakan himpunan dari keseluruhan urutan pendaratan yang diijinkan.
Dengan cara yang sama, diperoleh urutan pendaratan pesawat yang
memungkinkan seperti didata dalam Tabel 3.2.2.
Tabel 3.2.2 : Urutan pendaratan pesawat yang memungkinkan
Urutan
Pendaratan
Urutan 1 {1}
Urutan 3 {3}
Urutan 4 {1 } Urutan 5 {1 } Urutan 6 {3 } Urutan 7 {2 } Urutan 8 {3 } Urutan 9 {1 } Urutan 10 {1 }
Pada Tabel 3.2.2, pada urutan pertama hanya muncul 1 pesawat dalam
urutan tersebut. Hal ini berarti hanya pesawat 1 saja yang mendarat pada landasan
pacu tersebut. Sehingga dalam konteks urutan pertama ini pesawat 2 dan pesawat
3 tidak mendarat. Hal ini juga berlaku pada urutan ke-2 dan urutan ke-3. Untuk
urutan ke-4, yakni {1 } berarti hanya pesawat 1 dan 2 saja yang mendarat, yang dimulai dengan pendaratan pesawat 1 dan kemudian disusul oleh pendaratan
pesawat ke-2. Hal ini juga berlaku untuk urutan 5 sampai urutan 8. Kemudian
untuk urutan ke-9, yakni {1 }, berarti ke-3 pesawat mendarat pada landasan pacu yang sama, dimulai dari pendaratan pesawat 1, kemudian disusul
dengan pendaratan pesawat ke-2 dan diakhiri dengan pendaratan pesawat ke-3.
Urutan-urutan pendaratan yang ditulis dalam Tabel 3.1.2, tentu saja
memiliki nilai pinalti untuk setiap urutannya. Untuk menentukan total nilai pinalti
objektifnya. Sebagai contoh, untuk memperoleh total nilai pinalti dari urutan 4,
yakni {1 } maka total nilai pinalti ini dapat diperoleh dengan menyelesaikannya dengan metode pencabangan dan pembatasan menggunakan
bantuan software QM. Maka fungsi objektif dan kendala-kendala yang terjadi untuk urutan 4 ini, ialah :
Minimum :
( ) ( )
dengan kendala :
1) 9)
2) 10)
3) 10 11)
4) 12)
5) 13)
6) 14)
7) 15)
8)
dan diperoleh hasil :
Disini dapat dilihat bahwa, untuk penjadwalan (khusus untuk urutan {1
}) didapatkan untuk Dengan demikian, waktu pendaratan pesawat 1 dan pesawat 2 ialah pada menit ke 88 dan 98, dengan
Begitupula halnya dengan urutan ke-10, yang melibatkan 3 pesawat. Untuk
menentukan total nilai pinalti yang terjadi dari urutan 10, yakni {1 )} maka total nilai pinalti ini dapat diperoleh dengan menyelesaikannya dengan cara
yang sama. Maka fungsi objektif dan kendala-kendala yang dibangun untuk
urutan 10 ini, ialah :
Minimum :
( ) ( ) ( )
dengan kendala :
1) 13)
2) 14)
3) 15)
4) 10 16)
5) 10 17)
6) 18)
7) 19)
8) 20)
9) 21)
10) 22)
11) 23)
12)
Kemudian kendala-kendala diselesaikan dengan bantuan software QM for
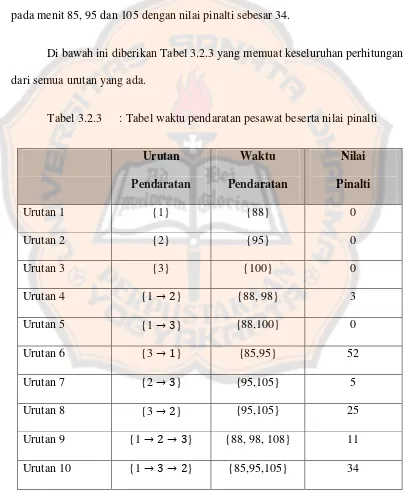
dari keluaran tersebut dapat kita ketahui bahwa penjadwalan untuk urutan {1
} didapatkan . Dengan demikian, waktu pendaratan pesawat 1, 3 dan 2 yang disarankan adalah
pada menit 85, 95 dan 105 dengan nilai pinalti sebesar 34.
Di bawah ini diberikan Tabel 3.2.3 yang memuat keseluruhan perhitungan
dari semua urutan yang ada.
Tabel 3.2.3 : Tabel waktu pendaratan pesawat beserta nilai pinalti