Eksponen Titik Keluar Dari Sebuah Kelas Digraf Dwiwarna Primitif Atas n-Titik

(1)

DIGRAF DWIWARNA PRIMITIF

Pada bab ini akan dibahas teorema, definisi dan landasan teori pada penelitian ini. Berikut akan dibahas mengenai digraf, digraf dwiwarna dan hubungan keduanya dengan primitif itas,terhubung kuat, eksponen dan eksponen titik.

2.1 Definisi

Sub-bab ini akan membahas definisi tentang digraf dan digraf dwiwarna secara ke-seluruhan.

2.1.1 Digraf

Andaikan V adalah sebuah himpunan berhingga yang tak kosong yang disebut sebagai titik (vertex) dan E adalah himpunan pasangan berurut dari titik V yang disebut sebagai edge, maka graf adalah suatu objek yang dibentuk dari himpunan V,dan himpunan E ⊆V ×V yang unsurnya disebut sebagai edge.

Digraf D adalah objek yang dibentuk dari himpunan V, dan himpunan A ⊆ V ×V yang unsurnya disebut sebagai arc dari D. Jika (u, v)∈ A merupakan sebuah arc pada digraf D, maka u sebagai titik awal dan v sebagai titik akhir. Titik V direpresentasikan dalam bentuk titik atau lingkaran kecil sedangkan arc direpsen-tasikan dalam bentuk garis berarah.

Barisan sejumlah titikv1, v2, ..., vmsehingga terdapat arc dalamDyang menghubungkan titik vi ke titik vi+1 untuk setiap i = 1,2,3, ..., m−1 disebut sebagai walk dengan

(2)

v1 →v2 →v3 →...→vm

untuk v1 6= vm maka disebut walk terbuka. Suatu walk yang tidak mengalami

pe-rulangan titik disebut sebagai path, sedangkan suatu path tertutup disebut sebagai cycle dan cycle yang memiliki panjang 1 disebut sebagai loop.

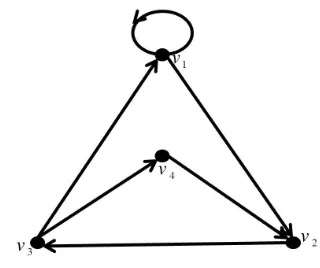
Contoh 2.1.1 Berikut merupakan representasi dari definisi diatas.

Gambar 2.1 : Digraf dengan 4 titik dan 6 arc

Digraf diatas memperlihatkan walk , path, cycle, dan loop sebagai berikut:

a. v1 →v2 →v3 →v4 →v2 adalah walk terbuka

b. v1 →v2 →v3 →v4 →v2 →v3 →v1 adalah walk tertutup namun bukan path

c. v1 →v2 →v3 →v4 adalah path terbuka

d. v1 →v2 →v3 →v1 adalah path tertutup atau disebut cycle

e. v1 →v1 adalah loop

2.1.2 Digraf Dwiwarna

(3)

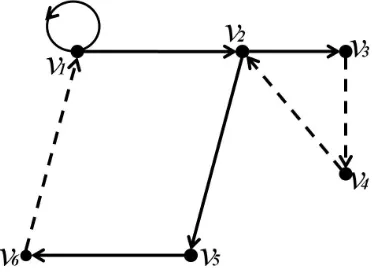
Arc merah (u, v) direpresentasikan dengan u→m v atau dengan tanda panah sedangkan arc biru (u, v) direpresentasikan dengan u→b v atau garis putus-putus. Contoh 2.1.2 Berikut gambar digraf dwiwarna

Gambar 2.2 : Digraf Dwiwarna dengan 6 titik 8 arc

Digraf dwiwarna diatas memperlihatkan himpunan vertex V = {v1, v2, v3, v4, v5, v6}

dengan uraian sebagai berikut :

a. Himpunan arc biru B ={(v3, v4),(v4, v2),(v6, v1)}

b. Himpunan arc merahR ={(v1, v2),(v2, v3),(v2, v5),(v5, v6),(v1, v1)}

merupakan suatu digraf dwiwarna dengan 6 vertex, 3 arc biru dan 5 arc merah.

Pada digraf dwiwarna juga terdapat walk, path, dan cycle. Suatu (h, k)-walk dalam digraf dwiwarna adalah sebuah walk denganharc merah dankarc biru sedan-gkan vektor ((r(w), b(w)) atau





r(w) b(w)



 merupakan komposisi dari walk w, dengan

r(w) adalah notasi dari jumlah arc merah dan b(w) adalah notasi dari jumlah arc biru dan l(w) =r(w) +b(w) adalah panjang walkwyang merupakan jumlah dari arc merah dan arc biru.

(4)

satu yang memiliki komposisi

Contoh 2.1.3 Berikut adalah contoh walk, path, cycle dan loop dari Gambar 2.2. Digraf dwiwarna diatas memperlihatkan :

1. v1

→v2 adalah walk terbuka.

2. v1 →m v2 →m v3 →b v4 adalah path terbuka.

→v1 adalah loop dengan komposisi 

2.2 Matriks Adjacency

Matriks adjacency dari digraf dan digraf dwiwarna dengan n-titik adalah suatu ma-triks berordon×nyang dinotasikan denganAdimana setiap entrinya adalah 1 atau 0.

2.1.2 Matriks Adjacency Digraf

Matriks adjacency pada Digraf D dengan n-titik yang dinotasikan sebagai A(D) = [aij] dengan entry sebagai berikut:

aij =

(

1, jika terdapat arc darivi kevj di D 0, jika sebaliknya

untuk i, j = 1,2,3, ..., n

(5)

2.2.2 Matriks Adjacency Digraf Dwiwarna

Pada digraf dwiwarna matriks adjacency dibagi menjadi 2 bagian berdasarkan warna arc yakni :

a. Matriks adjacency merah

Matriks adjacency merah yang berordo n ×n dinotasikan sebagai R = [rij] dengan entri adalah sebagai berikut:

rij =

(

1, jika terdapat arc merah dari vi ke vj diD(2) 0, jika sebaliknya

untuk i, j = 1,2,3, ..., n

Contoh 2.2.2 Berikut adalah matriks adjacency merah dari digraf dwiwarna yang diperoleh dari Gambar 2.2.



            

1 1 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0



            

b. Matriks adjacency biru

Matriks adjacency biru yang berordon×n dinotasikan sebagai B = [bij]dengan entri adalah sebagai berikut:

bij =

(

1, jika terdapat arc biru darivi kevj di D(2) 0, jika sebaliknya

untuk i, j = 1,2,3, ..., n.

(6)



            

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0



            

2.3 Primitifitas Digraf dan Digraf Dwiwarna Terhubung Kuat

Pada subbab ini akan dibahas mengenai digraf dan digraf dwiwarna terhubung kuat dan hubungannya dengan primitifitas.

2.3.1 Primitifas Digraf Terhubung Kuat

Suatu digraf D dikatakan terhubung kuat (strongly connected) jika untuk setiap pasang titik udan v di D terdapat walk dari uke v dan walk dari v keu.

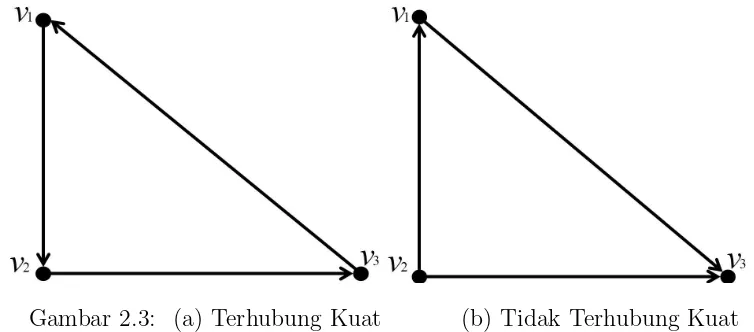
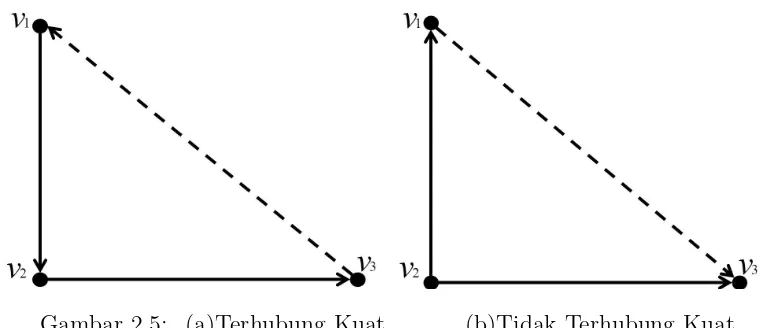
Contoh 2.3.1Berikut adalah digraf terhubung kuat dan tak terhubung kuat.

Gambar 2.3: (a) Terhubung Kuat (b) Tidak Terhubung Kuat

(7)

Lemma 2.3.1 Andaikan D adalah digraf terhubung kuat maka setiap titik u di D terletak pada cycle.

Bukti : Ambil sebarang titiku diD dan sebarang arc dari titikukev diD. Karena D adalah digraf terhubung kuat, maka terdapat path dari titiku kev dan path dari titik v ke u akibatnya terdapat path tertutup atau disebut sebagai cycle untuk se-tiap titikudiD. Dengan kata lain bahwa setiap titikudiDterletak pada suatu cycle.

Andaikan C = {γ1, γ2, ..., γq} merupakan himpunan semua cycle di D dan

misalkan notasi l(γi) merupakan panjang semua cycle pada digraf D untuk setiap i= 1,2,· · ·, q. Suatu digrafDterhubung kuat dikatakan primitif jika dan hanya jika pembagi persekutuan terbesar dari setiap panjang cycle di D adalah 1 (Brualdi dan Ryser,1991).

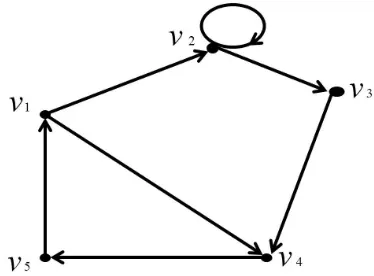
Contoh 2.3.2 Berikut adalah digraf terhubung kuat yang primitif.

Gambar 2.4 : Digraf Terhubung Kuat dan Primitif

Pada gambar 2.4 diperlihatkan bahwa l(γ1) dari cyclev1 →v2 →v3 →v4 →v5 →v1

adalah 5. Kemudian l(γ2) dari cycle v1 → v4 → v5 → v1 adalah 3. Dan l(γ3) dari

cycle tertutup v1 ke v1 adalah 1. Sehingga diketahui bahwa pembagi persekutuan

(8)

2.3.2 Primitifitas Digraf Dwiwarna Terhubung Kuat

Suatu digraf D dikatakan terhubung kuat (strongly connected) jika untuk setiap pasang titik udan v di D terdapat walk dari uke v dan walk dari v ke u.

Contoh 2.3.3Berikut adalah digraf dwiwarna terhubung kuat dan tidak terhubung kuat.

Gambar 2.5: (a)Terhubung Kuat (b)Tidak Terhubung Kuat

Gambar 2.5 memperlihatkan bahwa pada digraf dwiwarna (a) terdapat walk dari satu titik ketitik lainnya. Sedangkan (b) tidak terdapat walk dari v3 kev1.

Lemma 2.3.2 Andaikan D(2) adalah digraf dwiwarna terhubung kuat maka setiap titik u di D(2) terletak pada cycle.

Bukti : Ambil sebarang titik u di D(2) dan sebarang arc dari titik u ke v di D(2). KarenaD(2) adalah digraf dwiwarna terhubung kuat, maka terdapat path dari titiku kev dan path dari titikv keuakibatnya terdapat path tertutup atau disebut sebagai cycle untuk setiap titik u di D(2)_{. Dengan kata lain bahwa setiap titik} _u _di _D(2)

terletak pada suatu cycle.

(9)

titik (u, v) di D(2) _{terdapat (h, k)-walk dari} _u _ke _v _{dan walk dari} _v _ke_u.

Andaikan C = {γ1, γ2, ..., γq} merupakan himpunan semua cycle di D(2) dan

misalkan notasi l(γi) merupakan panjang semua cycle pada digraf dwiwarna D(2) untuk setiap i = 1,2,3,· · ·, q. S disebut sebagai matriks cycle adalah matriks yang berordo 2×q sebagai berikut

S =





r(γ1) r(γ2) · · · r(γq)

b(γ1) b(γ2) · · · b(γq) 



Kolom ke-qdari matrik cycleS merupakan komposisi dari cycleγq dan jumlah baris pada matriksSmenyatakan banyaknya warna padaD(2). Suatu digraf dwiwarna dikatakan primitif jika dan hanya jika pembagi persekutuan terbesar dari determinan-determinan matriks minor berordo 2×2 dariSadalah 1 (Fornasini dan Valcher,1997).

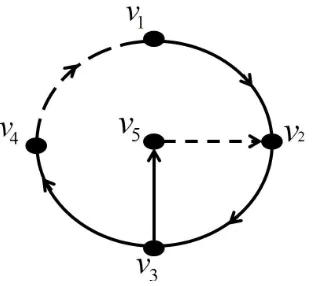
Contoh 2.3.4 Berikut adalah digraf dwiwarna terhubung kuat yang primitif.

Gambar 2.6 Digraf Dwiwarna Terhubung Kuat dan Primitif

Dari Gambar 2.6 diatas terdapat 2 cycle yaitu cycle yang pertama v1

m → v2

m →v3

m → v4

b

→ v1 dengan komposisi S1 = 



3 1



 dan cycle kedua adalah v5

b → v2

m → v3

m → v5

dengan komposisi S2 = 



2 1



, maka matriks cycle dari D(2) adalah S = 



3 2 1 1





(10)

2.4 Matriks Tak Negatif dan Digraf Dwiwarna

Suatu matriks A dikatakan matriks tak negatif jika untuk setiap entri dari matriks A= [aij] bernilai tak negatif atau dapat dinotasikan dengan aij ≥0 .

Contoh 2.4.1Berikut adalah matriks tak negatif.



   

1 0 0 0 1 0 0 0 1



   

sedangkan matriksA dikatakan postitif, jika untuk setiap entri dari matriksA= [aij] bernilai positif atau dapat dinotasikan dengan aij >0 .

Contoh 2.4.2 Berikut adalah matriks positif.



   

1 4 7 2 5 8 3 6 9



   

Pada suatu digrafD, terdapat suatu bilangan bulat positiflsehingga untuk setiap pasangan titik-titikudan v terdapat walk dari uke v dengan panjangl, maka bilan-gan bulat positif terkecil l disebut sebagai eksponen dari digraf D yang dinotasikan sebagai exp(D) (Brualdi dan Ryser,1991).

Proposisi 2.4 Andaikan A adalah suatu matriks adjacency dari digraf D. Entri ak

ij dari Ak menyatakan banyaknya walk dari titik vi ke vj dengan panjang k di D.

Bukti : Andaikan A suatu matriks adjacency dari digraf D, maka setiap entri aij dari A menyatakan arc dari titikvi kevj diD. Sehingga untukk = 1, terdapat entri a1_ij dariA1 menyatakan banyaknya walk dari titikvi kevj dengan panjang satu diD.

Asumsikan setiap entri ak

(11)

entriak+1

ij menyatakan banyaknya walk dari titikvi kevj dengan panjang k+ 1 diD, untuk setiap k ≥1 .

Perhatikan setiap walk dari titik vi ke vj di D dengan panjang k + 1 yang terdiri dari walk vi ke vl dengan panjang k dengan l = 1,2,3, .., n dan dilanjutkan dengan arc dari titikvl kevj. Sehinggaak

ilalj menyatakan walk dengan panjang k+ 1 dari titik vi ke vj di D untuk k = 1,2,3,· · ·, n. Jika terdapat walk dengan panjang k dari titik vi ke vj di D, maka ak

il = 0 sehingga akilalj = 0. Hal ini berarti tidak terdapat walk dengan panjang k + 1 dari titik vi ke vj yang melalui titik vl di D. Sehingga diperoleh jumlah walk dengan panjang k+ 1 dari titik vi kevj diD adalah

aki1a1j +aki2a2j+...+akinanj =

ij adalah benar menyatakan banyaknya walk dari titik vi ke vj yang panjangnya k+ 1 di D.

Contoh 2.4.1 Berikut adalah representasi menghitung eksponen dari digrafD. Dari Gambar 2.1 diatas diperoleh matriks adjacency sebagai berikut.

A=

Dari proposisi diatas, dengan mencari banyak walk dari titik vi kevj dengan panjang k, sehingga bilangan bulat positif terkecil k adalah eksponen dari digraf D. Perhatikan matriks Ak _untuk _k:

a. Untukk = 1, diperoleh A=

(12)

b. untuk k = 2, diperolehA2=

maka k = 2 bukan merupakan eksponen dari digraf karena tidak terdapat walk dengan panjang 2 dari titik v1 ke v4, v2 ke v2,v2 kev3,v3 kev4, dst.

maka k= 3 bukan merupakan eksponen dari digraf, karena tidak terdapat walk dengan panjang tiga dari titik v2 kev3,v3 kev4, dst.

maka k= 4 bukan merupakan eksponen dari digraf, karena tidak terdapat walk dengan panjang empat dari titik v2 ke v4, v4 ke v3, v4 ke v4, dst.

maka k= 5 bukan merupakan eksponen dari digraf, karena tidak terdapat walk dengan panjang lima dari titik v4 kev4.

(13)

Pada digraf dwiwarnaD(2)_{, eksponen dari digraf dwiwarna}_D(2)_{, di definisikan}

sebagai bilangan bulat positif terkecilh+k yang terdiri dari h arc merah dan k arc biru sehingga untuk setiap pasang titikudanv terdapat sebuah (h, k)-walk dari uke v, eksponen dari digraf dwiwarnaD(2) dinotasikan olehexp(D(2)_{)(Shader dan Suwilo,}

2003).

Andaikan A dan B adalah suatu matriks tak negatif berordo m ×m. Un-tuk bilangan tak negatif h dan k di definisikan (h, k)-Hurwitz product, (R, B)(h,k)

adalah jumlah keseluruhan matriks dari perkalianR sebanyakh kali danB sebanyak k kali.

Contoh 2.4.2 :

(R, B)(1,0) ₌_R _{dan (R, B)}(2,2)₌_R2_B2₊_RBRB₊_RB2_R₊_BRBR₊_B2_R2

Lemma 2.4.1 Jika (R, B) adalah matriks adjacency dari digraf dwiwarna. Maka (R, B)(h,k) _{adalah jumlah} _{(h, k)-walk dari} _vi _ke _vj _{pada digraf dwiwarna.}

Bukti : Pembuktian dilakukan dengan cara induksi, yakni jika h = 0 dan k = 1 maka (R, B)(0,1) ₌_B _{merupakan walk dari} _vi _ke _vj _{memiliki komposisi}





0 1



 pada

digraf dwiwarna . Kemudian jika h= 1 dan k = 0 maka (R, B)(1,0) ₌_R _merupakan

walk dari vi kevj memiliki komposisi





1 0



 pada digraf dwiwarna.

Kemudian diperlihatkan untuk semua bilangan bulat tak negatif h+k + 1 adalah benar dengan pembuktian sebagai berikut.

(R, B)(h+1,k) ₌_{R(R, B)}(h,k)₊_B_{(R, B)}(h+1,k−1)

sehingga R(R, B)(h,k) _{menyatakan bahwa terdapat walk dari}_vi _ke_vj _{dengan panjang}

(h, k) yang diikuti dengan sebuah arc merah, sedangkan B(R, B)(h+1,k−1) menyatakan

(14)

dari vi kevj.

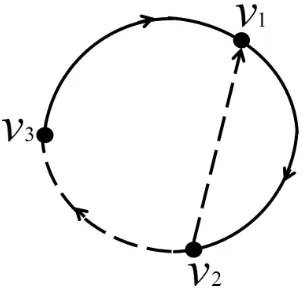
Contoh 2.4.3 Berikut adalah representasi menghitung eksponen digraf dwiwarna.

Gambar 2.7 : Digraf Dwiwarna dengan 3 titik dan 4 arc

Dari Gambar 2.7 digraf dwiwarna terhubung kuat yang primitif terdapat matriks

ad-jacency merah R =



   

0 1 0 0 0 0 1 0 0



   

dan matriks adjacency biru B =



   

0 0 0 1 0 1 0 0 0



   

.

Menggunakan Lemma 2.4.1, jika (R, B) adalah matriks adjacendy dari digraf dwi-warna. Maka (R, B)(h,k)_{adalah jumlah (h, k)-walk dari}_vi_ke_vj_{pada digraf dwiwarna.}

Sehingga h+k merupakan eksponen dari digraf bila matriks (R, B)(h,k) _adalah

ma-triks positif.

Dengan demikian perhatikan matriks adjacency merahRdan matriks adjacency biru B adalah sebagai berikut :

1. Untukh+k = 2 , maka diperoleh

a. (R, B)(2,0) ₌_R2 ₌ 

   

0 0 0 0 0 0 0 1 0



   

b. (R, B)(1,1) ₌_RB₊_BR₌ 

   

0 0 0 0 0 0 0 0 0



(15)

(16)

(17)

a. (R, B)(0,6) ₌_B6 ₌

(18)

se-hingga exp(D(2)_{) = 10 dengan komposisi 6 arc merah dan 4 arc biru yakni} 



6 4



.

2.5 Eksponen Titik Digraf dan Digraf Dwiwarna

Pada subbab ini akan dibahas definisi dan penentuan eksponen titik digraf dan digraf dwiwarna.

2.5.1 Eksponen Titik Digraf

Misalkan D adalah sebuah digraf primitif yang terdiri dari himpunan titik V(D) = {v1, v2, ..., vn}. Eksponen titik dari digraph D didefinisikan sebagai jumlah walk

dengan panjang minimumm yang menghubungkan titikvk ke setiap titik di D dino-tasikan γD(vk).

Misalkan Dadalah sebuah digraf dwiwarna primitif yang berordo n×n. Jika titik-titik di D adalah (v1, v2, ...vn) sehingga

γD(v1)≥γD(v2)≥...≥γD(vn)

MakaγD(vk) adalah tipe pertama generalisasi eksponen ke-kdariD, yang dinotasikan dengan expD(vk).

Contoh 2.5.1Berikut adalah bagaimana mencari eksponen titik dari masing-masing titik di digraf D, berdasarkan proposisi 2.4 entri aij harus bernilai positif.

Dari Contoh 2.4.1 diperoleh matriks-matriks dari Ak _:

1. Untuk k=3, pada baris pertama semua entri bernilai positif, makaexpD(v1) = 3.

2. Untuk k=4, pada baris ke-3 semua entri juga bernilai positif,makaexpD(v3) = 4.

3. Untuk k=5, pada baris ke-2 semua entri bernilai positif, maka expD(v2) = 5.

(19)

2.5.2 Eksponen Titik Digraf Dwiwarna

Misalkan D(2) _{adalah sebuah digraf dwiwarna primitif yang terdiri dari himpunan}

titik V(D) = {v1, v2, ..., vn}. Eksponen titik dari digraph dwiwarna D(2)

didefin-isikan sebagai jumlah walk dengan panjang minimumg+hyang menghubungkan titik vk ke setiap titik di D(2), dengang menyatakan jumlah arc merah danh menyatakan jumlah arc biru . Kemudian dinotasikan dengan γD(vk).

Misalkan Dadalah sebuah digraf dwiwarna primitif yang berordo n×n. Jika titik-titik di D(2) adalah (v1, v2, ..., vn), maka

γD(v1)≥γD(v2)≥...≥γD(vn)

sehingga γD(vk) adalah tipe pertama generalisasi eksponen ke-k dariD(2), yang dino-tasikan dengan exp_D(2)(vk) .

Dengan menggunakan operasi (g, h)-matriksHurwitz ProductRdanByang telah didefenisikan pada subbab 2.4. Untuk suatu bilangan positif terkecil g dan h yang masing-masing merupakan jumlah arc merah dan arc biru, sehinggag+h meru-pakan eksponen titik digraf dwiwarna untuk setiap baris ke-k dari matriks tersebut yang seluruh entrinya bernilai positif .

Contoh 2.5.2 Berikut mencari eksponen titik digraf dwiwarna dari masing-masing titik pada Gambar 2.6.

1. Untuk g+h=4, dengan

(R, B)(2,2) ₌_{R(R, B)}(1,2)₊_B_{(R, B)}(2,1)₌ 

   

1 0 1 2 1 1 0 0 0



   

pada baris ke-2 semua entri bernilai positif,maka exp_D(2)(v3) = 4 yang terdiri

dari 2 arc merah dan 2 arc biru yakni





2 2



(20)

2. Untuk g+h=5 dengan

(R, B)(3,2) ₌_{R(R, B)}(2,2)₊_B_{(R, B)}(3,1)₌ 

   

2 1 1 1 2 0 1 0 1



   

pada baris pertama semua entri bernilai positif, maka expD(2)(v₁) = 5 yang

terdiri dari 3 arc merah dan 2 arc biru yakni





3 2



.

3. Untuk g+h=6, dengan

(R, B)(4,2) ₌_{R(R, B)}(3,2)₊_B_{(R, B)}(4,1)₌ 

   

1 2 0 0 1 0 2 1 1



   

pada baris ke-3 semua entri bernilai positif, maka exp_D(2)(v2) = 6 yang terdiri

dari 4 arc merah dan 2 arc biru yakni





4 2



.

2.6 Sistem Persamaan Diophantine

Bentuk persamaaan Diophantine dapat dituliskan sebagai berikut

a1x1+a2x2 +a3x3+...+anxn=b

memiliki solusi bilangan bulat untuk semua bilangan bulat positif n dan koefisien-koefisien a1, a2, a3, ..., an tidak semuanya bernilai nol.

Teorema 2.6 Persamaan diophantine

a1x1+a2x2 +a3x3+...+anxn=b

(21)

Bukti : Sistem persamaan diophantine adalah himpunan dari m persamaan dio-phantine dalam n variabel yang sama, untuk m, n > 0. Berikut merupakan sistem persamaan diophantine.

Sistem persamaan diophantine tersebut dapat pula direpresentasikan dalam bentuk persamaan matriks Ax=b sebagai berikut

A=

Sistem persamaan diophantine memiliki solusi bilangan bulat jika dan hanya jika pembagi persekutuan terbesar dari determinan-determinan submatriks 2×2 dari A adalah ±1.

2.7 Formula Eksponen Titik Digraf Dwiwarna dengan Dua Cycle

Subbab ini dibahas bagaimana menentukan batas atas dan batas bawah eksponen titik digraf dwiwarna yang primitif yang memuat dua cycle.

Lemma 2.7.1 Andaikan D(2) adalah digraf dwiwarna primitif yang memuat dua cycle dengan matriks cycle S=





r(γ1) b(γ2)

b(γ1) r(γ2) 

. Misalkanvkadalah sembarang titik

dariD(2) _{dan terdapat sebuah}_{(g, h)}_-walk _{dari titik}_vk_{ke setiap titik}_vj_, _j _{= 1,}_2,_{· · ·}_{, n}

di D(2) dengan persamaan berikut

(22)

maka

 untuk sembarang bilangan bulat tak negatif u, v dan

untuk suatu path p(k,j) dari vk ke vj.

Bukti : Misalkanp(k,j)adalah path dari titikvkkevj untuk sembarangj = 1,2, ..., n.

KarenaD(2) memuat 2 cycle maka setiap walknya dapat didekomposisi ke dalam path dan cycle sebagai berikut :



dengan x1, x2 ≥0. Karena D(2) primitif, makaM memiliki invers. Dengan

menggu-nakan persamaan (1) dan (2), maka diperoleh :

S

 dan Lemma 2.7.1 terbukti.

Menggunakan Lemma 2.7.1 diperoleh teorema sebagai berikut.

Teorema 2.7.1 Andaikan D(2) adalah digraf dwiwarna primitif yang terdiri dari cycle γ1 dan γ2. Misalkan vk adalah titik diD(2). Untuk sembarang titik vi dan vj di

D(2)_{, didefinisikan} _u

0 =b(γ2)r(pk,j)−r(γ2)b(pk,j) danw0 =r(γ1)b(pk,j)−b(γ1)r(pk,j)

(23)





g h



=S





u w



sehingga diperoleh persamaan





u w



≥S−1 



r(p(k,j))

b(p(k,j)) 

=





b(γ2)r(pk,j)−r(γ2)b(pk,j)

r(γ1)b(pk,j)−b(γ1)r(pk,j) 

 (3)

untuk setiap path pk,j dari titikvk ke vj.

Untuk sembarang titikvj, j = 1,2, ..., n, diperoleh

u0 =b(γ2)r(pk,j)−r(γ2)b(pk,j)≥0 (4)

dan untuk sembarang titik vi, i= 1,2, ..., n, diperoleh

w0 =r(γ1)b(pk,i)−b(γ1)r(pk,i)≥0 (5)

sehingga u≥u0 dan w≥w0. Oleh Lemma 2.6.1 diperoleh 



g h



=S 



u w



≥S 



u0

w0 

 (6)

sehinggaexp_D(2)(vk) =g+h≥(r(γ1)+b(γ1))u0+(r(γ2)+b(γ2))w0 =l(γ1)u0+l(γ2)w0.

Teorema 2.7.1 menerangkan tentang batas bawah eksponen titik, sedangkan Proposisi 2.7.1 berikut akan menerangkan batas atas eksponen titik digraf dwiwarna yang primitif dari suatu titikv, dengan d(v, vk) merupakan jarak dari titikvk ke titik v sebagai walk terpendek dari vk ke titikv.

Proposisi 2.7.1 Asumsikan D(2) adalah digraf dwiwarna primitif atas n-titik. Mis-alkan v adalah sebuah titik di D(2) dengan exp(2)_D (vk). Untuk sembarang titik vk, k = 1,2, ..., n di D(2), expD(2)(vk)≤exp_D(2)(v) +d(vk, v).

Bukti : Untuk setiap k = 1,2, ..., n misalkan pk,v adalah (r(pk,v), b(pk,v))-path dari titik vk ke titik v dengan panjang d(vk, v). Terdapat (g, h)-walk dari titik v ke se-tiap titik vj, j = 1,2, ..., n di D(2) , sehingga exp_D(2)(v) = g +h. ini

(24)

titik vk ke setiap titik vj. Walk tersebut berjalan dari titik vk ke v dengan melalui (r(pk,v), b(pk,v))-path selanjutnya menuju ke titik vj melalui (g +h)-walk. Sehingga diperoleh exp_D(2)(vk)≤exp_D(2)(v) +d(vk, v).

Proposisi 2.7.2 Andaikan D(2) adalah digraf dwiwarna yang terdiri atas cycle γ1

danγ2. Misalkan titik vk adalah titik di D(2) yang terdapat pada cycleγ1 danγ2. Jika

untuk setiap i = 1,2, ..., n dan sembarang bilangan g dan h, terdapat path pk,i dari titik vk ke titik vi sehingga sistem persamaan

Sx+





r(p(k,i))

b(p(k,i)) 

=





g h