KUMPULAN SOAL JAWAB OLIMPIADE MATEMATIKA

===================================================================

Tema : TEORI BILANGAN

180.) Tentukan semua bilangan bulat positif n sehingga 1 2 1



Sehingga perlu ditulis

1

182.) Tunjukkan bahwa kuadrat sembarang bilangan bulat adalah dalam bentuk 3k dan 3k +1. Jawab :

Menurut contoh (no 172) maka kuadrat sembarang bilangan bulat dapat ditulis dalam bentuk p

Catatan notasi x y _{artinya x membagi habis y sehingga dapat ditulis ada bilangan bulat k dan}

sehingga y = xk. Jika x tidak membagi habis y , pada tulisan ini digunakan notasi x ~| y.

 (tidak bulat ). Kontradiksi diketahui l bulat. Jadi pengandaian salah bahwa 3~a_dan 3~b_{dengan diketahui 3a}2 _b2

 . Jadi haruslah jika _3a2 _b2

 maka 3a _dan 3b_.

184. )Tunjukkan bawa jika sisi-sisi suatu segitiga siku-siku semuanya bulat maka 3 membagi salah satu dari ketiga sisi tersebut.

Jawab :

Sebut panjang sisi-sisi adalah x, y, z dan _x2 _y2 _z2 _{dengan x, y dan z bilangan bulat positif.} Anggap bahwa _3x2 _y2

 maka dengan soal sebelumnya 3|x dan 3|y. Bukti selesai.

===================================================================

k (tidak habis dibagi 5).

Jadi 5~|n2 2n

 .

186.) Buktikan bahwa tidak ada bilangan prima triple yang dapat disusun dalam bentuk p, p +2, p + 4 kecuali tripel 3,5,7.

Jawab. Untuk p > 3 maka sembarang bilangan prima dapat ditulis dalam bentuk p = 6k + 1 atau p = 6k -1.

(i) Untuk p = 6k + 1 maka p +2 = 6k +1 +2 = 3(2k +1). Karena 2k + 1 > 1 maka jelas p +2 bukan prima (karena faktor-faktor prima hanyalah 1 dan dia sendiri).

(ii) Untuk p = 6k + 1 maka p +4 = 6k +1 +4 = 6k+5 = 6t-1.(jelas prima berdasarkan pengetahuan sebelum ini telah dibuktikan bahwa 6k +1 prima).

(iii) Untuk p = 6k - 1 maka p +2 = 6k -1 +2 = 6k + 1 (jelas prima, berdasarkan pengetahuan sebelum ini telah dibuktikan bahwa 6k +1 prima).

(iv) Untuk p = 6k - 1 maka p +4 = 6k -1 +4 = 6k+3 = 3(2k +1) . Karena 2k + 1 > 1 maka jelas p +2 bukan prima (karena faktor-faktor prima hanyalah 1 dan dia sendiri.

Jelas tidak ada tripel lain yang prima yang dapat dibentuk dalam p, p +2, p +4.

Yang terbesar yaitu 2 171 2  

n = 169 . Jadi n = 13.

188). Tunjukkan jika n bulat positif sehingga 2n + 1 berbentuk kuadrat maka n + 1 merupakan jumlahan 2 bilangan kuadrat berturutan .

===================================================================

208). Tentukan pecahan rasional yang sama dengan 0.3172 .

Jawab : Sebut bilangan tersebut x = 0.3172 = 0.3172727272…

10000x = 3172,727272… 100x = 31.727272…

209). Bilangan 2 digit dibagi oleh jumlah dari digit-digitnya. Berapakah sisa pembagian terbesar ?.

Jawab : Bilangan 2 digit yang mungkin adalah 10, 11, 12,…, 99. Sebutlah bilangan tersebut x = 10 a + b. (belum selesai).

210). Tunjukkan bahwa bilangan bulat



merupakan bilangan tak prima (komposit). Jawab :

akan diselidiki dapat tidaknya disusun dalam dalam 8p . (belum lengkap).

Perhatikan jika kesulitan dalam memperumum bentuk ambillah m = 3. Jadi ab + 1 = (111)(1005) + 1 = (1005)(111) +1

Secara umum m kita dapat beranalogi yaitu

ab + 1 =









1

Jelas bahwa 10m2 habis dibagi 3 (karena jumlah digit-digitnya habis dibagi 3).

212). Ditanyakan digit-digit apa yang muncul pada perkalian :



=================================================================== 3333 x 6666 = 22217778.

Secara umum diperoleh terdapat 2 sebanyak 665 7 sebanyak 665

1 sebanyak 1 dan 8 sebanyak 1.

213). Tunjukkan bahwa tidak ada bilangan bulat dengan sifat sbb : jika digit awal ‚disuppressed’ hasilnya adalah 1/35 dari bilangan mula-mula.

Jawab :

Perhatikan contoh no.200 untuk menyelesaikan hal ini. Jadi kita dapat memperoleh bentuk sifat

,

Agar y bulat maka _k.10n _{faktor yang sama dengan faktor 34. Sedangkan faktor-faktor 34}

adalah 1, 2, 17 dan 34. Karena 0k 9 _{maka k yang memenuhi hanyalah 1 dan 2. Jelas} bahwa k = 1 sudah memenuhi sehingga kita hanya memperhatikan k = 2.

Untuk k = 2 maka _y n ₁₀n

 . Padahal 17 bilangan prima dan

jelas bahwa 17 tidak membagi habis₁₀n _{untuk semua n asli. Sehingga terbukti tidak ada}

bilangan bulat dengan sifat (a)-(b).

214). Tunjukkan bahwa jumlahan semua bilangan bulat dengan n digit untuk n 3, adalah



Jawab : Perhatikan untuk n = 3 maka semua bilangan yang mungkin adalah 100,101, …,999. Jumlah bilangan adalah dengan menggunakan deret aritmatika yaitu

.

Banyaknya bilangan adalah 9 x ₁₀n1 _{jumlah semua bilangan tersebut adalah menggunakan} deret aritmatika yaitu



215.) Tunjukkan bahwa untuk sembarang bilangan bulat positif n, maka bentuk



 adalah bentuk kuadrat sempurna.

=================================================================== Jawab : Bilangan tersebut harus habis dibagi 15 (atau 3 dan 5). Bilangan yang habis dibagi 3 yaitu jika bilangan yang jumlah digit-digitnya habis dibagi 3. Karena bilangan tersebut hanya terdiri dari 8 dan 0 maka bilangan yang mungkin adalah 888. Akan tetapi karena harus bisa dibagi 15 maka bilangan tersebut 8880.

218) Tunjukkan bahwa bilangan desimal dengan angka dibelakang koma adalah semua bilangan asli (x = 0.1234567891011121314151617…) merupakan bilangan rasional.

Jawab : sebut bilangan tersebut x dan andaikan bilangan tersebut rasional. Berarti harus ada bilangan m dan n yang bulat sehingga x = m/n. Akan tetapi tidak mungkin. .

219). Diberikan 1/49 = 0.0204 … bla-bla.

221). Diberikan n adlalah bilangan bulat positif yang mungkin dan d adalah 1 digit dengan dasar 10 (basis 10). Tentukan n jika n/810 = 0.d25d25d25….

Jawab : Karena desimal berulang, bilangan tersebut dapat dinyatakan sebagai pecahan rasional maka yaitu diperoleh n/810 = d25/999.

Sehingga d₁₁₁25  ₉₀n atau (30)(d25) = n (37) .

n d

 37

) 25 ( 30

(bulat). Karena 37 tidak membagi habis (30) maka 37 harus bisa membagi (d25

sehingga d yang memenuhi adalah d = 9 sehingga 750 37

) 925 ( 30

 .

282). Buktikan jika sembarang bilangan kuadrat jika dibagi 13 selalu bersisa 0,1,3,4,9, 10, dan 12.

Bukti : Dari hal. 25 no.172 : bentuk kuadrat selalu dapat dinyatakan dalam 4t (jika bentuk kuadrat genap) atau 4t +1 (jika bentuk kuadrat ganjil).

Sebut _{x n}2

 dan diketahui n2 13ks, 0s12, s : bulat. (i) n2 4t

 maka 4t = 13 k + s .

s k t 

 (4 13 ) . Untuk 13k 0mod13sehingga yang kita perhatikan s = 4t. Kita mendaftar semua t yang mungkin sebagai berikut

t s= 4t Keterangan

0 0 memenuhi

1 4 memenuhi

2 8 tidak memenuhi

(sebagai salah satu jenis sisa dalam soal)

3 12 memenuhi

Jadi t yang memenuhi = 0,1,3

(ii) n2 4t

 +1, 4t + 1 = 13k +s

(4t + 1-13k) = s. sehingga dipilih s = 4t +1. Secara sama kita dapat mendaftar.

t s= 4t Keterangan

0 0 memenuhi

1 5 tidak memenuhi

=================================================================== soal)

2 9 memenuhi

3 13 sama artinya sisa 0

4 17 sama artinya sisa 4

Jadi t yang memenuhi = 0, 2

301). Tentukan digit terakhir dari

233333334

.

9987737 + 12

.

21327 + 12123

.

99987

Jawab : Untuk mendapatkan angka satuan maka cukup mencari hasil pembagian angka satuan dari tiap suku yang dibagi oleh 10, yaitu :

((4)(7) + (2)(7) + (3)(7)) mod 10 = (8 + 4 + 1) mod 10 = 3 mod 10.

283). Buktikan bahwa tidak ada bilangan bulat x dan y yang memenuhi 2 5 2 2   y

x _.

Bukti :

Menurut pengentahuan kita sebelum ini, bentuk kuadrat dapat dinyatakan dalam bentuk 4k (genap) atau 4k +1 (ganjil). Artinya 2 5 2 2

  y

x _{akan kita nyatakan dalam kedua bentuk ini.} Yaitu : 5_y2 _2 _{= 4(y}2 _{2) + (y}2_{2) -8}

= 4(_y2 _2_{) + ( y}2 _{-6).Untuk memenuhi sebagai bentuk 4k atau 4k +1 maka} disyaratkan

2

y _{-6 = 0 atau y}2 _{-6 = 1. Sehingga y}2 _{= 6 atau y}2_{= 7. Jelas tidak ada bilangan bulat y} yang memenuhi.

Catatan : pada bagian ini yang k = 2 2 

y _{(memuat y yang tidak kita ketahui).} Cara 2 :

Kita dapat menganggap bahwa _x2 _5_y2 _2 _{dibaca sebagai bentuk kuadrat yang dibagi 5} bersisa 2. Ditulis 2 2



x mod 5. Oleh karena itu kita akan mendaftar beberapa bilangan

kuadrat dan kita bagi 5. Kemudian kita selidiki sisanya, sebagaimana ditunjukkan pada Tabel berikut.

x _x2 _sisa

pembagian dengan 5

1 1 1

2 4 -1

3 9 -1

4 16 1

5 25 0

6 36 1

7 49 -1

8 64 -1

9 81 1

10 100 0

11 121 1

12 144 -1

Jika proses dilanjutkan maka hanya bersisa 0, -1 dan 1 (perlu juga dinyatakan dalam bentuk umum, tapi saat ini tidak ditulis).

284). Digit berapa yang harus ditulis untuk a dan b dalam 30a0b03 sehingga bilangan bulat tersebut habis dibagi 13.

Jawab :

Sebut u = 30a0b03 = 3 106 0 105 104 0 103 102 0 102 3  

 



 x ax x bx x

=================================================================== = 3 106 104 102 3

 

ax bx

x

Sedangkan 102 _9mod13_{= -4 mod 13. Bagian akhir yang digunakan pada perhitungan lebih} lanjut karena angka -4 lebih mudah daripada 9 jika dipangkatkan. Ekspresi u dapat ditulis u = 3(102)3



102



2 (102) 3

 

a b = (3( 4)3  42 ( 4) 3     

 a b ) mod 13

= 3(64)a 16 (4b)3

= [3(4(13)12)a 16 (4b)3] mod 13 =[ 3(-4)(13)(3) + 3(-12) + 16a -4b + 3] mod 13 = [0 -33 + 13a + 3a -4b ] mod 13

= [-7 + 3a -4b] mod 13 .

Karena dari soal bilangan yang diminta harus habis dibagi 13 maka diperoleh -7 + 3a -4b = 0. Atau 3a – 4b = 7. Untuk selanjutnya kita mencari a dan b yang mungkin dengan cara mendaftar sebagai berikut.

a 3a Persamaan 3a – 4b = 7, a dan b bulat

0 tidak dipenuhi

1. tidak dipenuhi 2. tidak dipenuhi 3. tidak dipenuhi 4. tidak dipenuhi 5. dapat, b = 2 6. tidak dipenuhi 7. tidak dipenuhi 8. tidak dipenuhi

9. b = 5

Jadi (a ,b) yang memenuhi adalah (5,2) dan (9,5).

285). Tentukan semua n, 1n25 sedemikian hingga 2 15 122   n

n dapat dibagi 6.

Petunjuk : nyatakan bahwa 2 15 122   n

n



(n +1)(n + 2) mod 6. Jawab : Berdasarkan pada petunjuk maka agar 2 15 122

  n

n habis dibagi 6 maka

(n +1)(n + 2) = 0 atau (n +1)(n + 2) = 6k . Untuk (n +1)(n + 2) = 0 tidak mungkin karena n tidak boleh negatif . Sehinggga haruslah (n +1)(n + 2) = 6k. Kita akan mnegusahakan dengan mendaftar semua n yang mungkin sehingga (n +1)(n + 2) = 6k.

n (n+1)(n+2) Persamaan (n +1)(n + 2) = 6k

1. (2)(3) 2. (3)(4) 3. (4)(5) 4. (5)(6) 5. (6)(7) 6. (7)(8) 7. (8)(9) 8. (9)(10) 9. (10)(11) 10. (11)(12)

Demikian seterusnya, maka akan diperoleh pola bahwa n = 3k -1 dan (3k -2) yang memenuhi.

286). n n n

=================================================================== 288).

289). Tentukan semua n bulat sehingga 10| 10 1



n _.

Jawab : Dicari bilangan yang dipangkatkan bersisa 9 sehingga jika ditambah dengan 1 habis dibagi 10. Kita ketahui bahwa bilangan yang bersatuan 9 adalah 3 dan 7. Dengan memperhatikan pola sebagai berikut .

9 berakhir 9 dan ₇10_berakhir 9.

Soal Test (Test Tengah Pelatihan Guru Berau, Kaltim 19 Nov-28 Nov 2010)

1. Hal 10 no 362 : Tentukan 10002 9992 9982 9972 ... 42 32 22 1

4. Hal 43 no 299 : Jika 62ab427 adalah suatu kelipatan 99, tentukan digit a dan b. 5. Hal 10 no 359 : Diberikan _{a b b c c a}

adalah barisan aritmatika. Tunjukkan bahwa _b2_,a2_,c2_{juga barisan aritmatika.}

===================================================================

Jelas bahwa ruas kiri < ruas kanan, sehingga berlaku pernyataan di atas pada n = 2. (ii) Pernyataan di atas dianggap berlaku (benar) pada n = k

yaitu

(iii) Perlu dibuktikan bahwa pernyataan di atas berlaku untuk n = k+ 1 yaitu perlu dibuktikan berlaku

Pebuktian dilakukan sebagai berikut : Ruas kiri = 2 2 2 2 _{( 1)}2

Sehingga hanya perlu dibuktikan

2

Karena keduanya negatif maka jelas bahwa

2

Jadi terbukti (*).

3. Hal 42 no 288 : Buktikan bahwa jika _9a3 _b3 _c3 Selain itu dari aljabar

a b c3 a3 b3 c3 3ab2 3ac2 3bc2 3a2b 3a2c 3b2c 6abc

Suatu bilangan habis dibagi n maka ada salah satu faktor yang juga habis dibagi n. Karena semua faktor sama maka dapat ditulis

 3

3 abc  3abc_.

Sesuai dengan sifat bilangan yang habis dibagi 3 adalah bilangan yang jumlah digit-digitnya habis dibagi 3. Sehingga

abc

===================================================================

4. Hal 43 no 299 : Jika 62ab427 adalah suatu kelipatan 99, tentukan digit a dan b. Jawab : Bilangan yang habis dibagi 99 adalah bilangan yang habis dibagi 9 dan 11.

Bilangan yang habis dibagi 9 adalah bilangan yang jumlah digit-digitnya habis dibagi 9 sehingga

6 + 2 + a + b + 4+ 2 + 7 = 9k , k bulat.

a + b + 21 = 9k . (Untuk 9k yang terdekat adalah 27.)

Cukuplah k = 1 dan jumlahkan kembali digit-digit pada ruas kiri yaitu a + b + 2 + 1 = 9

atau a + b = 6. (i)

Karena bilangan tersebut juga habis dibagi 11 maka perlu dibuat bahwa bilangan habis dibagi 11 jika jumlah selang-selingnya habis dibagi 11.

Sehingga 6 - 2 + a -b + 4 - 2 + 7 = 11.

Atau a- b = -2. (ii)

Jadi diperoleh 2 persamaan

a + b = 6, a- b = -2.

Kedua persamaan diselesaikan diperoleh a = 2 dan b = 4.

5. Hal 10 no 359 : Diberikan _{a b b c c a}   

1 , 1 , 1

adalah barisan aritmatika. Tunjukkan bahwa _b2_,a2_,c2_{juga barisan aritmatika.}

Jawab : Karena barisan aritmatika mempunyai beda yang sama maka berlaku

c b a c b a c

b       1 1 1

1

. Diperoleh

Ruas kiri =_b1_{c a}1_{b (}a_b b_c)(ab _bc_{) (b} a_c)(ac _b)

 

 

 

     

 .

Ruas kanan = _{c a b c}   

1 1

= _{c a b c} b_c_c_a_bc_a_c 

 ) ( )

( 1

= _(cb_a_)ba_c. Karena ruas kiri = ruas kanan maka

) )(

(b c a b

c a

 



= _c b_{a b}a _c

 



)

(  (a-c)(c + a) = (b-a)(b+a).

2 2 2

2 _{c b a}

a    .

Bentuk terakhir merupakan selisih antara 2 suku berturutan pada barisan _b2_,a2_,c2 _sama. Jadi _b2_,a2_,c2 _{merupakan barisan aritmatika.}

Tema : Kombinatorik

PRINSIP INKLUSI – EKSKLUSI

card (A) (dari kata cardinal) yang berarti banyaknya anggota A. Teorema :

=================================================================== diketahui 12% menyukai menonton dan membaca, 20% hanya menyukai menonton dan 15% hanya menyukai membaca. Berapa persen anak –anak yang menyukai ketiga aktivitas tersebut ?.

Jawab :

Berdasarkan prinsip Inklusi-Eksklusi untuk 3 himpunan A, B dan C :

) (

) (

) (

) ( )

( )

(

) (

C B card C

A card B

A card C

card B

card A

card

C B A card

 

 

 

 



 

+ card(A B C). (i)

Sebut A := banyaknya anak yang menyukai menonton = 45, B := banyaknya anak yang menyukai olah raga = 48,

C:= banyaknya anak yang menyukai membaca = 35,

Sebut pula card(A B) =x1 , card(A C) = 12 , card(B C) = x2;

) (AB C

card  = 20 ; card(C A B)15; card(A B C) = x .

Perhatikan notasi card(AB C)artinya banyaknya anggota A yang bukan dalam B

maupun C. Ditanyakan x.

Diketahui card(C A B)card(C)card(C (A B)). (ii)

Perhatikan bahwa



C (A B)



= (C A) (C B). Sehingga

card



C (A B)



= card(C A) card(C B).

Dari data diperoleh card



C (A B)



= 12 + x2- x . Gunakan hasil ini pada persamaan (ii) diperoleh yaitu

)) (

( )

( )

(CA B card C card C A B

card     

sehingga 15 = 35-12-x2+ x

atau -8 = - x2 + x. (iii)

Secara sama diperoleh

)) (

( )

( )

(AB C card A card A B C

card     

= card(A)[card(A B)card(AC)card(A BC)]. 20 = 45 – [x1+12-x].

-25+12= -x1+ x . Atau -13 = - x1+ x. (iv) Dari persamaan (ii) dan (iii) diperoleh

-13 = - x1 + (-8 + x2) ,

 -13 + 8 = - x1 + x2 ,

-5 = = - x1 + x2 atau x1 = 5 + x2. (v) Gunakan hasil (iii) – (v) dalam persamaan (i) , diperoleh

90 = 45 + 48 + 35 -x1 -12 -x2+ x.

 90 = 128 – (5 + x2) -12 -x2+ x .

 107 = 128 - 2x2+ x

 -21 = - 2x2+ x . (vi)

Dari persamaan (iii) dan (vi) diperoleh

 -21 = - 2x2+ x . -8 = - x2 + x.

Dengan mengalikan persamaan 2 dengan 2 diperoleh

===================================================================

Latihan soal

No. 423. Perhatikan himpunan bilangan A2,4,6,...,114

1. Berapa banyak anggota pada A ? 2. Berapa banyak yang dapat dibagi 3 ?. 3. Berapa banyak yang dapat dibagi 5 ? 4. Berapa banyak yang dapat dibagi 15 ?

5. Berapa banyak yang dapat dibagi 3, 5 atau keduanya ?. 6. Berapa banyak yang tidak dapat dibagi 3 atau 5 ?

7. Berapa banyak yang dapat dibagi tepat satu dari 3 atau 5 ?.

Jawab : hanya dijelaskan yang perlu yaitu yang dalam notasi himpunan . Dipergunakan notasi :  x := bilangan bulat terbesar yang lebih kecil dari x.

Notasi ini menjelaskan bahwa banyaknya anggota himpunan perlu bulat. (1) Sehingga : card (A) = _

    

2 114

= 57.

Dapat pula dengan cara menganggap anggota A adalah barisan aritmatika dengan beda 2 sehingga U_n U₁ (n1)b yaitu 144 = 2 + (n-1)(2) = 2 + 2n -2. Sehingga n = 57.

(2) Sebut A3 :anggota himpunan A yang dapat dibagi 3 

:

5

A _{anggota himpunan A yang dapat dibagi 5}

card (A3):= banyaknya anggota A yang dapat dibagi 3 maka card (A3):= ₃ 19 57

      

card (A5):= banyaknya anggota A yang dapat dibagi 5 maka card (A5):= ₅ 11 57

     

 _.

Catatan : Jika didaftar bilangan tersebut : A5 10,20,30,...,110. Himpunan tersebut

dapat dipandang sebagai barisan bilangan aritmatika dengan beda 10. Sehingga

b n U

Un  1 ( 1) yaitu 110 = 10 + (n – 1) (10) atau 110 = 10 n sehingga n = 11. card (A15) := banyaknya anggota A yang dapat dibagi 15.

Belum selesai.

No. 429 Suatu perusahaan asuransi mempunyai 10 000 pemegang polis. Setiap pemegang polis digolongkan dalam bentuk :

 muda atau tua

 laki-laki atau perempuan

 menikah atau singgel.

Dari pemegang polis ini, ada 3000 muda, 4600 laki-laki dan 7000 menikah. Pemegang polis digolongkan sebagai 1320 laki-laki muda, 3010 laki-laki menikah, dan 1400 menikah muda. Sedangkan 600 pemegang polis adalah laki-laki muda yang menikah. Berapa banyak pemegang polis yang muda , perempuan dan singgel.

Jawab :

Perkenalkan dulu notasi himpunan A = muda , B = laki-laki, C = Menikah Diketahui :

card(A) = 3000, card (B) = 4600 , card (C) = 7000 , card(A B) = 1320, card(B C)

=3010, card(A C)= 1400, card(A BC) = 600.

Yang ditanyakan dalam notasi himpunan adalah = card(AB C)

Yaitu

) (AB C

card  = card(A) – card(A (BC))

= card(A) -



card(A B)card(AC)



=================================================================== = card(A) card(A B)card(AC)card(A BC)

= … = 880.

Hal ini dapat ditunjukkan pada Gambar berikut.

No.461. Pada penyusunan nomer telepon dengan 7 digunakan digit yaitu 0,1,2,3,4,5,7,8_.

Tidak ada nomer telepon yang diijinkan menggunakan awal 0, 1 atau 5. Tentukan banyaknya nomer telepon yang mungkin dari kriteria berikut

(1). Semua digit boleh diulang

(2) Tidak ada digit yang boleh berulang

(3) Digit boleh diulang, tetapi nomer telepon harus genap (4) Digit dapat diulang, tetapi nomer telepon ganjil

(5) Digit-digit tidak boleh diulang dan nomer telepon harus ganjil. Jawab :

Misalkan posisi nomer telepon digambarkan pada kotak berikut

(1) Ada 8 digit yang mungkin , tetapi pada awal tidak boleh ada 0, 1 atau 5. Sehingga tinggal 5 digit yang boleh mengisi kotak pertama. Sedangkan setiap kotak ada 8 kemungkinan yang digambarkan pada gambar berikut

5 8 8 8 8 8 8

Jadi ada (5)(8)(8)(8)(8)(8)(8) = _5x86_. (2) Diperoleh

5 7 6 5 4 3 2

Susunan yang diperoleh = 5x7!

(3) Digit awal ada 5 macam; sedang digit belakang ada 4 macam . Digit yang lain dapat diulang (8) macam jadi

5 8 8 8 8 8 4

(4) Digit ganjil adalah 1,3,5,7 _{dan angka telepon ganjil adalah digit terakhir ganjil (ada 4}

macam) ; Yang didepan ada 5 macam sehingga diperoleh sama

5 8 8 8 8 8 4

(5) Hal ini dilakukan dengan memisahkan didepan genap dan didepan ganjil. Jika didepan genap maka diperoleh

3 6 5 4 3 2 4

Jika didepan ganjil dan hanya ada 4 macam tetapi 1 dan 5 tidak boleh, maka didepan hanya ada 2 macam digit. Sedangkan jika pada digit terakhir karena harus ganjil dan tidak boleh diulang. Jadi jika sudah digunakan didepan tidak bisa digunakan dibelakang. Jadi kemungkinan digit terakhir hanya ada 3 macam : yaitu digit (1, 3,5,7) – (3) atau (7) (yang dapat digunakan didepan. Artinya jika sudah digunakan didepan tidak boleh digunakan dibelakang.

===================================================================

2 6 5 4 3 2 3

Jadi banyaknya jenis nomer telepon dijumlahkan (ingat bahwa bilangan-bilangan pada kotak adalah banyaknya digit yang mungkin dapat mengisi) :

(6)(5)(4)(3)(2)[(3)(4) + (2)(3)].

No.466. Jelas bahwa ₉n

No.560 (AHSME 1990) Ada berapa banyak cara bilangan dengan 3 digit berbeda dalam urutan naik atau dalam urutan turun ?.

Jawab : Misal posisi 3 digit tersebut dengan garis garis berikut

(a) dengan urutan naik : Untuk menempati kotak pertama dapat diisi oleh 1, 2, 3,…,7 (0 tidak boleh, 9 tidak mungkin karena harus 3 digit yang berbeda, 8 juga tidak bisa karena hanya mungkin 1 digit ( yaitu 9 ) sedangkan kotak ketiga kosong). Setelah kotak pertama ditetapkan maka yang berikutnya dapat ditetapkan demikian pula kotak ketiga sebagaimana ditunjukkan pada Tabel berikut. Jadi ada (7)(7)(7) cara. Contoh :

1 2 3

2 3 4

3 4 5

4 5 6

5 6 7

6 7 8

7 8 9

(b) dengan urutan turun : Kita perlu menetapkan susunan yang dimulai dari kotak pertama . Hal ini ditunjukkan pada Tabel berikut sebagai contoh.

9 8 7

8 7 6

7 6 5

6 5 4

5 4 3

4 3 2

3 2 1

2 1 0

Jadi ada (8)(8)(8) susunan.

No 561. Ada berapa macam cara jika dari 20 orang siswa, ada 5 macam test yang harus diikuti oleh 4 orang siswa ?.

Jawab : Artinya setiap 4 siswa akan mengikuti test sedangkan 16 yang lain paling sedikit 1 macam test.

Banyaknya cara melakukan mengambil 4 orang dari 20 siswa yang harus 5 macam test adalah 

     

4 20

.

=================================================================== Bagian ini dapat ditulis sebagai _

 Oleh karena itu banyaknya susunan yang diinginkan :



No.567. Ada berapa permutasi dari kata CHICHICUILOTE dengan :

(a). Tidak ada syarat apapun ?.

(b). Jika kata dimulai dari suatu huruf I dan berakhir dengan huruf I . © Jika dimulai dengan I dan diakhiri dengan C

(f) Jika kata LOTE harus ada dan urutan demikian

Jawab : Diketahui ada 13 huruf dengan 3C, 2H, 3I , 1U, 1O, 1E. Jelas (a) Ada 13!.

(b). Dijelaskan dengan Tabel berikut, dimana 2 I pada awal dan akhir

I I

Oleh karena itu I yang satu boleh berada dimana saja bersama dengan huruf yang lain pada 11 kolom yang kosong tersebut. Karena ada 3C yang sama, 2H yang sama, maka ada susunan sebanyak :

! Secara sama hal ini ditunjukkan pada Gambar berikut ©.

I C

Sedangkan kotak yang lain diisi oleh yang lain ( termasuk 2 I) yaitu

!

(f). Karena kata LOTE harus ada dalam susunan demikian maka dipandang sebagai 1 posisi dan ada 10 cara memindahnya. Sedang huruf yang lain bebas , sehingga susuan yang diperoleh

Test Tengah 2 Pelatihan Guru-guru Berau

1. Soal no 426 : Dari 40 siswa , 30 orang dapat berenang dan 27 dapat bermain catur dan 5 yang tidak dapt melakukan keduanya. Berapa banyak siswa yang dapat berenang dan main catur ?

2. Soal 463 : Berapa banyak bilangan bulat nonnegatif dengan n digit yang tidak memuat digit 5 ?.

3. Soal no 496 : Bilangan 3 digit dibuat menggunakan digit-digit 1,3,7,8,9_.

(a). Berapa banyak bilangan bilangan tersebut ? (b) Berapa banyak yang genap ?.

©. Berapa banyak yang palindrom ?. (d) Berapa banyak yang dapat dibagi 3 ?.

4. Soal no 514 : Berapa banyak susunan yang dapat dibuat dari kata DRAUGHT dengan huruf hidup tak pernah dipisahkan ?.

===================================================================

Jawab :

1. Soal no 426 : Dari 40 siswa , 30 orang dapat berenang dan 27 dapat bermain catur dan 5 yang tidak dapt melakukan keduanya. Berapa banyak siswa yang dapat berenang dan main catur ?

Jawab : Diketahui 40 orang = card(S)

A := orang yang dapat berenang, card(A) = 30 B:= orang yang dapat bermain catur , card(B) = 27

5 )

(AUB c 

card

Ditanyakan card(A B)…

Dengan aturan himpunan : _{card(S) card(A B) card(A B)}c

 

 

40 = card(A B) + 5 . Sehingga card(A B) = 35.

Menurut Teorema Inklusi Eksklusi :

)

(A B

card  = card(A)card(B)card(A B) = 30 + 27 - card(A B)

35 = 30 + 27 - card(A B). Sehingga card(A B)= 57-35 = 22.

Banyaknya anak yang dapat berenang dan bermain catur adalah 22 orang.

Soal 463 : Berapa banyak bilangan bulat nonnegatif dengan n digit yang tidak memuat digit 5 ?.

Jawab : Untuk n = 1, ada 9 bilangan yaitu : 0,1,2,3,4,6,7,8,9. Untuk n 2: Untuk n =2, banyak bilangan : (8)(9)

n = 3, banyak bilangan := (8)(9)(9) n = 4, banyak bilangan = (8)(9)(9)(9) .

. .

n = k, banyak bilangan =     

1

) 9 )...( 9 )( 9 ( ) 8 (



k .

Yang dapat dipasang paling depan ada 8 digit yaitu : 1,2,3,4,6,7,8,9

Yang dapat dipasang pada urutan 2 dst ada 9 pilihan yaitu : 0,1,2,3,4,6,7,8,9 Sehingga banyak bilangan ₍₈₎₍₉₎n1_.

Soal no 496 : Bilangan 3 digit dibuat menggunakan digit-digit 1,3,7,8,9_.

(a). Berapa banyak bilangan bilangan tersebut ? (b) Berapa banyak yang genap ?.

©. Berapa banyak yang palindrom ?. (d) Berapa banyak yang dapat dibagi 3 ?. Jawab :

(a) Banyak bilangan yang terbentuk :

banyak bilangan digit ratusan ada 5 dan digit puluhan ada 5, digit satuan ada 5.

Sehingga banyak bilangan yang terbentuk ada = 5 x 5 x 5 = 125. (b) Banyak bilangan genap : Bilangan yang digit satuannya genap :

yang dapat dipilih sebagai digit satuan ada 1 yaitu 8 Jadi banyaknya bilangan genap ada : 5 x 5 x 1 = 25. ©. Banyak bilangan palindrom :

angka ratusan dan satuannya : ada 5 pilihan angka puluhan ada 5 pilihan.

Banyaknya bilangan palindrom = 5 x 5 = 25.

===================================================================

(a,b,c) Banyak permutasi (1,1,1) 3!/3!=1 (1,1,7) 3!/2! = 3 (1,3,8) 3!= 6 (1,7,7) 3!/2!=3

(1,8,9) 3!=6

(3,3,3) 3!/3!=1 (3,3,9) 3!/2!=3

(3,7,8) 3!=6

(3,9,9) 3!/2!=1 (7,7,7) 3!/3!=1

(7,8,9) 3!=6

(8,8,8) 3!/3!=1 (9,9,9) 3!/3!=1

Banyak bilangan yang habis dibagi 3 : 1+3+6+3+6+1+3+6+1+1+6+1+1= 41.

4. Soal no 514 : Berapa banyak susunan yang dapat dibuat dari kata DRAUGHT dengan huruf hidup tak pernah dipisahkan ?.

Diketahui kata DRAUGHT : Jika huruf hidup tak dipisahkan AU maka AU dianggap sebagai 1, berarti tempat huruf ada (5 +1) = 6. Huruf sis : DRGHT ada 5 permutasi = 5!. Sedangkan AU bisa dibalik UA sehingga ada 2! cara.

Banyaknya susunannya = 6 x 5!2! = 6x5x4x3x2x1x2 = 1440.

No 5:Soal 530 : Ada berapa cara kita dapat menulis bilangan 10 sebagai jumlahan dari 3 bilangan positif ?.Disini urutan penulisan 1 + 8 + 1 dianggap susunan yang berbeda dengan 8 + 1 +1.

Jawab : Banyknya cara menulis bilangan 10 sebagai jumlahan 3 bilangan positif : a + b + c

(a,b,c) Banyak permutasi

(1,1,8) 3!/2!=3

(1,2,7) 3!=6

(1,3,6) 3!

(1,4,5) 3!=6

(2,2,6) 3!/2!=3

(2,3,5) 3! = 6

(2,4,4) 3!/2!=3

(3,3,4) 3!/2!=3

Jadi banyak bilangan tersebut adalah = 3 + 6 + 6+ 6 + 3 + 6 +3 + 3 = 36. Cara lain : menggunakan Teorema : De Moivre :

=================================================================== Maka banyaknya bilangan 3 digit yang jumlah digitnya 10 adalah

. 36 ! 7 ! 2

! 9 2 9 1 3

1 10

                  

 

POST TEST Pelatihan Gur-Guru Matematika BERAU

1. Diketahui bilangan real positif a, b, dan c sedemikian hingga a_b _cb _ac , Tentukan

nilai _aa _bb _cc  

 

2 3

2 3

.

2. Tentukan nilai dari ... ₉₉ 1 ₁₀₀

6 5

1 4 3

1 3 2

1 2 1

1

        

 =…

3. Tentukan banyaknya bilangan yang terdiri dari paling banyak 3 angka dengan bilangan yang terbentuk tidak mempunyai angka kembar dan diambil dari angka 1,2,3,4,5,6,7,8.

4. Dua buah roda gigi masing-masing berjari-jari 90cm dan 30cm. Kedua roda gigi diketahui bersinggungan dan dikelilingi dengan erat sebuah rantai. Tentukan panjang rantai tersebut!.

.

JAWABAN SOAL POST TEST

No.1 Diketahui bilangan real positif a, b, dan c sedemikian hingga a_b _cb _ac, Tentukan nilai

c b a

c b a

 

 

2 3

2 3

.

Jawab : Diketahui bilangan real positif a, b, dan c sedemikian hingga a_b _cb _ac, Tentukan

nilai _aa _bb _cc  

 

2 3

2 3

no.1 Dengan diketahui _ba _cb _ac.

Dari a_b b_c diperoleh acb2

Dari _ba  _ac diperoleh bca2

Dari b_c  _ac diperoleh _{ab c}2 

Dijumlah ketiga ruas kiri dan kalikan dengan 2 yaitu 2(ac + bc + ab) = 2(_a2 _b2 _c2



 .).

Sehingga

0 2 2 2 2 2

2 2 2 2

    

 b c ab bc ac

a .

Atau  2 ( )2 ( )2 0     

b a c b c

a _.

=================================================================== Substitusikan hasil tersebut pada _aa _bb _cc



Dengan menjumlahkan semuanya diperoleh

100

No.3 Tentukan banyaknya bilangan yang terdiri dari paling banyak 3 angka dengan bilangan yang terbentuk tidak mempunyai angka kembar dan diambil dari angka 1,2,3,4,5,6,7,8. Jawab : hal ini diilustrasikan pada Gambar berikut

Karena bilangan terdiri paling banyak 3 digit, maka bilangan tersebut dapat 1 digit, 2 digit atau 3 digit.

(a). Bilangan dengan 1 digit terdiri dari 8 cara (b) Bilangan yang terdiri dari 2 digit :

(8)(7) = 56 karena ada 8 pilihan untuk angka puluhan dan 7 angka pilihan satuan karena yang sudah dipilih tidak boleh dipilih lagi.

©. Bilangan yang terdiri dari 3 angka :

Jika pada kotak pertama telah diisi maka digit lain diisi dari 7 yang lain. Pilihan pada kotak pertama ada 8 macam. Jadi banyaknya cara ada (8)(7)(6) cara.

Jadi banyaknya bilangan yang dapat disusun = 8 + 56 + 336 = 400.

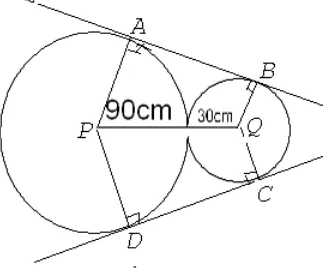
4. Dua buah roda gigi masing-masing berjari-jari 90cm dan 30cm. Kedua roda gigi diketahui bersinggungan dan dikelilingi dengan erat sebuah rantai. Tentukan panjang rantai tersebut!.

Gambar a.

Jawab : Berikut ini diberikan keterangan bukan sebagai materi jawaban terlebih dahulu tetapi menjelaskan kesalahan yang sering muncul pada jawaban peserta.

===================================================================

Gambar b.

Kembali pada soal.

Kita perlu menarik garis singgung yang menyinggung lingkaran besar dan menyinggung lingaran kecil yang segaris. Perlu diketahui pula sembarang garis singgung pada lingkaran pasti tegak lurus dengan jari-jari lingkaran. Hal ini ditunjukkan pada Gambar berikut.

Sebut sudut APQ1 QPD, Sedangkan sudut refleksi APQ+QPD adalah 1

 . dan sudut refleksi BQPPQCadalah BQC 2.

Sebutlah panjang busur yang besar untuk AD diberi simbol bsr(AD), panjang AB = |AB| , panjang busur BC = bsr(BC) dan panjang CD = |CD|.

Yang ditanyakan adalah panjang rantai yang mengelilingi kedua lingkaran. Hal ini berarti perlu ditentukan panjang AB = panjang DC, panjang busur AD dan panjang busur BC.

Untuk itu panjang rantai berarti :

Panjang rantai = bsr(AD) + |AB| + bsr(BC) + |CD|

= bsr(AD) +2 |AB| + bsr(BC) (karena |AB|=|CD|) Proses selanjutnya dilakukan beberapa tahap.

Tahap 1. Cari |AB|

Perhatikan segiempat PABQ : Dari titik Q , kita buat garis yang tegak lurus dan sejajar AB pada AP, memotong pada titik E sebagaimana ditunjukkan pada Gambar berikut.

=================================================================== Perhatikan PEQ: |PE| = 90 cm – 30cm = 60 cm.

|PQ| = (90 + 30)cm = 120 cm. Oleh karena itu |AB| = |EQ| = 1202 602 60 3



 .

Tahap 2. Menghitung panjang busur yang besar AD diperlukan mengetahui besar sudut yang menghadap busur tersebut yaitu 1(karena kita akan menggunakan formula :

panjang busur = kelilinglingkaran

360

busur dihadapan sudut

besar

0 x .

Untuk kita kita perlu menghitung besar sudut 1. Perhatikan segitiga AEQ yang siku-siku di E.

2 1 120

60

cos 1   

PQ EP

 .

Jadi 1= 600 /3. Sehingga ₃₆₀o _{2 360}o ₂₍₆₀o_{) 240}o

1

1     

 .

Panjang busr AD dapat dihitung yaitu bsr(AD) = ₃₆₀240o x2(90cm)120

o

.

Tahap 3. Kita perlu menghitung busur BC sbb:

Secara sama kita perlu mengetahui besar sudut yang menghadap busur tersebut, akan tetapi tidak bisa secara langsung. Kita perlu mengetahui besar sudut 2 yaitu dengan

memperhatikan segiempat PABQ.

) 90 90 60 ( ) 2 (

2  n  o  o o 

= (42) - ₂₄₀o

= ₃₆₀0 ₂₄₀0 ₁₂₀o



 .

Besar sudut 2= 3600 2(1200)120o.

Sehingga bsr(BC) = 2(30 ) 20

360 120



cm x

o o

.

Tahap 4 : Kita peroleh panjang rantai = 120₊₂₍₆₀ 3) + 20 ₌ 140_{+ 120} 3.

LATIHAN SOAL yang telah dikerjakan

Tema : GEOMETRI

Catatan : cocok untuk SMP

No.738 : Buktikan bahwa jumlah sudut luar dari suatu poligon konveks dengan n sisi adalah 

2

Jawab : Untuk mengilustrasikan hal ini ditunjukan terlebih dahulu oleh segitiga ( n = 3). Yang dimaksud sudut-sudut luar poligon adalah1 , ´2, 3.

Perhatikan bahwa 1+´2+ 3= ( a)(b)(c) = 3(abc)3  2 .

=================================================================== 1

 +´2+ 3+…+ n= ( 1)(2)...(n)

= n1...n

Diketahui bahwa jumlah sudut pada n-poligon adalah (n-2)  . Sehingga 1+´2+ 3+…+n= n(n2) = 2 .

===============================================================

CATATAN : USULAN KURIKULUM MATEMATIKA SMA

SMA TAHUN 1 – TAHUN 2

1. ALJABAR

2. CALCULUS : Jenis.- jenis Fungsi . Limit, Derivatif dan Integral dan pemanfaatan 3. TEORI BILANGAN

4. GEOMETRI ( Euclid): Segitiga, lingkaran, segi banyak 5. KOMBINATORIK

6. LOGIKA

7. PERTIDAKSAMAAN : rata-rata aritmatika, rata-rata geometri, rata-rata harmonika , dan berbagi jenis pertidaksamaan

8. STATISTIK DAN PROBABILISTIK

9. PEMODELAN MATEMATIKA : Manfaat kalkulus dalam analisa data, masalah persamaan diferensial untuk kegunaan diferensial dan integral