KATA PENGANTAR
MATLAB adalah sebuah bahasa pemrograman untuk komputasi teknik yang mengintegrasikan komputasi, visualisasi dan pemrograman dalam suatu lingkungan yang mudah digunakan. Permasalahan dan solusinya dapat diekspresikan dalam bentuk notasi-notasi matematis yang sudah dikenal. Dibandingkan dengan bahasa pemrograman lainnya seperti Fortran, Turbo Pascal ataupun Quick Basic, bahasa pemrograman MATLAB ini relatif lebih mudah dipelajari dan diaplikasikan untuk kebutuhan komputasi sederhana, rumit hingga sangat rumit. Para pemula yang pernah mempelajari metode-metode perhitungan numerik pasti akan merasa takjub dengan MATLAB ini, karena metode-metode numerik yang dipelajari dengan susah payah di bangku kuliah ternyata hanya merupakan hal kecil saja karena MATLAB akan dapat menyelesaikannya dengan sangat mudah dan sangat cepat.Buku ini disusun dengan satu tujuan, yakni memudahkan pengguna pemula, khususnya Mahasiswa Teknik Kimia yang sedang mempelajari MATLAB, dapat memahami MATLAB dengan lebih cepat sehingga mampu menyelesaikan permasalahan-permasalahan dalam teknik kimia, baik secara manual (perhitungan satu-satu, seperti layaknya kalkulator) atau secara pemrograman (perhitungan serentak). Bab I akan membahas tentang komponen-komponen dari MATLAB yang penting seperti matrik dan operasi-operasi matematika terhadap matrik. Pada bab II akan dibahas fungsi-fungsi MATLAB yang penting yang dapat dipergunakan untuk menyelesaikan banyak model-model matematika yang berhubungan dengan operasi-operasi teknik kimia. Terakhir, pada bab III akan dibahas contoh-contoh soal beserta jawabannya dan soal-soal untuk menguji tingkat pemahaman tentang penggunaan MATLAB ini.
Penyusun mengucapkan terima kasih kepada semua pihak yang telah membantu penyelesaian buku ini. Akhirnya, penyusun berharap semoga buku ini berguna untuk pengembangan perkuliahan mata kuliah Komputasi Proses atau Matematika Teknik Kimia pada Jurusan Teknik Kimia Politeknik Negeri Ujung Pandang.
Makassar, Oktober 2014 Penyusun
DAFTAR ISI
KATA PENGANTAR
... iii
DAFTAR ISI
...
... iv
Bab 1 MENGENAL MATLAB DAN KOMPONEN-KOMPONENNYA
1.1
Pendahuluan ... 1
1.2
Memulai MATLAB ... 1
1.3
Matrik ... 2
1.4
Ekspresi
1.4.1 Ekspresi Variabel ... 4
1.4.2 Ekspresi Angka ... 5
1.4.3 Ekspresi Operator ... 6
1.4.4 Ekspresi Fungsi ... 12
1.5
Operasi-Operasi Matematis dan Analisis Data
1.5.1 Fungsi-Fungsi Polinom dan Interpolasi ... 14
1.5.2 Permasalahan Harga Nol (fzero) ... 24
1.5.3 Integral Numerik (quad) ... 26
1.5.4 Regresi Polinom dan Linearisasi (bck slash) ... 27
1.5.5 Penyelesaian Sistem Persamaan Linear (back slash) ... 37
1.5.6 Penyelesaian Sistem Persamaan Non-Linear (fsolve) ... 37
1.5.7 Minimasi Fungsi (fminbnd dan fminsearch) ... 39
1.5.8 Persamaan Diferensial Ordiner (ode45 ; ode15i ; ode15s) ... 42
1.6
Latihan Soal-Soal ... 44
Bab 2 MEMBUAT PROGRAM MATLAB
2.1
Pendahuluan ... 50
2.2
Membuat M-File ... 50
2.2
Komponen-Komponen Program Dasar ... 51
2.3
Pemrograman M-File ... 51
2.3.1 Script ... 51
2.3.2 Function ... 52
2.4
Program Control Statements ... 55
2.4.1 Conditional Control ... 55
2.4.2 Loop Control ... 57
2.4.3 Break ... 59
2.5
Referensi Simbol-Simbol ... 60
2.6
Built-in Function ... 60
2.7
Grafik ... 60
2.7.1 Penggambaran dengan plot ... 60
2.7.2 Penggambaran dengan fplot ... 62
2.8
Beberapa Trik Pemrograman
2.8.1 Membuat Gambar Fungsi Polinom ... 64
2.8.2 Permasalahan Harga Nol ... 64
2.8.4 Permasalahan Metode Least Square ... 68
2.9 Latihan Soal-Soal ... 73
Bab 3 KOMPUTASI TEKNIK KIMIA
Pendahuluan
3.1 Pengayakan ... 80
3.2 Sieving ... 82
3.3 Hubungan Cp versus T ... 87
3.4 Hubungan P versus T ... 89
3.5 Proses Filtrasi Pada FTU ... 91
3.6 Continuous Countercurrent Dryer ... 93
3.7 Proses Level ... 95
3.8 Batch Sedimentation ... 96
3.9 Distilasi Sederhana Pada Tekanan Atmosfer ... 98
3.10 Flash Vaporization 1 ... 101
3.11 Flash Vaporization 2 ... 103
3.12 Kecepatan Aliran dalam Pipa ... 106
3.13 Tangki Berpengaduk ... 108
3.14 Reaksi Pembentukan Etil Ester ... 109
3.15 Bubble Point dan Dew Point ... 111
3.16 Plate Distillation ... 112
3.17 Persamaan Keadaan Untuk Real Gas ... 114
1
BAB 1
MENGENAL MATLAB
1.1 Pendahuluan
Pada bab ini Anda akan mempelajari MATLAB dan mencoba menyelesaikan beberapa permasalahan yang mungkin pernah diangkat pada mata kuliah Matematika Teknik atau mata kuliah lainnya dengan menggunakan fungsi-fungsi MATLAB atau fungsi-fungsi dengan algoritma buatan sendiri. Jika Anda menginginkan informasi yang lebih detail berkaitan dengan topik tertentu dan tidak terdapat dalam buku ini, maka Anda dipersilahkan mencari sendiri informasi tersebut pada help menu. Semua yang Anda butuhkan ada disana.
1.2 Memulai MATLAB
MATLAB pada sistem Windows dapat dijalankan melalui beberapa cara, misalnya dengan klik ganda pada ikon MATLAB pada desktop atau melalui start menu. Segera setelah MATLAB dijalankan, maka muncul MATLAB desktop, yang berisikan tools (graphical user interfaces) untuk mengatur file, variabel dan aplikasi-aplikasi. MATLAB desktop terdiri
atas Command Line Window, Command History, Current Directory,
Workspace, Help, dan Profiler. Gambar 1.1 berikut memperlihatkan
Command Line Window yang otomatis tampil ketika Anda menjalankan
MATLAB.
2
Anda dipersilahkan untuk meng-explore sendiri Command Line Windowpada MATLAB desktop ini. Jika Anda mengetikkan kode-kode MATLAB pada
Command Line Window dan setelah itu menekan tombol ENTER, maka
kode-kode tersebut langsung di eksekusi dan nilai-nilai variabel dan konstanta akan
tetap ada dan tersimpan didalam memori, tentu saja selama Anda belum
menghapusnya. Dengan Command Line Window ini, Anda dapat
menggunakan MATLAB selayaknya sebuah kalkulator yang canggih, yang memiliki kemampuan diatas rata-rata kalkulator yang ada.
Sebelum Anda dapat menggunakan MATLAB seperti selayaknya sebuah kalkulator, Anda perlu memahami terlebih dahulu tentang matrik, jenis-jenis ekspresi dan beberapa fungsi khusus yang dapat membantu Anda menyelesaikan permasalahan-permasalahan matematika dan sekaligus membuat suatu analisis / interpretasi data.
1.3
Matrik
Matrik di dalam MATLAB pada dasarnya adalah sekumpulan data yang tersusun dalam baris dan kolom sehingga seakan-akan membentuk bidang segi empat. Dalam hal ini, MATLAB mampu mengidentifikasi apakah suatu matrik merupakan sebuah matrik skalar, matrik kuadrat, vektor baris atau vektor kolom. Matrik skalar adalah matrik yang memiliki elemen matrik yang tersusun dalam 1 baris dan 1 kolom saja atau dengan kata lain hanya memiliki 1 elemen saja. Matrik yang elemen-elemennya tersusun dalam 1 kolom atau 1 baris saja disebut vektor, sehingga sehubungan dengan hal tersebut dikenal 2 jenis vektor, yakni vektor baris dan vektor kolom. Matrik yang elemen-elemennya tersusun sedemikian rupa sehingga memiliki jumlah baris yang sama banyak dengan jumlah kolom disebut matrik kuadrat.
Berikut ini adalah aturan atau cara penulisan yang digunakan dalam pembuatan matrik di dalam MATLAB:
(1) elemen elemen matrik yang terletak dalam 1 baris dipisahkan oleh tanda koma atau spasi
(2) pergantian setiap baris matrik menggunakan tanda semikolon ” ; ”
(3) semua elemen matrik diletakkan didalam tanda kurung sudut ” [ ] ”.
A=[1 3 5 ; 2 2 4]
3
Berikut adalah contoh data matrik dengan penulisan yang benar: A=10 A adalah matrik skalar dengan nilai 10 A=[1 4] dan B=[1;4] A adalah vektor baris dan B vektor kolom
Matrik A berdimensi 2 x 3 (2 baris dan 3 kolom) A=3:12 Vektor A bernilai 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 A=3:4:12 Vektor A bernilai 3 , 7 , 11
A=[3:4:12 4:4:10] Vektor A bernilai 3 , 7 , 11 , 4 , 8 A=[3:4:12 4:4:12] Vektor A bernilai 3 , 7 , 11 , 4 , 8 , 12
A=[3:4:12 ; 2:2:9] Ekspresi salah, dimensi matrik tidak konsisten A=[3:4:12 ; 4:4:12] Matrik A berdimensi 2 x 3 (2 baris dan 3 kolom) A=[3:4:12 ; 4:4:12]' Matrik A berdimensi 3 x 2 (3 baris dan 2 kolom)
Berikut adalah contoh cara mengakses data matrik (matrix indexing)
dengan penulisan yang benar:
Jika matrik A=[1 2 3 4 ; 5 6 7 8 ; 9 10 11 12], maka
A(1 : 3) adalah vektor baris [1 5 9], sedangkan A(1 : 5) adalah [1 5 9 2 6]
A(1 , 3) adalah elemen matrik A pada baris ke- 1 dan pada kolom ke- 3, yaitu 3
A(1 , 2 : 3) adalah sebuah vektor baris [2 3], yang mana merupakan elemen matrik A pada baris ke - 1 dan pada kolom ke- 2 dan ke- 3.
A(: , 2 : 4) adalah elemen-elemen matrik A pada semua baris dan kolom ke- 2, 3 dan 4. Ekspresi yang agak identik adalah A(: , 1)=[ ]. Mengapa disebut agak identik??
A([1 3] , 2 : 4) adalah elemen matrik A pada baris ke- 1 dan ke- 3 dan pada kolom ke- 2, 3, dan 4
A(2 : 3 , :).^2 adalah kuadrat setiap elemen matrik A pada baris ke- 2 dan 3
4
sum(A) adalah jumlah elemen matrik A pada setiap kolom, jadi [15 18 21 24] sum(sum(A)) adalah jumlah semua elemen matrik A, jadi [78] sum(sum(A).^2) menghasilkan [1566]. Mengapa??
Jika diketahui A=1 : 5, B=6 : 10, C=11 : 15, dan D=16 : 20, maka E=[A; B; C; D] adalah operasi untuk membuat matrik baru E dengan
baris ke-1 berisi vektor A, baris ke- 2 berisi vektor B, baris ke- 3 berisi vektor C dan baris ke- 4 berisi vektor D.
Sebaliknya F=[A' B' C' D'] adalah operasi untuk membuat matrik dengan kolom-kolom berisi A, B, C, dan D.
Untuk menghapus misalnya seluruh elemen pada baris ke- 2 dari matrik E, maka digunakan E(2 , :)=[ ].
Untuk menghapus misalnya seluruh elemen matrik F pada kolom 2 dan 4 , maka digunakan F(: , [2 4])=[ ]
1.4 Ekspresi
Seperti pada kebanyakan bahasa-bahasa pemrograman komputer pada umumnya, MATLAB juga menyediakan ekspresi-ekspresi matematis, diantaranya adalah ekspresi variabel, ekspresi angka, ekspresi operator dan ekspresi fungsi. Ekspresi-ekspresi pada MATLAB tersebut dapat dikatakan selangkah lebih maju dibandingkan dengan ekspresi-ekspresi pada bahasa pemrograman komputer yang lain, karena semua ekspresi MATLAB berbasis pada data matrik seperti akan Anda lihat pada pembahasan-pembahasan lebih lanjut.
1.4.1 Ekspresi Variabel
MATLAB tidak mensyaratkan variabel harus dideklarasikan atau diberi dimensi terlebih dahulu. Saat MATLAB mengeksekusi ekspresi-ekspresi yang Anda tuliskan dan menemukan suatu variabel baru, maka MATLAB secara otomatis akan membuat variabel baru tersebut dan menempatkannya pada memori internal MATLAB. Jika variabel sudah ada sebelumnya didalam memori, maka MATLAB hanya akan mengganti nilainya saja.
5
Nama variabel dimulai dari sebuah huruf tertentu, kemudian dapat diikutidengan sejumlah angka, huruf atau underscores ( _ ) atau gabungannya. Pada
prinsipnya, MATLAB dapat menerima 63 karakter sebagai nama dari variabel, dan
selain itu MATLAB juga membedakan antara huruf besar dan huruf kecil. Berikut adalah contoh nama variabel yang benar : a; A, a1, A2; WperD ; d_media_filter ; rho ; TebalCakeRataRata; fungsi_di_trial
1.4.2
Ekspresi
Angka
MATLAB mengekspresikan suatu angka dengan menggunakan notasi desimal dengan tambahan tanda titik desimal dan tanda plus atau minus. Pada notasi scientific digunakan simbol huruf e untuk menunjukkan perkalian dengan
10
pangkat.
Contoh : 1.2345e+002 1,2345 x 102
123,45
Angka merupakan tipe data numerik yang meliputi integer (bilangan bulat), single- dan double-precision floating-point numbers
(bilangan-bilangan nyata). Nilai maksimum dan minimum dari bilangan nyata dapat diperoleh melalui fungsi realmin dan realmax. Pada
default setting, semua angka disimpan pada memori internal MATLAB sebagai double-precision floating-point dan ditampilkan dengan 5 digit ( format short ), tetapi sesuai kebutuhan, angka juga dapat diubah penampilannya menjadi 15 digit ( format long ), eksponensial ( format short e atau format long e ), pecahan ( format rational ), dan heksa desimal ( format hex ). Anda dipersilahkan untuk mencoba satu-persatu
format-format di atas pada MATLAB desktop Command Line Window.
Bilangan kompleks merupakan tipe data numerik yang terdiri dari
2 bagian terpisah, yaitu bagian bilangan nyata dan bagian bilangan imaginer. Bagian bilangan imaginer dinyatakan dengan menggunakan tambahan huruf i atau j ( contoh bilangan kompleks : 1-2i ).
MATLAB juga menggunakan nilai-nilai khusus yang menyatakan – Inf , Inf ( infinity, tak terhingga, contoh: log(0), exp(10000) atau 1/0 ) dan NaN ( non a number, bukan angka, untuk menyatakan suatu bilangan nyata maupun bilangan kompleks, contoh: 2i/0, 0/0, Inf/Inf )
6
1.4.3 Ekspresi Operator
Operator-operator pada MATLAB terbagi dalam tiga kategori, yaitu operator aritmatika, operator relasional, dan operator logika.
Operator Aritmatika
Selain operator-operator dasar seperti penjumlahan (+),
pengurangan (–), perkalian (*), pembagian ( / ), dan perpangkatan ( ^ ), MATLAB juga menggunakan operator khusus, yakni perkalian antar elemen dari 2 matrik ( .* ), pembagian antar elemen dari 2 matrik ( ./ ) dan perpangkatan untuk elemen- elemen matrik ( .^ ) serta transpose ( ' ) dan kolon ( : ).
Berikut adalah penjelasan operator-operator tersebut dengan menggunakan contoh vektor A=[1 2 3] dan B=[2 3 4]
(1) Operasi A' dan A.' adalah transpose dari A menghasilkan vektor [1; 2; 3]
>> A=[1 2 3], A', A.' 1 2 3 ans = 1 2 3 ans = 1 2 3
7
(2) Operasi A+B atau A-B adalah penjumlahan atau pengurangan antara matrikA dan matrik B. Operasi matrik ini berhasil jika matrik A dan matrik B
memiliki ukuran yang sama atau salah satunya merupakan matrik skalar. >> A+B , A-B ans = 3 5 7 ans = -1 -1 -1
(3) Operasi A*B adalah perkalian antara matrik A dan B. Operasi berhasil jika jumlah kolom matrik A sama dengan jumlah baris matrik B, atau salah satunya merupakan skalar.
>> A*B
??? Error using ==> mtimes
Inner matrix dimensions must agree. >> A'*B , A*B' , 3*A
ans = 2 3 4 4 6 8 6 9 12 ans = 20 ans = 3 6 9
8
(4) Operasi A.*B adalah perkalian antar elemen matrik A dan B. Operasiberhasil jika A dan B berukuran sama atau salah satunya merupakan matrik skalar. >> A.*B , B.*A ans = 2 6 12 ans = 2 6 12
(5) Operasi A/B, baca A slash B Lihat referensi fungsi MATLAB : mrdivide. (6) Operasi A./B adalah pembagian antar elemen-elemen matrik dengan hasil A(i,j)/B(i,j). Operasi ini berhasil jika matrik A dan B memiliki dimensi sama atau salah satunya merupakan matrik skalar.
>> A/B , A./B ans = 0.6897 ans = 0.5000 0.6667 0.7500 Contoh-contoh lain : A/2 [0.5000 1.0000 1.5000] A./2 [0.5000 1.0000 1.5000]
2/A error, karena dimensi matrik tidak sesuai 2./A [2.0000 1.0000 0.6667]
9
(7) Operasi A\B, baca A backslash B. Lihat referensi fungsi : mldivide.Operasi backslash ( \ ) ini digunakan pada penyelesaian persamaan linear dan analisis regresi. Lihat sub bab 1.4.4 dan 1.4.5
(8) Operasi A^B : Lihat referensi fungsi : mpower. Jika salah satu matrik skalar, maka matrik lainnya harus matrik kuadrat.
>> A^B
??? Error using ==> mpower
At least one operand must be scalar. >> A^3
??? Error using ==> mpower Matrix must be square. >> 3^A
??? Error using ==> mpower Matrix must be square.
(9) Operasi A.^B menghasilkan matrik dengan elemen A(i,j) pangkat B(i,j).
Operasi ini berhasil jika A dan B memiliki dimensi yang sama atau salah satunya merupakan matrik skalar.
>> A.^B , B.^A ans =
1 8 81
ans =
10
Operator RelasionalOperator relasional membandingkan operand secara kuantitatif, dan meliputi lebih kecil dari ( < ), lebih kecil dari atau sama dengan ( <= ), lebih besar dari ( > ), lebih besar dari atau sama dengan ( >= ), sama dengan ( = = ), dan tidak sama dengan ( ~= ). Operator-operator relasional ini menghasilkan data logika berupa 1 untuk true dan 0 untuk
false. >> A=5, B=A*ones(3 , 3) A = 5 B = 5 5 5 5 5 5 5 5 5 >> X=A>=[1 2 3 ; 4 5 6 ; 7 8 10] , Y=B>=[1 2 3 ; 4 5 6 ; 7 8 10] X = 1 1 1 1 1 0 0 0 0 Y = 1 1 1 1 1 0 0 0 0
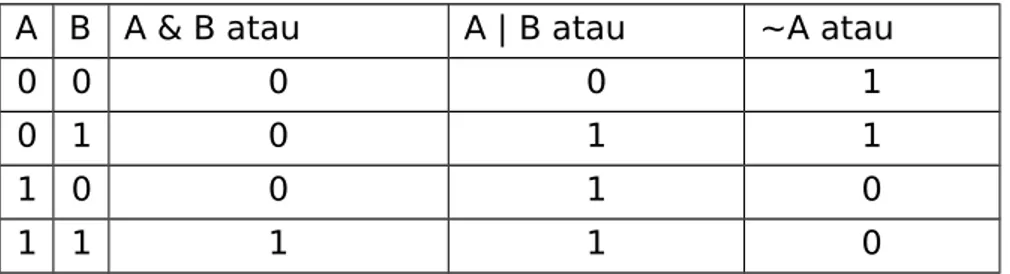
A B A & B atau and(A,B) A | B atau or(A,B) ~A atau not(A) 0 0 0 0 1 0 1 0 1 1 1 0 0 1 0 1 1 1 1 0
11
>> X==Y, X<=Y , X>=Yans = 1 1 1 1 1 1 1 1 1 ans = 1 1 1 1 1 1 1 1 1 ans = 1 1 1 1 1 1 1 1 1 Operator Logika
Tipe data logika merepresentasikan logika benar atau salah menggunakan angka 1 untuk benar dan 0 untuk salah. Operator logika menggunakan AND, OR, NOT atau dengan menggunakan simbol ” & ”, ” | ” , dan
” ~ ”.
Berikut adalah tabel logika yang dapat membantu Anda memahami operator-operator logika ini.
12
Contoh 1: Jika A=5; B=A*ones(3,3), maka ekspresi logikaX=A&B atau
X=and(A,B) akan menghasilkan matrik [1 1 1; 1 1 1; 1 1 1]. Buktikan!! Contoh 2: Ekspresi 3>6 menghasilkan 0 sedangkan ekspresi (5*10)>40 menghasilkan 1 dan ekspresi [30 40 50]>40 menghasilkan [0 0 1].
Contoh 3: Jika a=5; dan b=[4 5 6], maka ekspresi
or(a>=b,a>b) akan menghasilkan [1 1 0] sedangkan and(a>=b,a>b) menghasilkan [1 0 0]
1.4.4 Ekspresi Fungsi
MATLAB menyediakan fungsi standar dalam jumlah yang banyak sekali, seperti fungsi-fungsi matematika dasar (abs, sqrt, exp, sin , dan lain lain) dan matematika tinggi. Daftar fungsi-fungsi MATLAB ini dapat Anda lihat pada MATLAB online help, yakni di MATLAB-Functions-Alphabetical List
Fungsi-fungsi seperti sqrt dan abs merupakan built-in function dari MATLAB dengan kode-kode komputasi yang tidak dapat dilihat. Fungsi-fungsi lain yang bukan merupakan built-in function dapat dilihat kode-kode komputasinya dan dimodifikasi.
MATLAB juga menyediakan beberapa fungsi khusus yang menghasilkan konstanta-konstanta penting seperti pi untuk 3.14159265..., i atau j untuk unit bilangan imaginer, eps untuk ketelitian relatif yang setara dengan 2-52, namelengthmax untuk panjang maksimum nama
variabel, realmin dan realmax untuk angka floating-point
terkecil/terbesar, Inf untuk ketakterhinggaan dan NaN untuk bukan sebuah angka.
Nama-nama fungsi boleh diubah dan isinya diganti dengan nilai variabel baru, misalnya eps=1.e-6 dan pi=3.14
Fungsi-fungsi MATLAB selain built in function merupakan kelompok M-file function dan salah satunya adalah anonymous function. Konstruksi M-file function secara umum akan dijelaskan pada bab 2 , sedangkan konstruksi anonymous function secara umum mengikuti cara penulisan berikut :
13
Nama_Fungsi adalah suatu variabel yang melambangkan variabel bebasdari suatu persamaan tertentu. Adapun Daftar_Argumen adalah daftar semua variabel tidak bebas dari persamaan tersebut. Nama_Fungsi dan argumen juga merupakan suatu variabel sehingga mengikuti aturan penamaan untuk variabel.
y
1
2
Contoh 1: Untuk menghitung nilaifungsi
x
3
4
pada x = [1 2 3], maka>> y=@(x) 1 + 2./(x.^3+4); x1=[1 : 3]'; y1=y(x1); [x1 y1]
ans = 1.0000 1.400 0 2.0000 1.166 7 3.0000 1.064 5
Contoh 2: Jika r adalah fungsi dari x , y dan z,
misalnya
r
3x
2
2 y
3
3z
4 ,maka nilai r untuk x=1 ,y=2 dan z=3 didapat dengan kode-kode berikut: >> r=@(x,y,z) 3*x.^2+2*y.^3-2*z.^4; r(1,2,3)
ans = -143
MATLAB juga memiliki fungsi yang tidak membutuhkan masukan argumen. Perhatikan contoh pendefinisiannya berikut :
>> t=@( ) datestr(now) t = @( ) datestr(now) >> t( ) ans = 04-Oct-2014 04:51:39
Beberapa fungsi anonymous juga dapat didefinisikan sekaligus seperti:
A = {@(x) 3*x.^2, @(y) 2*y.^3, @(x,y) 3*x.^2+2*y.^3}
Ekspresi A{1}(2) adalah cara menjalankan fungsi pertama untuk x=2, sehingga operasi seperti A{1}(2)+A{2}(3) pada prinsipnya identis dengan A{3}(2,3)
Untuk memudahkan dalam membaca fungsi, terutama fungsi-fungsi yang panjang dan rumit, maka perlu melakukan trik penulisan seperti contoh berikut:
A1=@(x) 3*x.^2; A2=@(y) 2*y.^3; A3=@(x,y) 3*x.^2+2*y.^3; A={A1,A2,A3}
1.5 Operasi-Operasi Matematis dan Analisis
Data
Pada sub bab ini, Anda akan melihat MATLAB dapat dipergunakan seperti layaknya sebuah kalkulator dengan fasilitas yang efisien. Bersama dengan contoh-contoh yang sudah dibahas pada sub-sub bab sebelumnya, topik-topik bahasan pada sub-sub-bab ini juga akan memberikan pengetahuan pada Anda, bahwa MATLAB memang lebih baik dibandingkan dengan kalkulator biasa.
1.5.1 Fungsi-Fungsi Polinom dan Interpolasi
Anda dipersilahkan meng-explore sendiri fungsi built in untuk operasi- operasi standar terhadap polinom pada MATLAB online help di MATLAB- Mathematic-Polynomials and Interpolation.
Secara umum, sebuah fungsi polinom diwakili oleh vektor koefisien dari persamaan fungsinya. Sebagai contoh, misalnya diketahui sebuah fungsi polinom 3x5 – 2x2 + x -5 , maka untuk memasukkan fungsi ini ke dalam MATLAB digunakan ekspresi sebagai berikut:
>> p=[ 3 0 0 -2 1 -5 ] p =
Ingat : Vektor koefisien dari persamaan fungsi polinom dimulai dari
pangkat tertinggi hingga ke konstanta, bukan sebaliknya.
polyval(p,x)
Ekspresi polyval(p,x) akan menghasilkan nilai fungsi polinom yang diwakili oleh vektor koefisien p pada nilai x tertentu. Dalam hal ini nilai x bisa skalar (satu nilai saja) atau merupakan suatu vektor dengan beberapa elemen.
Contoh : Evaluasi nilai polinom x3 – 3 x2 – 13 x + 15 pada x=1, 2, 3, 4, dan 5 >> p=[1 -3 -13 15], r=polyval(p,[1 2 3 4 5]) p = 1 -3 -13 15 r = 0 -15 -24 -21 0
Ekspresi yang identik dengan ekspresi diatas adalah seperti berikut: >> p=[1 -3 -13 15]; x=[1:5]; r=polyval(p,x)
Dengan menggunakan fungsi MATLAB polyval ini, maka kita juga bisa mendefinisikan fungsi polinom dalam bentuk fungsi anonymous, sehingga contoh diatas juga dapat diselesaikan dengan cara sebagai berikut: >> p=[1 -3 -13 15]; y=@(x) polyval(p,x); x=[1:5]; r=y(x)
roots(p) dan poly(r)
Ekspresi r=roots(p) akan menghasilkan vektor sebagai titik-titik potong terhadap sumbu x dari fungsi polinom, yang mana berarti juga harga nol dari fungsi polinom tersebut, termasuk juga yang imajiner. Dalam hal ini p adalah vektor koefisien dari fungsi polinom yang dievaluasi.
Ekspresi q=poly(r) akan menghasilkan vektor koefisien fungsi polinom
berdasarkan masukan vektor r sebagai harga nol fungsi polinom yang dicari.
Contoh : Dari polinom p dengan persamaan x3 – 3 x2 – 13 x + 15 tentukanlah vektor r sebagai titik-titik potong terhadap sumbu x, kemudan buktikan dari vektor r tersebut dapat dihasilkan kembali vektor koefisien polinom p. >> p=[ 1 -3 -13 15 ], r=roots(p), q=poly(r) p = 1 -3 -13 15 r = 5.0000 -3.0000 1.0000 q = 1.0000 -3.0000 -13.0000 15.0000
Ekspresi r=roots(p) diatas menghasilkan vektor r=[5 ; -3 ; 0] sebagai harga nol dari polinom ( titik-titik potong terhadap sumbu x ). Sebaliknya, operasi berikutnya dengan q=poly(r) menghasilkan vektor koefisien fungsi polinom dengan urutan mulai dari pangkat tertinggi hingga konstanta.
Dari contoh ini terlihat bahwa fungsi-fungsi MATLAB roots dan poly merupakan sepasang fungsi yang sifatnya saling berkebalikan.
Polyder(p) dan polyint(p) atau polyint(p,k)
Ekspresi polyder(p) akan menghasilkan vektor koefisien polinom hasil diferensiasi fungsi polinom dengan koefisien p sedangkan ekspresi polyint(p) dan polyint(p,k) akan menghasilkan vektor koefisien polinom hasil integrasi tidak tentu dari fungsi polinom p. Dalam hal ini k adalah konstanta integrasi yang ditetapkan sepihak, artinya jika diinginkan hasil integrasi yang memiliki kontanta integrasi, maka nilai k harus ditetapkan.
Contoh 1: Diferensialkan polinom x2 - 2 x – 15 dan kemudian integralkan hasilnya.
>> p=[1 -2 -15]; d=polyder(p), q=polyint(d), qk=polyint(d,-15) d = 2 -2 q = 1 -2 0 qk = 1 -2 -15
Terlihat bahwa ekspresi polyint(d) menghasilkan vektor [1 -2 0], yang mana merupakan integral dari fungsi polinom d = 2x - 2 , dan konstanta integrasi ditetapkan sepihak sama dengan nol. Untuk mendapatkan kembali fungsi polinom p = x2 – 2x – 15, maka digunakan
polyint([2 -2],-15).
Untuk hitung integral tentu terhadap fungsi polinom, maka dapat dimanfaatkan secara bersama-sama fungsi MATLAB polyint dan polyval seperti contoh 2 berikut:
Contoh 2 : Integralkan polinom p = x2 – 2x – 15 dengan batas integrasi
atas dan bawah berturut-turut adalah 3 dan 0. >> p=[1 -2 -15]; q=polyint(p); Q=polyval(q,3)-polyval(q,0) Q =
-45
conv dan deconv
Ekspresi ab=conv(a,b) menghasilkan vektor hasil perkalian antara vektor koefisien polinom a dan b. Misal a = x + 5 ; b = x2 + 3 dan c = x - 1,
maka perkalian
>> a=[1 5]; b=[1 0 3]; c=[1 -1]; ab=conv(a,b), abc=conv(ab,c) ab =
1 5 3 15
abc =
1 4 -2 12 -15
Sebaliknya, jika polinom ab dibagi dengan b, maka operasi dalam
MATLAB-nya adalah sebagai berikut: >> [h s]=deconv(ab,b)
h = 1 5
s =
0 0 0 0
Dalam hal ini h adalah vektor koefisien polinom hasil pembagian dan s adalah vektor koefisien polinom sisa pembagian.
residue
Untuk menyederhanakan suatu pecahan polinom menjadi
pecahan-r pecahan-r pecahan-r
pecahan parsialnya dalam bentuk :
a ( x )
1
2
n
k (
x)
,b( x)
x
p1 x
p2
x
pn
maka digunakan fungsi MATLAB berikut: [r p k]=residue(a,b)
Contoh 1: Untuk mendapatkan pecahan-pecahan parsial dari polinom
2x
3
3x
2
32x
15
x
2
2x
15
>> a=[2 3 -32 15]; b=[1 2 -15]; [r p k]= residue(a,b) r = 0 0 p = -5 3 k = 2 -1
Hasil operasi ini memberi arti, bahwa pecahan polinom diatas dapat
disederhanakan menjadi pecahan-pecahan parsial dalam bentuk :
0
0
2x
1
2x
1
x
5 x
3
2x
3
3x
2
32x
20
Contoh 2: Sederhanakan pecahanberikut
x
2
2x
15
, maka >> a=[2 3 -32 20]; b=[1 2 -15]; [r p k]= residue(a,b) r = -0.6250 0.6250 p = -5 3 k = 2 -12x
3
3x
2
32x
20
0.6250 0.6250
Jadi :x
2
2x
15
x
5
x
3
2x
1
polyfit(x,y,n)
Jika vektor data x berpasangan dengan vektor data y dan dicari fungsi polinom yang memiliki kesalahan kuadrat terkecil ( SSE, sum of the squared errors, least square method ) terhadap semua data (x,y), maka hubungan fungsional y = f(x) sebagai suatu fungsi polinom orde ke- n tercakup melalui penggunaan fungsi MATLAB p=polyfit(x,y,n). Dalam hal ini, p adalah vektor koefisien dari persamaan fungsi polinom yang dicari. (baca keterangan lebih lanjut pada MATLAB online help).
Contoh 1 : Dari data x dan y berikut, nyatakan hubungan fungsional antara keduanya sebagai fungsi polinom order ke- 3 kemudian tentukan prediksi nilai y berdasarkan fungsi polinom tersebut untuk nilai x=[1 2 3 4 5]. Hitung pula nilai error kuadrat ( SSE) -nya.
x 1 2 3 7 8 10 y 9 11 11.3 12.5 13.1 22 >> x=[1 2 3 7 8 10]; y=[9 11 11.3 12.5 13.1 22]; p3=polyfit(x,y,3), polyval(p3,[1:5]) p3 = 0.0726 -0.9925 4.2963 5.6345 ans = 9.0108 10.8374 11.5496 11.5829 11.3727 >> SSE=sum((y-polyval(p3,x)).^2) SSE = 0.6715
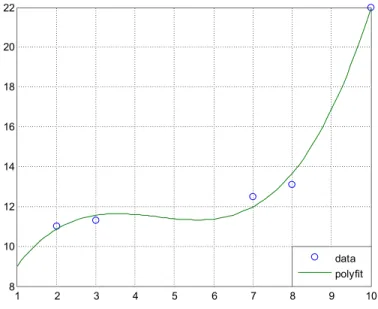
Untuk memperlihatkan kinerja fungsi polyfit ini, maka fungsi polinom p3 dapat dievaluasi nilai fungsinya y1 pada setiap nilai x1=[1:0.1:10] sebagai berikut :
data polyfit >> legend(4,'data','polyfit') 22 20 18 16 14 12 10 8 1 2 3 4 5 6 7 8 9 10
Gambar 1.2 : Interpretrasi data x dan y sebagai fungsi polinom
Gambar 1.2 yang dihasilkan memperlihatkan bahwa polyfit menghasilkan fungsi polinom dengan kurva fungsi yang tidak selalu melewati titik-titik data (x,y). Anda bisa membandingkannya nanti dengan fungsi MATLAB lainnya, misalnya interp1
Catatan : Anda hanya boleh mencocokkan 6 pasang data (x,y) diatas sebagai fungsi polinom order ke- 1 sampai dengan order ke- 5 saja.
Contoh 2 : Data x dan y berikut dicocokkan untuk memiliki hubungan fungsional sebagai fungsi polinom y = ax3 + b. Tentukan nilai a dan b terbaik dan perkiraan
data y untuk x=[2.5 3.5] x 1 2 3 4 5 6 y 5 26 83 194 377 650 >> x=1:6; y=[5 26 83 194 377 650]; r=[2.5 3.5]; >> ab=polyfit(x.^3,y,1), ab(1)*r.^3+ab(2) ab = 3.0000 2.0000
ans =
48.8750 130.6250
Pada contoh 2 terlihat modifikasi penggunaan polyfit(x,y,n), yang mana argumen x disubstitusikan dengan x.^3, sehingga pada akhirnya terbentuk persamaan fungsi polinom order 1. Perlakuan yang sama bisa juga diterapkan untuk argumen y.
interp1
Interpolasi adalah perkiraan nilai titik data yang terletak diantara titik-titik data yang sudah diketahui berdasarkan suatu asumsi bahwa semua titik-titik data tersebut dilewati oleh suatu kurva fungsi tertentu. Sedangkan ekstrapolasi adalah perkiraan nilai-nilai titik data diluar range dari titik data yang diketahui. Terdapat beberapa pilihan syntax interpolasi/ekstrapolasi, diantaranya adalah :
yi = interp1(x,y,xi)
yi = interp1(x,y,xi,'method')
yi = interp1(x,y,xi,'method','extrap')
Metode interpolasi diantaranya adalah 'linear', 'spline' dan 'cubic'.
Contoh 1 : Berdasarkan data x dan y pada tabel dibawah ini, tentukanlah nilai perkiraan data y pada x=[2.5 3.5] menggunakan a) polyfit dan b) menggunakan interpolasi linear dan spline.
x 1 2 3 4 5 6 y 5 26 83 194 377 650 >> x=1:6; y=[5 26 83 194 377 650]; r=[2.5 3.5]; >> p5=polyfit(x,y,5); polyval(p5,r) ans = 48.8750 130.6250 >> interp1(x,y,r), interp1(x,y,r,’spline’) ans = 54.5000 138.5000
data linear spline polyfit ans = 48.8750 130.6250
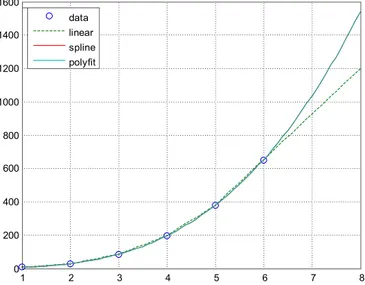
Contoh 2 : Evaluasi lebih lanjut Contoh 1 dengan membuat visualisasi data x dan y dan kurva nilai-nilai perkiraannya menggunakan polyfit dan interpolasi/ekstrapolasi pada xi=[1:0.1:8].
>> x=1:6; y=[5 26 83 194 377 650]; xi=[1:0.1:8]; >> p5=polyfit(x,y,5); fp5=@(x) polyval(p5,x); >> y1=interp1(x,y,xi,'linear','extrap '); >> y2=interp1(x,y,xi,'spline','extrap '); >> plot(x,y,'o',xi,y1,'--',,xi,y2,xi,fp5(x i)); >> grid on, legend(2,'data','linear','spline','polyfit') 1600 1400 1200 1000 800 600 400 200 0 1 2 3 4 5 6 7 8
Gambar 1.3 : Interpretasi data menggunakan interp1 versus polyfit
spline berhimpit dengan kurva polyfit, yang mana menunjukkan tingkat ketelitian perhitungan yang hampir sama. Anda dapat membuktikannya dengan ekspresi [y2' fp5(xi)']
1.5.2 Permasalahan Harga Nol ( fzero )
Permasalahan harga nol secara singkat dapat dijelaskan sebagai berikut: Pada suatu fungsi tertentu, misalnya y=f(x), ingin dicari nilai x sedemikian rupa
sehingga nilai y sama dengan 0. Nilai x yang dicari ini selanjutnya disebut harga nol.
Untuk menemukan satu harga nol suatu fungsi yang memiliki 1 variabel saja, MATLAB menyediakan fungsi fzero dengan syntax berikut:
x0 = fzero(fun, x)
Argumen fun adalah nama fungsi (anonymous atau M-file lainnya),
sedangkan x adalah nilai awal yang dianggap cukup dekat dengan harga nol yang dicari. Contoh 1: Selesaikan persamaan
x
3
x
1
0
>> y=@(x) x.^3-x-1; x0=fzero(y,2) x0 = 1.3247Contoh 2: Selesaikan persamaan : x=cos(x)
Untuk menemukan satu nilai dari x yang cocok dan sesuai dengan persamaan x=cos(x), maka mula-mula didefinisikan dahulu fungsi y dengan y=@(x) x-cos(x); atau y=@(x) cos(x)-x; Selanjutnya operasi x=fzero(y,1) akan menghasilkan x=
0.7391 sebagai nilai yang dicari.
Contoh 3: Ekspresi berikut menyelesaikan persamaan : ini >> y=@(x) 1./x-3./(x.^2-1)+x.^3./(x.^2+4)-0.5; x0=fzero(y,4) x0 = 2
1
3
x x
2
1
x
3x
2
4
Contoh 4: Untuk menemukan nilai x yang cocok dengan persamaan
3(2x 3)(x 5) 7 , maka ekspresi MATLAB yang benar adalah: >> y=@(x) 7-3*(2*x-3).*(x-5); a=fzero(y,1), b= fzero(y,6) a = 1.1935 b = 5.3065 Contoh 5: Diketahui
y
memiliki nilai tepat 4?
f ( x)
x
x
3
3
tersebutln( x)
. Pada nilai x berapa fungsi>> y=@(x) x./(x.^3+3)+log(x)-4; fzero(y,50) ans =
54.5798
Contoh 6: Diketahui koefisien polinom p=[1 2 3 4] . Berapa nilai x yang cocok supaya fungsi polinom tersebut memiliki nilai 6?
>> p=[1 2 3 4]; y=@(x) polyval(p,x)-6; x=fzero(y,1) x =
0.4780
Untuk mendapatkan nilai perkiraan nilai 50 pada contoh 5, sebenarnya telah dilakukan beberapa kali eksekusi fungsi fzero. Jika fzero memberikan hasil yang tidak diharapkan, MATLAB menyarankan untuk mengecek fungsinya apakah ada yang salah, lalu mencoba lagi dengan nilai perkiraan yang baru.
Untuk mendapatkan nilai perkiraan awal x yang paling dekat dengan akar persamaan fungsi yang dicari, dianjurkan membuat kurva fungsi tersebut
terlebih dahulu, misalnya dengan menggunakan fplot(y,[0 60]). Terlihat pada
kurva, bahwa titik potong terhadap sumbu x terletak diantara 50 dan 60. Berdasarkan kurva tersebut, maka ditetapkan nilai awal yang cukup dekat dengan harga nol yang dicari, misalnya 50.
Dari contoh-contoh yang ada, terlihat fungsi fzero hanya menghasilkan
1 harga nol saja. Harga nol lainnya (jika ada) dicari dengan menggunakan nilai awal yang lain.
1.5.3 Integral Numerik (
quad )
Untuk menyelesaikan perhitungan integral tentu seperti
b
q
f ( x) dx
a
dapat memanfaatkan fungsi MATLAB berikut: q=quad(f,a,b) dengan f adalah
nama fungsi ( bisa fungsi anonymous atau M-file lainnya ), dan a adalah batas
bawah integrasi serta b adalah batas atas integrasi.
Contoh 1: Ekspresi berikut untuk menyelesaikan hitung integral tentu : 2
q
x
2
3
dx
1 >> f=@(x) x.^2+3; q=quad(f,1,2) q = 5.3333Karena f adalah fungsi polinom order ke- 2, maka operasi diatas juga dapat diselesaikan dan diperbandingkan dengan fungsi MATLAB polinom berikut:
>> q=polyint([1 0 3]); hasil=polyval(q,2)-polyval(q,1) hasil =
Contoh 2: Tentukan nilai a
supaya
a
x
2
3
dx
1
1>> f=@(x) x.^2+3; g=@(a) quad(f,1,a)-1; fzero(g,2) ans =
1.2351
Karena f adalah fungsi polinom order ke- 2, maka
operasi berikut dapat
diperbandingkan. >> q=polyint([1 0 3]);y=@(a)polyval(q,a)-polyval(q,1)-1; fzero(y,2) ans = 1.2351 Atau dengan :
>> f=@(x) polyval([1 0 3],x); f1=@(a) quad(f,1,a)-1; fzero(f1,2) ans =
1.2351
1.5.4 Regresi Polinom dan Linearisasi
Regresi polinom adalah pencocokan secara least square
hubungan fungsional pasangan data x dan y sebagai fungsi polinom. Dalam hal ini order polinom dibatasi sebanyak jumlah pasangan data dikurangi satu. Jadi, jika terdapat 5 data x dan y, maka order fungsi polinom maksimal adalah 4. Meskipun demikian, fungsi polinom yang benar-benar cocok mewakili hubungan fungsional pasangan data x dan y bisa saja memiliki order dibawah 4 , seperti contoh-contoh berikut:
Contoh 1 : Jika data x=[0:5];y=[1 9 17 25 33 41] dicocokkan memiliki hubungan fungsional sebagai:
(1) y=ax (2) y=ax+1 (3) y=ax+b (4) y = ax2+bx+c
,maka untuk menentukan nilai a, b dan atau c yang cocok ( secara least square )
digunakan kode-kode MATLAB sebagai berikut: >> x=[0:5]; y=[1 9 17 25 33 41];
>> x=x'; y=y'; %data dibuat vektor kolom >> a=x\y %soal (1) a = 8.2727 >> a=x\(y-1) %soal (2) a = 8
>> ab=[x ones(size(x))]\y %soal (3) ab =
8.0000 1.0000
>> abc=[x.^2 x ones(size(x))]\y %soal (4) abc =
-0.0000 8.0000 1.0000
Catatan : Hasil-hasil ini dapat dibandingkan dengan cara yang sudah dipelajari pada mata kuliah Matek (topik bahasan Least Square : Regresi Polinom) sebagai berikut:
Untuk y=ax ,
a
xy
x
2
, sehingga penyelesaiannya dalam MATLAB :
>> a=sum(x.*y)/sum(x.^2) a = 8.2727 Untuk y=ax+b
a
x
y
n
xy
x
2
n
x
2
dan b y ax sehingga penyelesaiannya :
>> sx=sum(x); sy=sum(y); sxy=sum(x.*y); sx2=sum(x.^2); n=length(x); >> a=(sx*sy-n*sxy)/(sx^2-n*sx2),
b=sy/n-a*sx/n a = 8
b = 1
atau langsung dengan :
>> ab=[n sx; sx sx2]\[sy; sxy]; a=ab(2), b=ab(1) a =
8
b = 1.0000
Untuk y = ax2 + bx +c maka penyelesaiannya adalah:
>> sx=sum(x); sx2=sum(x.^2); sx3=sum(x.^3); sx4=sum(x.^4); >> sy=sum(y); sxy=sum(x.*y);sx2y=sum(x.^2.*y); n=length(x); >> RL=[n sx sx2; sx sx2 sx3; sx2 sx3 sx4]\[sy; sxy; sx2y];
>> a=RL(3), b=RL(2), c=RL(1) a = 0 b = 8 c = 1.0000
Kode-kode penyelesaian dengan MATLAB terlihat lebih sederhana dibandingkan dengan metode penyelesaiannya sendiri. Untuk seterusnya tanpa melupakan prinsip dasar dari metode least square sendiri, Anda diminta untuk menggunakan cara penyelesaian MATLAB ini dalam menyelesaikan semua permasalahan-permasalahan regresi atau linearisasi. Contoh 2: Diketahui data x dan y sesuai tabel dibawah.
x 1 2 3 4 5 6 7 8
y -7 -25.75 -54.55 -93.44 -142.36 -201.31 -270.26 -349.23
Jika data dicocokkan pada persamaan : y=
nilai a, b, c, d, dan e terbaik.
a x2 + b +c+dx+ex2, maka tentukanlahx >> x=[1:8]'; y=[-7 -25.75 -54.55 -93.44 -142.36 -201.31 -270.26 -349.23]';
>> m=[1./x.^2 1./x ones(size(x)) x x.^2]; RL=m\y; >> a=RL(1), b=RL(2), c=RL(3), d=RL(4), e=RL(5) a = 1.1039 b = -2.2008 c = 3.1222 d = -4.0274 e = -4.9980
Contoh 3: Diketahui x=[1 2 3 4 5]'; y=[6 20 58 132 254]'; Bentuk manakah yang paling cocok menggambarkan hubungan fungsional data x dan y?
1) y a xb 2) y a xb 4 3) y a xb c
Mula-mula, bentuk 1) dilinearisasi menjadi :
sehingga berdasarkan bentuk linearnya ini, maka :
ln( y) ln(a) b ln( x) ,
>> a1=exp(RL1(1)), b1=RL1(2), a1 = 5.0512 b1 = 2.3332 >> SSE1=sum((y-a1*x.^b1).^2) SSE1 = 1.5553e+003
Dengan cara sama, bentuk persamaan
ln( y 4) ln(a) b ln( x)
y a xb 4 juga dilinearisasi
menjadi
>> m=[ones(size(x)) log(x)]; RL2=m\log(y-4); a2=exp(RL2(1)), b2=RL2(2) a2 = 2.0000 b2 = 3.0000 >> SSE2=sum((y-(a2*x.^b2+4)).^2) SSE2 = 1.1304e-027
Nilai SSE pada bentuk 2) lebih kecil daripada nilai SSE pada bentuk 1) sehingga bentuk 2) lebih cocok menggambarkan hubungan fungsional antara data x dan y.
Bentuk 3) sendiri tidak dapat diselesaikan secara eksak menggunakan metode
linearisasi ini.
Contoh 4: Data x dan y pada tabel akan dicocokkan hubungan fungsionalnya
sebagai y a xbx c Tentukan nilai a, b dan c terbaik dan tentukan
error kuadratnya. x 0.1 0.2 0.3 0.4 0.5 y 0.4755 1.8534 2.4977 3 3.3227 Linearisas i
y a xbx c menghasilkan ln( y) ln(a) bx ln( x) c ln( x) , sehingga :
>> x=[0.1:0.1:0.5]'; y=[0.4755 1.1422 1.8534 2.4977 3]'; >> m=[ones(size(x)) x.*log(x) log(x)]; RL=m\log(y);
>> a=exp(RL(1)), b=RL(2), c=RL(3), sse=sum((y-a*x.^(b*x+c)).^2) a = 3.0005 b = -1.9995 c = 1.0000 sse = 2.7640e-009
Contoh 5: Diketahui x=1:5; y=2:6; z= [8 13 18 23 28]. Jika hubungan dari ke- 3
variabel tersebut dapat dinyatakan sebagai : 1) z ax by 2)
z
ax
2
by
2
c
3)z
a x
by
c,maka tentukan nilai a, b, atau c yang paling cocok.
>> x=1:5; y=2:6; z= [8 13 18 23 28]; m=[x' y']; RL1=m\z'; a1=RL(1), b1=RL(2) a1 = 1.098 8 b1 = -1.9995
>> m=[x'.^2 y'.^2 ones(size(x'))]; RL2=m\z'; a2=RL2(1), b2=RL2(2), c2=RL2(3) a2 = -2.5000 b2 = 2.500 0 c2 = 0.500 0
>> m=[ones(size(x')) log(x') log(y')]; RL3=m\z'; a3=RL3(1), b3=RL3(2),c3=RL3(3)
-31.5583
b3 = -26.8140 c3 = 57.1742
Berikut adalah kesimpulan pada penyelesaian persamaan regresi Yr=f(x)
dengan menggunakan pembagian kiri (back slash) ( \ ):
1) Data x dan y harus merupakan vektor kolom.
2) Buat matrik m yang elemen-elemennya sesuai dengan bentuk ekspresi data x pada fungsi Yr=f(x)), khusus untuk konstanta gunakan
ones(size((x))
3) Koefisien-koefisien yang dicari pada fungsi Yr=f(x) adalah m\y
Berdasarkan 3 hal di atas, semua permasalahan tentang regresi, baik pada regresi linear, regresi polinomial, ataupun regresi linear multi fungsi, dapat diselesaikan. Pada Tabel 1.2 dapat dilihat beberapa bentuk regresi dan linearisasi.
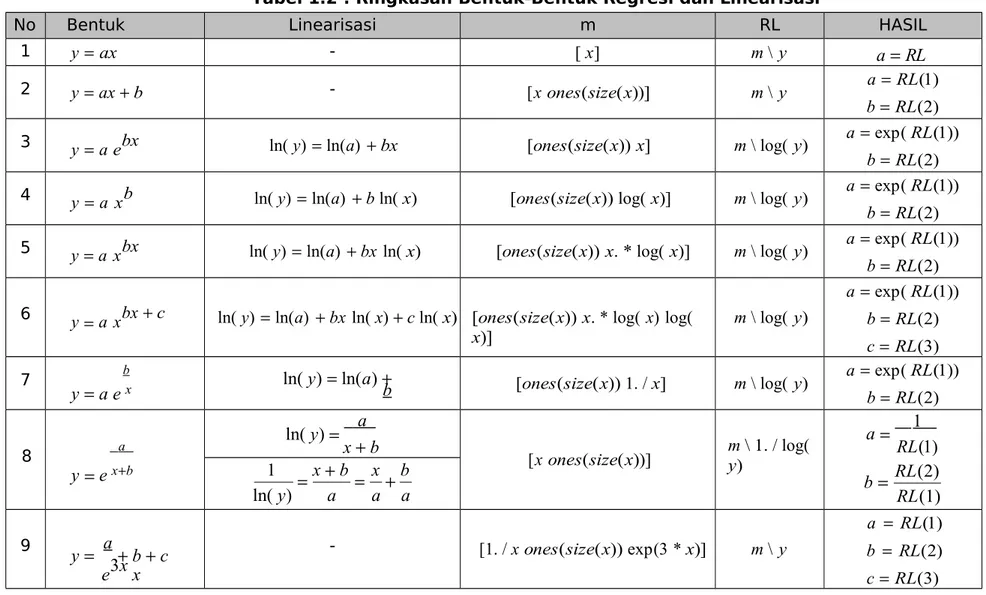
Tabel 1.2 : Ringkasan Bentuk-Bentuk Regresi dan Linearisasi
No Bentuk Linearisasi m RL HASIL
1 y ax - [ x] m \ y
a
RL
2 y ax b - [x ones(size(x))] m \ y a RL(1)
b RL(2)
3 y a ebx ln( y) ln(a) bx [ones(size(x)) x] m \ log( y) a exp( RL(1))
b RL(2)
4 y a xb ln( y) ln(a) b ln( x) [ones(size(x)) log( x)] m \ log( y) a exp( RL(1))
b RL(2)
5 y a xbx ln( y) ln(a) bx ln( x) [ones(size(x)) x. * log( x)] m \ log( y) a exp( RL(1))
b RL(2)
6 y a xbx c ln( y) ln(a) bx ln( x) c ln( x) [ones(size(x)) x. * log( x) log(
x)] m \ log( y) a exp( RL(1)) b RL(2) c RL(3) 7 b
y
a e
xln( y)
ln(a)
b
x
[ones(size(x)) 1. / x] m \ log( y) a exp( RL(1))
b RL(2) 8 a
y
e
xbln( y)
a
x
b
[x ones(size(x))] m \ 1. / log(y)a
1
RL(1)
RL(2)
b
RL(1)
1 x
b x b
ln( y) a a a
9y
a
b
c
e3x x
- [1. / x ones(size(x)) exp(3 * x)] m \ y a RL(1) b RL(2) c RL(3) .36
37
1.5.5 Penyelesaian Sistem Persamaan Linear
Jika diketahui sistem persamaan linear berikut : 2a + b + 3c = 13
2a + 3b - 2c = 2 a + 3b - c = 4
Mula-mula dibuat matrik koefisien dan vektor kolom kontanta dari persamaan linear diatas sebagai berikut:
>> Koef=[2 1 3 ; 2 3 -2 ; 1 3 -1]; Konst=[13 ; 2 ; 4];
Penyelesaian ala MATLAB adalah hasil pembagian kiri dari matrik koefisien Koef dan vektor konstanta Kons. Jadi :
>> abc=Koef \ Konst; a=abc(1), b=abc(2), c=abc(3) a = 1 b = 2 c = 3
1.5.6 Penyelesaian Sistem Persamaan Non Linear
Contoh-contoh berikut memperlihatkan cara penyelesaian sistem-sistem non linear yang terdiri dari 2 persamaan dalam bentuk fungsi implisit dengan 2 variabel.
38
Contoh 1 : Selesaikan persamaan non linear berikut:2a
2
b
4
0
a
3
2b
2
9
0
>> F = @(x) [2*x(1).^2 + x(2) - 4; x(1).^3 + 2*x(2).^2 - 9];
>> Tebakan_Awal = [2; 1]; % tebakan awal sebagai hasil penyelesaian >> xy = fsolve(F, Tebakan_Awal); x=xy(1), y=xy(2)
Optimization terminated: first-order optimality is less than options.TolFun. x =
1.0000
y = 2.0000
Contoh 2 : Selesaikan persamaan non linear berikut:
2a
3
a
2
b
3
2b
2
19
0
a
2
b
2
0.5 a b
6
0
>> f=@(x) [2*x(1).^3 + x(1).^2 + x(2).^3 + 2*x(2).^2 - 19; x(1).^2 + x(2).^2 + 0.5*x(1).*x(2) - 6];
>> xy=fsolve(f , [1 3]), xy=fsolve(f , [3 3]), xy=fsolve(f , [-3 3]) Optimization terminated: first-order optimality is less than options.TolFun. xy =
39
Optimization terminated: first-order optimality is less than options.TolFun. xy =1.6659 1.4269
Optimization terminated: first-order optimality is less than options.TolFun. xy =
-1.5200 2.3380
Anda bisa melihat, bahwa fsolve memiliki prinsip kerja mirip fzero, jadi untuk menemukan harga nol lain eksekusi fungsi harus diulang lagi dengan nilai awal yang lain. Anda disarankan membaca lebih lanjut tentang fsolve pada MATLAB online help.
1.5.7 Minimasi Fungsi ( fminbnd dan fminsearch )
Untuk mendapatkan nilai minimum fungsi, MATLAB menyediakan fungsi fminbnd untuk fungsi yang mengandung 1 jenis variabel saja pada interval tertutup [x1, x2] yang tetap dan fminsearch untuk fungsi yang mengandung beberapa jenis variabel.
Syntax :
x = fminbnd(fungsi,x1,x2) dan x = fminsearch(fungsi,x0) Contoh 1 : Tentukan minimum dari fungsi
polinom
y
f (x)
3x
3
4x
5
>> y=@(x) 3*x.^3 -4*x - 5; %y=@(x) polyval([3 0 -4 -5],x); fminbnd(y, 0, 4)
ans = 0.6667
Contoh 2: Diketahui vektor koefisien fungsi polinom p=[1 2 3 4 5 6 -7 -8 -9]. Tentukanlah titik-titik minimum dan maksimumnya.
>> p=[1 2 3 4 5 6 -7 -8 -9]; y=@(x) polyval(p , x); >> xmin=fminbnd(y , -20 , 20), ymin=y1(xmin) xmin = -1.3462 ymin = -14.2007
Jadi, pada interval dari -20 s/d 20, terdapat titik mínimum (-1,3462 ; -14,2007)
Untuk mencari titik maksimum, fungsi polinom harus dikalikan dengan faktor -1, sehingga :
>> y2=@(x) -polyval(p,x); xmax=fminbnd(y2,-20,20), ymax=y2(xmax) Benarkah telah dihasilkan titik maksimum??? Untuk membuktikan hal tersebut, kurva fungsi polinom digambarkan pada interval -20 s/d 20 dan pada interval -2 s/d 1.5 sebagai berikut:
10 x 10 3 140 2.5 120 2 1.5 100 80 60 1 40 0.5 20 0 0 -0.5 -20 -20 -15 -10 -5 0 5 10 15 20 -2 -1.5 -1 -0.5 0 0.5 1 1.5
Dari kurva diatas, terlihat jelas terdapat 2 titik mínimum absolut dan 1 titik
maksimum relatif. Hal ini membuktikan kebenaran titik mínimum yang sudah dihitung tetapi sekaligus juga membuktikan adanya titik mínimum lain dan kesalahan perhitungan titik maksimum yang dilakukan. Menyikapi hal ini, maka sangat baik untuk mengikuti saran berikut:
Buatlah terlebih dahulu kurva fungsinya sehingga dapat diperkirakan hal-hal
penting seperti titik-titik ekstrim dan titik-titik potong terhadap sumbu x dan titik- titik lainnya yang diamati.
Selanjutnya berdasarkan gambar fungsi diatas, titik-titik mínimum dan
titik maksimum ditentukan sebagai berikut:
>> y=@(x) polyval(p , x); xmin1=fminbnd(y , -2 , -1), xmin2=fminbnd(y , 0.5 , 1) xmin1 = -1.3462 xmin2 = 0.6106 >> ymin=y([xmin1 , xmin2]) ymin = -14.2007 -13.8561
Jadi, kurva memiliki 2 titik mínimum pada (-1,3462 ; -14,2007) dan (0,6106 ;
-13,8561). Berikutnya untuk titik maksimum :
>> y=@(x) -polyval(p , x); xmax=fminbnd(y , -1 , 0) , ymax=-y(xmax) xmax =
-0.4192
ymax = -7.2032
Jelaslah sudah, bahwa kurva fungsi perlu digambarkan terlebih dahulu
pada perhitungan yang membutuhkan masukan berupa interval seperti pada fminbnd atau nilai awal seperti pada fzero . Hal ini berguna untuk ketelitian perhitungan dan tidak menyesatkan “MATLAB”. Semakin sempit interval dan semakin dekat nilai awal dengan nilai yang dicari, maka MATLAB akan memberikan jawaban yang lebih eksak.
Contoh 3 : Tentukan minimum
dari
y
f (x
1, x
2)
100(x
2
x
1 2)
2
(1
x
1)
2 >> f= @(x) 100*(x(2)-x(1)^2)^2+(1-x(1))^2; x0=[2 2]; fminsearch(f , x0) ans = 1.0000 1.0000Berbeda dengan variabel x pada fminbnd, variabel x pada fminsearch merupakan sebuah vektor dari semua variabel fungsi sehingga pendefinisian fungsinya menggunakan ekspresi variabel x(1), x(2), x(3), dan seterusnya.
1.5.8 Persamaan Diferensial Dengan Nilai Awal
Pada MATLAB online help atau tepatnya pada
MATLAB-Mathematics- Differential Equations-Initial Value Problems for ODEs and
DAEs, Anda dapat menemukan beberapa jenis solver yang berbeda,
diantaranya adalah ode45 dan ode15s untuk fungsi
eksplisit
y' f (x, y) dan ode15i untuk fungsi impisit
f (x, y, y' ) 0 . Salah satu syntax –nya adalah : [X,Y] = ode45(odefun , Xspan , y0)
[X,Y] = ode15i(odefun , Xspan , y0 , dy0) Contoh 1: Persamaan
diferensial
y' y x dengan nilai awal (0 , 0) akan dicari
penyelesaian pada x = 0.2 ; 0.4 ; 0.6 dan 0,8, maka kode MATLAB-nya adalah:
>> D=@(x,y) y - x; x0=0; y0=0; %fungsi eksplisit >> Xspan=[x0 : 0.2 : 0.8];
ans = 0 0 0.200 0 -0.0214 0.400 0 -0.0918 0.600 0 -0.2221 0.800 0 -0.4255
Jika fungsi didefinisikan secara implisit, maka:
>> D=@(x,y,yp) y – x - yp; x0=0; y0=0; %fungsi implisit >> Xspan=[x0 : 0.2 : 0.8]; yp0=y0 - x0;
>> [x,y]=ode15i(D , Xspan , y0 , yp0); [x y] ans = 0 0 0.200 0 -0.0214 0.400 0 -0.0918 0.600 0 -0.2221 0.800 0 -0.4256
Contoh 2: Diketahui persamaan
diferensial
y'
x
2
2x
1
y
dengan nilai awal (1,0). Buatlah tabel penyelesaian pada x = 2 ; 5 ; 7 ; 10
>> D=@(x,y) x.^2+2*x-1-y; x0=1; y0=0; xspan=[x0 2 5 7 10]; >> [x y]=ode45(D , xspan , y0); [x y]
ans = 1.0000 0 2.0000 3.0000 5.0000 24.000 0 7.0000 47.999 3 10.000 0 99.000 5
x 1 2 3 4 5
y 0 14 44 96 176
1.6 Latihan Soal-Soal
Jika a=[1:4;5:8;9:12] dan b=[13:16;17:20;21:24], maka
(1) Jelaskan makna operasi-operasi berikut kemudian tentukan hasil operasinya a) a.*b b) a*b(1,:)' c) a(:,3) d) sum(a)
e) sum(a') f) sum(a(2,2:3)) g) sum(a(2,2:3).^2)
(2) Tentukan ekspresi yang diperlukan untuk menentukan ukuran, jumlah kolom dan jumlah baris matrik a
(3) Diketahui matrik A berukuran 6x7. Jika elemen matrik B diambilkan dari elemen-elemen matrik A dengan ketentuan bahwa:
a) Matrik B berukuran 3x3 dengan elemen-elemen pada baris ke- 1, 2, dan 3 berturut-turut adalah elemen-elemen matrik A pada baris ke-2, 4, dan 6 dan pada kolom ke- 1, 3, dan 4.
b) Matrik B berukuran 3x7 dengan elemen-elemen pada baris ke- 1, 2, dan 3 berturut-turut adalah kuadrat dari elemen-elemen matrik A pada baris
ke-1, 3, dan 6
Tentukan ekspresi yang diperlukan untuk membentuk matrik B diatas. (4) Hitung jumlah seluruh bilangan ganjil pada interval 3 s/d 999
(5) Hitung jumlah kuadrat dari seluruh bilangan ganjil pada interval 3 s/d 999 (6) Hitung jumlah rata-rata dari 1 s/d 1000; 1001 s/d 2001 dan 3001 s/d 4000 (7) Nyatakan bilangan 0.012333333333333... sebagai suatu pecahan
(8) Matrik A adalah matrik yang berukuran 4x6, nilai elemen-elemen pada baris ke- 1 adalah [1 2 3 4 5 6]. Tentukan matrik A tersebut jika nilai elemen-elemen pada baris ke- 2, 3, dan 4 berturut-turut merupakan elemen-elemen pada
pada baris ke- 1 pangkat nomor barisnya masing-masing.
a) Tentukan koefisien polinom yang paling cocok untuk hubungan a1) x vs y a2) x vs 1/(5x-y) a3) x vs
ln(y-30x) Selesaikan dengan prinsip dari polyfit dan regresi/linearisasi
b) Jika fungsi polinom yang berlaku dan benar adalah pada soal a1), maka b1) hitung nilai y pada x=1.5 , 2.5, 3.5 dan 4.5
b2) hitung nilai x jika y=45
b3) hitung integral fungsi tersebut dari 1.5 s/d 6
b4) hitung batas integrasi atas b jika integral fungsi dari 1 s/d b bernilai 3 b5) tentukan hasil bagi dan hasil kali polinom tersebut dengan (x-3)
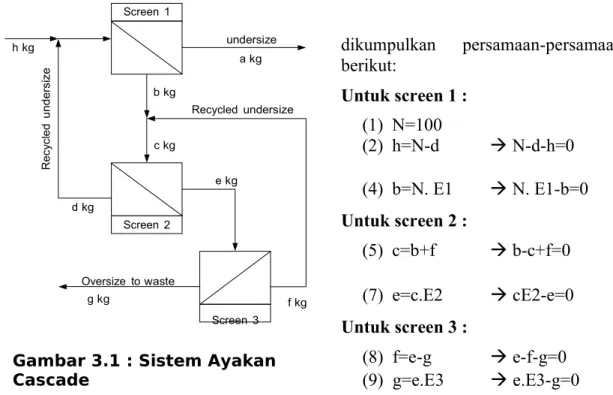
b6) hitung nilai maksimum/minimum dari fungsi polinom tersebut (10) Pada proses filtrasi pada dP= 0.5 bar dan diameter media filter
20 cm, diketahui data pengamatan berikut:
Volume Filtrat, L 1 2 3 4 5 6 7 8 9 9.5
Waktu, detik 45 92 160 290 405 586 788 1060 1328 1520
Rumus-rumus : Persamaan garis filtrasi adalah
t
r
ck
V
r
FV 2 A
2dP
A dP
k
V
ca ke ;V
FiltratV
cake
A x tebal cake
;
A
d
2 ;4
L
r
Fr
C 1 bar = 100000 Pa ;
0.001 Paa) Hitung slope dan intercept garis filtrasi menggunakan prinsip: a1) regresi a2) polyfit
b) Hitung
3
(11) Jika data pada soal no (9b1) akan diperlembut dan diperluas untuk x=1:0.1:5,
maka tentukan nilai y dengan menggunakan prinsip least square dan prinsip
interpolasi/ekstrapolasi
(12) Tabel berikut adalah data tentang suhu T dan kapasitas panas Cp suatu gas tertentu.
T[0K] 400 480 520
Cp[kal/(gmol K) 41 45 47
Hitunglah energi yang dibutuhkan untuk memanaskan 3 gmol gas dari 410
sampai 510K dengan data T dan Cp diatas.
T 2
Petunjuk : Gunakan rumus :
Q
C
pdT
.T 1 (13) Untuk fungsi
y
(2x
3)
2
x
4
3
2 , tentukanx
1
a) Nilai x supaya fungsi bernilai 0b) Nilai x supaya fungsi memiliki nilai 3
c) Nilai batas integrasi bawah a supaya integral fungsi diatas dari a s/d 7 bernilai 316
d) Nilai batas integrasi bawah a supaya integral fungsi diatas dari a s/d a+2 bernilai 316
(14) Hitung volume 40 kg CO2 pada kondisi standar. ( V = 20.4 m 3 )
(15) Hitung densitas N2 pada 270C dan 100 kPa (
1.123 kg / m
)(16) Diketahui persamaan diferensial
ordiner
y'
y
x
3
3x
2
2x
4
dengan nilai awal (0 ; 2). Tentukan nilai y untuk x=[1 3 6 9]
Jawaban Soal 1 .6
(1) a. [13 28 45 64; 85 108 133 160; 189 220 253 288] b. [150; 382; 614] ??
c. [3; 7; 11] semua elemen matrik pada kolom ke- 3 d. [15 18 21 24] jumlah elemen pada setiap kolom matrik a e. [10 26 42] jumlah elemen pada setiap baris matrik a
f. 13 yaitu jumlah dari a(2,2) =6 dan a(2,3)=7 g. 85 jumlah dari kuadrat a(2,2) dan a(2,3)
(2) A=size(a) ukuran matrik a nkolom=A(2) jumlah kolom matrik a nbaris=A(1) jumlah baris matrik a (3) a) B=A([2 4 6],[1 3 4]) b) B=[A(1,:).^2; A(3,:).^2; A(6,:).^2] (4) sum(3:2:999) (5) sum([3:2:999].^2) (6) sum([sum(1:1000) sum(1001:2001) sum(3001:4000)])/3 (7) 37/3000
(8) a=[1 2 3 4 5 6]; A=[a; a.^2; a.^3; a.^4] (9) x=[1 2 3 4 5]'; y=[0 14 44 96 176]';
a11) p1=polyfit(x,y,length(x)-1) a12) RL1=[x.^4 x.^3 x.^2 x ones(size(x))]\y a21) p2=polyfit(x, 1./ (5*x-y),length(x)-1)
a22) RL2=[x.^4 x.^3 x.^2 x ones(size(x))]\(1./(5*x-y)) a31) p3=polyfit(x, log(y+30*x),length(x)-1)
a32) RL3=[x.^4 x.^3 x.^2 x ones(size(x))]\ log(y+30*x) b1) x1=[1.5 2.5 3.5 4.5]; y1=polyval(p1,x1)
b2) y=@(x) polyval(p1,x)-45; x=fzero(y,1)
b3) polyval(polyint(p1),1.5)- polyval(polyint(p1),6) b4) q=polyint(p1); y=@(b) polyval(q,1)- polyval(q,b)-3;
b=fzero(y,1) b5) hasilbagi=deconv(p1,[1 -3]), hasilkali=conv(p1,[1 -3]) b6) tidak ada (10) t=[45 92 160 290 405 586 788 1060 1328 1520]';tc=3e-3; V=[1 2 3 4 5 6 7 8 9 9.5]'; dP=0.5e+5;d=0.2; A=pi/4*d*d; k=A*tc/V(length(V)); miu=0.001; a1) RL=[V ones(size(V))]\(t./V) a2) p=polyfit(V,t./V,1) b1) rc=RL(1)*2*A^2*dP/miu/k , rf=RL(2)*A*dP/miu, L=rf/rc b2) rc=p(1)*2*A^2*dP/miu/k , rf=p(2)*A*dP/miu, L=rf/rc (11) x=[1 2 3 4 5]';y=[0 14 44 96 176]'; p=polyfit(x,y,length(x)-1); y1=polyval(p, [1:0.1:5]'); y2=interp1(x,y,[1:0.1:5]');[y1 y2] (12) T=[400 480 520]; Cp=[41 45 47]; p=polyfit(T,Cp,2);
q=polyint(p); Q=3*(polyval(q,510)-polyval(q,410)) (13) y=@(x) (2*x-3).^2-(x.^4+3)/(x.^2+1); a) x=fzero(y,1) b) x=fzero(@(x) y(x)-3,1) c) x1=fzero(y,1);x2=fzero(y,10); L=abs(quad(y,x1,x2))+quad(y,x2,7)-316; f=@(a) abs(quad(y,a,x1)) +L;fzero(f,-3) d) f=@(a) quad(y,a,a+2)-316;a=fzero(f,10) (14) M=40; BM=44; R=8314; V=M/BM*R*273/101325 (15) T=27+273; BM=28; P=100e+3; R=8314;
rho=BM/R/T*P (16) Dy=@(x,y) y-x.^3+3*x.^2+2*x-4; xSpan=[0 1 3 6 9];
BAB 2
MEMBUAT PROGRAM MATLAB
2.1 Pendahuluan
Sebuah program MATLAB sebenarnya adalah sekumpulan ekspresi-ekspresi MATLAB seperti yang Anda biasa tuliskan dalam MATLAB command line window, tetapi kode-kode tersebut terkumpul dalam satu file dan akan dieksekusi oleh MATLAB secara berurutan, satu persatu dengan cepat sehingga mengesankan program tereksekusi secara serentak. Pada prinsipnya program MATLAB dapat dituliskan melalui penggunaan suatu
text editor dan disimpan dalam bentuk file dengan ekstensi .m pada folder tertentu yang dikehendaki sehingga membuat file tersebut masuk dalam kategori MATLAB M-file.
Bab ini akan membahas program MATLAB dasar dan beberapa trik pemrograman MATLAB. Melalui contoh-contoh yang diberikan, diharapkan Anda dapat dengan lebih mudah memahami MATLAB ini sehingga dapat dipergunakan untuk menyelesaikan beberapa permasalahan-permasalah matematis dan pada gilirannya nanti dapat menyelesaikan permasalahan-permasalahan pada bidang teknik kimia. Jika dalam penulisan program Anda mengalami keraguan tentang suatu syntax fungsi MATLAB, dianjurkan Anda mengkombinasikan text-editor dengan help navigator.
2.1. Membuat M-File
Sebuah M-file baru dapat dibuat dengan cara meng-klik menu MATLAB [File] kemudian memilih [New]-[M-File] atau langsung dengan
shortcut [New M-File] pada editor toolbar. Pada halaman kosong yang terbentuk Anda dapat menuliskan seluruh kode program dan mengeksekusi program dengan menekan tombol F5 untuk run dan melihat hasilnya di command line window.
2.2 Komponen-Komponen Program Dasar
Program MATLAB pada dasarnya adalah sekumpulan kode-kode yang dapat dikelompokkan sebagai variabel, keywords, konstanta-konstanta dan fungsi-fungsi, serta operator. Gabungan dari kode-kode tersebut membentuk ekspresi yang memiliki tujuan khusus. Beberapa ekspresi yang dituliskan berurutan dan dalam satu kelompok disebut blok. Jika Anda ingin belajar MATLAB lebih mendalam, maka Anda dipersilahkan
untuk meng-explore sendiri pada help menu, khususnya tentang
komponen-komponen dasar pada MATLAB- Programming.
2.3 Pemrograman M-File
M-File adalah file eksternal yang memiliki nama ekstensi .m , berisikan teks-teks komentar dan kode-kode dalam bahasa MATLAB seperti yang sudah pernah Anda lakukan saat melakukan perhitungan pada command line windows. M-File tidak memerlukan deklarasi variabel ataupun pembatas seperti begin/end. Teks-teks komentar yang ada harus diawali dengan tanda persen ( % ).
2.3.1 Script
Script adalah bentuk paling sederhana dari M-file yang tidak menerima masukan ( tidak memiliki argumen input ) atau menghasilkan argumen keluaran. Script dapat mengolah data yang sudah ada didalam memori internal MATLAB, atau membuat data baru. Meskipun script tidak menghasilkan keluaran argumen, setiap variabel yang dibuat tetap akan berada pada memori internal MATLAB sehingga dapat digunakan pada komputasi berikutnya. Sebagai tambahan, script juga dapat menghasilkan keluaran grafis menggunakan perintah sejenis plot.
Contoh : Script berikut menghitung rho untuk beberapa fungsi trigonometri, kemudian membuat beberapa gambar dalam sistem koordinat polar (Sumber : MATLAB online help).
% script utk menggambar "flower petal" Baris
teks/komentar theta = -pi:0.01:pi; % Komputasi rho(1,:) = 2 * sin(5 * theta) .^ 2;