MODEL SIRS PADA PROSES PENULARAN PENYAKIT INFLUENZA DENGAN POPULASI YANG TERINFEKSI VIRUS LIA MULYANAH

(1)

LIA MULYANAH

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2008

(2)

LIA MULYANAH

G54104018

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2008

(3)

in Infected Population. Supervisors : ALI KUSNANTO and ENDAR H. NUGRAHANI.

Influenza is a viral infectious disease in which its infection was studied using the SIRS model. In this paper the analysis of the influenza infection in a virus infected population with different initial quantity of population already infected.

Stability analysis of infection virus influence used SIRS Model produced 2 equilibrium points, in example one is called free of disease (T1) and the other is called an endemic case (T2).

The parameter value is related to the basic reproduction rate . If the basic reproduction rate was less than 1 (

0 R

0 1

R < ), the equilibrium point T1 was a stable node and the equilibrium point T2 was

an unstable spiral so virus was loss from population. If the basic reproduction rate was greater than 1 (R₀ >1), the equilibrium point T1 was a saddle and the equilibrium point T2 was a stable spiral

so virus stayed in population.

This work also compared the dynamic analysis of population with different parameter values, that is when initial population of infection I(0) is 1% and 10% from population. From the analysis, we have known that the 10% infected population was faster to stability than the 1% infected population.

(4)

Terinfeksi Virus. Dibimbing oleh ALI KUSNANTO dan ENDAR H. NUGRAHANI.

Penyakit influenza termasuk salah satu jenis penyakit menular yang disebabkan oleh virus influenza. Proses penularan penyakit ini dapat dimodelkan dengan menggunakan model SIRS. Dalam tulisan ini dianalisis penularan penyakit influenza pada populasi yang terinfeksi virus dengan jumlah individu yang terinfeksi awal berbeda.

Analisis kestabilan pada proses penularan virus influenza dengan menggunakan model SIRS ini menghasilkan 2 titik tetap, yaitu titik tetap tanpa penyakit (T1) dan titik tetap endemik (T2)

dengan beberapa nilai parameter. Nilai parameter ini ada kaitannya dengan konsep reproduksi dasar virus R₀. Ketika reproduksi dasar virus kurang dari 1 (R₀<1) titik tetap tanpa penyakit (T1)

simpul stabil, dan titik tetap endemik (T2) spiral tak stabil sehingga virus akan hilang dari populasi.

Ketika reproduksi dasar virus lebih besar dari 1 (R₀ >1) titik tetap tanpa penyakit (T1) akan sadel,

dan titik tetap endemik (T2) akan spiral stabil sehingga virus akan bertahan dalam populasi.

Selain menganalisis kestabilan, dibandingkan juga analisis untuk dinamika populasi dengan nilai parameter yang berbeda, yaitu ketika jumlah populasi awal yang terinfeksi virus I(0) 1% dari populasi dan 10% dari populasi. Dari hasil analisis diperoleh bahwa ketika populasi awal yang terinfeksi 10% dari populasi, maka populasi akan lebih cepat menuju kestabilan daripada ketika populasi awal yang terinfeksi 1% dari populasi.

(5)

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Oleh:

LIA MULYANAH

G54104018

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2008

(6)

NIM : G54104018

Menyetujui

Pembimbing I,

Drs. Ali Kusnanto, M.Si.

NIP : 131913135

Pembimbing II,

DR. Ir. Endar H. Nugrahani, MS

NIP : 131842411

Mengetahui

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Dr. Drh. Hasim, DEA

NIP : 131578806

(7)

karunia-Nya sehingga penulis dapat menyelesaikan karya ilmiah ini. Penyusunan karya ilmiah ini tidak terlepas dari bantuan berbagai pihak. Oleh karena itu, dalam kesempatan ini penulis mengucapkan terimakasih yang sebesar-besarnya kepada semua pihak yang telah membantu.

Terima kasih kepada Bapak Drs. Ali Kusnanto, M.Si. selaku dosen pembimbing 1 yang telah dengan sabar membimbing penulis sehingga penulis bisa menyelesaikan skripsi ini. Begitu pun untuk dosen pembimbing 2 Ibu DR. Ir. Endar H. Nugrahani, MS. Terima kasih kepada Bapak Ir. N. K. Kutha Ardana, M. Sc. yang telah bersedia menjadi dosen penguji.

Terima kasih penulis haturkan kepada semua dosen Departemen Matematika IPB yang telah memberikan ilmu dan motivasi kepada penulis. Terima kasih kepada semua staf Departemen Matematika IPB yang telah banyak membantu penulis, Bu Ade, Pak Yono, Pak Bono, Bu Marisi, Mas Deni, Bu Susi staf lainnya yang tidak bisa disebutkan semuanya.

Terima kasih untuk keluarga tercinta, Ibu yang tiada henti slalu mendukung dan tetap berdoa dengan penuh kasih sayang. Bapak yang slalu memberi smangat, doa, kepercayaan dan kasih sayangnya selama ini. Kedua adik ku, Eva dan Ai yang slalu membangkitkan smangat untuk segera menyelesaikan skripsi ini. Kakek, Nenek, ua, bibi, paman dan semua sepupu yang slalu menjadi sumber smangat. Terima kasih untuk Supriatna dan keluarga yang slama ini slalu membantu.

Teman-teman yang telah menjadi sahabat dan memberikan kenangan yang begitu indah dalam kebersamaan kita, Eli, Mukti, Rina, Janah, Rizul, Eva, Nidia, Ika, Sifa, Intan, Dian, Dee-dee, Liay, Mahar, Eni, Armi, Ayu, Ani, Tities, Tia, Fitri, Darwisah, Endit, Sita, Niken, Maryam, Peny, Uwi, Eci, Eneng, Reni, Roma, Ro’fah, Rangga M, Fariz, Adji, Fred, Mimin, Mahnur, Triyadi, Idris, Yaya, Mora, Iboy, Majid, Jali, Great dan semuanya yang tidak dapat disebutkan satu per satu. Kakak-kakak kelas Math 40: Teh Ulfa, Kak Abay, Kak Rusli, Teh Nci, Kak Aam yang telah membantu dan memberi smangat.

Teman-teman sekostan yang slalu menyemangati, Mel, Wheny, Widia, Jo, Ana, Efi, Sinta, Ipo, Ima, Riska, Kak Marna, Popon, Eri, Uni, Ika dan teh Reni. Dan semua pihak yang telah membantu yang tidak dapat penulis sebutkan satu per satu.

Semoga karya ilmiah ini bermanfaat bagi semua pihak, khususnya bagi pihak yang memiliki ketertarikan dalam bidang Matematika dan dapat menjadi inspirasi untuk penelitian-penelitian selanjutnya.

Bogor, Mei 2008

(8)

Penulis dilahirkan pada tanggal 3 Oktober 1985 di Ciamis. Penulis merupakan anak pertama dari tiga bersaudara, anak dari pasangan Maman Kusmanto dan Ebah Nurjanah.

Pada tahun 2001, penulis melanjutkan pendidikan ke jenjang pendidikan sekolah menengah umum di SMU Negeri 1 Ciamis. Pada tahun 2004, penulis lulus dari tingkat SMU dan melanjutkan pendidikan ke tingkat Perguruan Tinggi di Institut Pertanian Bogor (IPB). Penulis masuk IPB melalui jalur USMI dan mengambill program studi Matematika, Departemen Matematika, Fakultas matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor untuk tingkat Strata 1 (S1). Selama menjalani pendidikan di IPB, penulis memperoleh kesempatan untuk mendapatkan beasiswa PPA pada tahun 2005 dan 2006. Selain itu, penulis juga terlibat dalam beberapa kegiatan, antara lain mengikuti Program Guru Tambahan tingkat Sekolah Dasar (2004/2005), anggota Lingkar Muslim Matematika Himpro GUMATIKA (2005/2006, 2006/2007), Staf pengajar privat Kalkulus 1 Himpro GUMATIKA (2005/2006,2006/2007). Selain itu penulis juga aktif dalam berbagai kepanitiaan, diantaranya Penyambutan Mahasiswa Baru tahun 2005, Ramadhan In Action tahun 2005 dan 2006, Pesta Sains Nasional FMIPA IPB tahun 2006, Musyawarah Wilayah Ikahimatika tahun 2006, Welcome Ceremony Matematika tahun 2006 dan 2007.

(9)

1.1. Latar Belakang... 1

1.2. Tujuan... 1

LANDASAN TEORI ... 2

Sistem Persamaan Diferensial ... 2

Titik Tetap ... 2

Nilai Eigen dan Vektor Eigen... 2

Analisis Kestabilan Titik Tetap ... 3

Pelinearan ... 3

Model Primitif Penularan Virus ... 3

PEMBAHASAN ... 5

3.1. Perumusan Model... 5

3.2. Titik Tetap ... 6

3.2.1. Titik Tetap Tanpa Penyakit ... 6

3.2.2. Titik Tetap Endemik... 7

3.3. Analisis Kestabilan Titik Tetap ketika Populasi Awal yang Terinfeksi 1 Orang... 9

3.3.1. Analisis Kestabilan Titik Tetap untuk R0 < 1... 9

3.3.2. Analisis kestabilan titik tetap untuk R0 > 1 ... 12

3.4. Dinamika Populasi Penularan Virus Influenza... 15

3.4.1. Dinamika populasi untuk R0 < 1 ... 15

3.4.2. Dinamika populasi untuk R0 > 1 ... 18

Perbandingan Dinamika Populasi ketika Populasi Awal yang Terinfeksi 1% dan 10% dari Populasi untuk R0 < 1... 22

Perbandingan Dinamika Populasi ketika Populasi Awal yang Terinfeksi 1% dan 10% dari Populasi untuk R0 > 1... 24

KESIMPULAN... 25

DAFTAR PUSTAKA ... 26

(10)

Pencarian titik tetap dari persamaan (4), (5) dan (6) ... 29

Pencarian titik tetap dari persamaan (4), (5), (6) dengan menggunakan Mathematica . 31 Penentuan nilai eigen titik tetap tanpa penyakit ... 31

Penentuan nilai eigen titik tetap tanpa penyakit dengan Mathematica 6.0... 32

Penentuan nilai eigen titik tetap endemic... 32

Bukti ... 37

Gambar bidang fase ketika β =0.0002 dan v=0.9 dengan menggunakan Mathematica 5.2... 38

Gambar bidang fase ketika β=0.0001 dan v=0.9 dengan menggunakan Mathematica 5.2... 40

Gambar bidang fase ketika

β

=

0.0002

dan

v

=

0.4

dengan menggunakan Mathematica 5.2... 43

Gambar bidang fase ketika

β

=

0.0003

dan

v

=

0.4

dengan menggunakan Mathematica 5.2... 44

Program Mathematica untuk dinamika populasi ketika β = 0.0002 dan v = 0.9 ... 46

Program Mathematica ketika R₀<1 dan populasi yang terinfeksi 1% dari total populasi ... 49

Program Mathematica ketika R0<1 dan populasi yang terinfeksi 10% dari total populasi ... 50

Program Mathematica ketika R0 >1 dan populasi yang terinfeksi 1% dari total populasi ... 50

Program Mathematica ketika R₀ >1 dan populasi yang terinfeksi 10% dari total populasi ... 51

(11)

Gambar 2 Model SIRS pada populasi tertutup... 4

Gambar 3 Model SIRS pada populasi terbuka ... 4

Gambar 4 Diagram Model SIRS ... 5

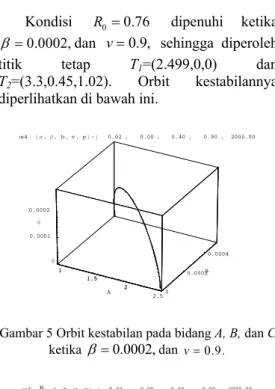
Gambar 5 Orbit kestabilan pada bidang A, B, dan C ketika β=0.0002,dan v=0.9... 9

Gambar 6 Proyeksi bidang fase pada bidang A, B ketika β=0.0002,dan v=0.9... 9

Gambar 7 Proyeksi bidang fase pada bidang A, C ketika β =0.0002,dan v=0.9... 10

Gambar 8 Proyeksi bidang fase pada bidang B, C ketika β =0.0002,dan v=0.9... 10

Gambar 9 Orbit kestabilan pada bidang A, B, dan C ketika β =0.0002,dan v=0.8... 10

Gambar 10 Proyeksi bidang fase pada bidang A, B ketika β =0.0002,dan v=0.8... 10

Gambar 11 Proyeksi bidang fase pada bidang A, C ketika β=0.0002,dan v=0.8... 10

Gambar 12 Proyeksi bidang fase pada bidang B, C ketika β =0.0002,dan v=0.8. ... 11

Gambar 13 Orbit kestabilan pada bidang A, B, dan C ketika β =0.0001,dan v=0.9... 11

Gambar 14 Proyeksi bidang fase pada bidang A, B ketika β =0.0001,dan v=0.9... 11

Gambar 15 Proyeksi bidang fase pada bidang A, C ketika β =0.0001,dan v=0.9. ... 12

Gambar 16 Proyeksi bidang fase pada bidang B, C ketika β =0.0001,dan v=0.9. ... 12

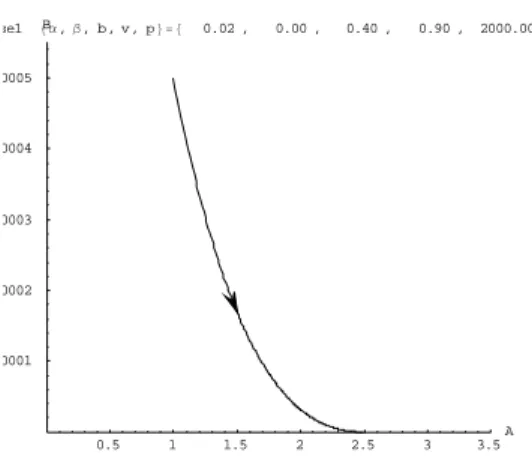
Gambar 17 Bidang fase tiga dimensi (A, B, C) ketika β =0.0002, dan v=0.5... 12

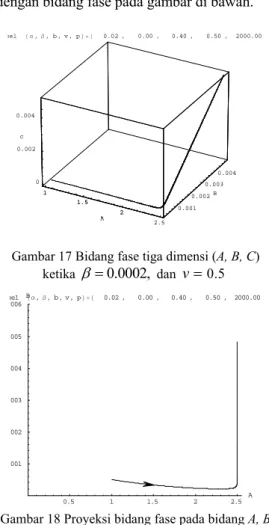
Gambar 18 Proyeksi bidang fase pada bidang A, B ketika β =0.0002, dan v=0.5... 12

Gambar 19 Proyeksi bidang fase pada bidang A, C ketika β=0.0002, dan v=0.5... 13

Gambar 20 Proyeksi bidang fase pada bidang B, C ketika β =0.0002, dan v=0.5... 13

Gambar 21 Bidang fase tiga dimensi (A, B, C) ketika β=0.0002,dan v=0.4... 13

Gambar 22 Proyeksi bidang fase pada bidang A, B ketika β =0.0002,dan v=0.4... 13

Gambar 23 Proyeksi bidang fase pada bidang A, C ketika β =0.0002,dan v=0.4... 14

Gambar 24 Proyeksi bidang fase pada bidang B, C ketika β=0.0002,dan v=0.4... 14

Gambar 25 Bidang fase 3 dimensi (A, B, C) ketika β=0.0003,dan v=0.4 ... 14

Gambar 26 Proyeksi bidang fase pada bidang A, B ketika β=0.0003,dan v=0.4 ... 14

Gambar 27 Proyeksi bidang fase pada bidang A, C ketika β=0.0003,dan v=0.4 ... 15

Gambar 28 Proyeksi bidang fase pada bidang B, C ketika β=0.0003,dan v=0.4 ... 15

Gambar 29 Dinamika populasi A terhadap waktu t... 16

Gambar 30 Dinamika populasi B terhadap waktu t... 16

Gambar 31 Dinamika populasi C terhadap waktu t... 16

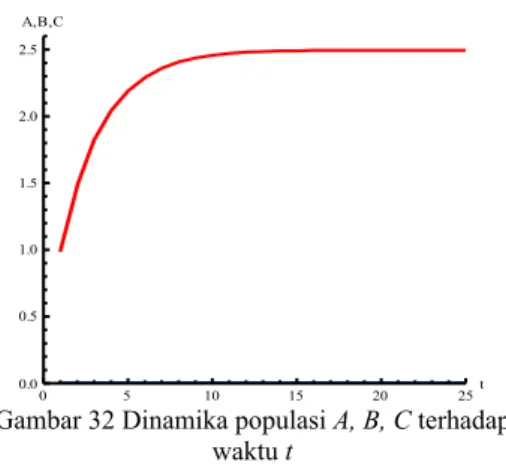
Gambar 32 Dinamika populasi A, B, C terhadap waktu t... 16

(12)

Gambar 59 Dinamika populasi A, B dan C terhadap waktu t... 23

(13)

1.1. Latar Belakang

Berbagai jenis penyakit saat ini semakin banyak. Salah satu penyebabnya, gaya hidup dan lingkungan yang semakin tidak sehat. Secara umum ada dua jenis penyakit, yaitu penyakit menular dan tidak menular. Dalam kelompok penyakit menular ada yang ringan dan ada yang berat. Yang ringan misalnya influenza dan diare. Sedangkan yang berat seperti HIV/AIDS, polio, demam berdarah, campak, TBC, malaria, flu burung, SARS, dan sederet penyakit lainnya. Menular atau tidaknya suatu penyakit tetap harus diwaspadai dan tidak boleh dianggap remeh. Sebab, ketika seseorang terkena suatu penyakit aktivitas kehidupannya akan terganggu. Apalagi jika penyakitnya sudah parah, bisa mengakibatkan kematian.

Pada penyakit menular, medium penularannya bermacam-macam. Ada yang karena kontak langsung dengan penderita, lewat udara, kotoran, atau lewat perantara binatang.

Virus influenza telah ada berabad-abad yang lalu dan telah menyebabkan kematian dan berbagai macam penyakit. Setiap tahun virus influenza menyerang 25-50 juta manusia, dan diperkirakan 20-40 ribu manusia di Amerika meninggal disebabkan oleh virus influenza.

Ada tiga tipe serologi virus influenza, yaitu tipe A, B, dan C. Tipe A dapat menginfeksi manusia dan hewan, sedangkan tipe B dan C hanya menginfeksi manusia.

Influenza adalah penyakit yang disebabkan oleh virus influenza pada saluran pernafasan dari hidung sampai trachea. Influenza (flu) yang merupakan suatu infeksi virus yang menyebabkan demam, hidung meler, sakit kepala, batuk, tidak enak badan (malaise) dan peradangan pada selaput lendir hidung dan saluran pernafasan. Influenza merupakan penyakit serius, tetapi sebagian besar penderita akan kembali sehat dalam waktu 7-10 hari. Selain menyerang manusia, ternyata virus influenza juga dapat ditemukan pada beberapa binatang, seperti unggas, babi, bebek, ikan paus, kuda, dan anjing laut. Jangka waktu seseorang terkena virus hingga munculnya gejala adalah satu sampai empat hari, dengan rata-rata dua hari. Sedangkan

periode seseorang dapat menularkan penyakitnya ke orang lain bervariasi untuk tiap usia.

Penularan sudah mulai terjadi dari sebelum penderita merasa sakit, yang berlanjut hingga tiga sampai tujuh hari setelah timbul gejala pertama pada orang dewasa. Sedangkan pada anak-anak dapat lebih dari satu minggu.

Untuk menganalisis dinamika penyebaran virus banyak metode yang dapat digunakan, diantaranya cellular automata yang pernah digunakan oleh Keeling dan Gillingan, forest-fire lattices yang digunakan oleh Rhodes dkk., sedangkan dalam tulisan ini akan dibahas pemodelan matematika untuk suatu penyakit menular dengan memisahkan populasi menjadi beberapa kelas, yang lebih dikenal dengan pendekatan SIRS.

Dalam tulisan ini akan dibahas model penyebaran penyakit menular yaitu influenza. Analisis kestabilan dan dinamika populasinya akan menjadi pembahasan. Pertama, ditentukan titik tetapnya yang terdiri dari titik tetap tanpa penyakit dan titik tetap endemik. Selanjutnya ditentukan matriks Jacobi dengan melakukan pelinearan setiap persamaan yang ada terhadap setiap variabel. Kemudian ditentukan nilai eigen dengan menyelesaikan persamaan karakteristik, nilai eigen tersebut akan digunakan untuk menganalisis kestabilan titik tetapnya. Selanjutnya laju reproduksi dasar virus ditentukan untuk mengetahui laju penularan penyakit tersebut dengan cara mengubah beberapa nilai parameter. Hal tersebut juga digunakan untuk menentukan bidang fasenya agar diketahui jenis kestabilannya. Dianalisis juga grafik dinamika populasi dengan beberapa nilai laju reproduksi dasar virus yang berbeda dengan mengubah beberapa parameter. Terakhir adalah membandingkan pengaruh dari jumlah populasi awal yang terinfeksi berbeda, yaitu 1% dan 10% dari total populasi.

1.2. Tujuan

Tujuan dari penulisan karya ilmiah ini adalah menganalisa penyebaran penyakit influenza menggunakan model SIRS dan menentukan kestabilan serta dinamika populasi untuk beberapa kondisi yang berbeda.

(14)

LANDASAN TEORI

Definisi 1 [Sistem Persamaan Diferensial

Linear (SPDL)]

Persamaan diferensial orde n dikatakan linear jika dapat ditulis dalam bentuk:

1 0 0( ) 1 ... 1( ) ( ) ( ) ( ) n n n n n n d x d x dx a t a t dt dt dt a t x a t f t − − − + + + = + (1.1)

dengan dan adalah fungsi dari

waktu t dan . ( ) a t f t( ) ( ) 0 a t ≠ (Farlow, 1994) Definisi 2 [Sistem Persamaan Diferensial

Mandiri]

Misalkan diberikan suatu sistem persamaan diferensial orde 1 sebagai berikut: 1 2 ( , ,...) dx x f x x dt = =& (1.2) f fungsi kontinu bernilai real, dengan laju perubahan dinyatakan dengan fungsi itu sendiri serta tidak berubah terhadap waktu, maka sistem (1.2) merupakan sistem persamaan differensial mandiri.

(Verhulst, 1990) Definisi 3 [Titik tetap]

Misalkan diberikan sistem persamaan diferensial (SPD) sebagai berikut

1 2 1 2

( , ,...), ( , ,...) n dx

x f x x x x

dt = =& ∈R (1.3)

Suatu titik _x*_{yang memenuhi}_{f x}_{( ) 0}* ₌ disebut titik keseimbangan atau titik tetap dari sistem (1.3).

(Verhulst, 1990) Definisi 4 [Titik tetap stabil]

Titik _x*_{adalah titik tetap sebuah SPD dan} ( )

x t adalah solusi yang memenuhi kondisi awal x(0)=x0 dan

* 0

x ≠ . Titik x _x* dikatakan titik tetap stabil jika terdapat

0 0

ε > , yang memenuhi sifat berikut: untuk setiap ε , ₁ 0<ε₁<ε₀, terdapat ε>0 sedemikian sehingga jika *

0 x −x < maka ε * 1 ( ) x −x t < , untuk setiap ε t t> 0.

(Szidarovszky & Bahill, 1998)

Definisi 5 [Titik Tetap Stabil Asimtotik Lokal]

Titik _x*_{dikatakan titik tetap stabil} asimtotik lokal jika titik _x*_{stabil dan terdapat}

0

ε> sedemikian sehingga jika * 0 x −x < ε maka _{lim ( )} *

t→∞x t =x .

(Szidarovszky & Bahill, 1998) Definisi 6 [Titik Tetap Stabil Asimtotik

Global] Titik *

x dikatakan titik tetap stabil asimtotik global jika titik _x*_{stabil dan}

, 0

n

x ∈ Ω ⊆ R _{lim ( )} * t→∞x t =x .

(Szidarovszky & Bahill, 1998) Definisi 4 menyatakan bahwa titik _x* stabil jika seluruh orbit (lintasan kurva dan yang menggambarkan solusi x t( )) berada pada radius ε , jika nilai awal (₁ x₀) yang dipilih cukup dekat dengan _x*_{. Pada Definisi} 5 (titik tetap stabil asimtotik lokal), dipilih nilai awal (x0) yang cukup dekat dengan

* x sehingga solusi x t( ) adalah _x*_untuk_t _. Sedangkan pada definisi 6 (titik tetap stabil asimtotik global), dipilih nilai awal (

→ ∞

0 x ) di luar radius ε sehingga solusi ₀ x t( ) adalah _x* untuk t→ ∞.

Definisi 7 [Titik Tetap Tidak stabil]

Misalkan _x*_{adalah titik tetap sebuah} SPD dan x t( )adalah solusi dengan nilai awal

0 (0)

x =x dengan *

0

x ≠x . Titik _x*_dikatakan titik tetap tidak stabil jika terdapat ε₀ >0, yang memenuhi sifat berikut: untuk setiap

0

ε> , 0< <ε ε₀, sedemikian sehingga jika * 0 x −x < maka ε * 0 ( ) x −x t < , untuk ε setiap t t> ₀.

(Szidarovszky & Bahill, 1998) Definisi 8 [Nilai Eigen dan Vektor Eigen] Misalkan adalah matriks , maka suatu vektor taknol di dalam disebut vektor eigen dari , jika untuk suatu skalar

A n n×

x _Rn

A λ , yang

(15)

λ

Ax = x, (1.4) vektor disebut vektor eigen yang bersesuaian dengan nilai eigen

x

λ . Untuk mencari nilai eigen dari matriks yang berukuran , maka persamaan (1.4) dapat dituliskan sebagai berikut:

A

n n× 0 λ − (A I)x = , (1.5) dengan matriks identitas. Persamaan (1.4) mempunyai solusi tak nol jika dan hanya jika

I

det (A−λI) = 0 (1.6) Persamaan (1.6) disebut persamaan karakteristik.

(Leon, 1998) Analisis Kestabilan Titik Tetap

Misalkan diberikan matriks berukuran sebagai berikut: A n n× 11 1 1 A n n n a a a a ⎛ ⎞ ⎜ = ⎜ ⎜ ⎟ ⎝ ⎠ L M O M L n ⎟ ⎟. Dengan persamaan

karakteristik det (A−λI) = 0, dan adalah matriks identitas, maka persamaan karakteristiknya menjadi: I 11 1 1 det 0 n n nn a a a a λ λ − ⎛ ⎞ ⎜ ₌ ⎜ ⎜ ₋ ⎟ ⎝ ⎠ L M O M L ⎟ ⎟ , sedemikian

sehingga akan diperoleh nilai eigen dari matriks tersebut.

Analisis kestabilan titik tetap dilakukan untuk setiap nilai eigen yang diperoleh, maka akan ada 4 kasus sebagai berikut:

1. Jika nilai eigennya real dan berbeda tanda, maka titik tetap bersifat sadel. 2. Jika semua nilai eigennya real dan

bertanda sama maka titik tetapnya merupakan simpul tak sejati (nodes). Jika bertanda positif maka nodes tak stabil. Jika bertanda negatif, maka nodes stabil. 3. Jika nilai eigennya merupakan complex

conjugate dengan bagian real yang positif maka titik tetap bersifat spiral tak stabil. Jika bagian realnya negatif maka titik tetap bersifat spiral stabil.

4. Jika nilai eigen merupakan imajiner murni, maka titik tetap bersifat center yang selalu stabil.

(Huntley & Johnson, 1983) Berdasarkan uraian di atas dapat disimpulkan bahwa kestabilan titik tetap mempunyai 3 perilaku sebagai berikut:

1. Stabil jika

a. Setiap nilai eigen real adalah negatif (λ_i <0 untuk setiap i).

b. Setiap komponen nilai eigen kompleks lebih kecil atau sama dengan nol, (Re(λ_i ≤0)untuk setiap i).

2. Tak stabil jika

a. Setiap nilai eigen real adalah positif (λi >0 untuk setiap i).

b. Setiap komponen nilai eigen kompleks lebih besar dari nol, (Re(λ_i >0)untuk setiap i).

3. Sadel jika perkalian dua buah nilai eigen real sembarang adalah negatif (λ λ_i _j < 0 untuk i dan j sembarang).

Pelinearan

Untuk suatu SPD taklinear, analisis kestabilannya dilakukan melalui pelinearan. Misalkan diberikan SPD taklinear sebagai berikut:

n U⊂R →R

&x=f(x): n_{. (1.7)} Dengan menggunakan ekspansi Taylor untuk suatu titik tetap

x

* , maka persamaan (1.7) dapat ditulis sebagai berikut:

( )x ϕ

= +

&x Ax . (1.8) Persamaan tersebut merupakan SPD taklinear dengan A adalah matriks Jacobi,

* * * 1 1 1 1 11 1 1 ( ) ( )_{x x} n n n n x x n n nn Df x Df x f f x x f f x x a a a a = = = = ∂ ∂ ⎡ ⎤ ⎢_∂ _∂ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢_∂ _∂ ⎥ ⎢ ⎥ ⎢_∂ _∂ ⎥ ⎣ ⎦ ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ L M O M L L M O M L A = =

dan ϕ( )x suku berorde tinggi yang bersifat 0

x

lim ( ) 0.ϕ x

→ = Selanjutnya pada

persamaan (1.8) disebut pelinearan dari sistem taklinear persamaan (1.7) yang didapatkan dalam bentuk

Ax

=

&x Ax. (Verhulst, 1990)

Model primitif penularan virus Misalkan x = Populasi koloni manusia,

y = Populasi virus, dengan asumsi sebagai berikut:

(16)

1. Laju kelahiran manusia α adalah konstan,

2. Infeksi virus menyebabkan peningkatan kematian terhadap penyakit, akibatnya , dengan g adalah fungsi sebarang,

( ) 0 g y >

3. Perkembangbiakkan partikel virus tergantung pada kehadiran manusia,

4. Dalam ketiadaan koloni manusia, partikel virus “mati“ atau menjadi tidak mampu bertahan hidup dengan laju γ. Persamaannya adalah sebagai berikut

[ ( )] dx , g y x dt = α− . dy _xy _y dt =β −γ

Dalam Model ini, populasi dibagi kedalam kelas-kelas yang berbeda sesuai dengan tingkat kesehatan anggotanya. Pembagian kelas-kelas tersebut terdiri dari kelas individu yang rentan terserang penyakit S, yang terinfeksi I, dan kelas individu yang telah pulih R dari individu yang terjangkit penyakit tidak dalam jangka waktu lama, karena mereka telah pulih dan kebal, sudah diisolasi atau sudah mati. Jika penyakit memberikan sistem kekebalan sementara kepada penderitanya, atau penderita yang telah pulih dapat terjangkit kembali, maka individu dapat juga bergerak dari kelas ketiga ke kelas pertama.

Jangka waktu epidemik dapat bervariasi dari minggu sampai tahun. Model klasik tentang teori epidemik telah dibuat oleh Kermack dan McKendrick (1927). Salah satu kasus khusus yang dipelajari digambarkan di bawah ini.

Gambar di atas menjelaskan laju perpindahan antara ketiga kelas dengan parameter β, yaitu laju penularan penyakit dan laju pemulihan v. Diasumsikan bahwa setiap pembagian kelas terdiri dari individu yang sama sehatnya atau sama sakitnya, dan tidak ada kelahiran atau kematian dalam populasi. (Dalam beberapa terminologi, model yang digambarkan pada gambar 1 disebut model SIR tanpa dinamika yang lebih rumit, karena perpindahan hanya dari kelas S ke I dan kemudian ke R).

Total populasi N dibagi menjadi kelas yang rentan terserang infeksi (S), yang terinfeksi (I), dan yang pulih (sembuh) dari penyakit (R). Laju penularan penyakit, pemulihan, dan laju hilangnya sistem kekebalan masing-masing β, v, dan γ konstan.

Persamaan yang dibuat Kermack dan McKendrick untuk penyakit yang diilustrasikan dalam gambar 1 adalah:

dS SI dt = −β dI _{SI vI} dt =β − dR vI dt =

Dapat ditunjukkan bahwa total populasi N = + +S I R tidak berubah. Persamaan tersebut tak linear. S, I, dan R adalah fungsi dari waktu t. Misalkan sistem kekebalan tubuh dapat hilang sehingga individu yang telah pulih menjadi terserang penyakit kembali (gambar 2). Persamaan dapat dituliskan menjadi: dS SI R dt = −β +γ dI _{SI vI} dt =β − dR vI R dt = −γ

Model di atas disebut model SIRS pada populasi tertutup. Sedangkan persamaan pada gambar 3 yang merupakan model SIRS pada populasi terbuka adalah

dS NS SI S dt =

δ

−

β

−

δ

+

γ

R dI SI I vI dt =β −δ − dR vI R R dt = −γ −δ 0

R merupakan rata-rata jumlah infeksi sekunder yang disebabkan oleh datangnya individu terinfeksi tunggal kedalam populasi β

S I v R

Gambar 1 model SIR

γ β

S I v R

Gambar 2 model SIRS pada populasi tertutup γ β _v N δ δ δ S I R δ

Gambar 3 model SIRS pada populasi terbuka

(17)

N yang rentan terserang penyakit, atau bisa juga dikatakan merupakan reproduksi dasar virus. Berikut adalah analisis untuk nilai R

0 R

0:

¾ R0 < 1 : Virus tidak dapat bertahan hidup

didalam populasi.

¾ R0 > 1 : Virus dapat bertahan hidup di

dalam populasi.

Analisis lebih lanjut mengenai model ini dapat dibuat kedalam suatu perhitungan, faktanya adalah bahwa total populasi:

N = + +S I R

tidak pernah berubah. Hal tersebut menjelaskan bahwa satu variabel, misalkan R dapat dihilangkan, sehingga model menjadi hanya dua persamaan.

PEMBAHASAN

3.1. Perumusan Model

Model ini dideskripsikan oleh Waltman (1974). Pada model ini total populasi yang merupakan fungsi dari waktu t dibagi menjadi tiga kelas yaitu; kelas individu yang rentan terserang penyakit dinotasikan dengan , kelas individu yang terinfeksi yaitu individu yang mampu menularkan penyakit ke individu lain dinotasikan dengan

( )

N t

S

I

, dan kelas yang sembuh yaitu individu yang terserang penyakit dan mati, atau terserang penyakit dan sembuh, atau individu yang diisolasi dari

rentan sampai sembuh dan imunitas permanen diperoleh dinotasikan dengan , atau dapat juga ditulis:

R

( )

N t

=

S t

+

I t

+

R t

Pada populasi, penyebaran penyakit menular mengikuti model dinamik SIRS (Susceptible -> Infected --> Removed --> Susceptible) dan proses analisis ini telah banyak dilakukan pada manusia dan mamalia (Anderson and May, 1978; Giesecko, 1994; Cairns, 1995). Proses penggambarannya diperlihatkan pada gambar 5.

Birth

β v

Susceptible

( S )

Infected

( I )

Remove

( R )

b α+ _b b

Gambar 4 Diagram Model SIRS

Model ini menggunakan beberapa asumsi, diantaranya:

Total populasi

N t

( )

konstan.

Perpindahan penyakit terjadi secara langsung, yang akan menghasilkan kepekatan individu per satuan waktu dan kepekatan

S

I

individu per satuan waktu.

Adanya kepastian proporsi populasi, yaitu

S

dan sisanya

I

. Persatuan waktu, proporsi individu

I

membuat

I

β

secara potensial merupakan

interaksi penularan.

Tingkat transmisi penularan penyakit

( )

β

proporsional terhadap tingkat

(18)

pertemuan individu yang rentan terkena penyakit dengan penular yang dimodelkan oleh perkalian

β

SI , dimana

β

adalah koefisien transmisi penularan. Persamaan dideskripsikan mengikuti model deterministik yang memasukkan nilai konstan untuk setiap parameternya. Setiap individu pada populasi memiliki kesempatan yang sama untuk berinteraksi dengan individu yang terinfeksi atau penular.

Individu yang sembuh dari infeksi dengan tingkat , mereka telah memiliki imunitas untuk infeksi selanjutnya pada periode waktu tertentu.

v

Semua parameter dan variable yang digunakan tak negatif.

Sebagaimana dideskripsikan Anderson (1982), koefisien transmisi penularan

β

ditentukan oleh 2 faktor, yaitu frekuensi interaksi yang terjadi secara langsung untuk kepekatan hewan yang rentan terserang penyakit dan kemungkinan adanya kontak pada transmisi patogen. Banyaknya individu pada waktu t untuk setiap kelas dinyatakan sebagai ,

S

I

, dan yang mana ketiganya merupakan fungsi dari . Pada saat diobservasi akan mengikuti persamaan:

R

t t 0

(

)

dS

S

bS

SI v

dt

=

+ −

−

β

+ R

(1)

(

dI

SI

b v I

dt

=

β

−

α

+ + )

(2)

dR

vI bR

dt

=

−

(3) dimana

S

adalah banyaknya individu dalam populasi yang rentan terserang penyakit.

I

adalah banyaknya individu dalam populasi yang terinfeksi dan dapat menularkan penyakit.

R

adalah banyaknya individu dalam populasi yang sembuh dari penyakit.

β

adalah koefisien transmisi (laju) penularan penyakit.

α

adalah tingkat mortalitas individu yang terinfeksi (penular).

v

adalah laju penyembuhan.

b

adalah tingkat mortalitas alami.

N adalah total populasi.

0

S

adalah laju awal populasi yang rentan terserang penyakit.

Selanjutnya digunakan skala berikut:

0

,

S

=

N A

I

=

N B

₀

,

dan

R N C

=

₀

.

Sekarang, setiap fungsi merupakan fraksi dari populasi awal

N

₀. Misal,

A t

( )

merupakan fraksi dari populasi awal yang rentan terserang penyakit. Dengan mensubstitusikan skala di atas ke dalam persamaan (1), (2) dan (3), maka akan diperoleh: 0

N

0

(

0

)

dA

A

bA

N AB vC

dt

=

+ −

−

β

+

(4) 0

(

dB

N AB

b v B

dt

=

β

−

α

+ + )

(5)

dC

vB bC

dt

=

−

(6)

Selanjutnya akan dicari titik tetap untuk model (4), (5) dan (6) yang kemudian akan dianalisis kestabilan di sekitar titik tetap tersebut.

3.2. Titik tetap

Analisis titik tetap pada SPD sering digunakan untuk menentukan solusi yang tidak berubah terhadap waktu, yaitu pada saat

0 dx

dt

=

,

0 dy

dt

=

, dan

0 dz

dt

=

. Titik tetap dari persamaan (4), (5) dan (6) akan diperoleh dengan menentukan

dA

0,

dt

=

0,

dB

dt

=

dan

0,

dC

dt

=

sehingga diperoleh persamaan dibawah ini: 0

(

0

)

A

+ −

bA

−

β

N AB vC

+

=

0

(7) 0

(

)

N AB

b v B 0

β

−

α

+ +

=

(8)

0 vB bC

−

=

(9)

Dari hasil analisis (lihat lampiran), akan diperoleh dua jenis titik tetap, yaitu titik tetap tanpa penyakit dan titik tetap endemik. 3.2.1. Titik tetap tanpa penyakit

Titik tetap tanpa penyakit diperoleh ketika

B

=

0

. Dengan mensubstitusikan nilai tersebut kedalam persamaan (7), (8), dan (9) maka akan diperoleh nilai

A

dan

C

.

(19)

Sehingga diperoleh titik tetap dari persamaan (4), (5) dan (6) yaitu

T

₁

A

0

,0,0

b

⎛

⎞

= ⎜

_⎝

⎟

_⎠

Misalkan persamaan (4), (5) dan (6) dituliskan sebagai berikut:

0 0

( , , )

(

)

x A B C

=

A

+ − −

bA

β

N AB vC

+

0 ( , , ) ( ) y A B C =

β

N AB−

α

+ +b v B ( , , ) z A B C =vB bC−

Dengan melakukan pelinearan pada system persamaan di atas, maka akan diperoleh matriks Jacobi:

dx

dA dB

dC

dy

J

dA dB

dC

dz

dA dB

dC

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

= ⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

0 0 0 0 ( ) 0 b N B N A v N B N A b v v

β

α

− − − ⎡ ⎢ =_⎢ − + ⎢ 0 b ⎤ ⎥ + _⎥ ⎥ − ⎣ ⎦

Pelinearan pada titik tetap akan menghasilkan matriks jacobi sebagai berikut:

1

T

0 0 0 0 0 0 ( ) 0 N A b b N A J b b v b β β _α − ⎡ 0 v v − ⎢ ⎢ ⎢ =_⎢ − + + ⎢ ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ − ⎢ ⎥ ⎢ ⎥ ⎣ ⎦

Untuk memperoleh nilai eigen digunakan persamaan karakteristik

det(

J

₀

−

λ

I

) 0

=

, sehingga akan diperoleh nilai eigen untuk matriks J0, yaitu: 1 2 0 0 3

(

)

b

N A

b v

b

λ λ

β

λ

α

=

= −

=

−

+ +

karena semua parameter tak negatif, maka

1 2

b

0 λ λ

=

= − <

sehingga kestabilan dititik

ini tergantung pada nilai eigen

λ

₃

.

Jika

3

0 λ

<

yang mana kondisi ini akan dipenuhi

ketika

N A

0 0

(

b v

b

)

β

_α

<

+ +

maka titik

tetap ini akan stabil dan sebaliknya jika

3

0 λ

>

yang berarti

N A

0 0

(

b v

)

b

β

_>

_α

_{+ +}

maka titik tetapnya akan sadel.

Kondisi stabil yang dipenuhi ketika

0 0

₍

N A

b v

b

)

β

_α

<

+ +

dapat ditulis dalam

0 0

₁

(

)

N A

b

b v

β

α

+ +

<

. 0 0

(

N A

b

b v)

β

α

+ +

merupakan

reproduksi dasar virus dalam populasi

R

₀.

Sehingga ketika 0 0

₁

(

)

N A

b

b v

β

α

+ +

<

atau 0

1 R

<

yang merupakan kondisi stabil maka virus tidak dapat bertahan di dalam populasi.

Sebaliknya, ketika 0 0

₁

(

)

N A

b

b v

β

α

+ +

>

atau

maka populasi tidak stabil karena virus akan bertahan dalam populasi.

0

1 R

>

Bisa disimpulkan bahwa titik tetap tanpa penyakit bersifat stabil asimtotik lokal jika dan hanya jika

R

₀

<

1

dan tidak stabil jika dan hanya jika

R

₀

>

1

.

3.2.2. Titik tetap endemik

Titik tetap endemic yaitu ketika ada individu yang terinfeksi dalam populasi. Dari persamaan (7), (8), dan (9) diperoleh titik tetap endemik

T

₂

=

(

x y z

, ,

)

, dengan

0

b v

x

N

α

β

+ +

=

0 0 2

(

)

(

)

(

)

b

b v

b A

N

y

b

b v

v

α

β

α

+ +

−

=

+ + −

0 0 2 0

( (

)

(

)

v b

b v

N A

z

N v

b

b v )

α

β

α

+ + −

=

−

+ +

Pelinearan pada titik tetap akan menghasilkan matriks jacobi sebagai berikut:

2

(20)

2 0 0 2 2 2 0 0 1 2 2 ( ) ( ) ( ) 0 0 0 bA N b b v b b b bv b v bA N b b v J b bv b v v b β α _α α β α α ⎡ − + + ⎤ − − − + + ⎢ ₊ ₊ ₋ ⎥ ⎢ ⎥ ⎢ − + + ⎥ = ⎢ ₊ ₊ ₋ ⎥ ⎢ ⎥ v v − ⎢ ⎥ ⎢ ⎥ ⎣ ⎦

Untuk memperoleh nilai eigen digunakan persamaan karakteristik

det(

J

₁

−

λ

I

) 0

=

, 2 0 0 2 2 2 0 0 2 2 ( ) ( ) ( ) 0 0 0 bA N b b v b b b bv b v bA N b b v b bv b v v b β α _λ _α α β α _λ α λ − + + − − − − + + + + − − + + 0 v v − = + + − − −

Sehingga diperoleh nilai eigen J1, yaitu:

1 ₃ a b λ → − − 3 2 2 2 3 1/ 3 2( 3 ) 3 [ 4( 3 ) ] a bc b d d a bc − + + + − + 2 2 3 3 [ 4( 3 ) 3 2 d d a bc b + + − + + ]1/ 3 2 3 a b λ → − + 2 2 2 3 1/ 3 3 (1 3)( 3 ) 3 4 [ 4( 3 ) ] i a bc b d d a bc + − + + + − + 2 2 3 3 (1 3)[ 4( 3 ) ] 6 2 i d d a bc b − + + − + − 1/ 3 3 ₃ a b λ → − + 2 2 2 3 1/ 3 3 (1 3)( 3 ) 3 4 [ 4( 3 ) ] i a bc b d d a bc − − + + + − + 2 2 3 3 (1 3)[ 4( 3 ) ] 6 2 i d d a bc b + + + − + − 1/ 3

dengan nilai

a b c

, ,

, dan dalam lampiran.

d

Berikut adalah tabel kondisi kestabilan dari dua titik tetap yang diperoleh.

Kondisi T1 T2 0 0

₍

₎

N A

b v

b

β

_α

<

+ +

atau

R

₀

<

1

Simpul stabil Spiral tak stabil 0 0

₍

₎

N A

b v

b

β

_>

_α

_{+ +}

atau

R

₀

>

1

Sadel Spiral stabil

Tabel 1 Dari tabel di atas terlihat bahwa kondisi kestabilan dari dua titik tetap yang diperoleh saling bertentangan, meskipun jenis kestabilannya berbeda. Ketika titik tetap yang pertama stabil, titik tetap yang kedua tidak stabil dan ketika titik tetap yang pertama sadel, titik tetap yang kedua stabil.

Selain itu, terlihat ada korelasi antara

R

₀ dengan titik tetap endemik, sehingga titik tetap endemik dapat dinyatakan dalam

R

₀ yaitu sebagai berikut.

0 0 A x bR = 0 2 1 ( 1) ( ) b R y v bα b v − = − + + 0 2 1 ( 1) ( ) v R z v bα b v − = − + +

Jika

R

₀

<

1

maka

x A

>

₀, karena

x

, , dan positif sehingga akan mengakibatkan

y

z

2

( )

bα+ + −b v v > . Artinya virus akan 0 hilang dari populasi jika populasi yang rentan terserang penyakit melebihi populasi awal yang rentan terserang penyakit. Dan

(21)

sebaliknya jika

R

₀

>

1

maka

x A

<

0,

sehingga , artinya virus

akan bertahan dalam populasi ketika populasi yang rentan terserang penyakit kurang dari populasi awal yang rentan terserang penyakit.

2

( )

bα+ + −b v v < 0

3.3. Analisis kestabilan titik tetap ketika populasi awal yang terinfeksi 1 orang Di sini akan digambarkan bidang fase dari persamaan (4), (5), (6). Hal ini membutuh nilai awal untuk masing-masing parameter dan variabel . Misal populasi awal kita sebut . Misalkan hanya ada satu individu yang terinfeksi ( ), sehingga populasi lainnya rentan terserang penyakit

. Kondisi awal lainnya , sehingga dipenuhi: (0) N 0 N (0) 1 I = 0 (0) 1 S =N − (0) 0 R =

(0)

N

=

S

+

I

+

R

.

Jika dituliskan secara menyeluruh, kondisi awal dari model ini adalah

(0)

(0) 1

S

=

N

−

(0) 1

I

=

(0) 0

R

=

Dengan menggunakan skala berikut

0

,

S

=

N A

I

=

N B

₀

,

dan

R N C

=

₀

.

Persamaan kondisi awal di atas akan menjadi

0

1 (0) 1

,

A

N

= −

0

1 (0)

,

B

N

=

C

(0) 0.

=

Pada proses penggambaran ini diambil nilai awal dari populasi . Selain kondisi awal di atas, dibutuhkan juga nilai dari parameter yang belum diketahui.

0 2000 N =

3.3.1. Analisis kestabilan titik tetap untuk

R0 < 1

Berikut adalah gambar bidang fase tiga dimensi dari persamaan (4), (5), dan (6) yang menunjukkan orbit kestabilannya. Dengan menggunakan Dynpac dari DynSys10. 71 pada Mathematica 5.2 ketika tingkat mortalitas alami b=0.4, dan α=0.02,

dengan nilai awal (0) 1 1 ,

2000 A = − 1 (0) , 2000 B = C(0) 0.= a. Ketika R0 = 0.76

Kondisi R0 =0.76 dipenuhi ketika 0.0002,

β = dan v=0.9, sehingga diperoleh

titik tetap T1=(2.499,0,0) dan

T2=(3.3,0.45,1.02). Orbit kestabilannya

diperlihatkan di bawah ini.

se4 8 α , β , b, v, p< = 8 0.02 , 0.00 , 0.40 , 0.90 , 2000.00 1 1.5 2 2.5 A 0 0.0002 0.0004 B 0 0.0001 0.0002 c 1 1.5 2 A

Gambar 5 Orbit kestabilan pada bidang A, B, dan C ketika β=0.0002,dan v=0.9. 0.5 1 1.5 2 2.5 3 3.5 A 0001 0002 0003 0004 0005 B se4 8α, β, b, v, p<=8 0.02 , 0.00 , 0.40 , 0.90 , 2000.00

Gambar 6 Proyeksi bidang fase pada bidang A, B ketika β=0.0002,dan v=0.9.

Dari gambar 6 terlihat bahwa orbit menuju titik T₁=(2.499, 0) sehingga

1 (2.499, 0)

T = berada pada bidang fase

tersebut, sedangkan titik

sangat jauh dari bidang fase. Hal ini menunjukkan bahwa T

2 (3.3,0.45) T =

1 stabil dengan jenis

(22)

0.5 1 1.5 2 2.5 3 3.5 A 0005 0001 0015 0002 0025 c se4 8α, β, b, v, p<=8 0.02 , 0.00 , 0.40 , 0.90 , 2000.00

Gambar 7 Proyeksi bidang fase pada bidang A, C ketika β =0.0002,dan v=0.9.

Gambar 7 yang merupakan proyeksi atau pencerminan orbit kestabilan dari gambar 5 terhadap sumbu A dan C menunjukkan bahwa

bersifat stabil karena dituju oleh orbit kestabilan sehingga

1 (2.499, 0) T =

berada pada bidang fase. Jenis kestabilannya

adalah node dan tak stabil

karena jauh dari bidang fase. 2 (3.3,1.02) T = 0.0001 0.0002 0.0003 0.0004 0.0005 B 0005 0001 0015 0002 0025 0003 0035 c se1 8α, β, b, v, p<=8 0.02 , 0.00 , 0.40 , 0.90 , 2000.00

Gambar 8 Proyeksi bidang fase pada bidang B, C ketika β =0.0002,dan v=0.9.

Gambar 8 merupakan proyeksi atau pencerminan dari orbit kestabilan tiga dimensi gambar 5 terhadap bidang B, C menunjukkan bahwa dituju oleh bidang fase. Hal ini menunjukkan bahwa T

1 (0, 0) T =

kestabilan node dan T2 tak stabil karena jauh

dari bidang fase.

b. Ketika R0 = 0.82

Berikut akan dianalisis untuk nilai R0

yang berbeda dengan mengubah parameter menjadi 0.8 sehingga diperoleh nilai R

v

0 yang

lebih besar yaitu R0 = 0.82 dengan titik tetap

T1=(2.499,0,0) dan T2=(3.05,0.58,1.16). se2 8α, β, b, v, p<=8 0.02 , 0.00 , 0.40 , 0.80 , 2000.00 1 1.5 2 2.5 A 0 0.0002 0.0004 B 0 0.0001 0.0002 c 1 1.5 2 A

Gambar 9 Orbit kestabilan pada bidang A, B, dan C ketika β =0.0002,dan v=0.8. 0.5 1 1.5 2 2.5 3 3.5 A 0001 0002 0003 0004 0005 B se2 8α,β, b, v, p<=8 0.02 , 0.00 , 0.40 , 0.80 , 2000.00

Gambar 10 Proyeksi bidang fase pada bidang A, B ketika β =0.0002,dan v=0.8.

Dari gambar terlihat bahwa titik tetap 1 (2.499, 0)

T = dituju oleh bidang fase

sehingga berada pada bidang fase dan titik tetap T₂ =(3.05, 0.58) jauh dari bidang fase. Ini menunjukkan bahwa T1 stabil dengan jenis

kestabilan node dan T2 tak stabil. Selain itu

terlihat pula bahwa dengan menurunkan nilai parameter kurva menjadi lebih curam jika dibandingkan dengan kurva sebelumnya.

v 0.5 1 1.5 2 2.5 3 3.5 A 0005 0001 0015 0002 0025 c se2 8α,β, b, v, p<=8 0.02 , 0.00 , 0.40 , 0.80 , 2000.00

Gambar 11 Proyeksi bidang fase pada bidang A, C ketika β =0.0002,dan v=0.8.

(23)

Dari gambar terlihat bahwa titik tetap dituju oleh bidang fase sehingga berada pada bidang fase dan titik

tetap jauh dari bidang fase.

Ini menunjukkan bahwa T 1 (2.499, 0)

T =

2 (3.05,1.16) T =

terlihat pula bahwa jika dibandingkan dengan kurva sebelumnya, dengan menurunkan nilai parameter v yang mengakibatkan nilai R0

menjadi lebih besar gambar bidang fase menjadi semakin mampat.

0.0001 0.0002 0.0003 0.0004 0.0005 B 0005 0001 0015 0002 0025 0003 0035 c se2 8α, β, b, v, p<=8 0.02 , 0.00 , 0.40 , 0.80 , 2000.00

Gambar 12 Proyeksi bidang fase pada bidang B, C ketika β =0.0002,dan v=0.8.

Dari gambar terlihat bahwa titik tetap dituju oleh bidang fase sehingga berada pada bidang fase dan titik tetap

jauh dari bidang fase. Ini menunjukkan bahwa T

1 (0, 0) T =

2 (0.58,1.16) T =

terlihat pula bahwa dengan menurunkan nilai parameter v yang mengakibatkan nilai R0

menjadi lebih besar, gambar bidang fase menjadi semakin sempit terlihat dari ujung bidang fase yang menurun.

c. Ketika R0 = 0.38

Berikut akan dianalisis untuk nilai R0

yang berbeda dengan mengubah nilai parameter β menjadi 0.0001, sehingga nilai R0 menjadi lebih kecil. Dengan perubahan

nilai β tersebut mengakibatkan nilai titik tetapnya juga berubah menjadi T1=(2.499,0,0)

dan T2=(6.6,2.33,5.24). se1 8α,β, b, v, p<=8 0.02 , 0.00 , 0.40 , 0.90 , 2000.00 1 1.5 2 2.5 A 0 0.0002 0.0004 B 0 0.00005 0.0001 0.00015 0.0002 c 1 1.5 2 A

Gambar 13 Orbit kestabilan pada bidang A, B, dan

C ketika β =0.0001,dan v=0.9. 0.5 1 1.5 2 2.5 3 3.5 A 0001 0002 0003 0004 0005 B se1 8α,β, b, v, p<=8 0.02 , 0.00 , 0.40 , 0.90 , 2000.00

Gambar 14 Proyeksi bidang fase pada bidang A, B ketika β =0.0001,dan v=0.9.

Dari gambar terlihat bahwa titik tetap 1 (2.499, 0)

T = dituju oleh bidang fase

sehingga berada pada bidang fase dan titik tetap T₂ =(6.6, 2.33) jauh dari bidang fase. Ini menunjukkan bahwa T1 stabil dengan jenis

terlihat pula bahwa dengan menurunkan nilai parameter β kurva menjadi lebih landai dibandingkan dengan kurva sebelumnya.

(24)

0.5 1 1.5 2 2.5 3 3.5 A 00005 0001 00015 0002 00025 c se1 8α,β, b, v, p<=8 0.02 , 0.00 , 0.40 , 0.90 , 2000.00

Gambar 15 Proyeksi bidang fase pada bidang A, C ketika β =0.0001,dan v=0.9.

Dari gambar terlihat bahwa titik tetap dituju oleh bidang fase sehingga berada pada bidang fase dan titik

tetap jauh dari bidang fase.

Ini menunjukkan bahwa T 1 (2.499, 0)

T =

2 (6.6,5.24) T =

terlihat pula bahwa dengan menurunkan nilai parameter β puncak kurva menjadi lebih rendah dibandingkan dengan kurva dengan nilai parameter β =0.0002,danv=0.9.

0.0001 0.0002 0.0003 0.0004 0.0005 B 00005 0001 00015 0002 00025 0003 00035 c se1 8α, β, b, v, p<=8 0.02 , 0.00 , 0.40 , 0.90 , 2000.00

Gambar 16 Proyeksi bidang fase pada bidang B, C ketika β =0.0001,dan v=0.9.

Dari gambar terlihat bahwa titik tetap dituju oleh bidang fase, sedangkan

titik tetap jauh dari bidang

fase. Ini menunjukkan bahwa T 1 (0, 0)

T =

2 (2.33,5.24) T =

1 stabil dengan

jenis kestabilan node dan T2 tak stabil. Selain

itu terlihat pula bahwa dengan menurunkan nilai parameter β ujung dari bidang fase menjadi lebih tinggi dibandingkan dengan bidang fase dengan nilai parameter

0.0002,

β = danv=0.9.

3.3.2. Analisis kestabilan titik tetap untuk

R0 > 1

Berikut akan dianalisis orbit kestabilan untuk nilai R0 > 1 dengan tingkat mortalitas

alami b=0.4,α=0.02, dengan nilai awal

yang sama yaitu (0) 1 1 ,

2000 A = − 1 (0) , 2000 B = dan C(0) 0.= a. Ketika R0 = 1.09

Kondisi R₀=1.09 dipenuhi ketika 0.0002,

β = dan v=0.5, dengan titik tetap T1=(2.499,0,0) dan T2=(2.3,0.27,0.34).

Diperoleh orbit kestabilan yang digambarkan dengan bidang fase pada gambar di bawah.

se1 8 α , β , b, v, p< = 8 0.02 , 0.00 , 0.40 , 0.50 , 2000.00 1 1.5 2 2.5 A 0.001 0.002 0.003 0.004 B 0 0.002 0.004 c 1 1.5 2 A

Gambar 17 Bidang fase tiga dimensi (A, B, C) ketika β =0.0002, dan v=0.5 0.5 1 1.5 2 2.5 A 001 002 003 004 005 006 B se1 8α,β, b, v, p<=8 0.02 , 0.00 , 0.40 , 0.50 , 2000.00

Gambar 18 Proyeksi bidang fase pada bidang A, B ketika β =0.0002, dan v=0.5

Gambar di atas merupakan proyeksi atau pencerminan dari orbit kestabilan tiga dimensi pada gambar 17 terhadap sumbu A, B. Bidang fase bergerak dari titik awal (

mendekati titik tetap tapi tidak berhenti di T

0.9995,0.0005) 1 (2.499, 0)

T =

(25)

berbelok menuju ke suatu nilai dari B, mungkin menuju ke titik tetap

. 2 (2.3, 0.27) T = 0.5 1 1.5 2 2.5 A 001 002 003 004 005 006 c se1 8α, β, b, v, p<=8 0.02 , 0.00 , 0.40 , 0.50 , 2000.00

Gambar 19 Proyeksi bidang fase pada bidang A, C ketika β=0.0002, dan v=0.5

Gambar di atas merupakan proyeksi atau pencerminan dari orbit kestabilan tiga dimensi pada gambar 17 terhadap sumbu A, C. Bidang fase bergerak dari titik awal (

0.9995, 0) 1 (2.499, 0)

T =

1, karena bidang fase tersebut

berbelok menuju ke suatu nilai dari B, mungkin menuju ke titik tetap

. 2 (2.3, 0.34) T = 0.001 0.002 0.003 0.004 0.005 0.006 B 001 002 003 004 005 006 c se1 8α, β, b, v, p<=8 0.02 , 0.00 , 0.40 , 0.50 , 2000.00

Gambar 20 Proyeksi bidang fase pada bidang B, C ketika β =0.0002, dan v=0.5.

Gambar di atas merupakan proyeksi atau pencerminan dari orbit kestabilan tiga dimensi pada gambar 17 terhadap sumbu B, C. Bidang fase bergerak dari titik awal (

menjauhi titik tetap , dan mungkin

menuju ke titik tetap .

0.0005, 0) 1 (0, 0)

T =

2 (0.27, 0.34) T =

Dari ketiga gambar di atas terlihat bahwa bidang fase menjauhi titik tetap T1, dan

mungkin menuju ke titik tetap T2. Hal ini

menunjukkan bahwa pada kondisi ini T1 sadel.

b. Ketika R0 = 1.22

Berikut dilakukan analisis untuk nilai 0.4,

v= sehingga menghasilkan nilai R0 yang

berbeda yang lebih besar. Kondisi tersebut menghasilkan titik tetap yang berbeda pula yaitu T1=(2.499,0,0) dan T2=(2.05,0.43,0.43).

Di bawah ini adalah gambar bidang fase dalam bentuk 3 dimensi.

se1 8α , β, b, v, p< =8 0.02 , 0.00 , 0.40 , 0.40 , 2000.00 1 1.5 2 2.5 A 0 0.1 0.2 B 0 0.1 0.2 c 1 1.5 2 A

Gambar 21 Bidang fase tiga dimensi (A, B, C) ketika β=0.0002,dan v=0.4 0.5 1 1.5 2 2.5 A .05 0.1 .15 0.2 .25 0.3 B se1 8α, β, b, v, p<=8 0.02 , 0.00 , 0.40 , 0.40 , 2000.00

Gambar 22 Proyeksi bidang fase pada bidang A, B ketika β=0.0002,dan v=0.4

Gambar di atas merupakan proyeksi atau pencerminan dari orbit kestabilan tiga dimensi pada gambar 21. Bidang fase bergerak dari

titik awal mendekati titik

tetap

(0.9995,0.0005) 1 (2.499, 0)

T = tapi tidak berhenti di T1.

Bidang fase terus bergerak naik menuju ke titik tetap T2 =(2.05,0.43). Ini menunjukkan bahwa T1 sadel. Selain itu, dengan

berkurangnya nilai mengakibatkan bidang fase semakin rapat dengan sumbu absis.

(26)

0.5 1 1.5 2 2.5 A .05 0.1 .15 0.2 .25 0.3 c se1 8α, β, b, v, p<=8 0.02 , 0.00 , 0.40 , 0.40 , 2000.00

Gambar 23 Proyeksi bidang fase pada bidang A, C ketika β =0.0002,dan v=0.4

Gambar di atas merupakan proyeksi atau pencerminan dari orbit kestabilan tiga dimensi pada gambar 21 terhadap sumbu A, C. Bidang fase bergerak dari titik awal (

0.9995, 0) 1 (2.499, 0)

T =

1. Bidang fase terus bergerak naik

menuju ke titik kestabilan .

Ini menunjukkan bahwa T

2 (2.05,0.43) T =

1 sadel. Selain itu,

dengan berkurangnya nilai mengakibatkan bidang fase semakin rapat dengan sumbu absis. v 0.05 0.1 0.15 0.2 0.25 0.3 B .05 0.1 .15 0.2 .25 0.3 c se1 8α,β, b, v, p<=8 0.02 , 0.00 , 0.40 , 0.40 , 2000.00

Gambar 24 Proyeksi bidang fase pada bidang B, C ketika β=0.0002,dan v=0.4

Gambar di atas merupakan proyeksi atau pencerminan dari orbit kestabilan tiga dimensi pada gambar 21 terhadap sumbu B, C. Bidang fase bergerak dari titik awal (

menjauhi titik kestabilan menuju titik kestabilan di . Selain itu, terlihat bahwa gambar bidang fase menjadi lebih landai. 0.0005, 0) 1 (0, 0) T = 2 (0.43, 0.43) T =

Dari ketiga gambar di atas terlihat bahwa bidang fase menjauhi titik tetap T1, dan

mungkin menuju ke titik tetap T2. Hal ini

menunjukkan bahwa pada kondisi ini T1 sadel.

Selain itu, dengan penurunan nilai mengakibatkan peningkatan untuk nilai B dan C.

v

c. Ketika R0 = 1.83

Berikut akan dilakukan analisis untuk perubahan nilai β yaitu dengan menaikkan nilai β menjadi 0.0003 dengan nilai

0.4,

v= dan parameter yang lain tetap, menghasilkan nilai R0 yang lebih besar yaitu

R0 = 1.83 , dan titik tetapnya menjadi

T1=(2.499,0,0) dan T2=(1.37,1.08,1.08). Di

bawah ini adalah gambar bidang fase dalam 3 dimensi. se1 8α, β, b, v, p<=8 0.02 , 0.00 , 0.40 , 0.40 , 2000.00 1 1.5 2 A 0 0.25 0.5 0.75 1 B 0 0.25 0.5 0.75 1 c 1 1.5 2 A

Gambar 25 Bidang fase 3 dimensi (A, B, C) ketika

0.0003, β = dan v=0.4 0.5 1 1.5 2 2.5 A 0.2 0.4 0.6 0.8 1 B se1 8α,β, b, v, p<=8 0.02 , 0.00 , 0.40 , 0.40 , 2000.00

Gambar 26 Proyeksi bidang fase pada bidang A, B ketika β=0.0003,dan v=0.4

Gambar di atas merupakan proyeksi dari gambar 25 terhadap sumbu A, B. Pada gambar di atas titik awal pergerakkan bidang fase tidak terlihat dengan jelas, hal ini karena skala nilai yang dihasilkan lebih besar daripada ketika β =0.0002. Di sini jelas terlihat bahwa bidang fase menuju titik tetap T2 di

(27)

0.5 1 1.5 2 2.5 A 0.2 0.4 0.6 0.8 1 c se1 8α,β, b, v, p<=8 0.02 , 0.00 , 0.40 , 0.40 , 2000.00

Gambar 27 Proyeksi bidang fase pada bidang A, C ketika β=0.0003,dan v=0.4

Gambar di atas merupakan proyeksi dari gambar 25 terhadap sumbu A, C. Pada gambar di atas titik awal pergerakkan bidang fase tidak terlihat dengan jelas, hal ini karena skala nilai yang dihasilkan lebih besar daripada ketika β =0.0002. Di sini jelas terlihat bahwa bidang fase menuju titik tetap T2 di

(1.37,1.08). 0.2 0.4 0.6 0.8 1 B 0.2 0.4 0.6 0.8 1 c se1 8α,β, b, v, p<=8 0.02 , 0.00 , 0.40 , 0.40 , 2000.00

Gambar 28 Proyeksi bidang fase pada bidang B, C ketika β=0.0003,dan v=0.4

Gambar di atas merupakan proyeksi dari gambar 25 terhadap sumbu B, C. Pada gambar di atas titik awal pergerakkan bidang fase terlihat seolah-olah dari titik (0,0) padahal sebenarnya bidang fase bergerak dari titik (0.0005,0), hal ini karena skala nilai yang dihasilkan lebih besar daripada ketika

0.0002. β =

Dari ketiga proyeksi di atas dapat dilihat bahwa dengan bertambahnya nilai β titik tetapnya semakin besar, begitu pula dengan nilai R0. Dengan semakin besarnya nilai titik

tetap mengakibatkan gambar bidang fase lebih jelas pada ujungnya tapi kurang jelas kondisi awalnya.

3.4. Dinamika populasi penularan virus influenza

Untuk mengamati pengaruh masuknya patogen atau virus ke dalam populasi pada waktu tertentu maka diperlukan kurva yang menunjukkan pengaruh masuknya patogen kedalam populasi hubungannya dengan periode waktu. Hal ini membutuh nilai awal untuk masing-masing parameter dan variabel . Pada proses penggambaran ini diambil nilai awal dari populasi . Selain kondisi awal di atas, dibutuhkan juga nilai dari parameter yang belum diketahui.

0 2000 N =

Dalam karya tulis ini dianalisis dinamika populasi untuk dua kondisi, yaitu ketika

0 1

R < dimana populasi akan stabil karena virus akan hilang dari populasi dan ketika dimana virus akan bertahan dalam populasi.

0 1

R >

3.4.1. Dinamika populasi untuk R0 < 1

Kondisi R₀<1 adalah kondisi dimana populasi akan stabil menuju musnahnya virus dari populasi. Dalam proses penggambarannya saya menggunakan Mathematica 6.0 yang dievaluasi ketika tingkat mortalitas alami dan tingkat mortalitas populasi yang terinfeksi

0.4, b=

0.02, α=

dengan nilai awal (0) 1 1 ,

2000 A = − 1 (0) , 2000 B = C(0) 0.=

Untuk nilai R₀ <1 ini akan dianalisis untuk tiga kondisi dengan mengubah nilai dan

v β sehingga diperoleh nilai R0 yang

berbeda yaitu R0=0.76, R0=0.81 dan R0 = 0.38

.

a. Ketika R0 = 0.76

Kondisi R0=0.76 dipenuhi ketika

0.0002,

β = dan v=0.9, sehingga diperoleh

(28)

0 5 10 15 20 25t 0.0 0.5 1.0 1.5 2.0 2.5 A

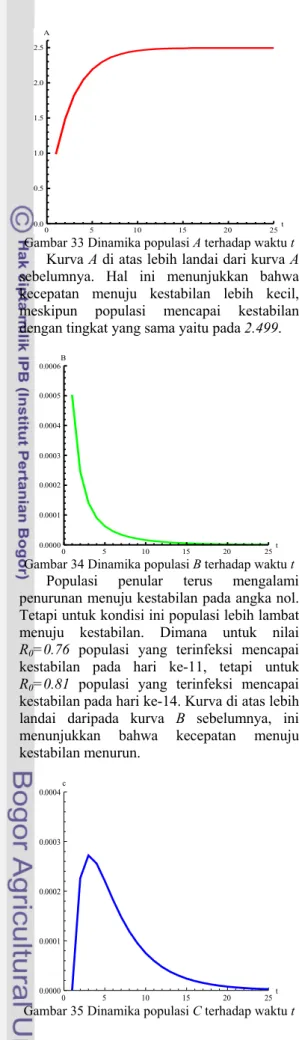
Gambar 29 Dinamika populasi A terhadap waktu t

Gambar di atas menyatakan bahwa populasi yang rentan terserang penyakit mengalami peningkatan yang signifikan pada waktu yang cukup singkat, tapi kemudian stabil pada angka 2.499 setelah 8 hari. Peningkatan tersebut terjadi karena pada kondisi ini

x A

>

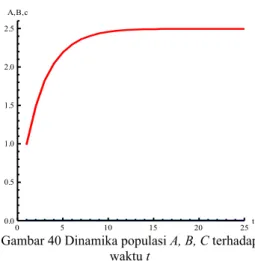
₀. 0 5 10 15 20 25t 0.0000 0.0001 0.0002 0.0003 0.0004 0.0005 0.0006B

Gambar 30 Dinamika populasi B terhadap waktu t

Gambar di atas menyatakan bahwa jumlah populasi yang terinfeksi mengalami penurunan yang sangat signifikan pada waktu yang sangat singkat. Kemudian mencapai kestabilan pada angka 0 dihari ke-11. Penurunan ini terjadi karena pada kondisi ini virus tidak dapat bertahan dalam populasi.

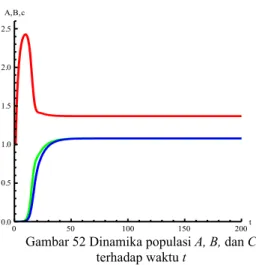
0 5 10 15 20 25t 0.0000 0.0001 0.0002 0.0003 0.0004c

Gambar 31 Dinamika populasi C terhadap waktu t

Gambar di atas menyatakan bahwa pada hari ke-1 laju kesembuhan meningkat tajam, kemudian pada hari ke-2 peningkatan yang terjadi tidak signifikan seperti hari pertama. Pada hari ketiga, laju kesembuhan mengalami penurunan yang tajam menuju kestabilan pada angka nol setelah hari ke-18. Jumlah populasi yang sembuh meningkat karena ketika banyak populasi yang terinfeksi maka populasi yang sembuh pun akan banyak hal ini karena laju kesembuhan yang cukup besar yaitu mendekati 1. Namun setelah mencapai tingkat tertentu populasi yang sembuh akan menurun, hal ini seiring dengan menurunnya jumlah populasi yang juga menurun.

0 5 10 15 20 25t 0.0 0.5 1.0 1.5 2.0 2.5 A,B,C

Gambar 32 Dinamika populasi A, B, C terhadap waktu t

Gambar di atas merupakan gabungan kurva A, B, dan C. Pada gambar di atas terlihat bahwa kurva B dan C berupa garis horizontal yang berada disumbu absis dan nilainya mendekati nol. Hal ini berarti jumlah populasi yang terinfeksi sedikit sehingga jumlah populasi yang sembuh pun sedikit. Inilah yang menyebabkan virus tidak dapat bertahan dalam populasi atau virus akan musnah dari populasi.

b. Ketika R0 = 0.81

Berikut adalah dinamika populasi ketika koefisien penularan penyakit β tetap dan laju kesembuhan diturunkan menjadi 0.8. Hal ini menaikkan nilai R

v

0 menjadi 0.81 dengan