LAPORAN TAHUNAN PENELITIAN HIBAH BERSAING
PEMODELAN REGRESI POISSON, BINOMIAL NEGATIF DAN POISSON TERGENERALISASI PADA KASUS KECELAKAAN
KENDARAAN BERMOTOR DI LALU LINTAS
TAHUN KE I DARI RENCANA II TAHUN
TIM PENGUSUL
Dr. Irwan, M.Si 0005106509 KETUA Devni Prima Sari,S.Si,M.Sc. 0020128403 ANGGOTA
Dibiayai oleh DIPA Universitas Negeri Padang
Sesuai dengan Surat Penugasan Pelaksanaan Penelitian Desentralisasi Melalui DIPA UNP tahun anggaran 2013 No. 298.a.45/UN35.2/PG/2013
Tanggal 31 Mei 2013
iii RINGKASAN
Pemodelan Regresi Poisson, Binomial Negatif dan Poisson Tergeneralisasi pada Kasus Kecelakaan Kendaraan Bermotor Di Lalu Lintas
v DAFTAR ISI
HALAMAN PENGESAHAN ... ii
RINGKASAN ... iii
PRAKATA ... iv
DAFTAR ISI ... v
DAFTAR TABEL ... vii
BAB 1 PENDAHULUAN ... 1
1.1 Latar Belakang ... 1
1.2 Perumusan Masalah ... 3
1.3 Tujuan Penelitian ... 3
1.4 Keutamaan dan Inovasi Penelitian ... 4
BAB 2 TINJAUAN PUSTAKA ... 5
2.1 Kendaraan Bermotor ... 5
2.2 Faktor-faktor Penyebab Kecelakaan Lalu Lintas ... 6
2.3 Variabel Random dan Fungsi Distribusi... 6
2.4 Keluarga Eksponensial ... 9
2.4.1 Distribusi keluarga eksponensial ... 9
2.4.2 Distribusi standar dalam format keluarga eksponensial ... 11
2.5 Estimasi Maksimum Likelihood (MLE) ... 14
2.6 Statistic Score ... 15
2.7 Generalized linear model (GLM) ... 18
2.7.1 Fungsi Link ... 20
2.7.2 Metode Iterasi Newton-Raphson ... 20
2.7.3 Estimasi Maksimum Likelihood ... 21
2.7.4 Fisher Scoring ... 23
2.7.5 Iteratively Weighted Least Square (IWLS) ... 23
2.8 Goodness Of Fit ... 24
2.8.1 Pearson Chi-square ... 25
2.8.2 Deviance ... 25
vi
BAB 3 TUJUAN DAN MANFAAT PENELITIAN ... 28
3.1 Tujuan Penelitian ... 28
3.2 Manfaat Penelitian ... 28
BAB 4 METODE PENELITIAN ... 29
BAB 5 HASIL DAN PEMBAHASAN ... 30
5.1 Model Regresi Poisson ... 30
5.1.1 Overdispersi ... 30
5.1.2 Percobaan Poisson ... 30
5.1.3 Distribusi Poisson ... 31
5.1.4 Model Regresi Poisson ... 33
5.1.5 Estimasi Parameter ... 34
5.1.6 Uji Ketepatan (Goodness of Fit) Model Regresi Poisson ... 35
5.2 Model Regresi Binomial Negatif ... 38
5.2.1 Overdispersi Metode Binomial Negatif ... 38
5.2.2 Distribusi Binomial Negatif ... 40
5.2.3 Estimasi parameter untuk model regresi binomial negatif ... 41
5.2.4 Uji ketepatan (goodness of fit) model regresi binomial negatif ... 44
5.3 Aplikasi Numerik ... 45
5.3.1 Data Penelitian ... 45
5.3.2 Proses Analisis Data ... 47
BAB 6 RENCANA TAHAPAN BERIKUTNYA ... 52
BAB 7 KESIMPULAN DAN SARAN ... 53
7.1 Kesimpulan ... 53
7.2 Saran ... 53
DAFTAR PUSTAKA ... 55
vii DAFTAR TABEL
Tabel 2.1 Faktor-faktor penyebab kecelakaan lalu-lintas jalan ... 6 Tabel 5.1 Rating factors dan ratingclasses untuk data penelitian ... 46 Tabel 5.2 Analisis deviance model regresi Poisson tiap rating classes ... 47 Tabel 5.3 Analisis deviance model regresi Poisson untuk tiap rating classes
yang sudah signifikan. ... 48 Tabel 5.4 Estimasi parameter untuk model Poisson rating classes yang
signifikan ... 49 Tabel 5.5 Estimasi parameter untuk model Binomial Negatif (MLE) rating
classes ... 49 Tabel 5.6 Estimasi parameter untuk model Binomial Negatif (MLE) rating
1 BAB 1 PENDAHULUAN
1.1 Latar Belakang
Kecelakaan lalu lintas merupakan masalah yang umum terjadi dalam penyelenggaraan sistem transportasi di banyak negara. Pada negara-negara berkembang, termasuk di Indonesia, kecelakaan lalu lintas ini cenderung mengalami peningkatan. PT Jasa Raharja (persero) mencatat, setiap 15 menit terdapat satu orang yang meninggal dunia di Indonesia karena kecelakaan lalu lintas. Ini terlihat dari tingginya biaya santunan kecelakaan yang diklaim kepada asuransi Jasa Raharja mencapai 1 Triliun rupiah setiap tahunnya. PT Jamsostek (Persero) mencatat klaim kecelakaan lalu lintas mendominasi dibanding kecelakaan kerja lainnya. Kepala PT Jamsostek (Persero) Cabang Tanjung Priok Muhammad Akip mengungkapkan, kecelakaan lalu lintas masih mendominasi daftar panjang kecelakaan kerja yang diklaim ke Jamsostek setiap tahunnya.
Jumlah kecelakaan yang tinggi akan menjadi salah satu faktor yang tidak menguntungkan bagi perusahaan asuransi kendaraan bermotor. Disamping itu, seluruh pihak harus lebih mewaspadai faktor-faktor yang menyebabkan terjadinya kecelakaan lalu lintas. Masih tingginya angka kecelakaan di jalan raya juga menjadi pekerjaan rumah besar bagi pemerintah.
faktor manusia memiliki kontribusi terbesar pada kecelakaan kendaraan bermotor, sehingga faktor tersebut sangat penting untuk diamati dalam upaya mengurangi terjadinya kecelakaan lalu lintas yang melibatkan kendaraan bermotor. Perbedaan karakteristik sosio-ekonomi, karakteristik pergerakan dan perilaku pengemudi kendaraan bermotor menjadi dasar pertimbangan dalam identifikasi faktor-faktor penyebab terjadinya kecelakaan.
kendaraan bermotor di lalu lintas, sehingga jumlah korban kecelakaan kendaraan bermotor akan semakin berkurang dari tahun ke tahun.
1.2 Perumusan Masalah
Dari latar belakang tersebut berikut ini dapat dirumuskan beberapa permasalahan yang menjadi kajian dalam penelitian ini, yaitu:
1. Mempelajari lebih jauh tentang estimasi parameter pada model regresi Poisson.
2. Mempelajari lebih jauh tentang masalah overdispersi yang sering terjadi pada model regresi Poisson.
3. Mempelajari model regresi Binomial Negatif dan Poisson Tergeneralisasi dalam mengatasi masalah overdispersi pada regresi Poisson.
4. Mengaplikasikan secara numerik model regresi Binomial Negatif dan Poisson Tergeneralisasi pada kasus kecelakaan kendaraan bermotor di lalu lintas di Kota Padang.
1.3 Tujuan Penelitian
1.4 Keutamaan dan Inovasi Penelitian
5 BAB 2
TINJAUAN PUSTAKA
Pada bab ini akan dibahas teori-teori yang digunakan sebagai dasar untuk membahas materi pada bab-bab selanjutnya.
2.1 Kendaraan Bermotor
Kendaraan adalah suatu sarana angkut di jalan yang terdiri atas kendaraan bermotor dan kendaraan tidak bermotor. Kendaraan bermotor adalah setiap kendaraan yang digerakkan oleh peralatan mekanik berupa mesin selain kendaraan yang berjalan di atas rel, terdiri dari kendaraan bermotor perseorangan dan kendaraan bermotor umum. Kendaraan tidak bermotor adalah kendaraan yang digerakkan oleh tenaga orang atau hewan (UU RI No. 22 Tahun 2009).
Jenis kendaraan bermotor, yaitu (UU RI No. 22 Tahun 2009):
1. Sepeda motor adalah kendaraan bermotor beroda dua dengan atau tanpa rumah-rumah dan dengan atau tanpa kereta samping atau kendaraan bermotor beroda tiga tanpa rumah-rumah.
2. Mobil penumpang adalah setiap kendaraan bermotor yang dilengkapi sebanyak-banyaknya 8 (delapan) tempat duduk tidak termasuk tempat duduk pengemudi, baik dengan maupun tanpa perlengkapan pengangkutan bagasi. 3. Mobil bus adalah setiap kendaraan bermotor yang dilengkapi lebih dari 8
(delapan) tempat duduk tidak termasuk tempat duduk pengemudi, baik dengan maupun tanpa perlengkapan pengangkutan bagasi.
4. Mobil barang adalah setiap kendaraan bermotor selain dari yang termasuk dalam sepeda motor, mobil penumpang dan mobil bus.
2.2 Faktor-faktor Penyebab Kecelakaan Lalu Lintas
Secara umum ada empat faktor utama penyebab kecelakaan; faktor pengemudi (road user), faktor kendaraan (vehicle), faktor lingkungan jalan (road environment) dan faktor cuaca. Kecelakaan yang terjadi pada umumnya tidak hanya disebabkan oleh satu faktor saja, melainkan hasil interaksi antar faktor lain.
Pada dasarnya faktor-faktor tersebut berkaitan atau saling menunjang bagi terjadinya kecelakaan. Namun, dengan diketahuinya faktor penyebab kecelakaan yang utama dapat ditentukan langkah-langkah penanggulangan untuk menurunkan jumlah kecelakaan. Berdasarkan penelitian yang pernah ada faktor penyebab kecelakaan dapat dikomposisikan dalam tabel 2.1 berikut :
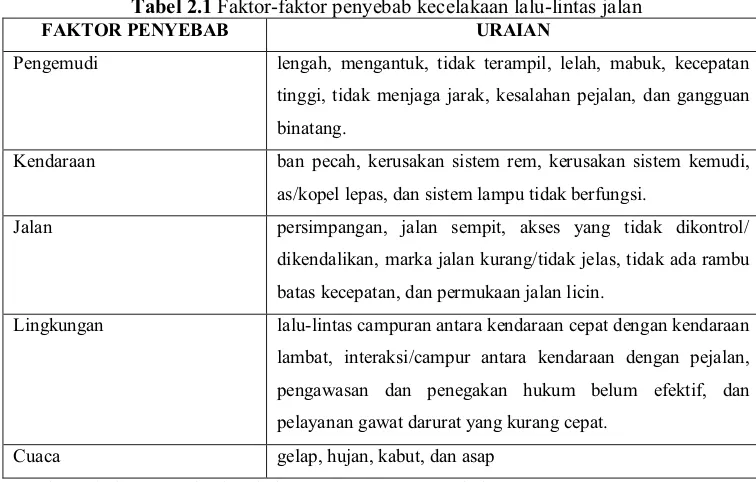
Tabel 2.1 Faktor-faktor penyebab kecelakaan lalu-lintas jalan
FAKTOR PENYEBAB URAIAN
Pengemudi lengah, mengantuk, tidak terampil, lelah, mabuk, kecepatan
tinggi, tidak menjaga jarak, kesalahan pejalan, dan gangguan
binatang.
Kendaraan ban pecah, kerusakan sistem rem, kerusakan sistem kemudi,
as/kopel lepas, dan sistem lampu tidak berfungsi.
Jalan persimpangan, jalan sempit, akses yang tidak dikontrol/
dikendalikan, marka jalan kurang/tidak jelas, tidak ada rambu
batas kecepatan, dan permukaan jalan licin.
Lingkungan lalu-lintas campuran antara kendaraan cepat dengan kendaraan
lambat, interaksi/campur antara kendaraan dengan pejalan,
pengawasan dan penegakan hukum belum efektif, dan
pelayanan gawat darurat yang kurang cepat.
Cuaca gelap, hujan, kabut, dan asap
Sumber: Direktorat Jenderal Perhubungan Darat ± Dept.Perhubungan
2.3 Variabel Random dan Fungsi Distribusi
Definisi 2.1 Variabel random ࢄ adalah suatu fungsi dengan daerah asal ࡿ dan daerah hasil bilangan real sedemikian sehingga ሺࢋሻ ൌ ࢞, dengan ܍ א ܁ dan ܠ א ज.
Definisi 2.2 Fungsi ݂ሺݔሻ adalah fungsi padat peluang untuk variabel random kontinu ܺ jika dan hanya jika memenuhi sifat berikut,
݂ሺݔሻ Ͳǡ ݑ݊ݐݑ݇ݏ݁݉ݑܽݔݎ݈݁ܽǡ ݀ܽ݊
݂ሺݔሻ݀ݔ ൌ ͳି .
Salah satu konsep penting dalam probabilitas adalah ekspektasi dan variansi dari variabel random. Berikut ini adalah beberapa definisi dan teorema mengenai ekspektasi dan variansi.
Teorema 2.1 Jika Y adalah suatu variabel random dengan fungsi densitas ݂ሺݕሻǡܽ dan ܾ adalah suatu konstanta, dan ݃ሺݕሻ dan ݄ሺݕሻ adalah fungsi real, maka
ܧሾܽ݃ሺܻሻ ܾ݄ሺܻሻሿ ൌ ܽܧሾ݃ሺܻሻሿ ܾܧሾ݄ሺܻሻሿ . Definisi 2.3 Variansi dari variabel random X diberikan oleh ܸܽݎሺܺሻ ൌ ܧሾሺܺ െ ߤሻଶሿ .
Teorema 2.2 Jika Y adalah suatu variabel random dari a dan b adalah suatu konstanta, maka
ܸܽݎሺܻܽ ܾሻ ൌ ܽଶܸܽݎሺܻሻ.
Distribusi kontinu yang sering terjadi dalam aplikasi adalah disribusi gamma. Distribusi ini berhubungan dengan suatu fungsi yang disebut fungsi gamma.
߁ሺ݊ሻ ൌ ݔ
݁ି௫݀ݔ ൌ ݊Ǩ .
Teorema 2.3 Fungsi Gamma mendukung sifat-sifat berikut: ߁ሺߢሻ ൌ ሺߢ െ ͳሻ߁ሺߢ െ ͳሻߢ ͳ
߁ሺ݊ሻ ൌ ሺ݊ െ ͳሻǨ .
Banyak keadaan yang menghendakinya mencatat sekaligus nilai-nilai beberapa variabel random dan tidak hanya melibatkan satu variabel random saja. Sehingga fungsi padat peluang gabungannya dapat kita lihat dari definisi-definisi berikut.
Definisi 2.5 Fungsi padat peluang (fpp) gabungan dari k-dimensi variabel random diskret ܺ ൌ ሺܺଵǡ ܺଶǡ Ǥ Ǥ Ǥ ǡ ܺ୩ሻ didefinisikan dengan
݂ሺݔଵǡ ݔଶǡ ǥ ǡ ݔሻ ൌ ܲሾܺଵൌ ݔଵǡ ܺଶൌ ݔଶǡ ǥ ǡ ܺ ൌ ݔሿ
Untuk semua nilai ݔ ൌ ሺݔଵǡ ݔଶǡ ǥ ǡ ݔሻܺǤ
Definisi 2.6 Jika pasangan ሺܺଵǡ ܺଶሻ dari variabel random kontinu dari fpp gabungan ݂ሺݔଵǡ ݔଶሻ, maka fpp marginal dari ܺଵ dan ܺଶ adalah
݂ଵሺݔଵሻ ൌ න ݂ሺݔଵǡ ݔଶሻ
ି ݀ݔଶ
݂ଶሺݔଶሻ ൌ ݂ሺݔି ଵǡ ݔଶሻ݀ݔଵ.
Definisi dari peluang bersyarat suatu kejadian bisa dilanjutkan pada konsep varabel random bersyarat, didasarkan pada definisi berikut ini.
Definisi 2.7 Jika ܺଵ dan ܺଶ adalah variabel random kontinu atau diskret dengan fpp gabungan ݂ሺݔଵǡ ݔଶሻ, kemudian fungsi kepadatan peluang bersyarat (fpp bersyarat) dari ܺଶ diberikan ܺଵൌ ݔଵ didefinisikan oleh
Untuk nilai ݔଵݏ݄݂݁݅݊݃݃ܽଵሺݔଵሻ Ͳ, dan nol lainnya.
Definisi 2.8 Jika ܺ dan ܻ adalah variabel random distribusi gabungan, kemudian ekspektasi dari ܻ diberikan ܺ ൌ ݔ diberikan oleh
ܧሺܻȁݔሻ ൌ ݕ݂ሺݕȁݔሻ
௬
ܻܺ
ܧሺܻȁݔሻ ൌ ݕ݂ሺݕȁݔሻି ݀ݕ jika X dan Y kontinu.
2.4 Keluarga Eksponensial
Distribusi keluarga eksponensial merupakan salah satu kunci pembangun
generalized linear modeling (GLM).
2.4.1 Distribusi keluarga eksponensial
Menurut (Jong & Heller, 2008) distribusi dari keluarga eksponensial dapat berbentuk:
݂ሺݕሻ ൌ ܿሺݕǡ ߶ሻ݁ݔ ቊݕߠ െ ܽሺߠሻ߶ ቋ (2.1)
dimana ߠ dan ߶ adalah parameter. Parameter ߠ disebut parameter kanonik dan ߶ parameter dispersi. Probabilitas fungsi yang dapat ditulis sebagai (2.1) dikatakan anggota keluarga eksponensial. Pemilihan fungsi ܽሺߠሻ dan ܿሺݕǡ ߶ሻ ditentukan oleh fungsi probabilitas aktual seperti binomial, normal atau Gamma
ܧሺݕሻ ൌ ܽሶሺߠሻǡܸܽݎሺݕሻ ൌ ߶ܽሷሺߠሻ. (2.2) Dimana ܽሶሺߠሻ dan ܽሷሺߠሻ adalah turunan pertama dan kedua dari ܽሺߠሻterhadap ߠ.
Bukti: ߲݂ሺݕሻ
߲ߠ ൌ ݂ሺݕሻ ቈ
kemudian kedua ruas diintegralkan terhadap y, න߲݂ሺݕሻ߲ߠ ݀ݕ ൌන ݂ሺݕሻ ቈݕ െ ܽሶሺߠሻ߶ ݀ݕ
߲
߲ߠන ݂ሺݕሻ ݀ݕ ൌ ܧ ቈ
ݕ െ ܽሶሺߠሻ ߶
dengan menggunakan Definisi 2.2 dan Teorema 2.1, kita peroleh sebagai berikut, ߲
߲ߠ ͳ ൌ
ܧሾݕሿ െ ܽሶሺߠሻ ߶
Ͳ ൌܧሾݕሿ െ ܽሶሺߠሻ߶
ܧሾݕሿ ൌ ܽሶሺߠሻ ൌ ߤ (2.3) dan
߲ଶ݂ሺݕሻ
߲ߠଶ ൌ ݂ሺݕሻ ቈݕ െ ܽሶሺߠሻ߶ ଶ
െ ݂ሺݕሻܽሷሺߠሻ߶
kemudian kedua ruas diintegralkan terhadap y,
න߲ଶ߲ߠ݂ሺݕሻଶ ݀ݕ ൌ න ݂ሺݕሻ ቈݕ െ ܽሶሺߠሻ߶
ଶ
݀ݕ െ න ݂ሺݕሻܽሷሺߠሻ߶ ݀ݕ
߲ଶ
߲ߠଶන ݂ሺݕሻ ݀ݕ ൌ ܧ ቊ
ݕ െ ܽሶሺߠሻ ߶ ቋ
ଶ
൩ െ ܧ ቈܽሷሺߠሻ߶
dengan mengunakan Definisi 2.2 dan Teorema 2.1, kita peroleh sebagai berikut, ߲ଶ
߲ߠଶͳ ൌ
ܧሾݕ െ ߤሿଶ
߶ଶ െ
ܽሷሺߠሻ ߶
Ͳ ൌܸܽݎሺݕሻ߶ଶ െܽሷሺߠሻ߶
ܸܽݎሺݕሻ ൌ ߶ܽሷሺߠሻ. (2.4)
ܽሷሺߠሻ ൌ߲ܽሶሺߠሻ߲ߠ ൌ߲ߤ߲ߠ ؠ ܸሺߤሻ (2.5)
dan karenanya ܸܽݎሺݕሻ ൌ ߶ܸሺߤሻ di mana ܸሺߤሻ disebut fungsi variansi, menunjukkan hubungan antara rataan dan varians.
2.4.2 Distribusi standar dalam format keluarga eksponensial
Beberapa anggota keluarga eksponensial, diantaranya adalah distribusi Poisson, distribusi normal, distribusi gamma dan distribusi binomial negatif. 1. Distribusi Poisson
Fungsi probabilitas Poisson adalah, ݂ሺݕሻ ൌ݁ିఓݕǨ ǡݕ ൌ Ͳǡͳǡʹǡ ǥߤ௬
Maka,
݂ሺݕሻ ൌ ݁ିఓݕǨ ൌ െߤ ݕ ߤ ߤ௬ ݕǨͳ
ൌ ݕǨ ሺݕ ߤ െ ߤሻͳ
ൌ ܿሺݕǡ ߶ሻ ݕߠ െ ܽሺߠሻ߶ ǡ
dengan ܿሺݕǡ ߶ሻ ൌ ଵ
௬Ǩǡ ߶ ൌ ͳǡ ߠ ൌ ሺߤሻ ܽሺߠሻ ൌ ߤ ൌ ݁ఏ.
Ini menunjukkan bahwa Poisson adalah termasuk keluarga eksponensial dan ܧሺݕሻ ൌ ܽሶሺߠሻ ൌ ݁ఏ ൌ ߤ
ܸܽݎሺݕሻ ൌ ߶ܽሷሺߠሻ ൌ ͳ ൈ ݁ఏ ൌ ߤ.
Distribusi Normal
݂ሺݕሻ ൌ ͳ
Ini menunjukkan bahwa distribusi Normal adalah termasuk keluarga eksponensial dan
ܽሶሺߠሻ ൌ ߠ ൌ ߤǡ ܸܽݎሺݕሻ ൌ ߶ܽሷሺߠሻ ൌ ߪଶǤ
2. Distribusi Gamma
Fungsi probabilitas Gamma adalah,
݂ሺݕሻ ൌīݕሺݒሻ ൬ିଵ ݕݒߤ ൰௩݁ି௬௩ ఓΤ ǡݕ Ͳǡ
Maka,
ൌ െ ݕ െ īሺݒሻ ݒ ݕ ݒ ݒ െ ݒ ߤ െݕݒߤ
ൌ ሺݒ െ ͳሻ ݕ െ īሺݒሻ ݒ ݒ െ ߤݒିଵݕሺെߤݒିଵିଵሻ
ൌ ݕሺ௩ିଵሻīሺݒሻ ቆǤ ݒ௩ ݕሺെߤିଵݒିଵሻ െ ߤቇ
ൌ ܿሺݕǡ ߶ሻ ൜ݕߠ ܽሺߠሻ߶ ൠ
dengan ܿሺݕǡ ߶ሻ ൌ ୷ ቀభషದದ ቁ
மభದīቀభ ದቁ
ǡ ߶ ൌ ݒିଵǡ ߠ ൌ െߤିଵܽሺߠሻ ൌ ሺെߠିଵሻ.
Ini menunjukkan bahwa Gamma adalah termasuk keluarga eksponensial dengan
ܧሺݕሻ ൌ ܽሶሺߠሻ ൌ െߠሺߠିଶሻ ൌ ߤǡ ܸܽݎሺݕሻ ൌ ߶ܽሷሺߠሻ ൌ ݒିଵ ͳ
ߠଶ ൌߤ ଶ
ݒ Ǥ
Distribusi ߯௩ଶ merupakan ܩሺݒǡ௩
ଶሻ, sehingga Chi-square juga merupakan
keluarga eksponensial. 3. Binomial negatif
Fungsi probabilitas binomial negatif adalah, ݂ሺݕሻ ൌīሺݕ ͳሻīሺݕ ݒሻīሺݒሻ ൬ݒ ߤ൰ݒ ௩൬ݒ ߤ൰ߤ ௬
di mana rataan ܧሺݕሻ ൌ ߤ, dan variansi adalah ܸܽݎሺݕሻ ൌ ߤ ߤଶݒିଵ. Maka,
݂ሺݕሻ ൌ ቈīሺݕ ͳሻīሺݕ ݒሻīሺݒሻ ൬ݒ ߤ൰ݒ ௩൬ݒ ߤ൰ߤ ௬
ൌ ܿሺݕǡ ߶ሻ ൜ݕߠ ܽሺߠሻ߶ ൠ
dengan ܿሺݕǡ ߶ሻ ൌ īሺ௬ା௩ሻ
īሺ௬ାଵሻīሺ௩ሻǡ ߶ ൌ ͳǡ ߠ ൌ ቀ ఓ
௩ାఓቁ ܽሺߠሻ ൌ െݒ ൫ͳ െ
݁ఏሻ.
Ini menunjukkan bahwa binomial negatif termasuk keluarga eksponensial dengan
ܧሺݕሻ ൌ ܽሶሺߠሻ ൌͳ െ ݁ݒ݁ఏఏ ൌ ߤǡ ܸܽݎሺݕሻ ൌ ߶ܽሷሺߠሻ ൌሺͳ െ ݁ݒ݁ఏఏሻଶൌ ߤ ߤଶݒିଵǤ
2.5 Estimasi Maksimum Likelihood (MLE)
MLE didasarkan pada pemilihan estimasi parameter yang memaksimalkan likelihood sampel yang diamati ݕଵǡ ǥ ǡ ݕ. Setiap ݕ merupakan realisasi dari ݂ሺݕሻ, dan demikian juga fungsi probabilitas ݂ሺݕሻ. Probabilitas tergantung ߠ dan, jika ߶ ada, fungsi probabilitas ditulis sebagai ݂ሺݕǢ ߠǡ ߶ሻ. Jika ݕ independen maka fungsi probabilitas gabungan adalah
݂ሺݕǢ ߠǡ ߶ሻ ൌ ෑ ݂ሺݕǢ ߠǡ ߶ሻ
ୀଵ
ܮሺߠǡ ߶ሻ ൌ ෑ ݂ሺݕǢ ߠǡ ߶ሻǤ
ୀଵ
(2.6)
Maka untuk memperoleh nilai ߠ߶ yang memaksimalkan ܮሺߠǡ ߶ሻ harus diderivatifkan dengan langkah-langkah sebagai berikut:
1. Nilai ߠ diperoleh dari derivatif pertama ߲
߲ߠ ܮሺߠǡ ߶ሻฬఏୀఏ ൌ Ͳ
߲ଶ
߲ߠଶܮሺߠǡ ߶ሻቤ ఏୀఏ
൏ Ͳ
Log-likelihood ݈ሺߠǡ ߶ሻ adalah logaritma dari likelihood:
݈ሺߠǡ ߶ሻ ൌ ݈݊ ݂ሺݕǢ ߠǡ ߶ሻ
ୀଵ
Ǥ (2.7)
Metode maksimum likelihood memilih nilai-nilai ߠ dan ߶ yang memaksimalkan likelihood atau ekuivalen, likelihood. Maksimalisasi log-likelihood lebih disukai karena lebih mudah untuk bekerja dengan analitis. Penduga maksimum likelihood (MLE) dari ߠ dan ߶ dilambangkan sebagai ߠ߶.
2.6 Statistic Score
Misalkan suatu variabel random kontinu Y memiliki fungsi kepadatan ݂ሺݕǢ ߠሻ yang tergantung kepada parameter tunggal ߠ (atau dalam kasus diskret, ݂ሺݕǢ ߠሻ adalah fungsi peluang). Fungsi log-likelihood adalah algoritma dari ݂ሺݕǢ ߠሻ sebagai fungsi dari ߠ, yaitu
݈ሺߠǢ ݕሻ ൌ ݂ሺݕǢ ߠሻǤ
Banyak hasil-hasil kunci pada GLM berhubungan dengan turunan pertama dari fungsi turunan pertama dari fungsi likelihood ini yaitu
ܷ ൌ݀ߠ݈݀
yang disebut dengan score.
݀ ݂ሺݕǢ ߠሻ ݀ߠ ൌ
ͳ ݂ሺݕǢ ߠሻ
݂݀ሺݕǢ ߠሻ
݀ߠ Ǥ (2.8)
Bila diambil ekspektasi dari (2.8), maka diperoleh ܧሺܷሻ ൌ න݀ ݂ሺݕǢ ߠሻ݀ߠ ݂ሺݕǢ ߠሻ݀ݕ ൌ න݂݀ሺݕǢ ߠሻ݀ߠ ݀ݕ
dengan pengintegralan terhadap y.
Selanjutnya, pengintegralan pada sisi kanan adalah න݂݀ሺݕǢ ߠሻ݀ߠ ݀ݕ ൌ݀ߠ݀ න ݂ሺݕǢ ߠሻ ݀ݕ ൌ݀ߠ ͳ ൌ Ͳ݀
karena ݂ሺݕǢ ߠሻ ݀ݕ ൌ ͳ. Dengan demikian,
ܧሺܷሻ ൌ Ͳ (2.9)
Jika (2.8) diturunkan terhadap ߠ dan kemudian diambil ekspektasinya, maka
ܧ ቆ݀ߠ݀ ݀ ݂ሺݕǢ ߠሻ݀ߠ ቇ ൌ݀ߠ ܧ ቆ݀ ݀ ݂ሺݕǢ ߠሻ݀ߠ ቇ
ൌ݀ߠ݀ න݀ ݂ሺݕǢ ߠሻ݀ߠ ݂ሺݕǢ ߠሻ݀ݕ
ൌ݀ߠ݀ න݂ሺݕǢ ߠሻͳ ݂݀ሺݕǢ ߠሻ݀ߠ ݂ሺݕǢ ߠሻ݀ݕ
ൌ݀ߠ݀ଶଶන ݂ሺݕǢ ߠሻ ݀ݕ
ൌ݀ߠ݀ଶଶͳ݀ݕ ൌ ͲǤ (2.10)
Karena ݂ሺݕǢ ߠሻ ݀ݕ ൌ ͳ. Bentuk ௗ
ௗఏ
ௗ ୪୭ ሺ௬Ǣఏሻ
ௗఏ ݂ሺݕǢ ߠሻ݀ݕ dapat ditulis
݀ ݀ߠන
݀ ݂ሺݕǢ ߠሻ
݀ߠ ݂ሺݕǢ ߠሻ݀ݕ ൌ න ݀ ݀ߠቈ
݀ ݂ሺݕǢ ߠሻ
݀ߠ ݂ሺݕǢ ߠሻ ݀ݕ
ൌ න݀ଶ ݂ሺݕǢ ߠሻ݀ߠଶ ݂ሺݕǢ ߠሻ݀ݕ න݀ ݂ሺݕǢ ߠሻ݀ߠ ݂݀ሺݕǢ ߠሻ݀ߠ ݀ݕǤ
Dengan mensubstitusi (2.8) pada bagian kedua dari persamaan di atas, diperoleh
ൌ න݀ଶ ݂ሺݕǢ ߠሻ݀ߠଶ ݂ሺݕǢ ߠሻ݀ݕ න ቈ݀ ݂ሺݕǢ ߠሻ݀ߠ
ଶ
݂ሺݕǢ ߠሻ݀ݕ ൌ Ͳ
dengan demikian,
ܧ ቈ݀ଶ ݂ሺݕǢ ߠሻ݀ߠଶ ൌ െܧ ቈ݀ ݂ሺݕǢ ߠሻ݀ߠ
ଶ
൩ (2.11)
dalam terminologi statistic score ditulis sebagai ܧሾܷƍሿ ൌ െܧሾܷଶሿ
dengan ܷƍ menotasikan turunan dari U terhadapߠ. Karena E[U] = 0, maka variansi dari U yang disebut dengan informasi, adalah
ܸܽݎሺܷሻ ൌ ܧሾܷଶሿ ൌെܧሾܷƍሿǤ (2.12) Secara umum, misalkan variabel random ܻଵǡ ܻଶǡ ǥ ǡ ܻே memiliki distribusi peluang yang bergantung kepada parameter-parameter ߚଵǡ ߚଶǡ ǥ ǡ ߚ. Dengan fungsi log-likelihood dari ܻଵǡ ܻଶǡ ǥ ǡ ܻே adalah
݈ሺߚǢ ݕሻ ൌ ݈ሺߚǢ ݕሻ ே
ୀଵ
ܷ ൌ߲݈ሺߚǢ ݕሻ߲ߚ ൌ
߲݈ሺߚǢ ݕሻ
߲ߚ ே
ୀଵ
dengan argumen yang sama dengan (2.9), maka
ܧ ቈ߲݈ሺߚǢ ݕ߲ߚ ሻ
ൌ Ͳ (2.13)
dan dengan demikian ܧ൫ߚ൯ ൌ Ͳ untuk setiap j.
Matrik informasi (information matrix) didefinisikan sebagai matriks variansi±kovariansi (variance-covariance matrix) dari ܷ, ܫ ൌ ܧሺ்ܷܷሻ dengan U
adalah vektor dari ܷଵǡ ܷଶǡ ǥ ǡ ܷ, sehingga
ܫ௦ ൌ ܧൣܷܷ௦൧ ൌ ܧ ቈ߲ߚ߲݈
߲݈ ߲ߚ௦Ǥ
Dengan argumen yang analog dengan kasus variabel random tunggal dengan parameter tunggal, maka
ܧ ቈ߲ߚ߲ଶ݈
߲ߚ௦ ൌ െܧ ቈ
߲݈ ߲ߚ
߲݈
߲ߚ௦ (2.14)
sehingga dengan demikian, elemen dari matriks informasi adalah
ܫ௦ ൌ െܧ ቈ ߲ ଶ݈
߲ߚ߲ߚ௦Ǥ (2.15)
2.7 Generalized linear model (GLM)
1. Distribusi dari variabel respon didasarkan pada keluarga ekponensial sehingga distribusi dari variabel respon tidak harus normal/mendekati normal. 2. Transformasi dari rataan variabel respon berhubungan linier dengan variabel
penjelas.
GLM penting dalam analisis data asuransi. Dengan data asuransi, asumsi model normal sering kali tidak berlaku. Sebagai contoh, ukuran klaim, frekuensi klaim dan terjadinya klaim pada satu polis adalah semua hasil yang tidak normal.
Diberi respon y, generalized linear model (GLM) adalah
݂ሺݕሻ ൌ ܿሺݕǡ ߶ሻ݁ݔ ൜ݕߠ െ ܽሺߠሻ߶ ൠ ǡ݃ሺߤሻ ൌ ݔ்ߚǤ (2.16)
dimana,
1. Persamaan ݂ሺݕሻ menyatakan bahwa distribusi respons merupakan keluarga eksponensial. Persamaan kedua menetapkan transformasi rataan, ݃ሺߤሻ , adalah berhubungan linear dengan variabel penjelas ݔ.
2. Pemilihan ܽሺߠሻ menentukan distribusi respon.
3. Pemilihan ݃ሺߤሻ, disebut link, menentukan bagaimana rataan terkait ke variabel penjelas ݔ. Dalam model linier normal, hubungan antara rataan dari y dan variabel-variabel penjelas ߤ ൌ ݔ்ߚ. Dalam GLM, diperumum menjadi ݃ሺߤሻ ൌ ݔ்ߚ, di mana ݃ adalah monoton, fungsi terdiferensialkan (seperti log
atau akar kuadrat).
5. Pengamatan pada ݕ diasumsikan independen.
2.7.1 Fungsi Link
Fungsi link adalah suatu fungsi yang menghubungkan ߤ ൌ ܧሺݕሻ dengan fungsi linear ࢞ࢀࢼ. Sebagian besar hasil regresi bergantung pada pemilihan fungsi link-nya. Suatu fungsi link disebut fungsi link kanonik (canonical link function) apabila ݃ሺߤሻ ൌ ߟ ൌ ߠ, dimana ߠ adalah parameter kanonik. Berikut beberapa fungsi link kanonik untuk beberapa distribusi.
Distribusi Fungsi Link Kanonik
Normal ߟ ൌ ߤ
Poisson ߟ ൌ ݈݃ߤ
Binomial ߟ ൌ ሾߨȀሺͳ െ ߨሻሿ
Gamma ߟ ൌ ߤିଵ
Invers ߟ ൌ ߤିଶ
2.7.2 Metode Iterasi Newton-Raphson
Metode Newton-Raphson adalah metode yang digunakan untuk menyelesaikan persamaan non-linear secara iteratif, misalnya mencari lokasi agar suatu fungsi maksimum pada persamaan likelihood. Dengan log-likelihood ݈ሺࢼሻ kita mengharapkan nilai డሺࢼሻ
డࢼ ൌ Ͳ dan maksimum.
Kita memperluas ߲݈ሺࢼሻȀ߲ࢼ mendekati ࢼ sehingga ߲݈ሺࢼሻ
߲ࢼ ൌ ݈ƍሺࢼሻ ൌሶ ݈ƍሺࢼሻ
߲ଶ݈ሺࢼሻ
߲ࢼ߲ࢼ࢚ሺࢼ െ ࢼሻǤ (2.17)
Persamaan (2.17) disamakan dengan nol sehingga diperoleh,
݈ƍሺࢼ
ሻ ߲ ଶ݈ሺࢼሻ
ࢼ ൌ ࢼെ ቈ߲
ࢼሺሻ dinotasikan sebagai nilai ࢼ pada iterasi ke-m. Diperoleh iterasi sebagai
berikut, merevisi ࢼ, mengarah pada urutan seperti yang dinyatakan di atas akan cepat konvergen. Pendekatan ini dapat diadaptasi ketika ࢼ adalah vektor. Perbarui persamaan (2.18) dengan matriks invers dimana ݈ƍሺࢼሻ adalah vektor dari turunan parsial ߲݈ ߲ߚΤ . Vektor ݈ƍሺࢼሻ disebut score vector, dan ݈ƍƍሺࢼሻ, matriks dari turunan parsial perkalian ߲ଶ݈Ȁ൫߲ߚ߲ߚ௦൯, disebut matriks Hessian. Tata cara mengevaluasi perulangan pada vektor skor dan matrik Hessian untuk memperbarui perkiraan seperti pada (2.18) disebut iterasi Newton-Raphson.
2.7.3 Estimasi Maksimum Likelihood
MLE dari ߚ dan ߶ diturunkan dengan memaksimalkan log-likelihood, yang didefinisikan,
dimana ݕ diasumsikan independen.
Untuk mencari maksimal, ݈ሺߚǡ ߶ሻ diturunkan terhadap ߚ.
2.7.4 Fisher Scoring
Fisher menyarankan menggantikan ݈ԢԢሺࢼሻ dalam (2.18) dengan ekspektasi ܧሾ݈ԢԢሺࢼሻሿ, dan menunjukkan bahwa ܧሾ݈ԢԢሺࢼሻሿ ൌ െܧሾ݈ᇱሺࢼሻ݈ᇱሺࢼሻ்ሿ.
Untuk menentukan ekspektasi dari turunan kedua, digunakan sifat pada (2.14) sehingga,
Matrik Hessian yang diharapkan (Expected Hessian Matrix) menjadi
െܧ ቆ߲ߚ߲ଶ݈
Iterasi untuk Fisher scoring menjadi
ߚሺ௧ାଵሻൌ ߚሺ௧ሻ ሾࢄࢀࢃࢄሿିࢄࢀࢃ (2.25)
dimana ࢃǡ ࢄǡ ߚሺ௧ሻǤ
2.7.5 Iteratively Weighted Least Square (IWLS)
ߚሺ௧ାଵሻൌ ߚሺ௧ሻ ሾࢄࢀࢃࢄሿିࢄࢀࢃǤ
Bentuk tersebut dapat dituliskan kembali menjadi: ߚሺ௧ାଵሻൌ ሾࢄࢀࢃࢄሿିࢄࢀࢃࢄߚሺ௧ሻ ሾࢄࢀࢃࢄሿିࢄࢀࢃ
ൌ ሾ்ܹܺܺሿିଵ൜்ܹܺܺߚሺ௧ሻ ்ܹܺ ൬߲ߟ
߲ߤ൰ሺݕ െ ߤሻൠ
ൌ ሾ்ܹܺܺሿିଵ்ܹܺ ൜ܺߚሺ௧ሻ ൬߲ߟ
߲ߤ൰ሺݕ െ ߤሻൠ
ൌ ሾ்ܹܺܺሿିଵ்ܹܺ ൜ߟ ൬߲ߟ
߲ߤ൰ሺݕ െ ߤሻൠ
ൌ ሾ்ܹܺܺሿିଵ்ܹܺ݃Ǥ (2.26)
݃ sering disebut sebagai working variate, yaitu :
݃ ൌ ߟ ൬߲ߟ߲ߤ൰ሺݕ െ ߤሻ (2.27)
݃ ൌ ߟ ൬߲ߟ߲ߤ
൰ ሺݕെ ߤሻ
dimana ߟ ൌ ்ܺߚ adalah prediktor linear.
Persamaan (2.26) merupakan hasil modifikasi dari metode Fisher scoring yang dapat dipandang sebagai Iteratively Weighted Least Square.
2.8 Goodness Of Fit
Menentukan suatu model dari suatu data dianggap sebagai cara untuk mengganti satu set data observasi dengan satu set nilai prediksinya (fitted values), Ɋො, yang diperoleh dari suatu model yang biasanya menyertakan parameter dengan jumlah yang relatif sedikit.
2.8.1 Pearson Chi-square
Ukuran lain yang biasa digunakan untuk uji goodnes of fit adalah Pearson Chi-square statistic (McCullagh & Nelder, 1989) yang didefinisikan sebagai
߯ଶ ൌ ሺݕെ ߤሻଶ
ܸܽݎሺߤሻ
ୀଵ
(2.28) Dimana ܸܽݎሺߤሻ yaitu fungsi variansi dari distribusi peluang datanya, dan ܸܽݎሺߤሻ ൌሺథ ሻ. Untuk sampel yang besar, Pearson Chi-square statistic
berdistribusi Chi-square dengan derajat bebas n-p, dimana n yaitu jumlah observasi dan p yaitu jumlah parameternya. Hipotesis untuk Pearson Chi-square statistic, yaitu:
ܪǣ ߤ ൌ ݁ሺߚ ߚଵݔଵ ڮ ߚݔሻ
ܪଵǣ ߤ ് ݁ሺߚ ߚଵݔଵ ڮ ߚݔሻ
ܪ diterima (yang berarti bahwa model regresinya tepat), yaitu jika nilai Pearson
Chi-square statistic, ܲ ൏ ߯ሺןǢିሻଶ . Atau bisa juga digunakan p-value
=൛߯ሺןǢିሻଶ ܲൟ untuk uji hipotesisnya, dimana ܪ diterima jika p-value !Į
2.8.2 Deviance
Deviance adalah sama dengan,
ܦ ൌ ʹ൫݈ሺ࢟Ǣ ࢟ሻ െ ݈ሺࣆǢ ࢟ሻ൯ (2.29)
di mana ݈ሺ࢟Ǣ ࢟ሻdan ݈ሺࣆǢ ࢟ሻadalah model log likelihood yang dievaluasi masing-masing di bawah ࣆ dan ࢟. Untuk sampel yang besar, Deviance-nya berdistribusi
Chi-square dengan derajat bebas n-p, di mana n adalah jumlah datanya dan p
adalah jumlah parameternya. Hipotesis yaitu:
ܪǣ ߤ ൌ ݁݁ݔሺߚ ߚଵݔଵ ڮ ߚݔሻ
ܪଵǣ ߤ ് ݁൫ߚ ߚଵݔଵ ڮ ߚݔ൯ (2.30)
ܪ diterima berarti bahwa model regresinya tepat atau bisa digunakan, yaitu jika
Deviance bisa digunakan untuk membandingkan model bersarang (nested model) jika digunakan estimasi maksimum likelihood (McCullagh & Nelder, 1989). Membandingkan antara model tereduksi dengan model penuh. Misalkan ܦଵ dan ݂݀ଵ merupakan Deviance dan derajat bebas untuk model penuh, dan ܦଶ
dan ݂݀ଶ merupakan Deviance dan derajat bebas untuk model yang tereduksi. Kemudian dicari selisih dari Deviance model tereduksi dengan Deviance model penuh,
οܦ ൌ ܦଶെ ܦଵ (2.31)
Dimana untuk sampel οܦ akan berdistribusi Chi-square dengan derajat bebasnya ݂݀ଶെ ݂݀ଵ (sebanyak j).
ܪ diterima, yang berarti bahwa variabel independen yang dikeluarkan
dari model penuhnya itu bernilai nol, yang berarti bahwa model tereduksi lebih baik dari model penuh, jika οܦ ൏ ߯ሺןǢሻଶ . Namun jika dari uji tersebut, model penuh masih lebih baik dari model reduksinya (ܪ ditolak), maka perlu dilihat lagi apakah masih ada variabel independen lain (selain yang pertama) yang tidak signifikan dalam model penuhnya. Jika tidak ada lagi maka model penuhnya bisa digunakan. Namun jika masih ada, maka dilakukan reduksi variabel lagi dan uji model reduksinya.
Keuntungan Deviance dibandingkan Pearson Chi-square statistic yaitu bahwa Deviance bisa digunakan untuk membandingkan model bersarang (nested model) jika digunakan estimasi maksimum likelihood (McCullagh & Nelder, 1989). Dalam hal ini membandingkan model tersarang berarti membandingkan antara model dengan nilai observasi sebenarnya dengan model dengan nilai prediksinya.
2.8.3 AIC dan BIC
Ketika beberapa model cocok, dapat membandingkan performa model-model alternatif berdasarkan beberapa likelihood langkah-langkah yang telah diusulkan dalam literatur statistik. Dua metode yang paling sering digunakan adalah ukuran Akaike Information Criteria (AIC) dan Bayesian Schwartz Information Criteria (BIC). AIC didefinisikan sebagai
ܣܫܥ ൌ െʹ݈ ʹ (2.32) dimana ݈menunjukkan log-likelihood dievaluasi di bawah ࣆ dan jumlah parameter.
Untuk ukuran ini, semakin kecil AIC, semakin baik model. BIC didefinisikan sebagai (Schwarz, 1978),
28 BAB 3
TUJUAN DAN MANFAAT PENELITIAN
3.1 Tujuan Penelitian
Tujuan dalam penelitian ini adalah untuk mengatasi overdispersi yang terjadi pada model regresi Poisson dengan menggunakan model regresi model Binomial Negatif dan Poisson Tergeneralisasi, kemudian mengestimasi parameter kedua model regresi. Dari dua tipe model regresi yang diperoleh, akan diuji ketepatan model. Kemudian diimplementasikan pada kasus kecelakaan kendaraan bermotor di lalu lintas di Kota Padang.
3.2 Manfaat Penelitian
29 BAB 4
METODE PENELITIAN
Tahapan metode yang dilakukan dalam penelitian ini adalah sebagai berikut:
1. Pengumpulan literatur yang berhubungan dengan Model Regresi Poisson, Binomial Negatif dan Poisson Tergeneralisasi.
2. Menentukan variabel respon dan variabel bebas.
3. Melakukan uji signifikansi dan interaksi antara faktor utama pada model regresi Poisson dengan melakukan Analisis Deviance.
4. Melakukan uji signifikansi dan interaksi antara faktor cabang pada model regresi Poisson dengan melakukan Analisis Deviance.
5. Membentuk model dugaan regresi Poisson.
6. Mereduksi model yang diperoleh dengan menggunakan signifikansi.
7. Estimasi semua parameter yang telah signifikan untuk model regresi Poisson. 8. Pendeteksian overdispersi pada data dengan melihat nilai Pearson Chi-square
dan Deviance yang dibagi dengan derajat bebasnya.
9. Lakukan kembali langkah (7) dan (8) untuk model regresi Binomial Negatif. 10. Identifikasi kebaikan model regresi Poisson dan Binomial Negatif dengan
melihat Pearson Chi-square,Deviance dan log-likelihood dalam permasalah-an overdispersi.
11. Melakukan interpretasi terhadap hasil yang diperoleh.
30 BAB 5
HASIL DAN PEMBAHASAN
5.1 Model Regresi Poisson
5.1.1 Overdispersi
Overdispersi merupakan salah satu masalah yang sering terjadi dalam analisis regresi Poisson. Distribusi Poisson sering dianjurkan dalam menghitung data tetapi distribusi ini tidaklah mencukupi karena data menampilkan variansi yang lebih besar dari yang diprediksikan oleh Poisson. Hal ini diistilahkan dengan overdispersi atau variansi ekstra-Poisson. Overdispersi bisa terjadi karena pengelompokkan di dalam populasi dan pengukuran atau percobaan secara berulang pada objek yang sama (McCullagh & Nelder, 1989).
Ada atau tidaknya overdispersi dapat dilihat dari nilai Deviance atau
Pearson Chi-square yang dibagi dengan derajat bebasnya. Apabila nilai pearson Chi-square dibagi dengan derajat bebas lebih besar daripada 1, ini menunjukkan nilai variansi yang lebih besar daripada rataan; overdispersi telah terjadi.
Permasalahan overdispersi biasanya terjadi pada kasus-kasus nyata. Untuk mengatasinya dapat dilakukan dua metode, yaitu:
1. Dengan mengansumsikan ܸܽݎሺݕሻ ൌ ߪଶߣ dan mengestimasi parameter ߪଶ, yang kemudian disebut dengan model Quasi-likelihood.
2. Dengan mengubah distribusi variabel respon menjadi binomial negatif, dimana lebih terdispersi daripada Poisson, yang kemudian disebut dengan model regresi binomial negatif.
5.1.2 Percobaan Poisson
kantor, banyaknya pertandingan yang ditunda karena hujan selama kompetisi sepak bola, dan sebagainya. Percobaan Poisson memiliki ciri-ciri sebagai berikut: 1. Banyaknya hasil percabaan yang terjadi dalam selang waktu atau daerah
tertentu tidak bergantung pada banyaknya hasil percobaan yang terjadi pada selang waktu atau daerah lain yang terpisah
2. Peluang terjadinya satu hasil percobaan selama selang waktu yang singkat sekali atau dalam suatu daerah yang kecil sebanding dengan panjang selang waktu tersebut/besarnya daerah tersebut dantik bergantung pada banyaknya hasil percobaan yang terjadi di luar selang waktu atau daerah tersebut.
3. Peluang bahwa lebih dari satu hasil percobaan akan terjadi dalam selang waktu yang relatif singkat atau dalam daerah yang kecil tersebut diabaikan. 5.1.3 Distribusi Poisson
Misalkan Yi merupakan variabel random hitungan klaim dalam i kelas, i = 1,2 ... n, dimana n menunjukkan jumlah rating classes. Jika Yi mengikuti distribusi Poisson, fungsi kepadatan peluang adalah,
ܲݎሺܻ ൌ ݕሻ ൌ݁
ܸܽݎሺܻሻ ൌ ܧ൫ܻଶ൯ െ ൫ܧሺܻሻ൯ଶ
ൌ ߣଶ ߣെ ሺߣሻଶ
ൌ ߣǤ
Terlihat bahwa: ܻ̱ܲ݅ݏݏ݊ሺߣሻǡ ܧሺܻሻ ൌ ܸܽݎሺܻሻ ൌ ߣז 5.1.4 Model Regresi Poisson
Dalam berbagai eksperimen, seringkali data cacah yang merupakan objek penelitian dipengaruhi oleh sejumlah variabel penjelas (explanatory). Sehingga untuk mengetahui pola hubungan kedua variabel tersebut, dapat digunakan suatu model regresi yang didasarkan pada distribusi Poisson. Pada regresi Poisson diasumsikan bahwa variabel dependen ܻ yang menyatakan jumlah (cacah) kejadian berdistribusi Poisson, diberikan sejumlah variabel independen ݔଵǡ ǥ ǡ ݔ.
Yi mengikuti distribusi Poisson, fungsi kepadatan peluang adalah, ܲݎሺܻȁݔଵǡ ǥ ǡ ݔሻ ൌ ݁
ିఒߣ௬
ݕǨ ǡ ݕ ൌ Ͳǡͳǡ ǥ
atau ܻ̱ܲ݅ሺߣሻǡ ݅ ൌ ͳǡʹǡ͵ǡ ǥ ǡ ݊.
Salah satu tujuan dari analisis regresi adalah untuk menentukan pola hubungan antara variabel respon dengan variabel penjelas. Selanjutnya, dalam regresi Poisson hubungan tersebut dapat dituliskan dalam bentuk:
ܧሾܻȁݔሿ ൌ ߣ ൌ ߚ ݔଵߚଵ ڮ ݔߚ
atau dalam bentuk vektor ditulis sebagai
ܧሾܻȁݔሿ ൌ ߣൌ ࢞ࢀࢼ (5.2)
Karena nilai ߣ Ͳ, maka digunakan fungsi link ߟ ൌ ሺ࢞ࢀࢼሻ atau ߟ ൌ ݈݃ߣ ൌ ࢞ࢀࢼ untuk menghubungkan ߣ ൌ ܧሾܻȁ࢞ሿ dengan fungsi linear
࢞ࢀࢼ, sehingga hubungan antara ߣ ൌ ܧሾܻȁ࢞ሿ dan ࢞ࢀࢼ menjadi tepat. Dengan
demikian, model regresi dapat ditulis dalam bentuk:
ܧሾܻȁ࢞ሿ ൌ ߣൌ ݁ݔሺ࢞ࢀࢼሻǡ ݅ ൌ ͳǡʹǡ ǥ ǡ ݊Ǥ (5.3)
5.1.5 Estimasi Parameter
Untuk mengestimasi parameter-parameter dalam regresi Poisson dapat digunakan metode estimasi maksimum likelihood (MLE). Metode estimasi maksimum likelihood dapat dilakukan jika distribusi data diketahui.
Langkah pertama yang dilakukan adalah menentukan fungsi likelihood
dari model regresi Poisson. Dengan mengasumsikan ܻଵǡ ܻଶǡ ǥ ǡ ܻ adalah variabel random yang mutually independent atau Yi ~ Poisson (ߣ), maka fungsi likelihood untuk model regresi Poisson adalah sebagai berikut:
ܮሺࢼሻ ൌ ෑ ܲሺݕǢ ࢼሻ
Selanjutnya dari fungsi likelihood diambil nilai lognya sehingga diperoleh fungsi log-likelihood dari persamaan di atas sebagai berikut:
݈݃ܮሺࢼሻ ൌ ݈݃ ൝ෑ ܲሺݕǢ ࢼሻ kovariat untuk observasi ke-i, maka diperoleh persamaan sebagai berikut:
Kemudian persamaan (5.5) diturunkan terhadap ߚ dan disamakan dengan
Setelah disamakan dengan nol, maka akan terdapat p (sejumlah parameter yang ada) persamaan. Dalam persamaan (5.6) terdapat suku ݁ݔ൫ࢄࢀࢼ൯ sehingga bentuk pasti (closed form) dari ȕ sulit ditentukan. Oleh karena itu, untuk mengestimasi parameter ȕ dilakukan secara iteratif dengan bantuan komputer yang didasarkan pada suatu prosedur (algoritma) iterasi yang disebut dengan
Iteratively Weighted Least Square (IWLS).
Untuk mempermudah penerapan pada regresi IWLS Poisson, notasi rataan Poisson, ߣ, akan diganti dengan ߤ. Dalam rangka mencari Ⱦ pada regresi Poisson log LȕGDSDWGLPDNVLPDONDQGHQJDQPHQJJXQDNDQPHWRGH:/6
߲ ሺࢼሻ
menghasilkan perkiraan kuadrat terkecil, ࢼ෩.
Hal ini menunjukkan bahwa hasil estimasi dengan MLE dan WLS sama. 5.1.6 Uji Ketepatan (Goodness of Fit) Model Regresi Poisson
Uji ketepatan model regresi Poisson dilakukan dengan dua cara yaitu,
5.1.6.1 Pearson Chi-square statistic untuk Model Regresi Poisson
Ukuran lain yang bisa digunakan untuk uji goodness of fit yaitu Pearson Chi-square statistic (McCullagh & Nelder, 1989) yang didefinisikan sebagai ߯ଶ ൌ ሺݕെ ߤሻଶ
ܸܽݎሺߤሻ
ୀଵ
dimana ܸܽݎሺߤሻ yaitu fungsi variansi dari distribusi peluang datanya dan ܸܽݎሺߤሻ ൌሺథ ሻ. Karena data yang diobservasi itu berdistribusi Poisson, maka
ܸܽݎሺߤሻ ൌ ߤ sehingga Statistik Pearson Chi-square untuk regresi Poissonnya
yaitu:
5.1.6.2 Deviance untuk Model Regresi Poisson
Deviance dapat diartikan sebagai logaritma dari uji likelihoodnya, yaitu: ܦ ൌ െʹ݈݃ ቂሺ࢟Ǣࣆሻሺ࢟Ǣ࢟ሻቃ ൌ ʹሺ݈݃ܮሺ࢟Ǣ ࢟ሻ െ ݈݃ܮሺ࢟Ǣ ࣆሻሻǤ (5.9)
Dalam persamaan tersebut, ܮሺ࢟Ǣ ࣆሻ adalah fungsi likelihood current model
sedangkan ܮሺ࢟Ǣ ࢟ሻ adalah fungsi likelihood saturated model dari distribusi Poisson. Adapun fungsi log-likelihoodcurrent model dituliskan sebagai berikut: ݈ሺࣆǡ ࢟ሻ ൌ ݈݃ܮሺࣆǡ ࢟ሻ
ൌ ݈݃ ෑ݁ିఓߤ
௬
ݕǨ
ୀଵ
ൌ ݈݃ ቆ݁ିఓߤ
௬
ݕǨ ቇ
ୀଵ
ൌ ሺݕ݈݃ߤെ ߤെ ݈݃ݕǨሻ
ୀଵ
Ǥ (5.10)
߯ଶ ൌ ሺݕെ ߤሻଶ
ߤ
ୀଵ
Sedangkan untuk saturated model, dimana nilai-nilai ߤ diganti dengan nilai ݕ (tanpa asumsi tentang keeratan hubungannya dengan variabel x nya), fungsi likelihoodsaturated model-nya yaitu:
ܮሺ࢟Ǣ ࢟ሻ ൌ ෑ ݂ሺݕǡ ݕሻ
Sehingga fungsi log-likelihoodsaturated model-nya menjadi ݈ሺ࢟Ǣ ࢟ሻ ൌ ݈݃ܮሺ࢟Ǣ ࢟ሻ
Sehingga Deviance, D, bisa diperoleh dengan mensubstitusi (5.10) dan (5.11) ke dalam (5.9) dan diperoleh
5.2 Model Regresi Binomial Negatif
5.2.1 Overdispersi Metode Binomial Negatif
Berdasarkan Poisson, rataan, ߣ, diasumsikan konstan atau homogen dalam kelas. Dengan asumsi ߣ untuk Gamma dengan rataan ܧሺߣሻ ൌ ߤ dan varians ܸܽݎሺߣሻ ൌ ߤଶݒିଵ , dan ܻȁߣ menjadi Poisson dengan rataan bersyarat
ܧሺܻȁߣሻ ൌ ߣdapat ditunjukkan bahwa distribusi marjinal ܻmengikuti distribusi
binomial negatif dengan fungsi kepadatan peluang,
ܲݎሺܻ ൌ ݕሻ ൌ න ܲݎሺܻ ൌ ݕȁߣሻ݂ሺߣሻ݀ߣ
Apabila overdispersi terjadi pada data yang dimodelkan dengan regresi Poisson, maka salah satu jalan yang dapat diambil adalah memodelkan ulang data tersebut dengan model yang lebih terdispersi. Dalam hal ini, model yang digunakan adalah model binomial negatif.
Misalkan Yi a 3RLVVRQȜi WHUKDGDS Ȝi itu sendiri adalah variabel
random dengan distribusi Gamma. Misalkan Yi_Ȝia3RLVVRQȜi)
Dapat ditunjukkan bahwa distribusi tak bersyarat dari yi adalah binomial
negatif, sebagai berikut:
Fungsi kepadatan peluang bersyarat dari yi adalah ܲݎሺܻ ൌ ݕȁߣሻ ൌ
షഊఒ
ܲݎሺߣሻ ൌ ͳ
Memanfaatkan definisi dari fungsi densitas bersyarat, maka didapat fungsi peluang bersama dari yiGDQȜi adalah
ܲݎሺݕǡ ߣሻ ൌ ܲݎሺߣሻܲݎሺܻൌ ݕȁߣሻ
Dengan diperolehnya fungsi peluang bersama dari yi GDQȜi, maka fungsi
peluang tak bersyarat dari yi adalah
ܲݎሺܻ ൌ ݕሻ ൌ න ͳ maka dengan demikian didapatkan
ൌ߁ሺݕ߁ሺݕݒሻ
Harga ekspektasi/rataan dari distribusi ini adalah ܧሺܻሻ ൌ ܧሾܧሺܻȁߣሻሿ ൌ ܧሺߣሻ ൌ ݒǤߤݒ
Dengan variansinya adalah ܸܽݎሺܻሻ ൌ ܧ൫ܻଶ൯ െ ሾܧሺܻሻሿଶ
5.2.2 Distribusi Binomial Negatif
Parameter berbeda dapat menghasilkan berbagai jenis distribusi binomial negatif. Misalnya, dengan mengambil vi = a-1, ܻmengikuti sebuah distribusi binomial negatif dengan rataan E (ܻ) = ߤ dan variansi Var (ܻ) = ߤ (1 + aߤ), di mana ܽ menunjukkan parameter dispersi (Lawless, 1987); (Cameron & Trivedi, 1986). Sehingga persamaan (5.14) menjadi,
ܲݎሺܻൌ ݕሻ ൌ߁ሺݕ ܽ akan menjadi distribusi Poisson. Jika a > 0, variansi akan melebihi rataan, Var(ܻ) > E(ܻ), dan distribusi memungkinkan overdispersi. Dalam tulisan ini, distribusi akan disebut sebagai binomial negatif.
5.2.3 Estimasi parameter untuk model regresi binomial negatif
Untuk mengestimasi parameter ߚ dan ܽ dalam regresi binomial negatif dapat digunakan metode estimasi maksimum likelihood (MLE) maupun metode moment. Langkah pertama yang dilakukan adalah menentukan fungsi likelihood
dari model regresi binomial negatif. ܧሺܻȁ࢞ሻ ൌ ߤ ൌ ݁ݔሺ࢞ࢀࢼሻ, maka fungsi
likelihood untuk model regresi binomial negatif adalah sebagai berikut: ܮሺࢼǡ ܽሻ ൌ ෑ ܲሺࢼǡ ܽሻ
Selanjutnya dari fungsi likelihood diambil nilai lognya sehingga diperoleh fungsi log-likelihood dari persamaan di atas sebagai berikut:
ൌ ݈݃ ෑȞሺݕȞሺܽ ܽିଵሻ െ ݈݃ ෑ ݕିଵሻ Ǩ
Menurut Lawless (1987), ሺூାሻ
ሺሻ ൌ ݇ ൈ ሺͳ ݇ሻ ൈ ǥ ൈ ሺܫ െ ͳ ݇ሻ untuk I
bilangan bulat. Sehingga, ൫௬ାషభ൯
ሺషభሻ ൌ ܽିଵൈ ሺͳ ܽିଵሻ ൈ ǥ ൈ ሺݕെ ͳ ܽିଵሻ. Maka, ݈݃ܮሺࢼǡ ܽሻ bisa ditulis tanpa fungsi Gamma dengan
݈݃ ቈȞሺݕȞሺܽ ܽିଵሻ ൌ ݈݃ܽିଵሻ ିଵ ሺͳ ܽିଵሻ ڮ ݈݃ሺݕ
െ ͳ ܽିଵሻ
݈݃ ቈȞሺݕȞሺܽ ܽିଵሻ ൌ ݈݃ ൬ିଵሻ ͳ ܽݎܽ ൰
௬ିଵ
ୀ
Likelihood untuk model regresi binomial negatif I dapat ditulis sebagai,
݈ሺࢼǡ ܽሻ ൌ ቐ݈݃ ሺͳ ܽݎሻ
Oleh karena itu, estimasi maksimum likelihood, ൫ࢼǡ ܽො൯, dapat diperoleh dengan memaksimalkan ݈ሺࢼǡ ܽሻterhadap ࢼ dan ܽ. Persamaan terkait adalah,
߲݈ሺࢼǡ ܽሻ
urutan kedua, dengan ࢼ tetap pada ࢼሺଵሻ, ݈ሺࢼǡ ܽሻ adalah dimaksimalkan terhadap ܽ , menghasilkan ܽሺଵሻ . Persamaan terkait adalah persamaan (5.18), dan permasalahan dapat dilakukan dengan menggunakan iterasi Newton-Raphson. Iterasi dengan ܽ dan ࢼ tetap, ൫ࢼǡ ܽො൯ nantinya akan diperoleh.
Pendekatan yang lebih mudah untuk mengestimasi ܽ adalah dengan menggunakan perkiraan yang disarankan oleh (Breslow, 1984), yaitu dengan menyamakan Pearson Chi-SquareStatistic dengan derajat bebas,
൫ݕ െ ܧሺܻሻ൯
ଶ
ܸܽݎሺܻሻ
ൌ ݊ െ
sehingga diperoleh,
ߤሺݕെ ߤሻଶ
ሺͳ ܽߤሻ
ൌ ݊ െ (5.19)
di mana n menunjukkan jumlah rating classes dan p jumlah parameter regresi. Prosedur iterasi seperti yang disebutkan di atas juga dapat digunakan, kali ini menghasilkan MLE dari ࢼ dan estimasi moment dari ܽ, ൫ࢼǡ ܽ൯.
Dalam tulisan ini, ketika ܽ diestimasi dengan MLE, model akan disebut sebagai binomial negatif I (MLE). Demikian juga, ketika diestimasi dengan metode moment, model akan disebut sebagai binomial negatif I (moment).
5.2.4 Uji ketepatan (goodness of fit) model regresi binomial negatif
Uji ketepatan model regresi binomial negatif dilakukan dengan dua cara yaitu, Pearson Chi-Square statistic dan deviance.
5.2.4.1 Pearson Chi-Square pada model regresi binomial negatif
Karena data yang diobservasi itu berdistribusi binomial negatif, maka ܸܽݎሺܻሻ ൌ ߤሺͳ ܽߤሻ sehingga Pearson Chi-Square Statistic untuk regresi binomial negatif I yaitu:
߯ଶൌ ሺݕെ ߤሻଶ
ߤሺͳ ܽߤሻ
ୀଵ
5.2.4.2 Deviance pada model regresi binomial negatif
Uji kecocokan suatu model terhadap data adalah pertanyaan alami yang timbul pada semua model statistik. Salah satu cara untuk menilai kecocokan model adalah dengan membandingkannya dengan model penuh (saturated model).
Deviance dinotasikan dengan D, didefinisikan sebagai ukuran jarak antara
saturated model dengan current model:
ܦ ൌ ʹሺ݈݃ܮሺ࢟Ǣ ࢇሻ െ ݈݃ܮሺࣆǢ ࢇሻሻ.
Bila model cocok, maka current model diharapkan dekat dengan (tapi tidak lebih besar dari) saturated model. Nilai deviance yang besar menunjukkan bahwa current model tidak bagus.
Sehingga bentuk persamaan di atas menjadi, ܦ ൌ ʹ ൜ݕ݈݃ ൬ݕߤ
൰ െ ሺݕ ܽ
ିଵሻ ݈݃ ൬ͳ ܽݕ
ͳ ܽߤ൰ൠ
ୀଵ
Ǥ (5.21)
5.3 Aplikasi Numerik
5.3.1 Data Penelitian
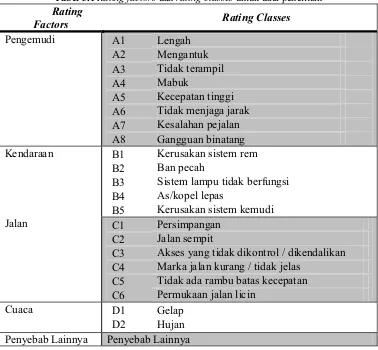
Data yang digunakan dalam penelitian ini adalah data sekunder dari laporan Unit Lakalantas Poltabes Padang selama tahun 2012. Rating factor dan
Tabel 5.1Rating factors dan ratingclasses untuk data penelitian Rating
Factors Rating Classes
Pengemudi A1 Lengah
A2 Mengantuk A3 Tidak terampil
A4 Mabuk
A5 Kecepatan tinggi A6 Tidak menjaga jarak A7 Kesalahan pejalan A8 Gangguan binatang Kendaraan B1 Kerusakan sistem rem
B2 Ban pecah
B3 Sistem lampu tidak berfungsi B4 As/kopel lepas
B5 Kerusakan sistem kemudi
Jalan C1 Persimpangan
C2 Jalan sempit
C3 Akses yang tidak dikontrol / dikendalikan C4 Marka jalan kurang / tidak jelas
C5 Tidak ada rambu batas kecepatan C6 Permukaan jalan licin
Cuaca D1 Gelap
D2 Hujan Penyebab Lainnya Penyebab Lainnya
Tabel 5.1 menunjukkan rating factors dan rating classes untuk jumlah kecelakaan. Berdasarkan laporan dari Unit Lakalantas Poltabes Padang selama tahun 2012 terdapat 540 kasus kecelakaan lalu lintas yang terjadi di Kota Padang. Data tersebut kemudian dikelompokkan berdasarkan faktor penyebabnya.
Variabel dalam penelitian ini terdiri dari variabel respon dan prediktor. Adapun variabel yang digunakan pada penelitian ini adalah:
1. Variabel respon (Dependent variable)
Dalam penelitian ini yang menjadi variabel respon adalah data angka jumlah kecelakaan tahun 2012.
2. Variabel bebas (independent variable) atau variabel penjelas
Lakalantas Poltabes Padang dan dikutip dari Direktorat Jenderal Perhubungan Darat Departemen Perhubungan, www.dephub.go.id.
Ada kalanya kita melakukan suatu regresi dimana variabel penjelas berupa data kualitatif. Jika data kualitatif tersebut memiliki m kategori, maka jumlah variabel dummy yang dicantumkan di dalam model adalah (m - 1).
5.3.2 Proses Analisis Data
Penelitian ini menggunakan tiga model regresi yaitu model regresi poisson, binomial negatif dan poisson tergeneralisasi pada kasus kecelakaan kendaraan bermotor di lalu lintas di Kota Padang. Pada penelitian ini digunakan bantuan software R. Adapun langkah-langkah yang dilakukan adalah sebagai berikut:
1. Membentuk peubah dummy pada variabel bebas.
2. Menguji signifikansi tiap rating classes dengan menggunakan analisis
deviance.
3. Mengestimasi parameter untuk tiap rating classes yang signifikan pada model regresi Poisson.
4. Mengestimasi parameter untuk tiap rating classes yang signifikan pada model regresi Binomial Negatif.
5. Memilih model terbaik.
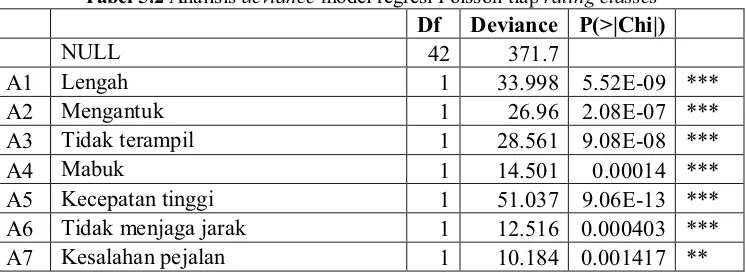
Untuk menguji signifikansi tiap rating classes digunakan analisis
deviance. Berikut ini akan disajikan hasil analisis deviance model regresi Poisson yang memuat tiap rating classes.
Tabel 5.2 Analisis deviance model regresi Poisson tiap rating classes
Df Deviance P(>|Chi|)
NULL 42 371.7
A1 Lengah 1 33.998 5.52E-09 ***
A2 Mengantuk 1 26.96 2.08E-07 ***
A3 Tidak terampil 1 28.561 9.08E-08 ***
A4 Mabuk 1 14.501 0.00014 ***
A5 Kecepatan tinggi 1 51.037 9.06E-13 ***
A6 Tidak menjaga jarak 1 12.516 0.000403 ***
A8 Gangguan binatang 1 11.286 0.000781 *** B1 Kerusakan sistem rem 1 11.279 0.000784 ***
B2 Ban pecah 1 5.088 0.024094 *
B3 Sistem lampu tidak berfungsi 1 1.927 0.165139
B4 As/kopel lepas 1 0.524 0.469311
B5 Kerusakan sistem kemudi 1 5.248 0.021972 *
C1 Persimpangan 1 14.557 0.000136 ***
C2 Jalan sempit 1 0.315 0.574905
C3 Akses yang tidak dikontrol / dikendalikan
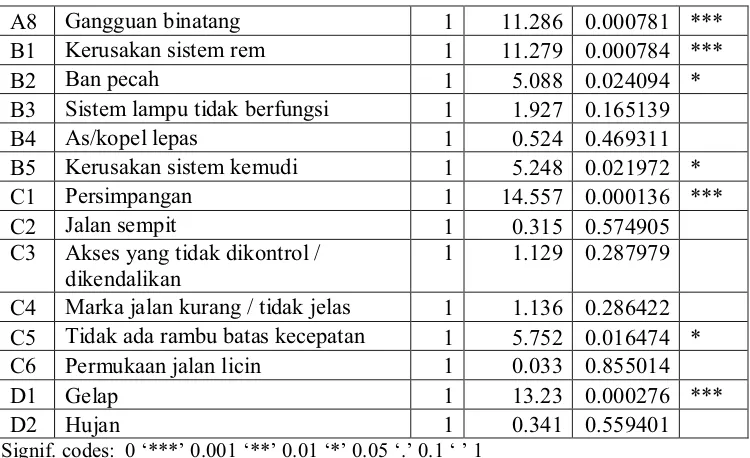
Dari Error! Reference source not found. terlihat bahwa terdapat rating classes yang tidak signifikan. Sehingga harus dilakukan kembali analisis deviance
dengan membuang pasangan rating classes yang tidak signifikan. Berikut adalah ini adalah analisis deviance model regresi Poisson untuk tiap rating classes yang telah signifikan.
Tabel 5.3 Analisis deviance model regresi Poisson untuk tiap rating classes yang sudah signifikan.
Dari hasil analisis deviansi model regresi Poisson untuk tiap rating classes
tidak terampil, mabuk, kecepatan tinggi, tidak menjaga jarak, kesalahan pejalan, kerusakan sistem rem, kerusakan sistem kemudi, persimpangan dan gelap. Hasil estimasi parameter untuk rating classes yang signifikan, dapat dilihat pada Tabel 5.4.
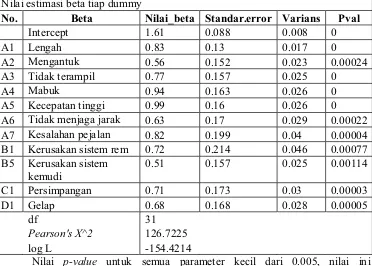
Tabel 5.4 Estimasi parameter untuk model Poisson rating classes yang signifikan Nilai estimasi beta tiap dummy
No. Beta Nilai_beta Standar.error Varians Pval
Intercept 1.61 0.088 0.008 0
A1 Lengah 0.83 0.13 0.017 0
A2 Mengantuk 0.56 0.152 0.023 0.00024
A3 Tidak terampil 0.77 0.157 0.025 0
A4 Mabuk 0.94 0.163 0.026 0
A5 Kecepatan tinggi 0.99 0.16 0.026 0
A6 Tidak menjaga jarak 0.63 0.17 0.029 0.00022
A7 Kesalahan pejalan 0.82 0.199 0.04 0.00004
B1 Kerusakan sistem rem 0.72 0.214 0.046 0.00077
B5 Kerusakan sistem kemudi
0.51 0.157 0.025 0.00114
C1 Persimpangan 0.71 0.173 0.03 0.00003
D1 Gelap 0.68 0.168 0.028 0.00005
df 31
Pearson's X^2 126.7225
log L -154.4214
Nilai p-value untuk semua parameter kecil dari 0.005, nilai ini mengidentifikasikan bahwa estimasi parameter sudah signifikan. Dari Tabel 5.4 terlihat bahwa terjadi overdispersi pada data karena nilai Pearson Chi-square
dibagi dengan derajat bebas nilainya lebih besar dari 1. Untuk mengatasi masalah overdispersi pada data cacah ini dapat diatasi dengan memodel-ulangkan dengan regresi binomial negatif.
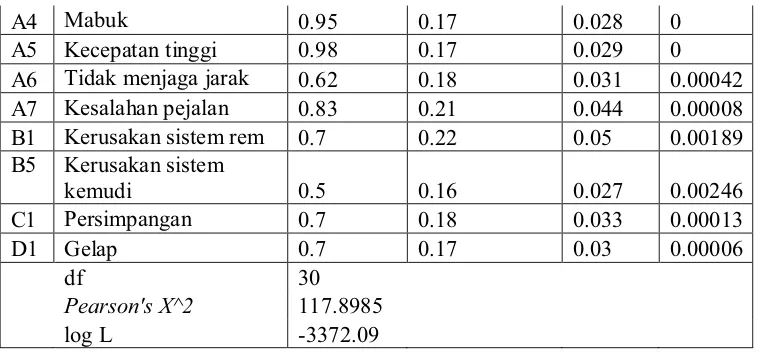
Tabel 5.5 Estimasi parameter untuk model Binomial Negatif (MLE) rating classes
Nilai a = 0.005753275
Nilai estimasi beta tiap dummy
No. Beta Nilai_beta Standar.error Varians Pval
Intercept 1.61 0.09 0.008 0
A1 Lengah 0.83 0.14 0.019 0
A2 Mengantuk 0.57 0.16 0.025 0.00029
A4 Mabuk 0.95 0.17 0.028 0
A5 Kecepatan tinggi 0.98 0.17 0.029 0
A6 Tidak menjaga jarak 0.62 0.18 0.031 0.00042
A7 Kesalahan pejalan 0.83 0.21 0.044 0.00008
B1 Kerusakan sistem rem 0.7 0.22 0.05 0.00189
B5 Kerusakan sistem
kemudi 0.5 0.16 0.027 0.00246
C1 Persimpangan 0.7 0.18 0.033 0.00013
D1 Gelap 0.7 0.17 0.03 0.00006
df 30
Pearson's X^2 117.8985
log L -3372.09
Setelah data yang sama seperti data yang digunakan untuk Tabel 5.4 dimodel ulangkan dengan model Binomial Negatif (MLE), terlihat bahwa permasalahan overdispersi yang terjadi pada model Poison mulai dapat teratasi. Hal ini dapat dilihat pada Tabel 5.5, dimana nilai Pearson Chi-square dibagi dengan derajat bebas nilainya mulai mendekati 1. Semua parameter pada data yang dimodel-ulangkan ini tetap signifikan.
Kemudian dengan menggunakan data sama, dilakukan pemodelan ulang dengan model Binomial Negatif (Moment). Hasilnya dapat dilihat pada Tabel 5.4 di bawah:
Tabel 5.6 Estimasi parameter untuk model Binomial Negatif (MLE) rating classes
Nilai a = 0.2557075
Nilai estimasi beta tiap dummy
No. Beta Nilai_beta Standar.error Varians Pval
Intercept 1.56 0.15 0.024 0
A1 Lengah 0.94 0.28 0.078 0.00079
A2 Mengantuk 0.74 0.31 0.095 0.01593
A3 Tidak terampil 0.95 0.33 0.106 0.00333
A4 Mabuk 1.02 0.33 0.108 0.0019
A5 Kecepatan tinggi 0.92 0.38 0.144 0.01478
A7 Kesalahan pejalan 0.92 0.46 0.209 0.04348
B1 Kerusakan sistem rem 0.53 0.47 0.221 0.25919
B5 Kerusakan sistem
kemudi 0.36 0.33 0.112 0.28433
C1 Persimpangan 0.49 0.39 0.156 0.21116
D1 Gelap 0.87 0.34 0.115 0.01027
df 30
Pearson's X^2 31
log L -1501.25
52 BAB 6
RENCANA TAHAPAN BERIKUTNYA
Setelah data yang sama seperti data yang digunakan untuk Tabel 5.4 dimodel ulangkan dengan model Binomial Negatif (MLE), terlihat bahwa permasalahan overdispersi yang terjadi pada model Poison mulai dapat teratasi. Hal ini dapat dilihat pada Tabel 5.5, dimana nilai Pearson Chi-square dibagi dengan derajat bebas nilainya mulai mendekati 1. Semua parameter pada data yang dimodel-ulangkan ini tetap signifikan.
53 BAB 7
KESIMPULAN DAN SARAN
7.1 Kesimpulan
Berdasarkan hasil analisis dan pembahasan model regresi Poisson yang diperoleh ternyata tidak memenuhi asumsi equi-dispersion sehingga digunakan model regresi binomial negatif untuk pemodelan kasus kecelakaan kendaraan bermotor di lalu lintas. Dari data diperoleh kesimpulan bahwa model regresi binomial negatif (MLE) dapat mengurangi permasalahan dalam data yang mengandung overdispersi. Dengan bentuk model sebagai berikut,
Ɋ ൌ ሺͳǤͳ ͲǤͺ͵ͳ ͲǤͷʹ ͲǤͺ͵ ͲǤͻͷͶ ͲǤͻͺͷ ͲǤʹ
ͲǤͺ͵ ͲǤͲͳ ͲǤͷͲͷ ͲǤͲͳ ͲǤͲͳሻ
Dimana faktor yang paling berpengaruh terhadap jumlah kecelakaan kendaraan bermotor di lalu lintas adalah pengemudi lengah, pengemudi mengantuk, pengemudi tidak terampil, pengemudi mabuk, kecepatan kendaraan tinggi, tidak menjaga jarak, kesalahan pejalan, kerusakan sistem rem, kerusakan sistem kemudi, jalan persimpangan dan cuaca gelap.
7.2 Saran
55 DAFTAR PUSTAKA
Bailey, Robert A., and Leroy J. Simon. "Two Studies in Automobile Insurance Ratemaking." ASTIN Bulletin, 1960: 192-217.
Bain, Lee J., and Max Engelhardt. Introduction to Probability and Matematical Statistic. California: Duxbury Press, 1991.
Breslow, N. E. "Extra-Poisson Variation in Log-Linear Models." Journal of the Royal Statistical Society, 1984: Blackwell Publishing for the Royal Statistical Society.
&DPHURQ$&ROLQGDQ3UDYLQ.7ULYHGL³(FRQRPHWULF0RGHOV%DVHGRQ&RXQW Data: Comparisons and Applications of Some EstimaWRUV DQG 7HVWV´
Journal of Applied Econometrics, 1986: 29-53.
&R['5³6RPH5HPDUNVRQ2YHUGLVSHUVLRQ´Biometrika, 1983: 269-274. Harrington, Scott E. "Estimation and Testing for Functional Form in Pure
Premium Regression Models." ASTIN Bulletin, 1986: 31-43.
Ismail, Noriszura, and Abdul Aziz Jemain. "Bridging Minimum Bias and Maximum Likelihood Methods through Weighted Equation." Casualty Actuarial Society Forum, 2005: 367-394.
Ismail, Noriszura, and Abdul Aziz Jemain. "Handling Overdispersion with Negative binomial and Generalized Poisson Regression Models." Casualty Actuarial Society Forum, 2007: 103-158.
Jong, P. d., & Heller, G. Z. (2008). Generalized Linear Models for Insurance Data. New York: Cambridge University Press.
/DZOHVV -HUDOG ) ³Negative binomial and Mixed Poisson 5HJUHVVLRQ´ The Canadian Journal of Statistics, 1987: 209-225.
McCullagh, P., dan J.A. Nelder. Generalized Linear Models. 2nd Edition. London: Chapman and Hall, 1989.
1HOGHU-$GDQ</HH³/LNHOLKRRG4XDVL-Likelihood and Pseudolikelihood: 6RPH&RPSDULVRQV´urnal of the Royal Statistical Society, 1992: 273-284. 5HQVKDZ $UWKXU ( ³0RGHOOLQJ WKH &ODLPV 3URFHVV LQ WKH 3UHVHQFH RI
Sari, Devni Prima. Penanganan Overdispersi dengan Model Regresi Binomial Negatif I Pada Faktor-Faktor yang Mempengaruhi Angka Kematian yang Disebabkan Oleh Kanker Paru-Paru. Prosiding Seminar Nasional Matematika UNS, 2010: 445-452.
Sari, Devni Prima. Penanganan Overdispersi dengan Model Regresi Binomial Negatif I dan Binomial Negatif II. Universitas Gadjah Mada, 2010.
Sari, Devni Prima. Kajian Overdispersi Pada Regresi Poisson dengan Menggunakan Regresi Poisson Tergeneralisasi I. Prosiding Seminar Nasional Matematika UNAND, 2011: 122-128.
Schwarz, Gideon. "Estimating the Dimension of a Model." The Annals of Statistics, 1978: 461-464.
UU RI No.22 Tahun 2009. Undang-Undang No. 22 Tahun 2009 tentang Lalu Lintas dan Angkutan Jalan. Diakses melalui www.polri.go.id tanggal 2 Januari 2013.
LAMPIRAN
1. INSTRUMENT
a) Model Regresi Poisson poisson<- function(data3) {
x=as.matrix(data3[,-(12)]) X=cbind(1,x)
Y=as.vector(data3[,12]) x=0
new.beta <- rep(c(0.001), dim(X)[2]) for (i in 1:length(Y))
{
beta=new.beta
miul=exp(as.vector(X%*%beta)) W=diag(miul)
I.inverse=solve(t(X)%*%W%*%X) k=(Y-miul)/miul
z=t(X)%*%W%*%k
new.beta=as.vector(beta+I.inverse%*%z) new.miul=exp(as.vector(X%*%new.beta))
loglikelihood=sum((Y*log(new.miul))-new.miul-lfactorial(Y)) Deviance=sum(Y*log(Y/miul)-(Y-miul))
pearson=sum((Y-miul)^2/new.miul) }
varians=as.vector (diag(I.inverse)) std.error=sqrt(varians)
df=dim(X)[1]-dim(X)[2] n=dim(X)[1]
p=dim(X)[2]
AIC=-2*loglikelihood+2*p BIC=-2*loglikelihood+p*log(n)
coef<-c(beta) SE<-c(std.error) tstat<-coef/SE
pval=2*pnorm(-abs(tstat))
frame=data.frame(beta=c("intercept","Lengah","Mengantuk","Tidak_terampi l","Mabuk","Kecepatan_tinggi","Tidak_menjaga_jarak","Kesalahan_pejalan" ,"Kerusakan_sistem_rem","Kerusakan_sistem_kemudi","Persimpangan","Gel ap"),nilai_beta=new.beta,standar.error=std.error,varians=round(varians,3),pv al=round(pval,5))
cat("nilai estimasi beta tiap dummy","\n") print(frame,digits=2)
cat("===============================================","\n") cat("df =",df,"\n")
cat("Pearson's X^2=",pearson,"\n") cat("Deviance =",Deviance,"\n") cat("log L =",loglikelihood,"\n") cat("AIC =",AIC,"\n")
cat("BIC =",BIC,"\n") }
poisson(data3)
b) Model Regresi Binomial Negatif (MLE) BN.mle<- function(data3)
new.beta <- rep(c(0.001), dim(X)[2]) for (i in 1:length(Y))
{ a=new.a beta=new.beta
miul= exp(as.vector(X%*%beta)) W=diag(miul/(1+ a*miul))
I.inverse=solve(t(X)%*%W%*%X) k=(Y-miul)/miul
z=t(X)%*%W%*%k