Model Program Stokastik Untuk Persoalan Penugasan Armada Penerbangan

MODEL PROGRAM STOKASTIK UNTUK

PERSOALAN PENUGASAN ARMADA

PENERBANGAN

TESIS

Oleh

ALFRED HASIHOLAN SILALAHI 087021053/MT

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MODEL PROGRAM STOKASTIK UNTUK

PERSOALAN PENUGASAN ARMADA

PENERBANGAN

T E S I S

Diajukan Sebagai Salah Satu Syarat

Untuk Memperoleh Gelar Magister Sains dalam Program Studi Magister Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Universitas Sumatera Utara

Oleh

ALFRED HASIHOLAN SILALAHI 087021053/MT

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

Judul Tesis : MODEL PROGRAM STOKASTIK UNTUK PERSO-ALAN PENUGASAN ARMADA PENERBANGAN Nama Mahasiswa : Alfred Hasiholan Silalahi

Nomor Pokok : 087021053 Program Studi : Matematika

Menyetujui, Komisi Pembimbing

(Prof. Dr. Opim Salim S, M.Sc) (Dr. Sutarman, M.Sc)

Ketua Anggota

Ketua Program Studi Dekan

(Prof. Dr. Herman Mawengkang) (Prof. Dr. Eddy Marlianto, M.Sc)

Telah diuji pada

Tanggal 17 Mei 2010

PANITIA PENGUJI TESIS

Ketua : Prof. Dr. Opim Salim S, M.Sc Anggota : 1. Dr. Sutarman, M.Sc

ABSTRAK

Armada perusahaan penerbangan biasanya mempunyai kelompok pesawat ganda, yang masing-masing mempunyai rancangan cockpit dan persyaratan spesifik awak pesawat. Setiap kelompok pesawat mempunyai tipe pesawat ganda yang mem-punyai kapasitas yang berbeda-beda. Dengan jadwal penerbangan tertentu, model penugasan armada berkenaan dengan penugasan pesawat ke leg-leg penerbangan untuk memaksimalkan laba dengan mempertimbangkan rencana perjalanan yang berdasarkan permintaan. Akan tetapi, karena managemen hasil terkait dengan peraturan penjadwalan awak pesawat, terlebih, keputusan ini harus diambil se-belum keberangkatan saat permintaan pasar masih sedikit tidak pasti, walaupun selanjutnya pada tahap kemudian, penugasan ulang tipe-tipe pesawat di dalam kelompok tertentu bisa dilakukan saat ramalan permintaan meningkat, sambil tetap mempertahankan jadwal awak pesawat. Dalam tesis ini, diajukan pen-dekatan mixed-integer programming stokastik dua-tahap di mana tahap pertama hanya mengambil keputusan penugasan kelompok tingkat-lebih-tinggi, sementara tahap kedua melaksanakan penugasan tingkat tipe berbasis-kelompok selanjut-nya menurut perkiraan realisasi permintaan pasar. Hasil beberapa percobaan numerik dipresentasikan untuk menunjukkan efikasi penggunaan model stokastik dan bukan model deterministrik tradisional yang hanya mempertimbangkan per-kiraan permintaan, dan untuk menunjukkan efisiensi algoritma yang diajukan dibandingkan dengan menyelesaikan model dengan menggunakan ekuivalen de-terministiknya.

ABSTRACT

An airlines fleet typically contains multiple aircraft families, each having a spe-cific cockpit design and crew requirement. Each aircraft family contains multiple aircraft types having different capacities. Given a flight schedule network, the fleet assignment model is concerned with assigning aircraft to flight legs to max-imize profit with respect to captured itinerary based demand. However, because of related yield management and crew scheduling regulations, in particular, this decision needs to be made well in advance of departures when market demand is still highly uncertain, although subsequently at preserving crew schedule. In this paper, we proposed a two-stage stochastic mixed-integer programming approach in which the first stage makes only higher-level family-assigment decision, while the seconds stages performs subsequent family based type-level assignments according to forecasted market demand realizations. Results of some numerical experiments are presented to exhibit the efficacy of using the stochastic model as opposed to the traditional deterministic model that considers only expected demand, and to demonstrate the efficiency of the proposed algorithms as compared with solving the model using its deterministics equivalent.

KATA PENGANTAR

Dengan segala kerendahan hati dan penuh sukacita, penulis mengucap-kan puji syukur ke hadirat Tuhan Yang Maha Kuasa atas segala anugrah dan berkat-Nya yang telah diberikan, sehingga penulis dapat menyelesaikan tesis de-ngan judul : MODEL PROGRAM STOKASTIK UNTUK PERSOALAN PENU-GASAN ARMADA PENERBANGAN. Tesis ini merupakan salah satu syarat untuk menyelesaikan studi pada Program Studi Magister Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam (FMIPA)Universitas Sumatera Utara.

Pada kesempatan ini, penulis menyampaikan terimakasih sebesar-besarnya kepada :

Prof. Dr. dr. Syahril Pasaribu, DTMH, M.Sc(CTM), Sp.A(K) selaku Rektor Universitas Sumatera Utara

Prof. Dr. Ir. T. Chairun Nisa, B, M.Sc selaku Direktur Pascasarjana Universitas Sumatera Utara yang telah memberikan kesempatan kepada penulis untuk mengikuti Program Studi Magister Matematika di FMIPA Universitas Su-matera Utara Medan.

Dr. Sutarman, M.Scselaku Dekan FMIPA USU dan Pembimbing Kedua yang juga telah banyak memberikan bimbingan kepada penulis dalam penulisan tesis ini

Prof. Dr. Herman Mawengkangselaku Ketua Program Studi Magister Mate-matika FMIPA Universitas Sumatera Utara yang telah banyak memberikan ban-tuan dalam penulisan tesis ini.

Dr. Saib Suwilo, M.Scselaku Sekretaris Program Studi Magister Matematika FMIPA Universitas Sumatera Utara.

Prof. Dr. Opim Salim S, M.Scselaku Pembimbing Utama yang telah banyak memberikan bimbingan dan arahan serta motivasi kepada penulis dalam penulisan tesis ini.

Saudari Misiani, S.Si selaku Staf Administrasi Program Studi Magister Ma-tematika FMIPA Universitas Sumatera Utara yang telah banyak memberikan pelayanan yang baik kepada penulis selama mengikuti perkuliahan.

Seluruh rekan-rekan Mahasiswa pada Program Studi Magister Matematika FMIPA Universitas Sumatera Utara yang telah memberikan bantuan moril dan dorongan kepada penulis dalam penulisan

Tak lupa penulis mengucapkan terimakasih sebesar-besarnya dan penghar-gaan setinggi-tingginya kepada orangtua dan mertua tercintaSt. Maruli Silala-hi, BA / Tiomina br SimanjuntakdanSabam M. Rajagukguk / Asmida br. Siregaryang telah mencurahkan kasih sayang dan dukungan kepada penulis, terlebih pada isteri tersayang Delima Christin Rajagukguk, SEyang dengan setia mendampingi dan membantu penulis selama mengikuti perkuliahan hing-ga sampai penulisan tesis ini. Terakhir, ucapan terimakasih kepada anak-anak tersayang Gracia Monica Silalahi, Anasthasya Silalahi, dan Yehezkiel Silalahi yang telah memberikan semangat dan dorongan kepada penulis dalam penulisan tesis ini.

Penulis menyadari bahwa tesis ini masih jauh dari sempurna, untuk itu penulis mengharapkan kritik saran untuk penyempurnaan tesis ini. Semoga tesis ini dapat bermanfaat bagi pembaca dan pihak-pihak lain yang memerlukannya. Terimakasih.

Medan, Penulis,

RIWAYAT HIDUP

Alfred Hasiholan Silalahi dilahirkan di Batu V Pematangsiantar pada tang-gal 31 Oktober 1969 dari pasangan Bapak St. Maruli Silalhi, BA & Ibu Tiomina br. Simanjuntak dan merupakan anak ke empat dari delapan bersaudara. Penulis menamatkan pendidikan Sekolah Dasar (SD) HKBP Batu IV Pematangsiantar tahun 1981, Sekolah Menengah Pertama (SMP) HKBP Batu IV Pematangsiantar tahun 1984, Sekolah Menengah Atas (SMA) PGRI 29 Perumnas Batu VI Pe-matangsiantar tahun 1987. Pada tahun 1987 memasuki Perguruan Tinggi Uni-versitas HKBP Nommensen Pematangsiantar jurusan PMIPA Program Studi Ma-tematika pada Jenjang Diploma III Proyek Pengembangan Pendidikan Tenaga Kependidikan (P 3TK) dan lulus tahun 1990. Kemudian pada tahun 1990 penulis melanjutkan perkuliahan ke jenjang Strata Satu (S-1) pada Universitas HKBP Nommensen Pematangsiantar dan lulus tahun 1991.

Silalahi dan 1 anak laki-laki bernama Yehezkiel Silalahi.

DAFTAR ISI

Halaman

ABSTRAK i

ABSTRACT ii

KATA PENGANTAR iii

RIWAYAT HIDUP v

DAFTAR ISI vii

DAFTAR TABEL ix

BAB 1 PENDAHULUAN 1

1.1 Latar Belakang 1

1.2 Perumusan Masalah 3

1.3 Tujuan Penelitian 3

1.4 Manfaat Penelitian 3

1.5 Metode Penelitian 3

BAB 2 TINJAUAN PUSTAKA 4

BAB 3 LANDASAN TEORI 6

3.1 Penugasan Armada dengan Pendekatan Stokastik 6 3.1.1 Model Penugasan Armada Stokastik Dua-Tahap 7 3.1.2 Strategi Penugasan Tipe-Pesawat Setelah Penyelesaian

SPFAM 16

BAB 4 PEMBAHASAN 20

4.2 Pendekatan Penyelesaian 21

4.2.1 Kerangka Berbasis-Dekomposisi 22

4.2.2 Analisa Polyhedral: Pengembangan SPFAM2 26 4.2.3 Pendekatan Penyelesaian Yang Diajukan 33

BAB 5 KESIMPULAN DAN SARAN 37

5.1 Kesimpulan 37

5.2 Saran 38

DAFTAR TABEL

Nomor Judul Halaman

3.1 Parameter untuk contoh 3.1 15

3.2 Solusi penugasan armada yang diperoleh melalui model 3.1, 3.2, dan

pendekatan determenistik 15

ABSTRAK

Armada perusahaan penerbangan biasanya mempunyai kelompok pesawat ganda, yang masing-masing mempunyai rancangan cockpit dan persyaratan spesifik awak pesawat. Setiap kelompok pesawat mempunyai tipe pesawat ganda yang mem-punyai kapasitas yang berbeda-beda. Dengan jadwal penerbangan tertentu, model penugasan armada berkenaan dengan penugasan pesawat ke leg-leg penerbangan untuk memaksimalkan laba dengan mempertimbangkan rencana perjalanan yang berdasarkan permintaan. Akan tetapi, karena managemen hasil terkait dengan peraturan penjadwalan awak pesawat, terlebih, keputusan ini harus diambil se-belum keberangkatan saat permintaan pasar masih sedikit tidak pasti, walaupun selanjutnya pada tahap kemudian, penugasan ulang tipe-tipe pesawat di dalam kelompok tertentu bisa dilakukan saat ramalan permintaan meningkat, sambil tetap mempertahankan jadwal awak pesawat. Dalam tesis ini, diajukan pen-dekatan mixed-integer programming stokastik dua-tahap di mana tahap pertama hanya mengambil keputusan penugasan kelompok tingkat-lebih-tinggi, sementara tahap kedua melaksanakan penugasan tingkat tipe berbasis-kelompok selanjut-nya menurut perkiraan realisasi permintaan pasar. Hasil beberapa percobaan numerik dipresentasikan untuk menunjukkan efikasi penggunaan model stokastik dan bukan model deterministrik tradisional yang hanya mempertimbangkan per-kiraan permintaan, dan untuk menunjukkan efisiensi algoritma yang diajukan dibandingkan dengan menyelesaikan model dengan menggunakan ekuivalen de-terministiknya.

ABSTRACT

An airlines fleet typically contains multiple aircraft families, each having a spe-cific cockpit design and crew requirement. Each aircraft family contains multiple aircraft types having different capacities. Given a flight schedule network, the fleet assignment model is concerned with assigning aircraft to flight legs to max-imize profit with respect to captured itinerary based demand. However, because of related yield management and crew scheduling regulations, in particular, this decision needs to be made well in advance of departures when market demand is still highly uncertain, although subsequently at preserving crew schedule. In this paper, we proposed a two-stage stochastic mixed-integer programming approach in which the first stage makes only higher-level family-assigment decision, while the seconds stages performs subsequent family based type-level assignments according to forecasted market demand realizations. Results of some numerical experiments are presented to exhibit the efficacy of using the stochastic model as opposed to the traditional deterministic model that considers only expected demand, and to demonstrate the efficiency of the proposed algorithms as compared with solving the model using its deterministics equivalent.

BAB 1

PENDAHULUAN

1.1 Latar Belakang

Setiap perusahaan penerbangan perlu memanfaatkan kapasitas peralatan-nya dengan efisien karena modal dan biaya operasional pesawat yang sangat tinggi dengan cara menjadwalkan pesawat secara bijaksana ke leg-leg penerba-ngan yang berbeda untuk mengakomodir permintaan penumpang sampai tingkat yang mungkin sehingga perusahaan memperoleh laba maksimal. Proses keputusan ini melibatkan armada kelompok-kelompok pesawat yang berbeda yang masing-masing terdiri dari tipe pesawat ganda yang mempunyai kapasitas spesifik yang disebut sebagai model penugasan armada penerbangan atau Fleet Assignment Model (FAM). Berdasarkan hasil penelitian dari para peneliti sebelumnya seperti Farkas (1995), Kniker (1998), Jacobs et al. (1999), Barnhart et al. (2002) dan Sherali et al. (2005), mengatakan pada umumnya setiap perusahaan penerba-ngan dapat menyelesaikan masalah penjadwalan pesawat 10-12 minggu sebelum keberangkatan karena keputusan penjadwalan awak pesawat ditentukan oleh tipe pesawat yang digunakan pada leg-leg penerbangan yang berbeda, dan menurut peraturan serikat pekerja, keputusan ini harus dipastikan 8-10 minggu sebelum keberangkatan

2

yang disebut denganmodel pengerahan ulang armada. Keputusan ini dilaksanakan dengan menggunakan model optimisasi berskala besar. Setelah tahap pengerahan-ulang armada, yang bisa dilaksanakan adalah hanya terbatas pada tukar-menukar pesawat antara leg-leg atau rute-rute yang mempunyai tempat keberangkatan dan tempat tujuan yang sama.

Penelitian ini, diajukan pendekatan program stokastik bilangan bulat cam-puran dua-tahap (Stochastic Mixed Integer Programming - SMIP), dimana tahap pertama hanya mengambil keputusan penugasan kelompok tingkat lebih-tinggi, selanjutnya tahap kedua melaksanakan penugasan tingkat tipe berbasis-kelompok menurut perkiraan realisasi permintaan pasar. Dengan mempertimbangkan keti-dakpastian permintaan sebelum tahap penentuan armada awal, tambahan flek-sibilitas dimasukkan ke dalam proses yang menawarkan peluang yang lebih bi-jaksana untuk direvisi, kemudian dilakukan analisa polyhedral atas model yang diajukan lalu mengembangkan pendekatan penyelesaian yang cocok.

Penelitian ini, difokuskan pada dua tahap. Tahap pertama disebut dengan tahap kerangka penugasan armada dinamik penugasan armada awal dan tahap kedua disebut dengan tahap pengerahan-ulang armada. Untuk menentukan be-rapa banyak penumpang yang diterima pada network penerbangan yang dijad-walkan, keputusan pengerahan armada ini dipadukan dengan komponen manage-men hasil. Permintaan yang datang dari penumpang multi-leg akan tergantung pada ketersediaan tempat duduk pada semua leg yang terlibat antara tempat ke-berangkatan dan tempat tujuan penumpang yang dikenal sebagai efek network. Serupa halnya, penumpang yang terbang pada leg tertentu tidak identik dengan bentuk pendapatan yang dihasilkan perusahaan penerbangan dan sumberdaya yang dikonsumsi oleh perusahaan penerbangan.

3

1.2 Perumusan Masalah

Perumusan masalah dalam penelitian ini adalah bagaimana memodelkan program stokastik untuk membuat perencanaan dalam menyelesaikan persoalan penugasan armada penerbangan dalam kondisi ketidakpastian.

1.3 Tujuan Penelitian

Tujuan dari penelitian ini adalah untuk menghasilkan dan menyelesaikan model program stokastik untuk persoalan penugasan armada penerbangan dalam kondisi ketidakpastian sehingga permintaan penumpang dapat dipenuhi dan juga perusahaan penerbangan dapat memaksimalkan laba.

1.4 Manfaat Penelitian

Penelitian ini diharapkan dapat memberikan kontribusi bagi perusahaan penerbangan yang mengalami masalah dalam penugasan armada penerbangan menentukan model dengan kondisi tidak pasti, serta menjadi acuan bagi peneliti lainnya dalam melakukan penelitian yang sama ataupun lebih kompleks lagi.

1.5 Metode Penelitian

BAB 2

TINJAUAN PUSTAKA

Program stokastik adalah sebuah kerangka untuk mengoptimasikan masa-lah pemodelan dalam kondisi ketidakpastian (uncertainly). Sedangkan optimasi kondisi kepastian (determenistik) dirumuskan dengan parameter-parameter yang diketahui. Masalah-masalah dunia nyata hampir selalu menyertakan beberapa parameter yang tidak diketahui. Ketika parameter hanya dikenal dalam batas-batas tertentu, salah satu pendekatan yang digunakan untuk mengatasi masalah-masalah seperti ini adalah pendekatan optimisasi kuat (robust optimization). Mo-del program stokastik dirumuskan, dipecahkan secara analisis atau dikontrol, dan di analisa dalam rangka untuk memberikan informasi yang berguna bagi pembu-at keputusan. Tujuannya adalah untuk mencari solusi yang layak dan optimal (dalam arti tertentu) untuk semua masalah.

Salah satu program yang diterapkan dan mempelajari model pogram stokastik adalah program linear dua-tahap. Di sini pembuat keputusan mengambil bebera-pa tindakan di tahap pertama, setelah terjadi peristiwa acak yang mempengaruhi hasil keputusan tahap pertama. Kemudian, sebuah keputusan lain/dapat diambil pada tahap kedua untuk mengkompensasikan efek buruk yang mungkin dialami sebagai akibat dari keputusan tahap pertama kebijakan yang optimal dari model seperti itu

Barnhart et al. (2002) dan Sherali et al. (2005), mengembangkan rumusan ini dari skenario tunggal (perkiraan permintaan), penugasan armada berbasis-rencana perjalanan dan model pengerahan-ulang armada.

kapa-5

BAB 3

LANDASAN TEORI

3.1 Penugasan Armada dengan Pendekatan Stokastik

7

3.1.1 Model Penugasan Armada Stokastik Dua-Tahap

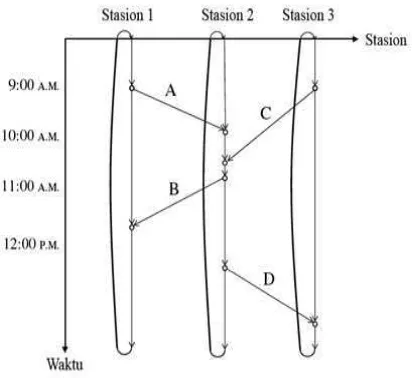
Masalah penugasan armada awal yang memasukkan peluang pengerahan-ulang armada akan dirumuskan dengan menggunakan program stokastik dua-tahap bilangan bulat campuran (SMIP). Rumusan ini dikembangkan oleh Barn-hart dkk. (2002) dan Sherali dkk. (2005) dari skenario tunggal (perkiraan per-mintaan), penugasan armada berbasis-rencana perjalanan dan model pengerahan-ulang armada yang didasarkan pada struktur network penerbangan waktu-ruang yang digambarkan dalam Gambar 1, yang biasanya digunakan dalam perumusan model penugasan armada (FAM) dan menggambarkan jadwal penerbangan yang diputuskan dengan proses penjadwalan perusahaan penerbangan sebelumnya.

Representasi network penerbangan waktu-ruang secara keseluruhan mene-tapkan himpunan network sedemikian, satu untuk masing-masing tipe armada dalam masing-masing kelompok. Ini memungkinkan waktu penerbangan tergan-tung tipe-armada dan waktu memutar (waktu yang dibutuhkan pesawat yang datang untuk bersiap untuk penerbangan lainnya). Jika waktu penerbangan dan waktu memutar tidak berbeda secara signifikan antara sebagian tipe armada ter-tentu, maka representasi network gabungan bisa dibentuk untuk tipe-tipe ini. Dalam subnetwork untuk tipe armada tertentu, jadwal waktu network vertikal terkait dengan masing-masing stasion, yang terdiri dari serangkaian node kejadi-an ykejadi-ang terjadi secara berkejadi-angkai di stasion ini. Node kejadikejadi-an ini menggambarkkejadi-an pertibaan atau keberangkatan penerbangan pada waktu spesifik.

Barnhart et al. (2001) dan sherali et. al (2005) mengatakan ada tiga tipe arc dalam subnetwork untuk masing-masing tipe armada, yaituarc ground yang ditunjukkan oleh panah melengkung yang menggambarkan pesawat tetap di sta-sion yang sama selama periode waktu tertentu,arc penerbanganyang ditunjukkan oleh panah vertikal yang menggambarkan leg-leg penerbangan danarc wraparound

8

Gambar 3.1 Struktur Network Penerbangan Waktu Ruang

Arc penerbangan menghubungkan node-node yang tepat pada jadwal waktu network yang berbeda-beda untuk masing tipe armada. Untuk masing-masing stasion, jumlah arc penerbangan yang tiba sama dengan jumlah arc pener-bangan yang berangkat, yang diberikan oleh proses penjadwalan untuk menjamin jadwal harian yang sama dan untuk menghindari munculnya tiket cuma-cuma. Persyaratan bahwa hanya satu tipe armada (dan karenanya hanya satu kelompok armada) dialokasikan pada masing-masing leg penerbangan secara bersama-sama mengatur flow yang terjadi pada subnetwork dengan tipe yang berbeda-beda, yang dengan demikian menjadikan semua subnetwork saling tergantung.

9

Himpunan

K : himpunan kelompok pesawat dalam armada, dengan indeksk(misalnya k = 1 bisa menotasikan kelompok Boeing B737).

Tk : himpunan tipe armada dalam kelompok k, dengan indeks t (misalnya T1bisa mencakup tipe B737-300 dan B737-500 dalam kelompok Boeing

B737).

T : himpunan semua tipe armada dalam keseluruhan armada, dimana T =

∪k∈KTk

Nt : himpunan node dalam network t tipe armada,t ∈T; dengan indeks n. Gt : himpunan arc ground dalam network t tipe armada, t ∈ T; dengan

indeks g.

Lk : himpunan leg penerbangan yang ditugaskan pada kelompok k (sebagai konsekuensi dari keputusan pengerahan armada awal yang akan diten-tukan), dengan indeks l.

L : himpunan semua leg penerbangan, di mana L=∪k∈KLk.

Π : himpunan semua rencana perjalanan (path) yang diidentifikasi yang akan dipertimbangkan dalam analisa, dengan indeks i.

Π(l) : himpunan rencana perjalanan (path) dalam Π yang lewat melalui leg

l, l∈L.

CSt : himpunan arc (arc penerbangan/leg penerbangan, l, dan arc ground, g) yang maju dalam waktu hingga jadwal waktu penghitungan (garis horizontal yang bersesuaian dengan waktu tetap) dalam networkt tipe pesawat, t∈T.

10

1 jika leg penerbanganlditerbangkan oleh kelompok pesawatk

(dalam masalah tahap pertama), l∈L, k ∈K

1 jika taraf 1 diterbangkan oleh tipe armadat (dalam masalah tahap kedua) dengan scenarios, l ∈L, k ∈K, s∈S

0 untuk lainnya ys

g : jumlah pesawat (tipe t) pada arc ground g dalam network t tipe armada untuk skenario s, g∈Gt, t∈T, s∈S

Ps

t : variabel artifisial untuk mencatat ketaklayakan dalam batasan ketersediaan pesawat untuk tipe t dan skenario s, t∈T, s∈S.

qs

t : jumlah penumpang yang diterbangkan (permintaan diterima) atas rencana perjalanan idengan skenario s, i∈Π, s∈S.

Parameter Permintaan dan Biaya µs

i : realisasi permintaan untuk rencana perjalanan i, i ∈ Π, dengan skenario s, s∈S.

µs _{: vektor realisasi permintaan atas seluruh rencana perjalanan dalam} Π dengan skenario s, s ∈S.

Clt : biaya pencakupan leg l dengan menggunakan armada tipe t, l ∈

L, t∈T

Capt : kapasitas armada tipe t, t∈T.

f_is : taksiran ongkos rata-rata untuk rencana perjalanan i dengan ske-nario s, i∈Π, s∈S.

ps _{: probabilitas untuk realisasi skenario s, s∈S.} At : jumlah pesawat tipe t yang tersedia,t∈T.

11

Notasi Lainnya

Qs(z, µs_{) : nilai tujuan tahap kedua untuk skenario s, dengan diketahuinya} keputusan pengerahan armadaz dari tahap pertama dan realisasi permintaan µs_{, s∈S.}

bfln =±1 : jika penerbangan l berawal/berakhir di node n (dalam network armada tipe t),l ∈L, n∈N, t∈T.

bggn =±1 : jika arc ground g berawal/berakhir di node n (dalam network armada tipe t),g ∈G, n∈N, t∈T.

Keacakan dinyatakan dengan menggunakan himpunan skenario diskritS, di mana setiap skenario s ∈S terkait dengan realisasi permintaanµs_{, ongkos yang} bersesuaian fs _{, dan probabilitas p}s _(dimanaP

s∈Sp

s _{= 1). Variabelz adalah} ke-putusan penugasan kelompok pesawat, dan xs _{adalah keputusan penugasan} tipe-pesawat atau, ekuivalen, keputusan pengerahan-ulang armada yang bersesuaian dengan masing-masing skenario s ∈ S. Di dalam prakteknya, permintaan bi-asanya ditaksir dengan menggunakan distribusi normal, karena distribusi kontinu biasanya jauh lebih sulit ditangani dalam perhitungan dan algoritma, rentang nilai permintaan yang mungkin bisa didiskritkan untuk menyatakan skenario diskrit, dan dengan demikian permintaan rata-rata dan probabilitas untuk setiap segmen yang didiskritkan diambil sebagai nilai µ dan nilai p yang bersesuaian. Dengan tergantung pada tingkat diskritisasi, pendekatan ini bisa menghasilkan terlalu banyak skenario yang perlu diperhatikan. Kemudian, dalam bagian 4.1.3, di-rancang proses penyusunan skenario yang menghasilkan representasi yang layak sambil menjaga ukuran masalah tetap bisa ditangani dengan mudah. Untuk saat ini, difokuskan pada pemodelan masalah.

Pada tahap pertama SPFAM dua-tahap yang diajukan, kelompok pesawat

per-12

jalanan. Kemudian SPFAM tahap-dua bisa dinyatakan sebagai berikut.

Model 3.1. : Program FAM Stokastik Dua-Tahap Yang Memper-timbangkan Pengerahan-ulang Armada:

di mana, untuk setiap s∈S, akan diperoleh : Qs(z, µs_{) = min}P

13

tahap-kedua yang masing-masing menyatakan batasan kapasitas dan batasan per-mintaan. Batasan (1j) mengatakan bahwa semua penerbangan untuk tiap jenis pesawat memenuhi ketersediaan awak pesawat. Secara teoritis, model ini dapat digeneralisir untuk mencakup keputusan penumpang tingkat-kelas-ongkos dengan mendefinisikan Π dalam batasan campuran penumpang ini sebagai himpunan ren-cana perjalanan dan kelas ongkos, seperti yang dibahas Smith (2004). Akan tetapi, ini meningkatkan ukuran masalah secara drastis, dan membutuhkan studi lebih lanjut untuk pengembangan pendekatan penyelesaian khusus yang sesuai.

Penyelesaian untuk Model 3.1 akan menghasilkan penugasan kelompok sawat ke leg penerbangan untuk FAM awal dan penugasan alternatip tipe pe-sawat dengan skenario yang berbeda-beda. Penugasan tingkat-tipe-alternatip ini bisa dipandang sebagai keputusan potensial untuk proses pengerahan-ulang ar-mada kemudian. Penugasan tingkat-kelompok ke leg tidak memutuskan tentang kapasitas yang dialokasikan ke leg penerbangan.

Sebagai alternatip, dapat didispensasikan dengan keputusan pengerahan-ulang armada berbasis-skenario dari tahap kedua dengan mendukung pemben-tukan masalah tahap-kedua linier (bukan diskrit) yang lebih mudah dikerjakan. Dalam kasus ini, masalah tahap-pertama itu sendiri memutuskan tentang penu-gasan tipe pesawat ke leg, dan meminimalkan biaya penupenu-gasan ini minus perkiraan pendapatan dari tahap kedua. Ini menghasilkan varian stokastik lain dari FAM awal yang mempertimbangkan permintaan rencana perjalanan sebagai berikut.

14

t (x, µs) adalah tujuan tahap-kedua (digunakan superskript R untuk menyatakan sudut pandang terbatas yang mengesampingkan pengerahan-ulang armada). Pada prinsipnya rumus ini merupakan FAM tingkat-OD (asal dan tujuan) dengan mempertimbangkan managemen pendapatan (RM) yang diajukan oleh Smith (2004), di mana tahap kedua adalah masalah managemen pendapatan tingkat-OD.

Dari sudut pandang implementasi, Model 3.2 lebih mudah dikerjakan dari-pada Model 3.1. Akan tetapi, dari sudut pandang pemodelan, Model 3.2 mem-batasi satu penugasan tingkat-tipe untuk semua realisasi permintaan; karenanya, nilai tujuan optimal untuk Model 3.1 setidaknya lebih baik untuk Model 3.2. Lebih jauh lagi, penugasan tingkat-tipe optimal yang diperoleh dari Model 3.2 bisa tidak layak berkenaan dengan penugasan tingkat-kelompok yang diperoleh dari Model 3.1. Contoh berikut membandingkan penyelesaian dari pendekatan stokastik sedemikian versus pendekatan deterministik. Dalam Bagian 4, akan dilakukan percobaan perhitungan lebih lanjut dengan menggunakan Model 3.2 dan menggunakan FAM deterministik dengan model pengerahan-ulang armada digerakkan-permintaan pasca-optimisasi.

Barnhart et al. (2001) dan sherali et. al (2005) membuat Contoh untuk mengillus-trasikan perbandingan Model 3.1, Model 3.2 dan pendekatan deterministik, de-ngan memperhatikan network hipotetis yang mempunyai 4 (empat) leg yang ter-diri dari dua trip putaran yang tak berimpit. Pada contoh ini dimisalkan him-punan berikut: K = {k1, k2}, Tk1 = {t1, t2}, Tk2 = {t2, t4}, S = {s1, s2} dan

Π =L ={l1, l2, l3, l4} (yaitu, semua rencana perjalanan hanya memuat leg

tung-gal). Kita hanya bisa menggunakan pesawat yang tersedia (yaitu,ψi =∞,∀t∈T, sehinggaPs

15

Tabel 3.1 Parameter untuk contoh 3.1

Biaya Skenario 1 Skenario 2 Rata-rata clt1 clt2 clt3 clt4 f

1

i µ1i fi2 µ2i fi¯ µi¯ l1 9,000 18,000 19,000 10,000 400 90 970 140 628 110

l2 9,000 17,000 18,000 10,000 430 100 1,000 150 658 120

l3 8,000 17,000 18,000 9,000 410 90 980 140 638 110

l4 8,000 18,000 19,000 9,000 530 90 990 140 714 110

Juga, andaikan bahwa masing-masing tipe hanya mempunyai satu pesawat yang tersedia, dan bahwa kapasitas untuk ke empat tipe masing-masing adalah 120, 138, 141 dan 123. Misalkan probabilitas untuk kedua skenario adalah ps1 ₌

0,6 danps2 _{= 0,4, dan dengan demikian ongkos dan permintaan rata-rata, ¯f dan}

¯

µ, diambil dari nilai yang diperlihatkan dalam dua kolom terakhir pada Tabel 1. Penugasan yang diperoleh dari Model 3.1, 3.2 dan pendekatan deterministik yang menggunakan nilai ongkos dan permintaan rata-rata diperlihatkan pada Tabel 2 berikut.

Tabel 3.2 Solusi penugasan armada yang diperoleh melalui model 3.1, 3.2, dan pendekatan determenistik

Model 3.1 Model 3.2 Deterministik

Kelompok Tipe di Tipe di Kelompok Tipe Kelompok Tipe bawahs1 bawah s2

l1 k2 t4 t3 k2 t4 k1 t1

l2 k2 t4 t3 k2 t4 k1 t1

l3 k2 t4 t3 k2 t4 k1 t1

l4 k2 t4 t3 k2 t4 k1 t1

Penugasan yang diperoleh dari Model 3.2 adalah untuk menugaskan pesawat tunggal tipet, dari kelompokk2 ke semua leg, penugasan yang diperoleh dari

pen-dekatan deterministik adalah menugaskan pesawat tunggal tipetdari kelompokk1

ke semua leg, sementara penugasan yang diperoleh dari Model 3.1 menggunakan pesawat dari kedua kelompok.

16

merangkumkan penugasan tipe dan nilai tujuan yang diperoleh dengan menggu-nakan ketiga pendekatan dengan kedua skenario ini.

Tabel 3.3 Pelaksanaan dari ketiga pendekatan dengan skenario yang berbeda

Model 3.1 Model 3.2 Deterministik

Skenario Skenario Skenario Skenario Skenario Skenario

s1 s2 s1 s2 s1 s2

Objektif -476,660 -127,600 -446,620 -125,600 -438,800 -129,600

Diharapkan -337,036 -318,212 -315,120

Perkiraan nilai tujuan pada table 3 untuk Model 3.1, Model 3.2 dan pen-dekatan deterministik masing-masing adalah -337,036, -318,212 dan -315,120. Karenanya, walaupun mempunyai ukuran masalah yang lebih kecil, Model 3.2 maupun pendekatan deterministik kehilangan ciri optimalitas dan fleksibilitas tertentu berkenaan dengan keputusan pengerahan-ulang armada dengan cara yang sama modeldapat digeneralisir. 3.1. digeneralisir untuk mengakomodasi keputusan penumpang tingkat kelas-ongkos dan, dengan cara serupa, keputusan penumpang setiap harinya. Model ini juga bisa diperluas untuk memasukkan efek penangkapan kembali (yaitu, routing ulang penumpang yang tidak bisa mewujud-kan rencana perjalanan pilihan-pertama mereka ke rencana perjalanan lain yang mempunyai asal dan tujuan yang sama) dengan memasukkan variabelqs

ij,∀ij ∈Π, untuk menotasikan permintaan atas rencana perjalananiyang diterbangkan atas rencana perjalanan j bila penangkapan kembali dipertimbangkan. Lebih jauh la-gi, rumus optimisasi kuat (RO) bisa dibentuk dari Model 3.1 untuk menstabilkan variabilitas antar-skenario. Dalam tulisan ini, akan difokuskan pada program stokastik dasar Model 3.1 (SPFAM) dan variannya Model 3.2, dengan memper-timbangkan motivasi pada saat keputusan diambil.

3.1.2 Strategi Penugasan Tipe-Pesawat Setelah Penyelesaian SPFAM

17

pada tipe subnetwork seperti yang diperkenalkan pada Bagian 3.1. Tahap kedua menugaskan tipe pesawat ke leg penerbangan dan menentukan permintaan yang diterima, tergantung pada skenario permintaan. Penugasan tipe armada dari tahap kedua ini bisa bervariasi antara skenario yang satu dengan skenario yang lain. Lebih jauh lagi, jika masalah ini tidak diselesaikan sampai optimal, ma-ka penyelesaian penugasan tipe-armada biner mungkin tidak ada tersedia. Ama-kan tetapi, penugasan tipe-armada yang layak dan konsisten sering dibutuhkan un-tuk managemen pendapatan dan sistem keputusan lainnya. Oleh karena itu, dalam bagian ini, penulis mengajukan strategi untuk merekonsiliasi penugasan-penugasan tipe armada yang berbeda yang terjadi akibat dari keputusan berbasis-skenario tahap-kedua.

Misalkan (¯z,x,¯ y,¯ q) adalah notasi penyelesaian yang diperoleh untuk SP-¯ FAM. Dalam penyelesaian ini, diasumsikan bahwa ¯zadalah biner, tetapi (¯x,y)tidak¯ selalu demikian , yang mungkin penyelesaian untuk masalah tahap-kedua adalah penyelesaian heuristik. Oleh karena itu, setiap kelompok pesawat dapat memu-tuskan leg penerbangan yang dicakup oleh setiap kelompok pesawat. Untuk sub-network terkait yang terdiri dari leg penerbangan yang dicakup masing-masing kelompok, perlu ditentukan penugasan tipe armada spesifik ke leg yang bers-esuaian. Model yang diajukan berikut adalah menyelesaikan masalah pengerahan armada untuk masing-masing kelompokk ∈K, di mana tujuannya untuk memi-nimalkan biaya pengerahan-ulang armada.

Definisikan ult menjadi sebuah variabel keputusan biner yang mempunyai nilai 1(satu) jika tipe armada t ditugaskan ke leg penerbangan l, dan 0 (nol) un-tuk lainnya, ∀l ∈ L, t ∈ T. Juga misalkan vg jumlah pesawat pada arc ground g ∀g ∈ G, t ∈ T. Misalkan cl

t,t adalah biaya yang terkait dengan pengerahan-ulang armada pada legl dari tipe yang dialokasikan mula-mulat menjadi tipe t,

∀l ∈ Lkt, t ∈ Tk. Biaya ini dapat mencakup biaya pribadi, biaya pemeliharaan dan biaya terkait-bandara (seperti yang ditanggung karena pergantian gerbang, dan juga biaya yang ditanggung karena ketidakpuasan penumpang). Kemudi-an P

s∈Sp sP

t∈Tkc

l

18

berbeda-beda untuk mengerahkan-ulang armada leg l dari tipe yang ditugaskan semula untuk tipe yang akan ditentukan t, ∀l ∈ Lk, t ∈ Tk. Karenanya, model berikut dapat diselesaikan untuk masing-masing kelompokk ∈K, di mana bata-san (3b) - (3e) diwarisi dari FAM kelompok tunggal dan fungsi tujuan (3a) memi-nimalkan total biaya pengerahan-ulang armada. Penyelesaian modelnya adalah penugasan tipe armada ke leg yang meminimalkan perkiraan biaya pengerahan-ulang armada masa mendatang.

Model 3.3. : Merekonsiliasi Penugasan Tipe-Armada Untuk Me-minimalkan Perkiraan Biaya Pengerahan-ulang Ar-mada:

Catatan 3.2. Perhatikan kasus khusus di mana : clt,t =

n _{θ jika t6=t}

0 jika t=t ∀l ∈Lk, t∈Tk (4) di mana θ adalah konstanta. Dalam kasus ini, fungsi tujuan (3a) di atas menjadi Minimalkan P

Dalam kasus ini, pengerahan-ulang armada atas semua leg dari suatu tipe yang semula ditugaskan ke suatu tipe lainnya diasumsikan juga tidak diinginkan. Dengan demikian sukuP

s∈Sp s_x¯s

19

menyatakan probabilitas bahwa leg l mempertahankan penugasan awalnya. Kare-nanya, fungsi tujuan (6) memaksimalkan total probabilitas penahanan penugasan awal atas semua leg.

Pada kasus - khusus lain di mana : cl

t,t =

n _{bl jikat6=t}

−al jikat=t ∀l∈Lk, t ∈Tk (7) di mana koefisien aj adalah tingkat preferensi atau ganjaran (biaya negatip) un-tuk mempertahankan penugasan tipe-armada semula atau awal, dan koefisien bt adalah penalti untuk setiap perubahan dalam penugasan ini, untuk masing-masing leg l. Dalam kasus ini, fungsi tujuan (3a) ekuivalen dengan

Maksimalkan P

Dengan menggunakan (1e) dan (3b), ini menghasilkan Maksimalkan P

Untuk nilai konstantaa1+b1 atasl, ini pada gilirannya tereduksi menjadi fungsi

BAB 4

PEMBAHASAN

4.1 Penyusunan Skenario

Listes dan Dekker (2005) juga menggunakan program stokastik dua-tahap untuk mengkaji manfaat pencocokan dinamik kapasitas pesawat dengan permin-taan penumpang, walaupun fokus mereka adalah pada pengambilan keputusan tentang komposisi armada. Dalam penyusunan skenario, mereka mendiskritkan masing-masing distribusi permintaan (tingkat-leg) menjadiSsegmen dengan pro-babilitas sama, dan memilih secara acak suatu permintaan sampel untuk masing-masing leg dari keS segmen ini. Percobaan numerik mereka menunjukkan bahwa 50 skenario sudah cukup untuk menangkap dampak variasi permintaan, dan de-ngan mempertimbangkan skenario tambahan tidak menghasilkan perubahan yang signifikan dalam penyelesaian yang diperoleh.

Pendekatan yang digunakan sama untuk menghasilkan skenario, tanpa me-lakukan segmentasi secara eksplisit atas distribusi kontinu. Untuk menghasilkan skenario, diambil secara acak sampel masing-masing permintaan tingkat-rencana perjalanan menurut distribusinya (diasumsikan berdistribusi normal terpancung). Masing-masing komposisi permintaan tingkat-rencana perjalanan yang sampelnya diambil membentuk satu skenario tertentu, dan dihasilkanS skenario sedemikian yang kemungkinannya sama.

bah-21

wa permintaan atas rencana perjalanan kelompok-kelompok yang berbeda saling lepas, sementara rencana perjalanan lainnya yang tidak termasuk dalam suatu kelompok selalu menangani permintaan rata-rata sendiri.

4.2 Pendekatan Penyelesaian

Model 3.1(SPFAM) adalah program mixed-integer stokastik dua-tahap (SM-IP) yang mempunyai variabel biner pada tahap pertama dan variabel biner dan kontinu pada tahap kedua. Fokusnya adalah untuk menugaskan kelompok pe-sawat ke network penerbangan dengan tujuan mempertahankan fleksibilitas yang cukup untuk kemudian direvisi pada penugasan tipe-armada. Jumlah penerba-ngan per hari dan rencana perjalanan yang diidentifikasi untuk perusahaan pener-bangan utama dengan mudah bisa mencapai ribuan dan jutaan, walaupun dalam kenyataannya, hanya himpunan gabungan rencana perjalanan yang representatif sedemikian untuk beberapa himpunan bagian penerbangan bisa digunakan un-tuk tujuan pemodelan. Jika jumlah tipe dipadu dengan duplikasi armada unun-tuk merealisasikan permintaan dan skenario ganda untuk masing-masing rencana per-jalanan, ini dapat menimbulkan masalah berskala sangat besar. Oleh karena itu, pendekatan penyelesaian yang cermat perlu dirancang untuk mengurangi beban kombinatorial yang sifatnya melekat.

22

4.2.1 Kerangka Berbasis-Dekomposisi

Sherali dan Fraticelli (2002) mengembangkan algoritma dekomposisi Ben-ders yang dimodifikasi untuk menyelesaikan SMIP di mana variabel tahap per-tama bernilai biner dan tahap kedua melibatkan variabel bilangan bulat cam-puran 0-1. Proses penyelesaiannya bergantian antara masalah utama dan sub-masalah yang bersesuaian dengan skenario yang berbeda-beda. Masalah utama diselesaikan melalui skema cabang-dan-batas/potong berbasis-LP dalam ruang variabel tahap pertama dan beberapa variabel tambahan yang menyatakan nilai fungsi tahap-kedua. Submasalah diselesaikan dengan menggunakan proses kon-veksifikasi berangkai (seperti proses teknik reformulasi-linierisasi (RLT) Sherali dan Adams 1990, 1994, 1999), dalam bentuk variabel campuran bilangan bulat.

Untuk memudahkan beban perhitungan dan menjaga fokus pada peneta-pan penugasan kelompok melalui SPFAM, akan diselesaikan model SPFAM1 yang diperlonggar, yang didefinisikan sebagai SPFAM dengan batasan biner untuk vari-abel s yang diperlonggar (tetapi batasan untuk variabel z tetap dipertahankan), dan karena (1h) diperketat menjadi (9c) maka akan menjadi sebagai berikut:

SPFAM1; Minimalkan P

s∈S

ps_{Qs(z, µ}s_{) (9a)}

dengan batasan (1b) dan (1c) (9b)

di mana, untuk setiap s∈S,

dengan batasan (1e) - (1g), dan (9d)

P

23 yang menghasilkan ketaksamaan yang sah dan lebih ketat. Perlu diperhatikan bahwa ketidakpastian dalam SPFAM (model 3.1) hanya ada dalam fungsi tujuan tahap-kedua dan ruas kanan tahap-kedua. Akan tetapi, penggunaan (9c) dan (10) dalam SPFAM1 memasukkan keacakan ke dalam matriks wacana, sambil mengetatkan representasi model.

Dalam konteks pengaplikasian dekomposisi Benders pada SPFAM1, masalah utama berbentuk :

Yang mencakup batasan tahap-pertama seperti beberapa tambahan tipe poto-ngan Benders (11c) yang dihasilkan dari submasalah sebagai berikut. Dalam im-plementasinya, ketika Branch and Bound memotong proses untuk masalah utama dalam menentukan penyelesaian z baru yang bernilai-biner untuk menyelesaikan masalah tahap-kedua (yaitu, submasalah) pada masing-masing skenario. Perlu di-catat bahwa kelebihan (1b) dan dengan menggunakan Π =S

k∈K

S

l∈LkΠ(l),

meng-24

gunakan potongan ini untuk iterasi awal guna mengembangkan deskripsi awal tentang fungsi nilai optimal.

Khususnya, diketahui penyelesaian biner ¯z dari (11), dapat kita pastikan Lk ∀k ∈ K. Kemudian, masalah yang terdekomposisi parsial ini mempunyai bentuk sebagai berikut, ∀k ∈K, s∈S;

Seperti yang dinyatakan di atas, untuk memudahkan beban perhitungan, ketimbang mengembangkan potongan Benders yang didasarkan pada submasalah (9c)-(9g) untuk setiap s ∈ S, diselesaikan masalah kelompok-tunggal terdekom-posisi (12) (untuk beberapa iterasi awal) dan dikembangkan potongan Benders untuk SPFAM1 dengan menggunakan penyelesaian dual optimal yang diperoleh dari masalah ini sebagai berikut.

25

di mana untuk penyelesaian masalah utama z¯tertentu, kita definisikan

Ki _≡

k∈K|i∈S

l∈LkΠ(l) ∀i∈Π

Bukti. Dari kelayakan dual untuk (12), dibentuk penyelesaian layak dual un-tuk sistem (9d)-(9g). Pertama kali didefinisikan φls _{≡ 0∀l ∈ L\{Lk}∀k ∈ K.} kemudian penyelesaian dual untuk (12) untuk setiap k ∈ K, digabungkan un-tuk mengkaji penyelesaian dual ¯φ1s_,φ¯2s_,φ¯3s_,φ¯4s_{, dan ¯φ}5s _{≡ maxk}

∈Kiφ¯5ks∀i∈Π

masing-masing terkait dengan batasan (9d)-(9f) untuk submasalah. Kelayakan dual berkenaan dengan kolomxs_{, y}s _{dan p}s _{tampak jelas dari kelayakan dual} un-tuk (12). Masih harus ditunjukkan bahwa ¯φ4s

l ∀l ∈ L dan maxk∈Kiφ¯5_iks∀i ∈ Π

masing-masing terkait dengan (9e) dan (9f), menghasilkan kelayakan dual berke-naan dengan kolom untukqs

t∀i∈Π. Dari dual untuk (12), diperoleh bahwa untuk setiap k∈ K,

dan karena itu ;

max dual untuk (9c)-(9g), dan juga (13) merupakan potongan Benders yang sah untuk SPFAM1.

Sepanjang menyangkut penyelesaian layak primal, untuk memutakhirkan nilai saat ini, dengan menotasikanqsk

t sebagai nilai optimal dariqsi∀i∈

S

l∈LkΠ(l),

26

Untuk memperoleh penyelesaian yang bahkan lebih mendekati penyelesaian untuk SPFAM (Model 3.1), selanjutnya dilaksanakan analisa polyhedral dalam bagian 4.2.2 atas Model 3.1 yang mencakup batasan biner untuk variabel xguna mengembangkan representasi model yang ditingkatkan untuk SPFAM. Pada mo-del yang dihasilkan ini,xakan diperlonggar menjadi bernilai kontinu untuk mem-peroleh model SPFAM2, dan kemudian akan diaplikasikan pempartisian Bender pada SPFAM2 dalam Bagian 4.2.3.

4.2.2 Analisa Polyhedral: Pengembangan SPFAM2

Potongan Benders yang dihasilkan atas masalah tahap-kedua, bisa tidak menghasilkan nilai x biner yang baik. Sherali et al. (2005) melaksanakan ana-lisa polyhedral atas versi deterministik dari model kelompok-tunggal yang seru-pa dengan model yang dikaji di sini, dan mengajukan beberaseru-pa rumusan ulang dan mekanisme pembentukan hull konveks parsial, bersama-sama dengan berba-gai kelas ketaksamaan yang sah, untuk mengetatkan representasi model. Secara khusus, perusahaan penerbangan menetapkan hasil berikut. Untuk setiapk ∈K dan l ∈Lk (didasarkan pada zik= 1), misalkan :

Kemudian hull konveks dari Z_lks diberikan dalam ruang dimensi lebih tinggi yang memasukkan variabel baru sebagai berikut : Qs

27

Sekarang akan dikaji substruktur yang serupa, tetapi satu yang mencakup variabel tahap-pertama dan tahap-kedua untuk skenario tertentu. Secara khusus, dapat diperhatikan subsistem berikut yang diekstraksi dari SPFAM (Model 3.1) untuk setiap l ∈L dan s ∈ S, di mana Capt diganti dengan ˜cs

lt∀t, seperti dalam (9c) dan (10).

Proposisi 4.2 Misalkan zs

l diberikan oleh (17) untuk setiap l∈L. Maka,

28

P

t∈T Qs

ilt=qis∀i∈Π(l), (18e)

xs_{≥0, Q}s_{≥0} (18f)}

Bukti. Persamaan (17a) dan (17b) dapat ditulis secara ekuivalen sebagai berikut:

zlk= P

t∈Tk

xs

lt ∀k∈K, (19a)

P

t∈T xs

lt= 1 (19b)

Dengan mencatat bahwa sistem (19b) dan (17c-17e) mempunyai bentuk yang sama dengan zs_lk dalam (15a-15d), dan bahwa (19a) menyamakan masing-masing variabel zlk menjadi sebuah ekspressi dalam variabel x yaitu dinilai biner secara otomatis untuk binerx, hasil berikut diperoleh dari representasi yang bersesuaian dari conv(zs

lk) yang diberikan oleh (16a-16c). Catatan Dalam kasus memasukkan zsc

l ke dalam hasil beberapa leg-leg yang

dip-ilih dapat menyebabkan peningkatan yang luar biasa dalam ukuran masalah, yang dapat memperoleh RLT yang valid atau potongan proyeksi yang diimplikasikan oleh himpunan ini ketika diperlukan melalui pemisahan masalah sebagai berikut. Notasikan ξs _{≡(z, x}s_{, q}s_{) dan misalkan (18) ditulis tersusun lebih rapi sebagai :}

W1ξs+W2Qs=h1 ←ψ1, (20a)

W3ξs+W4Qs≤0←ψ2 (20b)

(ξs_{, Q}s_{)≥0 (20c)}

Diberikan beberapa penyelesaian pecahan ¯ξs_{, untuk memungkinkan menghapus} ini dengan ketaksamaan yang sah dalam ruang variableξyang diimplikasikan oleh (20), masalah pemisahan dapat diselesaikan sebagai berikut:

Maksimalkan [ψT

1W1+ψ2TW3] ˜ξs−ψT1h1 (21a)

dengan batasan

ψT

29

[ψT

1W2+ψ2TW3] ˜ξs−ψT1h1 ≤1 (21c)

ψ1 unrestricted ψ2 ≥0 (21d)

di mana (21c) adalah sebuah batasan normalisasi. Jika nilai objektif dari masalah ini positip (yaitu, sama dengan satu disebabkan (21c)), maka akan kita peroleh potongan RLT sebagai berikut :

[ ˜ψT

1W1+ ˜ψ2TW3]ξs≤ψ˜1Th1 (22)

yang memotong ξ, di mana ¯ψ adalah penyelesaian optimal untuk masalah (21).

Selanjutnya, akan diajukan strategi lain yang didasarkan pada hasil Propo-sisi 4.2, yang dimotivasi oleh fakta bahwa himpunan variabel tambahan Qs

ilt∀i∈ Π, l ∈ L, t ∈ T, s ∈ S dapat meningkatkan ukuran masalah secara signifikan. Sebenarnya akan dibentuk subsistem alternatip yang memasukkan lebih sedikit variabel ke dalam rumus dengan penggabungan batasan-batasan secara layak ke dalam Zsc

l . Dan akhirnya, untuk setiap l ∈ L dan s ∈ S, masing-masing akan diganti dari (18c) dan (18d) atas t ∈ Tk∀k ∈ K, dan kemudian disubstitusikan Qzs

ilk =

P

t∈TkQ

s

ilt∀i∈Π(l), k∈K untuk memperoleh himpunan berikut: ˜

30

dengan xs

lt ∀t ∈ T, sambil mempertahankan (23a) itu sendiri, dan kemudian mensubstitusikan Vs Ini menghasilkan himpunan yang diangkat sebagai berikut:

˜

Proposisi 4.3 MisalkanZs

l danZlsv diberikan masing-masing oleh (17) dan (24)

untuk setiap l ∈ L dan s ∈ S. Maka, Zsv

l ⊇ Zls, dan titik ekstrim Zlsv

meng-hasilkan nilai biner untuk variabel z.

Bukti. Untuk setiap (¯z,x¯5_,q¯s_)∈zs bahwa di titik ekstrim dari ˜Zsv

l variabel z adalah bernilai biner. Untuk ini, perhatikan masalah linear programming berikut :

M inimalkan nc1.z+c2.x+c3.q : (z.x.q)∈Z˜lsv

o

(25) untuk vektor gradien tujuan (c1, c2, c3) untuk mana (25) mempunyai optimum

31

dengan menggunakan (24c). Kemudian fungsi objektif berbentuk P

k∈Kclkzlk+ tasan (24b), (24c) dan (24d) dapat dipisahkan dalam himpunan variabel masing-masing (Qzs

ilk, Vilks ), i ∈ Π(l), t ∈ Tk untuk setiap k ∈ K, dan tambahan lagi, masing-masing batasan yang bisa dipisahkan ini kita peroleh ruas kanannya yang ditentukan skalanya oleh zik. Karenanya, dualitas LP, untuk z ≥ 0 tetap (yang memenuhi (24a)), nilai optimal dari P

k∈K bisa diperoleh sebagai fungsi linier dari (zlk, k ∈ K). Karena itu, program linier (25) tereduksi dengan efektif menjadi :

minimalkan untuk vektor tujuan c yang tepat. Karena hipotesa optimum unik, dan dengan memperhatikan struktur dari (26), penyelesaian optimal ˆz, haruslah berbentuk :

ˆ

zlk∗ = 1danzlkˆ = 0,∀k ∈K\{k∗}untuk beberapa k∗ ∈K, (27) yang bernilai biner. Ini melengkapi bukti.

Serupa dengan kasusZ_lsc, masalah pemisahan yang didasarkan pada (24) un-tuk ˜Zsv_{dapat dibentuk untuk menghasilkan potongan RLT sesuai dengan Catatan} 4.1.

Untuk memperkenalkan SPFAM2, suatu model yang berada di antara SP-FAM, yang mengharuskan variabel x bernilai viner, dan SPFAM1, yang mem-perlonggar variabel x menjadi kontinu tanpa menambahkan batasan pengetatan terkait. Lebih tepatnya, pada SPFAM ditambahkan himpunan batasan hull kon-veks parsial yang didasarkan pada Proposisi 4.2 yang bersesuaian dengan him-punan leg yang dipilih Lij ⊆ L (akan diidentifikasi kemudian). Ini menghasilkan model berikut:

SPFAM2: M inimalkan P

s∈S

ps_{Qs(z, µ}s_{) (28a)}

dengan batasan (1b) dan (1c) (28b)

32

(1h) dengan Capi diganti oleh ˜cs

lt yang sedang digunakan (10)

∀l∈L\LQ, (28e)

Sebagai alternatip untuk penggunaan (18b)-(18f) di atas untukl∈LQ, bisa digu-nakan (24b)-(24g) sebagai gantinya untukl ∈LQuntuk memperoleh masalah yang lebih mudah dikerjakan. Sewaktu menyelesaikan submasalah terdekomposisi-kelompok, bisa diperoleh potongan Benders yang serupa dengan (13). Jika bata-san (18b)-(18f) digunakan untuk leg dalam LQ seperti yang didefinisikan dalam (28d)-(28j), maka serupa dengan (13) dari Proposisi 4.1, potongan Bender yang bersesuaian berbentuk :

Sebagai alternatip, jika batasan (24b)-(24g) digunakan untuk leg dalam LQ, po-tongan Bender yang bersesuaian berbentuk :

33

di mana ¯φvs t dan ¯φ

Qs

t adalah penyelesaian dual optimal yang masing-masing terkait dengan (24b) dan (24d), danKiq _{dan K}iQ _{didefinisikan serupa dengan K}i _dalam Proposisi 3.1 sebagai Kiq _≡

k ∈K|i∈S

Pendekatan penyelesaian untuk SPFAM2 diajukan dalam Algoritma 4.1 di bawah ini.

4.2.3 Pendekatan Penyelesaian Yang Diajukan

SPFAM1 dan SPFAM2 adalah dua varian kontinu dari SPFAM dalam Model 3.1, yang mempunyai tingkat relaksasi yang berbeda. Metodologi penyelesaian yang diajukan adalah mengaplikasikan kerangka dekomposisi Benders bersama-sama dengan teknik pemisahan dan pengetatan untuk menyelesaikan SPFAM1 dan SPFAM2 sehingga mendekati optimalitas.

Algoritma 4.1. (Untuk menyelesaikan SPFAM1 dari (9), dengan masalah utama yang didefinisikan dalam (11) dan submasalah SP yang didefinisikan dalam (9c)-(9f).

Inisialisasi: Inisialisasi penyelesaian saat ini z∗ adalah sebagai nol, dan seba-gai nilai tujuannya adalah v∗ = ∞. Selesaikan relaksasi-LP dari SPFAM1 (de-ngan variabel z, yang juga diperlonggar menjadi kontinu) dengan menggunakan dekomposisi Benders bersama-sama dengan himpunan kelayakan awal dan poto-ngan gabupoto-ngan seperti yang dinyatakan dalam Catatan 4.2 dan 4.3 di bawah. Tahap ini diakhiri jika LB ≥(1−e)U B untuk toleransi ε > 0, di mana LB dan UB masing-masing adalah batas bawah dan batas atas untuk relaksasi LP seba-gaimana dipertahankan metode Benders, atau hingga jumlah maksimum tertentu dari potongan Benders dihasilkan.

34

dekomposisi (12) untuk memaksimumkan potongan Benders untuk menghasilkan potongan Benders gabungan (13) yang akan digunakan dalam (11c). Kemudian submasalah eksak (9c)-(9g) diselesaikan dalam iterasi Benders selanjutnya untuk memperoleh potongan Benders (11c). Prosedur diakhiri dan berlanjut ke Tahap 2 bila gap relatip antara batas bawah danv∗lebih kecil dari yang ditetapkan p% op-timalitas, atau jika jumlah maksimum tertentu dari potongan Benders dihasilkan pada tahap ini.

Tahap 2. Tetapkan penugasan kelompok yang didasarkan pada penyelesaian z∗ _{saat ini. Selesaikan Model 3.3 dengan menggunakan pemecah program}

bila-ngan bulat campuran untuk memperoleh penugasan tipe armada.

Algoritma 4.2. (Untuk menyelesaikan SPFAM2 dari (28), dengan masalah uta-ma yang didefinisikan dalam (11) dan subuta-masalah SP yang didefinisikan dalam (28c)-(28j) ∀s∈S, dengan LQ diinisialisasi sebagai ∅).

Inisialisasi: Sama seperti tahap inisialisasi dalam Algoritma 3.1, tanpa mengupdate z∗ dan v∗.

Tahap 1. Kuatkan LQ dengan leg penerbangan l sedemikian sehingga nilai xyang bersesuaian relatip lebih terbagi-bagi seperti yang dijelaskan di bawah ini, dan sedemikian sehingga jumlah rencana perjalanan (path) yang memuat salah satu leg ini tidak melebihi jumlah yang ditetapkan Πmax:

LQ ←LQ∪

Update batasan submasalah (28d)-(28j) ∀s ∈ S dengan menggunakan informasi LQ saat ini. Selesaikan relaksasi LP dari SPFAM2 melalui dekomposisi Benders dengan menggunakan himpunan potongan Benders yang ada untuk menginisia-lisasi proses. Ulangi Tahap 1 sampai jumlah maksimum (cutH

max) dari potongan

Benders tertentu yang telah dihasilkan pada tahap ini atau LQ tidak lagi diku-atkan atau kardinalitasnya melampaui batas yang ditetapkan.

35

dekomposisi Benders, dengan menggunakan potongan Benders yang diperoleh dari tahap inisialisasi dan Tahap 1 sebagai himpunan ketaksamaan awal. Proses ini terkait dengan tahap 1 Algoritma 4.1, di mana, serupa dengan (13) dalam Propo-sisi 4.1, dihasilkan jumlah maksimum tertentu potongan Benders gabungan (29) atau (30) sebelum beralih menyelesaikan submasalah secara eksak. Prosedur ini diakhiri dan berlanjut ke Tahap 3 bila gap relatip antara batasa bawah dan v∗ lebih kecil dari p% optimalitas yang ditetapkan, atau jika jumlah maksimum ter-tentu potongan Benders dihasilkan pada tahap ini.

Tahap 3. Sama seperti Tahap 2 pada Algoritma 4.1.

Catatan 4.2 (Potongan Kelayakan Keseimbangan Network). Network pener-bangan waktu-ruang awal diasumsikan mempunyai jumlah arc penerpener-bangan ke-datangan dan keberangkatan yang sama untuk setiap stasion guna menjamin flow penugasan armada sirkulasi yang seimbang di setiap node. Akan tetapi, sete-lah penyelesaian-z tahap-satu diperoleh, subnetwork dibatasi hanya memuat leg penerbangan yang dialokasikan ke kelompok bersangkutan dari tahap pertama. Subnetwork yang dihasilkan juga bisa kehilangan ciri keseimbangan jadwal di atas untuk stasion, dan karenanya menjadikan batasan keseimbangan (1f) dan (12c) tidak layak. Aspek ini bisa ditangani melalui pembentukan potongan kelayakan (selain potongan optimalitas) dalam dekomposisi Benders, atau ekuivalen, dengan menggunakan variabel artifisial dalam batasan keseimbangan (1f) dan (12c) untuk menjamin wacana lengkap. Potongan awal dalam tahap pertama dapat juga dita-mbahkan untuk membantu menegakkan penugasan tingkat-kelompok untuk setiap stasion. Sebagai contoh misalnya, misalkanAmenotasikan himpunan stasion, de-ngan indeks a, dan misalkan bala ≡ ±1∀l ∈ L, a ∈ A menotasikan penerbangan l yang berasal/berakhir di stasion a, dan nol untuk lainnya. Kemudian dapat ditambahkan potongan-potongan berikut pada tahap pertama:

P

l∈L

balazlk= 0 ∀a∈ A, k ∈K (32)

36

sama. Untuk ini, dapat ditambahkan arc flow tiket gratis dari akhir hari ke masing stasion ke akhir hari untuk setiap stasion lainnya untuk masing-masing network tipe, yang memuat biaya tiket gratis yang tepat. Karena tidak ada penumpang diterima dan karenanya tidak ada laba dihasilkan atas penerbangan ini, flow atas arc tiket gratis ini akan dijauhkan dari penyelesaian submasalah. Dengan menghasilkan potongan Benders optimalitas, perusahaan penerbangan akan berusaha menentukan penugasan kelompok yang cenderung mengurangi bi-aya tiket gratis sedemikian sebesar mungkin atas skenario yang berbeda-beda. Catatan 4.3(Potongan Ketersediaan Gabungan). Dapat juga ditambahkan pa-da tahap pertama versi gabungan tertentu pa-dari batasan ketersediaan (1g) pa-dalam bentuk :

P

l∈L∪CS′ t t∈Tk

zlk≤ P

t∈Tk

At ∀k∈K (33)

BAB 5

KESIMPULAN DAN SARAN

5.1 Kesimpulan

38

5.2 Saran

Untuk penelitian masa mendatang, penulis menyarankan agar :

1. Pertimbangan tentang model yang memasukkan kelas ongkos yang berbeda-beda, isu penangkapan kembali, routing pemeliharaan dan variasi menu-rut hari. Walaupun model yang ditingkatkan ini bisa lebih sejalan dengan operasi perusahaan penerbangan di dalam praktek, padanan stokastiknya mungkin terlalu sulit diselesaikan. Mungkin lebih cocok menyelesaikan mo-del program stokastik yang lebih relatip sederhana, namun menantang, yang diajukan dalam tulisan ini untuk mengambil keputusan penugasan kelompok-ke-leg, dan kemudian menyelesaikan variant deterministik dari model yang ditingkatkan untuk melakukan penugasan tingkat-tipe pesawat di dalam kelompok yang dirancang.

DAFTAR PUSTAKA

Abara, J. 1989. Applying integer linear programming to the fleet assignment pro-blem. Interfaces19(4) 20 28.

Barnhart, C., T. S. Kniker, M. Lohatepanont. 2002. Itenerary-based airline fleet assignment. Transportation Sci. 36 199-217.

Farkas, A. 1995. The influence of network effects and yield management on airline fleet assignment decisions. Ph.D. disertatation. Massachusetts Institute of Technology, Cambridge, MA.

Jacobs, T. L., B. C. Smith, E. Johnson. 1999. O&D FAM: Incorporating passenger flow into the fleeting process. Proc. AGIFORS Sympos., New Orleans, LA, 128 161

Kniker, T. S. 1998. Itinerary-based airline fleet assignment. Ph.D. dissertation, Massachusetts Institute of Technology, Cambridge, MA.

Listes, O., R. Dekker, 2005. A scenario aggregation-based approach for deter-mining a robust airline fleet composition for dynamic capacity allocation.

Transportation Sci. 39(3) 367 382.

Mulvey, J. M., R. J. Vanderbei, S. A. Zenios. 1995. Robust optimization of large-scale systems. Operation Research.43(2) 264 281.

Pilla, V. L., J. M. Rosenberger, V. C. P. Chen, B. Smith. 2005. A statistical computer experiments approach to airline fleet assignment. Technical report COSMOS -05-03, The University of Texas at Arlington, Arlington, TX Sherali, H. D., W. P. Adams, 1990. A hierarchy of relaxations between the

contin-uous and convex hull characterizations for mixed-integer zero-one program-ming problems. Discrete Appl. Math.52(1) 83 106 .

Sherali, H. D., W. P. Adams, 1994. A hierarchy of relaxations and convex hull representations for zero-one programming problems.SIAM J. Discrete Math. 3(3) 411 430 .

Sherali, H. D., W. P. Adams, 1999. A Reformulation-Linearization Technique for Solving Discrete and Continuous Nonconvex Problems.Kluwer Academic Publishers, Boston, MA.

Sherali, H. D., B. M. P. Fraticelli, 2002. A modification of Benders decompososition algorithm for discrete subproblems: An approach for stochastic programs with integer resource. J. Global Optim. 22(2) 319 342.

Smith, B. C, 2004. Robust airline fleet assignment. Ph.D. dissertation, Georgia Institute of Technology, Atlanta, GA.

40

Talluri, T. K. 1996. Swapping applications in a daily airline fleet assignment. Trans-portation Sci. 30 237 248.