ANALISIS CELLULAR BEAM DENGAN METODE
PENDEKATAN DIBANDINGKAN DENGAN
PROGRAM ANSYS
TUGAS AKHIR
Diajukan untuk melengkapi syarat penyelesaian Pendidikan sarjana teknik sipil
060404116
Anton Wijaya
BIDANG STUDI STRUKTUR
DEPARTEMEN TEKNIK SIPIL
FAKULTAS TEKNIK
UNIVERSITAS SUMATERA UTARA
MEDAN
LEMBAR PENGESAHAN
ANALISIS CELLULAR BEAM DENGAN METODE PENDEKATAN
DIBANDINGKAN DENGAN PROGRAM ANSYS
TUGAS AKHIR
Diajukan untuk melengkapi syarat penyelesaian Pendidikan sarjana teknik sipil
06 0404 116
Anton Wijaya
Pembimbing
NIP.19590707 198710 1 001 Ir. Daniel Rumbi Teruna, MT
Pembanding I Pembanding II Pembanding III
Prof.Dr.Ing.Johannes Tarigan Ir.Sanci Barus, MT
NIP.19561224 198103 1 002 NIP.19520901 198112 1 001 NIP.19770623 20050 1 2001 Nursyamsi, ST, MT
Diketahui :
Ketua Departemen Teknik Sipil
Prof.Dr.Ing.Johannes Tarigan NIP.19561224 198103 1 002
BIDANG STUDI STRUKTUR
DEPARTEMEN TEKNIK SIPIL
ABSTRAK
Struktur bangunan yang kita kenal saat ini telah banyak menggunakan berbagai jenis balok yang berlubang pada bagian badan profil. Beberapa buku telah membahas balok dengan bukaan yang ada. Namun, dalam buku-buku tersebut masih jarang disajikan balok baja dengan bukaan berbentuk lingkaran . dalam tugas akhir ini, disajikan teori-teori tentang balok baja dengan bukaan lingkaran yang dikenal dengan cellular beam serta rumus pendekatan untuk menghitung lendutan yang terjadi pada balok baja tersebut. Selain itu dalam tugas akhir ini, disajikan cara kerja program ANSYS yang digunakan untuk penelitian terhadap suatu model yang rumit.
Pada akhir penulisan Tugas Akhir ini akan terlihat bagaimana pengaruh bukaan lingkaran dan tinggi profil yang dinaikkan setelah proses pembentukan cellular beam terhadap tegangan yang terjadi dan beban kritis yang dipikul yang dianalisis dengan melibatkan pengaruh nonlinearitas geometri dan nonlinearitas material. Semakin besar tegangan maksimum yang dianalisis maka beban yang dapat dipikul oleh model akan semakin besar dengan berbagai jenis bentang.
KATA PENGANTAR
Dewasa ini banyak kita temukan profil baja dengan bukaan pada bagian badan profil dalam suatu struktur bangunan baik sebagai balok biasa maupun balok kantilever. Dalam menganalisis profil baja tersebut, digunakan program ANSYS untuk menganalisis profil baja tersebut dengan analisis nonlinear agar mendapatkan hasil yang tidak bisa dihitung dengan cara manual.
Tugas akhir ini merupakan salah satu studi untuk mengenal profil bukaan berbentuk lingkaran yang dikenal dengan Cellular Beam dan cara kerja ANSYS untuk menganalisis suatu model yang rumit. Dengam bantuan buku ini, diharapkan studi mengenai Cellular Beam dan ANSYS terhadap struktur dapat lebih berkembang lagi.
Tugas akhir ini disusun untuk memenuhi dan melengkapi syarat penyelesaian pendidikan sarjana Teknik Sipil Universitas Sumatera Utara. Tugas akhir ini dapat disusun berkat adanya bimbingan dan kerjasama beberapa dosen maupun mahasiswa Universitas Sumatera Utara. Disamping itu, penulis juga mencari literature yang berhubungan dengan Cellular Beam dan program ANSYS.
Puji syukur dan terima kasih penulis panjatkan kehadirat Tuhan Yang Maha Esa dan beberapa pihak yang telah membantu dalam penyusunan Tugas Akhir ini. Penulis ingin mengucapkan terima kasih khususnya kepada beberapa pihak di bawah ini:
1. Bapak Ir. Daniel Rumbi Teruna, MT selaku dosen pembimbing yang telah bersedia meluangkan waktu untuk memberikan saran dan bimbingan
3. Bapak Prof. Dr. Ing. Johannes Tarigan selaku ketua Departemen Teknik Sipil Fakultas Teknik USU sekaligus dosen pembanding
4. Bapak Ir. Sanci Barus , MT selaku ketua koordinator bidang studi Struktur sekaligus dosen pembanding
5. Bapak Ir. Teruna Jaya, Msc selaku sekretaris Departemen Teknik Sipil Fakultas Teknik USU
6. Kedua orang tua penulis yang turut mendukung segala kegiatan akademis penulis
7. Rekan-rekan mahasiswa yang telah memberikan semangat kepada penulis 8. Para pegawai Departemen Teknik Sipil Fakultas Teknik USU atas
ketersediannya untuk mengurus administrasi Tugas akhir ini.
Walaupun dalam menyusun Tugas akhir ini penulis telah berusaha untuk mengkaji dan menyampaikan materi secara sistematis dan terstruktur, tetapi tentunya Tugas Akhir ini masih jauh dari sempurna. Kritik dan saran yang membangun tentulah sangat penulis harapkan di kemudian hari.
Medan, Juni 2009
DAFTAR ISI
III.1.2. Balok Dengan Rotasi Kecil ... III.1.3. Defleksi Dengan Integrasi Persamaan Momen Lentur ... III.1.4. Batasan Lendutan ... III.1.5. Defleksi Pada Cellular Beam ... III.2. Perilaku Balok Tanpa Kekangan Lateral ... III.2.1. Kuat Lentur Nominal Balok ... III.2.2. Tekuk Badan Profil Pada Cellular Beam ... III.2.3. Perhitungan Model Untuk Balok Dengan Bukaan Pada Badan Profil ... BAB IV. PERHITUNGAN CELLULAR BEAM DENGAN PROGRAM ANSYS ...
IV.1. Teori ANSYS ... IV.2. Nonlinear Geometri dan Nonlinear Material ... IV.3. Permodelan Balok Baja IWF Pada Program ANSYS ... IV.3.1. Pemodelan Elemen Garis Pada Balok Baja IWF ...
IV.3.1a. pemodelan elemen garis pada balok baja IWF (tahap
preprocessor) ...
IV.3.1b. pemberian beban dan analisis elemen garis pada balok baja IWF (tahap solution) ...
IV.3.1c. menampilkan hasil analisis elemen garis pada balok baja IWF (tahap postprocessing) ... IV.3.2. Pemodelan Elemen Solid Pada Balok Baja IWF ...
IV.3.2a. pemodelan elemen garis pada balok baja IWF (tahap
preprocessor) ...
IV.3.2b. pemberian beban dan analisis elemen garis pada balok baja IWF (tahap solution) ...
DAFTAR TABEL
DAFTAR GAMBAR
Gambar I.1.1. Balok Baja Dengan Bukaan Pada Bagian Badan Profil ... Gambar II.1.1. Batang Lentur ... Gambar II.1.2. Diagram Tegangan dan Regangan Pada Penampang Melintang
Balok ... Gambar II.1.3. Kurva Tegangan-Regangan Pada Balok Baja ... Gambar II.3.1. Proses Pembentukan Castellated Beam ... Gambar II.3.2. Parameter Pada Castellated Beam ... Gambar II.4.1. Proses Pembentukan Cellular Beam ... Gambar II.4.2. Hubungan Tegangan dan Regangan Pada Cellular Beam... Gambar II.4.3. Penjepit, lingkaran, e’ untuk Cellular Beam ... Gambar II.5.1. Cellular Beam Berdasarkan Fungsinya ... Gambar II.5.2. Cellular Beam Berdasarkan Bentuknya ... Gambar III.1.1. Kurva Defleksi Balok Kantilever ... Gambar III.1.2. Kurva Defleksi Sebuah Balok ... Gambar III.1.3. Syarat Batas Tumpuan Pada Perletakan ... Gambar III.1.4. Kondisi Kontiniuitas ... Gambar III.1.5. Defleksi Balok Sederhana Dengan Beban Terbagi Rata ...
Gambar III.1.6. diagram benda bebas yang digunakan dalam menentukan momen lentur M ...
Gambar III.2.2. Tekuk Lateral Pada Balok ... Gambar III.2.3. Balok Dengan Beban Momen Konstan Kekangan Lateral ... Gambar III.2.4. Kuat Momen Nominal Akibat Panjang Balok Tanpa Sokongan . Gambar III.2.5. Ilustrasi Tekuk Torsi Lateral Pada Balok ... Gambar III.2.6. gaya yang bekerja pada badan profil baja dan kegagalan balok baja
DAFTAR NOTASI
M : Momen Lentur, Kg.my : jarak yang diukur dari garis rotasi (garis netral),mm
ϵ
:
Reganganf : Tegangan, Mpa
Fy : Tegangan leleh baja, Mpa b : Lebar Penampang, mm d : Tinggi Penampang, mm
My : Momen Pada Saat Tegangan Mencapai Tegangan Leleh, Kg.m Mp : Momen Pada Saat Tegangan Mencapai Plastis, Kg.m
ξ : Shape Factor ( Faktor Bentuk) Ux : Perpindahan aksial pada sumbu X Uy : Perpindahan transversal pada sumbu Y
θ : Rotasi pada penampang melintang G : Modulus Geser, Kg/m
KT : Kekakuan Material 2
KG : Kekakuan Geometri L : Panjang bentang, m
∅ : sudut potongan pada bukaan badan profil
α : Rasio Ekspansi c : Panjang pengelasan
tf t
: tebal sayap profil baja IWF, mm w
A : Luas penampang melintang bahan, cm : tebal badan profil baja IWF, mm
I : Inersia penampang melintang bahan, cm 2
E : Modulus elastisitas bahan, kg/m
4
EI : Modulus kekakuan bahan, kg.m 2
Ixx : Inersia penampang X, cm 2
H : Tinggi profil baja cellular beam, mm 4
S : jarak antara titik tengah lingkaran ke titik tengah lingkaran lainnya pada Profil baja cellular beam, mm
Ao : Diameter lingkaran, mm dtee
q : beban terbagi rata, kg/m’
: jarak dari pinggiran atas lingkaran kef lens profil, mm
P : beban terpusat, kg
δ : defleksi / lendutan , mm
Mo : momen pada titik tertentu, kg.m Iy,ACB : momen inersia netto profil ACB, mm K
4
1
K
: koeffisien kelangsingan (L/H) dari balok cellular 2
Lb : panjang balok tanpa sokongan, m
: koeffisien sensitivitas balok cellular (L/S)
J : Konstanta torsi Cw : Konstanta warping
Mn : Momen Nominal, kg.m
ABSTRAK
Struktur bangunan yang kita kenal saat ini telah banyak menggunakan berbagai jenis balok yang berlubang pada bagian badan profil. Beberapa buku telah membahas balok dengan bukaan yang ada. Namun, dalam buku-buku tersebut masih jarang disajikan balok baja dengan bukaan berbentuk lingkaran . dalam tugas akhir ini, disajikan teori-teori tentang balok baja dengan bukaan lingkaran yang dikenal dengan cellular beam serta rumus pendekatan untuk menghitung lendutan yang terjadi pada balok baja tersebut. Selain itu dalam tugas akhir ini, disajikan cara kerja program ANSYS yang digunakan untuk penelitian terhadap suatu model yang rumit.
Pada akhir penulisan Tugas Akhir ini akan terlihat bagaimana pengaruh bukaan lingkaran dan tinggi profil yang dinaikkan setelah proses pembentukan cellular beam terhadap tegangan yang terjadi dan beban kritis yang dipikul yang dianalisis dengan melibatkan pengaruh nonlinearitas geometri dan nonlinearitas material. Semakin besar tegangan maksimum yang dianalisis maka beban yang dapat dipikul oleh model akan semakin besar dengan berbagai jenis bentang.
BAB I
PENDAHULUAN
I.1.
Umum
Pada bangunan-bangunan sekarang ini, khususnya bangunan baja terdapat berbagai macam permodelan struktur baik untuk bangunan bertingkat tinggi maupun bangunan yang berbentang lebar. Oleh karena kemajuan teknologi dan ilmu pengetahuan maka para ilwuwan membuat beberapa konsep baru untuk mengatasi masalah yang ada dan melakukan penghematan pemakaian bahan tetapi tidak mengurangi kekuatan struktur yang ada.
Pertanggungjawaban dari seorang perencana struktur tidak hanya didasarkan pada keamanan dan kemampuan pelayanan dari struktur yang ada tetapi dia juga harus berdasar atas kebutuhan fungsional yang didasarkan pada penggunaan struktur bangunan yang dimaksudkan. Pada saat merencanakan suatu struktur yang kuat pada bangunan bertingkat tinggi, bagian-bagian struktur baja yang secara tradisional terdiri dari balok dan girder dengan baja yang bagian badannya masih padat. Hal ini menyulitkan bagian dari pipa dan ducting ada pendingin udara yang membutuhkan kepuasan fungsional untuk di mana struktur itu digunakan. Dan juga untuk pemeliharaan bangunan untuk sekian lama itu dibutuhkan untuk memperbaiki ducting pendingin udara di tempat. Akibat hal ini, maka para ilmuwan mengembangkan system bukaan pada bagian badan baja untuk memudahkan pelayanan instalasi dan juga untuk pemeliharaan instalasi tersebut secara berkala dan untuk jangka waktu yang sangat lama.
girders, rangka batang dan sebagainya tetap dibutuhkan. Bentuk konstruksi ini menyediakan suatu ketinggian konstruksi yang lebih rendah dengan penempatan pelayanan instalasi.
Pengenalan suatu balok baja dengan bukaan pada bagian badan profil menunjukan distribusi tegangan dan juga pengaruh perilaku kegagalan. Akan tetapi, efisiensi dari perencanaan balok baja dan plat girder dengan bukaan pada bagian badan profil baja telah menjadi satu bagian penting pertimbangan di struktur yang modern.
Bentuk dari bukaan pada bagian badan baja akan tergantung pada pilihan perencana dan bukaan yang diinginkan. Tidak ada peraturan yang tetap dan cepat untuk mendedikasikan bentuk dari bukaan yang ada. Tetapi untuk kenyamanan perencana, bukaan dengan bentuk yang simetris seperti lingkaran dan bujur sangkar biasanya menjadi pilihan. Kekuatan dari balok tersebut dengan bukaan mungkin dihitung dengan cara deformasi plastis yang diakibatkan momen dan gaya geser pada daerah bukaan.
(a)
(b)
(c)
Yang akan dibahas adalah mengenai Cellular Beam . bukaan lingkaran pada bagian badan profil ini biasanya disebut dengan “ Cell “ . Sekarang-sekarang ini terjadi peningkatan dalam penggunaan castellated dan cellular beam. Untuk design standar saat ini untuk balok baja dengan bukaan pada bagian tengahnya di amerika serikat masih tidak seragam. Akibatnya masih digunakan rumus pendekatan dalam merencanakan balok baja dengan bukaan pada bagian badan profil baja. Dalam hal ini akan di bahas rumus pendekatan cellular beam terhadap lendutan . dan juga menampilkan gambar distribusi tegangan dan regangan , lateral buckling dengan menggunakan program ansys.
I.2.
Latar belakang masalah
Seiring dengan berkembangnya teknologi material dan struktur serta untuk memenuhi kebutuhan pelayanan instalasi-instalasi yang ada maka sekarang ini banyak dijumpai profil baja dengan bukaan pada bagian badan profil , salah satunya adalah Cellular Beam. Cellular beam memiliki keunggulan yaitu lebih ringan, lebih kuat serta lebih hemat .
I.3.
Maksud dan tujuan
Maksud dan tujuan penulisan tugas akhir ini adalah :
• Menghitung suatu rumus pendekatan terhadap lendutan dan kuat momen nominal yang disesuaikan dengan program ANSYS.
• Mengetahui distibusi tegangan dan regangan dengan program ANSYS.
• Membandingkan lendutan, tegangan dan momen nominal yang terjadi dengan metode manual dan ANSYS.
• Untuk mengetahui efektifitas pemakaian Cellular beam pada bangunan baja.
I.4.
Pembatasan masalah
Batasan-batasan pembahasan masalah dalam tugas akhir ini adalah :
• Struktur yang akan di tinjau adalah Beam Column dengan aplikasi balok dengan perletakan sederhana.
• Pembebanan terhadap struktur hanya merupakan beban terpusat pada tengah bentang balok.
• Profil yang digunakan adalah IWF yang dipabrikasi menjadi Cellular beam
• Peraturan yang digunakan adalah AISC tentang baja dengan bukaan pada bagian badan profil.
I.5.
Metodologi penulisan
Metode dalam penulisan tugas akhir ini adalah berupa kajian literature dan masukan dari dosen pembimbing.
Adapun urutan pennulisan tugas akhir ini adalah sebagai berikut : 1. Mencari dasar pengetahuan tentang cellular beam.
2. Pembahasan mengenai keuntungan pemakaian cellular beam , kenapa harus memakai cellular beam dan perbandingan efektifitas dengan material lainnya. 3. Mencari suatu rumus pendekatan pada struktur cellular beam terhadap
lendutan dan kuat momen nominal yang akan digunakan bagi para perencana. 4. Menampilkan pemodelan struktur cellular beam dengan program ANSYS
serta menampilkan hasil distibusi tegangan dan regangan serta lateral buckling yang terjadi.
BAB II
TEORI DASAR
II.1. Teori balok umum
Balok ataupun batang lentur adalah salah satu diantara elemen-elemen struktur yang paling banyak dijumpai pada setiap struktur. Balok adalah elemen struktur yang memikul beban yang bekerja tegak lurus dengan sumbu longitudinalnya. Hal ini menyebabkan balok itu melentur.
Gambar II.1.1. Batang Lentur
II.1.1. Perilaku lentur balok.
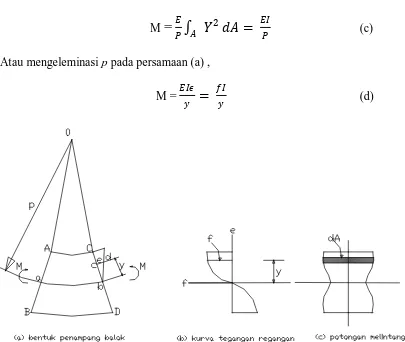
Pada gambar II.1.2. diperlihatkan suatu panjang balok lurus dimana telah dilenturkan pada radius p dengan momen M ; segmen yang ada dijadikan sebagai lentur murni. Berdasarkan dua potongan melintang AB dan CD terdapat suatu jarak yang terpisah, bagian yang sama 0ab dan bcd memberikan
ϵ
=
��
(a)
Dimana y adalah jarak yang diukur dari garis rotasi (garis netral). Tetapi, regangannya adalah jarak yang cocok dari garis netral. Variasi pada tegangan pada potongan melintang itu diberikan pada diagram bahan tegangan dan regangan, berputar 900
M = ∫ ����� (b)
dari orientasi konvensional, menyediakan garis regangan ϵ di skalakan melalui persamaan (a) dengan jarak y pada gambar II.1.2.b. momen lentur M diberikan dengan :
M
=
��
∫ �
2
�
��
=
��
� (c)
Atau mengeleminasi p pada persamaan (a) ,
M = ��� �
=
��
� (d)
Gambar II.1.2. (a) penampang balok ,(b) kurva tegangan regangan, (c) penampang melintang balok
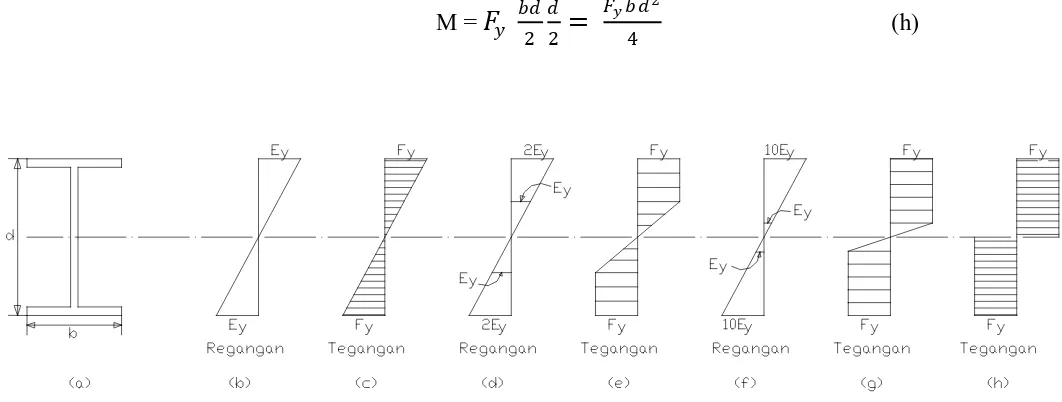
Perilaku lentur dari balok dengan penampang melintang persegi panjang menghasilkan suatu diagram leleh baja. Pada persamaan (d) membuat suatu garis tegangan yang panjang jika f ≤ Fy . ketika regangan mencapai puncak yaitu pada nilai ϵy
M = �� �/2
=
����2
6
(e)
, distribusi tegangan dan distribusi regangan di tampilkan pada gambar II.1.3.b dan c. momen di atas disebut momen leleh yaitu
M = 11
48 Fy b d
2
Momen ini hanya 37,5 persen dari momen leleh yang ada walaupun regangan maksimum yang dua kali lebih besar. masih jauh deformasi yang ditunjukan pada gambar II.1.3.f , dimana sudah 90 persen dari penampang sudah mencapai leleh. Momen yang dihasilkan yaitu
(f)
M = 0.249 Fy b d2
Pada gambar II.1.3.h ditunjukan bahwa momen telah mencapai plastis dimana momen yang ada lebih besar 0,4 persen dari momen pada regangan 10ϵ
(g)
y
M =
�
� ��2
�
2
=
����2
4
(h)
.
Gambar II.1.3. kurva tegangan-regangan pada balok baja
Momen pada persamaan (h) itu dinamakan ketahanan pada momen plastis. Yang disimbolkan dengan Mp . ini biasanya diambil nilai batasan. Rasio antara momen plastis dan momen leleh untuk penampang di atas yaitu
�� ��
=
� �
=
ξII.2. Teori Metode Elemen Hingga (FEM) .
Balok cellular yang merupakan material baja yang nonlinear dapat di analisis melalui rumus pendekatan yang berdasarkan metode elemen hingga. FEM merupakan salah satu metode yang digunakan untuk menghitung gaya-gaya dalam yang terjadi dalam suatu komponen struktur. Finite element methode juga dapat dipakai untuk perhitungan struktur, fluida, elektrik, static, dinamik, dan lain-lain. FEM juga dikenal sebagai metode kekakuan atau displacement methode karena yang didapat terlebih dahulu dari perhitungan adalah perpindahan baru kemudian mencari gaya batang. Dikarenakan perhitungan matematis yang kompleks, FEM secara utama dikembangkan untuk deformasi linear yang kecil dimana matriks kekakuan konstan. Pada kasus deformasi yang besar, matriks kekakuan dan gaya dalam menjadi fungsi dari perpindahan. Nonlinear FEM digunakan untuk memperbaiki parameter material dari pandangan pelat elastis yang tinggi. Dalam bab ini, dikembangkan model FEM nonlinear untuk deformasi geometri yang besar. dalam hal ini akan digunakan suatu model untuk memperbaiki deformasi yang ada pada struktur balok.
II.2.1. deskripsi model matematis.
Euler-Bernoulli beam (EB) teori secara luas digunakan untuk memodelkan deformasi yang kecil. Timoshenko beam (TB) teori memperluas persamaan EB untuk memperjelas untuk efek nonlinear seperti geser. Untuk lebih teliti, elemen kinematik pada balok dijelaskan dengan 3 dof per node yaitu perpindahan aksial pada sumbu X (Ux), perpindahan transversal pada sumbu Y (Uy) dan rotasi pada penampang melintang (θ). Teori EB mengasumsikan bahwa penampang melintang meninggalkan gaya normal untuk membentuk sumbu longitudinal, di mana TB menghapus kendala normal dengan memperkenalkan deformasi geser. Sebagai tambahan, kedua teori mengacuhkan perubahan dimensi dari bentuk penampang balok yang mengalami deformasi. Teori TB dapat digunakan untuk perilaku geometri nonlinear akibat perpindahan dan perputaran yang besar. walaupun lebih kompleks teori TB yang muncul agar lebih efisien dalam hal perhitungan FEM.
Balok tersebut dibagi menjadi beberapa bagian ( elemen hingga ) . elemen-elemen balok lurus dan memiliki 2 node. Maka dikumpulkan semua nodal dof ke dalam sistem vektor dof yang dinamakan vektor tetap :
U = [ �x1 �y1 θ1 . . . �xn �yn θn ]T
Dalam hal ini, diasumsikan untuk mengetahui material properti dari model yang ada seperti E modulus elastisitas, G yaitu modulus geser. Materialnya masih tetap linear elastis . gaya-gaya yang ada bekerja pada node balok yang dikumpulkan untuk membentuk vektor gaya yaitu :
f = [ fx1 fy1 fθ1 . . . fxn fyn fθn ]
Regangan merupakan suatu ukuran untuk mengubah bentuk objek, dalam hal ini yaitu panjang, sebelum dan sesudah terjadi deformasi yang diakibatkan beberapa beban yang ada. Tegangan adalah distribusi gaya-gaya dalam per satuan luas yang seimbang dan bereaksi terhadap gaya luar yang terjadi pada balok. Dalam kasus teori TB , ada tiga perbedaan komponen tegangan per elemen balok : regangan aksial yang diukur berdasarkan besar ukuran balok ( e ), regangan geser yang diukur berdasarkan perubahan sudut antara dua garis pada balok sebelum dan sesudah deformasi ( γ ) , dan ukuran perubahan kurva ( k ). Dari hal di atas , dapat dikumpulkan menjadi suatu vektor regangan balok secara umum :
hT = [ e1 γ1 k1 . . . e n-1 γ n-1 k n-1 ].
Resultan tegangan pada teori TB ditentukan gaya aksial N , gaya lintang V dan momen lentur M per satuan luas dari penampang melintang. Resultan tegangan secara umum :
z = [ N1 V1 M1 . . . N n-1 V n-1 M n-1 ]. Di mana n-1 adalah jumlah dari elemen balok.
Energi regangan dalam model sepanjang balok dapat ditulis sebagai integral panjang :
U = ∫ �� �hdX
Di mana L adalah panjang balok. Vektor gaya dalam bisa didapat dengan mengambil variasi pertama dari energi regangan sehubungan dengan perpindahan nodal :
P = ��
�� = ∫ �� �(u)zdX
KT = ��
��
=
∫ (�� ����
+
�����
)
� dX = (KM + KG
Di mana KT adalah kekakuan material dan KG adalah kekakuan geometri. Kekakuan material adalah konstan dan identik dengan matriks kekakuan linear pada balok Euler-Bernoulli C1 . kekakuan geometri mendatangkan variasi dari B dimana resultan tegangan tetap dan membawa balok nonlinear pada deformasi geometri yang besar.
)
II.3. Castellated beam
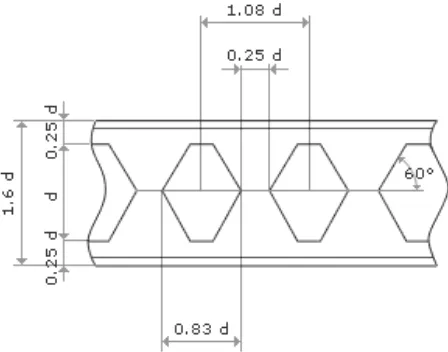
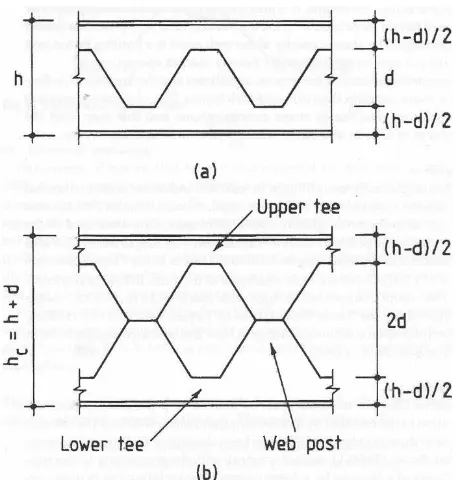
Castellated beam merupakan suatu profil baja yang mempunyai bukaan berbentuk segi enam. Castellated mengalami proses pemotongan pada bagian badan profil dengan pola zigzag. Salah satu bagian yang telah dipotong lalu diangkat dan disatukan bagian badannya dan terakhir dilakukan pengelasan pada bagian badan yang menempel ; hal ini dilakukan untuk meningkatkan tinggi dari profil awal (h) dengan tinggi potongan yang ada (d). bentuk castellated beam ditampilkan dalam gambar II.3.1.
Adapun keuntungan dari penggunaan castellated beam. Keuntungan yang utama yaitu meningkatkan kekakuan lentur secara vertikal; castellated beam telah dibuktikan lebih efisien untuk beban medium pada bentang panjang dimana perencanaannya dikontrol dengan kapasitas momen dan lendutan. Balok castellated, karena rasio kuat tariknya yang tinggi dengan berat dan pemeliharaan yang kecil, kadang-kadang secara menguntungkan dapat menggantikan penggunaan girder. Mereka digunakan dalam bangunan bertingkat, bangunan komersial dan bangunan industri, dan juga untuk rangka portal. Keuntungan balok castellated juga mencakup penampilan mereka yang mengesankan dan memungkinkan penggunaan daerah bukaan untuk pelayanan instalasi.
Adapun juga kerugian dari penggunaan balok castellated. Akibat adanya bukaan pada bagian badan profil, perilaku struktur dari balok castellated akan berbeda dari balok baja yang biasa. Karena perbedaan kemungkinan moda kegagalan atau moda kegagalan yang baru, mereka merupakan struktur nonlinear, dimana tidak bisa dianalisis dengan metode sederhana. Kapasitas geser pada bagian badan profil adalah suatu faktor yang terbatas, dan balok castellated tidak cocok untuk bentang pendek yang dibebani dengan berat. Deformasi geser pada bagian T nya sangat signifikan dan analisa lendutan lebih kompleks daripada balok yang bagian badan profil padat.
II.3.1. Analisa dan perencanaan balok castellated.
Gambar II.3.2.parameter pada castellated beam
• Sudut potongan (∅)
Sudut potongan mempengaruhi jumlah proses pemotongan balok castellated (N) per unit panjang dari balok . N akan kecil ketika sudut itu rata dan akan besar ketika bertahap. Percobaan telah menunjukan bahwa peningkatan jumlah N mempunyai pengaruh yang kecil untuk kekakuan elastis pada balok castellated, itu akan meningkatkan daktailitas dan kapasitas rotasi, percobaan yang ada menunjukan bahwa penyesuaian pada sudut 600
• Rasio ekspansi (α)
adalah suatu sudut standart yang efisien terhadap bangunan industri.
Rasio ekspansi merupakan suatu ukuran dari peningkatan tinggi balok yang dicapai pada proses pemotongan. Dalam teori tinggi balok baja yang biasa dapat hampir dua kali lipat, tetapi tinggi seluruhnya dari profil T adalah suatu faktor batas. Dalam pelaksanaan, tinggi dari potongan ‘d’ adalah setengah bagian dari tinggi hs
h , maka
T = ℎ�
4 , hC
Untuk sudut potongan 60
= ℎ�
2 + ℎ , α =
ℎ�
ℎ ≈ 1,5 0
α = 0.5ℎ�
√3
=
0.289 h• Panjang pengelasan (c)
s
Jika panjang pengelasan terlalu pendek . kemudian las pada bagian badan yang disambung akan mengalami kegagalan geser horizontal, dan apabila terlalu panjang akan mengalami kegagalan dalam lentur vierendeel, jadi keseimbangan yang beralasan antara dua moda kegagalan ini yaitu c = hs / 4.
II.4. Cellular Beam
Cellular beam telah membukt ikan menjadi salah satu jenis konstruksi baja yang berkembang paling signifikan sejak perkenalan mereka pada tahun 1987. Mereka saat ini telah digunakan di lebih dari 3500 proyek pembangunan pada 20 lebih Negara. Integritas structural dan criteria perencanaannya telah di verifikasi dengan mengikuti percobaan terhadap struktur cellular beam dalam skala besar.
Gambar II.4.1. Proses Pembentukan Cellular Beam
yang memiliki perencanaan pembebanan dengan tingkat medium sampai tinggi pada bentang portal atau bangunan yang medium sampai bentang yang panjang. Untuk sekarang-sekarang ini aplikasi dari cellular beam ini dari bangunan-bangunan komersial dan bangunan-bangunan industri termasuk daerah perpakiran yang berada pada daerah basement.
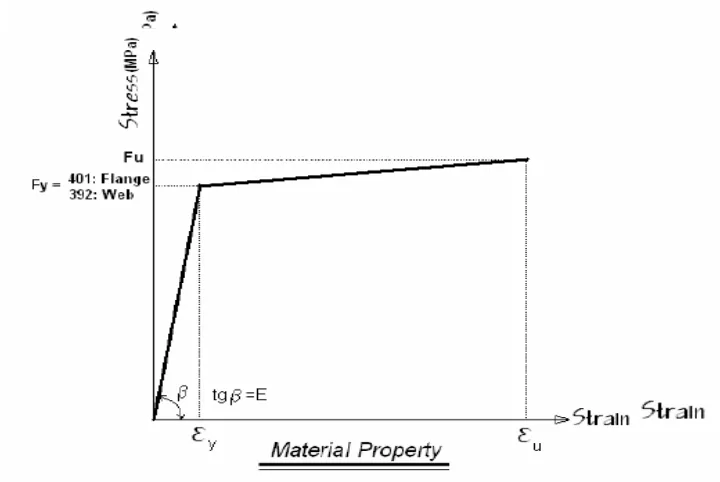
Pada bagian badan profil baja yang biasanya digunakan balok baja dengan profil I itu telah diadaptasikan dengan penambahan bukaan pada bagian badan profil baja di bawah panjang dari bentang yang ada. Penambahan dari bukaan lingkaran pada badan profil ini menghasilkan dalam suatu balok baja suatu berat yang sama bahkan lebih ringan daripada balok baja yang aslinya tetapi lebih kuat dan lebih tinggi disebabkan karena meningkatnya ketinggian bagian badan profil baja yang ada. Tambahan bukaan lingkaran pada bagian badan baja, juga menghasilkan suatu perbedaan distribusi tegangan pada bagian badan dan suatu moda kegagalan baru yang dihubungkan dengan balok baja tersebut. Adapun hubungan tegangan dan regangan pada cellular beam yang di tampilkan pada gambar II.1.1.
[image:34.595.147.507.484.725.2]
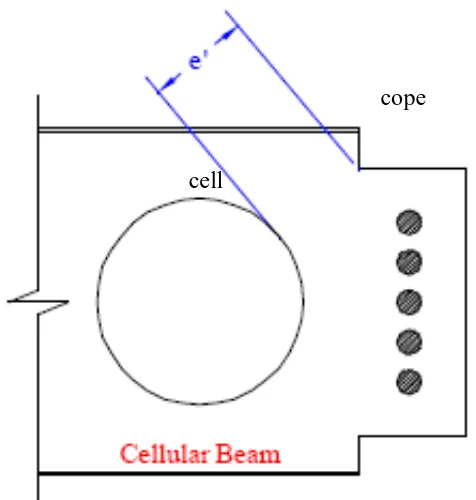
Apabila Cellular Beam digunakan untuk konstruksi, sebaiknya Cellular beam di beri Cope yaitu pemegang atau tanggulan pada sudut balok sehingga balok dapat dihubungkan dengan kolom yang ada. Penjepit yang ada itu di bedakan berdasarkan dimensi horizontal balok tersebut. Jarak antara pinggir penjepit dan pinggiran Cell adalah jarak e’ . untuk dimensi penjepit yang signifikan , jarak e’ bisa menjadi kecil dan hal itu akan mudah menyebabkan terjadinya kegagalan pada balok.
cope
cell
[image:35.595.204.442.306.556.2]
Gambar II.4.3.Penjepit, lingkaran, e’ untuk Cellular Beam
Studi tentang bukaan pada bagian badan profil sudah selesai di amerika serikat dan kanada, termasuk bentuk bujur sangkar, persegi panjang, lingkaran, konsentris dan eksentris bukaan pada baik komposit dan non-komposit balok baja.
Bagaimanapun , peraturan ini menutupi kemungkinan-kemungkinan yang jauh beda dan oleh karena itu , mereka sangat konservatif . dengan menggabungkan beberapa parameter, peraturan itu akan mungkin untuk mendapatkan hasil yang lebih fleksibel dan ekonomis untuk beberapa tipe keadaan.
Pada perencanaan bukaan pada balok baja ini dibutuhkan bantuan perencanaan. Bantuan perencanaan itu disediakan yang mengijinkan identifikasi dari balok baja yang ada. Aplikasi dari bantuan perencanaan ini menghindari penggunaan metode perhitungan analisis yang kompleks dan mahal.
Perencanaan yang di kembangkan untuk baik baja komposit dan non-komposit harus mengikuti batasan-batasan yang ada :
�
��
>
1.20 (1)ℎ
�� ≤ 3.76
�
���
(2)
��
2��
≤0.38
�
�
��
(3)
Dimana :
d = tinggi profil baja secara keseluruhan h = tinggi badan profil tanpa tinggi sayap tw
b
= tebal badan profil f
t
= lebar sayap profil f
E = modulus elastisitas baja = tebal sayap profil
Balok tersebut seharusnya diberi perletakan sederhana dan diberikan suatu faktor distribusi pembebanan yang seragam. Balok baja tersebut harus di lengkapi dengan bracing lateral untuk mencegah tekuk torsi dan tekuk lateral. Baja tersebut harus memiliki kekuatan leleh maksimum sebesar 50 ksi ( 350 Mpa ).
Bukaan sebaiknya memiliki bentuk yaitu bujur sangkar, persegi dengan aspek ratio sama dengan 2 ( panjang ao sama dengan 2 kali tinggi ho
Rasio panjang bentang dan tinggi profil baja balok, L/d, harus dalam batas 10 sampai 30, begitu juga untuk struktur baja komposit.
) dan begitu juga untuk bentuk lingkaran.
II.5. Jenis – Jenis Cellular Beam
Untuk bangunan-bangunan sekarang ini, para perencana dituntut tidak hanya merencanakan suatu struktur itu kuat ataupun tidak . akan tetapi, para perencana di tuntut untuk bisa merencanakan suatu struktur yang kuat, ekonomis, memberikan kemudahan pelayanan instalasi, serta tuntutan nilai arsitekturnya. maka, para perencana menciptakan berbagai macam jenis struktur , agar struktur tersebut dapat disesuaikan dengan keadaan yang ada serta permintaan pemilik bangunan.
Pada bagian ini akan dibahas berbagai jenis Cellular Beam yang dapat digunakan pada keaadan dan kondisi tertentu. Cellular beam dapat di bagi atas :
1. Cellular beam berdasarkan fungsinya :
• Cellular beam sebagai balok pada bangunan.
• Cellular beam sebagai pelat lantai
• Cellular beam sebagai kolom .
2. Cellular beam berdasarkan kombinasi pemakaian dengan material lain :
• Cellular beam yang komposit. 3. Cellular beam berdasarkan bentuk :
• Cellular beam berbentuk curve (lengkung).
• Cellular beam yang berbentuk non-prismatis / cantilever.
• Cellular beam yang berbentuk spine.
II.5.1. Cellular beam berdasarkan fungsinya.
A. Cellular beam sebagai Balok pada bangunan
Pada dasarnya cellular beam dirancang dan didesain sebagai balok yang digunakan pada struktur bangunan yang ada. Adapun pembagian penggunaan cellular beam sebagai balok bangunan yaitu balok pada area basement ( area perpakiran ) , balok pada pelat lantai dan balok pada bagian atap bangunan yang ada.
Salah satu keuntungan dari cellular beam yaitu penggunaannya pada area parker mobil. Pada bentang 16 meter dibawah beban area parker, cellular beam merupakan suatu material struktur yang paling efisien. Sebagai tambahan selain berat cellular beam yang ringan, ada 3 keuntungan dipakainya cellular beam pada area parker yaitu :
• Sebagai suatu penampilan dan bagian dari keamanan.
• Sebagai area ventilasi udara dari asap-asap yang ada.
Selain untuk area parkir juga digunakan untuk balok lantai dan balok atap banguna yang ada . Jenis Cellular beam yang dipakai pada pelat lantai dan atap sebenarnya sama dengan cellular beam yang ada yang berbeda adalah pada pelat lantai, besar bukaan yang ada sebesar 0,8 – 1,1 H sedangkan untuk balok atap bangunan besar bukaan sebesar 1,0 – 1,3 H , dimana H adalah tinggi profil Cellular Beam yang ada.
B. Cellular beam sebagai pelat lantai pada bangunan
Cellular beam sebagai pelat lantai merupakan suatu generasi baja yang baru yang secara keseluruhan terbentang yang digunakan sebagai pelat lantai dan dikenal dengan nama USFB ( Ultra Shallow Floor Beam ). USFB dapat digunakan pada ketebalan min 160 mm .
USFB terbentuk dengan cara pengelasan dua asimetris Cellular balok T sepanjang bagian badannya. Deck atau pelatnya duduk pada bagian sayap profil bagian bawah yang lebar. Proses penggabungan antara beton, metal decking dan USFB akan ditunjukan pada gambar II.5.1.
C. Cellular beam sebagai kolom pada bangunan .
Cellular kolom merupakan kolom yang paling efisien pada kasus-kasus yang ada di mana beban aksialnya kecil seperti kolom gable, kaki portal, kolom .
(a)
(b)
[image:41.595.170.523.42.246.2]
(d)
Gambar II.5.1. (a) cellular beam sebagai balok pada area parkir (b) cellular beam sebagai balok pada atap bangunan (c) potongan USFB untuk pelat lantai (d) cellular kolom .
II.5.2. Cellular beam berdasarkan kombinasi pemakaian dengan material lainnya. A. Cellular beam yang non komposit.
untuk struktur non komposit seperti yang telah dibahas diatas yaitu suatu struktur beam column yang hanya mengandalkan kekuatan dari material baja itu sendiri baik digunakan sebagai balok maupun kolom pada suatu struktur bangunan baja.
B. Cellular beam yang komposit.
Perkembangan popularitas dari penggunaan cellular beam pada lantai komposit muncul pada waktu yang sama seiring dengan perhatian atas perencanaan teknik keamanan terhadap bahaya api (panas).
Perkembangan dari berbagai inovasi sistem lantai komposit telah dilakukan. Investigasi dari perilaku balok komposit dengan bukaan pada badan profil dibandingkan dengan profil biasa telah menunjukan bahwa secara signifikan pelat meningkatkan kapasitas gaya geser daripada balok baja biasa. Hal ini menyebabkan naiknya kekakuan lentur dan kapasitas gaya geser pada bagian atas bukaan profil. Contoh Cellular beam komposit ini yaitu USFB.
II.5.3. Cellular beam berdasarkan bentuknya.
A. Cellular beam yang berbentuk curve atau lengkungan.
Ada 2 faktor yang mengkombinasikan untuk membuat cellular beam menjadi suatu bagian struktur lengkung yang paling ekonomis yaitu :
• Efisiensi struktur
Hal yang penting dari 2 kombinasi yang adalah efisiensi struktur. Ini merupakan suatu penampilan yang menghasilkan banyak keuntungan tanpa menambah berat yang menghasilkan penggunaan cellular beam pada bagian atap bangunan.
• Kemudahan untuk melengkung.
Dalam aplikasi lengkung, keuntungan dari cellular beam adalah kemudahan untuk melengkung. Dengan hanya suatu modifikasi yang tidak signifikan pada proses produksinya, cellular beam dengan cepat melengkung sesuai dengan radius yang dibutuhkan.
lebar yaitu diatas 30 m, serta penggunaan cellular beam yang lengkung lebih murah daripada balok baja biasa yang dilengkungkan maupun rangka batang.
B. Cellular beam yang berbentuk non-prismatis atau untuk kantilever.
Cellular beam menyediakan metode paling ekonomis dalam menghasilkan bagian baja yang non-prismatis. Balok non-prismatis ini bisa mempunyai cell yang ukuran diameter yang seragam, cell yang ukuran diameter yang bervariasi serta tanpa bukaan. Ada juga cellular beam yang non-prismatis digunakan pada bagian kantilever suatu bangunan dimana untuk kantilever biasanya dibuat dengan dua atau tiga ukuran bukaan yang berbeda untuk meminimalisasikan berat dari cellular beam tersebut tetapi meningkatkan kekuatan struktur yang ada.
C. Cellular beam yang sebagai spine.
( a )
( b )
[image:44.595.158.494.56.668.2]
( c )
II.6. Keuntungan dan kerugian dari penggunaan Cellular Beam
• Dari segi kekuatan struktur.
Jika dilihat dari segi struktur, maka cellular beam memiliki keuntungan yang sangat banyak diantaranya memiliki kemampuan kekakuan lentur struktur yang lebih besar , memiliki kapasitas untuk menahan gaya geser yang besar. berat Cellular beam juga akan berkurang dengan demikian beban aksial yang diterima oleh kolom menjadi lebih kecil sehingga dimensi kolom menjadi kecil dan perencana dapat melakukan penghematan bahan.
• Dari segi nilai ekonomisnya.
Untuk nilai ekonomis suatu cellular beam dapat dilihat dari penggunaan material yang ada sebab tidak diperlukan lagi suatu balok baja profil IWF yang memiliki inersia yang besar karena dari profil yang kecil dapat kita pabrikasi menjadi cellular beam yang memiliki inersia yang lebih besar sehingga akan menghemat penggunaan bahan yang ada. Begitu juga dengan berat cellular beam yang menjadi lebih ringan yang memberikan pengaruh terhadap pemakaian ukuran kolom bangunan yang lebih kecil.
• Dari segi integrasi pelayanan.
penyokong. Instalasi-instalasi di atas dapat dilewatkan melalui lubang bukaan yang ada pada balok sehingga tinggi lantai tetap bisa terjaga apabila ditutup dengan plafon yang ada.
• Tahan terhadap gaya dinamis.
Untuk gaya dinamis, kenapa dipilih cellular beam karena cellular beam menyediakan suatu pelat lantai yang lebih berkualitas dibandingkan dengan balok yang rendah dengan pelayanan yang penuh, dengan menggunakan ruang kosong di bagian atas secara keseluruhan dimana memaksimalkan inersia dan kekakuan.
Adapun hal yang memungkinkan suatu lantai untuk menerima suatu frekuensi di bawah 4 Hz untuk menghasilkan suatu lantai yang memiliki kualitas yang tinggi. SCI’s mengeluarkan suatu metode untuk perencanaan lantai yang berkualitas yaitu dengan menghitung faktor respon ( R ) , yang secara tidak langsung cocok ke lantai yang berkualitas.
R ≤ 12 Cocok untuk lantai kantor yang sibuk. R ≤ 8 Cocok untuk lantai kantor yang umum. R ≤ 4 Cocok untuk lantai kantor yang paling tinggi.
• Dari segi kebutuhan pemakaian.
bisa disesuaikan dengan keinginan arsitektur. Misalnya untuk bentang panjang yang lebih dari 30 meter maka bisa digunakan cellular beam yang dilengkungkan.
• Dibandingkan dengan Castellated beam
Jika dibandingkan dengan castellated beam, cellular beam memiliki keunggulan yaitu lebih ringan, dan cellular beam memiliki benuk geometri yang lebih fleksibel sesuai keadaan.
• Kerugian dari Cellular beam
Adapun kerugian yang dimiliki oleh cellular beam yaitu pembentukan cellular beam baik yang biasa ataupun melengkung harus dilakukan pabrikasi di workshop cellular beam, tidak bisa dilakukan di lapangan langsung, serta pada saat pabrikasi akan ada waste yang terbuang baik di bagian ujung dan sisa potongan semi-lingkaran yang ada.
II.7. Spesifikasi Cellular Beam .
1. Berdasarkan rasio tinggi / berat.
ao
S = 1,1a
= 1,0h – 1,3h o – 1,3a H
o
1= 1,4h – 1,6h
• Aplikasi : atap , bentang lebar, jembatan.
ao S = 1,2a
= 0,8h – 1,1h o – 1,7a H
o
2= 1,3h – 1,4h
• Aplikasi : lantai, area parkir, kolom, struktur di lepas pantai.
Spesifikasi dari cellular beam juga meliputi notasi pembacaan dari profil cellular beam yang ada. Berikut contah notasi untuk cellular beam yang simetris dan tidak simetris :
1. Notasi standart untuk cellular beam yang tidak simetris (ACB) yaitu seperti di bawah ini :
a b c d e f g
732 X 191/229 X 90 kg/m ACB. S355 (450 @ 650 )
a. 732 ( tinggi dalam mm ) b. 191 ( lebar sayap bagian atas ) c. 229 ( lebar sayap bagian bawah ) d. 90 ( berat dalam kg/m )
e. S355 ( mutu baja )
2. Notasi standart untuk cellular beam yang simetris (CUB) yaitu seperti dibawah ini :
a b c d e f
1160 X 267 X 134 kg/m CUB. S355 (800 @ 1000)
a. 1160 ( tinggi dalam mm ) b. 267 ( lebar sayap bagian atas ) c. 134 ( berat dalam kg/m ) d. S355 ( mutu baja )
e. 800 ( diameter cell dalam mm ) f. 1000 ( jarak antar cell )
Bentuk penampang juga merupakan bagian dari spesifikasi cellular beam , yaitu bentuk penampang dari awal hingga menjadi bentuk penampang cellular beam. Geometri dari cellular beam sangatlah fleksibel. Perubahan data cell pada ketinggian balok, menyebabkan suatu batasan pada bentuk penampang dari suatu bentuk IWF biasa. Untuk contohnya :
• Standart UB 762 x 267 x 147 kg/m
• Cells 800 mm dia @ 1000 mm
• Tinggi 1141 mm
• IXX 382897 cm
• Cells 750 mm dia @ 1125 mm 4
• Tinggi 1078 mm
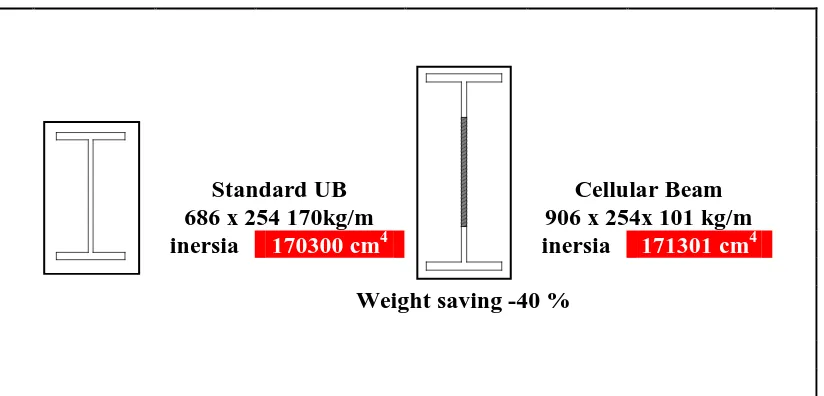
Pada contoh di bawah, menunjukan adanya pengurangan berat dari cellular beam dibandingkan dengan universal beam (UB) yang standart.
[image:51.595.111.523.138.336.2]Berikut ini merupakan tabel bentuk penampang dari standart UB menjadi cellular beam. Akan tetapi, tabel ini untuk balok jenis ini sangatlah terbatas dalam membantu seorang perencana. Bagaimanapun tabel ini Cuma hanya untuk tujuan pembelajaran saja.
Tabel II.7.1. tabel bentuk penampang dari standart UB menjadi Cellular Beam
yang di keluarkan perusahaan WESTOK.
Standard UB Cellular Beam
Section size Ixx Ixx Section size
1684318 1398 x 419 x 388 1468573 1389 x 419 x 343 1016 x 305 x 487 1020400 1085867 1490 x 305 x 249 1016 x 305 x 438 908900 915994 1480 x 305 x 222 1016 x 305 x 393 806600 915994 1480 x 305 x 222 1016 x 305 x 349 722100 737838 1364 x 305 x 201 1016 x 305 x 314 643200 737838 1364 x 305 x 201 1016 x 305 x 272 552900 554621 1257 x 292 x 176 1016 x 305 x 249 480300 486808 1149 x 267 x 173 1016 x 305 x 222 406900 486808 1149 x 267 x 173 914 x 419 x 388 719600 737838 1364 x 305 x 201 914 x 419 x 343 625800 629621 1263 x 292 x 194
Standard UB Cellular Beam
686 x 254 170kg/m 906 x 254x 101 kg/m
inersia 170300 cm4 inersia 171301 cm4
Weight saving -40 %
914 x 305 x 289 504200 554621 1257 x 292 x 176 914 x 305 x 253 436300 486808 1149 x 267 x 173 914 x 305 x 224 376400 382897 1141 x 267 x 147 914 x 305 x 201 325300 342081 1137 x 267 x 134 838 x 292 x 226 339700 342081 1137 x 267 x 134 838 x 292 x 194 279200 342081 1137 x 267 x 134 838 x 292 x 176 246000 342081 1137 x 267 x 134 762 x 267 x 197 240000 342081 1137 x 267 x 134 762 x 267 x 173 205300 222718 915 x 229 x 125 762 x 267 x 147 168500 171301 906 x 229 x 101 762 x 267 x 134 150700 171301 906 x 229 x 101
686 x 254 x 170 170300 171301 906 x 229 x 101
Ada juga tabel bentuk penampang yang ditawarkan oleh perusahaan macsteel. Bentuk geometrid dan data-data yang ada merupakan variable yang tidak terbatas. Tabel II.4.2. yang ada hanya mengikuti dua contoh untuk satu ukuran profil. Untuk perencanaan, perusahaan mecstell menawarkan program computer CELLBEAM AUTOMATE. Tabel di bawah ini hanya mengijinkan untuk pengecekan terhadap lendutan pada umumnya. Untuk pengecekan tekuk lateral dan tekuk torsi harus menggunakan CELLBEAM .
Tabel II.7.2. tabel bentuk penampang dari standart UB menjadi Cellular Beam
yang di keluarkan perusahaan MACSTEEL.
SECTION FLOOR (example only ) ROOF (example only)
H D S IXX ZEXX SXX ANET H D S IXX ZEXX SXX ANET (mm) (mm) (mm) cm4 cm3 cm3 cm2 (mm) (mm) (mm) cm4 cm3 cm3 cm2
203 x 133 x 25
289.8 200 300 4732 326.5 343.1 25 309.3 225 300 5384 348.2 364 24.7 203 x 133 x 30 293.4 200 300 5852 398.9 421 30.5 312.9 225 300 6656 425.5 446.8 30.1
254 x 146 x 31
359.7 250 375 8971 498.8 523.2 30.7 383.7 275 350 10262 534.9 559.3 30.6 254 x 146 x 37 364.3 250 375 11254 617.9 650.1 37.7 388.3 275 350 12859 662.3 694.7 37.7 254 x 146 x 43 367.9 250 375 13275 721.8 763 44.1 391.9 275 350 15160 773.7 815 44
305 x 102 x 25
435 300 450 8816 405.3 430.9 21.2 463.2 325 400 10124 437.1 463.9 21.4 305 x 102 x 29 438.6 300 450 10657 485.9 515.9 25.2 466.8 325 400 12214 523.3 554.6 25.4 305 x 102 x 33 442.6 300 450 12932 584.3 621.5 30.1 470.8 325 400 14801 628.7 667.4 30.3
305 x 165 x 40
433.3 300 450 17237 795.6 832.8 40.4 461.5 325 400 19718 854.5 893 40.6 305 x 165 x 46 436.5 300 450 20061 919.2 965.2 46.7 464.7 325 400 22934 987 1035 46.9 305 x 165 x 54 440.3 300 450 23670 1075 1134 354.7 468.5 325 400 27047 1155 1216 54.9
SECTION LANTAI (example only ) ATAP (example only)
H D S IXX ZEXX SXX ANET H D S IXX ZEXX SXX ANET (mm) (mm) (mm) cm4 cm3 cm3 cm2 (mm) (mm) (mm) cm4 cm3 cm3 cm2
406 x 140 x 39
571.2 400 600 24957 873.8 921.2 34.2 604.5 425 525 28367 938.5 989.7 34.8 406 x 140 x 46 576.4 400 600 31451 1091 1150 42.3 609.7 425 525 35662 1170 1233 42.9
406 x 178 x 54
575.8 400 600 37713 1310 1377 50.6 609.1 425 525 42739 1403 1475 51.2 406 x 178 x 60 579.6 400 600 43565 1503 1581 57.7 612.9 425 525 49297 1609 16913 58.4 406 x 178 x 67 582.6 400 600 49074 1685 1776 64.7 615.9 425 525 55511 1803 1900 65.4 406 x 178 x 74 586 400 600 55063 1879 1986 72.1 619.3 425 525 62247 2010 2123 72.9
457 x 191 x 67 648.3 450 675 59376 1832 1927 62.9 682.5 475 600 66618 1952 2054 63.7 457 x 191 x 74 651.9 450 675 67373 2067 2177 70.8 686.1 475 600 75522 2201 2318 71.6 457 x 191 x 82 654.9 450 675 74891 2287 2414 78.3 689.1 475 600 83924 2436 2571 79.2 457 x 191 x 89
658.3 450 675 82871 2518 2663 86.1 692.5 475 600 92809 2680 2833 87.1 457 x 191 x 98 662.1 450 675 92309 2789 2956 95.3 696.3 475 600 1E+05 2968 3145 96.3
533 x 210 x 82
759.1 525 775 96581 2545 2683 75.1 796.1 550 675 1E+05 2704 2854 76.2 533 x 210 x 92 763.9 525 775 1E+05 2942 3103 86.3 800.9 550 675 1E+05 3123 3296 87.5 533 x 210 x 101 767.5 525 775 1E+05 3263 3446 95.5 804.5 550 675 1E+05 3462 3659 96.8 533 x 210 x 109 770.3 525 775 1E+05 3530 3736 103 807.3 550 675 2E+05 3746 3966 105 533 x 210 x 122 775.3 525 775 2E+05 3989 4233 1167 812.3 550 675 2E+05 4232 4491 118.2
356 x 171 x 51 506.6 350 525 28501 1125 1182 49.3 535.7 375 475 32162 1201 1260 49.6 356 x 171 x 57 509.6 350 525 32342 1269 1137 55.6 538.7 375 475 36478 1354 1424 55.9 356 x 171 x 67 515 350 525 39223 1523 1611 66.5 554.1 375 475 44196 1625 1715 66.9
406 x 140 x 39
BAB III
PEMBAHASAN MASALAH
III.1. Defleksi Balok
Apabila suatu balok dengan sumbu longitudinal lurus dibebani oleh gaya-gaya lateral , maka sumbu tersebut akan terdeformasi menjadi suatu lengkungan yang di sebut kurva defleksi balok. Kelengkungan kurva defleksi juga untuk menentukan regangan normal dan tegangan normal pada balok. Dalam bab ini, akan ditentukan persamaan kurva defleksi dan juga mencari defleksi di titik-titik yang ditentukan disepanjang sumbu balok.
Perhitungan defleksi merupakan bagian penting di dalam analisis dan desain struktural. Sebagai contoh, mencari defleksi adalah hal penting dalam analisis struktur. Defleksi juga penting dalam analisis dinamik, seperti pada penyeledikan getaran pesawat terbang atau respons sebuah gedung tahan gempa.
III.1.1. Persamaan Diferensial Untuk Kurva Defleksi.
Semua prosedur untuk mencari defleksi balok didasarkan atas persamaan diferensial kurva defleksi dan hubungan-hubungan yang berkaitan dengan itu. Karena itulah, kita akan mulai dengan menurunkan persamaan dasar untuk kurva defleksi sebuah balok.
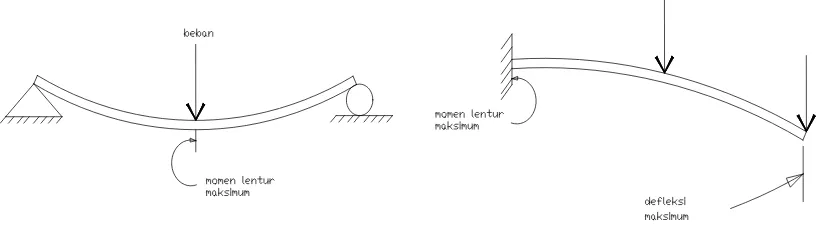
Untuk membahas hal tersebut, tinjau lah balok kantilever dengan beban terpusat yang bekerja ke atas di ujung bebas (gambar III.1.1.a). akibat aksi beban tersebut, sumbu balok berubah bentuk menjadi suatu lengkungan, seperti terlihat dalam gambar III.1.1.b . sumbu-sumbu referensi mempunyai titik pusat di ujung bebas balok, dengan sumbu x berarah ke kanan dan sumbu y berarah ke atas . sumbu z mempunyai arah keluar kertas. Dalam pembahasan ini, kita menganggap bahwa bidang xy adalah bidang simetri balok dan diasumsikan bahwa semua beban bekerja di bidang ini ( bidang lentur ) .
Gambar III.1.1. kurva defleksi balok kantilever.
Defleksi v adalah peralihan dalam arah y dan sembarang titik di sumbu balok
(gambar III.1.1.b). karena sumbu y adalah positif ka atas, maka defleksi juga positif ke atas. Untuk mendapatkan persamaan kurva defleksi, kita harus menyatakan persamaan kurva defleksi, kita harus menyatakan v sebagai fungsi dari x.
pada jarak x + dx dari titik pusat, juga ditunjukkan. Defleksi di titik kedua ini adalah v + dv, dimana dv adalah pertambahan kurva defleksi pada saat kita berjalan di sepanjang kurva dari m1 dan m2
Apabila balok ini melentur, maka yang terjadi bukan hanya defleksi di setiap titik di sepanjang sumbu, melainkan juga rotasi. Sudut rotasi θ dari sumbu balok adalah sudut antara sumbu x dan garis singgung kurva defleksi, seperti terlihat pada titik m
.
1 pada gambar yang dibesarkan dalam gambar III.1.2.b. untuk sistem sumbu yang telah dipilih ( sumbu x positif ke kanan dan sumbu y positif ke atas), sudut rotasi adalah positif apabila berlawanan jarum jam. Sudut rotasi dapat juga disebut dengan nama yaitu sudut kemiringan atau sudut singgung.
dθ
θ + dθ θ
[image:59.595.180.469.75.256.2]
x
Gambar III.1.2. Kurva Defleksi Sebuah Balok.
Sudut rotasi di titik m2 adalah θ + dθ, di mana dθ adalah pertambahan sudut apabila kita berjalan dari titik m1 ke titik m2
p dθ = ds (a)
. Dengan demikian, jika kita membuat garis normal terhadap garis singgung (gambar III.1.3.), sudut antara kedua normal ini adalah dθ. Titik potong kedua normal ini adalah pusat kelengkungan O’ (gambar III.1.3.a) dan jarak dari O’ ke kurva tersebut adalah radius kelengkungan p. dari gambar III.1.3. dapat dilihat bahwa
di mana dθ dalam radian dan ds adalah jarak di sepanjang kurva defleksi antara titik m1 dan m2
κ = 1 �
=
��
Kemiringan kurva defleksi adalah turunan pertama dv/dx dari defleksi v. dalam geometri, kemiringan adalah pertambahan dv dalam defleksi (apabila kita berjalan dari titik m1 ke titik m2
tan θ = ��
��
θ = arctan ��
��
(3-2) dalam gambar III.1.2.) dibagi dengan pertambahan dx dalam jarak di sepanjang sumbu x. karena dv dan dx sangat kecil tak hingga, maka kemiringan dv/dx sama dengan tangent dari sudut rotasi θ (gambar III.1.2.b). jadi,
Dengan cara yang sama, kita juga mendapatkan hubungan berikut :
cos θ = ��
��
sin θ = ��
��
(3-3) Perhatikan bahwa jika sumbu x dan y mempunyai arah seperti terlihat dalam gambar III.1.2.b. , kemiringan dv/dx adalah positif jika garis singgung kurva miring ke atas kanan.
Persamaan 3-1 sampai 3-3 didasarkan hanya atas tinjauan geometris, sehingga berlaku balok dengan bahan apapun. Selain itu, tidak ada batasan mengenai besarnya kemiringan dan defleksi.
III.1.2. Balok Dengan Rotasi Kecil
Hampir semua balok mengalami defleksi dan sudut rotasi yang sangat kecil pada kondisi kerja sehingga kurva defleksinya mempunyai kelengkungan yang sangat kecil. Dengan demikian, kita dapat melakukan pendekatan matematis yang sangat menyederhanakan analisis. Sebagai contoh, karena cos θ ≈ 1 apabila θ kecil, maka persamaan (3-3) menghasilkan
ds ≈ dx (b)
dan persamaan 3.1 menjadi
κ = 1 �
=
��
juga , karena tan θ≈ θ apabila θ kecil, maka kita dapat melakukan pendekatan dari persamaan (3-2) :
θ≈ tan θ = ��
�� (c)
jadi , jika rotasi balok kecil, maka kita dapat menganggap bahwa sudut rotasi θ dan kemiringan dv/dx sama.
Dengan mengambil turunan θ terhadap x dalam persamaan (c), kita
mendapatkan ��
��
=
�2���2
(d) Dengan menggabungkan persamaan ini dangan persamaan (3-4), kita memperoleh
hubungan antara kelengkungan suatu balok dan defleksinya :
κ = 1 �
=
�2�
��2
(3-5) persamaan ini berlaku untuk suatu balok dengan bahan apapun, asalkan rotasinya merupakan besaran kecil.
Jika bahan dari balok bersifat elastic linier dan mengikuti hokum Hooke, maka kelengkungannya adalah
κ = 1 �
=
�
��
(3-6)
di mana M adalah momen lentur dan EI adalah rigiditas lentur balok tersebut. Persamaan (3-6) menunjukan bahwa momen lentur positif menghasilkan kelengkungan positif dan momen lentur negatif menghasilkan kelengkungan negatif.
Dengan menggabungkan persamaan (3-5) dengan persamaan (3-6) maka kita dapatkan persamaan diferensial dasar untuk kurva defleksi suatu balok :
�2� ��2
=
�
Persamaan ini dapat diintegrasikan di setiap kasus khusus untuk mendapatkan defleksi v, asalkan momen lentur M dan rigiditas lentur EI diketahui sebagai fungsi dari x.
Persamaan lain dapat diperoleh dengan mengganti momen lentur M dengan gaya geser V dan intensitas beban q dari beban terdistribusi dari hubungan antara M, V, dan q :
-q = ��
��
V =
����
(3-8) Dengan mendiferensiasi persamaan (3-7) terhadap sumbu x dan selanjutnya mensubstitusikan rumus di atas untuk gaya geser dan beban, maka kita dapat memperoleh rumus-rumus tambahan. Dalam melakukan hal itu, kita akan meninjau dua kasus, balok nonprismatis dan balok prismatis.
Dalam kasus balok nonprismatis , rigiditas lentur EI adalah variable, sehingga kita menulis persamaan (3-7) dalam bentuk
EIX � 2�
��2
= M
(3-9a)
Di mana subskrip x dimasukan sebagai pengingat bahwa rigiditas lentur dapat bervariasi terhadap x. dengan mendiferensiasikan kedua sisi persamaan ini dan menggunakan persamaan (3-8), kita peroleh
� ��
�
EIx�2� ��2
�
=
��
��
= V
(3-9b)
� 2 ��2
�
EIx�2� ��2
�
=
��
Dalam balok prismatis (EI konstan ), persamaan diferensialnya menjadi
EI � 2�
��2
= M
EI �3���3
= V
EIUntuk memudahkan penulisan persamaan, tanda aksen seringkali digunakan untuk menandakan arti diferensiasi :
� 4�
��4
= -q
(3-10a,b,c)v’ ≡��
��
v’’ ≡ �2�
��2
v’’’ ≡ �3�
��3
v’’’’ ≡ �4�
��4
(3-11) dengan menggunakan notasi ini, kita dapat menyatakan persamaan diferensial untuk balok prismatis dalam bentuk berikut :
EIv’’ = M
EIv’’’ = V
EIv’’’’ = -q (3-12a,b,c) Kita akan menyebut persamaan-persamaan di atas masing-masing sebagai persamaan momen-lentur, persamaan gaya geser, dan persamaan beban.
III.1.3. Defleksi Dengan Integrasi Persamaan Momen Lentur.
Persamaan diferensial kurva defleksi telah siap dan telah didapatkan defleksi balok. Persamaan yang digunakan adalah persamaan momen lentur (persamaan 3-12a). karena persamaan ini mempunyai orde kedua, dua integrasi dibutuhkan. Integrasi pertama menghasilkan kemiringan v’ = dv/dx, dan yang kedua menghasilkan defleksi v.
Kita mulai analisis dengan menuliskan persamaan untuk momen lentur di balok. Karena hanya balok statis tertentu yang ditinjau, maka kita dapat memperoleh momen lentur tersebut dari diagram benda bebas dan persamaan keseimbangan.
konstanta integrasi. Lalu, kita integrasikan setiap persamaan kemiringan untuk memperoleh defleksi v yang berkaitan. Lagi-lagi, setiap integrasi menghasilkan konstanta baru. Jadi ada dua konstanta integrasi untuk setiap daerah pada balok. Konstanta-konstanta tersebut dicari dari kondisi yang diketahui mengenai kemiringan dan defleksi. Kondisi tersebut terdiri atas tiga kategori : (1) kondisi batas, (2) kondisi kontinuitas, dan (3) kondisi simetri.
Kondisi batas berkaitan dengan defleksi dan kemiringan pada tumpuan suatu balok . Sebagai contoh, ditumpuan sederhana (apakah sendi atau rol) defleksinya nol (gambar III.1.3.a), dan tumpuan jepit defleksi dan kemiringannya adalah nol (gambar III.1.3.b). Setiap kondisi batas memberikan satu persamaan yang dapat digunakan untuk mencari besarnya konstanta integrasi.
vA = 0 vB = 0 vA = 0 ; v’A
( a ) ( b )
= 0
Di titik C : (v)AC = (v) (v’)
CB AC = (v’)
Gambar III.1.4. kondisi kontinuitas di titik C CB
Kondisi simetri juga mungkin ada. Sebagai contoh, jika suatu balok sederhana memikul beban terbagi rata di seluruh panjangnya, kita dapat langsung mengetahui bahwa kemiringan dari kurva defleksi di titik tengah harus nol. Kondisi ini dapat diilustrasikan dengan balok sederhana AB yang memikul beban terbagi rata dengan intensitas q yang bekerja di seluruh bentang balok (gambar III.1.5). dari kondisi yang ada, dapat ditentukan persamaan kurva defleksi dan defleksi maksimum δmaks di titik tengah balok.
(a) δ θ
maks
A θB
(b)
Momen lentur di balok. Momen lentur di potongan melintang pada jarak x dari tumpuan kiri diperoleh dari diagram benda bebas dalam gambar III.1.6. reaksi di tumpuan tersebut adalah qL/2, sehingga rumus untuk momen lentur adalah
M = ���
2
-
��2
[image:66.595.243.460.159.358.2]2
(3-13)
Gambar III.1.6. diagram benda bebas yang digunakan dalam menentukan momen lentur M
Persamaan diferensial kurva defleksi. Dengan mensubstitusikan rumus untuk momen lentur (persamaan 3-13) kedalam persamaan diferensial (persamaan 3-12a), didapatkan
EIv’’ = ���
2
-
��2
2
(3-14)
Persamaan ini dapat diintegrasikan untuk mendapatkan kemiringan dan defleksi balok.
Kemiringan balok. Dengan mengalikan kedua sisi persamaan diferensial dengan dx dan mengintegrasikannya, kita peroleh persamaan berikut untuk kemiringan :
EIv’ = ��� 2
4
-
��3
6 + C1
Dimana C1 adalah konstanta integrasi. Untuk mengevaluasi konstanta C1
v’ = 0 apabila x = �
2
, kita amati dari simetri balok dan bebannya bahwa kemiringan dari kurva defleksi di tengah bentang sama dengan nol. Jadi, kita mempunyai kondisi simetri:
Kondisi ini dapat dinyatakan dalam bentuk v’ ��
2� = 0
dengan menerapkan kondisi ini ke dalam persamaan (a) maka
0 = ��
4
�
� 2�
2-
� 6�
� 2�
3+ C1 atau C1
Persamaan untuk kemiringan balok (persamaan a) menjadi
= -
�� 324
EIv’ = ��� 2
4
-
��3
6 +
-
��3
24
(b)
Atau v’ =
-
�24�� (L
3
– 6Lx2 + 4x3
Sebagaimana diduga, kemiringan bertanda negative ( artinya searah jarum jam ) di ujung kiri balok (x=0), positif di ujung kanan (x=L), dan sama dengan nol di titik tengah (x = L/2).
) (3-15)
Defleksi balok. Defleksi diperoleh dengan mengintegrasikan rumus kemiringan. Jadi, dengan mengalikan kedua sisi persamaan (b) dengan dx dan mengintegrasikannya, kita dapatkan
EIv =
��� 312
-
��4
24
-
��3�
24 + C2
Konstanta integrasi C
(c)
2
Dengan menerapkan kondisi ini dalam persamaan (c), maka C
dapat dievaluasi dari kondisi bahwa defleksi balok di tumpuan kiri sama dengan nol; artinya, v = 0 apabila x = 0, atau v(0) = 0 .
EIv = ��� 3
12
-
��4
24
-
��3�
24
(d)
Atau v =
-
��24�� (L
3
– 2Lx2 + x3
Persamaan ini memberikan defleksi di sembarang titik di sepanjang balok. Perhatikan bahwa defleksi adalah nol di kedua ujung balok (x=0 dan x=L) dan negative di lokasi lainnya. (defleksi ke bawah berharga negatif).
) (3-16)
Defleksi maksimum. Defleksi maksimum δmaks terjadi di titik tengah bentang (gambar III.1.5.b) dan diperoleh dengan menetapkan x sama dengan L/2 dalam persamaan (3-16). Namun, karena δmaks
δ
menunjukan besar defleksi maksimum dank arena defleksi v negatif apabila arahnya ke bawah, maka kita harus memasukkan tanda minus ke dalam persamaan tersebut, sebagai berikut:
maks = -v
�
�2
�
= -
��
24�� (L
3
– 2Lx2 + x3
δ
)
maks
δ
= ��
24��
�
L3
– 2L
�
�2
�
2 +�
� 2�
3�
maks δ= ��
24��
��
8L3
8
�
– 2L�
L2
4
�
+�
L3 8
��
maks δ = �� � 2�24��
��
8L3
8
�
–�
4L3
8
�
+�
L3
8
��
maks
δ
= ��
48��
�
5L3
8
�
maks =
5�L4
III.1.4. Batasan lendutan
Adapun batasan-batasan lendutan untuk keadaan kemampuan-layan batas harus sesuai dengan struktur, fungsi penggunaan, sifat pembebanan, serta elemen-elemen yang didukung oleh struktur tersebut. Batas lendutan maksimum diberikan dalam table III.1.1. sesuai dengan SNI 03-1729-2002 .
Table III.1.1. Batas Lendutan Maksimum
Komponen struktur dengan beban tidak terfaktor Beban tetap Beban sementara Balok pemikul dinding atau finishing getas L/360 -
Balok biasa L/240 -
Kolom dengan analisis orde pertama saja h/500 h/200 Kolom dengan analisis orde kedua h/300 h/200
Di mana L adalah panjang bentang dan h adalah tinggi tingkat ; beban tetap adalah beban mati dan beban hidup , beban sementara meliputi beban gempa atau beban angin.
III.1.5. Defleksi pada Cellular Beam.
Dalam hal ini, akan kita bahas perencanaan defleksi pada cellular beam berdasarkan penelitian yang dilakukan oleh Ancelormittal dan menghasilkan nama ACB ( Arcelormittal Cellular Beam ) yang merupakan suatu profil baja Cellular Beam yang diproduksi dan dibuat oleh perusahaan Arcelormittal.
Gambar III.1.7. defleksi pada tengah bentang dengan beban terbagi rata Untuk balok ACB pada bentang L.
Adapun rumus defleksi untuk ACB yaitu
δmaks =
5�L4 384���,���
* K1 * K
• K
2
1 adalah koeffisien kelangsingan (L/H) dari balok cellular. Nilai K1 dapat diperoleh melalui kurva pada gambar III.1.8.a. untuk nilai kelangsingan yang lebih besar dari 30, nilai tetap untuk koeffisien K1
• K
= 1,05 .
2 adalah koeffisien sensitivitas balok cellular yang merupakan fungsi dari jumlah bukaan yang ada. (L/S) . Nilai K2 dapat diperoleh melalui kurva pada gambar III.1.8.b. untuk rasio L/S yang lebih besar dari 15, nilai tetap untuk koeffisien K2
• E = modulus elastisitas baja = 200 kN/mm = 1,05 .
• I
2
y,ACB
• q = beban terbagi rata ( kN/m)
( a )
[image:71.595.155.499.38.526.2]( b )
Gambar III.1.8. kurva untuk menentukan (a) koeffisien K1 (b) koeffisien K2
III.2. Perilaku Balok Tanpa Kekangan Lateral
sayap. Flens tekan dari balok dapat dianggap sebagai kolom. Sayap diasumsikan sebagai kolom ini akan tertekuk dalam arah lemahnya akibat lentur terhadap suatu sumbu seperti 1-1. Namun karena web balok memberikan sokongan untuk mencegah tekuk dalam arah ini, maka flens akan cenderung tertekuk oleh lentur pada sumbu 2-2.
Gambar III.2.1. balok terkekang pada ujung-ujungnya
Tekuk lateral ( Kip ) adalah satu pergerakan / tekukan ke samping dari bagian yang tertekan dari batang / balok (flens dan pelat-badan yang berhubungan dengan flens itu) ke arah siku atas bidang kopel-lentur, berbareng dengan berputarnya penampang dari batang (gambar III.2.2).
Gambar III.2.2. tekuk lateral pada balok
Tekuk torsi lateral adalah kondisi batas yang menentukan kekuatan sebuah balok. Sebuah balok mampu memikul momen hingga mencapai momen plastis (Mp). Tercapainya atau tidaknya momen plastis, keruntuhan dari sebuah struktur balok adalah salah satu dari peristiwa berikut :
1. Tekuk lokal dari flens tekan
2. Tekuk lokal dari web dalam tekan lentur 3. Tekuk torsi lateral.
Ketiga macam keruntuhan tersebut dapat terjadi pad kondisi elastis maupun inelastis. Gambar III.2.3. menunjukan perilaku dari sebuah balok yang dibebani momen konstan M dengan bentang tak terkekang L. Empat kategori dari perilaku balok tersebut adalah :
2. Jika L diperbesar sehingga Lpd < L < Lp, maka balok dapat mencapai Mp
3. Bila panjang bentang tak terkekang diperbesar lagi (L
[image:74.595.136.54