ISOMETRI TERHADAP GEOMETRI INSIDENSI
TERURUT
(Skripsi)
Oleh
Damay Lisdiana
JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG
ABSTRAK
ISOMETRI TERHADAP GEOMETRI INSIDENSI TERURUT
Oleh
DAMAY LISDIANA
Suatu geometri dibentuk berdasarkan aksioma yang berlaku dalam geometri-geometri tersebut. Geometri yang dibentuk berdasarkan aksioma-aksioma insidensi disebut geometri insidensi. Sedangkan geometri insidensi yang telah diperkaya dengan aksioma urutan disebut geometri insidensi terurut. Dalam suatu geometri terdapat bagian tentang transformasi geometri. Transformasi geometri adalah bagian dari geometri yang membahas tentang perubahan (letak, bentuk, maupun penyajian) yang didasarkan dengan gambar dan matriks. Transformasi adalah perpindahan atau pemetaan suatu titik pada bidang kartesius ke bidang yang lain, atau T: R2⟶ R2 , (x , y) ⟶(x’ , y’).
Misalkan fungsi �: En ⟶ En adalah isometri, jika untuk semua titik P dan Q berada di En. Isometri merupakan suatu transformasi atas refleksi (pencerminan), translasi (pergeseran), dan rotasi (perputaran) apabila �(P) = P’, �(Q) = Q’ sehingga jarak = ′ ′ untuk setiap pasang titik P dan Q. Dengan menggunakan metode studi literatur, maka dibuktikan bahwa refleksi (pencerminan), translasi (pergeseran), dan rotasi (perputaran) adalah suatu isometri. Isometri memiliki sifat mempertahankan sebuah ruas garis dengan tiga titik segaris yang berurutan, mempertahankan keantaraan pada tiga titik segaris yang berurutan, mempertahankan titik tengah terhadap tiga titik segaris yang berurutan, mempertahankan kesebangunan, dan mempertahankan sudut antara dua garis. Pada suatu refleksi (pencerminan), translasi (pergeseran), dan rotasi (perputaran), diperoleh bahwa bentuk bayangan sama dan sebangun dengan bentuk aslinya.
Kata kunci : Geometri Insidensi, Geometri Insidensi Terurut, Geometri
ISOMETRI TERHADAP GEOMETRI INSIDENSI TERURUT
OLEH
DAMAY LISDIANA
Skripsi
Sebagai Salah Satu Syarat untuk Memperoleh Gelar SARJANA SAINS
Pada
Jurusan Matematika
Fakultas Matematika dan Ilmu Pengetahuan Alam
JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG
Judul Penelitian : ISOMETRI TERHADAP GEOMETRI INSIDENSI TERURUT
Nama Mahasiswa : Damay Lisdiana
NPM : 0917031004
Jurusan : Matematika
Fakultas : Matematika dan Ilmu Pengetahuan Alam
Bandar Lampung, Mei 2013
Menyetujui, Komisi Pembimbing
Pembimbing I Pembimbing II
Dr. Muslim Ansori, M.Si. Amanto, M. Si.
NIP.19720227 199802 1 001 NIP.19840627 200604 2 001
Mengetahui,
Ketua Jurusan Matematika
MENGESAHKAN
1. Tim Penguji
Ketua : Dr. Muslim Ansori, M.Si. ………...
Sekretaris : Amanto, M.Si …….....
Penguji
Bukan Pembimbing : Drs. Tiryono Ruby, M.sc ………...
2. Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam
Prof. Suharso, Ph. D. NIP.19690530 199512 1001
PERNYATAAN SKRIPSI MAHASISWA
Yang bertanda tangan di bawah ini:
Nama : Damay Lisdiana
Nomor Pokok Mahasiswa : 0917031004
Program Studi : Matematika
Jurusan : Matematika
Dengan ini menyatakan bahwa penelitian ini adalah hasil pekerjaan saya sendiri,
dan sepanjang pengetahuan saya tidak berisi materi yang telah dipublikasikan atau
ditulis oleh orang lain atau telah dipergunakan dan diterima sebagai persyaratan
penyelesaian studi pada universitas atau institut lain.
Bandar Lampung, Mei 2013 Yang menyatakan
RIWAYAT HIDUP
Penulis dilahirkan di Kedondong pada tanggal 17 Maret 1991, penulis merupakan
anak pertama dari dua bersaudara dari pasangan bapak Guno dan ibu Sudarti.
Penulis menyelesaikan Pendidikan Sekolah Dasar di SD Negeri 4 Kedondong
pada tahun 2003, setelah lulus SD penulis melanjutkan sekolah ke SLTP Negeri 1
Kedondong dan lulus pada tahun 2006. Kemudian, penulis melanjutkan sekolah
ke SMA Negeri 1 Gadingrejo dan lulus pada tahun 2009.
Pada tahun 2009 penulis masuk dan terdaftar sebagai mahasiswa di Universitas
Lampung melalui jalur Penelusuran Kemampuan Akademik dan Bakat (PKAB).
Penulis masuk pada Jurusan Matematika program studi Matematika S1 Fakultas
Matematika dan Ilmu Pengetahuan Alam. Selama menjadi mahasiswa penulis
aktif dalam kepengurusan Himpunan Mahasiswa Jurusan Matematika
Motto
Boleh jadi kamu membenci sesuatu, padahal ia amat baik bagimu, dan boleh jadi
kamu menyukai sesuatu, padahal ia amat buruk bagimu, Allah maha
mengetahui, sedang kamu tidak mengetahui.
(Al-Baqarah:216)
Jika engkau sanggup untuk tidak dikenal, maka lakukanlah. Apa sukarnya
engkau tidak dikenal? Apa sukarnya engkau tidak disanjung-sanjung? Tidak
mengapalah engkau tercela di hadapan manusia, selagi engkau terpuji di sisi
Allah.
(Al-Fudhayl ibn Iyadh)
Jadilah kamu sebagai sumber ilmu, pelita petunjuk, penerang rumah, obor pada
waktu malam dan pembaharu hati yang diketahui penduduk langit, namun
Dengan menyebut nama Allah yang Maha pengasih lagi Maha penyayang
PERSEMBAHAN
Dengan segala cinta dan kasih sayang kupersembahkan karya sederhana ini untuk orang-orang yang akan selalu berharga dalam hidupku:
Ibu dan Bapak
Terima kasih untuk cinta, kasih sayang, dukungan serta doa yang tiada terhingga untukku
Adik-adikku
Terima kasih untuk segala kasih sayang yang kalian berikan untukku
Sahabat-sahabatku
Terimakasih untuk kasih sayang, kesetiaan, kesabaran, dan dukungan yang selalu ada untukku
Para Pendidikku (Guru-guruku, Dosen-dosenku)
Terimakasih atas bimbingan yang diberikan pada ku hingga aku dapat melihat dunia dengan ilmu
Teman-teman GEOMETRI 2009
Terimakasih untuk segala dukungan dan bantuan yang diberikan untukku
Teman-teman kosan
ix SANWACANA
Assalamu’alaikum warahmatullah wabarakatuh
Segala puji bagi Allah SWT. yang senantiasa memberikan rahmat, dan
hidayah-Nya kepada penulis sehingga penulis dapat menyelesaikan skripsi ini yang
berjudul “Isometri Terhadap Geometri Insidensi Terurut” . Skripsi ini disusun
untuk memenuhi persyaratan memperoleh gelar Sarjana Sains Jurusan
Matematika di Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas
Lampung.
Keberhasilan penulisan skripsi ini tidak hanya dari penulis saja, tetapi
keberhasilan skripsi ini juga karena bantuan dari berbagai pihak. Oleh karena itu,
tidak lupa penulis mengucapkan terima kasih kepada:
1. Bapak Dr. Muslim Ansori, M.Si. selaku Pembimbing I, karena atas
bimbingan, bantuan dan kesabarannya yang selalu membimbing penulis
sehingga penulisan skripsi ini dapat terselesaikan;
2. Bapak Amanto, M.Si., selaku Pembimbing II yang selalu memberikan ide
serta masukan dan membimbing penulis dalam menyelesaikan skripsi;
3. Bapak Drs. Tiryono Ruby, M.Sc., Ph.D. selaku Pembahas sekaligus selaku
ketua Jurusan Matematika yang telah memotivasi dan memberikan saran dan
x 4. Ibu Widiarti, M.Si., selaku Pembimbing Akademik yang selalu membantu,
dan memberikan saran kepada penulis;
5. Dosen, staf dan karyawan jurusan Matematika serta civitas akademika
FMIPA;
6. Ibu dan Bapak, terima kasih atas kasih sayang, cinta dan doa – doa dari Ibu
dan Bapak, yang selalu mendukung, membimbing dan memberi motivasi bagi
penulis untuk tetap semangat;
7. Dila, Perti, Anna, Desi, Septi, Raisa, Indah dan sahabat-sahabat yang selalu
mendukung dan membantu penulis dalam pembuatan laporan ini;
8. Seluruh teman-teman Jurusan Matematika terutama angkatan 2009
(Geometri) yang telah banyak membantu dan memberikan masukan yang
sangat berarti dalam pembuatan skripsi ini.
9. Teman-teman kosan, Wo Cheri, Pipin, Anna, Alvin, Aryanti, dan Rama yang
selalu membantu dan memberikan saran dalam pembuatan skripsi ini.
Penulis menyadari skripsi ini masih banyak kekurangan. Oleh karena itu, penulis
mengharapkan kritik dan saran untuk menjadikan skripsi ini lebih baik lagi.
Wasaalamualaikum warahmatullah wabarakatuh.
Bandar Lampung, Mei 2013
Penulis,
xi
2.2 Geometri Insidensi Terurut ... 7
xii DAFTAR GAMBAR
Halaman GAMBAR
1. Tiga titik A, B, dan C yang kolinear ... 8
2. Sinar atau setengah garis ... 10
3. Garis �� yang memotong g ... 12
4. Titik A dan B yang berbeda dan terletak pada sisi g ... 14
5. Kedudukan antar sinar ... 15
6. Sudut ... 18
7. Perpotongan dua garis yang membentuk empat sudut ... ... 20
8. Isometri ... 21
9. Diagram Penelitian ... 25
10. Refleksi titik P terhadap garis g ... 27
11. Refleksi tiga titik berurutan A, B, dan C terhadap garis g ... 28
12. Jajar genjang CABD ... 32
13. Translasi objek segitiga dengan transformasi (10,20) ... 34
14. Rotasi dengan pusat P dan sudut rotasi � ... 35
15. Rotasi dua titik A dan B di R2 ... 36
1
I. PENDAHULUAN
1.1 Latar Belakang Masalah
Matematika merupakan salah satu cabang dari ilmu pengetahuan yang banyak
aplikasinya di berbagai bidang ilmu pengetahuan dan matematika itu sendiri.
Disiplin-disiplin utama di dalam matematika pertama muncul karena kebutuhan
akan perhitungan di dalam perdagangan, untuk memahami hubungan antar
bilangan, untuk mengukur tanah, dan untuk meramal peristiwa astronomi. Empat
kebutuhan ini dapat dikaitkan dengan pembagian-pembagian matematika ke
dalam pengkajian besaran, struktur, ruang, dan perubahan yaitu, aritmetika,
aljabar, geometri, dan analisis.
Geometri merupakan salah satu cabang matematika yang membahas mengenai
bentuk, bidang, dan ruang suatu benda. Dalam geometri, dipelajari hubungan
antar titik-titik, garis-garis, sudut-sudut, bidang-bidang, serta bangun datar dan
bangun ruang. Suatu geometri dibentuk berdasarkan aksioma yang berlaku dalam
geometri-goemetri tersebut. Selain aksioma, di dalam geometri juga diperlukan
unsur-unsur tak terdefinisi yaitu, titik, garis, dan bidang. Pengkajian tentang ruang
2
Geometri Euclides adalah geometri yang mempelajari tentang bidang datar yang
didasarkan pada definisi, teorema, aksioma dan asumsi-asumsi. Geometri
insidensi merupakan geometri yang mendasari geometri Euclides. Geometri
insidensi adalah geometri yang didasari oleh aksioma insidensi. Menurut David
Hilbert, geometri Euclides didasarkan pada lima kelompok aksioma, yaitu:
kelompok aksioma insidensi, kelompok aksioma urutan, kelompok aksioma
kekongruenan, aksioma kesejajaran Euclides, dan aksioma kekontinuan. Jadi
dapat dikatakan bahwa geometri Euclides adalah sebuah geometri insidensi yang
dilengkapi dengan kelompok aksioma-aksioma tersebut. Geometri insidensi
merupakan sebuah himpunan titik-titik bersama dengan himpunan bagian seperti
garis dan bidang yang memenuhi sistem aksioma sebagai berikut :
1. Garis adalah himpunan titik-titik yang mengandung paling sedikit dua
titik.
2. Dua titik yang berlainan terkandung dalam tepat satu garis (satu dan tidak
lebih dari satu garis).
3. Bidang adalah himpunan titik-titik yang mengandung paling sedikit tiga
titik yang tidak terkandung dalam satu garis (tiga titik tak segaris)
4. Tiga titik berlainan yang tak segaris terkandung dalam satu dan tidak
lebih dari satu bidang.
5. Apabila sebuah bidang memuat dua titik berlainan dari sebuah garis,
maka bidang itu akan memuat setiap titik pada garis tersebut (garis
3
6. Apabila dua bidang bersekutu pada sebuah titik maka kedua bidang itu
akan bersekutu pada titik kedua yang lain (ada titik lain di mana bidang
tersebut juga bersekutu).
Sedangkan geometri insidensi yang telah diperkaya dengan aksioma urutan
disebut dengan geometri insidensi terurut.
Berdasarkan dari latar belakang yang telah dijelaskan, maka penulis tertarik untuk
melakukan penelitian dengan judul “Isometri Terhadap Geometri Insidensi
Terurut”.
1.2 Batasan Masalah
Dalam penelitian ini, permasalahan yang dibahas dibatasi pada geometri insidensi
terurut dan isometri.
1.3 Tujuan
Tujuan dari penelitian ini adalah:
1. Mempelajari isometri terhadap geometri insidensi terurut.
2. Memperoleh sifat-sifat khusus isometri terhadap geometri insidensi
4
1.4 Manfaat
Manfaat dari penelitian ini adalah:
1. Memperluas serta menambah wawasan pengetahuan tentang kajian
matematika khususnya tentang isometri.
2. Manambah wawasan pengetahuan tentang sifat-sifat khusus isometri
5
II. TINJAUAN PUSTAKA
2.1 Geometri Insidensi
Suatu geometri dibentuk berdasarkan aksioma yang berlaku dalam
geometri-geometri tersebut. Geometri insidensi didasari oleh aksioma insidensi. Di dalam
sebuah geometri selain aksioma diperlukan juga unsur-unsur tak terdefinisi. Untuk
membangun suatu geometri diperlukan unsur tak terdefinisi sebagai berikut :
1. Titik.
Titik dilambangkan dengan bulatan kecil (.). Titik hanya mempunyai
posisi, tetapi titik tidak mempunyai panjang, lebar, maupun ketebalan.
2. Himpunan titik-titik yang dinamakan garis.
Garis dilambangkan dengan simbol . Garis mempunyai panjang tapi
tidak mempunyai lebar maupun ketebalan. Suatu garis bisa lurus,
melengkung, maupun kombinasi dari keduanya.
3. Himpunan titik-titik yang dinamakan bidang.
Bidang mempunyai panjang dan lebar tapi tidak mempunyai ketebalan.
Bidang adalah suatu permukaan di mana suatu garis yang menghubungkan
dua titik pada permukaan tersebut secara keseluruhan akan terletak pada
6
Ketiga unsur tak terdefinisi tersebut dikaitkan satu sama lain dengan sebuah
sistem aksioma.
Pada geometri insidensi sistem aksioma yang digunakan adalah sistem aksioma
insidensi yang terdiri dari enam aksioma, yaitu :
1.1Garis adalah himpunan titik-titik yang mengandung paling sedikit dua titik.
1.2Dua titik yang berlainan terkandung dalam tepat satu garis (satu dan tidak
lebih dari satu garis).
1.3Bidang adalah himpunan titik-titik yang mengandung paling sedikit tiga titik
yang tidak terkandung dalam satu garis (tiga titik tak segaris atau tiga titik
yang tak kolinear).
1.4Tiga titik berlainan yang tak segaris terkandung dalam satu dan tidak lebih
dari satu bidang.
1.5Apabila sebuah bidang memuat dua titik berlainan dari sebuah garis, maka
bidang itu akan memuat setiap titik pada garis tersebut (garis terkandung
dalam bidang itu, atau garis terletak pada bidang itu).
1.6Apabila dua bidang bersekutu pada sebuah titik maka kedua bidang itu akan
bersekutu pada titik kedua yang lain (ada titik lain dimana bidang tersebut
juga bersekutu).
Sebuah himpunan titik-titik bersama dengan himpunan bagian seperti garis dan
bidang yang memenuhi sistem aksioma 1.1 sampai dengan 1.6 disebut suatu
7
2.2 Geometri Insidensi Terurut
Geometri insidensi terurut adalah geometri insidensi yang telah diperkaya dengan
aksioma urutan.
2.2.1 Urutan Pada Garis
Urutan adalah salah satu pengertian yang amat mendasar dalam matematika.
Konsep urutan dapat dijumpai dalam kalkulus khususnya dalam himpunan
bilangan real. Secara matematika diperkenalkan pengertian urutan tersebut
dalam bentuk suatu aksioma yang selanjutnya akan dinamakan sistem Aksioma
Terurut. Sistem aksioma tersebut adalah sebagai berikut:
U1 : (ABC) mengakibatkan (CBA), (ABC)dibaca “titik B antara titik A dan titik
C”.
U2 : (ABC) mengakibatkan ~ (BCA) dan ~ (BAC), ~ (BCA) dibaca “tidak
(BCA)”.
U3 : Titik-titik A, B, C berlainan dan segaris jika dan hanya jika (ABC), (BCA),
atau (CAB).
U4 : Jika P segaris dan berbeda dengan A, B, C maka (APB) mengakibatkan
(BPC) atau (APC) tetapi tidak sekaligus dua-duanya.
8
a. Ruas Garis (Schaum’s, 2005)
Ruas garis lurus dilambangkan dengan . Ruas garis lurus adalah bagian
dari garis lurus yang berada di antara dua titik pada garis lurus tersebut,
termasuk kedua titik tersebut.
Jika suatu ruas garis dibagi menjadi bagian-bagian:
1. Panjang keseluruhan ruas garis sama dengan jumlah dari panjang
semua bagiannya.
2. Panjang keseluruhan ruas garis lebih besar dari panjang bagiannya
yang manapun.
3. Dua ruas garis yang mempunyai panjang sama dikatakan kongruen.
Jadi, jika AB = CD maka kongruen dengan , sehingga ditulis
≅ .
Jika suatu ruas garis dibagi menjadi dua bagian yang sama:
1. Titik bagiannya adalah titik tengah ruas garis tersebut.
10
Bukti:
1. Oleh karena ( � ) = ( � ), serta = � ( � ) dan
= � ( � ) maka = .
2. Misalkan X , maka ( � ). Ini berarti A, X, B segaris sehingga
X AB. Jadi AB.
3. Misalkan A . Jadi berlakulah (AAB). Ini berlawanan dengan U3. Jadi
A . Misalkan B Jadi berlakulah (ABB). Ini berlawanan dengan
U3. Jadi B .
4. Oleh karena A ≠ B, menurut U5, ada X sehingga (AXB). Jadi, X atau
himpunan tak kosong.
b. Sinar atau setengah garis Definisi 2.2 (Rawuh, 2009)
Jika ada dua titik A dan B, A ≠ B, maka himpunan H = � (� ) dinamakan sinar atau setengah garis. Sinar ditulis sebagai A/B (“A atas
B”). Kadang-kadang A/B dinamakan perpanjangan . Titik A dinamakan
suatu ujung sinar A/B.
X A B
11
mencukupi untuk bidang, sehingga untuk bidang dilengkapi dengan aksioma
U6 yang biasa disebut dengan Aksioma Pasch. Aksiomanya berbunyi sebagai
berikut:
U6 : Misalkan g sebuah garis yang sebidang dengan titik A, B, C tetapi g tidak
melalui A, B, atau C. apabila g memotong maka g memotong atau
13
Setengah bidang dengan tepi g disebut sebuah sisi dari g. Dua setengah bidang
yang berhadapan dengan sisi g dinamakan sisi yang berhadapan. Dua titik atau
dua himpunan titik dikatakan terletak pada sisi g yang sama apabila mereka
terletak pada setengah bidang bertepi g yang sama, mereka terletak pada sisi g
yang berhadapan apabila mereka terletak pada dua setengah bidang bertepi g
yang berhadapan.
Oleh karena setiap titik yang tidak pada g terletak pada tepat satu setengah
bidang bertepi g sedangkan setiap setengah bidang bertepi g memiliki
setengah bidang tunggal yang berhadapan, sehingga dapat ditarik kesimpulan
sifat-sifat berikut berdasarkan dari Aksioma Pash, yaitu:
1. Misalkan titik A dan B terletak pada sisi g yang sama dan B dan C pada sisi
g yang sama maka, A dan C juga pada sisi g yang sama.
2. Misalkan A dan B pada sisi g yang sama dan B dan C pada sisi g yang
14
3. Misalkan A dan B terletak pada sisi g yang berhadapan dan B dan C terletak
pada sisi g yang berhadapan maka A dan C terletak pada sisi g yang sama.
Teorema 2.5 (Rawuh, 2009)
Dua titik yang berbeda terletak pada sisi garis g yang sama jika dan hanya jika,
1. Kedua titik itu sebidang dengan g.
2. Tidak terletak pada g.
3. Ruas garis yang menghubungkan kedua titik itu tidak memotong g.
15
adalah untuk menjamin sinar-sinar dalam suatu relasi antara supaya sinar-sinar
itu berlainan. Pernyataan tersebut dapat pula dinyatakan dalam bentuk yang
16
1. O, A, C berlainan dan tak kolinear
2. O AC
3. dan tak kolinear.
Teorema 2.6 (Rawuh, 2009)
Jika ( ) Maka ( ).
Teorema 2.7 (Rawuh, 2009)
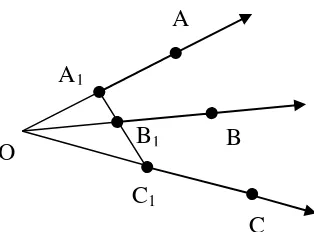
Jika ( ), maka tiap pasang sinar dalam ganda , , berlainan
dan tidak berlawanan.
Bukti:
Karena ( ), maka ada titik A1 , B1 , C1 sehingga (A1,
B1, C1). Jadi ₁ = , ₁ = , ₁ = . Karena dan berlainan
dan tidak berlawanan arah, maka ₁ dan ₁ berlainan dan tidak berlawanan
arah. Sehingga O A1 C1. (A1, B1, C1) mengakibatkan A1 B1 = A1 C1. Jadi O
A1 B1 ini berarti ₁ dan ₁ berlainan dan tidak berlawanan arah. Begitu pula
dan . Karena dan sama halnya dengan dan , sehingga
dan juga berlainan dan tidak berlawanan arah.
Teorema 2.8 (Rawuh, 2009)
Jika ( ), maka berlaku
17
dan C1 terletak pada sisi OB yang berhadapan. Sehingga menyebabkan A
18
titik akhir yang sama. Sinar-sinar tersebut merupakan sisi-sisi sudut,
sementara titik akhirnya merupakan titik sudutnya. Simbol untuk sudut adalah
atau .
Gambar 2.6. Sudut
Pengertian sudut menyangkut berbagai konsep, yaitu:
1. Sebuah gambar yang terdiri atas dua garis.
2. Daerah pada bidang yang dibatasi oleh dua garis yang berpotongan. A
B
19
3. Sebuah ukuran yang dinyatakan dengan bilangan real yang
menggambarkan selisih arah dua garis yang berpotongan.
Definisi 2.6 (Rawuh, 2009)
Misalkan ada tiga titik O, A, B yang berlainan dan tidak segaris himpunan
titik {O} disebut sudut dan ditulis sebagai AOB.
Jadi AOB = {O}. Sinar dan dinamakan sisi sudut dan
O dinamakan titik sudut.
Definisi 2.7(Rawuh, 2009)
Daerah dalam sebuah AOB, yang dilambangkan dengan D(AOB) adalah
himpunan titik X sehingga � antara dan atau dengan kata lain
D(AOB) = � ( � ) .
Daerah luar AOB, adalah himpunan titik X yang tidak dalam daerah dalam
maupun pada sudut tersebut. Daerah luar AOB ditulis sebagai L(AOB).
Definisi 2.8 (Rawuh, 2009)
Dua buah sudut yang bertitik ujung sama membentuk sepasang sudut yang
bertolak belakang apabila kedua kaki sudut yang satu berlawanan arah
20
Definisi 2.9 (Rawuh, 2009)
Dua garis l dan m dikatakan membentuk sebuah sudut, apabila titik sudutnya
berimpit dengan titik potong kedua garis itu dan apabila kedua kakinya
termuat dalam dua garis tersebut.
Teorema 2.10 (Rawuh, 2009)
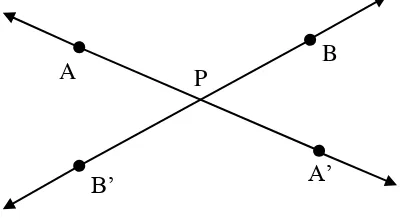
Dua garis yang berpotongan membentuk tepat empat buah sudut.
Bukti:
Misalkan l dan m berpotongan di P dan l ≠ m. Diambil A, A’ l, sehingga (APA’) dan B, B’ m sehingga (BPB’) maka A, P, B tidak segaris
Gambar 2.7. Perpotongan dua garis yang membentuk empat sudut
Jadi dan berlainan dan tidak berlawanan arah. Jadi ada APB yang
dibentuk oleh l dan m. Begitu pula ada sudut APB’, A’PB, A’PB’. P
A
A’
B
21
Jadi, suatu isometri adalah suatu transformasi titik yang mempertahankan jarak
22
Jika tiap persamaan tersebut, di sebelah kiri dikalikan dengan ̄¹ maka ̄¹
mempertahankan ketiga titik tersebut sehingga ̄¹ adalah suatu identitas.
23
III. METODE PENELITIAN
3.1 Waktu dan Tempat
Penelitian ini dilakukan di Jurusan Matematika Fakultas Matematika dan Ilmu
Pengetahuan Alam Universitas Lampung, pada semester genap tahun ajaran
2012/2013.
3.2 Metode Penelitian
Metode yang digunakan dalam penelitian ini adalah metode studi pustaka, yaitu
dengan mempelajari, memahami dan mengkaji mengenai buku-buku, jurnal
maupun makalah yang berhubungan dengan penelitian.
Dalam melakukan penelitian ini, ada langkah–langkah yang harus penulis lakukan
untuk mempermudah penulis dalam memperoleh maupun menyelesaikan hasil
penelitian. Langkah-langkah yang penulis lakukan dalam penelitian ini adalah
sebagai berikut:
1. Mengumpulkan referensi yang berhubungan dengan penelitian.
2. Menuliskan definisi-definisi dan teorema-teorema yang berhubungan dengan
24
3. Mempelajari dan memahami definisi-definisi dan teorema-teorema yang
berhubungan dengan penelitian.
4. Menguraikan dan menggunakan definisi-definisi dan teorema-teoremasebagai
acuan dalam melakukan penelitian untuk memperoleh hasil penelitian ini.
5. Melakukan penelitian tentang isometri pada geometri insidensi terurut.
6. Mencari sifat-sifat dari isometri pada geometri insidensi terurut.
25
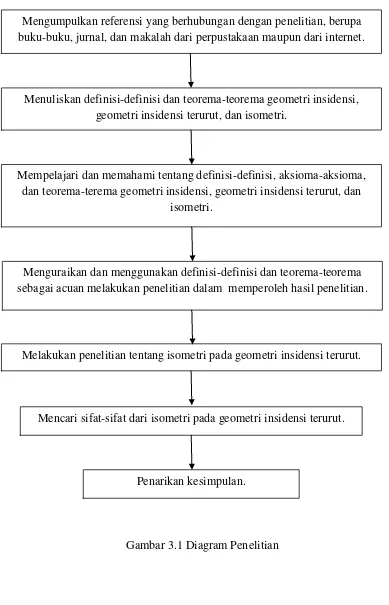
Gambar 3.1 Diagram Penelitian
Mengumpulkan referensi yang berhubungan dengan penelitian, berupa buku-buku, jurnal, dan makalah dari perpustakaan maupun dari internet.
Menuliskan definisi-definisi dan teorema-teorema geometri insidensi, geometri insidensi terurut, dan isometri.
Mempelajari dan memahami tentang definisi-definisi, aksioma-aksioma, dan teorema-terema geometri insidensi, geometri insidensi terurut, dan
isometri.
Menguraikan dan menggunakan definisi-definisi dan teorema-teorema sebagai acuan melakukan penelitian dalam memperoleh hasil penelitian.
Melakukan penelitian tentang isometri pada geometri insidensi terurut.
Mencari sifat-sifat dari isometri pada geometri insidensi terurut.
V. KESIMPULAN
Dari hasil pembahasan diperoleh kesimpulan bahwa, isometri merupakan
transformasi atas refleksi (pencerminan), translasi (pergeseran), dan rotasi
(perputaran). Pada suatu refleksi (pencerminan), translasi (pergeseran), dan rotasi
(perputaran), diperoleh bahwa bentuk bayangan sama dan sebangun dengan
bentuk aslinya. Isometri memiliki sifat mempertahankan sebuah ruas garis dengan
tiga titik segaris yang berurutan, mempertahankan keantaraan pada tiga titik
segaris yang berurutan, mempertahankan titik tengah terhadap tiga titik segaris
yang berurutan, mempertahankan kesebangunan, dan mempertahankan sudut
antara dua garis.
DAFTAR PUSTAKA
David Hilbert. 1971. Fondation of Geometry. Illinois: Open Court.
Edwin Moise. 1963. Elementary Geometry from Advance Standpoint. Addison Wesley Publishing Company, Inc.
G. E. Martin. 1932. Transformation Geometry: An Introduction to Symetry. New York: Springer.
Greenberg, Marvin J. 1973. Euclidean and Non-Euclidean Geometries. W.H. Freeman and Company.
Jennings, George A. 1997. Modern Geometry with Aplication. New York: Springer.
Rawuh. 2009. Geometri. Jakarta: UniversitasTerbuka.
Schaum’s. 2005. Geometri. Jakarta: Erlangga.
Wallace Edward C.N. and West Stephen F. 1992. Road to Geometry. Prentice Hall.