Fakultas Program Studi Tatap Muka Kode MK Disusun Oleh Ilmu Komputer Sistem
Informasi
03
87004 Ir. Pranto Busono M.Kom.TUGAS PERKULIAHAN
Logika
Matematika
Judul Tugas
HUKUM DAN PEMBUKTIAN
HIMPUNAN
Abstract
Deskripsi
Latihan untuk menyelesaikan berbagai macam bentuk Hukum pada himpunan Prinsip dualitas. Pembuktian pernyataan himpunan berdasarkan teori yang ada.
Ketentuan
Tugas bersifat openbook
Diperbolehkan bertanya tetapi tidak diperbolehkan dibuatkan orang lain Tidak diperbolehkan untuk copy – paste temannya
Luaran/Output
Mahasiswa mampu memahami dan dapat membuktikan pernyataan himpunan
Jadwal
- Tugas diberikan pada pertemuan ke 3.
- Jawaban dikumpulkan paling lambat satu minggu setelah tugas diberikan.
- Jawaban dikirim lewat e-mail : pranto@ batan.go.id
Penilaian
Bobot
Bobot nilai yang digunakan adalah A – F dengan nilai tertinggi adalah A dan terendah adalah F
1. Proses untuk mendapatkan penyelesaian masalah 2. Kesesuaian dan ketepatan hasil hitungan
3. Kecepatan Penyerahan Tugas
Daftar
Pustaka
1. Firrar Utdirartatmo, Teori Bahasa dan Otomata, Graha Ilmu, Yogyakarta, Edisi 2, 2005.
2. Jonhson, Ricard, Discrete Mathematics. Prentice Hall Int, New Jersey, 2001
3. Sri Kusumadewi, Hari Purnomo, Aplikasi Logika Fuzzy, Graha Ilmu, Yogyakarta, 2004.
4. Klin, George J dan Tina A. Folger, Fuzzy Sets, Uncertainty and Information, Prentice Hall Int, New Jersey, 1998.
5. Sumarna, Elektronika Digital, Graha Ilmu, Yogyakarta, 2006.
SOAL
1. Buktikan
A È (A Ç B) = A Ç (A È B)
a. Menggunakan diagram Venn b. Menggunakan tabel keanggotaan c. Menggunakan aljabar himpunan.
2. Buktikan
B
AÈ = AÇB
a. Menggunakan diagram Venn b. Menggunakan tabel keanggotaan c. Menggunakan aljabar himpunan.
3. Buktikan
B
AÇ = AÈB
Penyelesaian :
1. A È (A Ç B) = A Ç (A È B)
Buktikan :
a. Menggunakan diagram Venn b. Menggunakan tabel keanggotaan c. Menggunakan aljabar himpunan
Jawab :
a. Menggunakan Diagram Venn
= A Ç (A È B) (HK. Idempoten)
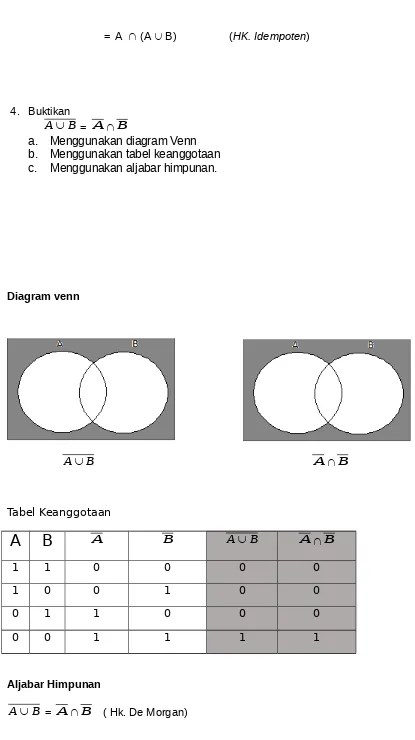
4. Buktikan
B
AÈ = AÇB
a. Menggunakan diagram Venn b. Menggunakan tabel keanggotaan c. Menggunakan aljabar himpunan.
Diagram venn
AÈB AÇB
Tabel Keanggotaan
A
B
A B AÈB AÇB1 1 0 0 0 0
1 0 0 1 0 0
0 1 1 0 0 0
0 0 1 1 1 1
Aljabar Himpunan
B
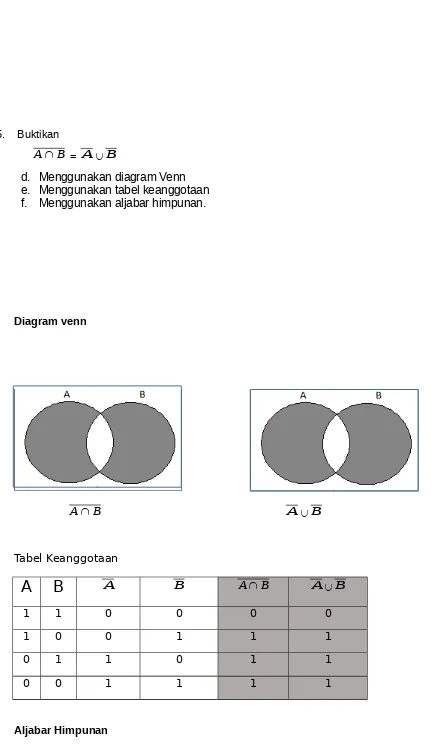
5. Buktikan
B
AÇ = AÈB
d. Menggunakan diagram Venn e. Menggunakan tabel keanggotaan f. Menggunakan aljabar himpunan.
Diagram venn
B
AÇ AÈB
Tabel Keanggotaan
A
B
A B AÇB AÈB1 1 0 0 0 0
1 0 0 1 1 1
0 1 1 0 1 1
0 0 1 1 1 1
B