Diktat Ajar Matematika Diktat Ajar Matematika

ii

DAFTAR ISI

Halaman

JUDUL

KATA PENGANTAR

………

i

DAFTAR ISI

………

ii

DAFTAR GAMBAR

………

iii

Bab I Sistem Bilangan

1.1

Himpunan Bilangan Real

………

1

1.2

Pertidaksamaan

………

2

1.3

Harga Mutlak

………

3

Tugas Mandiri Bab I

………

4

BAB II Fungsi dan Grafik

2.1

Pengertian Fungsi

………

5

2.2

Menggambar Grafik

………

6

2.3

Fungsi Trigonometri

………

7

Tugas Mandiri Bab II

………

9

BAB III Limit

3.1

Limit Fungsi Aljabar

………

10

3.2

Limit Fungsi Trigonometri

………

11

3.3

Kontinuitas

………

12

Tugas Mandiri Bab III

………

13

BAB IV Turunan / Diferensial

4.1.

Definisi Turunan

………

14

4.2.

Turunan Fungsi Aljabar

………

15

4.3.

Turunan Fungsi Trigonometris ………...………..

16

4.4.

Gradien Garis Singgung

………

17

4.5.

Fungsi Naik, Stasioner dan Fungsi Turun ...

19

Tugas Mandiri Bab IV

………

20

BAB V Turunan Fungsi Transenden

5.1

Pendahuluan

………

22

5.2

Fungsi Logaritma Natural

………

22

5.3

Fungsi Eksponen

………

23

5.4

Fungsi Inversi Trigonometri ………

25

5.5

Fungsi Hiperbolik

………

27

5.6

Fungsi Inversi Hiperbolik ………

28

Tugas Mandiri Bab V

………

29

BAB VI Turunan Fungsi Berbagai Variabel

6.1

Geometri Fungsi Dua Variabel ………

31

6.2

Turunan Parsial Fungsi Dua Variabel ...

32

6.3

Turunan Parsial Lebih Tinggi ………

33

6.4

Turunan Fungsi Implisit

………

33

6.5

Bidang Singgung dan Garis Normal ……….

34

6.6

Menentukan Jenis Titik Ekstrim ………

35

6.7

Turunan Parsial Fungsi Parameter ………

35

6.8

Diferensial Total

………

36

Tugas Mandiri Bab VI

………

37

iii

DAFTAR GAMBAR

Halaman

Gambar 1.1

Sketsa Bilangan Real

………

1

Gambar 1.2

Skala Bilangan

………

1

Gambar 1.3

Interval Hingga ………

1

Gambar 1.4

Interval tak Hingga ………

1

Gambar 2.1 Grafik Fungsi y = – x + |x| ……..….………

5

Gambar 2.2

Grafik Fungsi f(x)

………

6

Gambar 2.3

Grafik Fungsi f(x)

………

6

Gambar 2.4

Segitiga ABC

………

7

Gambar 2.5

Fungsi y = sin x

………

7

Gambar 2.6

Fungsi y = cos x

………

7

Gambar 2.7

Fungsi y = tan x

………

8

Gambar 2.8

Grafik y = 2sin ½ (x + 1/3

π

_{) ………...….}

₈

Gambar 2.9

Grafik y = sin2x dan y = cosx .………...….

8

Gambar 3.1

Sketsa Limit Barisan ………

10

Gambar 4.1 Gradien Garis Singgung ...………...……

17

Gambar 4.2

Fungsi Naik, Stasioner dan Fungsi Turun .………

18

Gambar 4.3

Grafik Fungsi y = x

3

+ x

2

……….

18

Gambar 4.4 Grafik Fungsi y = x

3

– x

2

– 8x + 2 …………...………

19

Gambar 6.1 Paraboloida Eliptik

………

31

Gambar 6.2 Bola pusat di (0, 0,0) jari-jari r ...……….………...

31

Gambar 6.3

Elipsoida berpusat di (0, 0, 0) ……...………

31

Gambar 6.4

Hiperboloida berdaun satu ………...………

32

Gambar 6.5

Silinder Parabolik

………

32

Gambar 6.6

Hiperboloida berdaun dua ………...………

32

Gambar 6.7

Kerucut Eliptik

………

32

1

BAB I

SISTEM BILANGAN

1.1 Himpunan Bilangan Real

Himpunan bilangan real terdiri atas bilangan rasional dan irrasional. Rincian terlihat pada gambar 1.1

Dikenal juga bilangan imajiner yaitu √ –1. Paduan bilangan real dan bilangan imajiner disebut bilangan kompleks. Ditulis a + b√ –1, dimana a dan b bilangan real. Bila i = √ –1 maka ditulis menjadi a + bi. Sifat-sifat urutan bilangan:

1. Trikotomi : jika x dan y suatu bilangan, berlaku: x < y atau x = y atau x > y 2. Transitif : jika x < y dan y < z maka x < z

3. Penambahan : jika x < y jika dan hanya jika x + z < y + z 4. Perkalian : jika z positip maka x < y jika dan hanya jika xz < yz

jika z negatip maka x < y jika dan hanya jika xz > yz

Skala bilangan merupakan penampilan secara grafis dari himpunan bilangan real oleh simbol titik-titik pada sebuah garis. Garis tersebut dinamakan garis bilangan. Setiap bilangan dinyatakan hanya oleh satu titik, dan demikian pula sebuah titik hanya mewakili sebuah bilangan. Jika a dan b adalah dua bilangan berbeda dan a < b, maka a terletak di sebelah kiri b pada garis bilangan tersebut.

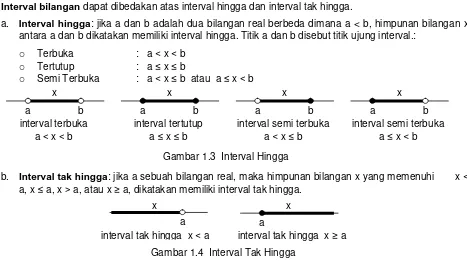
Interval bilangan dapat dibedakan atas interval hingga dan interval tak hingga.

a. Interval hingga: jika a dan b adalah dua bilangan real berbeda dimana a < b, himpunan bilangan x

antara a dan b dikatakan memiliki interval hingga. Titik a dan b disebut titik ujung interval.:

o Terbuka : a < x < b

o Tertutup : a ≤ x ≤ b

o Semi Terbuka : a < x ≤ b atau a ≤ x < b

b. Interval tak hingga: jika a sebuah bilangan real, maka himpunan bilangan x yang memenuhi x < a, x ≤ a, x > a, atau x ≥ a, dikatakan memiliki interval tak hingga.

x

a b

interval terbuka a < x < b

x

a b

interval tertutup a ≤ x ≤ b

x

a b

interval semi terbuka a < x ≤ b

x

a b

interval semi terbuka a ≤ x < b Gambar 1.3 Interval Hingga

Gambar 1.2 Skala Bilangan

– 4 – 3 – 2 – 1 0 1 2 3 4

π

2

1/2 -3/2

-5/2

Gambar 1.4 Interval Tak Hingga x

a interval tak hingga x < a

x a

interval tak hingga x ≥ a Gambar 1.1 Sketsa Bilangan Real

Bilangan rasional

Bilangan irrasional :

√

2 = 1,4242...., π = 3,14159..., dll. Bilangan real

bil. bulat

bil. pecahan b a

,

a dan b bulat

bil. bulat positip : 0, 1, 2, 3, 4, 5, …. bil. asli : 1, 2, 3, 4, 5, ….

2

1.2 Pertidaksamaan

Pernyataan a < b, a > b, a ≤ b, dan a ≥ b disebut pertidaksamaan dengan beberapa ketentuan, yaitu: (1) a > 0 jika dan hanya jika a positip

(2) a < 0 jika dan hanya jika a negatip (3) a > 0 jika dan hanya jika – a < 0 (4) a < 0 jika dan hanya jika – a > 0 (5) jika a < b dan b < c, maka a < c

(6) jika a < b dan c bilangan real, maka a + c < b + c (7) jika a < b dan c < d, maka a + c < b + d

(8) jika a < b dan c bilangan positip, maka ac < bc (9) jika a < b dan c bilangan negatip, maka ac > bc (10) jika 0 < a < b dan 0 < c < d, maka ac < bd

Teorema: | x |< a jika dan hanya jika – a < x < a dimana a > 0

| x |> a jika dan hanya jika x < – a atau x > a

Contoh : Tentukan himpunan penyelesaian pertidaksamaan berikut

1. – 5 ≤ 2x + 6 < 4 Jawab: – 11 ≤ 2x < – 2 → – 11/2 ≤ x < – 1 HP : { x : – 11/2 ≤ x < – 1 } 2. x2 – x < 6 Jawab: faktorisasi (x – 3)(x + 2) < 0 Titik pemecah x = – 2 dan x = 3

berdasarkan skema garis bilangan itu diperoleh HP : { x : – 2 ≤ x < 3 }

3. 3x2 – x – 2 > 0 Jawab: faktorisasi (3x + 2)(x – 1) > 0 , titik pemecah x = - 2/3 dan x = 1 berdasarkan skema garis bilangan itu diperoleh HP : { x : x < – 2/3 atau x > 1 }

4. 0

2 x

1 x

≥ +

−

Jawab:

Jangan mengalikan kedua ruas dengan x+2, sebab angka pengali itu bisa positip atau negatip, Ttitik pemecahnya yaitu x = – 2 dan x = 1.

untuk x = 1, nilainya 0 dan x = – 2, nilainya ∞ HP : { x : x < – 2 atau x ≥ 1 }

5. 1

2 x

5 x 2

≤ −

− _Jawab:

Jangan mengalikan kedua ruas dengan x – 2, tapi pindahkan angka 1 ke ruas kiri 0

1 2 x

5 x 2

≤ − −

−

→ 0

2 x

2 x 2 x

5 x 2

≤ − − − −

− _→

0

2 x

3 x

≤ − −

HP : { x : 2 < x ≤ 3 }

6. x3 – 5x2 + 4x ≤ 0 Jawab:

pertidaksamaan di atas dapat difaktorisasi menjadi x(x – 1)(x – 4) ≤ 0, sehingga terdapat 3 titik pemecah yaitu x = 0, x = 1, dan x = 4. Buat garis bilangan.

HP : { x : x ≤ 0 atau 1 ≤ x ≤ 4 }

7. (x + 1)(x – 1)2(x – 3) ≤ 0 Jawab: Ada 3 titik pemecah, yaitu x = – 1, x = 1, dan x = 3 HP : { x : – 1 ≤ x ≤ 3 }

– 2 3

0

₀

+ – +

2 3

∞ 0

+ – +

– 2/3 1

0 0

+ – +

– 2 1

∞ 0

+ – +

0 1

0 ₊ 0 – + 4

– 0

– 1 1

0 0

+ – +

3

8. Sebuah halaman berbentuk persegi panjang memerlukan pagar sepanjang 200 meter. Panjang salah satu sisinya adalah x meter.

Nyatakan luas L sebagai fungsi dari x. Tentukan pula daerah dari x. Jawab:

Panjang pagar = 200 m. Jika lebar = x m, panjang = 100 – x m. Luas y = panjang x lebar = x (100 – x).

Fungsi L = x(100 – x) syarat x > 0 dan 100 – x > 0 atau x < 100 Daerah x adalah 0 < x < 100 meter.

9. Sebuah kertas berukuran 10 x 14 cm akan dibuat kotak terbuka bagian atasnya. lalu kertas tersebut digunting ujung-ujungnya berbentuk bujur sangkar bersisi x.

Nyatakan volume kotak itu sebagai fungsi x dan tentukan daerah x. Jawab:

Berdasarkan sketsa di samping diperoleh: V = panjang x lebar x tinggi

V = (14 – 2x)(10 – 2x) x = 4(7 – x)(5 – x) x syarat volume > 0 atau V > 0, sehingga

4(7 – x)(5 – x) x > 0 Titik pemecah x = 0, x = 5, dan x = 7.

HP { x : 0 < x < 5 atau x > 7 } Namun x > 7 tidak mungkin sebab panjang = 14 – 2x akan menjadi negatip. Jadi daerah x adalah 0 < x < 5

1.3 Harga Mutlak

Harga mutlak | x | dari bilangan real x didefinisikan sebagai :

| x | = x jika x ≥ 0 dan

| x | = – x jika x < 0

Contoh :

1. Tentukan harga x yang memenuhi | 3x + 2 | = 5 Jawab: untuk 3x + 2 = 5, diperoleh x = 1

untuk – (3x + 2) = 5, atau – 3x – 2 = 5, diperoleh x = – 7/3 Jadi HP: { x: x = 1 atau x = – 7/3 }

2. Tentukan harga x yang memenuhi | 2x – 1 | = | 4x + 3 | Jawab: untuk 2x – 1 = 4x + 3, diperoleh x = – 2

untuk – (2x – 1) = 4x + 3, diperoleh x = – 1/3 Jadi HP: { x: x = – 2 atau x = – 1/3 }

3. Tentukan harga x yang memenuhi | 5x + 4 | = – 3

Jawab: Tidak ada harga x yang memenuhi sebab harga mutlak tidak mungkin negatip 4. Tentukan harga x yang memenuhi | x – 5 | < 4

Jawab: | x – 5 | < 4 sama dengan – 4 < x – 5 < 4 → 1 < x < 9. Jadi HP: { x: 1 < x < 9 }

5. Hitung: 13 + | – 1 – 4 | – 3 – | – 8 |

jawab: 13 + | – 1 – 4 | – 3 – | – 8 | = 13 + 5 – 3 – 8 = 7 6. Selesaikan | 3x – 5 |≥ 1

Jawab: untuk 3x – 5 ≤ – 1 diperoleh x ≤ 4/3 dan untuk 3x – 5 ≥ 1 diperoleh x ≥ 2 10 cm

14 cm x

x 14 – 2x

10 – 2x

0 5

0 ₊ – 0 +

7

– 0

4

TUGAS MANDIRI BAB I

Tugas Subbab 1.1

Sederhanakan

1.

Tugas Subbab 1.2

1. Tentukan nilai yang memenuhi 0

2. Suatu persegi panjang, panjangnya lebih 3 cm daripada lebarnya. Jika lebarnya x cm dan luasnya minimum 15 cm2, tentukan sistem pertidaksamaannya.

3. Jika y = 2x + 1 dan x2 – 8x + 15 < 0, tentukan nilai y yang memenuhi.

12. Selesaikan

x

14. Selesaikan

2

15. Selesaikan

3

Tugas Subbab 1.3

1. Jika | 2x – 3 | < 1 dan 2x < 3, tentukan x

5

BAB II

FUNGSI DAN GRAFIK

2.1 Pengertian Fungsi

Definisi : Fungsi f adalah suatu aturan padanan yang menghubungkan tiap obyek x dalam suatu himpunan, yang disebut daerah asal, dengan sebuah nilai unik f(x) dari himpunan kedua. Himpunan nilai yang diperoleh secara demikian disebut daerah hasil fungsi tersebut.

x disebut variabel bebas dan y = f(x) disebut variabel tak bebas. Contoh :

1. Diketahui f(x) = x2 – 2x, tentukan h

) 4 ( f ) h 4 (

f + −

Jawab: f(4) = 42 – 2.4 = 16 – 8 = 8

f(4+h) = (4+h)2 – 2(4+h) = 16 + 8h + h2 – 8 – 2h = 8 + 6h + h2

h ) 4 ( f ) h 4 (

f + −

= h

2 h h 6 +

= 6 + h

2. Diketahui g(x) = x 1

, tentukan

h ) a ( g ) h a (

g + −

Jawab:

h ) a ( g ) h a (

g + −

=

ah 2 a

1 h

1 . a ) h a (

h h

a 1 h a

1

+ − = +

− = − +

3. Jika f(x) = x2 – x maka tentukan f(x – 1)

Jawab f(x – 1) = (x – 1) 2 – (x – 1) = x2 – 2x + 1 – x + 1 = x2 – 3x + 2

Bila daerah asal tidak dirinci, berarti daerah asal itu adalah himpunan bilangan real terbesar, dimana aturan fungsi itu bermakna dan memberi nilai bilangan real. Daerah asal itu disebut daerah asal alamiah. Contoh:

1. Tentukan daerah asal alamiah untuk (a) f(x) = 3 x

1

− (b) g(t) = 9−t2 Jawab:

(a) daerah asal alamiah fungsi tersebut adalah x = seluruh bilangan real untuk x ≠ 3. (b) agar tidak menjadi bilangan imajiner, syaratnya 9 – t2≥ 0.

(3 + t)(3-t) ≥ 0. Titik pemecah t = – 3 dan t = 3, diperoleh – 3 ≤ t ≤ 3. Jadi daerah asal adalah HP: {t: – 3 ≤ t ≤ 3}

2. Diketahui : Daerah asal x = { – 4, – 3, – 2, – 1, 0, 1, 2} dan fungsi y = – x + | x | Tentukan : daerah hasil fungsi tersebut dan gambarkan grafiknya

Jawab: y = – x + | x |

x y

– 4 8

– 3 6

– 2 4

– 1 2

0 0

1 0

2 0

–4 –3 –2 –1 0 1 2 2 4 6 8

Fungsi y = – x +

x

sumbu x sumbu y

6

2.2 Menggambar Grafik

Beberapa fungsi khusus yang sering dijumpai adalah: a. Fungsi identitas : f(x) = x

b. Fungsi konstan : f(x) = a dimana a = konstanta c. Fungsi modulus (nilai mutlak) : f(x) = x jika x ≥ 0

–x jika x < 0 d. Fungsi tangga : 0 jika 0 ≤ x < 1

f(x) = 1 jika 1 ≤ x < 2 2 jika 2 ≤ x < 3

e. Fungsi linier : f(x) = ax + b, dimana a dan b konstanta

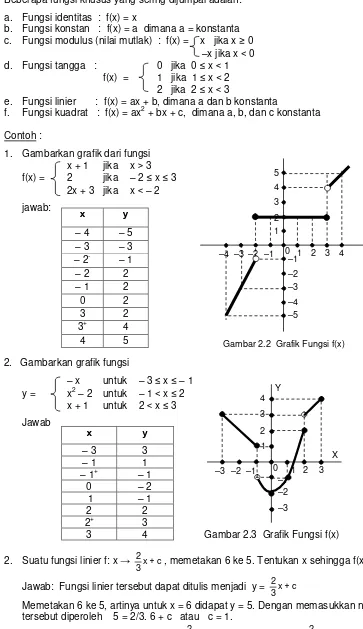
f. Fungsi kuadrat : f(x) = ax2 + bx + c, dimana a, b, dan c konstanta Contoh :

1. Gambarkan grafik dari fungsi x + 1 jika x > 3 f(x) = 2 jika – 2 ≤ x ≤ 3

2x + 3 jika x < – 2 jawab:

2. Gambarkan grafik fungsi

– x untuk – 3 ≤ x ≤ – 1 y = x2 – 2 untuk – 1 < x ≤ 2

x + 1 untuk 2 < x ≤ 3 Jawab

2. Suatu fungsi linier f: x → x c 3 2

+ , memetakan 6 ke 5. Tentukan x sehingga f(x) = 0

Jawab: Fungsi linier tersebut dapat ditulis menjadi y = x c 3

2 ₊

Memetakan 6 ke 5, artinya untuk x = 6 didapat y = 5. Dengan memasukkan nilai x dan y ke fungsi tersebut diperoleh 5 = 2/3. 6 + c atau c = 1.

Jadi persamaan tersebut adalah y = x 1 3

2 ₊

. Jika f(x) = 0, maka x 1 3

2 ₊

= 0, didapatkan x = – 2 3

x y

– 4 – 5

– 3 – 3 – 2- – 1

– 2 2

– 1 2

0 2

3 2

3+ 4

4 5

1 2 3 4 –2 –1

–3 –4

–1 –2 –3 1 2 3 4 5

0

–4 –5

Gambar 2.2 Grafik Fungsi f(x)

x y

– 3 3

– 1 1

– 1+ – 1

0 – 2

1 – 1

2 2

2+ 3

3 4 Gambar 2.3 Grafik Fungsi f(x) 0 1 2 3 –2 –1

–3

–1 –2 –3 1 2 3 4

7

2.3 Fungsi Trigonometri

Untuk mempelajari fungsi trigonometri, perlu diulang kembali rumus-rumus trigonometri : sin2x + cos2x = 1 1 + tan2x = sec2x 1 + cot2x = csc2x

Rumus penjumlahan Rumus pengurangan

sin(x + y) = sin x cos y + cos x sin y sin(x – y) = sin x cos y – cos x sin y cos(x + y) = cos x cos y – sin x sin y cos(x – y) = cos x cos y + sin x sin y tan(x + y) =

y tan x tan 1

y tan x tan

−

+ _{tan(x – y) =}

y tan x tan 1

y tan x tan

+ −

Rumus sudut ganda

sin 2x = 2 sin x cos x cos 2x = cos2 x – sin2 x = 1 – 2 sin2 x = 2 cos2 x – 1 tan 2x =

x tan x cot

2 1

x 2 cot

x cot 2 x 2 tan 1

x tan 2

− = − =

−

Rumus perkalian sin x cos y =

2 1

{sin(x+y) + sin(x – y)} sin x sin y = 2 1

{cos(x+y) – cos(x – y)}

cos x sin y = 2 1

{sin(x+y) – sin(x – y)} cos x cos y = 2 1

{cos(x+y) + cos(x – y)} Rumus faktor

sin x + sin y =

2 y x cos 2

y x sin

2 + − cos x + cos y =

2 y x cos 2

y x cos

2 + −

sin x – sin y =

2 y x sin 2

y x cos

2 + − cos x – cos y =

2 y x sin 2

y x sin

2 + −

−

Rumus Sinus Rumus Cosinus

γ = β =

α sin

c sin

b sin

a

a2 = b2 + c2 – 2 bc cos α b2 = a2 + c2 – 2 ac cos β

c2 = a2 + b2 – 2 ab cos γ

Persamaan

a. Jika sin x = sin a, maka . b. Jika cos x = cos a, maka

x = a + k.360o x = a + k.360o

x = (1800 – a) + k.3600 x = – a + k.360o

c. Jika tan x = tan a, maka x = a + k.180o d. Jika cot x = cot a, maka x = a + k.180o a. Fungsi Sinus :

Bentuk sederhana : y = sin x

dimana: x dalam satuan sudut atau radian y dalam satuan jarak

b. Fungsi Cosinus

Bentuk sederhana : y = cos x

dimana: x dalam satuan sudut atau radian y dalam satuan jarak

0o 90o 180o 270o 360o

Gambar 2.5 Fungsi y = sin x Y

X

0o 90o 180o 270o 360o

Gambar 2.6 Fungsi y = cos x Y

X

α β

γ C

B A

c

8

c. Fungsi Tangen

Bentuk sederhana : y = tan x

dimana: x dalam satuan sudut atau radian y dalam satuan jarak

Contoh :

1. Gambarkan sketsa grafik y = ) 3 1 x ( 2 1 sin

2 + π untuk interval 0o≤ x ≤ 360o. Jawab: 1/3 π = 60o

x y x y

0o 1 210o 1,414 30o 1,414 240o 1 60o 1,732 270o 0,518 90o 1,932 300o 0 120o 2 330o – 0,528 150o 1,932 360o – 1 180o 1,732

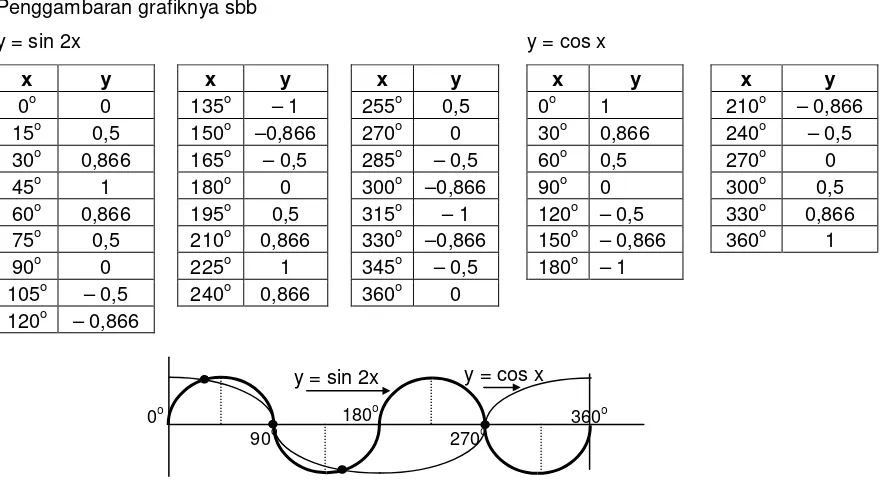
2. Tentukan titik potong persamaan y = sin 2x dan y = cos x dalam interval 0o≤ x ≤ 360o. Gambarkan sketsa kedua grafik dan titik potongnya.

Jawab

Bila kedua persamaan di atas dipotongkan diperoleh sin 2x = cos x atau sin 2 x = sin (90o – x) berdasarkan persamaan di atas diperoleh

a. 2x = 90o – x + k.360o didapat 3x = 90o + k.360o atau x = 30o + k.120o

untuk k = 0 maka x = 30o dan y = 0,866, untuk k = 1 maka x = 150o dan y = – 0,866 untuk k = 2 maka x = 270o dan y = 0

b. 2x = 180o – (90o – x) + k.360o didapat 2x = 90o + x + k.360o atau x = 90o + k.360o untuk k = 0 maka x = 90o dan y = 0

Jadi himpunan titik potong adalah { (30o, 0,866), (90o, 0), (150o, – 0,866), (270o, 0) } Penggambaran grafiknya sbb

y = sin 2x y = cos x

Gambar 2.9 Grafik y = sin 2x dan y = cos x

x y x y x y x y x y

0o 0 135o – 1 255o 0,5 0o 1 210o – 0,866

15o 0,5 150o –0,866 270o 0 30o 0,866 240o – 0,5 30o 0,866 165o – 0,5 285o – 0,5 60o 0,5 270o 0

45o 1 180o 0 300o –0,866 90o 0 300o 0,5

60o 0,866 195o 0,5 315o – 1 120o – 0,5 330o 0,866 75o 0,5 210o 0,866 330o –0,866 150o – 0,866 360o 1 90o 0 225o 1 345o – 0,5 180o – 1

105o – 0,5 240o 0,866 360o 0

120o – 0,866

0o 90o 180o 270o 360o

0 1

– 1

– 2 2

Gambar 2.8 Grafik y = ) 3 1 x ( 2 1 sin

2 + π

90o

180o

270o

360o 0o

y = sin 2x y = cos x

Gambar 2.7 Fungsi y = tan x X 00

1800 3600

Y

9

TUGAS MANDIRI BAB II

Tugas Subbab 2.1

1. Diketahui

2 2 x

1 x ) x ( f

+ −

= , hitung f(0), f(2a), dan f( x 1

)

2. Jika f(x) = 6 x

5 2 x 3

+ −

, hitunglah f(0) + 6f(2)

3. Jika f(x) = 6 x

5 2 x 3

+ −

, tentukan f(2) + 6 f(–3)

Tentukan daerah asal dari:

4. a. y = x2−16 b. y =

2 x 16

1 x 2 2 x

− + −

5. a. y = 1 2 x

1 2 x

+

− _{b. y =}

1 x

x 2 x

+ −

Tugas Subbab 2.2

1. Gambarkan sketsa grafik

a. y = x2 – 2x + 4 c. y = 2x2 – 4x + 3 b. y = x3 + x2 – 2x d. y = – 2x2 – 4x + 3 2. Gambarkan sketsa grafik

a. y =

5 x

) 3 x )( 2 x (

− −

− _{c. y = x}4

– 2 3. Gambarkan sketsa grafik

x2 + 1 jika x ≤ – 2 f(x) = 2x – x2 jika – 2 < x ≤ 1

x + 3 jika x > 1 4. Gambarkan sketsa grafik

x jika x ≤ – 2 f(x) = x3 – 1 jika – 2 < x ≤ 1

x2 + 3 jika x > 1 Tugas Subbab 2.3

A. Gambarkan sketsa grafik untuk 0o< x < 3600 1. y = sin x – cos x 2. y = 2 sin (x +

2

1_{π) + 1. 3. by = cos} 2

1 _x

4. y = 1 – cos 2x 5. x = sin 2y – 3 untuk 0o< y < 1800 B. Tentukan himpunan x untuk persamaan berikut

1. sin x = 0,5 untuk – 1800< x < 1800 4. sin x = cos 2x untuk 0o< x < 3600 2. cos x = 2

2

1 _{untuk 0}o_<

x < 7200 5. tan 2x = 3 3

1 _{untuk 0}o_<

x < 1800 C. Tentukan titik potong antara antara fungsi-fungsi berikut

1. y = sin 2x dengan y = cos x untuk – 1800< x < 1800 2. y = sin

2

1_{x dengan y = cos} 2

1_{x untuk 0}o_<

x < 7200 3. y = sin x + 1 dan y = – sin x – 1 untuk 0o< x < 3600 4. y = sin 3x dan y = 3

2

1 _{untuk 0}o_<

10

BAB III

LIMIT

3.1 Limit Fungsi Aljabar

Limit Barisan. Jika terdapat suatu barisan 1, 3/2, 5/3, 7/4, 9/5, …….., 2 – 1 /n, lalu diplotkan pada garis bilangan, maka untuk n sangat besar mendekati tak hingga, nilainya akan mendekati 2.

Dikatakan bahwa limit barisan adalah 2 atau ditulis: lim u lim (2 1/n) 2 n

n

n→∞ = →∞ − =

Gambar 3.1 Sketsa Limit Barisan

Limit Fungsi. Jika diketahui fungsi f(x) = x2, maka untuk x mendekati 2, fungsi akan bernilai 4. Bila fungsi itu disajikan dalam tabel akan terlihat sebagai berikut

x 1,9 1,99 1,999 1,9999 1,99999 1,999999 ... y 3,61 3,9601 3,996 3,9996 3,99996 3,999996 ...

Perhatikan, saat x semakin mendekati dua, maka y semakin mendekati 4. Secara matematis dituliskan sebagai

:

2 xlim ) x ( f 2

xlim→ = → x

2 = 4

Limit Kiri dan Limit Kanan

Jika x mendekati a dari kiri, ditulis x → a– disebut limit kiri Jika x mendekati a dari kanan, ditulis x → a+ disebut limit kanan

misalnya x → 2– maka nilai a = 1,9 1,99 1,999 1,9999 dan seterusnya x → 2+ maka nilai a = 2,1 2,01 2,001 2,0001 dan seterusnya

Gambar 3.2 Limit kiri dan limit kanan

Suatu fungsi dikatakan mempunyai limit jika limit kiri dan limit kanan ada dan bernilai sama. )

x ( f a x

lim − →

ada, berarti fungsi mempunyai limit kiri

) x ( f a x

lim + →

ada, berarti fungsi mempunyai limit kanan Jadi, f(x)

a xlim→

ada, berarti fungsi mempunyai limit kiri dan kanan dan bernilai limit sama

Contoh :

1. Tentukan limit untuk barisan berikut:

3, 5/2, 7/3, 9/4, 11/5, …….., 2+1/n, ……… Jawab : ) n 1 2 ( n

lim n u n

lim +

∞ → = ∞

→ = 2

2.

2 9 6 27 3

x 9 x 3 2 x 3 x

lim )

3 x )( 3 x (

) 9 x 3 2 x )( 3 x ( 3 x

lim 9 2 x

27 3 x 3 x

lim = =

+ + + → = + −

+ + − → = − − →

Perhatian! Pernyataan x a berarti x ≠ a

2

mendekati 2 dari kiri mendekati 2 dari kanan

0 1 2

11

3.2 Limit Fungsi Trigonometri

Dalam limit fungsi trigonometri dinyatakan persamaan sebagai berikut:

12

3.3 Kontinuitas

Fungsi f(x) disebut kontinu di x = x0, jika a. f(x0) terdefinisi

b. o x

x→lim f(x) ada c.

o x

x→lim f(x) = f(x0) Contoh :

Selidiki apakah fungsi berikut kontinu. Jika tidak, di titik mana fungsi tersebut diskontinu. 1. Fungsi

  

> −

≤ +

=

1 x untuk x 3

1 x untuk x 3 ) x ( f

Jawab: Melihat fungsi di atas, titik yang perlu diselidiki adalah di x = 1 a. Fungsi f(x0) = f(1) = 3 + 1 = 4 → fungsi tersebut ada untuk x = 1 b.

0 x x→lim

f(x) = − →1 x

lim 3 + x = 4 (limit kiri) 0 x x→lim

f(x) = + →1 x

lim 3 – x = 2 (limit kanan)

Karena limit kiri ≠ limit kanan, berarti tidak ada limit (syarat kedua tidak terpenuhi) Kesimpulan : fungsi tersebut diskontinu di x = 1

2. Fungsi

2 x

4 2 x ) x ( f

− −

= Jawab:

Titik yang perlu diselidiki adalah x = 2 dan x = – 2 Untuk x = 2

a. Fungsi f(x0) = f(2) =

0 0 2 2

4 4

= − −

= tak terdefinisi

syarat pertama tak terpenuhi. Jadi, fungsi diskontinu di x = 2 Untuk x = – 2

a. Fungsi f(x0) = f(–2) = 0 4 0 2 2

4 4

= − = − −

− _{→ fungsi tersebut ada untuk x = – 2}

b. 0 x x→lim

f(x) = 2 x→lim− x 2

4 2 x

− −

= 2

x→lim− x 2 ) 2 x )( 2 x (

− −

+ ₌

2 x→lim−

(x + 2) = 0

c. 0 x

x→lim f(x) = f(x0) = 0

Karena memenuhi ketiga syarat, maka fungsi kontinu di x = – 2

3. Fungsi f(x) =

1 x

5 x 4 2 x

− − +

untuk x ≠ ₁

6 untuk x = 1 Jawab: Titik yang perlu diselidiki adalah x = 1

a. Fungsi f(x0) = f(1) = 6

b. 0 x x→lim

f(x) = 1

xlim→ x 1 5 x 4 2 x

− − +

= 1

xlim→ x 1

) 1 x )( 5 x (

− −

+ _{= 6}

c. 0 x

x→lim f(x) = f(x0) = 6

13

TUGAS MANDIRI BAB III

Tugas Subbab 3.1

Hitunglah :

1.

Hitunglah:

1.

Selidiki kontinuitas fungsi-fungsi berikut dan gambarkan sketsa grafiknya

14

BAB IV

TURUNAN / DIFERENSIAL

4.1 Definisi Turunan

Turunan fungsi y = f(x) terhadap x di titik x = x0 didefinisikan sebagai:

x

3. Lintasan dengan persamaan s = t2 + 3t. Hitunglah kecepatan sesaat waktu t = 2 Jawab :

Kecepatan sesaat = dt Jadi kecepatan sesaat = 7 satuan kecepatan

4. Lintasan dengan persamaan s = (3t2 + 5) m dengan waktu t berubah dari 2 sampai 3 detik. Hitunglah kecepatan rata-rata.

15

4.2 Turunan Fungsi Aljabar

a. Turunan Fungsi y = axn

Jika diketahui suatu fungsi f(x) = axn, maka turunan pertama dari fungsi tersebut adalah: f’(x) = dan seterusnya

f(x) = ax, turunannya f’(x) = a f(x) = ax2, turunannya f’(x) = 2ax f(x) = ax3, turunannya f’(x) = 3ax2 Jadi: f(x) = axn, turunannya f’(x) = naxn-1

Contoh: Tentukan turunan dari fungsi berikut 1. f(x) = 23 2x Jawab : f(x) = 3

b. Turunan Fungsi dari Fungsi

Jika y = f(u) dan u = g(x), maka y = f{g(x)} adalah fungsi dari x. Jika y fungsi yang dapat diturunkan terhadap u dan u dapat diturunkan terhadap x, maka y = f{g(x)} adalah fungsi yang dapat diturunkan terhadap x.

Demikian pula, jika y = f(t) sedangkan x = g(t), maka turunan y terhadap x

16

c. Turunan Fungsi Lebih Tinggi

Jika y = f(x) adalah fungsi yang dapat diturunkan, turunannya disebut turunan pertama. Jika turunan pertama dapat diturunkan lagi maka turunannya disebut turunan kedua.

Ditulis

Demikian seterusnya turunan dari turunan kedua disebut turunan ketiga dinyatakan dengan

3

Contoh:

Jika y = 4x4 – x3 + 6x2 – 7x + 8 Tentukan

d. Turunan Fungsi Implisit

Persamaan f(x,y) = 0 pada suatu daerah tertentu menentukan y sebagai fungsi implisit dari x. Turunan y’ dapat diperoleh dengan salah satu cara berikut:

a. Jika mungkin, ubahlah fungsi implisit tersebut menjadi fungsi eksplisit y = g(x). Kemudian turunkan dengan cara biasa.

b. Pikirkan y sebagai fungsi x. Turunkan persamaan implisit tersebut terhadap x dan persamaan yang diperoleh diselesaikan untuk y’. Proses penurunan ini disebut penurunan implisit.

Contoh: Hitung

4.3 Turunan Fungsi Trigonometri

Turunan fungsi trigonometri y = sin x dapat diperoleh sebagai berikut:

f’(x) =

17

Berikut adalah hasil turunan dari fungsi trigonometri:

1. Fungsi y = sin u → dx dy

= cos u dx du

4. Fungsi y = cot u → dx dy

= –

csc

2u dx du

2. Fungsi y = cos u → dx dy

= – sin u dx du

5. Fungsi y = sec u → dx dy

= tan u sec u dx du

3. Fungsi y = tan u → dx dy

=

sec

2u dx du

6. Fungsi y = csc u → dx dy

= – cot u csc u dx du

Contoh : Hitunglah dx dy

untuk fungsi-fungsi berikut 1. y = x2 sin x Jawab :

dx dy

= 2x sin x + x2 cos x 2. y = tan2(3x2 – 2) Jawab :

dx dy

= 2 tan(3x2 – 2) sec2 (3x2 – 2) (6x) = 12x tan(3x2 – 2) sec2 (3x2 – 2) 3. sin y + cos x = 1 Jawab : cos y

dx dy

– sin x = 0 → dx dy

= y cos

x sin

4. sin y = cos 2x Jawab : cos y dx dy

= – 2sin 2x → dx dy

= y cos

x 2 sin 2 −

5. x cos y = sin(x+y) Jawab : cos y – x sin y dx dy

= cos(x+y) dx dy

+ cos(x+y) {– x sin y – cos(x+y)}

dx dy

= – cos y + cos(x+y) → dx dy

=

) y x cos( y sin x

) y x cos( y cos

+ +

+ −

4.4 Gradien Garis Singgung

Titik P(x, f(x)) adalah sebarang titik yang terletak pada kurva y = f(x). Garis singgung kurva pada titik P adalah garis lurus melalui P dengan gradien m, dimana: m = f’(x) =

dx dy

=

h ) x ( f ) h x ( f 0 h

lim + −

→ , jika limit itu ada.

Gambar 4.1 Gradien Garis Singgung Contoh soal:

1. Tentukan persamaan garis singgung pada kurva y =

3

x

2

−

5

x

di titik (1, – 2). Jawab: Gradien garis singgung kurva m =

dx dy

= 6x – 5. Pada titik (1, – 2), maka m = 6.1 – 5 = 1 Persamaan garis garis singgung dengan m = 1 dan melalui (1, – 2) adalah:

y – y1 = m (x – x1) → y – (– 2) = 1 (x – 1) → y = x – 3 adalah pers. garis singgung tsb. 2. Tentukan persamaan garis singgung pada kurva y =

2

x

2

−

x

+

3

sejajar garis y = 3x – 2

Jawab:

Gradien garis singgung kurva m1 = dx dy

= 4x – 1 sejajar berarti m1 = m2 Gradien garis y = x – 3 adalah m2 = 3 4x – 1 = 3, atau x = 1

Untuk x = 1, maka pada kurva y =

2

x

2

−

x

+

3

didapat y = 4. Jadi titik singgungnya (1,4) PGS yang diminta adalah: y – 4 = 3 (x – 1) → y = 3x + 1

f(x) f(x+h)

0 x

h x + h P(x, f(x))

Q(x+h, f(x+h)) y = f(x)

18

3. Tentukan persamaan garis singgung pada kurva y = x melalui titik (– 4, 0) Jawab: Kurva y = x, gradien garis singgung m =

dx dy

= x 2

1

Pers. garis menyinggung kurva di (x, x), melalui (– 4, 0) dengan m = x 2

1

y2 – y1 = m (x2 – x1) → 0 – x = x 2

1

(– 4 – x) kedua ruas dikalikan x, didapat – 2x = – 4 – x sehingga – x = – 4 atau x = 4

Untuk titik singgung x = 4 didapat y = 4 = 2, dan m = 4 2

1 =

4 1

Jadi, pers. garis singgungnya: y – 2 = 4 1

(x – 4) atau y = 4 1

x + 1

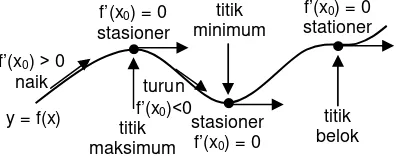
4.5 Fungsi Naik, Stasioner, dan Fungsi Turun

Ada 3 keadaan kurva berkaitan sifat turunannya, yaitu: 1. Jika f’(x0) > 0, fungsi y = f(x) naik di titik x = x0 2. Jika f’(x0) < 0, fungsi y = f(x) turun di titik x = x0 3. Jika f’(x0) = 0, fungsi y = f(x) stationer di titik x = x0

Gambar 4.2 Fungsi Naik, Stasioner, dan Fungsi Turun

Terdapat juga tiga keadaan titik stasioner berkaitan dengan turunan kedua fungsi, yaitu: a. Jika f’(x0) = 0 dan f”(x0) > 0, maka titik stasioner (x0, y0) adalah titik minimum

b. Jika f’(x0) = 0 dan f”(x0) < 0, maka titik stasioner (x0, y0) adalah titik maksimum c. Jika f’(x0) = 0 dan f”(x0) = 0, maka titik stasioner (x0, y0) adalah titik belok Contoh soal :

1. Tentukan titik-titik ekstrim pada persamaan y = x3 + x2 . Gambarkan sketsanya Jawab:

Turunan fungsi f’(x) = 3x2 + 2x = x (3x + 2)

Titik ekstrim terjadi jika f’(x) = 0, sehingga x (3x + 2) = 0.

Didapat x = 0 atau x = – 2/3. Untuk x = 0, maka y = 0, untuk x = – 2/3, maka y = 4/27 Jadi titik ekstrim terdapat pada titik (0, 0) dan titik (– 2/3, 4/27)

Untuk menyelidiki jenis titik ekstrim tersebut dihitung f”(x) = 6x + 2 Untuk titik (0, 0) diperoleh f”(x) = 2 > 0, titik tersebut adalah titik minimum

Untuk titik (– 2/3, 4/27) diperoleh f”(x) = – 2 < 0, titik tersebut adalah titik maksimum Sketsa grafik untuk kurva tersebut sebagai berikut

Gambar 4.3 Grafik y = x3 + x2 titik

maksimum

titik minimum

titik belok y = f(x)

f’(x0) > 0

naik _turun

f’(x0)<0

stasioner f’(x0) = 0

f’(x0) = 0 stationer f’(x0) = 0

stasioner

X Y

2

0 _{1 2}

– 1

– 1 – 2

1

titik minimum (0, 0)

19

2. Diketahui persamaan y = x3 – x2 – 8x + 2. Tentukan interval fungsi y naik dan turun. Gambarkan sketsa grafiknya

Jawab:

y = x3 – x2 – 8x + 2, fungsi naik jika dx dy _>

0 dan fungsi turun jika dx dy _<

0

dx dy

= 3x2 – 2x – 8 = (3x + 4) (x – 2). Titik pemecah x =

3

4

−

dan x = 2

Fungsi naik saat dx dy _>

0 dan fungsi turun saat f’(x ) < 0 Dari sketsa di samping diperoleh kesimpulan bahwa Fungsi naik untuk x <

3 4

− atau x > 2

Fungsi turun untuk 3 4

− < x < 2

Untuk menyelidiki sifat titik x = 3 4

− dan x = 2, maka dihitung 2 dx

y 2 d

= 6x – 2

Untuk x = 3 4

− diperoleh 2 dx

y 2 d

= – 10 < 0, maka titik tersebut adalah titik maksimum

Untuk x = 2 diperoleh 2 dx

y 2 d

= 10 > 0, maka titik tersebut adalah titik minimum

Untuk x = 3 4

− , didapat y = 27 230

dan untuk x = 2, didapat y = – 10. Jadi (

3 4 − ,

27 230

) adalah titik maksimum, sedangkan (2, – 10) adalah titik minimum Sketsa grafik untuk kurva tersebut sebagai berikut

Gambar 4.4 Grafik y = x3 – x2 – 8x + 2

3. Bagilah bilangan 150 menjadi 2 bagian sehingga perkalian bagian pertama dengan kuadrat bagian kedua menjadi bernilai maksimum. Tentukan nilai kedua bilangan itu.

Jawab :

Misalnya bilangan bagian kedua = x, maka bagian pertama = 150 – x

Jadi fungsinya menjadi f(x) = (150 – x) x2. Fungsi ini harus bernilai maksimum. Harga ekstrim terjadi jika f’(x) = 0, sehingga 300 x – 3 x2 = 0

Persamaan menjadi 3x (100 – x) = 0 didapat x = 0 dan x = 100. (x = 0 tidak memenuhi) f”(x) = 300 – 6x, untuk x = 100, maka f”(x) = – 300 < 0, jadi x = 100 bernilai maksimum. Jadi bilangan bagian pertama = 150 – 100 = 50 dan bagian kedua = 100.

(2, – 10) titik minimum (-4/3, 230/27)

titik maksimum

X

Y

0

y = x3 – x2 – 8x + 2

3 4

− 2

20

TUGAS MANDIRI BAB IV

Tugas Subbab 4.1

1. Hitung x y ∆ ∆

jika diberikan y = x2 + 4x dan x berubah dari 0,7 menjadi 0,85.

2. Tentukan kecepatan rata-rata jika t berubah dari 2 sampai 5 detik dan s = (2t2 + 5t – 3) m. 3. Tentukan turunan dari y =

1 x 2

1 x 2

+ −

4. Tentukan kemiringan dari kurva y = 1 x

4

+ di titik x = 1

5. Tentukan kemiringan garis singgung parabola y = – x2 + 5x – 6 di titik parabola memotong sumbu x.

Tugas Subbab 4.2

1. Tentukan dx

dy _{dari fungsi berikut}

a. y = 2x+2 x c. x = y + 5 e. x+ y = 1 b. y =

3 x2 1

d. y =

5 x

1 3

x −

2. Tentukan turunan dx dy

dari

a. y = (x3+6x−2)3 e.

1 3 x 2

1 3 x y

+ −

= i.

1 x

1 x y

+ − =

b. y = (x2+4)3(2x3−1)2 f. y=(x2+x+1)(2x2+3x) j. y= 2x+ 2x c. y = (x2−3)4 g.

2 ) 5 3 x (

) 2 2 x 3 ( ) 1 x 2 ( y

+ − +

= k.

x 4

3 ₄

x 6

y= +

d. y =

2 ) 2 x 2 a (

3

− , a konstan h.

2

x 1

x

y 

    

+

= l. y=2x2 2−x

3. Tentukan turunan dx dy

dari fungsi implisit berikut

a. x2y−xy3+3x2+2y2=0 c. y= xy+ xy e. xy3−x2y+x2−5x+6=0

b. 2

2 y x 2

y 3

x ₌

+ −

d. x4+3y−4x3y3=5x+1

4. Diketahui f(x)=2x3+9x2−24x+5. Jika f’(x) < 0, tentukan nilai x 5. Tentukan turunan pertama dan kedua dari persamaan berikut:

a. x3y+xy3 =2 untuk x = 1 b. x + xy + y = 2

Tugas Subbab 4.3

1. y = 2

1 _{tan x sin 2x 4. y = x (3 x + 4 cos x) 7. y =}

x cos x sin

x

+ 10. y = sinx cosx x sin x

+

2. y =

x 4 sin 1

x 4 cos

− 5. y = x sinx

x

+ 8. y = sinx cosx

x sin

+

3. y = tanx 6. y =

x cos 1

x sin x

+

+ _{9. y =}

x cos x sin

x cos x sin

21

Tugas Subbab 4.4

Tentukan persamaan garis singgung pada kurva : 1. y = 2x2 + 3 sejajar garis 8x – y + 3 = 0

2. y = 9 – x2 melalui titik di luar kurva (0, 11) 3. y =

2 x 2

1

melalui titik di luar kurva (1, – 2)

4. y = 3 x melalui titik singgung (8,2)

5. y = x (x – 1) (x – 2) di titik potong kurva dengan sumbu X. 6. y = (4x – 3)2 – 1 tegak lurus garis x + 2y – 11 = 0

7. Tentukan kedudukan titik-titik pada kurva y = 2 x3 + 13 x2 + 5x + 9 dimana garis singgung di titik-titik tersebut melalui (0, 0)

8. Jika garis singgung pada kurva y = ) x x b a

( + di titik (4, 8) mempunyai gradien 2, tentukan harga a dan b

Tugas Subbab 4.5

1. Selidiki apakah persamaan y = 2 x

1

− mempunyai nilai maksimum atau minimum. Tentukan pula interval fungsi y naik atau turun. Gambarkan sketsa grafiknya.

2. Selidiki fungsi y = 3x4−10x3 −12x2+ 60x−7 untuk titik belok, interval fungsi naik atau turun, serta titik maksimum dan minimum. Gambarkan sketsa grafiknya

3. Sebatang kawat 60 meter dipotong menjadi 2. Satu potong dibentuk menjadi lingkaran dan potongan kedua menjadi bujur sangkar. Agar luas kedua bentuk itu maksimum, tentukan panjang masing-masing potongan kawat tersebut.

4. Selembar karton berukuran 100 x 140 cm akan dibuat menjadi sebuah kotak tanpa tutup. Setiap sudut karton dipotong berbentuk bujur sangkar. Jika ingin diperoleh volume kotak maksimum, tentukan tinggi kotak tersebut.

5. Ongkos produksi x buah TV per hari Rp ( x2 35x 25 4

1 _{+ + ), harga jual total Rp (50 –} 2

1_{x). Berapa} buah televisi harus diproduksi per hari agar keuntungannya maksimum?

6. Diberikan y =

x

x

2

6

x

8

2

1 3 3

1

₊

₋

₊

_{. Tentukan titik-titik kritis, interval y naik dan turun, dan nilai} maksimum dan minimum. Gambarkan sketsa grafiknya.

7. Tunjukkan bahwa y = x3 – 8 tidak memiliki titik maksimum maupun minimum. 8. Tunjukkan bahwa y = x5 + 20 x – 6 adalah fungsi naik untuk semua nilai x. 9. Tunjukkan bahwa y = 1 – x3 – x7 adalah fungsi turun untuk semua nilai x.

10. Jika dalam sebuah lingkaran berjari-jari r akan digambarkan sebuah trapesium yang alasnya 2r dengan luas maksimum, buktikan luas trapesium itu = r2 3

4

3 _.

11. Tentukan titik maksimum dan minimum dari 2x2 – 4xy + 3y2 – 8x + 8y – 1 = 0.

12. Tentukan nilai absolut maksimum dan minimum dari y = (x – 3)2 dalam interval 0 ≤ x ≤ 4. 13. Tentukan persamaan garis melalui titik (3, 4) yang memotong kuadran pertama dalam bentuk

22

BAB V

TURUNAN FUNGSI TRANSENDEN

5.1 Pendahuluan

Salah satu fungsi non aljabar adalah fungsi transenden. Fungsi transenden mencakup antara lain fungsi logaritma, fungsi eksponen, fungsi trigonometri, dan fungsi hiperbolik

5.2 Fungsi Logaritma Natural

Dalam matematika dikenal bentuk logaritma natural : ln x = elogx dimana : e = (1 k)1/k bilangan e adalah irasional dan tak terukur

Telah dibuktikan secara matematis bahwa fungsi y = ln x turunannya dx

Catatan : Aturan dalam logaritma natural mirip logaritma biasa, yaitu: a. ln (ab) = ln a + ln b c. ln ab = b ln a b. ln

b a

= ln a – ln b d. ln e = 1 Contoh soal:

Tentukan turunan dari

b. Diferensiasi menggunakan logaritma natural

Diferensiasi secara logaritmik adalah membuat kedua ruas menjadi fungsi logaritma natural, sehingga menjadi ln y = ln f(x). Kedua ruas lalu diturunkan menjadi:

23

Contoh soal: Tentukan turunan dari 1. y = 2 log (x2 – 1) Jawab:

5.3 Fungsi Eksponen

Fungsi eksponen ada dua jenis, yaitu y = ex atau y = eu dan y = ax atau y = au Teorema: Jika a dan b adalah bilangan real maka berlaku:

ea + b = ea . eb ea – b = ea / eb eab = (ea)b = (eb)a

ax = ex ln a sehingga ln ax = x ln a Catatan

e adalah singkatan dari nama seorang ahli matematika dan fisika berkebangsaan Swiss, Leonhard Euler. a. Turunan fungsi y = ex

Fungsi y = ex diubah menjadi ln y = ln ex → ln y = x ln e → ln y = x. Jika fungsi tersebut diturunkan didapat, 1

24

b. Turunan fungsi y = ax

Fungsi y = ax diubah menjadi ln y = ln ax → ln y = x ln a. Jika diturunkan didapat, =

dx dy y 1

ln a atau = dx dy

y ln a = ax ln a

Jadi y = ax turunannya adalah = dx dy

ax ln a y = au turunannya adalah =

dx dy

au ln a dx du

Contoh soal:

Tentukan turunan dari y = 24x−1 Jawab: y = 24x−1 maka turunannya =

dx

dy ₂4x−1 _{ln 2 . 4 = 2}4x+1 _{ln 2}

c. Turunan fungsi y = xx dan f(x) = g(x)h(x)

Ada perbedaan antara fungsi pangkat dan fungsi eksponen, yaitu:

Fungsi pangkat : y = xa atau y = ua dimana bilangan pokok x atau u adalah variabel dan bilangan pangkat a tetap

Fungsi eksponen : y = ex atau y = eu dan y = ax atau y = au dimana bilangan pokok e atau a tetap dan bilangan pangkat x atau u adalah variabel

Namun, fungsi y = xx dan f(x) = g(x)h(x) bukanlah fungsi pangkat maupun eksponen, sebab bilangan pokok dan bilangan eksponen adalah variabel. Oleh karena itu, turunan untuk fungsi ini tidak boleh

menggunakan turunan untuk fungsi pangkat maupun eksponen. Untuk menurunkannya kedua ruas harus dijadikan logaritma natural.

Contoh soal: Tentukan turunan fungsi berikut 1. y = xx

Jawab: Ubah menjadi logaritma natural ln y = x ln x, turunkan x

x x ln dx dy y

1 _{= +}

= ln x + 1 Jadi y(lnx 1) xx(lnx 1) dx

dy _{= + = +}

2. y = xx2−2x → ln y = (x2 – 2x) ln x diturunkan x

1 ) x 2 2 x ( x ln ) 2 x 2 ( dx dy y

1 _{= − + −}

=

dx

dy

_x2 _2x

x − (2x ln x – 2 ln x + x – 2) Contoh soal esai:

1. Dalam suatu kondisi tertentu, laju pertumbuhan bakteri dinyatakan sebanding dengan jumlah bakteri yang ada. Jika ada 1000 bakteri saat ini, lalu 12 menit kemudian bertumbuh menjadi 2000 bakteri. Berapa lamakah bakteri tersebut menjadi 1.000.000?

Jawab:

Misal A = jumlah bakteri saat t, t = waktu, k = konstanta, dan dt dA

= laju pertumbuhan bakteri, maka laju pertumbuhan bakteri dinyatakan sebagai

dt dA

= k.A atau A dA

= k dt. Kedua ruas diintegralkan menjadi:

∫ = ∫ kdt

A dA

menghasilkan ln A = kt + C1 atau A = ekt+C1 = ekt eC1 Jika eC1 = C, didapat persamaan A = C kte

25

2000 = 1000.e12 k sehingga e12 k = 2 → 12k = ln 2 → k = 12

2 ln

= 0,05776 Jadi untuk A = 1.000.000, C = 1.000, dan k = 0,05776,

1.000.000 = 1.000 e0,05776t → e0,05776t = 1000 → 0,05776 t = ln 1000 t =

05776 , 0

1000 ln

= 119, 6. Jadi waktu yang diperlukan = 119, 6 menit

2. Sebatang besi panjangnya L meter pada suhu t dengan persamaan L = 60 e0,0001t. Hitung pertambahan panjang batang besi tersebut jika suhunya berubah dari 00 menjadi 250. Jawab:

L = 60 e0,0001t turunannya adalah

dt

dL

= 60 e0,0001t. 0,0001 Jadi perubahan panjang terhadap suhu dL = 0,006 e0,0001t dt Diketahui t1 = 0

0

, t2 = 25 0

, maka dt = 250 – 00 = 250, maka dL = 0,006 e0,0001x0 25 = 0,150 meter

5.4 Fungsi Inversi Trigonometri

Definisi untuk fungsi inversi trigonometri sebagai berikut:

a. y = arc sin x jika dan hanya jika siny = x untuk – π/2 ≤ y ≤π/2 b. y = arc cos x jika dan hanya jika cos y = x untuk 0 ≤ y ≤π c. y = arc tan x jika dan hanya jika tan y = x untuk – π/2 < y <π/2 d. y = arc cot x jika dan hanya jika cot y = x untuk 0 < y <π

e. y = arc sec x jika dan hanya jika sec y = x untuk – π≤ y ≤ – π/2, 0 ≤ y <π/2 f. y = arc csc x jika dan hanya jika csc y = x untuk – π≤ y ≤ – π/2, 0 < y ≤π/2

a. Turunan Fungsi y = arc sin x

y = arc sin x → sin y = x, kedua ruas diturunkan cos y dy = dx atau

y cos

1 dx dy ₌

sin y = x dan cos y = 1−x2 maka,

y cos

1 dx dy

= =

2 x 1

1

−

Jadi untuk y = arc sin x turunannya adalah _dxdy =

2 x 1

1 −

Secara umum y = arc sin u turunannya adalah = dx dy

dx du 2 u 1

1

−

b. Turunan Fungsi y = arc cos x

y = arc cos x → cos y = x, kedua ruas diturunkan – sin y dy = dx atau

y sin

1 dx dy ₌ −

cos y = x dan sin y = 1−x2 maka,

y sin

1 dx dy ₌ −

=

2 x 1

1

− −

Jadi untuk y = arc cos x turunannya adalah = dx dy

2 x 1

1 − −

Secara umum y = arc cos u turunannya adalah = dx dy

–

dx du 2 u 1

1

− y

1 x

2 x 1−

y 1

x

26

c. Turunan Fungsi y = arc tan x

y = arc tan x → tan y = x, kedua ruas diturunkan sec2 y dy = dx atau

y 2 sec

1 dx dy

=

tan y = x dan sec y =

x

2

+

1

maka,

y 2 sec

1 dx dy

= =

1 2 x

1 +

Jadi untuk y = arc tan x turunannya adalah = dx dy

1 2 x

1 +

Secara umum y = arc tan u turunannya adalah = dx dy

dx du

1 2 u

1 +

d. Turunan Fungsi y = arc cot x

y = arc cot x → cot y = x, kedua ruas diturunkan csc2 y dy = dx atau

y 2 csc

1 dx

dy −

=

cot y = x dan csc y =

x

2

+

1

maka,

y 2 csc

1 dx

dy −

= =

1 2 x

1 + −

Jadi: y = arc cot x turunannya adalah = dx dy

– 1 2 x

1 +

Secara umum y = arc cot u turunannya adalah = dx dy

–

dx du 1 2 u

1 +

e. Turunan Fungsi y = arc sec x

y = arc sec x → sec y = x, kedua ruas diturunkan sec y tan y dy = dx atau

y tan y sec

1 dx

dy

=

sec y = x maka tan y = x2−1

y tan y sec

1 dx

dy

= =

1 2 x x

1 −

Jadi: y = arc sec x turunannya adalah = dx dy

1 2 x x

1 −

Secara umum y = arc sec u turunannya adalah = dx dy

1 2 u u

1 − dx

du

f. Turunan Fungsi y = arc csc x

y = arc csc x → csc y = x, kedua ruas diturunkan – csc y cot y dy = dx atau

y cot y csc

1 dx

dy −

=

csc y = x maka cot y = x2−1

y cot y csc

1 dx

dy ₌ −

=

1 2 x x

1

− −

Jadi: y = arc csc x turunannya adalah = dx dy

–

1 2 x x

1 −

Secara umum y = arc csc u turunannya adalah = dx dy

–

1 2 u u

1 − dx

du y

x

1

1 2

x −

y x

1 1 2

x −

y x

1 1

2

x +

y 1

1 2

x +

27

Contoh : Tentukan turunan dari

1. y = arc cot 

5.5 Fungsi Hiperbolik

a. Definisi fungsi hiperbolik

1. Sinus hiperbolik : sinh x = Persamaan dasar mirip dengan fungsi trigonometri biasa:

Fungsi Hiperbolik Fungsi Trigonometri a. tanh x = b. Turunan Fungsi Hiperbolik

28

Secara umum: a. y = sinh u →

Contoh : Tentukan turunan dari 1. y = tanh (1 – x2) Jawab :

5.6 Fungsi Inversi Hiperbolik

29

TUGAS MANDIRI BAB V

Tugas Subbab 5.2

A. Tentukan turunan dari:

1. y = ln {(4x2 + 3) (2x – 1)} 6. y = ln cos2x 2. y = ln (x3 + 2) (x2 + 3) 7. y = (x2 – 2) ln sin x 3. y = ln

2 ) 4 x 3 (

4 x

− 8. xy + y ln x – ln y = 0 4. y = {ln (x3 – 4)2}3 9. xy (ln y + ln x) = 1 5. y = ln x(x3+3) 10. y = (lnx2)x2 B. Tentukan turunan dari fungsi-fungsi berikut

1.

1 2 x

1 2 x y

− +

= 3. 3

5 x 3 2 x

2 ) 3 2 x ( 2 x y

+ −

− =

2.

4 3 x 3

1 2 x y

− +

= 4. y =

2 x 1

2 ) 2 x 1 ( x

+ −

C. Tentukan turunan dari

1. y = alog (3x2 – 5) 4. y = log (ln x) 2. y = log3(2x+5)2 5. y = ln (log x)3 3. y = 5 log sin2 x

Tugas Subbab 5.3

a. Tentukan turunan dari fungsi berikut

1. y = ex2 4. y = e−xsin 2x 2, y = ex2lnx 5. y = e−x ln x 3. y =

x e x e

x e x e

− +

−

− _{6. y =}

ax e ax e

ax e ax e

− +

− −

b. Tentukan turunan dari

1. y = 5 x 3. y = 1 x 2

1 x 2

+ −

2. y = x2 3x 4. Y = (4x2−3x)3x2 c. Tentukan turunan dari

1. y = (x2+1)sinx 4. y = 3 x 7. y = 53x−4 10. y = xe+ex

2. y = 2 x e

x − 5. y = (x2−3)x+1 8. y = xlnx

3. y = (2x−1)x2+4 6. y = (lnx2)2x+3 9. y = (x2+1)10+10x2+1 d. Soal esai:

30

Tugas Subbab 5.4

Tentukan turunan dari

1. y2 sin x + y = arc tan x 5. y = ln ln sec 2x 9. y = arc sin ex 2. y =

2 x 2 a

x

−

– arc sin a x

6. y = 2 x

4 2

x −

+

2 x sec arc 2 1

10. y = arc sin x

3. y = x2 arccos x 2

7. y = xsin x 11. ln (x+y) = arc tan

y x

4. y = arc tan x 3

8. y = arc sin (x-1)

Tugas Subbab 5.5

A. Buktikan

1. cosh x + sinh x = ex 6. cosh 2x = cosh2 x + sinh2 x 2. cosh x – sinh x = e-x 7. sinh 2x = 2 sinh x cosh x 3.

2 1 x cosh x 2 1 2

sinh = − 8. sinh (x + y) = sinh x cosh y + cosh x sinh y 4. tanh 2x =

x 2 tanh 1

x tanh 2

+ 9. cosh (x + y) = cosh x cosh y + sinh x sinh y 5.

2 1 x cosh x 2 1 2

cosh = +

B. Tentukan turunan dari

1. y = x sech x2 4. y = csch2 (x2 + 1) 2. y = ln cosh x 5. y = a cosh

a x

3. y =

1

x

tanh

1

+

Tugas Subbab 5.6

31

BAB VI

TURUNAN FUNGSI BEBERAPA VARIABEL

6.1 Geometri Fungsi Dua Variabel

Persamaan z = f(x, y) atau F(x, y, z) = 0 bila dilukiskan pada ruang 3 dimensi dengan sistem koordinat XYZ, umumnya berbentuk permukaan. Untuk melukiskan permukaan, perlu diperhatikan 4 hal, yaitu: 1. Daerah definisi dan rentang fungsi f tersebut.

2. Sifat simetri fungsi f tersebut.

3. Kurva perpotongan dengan bidang koordinat (XOY, XOZ, dan YOZ) dengan memasukkan

• nilai z = 0 untuk mendapatkan kurva perpotongan permukaan dengan bidang XOY

• nilai y = 0 untuk mendapatkan kurva perpotongan permukaan dengan bidang XOZ

• nilai x = 0 untuk mendapatkan kurva perpotongan permukaan dengan bidang YOZ

4. Perpotongan dengan bidang lainnya, misal dengan bidang sejajar bidang XOY pada jarak z0 didapat dengan memasukkan z = z0, bidang sejajar bidang XOZ pada jarak y0 didapat dengan memasukkan y = y0, atau bidang sejajar bidang YOZ pada jarak x0 didapat dengan memasukkan x = x0. Kurva perpotongan disebut level kurva dan proyeksinya pada bidang koordinat disebut garis kontur.

Contoh :

a. Gambarkan permukaan 4 x2 + y2 = z

Jawab : Pers. tsb diubah menjadi z = 4 x2 + y2 Dalam bentuk z = f(x, y), daerah definisi Df adalah bidang XOY. Nilai z selalu positip sebab variabel x dan y dalam bentuk kuadrat. Rentang fungsi Rf adalah z ≥ 0. Level kurva didapat dari persamaan 4x2 + y2 = c dimana c bilangan riel > 0, ini persamaan elips pada z = c. Untuk y = 0, didapat z = 4 x2 yaitu persamaan parabola pada bidang XOZ. Untuk x = 0, didapat z = y2 yaitu persamaan parabola pada bidang YOZ.

Bentuk lukisannya sebagai berikut:

b. Gambarkan permukaan x2 + y2 + z2 = r2

Jawab : Persamaan itu dilukiskan sebagai bola dengan pusat di (0,0,0) dan jari-jari r. Untuk x = 0, persamaan memotong bidang YOZ menjadi y2 + z2 = r2 berupa lingkaran, untuk y = 0 memotong bidang XOZ menjadi x2 + z2 = r2 berupa lingkaran, untuk z = 0 memotong bidang XOY menjadi x2 + y2 = r2 berupa lingkaran.

c. Gambarkan permukaan 1

2 c

2 z 2 b

2 y 2 a

2 x

= +

+ dimana a, b, dan c positip, dan a = b Jawab :

Perpotongannya dengan bidang koordinat

• XOY, dengan z = 0 adalah 1 2 b

2 y 2 a

2 x

= +

a = b, membentuk persamaan lingkaran

• XOZ, dengan y = 0 adalah 1 2 c

2 z 2 a

2 x

= +

• YOZ, dengan x = 0 adalah 1 2 c

2 z 2 b

2 y

= +

keduanya membentuk persamaan elips. Jadi persamaan tersebut berbentuk elipsoida (elips putaran) Y

X

Z

Pada z = c, kurva berbentuk elips

Pada y = 0, z = 4 x2, dan x = 0, z = y2, kurva berbentuk parabola

Permukaan ini disebut paraboloida eliptik

Gambar 6.1 Paraboloida Eliptik

Z

Y

X (0, 0, 0)

Gambar 6.3 Elipsoida berpusat di (0, 0, 0)

Z

Y

X

(

0, 0, 0)

32

d. Gambarkan permukaan 1

2 c

2 z 2 b

2 y 2 a

2 x

= −

+ dimana a, b, dan c positip, dan a = b Jawab : Perpotongan persamaan itu dengan bidang:

• XOY, dengan z = 0 adalah 1 2 b

2 y 2 a

2

x _{+ =}

untuk a = b, membentuk persamaan lingkaran

• XOZ, dengan y = 0 adalah 1 2 c

2 z 2 a

2 x

= −

• YOZ, dengan x = 0 adalah 1 2 c

2 z 2 b

2 y

= −

keduanya membentuk persamaan hiperbola. Dengan demikian persamaan tersebut dilukiskan berbentuk hiperboloida berdaun satu.

e. Gambarkan permukaan z = y2

Jawab : Persamaan itu tidak memiliki variabel x, artinya nilai x dapat diambil sembarang. Perpotongan dengan bidang YOZ dengan x = 0 tetap adalah z = y2 yaitu berupa parabola. Permukaannya berbentuk silinder parabolik

f. Gambarkan permukaan 1

2 a

2 x 2 b

2 y 2 c

2 z

= −

− dimana a, b, dan c positip, dan a = b

Jawab: Persamaan tersebut menghasilkan gambar sebagaimana tercantum di samping. Jelaskan sendiri penyelesaiannya.

g. Gambarkan permukaan

2 2

2 2

2 2

c

z

b

y

a

x

=

+

dimana a, b, dan c positip, dan a = b

Jawab : Persamaan tersebut menghasilkan gambar sebagaimana di samping.

Jelaskan sendiri penyelesaiannya.

6.2 Turunan Parsial Fungsi Dua Variabel

Turunan parsial dari fungsi z = f(x, y) adalah:

T x z_

     ∂ ∂

= turunan parsial dari fungsi z terhadap x di T(xt, yt, zt) dimana y dianggap konstan

T y z       ∂

∂ _{= turunan parsial dari fungsi z terhadap x di T(x}

t, yt, zt) dimana x dianggap konstan Contoh:

Tentukan turunan parsial dari: a. z = x2 + y2 Jawab :

x

z

∂

∂

= 2x dan

y

z

∂

∂

= 2y

b. z = xy Jawab :

x

z

∂

∂

= y dan

y

z

∂

∂

= x

Y

Gambar 6.6 Hiperboloida berdaun dua

Z

X

Gambar 6.4 Hiperboloida berdaun satu

Z

Y

X

Gambar 6,5 Silinder parabolik

Z

Y

X

Gambar 6.7 Kerucut eliptik Y Z

33

6.3 Turunan Parsial Lebih Tinggi

Turunan parsial tingkat dua fungsi z = f(x, y) terbagi atas 4 macam, yaitu:

1.

Turunan parsial tingkat tiga fungsi z = f(x, y) terbagi atas 8 macam, yaitu:

1.

Tentukan semua turunan parsial tingkat dua untuk fungsi: a. z = x sin2y Jawab :

6.4 Turunan Fungsi Implisit

Persamaan f(x,y,z) = 0 adalah fungsi implisit dalam ruang tiga dimensi. Untuk menghitung dx dz

maka variabel z dan x diturunkan terhadap x dengan menganggap y konstan, dan untuk menghitung

dy dz

maka variabel z dan y diturunkan terhadap y dengan menganggap x konstan.

34

6.5 Bidang Singgung dan Garis Normal

Persamaan bidang yang menyinggung fungsi z = f(x, y) di titik T (x0, y0, z0) adalah:

Sedangkan, persamaan garis normalnya adalah: X = (x_o,y_o,z_o)+tN

dimana:

X = vektor garis normal Contoh:

Diketahui bidang permukaan z = x3 + x2y + y3 + y2x + 1. Tentukan :

a. Persamaan bidang singgung melalui titik T (1, 1, 5) pada permukaan tersebut. b. Persamaan garis normal

Jawab:

maka persamaan bidang singgung: )

garis normal

bidang singgung

bidang permukaan z = f(x, y) T(x0, y0,

z )

35

6.6 Menentukan Jenis Titik Ekstrim

Jika titik T (x0, y0, z0) adalah titik stasioner dari fungsi z = f (x, y) dan berlaku

maka berlaku ketentuan sebagai berikut: 1. Jika di T berlaku ∆ > 0, dan Jawab: Hitung turunan parsialnya, yaitu:

x

Titik stasioner didapat dari x

atas, disimpulkan titik tersebut minimum. 6.7 Turunan Parsial Fungsi Parameter

Jika diketahui suatu fungsi z = f (x, y) dimana x = f(t) dan y = f(t) maka turunan parsial z terhadap parameter t adalah:

t Contoh

1. Tentukan

36

x = t2 – 5t +7 →

t x ∂

∂ _{= 2t – 5 dan y = sin}2 t →

t y ∂

∂ _{= 2 sin t cos t = sin 2t}

t z ∂ ∂ ₌

x z ∂ ∂

t x ∂ ∂ ₊

y z ∂ ∂

t y ∂ ∂

= y 2 z 2

y 3

+ (2t – 5) + 2z 2y z 2 x 3

+

− _{sin 2t}

t z ∂ ∂ ₌

y 2 z 2

) 5 t 2 ( y 3

+

− ₊

y 2 z 2

t 2 sin ) z 2 x 3 (

+ −

2. Diketahui suatu persamaan volume silinder v = π_R2_{T, dimana R = jari-jarilingkaran}

silinder dan T = tinggi silinder

Jika pada silinder itu berlaku bahwa tingginya berkurang dengan kecepatan 0,3 cm/detik, dan jari-jarinya bertambah dengan kecepatan 0,5 cm/detik. Hitung kecepatan berubahnya volume silinder pada saat tingginya 10 cm dan jari-jari 7 cm.

Jawab: v = π_R2_{T maka}

R v ∂

∂

= 2π_{RT dan}

T v ∂ ∂

= π_R2 _sedangkan

t T ∂

∂ _{= – 0,3 cm/dt dan} t R ∂

∂ _{= 0,5 cm/dt}

Jadi kecepatan berubahnya volume silinder

t v ∂ ∂ ₌

R v ∂ ∂

t R ∂ ∂ ₊

T v ∂ ∂

t T ∂

∂ _{= 2πRT 0,5 + πR}2

(– 0,3) untuk T = 10 cm dan R = 7 cm maka

t v ∂ ∂

= 2π _{7 10 0,5 –} π ₇2 _{0,3 = (70 – 14,7)} π _{= 55,3}π _cm3_/dt

6.8 Diferensial Total

Jika z = f (x, y) maka diferensial total dari fungsi tersebut adalah dz = dx

x z ∂

∂ ₊

dy y z ∂ ∂

Artinya, jika pada x terjadi perubahan sebesar dx dan pada y terjadi perubahan sebesar dy maka pada z akan terjadi perubahan sebesar dz sebesar persamaan di atas.

Contoh:

1. Di lapangan akan dibuat empat persegi panjang dengan panjang 421 m dan lebar 314 m, setelah dipatok dan diukur kembali, diperoleh data baru panjangnya berubah menjadi 421,02 m dan lebarnya menjadi 313,97 m. Berapa perubahan (kesalahan) yang terjadi pada luasnya?

Jawab:

Luas = panjang x lebar. Misal Luas = L, panjang = x, dan lebar = y, maka L = xy x

L ∂

∂ _{= y dan} y L ∂

∂ _{= x, dx = 421,02 – 421 = 0,02 m dan dy = 313,97 – 314 = – 0,03 m}

dL = dx x L ∂

∂ _{+ dy}

y L ∂

∂ _{= y dx + x dy = 314 . 0,02 + 421 (– 0,03) = – 6,35 m}2

2. Tentukan nilai taksiran (4,02)1,1 sampai 3 desimal. Jawab : Ambil harga bulat, x = 4 maka dx = 4,02 – 4 = 0,02 dan y = 1 maka dy = 1,1 – 1 = 0,1

Fungsi tersebut adalah z = xy turunan parsialnya

x z ∂

∂ _{= yx}y−1 _{= 1. 4}0

= 1 dan y z ∂ ∂ _{= x}y

ln x = 41 ln 4 = 4 ln 4

dz = dx x z ∂

∂ _{+ dy}

y z ∂

∂ _{= yx}y−1 _{dx + x}y

ln x dy = 1. 0,02 + 4 ln 4. 0,1 ≈ 0,575

Jadi (4,02)1,1 = 41 + dz = 4 + 0,575 = 4,575 Check : 4,021,1 = 4,620071092

R T

37

TUGAS MANDIRI BAB VI

Tugas Subbab 6.3

Tentukan turunan parsial untuk fungsi berikut:

1. z = x2 sin y 4. z = x2 + 3xy + y2 7. z = x cos y – y cos x 2. z = ln x2+y2 5. z = arctan

x y

8. z = xy 3. z =

2 y

x

6. z =

2 x

y 2 y

x

−

9. Diketahui z = x2+y2 , buktikan z y z y x z

x =

∂ ∂ + ∂ ∂

10. Diketahui z = ln x2+y2, buktikan 1 y z y x z

x =

∂ ∂ − ∂ ∂

Tugas Subbab 6.4

Tentukan turunan parsial tingkat dua dan tiga untuk semua soal 1 – 8 di atas Tugas Subbab 6.5

1. Tentukan turunan x z ∂ ∂ _dan

y z ∂

∂ _{dari ysin(xz) – 2 tan x + y cos}2

x + xsin3z = 0

2. Diketahui persamaan

xy log z y e

x y z 2 x

+ = xy – xz + yz. Tentukan turunan x z ∂ ∂ _dan

y z ∂ ∂

3. Diketahui suatu persamaan implisit x2z – 3yz2 = – 2

Hitung x z ∂ ∂ _,

y z ∂ ∂ _,

2 x

z 2

∂ ∂ _,

2 y

z 2

∂ ∂ _,

x y

z 2

∂ ∂

∂ _{di titik (1, 1, 1)}

Tugas Subbab 6.6

1. Diketahui persamaan z = x

y x+

dan titik T (1, 1, 2) terletak pada permukaan tersebut. Tentukan persamaan bidang singgung dan persamaan garis normal yang melalui T. 2. Idem, persamaan z = x3 – 2xy + y2 dan titik T (1, – 1, 4)

3. Idem, persamaan z = x2+y2 dan titik T (4, – 3, 5) 4. Idem, persamaan z =

2 x

y 2 y

x

− dan titik T (1, – 1, 2)

5. Idem, persamaan z = 2 y

x

dan titik T (2, – 1, 2) Tugas Subbab 6.7

1. Tentukan nilai ekstrim dan jenisnya (jika ada) untuk fungsi-fungsi berikut: a. z = x3 + x2y – 2y3 + 3y2 d. z = 2x2 – y2 + 20x – 11y b. z = x3 + y3 + x2 – 5y2 – x + 3y e. z = 4xy2 – 2x2y – x c. z = x2 + y2 + 3xy

2. Akan dibuat sebuah kotak tanpa tutup atas dengan volume 108 cm3. Berapa ukuran kotak tersebut agar luas permukaannya minimum?

X

Y