www.elsevier.com/locate/dsw
Minimum ratio canceling is oracle polynomial for linear
programming, but not strongly polynomial, even for networks
(
S. Thomas McCormick
a;∗;1, Akiyoshi Shioura
b;2aFaculty of Commerce and Business Administration, University of British Columbia, Vancouver, BC, Canada V6T 1Z2 bDepartment of Mechanical Engineering, Sophia University, 7-1 Kioi-cho, Chiyoda-ku, Tokyo 102-8554, Japan
Received 8 February 1999; received in revised form 1 December 1999
Abstract
This paper shows that the minimum ratio canceling algorithm of Wallacher (Unpublished manuscript, Institut fur Ange-wandte Mathematik, Technische Universitat, Braunschweig (1989)) (and a faster relaxed version) can be generalized to an algorithm for general linear programs with geometric convergence. This implies that when we have a negative cycle oracle, this algorithm will compute an optimal solution in (weakly) polynomial time. We then specialize the algorithm to linear pro-gramming on unimodular linear spaces, and to the minimum cost ow and (dual) tension problems. We construct instances proving that even in the network special cases the algorithm is not strongly polynomial. c2000 Elsevier Science B.V. All rights reserved.
Keywords:Negative cycle canceling algorithm; Minimum ratio cycle; Linear programming problem; Unimodular linear space; Minimum cost ow; minimum cost tension
1. Introduction
A popular class of algorithms for the minimum cost ow problem is the cycle canceling algorithms. This
(An extended abstract of this paper appeared inProceedings of SODA 2000, pp. 944 –952.
∗Corresponding author. Fax: +1-604-822-9574.
E-mail addresses: [email protected] (S.T. Mc-Cormick), [email protected] (A. Shioura).
1Part of this research was done while visiting SORIE at Cornell University, and was supported by an NSERC Research Grant.
2Part of this research was done while visiting the Faculty of Commerce and Business Administration, University of British Columbia.
concept originates with Klein [12], and is based on the idea that pushing ow around negative-cost resid-ual cycles will improve the primal objective. The dresid-ual version of cycle canceling is cut canceling, originat-ing with Hassin [10]. Here we change node potentials across positive-valued cuts to improve the dual ob-jective. These algorithms are attractive since they are exible: algorithms with dierent behaviors can result from choosing dierent classes of negative cycles or positive cuts to cancel. See Shigeno et al. [21] for a recent survey of such algorithms.
A naive idea is to cancel most negative cycles, but these are NP-hard to compute, and do not lead to polynomial algorithms [26]. We could instead use the
polynomially computable most negative family of cy-cles, but this algorithm is again not polynomial, and the same is true for canceling a most positive (fam-ily of) cuts [21] (though canceling relaxed versions of these objects is polynomial [21]). Goldberg and Tarjan [7] popularized the idea of instead choosing to cancel a cycle whose ratio of cost to weight was min-imum. They chose the weight of each arc to be one, and showed that the resulting minimum mean cycle canceling algorithm is strongly polynomial.
Wallacher [23] considered several other possibili-ties for arc weights, and developed polynomial algo-rithms. One of his polynomial algorithms uses the arc weight given by the reciprocal of the residual capacity of the arc; we call this minimum ratiocycle cancel-ing. It turns out that this choice of arc weights makes it easy to prove a weakly polynomial iteration bound on the algorithm. Later, his algorithm was extended to linear programs with totally unimodular matrices by McCormick and Shioura [14], and to general in-teger programs by Schulz and Weismantel [20]. Re-cently, Wayne [24] applied the minimum ratio can-celing technique to generalized minimum cost ow to give the rst polynomial combinatorial algorithm for that problem. We combined Wayne’s ideas from [24] and our ideas from [14] to create the present paper. Subsequent to this paper a common generalization of it and [20] showed that the same ideas also work for mixed integer programs [13].
One aim of this paper is to show that Wallacher’s minimum ratio canceling algorithm generalizes to an algorithm for general linear programs that geometri-cally reduces the gap between the objective value of our current solution and the optimal objective value. When we have rational data and an oracle for nd-ing negative cycles we can show that this gap can be driven small enough that it is possible to round to an exact optimal solution in weakly polynomial time. We show that a faster, relaxed version of Wallacher’s al-gorithm also generalizes to linear programming.
An important special case of this is linear program-ming over a unimodular linear space, namely the solution set of the systemMx= 0 given by a totally unimodular matrixM. This is a common generaliza-tion of both primal and dual network ow. Karzanov and McCormick [11] showed that minimum mean cycle canceling can be generalized to a polynomial algorithm for linear programming in unimodular
linear spaces. We show that the specialization of min-imum ratio canceling to this case has a faster iteration bound.
Sections 3 and 4 show how our minimum ratio can-celing algorithm further specializes to both the pri-mal and dual of the minimum cost ow problem. The primal specialization is just Wallacher’s algo-rithm [23]. Although most algoalgo-rithms for the primal minimum cost ow problem have been dualized (e.g., [10,3,4,21]), we believe that our minimum ratio cut canceling tension algorithm is the rst dualization of the minimum ratio cycle canceling algorithm. We con-sider a problem equivalent to dual minimum cost ow called the minimum cost tension problem, which asks for a minimum cost set of potential dierences. This problem has a number of applications (see Rockafel-lar [18, Chapter 7F]) and algorithms of its own (see Hadjiat [9] or Karzanov and McCormick [11]).
Goldberg and Tarjan’s minimum mean cycle can-celing algorithm [8], and Ervolina and McCormick’s dual maximum mean cut canceling algorithm [4], dif-fer from our algorithms only in the choice of weights for the denominator of the ratio. Those algorithms are both strongly polynomial.
On the other hand, the running time analysis of our algorithms is quite similar to analyses of the most helpful cycle canceling algorithm of Weintraub [25] and Barahona and Tardos [2], and the dual most help-ful total cut canceling algorithm of Ervolina and Mc-Cormick [3]. Queyranne [16], and [3] show that these algorithms are not in general strongly polynomial.
Proving that the minimum ratio canceling algo-rithms are not strongly polynomial has implications beyond this paper. Our network ow algorithms are special cases of the Schulz and Weismantel [20], Wayne [24], and mixed integer program [13] results, so our proofs of non-strong polynomiality show that all of these algorithms are also not strongly polyno-mial.
2. A minimum ratio cycle canceling algorithm
In this section, we present a minimum ratio cycle canceling algorithm for the linear programming prob-lem. LetM be ann×m(m¿2) real matrix (we notate
M asn×minstead of the more usualm×nto match the canonical case whereM is the node-arc incidence matrix of a directed graph). PutJ={1;2; : : : ; m}. We are given costsc∈RJ, andupperandlower bounds
u ∈ (R∪ {+∞})J andl∈(R∪ {−∞})J. We deal with the following linear programming problem:
(LP) Minimize cTx=
back residual capacitiesbyr+
x(j) =u(j)−x(j) and
A cycle d is called augmenting (w.r.t. x) if capx(d)¿0, and negativeif cTd ¡0. In this paper, we assume that there exists no cycle d ∈ RJ such that supp(d)⊆{j∈J|l(j) =−∞; u(j) = +∞}and
cTd= 0. If such a cycle exists, then we can modify the problem (LP) without changing the optimal value by putting l(j) =u(j) = 0 for some j ∈ supp(d).
Note that this assumption assures the existence of an optimal extreme point of (LP).
Conditions for optimality and unboundedness of (LP) can be stated in terms of cycles:
Theorem 2.1. (i)x∈Pis optimal if and only if there is no negative augmenting cycle w.r.t. x. (ii) (LP)
is unbounded if and only if there is a negative cycle with capacity+∞.
Theorem 2.1(i) gives a generic algorithm for (LP): we can nd an optimal solution by iteratively nding and canceling negative cycles. The performance of this algorithm depends on the class of negative cycles we choose to cancel. We now describe the class of cycles we will choose to cancel. innite capacity, and (LP) is unbounded by Theorem 2.1(ii), and we have ruled out such instances. Thus
wx(d)¿0 for all negative cyclesd. Ifxis feasible but non-optimal to (LP) (so that some negative augment-ing cycle w.r.t.xexists), then aminimum ratio cycle
w.r.t.xis a (negative) augmenting cycle d minimiz-ing the ratiocTd=w representation is called a conformal realizationof y
That is, for an optimal solutiony∗∈RJof (MRC x), if y∗ is decomposed into cycles d1; d2; : : : ; dk in a conformal realization, then eachdiis also optimal for (MRCx)
Algorithm MINRATis described as follows:
AlgorithmMINRAT
Step 0:Find a feasible solutionx=x0∈Pof (LP).
Step 1: If there is no negative augmenting cycle, then stop; the vectorxis optimal.
Step 2:Find a minimum ratio cycled∈RJw.r.t.x. Let= capx(d).
Step 3: Cancel d by setting x′ =x+d. Go to
Step 1.
The next lemma shows that MINRATgeometrically reduces the gap between the current objective value and the optimal objective value, which is key to prov-ing that it terminates in a weakly polynomial number of iterations.
Lemma 2.2. Letx; x′∈Pbe feasible solutions in the current and next iterations ofMINRAT,respectively, and d∈RJ be the cycle chosen in Step 2.Also; let
Proof. Claim (i) is equivalent to
cT(x′
The denition ofimplies that
wx(x′−x) =wx(d) =wx(d)¿1: (4)
Combining (2) – (4) yields (1). Claim (ii) follows from (2) and (3).
Lemma 2.2 will allow us to get very close to an optimal extreme point. To get an exact optimal solu-tion we will round an approximate solusolu-tion using only
m calls to the oracle (this idea originated in Wayne [24]). This is based on the following lemma.
Lemma 2.3. A vectorx∈ Pis an extreme point of
P if and only if there exists no cycle d ∈ RJ with
supp(d)⊆{j∈J|l(j)¡ x(j)¡ u(j)}.
Based on Lemma 2.3, we can round a non-extreme point x ∈ P by iteratively nding a cycle d ∈ RJ this procedure terminates in at mostmiterations.
From now on we assume that entries of the matrix
M and the vectorsl; u, andcare rational numbers. As in Grotschel et al. [8], we dene theencoding lengthof numbers and vectors as follows. The encoding length of a rational numberris
hri= 2 +⌈log(|p|+ 1)⌉+⌈log(|q|+ 1)⌉;
where p and q (¿0) are relatively prime integers such thatr=p=q. The encoding length of a rational vectorx∈Qnishxi=P that there exists an feasible solutionx0and an optimal solution x∗ of (LP) such that hx0i and hx∗i are at
Theorem 2.4. If the matrix M and the vectors l,u are rational; thenMINRATnds an optimal solution inO(m4hBi+m3hUi+m2hCi)iterations.
Proof. This proof is similar to Wayne [24, Theorem 5]. Put= 2−(mhCi+4m2’)We rst nd a vector ˜x∈RJ withcT( ˜x−x∗)¡ 2=2 by using MINRAT. Lemma 2.2 (i) implies that MINRATrequires at most k iterations to compute ˜x, where k satises (1−1=m)kcT(x0 − x∗)¡ 2=2. This yields thatk= O(m4hBi+m3hUi+
m2hCi).
Suppose that xis a non-optimal extreme point and thatx∗is an optimal extreme point. Since the
denomi-nators of the rational numberscTxandcTx∗are at most
1=, we havecTx ¿ c Tx∗+2. Thus any extreme point ˆ
xwithcTxˆ6cTx˜must be optimal. We can obtain such an optimal extreme point ˆxof P by canceling cycles at mostmtimes, as explained after Lemma 2.3.
Therefore, MINRATis an oracle weakly polynomial algorithm for linear programming. In some applica-tions of this algorithm a special-purpose algorithm is available to solve the minimum ratio subproblem, and a reasonable initial solution is easily available. See Sections 3 and 4 below for such subroutines for pri-mal and dual network ow, or Wayne [24] for such a subroutine for generalized network ow.
2.1. A faster relaxed version of the algorithm
Wallacher [23] showed that when canceling min ratio cycles for minimum cost ow, it is possible to replace the (bottleneck) min ratio cycle computation with a much faster negative cycle computation, while keeping essentially the same iteration bound. Wayne [24], and Schulz and Weismantel [20] showed that the same idea works for generalized ows and integer programming. Here we show that this idea extends to linear programming.
Each scaling phasehas a xed parameter value
which is at most half the min ratio value at the begin-ning of the phase. For cycle dinRJ, we dene the
modied cost of dby c(d) =cTd−wx(d). Then it is easy to see that dhas negative modied cost if and only ifcTd=w
x(d)¡ . Such adcan be computed by a fast negative cycle subroutine, which is typically much faster than a min ratio cycle subroutine. For ex-ample, for generalized ow a negative cycle is a
fac-tor of about O(n) faster to compute than a min ratio cycle [24].
We keep canceling negative cycles w.r.t.cin the scaling phase until none are left (i.e., is at most the current min ratio value), at which point we set
←=2, and start a new phase. We call this version
relaxedMINRAT, or RMINRAT.
Lemma 2.5. There are at most2mcancellations per scaling phase ofRMINRAT.
Proof. First we show that canceling negative cycle
d(w.r.t.c) reduces the objective value by less than
. Rescale dso that capx(d) = 1, implying that the objective value decreases by cTd. In this rescaling
wx(d)¿1 since at least onejbecomes saturated. Thus
cTd ¡ w
x(d)6.
Letx0be the solution at the beginning of the phase,
x∗be an optimal solution, and0be the min ratio value forx0. Lemma 2.2 (ii) implies that06cT(x∗
−x0)=m, or cT(x∗−x0)¿m0¿2m. Since each cancellation in the phase bringscTxat leastcloser tocTx∗, there can be at most 2mcancellations in the phase.
Theorem 2.6. RMINRATnds an optimal solution in O(m4hBi+m3hUi+m2hCi)cancellations.
Proof. It takes O(m) cancellations in one scaling phase of RMINRAT to reduce our upper bound on
cT(x−x∗) from 2mto 2m(=2), i.e., by a factor of
two. It also takes O(m) cancellations of MINRAT to achieve the same reduction, so they enjoy the same iteration bound.
There are corresponding relaxed versions of all our subsequent specializations of MINRAT.
2.2. Specialization to linear programming on unimodular spaces
totally unimodular implies that any cycle is a multi-ple of a{0;±1}vector, and hence we regard a cycle as a{0;±1}vector. This implies that if the initialx0 is integral and landu are integral, then the current solutionxis integral in each iteration of MINRAT.
DeneC= maxj∈J|c(j)|,
JL={j∈J|l(j)¿− ∞};
JU={j∈J|u(j)¡+∞};
U= max
max
j∈JL|l(j)|;maxj∈JU|u(j)|
:
In this case we can get a sharper bound on the initial gap:
Lemma 2.7. There exists an optimal solution x∗ ∈
RJ of(LPU)with|x∗(j)
|6mU for allj∈J.
Proof. Letx′
∈RJ be an optimal solution of (LPU), and letx′=Pk
i=1idi(i¿0) be a conformal realiza-tion ofx′. Fori= 1; : : : ; k, deneJi={j∈JU|di(j) = +1} ∪ {j∈JL|d
i(j) =−1}. Then we claim that (i) ifJh6=∅, thenh6U,
(ii) ifJh=∅, andh¿ U, thenx′′=Pi6=hidi+Udh is also an optimal solution.
The claim implies thatx∗=Pk
i=1min{i; U}di is an optimal solution with|x∗(j)|6mU for allj∈J.
To prove claim (i), let j0 ∈Jh withdh(j0) = +1. Thenx′(j0)¿0 anddi(j0)¿0 for alli, which implies thath6x′(j0)6u(j0)6U. The case wheredh(j0) =
−1 is similar.
Now we show claim (ii). By Lemma 2.1(ii),dhis a nonnegative cycle, which impliescTx′′6cTx′. Hence, it suces to show thatl(j)6x′′(j)6u(j) for allj∈ J. Ifdh(j) = +1, thenl(j)6U6x′′(j)¡+∞=u(j) holds. The other cases are similar.
We now assume that our oracle nds an initialx0 satisfying the bound of Lemma 2.7 and computes min-imum ratio cycles.
Theorem 2.8. Ifc; u;and l are integral and the ini-tial feasible solutionx0 is integral;thenM
INRAT ter-minates inO(mlog(mCU))iterations.
Proof. The assumption on x0 and Lemma 2.7
im-ply that cT(x0 −x∗) is bounded by 2m2CU. Since
cT(x−x∗)¡1 implies thatxis optimal, Lemma 2.2(i)
implies that the algorithm terminates in at mostk it-erations, where k satises (1−1=m)k(2m2CU)¡1. This implies thatk ¡3mln(mCU).
Therefore, MINRATis a faster oracle weakly poly-nomial algorithm for (LPU) than for (LP). We again point out that special-purpose subroutines are avail-able for important special cases.
3. Specialization to the minimum cost ow problem
We are given a directed graphG=(N; A) with|N|=n
and|A|=m, upper and lower boundsu∈(R∪{+∞})A andl∈ (R∪ {−∞})A, and costsc ∈RA. For each node v∈ N, we denote the sets of arcs leaving and entering v by +v and −v, respectively. Then the
minimum cost ow problemis
(MCF) Minimize X a∈A
c(a)x(a)
subject toX a∈+v
x(a)−X a∈−v
x(a) = 0 (v∈N);
l(a)6x(a)6u(a) (a∈A):
IfM ∈ Rn×mis the node-arc incidence matrix ofG, then the ow conservation constraints can be written asMx= 0. Since thisM is totally unimodular, (MCF) is a special case of (LPU).
It is well known that the (matrix) cycles ofM are in 1–1 correspondence with the (graph) cycles ofG. Thus, the whole machinery of minimum ratio cancel-ing for (LPU) carries over to (MCF) without even needing to change terminology. We call the version of MINRATspecialized to (MCF) MINRAT-F. The spe-cialization of Theorem 2.8 to this case is:
Theorem 3.1(Wallacher [23]). If c; u; and l are integral;and the initial feasible owx0is integral and satises|x0(a)
|6mU for all a ∈ A; thenMINRAT-F terminates inO(mlog(nCU))iterations.
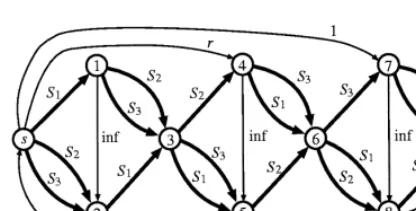
Fig. 1. A bad instance for MINRAT-F.
In order to show that MINRAT-F is not strongly poly-nomial, we now show a real-valued instance for which MINRAT-F does not terminate. Consider the network shown in Fig. 1, which is a modication of the one in Queyranne [16]. Each arc drawn by a bold arrow actually consists of three arcs in series with the same cost and bounds. The lower bound is 0 for each arc, and the upper bound is indicated in the gure. Dene
r= (√5−1)=2. The symbols ‘inf’,S1; S2, andS3 rep-resent the values +∞;(1 +r)=2;1=2, andr=2. These numbers satisfy the identities
S1−r=r3S1; S2−r2=r3S2 and S3−r3=r3S3;
and the inequalities 1¿ S1¿ r ¿ S2¿ r2¿ S3¿ r3
¿ S1−r=r3S1, etc., which are needed to understand the behavior of MINRAT-F on the network. The arc (t; s) has cost−1;and the four arcs (s;4);(s;7);(5; t), and (8; t) have large negative costs. Each of the other arcs has cost 0.
When MINRAT-F is applied to this network with the initial feasible ow x0 = 0 ∈ RA, it is easy to see that the rst iteration chooses the cycle with arcs {(s;7);(7;8);(8; t);(t; s)}, and the second iteration chooses the cycle with arcs
{(s;4);(4;5);(5; t);(t; s)}. These two cancellations saturate the arcs (s;4);(s;7);(5; t), and (8; t). The ow on the threekeyarcs is nowx12= 0; x45=r, and
x78= 1, and all other arcs have ow 0.
In the following iterations, the arcs with capacities 1 and r are never contained in canceled cycles, so the only negative-cost residual arc available is (t; s). Thus each further cycle Q consists of a shortest s-t
path (w.r.t. lengthswx), together with arc (t; s). Since 1=r+ 3=S1¡3=S2 (this is why each bold arc in Fig. 1 is a series of three arcs), the subpath containing the
backward (4;5) arc and the forward S1-arc (4;6) is shorter than the (5;6)S2 arc, so that the rst such shortest path uses only arcs with capaci-ties S1 and +∞. Since 1=r2 + 3=S2¡3=S3 and 1=r3+ 3=S
3¡3=r3S1, the next two cycles useS2and
S3 arcs, respectively, and we have a pattern that re-peats blocks of three iterations. For g= 1;2;3 the 3k−1 +gth iteration (k¿1) cancels the cycle
Q1={(s;1);(1;2);(2;3);(3;5);(4;5);(4;6);(6;8);
(7;8);(7; t);(t; s)};
Q2={(s;2);(1;2);(1;3);(3;4);(4;5);(5;6);(6;8);
(7;8);(7; t);(t; s)};
Q3={(s;2);(1;2);(1;3);(3;5);(4;5);(4;6);(6;7);
(7;8);(8; t);(t; s)};
whereQg consists of all arcs with capacities Sg, the three key arcs, and (t; s). The cycleQgcontains the key arc with ow 0 at the beginning of its iteration forward, and the two key arcs with positive ow backward. The iteration pushes r3k−3+g units of ow on Qg, which is determined by the backward key arc with a smaller ow hitting its lower bound of 0. The ow value on the key arcs andS1; S2, andS3 arcs changes as noted in Table 1.
Therefore, MINRAT-F requires an innite number of iterations. This proves:
Theorem 3.2. AlgorithmMINRAT-Fis not a nite al-gorithm for real data;so it is not a strongly polyno-mial algorithm.
4. Specialization to the minimum cost tension problem
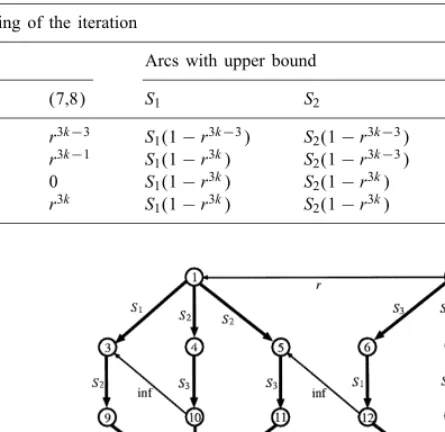
Table 1
Change of ow when MINRAT-F is applied to bad instance
Iter. MRC capx(Q) Flow at the beginning of the iteration
Key arcs Arcs with upper bound
(1,2) (4,5) (7,8) S1 S2 S3
3k Q1 r3k−2 0 r3k−2 r3k−3 S1(1−r3k−3) S2(1−r3k−3) S3(1−r3k−3) 3k+ 1 Q2 r3k−1 r3k−2 0 r3k−1 S1(1−r3k) S2(1−r3k−3) S3(1−r3k−3) 3k+ 2 Q3 r3k r3k r3k−1 0 S1(1−r3k) S2(1−r3k) S3(1−r3k−3) 3k+ 3 Q1 r3k+1 0 r3k+1 r3k S1(1−r3k) S2(1−r3k) S3(1−r3k)
Theminimum cost tension problemis
(MCT) Minimize X
a∈Ac(a)(a)
subject to l(a)6(a)6u(a) (a∈A);
∈RA: a tension:
Rockafellar [18] shows that (MCT) is equivalent to the dual of (MCF). DeneT to be the matrix whose rows are the incidence vectors of all fundamental cy-cles w.r.t. a maximal forest ofG. Thenis a tension if and only if T= 0, and T is a totally unimodu-lar matrix. Therefore (MCT) is also a special case of (LPU).
To describe the cycles ofT we need some notation. A cut is a nonempty proper subset of N. For any cut C⊂N, denote by +C (resp. −C) the sets of
arcs leaving (resp. entering) C. Then a vector d ∈ {0;±1}Ais a cycle ofT if and only if there is some cut
Csuch thatd(a) = +1 exactly on+C, andd(a) =−1 exactly on−C [18].
With this understanding, given a tension ∈ RA,
we can now dene residual capacities for arcs w.r.t., the capacity of a cutC w.r.t., the weight ofCw.r.t.
, and the cost of C. A cut isaugmentingw.r.t.if
r(a)¿0 on +C and r(a)¡0 on −C. We can-cel an augmenting cut by increasing i by cap(C) for i ∈ C, and leaving i the same for i 6∈ C. Al-gorithm MINRATspecializes into cancelling minimum ratio cuts, which we call MINRAT-T.
The specialization of Theorem 2.8 to this case is
Theorem 4.1. Ifc; u;andlare integral;and the ini-tial tension 0 is integral and satises |0(a)|6mU for all a ∈ A; then MINRAT-T terminates in O(mlog(nCU))iterations.
Fig. 2. A bad instance for MINRAT-T.
Such a 0 can be found in strongly polyno-mial time (Ahuja et al. [1]). The current best (strongly) polynomial bound for nding a mini-mum ratio cut is O(mTMC(m; n)) by Radzik [17]. HereTMC(m; n) is the time required for computing a minimum cut in a directed graph, and TMC(m; n) = O ( min{mnlog(n2= m); min{n2=3; √m}mlog(n2= m) logU}) by Goldberg–Tarjan [6] and Goldberg–Rao [5]. Therefore, MINRAT-T runs in (non-oracle) weakly polynomial time.
In order to show that MINRAT-T is not strongly poly-nomial, we now show a real-valued instance for which MINRAT-T does not terminate. The network in Fig. 2 is just the planar dual of the one in Fig. 1. Each arc drawn by a bold arrow actually consists of three parallel arcs with the same capacity and cost. The lower bound is 0 for each arc, and the upper bound is shown on each arc. The symbols ‘inf’,S1; S2 andS3 again represent the values +∞; (1 +r)=2; 1=2, andr=2. The arc (s; t) has cost −1, and four arcs (2;1); (s;2); (15; t), and (16;15) have large negative cost. Each of the other arcs has cost 0.
planar dual of a shortest path w.r.t. weights wx is a minimum cut w.r.t. weights w. Therefore, the behavior of MINRAT-T on the network in Fig. 2 exactly mimics the behavior of MINRAT-F on the network in Fig. 1. Thus MINRAT-T also requires an innite number of iterations, proving
Theorem 4.2. AlgorithmMINRAT-Tis not a nite al-gorithm for real data;so it is not a strongly polyno-mial algorithm.
Acknowledgements
We are grateful to Tomomi Matsui, Maurice Queyranne, Andreas Schulz, Maiko Shigeno, and Kevin Wayne for valuable discussion and comments.
References
[1] R.K. Ahuja, T.L. Magnanti, J.B. Orlin, Network Flows – Theory, Algorithms, and Applications, Prentice-Hall, Englewood Clis, NJ, 1993.
[2] F. Barahona, E. Tardos, Note on Weintraub’s minimum-cost circulation algorithm, SIAM J. Comp. 18 (1989) 579–583. [3] T.R. Ervolina, S.T. McCormick, Canceling most helpful total
cuts for minimum cost network ow, Networks 23 (1993) 41–52.
[4] T.R. Ervolina, S.T. McCormick, Two strongly polynomial cut canceling algorithms for minimum cost network ow, Discrete Appl. Math. 46 (1993) 133–165.
[5] A.V. Goldberg, S. Rao, Beyond the ow decomposition barrier, J. ACM 45 (1998) 753–782.
[6] A.V. Goldberg, R.E. Tarjan, A new approach to the maximum ow problem, J. ACM 35 (1988) 921–940.
[7] A.V. Goldberg, R.E. Tarjan, Finding minimum-cost circulations by cancelling negative cycles, J. ACM 36 (1989) 873–886.
[8] M. Grotschel, L. Lovasz, A. Schrijver, Geometric Algorithms and Combinatorial Optimization, Springer, Berlin, 1988. [9] M. Hadjiat, Un algorithme fortement polynomial pour la
tension de coˆut minimum base sur les cocycles de coˆuts moyens minimums, Technical Report, Groupe Intelligence Articielle, Faculte des Sciences de Luminy, Marseille France, 1994 (in French).
[10] R. Hassin, The minimum cost ow problem: a unifying approach to dual algorithms and a new tree-search algorithm, Math. Programming 25 (1983) 228–239.
[11] A.V. Karzanov, S.T. McCormick, Polynomial methods for separable convex optimization in unimodular spaces with applications, SIAM J. Comp. 26 (1997) 1245–1275. [12] M. Klein, A primal method for minimal cost ows,
Management Sci. 14 (1967) 205–220.
[13] S.T. McCormick, A. Schulz, A. Shioura, R. Weismantel, An oracle-polynomial primal augmentation algorithm for mixed integer programs, manuscript, May 2000.
[14] S.T. McCormick, A. Shioura, A minimum ratio cycle cancelling algorithm for linear programming problems with application to network optimization problems, manuscript, November 1996.
[15] N. Megiddo, Applying parallel computation algorithms in the design of serial algorithms, J. ACM 30 (1983) 852–865. [16] M. Queyranne, Theoretical eciency of the algorithm
‘Capacity’ for the maximum ow problem, Math. Oper. Res. 5 (1980) 258–266.
[17] T. Radzik, Parametric ows, weighted means of cuts, and fractional combinatorial optimization, in: P. Pardalos (Ed.), Complexity in Numerical Optimization, World Scientic, Singapore, 1993, pp. 351–386.
[18] R.T. Rockafellar, Network Flows and Monotropic Optimizatiion, Wiley, New York, 1984.
[19] A. Schrijver, Theory of Linear and Integer Programming, Wiley, New York, 1986.
[20] A.S. Schulz, R. Weismantel, A polynomial-time augmentation algorithm for integer programming, manuscript, Fachbereich Mathmatik, Technische Universitat Berlin, 1998.
[21] M. Shigeno, S. Iwata, S.T. McCormick, Relaxed most negative cycle and most positive cut cancelling algorithms for minimum cost ow, Math. Oper. Res. 25 (2000) 76–104. [22] E. Tardos, A strongly polynomial algorithm to solve combinatorial linear programs, Oper. Res. 34 (1986) 250– 256.
[23] C. Wallacher, A generalization of the minimum-mean cycle selection rule in cycle cancelling algorithms, unpublished manuscript, Institut fur Angewandte Mathematik, Technische Universitat Braunschweig, 1989.
[24] K. Wayne, A polynomial combinatorial algorithm for generalized minimum cost ow, Proceedings of the 31st Annual ACM Symposium on the Theory of Computing, 1999. [25] A. Weintraub, A primal algorithm to solve network ow problems with convex costs, Management Sci. 21 (1974) 87–97.