Metode primal affine-skaling untuk masalah program linear.

ABSTRAK

Untuk menyelesaikan masalah program linear, selain dengan metode grafik atau metode simpleks dapat juga diselesaikan dengan metode titik-dalam. Salah satu kelas dalam metode titik-dalam adalah metode primal affine-skaling. Untuk menentukan penyelesaian masalah program linear dengan metode primal affine-skaling dimulai dengan memilih titik-dalam awal, yaitu dari suatu daerah layak di ruang penyelesaian awal. Kemudian ditransformasi oleh transformasi affine-skaling, yaitu sedemikian sehingga hasil transformasi diposisikan dekat dengan pusat di ruang penyelesaian hasil transformasi ini. Hasil transformasi sebut saja . Langkah selanjutnya, dari dijalankan ke titik-dalam lain, yaitu

yang menggerakkan nilai sampai optimum dicapai sesuai dengan alur iterasi , dengan adalah arah layak turun tercuram (steepest descent) yang menyebabkan nilai fungsi berkurang dengan cepat. Dan

k x k

x k

T xk

k x k

y yk

1 + k

y f f

k y k k k

d y

y +1 = +α dk_y

k

α adalah besarnya langkah yang menyatakan seberapa jauh arah tersebut akan menuju ke titik optimum yang tetap berada pada daerah layak. Penyelesaian yang didapat di ruang penyelesaian tersebut ditransformasikan kembali dengan transformasi invers, yaitu

. Proses iterasi ini diulang hingga penyelesaian optimum dicapai. 1

− k T

ABSTRACT

Linear programming problems not only can be solved with graphic method or simplex method, but also it can be solved with interior-point method. One of the classes of the interior-point method is primal affine-scaling method. To find the solution of linear programming using primal affine-scaling method, we should start by selecting the interior-point solution , namely from inside feasible region in original solution space. Then, is transformed with an affine-scaling transformation, which is called , so that the selected interior-point solution is placed near the transformed feasible region. The image of called . Then, from we move to another interior-point , which improves the value of objective function , in accordance to the iteration . Here, is the direction of steepest descent that causes the fastest rate of decrease in the objective function. While

k x k

x k T

k

x yk

k

y yk+1

f yk+1 =yk +α_kdk_y dk_y

k

α is the step-length which gives how far the direction can move to the optimum point but it still remains in the feasible region. The solution, which is found in the solution space, is transformed back with inverse transformation, called . This process will be repeated until we obtain an optimum solution with the desired accuracy.

1 − k T

METODE PRIMAL AFFINE-SKALING

UNTUK MASALAH PROGRAM LINEAR

Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Oleh: Ajeng Retnojiwati

NIM : 013114013

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SANATA DHARMA YOGYAKARTA

2007

HALAMAN PERSEMBAHAN

“Dan apa saja yang kamu minta dalam doa dengan penuh

kepercayaan, kamu akan menerimanya.”

(Mat ius 21:22)

Terimakasih Tuhan Yesus

Engkau bantu aku melewati satu pergumulan lagi dalam hidup

Kupersembahkan karya ini untuk:

Tuhan Yesus dan Bunda Maria

Bapak, Ibu, Mas Purwiyadi, Mas

Sugeng, simbah dan keluargaku

ABSTRAK

Untuk menyelesaikan masalah program linear, selain dengan metode grafik atau metode simpleks dapat juga diselesaikan dengan metode titik-dalam. Salah satu kelas dalam metode titik-dalam adalah metode primal affine-skaling. Untuk menentukan penyelesaian masalah program linear dengan metode primal affine-skaling dimulai dengan memilih titik-dalam awal, yaitu dari suatu daerah layak di ruang penyelesaian awal. Kemudian ditransformasi oleh transformasi affine-skaling, yaitu sedemikian sehingga hasil transformasi diposisikan dekat dengan pusat di ruang penyelesaian hasil transformasi ini. Hasil transformasi sebut saja . Langkah selanjutnya, dari dijalankan ke titik-dalam lain, yaitu

yang menggerakkan nilai sampai optimum dicapai sesuai dengan alur iterasi , dengan adalah arah layak turun tercuram (steepest descent) yang menyebabkan nilai fungsi berkurang dengan cepat. Dan

k x k

x k

T xk

k x k

y yk

1 + k

y f f

k y k k k

d y

y +1 = +α dk_y

k

α adalah besarnya langkah yang menyatakan seberapa jauh arah tersebut akan menuju ke titik optimum yang tetap berada pada daerah layak. Penyelesaian yang didapat di ruang penyelesaian tersebut ditransformasikan kembali dengan transformasi invers, yaitu

. Proses iterasi ini diulang hingga penyelesaian optimum dicapai. 1

− k T

ABSTRACT

Linear programming problems not only can be solved with graphic method or simplex method, but also it can be solved with interior-point method. One of the classes of the interior-point method is primal affine-scaling method. To find the solution of linear programming using primal affine-scaling method, we should start by selecting the interior-point solution , namely from inside feasible region in original solution space. Then, is transformed with an affine-scaling transformation, which is called , so that the selected interior-point solution is placed near the transformed feasible region. The image of called . Then, from we move to another interior-point , which improves the value of objective function , in accordance to the iteration . Here, is the direction of steepest descent that causes the fastest rate of decrease in the objective function. While

k x k

x k T

k

x yk

k

y yk+1

f yk+1 =yk +α_kdk_y dk_y

k

α is the step-length which gives how far the direction can move to the optimum point but it still remains in the feasible region. The solution, which is found in the solution space, is transformed back with inverse transformation, called . This process will be repeated until we obtain an optimum solution with the desired accuracy.

1 − k T

KATA PENGANTAR

Puji syukur penulis panjatkan kepada Tuhan Yesus atas segala kasih dan perlindungan-Nya sehingga penulisan skripsi ini dapat terselesaikan. Skripsi ini disusun dalam rangka melengkapi salah satu syarat untuk memperoleh gelar Sarjana Sains pada Program Studi Matematika, Jurusan Matematika, Fakultas Matematika dan Ilmu Alam, Universitas Sanata Dharma Yogyakarta.

Penulisan skripsi ini tidak lepas dari bantuan dan dukungan dari berbagai pihak. Oleh karena itu, pada kesempatan ini penulis ingin menyampaikan ucapan terima kasih kepada:

1. Ibu Lusia Krismiyati, S.Si, M.Si sebagai dosen pembimbing yang penuh perhatian dan kesabaran telah membimbing serta memberi saran dan kritik kepada penulis selama proses penulisan skripsi ini.

2. Bapak Y.G. Hartono, S.Si, M.Sc sebagai dosen pembimbing dan selaku Ketua Program Studi Matematika, dosen pembimbing akademik dan dosen penguji yang telah memberikan dukungan, saran dan kritik dalam skripsi ini.

3. Bapak Ir. Ig. Aris Dwiatmoko, M.Sc selaku Dekan fakultas MIPA yang telah memberi dukungan dalm penulisan skripsi ini.

4. Ibu Any Herawati, S.Si, M.Si selaku dosen penguji yang telah memberikan saran dan kritik dalam skripsi ini.

5. Bapak dan Ibu dosen di Fakultas MIPA yang telah membimbing dan mendidik penulis selama menuntut ilmu di Universitas Sanata Dharma.

6. Bapak dan Ibu karyawan Universitas Sanata Dharma, khususnya sekretariat fakultas MIPA dan perpustakaan Universitas Sanata Dharma atas segala bantuan dan fasilitas yang telah diberikan.

7. Sahabat-sahabatku seperjuangan angkatan 2001: Very, Upik, Yuli, Dani, Tabita, Fanya, Andre, Indah, Ariel, Agnes, Erika, Wiwit, Deta, Maria, Rita, Alam, Vrysca, Daniel, Tedy, Ray, April, Ardi, serta kakak-kakak angkatan 1998, 1999, 2000 dan adik-adik angkatan 2002, 2003, 2004 yang telah membantu dan mendukung penulis.

8. Dhe-dhe dan keluarga yang telah memberi dukungan, semangat dan doanya. 9. Tien, Mei, Bayu, Helbin, Sinta, Heni, Henri, Mbak uci dan keluarga, mbak Novi,

Murni, Rini ikom, teman-teman Gloria Graha dan temen-temen radio masdha, yang telah memberi dukungan, semangat dan doanya.

10.Semua pihak yang telah membantu penulis baik secara langsung maupun tidak langsung hingga selesainya penulisan skripsi ini.

Penulis menyadari bahwa skripsi ini masih banyak kekurangannya. Oleh karena itu, penulis mengucapkan terima kasih bila ada kritik dan saran yang dapat membangun penulis. Penulis berharap semoga skripsi ini dapat bermanfaat dan menjadi referensi bagi pembaca.

Yogyakarta, 7 Februari 2007

Penulis

DAFTAR ISI

Halaman

HALAMAN JUDUL ……….…………..…. i

HALAMAN PERSETUJUAN PEMBIMBING ……….……….. ii

HALAMAN PENGESAHAN ……….. iii

HALAMAN PERSEMBAHAN ……….…..…… iv

PERNYATAAN KEASLIAN KARYA ……….……….…. v

ABSTRAK ……….……….….. vi

ABSTRACT ……….……….... vii

KATA PENGANTAR ……….……….…… viii

DAFTAR ISI ……….……….….. x

DAFTAR GAMBAR ………..… xiii

TABEL ……… xiii

BAB I PENDAHULUAN ………..…... 1

A. Latar Belakang Masalah ……….…. 1

B. Rumusan Masalah ……….…...…… 3

C. Pembatasan Masalah ……….…………...…. 4

D. Tujuan Penulisan ……….….. 4

E. Manfaat Penulisan ……... 4

F. Metode Penulisan ………..…………..…….. 5

G. Sistematika Penulisan ……….……….. 5

BAB II ORTOGONALITAS DAN OPTIMISASI UNTUK PERSOALAN

LINEAR ………. 6

A. Sistem Persamaan Linear Dan Matriks ………...…………. 6

B. Ruang Vektor ………..……….… 10

1. Ruang Vektor ………..…..………..………... 10

2. Hasil Kali Dalam Dan Ortogonalitas …... 22

3. Transformasi Linear ……….………… 31

C. Masalah Program Linear ………...…. . 32

1. Bentuk Standar Masalah Program Linear ……….. 32

2. Dualitas ………. . 37

D. Optimisasi Fungsi Untuk Persoalan Linear ………..…… 40

1. Optimisasi ……….. 40

2. Kelayakan ………...….... 41

E. Metode Arah Layak ………...…... 42

F. Metode Arah Turun Tercuram (Steepest Descent) …………... 44

BAB III METODE PRIMAL AFFINE-SKALING ………..…. 45

A. Metode Primal Affine-Skaling ………..……. 46

1. Transformasi Affine-Skaling ……….... 49

2. Menentukan Arah Layak ………..… 61

a. Bentuk Masalah Program Linear di Ruang Penyelesaian Hasil Transformasi ………. 61

b. Menentukan Arah Layak ………..…… 66

c. Perumusan Arah Langkah Dengan Arah Turun Tercuram ... 70

3. Menentukan Besar Langkah α_k ………..………...…… 74

B. Algoritma Primal Affine-Skaling ………...…..… 83

C. Aplikasi Metode Primal Affine-Skaling Untuk Menyelesaikan Masalah Program Linear Dengan Program Matlab ………...… 87

BAB IV PENUTUP ...….. 99

A. Kesimpulan ………...…….. 99

B. Saran ………...… 100

DAFTAR PUSTAKA ………. 101

LAMPIRAN ……….. 102

DAFTAR GAMBAR

Halaman

Gambar 1.1 Metode titik-dalam vs metode simpleks ……….. 2

Gambar 2.1 c=x+y ……….…. 28

Gambar 3.1 Ide transformasi affine-skaling ……….…………...…… 50

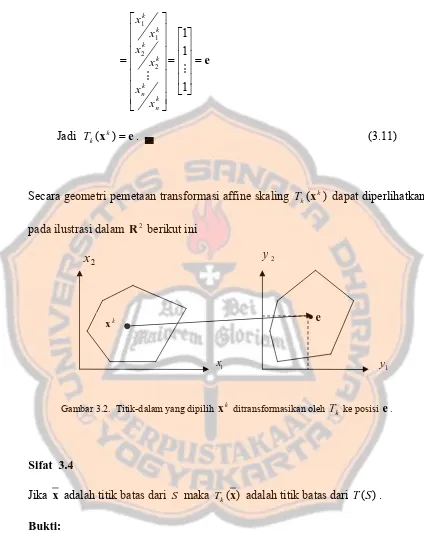
Gambar 3.2 Titik-dalam xk ditransformasikan oleh T_k ke posisi e ………... 54

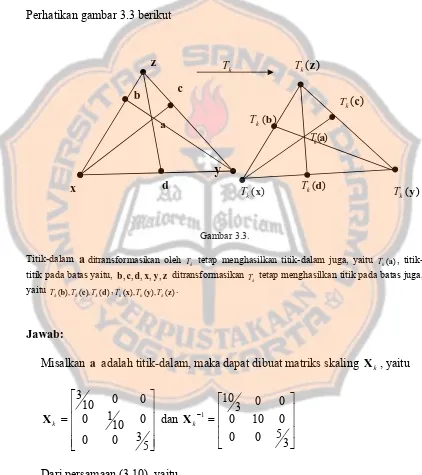
Gambar 3.3 Sifat-sifat dari transformasi affine-skaling ………. 59

Gambar 3.4 Daerah layak soal A ……… 65

Gambar 3.5 Daerah layak soal B ………...…. 66

Gambar 3.6 Proyeksi k ke ruang nol ……….. 71

c − Ak Gambar 3.7 Daerah layak sebelum dikenai transformasi affine skaling ……... 94

Gambar 3.8 Daerah layak yang sudah ditransformasi oleh transformasi affine skaling ……….. 95

TABEL Halaman Tabel 1 Hasil iterasi contoh 3.4 ………..…………. 103

Tabel 2 Hasil iter5asi contoh 3.5 ………. 104

BAB I

PENDAHULUAN

A. LATAR BELAKANG MASALAH

Masalah program linear adalah suatu masalah penyelesaian sistem

per-samaan linear. Masalah program linear dapat diselesaikan dengan cara metode

grafik atau metode simpleks. Pada metode grafik penyelesaiannya khusus

dikerja-kan hanya untuk dua variabel saja, sehingga apabila memuat lebih dari dua

varia-bel akan sulit menyelesaikannya. Meskipun dalam prakteknya masalah program

linear jarang yang hanya memuat dua variabel tetapi metode grafik

mempermu-dahkan orang dalam memahami pengertian-pengertian yang timbul dalam

ma-salah program linear. Untuk menyelesaikan mama-salah program linear yang memuat

dua atau lebih variabel dapat digunakan metode simpleks.

Ada metode lain yaitu metode titik-dalam yang dapat digunakan untuk

menyelesaikan masalah program linear yang memuat dua atau lebih variabel.

Perbedaan proses penyelesaian antara metode simpleks dan metode

titik-dalam, yaitu pada metode simpleks penyelesaian dilakukan dengan meninjau

setiap titik-titik sudut pada batas dari daerah layak hingga dicapai titik optimum.

Sedangkan pada metode titik-dalam dengan meninjau titik-titik yang berada dalam

daerah layak hingga dicapai titik optimum. Sehingga apabila program linear

me-muat masalah yang kompleks maka proses penyelesaian yang dilakukan dengan

metode titik-dalam dapat lebih cepat dan efisien dibandingkan dengan metode

yang kompleks maka program linear tersebut juga akan memiliki banyak titik

ba-tas. Sehingga dibutuhkan proses lebih panjang dibandingkan dengan metode

titik-dalam untuk mencapai titik optimum.

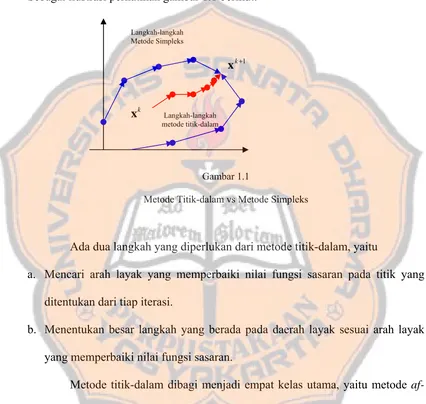
Sebagai ilustrasi perhatikan gambar 1.1 berikut:

Gambar 1.1

Metode Titik-dalam vs Metode Simpleks

Ada dua langkah yang diperlukan dari metode titik-dalam, yaitu

a. Mencari arah layak yang memperbaiki nilai fungsi sasaran pada titik yang

ditentukan dari tiap iterasi.

b. Menentukan besar langkah yang berada pada daerah layak sesuai arah layak

yang memperbaiki nilai fungsi sasaran.

Metode titik-dalam dibagi menjadi empat kelas utama, yaitu metode af-fine-skaling (affine-scaling method), metode proyektif (projective method) atau lebih dikenal dengan metode Karmarkar , metode path-following (path-following method), dan metode potensial-reduksi (potential-reduction method).

Dalam tulisan ini hanya akan dibahas metode affine-skaling. Metode af-fine-skaling adalah salah satu metode titik-dalam yang paling sederhana diantara

k x

Langkah-langkah Metode Simpleks

1

+ k x

semua metode titik-dalam. Disebut metode affine-skaling karena transformasi yang digunakan adalah transformasi affine-skaling. Metode affine-skaling yang akan digunakan dibatasi hanya untuk masalah primal program linear yang

meminimumkan fungsi sasaran. Sehingga metode ini disebut juga sebagai

me-tode primal affine-skaling.

Ide dasar metode primal affine-skaling yaitu dimulai dengan memilih suatu titik-dalam awal didalam daerah layak. Kemudian titik dalam yang dipilih

ditransformasi oleh transformasi affine-skaling sedemikian sehingga hasil transformasi titik-dalam yang dipilih diposisikan dekat dengan pusat di ruang

penyelesaian hasil transformasi. Hasil transformasi titik-dalam yang dipilih

dijalankan ke suatu titik-dalam lain dengan arah layak dan besar langkah yang

sesuai. Penyelesaian yang didapat di ruang penyelesaian tersebut ditransformasi

kembali dengan transformasi invers yang sesuai. Proses iterasi ini diulang hingga

penyelesaian optimum dicapai.

Selain dibahas metode primal affine-skaling juga akan dibahas aplikasinya dengan menggunakan program matlab untuk menyelesaikan masalah

program linear.

B. RUMUSAN MASALAH

Berdasarkan latar belakang masalah di atas, maka dibuat rumusan

seba-gai berikut:

1. Bagaimana menyelesaikan masalah program linear dengan menggunakan

2. Bagaimana aplikasi dari metode primal affine-skaling dengan mengguna-kan program matlab?

C. PEMBATASAN MASALAH

1. Penulis hanya akan membahas masalah dalam bentuk meminimumkan,

se-hingga masalah memaksimumkan harus diubah dalam bentuk

memini-mumkan, yaitu negatif dari maksimum fungsinya.

2. Metode yang digunakan adalah metode primal affine-skaling. 3. Transformasi yang digunakan adalah transformasi affine-skaling.

4. Daerah layak dari soal program linear adalah terbatas dan tidak kosong.

5. Hanya memuat variabel kurang dari atau sama dengan 10 (n≤10).

D. TUJUAN PENULISAN

Sesuai dengan latar belakang di atas, penulisan skripsi ini bertujuan

un-tuk menunjukkan langkah-langkah metode primal affine-skaling untuk menyele-saikan masalah program linear yang memuat n≤10 dan dapat dipertanggung-jawabkan langkah demi langkah.

E. MANFAAT PENULISAN

Manfaat dari penulisan skripsi ini adalah memberikan tambahan referensi

F. METODE PENULISAN

Metode yang digunakan dalam skripsi ini adalah penelitian kepustakaan,

yaitu dengan mempelajari buku-buku yang berkaitan dengan topik skripsi ini,

se-hingga dalam tulisan ini tidak ditemukan hal-hal yang baru.

G. SISTEMATIKA PENULISAN

Penulisan skripsi ini menggunakan sistematika sebagai berikut:

Bab I PENDAHULUAN

Bab ini berisi latar belakang masalah, perumusan masalah, pembatasan

masalah, tujuan penulisan, manfaat penulisan, dan metode penulisan.

Bab II ORTOGONALITAS DAN OPTIMISASI UNTUK PERSOALAN

LINEAR

Bab ini berisi tentang dasar teori yang berkaitan dan digunakan dalam

metode primal affine-skaling, yaitu mengenai sistem persamaan linear dan matriks, ruang vektor, masalah program linear, optimisasi fungsi

untuk persoalan linear, metode arah layak dan metode arah turun

tercuram.

Bab III METODE PRIMAL AFFINE-SKALING

Bab ini membahas tentang langkah-langkah metode primal affine-skaling dan aplikasinya menggunakan program matlab.

Bab IV PENUTUP

Bab ini berisi beberapa kesimpulan dan saran berdasarkan hasil

BAB II

ORTOGONALITAS DAN OPTIMISASI UNTUK PERSOALAN LINEAR

Pada bab ini akan dibahas hal-hal yang melandasi bab berikutnya.

De-finisi, teorema serta konsep-konsep mengacu pada daftar pustaka.

A. Sistem Persamaan Linear Dan Matriks Definisi 2.1 Persamaan Linear

Persamaan linear dalam n variabel x₁,x₂,L,x_n adalah persamaan yang dapat dinyatakan dalam bentuk

b x a x

a x

a_{1 1}+ _{2 2} +L+ _{n n} = (2.1)

dengan a1,a2,K,an dan b adalah konstanta real dan a1,a2,K,an tidak semua

sama dengan nol.

Definisi 2.2 Sistem Persamaan Linear

Suatu sistem persamaan linear m×n adalah himpunan m persamaan linear dengan n variabel, yang dapat dinyatakan dalam bentuk

⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧

1 1

1 21

1 11

x a

x a

x a

m

M

+ + +

2 2

2 22

2 12

x a

x a

x a

m +

+ +

L O L L

+ + +

m n mn

n n

n n

b x a

b x a

b x a

= = =

M

2 2

1 1

(2.2)

Dalam sistem persamaan linear m×n, dapat terjadi

n m n

m n

m= , > atau < . Apabila x1 =t1,x2 =t2,L,xn =tn dimana t1,t2,K,tn

adalah konstanta-konstanta real yang memenuhi semua persamaan linear dalam

sistem (2.2), maka pasangan terurut (t₁,t₂,K,tn) disebut penyelesaian atau

jawab dari sistem persamaan linear (2.2).

Definisi 2.3 Konsisten dan Tidak Konsisten

1. Sistem persamaan linear disebut konsisten jika sistem persamaan tersebut mempunyai penyelesaian.

2. Sistem persamaan linear disebut tidak konsisten jika sistem persamaan terse-but tidak mempunyai penyelesaian.

Sistem yang konsisten dapat mempunyai tepat satu penyelesaian atau mempunyai

banyak penyelesaian.

Sistem persamaan linear (2.2) di atas dapat dituliskan dengan notasi

ma-triks sebagai berikut:

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

= ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

m n

mn m

m

n n

b b b

x x x

a a

a

a a

a

a a

a

M M

L M O M M

L L

2 1 2

1

2 1

2 22

21

1 12

11

(2.3)

Atau lebih singkat ditulis Ax=b, dimana A=(a_ij) yaitu matriks koefisien,

( )

xj

=

Definisi 2.4Sistem Persamaan Linear Homogen

Suatu sistem persamaan linear disebut sistem persamaan linear homogen jika konstanta 0b_i = , untuk setiap i=1,2,...,m. Sistem persamaan linear homogen mempunyai bentuk umum:

⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ 1 1 1 21 1 11 x a x a x a m M + + + 2 2 2 22 2 12 x a x a x a m + + + L O L L + + + 0 0 0 2 1 = = = n mn n n n n x a x a x a

M (2.4)

Sistem persamaan linear homogen selalu konsisten karena

0 ..., , 0 , 0 ₂

1 = x = xn =

x selalu merupakan penyelesaian. Penyelesaian ini disebut

penyelesaian trivial. Jika ada penyelesaian lain maka penyelesaian itu disebut

penyelesian nontrivial.

Definisi 2.5Matriks Lengkap

Matriks lengkap dari sistem persamaan linear (2.2) adalah

⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 1 21 11 m a a a M 2 22 12 m a a a L O L L mn n n a a a M 2 1 ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ m b b b M 2 1

Definisi 2.6Operasi Baris Elementer

Operasi baris elementer pada suatu matriks adalah salah satu operasi:

2. Mengalikan suatu baris dengan konstanta tak nol, yakni mengalikan baris ke-i

dengan bilangan c,c≠0, dengan notasi cRi.

3. Mengganti suatu baris dengan hasil penjumlahan baris tersebut dan kelipatan

baris lain, yakni mengganti baris ke-i ditambah c kali baris ke- j, dengan no-tasi R_i +cR_j.

Definisi 2.7 Matriks Ekivalen Baris

Matriks B dikatakan ekivalen baris dengan matriks A jika terdapat matriks ele-menter E₁,E₂,...,E_k sehingga B=E_kE_k−1...E₁A atau A=E₁−1E₂−1...E_k−1B.

Dengan operasi baris elementer, matriks lengkap dari suatu sistem

per-samaan linear harus diubah menjadi suatu matriks dari sistem perper-samaan linear

yang mudah dicari jawabnya, yakni dengan matriks eselon.

Definisi 2.8Matriks Eselon

Matriks E disebut matriks eselon jika memenuhi dua sifat berikut:

1. Setiap baris yang hanya terdiri dari bilangan nol terletak sesudah baris yang

memuat elemen tak nol.

2. Pada setiap baris dari matriks E yang mempunyai elemen tak nol, elemen tak nol yang pertama harus terletak di kolom sebelah kanan elemen tak nol dari

baris sebelumnya.

B.Ruang Vektor 1. Ruang Vektor

Definisi 2.9 Ruang Vektor

Ruang Vektor atas lapangan F adalah himpunan tidak kosong V yang dileng-kapi dengan operasi penjumlahan dan operasi perkalian dengan skalar sedemikian

sehingga ∀x,y,z∈V dan ∀α,β∈F memenuhi syarat - syarat berikut: a. x+y∈V

b. x+y =y+x (sifat komutatif)

c. x+(y+z)=(x+y)+z (sifat asosiatif)

d. Terdapat elemen 0∈V,∀x∈V , x+0=x (unsur identitas)

e. ∀x∈V ∃(−x)∈V sehingga x+(−x)=0 (elemen invers)

f. αx∈V

g. α(x+y)=αx+αy (sifat distributif)

h. (α+β)x=αx+βx

i. 1x=x

j. (αβ)x=α(βx)

Contoh 2.1 Misalkan ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = n x x x M 2 1 x dan ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = n y y y M 2 1

y adalah vektor – vektor di Rn. Penjumlahan

pada Rn didefinisikan sebagai berikut:

n

n n n

n x y

y x y x y y y x x x R y x y

x ∀ ∈

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + + + = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ =

+ 2 2 , ,

1 1 2 1 2 1 M M

M (2.5)

dan operasi perkalian dengan skalar α di R didefinisikan sebagai berikut:

R R

x

x ∀ ∈ ∀ ∈

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = α α α α α

α 2 , ,

1 2 1 n n n x x x x x x M

M (2.6)

Tunjukkan bahwa Rn _{merupakan ruang vektor.} Bukti: Misalkan ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = n x x x M 2 1 x , ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = n y y y M 2 1

y , dan

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = n z z z M 2 1

z , ∀x,y,z∈Rn, ∀α,β∈R

a. Akan ditunjukkan x+y∈Rn. Sudah jelas (dari persamaan (2.5)) b. Akan ditunjukkan x+y=y+x

x y y

x = +

c. Akan ditunjukkan x+(y+z)=(x+y)+z ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + + + + + + = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + + + + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = + + ) ( ) ( ) ( )

( 2 2 2

1 1 1 2 2 1 1 2 1 n n n n n

n x y z

z y x z y x z y z y z y x x x M M M z y x ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + + + + + + = n n n y z x z y x z y x ) ( ) ( ) ( 2 2 2 1 1 1 M ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + + + = n n n z z z y x y x y x M M 2 1 2 2 1 1 z y x+ +

=( )

d. Akan ditunjukkan ada elemen identitas terhadap operasi penjumlahan.

Elemen identitasnya

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 0 0 0 M

0 sehingga

x 0 x = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + + + = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = + n n n x x x x x x x x x M M M M 2 1 2 1 2 1 0 0 0 0 0 0

e. Akan ditunjukkan mempunyai invers.

Invers dari

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = n x x x M 2 1

x adalah

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − = − n x x x M 2 1

x sehingga

0 x x = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − + − + − + = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = − + 0 0 0 ) ( ) ( ) ( )

( 2 2

1 1 2 1 2 1 M M M M n n n

n x x

x x x x x x x x x x

g. Akan ditunjukkan α(x+y)=αx+α y

y x y

x α α

α α α α α α α α α α α α α α = + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + + + = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + + + = + n n n n n n y y y x x x y x y x y x y x y x y x M M M M 2 1 2 1 2 2 1 1 2 2 1 1 ) (

h. Akan ditunjukkan (α +β)x=αx+βx

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + + + = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + + + = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + = + n n n n n n x x x x x x x x x x x x x x x x x x β β β α α α β α β α β α β α β α β α β α β α M M M M M 2 1 2 1 2 2 1 1 2 1 2 1 ) ( ) ( ) ( ) ( ) ( x x x β α + =

i. Akan ditunjukkan ada elemen identitas terhadap operasi perkalian

x x = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = n n n x x x x x x x x x M M M 2 1 2 1 2 1 1 1 1 1 1

j. Akan ditunjukkan (αβ)x=α(βx)

) ( _) ( ) ( ) ( ) ( ) ( ) ( ) ( 2 1 2 1 2 1 2 1 x

x α β

β β β α β α β α β α β α β α β α αβ β α = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = n n n n x x x x x x x x x x x x M M M

M . ~

Definisi 2.10 Subruang (Subspaces)

a. untuk x∈W dan sebarang skalar α∈F maka αx∈W

b. untuk x∈W dan y∈W maka vektor x+y∈W

maka W disebut subruang vektor dari V .

Definisi 2.11 Ruang Nol (Null Spaces)

Misalkan A adalah matriks berukuran m×n. Misalkan N(A) menyatakan him-punan semua penyelesaian dari sistem persamaan homogen Ax=0. Jadi

} {

)

(A = x∈Rn Ax=0

N (2.7)

) (A

N disebut sebagai ruang nol.

Contoh 2.2

Tunjukkan bahwa N(A)={x∈Rn Ax=0} merupakan ruang vektor.

Bukti: Misalkan ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = n x x x M 2 1 x , ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = n y y y M 2 1

y , dan

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = n z z z M 2 1

z , ∀x,y,z∈Rn, ∀α,β∈R

a. Akan ditunjukkan Ax+Ay∈N(A)

0 0 0 Ay Ax = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = + = + 0 0 0 0 0 0 0 0 0 M M M

Jadi Ax+Ay∈N(A)

= ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = + = + 0 0 0 0 0 0 0 0 0 0 0 0 M M M M 0 0 Ay

Ax 0+0=Ay+Ax

c. Akan ditunjukkan Ax+(Ay+Az)=(Ax+Ay)+Az

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = + + = + + 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ) ( ) ( M M M M M M 0 0 0 Az Ay Ax Az Ay Ax 0 0

0+ + = + +

=( ) ( )

d. Akan ditunjukkan ada elemen identitas terhadap operasi penjumlahan

Elemen identitasnya

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 0 0 0 M

0 sehingga

Ax 0 0

0 0

Ax = =

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = + = + 0 0 0 0 0 0 0 0 0 M M M

e. Akan ditunjukkan ada elemen invers

Invers dari

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = = 0 0 0 M 0

Ax adalah

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − = − = − 0 0 0 ) ( M 0

Ax sehingga

f. Akan ditunjukkan αAx∈N(A) ) ( 0 0 0 0 0 0 A 0 0

Ax = ∈N

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = = M M α α α

g. Akan ditunjukkan α(Ax+Ay)=αAx+αAy

(

0 0

)

Ax Ay

Ay

Ax α α

α α α α α α α α α = + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = + = + 0 0 0 0 0 0 0 0 0 0 0 0 ) ( M M M M

h. Akan ditunjukkan (α +β)Ax= =αAx+βAx

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + + + = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + = + = + 0 0 0 0 0 0 0 ) ( 0 ) ( 0 ) ( 0 0 0 ) ( ) ( ) ( β β β α α α β α β α β α β α β α β α M M M M Ax Ax Ax Ax β α + =

i. Akan ditunjukkan ada elemen identitas terhadap operasi perkalian

Ax 0 0

Ax = =

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = = 0 0 0 0 0 0 1 1 1 M M

j. Akan ditunjukkan (αβ)Ax=α(βAx)

) ( 0 0 0 0 ) ( 0 ) ( 0 ) ( 0 0 0 ) ( ) ( )

( Ax Ax α βAx

β β β α αβ αβ αβ αβ αβ αβ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = = M M

Teorema 2.1

} {

)

(A = x∈Rn Ax=0

N merupakan subruang dari n

R .

Bukti:

Akan dibuktikan bahwa N(A) adalah subruang dari n

R , yakni

a. Misalkan x∈N(A) dan α suatu skalar, maka A(αx)=α(Ax)=α0=0. Jadi αx∈N(A).

b.Misalkan x dan y adalah elemen – elemen dari N(A), maka

0 0 0 Ay Ax y x

A( + )= + = + = Jadi )x+y∈N(A .

Dari (a) dan (b) terbukti bahwa N(A) adalah subruang dari Rn. ▄

Definisi 2.12 Kombinasi Linear

Misalkan x₁,x₂,K,x_n adalah vektor – vektor dalam suatu ruang vektor V atas lapangan F . Jumlahan vektor-vektor yang berbentuk

n nx x

x α α

α_{1 1}+ _{2 2} +L+ (2.8)

disebut suatu kombinasi linear dari x₁,x₂,K,x_n, dengan skalarα₁,K,α_n∈F.

Definisi 2.13 Merentang (span)

Jika x₁,x₂,K,x_n adalah vektor-vektor pada ruang vektor V dan jika masing-masing vektor pada V dapat dinyatakan sebagai kombinasi linear dari

n x x

V dan dilambangkan S(x₁,x₂,K,x_n).

Teorema 2.2

Jika x₁,x₂,K,x_n adalah vektor-vektor dalam ruang vektor V maka )

, , ,

( _{1 2 n}

S x x K x adalah subruang dari V .

Bukti:

Misalkan β suatu skalar dan misalkan b=α₁x₁+α₂x₂ +L+α_nx_n adalah sebarang elemen dari S(x₁,x₂,K,x_n).

Maka βb=(βα₁)x₁+(βα₂)x₂ +L+(βα_n)x_n

Jadi βb∈S(x₁,x₂,K,x_n)

Selanjutnya akan ditunjukkan bahwa sebarang jumlah elemen-elemen dari

) , , ,

( _{1 2 n}

S x x K x juga berada dalam S(x₁,x₂,K,x_n)

Misalkan b=α₁x₁+α₂x₂ +L+α_nx_n dan c=β₁x₁+β₂x₂ +L+β_nx_n Maka b+c=(α₁+β₁)x₁ +(α₂ +β₂)x₂ +L+(α_n +β_n)x_n

Jadi b+c∈S(x₁,x₂,K,x_n)

Jadi S(x₁,x₂,K,x_n) adalah subruang dari V . ▄

Definisi 2.14 Himpunan Perentang

Himpunan }{x₁,x₂,K,x_n disebut himpunan perentang untuk ruang vektor V

Contoh 2.3

Misalkan e_i adalah vektor dalam n

R yang komponen ke-i adalah 1 dan kompo-nen yang lainnya semua sama dengan nol, untuk i=1,2,K,n. Jadi

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡ = ⎥

⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡ = ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡ =

1 0 0

, ,

0 1 0

,

0 0 1

2 1

M L

M

M e en

e .

Setiap vektor n

R

v∈ dapat dinyatakan sebagai kombinasi linear dari

vektor-vek-tor e₁,e₂,L,e_n tersebut, yaitu jika

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

=

n v v v

M

2 1

v adalah sebarang vektor dalam n

R ,

maka v =v₁e₁+v₂e₂ +L+v_ne_n. Oleh karena itu {e₁,e₂,L,e_n}adalah himpunan perentang untuk n

R . ~

Definisi 2.15 Bebas linear (linearly independent)

Vektor – vektor x1,x2,K,xn dalam ruang vektor V disebut bebas linear jika 0

x x

x +α + +αn n =

α_{1 1 2 2} L (2.9)

mengakibatkan semua skalar – skalar α₁,K,α_n harus sama dengan nol.

Definisi 2.16 Bergantung Linear (linearly dependent)

Vektor – vektor x1,x2,K,xn dalam ruang vektor V disebut bergantung linear

jika terdapat skalar – skalar α₁,K,α_n yang tidak semuanya nol sehingga

0 x x

x +α + +α_{n n} =

Definisi 2.17 Basis

Misalkan V suatu ruang vektor atas lapangan F . Himpunan vektor - vektor

{

x1,x2,.K,xn

}

membentuk basis untuk ruang vektor V jika dan hanya jika

a.

{

x1,x2,.K,xn

}

bebas linear

b.

{

x₁,x₂,.K,x_n

}

merentang V

Contoh 2.4

Tunjukkan bahwa

{

e₁,e₂,K,e_n

}

adalah basis.

Bukti:

Dalam contoh 2.3 telah ditunjukkan bahwa e₁,e₂,K,e_n merentang n

R . Bila

0 e e

e +v + +v_{n n} =

v_{1 1 2 2} L maka

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

= ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

0 0 0

2 1

M M

n v v v

, sehingga v₁ =v₂ =L=v_n =0.

Jadi e₁,e₂,K,e_n bebas linear.

Maka

{

e₁,e₂,K,e_n

}

merupakan basis untuk Rn. ~ Basis tersebut disebut basis baku untuk n

R

Definisi 2.18 Vektor-Vektor Baris dan Vektor-Vektor Kolom

Misalkan matriks

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

=

mn m

m

n n

a a

a

a a

a

a a

a

L M O M M

L L

2 1

2 22

21

1 12

11

A . Vektor-vektor dalam R1×n yaitu

[

a11 a12 a1n

]

1 = L

yang dibentuk dari baris-baris matriks A dinamakan vektor-vektor baris dari A

dan vektor-vektor dalam Rm, yaitu

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

=

1 21 11

1

m a a a

M

k ,

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

=

2 22 12

2

m a

a a

M

k ,

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

=

mn n n

n

a a a

M L 2 1

,k

yang dibentuk dari kolom-kolom matriks A, dinamakan vektor-vektor kolom

dari A.

Definisi 2.19 Ruang Baris dan Ruang kolom

a. Subruang yang direntang oleh m vektor baris matriks A merupakan subruang dari R1×n dan disebut ruang baris A.

b. Subruang yang direntang oleh n vektor kolom matriks A merupakan subruang dari Rm dan disebut ruang kolom A. Ruang kolom A dapat dinotasikan

{

m n

}

R(A)= b∈R b=Ax untuk x∈R

Definisi 2.20 Rank Dari Matriks

Rank dari matriks A berukuran m×n ditunjukkan dengan r(A). Rank matriks

2. Hasil Kali Dalam Dan Ortogonalitas Definisi 2.21 Ruang Hasil Kali Dalam

Hasil kali dalam pada ruang vektor V _{adalah sebuah operasi pada} V yang menunjuk setiap pasang vektor - vektor x dan y di dalam V sebuah bilangan real x,y _{yang memenuhi syarat berikut:}

a. x,x ≥0,∀x≠0dan x,x =0 jika hanya jika x=0. b. x,y = y,x ∀x,y∈V

c. αx+βy,z =α x,z +β y,z , ∀x,y,z∈V dan ∀α,β∈R

Sebuah ruang vektor V dengan hasil kali dalamnya disebut ruang hasil kali dalam .

Contoh 2.5

Ruang vektor Rn. Tunjukkan bahwa hasil kali skalar yang didefinisikan:

[

]

n n

n n T

y x y

x y x y y y x x

x = + + +

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

=

= K

M

L 2 _{1 1 2 2} 1

2 1

,y x y

x . (2.11)

adalah hasil kali dalam untuk n

R (yang disebut hasil kali dalam baku). Persamaan (2.11) dapat juga ditulis

∑

=

=

= n

i i i T

y x

1

,y x y

x (2.12)

dengan T

Bukti:

Ambil sebarang vektor

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = n x x x M 2 1 x , ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = n y y y M 2 1

y , dan

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = n z z z M 2 1

z dalam ruang

vektorRn dan sebarang skalar α,β∈R

a. Dibuktikan x,x =xTx≥0

Diketahui x,x =xTx

[

]

0

, 2 ₁2 ₂2 2

1

2

1 = + + + ≥

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = = _n n n T x x x x x x x x x K M L x x x x

Jadi x,x ≥0

)

(⇒ Diketahui x,x =0

Untuk x₁2 +x₂2 +...+x_n2 =0 diperoleh x₁ = x₂ =...= x_n =0

jadi x =0

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 0 0 0 2 1 M M n x x x )

(⇐ Diketahui x=0

Dibuktikan x,x =xTx=0

0 0 x x x

x, = T = T

[

]

Jadi xTx=0.0+0.0+K+0.0=0

b. Dibuktikan x,y = y,x ∀x,y∈Rn

yaitu dibuktikan x,y =xTy =yTx= y,x

y x y x = T

,

[

]

n n

n

n x y x y x y

y y y x x

x = + + +

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = K M

L 2 _{1 1 2 2} 1 2 1 n nx y x y x

y + + +

= _{1 1 2 2} K

[

]

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = n n x x x y y y M L 2 1 2 1 x y x y = ,

= T

Jadi xTy =yTx (2.13)

Jadi terbukti n

R y x x y y

x, = , ∀ , ∈

c. Dibuktikan αx+βy,z =α x,z +β y,z , ∀x,y,z∈Rn , ∀α,β∈R

[

]

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + + + = + n n n z z z y x y x y x M L 2 1 2 2 1 1 , α β α β α β β

αx y z

n n n

nz y z y z y z x

z x z

x α α β β β

α + + + + + + +

= _{1 1 2 2} K _{1 1 2 2} K

) (

)

(x₁z₁+x₂z₂ + +xnzn + y₁z₁ +y₂z₂ + +ynzn

[

]

[

]

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

+ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

=

n n

n n

z z z y y

y z

z z x x

x

M L

M

L 2

1

2 1 2

1

2

1 β

α

z y z xT β T

α +

= (2.14)

z y z

x, β ,

α +

=

Jadi terbukti n

R z y x z

y z

x z

y

x+β , =α , +β , , ∀ , , ∈

α

Dari (a), (b), (c) terbukti bahwa hasil kali dalam di ruang vektor Rn adalah hasil kali skalar x,y =xTy. ~

Definisi 2.22 Panjang atau norma

Jika x adalah sebuah vektor di dalam sebuah ruang hasil kali dalam n R , pan-jang atau norma dari x didefinisikan

2 2

2 2 1

)

( T = x +x + +x_n

= x x K

x (2.15)

Definisi 2.23 Ortogonal

Dua vektor dalam Rn, yaitu xdany, dikatakan orthogonal, dilambangkan

y x⊥ , jika

0 =

y

xT (2.16)

Definisi 2.24 Subruang Yang Ortogonal

Dua subruang vektor dalam n

X T = ∀ ∈

x y

x 0, dan y∈Y (2.17)

Jika X dan Y saling orthogonal, dapat ditulis sebagai X ⊥Y.

Teorema 2.3 b

Ax= adalah konsisten jika hanya jika b∈R(A)

Bukti:

) (⇒

Akan dibuktikan b∈R(A), artinya bberada di ruang kolom dari R(A) Misalkan A adalah matriks m×n dan x∈Rn

Karena Ax=b adalah konsisten maka Ax=b mempunyai penyelesaian Misalkan x adalah penyelesaian

Maka ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = n mn m m n n x x x a a a a a a a a a M L M O M M L L 2 1 2 1 2 22 21 1 12 11 Ax ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + + + + + + + + + = n mn m m n n n n x a x a x a x a x a x a x a x a x a L M L L 2 2 1 1 2 2 22 1 21 1 2 12 1 11 = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ m b b b M 2 1 b

Atau dapat ditulis

n in i

i

Perhatikan bahwa b merupakan vektor yang direntang oleh vektor-vektor kolom matriks A. Ini berarti b berada di ruang kolom A. Jadi b∈R(A)

) (⇐

Akan dibuktikan Ax=b adalah konsisten

Karena b∈R(A) maka b dapat direntangkan oleh oleh vektor-vektor kolom matriks A, yang dapat ditulis

n in i

i

i a x a x a x b = _{1 1}+ _{2 2} +L+

Berarti

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

=

n x x x

M

2 1

x memenuhi sistem Ax=b

Jadi x adalah penyelesaian Jadi Ax=b adalah konsisten. ▄

Teorema 2.4

Misalkan A matriks berukuran m×n . Andaikan matriks A mempunyai rank penuh m. Misalkan N(A) menyatakan ruang nol A dan R A( T) menyatakan ruang kolom dari AT maka N(A) dan R A( T) merupakan subruang yang saling orthogonal.

Bukti:

Misalkan x∈N(A) dan ( T)

R A y∈

Berarti cukup dibuktikan x⊥y, artinya xTy=0, )∀x∈N(A), y∈R(AT

} {

)

(A = x∈Rn Ax=0

N dan

{

n T m

}

T

R(A )= y∈R y=A z untunk z∈R

Maka xTy=xT(ATz)=(Ax)Tz

Karena Ax=0

Maka xTy=0Tz

Maka 0xTy=

Jadi x⊥y

Jadi N(A)⊥ ( T)

R A . ▄ )

( T

R A disebut juga sebagai ruang jawab dari y =ATz.

Dari teorema 2.4 telah diperlihatkan bahwa N(A)∈Rn dan R(AT)∈Rn

adalah subruang yang saling orthogonal. Misalkan x∈N(A) dan y∈R A( T) dan

y x

c= + , n R c∈ .

Gambar 2.1. c=x+y c

x

x dapat juga ditulis

y c

x= − (2.18)

Karena y =ATz, maka didapatkan

z A c

x= − T (2.19)

Kalikan kedua ruas dengan A, maka didapatkan

z AA Ac

Ax= − T

Diketahui bahwa Ax=0, maka didapatkan 0=Ac−AATz

z AA Ac= T z =(AAT)−1Ac

(2.20)

Subsitusikan persamaan (2.20) ke persamaan (2.19), maka didapatkan

Ac AA

A c

x= − T( T)−1 =[I−AT(AAT)−1A]c

=Pc (2.21)

dengan ]P=[I−AT(AAT)−1A (2.22)

Definisi 2.25 Matriks Proyeksi Orthogonal

Matriks P berukuran n×n, dengan P=[I−AT(AAT)−1A]

disebut matriks proyeksi ruang nol A atau matriks proyeksi orthogonal.

Perhatikan bahwa y∈R A( T), maka berdasarkan persamaan (2.20)

Rc Ac AA

A z A

dengan R =AT(AAT)−1A (2.24)

Sifat 2.1

Misalkan P adalah matriks proyeksi orthogonal berukuran n×n , dengan ]

) (

[I A AA 1A

P= − T T − maka

a. P2 =P

b. PT =P

Bukti:

a. Diketahui ]P=[I−AT(AAT)−1A

Maka P2 =[I−AT(AAT)−1A] [I−AT(AAT)−1A] =I 2−2I(AT(AAT)−1A)+AT(AAT)−1A

A AA AT( T)−1 = I−2(AT(AAT)−1A)+AT (AAT)−1A

= I−AT(AAT)−1A= P

b. T

P [ T( T) 1 ]T

A AA A

I− −

=

=I−AT((AAT)−1)T A

=I−AT((AAT)T)−1A

3. Transformasi Linear Definisi 2.26 Transformasi

Misalkan V dan W dua ruang vektor. Transformasi atau pemetaan atau fungsi T dari V ke dalam W adalah aturan yang memasangkan setiap elemen x

di V dengan satu dan hanya satu elemen di W. Untuk selanjutnya, transformasi ini ditulis

W V T : →

Ruang vektor V disebut daerah asal T. Nilai transformasi T untuk elemen

V ∈

x ditulis T(x) yang merupakan elemen di W. Elemen T(x) disebut peta

dari x.

Definisi 2.27 Transformasi Linear

Misalkan V dan Wdua ruang vektor. Transformasi T :V →W disebut transfor-masi linear jika

a. Untuk sebarang vektor x₁ dan x₂ di V berlaku

) ( ) ( )

(x₁ x₂ T x₁ T x₂

T + = + (2.25)

b. Untuk sebarang bilangan real s dan vektor x di V berlaku )

( )

(sx sT x

C. Masalah Program Linear

1. Bentuk Standar Masalah Program Linear

Perumusan masalah program linear dibagi menjadi dua, yakni fungsi

sa-saran dan kendala-kendala.

Definisi 2.28 Fungsi sasaran

Fungsi sasaran dalam masalah program linear dapat dinyatakan sebagai

∑

=

= p

j j jx c f

1

(2.27)

dengan p merupakan bilangan bulat yang menyatakan banyaknya variabel, x_j

merupakan variabel ke- j, dan c_j∈ R merupakan koefisien ongkos dari variabel ke- j, dengan j=1,K,p

Kendala-kendala dibagi dua, yakni kendala utama dan kendala tak

nega-tif.

Definisi 2.29 Kendala utama

Kendala utama masalah program linear berbentuk

(

)

∑

=

≥ = ≤

p

j

i j

ijx b a

1

,

, , i=1,2,...,m; j =1,K,p (2.28)

Definisi 2.30 Kendala Tak Negatif Kendala tak negatif berbentuk

; 0 ≥

j

x j =1,2,...,p. (2.29)

Untuk mencari penyelesaian dari sistem (2.28), kendala utama yang

ber-bentuk pertidaksamaan diubah menjadi persamaan, dengan cara sebagai berikut:

a. Kendala yang berbentuk ,

1

∑

=

≤

p

j

i j ijx b

a pada ruas kiri disisipkan variabel

pengetat (slack variable) s_i sedemikian sehingga dipenuhi:

∑

=

= +

p

j

i i j

ijx s b a

1

dengan si ≥0, i =1,2,...,m; j=1,2,...,p

Dalam hal ini,

jika ;

1

∑

=

=

p

j

i j ijx b

a i=1,2,...,m; j=1,2,...,p maka si =0

dan jika ;

1

∑

=

<

p

j

i j ijx b

a i=1,2,...,m; j=1,2,...,p maka s_i >0

b. Kendala yang berbentuk ,

1

∑

=

≥

p

j

i j ijx b

a pada ruas kanan disisipkan variabel

surplus (surplus variable) t_i sedemikian sehingga dipenuhi:

; 1

∑

=

+ =

p

j

i i j

ijx t b

a i =1,2,...,m; j =1,2,...,p

yang ekivalen dengan

∑

=

= −

p

j

i i j

ijx t b a

1

Dalam hal ini,

jika ;

1

∑

=

=

p

j

i j ijx b

a i=1,2,...,m; j=1,2,...,p maka t_i =0

jika ;

1

∑

=

>

p

j

i j ijx b

a i=1,2,...,m; j=1,2,...,pmaka 0t_i >

Dengan demikian kendala utama akan berubah menjadi sistem persamaan linear:

;

1

∑

=

= n

j

i j ijx b

a i=1,2,...,m; j=1,2,...,n (2.30)

yakni dengan memberi lambang variabel pengetat atau variabel surplus x_j dimu-lai dari j = p+1 sampai j =n, dengan n adalah banyaknya variabel x_j. Dan su-paya penyelesaian sistem (2.30) menjadi layak masih harus dipenuhi kendala tak

negatif

; 0 ≥

j

x j=1,2,...,n. (2.31)

Untuk menyesuaikan dengan bentuk kendala yang baru, fungsi sasaran

yang semula berbentuk

p p p

j j

jx cx c x c x c

f =

∑

= + + +

=

... 2 2 1 1 1

(2.32)

dilengkapi menjadi

n n p

p p p n

j j

jx cx c x c x c x c x c

f = = + + + + _{+ +} + +

=

∑

_{1 1 2 2} ... _{1 1} ...

1

(2.33)

Dengan demikian, suatu masalah program linear dapat dinyatakan dalam bentuk

sebagai berikut:

Maksimumkan (atau minimumkan)

∑

=

= n j

j jx c f

1

(2.34)

dengan kendala

;

1

∑

=

= n

j

i j ijx b

a i=1,2,...,m ;j=1,2,...,n. (2.35)

; 0 ≥

j

x j =1,2,...,n. (2.36)

Bentuk di atas (dengan semua kendala utama berbentuk persamaan) disebut ben-tuk standar dari masalah program linear.

Bentuk di atas bila ditulis dalam notasi matriks adalah sebagai berikut

Maksimumkan (atau Minimumkan) f =cTx (2.37)

dengan kendala Ax{≤,≥,=}b (2.38)

0

x≥ (2.39)

dengan x=

( )

x_j

( )

aij

=

A adalah koefisien matriks kendala

( )

bi

=

b adalah vektor suku tetap

( )

cj

=

Definisi 2.31 Penyelesaian Layak

Nilai-nilai variabel yang memenuhi kendala utama (2.38) dan kendala tak negatif

(2.39) disebut penyelesaian layak .

Pada umumnya sistem persamaan linear (2.38) mempunyai penyelesaian

takhingga banyak. Di antara penyelesaian-penyelesaian tersebut dicari juga yang

memenuhi (2.39), dan pada umumnya masih mempunyai penyelesaian takhingga

banyak. Kemudian di antara penyelesaian layak yang takhingga banyak ini dicari

yang mengoptimumkan fungsi sasaran, maka akan diperoleh penyelesaian

opti-mum.

Definisi 2.32 Penyelesaian Basis

Suatu vektor x merupakan penyelesaian basis, j