i
Skripsi
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains
Program Studi Matematika
Oleh:
Veronica Dwi Agustyaningrum NIM: 043114012
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
ii
Thesis
Presented as Partial Fulfillment of the Requirements To Obtain the SARJANA SAINS Degree
In Mathematics
By:
Veronica Dwi Agustyaningrum Student Number: 043114012
MATHEMATICS STUDY PROGRAM MATHEMATICS DEPARTMENT SCIENCE AND TECHNOLOGY FACULTY
SANATA DHARMA UNIVERSITY YOGYAKARTA
v
Skripsi ini kupersembahkan untuk:
Tuhan Yesus Kristus yang selalu membimbing dan memberkati setiap langkah hidupku
Bapak dan ibuku tercinta, Yohanes Sumarjono dan Christina Suyati
Kakakku tersayang, Yustina Ika Wahyuningsih Antonius Yudhi Anggoro
Semua teman dan sahabatku yang telah mendukungku hingga saat ini
vii
viii
, linear if and only if 2 of code word build a -dimension subspace from the vec-tor space that consist of all -tupel in over binary field , that is denoted by
x
sehingga penulis bisa menyelesaikan skripsi dengan judul “Kode Linear, Penguraian dan Pengelolaan Kesalahan” ini .
Penulis menyadari sepenuhnya bahwa banyak pihak yang telah memberikan dukungan, dorongan, kerjasama dan juga bimbingan sehingga akhirnya skripsi ini dapat selesai. Oleh karena itu, penulis mengucapkan banyak terima kasih kepada:
1. Ibu M.V. Any Herawati, S.Si., M.Si. selaku dosen pembimbing untuk kesabaran, bantuan, masukan serta telah meluangkan waktu untuk mendampingi penulis sejak awal hingga selesainya skripsi ini.
2. Romo Prof. Dr. Frans Susilo, SJ selaku dosen penguji yang telah memberi koreksi dan masukan kepada penulis.
3. Ibu Lusia Krismiyati, S.Si, M.Si. selaku Ketua Program Studi Matematika yang telah memberikan bantuan dan dorongan selama kuliah maupun dalam menyelesaikan skripsi ini.
4. Bapak Yosef Agung Cahyanta, S.T., M.T. selaku Dekan Fakultas Sains dan Teknologi.
5. Bapak Frederic Ezerman yang telah memberikan buku-buku pendukung tentang teori pengkodean.
xi
8. Bapak Yohanes Sumarjono dan Ibu Christina Suyati yang selalu memberi dukungan semangat dan menemani sehingga penulis dapat menyelesaikan pendidikan di tingkat perguruan tinggi.
9. Kakakku, Yustina Ika Wahyuningsih yang selalu memberi semangat dan bantuan selama masa perkuliahan dan proses penyelesaian skripsi ini. 10.Antonius Yudhi Anggoro yang selama ini selalu menemani, memberikan
dorongan semangat dan mau mendengarkan keluh-kesah di saat jatuh bangun dalam proses mengerjakan skripsi ini maupun saat masa perkuliahan.
11.Teman-teman mahasiswa angkatan 2004 program studi Matematika Universitas Sanata Dharma.
12.Teman-teman frater Projo di Kentungan yang selalu mendoakan dan memberikan dukungan selama penulis mengerjakan skripsi ini.
13.Banyak pihak yang tidak dapat penulis sebutkan satu persatu.
Yogyakarta, 28 September 2010
xii
HALAMAN JUDUL DALAM BAHASA INGGRIS ………. ii
HALAMAN PERSETUJUAN PEMBIMBING …...……… iii
HALAMAN PENGESAHAN ……….. iv
HALAMAN PERSEMBAHAN ………... v
HALAMAN PERNYATAAN KEASLIAN KARYA ……...…………. vi
HALAMAN ABSTRAK ……….……... vii
HALAMAN ABSTRACT ………... viii
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS ……… ix
KATA PENGANTAR ……….. x
DAFTAR ISI ……….………... xii
BAB I PENDAHULUAN ………...………….. 1
A. Latar Belakang Masalah ……… 1
B. Rumusan Masalah ……….……..……….. 3
C. Batasan Masalah ………...…... 3
D. Tujuan Penulisan ………..……...………….. 3
E. Manfaat Penulisan …………..………..……....…………. 3
F. Metode Penulisan ………..……….………....…... 4
xiii
C. Ruang Vektor ………...…..……….. 24
BAB III PENGURAIAN DAN PENGELOLAAN KESALAHAN, KODE LINEAR ……….. 52
A. Penguraian dan Pengelolaan Kesalahan, Kode Linear ....……… 52
3.1.1 Saluran Komunikasi ………. 52
3.1.2 Penguraian Kemungkinan Maksimum ………. 56
3.1.3 Jarak Hamming ……… 57
3.1.4 Penguraian Jarak Minimum ………. 59
3.1.5 Jarak Suatu Kode ………. 62
B. Kode Linear ………...………. 67
3.2.1 Kode Linear ………. 67
3.2.2 Bobot Hamming dari Kode Linear ……….. 70
3.2.3 Basis untuk Kode Linear ………. 73
3.2.4 Matriks Generator dan Matriks Pemeriksa ……….. 78
3.2.5 Ekivalensi dari Kode Linear ……… 85
3.2.6 Pengkodean Kode Linear ……… 87
xiv
1 A. Latar Belakang Masalah
Di jaman yang semakin modern ini, tuntutan akan sistem penyimpanan dan pengiriman data digital yang efisien semakin meningkat. Hal ini dipengaruhi oleh munculnya jaringan data berkecepatan tinggi untuk pengolahan dan penyimpanan serta pengiriman informasi digital dalam bidang militer, pemerintahan, keperluan pribadi, dan masih banyak hal lain. Perancangan sistem-sistem di atas menuntut penggabungan antara teknologi komputer dan komunikasi. Masalah utama dari perancangan suatu sistem sendiri adalah bagaimana mengendalikan kesalahan yang mungkin terjadi saat pengiriman sehingga diperoleh data yang benar. Salah satu cara yang dapat membantu merancang suatu sistem pengiriman data sehingga kesalahan yang mungkin terjadi saat pengiriman dapat dideteksi dan juga dapat dikoreksi/diperbaiki adalah teori pengkodean/penyandian.
Terdapat dua masalah pokok yang harus dihadapi oleh para perancang sistem penyimpanan atau pengiriman data, yaitu:
2. Sistem tersebut juga harus dapat memastikan bahwa bit-bit yang dikirim melalui saluran dapat diterima dengan benar, meskipun terjadi kesalahan saat pengiriman.
Dasar teori yang memberikan pemecahan masalah di atas diberikan oleh Claude Shannon pada tahun 1948. Shannon mengemukakan bahwa dengan penyandian/pengkodean informasi secara tepat, kesalahan yang mungkin terjadi saat pengiriman dapat dikurangi sampai pada tingkat yang diinginkan tanpa mengurangi kecepatan pengiriman. Sejak saat itu, banyak usaha dilakukan dalam menemukan metode perencanaan pengkodean untuk mengendalikan kesalahan yang mungkin terjadi.
Salah satu kode yang memiliki peran cukup penting dalam teori pengkodean yaitu kode linear. Dalam kode linear akan digunakan konsep-konsep mengenai ruang vektor dan sebagian besar penghitungannya akan dilakukan menggunakan matriks. Dengan kemampuannya mendeteksi -kesalahan dan mengoreksi --kesalahan, maka pesan yang dikirim dapat diterima dengan benar. Beberapa notasi yang akan digunakan yaitu, simbol digunakan untuk data informasi, untuk kata kode atau vektor yang akan dikirim, untuk vektor kesalahan dan untuk kata yang diterima. Kode linear
B. Rumusan Masalah
Masalah yang akan dibahas dalam skripsi ini adalah :
1. Apakah yang dimaksud dengan Teori Pengkodean? 2. Apakah yang dimaksud dengan kode linear?
3. Bagaimana sifat-sifat dari kode linear?
C. Batasan Masalah
Pembahasan dalam skripsi ini hanya dibatasi pada masalah teoritis saja dan tidak akan membahas mengenai aplikasi dari teori pengkodean terlebih kode linear sendiri.
D. Tujuan Penulisan
Tujuan dari penulisan skripsi ini adalah untuk memahami teori pengkodean yang secara khusus membahas lebih mendalam mengenai kode linear.
E. Manfaat Penulisan
F. Metode Penulisan
Penulisan skripsi ini menggunakan metode studi pustaka, yaitu dengan menggunakan buku-buku, jurnal ilmiah dan karangan ilmiah yang telah dipublikasikan sehingga di sini tidak disajikan hal baru dalam bidang matematika.
G. Sistematika Penulisan
BAB I PENDAHULUAN A. Latar Belakang B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penulisan G. Sistematika Penulisan
BAB II LAPANGAN BERHINGGA A. Lapangan
B. Sistem Persamaan Linear
BAB III PENGURAIAN DAN PENGELOLAAN KESALAHAN, KODE LINEAR
A. Penguraian dan Pengelolaan Kesalahan B. Kode Linear
6
A. Lapangan Definisi 2.1.1
Ring adalah suatu himpunan dengan dua operasi biner, penjumlahan (dinotasikan ) dan perkalian (dinotasikan , sedemikian hingga untuk semua , , di :
1. 2.
3. Terdapat elemen 0 di sedemikian hingga 0
4. Terdapat elemen – di sedemikian hingga 0 5.
6. dan
Definisi 2.1.2
1 1 untuk semua di disebut ring dengan elemen satuan. Elemen identitas terhadap perkalian pada suatu ring disebut elemen satuan.
Definisi 2.1.3
Andaikan adalah ring dengan elemen satuan. Suatu elemen di disebut
unit dari jika memiliki invers terhadap perkalian di .
Contoh 2.1.1
Himpunan semua bilangan bulat dengan penjumlahan dan perkalian biasa adalah ring komutatif dengan elemen satuan 1. Unit dari adalah 1 dan 1
Definisi 2.1.4
Jika setiap elemen tak nol di adalah unit, maka disebut ring divisi.
Lapangan adalah ring divisi yang komutatif.
Contoh 2.1.2
Suatu himpunan 0,1 dinotasikan dengan . Didefinisikan penjumlahan dan perkalian pada sebagai berikut:
+ 0 1 · 0 1
Lemma 2.1.1
Andaikan , dua elemen dari lapangan . Maka
i) 1
ii) 0 maka 0 atau 0
Bukti:
i) Dengan kata lain, harus ditunjukkan 1 0
1 1 1 (sifat elemen identitas perkalian)
1 1 (sifat komutatif)
1 1 (sifat distributif) 0
0 ii) Jika 0, maka
0 0
(sifat asosiatif) (sifat komutatif) 1 (sifat elemen invers)
1 (sifat komutatif)
Definisi 2.1.5
Suatu lapangan yang hanya memuat elemen berhingga disebut lapangan berhingga dan dinotasikan dengan .
Definisi 2.1.6
Andaikan , dan 1 adalah bilangan bulat. Dikatakan kongruen
dengan , ditulis sebagai
jika | , dengan kata lain membagi .
Contoh 2.1.3
a) 90 ≡ 30 (mod 60) dan 15 ≡ 3 (mod 12) b) 0 (mod ) berarti |
c) 0 (mod 2) berarti adalah bilangan genap d) 1 (mod 2) berarti adalah bilangan ganjil
Teorema 2.1.1
(2.1)
dimana ditentukan secara tunggal oleh dan , dan 0 1. Oleh karena itu, suatu bilangan bulat kongruen dengan tepat satu dari
0, 1, … , 1 modulo .
Bukti:
Akan dibuktikan melalui gambar di bawah ini:
0, 0 ─── ─── ─── … ─ ───•── ─
0 2 1
0, 0 ─ ───•── ─ … ─── ─── ───
1 0 2 Pada sumbu-x real di geometri analitik, beri tanda pada kelipatan dari dan posisi . Pertama andai berada pada kelipatan dari dan dapat diambil/ditetapkan 0. Kedua andai berada diantara dua kelipatan dari . Jika kasus kedua yang terjadi, misal kelipatan pertama dari yang berada di sebelah kiri dari . Maka (ditunjukkan pada gambar di atas) merupakan jarak antara dan . Dengan catatan 0 .
Ketunggalan dari dan mengikuti karena jika bukan kelipatan dari dan kita mengambil 0, maka terdapat suatu kelipatan tunggal/unik dari di sebelah kiri dan jaraknya tak sebanyak dari .
Definisi 2.1.7
Bilangan bulat pada persamaan 2.1 di atas disebut sisa dari dibagi oleh ,
dinotasikan .
Jika (mod ) dan (mod ), maka (mod ), (mod ), (mod ).
Untuk bilangan bulat 1, dinotasikan dengan atau ⁄
didefinisikan sebagai himpunan 0,1, … , 1 dan didefinisikan penjumlahan ⊕ dan perkalian ⊙ di sebagai berikut:
sisa dari bila dibagi , dinotasikan mod , dan
sisa dari bila dibagi , dinotasikan mod .
Teorema 2.1.2
adalah lapangan bila dan hanya bila prima. Bukti:
Andaikan bukan bilangan prima dan untuk dua bilangan bulat
1 , . Jadi 0, 0. Tetapi 0 di . Disini
terdapat kontradiksi dengan Lemma 2.1.1 (ii). Jadi, bukan lapangan. (⇐) Misalkan prima. Untuk setiap elemen tak nol , 0 ,
maka relatif prima terhadap . Jadi, menurut teorema dalam teori bilangan, terdapat dua bilangan bulat , dengan 0 1
sedemikian hingga 1, maka 1 mod . Oleh karena
itu . Ini berarti sifat elemen invers terhadap perkalian dipenuhi. Jadi adalah lapangan.
∎
Untuk suatu ring , bilangan bulat 1 dan , dinotasikan dengan atau yaitu banyaknya elemen
Definisi 2.1.8
Teorema 2.1.3
Karakteristik dari suatu lapangan adalah 0 atau bilangan prima. Bukti:
Jelas bahwa 1 bukan karakteristik dari lapangan karena 1 1 1 0.
Andaikan karakteristik dari suatu lapangan adalah bukan bilangan prima. Misalkan untuk bilangan bulat positif 1 , . Jika diambil
1 dan 1, dimana 1 adalah elemen identitas terhadap perkalian di , maka
1 1 1 1 1 1 0
Berdasarkan Lemma 2.1.1, maka 0 atau 0, berarti 1 0 atau
1 0. Oleh karena itu, terdapat kontradiksi dengan definisi karakteristik lapangan . Jadi, karakteristik suatu lapangan adalah 0 atau bilangan prima.
∎
Definisi 2.1.9
Suatu himpunan bagian E dari lapangan F yang juga merupakan lapangan terhadap operasi di F disebut lapangan bagian.
Teorema 2.1.4
Bukti:
¾ Pilih elemen dari . Klaim bahwa 0 , 1 , … , 1 adalah elemen-elemen yang berbeda.
Buktinya, jika untuk suatu 0 1, maka
0
0 dan 0 1.
Karakteristik dari adalah , maka 0, atau .
¾ Jika 0 , 1 , … , 1 , sudah dibuktikan. Selanjutnya,
pilih elemen di \ 0 , 1 , … , 1 . Klaim bahwa
adalah sepasang elemen yang saling berbeda untuk semua
0 , 1.
Buktinya, jika
Disini terdapat kontradiksi pada pemilihan . Karena , maka persamaan 2.2 di atas dapat dinyatakan sebagai pasangan terurut
, , .
Karena hanya memiliki banyak elemen berhingga, maka dengan cara yang sama dapat diperoleh elemen-elemen , , … , sedemikian hingga
\ , , … , , 2 ,
Dan
, , … , .
Dengan cara yang sama, dapat ditunjukkan bahwa
adalah elemen-elemen yang berbeda untuk semua ,
1,2, … , . Jadi, | | .
∎
B. Sistem Persamaan Linear
Sebuah garis yang terletak pada bidang dapat dinyatakan secara aljabar dalam suatu persamaan berbentuk:
dimana , , … , dan merupakan konstanta real. Variabel-variabel dalam persamaan linear seringkali disebut sebagai faktor-faktor yang tidak diketahui.
Definisi 2.2.1
Solusi dari persamaan linear adalah suatu
urutan dari bilangan , , … , sedemikian hingga persamaan tersebut
akan terpenuhi jika menggantikan , , … , . Kumpulan
semua solusi dari persamaan itu disebut himpunan solusi atau kadang kala disebut sebagai solusi umum dari persamaan tersebut.
Definisi 2.2.2
Sejumlah tertentu persamaan linear dalam variabel , , … , disebut sistem persamaan linear. Urutan sejumlah bilangan , , … , merupakan solusi
dari persamaan tersebut jika , , … , merupakan solusi dari setiap persamaan di dalam sistem tersebut.
Perkalian matriks memiliki aplikasi penting dalam sistem persamaan linear. Perhatikan sistem yang terdiri dari persamaan linear dengan faktor yang tidak diketahui berikut ini:
Karena dua matriks adalah setara jika dan hanya jika entri-entri yang bersesuaian adalah setara, maka kita dapat menukar persamaan dalam sistem ini dengan persamaan matriks tunggal
Matriks 1 pada ruas kiri persamaan di atas dapat ditulis sebagai hasil kali, sehingga diperoleh
… …
…
Matriks pada persamaan di atas disebut matriks koefisien dari sistem tersebut. Matriks yang diperbesar dari sistem tersebut diperoleh dengan menggabungkan ke sebagai kolom terakhir, sehingga bentuk matriks yang diperbesar menjadi
|
… …
…
| | | |
Definisi 2.2.3
Operasi baris elementer pada suatu matriks adalah setiap satu dari tiga operasi berikut ini:
1. Mengalikan baris dengan konstanta tak nol. 2. Menukar posisi dua baris.
3. Menambahkan kelipatan satu baris ke baris lainnya.
Definisi 2.2.4
Matriks dalam bentuk eselon baris tereduksi adalah matriks yang memenuhi sifat-sifat berikut ini:
2. Jika terdapat baris yang seluruhnya terdiri dari nol, maka baris-baris ini akan dikelompokkan bersama pada bagian paling bawah dari matriks.
3. Jika terdapat dua baris berurutan yang tidak seluruhnya terdiri dari nol, maka 1 utama pada baris yang lebih rendah terdapat pada kolom yang lebih kanan dari 1 utama pada baris yang lebih tinggi.
4. Setiap kolom yang memiliki 1 utama memiliki nol pada tempat-tempat lainnya.
Matriks yang memenuhi tiga sifat pertama di atas disebut dalam bentuk eselon baris.
Definisi 2.2.5
Dua matriks dikatakan ekivalen baris jika salah satu barisnya dapat diperoleh dari baris yang lain dengan serangkaian operasi baris elementer.
Definisi 2.2.6
Contoh 2.2.1
Selesaikan persamaan linear berikut ini
1 0 0 4 1 0 1 0 2 6 0 0 1 3 2
Sistem persamaan yang bersesuaian adalah
4 1
2 6
3 2
Karena , dan bersesuaian dengan 1 utama pada matriks yang diperbesar maka ketiganya disebut sebagai variabel utama. Variabel-variabel yang bukan utama (dalam hal ini ) disebut sebagai variabel bebas. Dengan menyelesaikan variabel-variabel utama dalam bentuk variabel bebas akan diperoleh
1 4
6 2
2 3
1 4 , 6 2 , 2 3 ,
Nilai-nilai sebarang yang ditetapkan untuk variabel-variabel bebas biasanya disebut parameter.
Definisi 2.2.7
Suatu sistem persamaan linear disebut homogen jika semua bentuk konstantanya adalah 0, yaitu sistem ini memiliki bentuk
0
0
0
Setiap sistem persamaan linear homogen adalah konsisten karena semua sistem tersebut memiliki solusi 0, 0, … , 0. Solusi ini disebut
solusi trivial. Jika tedapat solusi lain, maka solusi-solusi yang bukan trivial disebut solusi nontrivial.
Contoh 2.2.2
Selesaikan sistem persamaan linear homogen berikut
2 3 0
2 0
0 Penyelesaian:
Matriks yang diperbesar untuk sistem tersebut adalah
2 1 1 0 2 1 1 0 1 2 2 1 0 3 0 1 1 1 1 1 0 0 0 0
Dengan mereduksi matriks tersebut menjadi bentuk eselon baris, diperoleh
1 1 0 0 1 0 0 0 1 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0
Sistem persamaan yang bersesuaian adalah
0
0 0 Dengan menyelesaikan variabel-variabel utama diperoleh
0 Jadi, solusi umumnya adalah
, , , 0, .
Teorema 2.2.1
Suatu sistem persamaan linear homogen dengan jumlah faktor yang tidak diketahui lebih banyak dari jumlah persamaan, memiliki tak terhingga banyaknya solusi.
Bukti:
Pada contoh 2.2.2 menggambarkan dua hal penting dalam penyelesaian sistem persamaan linear homogen. Pertama, tidak satu pun dari ketiga operasi baris elementer mengubah nol terakhir pada matriks yang diperbesar, sehingga sistem persamaan yang bersesuaian dengan bentuk eselon baris tereduksi dari matriks yang diperbesar juga harus merupakan sistem yang homogen. Kedua, tergantung apakah bentuk eselon baris tereduksi dari matriks yang diperbesar memiliki suatu baris nol, jumlah persamaan dalam sistem yang tereduksi akan sama atau lebih sedikit dari jumlah persamaan dalam sistem aslinya. Jadi, jika suatu sistem homogen memiliki persamaan dengan faktor yang tidak diketahui, dimana , dan jika di dalam bentuk eselon baris tereduksi dari matriks yang diperbesar terdapat baris tak nol, maka akan diperoleh . Selanjutnya sistem persamaan yang bersesuaian dengan bentuk eselon baris tereduksi dari matriks yang diperbesar akan memiliki bentuk
… ∑ 0
… ∑ 0
dimana , , … , adalah variabel-variabel utama dan ∑ menotasikan jumlah-jumlah yang melibatkan variabel-variabel bebas . Dengan menyelesaikan variabel-variabel utama akan menghasilkan
∑
∑
∑
Seperti dalam contoh 2.2.2, dapat ditetapkan nilai-nilai sebarang untuk variabel-variabel bebas pada sisi kanan sehingga didapatkan tak terhingga banyaknya solusi untuk sistem tersebut.
∎
C. Ruang Vektor atas Lapangan Berhingga Definisi 2.3.1
Andaikan lapangan berhingga dengan orde . Suatu himpunan tak kosong , dilengkapi penjumlahan dan perkalian skalar dengan elemen di disebut
ruang vektor atas jika memenuhi semua kondisi di bawah ini:
Untuk semua , , dan , :
iii) Terdapat elemen 0 dengan sifat 0 0 untuk semua
iv) Untuk setiap terdapat elemen di , disebut – sedemikian hingga
0
v) vi) vii) viii) ix)
x) Jika 1 adalah elemen identitas terhadap perkalian di , maka 1
Contoh 2.3.1
Misalkan himpunan semua vektor yang panjangnya dengan entri-entri di sebagai berikut:
, , … ,
Didefinisikan penjumlahan vektor untuk secara per komponen, menggunakan penjumlahan yang didefinisikan pada , sedemikian hingga, jika
, , … , dan , , … ,
maka
Didefinisikan juga perkalian skalar untuk secara per komponen, sedemikian hingga, jika
, , … , dan
maka
, , … , .
Notasi merupakan vektor nol 0,0, … ,0 .
Pada akhirnya, dapat ditunjukkan bahwa memenuhi semua aksioma ruang vektor. Jadi, merupakan suatu ruang vektor.
Kadang kala vektor , , … , dinyatakan secara sederhana sebagai … .
Contoh 2.3.2
Misalkan terdiri dari suatu elemen tunggal, yang dinotasikan dengan 0, dan didefinisikan
0 0 0 dan 0 0
untuk semua skalar . Dapat ditunjukkan bahwa semua aksioma ruang vektor dipenuhi oleh . Ruang vektor ini disebut sebagai ruang vektor nol dan ditulis
Definisi 2.3.2
Suatu himpunan bagian tak kosong dari ruang vektor disebut ruang bagian dari jika sendiri merupakan ruang vektor terhadap penjumlahan vektor dan perkalian skalar yang sama seperti di .
Teorema 2.3.1
Himpunan bagian tak kosong dari ruang vektor atas adalah ruang bagian dari bila dan hanya bila:
i) Jika dan adalah vektor-vektor di , maka berada di . ii) Jika di dan sebarang vektor pada , maka berada pada . Bukti:
Jika adalah suatu ruang bagian dari ruang vektor atas , maka semua aksioma ruang vektor terpenuhi, khususnya aksioma 1 dan 6 berlaku. Tetapi aksioma-aksioma ini secara tepat adalah syarat (i) dan (ii).
Misalkan adalah sebarang vektor pada . Menurut syarat (ii), berada pada untuk setiap skalar . Dengan mengatur 0 diperoleh
0 0 berada pada . Dan dengan mengatur 1, maka 1 berada pada .
∎ Suatu himpunan bagian tak kosong dari ruang vektor atas disebut tertutup terhadap penjumlahan jika syarat (i) pada teorema 2.3.1 berlaku, dan dikatakan tertutup terhadap perkalian jika syarat (ii) berlaku. Jadi, teorema 2.3.1 menyatakan bahwa adalah ruang bagian dari ruang vektor atas bila dan hanya bila tertutup terhadap penjumlahan dan tertutup terhadap perkalian skalar.
Definisi 2.3.3
Jika adalah suatu sistem persamaan linear, maka setiap vektor yang memenuhi persamaan ini disebut sebagai vektor solusi dari sistem tersebut. Vektor-vektor solusi dari suatu sistem linear yang homogen membentuk ruang vektor yang disebut ruang solusi dari sistem tersebut.
Definisi 2.3.4
adalah vektor berbentuk dimana , , … , adalah skalar.
Definisi 2.3.5
Dimisalkan ruang vektor atas . Suatu himpunan vektor-vektor
, , … , di bebas linear jika
0 0.
Himpunan vektor-vektor di dikatakan bergantung linear jika himpunan tersebut tidak bebas linear, yaitu jika terdapat , , … , , tidak semua
nol, sedemikian hingga 0.
Definisi 2.3.6
Andaikan ruang vektor atas dan , , … , adalah himpunan bagian tak kosong dari . Rentang dari didefinisikan sebagai berikut
| .
Jika , didefinisikan 0 .
Teorema 2.3.2
Menurut Teorema 2.3.1, adalah ruang bagian dari bila dan hanya bila tertutup terhadap penjumlahan dan tertutup terhadap perkalian skalar. Berdasarkan Definisi 2.3.5, merupakan himpunan semua kombinasi linear dari elemen-elemen di dimana . Oleh karena itu,
tertutup terhadap penjumlahan dan perkalian skalar. Jadi, merupakan ruang bagian dari ruang vektor .
∎
Teorema 2.3.3
Jika ruang bagian dari , maka . Bukti:
Diketahui : ruang bagian dari Dibuktikan :
Harus ditunjukkan dan Andai : , , … ,
Akan dibuktikan: Misal:
Maka dapat dinyatakan dalam bentuk kombinasi linear sebagai berikut
dimana , untuk semua 1,2, … , .
Akan dibuktikan: Misal :
Maka dapat dinyatakan sebagai berikut
0 0 1 0
Dengan kata lain, dapat dinyatakan sebagai kombinasi linear dari elemen-elemen di . Berdasarkan definisi rentang, maka .
Jadi, karena dan , maka .
∎
Contoh 2.3.3
Jika 2 dan 0001, 0010, 0100 , maka
0000, 0001, 0010, 0100, 0011, 0101, 0110, 0111 .
Definisi 2.3.7
Andaikan ruang vektor atas . Himpunan bagian tak kosong
, , … , dari disebut basis untuk jika dan bebas
linear.
Teorema 2.3.4
untuk , , … , . Bukti:
Karena adalah basis dari , maka bebas linear dan merentang . Dengan demikian, setiap vektor pada dapat dinyatakan sebagai kombinasi linear dari vektor-vektor pada . Untuk melihat bahwa hanya terdapat satu cara untuk menyatakan suatu vektor sebagai suatu kombinasi linear dari vektor-vektor pada , dimisalkan vektor-vektor dapat ditulis sebagai
dan juga sebagai
.
Dengan mengurangkan persamaan kedua dengan persamaan pertama menghasilkan
0 .
Karena ruas kanan dari persamaan di atas adalah suatu kombinasi linear dari vektor-vektor pada dan bebas linear, maka diperoleh
0, 0, … , 0
berarti
, , … ,
Jadi, setiap vektor hanya dapat dinyatakan dalam bentuk
Definisi 2.3.8
Suatu ruang vektor tak nol disebut berdimensi terhingga jika terdiri dari himpunan terhingga vektor-vektor , , … , yang membentuk suatu basis. Jika tidak terdapat himpunan semacam ini, disebut sebagai
berdimensi takterhingga.
Teorema 2.3.5
Misalkan adalah suatu ruang vektor berdimensi terhingga dan
, , … , adalah basis sebarang.
a. Jika suatu himpunan memiliki vektor lebih dari , maka himpunan tersebut bersifat tidak bebas linear.
b. Jika suatu himpunan memiliki vektor kurang dari , maka himpunan tersebut bersifat merentang .
Bukti:
a. Misalkan , , … , adalah himpunan sebarang yang terdiri dari vektor pada , dimana . Akan ditunjukkan bahwa tidak bebas linear. Karena , , … , adalah suatu basis, maka setiap dapat dinyatakan sebagai kombinasi linear dari vektor-vektor pada , misalkan
Untuk menunjukkan bahwa tidak bebas linear, harus ditunjukkan terdapat skalar-skalar , , … , yang tidak semuanya nol, sedemikian hingga
0 (2.4) Dengan menggunakan persamaan-persamaan pada (2.3), maka persamaan (2.4) dapat ditulis kembali sebagai berikut
0
Jadi, dari kebebasan linear dari , masalah pembuktian bahwa adalah himpunan tidak bebas linear hanya menjadi pembuktian bahwa terdapat skalar-skalar , , … , yang tidak semuanya nol, yang memenuhi
0
0 (2.5)
Tetapi (2.5) memiliki lebih banyak faktor yang tidak diketahui dibanding jumlah persamaannya, sehingga berdasarkan teorema 2.2.1 terdapat solusi-solusi nontrivial.
b. Misalkan , , … , adalah himpunan sebarang yang terdiri dari vektor pada , dimana . Akan ditunjukkan bahwa tidak merentang . Pembuktiannya akan dilakukan dengan menggunakan kontradiksi, yaitu dengan mengasumsikan merentang .
Jika merentang , maka setiap vektor pada adalah kombinasi linear dari vektor-vektor pada . Khususnya, setiap vektor basis adalah kombinasi linear dari vektor-vektor pada , misalnya
(2.6)
Untuk memperoleh kontradiksi, akan ditunjukkan bahwa terdapat skalar
, , … , yang tidak semuanya nol sedemikian hingga
0 (2.7) Tetapi perhatikan bahwa (2.6) dan (2.7) memiliki bentuk yang sama dengan (2.3) dan (2.4) kecuali bahwa dan dipertukarkan dan demikian pula untuk dan -nya. Jadi diperoleh
0
0
Sistem linear ini memiliki lebih banyak faktor yang tidak diketahui disbanding jumlah persamaannya. Oleh karena itu, menurut teorema 2.2.1 sistem tersebut memiliki solusi-solusi nontrivial.
∎
Teorema 2.3.6
Semua basis untuk ruang vektor berdimensi terhingga memiliki jumlah vektor yang sama.
Bukti:
Berdasarkan teorema 2.3.4, jika , , … , adalah basis sebarang untuk ruang vektor , maka semua himpunan pada yang merentang dan bebas linear harus memiliki tepat vektor. Jadi, semua basis untuk harus memiliki jumlah vektor yang sama dengan basis sebarang .
∎
Definisi 2.3.9
Banyaknya vektor dalam himpunan basis dari ruang vektor disebut dimensi
Teorema 2.3.7
Misalkan ruang vektor atas . Jika dim , maka i) memiliki elemen.
ii) memiliki
!∏ basis yang berbeda.
Bukti:
i) Jika , , … , adalah basis untuk , maka
, , … , .
Karena , maka terdapat pilihan untuk setiap , , … , . Oleh karena itu, memiliki banyaknya elemen.
ii) Dimisalkan , , … , basis untuk . Karena 0, maka terdapat 1 pilihan untuk . Untuk suatu basis, maka
. Jadi ada pilihan untuk . Dengan cara yang sama,
untuk setiap sedemikian hingga 2, , , … , ,
maka terdapat pilihan untuk . Oleh karena itu, terdapat
∏ urutan yang berbeda dari -tupel , , … , . Karena urutan dari , , … , tidak diperhitungkan untuk suatu basis, maka jumlah basis yang berbeda untuk adalah
!∏ .
∎
Definisi 2.3.10
i) Hasil kali titik dari dan didefinisikan sebagai
. ii) Dua vektor dan dikatakan ortogonal jika 0.
iii) Dimisalkan himpunan bagian tak kosong dari . Komplemen ortogonal
dari didefinisikan
0 .
Jika , maka .
Teorema 2.3.8
Jika merupakan ruang bagian dari ruang vektor untuk setiap himpunan
bagian dari , maka .
Bukti:
Jelas dipenuhi berdasarkan teorema 2.3.3.
∎
Contoh 2.3.4
i) Misal 2 dan 4. Jika 1111 , 1110 , 1001 ,
maka
1 1 1 1 1 1 1 0 1,
1 1 1 0 1 0 1 1 0,
Jadi, dan ortogonal.
ii) Misal 2 dan 0100, 0101 . Untuk menentukan , diandaikan . Maka
0100 0 0,
0101 0 0.
Jadi diperoleh 0. Karena dan dapat 0 atau 1, maka dapat disimpulkan bahwa
0000, 1000, 0010, 1010 .
Definisi 2.3.11
Jika adalah suatu matriks , maka ruang bagian yang direntang oleh vektor-vektor baris dari disebut ruang baris dari dan ruang bagian yang direntang oleh vektor-vektor kolom dari disebut ruang kolom dari . Ruang solusi dari sistem persamaan yang homogen 0 disebut ruang nul dari .
Teorema 2.3.9
Suatu persamaan linear adalah konsisten bila dan hanya bila berada pada ruang kolom dari .
… …
…
dan
Jika , , … , menotasikan vektor-vektor kolom dari , maka hasilkali dapat dinyatakan sebagai suatu kombinasi linear dari vektor-vektor kolom tersebut dengan koefisien-koefisien dari , yaitu
(2.8) Jadi, suatu sistem linear yang terdiri dari persamaan dengan variabel dapat ditulis sebagai
(2.9) Dimana disimpulkan bahwa adalah konsisten bila dan hanya bila dapat dinyatakan sebagai kombinasi linear dari vektor-vektor kolom dari , atau secara ekivalen, bila dan hanya bila berada pada ruang kolom dari .
∎
Teorema 2.3.10
Operasi baris elementer tidak mengubah ruang nul suatu matriks. Bukti:
terhadap suatu matriks tidak mengubah himpunan solusi dari sistem linear
0 yang bersesuaian, atau dengan kata lain, tidak mengubah ruang nul dari .
∎
Teorema 2.3.11
Operasi baris elementer tidak mengubah ruang baris suatu matriks. Bukti:
Misalkan vektor-vektor baris dari matriks adalah , , … , , dan misalkan diperoleh dari dengan melakukan suatu operasi baris elementer. Akan ditunjukkan bahwa setiap vektor pada ruang baris dari juga terdapat pada ruang baris dari , dan sebaliknya setiap vektor pada ruang baris dari juga terdapat pada ruang baris dari .
Perhatikan kemungkinan berikut: jika operasi baris merupakan pertukaran baris, maka dan memiliki vektor baris yang sama dan sebagai konsekuensinya memiliki ruang baris yang sama. Jika operasi baris merupakan perkalian dari suatu dengan suatu skalar tak nol atau penjumlahan dari kelipatan satu baris dengan lainnya, maka vektor-vektor baris
, , … , dari adalah kombinasi linear dari , , … , . Jadi,
Karena diperoleh dari dengan melakukan suatu operasi baris, dapat diperoleh dari dengan melakukan operasi inversnya. Jadi, argumentasi di atas menunjukkan bahwa ruang baris dari terletak pada ruang baris dari .
∎
Teorema 2.3.12
Jika dan adalah matriks-matriks yang ekivalen baris, maka:
a. Suatu himpunan vektor-vektor kolom tertentu dari adalah bebas linear bila dan hanya bila vektor-vektor kolom yang bersesuaian dari
adalah bebas linear.
b. Suatu himpunan vektor-vektor kolom tertentu dari membentuk suatu basis untuk ruang kolom dari bila dan hanya bila vektor-vektor kolom yang bersesuaian dari membentuk suatu basis untuk ruang kolom dari .
Bukti:
0 dan 0
memiliki himpunan solusi yang sama. Jadi, sistem pertama memiliki solusi nontrivial bila dan hanya bila hal yang sama berlaku untuk sistem yang kedua. Tetapi jika vektor-vektor kolom dari dan berturut-turut adalah
, , … , dan , , … ,
Maka menurut persamaan 2.8, kedua sistem tersebut dapat ditulis kembali sebagai
0 (2.10) Dan
0 (2.11) Jadi, persamaan 2.10 memiliki solusi nontrivial untuk , , … , bila dan hanya bila hal yang sama berlaku untuk persamaan 2.11. Ini mengimplikasikan bahwa vektor-vektor kolom dari adalah bebas linear bila dan hanya bila hal yang sama berlaku untuk .
hanya bila vektor-vektor kolom yang bersesuaian dari juga membentuk basis untuk ruang kolom dari .
∎
Teorema 2.3.13
Jika dan adalah matriks-matriks yang ekivalen baris, maka:
a. Vektor-vektor baris dengan 1 utama (yaitu vektor-vektor baris tak nol) membentuk suatu basis untuk ruang baris dari ,
b. Vektor-vektor kolom dengan 1 utama dari vektor-vektor baris membentuk suatu basis untuk ruang kolom dari .
Bukti:
a. Menurut teorema 2.3.11, operasi baris elementer tidak mengubah ruang baris suatu matriks. Oleh karena itu, dan memiliki ruang baris yang sama. Misalkan diketahui matriks adalah matriks eselon berukuran yang diperoleh dari dengan melakukan operasi baris elementer. Dimisalkan pula vektor baris pertama dari adalah vektor-vektor baris tak nol sebagai berikut
0 0 0 0 0 0 0 … … … … 0
Vektor-vektor baris dari adalah
0, , … ,
0,0, … ,
Akan ditunjukkan bahwa vektor baris tak nol tersebut bebas linear. Untuk itu harus dicari konstanta-konstanta , , … , dari persamaan
0
atau
, , … , 0,0, … ,0
Dilihat komponen pertama menghasilkan 0. Kemudian
komponen kedua, yaitu , karena 0 maka 0.
Dengan cara yang sama dapat dicari konstanta-konstanta berikutnya hingga konstanta ke- , yaitu 0. Ini berarti bahwa vektor-vektor tersebut bebas linear. Karena vektor baris dari membangun ruang baris dari , maka vektor baris dari juga membangun ruang baris dari . Jadi, ruang baris dari dan mempunyai dimensi , atau rank baris dari matriks dan sama dengan .
Akan ditunjukkan bahwa dimensi ruang kolom dari matriks adalah . Karena dan dua matriks yang ekivalen, maka dua sistem persamaan linear homogen
0 dan 0 mempunyai himpunan solusi yang sama.
Misalkan , , … , adalah vektor-vektor kolom dari dan
, , … , adalah vektor-vektor kolom dari . Jika
, , … , , maka
Karena memenuhi kedua persamaan di atas atau tidak memenuhi kedua persamaan, maka
0
bila dan hanya bila
0
membangun ruang kolom dari . Oleh karena itu, ruang kolom dari mempunyai dimensi , atau rank kolom dari matriks sama dengan . ∎
Teorema 2.3.14
Jika adalah suatu matriks sebarang, maka ruang baris dan ruang kolom dari memiliki dimensi yang sama.
Bukti:
Misalkan adalah bentuk eselon baris sebarang dari . Berdasarkan teorema 2.3.10, maka
dim (ruang baris dari dim (ruang baris dari dan menurut teorema 2.3.11 b, maka
dim (ruang kolom dari dim (ruang kolom dari
jadi, bukti ini akan menjadi sempurna jika dapat ditunjukkan bahwa ruang baris dan ruang kolom dari memiliki dimensi yang sama. Tetapi dimensi ruang baris dari adalah banyaknya baris tak nol dan dimensi ruang kolom dari adalah banyaknya kolom yang mengandung 1 utama (teorema 2.3.12). Akan tetapi, baris-baris tak nol tepatnya merupakan baris-baris dimana terdapat 1 utama, sehingga banyaknya 1 utama dan banyaknya baris tak nol adalah sama. Hal ini menunjukkan bahwa ruang baris dan ruang kolom dari memiliki dimensi yang sama.
Definisi 2.3.12
Dimensi dari ruang baris dan ruang kolom dari suatu matriks disebut rank
dari dan dinyatakan sebagai rank( ). Dimensi ruang nul dari disebut sebagai nulitas dari dan dinyatakan sebagai nulitas( ).
Contoh 2.3.5
Tentukan rank dan nulitas dari matriks
1 3 2 4 2 7 5 9 0 2 2 2 4 0 4 4 5 1 6 4 3 4 1 7 Penyelesaian:
Bentuk eselon baris tereduksi dari adalah
1 0 0 0 0 1 0 0 4 2 0 0 28 12 0 0 37 16 0 0 13 5 0 0 (1)
Karena terdapat dua baris tak nol (atau secara ekivalen, dua 1 utama), ruang baris dan ruang kolomnya berdimensi dua, sehingga rank( 2. Untuk menentukan nulitas dari , harus ditentukan dimensi dari ruang solusi sistem linear 0. Sistem ini dapat diselesaikan dengan mereduksi matriks yang diperbesar menjadi bentuk eselon baris tereduksi. Matriks yang dihasilkan akan identik dengan (1), kecuali dengan tambahan satu kolom nol terakhir, dan sistem persamaan yang bersesuaian adalah
2 12 16 5 0
Atau, untuk menyelesaikan variabel-variabel utama
4 28 37 13
2 12 16 5
Maka solusi umum dari sistem tersebut adalah
4 28 37 13
2 12 16 5 (2)
Atau secara ekivalen
4 2 1 0 0 0 28 12 0 1 0 0 37 16 0 0 1 0 13 5 0 0 0 1 (3)
Keempat vektor pada ruas kanan (3) membentuk basis untuk ruang solusi, sehingga nulitas 4.
Teorema 2.3.15
Bukti:
Karena memiliki kolom, maka sistem linear homogen 0 memiliki variabel. Variabel ini terbagi dalam dua kategori, variabel utama dan variabel bebas. Jadi,
Tetapi banyaknya variabel utama adalah sama dengan banyaknya 1 utama di dalam bentuk eselon baris tereduksi dari , dan angka ini merupakan rank dari
. Jadi,
Banyaknya variabel bebas sama dengan nulitas dari . Hal ini terjadi karena nulitas dari adalah dimensi ruang solusi dari 0, yang sama dengan banyaknya parameter pada solusi umum, yang sama dengan banyaknya variabel bebas. Jadi,
∎
Teorema 2.3.16
Andaikan himpunan bagian dari , maka
dim dim .
Bukti:
Misal dim 1 dan , , … , basis dari . Akan
ditunjukkan dim dim . Ingat bahwa bila dan
hanya bila
0,
yang sama artinya memenuhi 0, dimana adalah matriks
yang baris ke- nya adalah . Untuk lebih jelasnya, perhatikan sistem persamaan di bawah ini:
0
0
0
Dapat diubah menjadi
… … …
0 0 0
52
KODE LINEAR
A. Penguraian dan Pengelolaan Kesalahan 3.1.1 Saluran Komunikasi
Definisi 3.1.1.1
Alfabet kode adalah suatu himpunan , , … , berukuran ,
dimana merupakan bilangan bulat positif yang disebut simbol kode.
i) Kata q-ary dengan panjang atas adalah suatu barisan
… dimana untuk semua . Sama artinya, dapat dipandang sebagai vektor , , … , .
ii) Kode blok q-ary dengan panjang atas adalah suatu himpunan tak
kosong dari kata -ary yang memiliki panjang sama dengan . iii) Elemen dari disebut kata kode di .
iv) Jumlah dari kata kode di , dinotasikan dengan | |, disebut ukuran dari .
v) Suatu kode blok dengan panjang dan ukuran dinyatakan sebagai
Pada kenyataannya, kode alfabet yang akan digunakan merupakan lapangan berhingga dengan order .
Contoh 3.1.1.1
Suatu kode atas kode alfabet 0,1 disebut kode biner, simbol kode untuk kode biner adalah 0 dan 1. Beberapa contoh kode biner yaitu:
1. 00, 01, 10, 11 adalah kode 2,4 .
2. 000, 011, 101, 111 adalah kode 3,4 .
3. 0011, 0101, 1010, 1100, 1001, 0110 adalah kode 4,6 .
Definisi 3.1.1.2
Saluran komunikasi adalah suatu himpunan yang terdiri dari alfabet
saluran berhingga , , … , dengan probabilitas saluran
pengirimanƤ memenuhi
Ƥ 1
Definisi 3.1.1.3
Suatu saluran komunikasi disebut tanpa memori jika hasil dari setiap satu pengiriman tidak bergantung dengan hasil pengiriman sebelumnya,
sedemikian hingga jika … dan … adalah kata
yang panjangnya , maka
Ƥ | Ƥ |
Definisi 3.1.1.4
Saluran simetri q-ary adalah saluran tanpa memori yang memiliki
saluran alfabet berukuran sedemikian hingga
i) Setiap simbol yang dikirim memiliki probabilitas sama 1 2⁄ dari simbol yang diterima dengan kesalahan.
ii)Jika suatu simbol diterima dengan kesalahan, maka setiap 1 kesalahan yang mungkin terjadi memiliki kemungkinan yang sama.
Secara khusus, saluran simetri biner (SSB) merupakan saluran tanpa memori yang memiliki saluran alphabet 0,1 dan saluran probabilitas
Ƥ 1 |0 Ƥ 0 |1
Jadi, probabilitas dari setiap bit kesalahan pada saluran simetri biner adalah , disebut probabilitas penyeberangan jalan dari saluran simetri biner.
Contoh 3.1.1.2
Andaikan kata kode dari kode 000, 111 akan dikirim melalui SSB dengan probabilitas penyeberangan jalan 0,05. Misalkan kata 110 diterima. Di-sini akan dicoba untuk menemukan kata kode yang paling mungkin dikirim dengan menghitung saluran probabilitas pengiriman:
Ƥ 110 |000
Ƥ 1 |0 Ƥ 0 |0
0,05 0,95
0,002375
Ƥ 110 |111
Ƥ 1 |1 Ƥ 0 |1
0,95 0,05
0,045125
3.1.2 Penguraian Kemungkinan Maksimum
Pada saluran komunikasi dengan kode, hanya kata kode yang akan dikirim. Diandaikan kata diterima. Dalam hal ini, diketahui bahwa kesalahan mungkin saja terjadi. Oleh karena itu, dibutuhkan suatu aturan untuk dapat menemukan kata kode yang mungkin dikirim. Aturan seperti itu disebut sebagai aturan penguraian.
Definisi 3.1.2.1
Andaikan kata kode dari kode akan dikirim melalui saluran komunikasi. Jika kata diterima, maka akan dihitung probabilitas saluran pengiriman
Ƥ |
untuk semua kata kode . Aturan penguraian kemungkinan
maksimum akan menyimpulkan bahwa adalah kata kode yang paling
mungkin dikirim jika memiliki probabilitas saluran pengiriman paling besar, sedemikian hingga:
Ƥ | Ƥ |
Aturan penguraian kemungkinan maksimum terdiri dari dua jenis, yaitu: 1. Penguraian kemungkinan maksimum lengkap. Jika kata diterima,
lebih dari satu kata kode yang memiliki probabilitas paling besar, maka dipilih satu diantaranya.
2. Penguraian kemungkinan maksimum tak lengkap. Jika kata diterima, akan dicari kata kode yang paling mungkin dikirim. Jika terdapat lebih dari satu kata kode yang memiliki probabilitas paling besar, maka dilakukan pengiriman ulang.
3.1.3 Jarak Hamming
Misalkan kata kode dari suatu kode akan dikirim melalui SSB dengan probabilitas penyeberangan 1 2⁄ . Jika kata diterima, maka untuk setiap kata kode probabilitas saluran pengirimannya diberikan sebagai berikut
Ƥ | 1
dimana adalah panjang dari , dan adalah jumlah kedudukan dimana
dan berbeda. Karena 1 2⁄ , berarti 1 , jadi
Definisi 3.1.3.1
Andaikan dan kata dengan panjang atas alfabet . Jarak Hamming dari ke , dinotasikan , , didefinisikan sebagai jumlah tempat
dimana dan berbeda. Jika … dan … , maka
, , , , (3.1)
dimana dan dianggap sebagai kata yang panjangnya 1, dan
, 1 0
Contoh 3.1.3.1
Misalkan 0,1 dan andaikan 01010, 01101, 11101. Maka
, 3
, 1
, 4
Teorema 3.1.3.1
Andaikan , , kata yang panjangnya atas . Maka
i) 0 ,
ii) , 0 bila dan hanya bila
iii) , ,
Bukti:
Untuk (i), (ii) dan (iii) jelas terpenuhi berdasarkan definisi jarak Hamming diatas. Berikut ini akan dibuktikan sifat keempat dengan menggunakan persamaan (3.1) di atas. Jika , maka (iv) jelas benar karena , 0. Jika , maka atau . Jadi (iv) benar.
∎
3.1.4 Penguraian Jarak Minimum
Definisi 3.1.4.1
Andaikan kata kode dari kode akan dikirim melalui saluran komunikasi. Jika kata diterima, aturan penguraian jarak minimum akan menguraikan menjadi jika , paling kecil diantara semua kata kode di , sedemikian hingga
, , (3.2)
dikirim, sedangkan aturan penguraian tak lengkap meminta dilakukan pengiriman ulang.
Teorema 3.1.4.1
Untuk SSB dengan probabilitas penyeberangan 1 2⁄ , aturan penguraian kemungkinan maksimum sama dengan aturan penguraian jarak minimum.
Bukti:
Misalkan merupakan kode yang digunakan dan adalah kata yang diterima (dengan panjang ). Untuk setiap vektor yang panjangnya , dan untuk setiap 0 ,
, Ƥ | 1
Karena 1 2⁄ , maka
1 1 1 1
Berdasarkan definisi 3.1.2.1, aturan penguraian kemungkinan
maksimum menguraikan menjadi sehingga
Ƥ | adalah nilai yang terbesar, dengan kata lain nilai , paling kecil. Jadi, aturan penguraian kemungkinan maksimum sama dengan aturan penguraian jarak minimum.
Mulai sekarang, diasumsikan bahwa semua SSB memiliki probabilitas penyeberangan 1 2⁄ . Akibatnya, dapat digunakan aturan penguraian jarak minimum untuk menunjukkan penguraian kemungkinan maksimum.
Contoh 3.1.4.1
Misal 000, 0011, 1000, 1100, 0001, 1001 adalah suatu kode biner. Kata kode di akan dikirim melalui SSB. Andaikan diterima
0111, maka
0111, 0000 3
0111, 0011 1
0111, 1000 4
0111, 1100 3
0111, 0001 2
0111, 1001 3
3.1.5 Jarak Suatu Kode
Definisi 3.1.5.1
Untuk suatu kode yang memuat paling tidak dua kata, jarak dari , dinotasikan , adalah
, | , ,
Definisi 3.1.5.2
Suatu kode dengan panjang , ukuran dan jarak dinyatakan sebagai kode , , . Nilai , dan disebut parameter dari kode.
Contoh 3.1.5.1
Suatu kode biner 00000, 00111, 11111 . Maka 2 karena
00000, 00111 3
00000, 11111 5
00111, 11111 2
Jadi, adalah kode biner 5,3,2 .
Definisi 3.1.5.3
Misal adalah bilangan bulat positif. Suatu kode mendeteksi
u-kesalahan jika perubahan setiap kata kode pada posisi tidak
menghasilkan kata kode yang lain. Kode tepat mendeteksi
-kesalahan jika mendeteksi -kesalahan tetapi tidak mendeteksi
1 -kesalahan.
Contoh 3.1.5.2
Kode biner 00000, 00111, 11111 mendeteksi 1-kesalahan karena perubahan setiap kata kode pada satu posisi tidak menghasilkan kata kode yang lain. Dengan kata lain,
00000 00111 membutuhkan perubahan tiga posisi
00000 11111 membutuhkan perubahan lima posisi
00111 11111 membutuhkan perubahan dua posisi
Jadi, tepat mendeteksi 1-kesalahan, dengan merubah dua posisi pertama dari 00111 akan menghasilkan kata kode lainnya, yaitu 11111 (jadi bukan kode pendeteksi 2-kesalahan).
Teorema 3.1.5.1
Suatu kode adalah pendeteksi -kesalahan bila dan hanya bila
dengan kata lain kode dengan jarak merupakan kode tepat pendeteksi
1 -kesalahan. Bukti:
Diandaikan 1. Jika dan terdapat sedemikian
hingga 1 , , maka . Oleh karena itu,
pendeteksi -kesalahan.
Andaikan 1, dengan kata lain , maka
terdapat , sedemikian hingga 1 , . Oleh
karena itu, mulai dengan pemilihan dan kesalahan 1
sedemikian hingga menghasilkan kata , yaitu kata kode yang lain di . Jadi, bukan kode pendeteksi -kesalahan.
∎
Definisi 3.1.5.4
Misal adalah bilangan bulat positif. Suatu kode adalah pengoreksi
-kesalahan jika penguraian jarak minimum mampu mengoreksi
kesalahan atau kurang, diasumsikan aturan penguraian tak lengkap digunakan. Kode tepat mengoreksi -kesalahan jika mengoreksi -kesalahan tetapi tidak mengoreksi 1 -kesalahan.
Contoh 3.1.5.3
penguraian jarak minimum, dapat dilihat bahwa:
i) Jika 000 dikirim dan terjadi satu kesalahan pada pengiriman, maka kata yang diterima 000, 010 atau 001 akan diuraikan menjadi 000. ii)Jika 111 dikirim dan terjadi satu kesalahan pada pengiriman, maka
kata yang diterima 110, 101 atau 011 akan diuraikan menjadi 111. Pada semua kasus, kesalahan tunggal akan diperbaiki. Oleh karena itu, merupakan kode pengoreksi 1-kesalahan.
Jika terjadi paling sedikit dua kesalahan, aturan penguraian akan menghasilkan kata kode yang salah. Sebagai contoh, jika 000 dikirim dan 011 diterima, maka 011 akan diuraikan menjadi 111 menggunakan aturan penguraian jarak minimum. Jadi, adalah kode pengoreksi tepat 1-kesalahan.
Teorema 3.1.5.2
Suatu kode adalah pengoreksi -kesalahan bila dan hanya bila
2 1, dengan kata lain kode dengan jarak merupakan kode pengoreksi tepat 1 2⁄ -kesalahan. Disini, adalah bilangan bulat terbesar kurang dari atau sama dengan .
Bukti:
pengiriman, maka , . Oleh karena itu, untuk setiap kata kode
, , maka
, , ,
2 1
1
,
Jadi, akan diuraikan menjadi jika aturan penguraian jarak minimum digunakan. Ini menunjukkan bahwa adalah kode pengoreksi -kesalahan.
(⇒) Andaikan pengoreksi -kesalahan. Jika 2 1, maka
terdapat kata kode yang berbeda , dengan , 2 .
Diklaim bahwa jika dikirim dan terjadi paling banyak -kesalahan, maka penguraian jarak minimum akan menguraikan kata yang diterima sebagai , atau jarak antara kata yang dikirim terhadap sama dengan jarak antara kata yang diterima dengan . Akan ditunjukkan terdapat kontradiksi dengan asumsi bahwa pengoreksi -kesalahan.
Selanjutnya diasumsikan bahwa dan berbeda tepat pada
posisi pertama, dimana 1 2 . Jika disimbolkan sebagai berikut:
… … …
Jika adalah kata yang diterima, maka
, ,
Jadi, , , , pada kasus ini diuraikan sebagai , atau
, , .
∎
B. Kode Linear
3.2.1 Kode Linear
Definisi 3.2.1. 1
Kode linear dengan panjang atas adalah ruang bagian dari .
Definisi 3.2.1.2
Andaikan kode linear di .
i) Kode dual dari adalah
ii)Dimensi dari kode linear adalah dimensi dari sebagai ruang vektor atas , dinotasikan dim .
Teorema 3.2.1.1
Andaikan kode linear dengan panjang atas . Maka, i) | |
ii) adalah kode linear dan dim dim iii)
Bukti:
i) Jelas dipenuhi berdasarkan teorema 2.2.4.
ii) Menurut teorema 2.2.5 dan teorema 2.2.7 jelas dipenuhi pula.
iii) Untuk membuktikan maka harus ditunjukkan bahwa . Misal . Untuk menunjukkan bahwa , harus
ditunjukkan 0 untuk semua . Karena dan ,
berdasarkan definisi , maka 0. Jadi .
∎
Kode linear yang panjangnya dan berdimensi atas disebut kode -ary , atau, jika konteksnya jelas , dapat disebut
kode , . Dapat juga dinyatakan kode linear , . Jika jarak dari
Definisi 3.2.1.3
Misal adalah suatu kode linear.
i) self-orthogonal jika .
ii) self-dual jika .
Teorema 3.2.1.2
i) Dimensi dari suatu kode self-ortogonal dengan panjang harus
2
⁄ .
ii) Dimensi dari kode self-dual dengan panjang adalah ⁄2. Bukti:
i) Berdasarkan definisi 3.2.1.3, kode self-orthogonal jika . Berarti dim dim . Diandaikan dim ⁄2. Menurut teorema 3.2.1.1,
dim dim
dim dim
⁄2
Terdapat kontradiksi. Jadi dim harus ⁄2.
ii) Berdasarkan definisi 3.2.1.3, kode self-dual jika . Berarti
dim dim . Diandaikan dim ⁄2. Misal dim
2
⁄ . Menurut teorema 3.2.1.1,
dim dim
⁄2
Terdapat kontradiksi. Jadi dim ⁄2.
∎
3.2.2 Bobot Hamming dari Kode Linear
Ingat bahwa jarak Hamming , antara dua kata , telah dibahas pada sub-subab 3.
Definisi 3.2.2.1
Misalkan adalah kata di . Bobot Hamming dari , dinotasikan dengan , didefinisikan sebagai jumlah koordinat tak nol di , sedemikian hingga
,
dimana adalah kata nol, yaitu kata yang semua elemennya 0.
Untuk setiap elemen di , bobot Hamming dapat
didefinisikan sebagai berikut
, 0 1 0 00
dapat didefinisikan demikian
Lemma 3.2.2.1
Jika , , maka , .
Bukti:
Untuk , , menurut definisi 3.1.3.1 , 0 jika . Hal itu benar bila dan hanya bila 0 atau, dengan kata lain,
0.
∎
Lemma 3.2.2.2
Jika , , maka , .
Bukti:
Dimisalkan … dan … di . Untuk semua
, 1 , 1 bila dan hanya bila . Oleh karena itu,
pasa-ngan , menyumbang 1 ke bila dan hanya bila
pasangan , menyumbang 1 ke , . Jadi, , , .
∎
Definisi 3.2.2.2
… .
Definisi 3.2.2.3
Andaikan suatu kode. Bobot Hamming minimum dari , dinotasikan , adalah bobot terkecil dari kata kode tak nol di .
Teorema 3.1.7.1
Misal kode linear atas . Maka . Bukti:
Berdasarkan lemma 3.2.2.1, untuk setiap kata , maka , . Menurut definisi 3.2.2.3, terdapat , sedemikian
hingga , . Jadi diperoleh
,
karena .
Untuk selanjutnya, diasumsikan 0 atau dinotasikan \ 0 . Terdapat \ 0 sedemikian hingga . Jadi diperoleh
, 0 .
Karena dan , maka .
Contoh 3.2.2.1
Misal adalah kode linear biner 0000, 1000, 0100, 1100 . Bobot dari setiap kata kode tak nol dari adalah sebagai berikut:
1000 1
0100 1
1100 2
Jadi, 1.
Di bawah ini disebutkan beberapa keuntungan dari kode linear sebagai berikut:
a) Kode linear merupakan ruang vektor. Oleh karena itu, kode tersebut dapat digambarkan secara lengkap dengan menggunakan basis (akan ditunjukkan dalam subbab berikutnya).
b) Jarak dari suatu kode linear sama dengan bobot terkecil dari kata kode tak nol dalam kode tersebut.
3.2.3 Basis untuk Kode Linear
Diingatkan kembali mengenai dua fakta dari aljabar linear:
a) Setiap matriks atas dapat diuraikan menjadi bentuk eselon
serangkaian operasi baris elementer. Dengan kata lain, suatu matriks ekivalen baris dengan matriks yang lain pada BEB atau BEBT.
b) Untuk suatu matriks yang diberikan, BEBTnya tunggal, tapi mungkin memiliki BEB yang berbeda.
Berikut ini akan diperkenalkan tiga algoritma untuk mencari basis dari suatu kode:
Algoritma 3.1
Masukan : himpunan bagian tak kosong dari
Keluaran: basis untuk , kode linear yang dibangun oleh
Langkah-langkah : Bentuk matriks dimana baris-barisnya adalah
kata-kata di . Gunakan operasi baris elementer untuk mendapatkan bentuk eselon baris dari . Kemudian baris-baris tak nol pada bentuk eselon baris dari merupakan basis untuk .
Contoh 3.2.3.1
Tentukan basis untuk , dimana
11110, 01111, 10001 .
11110 01111 10001
11110 01111 01111
11110 01111 00000
Jadi, 11110, 01111 adalah basis untuk .
Algoritma 3.2
Masukan : himpunan bagian tak kosong dari
Keluaran: basis untuk , kode linear yang dibangun oleh
Langkah-langkah : Bentuk matriks dimana kolom-kolomnya adalah
Berdasarkan teorema 2.3.13, maka algoritma di atas juga menghasilkan basis untuk ruang kolom dari matriks , yaitu basis untuk kode .
Contoh 3.2.3.2
Misal 2. Tentukan basis untuk , dimana
11101, 10110, 01011, 11010 .
1101 1011 1100 0111 1010 1101 0110 0001 0111 0111 1101 0110 0001 0111 0000 1101 0110 0001 0001 000 1101 0110 0001 0000 0000
Karena kolom 1, 2 dan 4 pada bentuk eselon baris adalah kolom utama, maka berdasarkan algoritma 3.2, kolom-kolom dari matriks pada bentuk awal yang bersesuaian dengan kolom utama merupakan basis untuk . Jadi, 11101, 10110, 11010 adalah basis untuk .
Algoritma 3.3
Masukan : himpunan bagian tak kosong dari
Keluaran: basis untuk kode dual , dimana
Langkah-langkah : Bentuk matriks dimana baris-barisnya adalah kata
bentuk eselon baris tereduksi. Andai matriks yang terdiri dari semua baris tak nol pada bentuk eselon baris tereduksi sebagai berikut:
0
Matriks memuat kolom utama. Ubah urutan kolom dari menjadi bentuk
|
dimana merupakan matriks identitas . Bentuk matriks sebagai berikut:
|
dimana adalah transpose dari .
Contoh 3.2.3.3
Tentukan basis untuk kode dual dimana
11101, 10110, 01011, 11010 .
|
10001 01011 00111 00000
Selanjutnya dibentuk matriks sebagai berikut
| 0 1 1 1 01 1 1 0 1
Jadi, 01110, 11101 adalah basis untuk kode dual .
3.2.4 Matriks Generator dan Matriks Pemeriksa
Definisi 3.2.4.1
i) Matriks generator untuk kode linear adalah matriks dimana
baris-barisnya merupakan basis untuk .
ii)Matriks pemeriksa untuk kode linear adalah matriks generator
untuk kode dual .
Teorema 3.2.4.1
i) Jika adalah kode linear , , maka matriks generator untuk adalah matriks dan matriks pemeriksa untuk adalah matriks
.
iv) Baris-baris dari suatu matriks generator adalah bebas linear. Hal yang sama juga dipenuhi oleh baris-baris pada matriks pemeriksa.
Bukti:
i) Diandaikan adalah kode linear , , maka memiliki panjang dan berdimensi . Berdasarkan definisi 3.2.4.1, maka matriks generator untuk berukuran . Selanjutnya akan ditunjukkan bahwa matriks pemeriksa untuk berukuran . Menurut teorema 3.2.1.1 bagian (ii), dim dim . Oleh karena itu, diperoleh
dim dim
dim dim
dim
Jadi, berdasarkan definisi 3.2.4.1 dapat disimpulkan bahwa matriks pemeriksa untuk berukuran .
ii) Jelas dipenuhi berdasarkan penjelasan pada algoritma 3.3 subbab sebelumnya.
iv) Jelas dipenuhi berdasarkan definisi matriks generator dan matriks pemeriksa di atas.
∎
Definisi 3.2.4.2
i) Matriks generator dengan bentuk | dikatakan bentuk standar. ii) Matriks pemeriksa dalam bentuk | dikatakan bentuk standar.
Lemma 3.2.4.1
Andaikan kode linear , atas , dengan matriks generator . Maka:
i) termasuk di bila dan hanya bila ortogonal dengan setiap baris di , secara simbolik: 0.
ii) Secara khusus, jika diberikan matriks berukuran , maka adalah matriks pemeriksa untuk bila dan hanya bila baris-baris dari bebas linear dan 0.
Bukti:
i) Andaikan adalah baris ke- dari . Oleh karena itu,
untuk semua 1 , dan setiap dapat dinyatakan sebagai kombinasi linear
Jika , maka 0 untuk semua . Jadi ortogonal dengan untuk semua 1 , sedemikian hingga 0.
Sebaliknya, jika 0 untuk semua 1 , maka untuk
semua ,
0
Jadi, .
ii) Jika matriks pemeriksa untuk , maka baris-baris di bebas linear. Karena baris-baris di adalah kata kode di , maka
0.
Sebaliknya, jika 0, maka baris-baris di termuat dalam . Karena baris-baris di bebas linear, maka ruang baris dari berdimensi . Jadi ruang baris dari adalah . Dengan kata lain, adalah matriks pemeriksa untuk .
∎
Teorema 3.2.4.2
Misal kode linear , atas , dengan matriks pemeriksa . Maka i) termasuk di bila dan hanya bila ortogonal dengan setiap
ii)Secara khusus, jika diberikan matriks berukuran , maka adalah matriks generator untuk bila dan hanya bila baris-baris di bebas linear dan 0.
Bukti:
i) (⇒) Andaikan adalah baris ke- dari . Oleh karena itu,
untuk semua 1 , dan setiap dapat dinyatakan sebagai kombinasi linear
dimana , , … , .
Jika , maka 0 untuk semua . Jadi ortogonal dengan untuk semua 1 , sedemikian hingga 0.
Sebaliknya, jika 0 untuk semua 1 , maka untuk
semua ,
0
Jadi, .
Sebaliknya, jika 0, maka baris-baris di termuat dalam . Karena baris-baris di bebas linear, maka ruang baris dari berdimensi . Jadi ruang baris dari adalah . Dengan kata lain, adalah matriks generator untuk .
∎
Teorema 3.2.4.3
Andaikan kode linear dan matriks pemeriksa untuk . Maka
i) memiliki jarak bila dan hanya bila setiap 1 kolom di bebas linear.
ii) memiliki jarak bila dan hanya bila memiliki kolom yang bergantung linear.
Bukti:
i) Andaikan , , … , adalah kata dengan bobot 0. Dimisalkan koordinat tak nol pada posisi , , … , , maka 0 jika , , … , . Misal 1 menotasikan kolom ke- di .
Berdasarkan lemma 3.2.4.1, memuat kata taknol
, , … , dengan bobot bila dan hanya bila
Untuk menunjukkan bahwa jarak dari sama artinya dengan menyatakan bahwa tidak memuat kata tak nol dengan bobot
1, yang ekivalen dengan mengatakan bahwa setiap 1 kolom atau kurang di bebas linear.
ii)Untuk menunjukkan bahwa jarak dari sama artinya dengan menyatakan bahwa memuat kata tak nol dengan bobot , yang ekivalen dengan menyatakan bahwa memiliki kolom yang bergantung linear.
∎
Akibat dari teorema di atas adalah sebagai berikut:
Jika dimisalkan adalah kode linear dan matriks pemeriksa untuk , maka pernyataan di bawah ini ekivalen:
i) memiliki jarak .
ii)Setiap 1 kolom dari bebas linear dan memiliki kolom yang bergantung linear.
Contoh 3.2.4.1
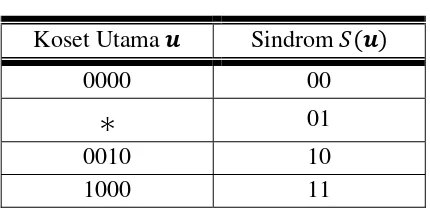
Misal kode linear biner dengan matriks pemeriksa
Dengan pemeriksaan dapat dilihat bahwa tidak terdapat kolom nol dan tidak ada dua kolom di yang jumlahnya , jadi setiap dua kolom di bebas linear. Akan tetapi, hasil jumlahan kolom 1, 3 dan 4 adalah , jadi ketiga kolom tersebut bergantung linear. Oleh karena itu, jarak dari
adalah 3.
Teorema 3.2.4.4
Jika | adalah matriks generator bentuk standar dari kode
, , maka matriks pemeriksa untuk adalah | . Bukti:
Dengan jelas persamaan 0 dipenuhi. Dengan mengingat
koordinat terakhir, jelas bahwa baris-baris di bebas linear. Jadi, berdasarkan lemma 3.2.4.1 bagian (ii), adalah matriks pemeriksa untuk .
∎
3.2.5 Ekivalensi dari Kode Linear
Definisi 3.2.5.1
i) Permutasi dari digit dalam kata kode tersebut.
ii)Perkalian simbol-simbol pada posisi tertentu dengan suatu skalar tak nol.
Teorema 3.2.5.1
Setiap kode linear ekivalen dengan kode linear yang memiliki matriks
generator pada bentuk standar. Bukti:
Jika matriks generator untuk , pada bentuk eselon baris tereduksi. Susun kembali kolom-kolom pada bentuk eselon baris tereduksi sehingga diperoleh kolom-kolom utama dan matriks identitas. Matriks yang dihasilkan, , pada bentuk standar merupakan matriks generator untuk kode ekivalen dengan kode .
∎
Contoh 3.2.5.1
Misal kode linear biner dengan matriks generator
1100001 0010011 0001001