BAB II ALJABAR LINIER

BAB II ALJABAR LINIER

Aljabar linier adalah salah satu dasar dalam penelitian operasional sebab masalah-masalah penelitian operasional akan lebih mudah diselesaikan dengan menggunakan konsep aljabar linier. Oleh sebab itu pada bab ini akan di bahan daras-dasar aljabar linier.

2.1 Vektor

Secara matematis vector terdiri dari orde n, sebagai contoh orde dengan pasangan berurutan (3,2) adalah vector berorde 2. Vektor dinyatakan dalam bentuk

a,

b,

c,

x

dan seterusnya.

Vektor a =

( )

3,2 dan vector

⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 3 2 5

b , dimana 3 dan 2 disebut sebagai komponen dari

vektor

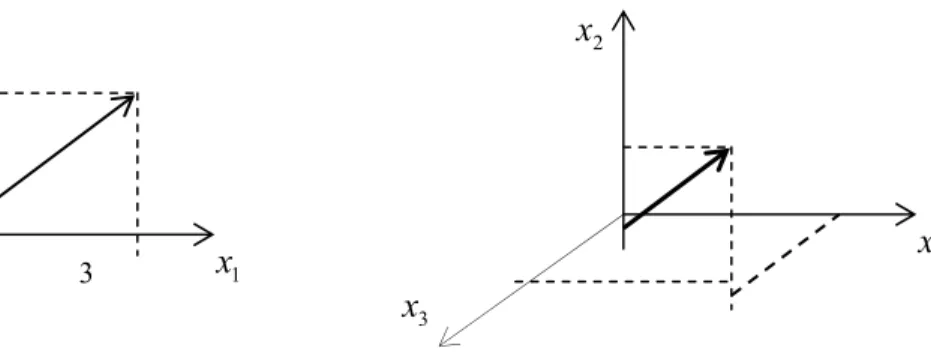
a

secara grafis dapat dilihat berturut-turut pada Gambar 2.1 dan 2.2.

2

3

Gambar 2.1 Vektor dalam dua dimensi Gambar 2.2 Vektor dalam tiga dimensi 3

x

1 x x1 2 x

2.2 Operasi vektor

Kesamaan Dua buah vector

a

dan b dikatakan sama jika dan hanya jika komponen dari vektor

a

dan b adalah sama.

(

a

1

,

a

2

,

L

,

a

n

)

=

a

dan

a

=

(

b

₁

,

b

₂

,

_L

,

b

_n

)

, maka

b

a= jika dan hanya jika

a

₁

=

b

₁

,

a

₂

=

b

₂

,

_L

,

a

_n

=

b

_n. (2.1) Penjumlahan Dua buah vector atau lebih yang berada dalam ruang yang sama dapat

dijumlahkan dengan cara menjumlahkan komponen-komponen yang bersesuaian.

(

a

1

,

a

2

,

L

,

a

n

)

=

a

dan

b

=

(

b

₁

,

b

₂

,

_L

,

b

_n

)

, maka

(

a

1

+

b

a

+

b

a

n

+

b

n

)

=

+

=

a

b

₁

,

_{2 2}

,

_L

,

c

. (2.2)

Misalkan vektor a=

( )

2,4 dan b=

( )

3,1 , maka penjumlahan vector

a

dan b adalah

( ) ( ) ( )

2,4 + 3,1 = 5,5 =

+ =a b

c ,

Secara grafis dapat dilihat pada Gambar 2.3.

Perkalian vektor dengan skalar Vektor dapat dikalikan dengan sebuah skalar k,

(

)

(

,

,

,

)

.

,

,

,

2 1 2 n n 1

ka

ka

ka

a

a

a

k

k

=

=

_L

a

(2.3)

Jika a=

( )

1,2 dan skalar k =2, secara grafis dapat diperlihatkan pada Gambar 2.4

Gambar 2.3 Penjumlahan vektor x1 Gambar 2.4 Perkalian vektor dengan skalar x1 2 x 2 x

2

4

5 5

Perkalian vektor dengan skalar memenuhi hukum asosiatif

k

(

m

a

)

=

(

km

)

a

, dan hukum distributif

k

(

a

+

b

)

=

(

k

a

+

k

b

)

dan

(

k

+

m

)

a

=

k

a

+

k

a

.

Pengurangan Dua buah vektor atau lebih dalam ruang yang sama dapat dikurangkan, dinotasikan a-b.

(

a

1

,

a

2

,

L

,

a

n

)

=

a

dan

b

=

(

b

₁

,

b

₂

,

_L

,

b

_n

)

, maka

(

a

1

,

a

2

,

L

,

a

n

)

+

(

−

1

)

(

b

1

,

b

2

,

L

,

b

n

)

=

−

=

a

b

c

(

) (

)

(

)

(

,

,

,

)

.

,

,

,

,

,

,

,

,

,

2 1 2 2 1 1 2 1 2 n n n n n 1

c

c

c

b

a

b

a

b

a

b

b

b

a

a

a

L

L

L

L

=

−

−

−

=

−

−

−

+

=

. (2.4)

Misalkan vektor a=

( )

2,4 dan b=

( )

3,1 , maka penjumlahan vector

a

dan b adalah

( ) ( ) ( )

6,4 − 3,1 = 3,3 =

− =a b

c

Inner Product Dua buah vektor dalam ruang yang sama dapat dikalikan yang disebut inner product

∑

=

=

+

+

+

=

=

n j j j n n

b

a

b

a

b

a

b

a

1 2 2 1 1

L

a.b

α

(2.5)

Inner product memenuhi hukum komutatif

b.a

a.b= dan memenuhi kondisi berikut

(

b c

) (

b c

)

a a.b a.c

a + = + = +

(

a+b

)(

c+d

)

=a.c+a.d+b.c+b.d

Perlu diperhatikan a.a≥0. Inner product sama dengan nol (a.a=0) jika dan hanya jika 0

=

a .

Dua buah vektor disebut orthogonal jika inner product-nya sama dengan nol. Jikaa=

( )

3,2 dan b=

( )

2,-3 adalah orthogonal, karena

a.b

=

3

(

2

)

+

2

(

−

3

)

=

0

. Vektor norm

∑

=

=

+

+

+

=

=

n j j n n

a

a

a

a

a

a

a

1 2 2 2 1 1

L

a.b

a

(2.7)

2.3 Linear Dependent dan Independent

Himpunan vektor a₁,a₂,_L,a_n yang berada dalam ruang yang sama

R

n dikatakan ”Linearly dependent” atau saling bergantung linier bila ada suatu himpunan dari n skalar yaitu

α

₁

,

α

₂

,

_L

,

α

_n tidak semuanya nol atau paling sedikit satu

α

≠0, bila hasil kombinasi liniernya adalah vektor nol (null vector). Jadi

0 a a a_{1 2 2 n n} 1 +

α

+ +

α

=

α

_L (2.8)

dimana 0 adalah vektor nol.

Sedangkan apabila dari n skalar yaitu

α

₁

,

α

₂

,

_L

,

α

_n masing-masing mempunyai nilai nol disebut lynearly independent atau saling bebas linier. Jadi dalam hal ii dapat ditulis:

0

2

1

=

α

=

=

α

n

=

α

_L

(2.9)

Himpunan vektor a₁,a₂,_L,a_n dalam ruang

_R

n _{adalah linear independent jika salah satu} dari vektor tersebut adalah suatu kominasi linier dari vektor-vektor lainnya. Jika salah satu dari vektor tersebut adalah suatu kombinasi linier dari vektor-vektor lainnya, vektor-vektor tersebut, salah satunya adalah a_n . Maka

1 n-1 n-1 1 n a a a =

α

+_L+

α

(2.10) atau

0

a

a

a

_{1 n-1 n-1} 1

+

+

α

+

(

−

1

)

n

=

α

_L

.

Dengan demikian dapat disimpulkan bahwa dari seluruh skalar

α

tidak seluruhnya nol, tetapi (-1) dan disebut linear independent.

Sedangkan apabila

0

1

=

∑

= n i i i

a

α

adalah linear independent, maka

α

_i adalah

0

2

1

=

α

=

=

α

n

=

α

_L

. Jika salah satu

α

, maka jelas bahwa vektor-vektor tersebut linearly dependent. Jadi 0=0a₁+_L+0a_n, adalah linearly dependent.

2.4 Basis

Vektor x₁,x₂,_L,x_m merupakan himpunan spanning dari ruang

E

n, jika setiap vektor pada

E

n dapat ditulis sebagai kombinasi linier dari

x

_i.Dengan menggunakan pemikiran dari ruang vektor dan linearly independent, dapat diuraikan tentang suatu basis dari suatu ruang vektor.

Himpunan spanning x₁,x₂,_L,x_n adalah basis untuk

E

n jika vektor-vektornya adalah linearly independent. Jadi basis dari

_E

2 _{memuat basis dua vektor, begitu juga basis untuk}

3

E

memuat tiga vektor.

Ambil x₁,x₂,_L,x_n adalah basis untuk

E

n, misalkan dalam

E

nterdapat vektor lain dalam a≠0. Maka

∑

=

=

n i i i 1

x

a

α

(2.11) 2.6 Matriks

Definisi 2.1 Matriks adalah kumpulan dari elemen yang disusun dalam bentuk baris dan kolom, banyaknya baris dan kolom menunjukan orde dari matriks.

Bentuk umum dari matriks orde n×m:

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = nm n n m m a a a a a a a a a A L M M L L 2 1 2 22 21 1 12 11 (2.12) 2.6.1 Operasi matriks

Penjumlahan/pengurangan Dua buah matriks atau lebih dapat dijumlahkan/ dikurangkan jika mempunyai orde yang sama, kemudian unsur-nsur yang bersesuaian dijumlahkan/dikurangkan.

Perkaalian matriks dengan skalar Jika

A

=

[ ]

a

_ij . Maka A dapat dikalikan dengan skalar

α

, sehingga

[ ]

a

ij

A

α

α

=

(2.13)

Perkalian matriks dengan skalar memenuhi hukum komutatif.

[

A B

]

α

A

α

B

α

+ = + dan

(

α

+ )

β

A

=

α

A

+

β

B

.

Perkalian matriks Dua buah matriks

A

dan

B

dapat dikalikan jika dan hanya jika banyaknya kolom pada matriks

A

sama dengan banyaknya baris pada matriks

B

. Jadi dalam menentukan apakah dua buah matriks dapat dikalikan atau tidak dan sekaligus untuk menentukan orde dari hasil perkaliannya, maka harus yakin bahwa banyaknya kolom pada matriks A sama dengan banyaknya baris pada matriks B.

p m p n n m

B

C

A

_×

⋅

_×

=

_× (2.14)

Perkalian matriks tidak memenuhi hukum komutatif

A

⋅

B

≠

B

⋅

A

, tetapi di dalam hal khusus bisa berlaku

A

⋅

B

=

B

⋅

A

(matriks COMUTE).

⎥

⎦

⎤

⎢

⎣

⎡

=

2

1

2

1

2

3

A

dan ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ 2 1 1 2 3 1 B , maka

⎥

⎦

⎤

⎢

⎣

⎡

=

=

11

6

13

8

.

B

A

C

.

Sifat perkalian matriks Perkalian matriks memenuhi:

1. Hukum distibutif terhadap penjumlahan:

A

(

B

+ )

C

=

AB

+

AC

. 2. Hukum assosiatif perkalian:

A

(

B

⋅

C

)

=

(

A

⋅

B

)

C

Jenis-jenis maatriks

1) Matriks Identitas adalah suatu matriks dimana semua unsurnya bernilai nol kecuali unsur pada diagonal utama sama dengan 1.

3) Matriks simetris adalah suatu matriks kuadrat dimana unsur

a

_ij

=

a

_ji untuk

n

j

i

,

=

1

,

2

,

_L

,

.

4) Skew-symetrik matrix adalah suatu matriks kuadrat dimana

n

j

i

a

a

_ij

=

−

_ij

,

,

=

1

,

2

,

_L

,

.

5) Matrriks diagonal adalah suatu matriks semua unsurnya sama dengan nol kecuali unsur pada diagonal utama tidak sama dengan nol.

6) Matriks nol adalah suatu matriks dimana semua unsurnya sama dengan nol. 7) Matriks non singulir adalah suatu matriks dimana nilai dari determinannya tidak

sama dengan nol.

8) Matriks conpormable, matriks A dikatakan conpormable terhadap B jika banyaknya kolom pada matriks A sama dengan banyaknya baris pada matriks B. 9) Matriks idempoten

10) Matriks partisi adalah suatu matriks yang dibagi menjadi matriks yang lebih kecil ordenya (sub matriks).

11)

α

[

A+B

]

=

α

A+

α

Bpada segitiga atas sama tyaiPerkalian dua buah 2.6.2 Matriks transpose

Jika matriks

A

berorde m×n. Maka transpose dari matrika

A

adalah

A

T. Dimana unsur-unsur baris pada matriks

A

merupakan unsur-unsur kolom pada

_A

T_.

Beberapa properti dari traspose matriks: 1.

( )

A

T T

₌

A

2.

(

A

+

B

)

T

=

A

T

+

B

T, dimana orde matriks

A

sama dengan orde dari

B

. 3.

( )

AB

T

=

B

T

A

T

2.6.3 Operasi baris elementer

Tiga dasar dari dari operasi baris elementer suatu matriks

1. Baris ke-i dapat ditukar dengan baris ke-j dan sebaliknya. 2. Baris ke-i dapat dikalikan dengan skalar

α

.

3. Baris ke-j dapat tukar dengan baris ke-j yang ditambah dengan skalar

α

. Jika ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = 2 4 2 1 2 2 A

1. Baris ke-1 dari matriks

A

ditukar dengan baris ke 2, diperoleh

⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = 2 4 2 2 2 1 1 A

2. Baris ke-2 dari matriks A₁dikalikan dengan 2, diperoleh

⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = 2 4 4 4 2 1 2 A

3. Baris ke-3 dari matriks A₁ ditambah 3, kemudian ditukar dengan baris ke-1, maka diperoleh ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = 2 1 2 2 5 7 3 A 2.7.4 Determinan

Determinan diperoleh dari matriks kuadrat, determinan dari matriks

A

ditulis A. Jika diketahui matriks

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = 22 21 12 11 a a a a A , maka 12 21 22 11a a a a A = − Jika ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = 33 32 31 23 22 21 13 12 11 a a a a a a a a a A , maka

32 31 22 21 13 33 31 23 21 12 33 32 23 22 11 _{a a} a a a a a a a a a a a a a A = − +

Sehingga secara umum dika terdapat matiks A berorde

n

×

n

maka determinan dari matriks A adalah:

∑

=

=

n i i i

A

a

A

1 1 1 (2.15) Sifat-sifat determinan

1. Pergantian baris an kolom atau sebaliknya tidak akan mempengaruhi nilai determinan A = A' 12 11 22 21 22 21 12 11 a a a a a a a a =

2. Jika dalam suatu baris atau kolom elemen-elemennya bernilai nol, maka nilai determinan ama dengan nol.

3. Jika setiap elemen pada suatu baris atau kolom dikalikan dengan suatu skalar

α

, maka nilai determinan akan menjadi

α

kali nilai determinan semula.

4. Bila dua buah baris atau kolom di tukar tempatnya, maka tanda determinan akan berubah, akan tetapinilai mutlaknya tetap.

5. Jika dua buah baris atau kolom sama elemen-elemennya, maka nilai determinanya sama dengan nol.

6. Suatu determinan nilainya tidak akan beruah ila elemen-elemen pada suatu baris atau kolom dikalikan dengan konstanta, kemudian ditambahkan atau dikurankan pada elemen-elemen baris atau kolom lainnya.

7. Determinan dari perkalian dua uah matriks sama denan hasil kali determinan matriks-matriks tersebut.

8. Determinan dari matrriks diagonal adalah hasil kali elemen-elemen diagonalnya.

Misalkan matriks A orde m×n, apabila dari matrriks A ini dipilih beberapa beberapa baris sebanyak

s

,

s

<

m

dan beberapa kolom sebanyak t,t<n, maka elemen-elemen dari s baris dan t kolom ini akan merupakan suatu matriks minor dari A.

Definisi 2.1 Jika matriks A sedikit-dikitnya mengandung suatu ninor determinan yang tidak lengkap (nilai = 0) dan ternyata terdiri dari r baris, akan tetapi untuk minor determinan yang lain pasti akan lenyap, apabila minor metriksnya terdiri dari (r – 1) baris, maka dalam hal ini matriksnya A mempunyai RANK = r dan ditulis r(A) = r.

⎥

⎦

⎤

⎢

⎣

⎡

=

1

2

2

2

1

1

1

1

A

0

2

2

1

1

1

=

=

A

, A₂ =1 =1, jadi r(A) = 1.

⎥

⎦

⎤

⎢

⎣

⎡

=

0

0

1

0

0

0

0

1

B

,

1

1

0

0

1

=

=

B

, jadi r(B) = 2.

Definisi 2.2 Kalau A matriks kuadrat dengan m baris dan n kolom, jika

r

(

A

)

=

r

=

n

, maka A dikatakan matriks non singulir dan jika r <n, maka matriks dikatakan singulir.

Rank matriks mempunyai peranan yang penting dalam penyelesaian persamaan linier simultan, sebab dengan mengetahui besarnya rank dari matriks koefisien, bisa ditentukan apakah persamaan tersebut mempunyai jawab atau tidak.

Mencari rank dengan menggunakan transformasi elementer

20 5 5 1 10 2 = A , tentukan rank A? Langkah-langkah

1. Kalikan baris pertama dengan

2

1

20 5 5 1 5 1

2. Kurangkan baris pertama pada baris kedua

20 5 0 0 5 1

4. Kalikan baris ketiga dengan

5

1

4 1 0 0 5 1

5. Kurangkan baris pertama pada baris ketiga

1 0 0 0 5 1 −

6. Kalikan baris ketiga dengan

−

1

1 0 0 0 5 1

7. Baris ke 1 dikurang 5 kali baris ketiga

0 0 1 0 0 1 1 0 0 0 0 1 = Jadi

rank

A

=

2

.

Jika C = A×B, maka

r

(

c

)

=

min{

r

(

A

),

r

(

B

)}

. 2.6.6 Matriks decomposible

Statu matriks

A

_n×n dikatakan decomposible jika dengan pertukaran beberapa baris dan kolom-kolom yang bersesuaian memungkinkan untuk memperoleh nol matriks pada pojok sebelaah kiri bawah, sehingga

A

dapat ditulis:

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = 22 12 11 0 A A A

A , dimana A₁₁ dan A₂₂ merupakan matriks kuadrat.

Jika sebaliknya disebut indecomposible. Supranto 1974.

2.6.7 Inverse matriks

Definisi 2.3

A

adalah matriks matriks kuadrat dengan ordo n×n dan

I

_n suatu matriks identitas, jika ada matriks kuadrat

_A

−1 _{sedemikian sehingga berlaku relasi}

I

A

A

AA

−1

=

−1

=

_{, maka}

_A

−1 _{disebut imverse dari matriks}

_A

_. Cara mencari inverse matriks

1. Metode substitusi

⎥

⎦

⎤

⎢

⎣

⎡

=

5

3

3

2

A

I

A

A

⋅

−1

=

_{, misalkan}

⎥

⎦

⎤

⎢

⎣

⎡

=

−

c

b

d

a

A

1

⎥

⎦

⎤

⎢

⎣

⎡

=

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

1

0

0

1

5

3

3

2

c

b

d

a

⎥

⎦

⎤

⎢

⎣

⎡

=

⎥

⎦

⎤

⎢

⎣

⎡

+

+

+

+

1

0

0

1

5

3

3

3

3

2

3

2

d

b

c

a

d

b

c

a

1 5 3 0 3 2 0 3 3 1 3 2 = + = + = + = + d b d b c a c a

3

,

3

,

5

=

−

=

−

=

b

c

a

dan d =2

Jadi

_⎥

⎦

⎤

⎢

⎣

⎡

−

−

=

−

2

3

3

5

1

A

2.6.8 Metode Adjoint matriks

Jika matriks

A

adalah matriks kuadrat dengan ordo n×n, dan setiap elemen dari matriks mempunyai ko-faktor, yaitu elemen

a

_ij mempunyai ko-faktor

K

_ij

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = = nn n n n n ij K K K K K K K K K K K L M L M M L L 2 1 2 22 21 1 12 11 ) ( (2.16)

Adjoint matriks adalah suatu matriks yang elemen-elemennya terdiri dari transpose dari semua kofaktor dari elemen-elemen matriks.

Jika

K

_ij kofaktor dari

A

, maka ) ( ) ( T _ji ij T _{K K} K A adj = = = . (2.17) ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = = nn n n n n T K K K K K K K K K K A adj L M L M M L L 2 1 2 22 21 1 12 11 ) (

dimana

A

_i1=kofaktor , elemen ₁

=

(

−

1

)

i+1

×

i

a

determinan dari matriks kofaktor dari A.

⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = 1 2 4 3 3 1 0 1 4 A

3

1

2

3

3

11 11

⎥

⇒

=

−

⎦

⎤

⎢

⎣

⎡

=

K

M

11

1

4

3

1

12 12

⎥

⇒

=

⎦

⎤

⎢

⎣

⎡

=

K

M

10

2

4

3

1

13 13

⎥

⇒

=

−

⎦

⎤

⎢

⎣

⎡

=

K

M

1

1

2

0

1

21 21

⎥

⇒

=

−

⎦

⎤

⎢

⎣

⎡

=

K

M

4

1

4

0

4

22 22

⎥

⇒

=

⎦

⎤

⎢

⎣

⎡

=

K

M

4

2

4

1

4

23 23

⎥

⇒

=

−

⎦

⎤

⎢

⎣

⎡

=

K

M

3

3

3

0

1

31 31

⎥

⇒

=

⎦

⎤

⎢

⎣

⎡

=

K

M

12

3

1

0

4

32 32

⎥

⇒

=

−

⎦

⎤

⎢

⎣

⎡

=

K

M

11

3

1

1

4

33 33

⎥

⇒

=

⎦

⎤

⎢

⎣

⎡

=

K

M

⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − = 11 12 3 4 4 1 10 11 3 ij K ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − = = 11 4 10 12 4 11 3 1 3 ) ( T ij K A adj

Definisi 2.4 Matriks

A

adalah matriks kuadrat ordo n×n, dan merupakan matriks yang non-singulir yaitu

det(

A

)

≠

0

,

K

_ij merupakan kofaktor dari elemen

a

_ij, maka inverse dari

A

dirumuskan sebagai berikut:

) det( ) ( ) det( 1 1 A K A adj A A T = = − _{. (2.18)}

Dari contoh di atas maka inverse matriks

A

adalah 1 − = A

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

−

−

−

−

=

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

−

−

−

−

−

−

=

=

−

11

4

10

12

4

11

3

1

3

11

4

10

12

4

11

3

1

3

1

)

(

1

1

_adj

_A

A

A

2.7 Himpunan konveks

Ambil

E

adalah ruang linier (riil) dan

X

⊆

E

.

Definisi 2.5 Ştefănescu [9]

X

adalah konveks jika

λ

x₁ +(1−

λ

)x₂ ∈X, dimana X

x

x₁, ₂ ∈ dan

λ

∈

[

0

,

1

]

.

Proposisi 2.1

X

adalah konveks jika dan hanya jika:

X

x

X

x

x

x

N

k

n i i i k i i k

∈

∈

=

⇒

∈

∈

∑

∑

= =1 1 3 2 1 2 1

,

,

,

,

,

,

,

[

0

,

1

],

1

,

_L

λ

λ

_L

λ

λ

λ

Irisan dari himpunan konveks adalah konveks.

Definisi 2.6 Ştefănescu [9] Konveks hull dari

X

(coX) adalah irisan dari semua himpunan konveks pada X. Dengan kata lain bahwa himpunan konveks dari E termuat dalam X.

Definisi 2.7 Supporting hyperplane dari

X

adalah suatu hyperplane H _p,α dengan properties:

a. X ∩H _p,α ≠

φ

b.

X

⊆

{

x

∈

E

p,

x

≤

α

}

atau

X

⊆

{

x

∈

E

p,

x

≥

α

}

.

Hyperplane

H

dalam

E

n didefinisikan bahwa himpunan dari titik

=

(

x

₁

,

x

₂

,

_L

,

x

_n

)

yang memenuhi persamaan

b

x

h

x

h

x

h

_{1 1}

+

_{2 2}

+

_L

+

_{n n}

=

atau b = ,

untuk nilai-nilai

h

_i (tidak semua

h

_i

≠

0

) dan b. Jadi jika untuk

E

2 diperoleh bentuk garis b x h x h_{1 1}+ _{2 2} = .

Pada

E

3 diperoleh persamaan bidang.

b

x

h

x

h

x

h

_{1 1}

+

_{2 2}

+

_{3 3}

=

.

Hyperplane

E

n dibagi dalam dua bagian, dinotasikan dengan

{

b

}

H+ = ≥ _{dan H}− ₌

{

_≤b

}

_.

Sebagai contoh ambil persamaan bidang 3x₁ − x2 ₂ =6. Maka

{

b

}

H+ = ≥ _{didefinisikan}

6

2

3

:

₁

−

₂

≥

+

_x

_x

H

dan

H

− didefinisikan

6

2

3

:

₁

−

₂

≤

−

_x

_x

H

.

Titik-titik pada garis 3x₁− x2 ₂ =6, berada pada kedua bagian tersebut.

Hyperplane adalah himpunan konveks. Jika ₁ dan ₂ ada pada hyperplane, sehingga b

=

1 dan 2 =b

Ambil =

λ

+(1−

λ

) ₂, kombinasi konveks dari ₁ dan ₂. Maka

[

λ

x1+(1−

λ

)x2

]

= 2 1 (1 ) x x

λ

λ

+ − = b b b = − + =

λ

(1

λ

)

Jadi adalah pada hyperplane. Dengan cara yang sama dapat dibuktikan bahwa bagian ruang

H

+

dan

H

− adalah juga konveks.