Penarikan Sampel Acak Sederhana

Teknik Sampling

Penarikan Sampel Acak Sederhana

Ukuran sampel

•Semakin besar, semakin byk informasi yg diperoleh •Sangat terkait dengan

biaya yang dikeluarkan

Tujuan

Penarikan Sampel

Mengambil kesimpulan mengenai populasi berdasarkan informasi yang

terkandung pada sampel

Variasi dalam data

•Dikontrol dengan metode pemilihan sampel yang tepat •Bila dirancang dengan tepat, biaya yang dikeluarkan

untuk melakukan pengamatan

•Bila dirancang dengan tepat, dapat menghemat biaya, informasi akurat

TPS Acak

Sederhana

Suatu teknik Penarikan sampel dimana setiap kemungkinan sampel berukuran n yang diambil dari suatu populasi berukuran N mempunyai kesempatan yang sama untuk terpilih,

Contoh Kasus

1

Seorang dokter gigi tertarik utk menge-tahui efektifitas dari suatu bahan dalam mengurangi

mengu-2

Manager HRD sebuah perusahaan ingin mengetahui preferensi karyawan di prsh tersebut

3

Direktur pemasaran sebuah perusahaan ingin menduga total penjualan produk nya pada tahun lalu mengurangi

mengu-rangi gigi berlubang. Studi tersebut dilakukan terhadap N=1000 siswa di sebuah sekolah di prsh tersebut mengenai berbagai alternatif skema asuransi kesehatan

nya pada tahun lalu

MASALAH : • Bagaimana menarik sampel

Cara memilih sampel acak sederhana

LOTERE

BIL. ACAK

(KOMP)

• Menuliskan nomor atau identitas lain

dari elemen populasi pada kertas, kmd

mengambil mengambil n kertas secara

acak. Elemen dengan identitas sesuai

kertas diambil sebagai sampel

• Biasanya kalau populasi kecil

• Beri nomor setiap anggt pop dg 1,2,... N

• Bangkitkan n bil acak dengan komputer

• Sekat bil. Acak sesuai dengan ukuran

(KOMP)

TABEL BILANGAN

ACAK

• Sekat bil. Acak sesuai dengan ukuran

populasi dan buat aturan shg setiap

elemen diwakili oleh bilangan yang

sama banyak

Penggunaan Tabel bilangan Acak

Beri nomor utk

1

2

3

Pilih sampel

4

Bangkitkan bil. Acak dari tabel acak.

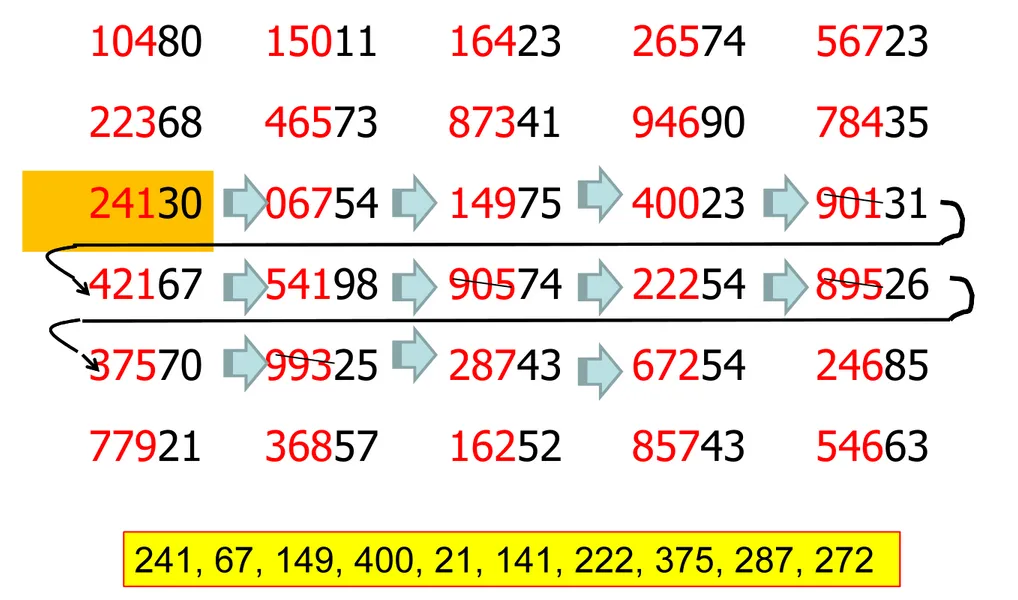
Beri nomor utk setiap elemen populasi Perhatikan hanya bbrp angka sesuai ukuran populasi N ≤10 : 1 angka 10<N ≤ 100 : 2 angka 100<N ≤ 1000 : 3.angka : Pilih sampel Mis N =400 (perhatikan 3 angka) 001 : elemen 1 002 : elemen 2 : 400 : elemen 400 401 : elemen 1 402 : elemen 2 : 800 : elemen 400 801-999 abaikan

Tabel bilangan Acak (N=400, n=10)

567

23

265

74

164

23

150

11

104

80

784

35

946

90

873

41

465

73

223

68

901

31

400

23

149

75

067

54

241

30

895

26

222

54

905

74

541

98

421

67

246

85

672

54

287

43

993

25

375

70

546

63

857

43

162

52

368

57

779

21

241, 67, 149, 400, 21, 141, 222, 375, 287, 272

Pendugaan Nilai Tengah Populasi

Penduga tengah populasi

n

y

y

n i i

∑

=

=

=

1

ˆ

µ

dengan :

•

Nilai tengah (PTB)

E

(

y

)

₌

µ













−

−

=

1

)

(

2

N

n

N

n

y

V

σ

• Ragam

Diduga dengan s

2 2 2

1

)

(

σ

−

=

N

N

s

V

Karena maka











 −

=

N

n

N

n

s

y

V

2

)

(

Finite pop correction factor

Pendugaan Nilai Tengah Populasi

Penduga tengah populasi

Dugaan Ragam

n

y

y

n i i

∑

=

=

=

1

ˆ

µ













−

=

N

n

N

n

s

y

V

2

)

(

ˆ

)

(

₋

2

∑

2

₋

2

∑

y

y

y

n

y

n n

dengan

Selang dugaan

:

Cat

: Jika N>>>n maka fpc

1 shg (biasanya n/N ≤ 0.05)

1

1

)

(

1 2 2 1 2 2

−

−

=

−

−

=

∑

∑

= =

n

y

n

y

n

y

y

s

i i i i

n

s

y

V

2

)

(

ˆ

=

)

(

ˆ

2

V

y

y

_±

Batas Kesalahan

Contoh Kasus

Suatu sampel acak berukuran n=9 catatan biaya perawatan

pasien yang

pernah

dirawat di ruang VIP RS ‘Sehat’

diambil dari untuk menduga rata-rata biaya perawatan di

ruang VIP dari N=484 catatan biaya yang ada (tentukan

elemen/unit PS/kerangka PS). Diperoleh sampel sbb

Pasien Biaya (jt rupiah

Y1 33.5

Dugalah µ, rata-rata biaya

Y2 32.0 Y3 52.0 Y4 43.0 Y5 40.0 Y6 41.0 Y7 45.0 Y8 42.5 Y9 39.0

perawatan dan hitung batas

kesalahan pada penduga

tersebut (tingkat

keperca-yaan 95%)

Contoh Kasus

Pasien Biaya Y1 33.5 Y2 32.0 Y3 52.0 Y4 43.0 Y5 40.0 Y6 41.0 Y7 45.0

n

n

y

y

n i i

0

.

39

...

0

.

32

5

.

33

ˆ

1

+

+

+

=

=

=

∑

=

µ

Nilai dugaan rata-rata biaya rawat

rupiah

juta

89

.

40

9

368

=

=

Untuk menghitung batas keslahan, hitung dulu s2 n Y7 45.0 Y8 42.5 Y9 39.0

67

.

35

1

9

)

89

.

40

(

9

)

0

.

39

...

0

.

32

5

.

33

(

1

2 2 2 2 1 2 2 2

=

−

−

+

+

+

=

−

−

=

∑

=

n

y

n

y

s

n i i Batas kesalahan

94

.

3

484

9

484

9

67

.

35

2

2

)

(

ˆ

2

2

=













−

=











 −

=

=

N

n

N

n

s

y

V

B

Diduga, rata-rata biaya rawat pasien di ruang VIP RS tersebut adalah 40.89 juta rupiah dengan batas kesalahan pendugaan 3.94 juta (tk kepercayaan 95%

Pendugaan Total Populasi

sehingga penduga total populasi

n

y

N

y

N

N

n i i

∑

=

=

=

=

ˆ

1

ˆ

µ

τ

Total populasi

:

µ

τ

₌

N

n













−

−

=

=

=

1

)

(

)

(

)

ˆ

(

2 2 2

N

n

N

n

N

y

V

N

y

N

V

V

τ

σ

Dengan ragam











 −

=

N

n

N

n

s

N

V

2 2

)

ˆ

(

ˆ

τ

Penduga bagi ragam

τ

ˆ

Pendugaan Total Populasi

Penduga total populasi

n

y

N

y

N

N

n i i

∑

=

=

=

=

ˆ

1

ˆ

µ

τ

Penduga bagi ragam

τ

ˆ











 −

=

N

n

N

n

s

N

V

2 2

)

ˆ

(

ˆ

_τ

Batas kesalahan











 −

=

=

N

n

N

n

s

N

V

B

2 2

2

)

ˆ

(

ˆ

2

τ

Suatu perusahaan ingin mengetahui berapa lama waktu yang

digunakan oleh karyawannya secara tidak efektif (untuk

kegiatan ngobrol, internetan, dll) dalam seminggu. Untuk itu,

diambil sampel acak yang terdiri dari 50 orang karyawan, dan

diperoleh rata-rata lamanya waktu yang digunakan secara tidak

efektif adalah 10.31 jam dengan s

2

_{=2.25 jam. Jika perusahaan}

efektif adalah 10.31 jam dengan s

2

_{=2.25 jam. Jika perusahaan}

tersebut memiliki 750 karyawan, dugalah total waktu yang

dihabiskan oleh semua karyawan untuk kegiatan-kegiatan

tersebut. Berikan batas kesalahan pendugaan.

Contoh Kasus

5

.

7732

)

31

.

10

(

750

ˆ

₌

N

y

₌

₌

τ

Nilai dugaan total lamanya waktu yang digunakan secara tidak efektif

jam

Dugaan ragam penduga

jam

n

N

s

N

V

B

2

ˆ

(

ˆ

)

2

2

750

2

2

.

25

750

50

307

.

4

2 2

_

 −

_



=

_



−

_



=

=

=

τ

Diduga, total lamanya waktu yang dihabisjan oleh seluruh karyawan secara tidak efektif adalah 7732.5 jam dengan batas kesalahan pendugaan sebesar 307.4 jam

jam

N

n

N

V

B

307

.

4

750

50

750

2

2

)

ˆ

(

ˆ

2

2 2



=







=









=

=

τ

Diduga, total lamanya waktu yang dihabisjan oleh seluruh karyawan secara tidak efektif adalah 7732.5 jam dengan kesalahan pendugaan kurang dari 307.4 jam

Penentuan Ukuran Sampel

• Dana

• Waktu

• Tenaga

Sampel berukuran besar

Sampel berukuran kecil

• Biaya besar, terkadang terlalu besar

• Informasi yang diperoleh banyak

• Biaya sedikit

• Informasi yang diperoleh tidak mencukupi

Penentuan Ukuran Sampel













−

−

=

=

1

2

)

(

2

2

N

n

N

n

y

V

B

σ

D

N

n

N

n

B

=













−

−

=

1

4

2 2

σ

)

(

2

)

(

2

V

N

y

N

2

V

y

B

₌

₌













−

−

=

1

2

2 2

N

n

N

n

N

B

σ

D

N

n

N

n

N

B

=













−

−

=

1

4

2 2 2

σ

Pendugaan Nilai Tengah

_{Pendugaan Total}

2 2

)

1

(

N

D

N

σ

n

σ

n

₋

₌

₋

[

2

]

2

)

1

(

N

D

σ

N

σ

n

₋

₊

₌

2 2

)

1

(

σ

σ

+

−

=

D

N

N

n

N

n

N



−

₁



4

2 2

)

1

(

N

D

N

σ

n

σ

n

₋

₌

₋

[

2

]

2

)

1

(

N

D

σ

N

σ

n

₋

₊

₌

Dengan

2 2 2

4

/

4

/

N

B

D

B

D

=

=

Untuk menduga nilai tengah

Untuk menduga total

Bila tdk diket., duga ragam dg

σ

ˆ

₌

Range

17/11/2014

Dinas Perindustrian Sumbar ingin menduga rata-rata modal dari usaha

tenunan yang ada di Sumbar. Meskipun data awal yang dapat digunakan

untuk menduga ragam populasi tidak tersedia, namun diketahui bahwa

modal usaha tenunan tersebut berkisar dari 20 juta – 100 juta. Diketahui

bahwa terdapat 225 usaha tenunan di Sumbar, tentukan berapa besarnya

contoh yang harus diambil apabila diinginkan kesalahan sampling

sebesar Rp 4 juta dengan tingkat kepercayaan 95%.

70

44

.

69

400

)

4

)(

1

225

(

)

400

(

225

)

1

(

2 2

≈

=

+

−

=

+

−

=

σ

σ

D

N

N

n

Dengan B=4 juta, diperoleh

D=B

2

_{/4 = 16/4= 4}

Simpangan baku populasi diduga dari

Jadi ukuran sampel yang harus diambil adalah

400

ˆ

20

4

80

4

)

20

100

(

4

ˆ

=

=

→

2

=

−

=

=

σ

σ

Range

Seorang ahli peternakan ingin mengetahui berapa total pertambahan

berat badan anak ayam dalam 0- 4 bulan untuk 1000 anak ayam yang

menetas pada periode terakhir. Tentu saja menghitung berat seluruh anak

ayam akan menghabiskan waktu dan membosankan. Karena itu

diputus-kan untuk mengambil sampel acak sederhana. Studi yang sama

sebelum-nya menunjukkan bahwa ragam populasi kira-kira bernilai 36 (gram).

Dengan tingkat kepercayaan 95% dan batas kesalahan 1000 gram ,

tentukan ukuran contoh yang diperlukan untuk penelitian di atas.

Dengan batas kesalahan B=1000 gr, diperoleh :

Diketahui dari studi sebelumnya bahwa ragam kenaikan berat 36 gr

Ukuran contoh yang diperlukan adalah

(

)

(

1000

)

0.25

.

4

1000

N

4.

B

D

2 2 2 2

=

=

=

126

125.98

36

999(0.25)

1000(36)

σ

1)D

(N

Nσ

n

₂ 2

≈

=

+

=

+

−

=

Pendugaan Proporsi

Pertanyaan Penelitian :

• Berapa proporsi siswa SMU di kota Padang yang tidak

lulus UN?

• Berapa persen bibit kedele yang mengecambah?

• Berapa proporsi RT yang hidup di bawah garis

pendugaan A ≈ Pendugaan

τ

Sukses : A Gagal : N-A Populasi a n-a Sampel

Pendugaan Proporsi

A = Total populasi

p = nilai tengah populasi

Kej.sukses diberi nilai y= 1

Kej.gagal diberi nilai y=0

pendugaan A ≈ Pendugaan

τ

pendugaan p ≈ Pendugaan

µ

Populasi (Ukuran N)

Prop. populasi

:

Sampel (Ukuran n)

Prop. sampel

:

n

a

p

ˆ

₌

/











 −

−

=

N

n

N

n

q

p

p

V

1

ˆ

ˆ

)

ˆ

(

ˆ

n

A

p

₌

/

n

a

y

p

ˆ

/

=

=

PENDUGA PROPORSI

)

ˆ

(

ˆ

2

V

p

B

₌

Seorang mahasiswa Jur.Matematika ingin menduga proporsi mahasiswa

tingkat akhir FMIPA Unand yang berencana untuk melanjutkan studinya

ke jenjang pascasarjana. Karena populasi yang dihadapi cukup besar,

maka ia memutuskan untuk mengambil sampel acak sederhana. Dari 400

orang mahasiswa tingkat akhir, ia mengambil sampel acak berukuran 100

orang.

Untuk setiap mahasiswa yang berencana untuk melanjutkan

studinya, ia memberikan nilai pengamatan yi=1 dan jika tidak, ia

memberikan

nilai yi=0.

Dari 100 mahasiswa tersebut, ia mencatat

terdapat 15 mahasiswa yang ingin melanjutkan studinya.

Dugalah

terdapat 15 mahasiswa yang ingin melanjutkan studinya.

Dugalah

proporsi semua mahasiswa tingkat akhir FMIPA yang berencana

nelanjutkan studinya beserta kesalahan pendugaannya.

Nilai dugaan proporsi mahasiswa yang akan melanjutkan studi

Batas kesalahan pendugaan

15

.

0

100

/

15

ˆ

=

=

=

y

p

ˆ

ˆ

ˆ

₌

 −



=

p

q

N

n

Jadi diduga 15% mahasiswa tingkat akhir FMIPA Unand

berencana melanjutkan studinya ke jenjang pascasarjana dengan

kesalahan pendugaan sebesar 5.9%

059

.

0

300

100

300

1

100

)

85

.

0

)(

15

.

0

(

2

1

ˆ

ˆ

2

)

ˆ

(

ˆ

2

=













−

−

=











 −

−

=

=

N

n

N

n

q

p

p

V

B

Penentuan ukuran contoh untuk pendugaan

proporsi

Ukuran contoh untuk menduga

µ

:

Subsitusi

σ

2

= pq, diperoleh:

2 2

σ

1)D

(N

N σ

n

+

−

=

Subsitusi

σ

2

= pq, diperoleh:

p diperoleh dari studi sebelumnya. Jika tidak tersedia,

gunakan p=1/2

pq

1)D

(N

Npq

n

+

−

=

D = B

2

/4

Dalam suatu penelitian pasar (

marketing riset

) ada 2000

Rumah tangga yang akan diteliti untuk memperkirakan

berapa proporsi ibu rumah tangga yang tak menyenangi

barang konsumsi tertentu. Guna menghemat biaya diambil

contoh acak sederhana ibu rumah tangga yang akan

diwawancarai. Oleh karena penelitian seperti ini belum

pernah dilakukan maka nilai proporsi populasi tidak diketahui.

diwawancarai. Oleh karena penelitian seperti ini belum

pernah dilakukan maka nilai proporsi populasi tidak diketahui.

Tentukan ukuran contoh yang diperlukan bila diingikan batas

kesalahan pendugaan sebesar 0.05 dan tingkat kepercayaan

95%.

Dari soal diketahui

:

N = 2000, B = 0.05

Karena p tdk diket,

digunakan p=0.5

(0.5)(0.5)

00625)

(1999)(0.0

(0.5)

(0.5)

(2000)

+

=

p)

p(1

1)D

(N

p)

-Np(1

n

−

+

−

=

sehingga

:

D = B

2

_{/ 4}

= (0.05)

2

_{/ 4}

= 0.000625

(0.5)(0.5)

00625)

(1999)(0.0

₊

334

47

.

333

499

.

1

500

≈

=

=

1. Seorang psikolog akan menduga rata-rata waktu yang diperlukan untuk merespons suatu stimulus (rangsang) di antara 200 orang pasien penderita gangguan mental di rumah sakit A.

a. Berapa ukuran sampel yang harus diambilnya jika ia menginginkan batas kesalahan pendugaan sebesar 0.5 detik. Tidak terdapat informasi

mengenai ragam populasi, namun dari pengalaman psikolog tersebut, waktu reaksi berkisar antara 1 detik sampai 3 detik

b. Misalkan akhirnya psikolog tersebut menarik sampel acak sederhana

berukuran 50 orang pasien di RS A. Diperoleh waktu reaksi rata-ratanya sebesar 2.1 detik dan simpangan baku sebesar 0.4 detik, dugalah waktu sebesar 2.1 detik dan simpangan baku sebesar 0.4 detik, dugalah waktu rata-rata yang diperlukan seluruh pasiend RS tersebut untuk merespons stimulus tersebut dan sertakan batas kesalahan pendugaan (pada taraf kepercayaan 95%). Apa interpretasi anda dari hasil yang anda peroleh.

2. Psikolog tersebut juga tertarik untuk mengetahui proporsi pasien RS tersebut yang dirawat akibat ketergantungannya terhadap narkoba. Dari 50 pasien tersebut, ia mencatat bahwa 21 orang pasien mengalami gangguan

kejiwaan akibat ketergantungannya terhadap narkoba. Dugalah proposi yang sesungguhnya dari banyaknya pasien yang mengalami gangguan jiwa karena narkoba (dengan taraf kepercayaan sebesar 95%