Pertemuan 14 Turunan Parsial
14.1 Pendahuluan
Dalam mempelajari fenomena dunia nyata, suatu obyek yang diselidiki biasanya tergantung pada dua atau lebih variabel. Jadi kita perlu memperluas ide awal Kalkulus mengenai fungsi atas satu variabel menjadi fungsi atas beberapa variabel. Turunan dari fungsi atas beberapa variabel lebih bervariasi dan menarik karena banyaknya cara berbeda tiap variabel saling berinteraksi. Integralnya pun mengarah pada variasi penerapan yang lebih beragam.
14.2 Fungsi atas Beberapa Variabel Definisi 14.1 Fungsi atas variabel bebas
Misalkan adalah suatu himpunan atas -tuples bilangan real ( ). Suatu fungsi nilai real pada adalah suatu aturan yang memetakan suatu bilangan real unik
( )
ke tiap elemen dalam . Himpunan merupakan domain fungsinya. Himpunan nilai yang dipilih oleh adalah range fungsinya. Simbol merupakan variabel terikat dari , dan dikatakan sebagai suatu fungsi dari variabel bebas hingga . Kita sebut pula
sebagai variabel input fungsi dan sebagai variabel output fungsi.
Contoh 14.1 Menghitung fungsi
Nilai dari ( ) √ pada titik ( ) adalah ( ) √ √
dikenal sebagai fungsi jarak dari titik pusat ke titik ( ) dalam koordinat ruang Kartesius.□
Contoh 14.2 Domain dan Ranges a. Fungsi atas 2 variabel
Definisi 14.2 Titik interior dan titik batas, terbuka, tertutup
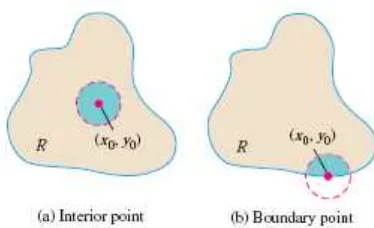
Suatu titik ( ) dalam suatu daerah (himpunan) dalam bidang- adalah suatu titik interior dari jika merupakan pusat dari suatu lingkaran dengan jari-jari positif yang terletak seluruhnya dalam (Gambar 14.1). Suatu titik ( ) adalah titik batas dari jika tiap lingkaran yang berpusat di ( ) mengandung titik-titik yang terletak di luar dan titik-titik yang terletak di dalam . (Titik batas itu sendiri tidak harus berada di dalam ).
Titik-titik interior dalam suatu daerah, sebagai suatu himpunan, membentuk interior dari daerah tersebut. Titik-titik batas daerah tersebut membentuk batasnya. Suatu daerah terbuka jika hanya terdiri atas titik-titik interior. Suatu daerah tertutup jika mengandung seluruh titik-titik batasnya (Gambar 14.2).
Gambar 14.1 Titik-titik interior dan titik-titik batas dari suatu daerah . Suatu titik interior pasti merupakan titik dari . Suatu titik batas belum tentu merupakan bagian dari .
(Thomas’s Calculus, 11th
ed, p.967)
Definisi 14.3 Daerah terbatas dan tidak terbatas dalam bidang
Suatu daerah dalam bidang dikatakan terbatas jika terletak di dalam suatu cakram (lingkaran) dengan jari-jari tertentu. Suatu daerah dikatakan tidak terbatas jika sebaliknya.
Definisi 14.4 Level curve, grafik, permukaan
Himpunan titik-titik dalam bidang dimana suatu fungsi ( ) memiliki suatu nilai konstan
( ) disebut suatu level curve dari . Himpunan seluruh titik ( ( )) dalam ruang, untuk ( ) dalam domain dari , disebut sebagai graph (grafik) dari . Grafik dari disebut juga surface (permukaan) ( ).
Contoh 14.3 Menggambar fungsi atas 2 variabel
Gambarkan grafik ( ) dan plot level curves ( ) ( ) , dan ( ) dalam domain dari dalam bidang tersebut.
Jawaban
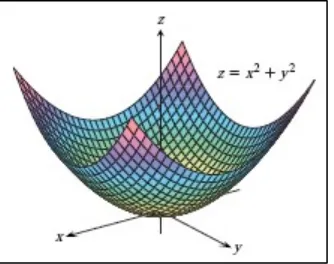
Domain dari adalah keseluruhan bidang- , dan range dari adalah himpunan atas bilangan real kurang dari sama dengan . Grafiknya merupakan parabola
, yang sebagian ditunjukkan dalam Gambar 14.3.
Level curve ( ) adalah himpunan titik-titik dalam bidang- dimana ( )
yang merupakan lingkaran dengan jari-jari berpusat di titik pusat. Demikian pula, level curves ( ) dan ( ) (Gambar 14.3) adalah lingkaran
( )
( )
Gambar 14.3 Grafik dan level curve yang dipilih dari fungsi ( ) . (Thomas’s Calculus, 11th
ed, p.967) Definisi 14.5 Level surface
Himpunan titik-titik ( ) dalam ruang dimana suatu fungsi atas tiga variabel memiliki suatu nilai konstan ( ) disebut sebagai suatu level surface dari .
Definisi 14.6 Titik-titik interior dan batas untuk daerah ruang
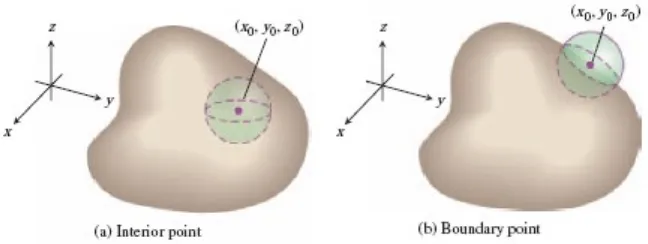
Suatu titik ( ) dalam suatu daerah dalam suatu ruang adalah suatu titik interior dari jika merupakan pusat dari suatu bola solid yang terletak seluruhnya dalam (Gambar 14.4a). Suatu titik ( ) adalah titik batas dari jika tiap bola yang berpusat di ( ) mengandung titik-titik yang terletak di luar dan titik-titik yang terletak di dalam (Gambar 14.4b). Interior dari adalah himpunan titik-titik interior dari . Batas dari adalah himpunan titik-titik batas dari .
Suatu daerah dikatakan terbuka jika keseluruhannya terdiri atas titik-titik interior. Suatu daerah dikatakan tertutup jika mengandung seluruh batasnya.
Gambar 14.4 Titik-titik interior dan titik-titik batas dari suatu daerah dalam ruang. (Thomas’s Calculus, 11th
ed, p.970) 14.3 Turunan Parsial
Definisi 14.7 Turunan parsial terhadap dan terhadap
Turunan parsial dari ( ) terhadap pada titik ( ) adalah
|( )
( ) ( )
dengan catatan limitnya ada.
Turunan parsial dari ( ) terhadap pada titik ( ) adalah
|( ) ( )|
dengan catatan limitnya ada.
Contoh 14.4 Mencari turunan parsial pada suatu titik Temukan nilai dari ⁄ dan ⁄ pada titik ( ) jika
( )
Jawaban
Untuk menemukan ⁄ , kita perlakukan sebagai suatu konstanta dan turunkan terhadap :
( )
Nilai ⁄ pada ( ) adalah ( ) ( )
Untuk menemukan ⁄ , kita perlakukan sebagai suatu konstanta dan turunkan terhadap :
( )
Nilai ⁄ pada ( ) adalah ( ) □ Contoh 14.5 Mencari turunan parsial pada suatu fungsi Tentukan ⁄ jika ( ) .
Jawaban
Kita perlakukan sebagai suatu konstanta dan sebagai suatu hasil kali dari dan :
( ) ( ) ( ) ( )
( )
Contoh 14.6 Turunan parsial bisa jadi berbeda Tentukan dan jika
( )
Jawaban
(
Dengan sebagai konstanta, kita peroleh
( dan sebagai fungsi terdiferensiasi atas :
( ) ( )
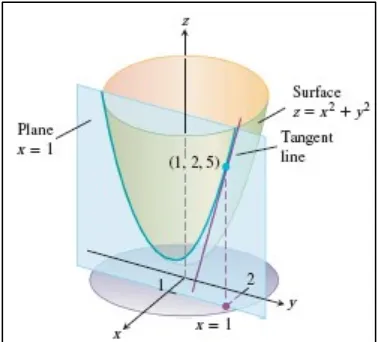
Contoh 14.8 Mencari slope suatu permukaan dalam
Gambar 14.5 Tangent terhadap kurva irisan dari bidang dan permukaan pada titik ( ).
(Thomas’s Calculus, 11th ed, p.970) Jawaban
Slope merupakan nilai dari turunan parsial ⁄ pada ( ):
|( ) ( )|( ) |( ) ( )
Untuk mengeceknya, kita dapat memperlakukan parabola tersebut sebagai suatu grafik fungsi satu variabel ( ) dalam bidang dan mencari slopenya pada . Slope yang dihitung dengan menggunakan turunan biasa, adalah
| ( )| |
Contoh 14.9 Fungsi atas 3 variabel
Jika , dan adalah variabel-variabel bebas dan
( ) ( )
maka
[ ( )] ( )
( ) ( ) ( )
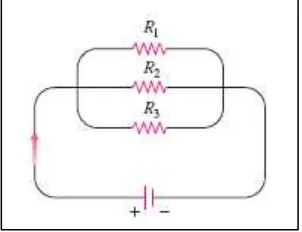
Contoh 14.10 Hambatan listrik paralel
(Gambar 14.6). Tentukan nilai dari ⁄ saat , dan ohm.
Gambar 14.6 Resistors yang disusun seperti ini dikatakan terhubung secara paralel. Persamaan hambatan dihitung dengan rumus
(Thomas’s Calculus, 11th
ed, p.989) Jawaban
Untuk menemukan nilai dari ⁄ , kita perlakukan dan sebagai konstanta dan dengan menggunakan turunan implisit kita turunkan kedua sisi persamaan terhadap :
( ) ( )
( )
Saat , dan ,
jadi dan
(
) ( )
Turunan Parsial dan Kekontinuan
variabel, dimana keberadaan suatu turunan mengakibatkan kekontinuan. Namun demikian, jika turunan-turunan parsial dari ( ) ada dan kontinu sepanjang lingkaran yang berpusat di ( ), maka kontinu pada ( ).
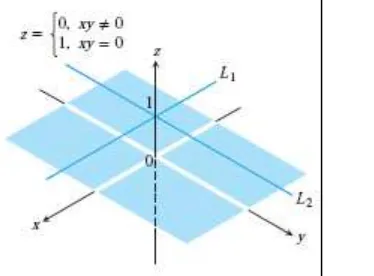
Contoh 14.11 Parsial ada, namun diskontinu Misal
( ) {
(Gambar 14.7).
a. Temukan limit dari saat ( ) mendekati ( ) sepanjang garis . b. Buktikan bahwa tidak kontinu pada titik pusat.
c. Tunjukkan bahwa baik turunan parsial ⁄ maupun ⁄ ada di titik pusat.
Gambar 14.7 Grafik fungsi pada Contoh 14.11 terdiri atas garis dan dan empat kuadran terbuka pada bidang- . Fungsinya memiliki turunan parsial pada titik pusat,
namun tidak kontinu di sana. (Thomas’s Calculus, 11th
ed, p.990) Jawaban
a. Karena ( ) selalu nol sepanjang garis (kecuali di titik pusat), kita peroleh
( ) ( ) ( )| ( ) ( )
b. Karena ( ) , limit pada bagian (a) membuktikan bahwa tidak kontinu pada ( ).
c. Untuk menemukan ⁄ pada ( ), kita perlakukan tetap pada . Maka ( ) untuk seluruh , dan grafik adalah garis pada Gambar 14.7. Slope dari garis ini pada suatu adalah ⁄ . Jadi, ⁄ pada ( ). Demikian pula, ⁄ merupakan slope dari garis pada suatu , jadi ⁄ pada ( ).□
Turunan Parsial Tingkat Kedua
Persamaan tersebut berarti
(
) ( )
dan seterusnya. Perhatikan urutan dimana turunan dikerjakan:
( ) pertama turunkan terhadap , baru terhadap . Contoh 14.12 Mencari turunan parsial tingkat kedua
Jika ( ) , tentukan
Jawaban
( )
( )
Sehingga,
(
) ( )
(
) ( )
(
) ( )
(
) ( )
Teorema 14.1 Teorema Turunan Gabungan
Jika ( ) dan turunan parsialnya , dan terdefinisi di dalam suatu daerah
( ) ( )
Contoh 14.13 Memilih tingkat turunan Tentukan ⁄ jika
Jawaban
Simbol ⁄ memberitahu kita untuk menurunkan fungsi pertama terhadap dan kemudian terhadap . Jika kita tunda penurunannya terhadap , melainkan menurunkannya terhadap terlebih dahulu, maka kita dapatkan jawabannya dengan lebih cepat. Dalam dua langkah,
a
Jika kita turunkan terhadap terlebih dahulu, kita peroleh ⁄ juga.□ Contoh 14.14 Menghitung turunan parsial tingkat empat
Tentukan jika ( ) . Jawaban
Pertama kita turunkan terhadap variabel , lalu , lalu kembali, dan terakhir terhadap :
Teorema 14.2 Teorema Increment untuk fungsi atas dua variabel
Misalkan bahwa turunan parsial pertama dari ( ) terdefinisi sepanjang suatu daerah terbuka yang mengandung titik ( ) dan bahwa dan kontinu pada ( ). Maka perubahan
( ) ( )
dalam nilai dari yang dihasilkan perpindahan dari ( ) ke titik lain ( ) dalam memenuhi persamaan dengan bentuk
dimana tiap saat .
Definisi 14.8 Fungsi terdiferensiasi
Sebuah fungsi ( ) terdiferensiasi pada ( ) jika ( ) dan ( ) ada
dan memenuhi suatu persamaan dengan bentuk
( ) ( )
dimana tiap saat . Kita katakan diferensiabel jika terdiferensiasi pada setiap titik dalam domainnya.
Akibat Teorema 14.2 Kekontinuan dari turunan parsial berarti terdiferensiasi
Jika turunan parsial dan dari suatu fungsi ( ) kontinu sepanjang suatu daerah
terbuka , maka terdiferensiasi pada setiap titik dari .
Teorema 14.3 Terdiferensiasi berarti kontinu
Jika suatu fungsi ( ) terdiferensiasi pada ( ), maka kontinu pada ( ).
14.4 Aturan Rantai
Teorema 14.4 Aturan Rantai untuk fungsi dua variabel bebas
Jika ( ) memiliki turunan-turunan parsial kontinu dan dan jika ( )
( ) merupakan fungsi-fungsi terdiferensiasi atas , maka komposisi ( ( ) ( )) adalah fungsi terdiferensiasi atas dan
( ( ) ( )) ( ) ( ( ) ( )) ( )
atau
Contoh 14.15 Menerapkan aturan rantai
Gunakan aturan rantai untuk menemukan turunan dari
terhadap sepanjang jalur . Apakah nilai turunannya saat ⁄ ?
Jawaban
Dalam contoh ini, kita dapat memeriksa hasilnya dengan perhitungan langsung. Sebagai suatu fungsi atas ,
sehingga
( )
Pada nilai yang diberikan dari , ( )
⁄ ( )
Teorema 14.5 Aturan Rantai untuk fungsi tiga variabel bebas
Jika ( ) adalah fungsi terdiferensiasi dan , dan adalah fungsi-fungsi terdiferensiasi atas , maka adalah fungsi terdiferensiasi atas dan
Contoh 14.16 Perubahan nilai fungsi sepanjang spiral Tentukan ⁄ jika
Dalam contoh ini nilai dari berubah sepanjang jalur suatu spiral. Apakah nilai turunannya pada saat ?
Teorema 14.6 Aturan Rantai untuk dua variabel bebas dan tiga variabel tengah
sebagai suatu fungsi terdiferensiasi atas . Maka pada suatu titik dimana ,
Contoh 14.19 Turunan implisit
Jawaban
Ambil ( ) . Maka
Perhitungan ini lebih pendek dibandingkan dengan perhitungan satu variabel untuk mencari turu a implisit sebagaima a ya g sebelum ya per ah kita pelajari.□
14.5 Nilai Ekstrim dan Saddle Points
Definisi 14.9 Local maximum, local minimum
Misalkan ( ) terdefinisi dalam suatu daerah yang mengandung titik ( ). Maka
1. ( ) adalah nilai local maximum dari jika ( ) ( ) untuk seluruh domain titik ( ) dalam suatu lingkaran terbuka yang berpusat di ( ).
2. ( ) adalah nilai local minimum dari jika ( ) ( ) untuk seluruh domain titik ( ) dalam suatu lingkaran terbuka yang berpusat di ( ).
Teorema 14.8 Uji turunan tingkat pertama untuk nilai ekstrim lokal
Jika ( ) memiliki suatu nilai local maximum atau minimum pada suatu titik interior
( ) dari domainnya dan jika turunan parsial tingkat pertamanya ada, maka ( ) dan ( ) .
Definisi 14.10 Titik kritis
Suatu titik interior dari domain suatu fungsi ( ) dimana baik dan nol, atau salah satu atau kedua dan tidak ada, merupakan titik kritis dari .
Definisi 14.11 Titik pelana (saddle point)
Suatu fungsi terdiferensiasi ( ) memiliki suatu titik pelana pada suatu titik kritis ( ) jika dalam setiap lingkaran terbuka yang berpusat di ( ) terdapat domain titik-titik ( ) dimana ( ) ( ) dan domain titik-titik ( ) dimana ( ) ( ). Titik yang
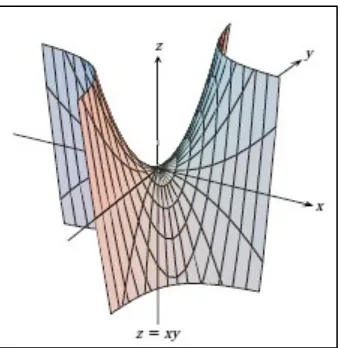
Gambar 14.8 Titik-titik pelana pada titik pusat. (Thomas’s Calculus, 11th
ed, p.1029) Contoh 14.20 Mencari nilai ekstrim lokal
Temukan nilai ekstrim lokal dari ( ) . Jawaban
Domain dari adalah keseluruhan bidang (jadi tidak ada titik-titik batas) dan turunan parsial dan ada dimanapun. Oleh karenanya, nilai ekstrim lokal dapat terjadi hanya pada saat
Satu-satunya kemungkinan adalah pada titik pusat, dimana nilai dari adalah nol. Karena tidak pernah negatif, kita dapat melihat bahwa titik pusatnya merupakan suatu lokal minimum (Gambar 14.9).□
Gambar 14.9 Grafik fungsi ( ) adalah parabola . Fungsi tersebut memiliki suatu nilai lokal minimum pada titik pusat.
(Thomas’s Calculus, 11th
ed, p.1029) Contoh 14.21 Menentukan titik pelana
Jawaban
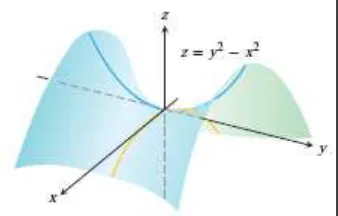
Domain dari adalah keseluruhan bidang (jadi tidak ada titik-titik batas) dan turunan parsial dan ada dimanapun. Oleh karenanya, nilai ekstrim lokal dapat terjadi hanya pada titik pusat ( ). Namun demikian, sepanjang sumbu- positif, memiliki nilai ( ) ; sepanjang sumbu- positif, memiliki nilai ( ) . Oleh karena itu, setiap lingkaran terbuka dalam bidang- yang berpusat di ( ) mengandung titik-titik dimana fungsi tersebut positif dan negatif. Fungsi tersebut memiliki suatu titik pelana pada titik pusat (Gambar 14.10) dibandingkan suatu nilai ekstrim lokal. Kita simpulka bahwa fu gsi tersebut ti ak memiliki ilai ekstrim lokal.□
Gambar 14.10 Titik pusatnya merupakan titik pelana dari fungsi ( ) . Tidak ada nilai ekstrim lokal.
(Thomas’s Calculus, 11th
ed, p.1030) Teorema 14.9 Uji turunan tingkat dua untuk nilai ekstrim lokal
Misalkan bahwa ( ) dan turunan parsial tingkat pertama dan keduanya kontinu dalam sebuah lingkaran berpusat pada ( ) dan bahwa ( ) ( ) . Maka,
i. memiliki suatu local maximum pada ( ) jika dan pada ( ).
ii. memiliki suatu local minimum pada ( ) jika dan pada ( ).
iii. memiliki suatu titik pelana pada ( ) jika pada ( ).
iv. Tes tidak memiliki kesimpulan pada ( ) jika pada ( ). Dalam kasus ini, kita harus menemukan cara lain untuk menentukan sifat dari pada ( ). Contoh 14.22 Menemukan nilai ekstrim lokal
Temukan nilai ekstrim lokal dari fungsi
( )
Fungsi tersebut terdefinisi dan terdiferensiasi untuk seluruh dan dan domainnya tidak memiliki titik batas. Oleh karenanya fungsi tersebut memiliki nilai ekstrim hanya pada titik-titik dimana dan bernilai nol. Dengan demikian,
atau
Oleh karenanya, titik ( ) merupakan satu-satunya titik dimana dapat memiliki nilai ekstrim. Untuk mengeceknya, kita hitung
Diskriminan dari pada ( ) ( ) adalah
( )( ) ( )
Kombinasi dari
a
memberitahu kita bahwa memiliki suatu local maximum pada ( ). Nilai dari pada titik ini adalah ( ) .□
Contoh 14.23 Mencari nilai ekstrim lokal Tentukan nilai ekstrim lokal dari ( ) . Jawaban
Karena terdiferensiasi dimana saja (Gambar 14.11), dapat diasumsikan nilai ekstrim hanya pada
a
Dengan demikian, titik pusat merupakan satu-satunya titik dimana mungkin memiliki suatu nilai ekstrim. Untuk melihat apa yang terjadi, kita hitung
Diskriminannya,
Gambar 14.11 Permukaan memiliki suatu titik pelana pada titik pusat. (Thomas’s Calculus, 11th
ed, p.1031) Contoh 14.24 Menemukan absolute extrema
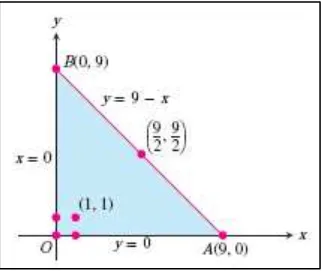
Temukan nilai absolut maksimum dan minimum dari
( )
pada daerah segitiga pada kuadran pertama yang dibatasi oleh garis .
Jawaban
Karena terdiferensiasi, satu-satunya tempat dimana dapat mengasumsikan nilai-nilai ini adalah titik-titik di dalam segitiga (Gambar 14.12) dimana dan titik-titik pada batasnya.
a. Titik interior. Untuk ini kita peroleh
merujuk pada titik tunggal ( ) ( ). Nilai dari adalah
( ) b. Titik batas. Kita ambil segitiga satu sisi pada satu waktu:
i. Pada ruas . Fungsi
( ) ( )
sekarang dapat dianggap sebagai fungsi atas terdefinisi pada interval tertutup . Nilai-nilai ekstrimnya dapat muncul pada titik-titik ujung
ima a ( )
ima a ( )
dan pada titik-titik ujung dimana ( ) . Satu-satunya titik interior dimana ( ) adalah , dimana
( ) ( ) ii. Pada ruas dan
Kita tahu dari sifat simetri dari dalam dan dan dari analisis yang baru saja dilakukan bahwa calon untuk ruas ini adalah
( ) ( ) ( )
iii. Kita telah menghitung nilai-nilai pada titik-titik ujung dari , jadi hanya perlu melihat pada titik-titik interior dari . Dengan , kita peroleh
( ) ( ) ( ) Dengan menetapkan ( ) diperoleh
Pada nilai ini,
a ( ) ( )
Akhirnya, kita daftarkan seluruh calon: ( ⁄ ). Nilai maksimum adalah , dimana dianggap pada ( ). Nilai minimum adalah , dimana dianggap pada ( ) dan ( ).□
Gambar 14.12 Daerah segitiga ini adalah domain dari fungsi pada Contoh 14.24. (Thomas’s Calculus, 11th
ed, p.1031) 14.6 Turunan Parsial dengan Variabel Terikat
Contoh 14.25 Menemukan turunan parsial dengan variabel bebas terbatas yang diketahui Tentukan ⁄ pada titik ( ) ( ) jika
dan dan adalah variabel-variabel bebas. Jawaban
Tidaklah umum untuk menghapus dalam ekspresi . Oleh karenanya, kita turunkan kedua persamaan secara implisit terhadap , dengan menganggap dan sebagai variabel-variabel bebas dan dan sebagai variabel-variabel terikat. Diperoleh
Persamaan-persamaan ini sekarang dapat digabungkan untuk menyatakan ⁄ dalam suku , dan . Kita selesaikan persamaan di atas untuk ⁄ diperoleh
dan substitusikan ke persamaan sebelumnya
Nilai dari turunan ini pada ( ) ( ) adalah ( )
( ) ( )
( )( )
( )
Contoh 14.26 Menemukan turunan parsial dengan variabel notasi terbatas yang diketahui Temukan ( ⁄ ) jika dan .
Jawaban
Dengan bebas, kita peroleh
( )
( )
( ) ( )
( )
14.7 Formula Taylor untuk Dua Variabel Rumus Taylor untuk ( ) pada titik ( )
Misalkan ( ) dan turunan parsialnya hingga tingkat adalah kontinu dalam suatu daerah persegi terbuka yang berpusat di titik ( ). Maka, melalui ,
( )
( ) ( )|( ) ( )|( )
( )|( )
( ) |( ) ( ) ( )
|
Rumus Taylor untuk ( ) pada titik pusat
( ) ( ) ( )
( ) ( )
( ) ( )
| ( )
Contoh 14.27 Menemukan perkiraan kuadratik
Tentukan suatu perkiraan kuadratik untuk ( ) di dekat titik pusat. Seberapa akurat perkiraan tersebut jika | | dan | | ?
Jawaban
Kita ambil untuk persamaan di atas:
( ) ( ) ( ) ( )
( )( )
dengan
( ) |( ) ( ) |( )
( ) |( ) ( ) |( )
( ) |( ) ( ) |( )
kita peroleh
( ( ) ( ) ( ))
Error dalam perkiraan tersebut adalah
( ) |( )
Turunan ketiganya tidak pernah melebihi dalam nilai absolut karena merupakan hasil kali sinus dan cosinus. Juga, | | dan | | . Dengan demikian,
| ( )| (( ) ( ) ( ) ( ) ) ( )