Pertemuan 12
Conic Sections dan Koordinat Kutub
12.1 Pendahuluan
Pada pertemuan kali ini, kita akan melihat definisi geometri dari parabola, elips, dan hiperbola, hingga persamaan standarnya masing-masing. Kurva-kurva ini disebut conic sections (conics), dan dapat memodelkan jalur yang dilalui oleh planet, satelit, dan benda lainnya. gerakan planet juga paling baik dideskripsikan dengan bantuan koordinat kutub, sehingga kita juga akan melihat kurva, turunan, dan integral dari sistem koordinat kutub ini. 12.2 Conic Sections dan Persamaan Kuadratik
Definisi 12.1 Parabola, Focus, dan Directrix
Suatu himpunan yang terdiri atas seluruh titik dalam sebuah bidang yang memiliki jarak yang sama dari suatu titik tetap tertentu dan suatu garis tertentu dalam bidang tersebut merupakan suatu parabola. Titik tetap tertentu tersebut adalah focus dari parabola, dan garis tetap tersebut adalah directrix.
Gambar 12.1 Beberapa bentuk standar parabola (Thomas’s Calculus, 11th
ed, p.686-687)
Tabel 12.1 Persamaan bentuk standar parabola dengan titik pada titik pusat ( ) Persamaan Focus Directrix Sumbu Terbuka
( ) Sumbu- Atas
( ) Sumbu- Bawah
( ) Sumbu- Kanan
( ) Sumbu- Kiri
Contoh 12.1
Jawaban
Kita temukan nilai dari dalam persamaan standar : s h a
Kemudian kita temukan focus dan directrix untuk nilai Focus: ( ) ( )
Directrix: a au □ Definisi 12.2 Elips, Foci
Suatu elips adalah himpunan titik-titik dalam sebuah bidang yang jaraknya dari dua titik tetap tertentu dalam bidang tersebut memiliki suatu jumlahan konstan. Kedua titik tetap tersebut adalah foci dari elips.
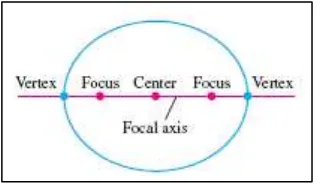
Definisi 12.3 Focal Axis, Center, Vertices
Garis yang melalui foci dari suatu elips adalah focal axis elips tersebut. Titik dalam pertengahan sumbu antara kedua foci adalah center. Titik dimana focal axis dan elips beririsan adalah titik-titik elips (Gambar 12.2).
Gambar 12.2 Titik-titik pada focal axis dari suatu elips (Thomas’s Calculus, 11th
ed, p.688) Persamaan bentuk standar untuk elips yang berpusat pada titik pusat Foci pada sumbu- : ( )
Jarak center ke focus: √ Foci: ( )
Jarak center ke focus: √ Foci: ( )
Vertices: ( )
Dalam tiap kasus, adalah semimajor axis dan adalah semiminor axis.
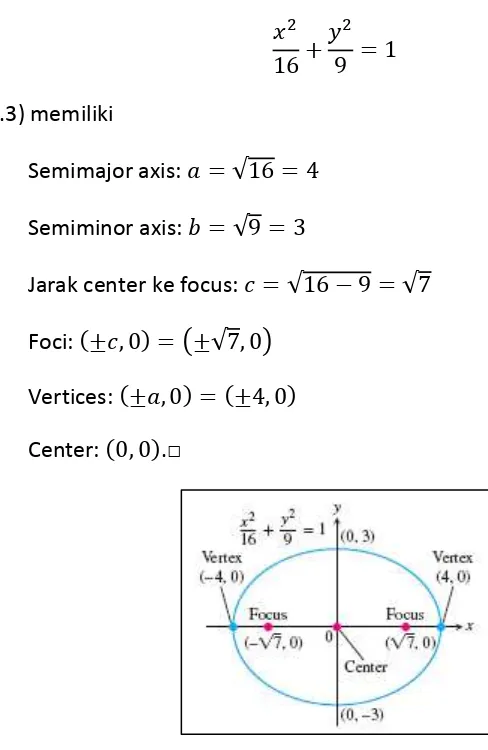
Contoh 12.2 Major axis horizontal Elips
(Gambar 12.3) memiliki
Semimajor axis: √ Semiminor axis: √
Jarak center ke focus: √ √ Foci: ( ) ( √ )
Vertices: ( ) ( ) Center: ( ).□
Gambar 12.3 Suatu elips dengan sumbu major horizontal (Thomas’s Calculus, 11th
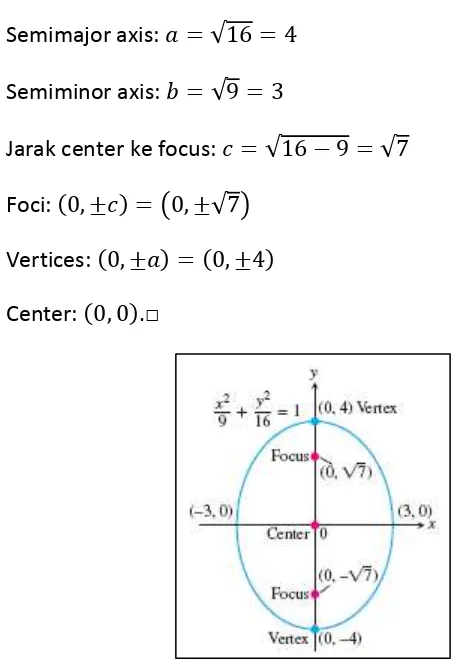
ed, p.689) Contoh 12.3 Major axis vertical
Elips
diperoleh dengan menukar nilai dan pada Contoh 12.2 sebelumnya memiliki suatu sumbu major vertical (Gambar 12.4),
Semimajor axis: √ Semiminor axis: √
Jarak center ke focus: √ √ Foci: ( ) ( √ )
Vertices: ( ) ( ) Center: ( ).□
Gambar 12.4 Suatu elips dengan sumbu major vertical (Thomas’s Calculus, 11th
ed, p.689) Definisi 12.4 Hiperbola, Foci
Suatu hiperbola adalah himpunan titik-titik dalam suatu bidang yang jaraknya dari dua titik tetap dalam bidang tersebut memiliki suatu selisih konstan. Kedua titik tetap tersebut adalah foci dari hiperbola.
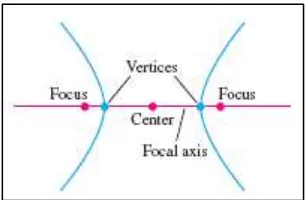
Definisi 12.5 Focal Axis, Center, Vertices
Gambar 12.5 Titik-titik pada focal axis dari suatu hiperbola (Thomas’s Calculus, 11th
ed, p.691)
Persamaan bentuk standar untuk hiperbola yang berpusat pada titik pusat
Foci pada sumbu- :
Jarak center ke focus: √ Foci: ( )
Vertices: ( )
Asymptotes:
Foci pada sumbu- :
Jarak center ke focus: √ Foci: ( )
Vertices: ( )
Asymptotes: Contoh 12.4 Foci pada
sumbu-Persamaan
(Gambar 12.6) memiliki
Jarak center ke focus: √ √ Foci: ( ) ( )
Center: ( )
Asymptotes: a au √ □
Gambar 12.6 Hiperbola dan asymptotesnya untuk Contoh 12.4 (Thomas’s Calculus, 11th ed, p.692)
Contoh 12.5 Foci pada sumbu-Persamaan
(Gambar 12.7) memiliki
Jarak center ke focus: √ √ Foci: ( ) ( )
Vertices: ( ) ( ) Center: ( )
Asymptotes: a au
√ □
(Thomas’s Calculus, 11th
ed, p.692) 12.3 Pengelompokkan Conic Sections
Sekarang diperkenalkan suatu bilangan baru yang disebut eccentricity dari suatu conic section. Eccentricity dapat menunjukkan tipe conic section (lingkaran, elips, parabola, atau hiperbola), dan menjelaskan beberapa sifat umum conic section (untuk elips dan hiperbola). Definisi 12.6 Eccentricity dari suatu elips
Orbit dari komet Halley adalah suatu elips dengan panjang unit astronomi dan lebar unit astronomi (satu unit astronomi adalah , semimajor axis dari orbit
Contoh 12.7 Menemukan vertices dari suatu elips
Tentukan vertices dari suatu elips yang memiliki eccentricity yang foci-nya terletak pada titik ( ).
Jawaban
cara berikut. Misalkan bahwa jarak suatu titik dari suatu titik tetap (focus) adalah suatu kelipatan konstan dari jaraknya terhadap suatu garis tetap (directrix). Maka,
dimana merupakan kelipatan konstan. Jalur yang ditelusuri oleh adalah
a. Suatu parabola jika
Temukan suatu persamaan Kartesius untuk hiperbola yang berpusat pada titik pusat yang memiliki focus pada ( ) dan garis sebagai directrix-nya.
Jawaban
Pertama kita cari eccentricity dari hiperbola tersebut. Focusnya adalah
Setelah memperoleh , sekarang kita dapat mencari persamaan yang diinginkan dari persamaan . Perhatikan Gambar 12.8, diperoleh
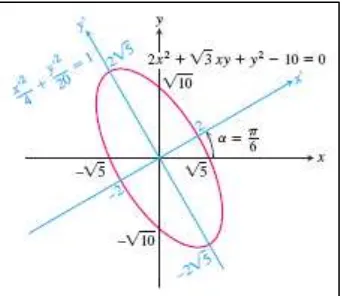
Sumbu- dan diputar dengan sudut sebesar ⁄ radians dari titik pusat. Temukan suatu
Gambar 12.8 Hiperbola untuk Contoh 12.10 ( dan adalah koordinat barunya) (Thomas’s Calculus, 11th
ed, p.703)
Jika kita terapkan persamaan sumbu koordinat yang berotasi ke persamaan kuadratik, kita peroleh persamaan kuadratik yang baru,
Koefisien yang lama dan baru saling berhubungan oleh persamaan berikut
( )
Sumbu koordinat akan diputar sebesar sudut untuk menghasilkan suatu persamaan bagi kurva substitusikan nilai-nilai ini ke persamaan sudut rotasi untuk memperoleh nilai :
√ √
Dengan aturan segitiga siku-siku, kita dapat menentukan salah satu sudut yang berlaku adalah ⁄ , sehingga ⁄ . Dengan substitusi ⁄ √
Gambar 12.9 Conic sections Contoh 12.11 (Thomas’s Calculus, 11th
ed, p.704) Kita tidak perlu menghapus suku- dari persamaan
untuk mengetahui jenis conic section yang dinyatakan oleh persamaan tersebut. Jika kita hanya ingin mengetahui jenis kurva yang terbentuk, maka kita dapat menggunakan uji diskriminan.
Uji diskriminan
Dengan pemahaman bahwa beberapa kasus dapat menjadi pengecualian, persamaan kuadratik adalah
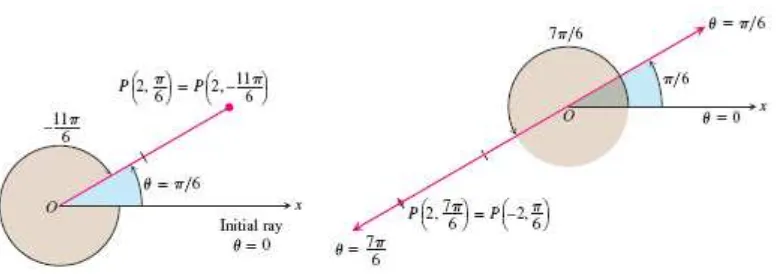
Gambar 12.10 Koordinat Kutub tidaklah unik dan dapat memiliki nilai negatif (Thomas’s Calculus, 11th
ed, p.714) Contoh 12.13 Menemukan Koordinat Kutub
Temukan seluruh koordinat kutub dari titik ( ⁄ ). Jawaban
Kita gambarkan initial ray dari sistem koordinat, lalu menggambarkan garis dari titik pusat dengan sudut ⁄ radians terhadap initial ray, dan tandai sebagai titik ( ⁄ ) (Gambar 12.11). Kemudian kita cari sudut-sudut pasangan lainnya dari dimana dan .
Gambar 12.11 Titik ( ⁄ ) memiliki banyak pasangan koordinat kutub lainnya (Thomas’s Calculus, 11th
ed, p.715) Untuk , daftar sudut yang sama adalah
Untuk , daftar sudutnya adalah
Pasangan koordinat yang berkaitan dengan adalah
dan
( )
Saat , diperoleh ( ) dan ( ). Saat , diperoleh ( ) dan ( ), da s rus ya.□
Persamaan Kutub dan Grafiknya Persamaan Grafik
Lingkaran dengan jari-jari | | berpusat di
Garis melalui membuat sudut terhadapt initial ray
Persamaan dengan bentuk dan dapat dikombinasikan untuk mendefinisikan daerah, ruas garis, dan sudut.
Contoh 12.14 Menentukan grafik
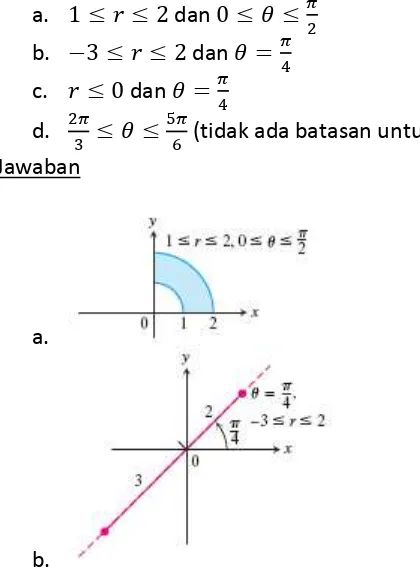
Gambarkan grafik kumpulan titik-titik dimana koordinat kutubnya memenuhi kondisi berikut.
a. dan b. dan c. dan
d. (tidak ada batasan untuk ) Jawaban
a.
c.
d.
Persamaan yang menghubungkan Koordinat Kutub dan Koordinat Kartesius
Gambar 12.12 Ilustrasi yang menggambarkan hubungan Koordinat Kutub dan Kartesius (Thomas’s Calculus, 11th
ed, p.716) Contoh 12.15 Mengubah Kartesius ke dalam Kutub
Tentukan persamaan kutub untuk lingkaran ( ) (Gambar 12.13).
(Thomas’s Calculus, 11th Contoh 12.16 Mengubah Kutub ke dalam Kartesius
( ) pada grafik
( ) ( ) ( ) pada grafik.
Saat naik dari ke , turun dari ke , dan naik dari nilai minimum ke nilai maksimum . Saat terus naik dari ke , naik dari kembali ke dan turun dari ke . Kurva mulai berulang saat karena cosinus memiliki periode . kurva meninggalkan titik pusat dengan slope ( ) dan kembali ke titik pusat dengan slope ( ) .
Kita buat sebuah tabel nilai dari hingga , gambar titik-titik tersebut, dan gambar kurva yang melalui titik-titik dengan suatu horizontal tangent pada titik pusat, kemudian mencerminkannya terhadap sumbu- sehingga diperoleh grafik utuh (Gambar 12.14). Kurva ya rb uk d s bu card o d kar a m y rupa b uk ja u .□
Gambar 12.14 Langkah-langkah dalam menggambar cardioid (Thomas’s Calculus, 11th
ed, p.720) 12.7 Area dan Panjang dalam Koordinat Kutub
Luas area dari daerah berbentuk kipas diantara titik pusat dan kurva ( ) ∫
Gambar 12.15 Luas diferensial untuk kurva ( ) (Thomas’s Calculus, 11th
ed, p.726) Contoh 12.18 Menemukan luas area
Temukan luas area daerah dalam bidang yang ditutupi oleh cardioid ( ). Jawaban
Kita gambarkan cardioid (Gambar 12.16) dan tentukan bahwa jari-jari menyapu daerah tepat satu kali saat berjalan dari ke . Dengan demikian luas areanya adalah
∫
∫ ( )
∫ ( ) ∫ ( )
∫ ( )
[ ] □
Gambar 12.16 Cardioid dalam Contoh 12.18 (Thomas’s Calculus, 11th
∫ ∫ ∫ ( )
Contoh 12.19 Menemukan luas area diantara kurva kutub
Temukan luas daerah yang terletak di dalam lingkaran dan di luar cardioid .
Jawaban
Kita gambarkan daerah untuk menentukan batasannya dan cari batasan dari integrasi (Gambar 12.17). Kurva yang di luar adalah , kurva di dalam adalah , dan
berjalan dari ⁄ hingga ⁄ . Luas areanya adalah ∫ ⁄⁄ ( )
∫ ⁄ ( ) simetri ∫ ( ( ⁄ ))
∫ ( ⁄ ) ∫ ⁄ ( )
[ ] ⁄ □
Gambar 12.17 Daerah dan batasan integrasi untuk Contoh 12.19 (Thomas’s Calculus, 11th
ed, p.727) Panjang dari suatu kurva kutub
∫ √ ( ) Contoh 12.20 Menemukan panjang dari suatu cardioid Temukan panjang dari cardioid .
Jawaban
Kita gambarkan cardioid tersebut untuk menentukan batasan integrasi (Gambar 12.18).
Gambar 12.18 Menghitung panjang suatu cardioid (Contoh 12.20) (Thomas’s Calculus, 11th
ed, p.728)
Titik ( ) menelusuri kurva satu kali, berlawanan arah jarum jam saat berjalan dari ke , sehingga ini merupakan nilai-nilai yang kita ambil sebagai dan .
Dengan
diperoleh
(
) ( ) ( )
dan
∫ √ ( ) ∫ √
∫ | |
∫ u uk
[ ]
12.8 Conic Sections dalam Koordinat Kutub
Persamaan kutub standar untuk garis
Jika titik ( ) adalah kaki tegak lurus dari titik pusat ke garis , dan , maka persamaan untuk adalah
( )
Contoh 12.21 Mengubah suatu persamaan kutub garis menjadi bentuk Kartesius
Gunakan identitas ( ) untuk menemukan suatu persamaan Kartesius untuk garis dalam Gambar 12.19.
Gambar 12.19 Persamaan kutub standar dari garis diubah menjadi persamaan Kartesius (Thomas’s Calculus, 11th
ed, p.728) Jawaban
( )
( )
√
√
Persamaan kutub untuk lingkaran dengan jari-jari dan berpusat di ( ) adalah ( )
Contoh 12.22 Lingkaran melalui titik pusat
Radius Center (polar coordinates) Polar equations
( )
( ⁄ )
⁄ ( ⁄ )
( ⁄ ) Persamaan kutub untuk suatu conic dengan eccentricity
dimana merupakan directrix vertical.
Persamaan di atas menunjukkan suatu elips jika , suatu parabola jika , dan suatu hiperbola jika .
Contoh 12.23 Persamaan kutub untuk beberapa conics
Gambar 12.20 Persamaan untuk conic sections dengan eccentricity , namun lokasi directrix yang berbeda-beda
(Thomas’s Calculus, 11th
ed, p.735) Contoh 12.24 Persamaan kutub untuk suatu hiperbola
Temukan suatu persamaan untuk hiperbola dengan eccentricity ⁄ dan directrix . Jawaban
( ( ⁄ ) ⁄ )
Persamaan kutub untuk elips dengan eccentricity dan semimajor axis ( )
Contoh 12.25 Orbit planet Pluto
Temukan suatu persamaan kutub untuk suatu elips dengan semimajor axis AU (astronomical units) dan eccentricity . Ini merupakan perkiraan ukuran orbit Pluto mengelilingi matahari.
Jawaban
Pada titik terdekatnya (perihelion) dimana , Pluto memiliki jarak
dari matahari. Pada titik terjauhnya (aphelion) dimana , Pluto memiliki jarak
dar ma ahar (Gambar 12.21).□
Gambar 12.21 Orbit dari Pluto (Thomas’s Calculus, 11th