pada suatu kurva.
A. Garis singgung
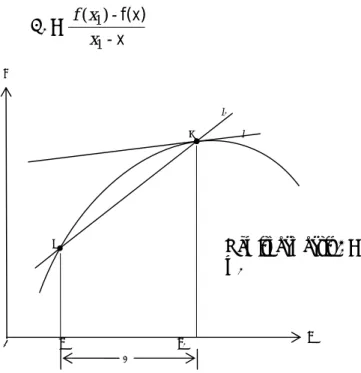
Garis singgung adalah garis yang menyinggung suatu titik tertentu pada suatu kurva. Pengertian garis singgung tersebut dapat dilihat pada Gambar 1a. Akan tetapi jika terdapat dua buah titik pada suatu kurva maka berkemungkinan garis singgung yang menyinggung salah satu titik akan memotong kurva pada titik lainnya. Untuk lebih jelasnya dapat dilihat pada Gambar 1b.
Untuk mendapatkan pengertian yang lebih jelas mengenai garis singgung kita perlu mendefinisikan kemiringan garis singgung l pada titik A(x1,f(x1)) yang terletak pada grafik fungsi. Selanjutnya pada grafik fungsi tersebut kita pilih suatu titik B(x,f(x)). Jika kita hubungkan titik A dan B maka akan terbentuk garis l1 yang mempunyai kemiringan :
A
l
(a)
(b)
Gambar 1. garis singgung A
B l
m1 =
x -
f(x) -
1 1) (
x x f
Jika f(x) kontinu pada selang [A,B] maka kita dapat mendekatkan titik B ke titik A dengan jalan memperkecil jarak antara x dan x1. Dalam bentuk limit hal tersebut dapat ditulis dalam bentuk :
x
x m f
x x x
x = −
→
→ x1
f(x) - ) lim (
lim 1 1
1 1
Persaman ini adalah kemiringan garis l1 jika x mendekati x1. Jika kita perhatikan Gambar 2 maka kita dapat melihat bahwa kemiringan garis l1 jika x mendekati x1 adalah mendekati kemiringan garis l. Dalam bentuk limit dapat ditulis :
m
x x m f
x x x
x =
= −
→
→ x1
f(x) - ) lim (
lim 1 1
1 1
Jadi :
x
x m f
x
x −
= → x1
f(x) - ) lim ( 1
1
l1
A l
B
x x1
h 0 x
y
Gambar 2. Kemiringan garis
Kemirngan garis l1= m1
Karena x1 – x = h, maka
h f(x) - ) lim (
0
h x m f
h
= +
→
Jika dimisalkan h = ∆x, maka
x f(x) -
∆
∆
∆
) lim (
0
x x m f
x
= +
→
Tiga persamaan adalah kemiringan garis l pada titik (x, f(x))
Contoh 1 :
Diketahui f(x) = 3x2 + 5. Tentukan kemiringan dan persamaan garis singgung yang melalui titik (a,a2)
Penyelesaian :
x f(x) -
∆
∆
∆
) lim (
0
x x m f
x
= +
→
x
x x
x x
x
x
x ∆
∆
∆
∆
∆
∆
∆
5 3 5 6
lim 3 5 )
( lim 3
2 2
0 2
0
−
− + +
= +
− +
= +
→
→
2
2 x 3( x)
x 3x - 5
x x x
x 6 3 6
lim
0 + =
= → ∆
∆
Jadi m = 6x (*)
Persamaan garis singgung : y = mx + n (**) Karena garis singgung melalui titik (a,a2) maka : persamaan (*) menjadi :m = 6a
persamaan (**) menjadi : a2 = 6a2 + n. Sehingga n = -5a2 Persamaan garis singgung menjadi : y = 6ax – 5a2
B. Turunan
Turunan adalah hasil dari proses differensiasi suatu fungsi. Differensiasi dapat dimisalkan sebagai suatu mesin yang memproses masukan f(x) menjadi turunan f(x) atau f ’(x).
Selanjutnya turunan didefinisikan sebagai kemiringan garis yang menyinggung kurva f(x)di titik (x, f(x)). Berdasarkan persamaan 4.3 dan Gambar 4.3 maka definisi turunan dapat ditulis dalam bentuk :
x x
x f x x f
f
x
x −
= −
→ 1
1) ( ) lim (
) ( '
1
, jika nilai limitnya ada
Jika persamaan di atas dapat dipenuhi berarti f(x) dapat didifferensiasikan (differensiable) pada x. Maka dikatakan f(x) mempunyai turunan pada x.
Contoh 2
Jika f(x) = 2x2 + 5x – 7, tentukan f ’(x), f ’(c) dan f ’(3) Penyelesaian :
f(x) = 2x2 + 5x – 7
f(x+∆x) = 2(x+∆x)2 + 5(x+∆x) – 7 = 2x2 + 4x∆x +2(∆x)2 + 5x + 5∆x – 7 f(x+∆x) – f(x) = 4x∆x + 2(∆x)2 + 5∆x
5 4 5 2 4 5 lim
) ( 2 lim 4
) ( ) lim (
) ( '
0 2
0
0 + − = + + = + + = +
= → → → x x x
x
x x
x x x
x f x x x f
f
x x
x ∆
∆
∆
∆
∆
∆
∆
∆
∆
∆
Jadi : f'(x)= x4 +5 f'(c)= c4 +5 f'(3)=4(3)+5=17
Catatan: Selain notasi 'f , turunan fungsi y = f(x) juga dapat dituliskan dengan notasi dy/dx .
Pada uraian terdahulu telah dijelaskan bahwa suatu fungsi f dikatakan differensiable jika memenuhi persamaan 4.6, yaitu :
Jika :
x x f x x f
x ∆
∆
∆
) ( ) lim (
0
− +
→ ada, maka
x x f x x x f
f
x ∆
∆
∆
) ( ) lim (
) ( '
0
−
= +
→
f(x+∆x)- f(x)= x
x x f x x
f ∆
∆
∆ − •
+ ) ( )
(
x x x f x x x f
f x x f
x x
x ∆
∆
∆ ∆
∆
∆
∆ 0 0 ( ) ( ). lim0
lim )) ( ) ( (
lim→ → →
−
= +
−
+ = 'f (x) . 0 = 0
Sehingga : lim ( ) lim ( )
0
0 f x x f x
x
x→ + = →
∆
∆ ∆ → lim ( ) ( )
0 f x f x
x =
∆ → (terbukti)
Jadi jika f adalah fungsi yang differensiabel pada x maka f dikatakan kontinu pada x.
Sebaliknya jika f adalah fungsi yang kontinu pada x, maka tidak secara otomatis f differensiable pada x.
C. Sifat – sifat turunan 1. Turunan bilangan konstan
Jika c suatu bilangan konstan dan y didefinisikan sebagai : y = f(x) = c maka = f'(x)=0
dx dy
2. Jika n adalah sembarang bilangan bulat, k adalah sembarang bilangan ril dan jika y didefinisikan sebagai :
y = f(x) = kxn maka = f'(x)=knxn−1 dx
dy
Contoh 3
Tentukan turunan pertama dari f(x) = 5x7 Penyelesaian :
6 1
7 35
) 7 )(
5 ( ) (
' x x x
dx f
dy = = − =
3. Aturan penjumlahan
Jika f dan g adalah dua buah fungsi dan h adalah fungsi yang didefinisikan sebagai :
y = h(x) = f(x) + g(x) maka f'(x) g'(x) dx
dy= +
Contoh 4 :
Diketahui y = 5x6 + 2x-3. Tenrtukan dxdy Penyelesaian :
f(x) = 5x6 g(x) = 2x-3
f’(x) = 30x5 g’(x) = -6x-4 dx =
dy f’(x) + g’(x) = 30x5 – 6x-4
4. Aturan perkalian
Jika f dan g adalah dua buah fungsi dan h adalah fungsi yang didefinisikan sebagai :
y = h(x) = f(x).g(x) maka f'(x)g(x) f(x)g'(x) dx
dy = +
Contoh 5 :
Diketahui y = (3x5 + 2x-2)(7x+3) Tentukan
dxdy
Penyelesaian :
f(x) = 3x5 + 2x-2 g(x) = 7x+3 f’(x) = 15x4 – 4x-3 g’(x) = 7
dy = 126xdx 5 + 45x4 - 14x-2 – 12x-3 5. Aturan pembagian
Jika f dan g adalah dua buah fungsi dan h adalah fungsi yang didefinisikan sebagai : y = h(x) =
) (
) (
x g
x
f maka
[ ( )]2
) ( ' ) ( ) ( ) ( '
x g
x g x f x g x f dx
dy= −
Contoh 6 :
Tentukan turunan dari h(x) = 3
2 4
4 3 2
x x x −
Penyelesaian :
2 3
2 2 4 3
3
2 (4 )
) 12 )(
3 2 ( ) 4 )(
6 8 ( )]
( [
) ( ' ).
( ) ( ).
( ) ' ( '
x
x x x x
x x x
g
x g x f x g x x f
h = − = − − −
= 6
4 6
6
4 6 4
6
16 60 12
16
36 24 24
32
x x x
x
x x x
x − − − = −
= 2
2
4 15 3
x x −
6. Turunan fungsi komposisi
Jika y = f(u) dan u = g(x) maka
dx du du dy
dxdy = Persamaan ini disebut aturan rantai
Contoh 7 : Tentukan
dxdy jika y = (4x3 + 5x2 – x + 4)3 Penyelesaian :
Misal u = 4x3 + 5x2 – x + 4 y = u3 =12x2+10x−1
dx
du 2
du 3u dy = = =3u2(12x2+10x−1)
dx du du dy dx dy
=3(12x2+10x−1)(4x3+5x2−x+4)2
Soal-soal
Tentukan turunan dari fungsi-fungsi berikut !
1. f(t) = at2 – bt + 17 6. ⎥⎦⎤
⎢⎣⎡ +
⎥⎦⎤
⎢⎣⎡
= x
x x x
f 1
5 4 4
) 5
( - 3x
2. f(x) = 2x-5 + 35x2 7. g(t) = (at2+bt+c)2(3at–7)5
3. ⎥⎦⎤
⎢⎣⎡ +
= 2
x x x
g 2
)
( 8.
c w
aw w b
g +
= − 2
) (
4. h(x) =
1 2
5 4 ⎥⎦⎤
⎢⎣⎡ + x
x 9. 3
2 2
) (
) ) (
(
d ct
bt t at
f −
= −
5. w(x) =
3
4 3
7 ⎥⎦⎤
⎢⎣⎡ - 2x +
x 10.
5 ) 3 ) (
(
2
+
= − t t t g
D. Turunan fungsi-fungsi trigonometri 1. Jika y = sin x maka = f'(x)=cos x
dx
dy
Bukti :
x
x x
x x
x f x x x f
dx f dy
x
x ∆
∆
∆
∆
∆
∆
sin ) lim sin(
) ( ) lim (
) ( '
0 0
−
= +
−
= +
= → →
x
x x x x x
x ∆
∆
∆
∆
sin sin
cos cos
lim sin
0
−
= +
→
x
x x x
x
x ∆
∆
∆
∆
sin cos ) 1 (cos lim sin
0
+
= −
→
⎥⎦⎤
⎢⎣⎡ − +
= → x
x x x
x x
x ∆
∆
∆
∆
∆
cos sin ) 1 sin (cos
lim
0
x
x x x
x x
x
x ∆
∆
∆
∆
∆
∆
lim sin 1 cos
lim cos sin
0
0 →
→ − +
=
= (sin x)(0) + (cos x)(1) = cos x (terbukti)
2. Jika y = sin u dan u = f(x) maka
dx u du dx
dy=cos .
3. Jika y = f(x) = cos x maka dxdy =f'(x)=−sinx 4. Jika y = cos u dan u = f(x) maka dxdy =−sinudxdu Contoh 8 :
Jika y = sin(π-2x), tentukan dxdy Penyelesaian :
Misal u = π - 2x y = sin u =−2
dx
du u
du dy =cos
(cosu)( 2) 2cos( 2x) dx
du du dy dx
dy = = − =− π −
Contoh 9 : Jika y =
cos2x tentukan dxdy Penyelesaian :
Misal u =
2x y = cos u =1/2
dx
du u
du
dy =−sin
2 2
)(1 sin
( x
dx u du du dy dx
dy sin
2 -1 )=
−
=
=
Contoh 10
Jika y = sin 2x cos 3x, tentukan dy dx Penyelesaian :
Misal u = sin 2x v = cos 3x
x
dx
du =2cos2 =−3sin3x dx
dv
. (2cos2x)(cos3x) (sin2x)( 3sin3x) dx
udv dx v du dx
dy = + = + −
=2cos2x.cos3x−3sin2x.sin3x
Contoh 11 Jika y =
x x 4 cos
3
sin , tentukan dxdy Penyelesaian :
Misal u = sin 3x v = cos 4x
x
dx
du =3cos3 =−4sin4x dx
dv
2 2
) 4 (cos
) 4 sin 4 )(
3 (sin ) 4 )(cos 3 cos 3 . (
.
x
x x
x x
v dx u dv dx v du
dx
dy − = − −
=
x
x x x
x
4 cos
4 sin . 3 sin 4 4 cos . 3 cos 3
2
= +
5. Jika y = f(x) = tan x maka = f'(x)=sec2 x dx
dy
6. Jika y = tan u maka
dx u)du (sec2
dx =
dy
Contoh 12
Jika y = 5 tan 3x, tentukan dxdy Penyelesaian :
Misal u = 3x y = 5 tan u =3
dx
du u
du
dy 2
sec
=5
u u x
dx du du dy dx
dy = =(5sec2 )(3)=15sec2 =15sec23
7. Jika y = f(x) = cot x maka = f'(x)=−csc2 x dx
dy
8. Jika y = cot u maka
dx u)du csc2
(−
dx =
dy
Contoh 13 :
Jika y = x
3 cot1 2
1 , tentukan dxdy Penyelesaian :
Misal u = x
1 y = 3 cotu 2 1
3
=1 dx
du u
du
dy 2
2csc
−1
=
u u x
dx du du dy dx dy
3 csc 1 6 csc 1
6 ) 1 3 )(1 2csc
(−1 2 =− 2 =− 2
=
=
9. Jika y = f(x) = sec x maka f x x x dx
dy= '( )=sec tan
10. Jika y = sec u maka
dx u)du dx u
dy=(sec tan
11. Jika y = f(x) = csc x maka f x x x dx
dy = '( )=−csc cot
12. Jika y = csc u maka
dx u)du dx u
dy=(−csc cot
Contoh 15 :
Jika y = csc( x) 3
1 π− , tentukan
dx dy
Penyelesaian :
Misal u = π-x y = 31cscu
=−1 dx
du ucotu
du
dy csc
3
−1
=
x) - cot(
cotu
cotu csc(π ) π
3 csc 1
3 ) 1 1 )(
3csc
( 1 u u x
dx du du dy dx
dy = = − − = = −
Soal-soal
Tentukan turunan pertma dari fungsi-fungsi berikut !
1. f(x) = )
3 sin(2x −π
6. f(x) = )
(3 csc4 π −x 2. f(x) = cos )
3 x
( −2π 7. g(t) = sin2tcos t 2
1 π
3. f(x) = tan3 x 8. h(w) =
) cos(
) sin(
bw aw
−
− π
π
4. h(x) = cot3x 9. g(t) =
) cos(
2
2 sin t b
t at
−
−
5. h(x) = )
3 (2 sec5 x −π
10. g(t) =
t t 3 sin cos2tsin
E. Turunan fungsi-fungsi trigonometri invers
Berikut beberapa turunan fungsi invers trigonometri ( fungsi siklometri) 1. Jika y = f(x) = arcsin x maka
x2 1 ) 1 x ( ' dx f dy
−
=
=
Bukti :
y = arcsinx → sin y = x → 1
dx dx dx ydy
cos = = →
y cos
1 dx dy=
Selanjutnya perhatikan segitiga berikut ini !
sin y = x cos y = 1−x2
1 2
1 dx x
dy
= − (terbukti)
1 x− 2 2. Jika y = arcsin u dan u = f(x) maka
dx du dx u
dy 1 2
1
= −
Contoh 16 :
Jika y = )
3 arcsin( 1 8
3 − x , tentukan dy dx Penyelesaian :
Misal u = −31x y = 83arcsinu
dxdu=−31
1 2
1 8 3 du u dy
= −
2 2
9 1 1 8
1 3
1 1
1 8 3
u x dx
du du dy dx dy
−
−
⎥⎦=
⎢⎣ ⎤
− ⎡−
=
=
3. Jika y = f(x) = arccos x maka
1 2
) 1 ( '
x x
dx f dy
− −
=
=
1 x
y
4. Jika y = arccos u dan u = f(x) maka
dx du dx u
dy 1 2
1
− −
=
Contoh 17 :
Jika y =−3arccos2x, tentukan
dx dy Penyelesaian :
Misal u = 2x y = −3arccosu
dxdu =2
1 2
3 1 du u dy
= −
2
2 1 4
) 6 2 ( 1 3 1
x dx u
du du dy dx dy
= −
= −
=
5. Jika y = f(x) = arctan x maka 2
x 1 ) 1 x ( ' dx f dy
= +
=
6. Jika y = arctan u dan u = f(x) maka dxdu
u 1
1 dx dy
+ 2
=
Contoh 18 :
Jika y = x
3 arctan1 5
3 , tentukan
dx dy Penyelesaian :
Misal u = 13x y = 53arctanu dxdu =31 2
u 1
1 5 3 du dy
= +
9 ) 1 1 ( 5
1 3
1 1
1 5 3
2 2
u x dx
du du dy dx dy
+
⎥⎦=
⎢⎣ ⎤
⎡
= +
=
7. Jika y = f(x) = arccot x maka 2
x 1 ) 1 x ( ' dx f dy
− +
=
=
8. Jika y = arccot u dan u = f(x) maka dxdu
u 1
1 dx dy
+ 2
−
=
Contoh 19 :
Jika y = 2 arccot 3x, tentukan dxdy Penyelesaian :
Misal u = 3x y = 2 arccot u dxdu =3 2
u 1 2 1 du dy
− +
=
2 2
x 9 1 ) 6 3 u ( 1 2 1 dx du du dy dx dy
− + + =
−
=
=
9. Jika y = f(x) = arcsec x maka
1 x x ) 1 x ( ' dx f dy
2−
=
=
10. Jika y = arcsec u dan u = f(x) maka dxdu
1 u u
1 dx dy
2−
=
Contoh 20 :
Jika y = arcsec ) (π2 −x
, tentukan dxdy Penyelesaian :
Misal u = −x 2
π y = arcsec u
=−1 dx
du
1 1
2 −
= u du u dy
1 2 )
( 2 ) ( ) 1 1 ( 1 1
2
2 − − −
−
=
− −
=
=
x u x
dx u du du dy dx dy
π π
11. Jika y = f(x) = arccsc x maka
1 ) 1
(
' =− 2−
=
x x x dx f
dy
12. Jika y = arcsec u dan u = f(x) maka
dx du u
dx u dy
1 1
2 −
−
=
Contoh 21 :
Jika y = arccsc(x−2π), tentukan
dx dy Penyelesaian :
Misal u = x−2π y = arccsc u dxdu =1
1 u u
1 du
dy
2−
−
=
1 2) x ( 2) x ( ) 1 1 ( 1 u u
1 dx
du du dy dx dy
2 2
π − π −
−
−
=
−
−
=
=
Soal-soal
Carilah turunan pertama dari soal-soal berikut ! 1. y = arcsin(π-x) 3. y = arccoscos2xx
2. y = -3 arccos 4x 4. y = arctan x – sin 3x
F. Turunan fungsi eksponensial
1. Jika y = f(x) = ex maka = f' x( )= dx
dy ex
2. Jika y = eu dan u = f(x) maka dxdy =eudxdu
Contoh 22 :
Jika y = −2ea−bx, tentukan dxdy Penyelesaian :
Misal : u = a – bx dxdu= -b
dxdy =(ea−bx)(−b)=−bea−bx
G. Turunan fungsi logaritma
1. Jika y = f(x) = ln x maka = f' x( )= dx
dy
1 x 2. Jika y = ln u dan u = f(x) maka
dx du u dx
dy =1
Contoh 23 :
Jika y = e2x ln31x tentukan dxdy
Penyelesaian : Misal : u = e2x v = ln31x dxdu=2e2x dxdv = x1
⎥
⎦
⎢ ⎤
⎣
⎡ +
= +
= +
= x
x 1 3 ln1 2 x e
e 1 3x ln1 e dx 2 .dv u v dx. du dx
dy 2x 2x 2x
3. Jika y = f(x) = alog x maka dxdy =f'(x)= (ln1a)x 4. Jika y = alog u dan u = f(x) maka dxdy =(ln1a)udxdu Contoh 24 :
Jika y = 7log(3-5x) tentukan dxdy
Penyelesaian : Misal : u = 3 – 5x → dxdu=−5 dxdy =(ln1a)udxdu=(ln7)(−35−5x) Soal-soal
Tentukan turunan pertama dari fungsi-fungsi berikut !
1. y = xe3x 4. y = 24x
e x 3 ln
x 7. y = lne4x
3x 1
10. y =
x ln e
e x 5 ln x
x
− x