logika matematika dan pembuktian matemat

Pokok-pokok bahasan

1.1 logika dan pernyataan 1.2 a. Konjungsi

b. disjungsi c. implikasi d. biimplikasi

1.3 negasi atau ingkara

1.4 konvers,invers dan kontraposisi 1.5 pernyataan kuantor

1.6 penarikan kesimpula

PENGERTIAN LOGIKA DAN PERNYATAAN

1

LOGIKA MATEMATIKA

Kebenaran seuatu teori yang dikemukakan seriap ilmuan, matematikawan maupun para ahli merupakan hal yang sangat menentukan reputasi mereka . untuk mendapatkan hal tersebut, mereka akan berusaha untuk mengaitkan suatu fakta atau valid. Sebagai akibatnya, logika adalah ilmu yang sangat penting dipelajari. Di dalam mata pelajaran matematika maupun IPA , aplikasi logika seringkali ditemukan meskipun tidak secara formal disebut sebagai belajar logika, bagian ini akan membahas tentang logika yang di dahului dengan pengertian penalaran, diikuti dengan pernyataan, berakit-rakit membentuk : negasi, konjungsi, disjungsi, implikasi dan biimplikasi.

A. PENGERTIAN LOGIKA

Ada pernyataan menarik yang dikemukakan mantan presidden AS Thomas jefferson sebagai mana dikutip copi (1978) berikut ini, “ in a republican natio, whose citizes are to be led by reason and persuasion and not by force, the art of reasoning becomes of first importance” (p.vii). pernyataan itu mnunjukan pentingnya logika, penalaran dan argumentasi dipelajari dan dikembangkan disuatu negara sehingga setiap warga ngara akan dapat dipimpin dengan daya nalar (otak) dan bukannya dengan kekuatan (otak) saja. Karenanya, seperti yang dinyatakan mantan presiden AS tadi, seni bernalar merupakan hala yang sangat penting. Di samping itu, copi (1978) juga mngutip pendapat juliana geren pilon yang senada dengan yang diucapkan mantan presiden AS tadi: “civilized life depends upon the success of reason in social intercourse, the prevalence of logic over violence in terpersonal conflict” (p.vii)

penurunan-peurunan kesimpilan yang sahih (valid, correct) dan yang tidak sahih (tidak valid, incorrect). Proses berpikir yang terjadi saat peurunan atau menarik kesimpulan dari pernyataan-pernyataan yang diketahui benar atau dianggap benar itu sering juga disebut dengan penalaran (reasoning).

B. PERNYATAAN

Diulai sejak ia masih kecil, setiap manusia, sedikit demi sedikit melengkapi perbendaharaan kata-katanya. Disaat berkomunikasi seseorang harus menyusun kata-kata yang dimilikinya menjadi suatu kalimat yang memiliki arti atau bermakana. Kalimat adalah susunan kata-kata yang memiliki arti yang dapat berupa pernyataan (“pintu itu tertutup.”), pernyataan (“apakah pintu itu tertutup?”), perintah (“tutup pintu itu!”), ataupun permintaan(“tolong pintunya ditutup”). Dari empat macam kalimat tersebut, hanya pernyataan saja yang bernilai benar atau salah, tetapi tidak sekaligus benar atau salah. Meskipun para ilmuan, matematika ataupun ahli-ahli lainn7a seringmenggunakan beberapa macam kalimat tersebut dalam kehidupan sehari-harinya namun hanya pernyataan saja yang menjadi perhatian mereka dalam mengembangkan ilmunya.

Setiap ilmuan matematikawan ataupun ahli-ahli lainnya akan berusaha untuk menghasilkan suatu pernyataan atau teori yang benar. Suatu ernyataan (termasuk teori) tidak akan ada artinya jika tidak bernilai benar. Karenanya, pembicaraan mengenai benar tidaknya suatu kalimat yang memuat suatu teori telah menjadi pembicaraan dan perdebatan para ahli filsafat dan logika sejak dahulu kala. Beberapa nama yang patut diperhitungkan karena telah berjasa untuk kita adalah plato (427-347), aristoteles (384-322 SM), charles s peirce (1839-1914) dan bertrand russell (1872-1970). Paparan berikut akan membicarakan tentang kebenaran dalam arti bilamana disebut salah. Untuk menjelaskan tentang kriteria kebenaran ini perhatikan dua kalimat berikut:

a. Semua manusia akan mati.

Pernytaan dari dua kalimat tersebut, kalimat manakah yang bernila benar dan manakah yang berniai salah. Pernyataan selanjutnya, mengapa kalimat tersebut dikategorikan bernilai benar atau salah. Dan bilamana suatu kalimat dikategorikan sebagai kalimat yang bernilai benar atau salah. Untuk menjawab pertanyaan tersebut , suriasumantri (1988) menyatakan bahwa ada tiga teori yang berkait dengan kriteria kebenaran ini yaitu : teori korespondensi dan koherensi pragmatis. Namun sebagan buku hany membicarakan duateori saja, yaitu korespondensi dan teori koherensi sehingga pembicaraan kita hanya berkait dengan dua teori terswebut.

1. Teori korespondensi

Teori korespondensi (the correspondence of truth) menunjukan bahawa suatu kalimat akan bernilai benar jika hal-hal yang terkandung di dalam pernyataan tersebut sesuai atau cocok dengam keadaan yang sesungguhnya. Contohnya “bandung adalah ibukota provinsi jawa barat” merupakan suatu pernyataan yang bernilai benar karena kenyataannya memang demikian. Yaitu bandung memang benar merupakan ibukota provinsi jawa barat. Namun pernyataan “ jakarta adalah ibu kota provinsi jawa tengah”, menurut teori ini akan bernilai salah karena hal-hal yang terkandung didalam pernyataan itu tidak sesuai dengan kenyataannya.

Teori korespondensi adalah kalimat yang tertutup kemungkinan untuk ditanggapi berbeda.

Contoh : ibu kota negara indonesia adalah jakarta

Kalimat pernyataan diatas tidak mungkin salah kebenarannya, karena sesuai dengan fakta bahwa jakarta adalah ibu kota negara indonesia

2. Teori koherensi

Pengetahuan aljabar telah didasarkan pada pernyataan pangkal yang dianggap benar. Pernyataan yang dianggap benar itu disebut aksioma atau postulat.

Teori koherensi adalah kalimat yang terbuka kemungkinan untuk ditanggapi berbeda.

Contoh : teorema seperti –b + (a+b) = a dapat dibuktikan dengan cara berikut:

-b + (a+b) = -b + (b+a) aks 3 - komutatif =(-b+b) + a aks 2 - asosiatif

=0 + a aks 6 - invers

= a aks 5 – identitas

1) Tertutup, a+b ∈ R dan a,b ∈ R

2) Asosiatif, a+(b+c) = (a+b)+c dan a.(b.c) = (a.b).c 3) Komutatif, a+b = b+a dan a.b = b.a

4) Distributif, a.(b+c) = a.b + a.c dan (b+c).a=b.a+c.a 5) Identitas, a+0 = 0+a = a dan a.1 = 1.a = a

Latihan 1.1

1. Manakah diantara kalimat berikut yang merupakan pernyataan. aX+3=2

b. X+3=2 adalah suatu pernyataan. c. 111 adalh bilangan prima

d. Tadi pagi fahmi bertanya “pak guru kapan ulangan?” e. 2n+1= untuk n ∈ A adalah bilangan ganjil

2. andi berbohong pada hari senin, selasa, dan rabu sedangkan pada hari-hari yang lain ia berkata benar. Teman karibnya, si badu berbohong pada hari kamis, jumat, dan sabtu, sedangkan pada hari-hari yang lain ia berkata benar. Pada suatu hari-hari, andi berkata “ kemarin adalah hari dimana saya berbohong.” Badu lalu menimpali : “kemarin adalah hari dimana saya berbohong juga”.

a. Pada hari apakah mereka berdua dapat menyatakan hal itu.

b. Jika mereka berdua sama-sama menyatakan bahwa hari kemarin adalah hari di mana mereka berkata benar, pada hari-hari apakah mereka berdua dapat menyatakan hal itu?

3. Pada suatu rumah makan , ANDI seorang SOPIR sedang duduk mengelilingi meja berbentuk persegi dengan tiga orang temannya. Ketiga teman Andi tersebut bekerja sebagai KLASI, PILOT, dan MARKONIS.

Tentukan pekerjaan Budi jika: andi duduk di sebelah kiri CHANDRA, BUDI duduk disebelah kanan kelasi dan DANI duduk berhadapan dengan chandra bukanlah seorang pilot.

a. Toni tidak pernah berbohong. Didi kadang-kadang berbohong. Sedangkan hory selalu berbohng

b. Mereka memakai kaos HIJAU, KUNING dan MERAH

c. Siswa yang memakai kaos kuing, menyatakan bahwa siswa yang berkaos merah adalah hory

d. Siswa yang memakai kaos merah menyatakan bahwa dirinya adalah didi

e. Siswa terakhir yang memakai kaos hijau , menyatakan bahwa siswa yang berkaos merah adalah toni

a. KONJUNGSI (Ʌ)

Konjungsi adalah suatu pernyataan majemuk yang menggunakan praktik “dan, tetapi, namun” (p ʌ q) dibaca (p atau q)

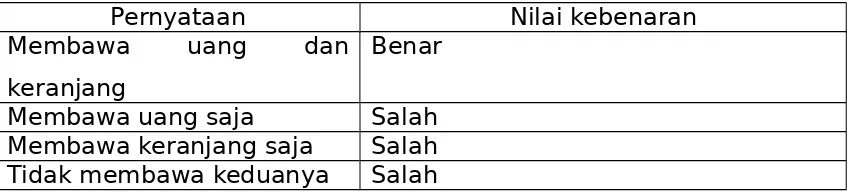
contoh: “ibu akan pergi kepasar ia hanya membawa uang dan keranjang karna nanti tidak diberi kantong untuk membawa barang-barangnya.

Pernyataan tersebut ekuivalen dengan dua pernyataan tunggal berikut : “ibu membawa uang” dan “ibu membawa keranjang”

Pernyataan Nilai kebenaran

Membawa uang dan keranjang

Benar Membawa uang saja Salah Membawa keranjang saja Salah Tidak membawa keduanya Salah

pernyataan

 Ibu membawa uang dan keranjang, ibu bisa kepasar dan membeli keperluan yg akan di belinya dan bisa dibawa menggunakan keranjang  Ibu hanya membawa uang saja, ibu bisa membeli keperluan yg akan di belinya, tadi dia tidak bisa membawanya karena tidak membawa keranjang

 Ibu hanya membawa keranjang saja, tidak bisa membeli apapun karna tidak membawa uang sebagai alat tukar

 Tidak membawa keduanya, tidak jadi kepasar karna tdak membawa keduanya

Tabel kebenaran (A ʌ B)

A B A ʌ B

B B B

B S S

1.2

S B S

S S S

Dasar dari tabel kebenaran adalah teori peluang

Atau teori peluang A B A= membawa uang

B B= membawa keranjang

B S

B

S S

Tabel tersebut tidak berlaku untuk consol “ibu igin berbelanja ke pasar dia ingin membeli sepatu dan sandal”

Pernyataan Nilai kebenaran

Ibu membeli sepatu dan sandal Benar

Ibu membeli sepatu Benar

Ibu membeli sandal Benar

Ibu tidak membeli keduaduanya Salah Pernyataan:

 Ibu jadi berbelanja karena membeli dua-duanya sepatu dan sandal  Ibu jadi belanja karena karna ibu membeli membeli sepatu

 Ibu jadi belanja karena ibu membeli sandal  Tidak

Tabel kebenaran

Misalkan: p = membeli sepatu q = membeli sandal

kata kuncinya “jika salah satunya benar maka bernilai benar”

tabel tersebut merupakan tabel kebenaran disjungsi, bukan konjungsi.

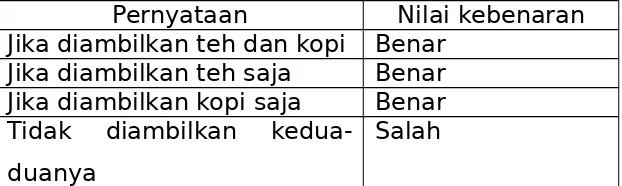
Contoh: “ayah menyuruh saya untuk mengambilkan segelas kopi atau segelas teh yang akan dia minum.

Pernyataan Nilai kebenaran Jika diambilkan teh dan kopi Benar

Jika diambilkan teh saja Benar Jika diambilkan kopi saja Benar Tidak diambilkan

kedua-duanya

Salah

 Jika diambilkan teh dan kopi, ayah bisa minum  Jika diambilkan teh saja, ayah bisa minum  Jika diambilkan kopi saja, ayah bisa minum

 Jika tidak diambilkan kedua-duanya, ayah tidak bisa minum

Tabel kebaran (p ᴠ q)

P=diambilkan kopi Q=diambilkan teh

Kata kuncinya untuk disjungsi inclusif “jika semuanya salah maka bernilai salah”

Kata kuncnya “ jika semuanya benar maka bernilai salah”

“ jika

semuanya salah maka bernilai salah”

“ jika salah satu benar maka bernilai benar”

c. IMPLIKASI ( ⟶ )

Misalkan ada dua pernyataan p dan q yang sering menjadi perhatian para ilmuan maupun matematikawan adalah menunjukkan atau membuktikan bahwa jika p bernilai benar akan mengakibatkan q bernilai benar juga. Untuk mencapai keinginannya tersebut, diletakkan kata “jika” sebelum pernyataan pertama dan pernyataan kedua sehingga didapatkan suatu pernyataan majemuk yag disebut dengan implikasi, pernyataan bersyarat kondisional ayau hypothetical dengan notasi “ → ” seperti ini . (p → q)”

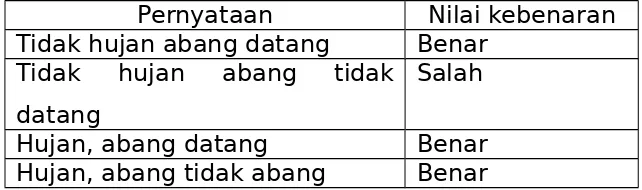
Contoh: “jika tidak hujan maka abang akan datang”

Pernyataan Nilai kebenaran Tidak hujan abang datang Benar

Tidak hujan abang tidak datang

Salah

Hujan, abang datang Benar Hujan, abang tidak abang Benar

Tabel pembuktian 1.2

X Y x → y

B B B

B S S

S B B

Contoh yang tidak sesuai “jika kambing hidup maka bernafas” pernyataan

 Jika Kambing hidup maka ia bernafas  Jika kambing hidup maka ia tidak bernafas  Jika kambing mati maka ia bernafas

 Jika kambing mati maka ia tidak bernafas

pernyataan Nilai

kebenaran Jika Kambing hidup maka

bernafas

Benar Jika kambing hidup maka ia tidak

bernafas

Salah

Jika kambing mati maka ia bernafas

salah Jika kambing mati maka ia tidak

bernafas

Karena tabel kebenaran ini merupakan tabel biimplikasi maka tabel ini bukan termasuk contoh implikasi

d. BIIMPLIKASI ( ⟷ )

Biimplikasi atau bikondisional adalah pernyataan majemuk dari dua pernyataan p dan q yang dinnotasikan dengan p ↔ q yang bernilai sama

dengan (p → q) ˄ (q → p) sehingga dapat dibaca : “p jika dan hanya jika q” atau “p bila dan hanya bila q” tabel kebenaran dari (p ↔ q) adalah:

contoh: “ kambing hidup jika dan hanya jika bernafas”

Pernyataan Nilai kebenarannya

kambing hidup jika dan hanya jika bernafas

Benar kambing hidup jika dan hanya jika tidak

bernafas

Salah

kambing mati jika dan hanya jika bernafas

Salah kambing mati jika dan hanya jika tidak

bernafas

Contoh yang tidak sesuai “ abang datang jika dan hanya jika tidak hujan”  Abang datang jika dan hanya jika tidak hujan

 Abang datang jika dan hanya jika hujan

 Abang tidak datang jika dan hany jika tidak hujan  Abang tidak datang jika dan hanya jika hujan

Pernyataan Kebenar

an Abang datang jika dan hanya jika tidak hujan

Benar Abang datang jika dan hanya jika hujan Benar Abang tidak datang jika dan hany jika tidak

hujan

Salah Abang tidak datang jika dan hanya jika

hujan

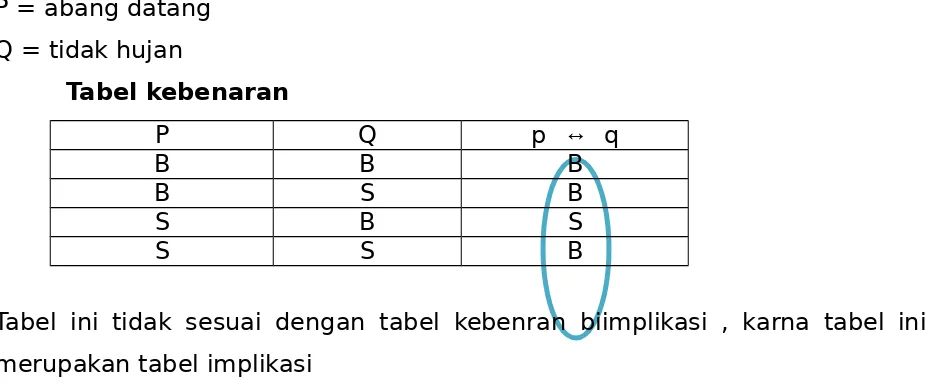
P = abang datang Q = tidak hujan

Tabel kebenaran

P Q p ↔ q

B B B

B S B

S B S

S S B

Tabel ini tidak sesuai dengan tabel kebenran biimplikasi , karna tabel ini merupakan tabel implikasi

Latihan 1.2

1. Tetukan nilai kebenaran dari pernyataan berikut! a. 3+2=6 ↔ 4+2=5

b. 3+2=5 ↔ 4+2=5

c. 3+2=5 atau jakarta ibu kota diaceh. d. Jika x2 _{=4 maka x=2}

e. Jika x= -2 maka x2₌₄

f. Jika 3x+4=2 dan x ∈ B , maka x = -1 2. Jika p: 10 habs dibagi 5

nyatakan dalam kalimat sehari-hari pernyataan-pernyataan di bawah ini lalu tentukan nilai kebenarannya

a. p

3. jika a : lisa gadis cantik dan b : lisa gadis cerdas,

nyatakan pernyataan dibawah ini dengan menggunaka a, b dan simbol-simbol logika matematika.

a. Lisa gadis yang cantik namun tidak cerdas b. Lisa gadis yang tidak cantik dan tidakcerdas

c. Meskipun lisa bukanlah gadis yang cantik namun ia gadis yang cerdas d. Lisa gadis yang cantik sekaligus juga gadis yang cerdas

e. Tidak benar bahwa lisa gadis yang cantik dan cerdas f. Jika lisa gadis yang cantik maka ia tidak cerdas

g. Jika lisa gadis yang tidak cantik maka ia tidak cerdas. 4. a. p→ q ↔ p ᴠ q

b. pʌq →(qʌ q → rʌq)

c.

_[

( p → r)ᴠ(p → q)

_]

ʌr

5. Tentukan nilai kebenaran berikut

a. 3 ≤ 7 dan 4 adalah bilangan ganjil b. 3 ≤ 7 atau 4 adalah bilangan ganjil c. 2+1=3 atau 4 ¿ 4

d. 5 adalah bilangan ganjil atau bisa dibagi dengan 4 e. Tidak benar bahwa 2+2=5 dan 5 ¿ 7

f. Tidak benar bahwa 2+2=5 atau 5 ¿ 7 g. 3 ≥ 3

6. Misalkan p = adalah 7 bilangan genap, g = 3+1=4 dan r = 24 habis dibagi dengan 8

a. Tuliskan simbolnya dan tetapkan nilai kebenarannya

- Tidak benar bahwa 7 adalah bilangan ganjl atau 3+1=4

- 3+1=4 dan 24 tidak habis dibagi 8

b. Tuliskan kata-kata berikut dan tetapkan nilai kebenarannya

- P v q

- (r Ʌ q)

- r v q

5. Buatlah tabel kebenaran untuk :

a. p v q

c. 8 habis dibagi 3 dan tidak habis dibagi 4

7. misalkan kita mendefinisikan (*) penyambung, dengan mengatakan bahwa p * q bernilai benar hanya jika q benar dan p salah selain itu bernilai salah

a. menuliskan tabel kebenaran untuk p*q b. menuliskan tabel kebenaran untuk q*p c. menuliskan tabel kebenaran untuk (p*p) *q

8. mari kita melambangkan "eksklusif atau" kadang-kadang digunakan dalam percakapan biasa dengan ⊕. sehingga p ⊕ q akan bernilai benar ketika tepat satu dari p, q adalah benar dan yang lainnya salah

a. tuliskan tabel kebenaran untuk p ⊕ q

b. tuliskan tabel kebenaran untuk p ⊕ p dan (p ⊕ q) ⊕ q

c. tunjukkan tabel kebenaran untuk (p Ʌ q)⊕ (p ⊕ q) adalah sama dengan tabel kebenaran untuk p v q

Ingkaran atau negasi suatu pernyataan

Jika p adalah “jakarta ibu kota negara indonesia” maka negas atau ingkaran dari pernyataan p tersebut adalah p yaitu: “jakarta bukan ibukota negara indonesia” atau “tidak benar bahwa jakarta ibu kota negara indonesia”

(p ʌq) ≡ p ˅ q

(pʌ q) ≡ p ˅ q

Implikasi

p ˅ q ≡ p → q

( p ˅ q) ≡ (p → q)

pʌ q ≡ (p → q)

biimplikasi p ↔ q

(p → q) ʌ(q → p) ≡ p ↔ q

[(p → q) ʌ(q → p) ≡ (p ↔ q)

(p → q) ˅ (q → p) ≡ (p ↔ q)

(pʌ q) ˅ (q ʌ p) ≡ (p ↔ q)

1. Negasi suatu konjungsi

Konjungsi adalah suatu pernyataan majemuk yang menggunakan perakit “dan”

Contohnya, pernyataan adi berikut ini: “heru makan nasi dan minum kopi”

P Q p˄q

p q p ˅ q

B B B S S S

B S S S B B

S B S B S B

S S B B B B

2. Negasisuatu disjungsi

Disjungsi adalah suatu pernyataan majemuk yang menggunakan perakit “atau”

Contohnya, pernyataan adi berikut :heru makan nasi atau minum kopi.” Suatuakhirnya, disjungsi p ˅ q akan bernilai salah hanya jika kompenen-kompenennya, yaitu baik p maupun q keduanya bernilai salah, yang selain itu akan bernilai benar. Karenanya, negasinya adalah “ heru tidak makan nasi dan tidak minum kopi,” sebagai mana ditunjukkan tabel kebenaran berikut :

P Q p ˅ q

p q p ˄ q

B B B S S S

B S B S B S

S B B B S S

S S S B B B

3. Negasi suatu implikasi

Perhatikan pernyataan berikut yang merupakan suatu implikasi: “jika hari hujan maka heru membawa payung”

Negasi dari implikasi diatas adalah “hari hujan akan tetapi andi tidak membawa patung”

Sehingga (p → q) ≡ p˄ q seperti ditunjukkan tabel kebenaran berikut ini:

P Q

q

B B S B S

B S B S B

S B S B S

S S B B S

Berdasarkan penjelasan diatas p → q ≡ [ (p → q)] ≡

(p˄ q) ≡ p˅q

4. Negasi suatu biimplikasi

Biimplikasi atau bikondisional adalah pernyataan majemuk dari dua pernyataan p dan q yang dinotasikan dengan p ↔ q yang ekuivalen (p → q) ˄(q → p) sehingga:

(p ↔ q) = [(p → q) ˄( q → p)]

= [( p˅q) ˄( q˅p)]

= ( p˅q) ˅ (

q˅p)

= (p˄ q) ˅( q˄ p)

Latihan 1.3

1. Tetukan nilai kebenaran dari pernyataan berikut! g. 3+2=6 ↔ 4+2=5

h. 3+2=5 ↔ 4+2=5

j. Jika x2 _{=4 maka x=2}

k. Jika x= -2 maka x2₌₄

l. Jika 3x+4=2 dan x ∈ B , maka x = -1 2. Jika p: 10 habs dibagi 5

q: 8 adalah blangan prima

nyatakan dalam kalimat sehari-hari pernyataan-pernyataan di bawah ini lalu tentukan nilai kebenarannya

k. p

l. q

m. p Ʌ q n. p v q

o. p Ʌ q

p. p Ʌ q

q. p Ʌ q

r. p → q s. p ↔ q

t. (p v q) → ( p v q)

2. buatkah negasi dari pernyataan ini

a. p → q ↔ p v q

b. p Ʌ q → (q Ʌ q → r Ʌ q)

c. [( p → r) v (p → q) Ʌ r

KONVERS, INVERS DAN KONTRAPOSISI

Pengertian dan contohnya, perhatikan pernyataan ini

Jika anda menggunakan bayclin maka baju akan putih bersih

Jika tidak menggunakan bayclin maka baju anda tidak akan putih bersih

Kesimpulan

P ≡ b=menggunakan bayclin q ≡ b=baju putih bersih

Menggunakan bayclin baju putih bersih Benar Menggunakan bayclin baju tidak putih bersih Salah Tidak menggunakna baylin baju putih bersih Benar Tidak menggunakan bayclin baju tidak putih

Implikasi invers kontra komperensi

LATIHAN 1.4

1. Tentukan konvers, invers, dan kontraposisi dari implikasi berikut :

a. Jika suatu bendera adalah bendera Jepang, maka ada bintang pada bendera tersebut.

b. a ¿ 0 → a3>¿ 0.

c. a ¿ 0 → ab ¿ 0.

d. Jika dua persegi panjang kongruen maka luasnya sama. e. x ¿ 3 → x2 _{¿ 9.}

f. Jika segitiga ABC adalah segita sama sisi maka sisi-sisi segita tersebut sama panjang.

2. Tentukan nilai kebenaran implikasi, konvers, invers, dan kontraposisi dari soal diatas.

3. Cari:

a. Kontrapositif dari ¬ p → q. b. Kebalikan dari ¬ q → p.

c. Kebalikan dari kebalikan dari q → ¬ p. d. Para negations dari p → ¬ q.

e. Kebalikan dari ¬ p ∧ q.

4. Menunjukkan yang mana dari pernyataan berikut ini yang bernilai benar

a. Jika 2 + 1 = 4 maka 3 + 2 = 5.

b. Merah putih jika dan hanya jika hijau biru. c. 2 + 1 = 3 dan 3 + 1 = 5 4 menyiratkan aneh. d. Jika 4 adalah aneh maka 5 aneh.

PERNYATAAN BERKUANTOR

A. KALIMAT TERBUKA, PERNYATAAN DAN KUANTOR

Perhatikan tiga kalimat berikut:

(1)3+4=6 (2) x2_{-5x+6=0 , x ∈ A dan (3) 2x+5 ¿ 4 , x ∈ A}

Tiga kalimat matematika seperti diatas dapat digunakan sebagai salah satu alternatif untuk memulai proses pembelajaran kuantor. Hanya kalimat pertama yang merupakan pernyataan. Kalimat kedua dan ketiga belum dapat ditentukan niloai kebenarnnya sebelum variabel x-nya diganti dengan salah satu anggota semesta pembicaraannya, karenanya, kalimat kedua dan ketiga dikategorikan sebagai kalimat pembuka.

“tidak ada x....”, sehingga untuk kalimat terbuka kedua didapat kalimat-kalimat berikut:

(1)Untuk setiap /semua bilangan Sali x, x2_{-5x+6=0 (2) terdapat}

bilangan aslix sedemikain sehingga x2_{-5x+6=0 dan (3) tidak ada}

bilangan asli x sedemikian sehingga x2_-5x+6=0

Sekarng, dapatkah anda menentukan nilai kebenaran ketiga kalimat diatas? Beberapa kata yang dikenal sebagai kuantor tersebut menunjukkan atau terkait dengan banyaknya pengganti perubah x, yaitu semua, beberapa, ataupun tidak ada. Sehingga didapatkan suatu pernyataan berkuantor yang bernilai benar saja atau salah saja, wheeler (1977:23) menyatakan “ quantifiers are most useful in rewriting assertions that cannot be classified as true or false...so that they can be classified either as true or false.” Ada dua jenis kuantor, yaitu kuantor universal (kuantor umum) dan kuantor eksistensial (kuantor khusus).

A. Kuantor universal

Kuantor jenis ini mempunyai lambang ∀ dan dibaca “untuk setiap” atau “untuk semua”. Misalkan p(x) adalh suatu kalimat terbuka , pernyataan ∀ x. P(x) dibaca, “untuk setiap x berlaku p(x)” atau “untuk semua x berlaku p(x)”, berikut ini adalah beberapa contoh pernyataan berkuantor universal:

1. “semua artis adalah cantik. “pernyataan berkuantor universal ini menggambarkan

adanya dua hmpunan , yaitu himpunan artiss dan himpunan orang cantik.

bahwa setiap artis yang merupakan anggota himpunan artis adalah cantik. Namun pernyataan berkuantor universal tadi akan benilai salah jika dapat ditunjukkan adanya salah satu atau beberapa orang yang dapat dikategorikan sebagai artis namun ia tidak termasuk pada kriteria cantik. Contoh yang menunjukkan salahya suatu pernyataan berkuantor universal ini disebut dengan counterexample atau contoh sangkalan sebagai manadinyatakan clemes, o’daffer, dan conney (1984:49) berikut: “A counterexample is a single example that shows a generalization to be false”

5. Jika (px) adalah “x+4 ¿ 1” dengan x adalah peubah pada himpunan

bilangan bulat B maka ( ∀ x ∈ B) p(x) adalah ( ∀ x ∈ B) x+4 ¿ 1 dan dibaca “untuk setiap bilangan bulat x berlaku x+4 ¿ 1.” Pernyataan

ini bernilai salah, karena jika x-nya diganti dengan bilangan blat -5 misalnya akan didapat pernyataan -5+4 ¿ 1 yang bernilai salah .

6. Jikaq q(n) berarti : 2n_{-1 adalh bilangan prima untuk n bilangan bulat ,}

maka ( ∀n∈ B) q(n) berarti : ( ∀n∈ B) 2n_{-1 adalah bilangan prima, dan}

dibaca: “untuk setiap bilangan bulat n berlaku 2n_{-1 adalah bilangan}

prima”.

Pernyataan ini bernilai salah .

Contoh

A=mahasiswa kelas 1-b

B=mahasiswa gemar mncontek

Ada mahasiswa kelas 1-b yang gemar mencontek

Semua mahasiswa yang gemar mencontek merupakan mahasiswa kelas 1-b A

Kuantor : 1. Universal mencakup seluruh anggota domain { ∀ ) Bisa ditandai denga kata, semua seluruh , setiap tiap dll 2. eksistensial, mencakup sebagian anggota domain ( ∃ )

Bsa ditandai dengan kata : sebagia, beberapa, ada, nilai terdapat dll

Contoh:

1. Jumlah dua bilangan genap adalah bilangan genap 2. Semua laki-laki adalah buaya darat

3. ∀ x ∈ N, x2_{-x+41 adalah bilangan prima}

4. ∃ x ∈ N ∈ n1 + n2 ∈ N

Jawab:

1. Bilangan genap dapat dinyatakan dengan 2n, n ∈ N Sehingga 2n1+n2 = 2(2n1+n2)

Di dapat 2(2n1+n2)=2p yang merupakan bilangan genap

Kesimpulan benar

2. Bukti : bapak saya laki-laki, menurut ibu saya , bapak saya bukan buaya darat

Kesimpulan salah

3. Bukti : ambil x=41 sehingga 412_-41+41=412

Bukan merupakan bilangan prima

- Semua bilangan berpangkat jika dihitung hasilnya bukan bilangan prima

Kesimpulan salah

4. Bukti: tukul arwana menurut pendapat saya tidak tampan Kesimpulan salah

5. ∃ x ∈ N ∋ n1 + n2 ∈ N

Berdasarkan aksioma ketertutupan bilagan asli dalam penjumlahan ∀x∈ N, x1+x2 ∈ N

Kesimpulan premi salah

Menentukan semua itu benar atau tidak

universal : harus dibuktikan secara umum, jangan diambil contoh satu persatu

eksistensial: untuk membenarkan suatu pernyataan hanya perlu mengambil satu

Untuk menyalahkan suatu pernyataan

Universal: Untuk menyalahkan suatu pernyataan universal hanya perlu

mengambil satu contoh yang tidak sesuai dengan pernyataan

Eksistensial p(x1) ˅ P(x2) v...v P(xn) ≡ B

∃ x1 p(x) jika salah satu benar bernilai benar , berlambang (v)

Universal (x1) Ʌ P(x2) Ʌ ... Ʌ P(xn) ≡ B

∀ x1 P(x) jika semua bilangan benar maka bernilai benar,

berlambang (Ʌ)

Contoh

1. Terdapat bilangan ganjil yang kurang dari atau sama dengan 4 P (3) v p(5) v p(7) ≡ B (eksistensial) ∃ x1 p(x)

Jawab:

P (3) v p(5) v p(7) ≡ B (eksistensial) ∃ x1 p(x)

B v S v S ≡ B

2. Jumlah dua blanga yang berbeda di A adalah kurang dari atau sama dengan 12

A= {3,5,7} Jawab:

P(3+5) Ʌ P(3+7) Ʌ P(5+7) ≡ B (universal) ∀ x1 P(x ,y)

B Ʌ B Ʌ B ≡

Misal : x dan y merupakan orang. L (x,y) = x mencintai y

- ∀ x ∀ y L (x,y) =semua x mencintai semua y - ∃ y ∀ x L (x,y) =semua x mncintai bberapa y

Tambahan ketentuan

∀ x (P(x) Ʌ Q(x)) ≡ ∀ x P(x) Ʌ ∀ x Q(x) semua (Ʌ)

∃ x (P(x) v Q(x)) ≡ ∃ x P(x) v ∃ x Q(x) beberapa (v)

1. Semua singa menyeramkan P(x) = x merupakan singa q(x) = x menyeramkan

p(x) Ʌ q(x) p(x) Ʌ q(x) terdapat semua singa dan ia menyeramkan

premi tersebut kurang tepat karena belum

pembuktian tentu semua singa itu menyeramkan

p(x) q(x) jika terdapat semua singa maka ia menyeramkan

premi tersebut tepat karena sudah tertera pada kalimatnya.

Kesimpulan: ∀ x ∈ D , P(x) → q(x)

Arguments and the principle (pembuktian tidak langsung) Of demonstration

P(x1)

P(x2)

P(x3)

: P(xn)

Latihan 1.5

1. Tentukan nilai kebenaran dari setiap pernyataan berikut ini. a. Setiap perwira TNI adalah laki-laki.

b. Beberapa Gubernur di Indonesia adalah perempuan.

c. Setiap bilangan jika dipangkatkan 0 akan bernilai sama dengan 1. d. Setiap bilangan memiliki lawan (invers penjumlahan).

e. Setiap bilangan memiliki kebalikan (invers perkalian). f. Setiap persegi adalah jajargenjang.

g. Setiap jajargenjang adalah trapesium.

h. Terdapat bilangan sedemikian sehingga setiap bilangan jika ditambahkan ke bilangan tersebut akan menghasilkan bilangan itu sendiri.

i. Terdapat bilangan sedemikian sehingga setiap bilangan jika dibagi dengan bilangan tersebut akan menghasilkan bilangan itu sendiri. j. Setiap jajargenjang memiliki simetri setengah putaran.

l. Setiap tahun yang habis dibagi 4 adalah tahun kabisat.

2. Menerjemahkan berikut ke dalam bentuk simbolis, menunjukkan pilihan yang tepat untuk domain:

a. Terdapat sebuah integer x sehingga 4 = x + 2. b. Untuk semua x integer, 4 = x + 2.

c. Setiap segitiga sama sisi adalah pigura yg sudutnya sama. d. Semua siswa seperti logika.

e. Beberapa siswa menyukai logika.

f. Tidak ada orang yang merupakan sebuah pulau. g. Setiap orang yang memahami logika menyukainya. h. Setiap orang memiliki seorang ibu.

i. Di antara semua integer ada beberapa yang bilangan prima. j. Bilangan bulat Beberapa bahkan dan habis dibagi 3.

k. Beberapa bilangan bulat bahkan atau dibagi 3. l. Semua kelompok siklik adalah abelian.

m. Setidaknya salah satu surat dalam pisang adalah vokal. n. Suatu hari bulan depan adalah hari Jumat.

o. x ^ 2 - 4 = 0 memiliki solusi positif.

p. Setiap solusi dari x ^ 2 - 4 = 0 adalah positif. q. Tidak ada solusi dari x ^ 2 - 4 = 0 adalah positif. r. Salah satu kandidat akan menjadi pemenang.

penarikan kesimpulan

3. Addition p bernilai benar

pvq jika salah satu benar maka bernilai benar

4. Simplify p Ʌq p dan q bernilai benar Penyederhanaan p

q 5. Conjunction p

Penyatuan q

pɅq

6. Odus ponen p

P q q

7. Modus tolens q

P q

p

8. Hipothetical syllogis p q q r

p r

9. Disjunction syllogism p v q

p

q

10. Universal instantion ∀ x P(x) P(c)

11. Eksistensial instantion ∃ x P(x) P (c)

12. Universal generalization p(c) ∀ x P(x)

13. Eksistensial generalization p(c) ∃ x P(x)

Resolution

1. [(pvq) Ʌ( pvr)] → (qvr) Pvq

pvr Q v r

Resolusi

i. = p = benar

p= salah

kemungkinan

P v q B v q B v (s/b) ≡ B q=(s/b)

p v r S v r S v B ≡ B r = B

q v r q v r karna r = B, q=(b/s) karna

(v)disjungsi jika salah satu benar

maka bernilai

benar benar

ii. P = salah

p= benar

P v q S v q S v B ≡ B q=B

p v r B v r B v (S/B) ≡ B r =

(S/B)

2. (pɅq)vr ≡ (p v r)Ʌ(q v r)

r → s r Ʌ s

p v s p v s

p v r r = benar

q v r r =salah r

S P v s

Latihan 1.6

1. Semua singa menyeramkan

Beberapa singa tidak minum kopi

Beberapa yang menyeramkan tidak minum kopi

2. Ada tiga buah hipotesis

Jika kau mengirimi ku e-mail maka aku akan menyelesaikan tugas Jika kau tidak mengirimiku e-mail maka aku akan tidur lebih awal

Jika saya tidak menyelesaikan tugas maka ketka bangun tidur saya merasa segar

3. Ada tiga buah hipotesis

1. Mungkin saya sedang bermimpi/berhalusinasi 2. Saya tidak sedang bermimpi

3. Jika saya berhalusinasi maka saya melihat wajah berbikini

Dit: buat kesimpulan yang dapat dibuat dari 3 hipotesis tersebut 4. Ada 4 hipotesis

1. Hari tidak cerah dan dingin

2. Jika kita bernang maka hari cerah

3. Jika kita tidak berenang maka kita main kano 4. Jika kita main kano maka pulang lebih awal

buat kesimpulan

PEMBUKTIAN MATEMATIKA

POKOK-POKOK BAHASA 2.1 metode of proof 2.2

2.1 model

Modal :

 Analisis = mencari komposisi

 Sintesis = sesuatu yang kecil untuk dibuat menjadi sesuatu yang utuh / lebih

 Deduktif = suatu konsep didasari oleh suatu konsep lainnya / konsep-konsep sebelumnya

 Induktif = melihat pola / keteraturan

 Abduktif = terdapat tahapan yang harus di tempuh untuk mendapatkan suatu hasil.

Langsung berbentuk implikasi (p → q) Pembuktian

Tidak langsung berbentuk kontrapositif ( q → p)

Pembuktian dibagi menjadi 2 cara, yaitu :

1. Pembuktian langsung, adalah pembuktian yang biasanya dinyatakan dalam bentuk implikasi (p → q)

Teorema dalam penjumlahan bilangan bulat.

1. Genap + genap = genap

M & n bilangan bulat

Bilangan genap dapat di tuliskan dengan 2p, p ∈ B Misal m = 2q

Bilangan ganjil dapat di tuliskan degan 2p+1 , p ∈ B Bilangan genap dapat di tuliskan dengan 2p, p ∈ B Misal m = 2q+1 maka ganjil + ganjil = genap 3. Genap + ganjil =

M & n bilangan bulat

Misal (q+r)=s

Di dapat 2(q+r)+1 = 2S+1 (ganjil) maka ganjil + ganjil = ganjil

teorema perkalian dalam bilangan bulat

1. Genap x genap = genap

M & n bilangan bulat

Bilangan ganjil dapat di tuliskan degan 2p+1 , p ∈ B Bilangan genap dapat di tuliskan dengan 2p, p ∈ B Misal m = 2q+1

Bilangan ganjil dapat di tuliskan degan 2p+1 , p ∈ B Bilangan genap dapat di tuliskan dengan 2p, p ∈ B Misal m = 2q+1

Karena sudah di buktikan pada pembuktian no 3 Teorema dalam (- ) & (+)

1. (+ ) x (+)

Misal m x n ¿ 0, dimana m,n adalah bilangan rill (m,n ∈ R)

M x n = n + n + ... + n Sebanyak m

Karena (n) nya positif jadi kita menggunakan teorema yang positif

Teorema penjabarannya

a ¿ 0 & b ¿ 0 → a+b ¿ 0 a ¿ 0

b ¿ 0 +

a+b ¿ 0

sehingga n + n +... ...+ n ¿ 0 positif karna lebih dari 0

sebanyak M

m x n = m.n ¿ 0 (+) x (+) = (+)

2. (+ ) x (-)

Misal m ¿ 0 dan n ¿ 0 dimana m,n adalah bilangan rill (m,n ∈

R)

M x n = n + n + ... + n Sebanyak m

Karena (n) nya negatif jadi kita menggunakan teorema yang negatif

Teorema penjabarannya

a ¿ 0 & b ¿ 0 → a+b ¿ 0 a ¿ 0 b ¿ 0

a+b ¿ 0

sehingga n + n +... ...+ n ¿ 0 negatif karna lebih dari 0

sebanyak M

m x n = m.n ¿ 0 (+) x (-) = (-)

Karna teorema sama seperti no 3 dan sudah di buktikan pada teorema no 3

4. (- ) x (-) = (+)

Misal dalam perkalian dengan 0 (-m) x 0 =0

(-m) x (n-n) = 0

(-m) x (n+(-n)) = 0 → aksioma distributif [(-m x n)] + [(-m) x (-n)]

Misal (-m) x (-n) = p [-m x n] + p =0

P = 0- [-m n] P = 0 + mn P = mn

Dengan kata lain p = (-m) x (-n) = mn (positif)

Pembuktian tidak langsung

Kontapositif (p → q) ( q → p)

Consol

1. Misal m dan m adalah bilangan genap dan m + n adalah bilangan ganjil.

Maka m = 2j dan m+n =2k+1 , j dan k termasuk bilangan bulat.

Oleh karena itu n adalah ganjil maupun genap, yang melengkapi bukti, bahwa itu kontradiksi

Jwb

dik: M,n genap m+n genap

P q

M + n ganjil m ganjil

q m genap

N genap n=...? Jwb:

Pembuktian 1 pembuktian 2

Misal m= ganjil misal m=genap

M+n =2k+1 M+n =2k+1

M=2 j+1 M=2 j

N=n+m-m N=n+m-m

N=(n+m)-m N=(n+m)-m

N=(2k+1)-(2j+1) N=(2k+1)-(2j)

N=2k-2j =2(k-j) genap N=2k-2j+1 =2(k-j)+1 ganjil

M=ganjil n=genap m=genap n ganjil

Pembuktian formal dan nonformal

1. Pembuktian Formal

Pembuktian formal adalah pembuktian yang kalimat pernyataannya menggunakan kalimat logika. Jadi untuk pembuktiannya harus dibuktikan dengan formal.

Contoh :

Dengan n ¿ 0, n adalah bilangan ganjil jika dan hanya jika 5n +¿ 6 merupakan bilangan ganjil. (p ↔ q ≡ (p → q) ∧ (q → p)) Bukti :

 p → q

“jika ganjil maka 5n+6 ganjil

Diketahui : n bilangan ganjil atau dapat dinyatakan dengan 2k+1 , k ∈B

Ditanyakan : pembuktian bahwa 5n+6 adalah ganjil Jawab : 5n+6 =5(2k+1)+6

=10k+11 =10k+10+1 =2(5k+5)+1

“jika, 5n+6 ganjil maka n ganjil”

Kontrapositif, dari q → p adalah p → q

Diketahui :Di misalkan n genap atau dapat dinyatakan dengan n=2j, j ∈B

Ditanyakan : pembuktian bahwa 5n+6 adalah genap Jawab : : 5n+6 =5(2j)+6

=10j+6 =2(5j+3)

Dengan kata lain 5n+6 adalah genap, berdasarkan pembuktian p → q dan q → p.

Sehingga teorema benar

2. Pembuktian tidak Formal

Pembuktian tidak formal adalah pembuktian yang kalimatnya bukan merupakan kalimat logika. Jadi untuk pembuktiannya dibuktikan secara tidak formal.

Contoh :

1. Buktikan bahwa tidak ada bilangan x rasional sehingga x2 _{¿ 2.} Bukti :

Anggap x merupakan bilangan rasional, sehingga x dapat dinyatakan dengan a

Dengan kata lain b2 merupakan bilangan genap.

∴ x bilangan rasional adalah SALAH, yang benar x adalah bilangan Irasional

Kalau kalimat pembuktiannya merupakan kalimat logka maka dibuktikan

harus secara formal

Kalau kalimat pembuktiannya bukan merupakan kalimat logka maka dibuktikan secara formal

Contoh: q diketahui: ¿ 2 + ¿ 1=180o pelurus

2 1 ¿ 2 + ¿ 4 = akibat aksioma

4 3 pelurus dan

playfar P k

diketahui : ¿ 2 + ¿ 1=180o pelurus

j ¿ 2 + ¿ 4 = akibat aksioma pelurus dan playfar J // j’ dipotong oleh k di p dan q

Ditanyakan : ¿ 2 = ¿ 3

Jawab : ¿ 1 + ¿ 2 =180o (pelurus)

¿1 + ¿ 3 = 180 (playfar)

Seingga ¿1 + ¿ 2 = ¿ 1 + ¿ 3...Terbukti

Contoh

3. tunjukkan bahwa minimal atau setidaknya ada 1 bilangan real a1,a2,a3,...an yang lebih dari atau sama dengan rata-ratanya

diketahui : a1+a2+a3,...an = A

n

ditanyakan : tunjukan a1+a2+a3,...an = A lebih dari atau sama

dengan rata2nya n j

jawab : asumsikan a1,a2,a3,...an ¿ A

maka a1+a2+a3,...an ¿ n.A

sehingga bila pertidak samaan dibagi dengan n di dapat a1+a2+a3,...an ¿ n.A

4. buktikan bahwa minimal(a, minimal (b,c) = minimal (minimal (a,b),c) untuk semua a,b,c ∈ R

1. a ≤ b ≤ c

minimal (a, minimal n(b,c)) = minimal (minimal (a,b),c) minimal (a,b) = (a,c)

a = a

2. a ≤ c ≤ b

minimal (a, minimal n(b,c)) = minimal (minimal (a,b),c) minimal (a,c) = (a,c)

a = a

3. b ≤ a ≤ c

minimal (a, minimal n(b,c)) = minimal (minimal (a,b),c) minimal (a,b) = (b,c)

b = b

4. b ≤ c ≤ a

minimal (a, minimal n(b,c)) = minimal (minimal (a,b),c) minimal (a,b) = (b,c)

b = b

5. c ≤ a ≤ b

minimal (a, minimal n(b,c)) = minimal (minimal (a,b),c) minimal (a,c) = (a,c)

c = c

Latihan 2.1

Teorema: jika x dan y bilangan bulat maka x - y adalah bilangan bulat. a. "Bukti 1": Misalkan x dan y keduanya bilangan ganjil. Maka terdapat

bilangan bulat j, k sehingga x = 2j + 1 dan y = 2k + 1. maka Jadi y adalah ganjil, kontradiksi.

c. "Bukti 3": Misalkan x - y adalah bilangan ganjil. Maka terdapat j bilangan bulat sedemikian rupa sehingga x - y = 2j + 1. Jika y bahkan kita selesai, sehingga misalkan y bilangan ganjil , katakan y = 2k + 1 untuk beberapa j bilangan bulat. demikian

x = x - y + y = 2j +1 - (2k + 1) = 2 (j - k) Jadi x adalah genap dan bukti selesai.

d. "Bukti 4": Misalkan x bbilangan genap dan x - y jugabilangan genap. Kemudian terdapat j bilangan bulat, k sedemikian sehingga x = 2j dan x - y = 2k. demikian

y = x - (x - y) = 2j - 2k = 2 (j - k) sehingga y adalah bilangan genap

e. "Bukti 5": Misalkan x, y bilangan genap dan x - y adalah bilangan ganjil . Kemudian terdapat bilangan bulat j dan k sehingga x = 2j

dan y = 2k. sekarang

x - y = 2j - 2k = 2 (j - k)

sehingga x - y bilangan genap, Tapi ini bertentangan dengan asumsi kita bahwa x - y adalah ganjil sehingga bukti selesai.

f. "Bukti 6": Suppode bahwa x - y adalah ganjil, katakanlah x - y = 2j + 1 untuk beberapa j bilangan bulat. jika x adalah ganjil kita sudah selesai, jadi menganggap bahwa x bahkan, katakanlah x = 2k untuk

beberapa k bilangan bulat. kemudian

y = x - (x - y) = 2k - (2j + 1) = 2 (k - j) - 1 = 2 (k - j - 1) + 1 sehingga y bilangan ganjil dan kami selesai.

g. "Bukti 7": Misalkan x dan y keduanya bilangan genap. Maka terdapat bilangan bulat j, k sehingga x = 2j dan y = 2k. maka

h. "Bukti 8": Misalkan x - y bilangan genap. Kemudian jika x adalah ganjil kita sudah selesai, sehingga menganggap bahwa x adalah genap. Kemudian terdapat bilangan bulat j, k seperti bahwa x - y = 2j dan x = 2k.maka sehingga y bilangan genap dan kita selesai.

j. "Bukti 10": Misalkan x dan y adalah bilangan ganjil dan x - y adalah bilangan ganjil. Kemudian ada keluar bilangan bulat j, k sehingga x = 2j + 1, y = 2k + 1. Dengan demikian kita memiliki

x - y = 2j + 1 - (2k + 1) = 2 (j - k)

sehingga x - y adalah baik ganjil dan genap, kontradiksi.

2. Untuk dugaan berikut, membuktikan yang benar dan memberikan counterexample untuk yang salah:

a. Jika x adalah integer dan 4x bilangan positif maka x adalah bilangan positif.

b. Jika x adalah bilangan bulat genap maka 4x adalah genap. c. Jika x adalah bilangan bulat dan x ^ 2 adalah genap maka x

genap.

d. Jika x adalah integer dan 3x genap maka x adalah genap. e. Jika x, y, z adalah bilangan bulat dan x + y + z adalah ganjil

maka ganjil x, y, z adalah gajil.

.

induksai matemaitka

dipergunakan hanya untuk yang berkaitan dengan bilangan asli N himpunan bilangan asli

Well ordered principle (wop) dari N

Perinsip induksi matematik (versi 1)

Misal S ∈N memenuhi sifat-sifat berikut: 1. 1 ∈ S

2. Jika k ∈ S maka k+1 ∈ S, untuk ∀ k ∈ N maka S = N  Misal p(n) adalah pernyataan yang memuat n (tentang n)

Perinsip induksi matematik (versi 2)

Misalkan p(n) , n ∈ N memenuhi sifat 1. P(1) benar

2. Jika p(k) benar untuk k ∈ N maka p (k+1) benar Sehingga p(k) benar untuk ∀ n ∈ N

Prinsip induksi matematika (versi 3)

Misalkan p(n) dengan n1, ≥ no , n1, no ∈ N yang memenuhi

1. P(no)

2. jika p(k) benar untuk k ≥ no maka p(k+1) benar, sehingga p(n) benar

∀ n ≥ no

Aplikasi Contoh Contoh 1 :

1 +¿ 2 +3+¿ …. +¿ n ¿ n

2 (n +¿ 1)

- Untuk n ¿ 1

1 ¿ 1

2 (1 +¿ 1)

1 ¿ 1

2 . 2

1 ¿2

2

1 ¿ 1 ….. terbukti

- Asumsikan benar untuk n ¿ k

1 +¿ 2 +3+¿ …. +¿ k ¿ n

2 (k +¿ 1)

(k+1)(1+1/(k+1)) = (k+1)+1 Akan dibuktikan untuk n= k+1

KUNCI JAWABAN Latihan 1.1

1. a. Merupakan sebuah pernyataan terbuka , karna akan bernilai benar jika x=-1 b. Sebuah pernyataan karna dampak dari no 1

c. Merupakan sebuah pernyataan, tapi bukan bilangan prima, karna 111 bisa di bagi dengan 3 dan 37

d. Merupakan pernyataan terbuka, karna belum tentu yang bertanya fahmi karna dalam pertanyaannya tidak dicantumkan nama fahmi

e. Merupakan pernyataan terbuka, karna ∈ A jika dikali 2 bernilai genap dan jika ditambah 1 jadi bernilai ganjil

2. A. Pada hari-hari apakah mereka berdua dapat menyatakan hal itu ?

B. Jika mereka berdua sama-sama menyatakan bahwa hari kemarin adalah hari dimana mereka berkata benar, pada hari-hari apakah mereka berdua dapat menyatakan hal itu ?

Senin Selasa Rabu Kamis Jum’at Sabtu Minggu Andi Bohong Bohong Bohong Jujur Jujur Jujur Jujur Badu Jujur Jujur Jujur Bohong Bohong Bohong Jujur

3. - andi seorang sopir

- Dani duduk berhadapan dengan candra - Candra bukan seorang pilot

- Andi duduk di sebelah kiri candra - Budi duduk di sebelah kanan klasi

pilot dani

sopir markonis andi budi

klasi candra

jadi andi seorang sopir dani seorang pilot budi seorang markonis candra seorang klasi

4. - Toni tidak pernah berbohong

- Pada poin d yg berpendapat adalah didi dan pada poin e yg brpendapat bukan toni, berarti toni belum berpendapat, sedangkan di poin c yang memakai kaos kuning adalah hori berarti yng memakai kaos kuning adalah tony

- karna toni tidak pernah berbohong berarti yang memakai kaos merah adalah hory terdapat pada poin c

jadi yang memakai kaos kuning adalah didi

kaos merah adalah hory

kaos hijau adalah didi

Latihan 1.2

1. a. 3 + 2 = 6 ↔ 4 + 2 = 5.

S S B

b. 3 + 2 = 5 → 4 + 2 = 5.

B S S

c. 3 + 2 = 5 atau Jakarta ibukota DI Aceh.

B ᴠ S B d. Jika _x2 _{= 4 maka x = 2}

Jika ≠2 maka x2_{≠4 terdapat x=-2 dimana x≠2, sehingga}

x2_{=4, sedangkan disitu}

tertera bahwa x2_{≠4 → soal diatas bernilai}

salah

e. Jika x = -2 maka _x2 _{= 4.}

Jika x2_{=4 maka x= -2}

Jika ≠ -2 maka x2_{≠4 terdapat x=2 dimana x≠-2, sehingga x}2_=4,

sedangkan disitu tertera bahwa x2_{≠4 → soal}

diatas bernilai salah

c. 10 habis dibagi 5 dan 8 adalah bilangan prima

Benar ∧ salah ≡ salah

d. 10 habis dibagi 5 atau 8 adalah bilangan prima

Benar v salah ≡ benar

e. 10 tidak habis dibagi 5 dan 8 adalah bukan bilangan prima

salah ∧ benar ≡ salah

f. 10 tidak habis dibagi 5 dan 8 adalah bilangan prima

salah ∧ salah ≡ salah

g. 10 habis dibagi 5 dan 8 bukan bilangan prima

Benar ⋀ benar ≡ benar

h. 10 habis dibagi 5 maka 8 adalah bilangan prima

benar ⟶ salah ≡ salah

i. 10 habis dibagi 5 jika dan hanya jika 8 adalah bilangan prima

benar ⟷ salah ≡ salah

j. Jika (10 habis dibagi 5 atau 8 bukan bilangan prima) maka (10 tidak habis dibagi 5 atau 8 bilagan prima)

(benar ∨ benar) ⟶ (salah ∨ salah)

Benar ⟶ salah ≡ salah

S B S B S S B B S

d. 5 adalah bilangan ganjil atau bisa dibagi dengan 4

B ∨ S ≡ B

6. a. Tuliskan simbolnya dan tetapkan nilai kebenarannya a. 3+1 ≠ 4 dan 24 habis dibagi 8

∼ q ∧ r S ∧ B ≡ B

b. Tidak benar bahwa 7 adalah bilangan ganjl atau 3+1=4 ∼ ( ∼ P ∨ q)

∼ (B ∨ B) ≡ S c. 3+1=4 dan 24 tidak habis dibagi 8

q ∧ ∼ r

B ∧ S ≡ S

b. Tuliskan kata-kata berikut dan tetapkan nilai kebenarannya

a. P v q

7 adalah bilangan genap atau 3+1 ≠ 4

S ∨ S ≡ S

b. (r Ʌ q)

Tidak benar bahwa 24 habis dibagi 8 dan 3+1= 4 ∼ (B ∧ B) ≡ ∼ (B) ≡ S

c. r v q

24 tidak habis dibagi 8 atau 3+1 ≠ 4

8. a. 3 - 4 ≥ 7

b. 3 + 1 ≠ 5 dan 2 ¿ 4

c. 8 tidak habis dibagi 3 dan habis dibagi 4

9. a. menuliskan tabel kebenaran untuk p*q

p q P *

b. menuliskan tabel kebenaran untuk q * p

c. menuliskan tabel kebenaran untuk (p * p) * q

p q p *

a. tuliskan tabel kebenaran untuk p ⊕ q

b. tuiskan tabel kebenaran untuk p ⊕ q dan (p ⊕ q) ⊕ q dengan tabel kebenaran untuk p v q

b. tunjukkan bahwa tidak ada

bedanya jika kita mengambil kedua "atau" dalam "dan / atau" menjadi inklusif (v) atau eksklusif (⊕)

soal diatas bernilai benar

i. Jika x ≠ -2 maka x2 _{≠ 4.}

Jika = -2 maka x2_{=4 terdapat x=-2 dimana x=-2, sehingga x}2_=4,

Soal diatas bernilai benar j. Jika 3x + 4 ≠ 2 dan x ∈ B, maka x = -1.

b. tidak benar bahwa 8 adalah bukan bilangan prima (benar) ≡ salah

k. tidak benar bahwa 10 habis dibagi 5 dan 8 adalah bilangan prima

(Benar ∧ salah ) ≡ benar

l. tidak benar bahwa 10 habis dibagi 5 atau 8 adalah bilangan prima

(Benar v salah ) ≡ salah

m. tidak benar bahwa 10 tidak habis dibagi 5 dan 8 adalah bukan bilangan prima

(salah ∧ benar ) ≡ benar

n. tidak benar bahwa 10 tidak habis dibagi 5 dan 8 adalah bilangan prima

(salah ∧ salah ) ≡ benar

o. tidak benar bahwa 10 habis dibagi 5 dan 8 bukan bilangan prima

(Benar ⋀ benar ) ≡ salah

p. tidak benar bahwa 10 habis dibagi 5 maka 8 adalah bilangan prima

(benar ⟶ salah ) ≡ benar

q. tidak benar bahwa 10 habis dibagi 5 jika dan hanya jika 8 adalah bilangan prima

(benar ⟷ salah ) ≡ salah

r. tidak benar bahwa Jika (10 habis dibagi 5 atau 8 bukan bilangan prima) maka (10 tidak habis dibagi 5 atau 8 bilagan prima)

Latihan 1.4

1. a. - konvers : jngnya maka bendera tersebut bendera jepang

- Invers : jika ada bendera yang bukan bendera jepang maka bendera tersebut

tidak ada bintangnya

- Kontraposisi : jika bendera tersebut tidak ada vbintangnya maka bendera tersebut

bukan bendera jepang

b. - konvers : a3 _{¿ 0 ⟶ a ¿ 0}

- Invers : a ≤ 0 ⟶ a3 _{≤ 0}

- Kontraposisi : a3 _{≤ 0 ⟶ a ≤ 0}

c. - konvers : ab = 0 ⟶ a= 0 - Invers : a ≠ 0 ⟶ ab ≠ 0 - Kontraposisi : ab ≠ 0 ⟶ a ≠ 0

-- konvers : jika luas persegi luasnya sama panjangnya juga sama - Invers : jika dua persegi pajang tidak sama panjang maka luasnya

tidak sama

- Kontraposisi : jika dua persegi luasnya tidak sama maka panjangnya juga tidak sama

d. - konvers : x2_{= 9 ⟶ x= 3}

- Invers : x ≠ 3 ⟶ x2 _{≠ 9}

- Kontraposisi : x2 _{≠ 9 ⟶ x =3}

e. - konvers : jika segitiga ABC sama panjang maka segitiga sama sisi - Invers : jika segitiga ABC adalah segitiga tidak sama sisi maka

tersebut tidak sama panjang

- Kontraposisi : jika sisi-sisi segitiga tersebut tidak sama panjang maka segitiga ABC

adalah segitiga tidak sama sisi

2. a. - Implikasi p → q - konvers q → p

B → S ≡ S B → B ≡ S

- Invers p → q - kontraposisi

q → p

S → S ≡ B S → S ≡ B

b. - Implikasi p → q - konvers q → p

B → B ≡ B B → B ≡ B

- Invers p → q - kontraposisi

q → p

S → S ≡ B S → S ≡ B

d. - Implikasi p → q - konvers q → p

B → S ≡ S B → B ≡ S

- Invers p → q - kontraposisi

q → p

S → S ≡ B S → S ≡ B

e. - Implikasi p → q - konvers q → p

B → S ≡ S B → B ≡ S

- Invers p → q - kontraposisi

q → p

S → S ≡ B S → S ≡ B

f. - Implikasi p → q - konvers q → p

B → S ≡ S B → B ≡ S

- Invers p → q - kontraposisi

q → p

b. c. d. e. f.

5. Menunjukkan yang

mana dari pernyataan berikut ini yang bernilai benar a. Jika 2 + 1 = 4 maka 3 + 2 = 5.

S → B ≡ B

b. Merah putih jika dan hanya jika hijau biru.

S ↔ S ≡ B

c. 2 + 1 = 3 dan 3 + 1 = 5 4 menyiratkan aneh.

S ↔ S ≡ B

d. Jika 4 adalah aneh maka 5 aneh.

S ↔ B ≡ B

e. Jika 4 adalah aneh maka 5 bahkan.

S ↔ S ≡ B

f. Jika 5 adalah aneh maka 4 aneh.

S ↔ B ≡ s

Latihan 1.5 1. A.

m. Beberapa Gubernur di Indonesia adalah perempuan.

n. Setiap bilangan jika dipangkatkan 0 akan bernilai sama dengan 1. o. Setiap bilangan memiliki lawan (invers penjumlahan).

p. Setiap bilangan memiliki kebalikan (invers perkalian). q. Setiap persegi adalah jajargenjang.

r. Setiap jajargenjang adalah trapesium.

t. Terdapat bilangan sedemikian sehingga setiap bilangan jika dibagi dengan bilangan tersebut akan menghasilkan bilangan itu sendiri. u. Setiap jajargenjang memiliki simetri setengah putaran.

v. Beberapa siswa menganggap matematika itu sulit. w. Setiap tahun yang habis dibagi 4 adalah tahun kabisat.

3. Menerjemahkan berikut ke dalam bentuk simbolis, menunjukkan pilihan yang tepat untuk domain:

t. Terdapat sebuah integer x sehingga 4 = x + 2. u. Untuk semua x integer, 4 = x + 2.

v. Setiap segitiga sama sisi adalah pigura yg sudutnya sama. w. Semua siswa seperti logika.

x. Beberapa siswa menyukai logika.

y. Tidak ada orang yang merupakan sebuah pulau. z. Setiap orang yang memahami logika menyukainya. aa. Setiap orang memiliki seorang ibu.

bb. Di antara semua integer ada beberapa yang bilangan prima. cc.Bilangan bulat Beberapa bahkan dan habis dibagi 3.

dd. Beberapa bilangan bulat bahkan atau dibagi 3. ee. Semua kelompok siklik adalah abelian.

ff. Setidaknya salah satu surat dalam pisang adalah vokal. gg. Suatu hari bulan depan adalah hari Jumat.

hh. x ^ 2 - 4 = 0 memiliki solusi positif.

Latihan 1.6 1. 1. p → q

2. p → r

3. r → s

jwb 4. q → p kontrapositif (1)

5. p → s HS (2) dan (3)

6. q → s HS (4) dan (6)

2. 1. R ∨ H 2. ∼ R 3. H → G

4. H DS (2) dan (1)

5. G MP (3) dan (4)

6. H ∧ G konjungsi (4) dan (5)

4. 1. ∼ p ∧ q 2. r → p

3. r → s

4. s → t

5. p simplify (1)

6. q simplify (1)

7. r MT (5) dan (2)

8. S MT (7 dan (3)