Logika Matematika (1)Logika Matematika (1) Logika Matematika (1)

LOGIKA MATEMATIKA

RESUME MATEMATIKA DASAR

Oleh:

Dwi Rahmasari Kinasih Gusti 161810101042

Khurnia Palupi 161810101046

Wahyu Gumilang 161810101062

JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS JEMBER

LOGIKA MATEMATIKA 1. Pengertian Umum Logika

Definisi logika memiliki rumusan yang berbeda menurut para ahli meskipun sebenarnya rumusan-rumusan tersebut intinya adalah hal yang sama. Seperti “Logika adalah suatu studi yang sistimatik tentang struktur proposisi dan syarat-syarat umum mengenai penalaran yang sahih dengan menggunakan metode yang mengesampingkan isi atau bahan proposisi dan hanya membahas bentuk logisnya saja. (Soekadijo,1983)

Logika matematika adalah pola berpikir berdasarkan penalaran dan dapat di uji kebenarannya secara matematika. (Irfan,2010)

Logika matematika meliputi: logika pernyataan atau proposisi

(propositional logic) suatu yang menelaah manipulasi antar pernyataan dan logika penghubung atau predikat (predicate logic) yang menelaah manipulasi

hubungan relasioanal antara pernyataan pertama dengan pernyataan kedua. Oleh karena itu logika matematika adalah ilmu yang menelaah manipulasi antar pernyataan matematika (mathematical Statement). (Irfan,2010)

Notasi merupakan suatu alat bantu yang digunakan untuk menyatakan sesuatu. Notasi digunakan untuk menyingkat kalimat verbal dengan suatu simbol yang ringkas. Ada beberapa hal yang harus diperhatikan dalam penggunaan notasi, seperti:

1. Ada beberapa simbol yang telah secara tetap sudah digunakan untuk menunjukkan hal-hal tertentu. Misalnya, notasi π digunakan untuk lambang bilangan irasional 3,1415....

2. Sekali simbol telah diperkenalkan sebagai wakil suatu objek, maka simbol tersebut digunakan untuk objek tersebut. (Tirta,2002)

Namun sebelum melangkah lebih jauh, kita perlu memahami terlebih dahulu pengertian pernyataan dan pengertian penghubung. Berikut ini diberikan definisi suatu pernyataan :

A. Pengertian 1. Kalimat terbuka

Atau dengan kata lain kalimat yang masih bervariabel. Contoh : a. 2x + 5 = 7

b. x2 + 1 = 10

c. Jarak kota A dan kota B 200 km d. Usia A lebih muda dari B, dll.

2. Pernyataan

Jika variabel pada kalimat terbuka diganti maka akan menjadi pernyataan. Dan pernyataan

tersebut dapat bernilai salah atau benar. Contoh pernyataan

a. 2 x 5 = 10 b. 20 : 2 = 6

c. Toni lebih muda dari Susi Pernyataan a bernilai benar Pernyataan b bernilai salah

Pernyataan c bisa benar atau salah

2.1 Pernyataan Tunggal dan Negasinya

Pernyataan disebut juga dengan kalimat deklaratif, stetemen, maupun

proposisi. Akan tetapi ada beberapa ahli yang membedakan istilah pernyataan dan proposisi, namun ada pula yang menyamakannya. Pernyataan sendiri merupakan suatu kalimat yang bernilai benar atau salah tetapi tidak kedua-duanya. Istilah benar dan salah merupakan istilah bagi kita yang menganggap pernyataan tersebut bernilai benar ataupun pernyataan tersebut bernilai salah karena sudah ada acuan untuk hal tersebut. Contoh:

1. Belalang adalah serangga

2. Lumajang merupakan kota pisang di Jawa Timur

Sebuah pernyataan atau proposisi adalah sebuah kalimat deklaratif yang mempunyai tepat satu nilai

Operasi ini merupakan operasi monar yaitu suatu operasi yang dikenakan pada satu pernyataan yang dilambangkan dengan “~“. Ingkaran dari pernyataan p adalah ~ p yang dibaca “bukan p”. Jadi operasi ingkaran adalah operasi yang mengingkari suatu pernyataan.

Ingkaran/Negasi dari suatu pernyataan adalah pernyataan lain yang diperoleh dengan menambahkan kata ”tidak” atau menyisipkan kata ”bukan” pada pernyataan semula. Ingkaran dari suatu pernyataan p disajikan dengan lambang atau ~p. Bila peryataan p bernilai benar, maka ingkarannya bernilai salah begitupun sebaliknya. Berikut ini tabel kebenaran untuk negasi:

P ~p

B S

S B

Pernyataan tunggal yaitu pernyataan yang hanya memuat satu pokok persoalan. Pernyataan tunggal pada umumnya dinyatakan dengan huruf-huruf kecil seperti p dan q.

Berikut ini adalah beberapa contoh kalimat tunggal p : 3 adalah bilangan ganjil

q : 7 adalah bilangan prima

r : 10 adalah bilangan berlebih/abundan

(i) nilai kebenaran p adalah benar,τ(p) = B (benar) (ii) nilai kebenaran q adalah salah, τ(q) = B (benar) (iii) nilai kebenaran r adalah salah, τ(r) = S (salah)

Tabel Kebenaran Negasi Pernyataan Tunggal

Negasi dari pernyataan p adalah suatu pernyataan yang bernilai salah jika p benar dan bernilai benar jika p salah.

P ¬p

B S

p : Lima (5) adalah bilangan prima; q : sepuluh (10) adalah bilangan abundan. Jawab :

Untuk mencari negasi yang tepat dari pernyataan-pernyataan tersebut pertama kita buat pernyataan berikut :

¬p : tidak benar 5 adalah bilangan prima; : lima (5) adalah bukan bilangan prima;

¬q : tidak benar 10 adalah bilangan abundan/(Tirta,2002) 2.2Pernyataan majemuk dan negasinya

1. Konjungsi

Operasi konjungsi merupakan operasi biner yaitu suatu operasi yang dikenakan pada dua pernyataan yang dilambangkan dengan tanda “ ”. Dua_˄ pernyataan pada operasi ini ditulis dengan kata “dan”.

Jika p dan q dua pernyataan , maka p ˄q bernilai benar jika p dan q keduanya bernilai benar, sebaliknya p˄q bernilai salah jika salah satu dari p atau q bernilai salah atau keduanya salah. Berikut ini tabel nilai kebenaran untuk operasi konjungsi:

P Q p ∧ q

B B B

B S S

S B S

S S S

(Apriyanti, Shariyah, 2013) Contoh :

r : Rina suka membaca buku s : Rina suka menonton tv

r ∧ s : Rina suka membaca buku dan menonton tv Negasi Konjungsi

P q p ∧ q ¬(p ∧ q)

B B B S

B S S B

S S S B

Contoh :

Pernyataan : p Pernyataan : q p^q

SMK 1 Sragen berada di Kabupaten Sragen (B)

Sragen termasuk ke dalam wilayah Jawa Tengah (B)

B

Jumlah sudut dalam suatu

segitiga selalu 180° (B) Besar sudut segitiga samasisi adalah 90° (S) S Dua adalah bilangan

ganjil (S) Dua adalah bilangan prima (B) S

2 + 6 = 7 (S) 6 = 7 – 2 (S) S

2. Disjungsi

Operasi disjungsi juga merupakan operasi biner yang dilambangkan dengan tanda ”v”. Operasi ini menggabungkan dua pernyataan menjadi satu dengan kata hubungan “atau”. (Apriyanti, Shariyah, 2013)

P Q p ∨ q

B B B

B S B

S B B

S S S

Contoh:

p : Kiki meminjam flashdisk q : Kiki sedang sarapan

pvq : Kiki meminjam flashdisk atau sedang sarapan Contoh:

Konjungsi

Pernyataan majemuk p dan q disebut Konjungsi dari p dan q dinyatakan dengan: p^q

Pernyataan : p Pernyataan : q p Vq SMK 1 Sragen berada di

Kabupaten Sragen (B)

Sragen termasuk ke dalam

wilayah Jawa Tengah (B) B

Jumlah sudut dalam suatu segi

tiga selalu 180o (B)

Besar sudut segitiga sama sisi

adalah 90o (S)

B

Dua adalah bilangan

ganjil (S) Dua adalah bilangan prima (B) B

2 + 6 = 7 (S) 6 = 7 – 2 (S) S

Negasi Disjungsi

P Q p ∨ q ¬( p ∨ q)

B B B S

B S B S

S B B S

S S S B

Disjungsi Inklusif yaitu apabila dalam suatu pernyataan terdapat salah satu atau kedua komponennya bernilai benar.

P Q p ∨ q

B B B

B S B

S B B

S S S

Disjungsi Eksklusif yaitu apabila dalam suatu pernyataan terdapat salah satu diantaranya bernilai benar saja.

p q p∨ q

B B S

B S B

S B B

S S S

Disjungsi :

Pernyataan majemuk p dan q disebut Disjungsi dari p dan q dinyatakan dengan: ” p V q ”

adalah sebuah pernyataan bernilai benar jika pernyataan p dan q salah satu atau

3. Tautologi dan Kontradiksi

Tautologi adalah pernyataan majemuk yang selalu bernilai benar tanpa

memandang nilai kebenaran komponennya. Tautologi dilambangkan dengan hiruf T.

Kontradiksi adalah pernyataan majemuk yang selalu bernilai

salah tanpa memandang nilai kebenaran dari komponennya. Kontradiksi dilambangkan dengan huruf F.

Contoh:

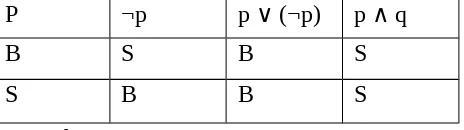
(i) p ∨ (¬p) adalah suatu tautologi. (ii) p ∧ (¬p) adalah suatu kontradiksi.

Tabel kebenaran untuk tautologi dan kontradiksi tersebut dapat dilihat:

P ¬p p ∨ (¬p) p ∧ q

B S B S

S B B S

Contoh

Tunjukkan bahwa p∨~p adalah tautology dan p∧~p adalah kontradiksi

Jawab

p ~p p∨~p p∧~

p

B S B S

S B B S

Dari table tersebut dapat kita simpulkan bahwa p∨~p adalah Tautologi dan p∧~p adalah Kontradiksi.

Tunjukkan bahwa pernyataan (p→q) → ~q adalah tautology Jawab :

p q p→q (p→q

) ~q (p→q) → ~q

B B B S S B

B S S B B B

S B B S B B

S S B S B B

Dapat disimpulkan bahwa pernyataan (p→q) → ~q adalah tautology

Tambahan

Aljabar pernyataan

Susunan pernyataan majemuk dapat juga dianggap sebagai hasil operasi dari beberapa pernyataan dengan perakit-perakit pernyataan sebagai operasi hitung. Sedangkan sebagai pengganti kesamaan dalam logika kita mengenal ekuivalensi, (≡).

Operasi beserta pernyataannya ini dikenal dengan istilah aljabar

pernyataan atau kalkulus pernyataan. Dua pernyataan dikatakan ekuivalen jika pernyataan-pernyataan tersebut mempunyai nilai kebenaran yang sama untuk setiap keadaan komponennya .

Jika τ P (pl, p2, ..., pn) = τ Q(ql, q2, ..., qn) maka P (pl, p2, ..., pn) ≡ Q(ql, q2, ..., qn).

DEFINISI Tautologi:

Sebuah pernyataan dikatakan bernilai Tautologi (valid), jika pernyataan tersebut bernilai benar terhadap setiap pemberian nilai kebenaran bagi setiap variabelnya. Kontradiksi:

Bentuk Rangkap dan Prinsip Kerangkapan

Salah satu sifat yang sangat menarik dalam aljabar logika adalah sifat rangkap atau dual dari suatu pernyataan majemuk.

Bentuk rangkap (dual) dari kalimat majemuk P(p1, p2, · · · , pn) adalah bentuk yang diperoleh dengan menggantikan tanda ∨ dengan ∧ dan sebaliknya, demikian juga F dengan T dan sebaliknya secara serempak.

Contoh :

(i) bentuk rangkap dari p ∧ (q r∨ ) adalah p ∨(q r∧ ); (ii) bentuk rangkap dari p ∨ (¬p) ≡ T adalah p ∧ (¬p) ≡ F

(Prinsip kerangkapan/dualitas). Jika suatu pernyataan (teorema) sudah terbukti kebeharannya maka bentuk rangkapnya juga valid.

(i) Bentuk p∨ (¬p) ≡ T adalah valid (merupakan tautologi), maka bentuk p ∧ (¬p) ≡ F juga valid (merupakan kontradiksi);

(ii) Bentuk p ∧ p ≡ p adalah valid, maka bentuk p ∨ p ≡ p juga valid.

Berikut disampaikan beberapa sifat dasar aljabar kalimat yang dapat dibuktikan dengan membuat tabel kebenaran dari bentuk aljabar yang bersangkutan.

 (Negasi ganda)

 ¬(¬p)) ≡ p

 (Hukum Komutatif/ pertukaran).

(p ∧ q) ≡ (q ∧ p)

 (p ∨ q) ≡ (q ∨ p)

 (Hukum Assosiatif/ pengelompokan).

 p ∧ (q ∧ r) ≡ (p ∧ q) ∧ r

p ∨ (q ∨ r) ≡ (p ∨ q) ∨ r

 (Hukum Identitas).

 p ∧ F ≡ F dan

p ∧ T ≡ p

p ∨ T ≡ T dan p ∨ F ≡ p

 p ∧ (¬p) ≡ F

dan (¬F) ≡ T

p ∨ (¬p) ≡ T dan (¬T) ≡ F

 (Hukum De Morgan).

 ¬(p ∧ q) ≡

¬(p) ∨ (¬q)

¬(p ∨ q) ≡ (¬p) ∧ (¬q)

 (Hukum Distributif).

 p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r) p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)

 (Hukum Idempoten).

 p ∧ p ≡ p p ∨ p ≡ p

 (Hukum Absorpsi /Penyerapan).

 p ∧ (p ∨ q) ≡

p dan p ∨ (p ∧ (¬q)) ≡ p

p ∨ (p ∧ q) ≡ p dan p ∧ (p ∨ (¬q) ≡ p

 (Komplementasi Gabungan).

 p ∧ ((¬p) ∨ q)

≡ p ∧ q

 p ∨ ((¬p) ∧ q)

 Hukum-hukum di atas dapat dibuktikan dengan membuat tabel kebenarannya. Selanjutnya hukum-hukum di atas dapat digunakan untuk membuktikan ekuivalensi yang lain. Jika diminta, maka pembuktian harus diturunkan dari kesepuluh hukum diatas (bukan dengan tabel kebenaran). Bahkan dalam sistem deduksi yang akan kita pelajari pada bab berikutnya asumsi dasar (aksioma) yang kita pakai sebagai dasar lebih terbatas lagi dan yang lainnya harus kita turunkan dengan menggunakan aksioma-aksioma atau definisi yang diketahui. Sebenarnya hukum absorpsi dapat dibuktikan secara deduktif (bukan menggunakan tabel kebenaran) dengan menggunakan sifat-sifat sebelumnya. Dalam logika sangat penting sekali menunjukkan alasan yang dipergunakan pada setiap langkah. Bukti hukum absorpsi/ penyerapan adalah sebagai berikut ini.

 (lihat Sulistyaningsih (1984)

 p ∧ (p ∨ q) ≡ (p ∨ F) ∧ (p ∨ q) identittas

 ≡ p ∨ (F ∧ q) distributif

≡ p ∨ F identitas

 Tambahan

(Operator Dagger).

 p ↓ q = ¬p ∧ ¬q (bersama-sama)

 Dari Definisi 1.12 dan Definisi 1.13, kita dapat turunkan sifat atau aksioma berikut:

 Teorema 1.13.

 p/q = ¬(p ∧ q)

 p ↓ q = ¬(p ∨ q)

 Tabel 1.1: Tabel Kebenaran Operator Stroke dan Dagger



P



Q



¬



¬



p



p

1 1 0 0 0 1

 Catatan: Untuk menghindarkan penggunaan kurung yang terlalu banyak, maka diadakan kesepakatan bahwa dalam aljabar pernyataan,

urutan/hirarki operasi ¬, ∧, ∨ adalah yang pertama ¬, lalu diikuti ∧ dan ∨. Contoh

 ¬p ∧ ¬q ∨ p ∧ q ≡ (¬p) ∧ (¬q) ∨ (p ∧ q)



 4. Negasi

 Negasi disebut juga ingkaran atau pengingkaran . Ingkaran dari suatu pernyataan diperoleh dengan menambahkan” tidak benar” di awal kalimat, atau dengan cara menyisipkan kata ” tidak” atau ” bukan” pada pernyataan tersebut.

Misalkan p adalah adalah pernyataan.







Berikut adalah tabel kebenaran pernyataan negasi





Contoh :

 Pernyataan : p  Negasi (ingkaran) : ~p

 Sembilan adalah bilangan prima (S)

 Sembilan bukan bilangan prima (B)

 Semua tumbuhan adalah  Tidak semua tumbuhan adalah

Negasi p adalah: Untuk sembarang pernyataan p, negasi dari p dilambangkan dengan ~ dan dibaca “ bukan p” Suatu pernyataan yang bernilai salah (S ) jika p benar (B), dan bernilai benar (B ) jika p salah (S) (Ary,2008)

makhluk hidup (B) makhluk hidup (S)



5. Implikasi

 Implikasi yaitu pernyataan yang bernilai salah ketika hipotesisnya bernilai benar sedangkan konklusinya bernilai salah. Selain itu, maka implikasi bernilai benar. Secara matematis kalimat dalam bentuk “jika p maka q”

dinotasikan dengan “p → q” disebut implikasi. Selanjutya “p → q” dapat dibaca “jika p maka q”, “p hanya jika q”, “p syarat cukup untuk q” atau “q syarat perlu untuk p”. notasi p disebut dengan anteseden/ hipotesis, sedangkan notasi q disebut dengan konsekuen/ konklusi/ kesimpulan.

 Tabel kebenaran implikasi



Dari suatu pernyataan bersyarat “ p ⇒ q ” yang diketahui dapat dibuat pernyataan lain sebagai berikut :

 1) q ⇒ p disebut pernyataan Konvers dari p ⇒ q

 2) ~p ⇒ ~q disebut pernyataan Invers dari p ⇒ q

 3) ~q ⇒ ~p disebut pernyataan Kontraposisi dari p ⇒ q

Dari pernyataan berbentuk implikasi dapat kita turunkan pernyataan-pernyataan baru yang disebut invers, konvers, dan kontraposisi.

 Implikasi : p → q

 Inversnya : ~p ⇒ ~q

p→q  ~p→~q 

q→p  ~q→~p 

invers

konvers kontra _{positif konvers}

invers

 Kontraposisinya : ~q ⇒ ~p

 Tabel kebenaran invers, konvers dan kontra positif



 Dari tabel tersebut dapat kita simpulkan: 1. p → q ≡ ¬q → ¬p dan

 Hubungan antara implikasi, invers, konvers dan kontra positifnya ditunjukkan dengan gambar berikut:







Implikasi :

Pernyataan majemuk p dan q disebut implikasi (pernyataan bersyarat) adalah sebuah pernyataan majemuk yang dilambangkan :

” p → q ”



 Sragen termasuk ke dalam

wilayah Jawa Tengah (B)

 B

 Jumlah sudut dalam suatu segi tiga selalu 180° (B)

 Besar sudut segitiga sama sisi adalah 90° (S)

 S

 Dua adalah bilangan ganjil (S)

 Dua adalah bilangan prima (B)

 B

 2 + 6 = 7 (S)  6 = 7 – 2 (S)  B



 Berikut adalah table kebenaran dari Konvers, Invers, dan Kontraposisi.

S B B S

Komponen Implikasi Konvers Invers Kontraposisi

Berdasarkan table kebenaran di atas, dapat disimpulkan bahwa: - Implikasi ekuivalen dengan kontraposisi

- Konvers ekuivalen dengan Invers 6. Biimplikasi

 Pernyataan p dan q apabila dirangkai dengan menggunakan hubungan “jika dan hanya jika“ sehingga menjadi “p jika dan hanya jika q ” atau dilambangkan dengan : “ p ⇔q ” suatu pernyataan majemuk disebut dengan biimplikasi. Pernyataan majemuk biimplikasi menyiratkan suatu gabungan dari: p ⇔q dan q⇔p

 Tabel kebenaran biimplikasi



(ii) 5 adalah bilangan ganjil ↔ 4 adalah bilangan genap (S)



 Contoh :

kebe nara

n

 ABCD adalah persegi⇔ABCD segi empat yang sisinya sama

 B

 n adalah bilangan prima⇔n habis dibagi 7 S  S

 SMK 1 Sragen terletak di Jawa Tengah ⇔Sragen adalah Kota yang ada di Yogyakarta S

 S

 Grafik f(x) bukan garis lurus ⇔ f(x) adalah fungsi yang tidak linier B

 B















 Tambahan

 Implikasi Logis dan Ekuivalensi Logis

 Sejauh ini kita memahami bahwa nilai kebenaran suatu implikasi bergantung pada nilai kebenaran hipotesis dan konklusinya. Ada bentuk khusus dari suatu implikasi yang nilainya selalu benar tanpa bergantung pada nilai kebenaran dari hipotesis dan konklusinya. Implikasi semacam ini disebut implikasi logis.

 Definisi Suatu implikasi dikatakan implikasi logis (dinotasikan dengan p ⇒ q), jika implikasinya merupakan tautologi tanpa memandang nilai kebenaran komponen-komponennya. Dengan kata lain P (pl, p2, ...) ⇒ Q(ql, q2, ...) jika P (pl, p2, ...) → Q(ql, q2, ...) ≡ TSeperti halnya nilai kebenaran implikasi, nilai kebenaran biimplikasi juga ditentukan oleh nilai kebenaran masing-masing komponennya. Jika suatu biimplikasi selalu bernilai benar maka dia disebut ekuivalensi logis, yang dinotasikan dengan ⇔. Definisi 2.5. Suatu biimplikasi dikatakan ekuivalensi logis, jika

Biimplikasi:

Pernyataan majemuk p dan q disebut biimplikasi (pernyataan bersyarat dua arah) adalah sebuah pernyataan majemuk yang dilambangkan :

” p ⇔ q ”

biimplikasinya merupakan tautologi, yaitu : P (pl, p2, ...) ⇔ Q(ql, q2, ...) jika P (pl, p2, ...) ↔ Q(ql, q2, ...) ≡ T.

 (Ekuivakensi disjungsi dan implikasi (EDI)).

 p → q ≡ ¬p ∨ q

 (Ekuivalensi biimplikasi dengan disjungsi, konjungsi).

 p ↔ q ≡ (¬p ∨ q) ∧ (p ∨ ¬q)

 Salah satu cara untuk membuktikan adanya implikasi logis adalah dengan membuktikan bahwa implikasinya adalah suatu tautologi.

 p → (p ∨ q) ≡ ¬p ∨ (p ∨ q)

 ≡ (¬p ∨ p) ∨ q hukum asosiatif ≡ T ∨ q hukum komplemen

≡ T hukum identitas

 Maka p ⇒ (p ∨ q).

 (p ∧ q) → q ≡ ¬(p ∧ q) ∨ q

 ≡ (¬p ∨ ¬q) ∨ q hukum De Morgan ≡ ¬p ∨ (¬q ∨ q) hukum Asosiatif

≡ ¬p ∨ T hukum komplemen

≡ T hukum identitas.

 Negasi Pernyataan Bersyarat

 Negasi kalimat bersyarat dicari melalui negasi dari ekuivalensinya yang terdiri atas perakit-perakit dasar. Ingat bahwa negasi tidak sama baik dengan invers maupun konvers.

 (Negasi Implikasi). Negasi implikasi adalah ¬(p → q) ≡ p ∧ ¬q. (2.7)

Bukti:

¬(p → q) ≡ ¬(¬p ∨ q)

 ≡ ¬(¬p)) ∧ ¬q De Morgan

≡ p ∧ ¬ q negasi ganda

Ada beberapa variasi bentuk negasi biimplikasi seperti dinyatakan dalam teorema berikut.

 (Negasi biimplikasi). Negasi bimplikasi adalah

 ¬(p ↔ q) ≡ ¬(p → q) ∨ ¬(p → q)

 ≡ (p ∧ ¬q) ∨ (¬p ∧ q) ≡ ¬p ↔ q

≡ p ↔ ¬q

 Bukti:

¬(p ↔ q) ≡ ¬(p → q) ∧ (q → p)

 ≡ ¬(p → q) ∨ ¬(p → q) De Morgan

≡ (p ∧ ¬q) ∨ (¬p ∧ q) Teorema 2.7

≡ (p ∧ ¬q) ∨ ¬p ∧ (p ∧ ¬q) ∨ q distributif ≡ T ∧ (¬q ∨ ¬p) ∧ (p ∨ q) ∧ T distributif

≡ (¬q ∨ ¬p) ∧ (p ∨ q) identitas

≡ (¬q ∨ ¬p) ∧ (p ∨ q) identitas

≡ (¬q ∨ ¬p) ∧ (¬¬p ∨ q) negasi dobel

≡ ¬p ↔ q atau,

≡ (¬q ∨ ¬p) ∧ (p ∨ ¬¬q) negasi dobel

≡ p ↔ ¬q.

 Dengan demikian pernyataan “Saya datang jika dan hanya jika cuaca cerah” mempunyai negasi : “Saya datang jika dan hanya jika cuaca tidak cerah” atau “Saya tidak datang jika dan hanya jika cuaca cerah”. Untuk

meyakinkan ekuivalensi variasi bentuk-bentuk negasi biimplikasi, kita dapat membuat tabel kebenarannya.

Kalimat matematika, kalimat terbuka, kalimat tertutup

 Dalam pembahasan matematika, banyak dilibatkan kalimat-kalimat ataupun pernyataan-pernyataan yang memuat simbol-simbol matematika. Kalimat-kalimat

tersebut ada yang berbentuk pernyataan ada yang tidak.

seperti peubah, tetapan dan operator lainnya.

Kalimat matematika terbuka adalah kalimat matematika yang belum bisa dinilai benar atau salah.

Kalimat matematika tertutup (disebut juga pernyataan matematis) adalah kalimat matematika yang sudah bisa dinilai benar atau salah.

Contoh : Kalimat p(x) : x + 2 ≥ 7, adalah suatu kalimat matematika terbuka, karena belum bisa dinilai bear atau salah. Misalkan semesta

pembicaraannya adalah himpunan semua bilangan real. Berarti x adalah anggota dari himpunan bilangan real. Jika kita gantikan x dengan sembarang bilangan real x ≥ 5 maka terbentuklah pernyataan yang bernilai benar. Sebaliknya jika kita gantikan x dengan bilangan-bilangan x < 5 , maka terbentuk pernyataan yang bernilai salah.

 Pada kalimat terbuka p(x) dengan semesta U, setiap kali kita mengambil elemen u dari U, maka p(x) = p(u) bernilai tepat salah satu benar atau salah. Semua elemen x ∈ U yang menyebabkan p(x) bernilai benar disebut himpunan penyelesaian/ himpunan kebenaran (truth set/ solution set) dari p dan dinotasika dengan Tp.

 Untuk p, kalimat terbuka pada U, maka untuk setiap u ∈ U atau τ(p(u)) = 1, atau τ(p(u)) = 0.

Himpunan kebenaran atau himpunan penyelesaian adalah himpunan semua unsur dari semesta pembicaraan yang menyebabkan terjadinya kalimat/

pernyataan yang bernilai benar. Tp = {u ∈ U, τp(u) = 1}

 Contoh:

(i) Perhatikan kalimat terbuka : x + 2 ≥ 10, x bilangan asli, maka Tp ={x ≥ 8, x bilagan asli }.

(ii) Misalkan p(x); x2 < 0 ; x bilangan real, maka Tp = _∅

(iii) Misalkan p(y); y2 ≥ 0; y bilangan real, maka Tp = U = <. Semua bilangan real jika dikuadratkan akan lebih atau sama dengan nol.

 Suatu kalimat terbuka dapat dinyatakan kalimat tertutup dengan menggantikan peubahnya dengan tetapan dari semesta pembicaraannya.

(i) Misalkan p(n) : n+2 > 8 adalah kalimat terbuka, misalnya pada semesta N (himpunan semua bilangan asli), maka

(a) p(2) : 2 + 2 > 8 adalah pernyataan salah. (b) p(8) : 8 + 2 > 8 adalah pernyataan benar.

(ii) q(x) : x2 − 2x + 1 = 0 adalah kalimat terbuka pada <, maka: (a) q(2) : 22 − 2.2 + 1 = 0 adalah pernyataan salah dan

(b) q(1) : 12 − 2.1 + 1 = 0 adalah pernyataan benar

Telah disampaikan diatas bahwa jika p(x) kalimat terbuka pada semesta U maka p(x) bisa benar untuk semua x ∈ U, yaitu Tp = U. Benar untuk beberapa

atau tak satu pun x ∈ U. Secara implisit ini berarti dengan memberikan kata-kata : Setiap, beberapa atau tak satupun , di depan kalimat terbuka tasi maka kalimat terbuka tadi maka kalimat terbuka tadi akan menjadi pernyataan yang bernilai benar atau salah.

1. p(x) : x + 2 ≥ 8 adalah kalimat terbuka pada N, maka :

(a) untuk semua x ∈ N berlaku x + 2 ≥ 8, adalah pernyataan salah, (b) ada x bilangan asli yang bersifat x + 2 ≥ 8 adalah benar.

7. Kuantor

 Istilah-istilah : terdapat , semua/ setiap, dengan demikian, dan sejenisnya, dapat digunakan untuk mengukur keberadaan himpunan penyelesaian (unsur-unsur yang menyebabkan p(x) bernilai benar). Kata-kata ini dalam logika disebut kuantor/ quantifier (to quantify = mengukur). Kuantor dibedakan menjadi kuantor universal dan kuantor eksistensial.

 Kuantor Universal

 Simbol  yang dibaca “untuk semua” atau “untuk setiap” disebut kuantor

umum. Jika p(x) adalah fungsi proposisi pada suatu himpunan A maka (x  A) p(x)

atau x, p(x) atau x p(x) adalah suatu pernyataan yang dapat dibaca sebagai “Untuk setiap x elemen A, p(x) merupakan pernyataan “Untuk semua x, berlaku p(x)”. (Apriyanti, Shariyah, 2013)

“untuk semua/ setiap x ∈ U x bersifat p” atau “semua x bersifat p”, atau “untuk semua x pernyataan p(x) adalah benar”.

 Nilai kebenaran pernyataan yang mengandung kuantor universal adalah τ(∀x, p(x)) = 1 jika dan hanya jika Tp = U.

Misalkan:

(i) p(x) : x + 2 ≥ 3 dengan semesta N, maka Tp = N. sehingga ∀x ∈ N, x + 2 ≥ 3 adalah benar. Demikian juga dengan

(ii) p(x) : x + 2 = 10 dengan semesta N maka Tp = {8}, sehingga ∀x ∈ N, x + 2 = 10 adalah salah.

 Dengan cara yang sama dapat dibuktikan bahwa (iii) ∀x ∈ R<, x2 < 0 adalah salah dan

(iv) ∀x ∈ R <, x2 + 2x + 8 > 0 adalah benar.

 (Tirta,2002)

 Kuantor Eksistensial

 Pernyataan ”untuk beberapa x, P(x)” dikatakan sebagai pernyataan kuantor

eksistensial dan secara simbulik ditulis sebagai berikut "x; P(x) " Simbul ”” disebut kuantor eksistensial (existensial quantifier). (Irfan, 2010)

 Misalkan p adalah suatu kalimat terbuka pada semesta U, maka:

∃x ∈ U, p(x) atau ∃x, 3 p(x) atau ∃x, 3 τ(p(x)) = 1 adalah pernyataan yang dibaca : “terdapat x yang bersifat p”, atau “beberapa x bersifat p”, atau “paling sedikit satu x bersifat p. Notasi ∃ yang dibaca : “beberapa” , “terdapat”, “paling sedikit satu ”.

Nilai kebenaran kuantor eksistensial adalah τ(∃x, p(x)) = 1, jika dan hanya jika Tp 6= _∅.

 Contoh

 (i) p(x) : x2 − 4x + 4 = 0 untuk semesta <, dengan Tp = {2},

 maka ∃x, x2 −4x + 4 = 0 adalah salah.

 Dalam menggunakan kata-kata “terdapat x”, biasanya ditambahkan juga istilah “sedemikian sehingga” yang dalam logika dinotasikan dengan “3 ”



 Contoh :

 Notasi logika dari pernyataan “terdapat bilangan asli sedemikian sehingga kuadratnya lebih dari 26 tetapi tidak lebih dari 100” adalah ∃x ∈ N, 3 26 < x2 ≤ 100.

 Kuantor Universal dan eksistensial masing-masing dapat digunakan untuk mendefinisikan Irisan dan gabungan dari keluarga himpunan {Ai, i = 1,2,3, · · · };

(i) Irisan (Interseksi) keluarga himpunan. adalah himpunan yang beranggotakan unsur-unsur yang muncul pada setiap himpunan, yaitu:

∩ Ai = {x|x ∈ Ai, ∀i ∈ I}

(ii) Gabungan (Union) dari keluarga himpunan adalah himpunan yang beranggotakan unsur-unsur yang cukup muncul pada salah satu himpunan

Ai tadi ∪ Ai = {x|∃i ∈ I 3 x ∈ Ai}

 (Tirta, 2002)

 Negasi Kuantor

 Jika p(x) adalah manusia tidak kekal atau x tidak kekal, maka “Semua manusia adalah tidak kekal” atau x p(x) bernilai benar, dan “Beberapa manusia kekal” atau x ~ p(x) bernilai salah. Pernyataan di atas dapat dituliskan

dengan simbol :~ [x p(x)] x ~ p(x). (Apriyanti, Shariyah, 2013)



(∀x ∈ M)(x berhati dengki )) ≡ ∀x ∈ M, d(x)

 ¬(∀x ∈ M)(x berhati dengki )) ≡ ¬∀x ∈ M, d(x)

 ∃(x ∈ M)(x tidak berhati dengki) ≡ (∃x ∈ M 3 d(x))

 (Tirta, 2002)



 TABEL KEBENARAN (Truth Table)

 Untuk mengevaluasi apakah sebuah pernyataan majemuk benar atau salah kita perlu table kebenaran dari kalimat penghubung yang ada dalam pernyataan tersebut. Untuk sembarang pernyataan p dan q, rangkuman tabel kebenaran dari semua penghubung adalah sebagai berikut:

 P  q  ~

Misalkan P(x) merupakan sebuah pernyataan yang mengandung variabel x dan D adalah sebuah himpunan. Kita sebut P sebuah fungsi pernyataan (dalam D) jika untuk setiap x di D, P(x) adalah pernyataan. Kita sebut D daerah asal pembicaraan (domain of discourse) dari P.

DEFINISI

Misalkan P(x) adalah fungsi pernyataan dengan daerah asal D.

1. Pernyataan ”untuk setiap x, P(x)” dikatakan sebagai pernyataan kuantor universal dan secara simbulik ditulis sebagai berikut "x; P(x) "

Simbul ”” disebut kuantor universal (universal quantifier).

2. Pernyataan ”untuk beberapa x, P(x)” dikatakan sebagai pernyataan kuantor eksistensial dan secara simbulik ditulis sebagai berikut "x; P(x) "

 

 Contoh :

Berikut ini beberapa contoh fungsi pernyataan dan himpunan daerah asal : 1. n 2 + 2n adalah bilangan ganjil, dengan daerah asal himpunan bilangan bulat. 2. x 2 - x - 6 = 0 , dengan daerah asal himpunan bilangan real.

3. Seorang pemain bisbol memukul bola melampaui 300 ft pada tahun 1974, dengan daerah asal himpunan pemain bisbol.(Irfan,2010)

 

8. Silogisme, Modus Tollens, dan Modus Ponens

 Silogisme Modus Ponens dan Modus Tollens adalah metode atau cara yang digunakan dalam menarik kesimpulan. Proses penarikan kesimpulan terbagi atas beberapa hipotesa yang diketahui nilai kebenarannya yang kemudian dengan menggunakan prinsip-prinsip logika diturunkan suatu kesimpulan

(konklusi). Penarikan kesimpulan ini disebut dengan argumentasi.

Prinsip-prinsip logika yang digunakan untuk menarik suatu kesimpulan adalah sebagai

berikut :

i. Argumen dikatakan berlaku atau sah:

Jika konjungsi dari hipotesa-hipotesanya berimplikasi dengan kesimpulan ii. Misalkan hipotesa yang diketahui adalah a dan b sedangkan kesimpulannya adalah c, Argumen yang berlaku atau sah :

p∧q→c

iii. Argumen dikatakan berlaku atau syah:

Jika hipotesa-hipotesanya benar maka kesimpulannya juga benar.

iv. Argumen disusun dengan cara menuliskan hipotesa - hipotesanya barus demi baris kemudian dibuat garis mendatar dan kesimpulan diletakkan baris paling bawah sebagai berikut :

a hipotesa 1 b hipotesa 2

∴ c kesimpulan

1. Silogisme

Proses penarikan kesimpulan yang menggunakan sifat menghantar dari pernyataan implikasi, yaitu dilakukan dengan cara menyusun baris – baris : p→q hipotesa 1

q→r hipotesa 2

∴ p→r kesimpulan

Dalam bentuk implikasi, silogisme dapat ditulis menjadi: (p→q )^( q→r) → (p→r)

Silogisme dikatakan sah jika nilai dari bentuk implikasi tersebut merupakan tautologi

Jawab:

Hipotesa 1 : Jika n bilangan ganjil maka n2 _ganjil.

 p q

 Hipotesa 2 : Jika n2 _{ganjil maka n}2_{+1 genap.}

 q r

 Kesimpulan: p→r

Jadi, kesimpulannya adalah: Jika n bilangan ganjil maka n2_{+1 genap} 2. Modus Ponens

Proses penarikan kesimpulan yang menggunakan sifat menghantar dari pernyataan implikasi, yaitu dilakukan dengan cara menyusun baris – baris :

 p→q hipotesa 1 p hipotesa 2

∴ q kesimpulan

Dalam bentuk implikasi, modus ponens dapat ditulis menjadi: (p→q) ∧ p→q

Modus Ponens dikatakan sah jika nilai dari bentuk implikasi tersebut merupakan

tautologi

Berikut ini adalah table kebenarannya.



Jawab:

Hipotesa 1 : Jika n bilangan ganjil maka n2 _ganjil.

 p q



 Hipotesa 2 : n bilangan ganjil.

 p

 Kesimpulan: q

Jadi, kesimpulannya adalah: n2 _ganjil 3. Modus Tollens

Proses penarikan kesimpulan yang menggunakan sifat menghantar dari pernyataan

implikasi, yaitu dilakukan dengan cara menyusun baris – baris : p→q hipotesa 1

~q hipotesa 2

∴~p kesimpulan

Dalam bentuk implikasi, modus tollens dapat ditulis menjadi: (p→q ) ∧ ~q→~p

Modus Tollens dikatakan sah jika nilai dari bentuk implikasi tersebut merupakan

tautologi

Berikut ini adalah table kebenarannya.



Cara lain untuk menunjukkan sah atau tidaknya sebuah Modus Tollens adalah

dengan mengambil kontaposisi dari argument sebagai berikut: p→q

Kontraposisi: ~q→~p Contoh

Tentukan kesimpulan dari argument berikut: Hipotesa 1 : Jika n bilangan ganjil maka n2 _ganjil. Hipotesa 2 : n2 _{tidak ganjil.}

Jawab:



Hipotesa 1 : Jika n bilangan ganjil maka n2 _ganjil.

 p q

 Hipotesa 2 : n2 _{tidak ganjil.}

 ~q

 Kesimpulan: ~p

Jadi, kesimpulannya adalah: n bilangan tidak ganjil

















































 DAFTAR PUSTAKA



 Apriyanti, Nia dan Sharifah, 2013. Logika Matematika, Cirebon: Shania Universitas Swadaya Gunung Jati

 Bandung Ary S.,dkk.2008. Matematika SMK Bisnis dan Manajemen. Jakarta:Departemen

 Irfan, Muhammad, 2010. Matematika SMK Bisnis dan Manajemen, Jakarta

 Tirta, I Made, 2002. Pengantar Dasar Matematika, Jember: Unit Penerbit FMIPA Universitas Jember