PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI

(1)

i

Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika

Oleh :

Singgih Satriyo Wicaksono NIM : 111414064

PROGRAM STUDI PENDIDIKAN MATEMATIKA

JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

UNIVERSITAS SANATA DHARMA YOGYAKARTA

(2)

ii SKRIPSI

LUAS PADA GEOMETRI HIPERBOLIK

Oleh :

Singgih Satriyo Wicaksono NIM : 111414064

Telah disetujui oleh :

Pembimbing,

(3)

iii SKRIPSI

LUAS PADA GEOMETRI HIPERBOLIK

Dipersiapkan dan ditulis oleh : Singgih Satriyo Wicaksono

NIM : 111414064

Telah dipertahankan di depan panitia penguji pada tanggal 29 Juli 2015

dan dinyatakan memenuhi syarat

Susunan Panitia Penguji

Nama Lengkap Tanda Tangan Ketua : Dr. Marcellinus Andy Rudhito, S.Pd. ………... Sekretaris : Ch. Enny Murwaningtyas, S.Si., M.Si. ……….. Anggota : 1. Drs. Sukardjono, M.Pd. ………... 2. Ch. Enny Murwaningtyas, S.Si., M.Si. ………... 3. Veronika Fitri Rianasari, M.Sc. ………...

Yogyakarta, 29 Juli 2015

Fakultas Keguruan dan Ilmu Pendidikan Universitas Sanata Dharma

Dekan,

(4)

iv

PERSEMBAHAN

Takut akan Tuhan adalah permulaan pengetahuan. Amsal 1 : 7

Skripsi ini untuk Ibuku dan adikku, almamaterku, dan setiap orang yang membacanya.

(5)

PERNYATAAN KEASLIAN KARYA

Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini

tidak memuat karya atau bagian orang lain, kecuali yang telah disebutkan dalam kutipan dan daft ar pustaka s eb agaiman a lay akny a kary a ilmi ah.

(6)

LEMBAR PERNYATAAN PERSETUJUAN

PUBLIKASI KARYA

ILMIAH

UNTUK KEPENTINGAN AKADEMIK

Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma :

Nama

NIM

: Singgih Satriyo Wicaksono :111414064

Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan Universitas Sanata Dharma sebuah karya ilmiah yang berjudul :

LUAS PADA GEOMETRI HIPERBOLIK

Dengan demikian saya memberikan kepada Perpustakaan Universitas Sanata Dharma

untuk

menyimpannya, mengalihkan dalam bentuk

media

lain, mengolahnya dalam bentuk pangkalan data, mendistribusikan secara terbatas, dan mempublikasikan di internet atau media lain demi kepentingan akademis tanpa meminta

ijin

dari saya maupun memberikan royalti kepada saya selama tetap mencantumkan nama saya sebagai penulis.

Demikian pernyataan ini saya buat dengan sebenarnya.

Yogyakarta,29 luh 2015 Yang menyatakan,

(7)

vii ABSTRAK

Singgih Satriyo Wicaksono, 2015. Luas pada Geometri Hiperbolik. Skripsi. Program Studi Pendidikan Matematika, Jurusan Pendidikan dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma, Yogyakarta.

Geometri hiperbolik adalah geometri yang berdasarkan pada postulat kesejajaran Lobachevski. Postulat tersebut berisi, “Diasumsikan suatu garis l dan suatu titik P yang tidak pada l, paling tidak ada dua garis 𝑙′_{, 𝑙′′ yang memuat P dan}

sejajar dengan l.” Defek suatu segitiga didefinisikan sebagai 180 dikurang jumlah sudut dalam segitiga. Di dalam geometri hiperbolik jumlah sudut dalam segitiga adalah kurang dari 180.

Dalam geometri hiperbolik, luas daerah segitiga (daerah triangular) didefinisikan sebagai defek dari segitiga yang bersesuaian. Suatu daerah segibanyak dapat diekspresikan sebagai gabungan daerah triangular yang terbatas jumlahnya. Luas dearah segibanyak didefinisikan sebagai total defek suatu daerah segibanyak, yaitu jumlah defek daerah triangular dari sembarang triangulasi terhadap daerah segibanyak tersebut.

(8)

viii ABSTRACT

Singgih Satriyo Wicaksono, 2015. Hyperbolic Geometry Area. Thesis. Mathematics Education Study Program, Mathematics and Science Education Deparment, Faculty of Teacher Training and Education, Sanata Dharma University, Yogyakarta.

Hyperbolic geometry is geometry which depends on Lobachevski Parallel Postulate. That postulate states, “Given a line l and a point P not on l, there are at least two lines l', l" which contain P and are parallel to l.” The defect of triangle is defined as 180 minus the angle sum of a triangle. Under hyperbolic geometry the angle sum of a triangle is less than 180.

In hyperbolic geometry, the area of triangle region is defined as the defect of the corresponding triangle. Polygon region can be expressed as the union of a finite number of triangular regions. The area of a polygon region is defined as total defect of a polygon region, that is the sum of the defect of the triangular region of any triangulation of that polygon region.

(9)

ix

KATA PENGANTAR

Segala puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Esa, karena atas berkat dan karuniaNya penulis dapat menyelesaikan skripsi yang berjudul “Luas pada Geometri Hiperbolik” ini.

Banyak tantangan dan hambatan yang penulis temui selama proses menyelesaikan skripsi ini. Namun penulis bersyukur dapat melaluinya. Dukungan, bantuan, dan doa dari banyak pihak telah menjadikan penulis tetap bersemangat dalam menyelesaikan skripsi ini. Untuk itu pada kesempatan kali ini penulis dengan sepenuh hati ingin mengucapkan terima kasih kepada beberapa pihak, diantaranya:

1. Bapak Rohandi, Ph.D. selaku dekan Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma.

2. Bapak Dr. M. Andy Rudhito, S.Pd. selaku kaprodi Pendidikan Matematika, Universitas Sanata Dharma.

3. Bapak Drs. Sukardjono, M.Pd. selaku dosen pembimbing yang telah banyak memberikan masukan dan nasihat kepada penulis selama menyusun skripsi.

4. Ibu V. Fitri Rianasari, S.Pd, M.Sc. selaku dosen pembimbing akademik yang telah banyak membimbing dan memberikan perhatian kepada penulis.

(10)

x

5. Ibu Ch. Enny Murwaningtyas, S.Si., M.Sc. selaku dosen penguji yang telah banyak memberikan masukan dan kritik yang membangun sehingga skripsi ini menjadi lebih baik.

6. Seluruh dosen Pendidikan Matematika yang telah memberikan ilmu selama penulis berkuliah di Universitas Sanata Dharma.

7. Seluruh staf sekretariat JPMIPA, Ibu Tari, Bapak Sugeng, Mas Arif, dan Mas Made yang telah banyak membantu memberikan pelayanan kesekretariatan selama ini.

8. Ibuku dan adikku Cahyo yang selalu mendukung, memberikan semangat, serta selalu berdoa untukku.

9. Keluarga Pakde Mulyana yang telah memberi banyak bantuan dan dukungan selama penulis kuliah. Juga mas Ony dan mas Anto yang banyak memberi bimbingan dan bantuan.

10. Keluarga Bapak Mattew Warren dan Ibu Selvi Kastanya yang telah banyak sekali membantu dan membimbing penulis selama kuliah.

11. Teman seperjuangan Pilipus Neri Agustima, yang telah banyak membantu penulis. Teman bertukar pikiran, teman main dota, teman yang baik dan juga menginspirasi.

12. Teman-teman Pendidikan Matematika angkatan 2011 dan teman-teman bimbingan Bapak Sukardjono yang selalu memberikan semangat, juga sebagai tempat berbagi suka duka mengerjakan skripsi.

13. Teman-teman PMK Oikumene. Trimakasih atas kesaksian-kesaksian yang menguatkan.

(11)

xi

14. Teman-teman Youth GBI Bethesda atas segala canda tawa dan semangat yang diberikan kepada penulis. Juga buat Kak Eva, pendengar yang baik untuk cerita-cerita penulis.

15. Semua pihak yang telah membantu dan tidak dapat disebutkan satu persatu.

Semoga tulisan ini dapat memberikan manfaat dan wawasan lebih kepada setiap pembaca. Tuhan memberkati.

Yogyakarta, 29 Juli 2015

(12)

xii DAFTAR ISI

HALAMAN JUDUL ... i

HALAMAN PERSETUJUAN PEMBIMBING ... ii

HALAMAN PENGESAHAN ... iii

HALAMAN PERSEMBAHAN ... iv

PERNYATAAN KEASLIAN KARYA ... v

PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH ... vi

ABSTRAK ... vii

ABSTRACT ... viii

KATA PENGANTAR ... ix

DAFTAR ISI ... xii

DAFTAR SIMBOL ... xiv

DAFTAR GAMBAR ... xvi

BAB I ... 1 PENDAHULUAN ... 1 1.1 Latar Belakang ... 1 1.2 Rumusan Masalah ... 2 1.3 Batasan Masalah ... 3 1.4 Tujuan Penelitian ... 3 1.5 Manfaat Penelitian ... 3 1.6 Metode Penelitian ... 4 1.7 Sistematika Penulisan ... 4 BAB II ... 6 LANDASAN TEORI ... 6

2.1 Pengenalan Geometri Non-Euclid ... 6

2.2 Geometri Insiden ... 8

2.3 Fungsi Jarak ... 11

2.4 Keantaraan ... 13

(13)

xiii

2.6 Kekonvekan dan Pemisahan ... 31

2.7 Kekontinuan ... 44

2.8 Ukuran Sudut ... 47

2.9 Postulat Luas ... 51

2.10 Sudut Luar Segitiga dan Konsekuensinya ... 55

2.11 Segiempat Saccheri dan Jumlah Sudut dalam Segitiga ... 62

2.12 Fungsi Kritis ... 67

BAB III ... 75

LUAS PADA GEOMETRI HIPERBOLIK ... 75

3.1 Jumlah Sudut dalam Segitiga pada Geometri Hiperbolik ... 75

3.2 Defek Segitiga ... 82

3.3 Triangulasi dan Subdivisi ... 90

3.4 Defek Daerah Segibanyak ... 97

BAB IV ... 115

PENUTUP ... 115

4.1 Kesimpulan ... 115

4.2 Saran ... 116

(14)

xiv

DAFTAR SIMBOL

𝒮 : himpunan semua titik ℒ : himpunan garis-garis 𝒫 : himpunan bidang-bidang ℝ : himpunan bilangan real ℛ : himpunan daerah segibanyak 𝐴, 𝐵, 𝐶 : titik-titik

𝑘, 𝑙, 𝑚 : garis-garis 𝐴𝐵

̅̅̅̅ : ruas garis atau segmen garis dengan titik akhir A dan B 𝐴𝐵

⃡ : garis yang melalui titik A dan titik B 𝐴𝐵

: sinar garis dengan titik akhir A 𝐴𝐵 : panjang 𝐴𝐵̅̅̅̅ atau jarak 𝐴 ke 𝐵 𝐴 − 𝐵 − 𝐶 : titik B diantara titik A dan titik C ∠𝐴𝐵𝐶 : sudut ABC

𝑚∠𝐴𝐵𝐶 : ukuran sudut ABC ∆𝐴𝐵𝐶 : segitiga ABC □𝐴𝐵𝐶𝐷 : segiempat ABCD 𝐻₁, 𝐻₂ : bidang setengah 𝑐(𝑎) : bilangan kritis 𝛿 : defek ∥ : sejajar | : asimtotik ⊥ : tegak lurus

(15)

xv

~ : sebangun ≅ : kongruen ∪ : gabungan ∩ : irisan

∈ : elemen atau anggota ∞ : tak hingga

sup : supremum inf : infimum

(16)

xvi

DAFTAR GAMBAR

Gambar 2.2.1 Garis ... 9

Gambar 2.2.2 Segmen Garis ... 9

Gambar 2.2.3 Sinar Garis ... 9

Gambar 2.3.1 Garis Bilangan I ... 11

Gambar 2.4.1 Keantaraan I ... 13

Gambar 2.4.2 Keantaraan II ... 13

Gambar 2.4.3 Garis Bilangan II... 17

Gambar 2.4.4 Ilustrasi Teorema 2.4.6 ... 19

Gambar 2.5.1 Segmen Garis ... 19

Gambar 2.5.2 Sinar Garis ... 20

Gambar 2.5.3 Sudut ... 20

Gambar 2.5.4 Segitiga ... 21

Gambar 2.5.5 Sudut-sudut Berpotongan ... 22

Gambar 2.5.7 Ilustrasi I Teorema 2.5.3 ... 25

Gambar 2.5.8 Ilustrasi II Teorema 2.5.3 ... 25

Gambar 2.5.9 Ilustrasi III Teorema 2.5.3 ... 26

Gambar 2.5.10 Sudut Yang Sama ... 27

Gambar 2.5.12 Ilustrasi II Teorema 2.5.5... 30

Gambar 2.6.1 Himpunan Konvek ... 31

Gambar 2.6.2 Himpunan Tidak Konvek ... 32

Gambar 2.6.3 Pemisahan Bidang ... 33

(17)

xvii

Gambar 2.6.9 Interior dan Eksterior Sudut... 40

Gambar 2.6.13 Interior Segitiga ... 43

Gambar 2.7.3 Teorema Crossbar ... 46

Gambar 2.8.1 Ukuran Sudut I ... 47

Gambar 2.8.2 Ukuran Sudut II ... 48

Gambar 2.8.3 Pembentukan Sudut ... 49

Gambar 2.8.4 Pembentukan Sudut ... 49

Gambar 2.8.5 Dua Sudut Membentuk Pasangan Linear ... 50

Gambar 2.8.6 Dua Sudut Berpelurus ... 50

Gambar 2.9.1 Daerah Triangular ... 51

Gambar 2.9.2 Daerah Segibanyak ... 51

Gambar 2.9.3 Pembagian Daerah Jajargenjang ... 52

Gambar 2.9.4 Postulat Penjumlahan ... 54

Gambar 2.9.5 Triangulasi ... 54

Gambar 2.11.1 Segiempat Saccheri I ... 62

Gambar 2.11.2 Segiempat Saccheri II ... 63

Gambar 2.11.3 Segiempat Saccheri III ... 64

(18)

xviii

Gambar 2.12.1 Supremum dan Infimum ... 67

Gambar 2.12.2 Garis Sejajar Pada Geometri Hiperbolik ... 69

Gambar 2.12.3 Fungsi Kritis ... 70

Gambar 3.1.1 Segitiga Terbuka ... 76

Gambar 3.1.2 Segitiga Asimtotik ... 77

Gambar 3.1.4 Segiempat Saccheri IV ... 79

Gambar 3.1.5 Jumlah Sudut Dalam Segitiga Siku-siku Pada Geometri Hiperbolik ... 80

Gambar 3.1.6 Jumlah Sudut Dalam Segitiga Pada Geometri Hiperbolik ... 81

Gambar 3.2.2 Segitiga Kongruen Pada Geometri Hiperbolik ... 83

Gambar 3.3.1 Segibanyak Konvek ... 91

Gambar 3.3.2 Triangulasi Bintang ... 92

Gambar 3.3.6 Ilustrasi III Teorema 3.3..2 ... 95

Gambar 3.3.7 Segibanyak Yang Ekuivalen ... 96

Gambar 3.4.1 Segitiga ... 97

Gambar 3.4.2 Jumlah Defek Triangulasi Bintang ... 99

Gambar 3.4.3 Triangulasi Bintang Daerah Segibanyak ... 101

Gambar 3.4.4 Triangulasi Batas ... 102

(19)

xix

(20)

1 BAB I

PENDAHULUAN

1.1 Latar Belakang

Kata “geometri” berasal dari kata Yunani “geometrein” (geo = bumi, dan metrein = ukuran) yang berarti ilmu pengukuran bumi. Pada mulanya, geometri adalah ilmu yang digunakan untuk mengukur lahan pertanian. Sejarahwan Yunani, Herodotus (5 tahun sebelum masehi), mengatakan orang-orang Mesir lah yang pertama kali menggunakan subjek geometri, tetapi negara-negara kuno lain (Babylonia, India, Cina) juga mempunyai beberapa informasi geometri (Greenberg, 1980 : 5).

Selama lebih dari 2000 tahun, “Elements” buku yang ditulis oleh Euclid sekitar 300 tahun sebelum masehi dianggap sebagai model dari penalaran matematika. Sampai abad ke-20, buku Euclid ini masih menjadi dasar pembelajaran geometri di sekolah-sekolah. Geometri Euclid ini mengandung postulat kesejajaran (parallel postulate) yang merupakan postulat terakhir dari lima postulat yang ada dalam geometri Euclid. Beberapa matematikawan menganggap postulat kesejajaran ini tidak sederhana dan mencoba membuktikannya. Beberapa matematikawan yang mencoba membuktikan postulat kesejajaran Euclid adalah Proclus (410-485), John Wallis (1616-1703), dan Girolamo Saccheri (1667-1733). Namun usaha ini tidak berhasil. Kegagalan dalam 20 abad akhirnya memicu sebuah pencetusan keraguan pemikiran matematikawan sehingga

(21)

pada 1830 J. Bolyai (1802-1860), seorang staf angkatan darat Hungaria, N.I. Lobachevsky (1793-1856), seorang Profesor matematika Rusia pada Universitas Kazan, dan sang agung Gauss sendiri telah mengembangkan secara independen teori geometri berdasarkan kontradiksi postulat kesejajaran Euclid (Prenowitz & Jordan, 1965: 53). Kemudian geometri ini dinamakan geometri hiperbolik.

Area atau luas dalam geometri Euclid dinyatakan dalam banyaknya persegi satuan yang tepat menimpa suatu bangun. Prosedur ini tidak dapat diterapkan dalam geometri hiperbolik karena dalam geometri hiperbolik tidak terdapat persegi. Lalu bagaimana menyatakan ukuran luas dalam geometri hiperbolik? Selama ini geometri yang telah dipelajari oleh penulis merupakan geometri Euclid. Oleh karena itu penulis ingin mengetahui geometri Non-Euclid terutama luas pada geometri hiperbolik.

1.2 Rumusan Masalah

1. Apa yang dimaksud geometri hiperbolik?

2. Bagaimana nilai defek segitiga dan segibanyak pada geometri hiperbolik?

(22)

1.3 Batasan Masalah

Luas yang dibahas dalam skripsi ini adalah luas dalam geometri hiperbolik.

1.4 Tujuan Penelitian

Penelitian ini bertujuan untuk :

1. Untuk mengetahui definisi geometri hiperbolik.

2. Untuk mengetahui nilai defek segitiga dan segibanyak pada geometri hiperbolik.

3. Untuk mengetahui luas segitiga dan segibanyak pada geometri hiperbolik.

1.5 Manfaat Penelitian

Manfaat yang dapat diambil dari penelitian ini adalah sebagai berikut :

1. Bagi Pembaca

Pembaca dapat menambah pengetahuan mengenai geometri hiperbolik dan luas pada geometri hiperbolik.

2. Bagi Penulis

Penulis dapat menambah pengetahuan mengenai geometri hiperbolik dan luas pada geometri hiperbolik.

3. Bagi Universitas

Universitas dapat menambah koleksi skripsi dalam bidang geometri.

(23)

1.6 Metode Penelitian

Metode penelitian yang digunakan dalam skripsi ini adalah metode studi pustaka, yaitu dengan membaca referensi-referensi mengenai geometri hiperbolik. Pembahasan dalam skripsi ini banyak mengacu pada buku Elementary Geometry from an Advanced Standpoint Third Edition, karangan Edwin E. Moise (1990) dan buku Geometry : A Metric Approach

with Model Second Edition, karangan Richard S. Milman dan George D.

Parker (1991).

Langkah-Langkah yang dilakukan dalam penelitian ini adalah:

1. Membaca berbagai referensi mengenai topik geometri hiperbolik. 2. Menyajikan kembali definisi-definisi serta teorema-teorema yang

menjadi dasar dalam mempelajari geometri hiperbolik, khususnya dalam skripsi ini mengenai luas dalam geometri hiperbolik.

3. Menyusun seluruh materi yang telah dikumpulkan secara runtut agar memudahkan pembaca dalam memahaminya.

1.7 Sistematika Penulisan

Bab pertama berupa pendahuluan. Pendahuluan ini berisi tentang latar belakang, rumusan masalah, batasan masalah, tujuan, manfaat, metode penelitian, dan sistematika penulisan.

Bab dua berisi tentang dasar-dasar yang akan digunakan dalam membahas defek dan luas pada geometri hiperbolik. Pertama disajikan

(24)

postulat-postulat dan definisi-definisi dasar dalam geometri yang terangkum dalam materi geometri insiden, fungsi jarak, segmen, sinar, sudut, dan segitiga, ukuran sudut, dan postulat luas. Kemudian dibahas mengenai keantaraan, kekonvekkan dan pemisahan, serta kekontinuan yang akan banyak digunakan dalam membahas materi selanjutnya. Selanjutnya diberikan materi mengenai jumlah sudut dalam segitiga pada geometri hiperbolik yang terangkum dalam materi sudut luar segitiga dan konsekuensinya, segiempat Saccheri dan jumlah sudut dalam segitiga, dan fungsi kritis.

Bab tiga membahas mengenai luas pada geometri hiperbolik. Materi-materi yang disajikan adalah jumlah sudut dalam segitiga pada geometri hiperbolik, defek segitiga, triangulasi dan subdivisi, dan defek segibanyak.

Bab empat berisi kesimpulan dari pembahsan pada bab tiga serta saran yang diberikan penulis kepada pembaca yang ingin melanjutkan penelitian ini.

(25)

6 BAB II

LANDASAN TEORI

2.1 Pengenalan Geometri Non-Euclid

Sub bab ini berisi sejarah singkat penemuan geometri hiperbolik (geometri Lobachevsky) dan geometri Eliptik (geometri Riemann) yang termasuk dalam geometri non-Euclid. Selama lebih dari 2000 tahun, “Elements” buku yang ditulis oleh Euclid sekitar 300 tahun sebelum masehi dianggap sebagai model dari penalaran matematika. Buku yang ditulis Euclid ini mengandung lima postulat. Postulat yang kelima disebut postulat kesejajaran (kemudian disebut postulat kesejajaran Euclid). Dalam kurun waktu yang lama matematikawan percaya bahwa geometri Euclid merupakan satu-satunya teori ruang yang mungkin dan mendeskripsikan secara tepat dunia nyata. Tetapi ketika posisi dari geometri Euclid dikritisi oleh penemuan geometri non-Euclid pada abad sembilan belas, para matematikawan mulai tergoncang. Sebuah revolusi pada matematika terjadi, sebanding dengan revolusi Copernicus pada astronomi dan revolusi Darwin pada biologi.

Sebelum ditemukannya geometri non-Euclid, ada beberapa matematikawan yang menganggap bahwa postulat kesejajaran Euclid tidak sederhana dan mencoba membuktikannya. Beberapa matematikawan yang mencoba membuktikan postulat kesejajaran Euclid adalah Proclus (410-485), John Wallis (1616-1703), dan Girolamo Saccheri (1667-1733).

(26)

Namun usaha ini tidak berhasil. Kegagalan dalam setiap usaha pembuktian postulat kesejajaran Euclid pada akhirnya menuntun pada kesadaran bahwa postulat kesejajaran tersebut tidak pasti, dan dimungkinkan adanya teori lain dari geometri. Teori yang lain tersebut dinamakan geometri non-Euclid, yaitu teori yang tidak berdasarkan pada posulat kesejajaran Euclid.

Kegagalan dalam 20 abad akhirnya memicu sebuah pencetusan keraguan pemikiran matematikawan sehingga pada 1830 J. Bolyai (1802-1860), seorang staf angkatan darat Hungaria, N.I. Lobachevsky (1793-1856), seorang Profesor matematika Rusia pada Universitas Kazan, dan sang agung Gauss sendiri telah mengembangkan secara independen teori geometri berdasarkan kontradiksi postulat kesejajaran Euclid (Prenowitz & Jordan, 1965: 53). Kemudian geometri ini dinamakan geometri hiperbolik. Bolyai dan Lobachevsky berhasil menyaingi postulat kesejajaran Euclid. Kemudian matematikawan meniru untuk membangun teori geometri non-Euclid lainnya. Selanjutnya, pada 1854, seorang matematikawan Jerman B. Riemann memperkenalkan teori non-Euclid yang berbeda dari geometri hiperbolik berdasarkan pada asumsi bahwa tidak ada garis yang sejajar. Kemudian geometri Riemann ini dinamakan geometri eliptik.

Geometri Euclid, geometri hiperbolik, dan geometri eliptik merupakan teori-teori geometri yang berbeda. Ketiga geometri ini berdasar pada postulat kesejajarannya masing-masing. Geometri hiperbolik dan

(27)

geometri eliptik termasuk dalam geometri non-Euclid karena postulat kesejajarannya tidak berdasarkan pada postulat kesejajaran Euclid.

2.2 Geometri Insiden

Menurut Prenowitz dan Jordan (1965: 119), insiden merupakan suatu relasi geometri yang paling dasar. Sebagai contoh diberikan relasi insiden dengan pernyataan berikut, “Sebuah titik terletak pada sebuah garis,” yang ekuivalen dengan “Sebuah garis melalui suatu titik.” Pernyataan lain yang mengekspresikan relasi insiden adalah, “Sebuah titik pada sebuah bidang”, “Sebuah garis pada sebuah bidang”, “Dua garis berpotongan.” Jadi relasi insiden mengekpresikan keterkaitan posisi antara titik, garis, dan bidang.

Ruang (space) akan dianggap sebagai himpunan 𝒮, adalah himpunan semua titik pada ruang. Selanjutnya diberikan himpunan bagian dari 𝒮, yang disebut garis-garis (lines) dinyatakan dengan ℒ, dan himpunan bagian dari 𝒮 yang disebut bidang-bidang (planes) dinyatakan dengan 𝒫. Maka anggota dari 𝒮, ℒ, dan 𝒫 berturut-turut disebut titik-titik, garis-garis, dan bidang-bidang.

Titik, garis, dan bidang tidak didefinisikan.

Suatu garis akan memanjang sampai tak hingga pada kedua arahnya seperti berikut :

(28)

Tanda panah mengindikasikan bahwa walaupun garis digambar terbatas dengan panjang tertentu, namun garis tetap memanjang sampai tak hingga.

Selanjutnya akan dibahas tentang segmen atau ruas garis, yang dapat digambarkan sebagai berikut :

Suatu Segmen dengan titik pangkal P dan Q, seperti Gambar 2.2.2 dilambangkan dengan 𝑃𝑄̅̅̅̅.

Suatu segmen diperpanjang sampai tak hingga hanya pada salah satu arah disebut sinar, dan dapat digambarkan seperti berikut :

Suatu sinar dengan titik pangkal P dan melalui 𝑃𝑄̅̅̅̅, seperti Gambar 2.2.3 dilambangkan dengan 𝑃𝑄 . Segmen dan sinar akan dibahas lebih lanjut pada sub bab 2.5.

Berikut akan dijelaskan postulat geometri insiden (Moise, 1990: 44).

Gambar 2.2.1 Garis

Gambar 2.2.3 Sinar Garis

P Q

(29)

I-0 Semua garis dan bidang adalah himpunan dari titik-titik.

Jika suatu garis l adalah himpunan bagian dari suatu bidang E, maka dikatakan l berada pada E. Jika titik P himpunan bagian dari suatu garis l, maka dikatakan P pada l atau l melalui P. Jika P himpunan bagian dari E, maka dikatakan P pada E atau E melalui P.

Definisi 2.2.1 (Moise, 1990: 44)

Titik-titik yang berada pada satu garis disebut kolinear, dan titik-titik yang berada pada satu bidang disebut koplanar.

I-1 Diberikan sembarang dua titik berbeda, ada tepat satu garis yang memuat dua titik tersebut.

Jika titik-titik tersebut adalah P dan Q, maka garis yang memuat titik-titik tersebut dilambangkan dengan 𝑃𝑄⃡ .

I-2 Diberikan sembarang tiga titik non kolinear berbeda, ada tepat satu bidang yang memuat titik-titik tersebut.

I-3 Jika dua titik berada pada suatu bidang, maka garis yang memuat titik-titik tersebut berada pada bidang yang sama.

I-4 Jika dua bidang berpotongan, maka perpotongannya adalah suatu garis.

(30)

2.3 Fungsi Jarak

Setiap pasang titik akan berkorespodensi dengan suatu bilangan real yang disebut jarak antara kedua titik tersebut. Diperlukan suatu fungsi jarak d, yang tergantung pada postulat berikut (Moise, 1990: 56):

D-0 d adalah suatu fungsi

d :𝒮 × 𝒮 → ℝ.

D-1 Untuk setiap P, Q, 𝑑(𝑃, 𝑄) ≥ 0.

D-2 𝑑(𝑃, 𝑄) = 0 jika dan hanya jika P = Q. D-3 𝑑(𝑃, 𝑄) = 𝑑(𝑄, 𝑃) untuk setiap P dan Q.

Selanjutnya agar lebih ringkas 𝑑(𝑃, 𝑄) akan ditulis dengan PQ.

Penandaan titik pada suatu garis dengan bilangan-bilangan dapat diterapkan seperti penandaan titik pada sumbu-x dalam geometri analitik.

Jika ini dilakukan, akan didapat korespodensi satu-satu

𝑓: 𝑙 ↔ ℝ

Gambar 2.3.1 Garis Bilangan I

-1 0 1 𝑥1

𝑥₂

P R Q

(31)

diantara titik-titik pada 𝑙 dan bilangan real. Jika 𝑥 = 𝑓(𝑃), maka x disebut sebagai koordinat titik P. Pada Gambar 2.3.1 koordinat P, Q, R, dan T adalah 0, 𝑥₁, 1, dan 𝑥₂.

Selanjutnya akan dijelaskan jarak antara dua titik.

Definisi 2.3.1 (Moise, 1990: 58)

Diberikan

𝑓: 𝑙 ↔ ℝ

adalah korespondensi satu-satu diantara suatu garis 𝑙 dan bilangan real. Untuk semua titik-titik A, B pada 𝑙, didapat

𝐴𝐵 = |𝑓(𝐴) − 𝑓(𝐵)|,

Kemudian f adalah suatu sistem koordinat untuk 𝑙. Untuk setiap titik A pada 𝑙, bilangan 𝑥 = 𝑓(𝐴) disebut koordinat titik A.

Sebagai contoh diberikan titik A dan B, sehingga 𝑓(𝐴) = 5 dan 𝑓(𝐵) = −7. Tentukan AB !

Jawab :

(32)

= |5 − (−7)| = |12| = 12

D-4 Postulat aturan (The Ruler Postulate).

Setiap garis memiliki sistem koordinat.

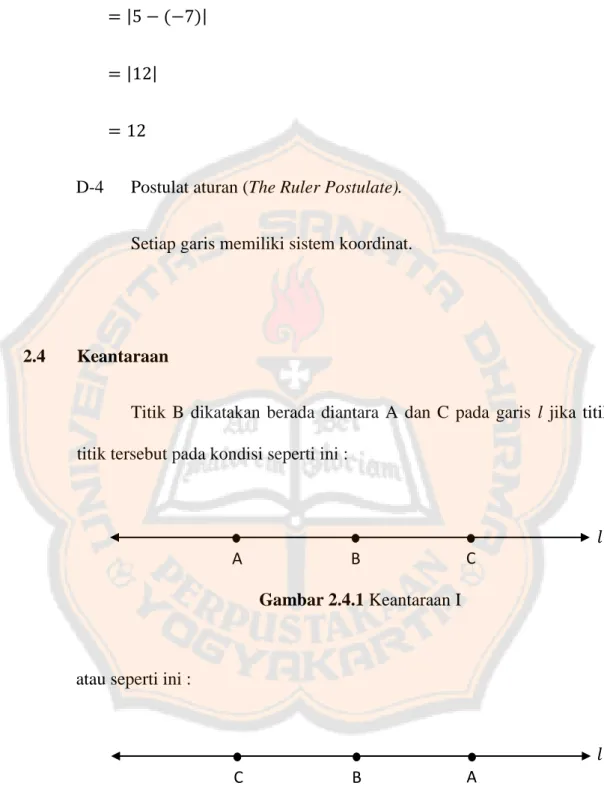
2.4 Keantaraan

Titik B dikatakan berada diantara A dan C pada garis l jika titik-titik tersebut pada kondisi seperti ini :

atau seperti ini :

Gambar 2.4.1 Keantaraan I A B C 𝑙 Gambar 2.4.2 Keantaraan II C B A 𝑙

(33)

Definisi 2.4.1 (Moise, 1990: 60)

Diberikan A, B, dan C adalah tiga titik berbeda yang kolinear. Jika 𝐴𝐵 + 𝐵𝐶 = 𝐴𝐶,

maka B diantara A dan C. Kemudian ini dilambangkan dengan A-B-C.

Teorema 2.4.1 (Moise, 1990: 60)

Jika A-B-C, maka C-B-A.

Bukti : 𝐶𝐵 + 𝐵𝐴 = 𝐵𝐴 + 𝐶𝐵 = 𝐴𝐵 + 𝐵𝐶 = 𝐴𝐶 = 𝐶𝐴 Didapat bahwa 𝐶𝐵 + 𝐵𝐴 = 𝐶𝐴. Jika 𝐴𝐵 + 𝐵𝐶 = 𝐴𝐶, maka 𝐶𝐵 + 𝐵𝐴 = 𝐶𝐴.

(34)

Lema 2.4.2 (Moise, 1990: 61)

Diberikan suatu garis l dengan sistem koordinat f dan tiga titik berbeda A, B, dan C pada l dengan koordinat berturut-turut x, y, dan z. Jika x-y-z, maka A-B-C.

Bukti :

(1) Jika 𝑥 < 𝑦 < 𝑧, maka

𝐴𝐵 = |𝑦 − 𝑥| = 𝑦 − 𝑥 Karena 𝑦 − 𝑥 > 0. Untuk alasan yang sama

𝐵𝐶 = |𝑧 − 𝑦| = 𝑧 − 𝑦 dan

𝐴𝐶 = |𝑧 − 𝑥| = 𝑧 − 𝑥. Oleh karena itu

𝐴𝐵 + 𝐵𝐶 = (𝑦 − 𝑥) + (𝑧 − 𝑦) = 𝑧 − 𝑥

= |𝑧 − 𝑥| = 𝐴𝐶 Sehingga A-B-C

(2) Jika 𝑧 < 𝑦 < 𝑥. Dengan cara yang sama seperti (1) didapat C-B-A. Dengan Teorema 2.4.1 didapat A-B-C. □

(35)

Teorema 2.4.3 (Moise, 1990: 61)

Sembarang tiga titik berbeda pada suatu garis, ada tepat satu titik berada diantara dua titik yang lain.

Bukti :

(1) Diberikan f sistem koordinat untuk suatu garis dan x, y, z adalah koordinat titik-titik A , B, dan C. Satu dari bilangan x, y, dan z berada diantara dua yang lain. Dengan Lema 2.4.2, ini berarti titik A, B, atau C berada diantara dua titik yang lain.

(2) Akan dibuktikan bahwa jika A-B-C, maka tidak ada diantara dua kondisi B-A-C dan A-C-B yang terpenuhi. Jika B-A-C, maka

𝐵𝐴 + 𝐴𝐶 = 𝐵𝐶. Telah diberikan

𝐴𝐵 + 𝐵𝐶 = 𝐴𝐶. Dengan menjumlahkannya didapat

𝐵𝐴 + 𝐴𝐶 + 𝐴𝐵 + 𝐵𝐶 = 𝐴𝐶 + 𝐵𝐶 atau

2𝐴𝐵 = 0.

Sehingga AB = 0. Ini tidak mungkin, sebab A ≠ B.

Pembuktian untuk A-C-B tidak terpenuhi sama seperti langkah-langkah diatas. □

(36)

Teorema 2.4.4 (Moise, 1990: 63)

Jika A dan B sembarang dua titik, A ≠ B, maka (1) ada titik C sehingga A-B-C dan (2) ada titik D sehingga A-D-B.

Bukti :

Ambil suatu sistem koordinat f untuk suatu garis 𝐴𝐵⃡ yang memuat A dan B.

Andaikan x, y koordinat titik A dan B, dengan x < y. Diberikan 𝐶 = 𝑓−1_{(𝑦 + 1).}

Maka A-B-C, karena 𝑥 < 𝑦 < 𝑦 + 1. Selanjutnya, diberikan 𝐷 = 𝑓−1₍𝑥 + 𝑦 2 ) Sebab x < y, maka 2𝑥 < 𝑥 + 𝑦 < 2𝑦 sehingga

Gambar 2.4.3 Garis Bilangan II

A 𝑥 B 𝑦 D 𝑥 + 𝑦 2 C 𝑦 + 1

(37)

𝑥 <𝑥 + 𝑦 2 < 𝑦

Jadi A-D-B. □

Teorema 2.4.5 (Moise, 1990: 63)

Jika A-B-C, maka A, B, dan C adalah tiga titik berbeda pada garis yang sama.

Bukti :

Berdasarkan Definisi 2.4.1, titik A, B, dan C adalah tiga titik berbeda. □

Teorema 2.4.6

Jika A-B-C dan A-C-D, maka A-B-D.

Bukti :

Ambil a, b, c, d berturut-turut sebagai koordinat titik A, B, C, dan D. Karena A-B-C maka a < b < c atau c < b < a. Karena A-C-D, maka a < c < d atau d < c < a.

Dari A-B-C dapat dipilih salah satu dari kondisi a < b < c atau c < b < a. Ambil a < b < c, didapat a < c. Dari A-C-D, kondisi d < c < a akan kontrdiksi dengan a < c, sehingga diambil a < c < d.

(38)

Telah diambil a < b < c dan a < c < d, sehingga didapat a < b < c < d. Akibatnya a < b < d. Berdasarkan Lema 2.4.2 karena a-b-d, maka A-B-D.□

2.5 Segmen, Sinar, Sudut, dan Segitiga

Definisi 2.5.1 (Moise, 1990: 64)

Jika A dan B adalah dua titik, maka segmen 𝐴𝐵̅̅̅̅ adalah himpunan yang memuat A dan B, bersama dengan semua titik diantara A dan B.

Definisi 2.5.2 (Moise, 1990: 65)

Sinar 𝐴𝐵 didefinisikan sebagai himpunan semua titik C pada garis 𝐴𝐵⃡ sehingga A tidak diantara B dan C. Sinar 𝐴𝐵 juga dapat didefinisikan

Gambar 2.5.1 Segmen Garis

A B

𝐴𝐵

̅̅̅̅ 𝐴𝐵⃡

A B C D

(39)

sebagai gabungan dari (1) segmen 𝐴𝐵̅̅̅̅ dan (2) himpunan semua titik C sehingga A-B-C. Titik A disebut titik pangkal dari sinar 𝐴𝐵 .

Definisi 2.5.3 (Moise, 1990: 65)

Sudut adalah gabungan dari dua sinar yang memiliki titik pangkal yang sama, tetapi dua sinar tersebut tidak pada garis yang sama. Jika suatu sudut adalah gabungan dari 𝐴𝐵 dan 𝐴𝐶 , maka sinar-sinar tersebut disebut sisi dari sudut. Titik A disebut titik sudut. Sudut tersebut disimbolkan dengan ∠𝐵𝐴𝐶. Catatan ∠𝐵𝐴𝐶 = ∠𝐶𝐴𝐵. Gambar 2.5.3 Sudut A B C 𝐴𝐵 A B

(40)

Definisi 2.5.4 (Moise, 1990: 65)

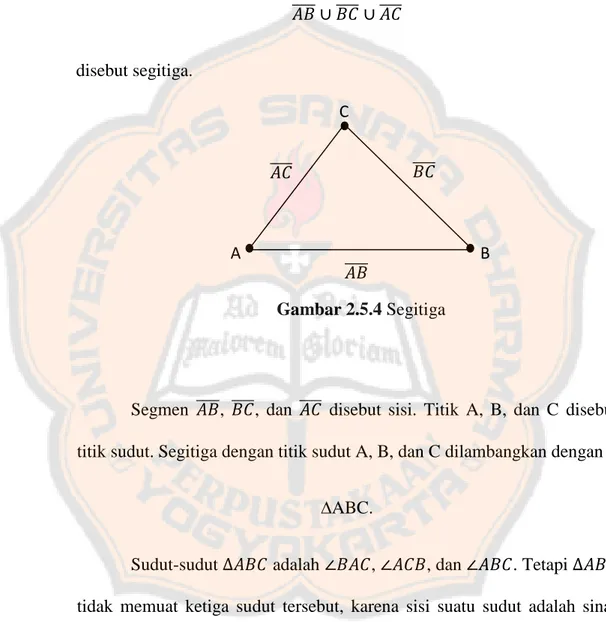
Jika A, B, dan C adalah tiga titik yang tidak segaris, maka himpunan

𝐴𝐵

̅̅̅̅ ∪ 𝐵𝐶̅̅̅̅ ∪ 𝐴𝐶̅̅̅̅ disebut segitiga.

Segmen 𝐴𝐵̅̅̅̅, 𝐵𝐶̅̅̅̅, dan 𝐴𝐶̅̅̅̅ disebut sisi. Titik A, B, dan C disebut titik sudut. Segitiga dengan titik sudut A, B, dan C dilambangkan dengan

∆ABC.

Sudut-sudut ∆𝐴𝐵𝐶 adalah ∠𝐵𝐴𝐶, ∠𝐴𝐶𝐵, dan ∠𝐴𝐵𝐶. Tetapi ∆𝐴𝐵𝐶 tidak memuat ketiga sudut tersebut, karena sisi suatu sudut adalah sinar dan sisi segitiga adalah segmen. Jika semua sudut digambar, maka gambarnya akan terlihat seperti gambar berikut.

A B C 𝐴𝐵 ̅̅̅̅ 𝐴𝐶 ̅̅̅̅ 𝐵𝐶̅̅̅̅ Gambar 2.5.4 Segitiga

(41)

Teorema 2.5.1 (Moise, 1990: 66)

Diberikan titik A dan titik B sembarang titik yang berbeda, maka 𝐴𝐵̅̅̅̅ = 𝐵𝐴

̅̅̅̅. Bukti :

Diketahui A dan B sembarang titik berbeda. Dari Definisi 2.5.1, segmen 𝐴𝐵

̅̅̅̅ adalah himpunan titik A dan titik B, bersama dengan semua titik X, sehingga A-X-B. Dapat ditulis 𝐴𝐵̅̅̅̅ = {A ∪ B ∪ X′ | X′ adalah himpunan semua titik X sehingga A-X-B}

Segmen 𝐵𝐴̅̅̅̅ adalah himpunan titik B dan titik A, bersama dengan semua titik X, sehingga B-X-A. Dapat ditulis 𝐵𝐴̅̅̅̅ = {B ∪ A ∪ X′ | X′ adalah himpunan semua titik X sehingga B-X-A}

Teorema 2.4.1 menjamin bahwa untuk setiap titik X, jika A-X-B maka B-X-A. Sehingga,

𝐵𝐴

̅̅̅̅ = {B ∪ A ∪ X′ | X′ adalah himpunan semua titik X sehingga B-X-A}

Gambar 2.5.5 Sudut-sudut Berpotongan

A

B C

(42)

= {A ∪ B ∪ X′ | X′ adalah himpunan semua titik X sehingga A-X-B}

= 𝐴𝐵̅̅̅̅ □

Teorema 2.5.2

Jika A-B-C, maka 𝐴𝐵̅̅̅̅ ∪ 𝐵𝐶̅̅̅̅ = 𝐴𝐶̅̅̅̅. Bukti :

Dari Definisi 2.5.1, 𝐴𝐶̅̅̅̅ adalah himpunan titik A dan C, bersama dengan semua titik di antara A dan C. Dapat ditulis 𝐴𝐶̅̅̅̅ = { A ∪ C ∪ Z′ | Z′ adalah himpunan semua titik Z sehingga A-Z-C}.

Diketahui A-B-C. Dari Definisi 2.4.1, A, B, dan C adalah titik-titik yang kolinear. Dari Teorema 2.4.4 dapat diambil titik X dan Y sehingga A-X-B dan B-Y-C.

𝐴𝐵

̅̅̅̅ = {A ∪ B ∪ X′ | X′ adalah himpunan semua titik X sehingga A-X-B} 𝐵𝐶

̅̅̅̅ = {B ∪ C ∪ Y′ | Y′ adalah himpunan semua titik Y sehingga B-Y-C} Diketahui A-B-C dan A-X-B, sehingga berdasarkan pada Teorema 2.4.6 didapat A-X-C untuk setiap X.

Gambar 2.5.6 Ilustrasi Teorema 2.5.2

A B C

(43)

Diketahui A-B-C dan B-Y-C, sehingga berdasarkan pada Teorema 2.4.6 didapat A-Y-C untuk setiap Y.

Oleh karena itu setiap anggota dari X′ dan Y′ berada diantara A dan C, sehingga X′_{dan Y′ merupakan anggota dari Z}′_{. Sehingga Z}′_{= {X}′_{∪ Y′ ∪ B}

| X′ adalah himpunan semua titik X sehingga A-X-B, Y′ adalah himpunan semua titik Y sehingga B-Y-C }.

𝐴𝐵

̅̅̅̅ ∪ 𝐵𝐶̅̅̅̅ = { A ∪ B ∪ C ∪ X′ ∪ Y′ | X′ adalah himpunan semua titik X sehingga A-X-B, Y′ adalah himpunan semua titik Y sehingga B-Y-C }

= { A ∪ C ∪ Z′ | Z′ adalah himpunan semua titik Z sehingga A-Z-C}

= 𝐴𝐶̅̅̅̅ □

Teorema 2.5.3 (Moise, 1990: 66)

Jika C adalah titik pada 𝐴𝐵 , C ≠ A, maka 𝐴𝐵 = 𝐴𝐶 . Bukti :

Dari Definisi 2.5.2, sinar 𝐴𝐵 adalah gabungan dari segmen 𝐴𝐵̅̅̅̅ dan himpunan semua titik Q sehingga A-B-Q. Dapat ditulis 𝐴𝐵 = {𝐴𝐵̅̅̅̅ ∪ Q′ | Q′ adalah himpunan semua titik Q sehingga A-B-Q}.

(44)

Jika B = C, maka 𝐴𝐵 dan 𝐴𝐶 adalah himpunan yang sama, sehingga 𝐴𝐵 = 𝐴𝐶

. Selanjutnya akan diambil B ≠ C. Dari Teorema 2.4.4 dapat diambil titik C sehingga A-C-B dan A-B-C.

Untuk kondisi A-C-B, dari Teorema 2.5.2 didapat 𝐴𝐶̅̅̅̅ ∪ 𝐶𝐵̅̅̅̅ = 𝐴𝐵̅̅̅̅. Sinar 𝐴𝐶

adalah gabungan dari segmen 𝐴𝐶̅̅̅̅ dan himpunan semua titik R sehingga A-C-R. Dapat ditulis 𝐴𝐶 = {𝐴𝐶̅̅̅̅ ∪ R′ | R′ adalah himpunan semua titik R sehingga A-C-R}.

Ambil titik S sembarang titik pada 𝐶𝐵̅̅̅̅ − 𝐶. Setiap titik S memenuhi A-C-S, sehingga 𝐶𝐵̅̅̅̅ − 𝐶 ∈ 𝐴𝐶 .

Untuk setiap Q ∈ Q′, A-C-B dan A-B-Q, maka A-C-Q (Teorema 2.4.6), sehingga Q′_{∈ 𝐴𝐶}_.

𝐴𝐶

̅̅̅̅ ∪ (𝐶𝐵̅̅̅̅ − 𝐶) dan 𝐴𝐶̅̅̅̅ ∪ 𝐶𝐵̅̅̅̅ merupakan himpunan yang sama, sehingga 𝐴𝐶

̅̅̅̅ ∪ (𝐶𝐵̅̅̅̅ − 𝐶) = 𝐴𝐶̅̅̅̅ ∪ 𝐶𝐵̅̅̅̅ = 𝐴𝐵̅̅̅̅.

A B _Q

Gambar 2.5.7 Ilustrasi I Teorema 2.5.3

Gambar 2.5.8 Ilustrasi II Teorema 2.5.3

(45)

Sehingga 𝐴𝐶 = {𝐴𝐶̅̅̅̅ ∪ 𝐶𝐵̅̅̅̅ ∪ Q′ | Q′ adalah himpunan semua titik Q sehingga A-B-Q}

= {𝐴𝐵̅̅̅̅ ∪ Q′ | Q′ adalah himpunan semua titik Q sehingga A-B-Q}

= 𝐴𝐵

Untuk kondisi A-B-C, dengan Teorema 2.5.2 didapat 𝐴𝐵̅̅̅̅ ∪ 𝐵𝐶̅̅̅̅ = 𝐴𝐶̅̅̅̅. Sinar 𝐴𝐶 = {𝐴𝐶̅̅̅̅ ∪ T′ | T′ adalah himpunan semua titik T sehingga A-C-T}.

Ambil U sembarang titik pada 𝐵𝐶̅̅̅̅ − 𝐵. Setiap titik U memenuhi A-B-U, maka setiap titik U ∈ Q′. Setiap titik T memenuhi A-B-T, maka setiap titik T ∈ Q′.

𝐴𝐵

̅̅̅̅ ∪ (𝐵𝐶̅̅̅̅ − 𝐵) dan 𝐴𝐵̅̅̅̅ ∪ 𝐵𝐶̅̅̅̅ merupakan himpunan yang sama, sehingga 𝐴𝐵

̅̅̅̅ ∪ (𝐵𝐶̅̅̅̅ − 𝐵) = 𝐴𝐵̅̅̅̅ ∪ 𝐵𝐶̅̅̅̅ = 𝐴𝐶̅̅̅̅.

Sehingga 𝐴𝐵 = {𝐴𝐵̅̅̅̅ ∪ 𝐵𝐶̅̅̅̅ ∪ T′ | T′ adalah himpunan semua titik T sehingga A-C-T}

= {𝐴𝐶̅̅̅̅ ∪ T′ | T′ adalah himpunan semua titik T sehingga A-C-T}

Gambar 2.5.9 Ilustrasi III Teorema 2.5.3

(46)

= 𝐴𝐶

Telah ditunjukan bahwa dimanapun letak C pada 𝐴𝐵 , dengan A ≠ C, maka 𝐴𝐵

= 𝐴𝐶 . □

Teorema 2.5.4 (Moise, 1990: 66)

Jika 𝐵₁ dan 𝐶₁ adalah titik-titik pada 𝐴𝐵 dan 𝐴𝐶 , dengan 𝐵₁, 𝐶₁ ≠ 𝐴, maka ∠𝐵𝐴𝐶 = ∠𝐵1𝐴𝐶1.

Bukti :

𝐵₁ pada 𝐴𝐵 dan 𝐵₁ ≠ 𝐴, maka berdasarkan Teorema 2.5.3 didapat 𝐴𝐵 = 𝐴𝐵1

.

𝐶₁ pada 𝐴𝐶 dan 𝐶₁ ≠ 𝐴, maka berdasarkan Teorema 2.5.3 didapat 𝐴𝐶 = 𝐴𝐶1 . A B C 𝐵1 𝐶₁

(47)

Berdasarkan Definisi 2.5.3, sudut adalah gabungan dari dua sinar yang memiliki titik pangkal yang sama, tetapi dua sinar tersebut tidak pada garis yang sama. Dapat ditulis

∠𝐵𝐴𝐶 = {𝐴𝐵 ∪ 𝐴𝐶 | 𝐴𝐵 ∩ 𝐴𝐶 = A} = {𝐴𝐵 ∪ 𝐴𝐶1 | 𝐴𝐵1 ∩ 𝐴𝐶1 = A} 1

=∠𝐵1𝐴𝐶1 □

Teorema 2.5.5 (Moise, 1990: 66)

Jika 𝐴𝐵̅̅̅̅ = 𝐶𝐷̅̅̅̅, maka titik A, B sama dengan titik C, D. Bukti :

Andaikan A, B tidak sama dengan titik C, D. Ambil a dan b sebagai koordinat titik A dan B, sehingga a < b. Ambil c dan d sebagai koordinat titik C dan D, sehingga c < d. Andaikan A, B, C dan D terletak pada garis

l.

Berikut akan diberikan kemungkinan letak a, b, c, dan d.

(1) a < b < c < d (2) a < c < b < d (3) a < c < d < b (4) c < a < d < b

(48)

(5) c < d < a < b

Gambar berikut merepresentasikan kemungkinan-kemungkinan di atas.

Dari kemungkinan (1), (2), (3), (4), dan (5) terlihat bahwa anggota himpunan segmen 𝐴𝐵̅̅̅̅ dan 𝐶𝐷̅̅̅̅ tidak sama. Sebagai contoh pada kondisi (3) a < c < d < b. Berdasarkan Teorema 2.4.4 ada titik X dengan koordinat x sehingga A-X-C. Karena a < c maka a < x < c.

Dari Definisi 2.5.1 segmen 𝐴𝐵̅̅̅̅ adalah himpunan titik A dan B bersama dengan semua titik di antara titik A dan B. Titik X berada di antara A dan B karena a < x < b, sehingga X ∈ 𝐴𝐵̅̅̅̅. Titik X ∉ 𝐶𝐷̅̅̅̅ karena x < c < d, yang berarti X tidak di antara C dan D. Karena ada titik X sehingga X ∈ 𝐴𝐵̅̅̅̅ dan X ∉ 𝐶𝐷̅̅̅̅, maka 𝐴𝐵̅̅̅̅ ≠ 𝐶𝐷̅̅̅̅. Hal ini kontradiksi dengan pernyataan 𝐴𝐵̅̅̅̅ = 𝐶𝐷̅̅̅̅, sehingga A, B sama dengan titik C, D.

b a c d a c b d (1) (2) 𝑙 𝑙 b a c d c a d b (3) (4) 𝑙 𝑙 b a c d (5) 𝑙

(49)

Untuk kasus A, B pada garis l dan C, D pada garis k, dengan l ≠ k. Ada tiga kemungkinan posisi segmen 𝐴𝐵̅̅̅̅ terhadap segmen 𝐶𝐷̅̅̅̅ yang akan dipaparkan sebagai berikut :

(1) l dan k sejajar, sehingga segmen 𝐴𝐵̅̅̅̅ sejajar dengan segmen 𝐶𝐷̅̅̅̅. (2) L dan k berpotongan, segmen 𝐴𝐵̅̅̅̅ tidak memotong segmen 𝐶𝐷̅̅̅̅. (3) L dan k berpotongan, segmen 𝐴𝐵̅̅̅̅ memotong segmen 𝐶𝐷̅̅̅̅.

Untuk kasus (1) dan (2), A, B tidak kolinear dengan C, D sehingga setiap titik di antara A dan B tidak di antara C dan D. Jadi 𝐴𝐵̅̅̅̅ ≠ 𝐶𝐷̅̅̅̅. Untuk kasus (3) 𝐴𝐵̅̅̅̅ dan 𝐶𝐷̅̅̅̅ berpotongan disuatu titik. Andaikan titik potong tersebut adalah titik X. Maka A-X-B dan C-X-D. Berdasarkan Teorema 2.4.4 ada titik Y sehingga Y-X. Telah didapat Y-X dan

A-A B C D (2) A B C D (1) A _B C _D (3)

(50)

X-B, berdasarkan Teorema 2.4.6, maka didapat A-Y-B. Titik Y di antara A dan B, tetapi titik Y tidak di antara C dan D karena C, D, dan Y tidak kolinear. Ada titik Y sehingga Y ∈ 𝐴𝐵̅̅̅̅ dan Y ∉ 𝐶𝐷̅̅̅̅, maka 𝐴𝐵̅̅̅̅ ≠ 𝐶𝐷̅̅̅̅. Telah ditunjukan bahwa untuk kasus (1), (2), dan (3) didapat 𝐴𝐵̅̅̅̅ ≠ 𝐶𝐷̅̅̅̅. Hal ini kontradiksi dengan pernyataan 𝐴𝐵̅̅̅̅ = 𝐶𝐷̅̅̅̅, sehingga A, B tidak sama dengan C, D. □

2.6 Kekonvekan dan Pemisahan

Definisi 2.6.1 (Moise, 1990: 72)

Suatu himpunan A dikatakan konvek jika untuk setiap dua titik P, Q ∈ A, setiap segmen 𝑃𝑄̅̅̅̅ berada di dalam A. Sebagai contoh diberikan tiga bangun yang konvek.

Himpunan A, B, dan C adalah daerah bidang. Sebagai contoh, A adalah gabungan segitiga dan himpunan semua titik yang ada di dalam

P Q A P Q C P Q B

(51)

segitiga. Pada Gambar 2.6.1 terlihat bahwa setiap segmen 𝑃𝑄̅̅̅̅ selalu berada di dalam A, B, dan C.

Selanjutnya akan diberikan contoh bangun yang tidak konvek.

Himpunan D, E, dan F adalah contoh bangun yang tidak konvek. Untuk menunjukan suatu bangun tidak konvek, misal bangun D, cukup ditunjukan bahwa ada dua titik P, Q ∈ D sehingga segmen 𝑃𝑄̅̅̅̅ tidak berada di dalam D.

Suatu himpunan konvek bisa saja tipis dan kecil. Sebagai contoh, setiap segmen 𝑃𝑄̅̅̅̅ adalah himpunan konvek. Himpunan yang beranggotakan satu titik juga konvek.

Suatu himpunan konvek juga bisa sangat besar. Sebagai contoh, himpunan ruang S adalah suatu himpunan konvek. Semua garis dan bidang juga konvek, karena tidak dapat ditemukan suatu segmen 𝑃𝑄̅̅̅̅ dimana P,Q anggota suatu garis atau bidang sehingga segmen 𝑃𝑄̅̅̅̅ tidak di dalam himpunan suatu garis atau bidang tersebut.

D P Q P Q F P Q E

(52)

Definisi 2.6.2

Diberikan sembarang garis l pada bidang E, himpunan bagian dari E yang tidak pada l membentuk dua himpunan yang disebut bidang setengah dan garis l disebut batas dari bidang setengah.

Sebagai contoh pada Gambar 2.6.3 𝐻1 adalah bagian dari bidang

pada sebelah kiri atas garis l dan 𝐻₂ adalah bagian dari bidang pada sebelah kanan bawah garis l. Himpunan 𝐻₁ dan 𝐻₂ disebut bidang setengah. Seperti telah dijelaskan sebelumnya, dengan menunjukan beberapa contoh segmen 𝑃𝑄̅̅̅̅, 𝐻₁ dan 𝐻₂ merupakan himpunan konvek.

Gambar 2.6.3 Pemisahan Bidang

P Q P Q l 𝐻1 𝐻₂ P Q

(53)

Postulat Pemisahan Bidang atau Plane Separation Axiom (PSA)

(Moise, 1990: 74)

Diberikan suatu garis dan bidang yang memuat garis tersebut. Himpunan semua titik pada bidang yang tidak pada garis adalah gabungan dua himpunan berbeda sehingga :

(1) Kedua himpunan tersebut konvek

(2) Jika titik P pada salah satu himpunan dan titik Q pada himpunan yang lain, maka segmen 𝑃𝑄̅̅̅̅ memotong garis.

Teorema 2.6.1 (Moise, 1990: 74)

Diberikan ∆ABC dan garis l. Jika l memuat titik E, dengan A-E-C, maka l memotong 𝐴𝐵̅̅̅̅ atau 𝐵𝐶̅̅̅̅.

A C

B

E

l

(54)

Bukti :

Andaikan l tidak memotong 𝐴𝐵̅̅̅̅ atau 𝐵𝐶̅̅̅̅. Maka A dan B pada pihak yang sama terhadap l dan B dan C pada pihak yang sama terhadap l. Oleh karena itu A dan C pada pihak yang sama terhadap l. Ini tidak mungkin karena A-E-C. □

Teorema 2.6.2 (Moise, 1990: 75)

Jika A dan B adalah himpunan konvek, maka 𝐴 ∩ 𝐵 juga konvek. Bukti :

Teorema ini akan dibuktikan dengan kontradiksi. Andaikan 𝐴 ∩ 𝐵 tidak konvek. Ambil titik-titik 𝑃, 𝑄 ∈ 𝐴 ∩ 𝐵, maka 𝑃, 𝑄 ∈ 𝐴 dan 𝑃, 𝑄 ∈ 𝐵. 𝑃𝑄̅̅̅̅ ∈ 𝐴 dan 𝑃𝑄̅̅̅̅ ∈ 𝐵 karena A dan B konvek dan ada titik R dimana P-R-Q sehingga 𝑅 ∉ 𝐴 ∩ 𝐵. Ini tidak mungkin karena A dan B konvek. Kontradiksi. □

Definisi 2.6.3 (Moise, 1990: 76)

Andaikan E suatu bidang. Jika

(55)

seperti pada postulat pemisahan bidang, maka 𝐻1 dan 𝐻2 disebut pihak

yang berlawanan terhadap l.

Teorema 2.6.3 (Moise, 1990: 76)

Jika A dan B pada pihak yang berlawanan terhadap garis l dan B dan C pada pihak yang berlawanan terhadap garis l, maka A dan C pada pihak yang sama terhadap l.

Bukti :

Ambil suatu bidang E dan garis l pada E. l membagi E kedalam dua bidang setengah 𝐻₁ dan 𝐻₂. Andaikan A pada 𝐻₁, maka B pada 𝐻₂ karena A dan B pada pihak yang berlawanan terhadap l. B pada 𝐻₂, maka C pada 𝐻₁ karena B dan C pada pihak yang berlawanan terhadap l. Didapat A dan C pada 𝐻₁, sehingga A dan C berada pada pihak yang sama terhadap l. □

𝐻₁ 𝐻₂ A B C l

(56)

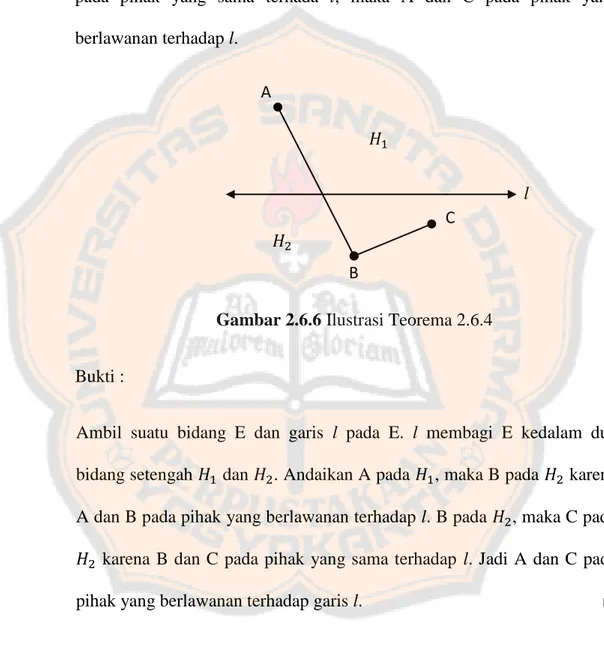
Teorema 2.6.4 (Moise, 1990: 76)

Jika A dan B pada pihak yang berlawanan terhadap garis l dan B dan C pada pihak yang sama terhada l, maka A dan C pada pihak yang berlawanan terhadap l.

Bukti :

Ambil suatu bidang E dan garis l pada E. l membagi E kedalam dua bidang setengah 𝐻₁ dan 𝐻₂. Andaikan A pada 𝐻₁, maka B pada 𝐻₂ karena A dan B pada pihak yang berlawanan terhadap l. B pada 𝐻₂, maka C pada 𝐻2 karena B dan C pada pihak yang sama terhadap l. Jadi A dan C pada

pihak yang berlawanan terhadap garis l. □

Definisi 2.6.4 (Moise, 1990: 76)

Jika A-B-C, maka sinar 𝐵𝐴 dan 𝐵𝐶 disebut sinar yang berlawanan.

𝐻₁ 𝐻₂ A B C l

(57)

Teorema 2.6.5 (Moise, 1990: 76)

Diberikan sebuah garis dan sinar yang memiliki titik pangkal pada garis yang diberikan, tetapi tidak berhimpit dengan garis tersebut. Kemudian semua titik pada sinar, kecuali titik pangkal, berada pada pihak yang sama terhadap garis tersebut.

Bukti :

Diberikan garis l dan sinar 𝐴𝐵 dengan 𝐴 ∈ 𝑙. Akan dibuktikan 𝐴𝐵 − 𝐴 berada pada pihak yang sama terhadap garis tersebut.

Andaikan 𝐴𝐵 memuat titik C sehingga B dan C berada pada pihak yang berlawanan terhadap l. Maka 𝐵𝐶̅̅̅̅ memotong l disuatu titik, dan titik ini harus A, karena 𝐵𝐶̅̅̅̅ terletak pada 𝐴𝐵 , dan 𝐴𝐵 memotong l hanya di A.

A B C

Gambar 2.6.7 Sinar Yang Berlawanan

A

B

l

(58)

Oleh karena itu C-A-B. Tetapi ini tidak mungkin. Dengan Definisi 2.5.2, sinar 𝐴𝐵 adalah himpunan titik C dari garis 𝐴𝐵⃡ sehingga A tidak diantara B dan C. Oleh sebab itu semua titik pada sinar, selain A, berada pada pihak yang sama terhadap l. □

Teorema 2.6.6 (Moise, 1990: 77)

Diberikan garis l dan A titik pada l, dan B titik yang tidak pada l. Maka semua titik dari 𝐴𝐵̅̅̅̅ − 𝐴 berada pada pihak yang sama terhadap l.

Bukti :

Berdasarkan Teorema 2.6.5 𝐴𝐵 − 𝐴 berada pada pihak yang sama terhadap l. Karena 𝐴𝐵̅̅̅̅ − 𝐴 berada pada 𝐴𝐵 − 𝐴, maka 𝐴𝐵̅̅̅̅ − 𝐴 juga berada pada pihak yang sama terhadap l. □

Definisi 2.6.5 (Moise, 1990: 77)

Diberikan ∠𝐵𝐴𝐶. Interior ∠𝐵𝐴𝐶 adalah irisan pihak 𝐴𝐶⃡ yang memuat B dan pihak 𝐴𝐵⃡ yang memuat C. Maka suatu titik D interior ∠𝐵𝐴𝐶 jika D dan B berada pada pihak yang sama dari 𝐴𝐶⃡ dan jika D dan C berada pada pihak yang sama dari 𝐴𝐵⃡ . Jadi, interior suatu sudut adalah irisan dua bidang setengah. Eksterior ∠𝐵𝐴𝐶 adalah himpunan semua titik yang tidak pada ∠𝐵𝐴𝐶 dan interior ∠𝐵𝐴𝐶.

(59)

Teorema 2.6.7 (Moise, 1990: 78)

Setiap sisi segitiga, kecuali titik sudutnya berada di dalam interior sudut di hadapannya.

Diberikan ∆𝐴𝐵𝐶, ∠𝐴 = ∠𝐵𝐴𝐶 merupakan sudut dihadapan sisi 𝐵𝐶̅̅̅̅.

Bukti :

(1) Pertama gunakan Teorema 2.6.6 pada garis 𝐴𝐶⃡ dan segmen 𝐵𝐶̅̅̅̅. Didapat 𝐵𝐶̅̅̅̅ − 𝐶 berada pada pihak yang memuat B.

(2) Selanjutnya gunakan Teorema 2.6.6 pada garis 𝐴𝐵⃡ dan segmen 𝐵𝐶̅̅̅̅. Didapat 𝐵𝐶̅̅̅̅ − 𝐵 berada pada pihak 𝐴𝐵⃡ yang memuat C.

(3) Dari (1) dan (2), 𝐵𝐶̅̅̅̅ − {𝐵, 𝐶} berada pada interior ∠𝐵𝐴𝐶. □

Gambar 2.6.9 Interior dan Eksterior Sudut

Interior Eksterior Eksterior A B C D A B C

(60)

Teorema 2.6.8 (Moise, 1990: 78)

Jika F berada di dalam interior ∠𝐵𝐴𝐶, maka 𝐴𝐹 − 𝐴 berada di dalam interior ∠𝐵𝐴𝐶.

Bukti :

(1) Dari Definisi 2.6.5, F dan B pada pihak yang sama terhadap 𝐴𝐶⃡ . Dengan Teorema 2.6.5, 𝐴𝐹 − 𝐴 berada pada pihak yang sama terhadap 𝐴𝐶

⃡ yang memuat F. Oleh karena itu 𝐴𝐹 − 𝐴 terletak pada pihak yang memuat B.

(2) Dari Definisi 2.6.5, F dan C pada pihak yang sama terhadap 𝐴𝐵⃡ . Dengan Teorema 2.6.5, 𝐴𝐹 − 𝐴 berada pada pihak yang sama terhadap 𝐴𝐵

⃡ yang memuat F. Oleh karena itu 𝐴𝐹 − 𝐴 terletak pada pihak yang memuat C.

Dari (1) dan (2) memenuhi bahwa 𝐴𝐹 − 𝐴 berada di dalam interior ∠𝐵𝐴𝐶.

□

A

B

C F

(61)

Teorema 2.6.9 (Moise, 1990: 79)

Diberikan ∆ABC dan titik F,D,G sehingga B-F-C, A-C-D, dan A-F-G. Maka G di dalam interior ∠𝐵𝐶𝐷.

Bukti :

(1) Karena A-F-G, G berada pada 𝐴𝐹⃡ , dan A tidak di antara G dan F. Oleh karena itu G pada 𝐴𝐹 . Karena G ≠ A, G pada 𝐴𝐹 − 𝐴.

(2) Dengan Teorema 2.6.7, titik F di dalam interior ∠𝐵𝐴𝐶. Dari Teorema 2.6.8, 𝐴𝐹 − 𝐴 berada pada interior ∠𝐵𝐴𝐶. Oleh karena itu G dan B pada pihak yang sama terhadap 𝐴𝐶⃡ (=𝐶𝐷⃡ ).

(3) A dan G pada pihak yang berlawanan terhadap 𝐵𝐶⃡ , dan A dan D pada pihak yang berlawanan terhadap 𝐵𝐶⃡ . Oleh karena itu G dan D pada pihak yang sama terhadap 𝐵𝐶⃡ .

Dari (2) dan (3), G di dalam interior ∠𝐵𝐶𝐷. □

A _C

B

D F _G

(62)

Selanjutnya akan didefinisikan interior suatu segitiga.

Definisi 2.6.6 (Moise, 1990: 80)

Interior ∆ABC didefinisikan sebagai irisan tiga himpunan berikut : (1) Pihak 𝐴𝐵⃡ yang memuat C

(2) Pihak 𝐴𝐶⃡ yang memuat B (3) Pihak 𝐵𝐶⃡ yang memuat A

Teorema 2.6.10 (Moise, 1990: 80)

Interior segitiga adalah himpunan konvek.

Bukti :

Diberikan sembarang ∆ABC. 𝐻_𝐴𝐵⃡ sebagai bidang setengah yang memuat

C, 𝐻_𝐴𝐶⃡ sebagai bidang setengah yang memuat B dan 𝐻𝐵𝐶⃡ sebagai bidang

setengah yang memuat A. Dari Definisi 2.6.6, interior ∆ABC adalah A

B

C

(63)

𝐻_𝐴𝐵⃡ ∩ 𝐻𝐴𝐶⃡ ∩ 𝐻𝐵𝐶⃡ . 𝐻𝐴𝐵⃡ , 𝐻𝐴𝐶⃡ , dan 𝐻𝐵𝐶⃡ konvek. Sehingga 𝐻𝐴𝐵⃡ ∩ 𝐻𝐴𝐶⃡ ∩

𝐻_𝐵𝐶⃡ juga konvek (lihat Teorema 2.6.2). □

2.7 Kekontinuan

Teorema 2.7.1 (Moise, 1990: 81)

Diberikan garis l, titik-titik A dan B pada l, A ≠ B, dan F dan G titik pada pihak yang berlawanan terhadap l. Maka 𝐴𝐹̅̅̅̅ tidak memotong 𝐵𝐺 .

Bukti :

(1) Dari Teorema 2.6.6, 𝐴𝐹̅̅̅̅ − 𝐴 berada pada pihak yang memuat F. (2) Dari Teorema 2.6.5, 𝐵𝐺 − 𝐵 berada pada pihak yang memuat G. Dari (1) dan (2) didapat bahwa 𝐵𝐺 − 𝐺 tidak memotong 𝐴𝐹̅̅̅̅ − 𝐴. Oleh karena itu 𝐵𝐺 dan 𝐴𝐹̅̅̅̅ tidak berpotongan. □

A

B F

(64)

Teorema 2.7.2 (Moise, 1990: 81)

Dalam ∆ABC diberikan F titik diantara A dan C, dan D suatu titik sehingga D dan B pada pihak yang sama terhadap 𝐹𝐶⃡ . Maka 𝐹𝐷 memotong 𝐴𝐵̅̅̅̅ atau 𝐵𝐶̅̅̅̅.

Bukti :

(1) Diberikan G suatu titik sehingga G-F-D. Maka G dan D berada pada pihak yang berlawanan terhadap 𝐴𝐶⃡ , jadi G dan B pada pihak yang berlawanan terhadap 𝐴𝐶⃡ . Terlihat

𝐹𝐷

⃡ = 𝐹𝐷 ∪ 𝐹𝐺

(2) Gunakan Teorema 2.7.1 pada garis 𝐴𝐶⃡ , segmen 𝐴𝐵̅̅̅̅, dan sinar 𝐹𝐺 . Ini berlaku bahwa 𝐹𝐺 tidak memotong 𝐴𝐵̅̅̅̅.

(3) Dengan cara yang sama, didapat 𝐹𝐺 tidak memotong 𝐵𝐶̅̅̅̅.

D F G A _C B E ?

(65)

(4) Dengan Teorema Pasch didapat bahwa 𝐹𝐷⃡ memotong 𝐴𝐵̅̅̅̅ atau 𝐵𝐶̅̅̅̅. Telah ditunjukan bahwa 𝐹𝐺 tidak memotong 𝐴𝐵̅̅̅̅ atau 𝐵𝐶̅̅̅̅, maka pastilah 𝐹𝐷 memotong 𝐴𝐵̅̅̅̅ atau 𝐵𝐶̅̅̅̅. □

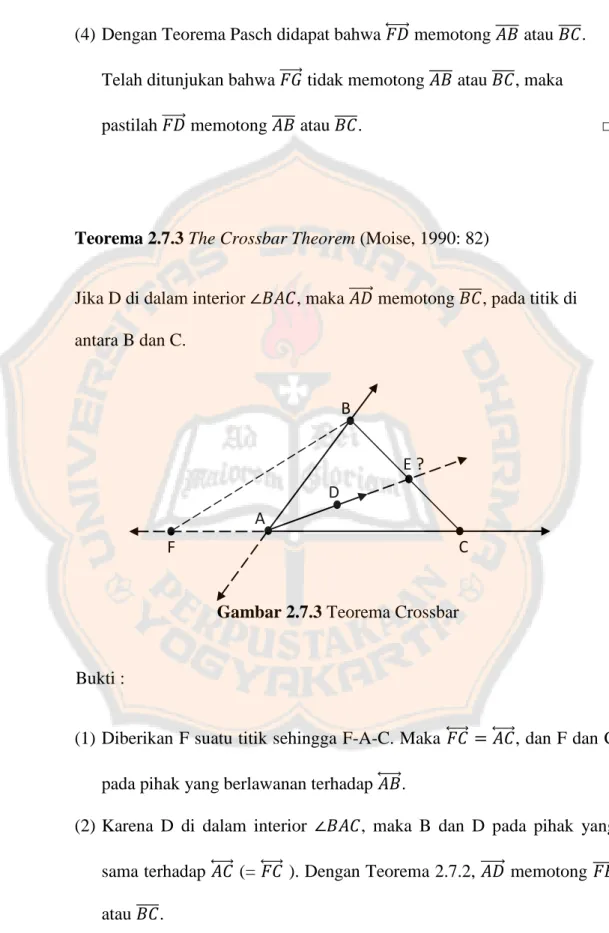
Teorema 2.7.3 The Crossbar Theorem (Moise, 1990: 82)

Jika D di dalam interior ∠𝐵𝐴𝐶, maka 𝐴𝐷 memotong 𝐵𝐶̅̅̅̅, pada titik di antara B dan C.

Bukti :

(1) Diberikan F suatu titik sehingga F-A-C. Maka 𝐹𝐶⃡ = 𝐴𝐶⃡ , dan F dan C pada pihak yang berlawanan terhadap 𝐴𝐵⃡ .

(2) Karena D di dalam interior ∠𝐵𝐴𝐶, maka B dan D pada pihak yang sama terhadap 𝐴𝐶⃡ (= 𝐹𝐶⃡ ). Dengan Teorema 2.7.2, 𝐴𝐷 memotong 𝐹𝐵̅̅̅̅ atau 𝐵𝐶̅̅̅̅.

Gambar 2.7.3 Teorema Crossbar

D F E ? A C B

(66)

(3) Karena F dan C pada pihak yang berlawanan terhadap 𝐴𝐵⃡ , dan C dan D pada pihak yang sama terhadap 𝐴𝐵⃡ , maka F dan D pada pihak yang berlawanan terhadap 𝐴𝐵⃡ .

(4) Gunakan Teorema 2.7.1 pada garis 𝐴𝐵⃡ , segmen 𝐹𝐵̅̅̅̅, dan sinar 𝐴𝐷 . Didapat 𝐴𝐷 tidak memotong 𝐹𝐵̅̅̅̅.

Dari (2) dan (4) memenuhi bahwa 𝐴𝐷 memotong 𝐵𝐶̅̅̅̅, di titik E yang berbeda dengan B. Jika E = C, maka A, D, dan C kolinear, dan ini tidak benar. Oleh karena itu B-E-C. □

2.8 Ukuran Sudut

Definisi 2.8.1 (Moise, 1990: 93)

Diberikan suatu fungsi 𝑚 ∶ 𝒜 → ℝ, dengan 𝒜 adalah himpunan semua sudut dan ℝ adalah himpunan bilangan real. Tulis 𝑚(∠𝐴𝐵𝐶) untuk menyimbolkan ukuran dari ∠𝐴𝐵𝐶. Agar lebih ringkas, selanjutnya 𝑚(∠𝐴𝐵𝐶) akan ditulis dengan 𝑚∠𝐴𝐵𝐶.

Gambar 2.8.1 Ukuran Sudut I

45𝑜

B

D A

(67)

Ukuran ∠𝐴𝐵𝐶 dan ∠𝐷𝐵𝐶 dapat ditulis 𝑚∠𝐴𝐵𝐶 = 90 dan 𝑚∠𝐷𝐵𝐶 = 45. Ukuran ∠𝐴𝐵𝐶 tidak ditulis 𝑚∠𝐴𝐵𝐶 = 90𝑜_{, karena nilai}

dari fungsi m adalah bilangan real. Pada sisi yang lain, penandaan sudut pada gambar menggunakan tanda derajat untuk mengindikasikan bahwa huruf atau angka dengan tanda derajat berarti ukuran suatu sudut.

Gambar 2.8.2 menunjukan bahwa

𝑚∠𝐴𝐵𝐶 = 45 dan

𝑚∠𝑃𝑄𝑅 = 𝑟.

Berikut akan diberikan beberapa postulat ukuran sudut. (Moise, 1990: 95)

M-1 m adalah fungsi 𝒜 → ℝ, dimana 𝒜 adalah himpunan semua sudut

dan ℝ adalah himpunan bilangan real.

M-2 Untuk setiap ∠𝐴, 𝑚∠𝐴 adalah antara 0 dan 180.

Gambar 2.8.2 Ukuran Sudut II

Q R P 𝑟𝑜 B A C 45𝑜

(68)

M-3 Postulat Pembentukan Sudut (The Angle Construction Postulate). Diberikan 𝐴𝐵 suatu sinar pada batas bidang setengah H. untuk setiap bilangan r diantara 0 dan 180, ada tepat satu sinar 𝐴𝑃 , dengan P pada H, sehingga 𝑚∠𝑃𝐴𝐵 = 𝑟.

M-4 Postulat Penjumlahan Sudut (The Angle Addition Postulate). Jika D di dalam interior ∠𝐵𝐴𝐶, maka

𝑚∠𝐵𝐴𝐶 = 𝑚∠𝐵𝐴𝐷 + 𝑚∠𝐷𝐴𝐶

Dua sudut membentuk suatu pasangan linear jika sudut-sudut tersebut terlihat seperti berikut :

Gambar 2.8.3 Pembentukan Sudut

𝑟𝑜

Q R

P 𝐻

Gambar 2.8.4 Pembentukan Sudut

D 𝑟𝑜 𝑠𝑜 (𝑟 + 𝑠)𝑜 A _B C

(69)

Jika 𝐴𝐵 dan 𝐴𝐶 sinar yang berlawanan, dan 𝐴𝐷 suatu sinar yang tidak pada 𝐴𝐵⃡ , maka ∠𝐷𝐴𝐵 dan ∠𝐷𝐴𝐶 membentuk pasangan linear.

Definisi 2.8.2 (Moise, 1990: 96)

Jika 𝑚∠𝐴𝐵𝐶 + 𝑚∠𝐷𝐸𝐹 = 180, maka kedua sudut tersebut dikatakan berpelurus. Definisi ini tidak tergantung pada letak sudut, tetapi hanya tergantung pada ukuran sudutnya. Artinya kedua sudut yang dimaksud tidak harus bersisian.

M-5 Postulat Pelurus (The Supplement Postulate). Jika dua sudut membentuk pasangan linear, maka kedua sudut tersebut berpelurus.

Gambar 2.8.5 Dua Sudut Membentuk

Pasangan Linear D A B C 𝑠0 𝑟0

Gambar 2.8.6 Dua Sudut Berpelurus

A B C

(70)

2.9 Postulat Luas

Definisi 2.9.1 (Moise, 1990: 184)

Suatu daerah triangular adalah bangun yang terbentuk dari gabungan segitiga beserta interiornya, seperti gambar berikut :

Sisi segitiga disebut batas daerah, dan titik sudut segitiga disebut titik sudut daerah.

Suatu daerah segibanyak adalah bangun seperti salah satu di bawah ini :

Gambar 2.9.1 Daerah Triangular

(71)

Definisi 2.9.2 (Moise, 1990: 184)

Suatu daerah segibanyak adalah bangun bidang yang dapat diekspresikan sebagai gabungan dari daerah triangular yang terbatas jumlahnya, sehingga jika dua daerah triangular beririsan, irisannya adalah suatu batas atau suatu titik sudut dari dua daerah triangular tersebut.

Gambar 2.9.2 menandakan bahwa daerah segibanyak dapat dibagi ke dalam daerah-daerah triangular. Tentunya, tidak ada kekhasan bagaimana cara suatu daerah segibanyak dapat dibagi ke dalam daerah-daerah triangular. Pada faktanya jika pembagian ini dilakukan untuk suatu bentuk tertentu, ini dapat dilakukan dalam banyak sekali cara (tak hingga). Sebagai contoh, suatu jajargenjang dengan interiornya dapat dibagi dalam paling tidak beberapa cara ini.

Definisi 2.9.3 (Moise, 1990: 185)

Diberikan suatu fungsi luas 𝛼, dimana untuk setiap daerah segibanyak berkorespondensi dengan suatu bilangan positif yang disebut luas.

(72)

Diberikan ℛ sebagai himpunan semua daerah segibanyak, sehingga 𝛼: ℛ ⟶ ℝ.

Selanjutnya akan diberikan beberapa postulat luas.

A-1 𝛼 adalah fungsi ℛ ⟶ ℝ, dimana ℛ adalah himpunan semua daerah segibanyak dan ℝ adalah himpunan semua bilangan real. Dapat ditulis 𝛼: ℛ ⟶ ℝ; ℛ = { 𝑅|𝑅 adalah daerah segibanyak}; ℝ = himpunan semua bilangan real.

A-2 Untuk setiap daerah segibanyak 𝑅, 𝛼(𝑅) > 0. Dapat ditulis 𝛼(𝑅) > 0, ∀ 𝑅 ∈ ℛ.

A-3 The Congruence Postulate. Jika dua daerah triangular kongruen, maka keduanya memiliki luas yang sama.

Diberikan 𝑇₁, 𝑇₂ adalah daerah triangular, 𝛼(𝑇₁) = 𝛼(𝑇₂), 𝑇₁ ≅ 𝑇2.

A-4 The Additivity Postulate. Jika dua daerah segibanyak berpotongan

hanya pada batas dan titik sudutnya, maka luas gabungan dua daerah segibanyak tersebut adalah gabungan dari luasnya.

Diberikan 𝑅₁, 𝑅₂ adalah daerah segibanyak. Jika 𝑅₁∩ 𝑅₂ = ℓ, dengan ℓ = himpunan garis-garis, maka 𝛼(𝑅₁∪ 𝑅₂) = 𝛼(𝑅₁) + 𝛼(𝑅₂).

(73)

Definisi 2.9.4 (Moise, 1990: 204)

Diberikan suatu daerah segibanyak R, diekspresikan sebagai gabungan dari daerah triangular yang terbatas, beririsan hanya pada batas dan titik sudutnya. Himpunan K yang anggota-anggotanya daerah triangular disebut komplek, dan disebut triangulasi dari R.

Pada Gambar 2.9.5, komplek K adalah himpunan {𝑇₁, 𝑇₂, 𝑇₃, 𝑇₄, 𝑇₅}. 𝑅₁ 𝑅₂

Gambar 2.9.4 Postulat Penjumlahan

𝑇₁ 𝑇₂ 𝑇3

𝑇₄

𝑇5

(74)

R dan K adalah objek yang berbeda. R adalah himpunan titik-titik yang banyaknya tak hingga, sedangkan K adalah himpunan daerah triangular yang terbatas.

2.10 Sudut Luar Segitiga dan Konsekuensinya

Teorema 2.10.1 (Prenowitz & Jordan, 1965: 22)

Sebuah sudut luar segitiga lebih besar dari kedua sudut dalam yang tidak bersisian dengan sudut tersebut.

Bukti :

Diberikan sembarang ∆ABC, ambil D pada 𝐵𝐶 , sehingga B − C − D. Pertama-tama akan ditunjukan bahwa ∠ACD lebih besar dari ∠A.

Ambil E sebagai titik tengah AC̅̅̅̅ dan ambil F pada 𝐵𝐸 sehingga 𝐵𝐸 = 𝐸𝐹. Sebab 𝐴𝐸 = 𝐸𝐶, 𝐵𝐸 = 𝐸𝐹, dan 𝑚∠𝐴𝐸𝐵 = 𝑚∠𝐶𝐸𝐹, maka ∆𝐴𝐸𝐵 ≅

Gambar 2.10.1 Ilustrasi I Teorema 2.10.1

E

A F

(75)

∆𝐶𝐸𝐹 (Sisi,Sudut,Sisi), akibatnya 𝑚∠𝐵𝐴𝐸 = 𝑚∠𝐹𝐶𝐸. Karena 𝑚∠𝐴𝐶𝐷 > 𝑚∠𝐹𝐶𝐸, maka 𝑚∠𝐴𝐶𝐷 > 𝑚∠𝐵𝐴𝐶 = 𝑚∠𝐴.

Selanjutnya ambil H pada 𝐴𝐶 , sehingga A-C-H. Akan ditunjukan 𝑚∠𝐵𝐶𝐻 > 𝑚∠𝐵.

Cara yang digunakan sama dengan pembuktian diatas. Ambil M sebagai titik tengah 𝐵𝐶̅̅̅̅, kemudian ambil N pada 𝐴𝑀 sehingga 𝐴𝑀 = 𝑀𝑁. Sebab 𝐵𝑀 = 𝐶𝑀, 𝐴𝑀 = 𝑁𝑀, dan 𝑚∠𝐴𝑀𝐵 = 𝑚∠𝑁𝑀𝐶, maka ∆𝐴𝐵𝑀 ≅ ∆𝑁𝐶𝑀. Sehingga 𝑚∠𝑁𝐶𝑀 = 𝑚∠𝐴𝐵𝑀. Karena 𝑚∠𝐵𝐶𝐻 > 𝑚∠𝑁𝐶𝑀, maka 𝑚∠𝐵𝐶𝐻 > 𝑚∠𝐴𝐵𝑀 = 𝑚∠𝐵. □

Teorema 2.10.2 (Prenowitz & Jordan, 1965: 24)

Jumlah ukuran dua sudut segitiga kurang dari 180. N

Gambar 2.10.2 Ilustrasi II Teorema 2.10.1

B

A

C

H M