BAB 7
MOMEN, KEMIRINGAN DAN KERUNCINGAN
A.
MomenMisalkan diberikan variable 𝑥 dengan harga- harga : 𝑥1 ,𝑥2 ,….,𝑥𝑛. Jika A = sebuah bilangan tetap dan r = 0, 1, 2…, n maka momen ke-r sekitar A, disingkat 𝑚𝑟′, didefinisikan oleh hubungan :
𝑚𝑟′ = ∑(𝑥𝑖− 𝐴)𝑟 𝑛 … … … . (1) Menurut Gasperz (1989:87) 𝑚𝑟∗= ∑𝑛 (𝑋𝑗− 𝐴)𝑟 𝑗=1 𝑛 = ∑𝑑𝑟 𝑛 Dimana d = X - A
Menurut Amudi Pasaribu (1975:123),
𝑚ℎ=(1𝑛) ∑(𝑥𝑖− 𝑎)ℎ 𝑘
𝑖=𝑗
Untuk A = 0 didapat momen ke-r sekitar nol atau disingkat momen ke-r (momen sekitar titik asal):
𝑚𝑜𝑚𝑒𝑛 𝑘𝑒 − 𝑟 = ∑ 𝑥𝑖𝑟 𝑛 … … … . . (2) Menurut Gasperz (1989:87) 𝑋𝑟=𝑋1 𝑟 + 𝑋 2 𝑟 + ⋯ + 𝑋 𝑛 𝑟 𝑛 = ∑𝑛𝑗=1𝑋𝑗𝑟 𝑛 = ∑𝑋𝑟 ௰ Menurut Amudi Pasaribu (1975:122),
𝑚ℎ=(1𝑛) ∑𝑥𝑖ℎ 𝑘 𝑖=𝑗
Dari rumus (2) maka untuk r =1 didapat rata-rata 𝑥. Jika A = 𝑥 kita peroleh momen ke-r sekitar rata-rata, biasa disingkat dengan 𝑚𝑟. Jadi didapat :
𝑚𝑟= ∑(𝑥𝑖− 𝑥)𝑟 𝑛 … … … . (3) Menurut Gasperz (1989:87) 𝑚𝑟= ∑𝑛 (𝑋𝑗− 𝑋)𝑟 𝑗=1 𝑛 = ∑(𝑋 − 𝑋)𝑟 𝑛
Menurut Amudi Pasaribu (1975:123),
𝑚ℎ=(1𝑛) ∑(𝑥𝑖− 𝑥)ℎ 𝑘
𝑖=𝑗 Untuk r =2, rumus (3) memberikan varians 𝑠2.
Untuk membedakan apakah momen itu untuk sampel atau populasi maka dipakai simbol: 𝑚𝑟 dan 𝑚𝑟′ untuk momen sampel dan µ𝑟 𝑑𝑎𝑛 µ𝑟′untuk momen populasi .
jika 𝑚𝑟 𝑑𝑎𝑛 𝑚𝑟′ adalah statistik sedangkan µ𝑟 𝑑𝑎𝑛 µ𝑟′adalah parameter.
Jika data telah disusun dalam dalam bentuk distribusi frekuensi, maka rumus-rumus diatas berturut-turut berbentuk :
𝑚𝑟′= ∑𝑓𝑖(𝑥𝑖− 𝐴)𝑟 𝑛 … … … . (4) Menurut Gasperz (1989:91), 𝑚𝑟∗ = ∑𝑛𝑗=1𝑓𝑗(𝑋𝑗− 𝐴)𝑟 𝑛 = ∑𝑓 (𝑋 − 𝐴)𝑟 𝑛 Menurut Amudi Pasaribu (1975:123),
𝑚ℎ=(1𝑛) ∑(𝑥𝑖− 𝑎)ℎ𝑓𝑖 𝑘 𝑖=𝑗 𝑚𝑜𝑚𝑒𝑛 𝑘𝑒 − 𝑟 =∑ 𝑓𝑖𝑥㐳𝑟 𝑛 … … … . . (5) Menurut Gasperz (1989:91) 𝑋𝑟=𝑓1𝑋1 𝑟 + 𝑓 2𝑋2𝑟+ ⋯ + 𝑓𝑘𝑋𝑘 𝑟 𝑛 = ∑ 𝑓𝑗𝑋 𝑗 𝑟 𝑛 𝑗=1 𝑛 = ∑𝑓𝑋𝑟 𝑛 Menurut Amudi Pasaribu (1975:122),
𝑚ℎ=(1𝑛) ∑𝑥𝑖ℎ𝑓𝑖 𝑘 𝑖=𝑗 𝑚𝑟 = ∑𝑓𝑖(𝑥𝑖− 𝑥)𝑟 𝑛 … … … . (6) 𝑑𝑒𝑛𝑔𝑎𝑛 𝑛 = ∑ 𝑓𝑖 ,𝑥𝑖= 𝑡𝑎𝑛𝑑𝑎 𝑘𝑒𝑙𝑎𝑠 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙 𝑑𝑎𝑛 𝑓𝑖= 𝑓𝑟𝑒𝑘𝑢𝑒𝑛𝑠𝑖 𝑦𝑎𝑛𝑔 𝑠𝑒𝑠𝑢𝑎𝑖 𝑑𝑒𝑛𝑔𝑎𝑛 𝑥𝑖 Menurut Gasperz (1989:91) 𝑚𝑟 = ∑ 𝑓〱(𝑋𝑗− 𝑋) 𝑟 𝑛 𝑗=1 𝑛 = ∑𝑓(𝑋 − 𝑋)𝑟 𝑛
Menurut Pasaribu (1975:123),
𝑚ℎ=(1𝑛) ∑(𝑥𝑖− 𝑥)ℎ 𝑘
𝑖=𝑗
𝑓𝑖 Dengan menggunakan cara sandi, rumus empat menjadi :
𝑚𝑟′ = 𝑝𝑟
∑𝑓𝑖𝑐𝑖𝑟
𝑛 … … … . (7) Dengan p = panjang kelas interval, 𝑐𝑖 = variable sandi.
Menurut Gasperz (1989:91)
𝑚𝑟∗ = 𝑐𝑟
∑𝑘 𝑓𝑗𝑢𝑗𝑟 𝑗=1
𝑛
Dari 𝑚𝑟′ , harga-harga 𝑚𝑟 untuk beberapa r, dapat ditentukan berdasarkan hubungan : 𝑚2= 𝑚2′− (𝑚1′) 2 𝑚3= 𝑚3′− 3𝑚1′𝑚2′ + 2(𝑚1′) 3 𝑚4= 𝑚4′− 4𝑚1′𝑚3′ + 6(𝑚1′) 2 𝑚2′ + 3(𝑚 1 ′)4 Menurut Gasperz (1989:96) 𝑚1= 0 𝑚2= 𝑚2∗ − (𝑚1∗)2 𝑚3= 𝑚3∗ − 3𝑚1∗𝑚2∗+ 2(𝑚1∗)3 𝑚4= 𝑚4∗ − 4𝑚 1 ∗𝑚 2 ∗+ 6(𝑚 1 ∗)2𝑚 2 ∗− 3(𝑚 1 ∗)4
Contoh: Untuk menghitung empat buah momen sekitar rata-rata untuk data dalam daftar distribusi frekuensi, kita lakukan sebagai berikut.
DATA 𝒇𝒊 𝒄𝒊 𝒇𝒊𝒄𝒊 𝒇𝒊𝒄⍖𝟐 𝒇𝒊𝒄𝒊𝟑 𝒇𝒊𝒄𝒊𝟒 60 – 62 63 – 65 66 – 68 69 – 71 72 – 74 5 18 42 27 8 -2 -1 0 1 2 -10 -18 0 27 16 20 18 0 27 32 -40 -18 0 27 64 80 18 0 27 128 jumlah 100 0 15 97 33 253
Dengan menggunakan rumus (7) maka : 𝑚1′= 𝑝1 ∑𝑓𝑖𝑐𝑖1 𝑛 = 3 15 100= 0,45 𝑚2′ = 𝑝2 ∑𝑓𝑖𝑐𝑖2 𝑛 = 32 97 100= 8,73 𝑚3′ = 𝑝3 ∑𝑓𝑖𝑐𝑖3 𝑛 = 33 33 100= 8,91 𝑚4′= 𝑝4 ∑ 𝑓𝑖𝑐𝑖 4 𝑛 = 3 4 253 100= 204,93 Sehingga dengan menggunakan hubungan di atas :
𝑚2= 𝑚2′− (𝑚1′) 2 = 8,73 − (0,45)2= 8,53 𝑚3= 𝑚3′− 3𝑚1′𝑚2′ + 2(𝑚1′) 3 = 8,91 − 3(0,45)(8,73)+ 2(0,45)3= −2,69 𝑚4= 𝑚4′− 4𝑚1′𝑚3′ + 6(𝑚1′) 2 𝑚2′ + 3(𝑚 1 ′)4 = 204,93 − 4 (0,45)(8,93)+ 6(0,45)2(8,73)+ 3(0,45)4= 199,38 Dari hasil ini didapat varians 𝑠2= 𝑚
2 = 8,53
B.
Kemiringan (Kemencengan)Hasan (2009:125) menyatakan kemencengan atau kecondongan (skewness) adalah tingkat ketidaksimetrisan atau kejauhan simetri dari sebuah distribusi. Menurut Somantri (2006:147), ukuran kemiringan adalah suatu ukuran yang dapat digunakan untuk menentukan miring tidaknya suatu kurva distribusi. Menurut Gasperz (1989:98), ukuran kemenjuluran atau kemencengan (skewness) merupakan suatu ukuran yang menunjukkan sejauh mana pergeseran dari bentuk yang simetri untuk suatu sebaran atau distribusi. Sedangkan menurut Herrhyanto dan Hamid (2008 : 6.2), ukuran kemiringan adalah ukuran yang menyatakan sebuah model distribusi yang mempunyai kemiringan tertentu.
Jadi ukuran kemiringan adalah suatu ukuran yang dapat digunakan untuk menentukan miring tidaknya suatu kurva distribusi dibandingkan dengan bentuk yang simetri.
C.
Keruncingan atau KurtosisKeruncingan atau kurtosis adalah tingkat kepuncakan dari sebuah distribusi yang biasanya diambil secara relatif terhadap suatu distribusi normal. (Hasan, 2009:137). Menurut Gasperz (1989: 104), kurtosis adalah suatu ukuran tentang keruncingan dari sebuah sebaran, yang biasanya dibandingkan dengan sebaran normal. Menurut Somantri
(2006:151), kurtosis merupakan tingkat menggunungnya suatu distribusi, yang umumnya dibandingkan dengan distribusi normal”. Sedangkan menurut Herrhyanto dan Hamid (2008 : 6.12), kurtosis adalah derajat kepuncakan dari suatu distribusi, biasanya diambil relatif terhadap distribusi normal.
Jadi keruncingan adalah tingkat kepuncakan dari sebuah distribusi, yang biasanya dibandingkan dengan distribusi normal.
D.
Koefisien Momen KemiringanUntuk mengetahui bahwa konsentrasi distribusi menceng ke kanan atau menceng ke kiri, dapat digunakan metode-metode berikut :
1. Koefisien Kemencengan Pearson
Koefisien Kemencengan Pearson merupakan nilai selisih rata-rata dengan modus dibagi simpangan baku. (Hasan, 2009:126). Koefisien Kemencengan Pearson dirumuskan sebagai berikut:
𝑠𝑘 =𝑥 − 𝑀𝑜 𝑠 Keterangan :
sk = koefisien kemencengan Pearson
s = simpangan baku 𝑀𝑜 = modus
Apabila secara empiris didapatkan hubungan antar nilai pusat sebagai : 𝑥 − 𝑀𝑜 = 3(𝑥 − 𝑀𝑒)
Maka rumus kemencengan diatas dapat diubah menjadi: 𝑠𝑘 =3(𝑥 − 𝑀𝑒)
𝑠 2. Koefisien Kemencengan Bowley
Koefisien kemencengan Bowley berdasarkan pada hubungan kuartil-kuartil (Q1, Q2 dan Q3) dari sebuah distribusi. (Hasan, 2009:125). Begitu pula menurut Gasperz (1989:101) bahwa “Bowley (A.L Bowley) mendasarkan rumusnya pada nilai-nilai kuartil dari suatu sebaran (distribution)”.
Koefisien kemencengan Bowley dirumuskan : 𝑠𝑘𝐵=
(𝑄3− 𝑄2) − (𝑄2− 𝑄1) (𝑄3− 𝑄2) + (𝑄2− 𝑄1)
𝑎𝑡𝑎𝑢 𝑠𝑘𝐵=
𝑄3−2𝑄2+ 𝑄1 𝑄3−𝑄1
Keterangan : skB = koefisien kemencengan Bowley; Q = kuartil
3. Koefisien Kemencengan Persentil
Gasperz (1989:102) mengatakan “Ukuran Kelly merupakan suatu ukuran moderat antara ukuran Pearson yang didasarkan pada semua bagian data dan ukuran Bowley yang didasarkan pada 50% dari bagian data. Kelly mendasarkan pada sebaran antara persentil 90 (𝑃90) dan persentil 10 (𝑃10). Jadi Koefisien Kemencengan Persentil didasarkan atas hubungan antar persentil (P90, P50 dan P10) dari sebuah distribusi (Hasan, 2009:132).
Koefisien Kemencengan Persentil dirumuskan :
𝑠𝑘𝑃=(𝑃90− 𝑃50) − (𝑃50− 𝑃10) (𝑃90− 𝑃50) + (𝑃50− 𝑃10) 𝑎𝑡𝑎𝑢 𝑠𝑘𝑃=
𝑃90−2𝑃50+ 𝑃10 𝑃90−𝑃10
skP = koefisien kemecengan persentil , P = persentil 4. Koefisien Kemencengan Momen
Koefisien Kemencengan Momen didasarkan pada perbandingan momen ke-3 dengan pangkat tiga simpangan baku. Koefisien kemencengan momen dilambangkan dengan α3. Koefisien kemencengan momen disebut juga kemencengan relatif. (Hasan, 2009:133)
Menurut Gasperz (1989:103), kemenjuluran relatif α3 digunakan sebagai pengukuran kemenjuluran sekitar rata-rata sebaran teoritis (distribusi teoritis). Menurut Somantri (2006:149), koefisien alpha ketiga merupakan rata-rata penyimpangan data dari rata-ratanya dipangkatkan tiga, dibagi dengan simpangan baku pangkat tiga. Jadi koefisien kemencengan momen adalah nilai perbandingan momen ke-3 dengan pangkat tiga simpangan baku.
Untuk mencari nilai α3, dibedakan antara data tunggal dan data berkelompok. a. Untuk data tunggal
Koefisien kemencengan momen untuk data tunggal dirumuskan sebagai: á3 =𝑀𝑠33 =
1
𝑛∑(𝑥 − 𝑥)3 𝑠3 á3= koefisien kemecengan momen
Menurut Gasperz (1989:103), 捦3=𝑚3 𝑠3 𝑎𝑡𝑎𝑢 𝑎3= 𝑚3 (√𝑚2)3 Menurut Pasaribu (1975:128), á3 =𝑚𝑠33=𝑛𝑠13∑(𝑥𝑖− 𝑥)3 𝑛 𝑖=1 b. Untuk data berkelompok
Koefisien kemencengan momen untuk data berkelompok dirumuskan α3=〱3 s3 = 1 n∑(x − x)3f s3 atau α3=C3 s3 = ( ∑ fu3 n − 3 ( ∑ fu2 n ) ( ∑ fu n ) + 2 ( ∑ fu n ) 3 ) Menurut Pasaribu (1975:128), á3=𝑚𝑠33=𝑛𝑠13∑(𝑥𝑖− 𝑥)3 𝑛 𝑖=1 𝑓𝑖 atau α3=C3 s3 = ( ∑ fu3 n − 3 ( ∑ fu2 n ) ( ∑ fu n ) + 2 ( ∑ fu n ) 3 )
dalam pemakaiannya, rumus kedua lebih praktis dan lebih mudah perhitungannya.
E.
Koefisien Momen KeruncinganUntuk mengetahui keruncingan suatu distribusi, ukuran yang sering digunakan adalah koefisien kurtosis persentil.
1. Koefisien keruncingan
Koefisien keruncingan atau koefisien kurtosis dilambangkan dengan α4 (alpha 4). Untuk mencari nilai koefisien keruncingan, dibedakan antara data tunggal dan data kelompok.
a. Untuk data tunggal
α4= 1 n∑(x − x)4 s4 Menurut Gasperz (1989:103), 𝑎4=𝑚4 𝑠4 𝑎𝑡𝑎𝑢 𝑎4= 𝑚4 𝑚22 Menurut Pasaribu (1975:131),
á4 =𝑚4 𝑠4 = 1 𝑛𝑠4∑(𝑥𝑖− 𝑥) 4 𝑛 𝑖=1 b. Untuk data kelompok
α4= 1 n∑(x − x)4f s4 atau α4= C4 n4= ( ∑ fu4 n − 4 ( ∑ fu3 n ) ( ∑ fu n ) + 6 ( ∑ fu2 n ) ( ∑ fu n ) 2 − 3 (∑ fu n ) 4 ) Menurut Pasaribu (1975:131), á4 =𝑚4 𝑠4 = 1 𝑛𝑠4∑(𝑥𝑖− 𝑥) 4𝑓 𝑖 𝑛 𝑖=1 2. Koefisien kurtosis persentil
Koefisien kurtosis persentil dilambangkan dengan K (kappa). Untuk distribusi normal, nilai K=0,263 . Koefisien kurtosis persentil, dirumuskan :
K = 1
2 (Q3− Q1) P90− P10
F.
Sifat Distribusi Data Berdasarkan Koefisien Momen Kemiringan Dan Koefisien Momen Keruncingan.1. Sifat Distribusi Data Berdasarkan Koefisien Momen Kemiringan
Sebuah distribusi yang tidak simetris akan memiliki rata-rata, median dan modus yang tidak sama besarnya (𝑥 ≠ 𝑀𝑒≠ 𝑀𝑜). Sehingga distribusi akan terkonsentrasi pada salah satu sisi dan kurvanya akan menceng.
Jika distribusi memiliki ekor yang lebih panjang ke kanan daripada yang ke kiri maka distribusi disebut menceng ke kanan atau memiliki kemencengan positif. Sebaliknya, jika distribusi memiliki ekor yang lebih panjang ke kiri daripada yang ke kanan maka distribusi disebut menceng ke kiri atau memiliki kemencengan negatif.
Jika nilai sk dihubungkan dengan keadaan kurva maka :
a. 𝑠𝑘 = 0 kurva memiliki bentuk simetris
b. 𝑠𝑘 ˃ 0 nilai-nilai terkonsentrasi pada sisi sebelah kanan (𝑥 terletak disebelah
kanan 𝑀𝑜 ) sehingga kurva memiliiki ekor memanjang ke kanan, kurva menceng ke kanan atau menceng positif.
c. 𝑠𝑘 ˂ 0 nilai-nilai terkonsentrasi pada sisi sebelah kiri (𝑥 terletak disebelah
kiri 𝑀𝑜 ) sehingga kurva memiliiki ekor memanjang ke kiri, kurva menceng ke kiri atau menceng negatif.
Berikut ini gambar kurva dari distribusi yang menceng ke kanan (menceng positif) dan menceng ke kiri (menceng negatif).
Mo 𝑥 𝑥 Mo
(a) (b)
Gambar 1
Keterangan : Kemencengan Distribusi (a) Menceng ke kanan (b) Menceng ke kiri a. Koefisien Kemencengan Pearson
Contoh soal :
Berikut ini adalah data nilai ujian statistik dari 40 mahasiswa sebuah universitas
Nilai Ujian Frekuensi
31 – 40 41 – 50 51 – 60 61 – 70 71 – 80 81 – 90 91 – 100 4 3 5 8 11 7 2 Jumlah 40
Penyelesaian: Nilai X F U u 2 F u f u 2 31 – 40 41 – 50 51 – 60 61 – 70 71 – 80 81 – 90 91 – 100 35,5 45,5 55,5 65,5 75,5 85,5 95,5 4 3 5 8 11 7 2 -4 -3 -2 -1 0 1 2 16 9 4 1 0 1 4 -16 -9 -10 -8 0 7 4 64 27 20 8 0 7 8 Jumlah 40 -32 134 𝑥 = 𝑀 + 𝐶∑∑𝑓𝑢𝑓 = 75,5 + 10(−3240 )= 75,5 − 8 = 67,5 𝑠 = 𝐶√∑ 𝑓𝑢2 𝑛 − ( ∑ 𝑓𝑢 𝑛 ) 2 = 10√134 40 − ( −32 40 ) 2 = 10(1,646) = 16,46 𝑀𝑒= 𝐵 + 1 2 𝑛 −(∑𝑓2)𝑜 𝑓𝑀𝑒 . 𝐶 = 60,5 + 1 2 40 − 12 8 . 10 = 60,5 + 10 = 70,5 𝑀𝑜= 𝐿 +𝑑 𝑑1 1+ 𝑑2. 𝐶 = 70,5 + 3 3 + 4= 70,5 + 4,29 = 74,34 𝑠𝑘 = 𝑥 − 𝑀𝑜 𝑠 = 67,5 − 74,34 16,46 = −0,42 Dengan menggunakan cara lain :
𝑠𝑘 =3(𝑥 − 𝑀𝑒) 𝑠
𝑠𝑘 =3(67,5 − 70,5)
16,46 = −0,5
Oleh karena nilai sk-nya negatif (-0,42) maka kurvanya menceng ke kiri atau menceng negatif.
b. Koefisien Kemencengan Bowley
Koefisien kemencengan Bowley sering juga disebut Kuartil Koefisien. Kemencengan.Apabila nilai skB dihubungkan dengan keadaan kurva, didapatkan : a. Jika Q3 - Q2 = Q2 - Q1 atau Q3 + Q1 - 2Q2 = 0 maka skB = 0 dan distribusi
datanya simetri
b. Jika Q1 = Q2 maka skB = 1 dan distribusi datanya miring ke kanan c. Jika Q2 = Q3 maka skB = -1 dan distribusi datanya miring ke kiri
d. skB = ± 0,10 menggambarkan distribusi yang menceng tidak berarti dan skB> 0,30 menggambarkan kurva yang menceng berarti.
Contoh soal :
Tentukan kemencengan kurva dari distribusi frekuensi berikut : Nilai Ujian Matematika Dasar I dari 111 mahasiswa, 1997
Nilai Ujian Frekuensi
20,00 – 29,99 30,00 – 39,99 40,00 – 49,99 50,00 – 59,99 60,00 – 69,99 70,00 – 79,99 4 9 25 40 28 5 Jumla h 111 Penyelesaian: Kelas 𝑄1= 𝑘𝑒𝑙𝑎𝑠 𝑘𝑒 − 3 𝑄1 = 𝐵1+ 1 4 𝑛 −(∑𝑓1)𝑜 𝑓𝑄1 . 𝐶 = 39,995 + 27,75 − 13 25 . 10 = 45,895 Kelas 𝑄2= 𝑘𝑒𝑙𝑎𝑠 𝑘𝑒 − 4 𝑄2 = 𝐵2+ 1 2 𝑛 −(∑𝑓2)𝑜 𝑓𝑄2 . 𝐶 = 49,995 + 55,5 − 38 40 . 10 = 54,37 Kelas 𝑄3= 𝑘𝑒𝑙𝑎𝑠 𝑘𝑒 − 5 𝑄3 = 𝐵3+ 3 4 𝑛 −(∑𝑓3)𝑜 𝑓𝑄3 .𝐶 = 59,995 + 83,25 − 78 28 . 10 = 61,87
𝑠𝑘𝐵=𝑄3− 2𝑄2+ 𝑄1 𝑄3− 𝑄1 =
61,87 − 2(54,37)+ 45,895
61,87 − 45,895 = −0,06 Karena 𝑠𝑘𝐵 negative (−0,06) maka kurva maka kurva menceng ke kiri. c. Koefisien Kemencengan Persentil
Contoh Soal:
Tentukan kemencengan kurva dari distribusi frekuensi berikut: Nilai Ujian Matematika Dasar I dari 111 mahasiswa, 1997
Nilai Ujian Frekuensi 20,00 – 29,99 30,00 – 39,99 40,00 – 49,99 50,00 – 59,99 60,00 – 69,99 70,00 – 79,99 4 9 25 40 28 5 Jumlah 111 Penyelesaian: Kelas 𝑃10= 𝑘𝑒𝑙𝑎𝑠 𝑘𝑒 − 2 𝑃10= 𝐵𝑏+ 1 10𝑛−(∑𝑓1)𝑜 𝑓𝑄1 . 𝐶 = 29,995 + 11,1−4 9 . 10 =37,885 Kelas 𝑃50= 𝑘𝑒𝑙𝑎𝑠 𝑘𝑒 −4 𝑃50= 𝐵𝑏+ 1 2 𝑛 −(∑𝑓1)𝑜 𝑓𝑄1 .𝐶 = 49,995 + 55,5 − 38 9 . 10 = 69,44 Kelas 𝑃90= 𝑘𝑒𝑙𝑎𝑠 𝑘𝑒 −5 𝑃90= 𝐵𝑏+ 9 10 𝑛 −(∑𝑓1)𝑜 𝑓𝑄1 . 𝐶 = 59,995 + 99,9 − 78 9 . 10 = 84,33 𝑠𝑘𝑃=𝑃90−2𝑃𝑃 50+ 𝑃10 90−𝑃10 = 84,33 − 2(69,44)+ 37,885 84,33 − 37,885 = −0,36 Karena 𝑠𝑘𝐵 negative (−0,36) maka kurva maka kurva menceng ke kiri.
d. Koefisien Kemencengan Momen
Apabila nilai α3dihubungkan dengan keadaan kurva, didapatkan : a. Untuk distribusi simetris (normal), nilai α3= 0,
b. Untuk distribusi menceng ke kanan, nilai α3 = positif, c. Untuk distribusi menceng ke kiri, nilai α3= negatif,
d. Menurut Karl Pearson, distribusi yang memiliki nilai α3 > ± 0,50 adalah distribusi yang sangat menceng
e. Menurut Kenney dan Keeping, nilai α3 bervariasi antara ± 2 bagi distribusi yang menceng.
2. Sifat Distribusi Data Berdasarkan Koefisien Momen Keruncingan
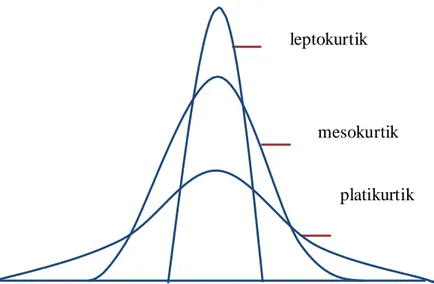
Berdasarkan keruncingannya, kurva distribusi dapat dibedakan atas tiga macam, yaitu sebagai berikut :
a. Leptokurtik : Merupakan distribusi yang memiliki puncak relatif tinggi. b. Platikurtik : Merupakan distribusi yang memiliki puncak hampir mendatar c. Mesokurtik : Merupakan distribusi yang memiliki puncak tidak tinggi dan
tidak mendatar
Bila distribusi merupakan distribusi simetris maka distribusi mesokurtik dianggap sebagai distribusi normal. Dari hasil koefisien kurtosis, ada tiga kriteria untuk mengetahui model distribusi dari sekumpulan data, yaitu koefisien keruncingan atau koefisien kurtosis dilambangkan dengan α4 (alpha 4). Jika hasil perhitungan koefisien keruncingan diperoleh :
1) Nilai lebih kecil dari 3, maka distribusinya adalah distribusi pletikurtik 2) Nilai lebih besar dari 3, maka distibusinya adalah distribusi leptokurtik 3) Nilai yang sama dengan 3, maka distribusinya adalah distribusi mesokurtik
leptokurtik
mesokurtik
platikurtik
Gambar 2. Kurva Keruncingan a) Koefisien keruncingan
Contoh soal : tentukan keruncingan kurva dari data 2,3,6,8,11! Penyelesaian : 𝑋 = 6 𝑠 = 3,67 X 𝑋 − 𝑋 (𝑋 − 𝑋)4 2 3 6 8 11 -4 -3 0 2 5 256 81 0 16 625 Jumlah 0 978 α4= 1 n∑(x − x)4 s4 = 1 5 978 (3,67)4= 195,6 181,4= 1,08
Karena nilainya 1,08 (lebih kecil dari 3) maka distribusinya adalah distribusi platikurtik.
b) Koefisien kurtosis persentil
Jika hasil perhitungan koefisien keruncingan diperoleh :
a) Nilai lebih kurang dari 0,263, maka distribusinya adalah distribusi pletikurtik b) Nilai lebih lebih dari 0,263, maka distibusinya adalah distribusi leptokurtik c) Nilai yang sama dengan 0,263, maka distribusinya adalah distribusi mesokurtik
Contoh soal :
Berikut ini disajikan tabel distribusi frekuensi dari tinggi 100 mahasiswa universitas XYZ.
a. Tentukan koefisien kurtosis persentil (K) !
b. Apakah distribusinya termasuk distribusi normal !
Tinggi (inci) frekuensi (f) 60 – 62 63 – 65 66 – 68 69 – 71 72 – 74 5 18 42 27 8 Jumlah 100 Penyelesaian : Kelas Q1= kelas ke − 3 Q1 = B1+ 1 4 n −(∑f1)o fQ1 . C = 65,5 + 25 − 23 42 . 3 = 65,64 Kelas Q3= kelas ke − 4 Q3= B3+ 3 4 n −(∑f3)o fQ3 . C = 68,5 + 75 − 65 27 . 3 = 69,61 Kelas P10= kelas ke − 2 P10= B10+ 10 100 n −(∑f10)o fP10 . C = 62,5 + 10 − 5 18 . 3 = 63,33 Kelas P90= kelas ke − 4 P90= B90+ 90 100 n −(∑f90)o fP90 . C = 68,5 + 90 − 65 27 . 3 = 71,28 Koefisien kurtosis persentil (K) adalah :
K = 1 2 (Q3− Q1) P90− P10 = 1 2 (69,61 − 65,64) 71,28 − 63,33 = 0,25
DAFTAR PUSTAKA
Akbar, Purnomo Setiady dan Husaini Usman. 2006. Pengantar Statistika Edisi Kedua. Jakarta : PT Bumi Aksara
Akdon dan Riduwan .2013. Rumus dan Data dalam Analisis Statistika. Bandung : Alfabeta. Dajan, Anto, 1986. “Pengantar Metode Statistik Jilid II”. Jakarta : LP3ES .
Furqon. 1999. Statistika Terapan Untuk Penelitian. AFABETA:Bandung Gaspersz, Vincent. 1989. Statistika. Armico:Bandung
Hamid, H.M. Akib dan Nar Herrhyanto. 2008. Statistika Dasar. Jakarta : Universitas Terbuka.
Harinaldi, 2005. “Prinsip-prinsip Statistik untuk Teknik dan Sains”. Jakarta : Erlangga.
Hasan, M. Iqbal. 2011. Pokok – Pokok Materi Statistika 1 ( Statistik Deskriptif ). Jakarta : PT Bumi Aksara
Herrhyanto, Nar. 2008. Statistika Dasar. Jakarta: Universitas Terbuka.
Mangkuatmodjo, Soegyarto. 2004. Statistika Lanjutan. Jakarta: PT Rineka Cipta. Pasaribu, Amudi. 1975. Pengantar Statistik. Gahlia Indonesia : Jakarta
Rachman,Maman dan Muchsin . 1996. Konsep dan Analisis Statistik. Semarang : CV. IKIP Semarang Press
Riduwan . 2010. Dasar-dasar Statistika. Bandung : Alfabeta.
Saleh,Samsubar. 1998. STATISTIK DESKRIPTIP. Yogyakarta : UPP AMP YKPN.
Siregar,Syofian. 2010. Statistika Deskriptif untuk Penelitian Dilengkapi Perhitungan Manual dan Aplikasi SPSS Versi 17. Jakarta : Rajawali Pers.
Somantri, Ating dan Sambas Ali Muhidin. 2006. Aplikasi statistika dalam Penelitian. pustaka ceria : Bandung
Subana,dkk. 2000. Statistik Pendidikan. Pustaka Setia:Bandung
Sudijono, Anas. 2008. Pengantar Statistik Pendidikan. Raja Grafindo Persada.Jakarta Sudijono, Anas. 2009. Pengantar Statistik Pendidikan. Jakarta : PT RajaGrafindo Persada. Sudijono, Anas. 1987. Pengantar Statistik Pendidikan. Jakarta : PT RajaGrafindo Persada. Sudjana, M.A., M.SC.2005. METODE STATISTIKA. Bandung: Tarsito
Sugiyono. 2014. Statistika untuk Penelitian. Bandung : Alfabeta.
Supranto, 1994. “Statistik Teori dan Aplikasi Jilid 2”. Jakarta : Erlangga.
Usman, Husaini & Setiady Akbar, Purnomo.2006. PENGANTAR STATISTIKA. Yogyakarta: BUMI AKSARA.