Komputasi untuk Sains, (Fortran)

(1)

Komputasi untuk Sains dan Teknik

Dr. Eng. Supriyanto, M.Sc

Edisi I

Laboratorium Jaringan Komputer Departemen Fisika-FMIPA

(2)

(3)

(4)

(5)

(6)

(7)

Kata Pengantar

Sarjana geofisika harus mampu menunjukkan kemauan dan kemampuan untuk dapat mem-formulasikan masalah, menyusun hipotesis, metode dan solusi serta mampu menyelesaikan masalah-masalah tersebut secara mandiri.

(8)

(9)

Daftar Isi

Lembar Persembahan i

Kata Pengantar v

Daftar Isi vii

Daftar Gambar xi

Daftar Tabel xiii

1 Matrik dan Komputasi 1

1.1 Pengenalan Matrik . . . 1

1.2 Inisialisasi matrik dalam memori komputer . . . 2

1.3 Macam-macam matrik . . . 2

1.3.1 Matrik transpose . . . 2

1.3.2 Matrik Bujursangkar . . . 2

1.3.3 Matrik Simetrik . . . 3

1.3.4 Matrik diagonal . . . 3

1.3.5 Matrik diagonal dominan . . . 3

1.3.6 Matrik identitas . . . 3

1.3.7 Matrik upper-triangular . . . 4

1.3.8 Matrik lower-triangular . . . 4

1.3.9 Matrik tridiagonal . . . 4

1.3.10 Vektor-baris dan Vektor-kolom . . . 4

1.4 Operasi matematika . . . 5

1.4.1 Penjumlahan matrik . . . 5

1.4.2 Komputasi penjumlahan matrik . . . 6

1.4.3 Perkalian matrik . . . 7

1.4.4 Komputasi perkalian matrik . . . 8

1.4.5 Perkalian matrik dan vektor-kolom . . . 9

1.4.6 Komputasi perkalian matrik dan vektor-kolom . . . 10

1.4.7 Matrik positif-definite . . . 10

1.5 Penutup . . . 11

2 Metode Eliminasi Gauss 13 2.1 Penyederhanaan . . . 13

2.2 Matrik dan Eliminasi Gauss . . . 17

2.3 Algoritma eliminasi Gauss . . . 19

(10)

2.3.1 Algoritma . . . 21 2.4 Penutup . . . 24

3 MetodeLU Decomposition 27

3.1 Penyederhanaan . . . 27

4 Invers Matrik dan Eliminasi Gauss 37

5 Iterasi Jacobi 45

6 Iterasi Gauss-Seidel 53

7 IterasiSuccesive-Over-Relaxation 59

8 Interpolasi Lagrange 63

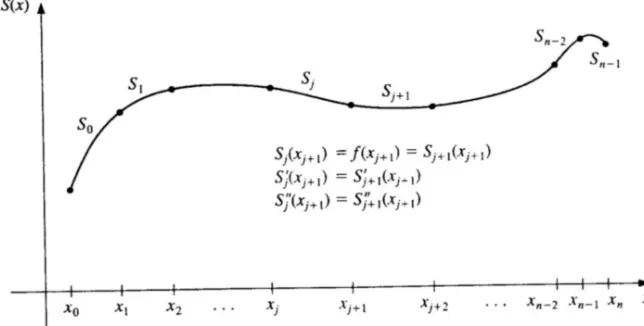
9 Interpolasi Cubic Spline 67

10 Metode Euler 77

11 Metode Runge Kutta 81

12 Metode Finite Difference 89

13 Integral Numerik 95

14 Metode Newton 101

15 Metode Monte Carlo 103

16 Inversi Linear 107

(11)

ix

17 Inversi Non-Linear 111

(12)

(13)

Daftar Gambar

9.1 Fungsif(x)dengan sejumlah titik data . . . 67

9.2 Pendekatan dengan polinomial cubic spline . . . 68

9.3 Profil suatu object . . . 73

9.4 Sampling titik data . . . 73

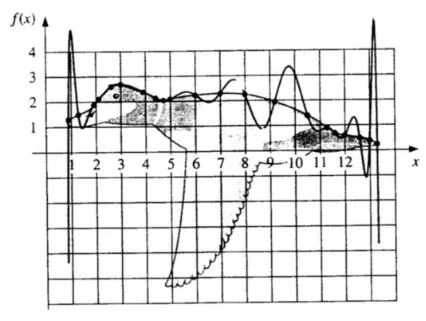
9.5 Hasil interpolasi cubic spline . . . 74

9.6 Hasil interpolasi lagrange . . . 74

10.1 Metode Euler . . . 78

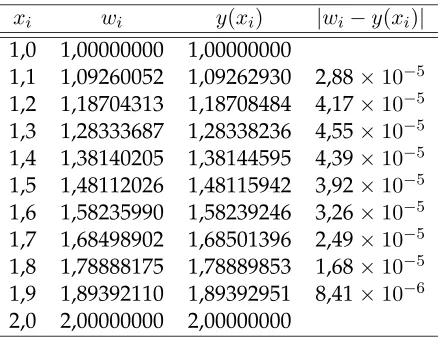
10.2 Trend error metode euler . . . 80

11.1 Rangkaian RC . . . 84

11.2 Kurva muatanqterhadap waktut . . . 88

13.1 Metode Trapezoida . . . 96

13.2 Metode Simpson . . . 96

13.3 Metode Composite Simpson . . . 99

14.1 Metode Newton . . . 102

15.1 Lingkaran dan bujursangkar . . . 104

15.2 Dart yang menancap pada bidang lingkaran dan bujursangkar . . . 104

15.3 Dart yang menancap pada bidang 1/4 lingkaran dan bujursangkar . . . 105

(14)

(15)

Daftar Tabel

7.1 Gauss-Seidel . . . 60 7.2 Relaksasi denganω= 1,25 . . . 60

(16)

(17)

Bab 1

Matrik dan Komputasi

✍Objektif :

⊲ Mengenalkan matrik dan jenis-jenis matrik.

⊲ Mengenalkan operasi penjumlahan dan perkalian matrik.

⊲ Mendeklarasikan elemen-elemen matrik ke dalam memori komputer.

⊲ Membuat script operasi matrik.

1.1 Pengenalan Matrik

Notasi suatu matrik berukurannxm ditulis dengan huruf besar dan dicetak tebal, misalnya

An×m. Huruf n menyatakan jumlah baris, dan huruf m jumlah kolom. Matrik terdiri dari

elemen-elemen matrik yang dinyatakan dengan huruf kecil diikuti angka-angka indeks, mis-alnyaaij, dimanai menunjukan posisi baris ke-idanj menentukan posisi kolom ke-j.

A= (aij) =

     

a11 a12 . . . a1m

a21 a22 . . . a2m ..

. ... ...

an1 an2 . . . anm

     

(1.1)

Contoh 1: MatrikA2×3

A=

"

3 8 5 6 4 7

#

dimana masing-masing elemennya adalaha11 = 3, a12 = 8, a13 = 5, a21 = 6, a22 = 4, dan a23= 7.

Contoh 2: MatrikB3×2

B=

  

1 3 5 9 2 4

  

(18)

dimana masing-masing elemennya adalahb11 = 1, b12 = 3, b21 = 5, b22 = 9, b31 = 2, dan

b32= 4.

1.2 Inisialisasi matrik dalam memori komputer

Dalam bahasa pemrograman Fortran77, cara mengisi memori komputer dengan elemen-elemen matrikA2×3, sesuai dengan Contoh 1 adalah

A(1,1) = 3

A(1,2) = 8

A(1,3) = 5

A(2,1) = 6

A(2,2) = 4

A(2,3) = 7

Sedangkan untuk matrikB3×2, sesuai Contoh 2 adalah

B(1,1) = 1

B(1,2) = 3

B(2,1) = 5

B(2,2) = 9

B(3,1) = 2

B(3,2) = 4

1.3 Macam-macam matrik

1.3.1 Matrik transpose

Operasi transpose terhadap suatu matrik akan menukar posisi kolom menjadi posisi baris demikian pula sebaliknya. Notasi matrik tranpose adalahAT atauAt.

Contoh 3: Operasi transpose terhadap matrikA

A=

"

3 8 5 6 4 7

#

At=

  

3 6 8 4 5 7

  

1.3.2 Matrik Bujursangkar

Matrik bujursangkar adalah matrik yang jumlah baris dan jumlah kolomnya sama.

Contoh 4: Matrik bujursangkar berukuran 3x3 atau sering juga disebut matrik bujursangkar orde 3

A=

  

1 3 8 5 9 7 2 4 6

(19)

1.3. MACAM-MACAM MATRIK 3

1.3.3 Matrik Simetrik

Matrik simetrik adalah matrik bujursangkar yang elemen-elemen matrikAbernilai sama den-gan matrik transpose-nya (At).

Contoh 5: Matrik simetrik

A=

1.3.4 Matrik diagonal

Matrik diagonal adalah matrik bujursangkar yang seluruh elemen-nya bernilai 0 (nol), kecuali elemen-elemen diagonalnya.

Contoh 6: Matrik diagonal orde 3

A=

1.3.5 Matrik diagonal dominan

Matrik diagonal dominan adalah matrik bujursangkar yang memenuhi

|aii|> n

X

j=1,j6=i

|aij| (1.2)

dimanai=1,2,3,..n. Coba perhatikan matrik-matrik berikut ini

A= matrikAdisebut matrik diagonal dominan. Sekarang perhatikan elemen diagonal matrikB,

|6_|<_|4_|+_{| −}3_|,| −2_|<_|4_|+_|0_|, dan|1_|<_{| −}3_|+_|0_|. Dengan demikian, matrikBbukan matrik diagonal dominan.

1.3.6 Matrik identitas

(20)

Contoh 7: Matrik identitas orde 3

1.3.7 Matrik upper-triangular

Matrik upper-tringular adalah matrik bujursangkar yang seluruh elemen dibawah elemen di-agonal bernilai 0 (nol).

Contoh 8: Matrik upper-triangular

A=

1.3.8 Matrik lower-triangular

Matrik lower-tringular adalah matrik bujursangkar yang seluruh elemen diatas elemen diago-nal bernilai 0 (nol).

Contoh 9: Matrik lower-triangular

A=

1.3.9 Matrik tridiagonal

Matrik tridiagonal adalah matrik bujursangkar yang seluruh elemen bukan 0 (nol) berada dis-ekitar elemen diagonal, sementara elemen lainnya bernilai 0 (nol).

Contoh 10: Matrik tridiagonal

A=

1.3.10 Vektor-baris dan Vektor-kolom

Notasi vektor biasanya dinyatakan dengan huruf kecil dan dicetak tebal. Suatu matrik dina-makan vektor-baris berukuran m, bila hanya memiliki satu baris danm kolom, yang diny-atakan sebagai berikut

a=ha11 a12 . . . a1m

i

=ha1 a2 . . . am

i

(21)

1.4. OPERASI MATEMATIKA 5

Sedangkan suatu matrik dinamakan vektor-kolom berukurann, bila hanya memiliki satu kolom dannbaris, yang dinyatakan sebagai berikut

a=

1.4 Operasi matematika

1.4.1 Penjumlahan matrik

Operasi penjumlahan pada dua buah matrik hanya bisa dilakukan bila kedua matrik tersebut berukuran sama. Misalnya matrikC2×3

C=

"

9 5 3 7 2 1

#

dijumlahkan dengan matrikA2×3, lalu hasilnya (misalnya) dinamakan matrikD2×3

D=A+C

Tanpa mempedulikan nilai elemen-elemen masing-masing matrik, operasi penjumlahan antara matrikA2×3 danC2×3, bisa juga dinyatakan dalam indeks masing-masing dari kedua matrik

tersebut, yaitu

Dijabarkan satu persatu sebagai berikut

(22)

Dari sini dapat diturunkan sebuah rumus umum penjumlahan dua buah matrik

dij =aij+cij (1.5)

dimanai=1,2,..,ndanj=1,2,..,m. Sementaranadalah jumlah baris, danmadalah jumlah kolom.

1.4.2 Komputasi penjumlahan matrik

Berdasarkan contoh operasi penjumlahan di atas, maka secara komputasi dengan bahasa pem-rograman Fortran77, operasi penjumlahan antara matrikA2×3danC2×3adalah

do i=1,2

do j=1,3

D(i,j)=A(i,j)+C(i,j)

end do

Perlu dicatat bahwa ukuran matrik tidak terbatas hanya 2x3. Tentu saja anda bisa mengubah ukurannya sesuai dengan keperluan atau kebutuhan anda. Jika ukuran matrik dinyatakan secara umum sebagainxm, maka bentuk pernyataan komputasinya menjadi

do i=1,n

do j=1,m

D(i,j)=A(i,j)+C(i,j)

end do

Sekarang, mari kita lengkapi dengan contoh sebagai berikut: diketahui matrikA2×3

A=

"

3 8 5 6 4 7

#

dan matrikC2×3

C=

"

9 5 3 7 2 1

#

Program untuk menjumlahkan kedua matrik tersebut adalah:

1 A(1,1) = 3

2 A(1,2) = 8

3 A(1,3) = 5

4 A(2,1) = 6

5 A(2,2) = 4

6 A(2,3) = 7

7 C(1,1) = 9

8 C(1,2) = 5

(23)

10 C(2,1) = 7

11 C(2,2) = 2

12 C(2,3) = 1

13 n=2

14 m=3

15 do i=1,n

16 do j=1,m

17 D(i,j)=A(i,j)+C(i,j)

18 end do

19 end do

1.4.3 Perkalian matrik

Operasi perkalian dua buah matrik hanya bisa dilakukan bila jumlah kolom matrik pertama sama dengan jumlah baris matrik kedua. Jadi kedua matrik tersebut tidak harus berukuran sama seperti pada penjumlahan dua matrik. Misalnya matrikA2×3 dikalikan dengan matrik B3×2, lalu hasilnya (misalnya) dinamakan matrikE2×2

E2×2 =A2×3.B3×2

E =

"

3 8 5 6 4 7

#   

1 3 5 9 2 4

  

=

"

3.1 + 8.5 + 5.2 3.3 + 8.9 + 5.4 6.1 + 4.5 + 7.2 6.3 + 4.9 + 7.4

#

=

"

53 101 40 82

#

Tanpa mempedulikan nilai elemen-elemen masing-masing matrik, operasi perkalian antara matrikA2×3 danB3×2, bisa juga dinyatakan dalam indeks masing-masing dari kedua matrik

tersebut, yaitu

"

e11 e12 e21 e22

#

=

"

a11.b11+a12.b21+a13.b31a11.b12+a12.b22+a13.b32 a21.b11+a22.b21+a23.b31a21.b12+a22.b22+a23.b32

#

Bila dijabarkan, maka elemen-elemen matrikE2×2adalah

(24)

kemudian secara sederhana dapat diwakili oleh rumus berikut

eij =

3

X

k=1 aikbkj

dimanai=1,2, danj=1,2.

Berdasarkan contoh ini, maka secara umum bila ada matrikAn×myang dikalikan dengan ma-trikBm×p, akan didapatkan matrikEn×pdimana elemen-elemen matrikEmemenuhi

eij = m

X

k=1

aikbkj (1.6)

dengani=1,2,. . . ,ndanj=1,2. . . ,p

1.4.4 Komputasi perkalian matrik

Komputasi operasi perkalian antara matrikA2×3danB3×2dilakukan melalui 2 tahap; pertama

adalah memberikan nilai 0 (nol) pada elemen-elemen matrikE2×2dengan cara

do i=1,2

do j=1,2

E(i,j)=0.0

end do

kedua adalah menghitung perkalian matrik dengan cara

do i=1,2

do j=1,2

do k=1,3

E(i,j)=E(i,j)+A(i,k)*B(k,j) end do

end do

Tentu saja anda bisa mengubah ukurannya sesuai dengan keperluan atau kebutuhan anda. Jika ukuran matrikAdinyatakan secara umum sebagainxmdan matrikBberukuranmxp, maka bentuk pernyataan komputasinya menjadi

do i=1,n

do j=1,p

E(i,j)=0.0

end do

do i=1,n

(25)

do k=1,m

E(i,j)=E(i,j)+A(i,k)*B(k,j) end do

end do

dimana akan diperoleh hasil berupa matrikEyang berukurannxp.

1.4.5 Perkalian matrik dan vektor-kolom

Operasi perkalian antara matrik dan vektor-kolom sebenarnya sama saja dengan perkalian an-tara dua matrik. Hanya saja ukuran vektor-kolom boleh dibilang spesial yaitumx1, dimana

mmerupakan jumlah baris sementara jumlah kolomnya hanya satu. Misalnya matrik A, pa-da contoh 1, dikalikan dengan vektor-kolom x yang berukuran3 x 1 atau disingkat dengan mengatakan vektor-kolomxberukuran3, lalu hasilnya (misalnya) dinamakan vektor-kolomy

y=Ax

y =

"

3 8 5 6 4 7

#   

2 3 4

  

=

"

3.2 + 8.3 + 5.4 6.2 + 4.3 + 7.4

#

=

"

50 52

#

Sekali lagi, tanpa mempedulikan nilai elemen-elemen masing-masing, operasi perkalian antara matrikAdan vektor-kolomx, bisa juga dinyatakan dalam indeksnya masing-masing, yaitu

"

y1 y2

#

=

"

a11.x1+a12.x2+a13.x3 a21.x1+a22.x2+a23.x3

#

Bila dijabarkan, maka elemen-elemen vektor-kolomyadalah

y1 =a11.x1+a12.x2+a13.x3 y2 =a21.x1+a22.x2+a23.x3

kemudian secara sederhana dapat diwakili oleh rumus berikut

yi=

3

X

(26)

dimanai=1,2.

Berdasarkan contoh tersebut, secara umum bila ada matrikAberukurannxmyang dikalikan dengan vektor-kolomxberukuranm, maka akan didapatkan vektor-kolomyberukurannx1

dimana elemen-elemen vektor-kolomymemenuhi

yi= m

X

j=1

aijxj (1.7)

dengani=1,2,. . . ,n.

1.4.6 Komputasi perkalian matrik dan vektor-kolom

Sama seperti perkalian dua matrik, komputasi untuk operasi perkalian antara matrikA beruku-rannxmdan vektor-kolomxberukuranmdilakukan melalui 2 tahap; pertama adalah mem-berikan nilai 0 (nol) pada elemen-elemen vektor-kolomyyang berukurann. Lalu tahap kedua adalah melakukan proses perkalian. Kedua tahapan ini digabung jadi satu dalam program berikut ini

do i=1,n

Y(i)=0.0

end do

do i=1,n

do j=1,m

Y(i)=Y(i)+A(i,j)*X(j) end do

end do

1.4.7 Matrik positif-definite

Suatu matrik dikatakanpositif-definitebila matrik tersebut simetrik dan memenuhi

xtAx>0 (1.8)

Contoh 11: Diketahui matrik simetrik berikut

A=

  

2 ₋1 0 −1 2 ₋1

0 ₋1 2

(27)

1.5. PENUTUP 11

untuk menguji apakah matrikAbersifatpositif-definit, maka

xtAx = hx1 x2 x3

i   

2 ₋1 0 −1 2 ₋1

0 ₋1 2

  

  

x1 x2 x3

  

= hx1 x2 x3

i   

2x1−x2 −x1+ 2x2−x3

−x2+ 2x3

  

= 2x2₁₋2x1x2+ 2x22−2x2x3+ 2x23

= x2₁+ (x2₁₋2x1x2+x22) + (x22−2x2x3+x23) +x23 = x2₁+ (x1−x2)2+ (x2−x3)2+x23

Dari sini dapat disimpulkan bahwa matrikAbersifatpositif-definite, karena memenuhi

x2₁+ (x1−x2)2+ (x2−x3)2+x23 >0

kecuali jikax1=x2=x3=0.

1.5 Penutup

(28)

(29)

Bab 2

Metode Eliminasi Gauss

✍Objektif :

⊲ _{Mengenalkan operasi penjumlahan dan perkalian matrik.}

2.1 Penyederhanaan

Secara umum, sistem persamaan linear dinyatakan sebagai berikut

Pn: an1x1+an2x2+...+annxn=bn (2.1) dimanaadanbmerupakan konstanta,xadalah variable,n= 1,2,3, ....

Contoh pertama

Misalnya ada sistem persamaan linear yang terdiri dari empat buah persamaan yaitu P1, P2,P3, danP4seperti berikut ini:

P1: x1 + x2 + 3x4 = 4

P2: 2x1 + x2 − x3 + x4 = 1 P3: 3x1 − x2 − x3 + 2x4 = -3 P4: −x1 + 2x2 + 3x3 − x4 = 4

Problem dari sistem persamaan linear adalah bagaimana mencari nilai pengganti bagi vari-abelx1,x2,x3, danx4sehingga semua persamaan diatas menjadi benar. Langkah awal

penye-lesaian problem tersebut adalah dengan melakukan penyederhanaan sistem persamaan linear. Ada banyak jalan untuk mendapatkan bentuk yang lebih sederhana, namun masalahnya, ki-ta ingin mendapatkan sebuah algoritma program yang nantinya bisa berjalan di komputer, sedemikian rupa sehingga apapun persamaannya, bisa disederhanakan oleh komputer. Kita akan berpatokan pada tiga buah aturan operasi untuk menyederhanakan sistem persamaan

(30)

linear di atas, yaitu

• PersamaanPidapat dikalikan dengan sembarang konstantaλ, lalu hasilnya ditempatkan di posisi persamaanPi. Simbol operasi ini adalah(λPi)→(Pi).

• PersamaanPj dapat dikalikan dengan sembarang konstanta λ kemudian dijumlahkan dengan persamaanPi, lalu hasilnya ditempatkan di posisi persamaanPi. Simbol operasi ini adalah(Pi+λPj)→(Pi).

• PersamaanPidanPj dapat bertukar posisi. Simbol operasi ini adalah(Pi)↔(Pj). Maka dengan berpegang pada aturan-aturan tersebut, problem sistem persamaan linear di atas akan diselesaikan dengan langkah-langkah berikut ini:

1. Gunakan persamaanP1untuk menghilangkan variabelx1 dari persamaanP2, P3 danP4

dengan cara(P2−2P1)→(P2),(P3−3P1)→(P3)dan(P4+P1)→(P4). Hasilnya akan

seperti ini

P1 : x1+x2+ 3x4 = 4, P2 : −x2−x3−5x4 = −7, P3 : −4x2−x3−7x4 = −15,

P4 : 3x2+ 3x3+ 2x4 = 8

2. Gunakan persamaan P2 untuk menghilangkan variabel x2 dari persamaan P3 dan P4

dengan cara(P3−4P2)→(P3)dan(P4+ 3P2)→(P4). Hasilnya akan seperti ini

P1 : x1+x2+ 3x4 = 4, P2: −x2−x3−5x4 = −7, P3 : 3x3+ 13x4 = 13, P4 : −13x4 = −13

Kalaux3masih ada di persamaanP4, dibutuhkan satu operasi lagi untuk menghilangkan-nya. Namun hasil operasi pada langkah ke-2 ternyata sudah otomatis menghilangkanx3.

Bentuk akhir dari keempat persamaan di atas, dikenal sebagai bentuktriangular.

Sampai dengan langkah ke-2 ini, kita berhasil mendapatkan sistem persamaan linear yang lebih sederhana. Apa yang dimaksud dengan sederhana dalam konteks ini? Su-atu sistem persamaan linear dikatakan sederhana bila kita bisa mendapatkan seluruh ni-lai pengganti variabelnya dengan cara yang lebih mudah atau dengan usaha yang tidak memakan waktu lama dibandingkan sebelum disederhanakan. Sekali kita mendapatkan nilai pengganti bagi variabelx4, makax3,x2 danx1akan diperoleh dengan mudah dan

cepat, sebagaimana yang dijelaskan pada langkah berikutnya.

(31)

2.1. PENYEDERHANAAN 15

akhirnyax1.

P4 : x4 = −

13

−13 = 1, P3: x3 =

1

3(13−13x4) = 1

3(13−13) = 0, P2 : x2 =₋(₋7 + 5x4+x3) = ₋(₋7 + 5 + 0) = 2,

P1 : x1= 4₋3x4₋x2 = 4₋3₋2 =₋1

Jadi solusinya adalah x1 = −1, x2 = 2, x3 = 0 danx4 = 1. Coba sekarang anda cek,

apakah semua solusi ini cocok dan tepat bila dimasukan ke sistem persamaan linear yang pertama, yaitu yang belum disederhanakan?

(32)

Contoh kedua

Misalnya ada sistem persamaan linear, terdiri dari empat buah persamaan yaituP1,P2,P3,

danP4seperti berikut ini:

P1 : x1 − x2 + 2x3 − x4 = -8 P2 : 2x1 − 2x2 + 3x3 − 3x4 = -20

P3 : x1 + x2 + x3 = -2

P4 : x1 − x2 + 4x3 + 3x4 = 4

Seperti contoh pertama, solusi sistem persamaan linear di atas akan dicari dengan langkah-langkah berikut ini:

1. Gunakan persamaanP1 untuk menghilangkanx1 dari persamaanP2, P3 danP4 dengan

cara(P2−2P1)→(P2),(P3−P1)→(P3)dan(P4−P1)→(P4). Hasilnya akan seperti ini P1 : x1−x2+ 2x3−x4 = −8,

P2 : −x3−x4 = −4, P3: 2x2−x3+x4 = 6, P4 : 2x3+ 4x4 = 12

Perhatikan persamaanP2! Akibat dari langkah yang pertama tadi, x2 hilang dari

per-samaanP2. Kondisi ini bisa menggagalkan proses triangularisasi. Untuk itu, posisi P2

mesti ditukar dengan persamaan yang berada dibawahnya, yaitu P3 atau P4. Supaya

proses triangularisasi dilanjutkan kembali, maka yang paling cocok adalah ditukar den-ganP3.

2. Tukar posisi persamaanP2 dengan persamaanP3,(P2 _↔P3). Hasilnya akan seperti ini

P1 : x1−x2+ 2x3−x4 = −8, P2: 2x2−x3+x4 = 6, P3: −x3−x4 = −4, P4 : 2x3+ 4x4 = 12

3. Gunakan persamaanP3untuk menghilangkanx3 dari persamaanP4 dengan cara(P4 − 2P3)→(P4). Hasilnya akan seperti ini

P1: x1₋x2+ 2x3₋x4 = ₋8, P2 : 2x2−x3+x4 = 6,

P3: −x3−x4 = −4,

P4 : 2x4 = 4

(33)

2.2. MATRIK DAN ELIMINASI GAUSS 17

4. Selanjutnya adalah proses backward-substitution. Melalui proses ini, yang pertama kali didapat solusinya adalahx4, kemudianx3, lalu diikutix2, dan akhirnyax1.

P4: x4 =

Berdasarkan kedua contoh di atas, untuk mendapatkan solusi sistem persamaan linear, diperlukan operasitriangularisasidan prosesbackward-substitution. Katabackward-substitution

kalau diterjemahkan kedalam bahasa indonesia, menjadisubstitusi-mundur. Gabungan pros-es triangularisasi dan substitusi-mundur untuk menyelpros-esaikan sistem persamaan linear dike-nal sebagai metodeeliminasi gauss.

2.2 Matrik dan Eliminasi Gauss

Sejumlah matrik bisa digunakan untuk menyatakan suatu sistem persamaan linear. Sejenak, mari kita kembali lagi melihat sistem persamaan linear secara umum seperti berikut ini:

a11x1+a12x2+. . .+a1nxn = b1 a21x1+a22x2+. . .+a2nxn = b2 . . . = . . . . . . = . . . an1x1+an2x2+. . .+annxn = bn

Sementara, kalau dinyatakan dalam bentuk operasi matrik, maka akan seperti ini:



(34)

berukurannx(n+ 1)seperti berikut ini:

Berdasarkan contoh pertama yang ada dihalaman depan catatan ini, saya akan tunjukkan proses triangularisasi dan substitusi-mundur dalam operasi matrik terhadap sistem persamaan linear yang terdiri dari empat persamaan matematika, yaitu (silakan lihat kembali contoh perta-ma):

Lalu kita dapat membuat matrik augment sebagai berikut:



Kemudian kita lakukan operasi triangularisai terhadap matrik augment, dimulai dari kolom pertama, yaitu

lalu dilanjutkan ke kolom berikutnya



(35)

masing-2.3. ALGORITMA ELIMINASI GAUSS 19

masing elemen berikut ini:



Dengan memperhatikan angka-angka indeks pada matrik augment di atas, kita akan menco-ba membuat rumusan proses substitusi-mundur untuk mendapatkan seluruh nilai pengganti variabelx. Dimulai darix4,

ini dapat dinyatakan dalam rumus umum, yaitu

xn=

ini juga dapat dinyatakan dalam rumus umum yaitu:

xi=

ai,n+1−Pn_j₌_i₊₁aijxj

aii

Proses triangularisasi dan substitusi-mundur dibakukan menjadi algoritma metode elimi-nasi gauss yang dapat diterapkan dalam berbagai bahasa pemrograman komputer, misalnya fortran, C, java, pascal, matlab, dan lain-lain.

2.3 Algoritma eliminasi Gauss

Secara umum, sistem persamaan linear adalah sebagai berikut:

a11x1+a12x2+. . .+a1nxn = b1 a21x1+a22x2+. . .+a2nxn = b2

..

. ... = ...

an1x1+an2x2+. . .+annxn = bn Algoritma dasar metode eliminasi gauss, adalah sebagai berikut:

(36)

yang berukurannx(n+ 1)seperti berikut ini:

Jelas terlihat bahwa elemen-elemen yang menempati kolom terakhir matrik augment adalah nilai daribi; yaituai,n+1=bidimanai= 1,2, ..., n.

2. Periksalah elemen-elemen pivot. Apakah ada yang bernilai nol? Elemen-elemen pivot adalah elemen-elemen yang menempati diagonal suatu matrik, yaitu a11, a22, ..., ann atau disingkataii. Jikaaii6= 0, bisa dilanjutkan ke langkah no.3. Namun, jika ada elemen diagonal yang bernilai nol,aii = 0, maka baris dimana elemen itu berada harus ditukar posisinya dengan baris yang ada dibawahnya,(Pi) ↔ (Pj)dimanaj =i+ 1, i+ 2, ..., n, sampai elemen diagonal matrik menjadi tidak nol,aii6= 0. (Kalau kurang jelas, silakan lihat

lagi contoh kedua yang ada dihalaman 3. Sebaiknya, walaupun elemen diagonalnya tidak nol, namun mendekati nol (misalnya 0,03), maka proses pertukaran ini dilakukan juga).

3. Proses triangularisasi. Lakukanlah operasi berikut:

Pj−

4. Hitunglah nilaixndengan cara:

xn=

(37)

2.3. ALGORITMA ELIMINASI GAUSS 21

2.3.1 Algoritma

Algoritma metode eliminasi gauss untuk menyelesaikannxnsistem persamaan linear.

P1: a11x1+a12x2+. . .+a1nxn = b1 P2: a21x1+a22x2+. . .+a2nxn = b2

..

. ... ... = ...

Pn: an1x1+an2x2+. . .+annxn = bn

INPUT: sejumlah persamaan linear dimana konstanta-konstanta-nya menjadi elemen-elemen matrik augmentA= (aij), dengan1≤i≤ndan1≤j≤n+ 1.

OUTPUT: solusi x1, x2, x3, ..., xn atau pesan kesalahan yang mengatakan bahwa sistem per-samaan linear tidak memiliki solusi yang unik.

• Langkah 1:Inputkan konstanta-konstanta dari sistem persamaan linear kedalam elemen-elemenmatrik augment, yaitu suatu matrik yang berukurannx(n+ 1)seperti berikut ini:

• Langkah 3: Definisikanpsebagai integer dimanai _≤p _≤ n. Lalu pastikan bahwa

api 6= 0. Jika ada elemen diagonal yang bernilai nol (aii = 0), maka program harus mencari dan memeriksa elemen-elemen yang tidak bernilai nol dalam kolom yang sama dengan kolom tempat elemen diagonal tersebut berada. Jadi saat proses ini berlangsung, integeri(indeks dari kolom) dibuat konstan, sementara integerp (in-deks dari baris) bergerak darip = isampaip = n. Bila ternyata setelah mencapai elemen paling bawah dalam kolom tersebut, yaitu saat p = n tetap didapat nilai

api = 0, maka sebuah pesan dimunculkan: sistem persamaan linear tidak memiliki solusi yang unik. Lalu program berakhir: STOP.

• Langkah 4: Namun jika sebelum integerp mencapai nilaip = n sudah diperoleh elemen yang tidak nol (api 6= 0), maka bisa dipastikan p 6= i. Jika p 6= i maka lakukan proses pertukaran (Pp)↔(Pi).

• Langkah 5:Untukj=i+ 1, .., n, lakukan Langkah 6 dan Langkah 7.

• Langkah 6:Tentukanmji,

mji=

aji

(38)

• Langkah 7:Lakukan proses triangularisasi,

(Pj −mjiPi)→(Pj)

• Langkah 8: Setelah proses triangularisasi dilalui, periksalahann. Jikaann = 0, kirimkan pesan:sistem persamaan linear tidak memiliki solusi yang unik. Lalu program berakhir: STOP.

• Langkah 9:Jikaann 6= 0, lakukan proses substitusi mundur, dimulai dengan menentukan

xn,

xn=

an,n+1 ann

• Langkah 10:Untuki=n₋1, ...,1tentukanxi,

xi =

ai,n+1−Pnj=i+1aijxj

aii

• Langkah 11:Diperoleh solusi yaitux1, x2, ..., xn. Algoritma telah dijalankan dengan

suk-ses. STOP.

Saya telah membuat program sederhana dalam fortran untuk mewujudkan algoritma elim-inasi gauss. Saya berasumsi bahwa anda sudah menguasai dasar-dasar pemrograman dalam fortran. Program ini sudah dicoba di-compile dengan fortran77 under Linux Debian dan visual-fortranunder windows-XP.

Langkah-langkah yang tercantum pada program ini disesuaikan dengan langkah-langkah yang tertulis di atas. Dalam program ini, ukuran maksimum matrik augment adalah 10 x 11, untuk mencari 10 variabel yang tidak diketahui. Jika anda bermaksud memperbesar atau memperke-cil ukuran matrik augment, silakan sesuaikan angka ukuran matrik yang anda inginkan pada statemen pertama dari program ini, yaitu statemen DIMENSION. Inilah programnya,

DIMENSION A(10,11), X(10)

REAL MJI

WRITE (*,*) ’=PROGRAM ELIMINASI GAUSS=’ WRITE (*,*)

C LANGKAH 1: MEMASUKAN NILAI ELEMEN-ELEMEN MATRIK AUGMENT

WRITE (*,’(1X,A)’) ’JUMLAH PERSAMAAN ? ’ READ (*,*) N

WRITE (*,*)

WRITE (*,*) ’MASUKAN ELEMEN-ELEMEN MATRIK AUGMENT’ M = N + 1

DO 50 I = 1,N

DO 60 J = 1,M

(39)

2.3. ALGORITMA ELIMINASI GAUSS 23

60 CONTINUE

50 CONTINUE

WRITE (*,*)

C MENAMPILKAN MATRIK AUGMENT

WRITE (*,’(1X,A)’) ’MATRIK AUGMENT:’ DO 110 I = 1,N

WRITE (*,’(1X,5(F14.8))’) (A(I,J),J=1,M)

110 CONTINUE

WRITE (*,*)

C LANGKAH 2: MEMERIKSA ELEMEN-ELEMEN PIVOT DAN PROSES TUKAR POSISI

NN = N-1

DO 10 I=1,NN

C LANGKAH 3: MENDEFINISIKAN P

P = I

100 IF (ABS(A(P,I)).GE.1.0E-20 .OR. P.GT.N) GOTO 200

P = P+1

GOTO 100

200 IF(P.EQ.N+1)THEN

C MENAMPILKAN PESAN TIDAK UNIK

WRITE(*,5) GOTO 400

END IF

C LANGKAH 4: PROSES TUKAR POSISI

IF(P.NE.I) THEN

DO 20 JJ=1,M

C = A(I,JJ)

A(I,JJ) = A(P,JJ)

A(P,JJ) = C

20 CONTINUE

END IF

C LANGKAH 5: PERSIAPAN PROSES TRIANGULARISASI

JJ = I+1

DO 30 J=JJ,N

C LANGKAH 6: TENTUKAN MJI

MJI = A(J,I)/A(I,I)

C LANGKAH 7: MELAKUKAN PROSES TRIANGULARISASI

DO 40 K=JJ,M

A(J,K) = A(J,K)-MJI*A(I,K)

40 CONTINUE

A(J,I) = 0

(40)

10 CONTINUE

C MENAMPILKAN HASIL TRIANGULARISASI

WRITE (*,’(1X,A)’) ’HASIL TRIANGULARISASI:’ DO 120 I = 1,N

WRITE (*,’(1X,5(F14.8))’) (A(I,J),J=1,M)

120 CONTINUE

C LANGKAH 8: MEMERIKSA ELEMEN A(N,N)

IF(ABS(A(N,N)).LT.1.0E-20) THEN

C MENAMPILKAN PESAN TIDAK UNIK

WRITE(*,5) GOTO 400

END IF

C LANGKAH 9: MENGHITUNG X(N)

X(N) = A(N,N+1)/A(N,N)

C LANGKAH 10: PROSES SUBSTITUSI MUNDUR

L = N-1

DO 15 K=1,L

I = L-K+1

JJ = I+1

SUM = 0.0

DO 16 KK=JJ,N

SUM = SUM+A(I,KK)*X(KK)

16 CONTINUE

X(I) = (A(I,N+1)-SUM)/A(I,I)

15 CONTINUE

C LANGKAH 11: MENAMPILKAN HASIL PERHITUNGAN

WRITE (*,*) WRITE (*,7) DO 18 I = 1,N

WRITE (*,’(1X,A,I2,A,F14.8)’) ’X(’,I,’) = ’,X(I)

18 CONTINUE

400 STOP

5 FORMAT(1X,’SISTEM LINEAR TIDAK MEMILIKI SOLUSI YANG UNIK’)

7 FORMAT(1X,’SOLUSI UNIK’)

END

2.4 Penutup

(41)

2.4. PENUTUP 25

(42)

(43)

Bab 3

Metode

LU Decomposition

✍Objektif :

Pada semua catatan yang terdahulu, telah diulas secara panjang lebar bahwa sistem persamaan linear dapat dicari solusinya secara langsung dengan metode eliminasi gauss. Namun perlu juga diketahui bahwa eliminasi gauss bukan satu-satunya metode dalam mencari solusi sistem persamaan linear, misalnya ada metode matrik inversi seperti yang dijelaskan pada catatan yang paling terakhir. Terlepas dari masalah in-efisiensi penyelesaiannya, yang jelas metode invers matrik bisa digunakan untuk menyelesaikan sistem persamaan linear.

Nah, pada catatan kali ini, saya ingin mengetengahkan sebuah metode yang lain untuk menyelesaikan sistem persamaan linear, yaitumetode faktorisasi matrikyang umum dikenal sebagai LU-decomposition. Metode ini sekaligus menjadi pengantar menuju metode Singular Value Decomposition, (SVD), suatu metode yang saat ini paling “handal” dalam menyelesaikan sistem persamaan linear dan merupakan bagian dari metodeleast square.

Seperti biasa, kita berasumsi bahwa sistem persamaan linear dapat dinyatakan dalam op-erasi matrik

Ax=b (3.1)

Pada metodeLU-decomposition, matrik A difaktorkan menjadi matrik L dan matrik U, dimana dimensi atau ukuran matrik L dan U harus sama dengan dimensi matrik A. Atau dengan kata lain, hasil perkalian matrik L dan matrik U adalah matrik A,

A=LU (3.2)

(44)

sehingga persamaan (9.2) menjadi

LUx=b

Langkah penyelesaian sistem persamaan linear dengan metodeLU-decomposition, diawali den-gan menghadirkan vektorydimana,

Ux=y (3.3)

Langkah tersebut tidak bermaksud untuk menghitung vektory, melainkan untuk menghitung vektor x. Artinya, sebelum persamaan (3.3) dieksekusi, nilai-nilai yang menempati elemen-elemen vektor yharus sudah diketahui. Lalu bagaimana cara memperoleh vektory? Begini caranya,

Ly=b (3.4)

Kesimpulannya, metodeLU-decompositiondilakukan dengan tiga langkah sebagai berikut:

• Melakukan faktorisasi matrik A menjadi matrik L dan matrik U→A=LU.

• Menghitung vektorydengan operasi matrikLy=b. Ini adalah prosesforward-substitution

atau substitusi-maju.

• Menghitung vektorxdengan operasi matrikUx=y. Ini adalah prosesbackward-substitution

atau substitusi-mundur.

MetodeLU-decompositionbisa dibilang merupakan modifikasi dari eliminasi gauss, karena beberapa langkah yang mesti dibuang pada eliminasi gauss, justru harus dipakai oleh LU-decomposition. Untuk lebih jelasnya, perhatikan contoh berikut ini. Diketahui sistem persamaan linear sebagai berikut

P1: x1 + x2 + 3x4 = 4

P2: 2x1 + x2 − x3 + x4 = 1 P3: 3x1 − x2 − x3 + 2x4 = -3 P4: −x1 + 2x2 + 3x3 − x4 = 4

Sistem tersebut dapat dinyatakan dalam operasi matrikAx=y,



(45)

Lain halnya dengan metode LU-decompositiondimana vektorb tidak mengalami perubahan. Yang berubah hanya matrik A saja, yaitu menjadi matrik L dan matrik U,A=LU

A=

Jadi matrik L dan U masing-masing adalah

L=

Coba bandingkan matrik U di atas dengan matrik hasil triangularisasi dari metode eliminasi gauss pada persamaan (3.6), sama persis bukan? Jadi, cara memperoleh matrik U adalah den-gan proses triangularisasi! Lantas, bagaimana cara memperoleh matrik L? Begini caranya: (1) elemen-elemen diagonal matrik L diberi nilai 1 (Asal tahu saja, cara ini dikenal dengan metode

Doolittle). (2) elemen-elemen matrik L yang berada di atas elemen-elemen diagonal diberi ni-lai 0. (3) sedangkan, elemen-elemen matrik L yang berada di bawah elemen-elemen diago-nal diisi dengan faktor pengali yang digunakan pada proses triangularisasi eliminasi gauss. Misalnya pada operasi (P2 ₋2P1) _→ (P2), maka faktor pengalinya adalah 2; pada operasi

(P3−3P1)→(P3), maka faktor pengalinya adalah3, dan seterusnya.

Inilah letak perbedaannya, seluruh faktor pengali tersebut sangat dibutuhkan pada metode

LU-decompositionuntuk membentuk matrik L. Padahal dalam metode eliminasi gauss, seluruh faktor pengali tersebut tidak dimanfaatkan alias dibuang begitu saja. Disisi lain, vektorbtidak mengalami proses apapun sehingga nilainya tetap. Jadi, proses konversi matrik pada metode

LU-decompositionhanya melibatkan matrik A saja!

(46)

Langkah berikutnya adalah menentukan vektory, dimanaLy=b,

Dengan proses substitusi-maju, elemen-elemen vektorydapat ditentukan,

y1 = 4, 2y1+y2 = 1, 3y1+ 4y2+y3 = −3, −y1₋3y2+y4 = 4

maka diperolehy1= 4,y2 =−7,y3 = 13,y4=−13.

Langkah terakhir adalah proses substitusi-mundur untuk menghitung vektorx, dimanaUx=

y,

Melalui proses ini, yang pertama kali didapat solusinya adalahx4, kemudianx3, lalu diikuti x2, dan akhirnyax1.

ian sistem persamaan linear dengan metodeLU-decomposition.

Sekali matrik A difaktorkan, maka vektorbbisa diganti nilainya sesuai dengan sistem per-samaan linear yang lain, misalnya seluruh nilai di ruas kanan diganti menjadi

P1 : x1 + x2 + 3x4 = 8

(47)

Dalam operasi matrik menjadi



Perhatikan baik-baik! Matrik A sama persis dengan contoh sebelumnya. Perbedaannya hanya pada vektorb. Selanjutnya, dengan metodeLU-decomposition, persamaan (3.8) menjadi



Silakan anda lanjutkan proses perhitungannya dengan mencari vektory sesuai contoh yang telah diberikan sebelumnya. Pada akhirnya akan diperoleh solusi sebagai berikut: x1 = 3, x2 =−1,x3= 0, dany4= 2.

Sekarang saatnya saya tunjukkan algoritma metode LU decomposition. Algoritma ini dibu-at untuk menyelesaikan sistem persamaan linear, dengan cara menfaktorkan mdibu-atrikA= (aij) berukuran nxn menjadi matrikL = (lij) dan matrikU = (uij)dengan ukuran yang sama. Algoritma LU-decomposition yang anda lihat sekarang merupakan modifikasi dari algorit-ma eliminasi gauss. Silakan anda periksa langkah-langkah algorit-mana saja yang telah mengalami modifikasi! Tapi asal tahu saja bahwa ini bukan satu-satunya algoritma untuk mendapatkan matrik LU. Sejauh yang saya tahu, ada algoritma lain untuk tujuan yang sama, dimana algo-ritma tersebut membutuhkan matrik permutasi untuk menggeser elemen pivot yang bernilai nol agar terhindar dari singular. Nah, sedangkan algoritma yang akan anda baca saat ini, sama sekali tidak “berurusan” dengan matrik permutasi. Algoritma ini cuma memanfaatkan “trik” tukar posisi yang sudah pernah dibahas di awal-awal catatan khususnya ketika membahas konsep eliminasi gauss.

Satu lagi yang harus saya sampaikan juga adalah bahwa dalam algoritma ini, elemen-elemen matrik L dan matrik U digabung jadi satu dan menggantikan seluruh elemen-elemen-elemen-elemen matrik A. Perhatian! cara ini jangan diartikan sebagai perkalian matrik L dan matrik U menjadi matrik A kembali. Cara ini dimaksudkan untuk menghemat memori komputer. Suatu aspek yang tidak boleh diabaikan oleh para programer. Marilah kita simak algoritmanya bersama-sama!

INPUT: dimensin; nilai elemenaij,1≤i, j ≤n; nilai elemenbi.

OUTPUT: solusi x1, x2, x3, ..., xn atau pesan kesalahan yang mengatakan bahwa faktorisasi tidak mungkin dilakukan.

(48)

elemen-elemen matrik A dan vektorb, seperti berikut ini:

• Langkah 3: Definisikanpsebagai integer dimanai _≤p _≤ n. Lalu pastikan bahwa

api6= 0. Langkah dilakukan bila ditemukan elemen diagonal yang bernilai nol (aii=

0). Ketika ada elemen diagonal yang bernilai nol, maka program harus mencari dan memeriksa elemen-elemen yang tidak bernilai nol dalam kolom yang sama dengan kolom tempat elemen diagonal tersebut berada. Jadi saat proses ini berlangsung, integeri(indeks dari kolom) dibuat konstan, sementara integerp(indeks dari baris) bergerak dari p = isampai p = n. Bila ternyata setelah mencapai elemen paling bawah dalam kolom tersebut, yaitu saat p = n tetap didapat nilai api = 0, maka sebuah pesan dimunculkan: sistem persamaan linear tidak memiliki solusi yang unik. Lalu program berakhir: STOP.

• Langkah 4: Namun jika sebelum integerp mencapai nilaip = n sudah diperoleh elemen yang tidak sama dengan nol (api6= 0), maka bisa dipastikanp6=i. Jikap6=i maka lakukan proses pertukaran (Pp)↔(Pi).

• Langkah 5:Untukj=i+ 1, .., n, lakukan Langkah 6 dan Langkah 7.

• Langkah 6:Tentukanmji,

mji=

aji

aii

• Langkah 7:Lakukan proses triangularisasi,

(Pj −mjiPi)→(Pj)

• Langkah 8:Nilaimjidisimpan keaji,

aji=mji

(49)

• Langkah 10:Lakukan proses substitusi-mundur, dimulai dengan menentukanxn,

xn=

an,n+1 ann Untuki=n₋1, ...,1tentukanxi,

xi =

ai,n+1−Pn_j₌_i₊₁aijxj

aii

• Langkah 11:Diperoleh solusi yaitux1, x2, ..., xn. Algoritma telah dijalankan dengan

suk-ses. STOP.

Algoritma di atas telah diimplementasi kedalam program yang ditulis dengan bahasa For-tran. Program tersebut sudah berhasil dikompilasi dengan visual fortran (windows) dan g77 (debian-linux). Inilah programnya:

DIMENSION A(10,11), B(10), Y(10), X(10)

REAL MJI

WRITE(*,*)

WRITE(*,*) ’==> FAKTORISASI MATRIK: LU DECOMPOSITION <==’ WRITE (*,*)

C LANGKAH 1: MEMASUKAN NILAI ELEMEN-ELEMEN MATRIK A DAN VEKTOR B

WRITE (*,*)

WRITE (*,*) ’MASUKAN ELEMEN-ELEMEN MATRIK A’ DO 50 I = 1,N

DO 60 J = 1,N

WRITE (*,’(1X,A,I2,A,I2,A)’) ’A(’,I,’,’,J,’) = ’ READ (*,*) A(I,J)

60 CONTINUE

WRITE (*,’(1X,A,I2,A)’) ’B(’,I,’) ? ’ READ (*,*) B(I)

WRITE (*,*)

50 CONTINUE

WRITE (*,*)

C MENAMPILKAN MATRIK A

WRITE (*,’(1X,A)’) ’MATRIK A:’ DO 110 I = 1,N

WRITE (*,6) (A(I,J),J=1,N)

110 CONTINUE

WRITE (*,*)

(50)

NN = N-1

DO 10 I=1,NN

P = I

P = P+1

GOTO 100

C MENAMPILKAN PESAN TIDAK DAPAT DIFAKTORKAN

WRITE(*,8) GOTO 400

END IF

IF(P.NE.I) THEN

DO 20 JJ=1,N

C = A(I,JJ)

A(I,JJ) = A(P,JJ)

A(P,JJ) = C

20 CONTINUE

END IF

JJ = I+1

DO 30 J=JJ,N

MJI = A(J,I)/A(I,I)

C LANGKAH 7: PROSES TRIANGULARISASI

DO 40 K=JJ,N

A(J,K) = A(J,K)-MJI*A(I,K)

40 CONTINUE

C LANGKAH 8: MENYIMPAN MJI KE A(J,I)

A(J,I) = MJI

30 CONTINUE

10 CONTINUE

C MENAMPILKAN MATRIK LU

WRITE (*,’(1X,A)’) ’MATRIK LU:’ DO 120 I = 1,N

WRITE (*,6) (A(I,J),J=1,N)

120 CONTINUE

WRITE (*,*)

C LANGKAH 9: SUBSTITUSI-MAJU

(51)

DO 15 I=2,N

SUM = 0.0

DO 16 J=1,I-1

SUM = SUM+A(I,J)*Y(J)

16 CONTINUE

Y(I) = B(I)-SUM

15 CONTINUE

C MENAMPILKAN VEKTOR Y

WRITE (*,’(1X,A)’) ’VEKTOR Y:’ DO 138 I = 1,N

WRITE (*,6) Y(I)

138 CONTINUE

WRITE (*,*)

C LANGKAH 10: SUBSTITUSI-MUNDUR

X(N) = Y(N)/A(N,N)

DO 24 K=1,N-1

I = N-K

JJ = I+1

SUM = 0.0

DO 26 KK=JJ,N

SUM = SUM+A(I,KK)*X(KK)

26 CONTINUE

X(I) = (Y(I)-SUM)/A(I,I)

24 CONTINUE

C LANGKAH 11: MENAMPILKAN SOLUSI DAN SELESAI

WRITE (*,’(1X,A)’) ’SOLUSI:’ DO 18 I = 1,N

WRITE (*,’(1X,A,I2,A,F14.8)’) ’X(’,I,’) = ’,X(I)

18 CONTINUE

WRITE(*,*)

WRITE(*,*) ’SELESAI --> SUKSES’ WRITE(*,*)

400 CONTINUE

6 FORMAT(1X,5(F14.8))

8 FORMAT(1X,’TIDAK DAPAT DIFAKTORKAN’)

END

(52)

(53)

Bab 4

Invers Matrik dan Eliminasi Gauss

✍Objektif :

Secara umum, sistem persamaan linear adalah sebagai berikut:

a11x1+a12x2+. . .+a1nxn = b1 a21x1+a22x2+. . .+a2nxn = b2 . . . = . . . . . . = . . . an1x1+an2x2+. . .+annxn = bn

Sistem persamaan linear tersebut dapat dinyatakan dalam bentuk operasi matrik,

Ax=b (4.1)

sehingga bentuknya menjadi seperti ini:

(54)

dimana

Dalam kaitannya dengan invers matrik, matrikAdisebut matriknon-singular jika matrik A

memiliki matrik invers dirinya yaituA−1. Atau dengan kata lain, matrikA−1 adalah invers dari matrik A. Jika matrik A tidak memiliki invers, maka matrik A disebut singular. Bila matrikAdikalikan dengan matrikA−1maka akan menghasilkan matrik identitasI, yaitu suatu matrik yang elemen-elemen diagonalnya bernilai 1.

AA−1 =I=

Bila keduanya dikalikan, maka akan menghasilkan matrik identitas,

AA−1=

Lalu bagaimana cara mendapatkan matrik invers,A−1? Persamaan (4.2) bisa dijadikan pedo-man..

i11 i12 i13 i21 i22 i23

dalam hal ini matrikA−1adalah

(55)

Elemen-elemen matrik invers, A−1 dapat diperoleh dengan menerapkan metode eliminasi gauss. Diawali dengan membentuk matrik augment:



Langkah berikutnya, matrik augment yang telah mengalami triangularisasi tersebut dipecah menjadi tiga buah matrik augment seperti berikut ini:



Langkah pamungkasnya adalah melakukan proses substitusi mundur pada ketiga matrik aug-ment di atas, sehingga diperoleh:

i11=−2₉

Hasil tersebut digabung menjadi sebuah matrik, yaitu matrikA−1,

A−1=

Keberadaan matrikA−1 bisa digunakan untuk menyelesaikan sistem persamaan linear (men-cari nilai x), dengan cara sebagai berikut

Ax = b A−1Ax = A−1b

Ix = A−1b

x = A−1b (4.3)

(56)

persamaan linear

x1+ 2x2−x3 = 2 2x1+x2 = 3 −x1+x2+ 2x3 = 4

Bila dikonversikan kedalam operasi matrik menjadi



Berdasarkan persamaan (4.3), maka elemen-elemen vektorxdapat dicari dengan cara

x=A−1b

Akhirnya diperoleh solusix1 = 7/9,x2 = 13/9, danx3 = 5/3. Penyelesaian sistem persamaan

linear menjadi lebih mudah bila matrik A−1 sudah diketahui. Sayangnya, untuk mendap-atkan matrikA−1, diperlukan langkah-langkah, seperti yang sudah dibahas pada contoh per-tama di atas, yang berakibat in-efisiensi proses penyelesaian (secara komputasi) bila diband-ingkan dengan metode eliminasi gauss untuk memecahkan sistem persamaan linear. Namun bagaimanapun, secara konseptual kita dianjurkan mengetahui cara bagaimana mendapatkan matrikA−1.

Saya telah memodifikasi program eliminasi gauss yang terdahulu, untuk keperluan perhitun-gan matrik invers. Program ini ditulis denperhitun-gan bahasa fortran, sudah berhasil dikompilasi dalam Linux Debian (g77) dan Windows XP (Visual Fortran). Inilah programnya,

DIMENSION A(10,20), D(10,10), X(10)

REAL MJI

INTEGER TKR, BK, TK, Q

WRITE (*,*) ’=PROGRAM INVERS MATRIK DENGAN ELIMINASI GAUSS=’ WRITE (*,*)

C LANGKAH 1: MEMASUKAN NILAI ELEMEN-ELEMEN MATRIK A

WRITE (*,*)

WRITE (*,*) ’MASUKAN ELEMEN-ELEMEN MATRIK A’ M = N + 1

(57)

DO 60 J = 1,N

60 CONTINUE

50 CONTINUE

C LANGKAH 2: MENDEFINISIKAN MATRIK IDENTITAS

WRITE (*,*) ’MENDEFINISIKAN MATRIK IDENTITAS’ DO 70 I = 1,N

DO 80 J = M,N+N

A(I,J) = 0

IF (I+N .EQ. J) THEN

A(I,J) = 1

END IF

80 CONTINUE

70 CONTINUE

WRITE (*,*)

C MENAMPILKAN MATRIK AUGMENT

WRITE (*,’(1X,A)’) ’MATRIK AUGMENT:’ DO 110 I = 1,N

WRITE (*,’(1X,5(F14.8))’) (A(I,J),J=1,N+N)

110 CONTINUE

WRITE (*,*)

C MENGHITUNG JUMLAH TUKAR (TKR) POSISI. MULA2 TKR = 0

TKR = 0

C MENGHITUNG JUMLAH OPERASI BAGI/KALI (BK).

BK = 0

C MENGHITUNG JUMLAH OPERASI TAMBAH/KURANG (TK).

TK = 0

C LANGKAH 3: MEMERIKSA ELEMEN2 PIVOT DAN PROSES TUKAR POSISI

NN = N-1

DO 10 I=1,NN

P = I

P = P+1

GOTO 100

C MENAMPILKAN PESAN SINGULAR

WRITE(*,5) GOTO 400

(58)

IF(P.NE.I) THEN

DO 20 JJ=1,N+N

C = A(I,JJ)

A(I,JJ) = A(P,JJ)

A(P,JJ) = C

TKR = TKR + 1

20 CONTINUE

END IF

JJ = I+1

DO 30 J=JJ,N

MJI = A(J,I)/A(I,I)

BK = BK + 1

C LANGKAH 8: MELAKUKAN PROSES TRIANGULARISASI

DO 40 K=JJ,N+N

A(J,K) = A(J,K)-MJI*A(I,K) BK = BK + 1

TK = TK + 1

40 CONTINUE

A(J,I) = 0

30 CONTINUE

10 CONTINUE

C MENAMPILKAN HASIL TRIANGULARISASI

WRITE (*,’(1X,A)’) ’HASIL TRIANGULARISASI:’ DO 120 I = 1,N

WRITE (*,’(1X,5(F14.8))’) (A(I,J),J=1,N+N)

120 CONTINUE

C LANGKAH 9: MEMERIKSA ELEMEN A(N,N)

IF(ABS(A(N,N)).LT.1.0E-20) THEN

C MENAMPILKAN PESAN SINGULAR

WRITE(*,5) GOTO 400

END IF

DO 500 J = 1,N

Q=N+J

C LANGKAH 10: MENGHITUNG A(N,N)

D(J,N) = A(N,Q)/A(N,N)

BK = BK + 1

(59)

L = N-1

DO 15 K=1,L

I = L-K+1

JJ = I+1

SUM = 0.0

DO 16 KK=JJ,N

SUM = SUM+A(I,KK)*D(J,KK) BK = BK + 1

TK = TK + 1

16 CONTINUE

D(J,I) = (A(I,Q)-SUM)/A(I,I)

BK = BK + 1

TK = TK + 1

15 CONTINUE

500 CONTINUE

C LANGKAH 12: MENAMPILKAN HASIL PERHITUNGAN

WRITE (*,*)

WRITE (*,’(1X,A)’) ’MATRIK INVERS:’ DO 220 I = 1,N

WRITE (*,’(1X,5(F14.8))’) (D(J,I),J=1,N)

220 CONTINUE

WRITE(*,8) TKR WRITE(*,9) BK WRITE(*,11) TK

400 STOP

5 FORMAT(1X,’MATRIK A BERSIFAT SINGULAR’)

8 FORMAT(1X,’JUMLAH TUKAR POSISI = ’,3X,I5)

9 FORMAT(1X,’JUMLAH OPERASI BAGI/KALI = ’,3X,I6)

11 FORMAT(1X,’JUMLAH OPERASI JUMLAH/KURANG = ’,3X,I6)

END

(60)

(61)

Bab 5

Iterasi Jacobi

✍Objektif :

Sebelum kita membahas metode iterasi untuk menyelesaikan problem sistem persamaan lin-ear, saya ingin menyampaikan satu hal yang sangat sederhana, yaitu tentang cara merepre-sentasikan elemen-elemen suatu vektor-kolom. Sebagaimana tertulis pada catatan catatan se-belumnya, biasanya suatu vektor-kolom ditulis sebagai

x=

     

x1 x2

.. .

xn

     

(5.1)

Dengan operasi transpose, vektor-kolom tersebut dapat dinyatakan sebagai

x=hx1 x2 . . . xn

it

(5.2)

Contoh:

x=

     

3 −2

8 5

     

=h3 ₋2 8 5it

(62)

Cara penulisan seperti ini digunakan untuk menyatakan vektor-kolom pada suatu kalimat di-dalam paragraf. Alasannya supaya tidak terlalu menyita banyak ruang penulisan. Sementara, persamaan (1), lebih sering digunakan pada penulisan operasi matrik. Satu hal lagi, pada paragraf-paragraf berikutnya, saya persingkat penulisan istilah vektor-kolom menjadi vektor saja.

Pengenalan norm

Vektorx= (x1;x2;...;xn)tmemiliki normℓ2 danℓ∞yang didefinisikan sebagai

ℓ2 =kxk2 ={

n

X

i=1

x2_i_}1/2 (5.3)

dan

ℓ∞=kxk∞= max

1≤i≤n|xi| (5.4)

Contoh:x= (3;₋2; 8; 5)T _{memiliki norm}_ℓ

2 yaitu

ℓ2 =kxk2=

p

(3)2_{+ (}₋₂₎2_{+ (8)}2_{+ (5)}2_{= 10,}₀₉₉₅

dan normℓ∞yaitu

ℓ∞=kxk∞= max{(3),(−2),(8),(5)}= 8

Saya menyarankan agar kedua norm ini diingat-ingat dengan baik, karena akan banyak dis-inggung pada catatan-catatan berikutnya.

Pengenalan metode iterasi

Sekarang kita mulai pembahasan tentang metode iterasi untuk menyelesaikan problem sistem persamaan linear. Metode ini berbeda dengan metode-metode yang telah dijelaskan sebelum-nya, dimana metode ini dimulai dengan menentukan nilai awal (initial value) untuk setiap elemen vektor x. Kemudian berdasarkan nilai awal tersebut, dilakukan langkah perhitungan untuk mendapatkan elemen-elemen vektor x yang baru.

x(baru)=Tx(lama)+c

atau

xk=Txk−1+c (5.5)

dimanak= 1,2,3, ...

(63)

Lalu, sistem persamaan tersebut diubah susunannya menjadi seperti ini

x1 =

dengan) sebagaix(baru). Sementara nilai x1, x2, x3 danx4 yang berada di ruas kanan tanda = (baca: sama dengan) sebagaix(lama)_{. Sistem persamaan tersebut menjadi seperti ini}

x(₁baru) = 1

atau seperti ini

x(₁k) = 1

Sehingga bentuk sistem persamaan yang terakhir ini dapat dinyatakan dalam persamaan ma-trik sebagai berikut

(64)

Padak= 1,

x(1)sebagai berikut

x(1)₁ = 6

tungan tersebut diulangi kembali dengan nilaik= 2. Lalu nilai-nilaix(1)= (0,6000; 2,2727;₋1,1000; 1,8750

dimasukan ke ruas kanan,

x(2)₁ = 1

(65)

k 0 1 2 3 4 ... 9 10

x(₁k) 0,0000 0,6000 1,0473 0,9326 1,0152 ... 0,9997 1,0001

x(₂k) 0,0000 2,2727 1,7159 2,0530 1,9537 ... 2,0004 1,9998

x(₃k) 0,0000 -1,1000 -0,8052 -1,0493 -0,9681 ... -1,0004 -0,9998

x(₄k) 0,0000 1,8852 0,8852 1,1309 0,9739 ... 1,0006 0,9998

maka kita akan memperoleh nilai-nilaix(3) = (0,9326; 2,0530;₋1,0493; 1,1309)t. Lalu proses perhitungan diulangi lagi dengank= 4. Begitu seterusnya proses ini diulang-ulang lagi untuk nilai-nilaikberikutnya. Proses yang berulang ini disebutiterasi. Sampai denganx(3) di atas, kita sudah melakukan tiga kali proses iterasi. Lantas sampai kapankah proses iterasi ini terus berlanjut? Jawabnya adalah sampaix(baru)mendekati solusi yang sesungguhnya, yaitu

x= (1; 2;₋1; 1)t

Dengan kata lain, proses iterasi harus di-stop atau dihentikan bila x(baru) sudah mendekati solusi. Lalu kriteria apa yang digunakan sehingga suatu hasil iterasi bisa dikatakan paling dekat dengan solusi yang sebenarnya? OK, simpan dulu pertanyaan ini, marilah kita amati hasil seluruh iterasi dari iterasi yang pertama hingga iterasi yang ke sepuluh. Tabel di atas ini menampilkan hasil perhitungan hingga iterasi yang ke sepuluh. Kita bisa saksikan bahwa hasil iterasi ke-1,x(1) = (0,6000; 2,2727;₋1,1000; 1,8852)adalah hasil yang paling tidak mendekati solusix= (1; 2;₋1; 1)t. Dibandingkan dengan hasil iterasi ke-2, jelas terlihat bahwa hasil iterasi ke-2 lebih mendekati solusi. Kalau terus diurutkan, maka hasil iterasi ke-10 merupakan hasil yang paling dekat dengan solusi.

Dengan memanfaatkan perhitungan norm, secara kuantitatif dapat disimpulkan bahwa it-erasi yang ke-10 adalah yang paling dekat dengan solusi. Pada tabel dibawah ini, saya meng-gunakan normℓ2, sedangkan hasil perhitungan norm, saya beri nama epsilon,ǫ. Jadi semakin

kecil nilai epsilon,ǫ, hasil iterasinya semakin dekat dengan solusi.

Kembali ke pertanyaan penting yang tadi yaitu kriteria apa yang digunakan sehingga su-atu hasil iterasi bisa dikatakan paling dekat dengan solusi yang sebenarnya? Jawabnya adalah besar kecilnya nilaiǫ. Artinya kalau nilaiǫditentukan sebesar 0,2 , maka iterasi akan berhen-ti pada iterasi yang ke-4. Atau kalau nilai ǫ ditentukan sebesar 0,001 , maka proses iterasi akan berhenti pada iterasi yang ke-10. Kesimpulannya, semakin kecil nilai ǫ, semakin pan-jang proses iterasinya, namun hasil akhirnya semakin dekat dengan solusi sebenarnya. Jadi nilaiǫberperan penting untuk menghentikan proses iterasi. Dalam hal ini,ǫdisebut sebagai stopping-criteria.

Metode yang baru saja kita bahas ini disebut metodeIterasi Jacobi. Metode ini bertujuan

normℓ2 °°x(2)−x(1) ° °

2

°

°x(3)−x(2) ° °

2

°

°x(4)−x(3) ° °

2 ...

°

°x(10)−x(9) ° °

2

(66)

mencari nilai-nilai pengganti variabel-variabel x dengan perumusan

x(_ik)=

Pn

j=1

³

−aijx(_jk−1)

´

+bi

aii (5.7)

dimanai=1,2,3,...,n.

Algoritma Iterasi Jacobi

• Langkah 1: Tentukank=1

• Langkah 2: Ketika (k_≤N) lakukan Langkah 3-6

– Langkah 3: Untuki=1,...,n, hitunglah

xi= −

Pn

j=1(aijXOj) +bi aii

– Langkah 4: Jikakx−XOk< ǫ, maka keluarkan OUTPUT (x1, ..., xn) lalu STOP – Langkah 5: Tentukank=k+1

– Langkah 6: Untuki=1,...n, tentukanXOi =xi

• Langkah 7: OUTPUT (’Iterasi maksimum telah terlampaui’) lalu STOP

Program dalam Fortran

IMPLICIT NONE

DIMENSION A(10,10),B(10),X(10),XO(10)

REAL A,B,X,XO,EPS,NORM,S

INTEGER N,I,J,K,ITMAX

WRITE(*,*) ’==> ITERASI JACOBI UNTUK SISTEM LINEAR <==’ WRITE(*,*)

WRITE (*,*) ’MASUKAN ELEMEN-ELEMEN MATRIK A DAN VEKTOR B’ DO 52 I = 1,N

DO 62 J = 1,N

62 CONTINUE

WRITE (*,*)

52 CONTINUE

(67)

READ (*,*) ITMAX

WRITE (*,’(1X,A)’) ’NILAI EPSILON ATAU TOLERANSI ? ’ READ (*,*) EPS

WRITE (*,*) ’MASUKAN NILAI AWAL UNTUK XO’ DO 72 I = 1,N

WRITE (*,’(1X,A,I2,A)’) ’XO(’,I,’) ? ’ READ (*,*) XO(I)

72 CONTINUE

WRITE (*,*)

WRITE (*,6) (A(I,J),J=1,N)

110 CONTINUE

WRITE (*,*)

C MENAMPILKAN VEKTOR B

WRITE (*,’(1X,A)’) ’VEKTOR B:’ DO 111 I = 1,N

WRITE (*,6) B(I)

111 CONTINUE

WRITE (*,*)

C LANGKAH 1

K = 1

C LANGKAH 2

100 IF(K.GT.ITMAX) GOTO 200

C LANGKAH 3

NORM = 0.0

DO 10 I = 1,N

S = 0.0

DO 20 J=1,N

S = S-A(I,J)*XO(J)

20 CONTINUE

S = (S+B(I))/A(I,I)

IF (ABS(S).GT.NORM) NORM=ABS(S)

X(I) = XO(I)+S

10 CONTINUE

WRITE(*,’(1X,A,I3)’) ’ITERASI KE-’, K WRITE(*,’(1X,A,F14.8)’) ’NORM = ’, NORM

WRITE(*,’(1X,A,I3,A,F14.8)’) (’X(’,I,’) = ’, X(I),I=1,N) WRITE(*,*)

(68)

IF(NORM.LE.EPS) THEN

WRITE(*,7) K,NORM GOTO 400

END IF

C LANGKAH 5

K = K+1

C LANGKAH 6

DO 30 I=1,N

XO(I) = X(I)

30 CONTINUE

GOTO 100

C LANGKAH 7

200 CONTINUE

WRITE(*,9)

400 STOP

5 FORMAT(1X,I3)

6 FORMAT(1X,(6(1X,F14.8)))

7 FORMAT(1X,’KONVERGEN PADA ITERASI YANG KE- ’,I3,

*’ , NORM= ’,F14.8)

9 FORMAT(1X,’MELEBIHI BATAS MAKSIMUM ITERASI’)

END

(69)

Bab 6

Iterasi Gauss-Seidel

✍Objektif :

Metode Iterasi Gauss-Seidel merupakan modifikasi dari metode Iterasi Jacobi. Modifikasi tersebut terletak pada rumus berikut:

x(_ik) = −

Pi−1

j=1

³

aijx(_jk)

´

−Pn

j=i+1

³

aijx(_jk−1)

´

+bi

aii (6.1)

Untuk lebih jelasnya, marilah kita perhatikan contoh berikut, diketahui sistem persamaan linearAx=byaitu

10x1−x2+ 2x3 = 6 −x1+ 11x2−x3+ 3x4 = 25

2x1₋x2+ 10x3₋x4 = ₋11 3x2₋x3+ 8x4 = 15

(70)

Lalu, sistem persamaan tersebut diubah susunannya menjadi seperti ini nilai-nilaix(1)sebagai berikut

x(1)₁ = 0,6000 x(1)₂ = 2,3272 x(1)₃ = ₋0,9873 x(1)₄ = 0,8789

Lalu proses perhitungan diulangi lagi dengan k = 2. Begitu seterusnya proses ini diulang-ulang lagi untuk nilai-nilai k berikutnya sampai x(k) mendekati solusi yang sesungguhnya, yaitu

x= (1; 2;₋1; 1)t

Marilah kita amati hasil seluruh iterasi. Tabel di bawah ini menampilkan hasil perhitungan hingga iterasi yang ke-5. Kita bisa saksikan bahwa dibandingkan dengan iterasi Jacobi, prob-lem sistem persamaan linear yang sama, bisa diselesaikan oleh metode iterasi Gauss-Seidel dalam 5 kali iterasi.

k 0 1 2 3 4 5

x(₁k) 0,0000 0,6000 1,030 1,0065 1,0009 1,0001

x(₂k) 0,0000 2,3272 2,037 2,0036 2,0003 2,0000

x(₃k) 0,0000 -0,9873 -1,014 -1,0025 -1,0003 -1,0000

x(₄k) 0,0000 0,8789 0,9844 0,9983 0,9999 1,0000

Dari kasus ini, bisa kita simpulkan bahwa iterasi Gauss-Seidel bekerja lebih efektif diband-ingkan iterasi Jacobi. Ya.., memang secara umum demikian, akan tetapi ternyata ditemukan kondisi yang sebaliknya pada kasus-kasus yang lain.

Algoritma Iterasi Jacobi

• Langkah 1: Tentukank=1

(71)

– Langkah 3: Untuki=1,...,n, hitunglah

xi= −

Pi−1

j=1aijxj −Pnj=i+1aijXOj+bi

aii

– Langkah 4: Jikakx₋XO_k< ǫ, maka keluarkan OUTPUT (x1, ..., xn) lalu STOP

– Langkah 5: Tentukank=k+1

– Langkah 6: Untuki=1,...n, tentukanXOi =xi

• Langkah 7: OUTPUT (’Iterasi maksimum telah terlampaui’) lalu STOP

Program dalam Fortran

IMPLICIT NONE

DIMENSION A(10,10),B(10),X(10),XO(10)

REAL A,B,X,XO,EPS,NORM,S1,S2

INTEGER N,I,J,K,ITMAX

WRITE(*,*)

WRITE(*,*) ’==> ITERASI GAUSS-SEIDEL UNTUK SISTEM LINEAR <==’ WRITE(*,*)

WRITE (*,*) ’MASUKAN ELEMEN-ELEMEN MATRIK A DAN VEKTOR B’ DO 52 I = 1,N

DO 62 J = 1,N

62 CONTINUE

WRITE (*,*)

52 CONTINUE

WRITE (*,’(1X,A)’) ’JUMLAH ITERASI MAKSIMUM ? ’ READ (*,*) ITMAX

WRITE (*,’(1X,A)’) ’NILAI EPSILON ATAU TOLERANSI ? ’ READ (*,*) EPS

WRITE (*,*) ’MASUKAN NILAI AWAL UNTUK XO’ DO 72 I = 1,N

WRITE (*,’(1X,A,I2,A)’) ’XO(’,I,’) ? ’ READ (*,*) XO(I)

72 CONTINUE

(72)

WRITE (*,6) (A(I,J),J=1,N)

110 CONTINUE

WRITE (*,*)

C MENAMPILKAN VEKTOR B

WRITE (*,’(1X,A)’) ’VEKTOR B:’ DO 111 I = 1,N

WRITE (*,6) B(I)

111 CONTINUE

WRITE (*,*)

C LANGKAH 1

K = 1

C LANGKAH 2

100 IF(K.GT.ITMAX) GOTO 200

C LANGKAH 3

DO 10 I = 1,N

S1 = 0.0

DO 20 J=I+1,N

S1 = S1-A(I,J)*XO(J)

20 CONTINUE

S2 = 0.0

DO 23 J=1,I-1

S2 = S2-A(I,J)*X(J)

23 CONTINUE

X(I) = (S2+S1+B(I))/A(I,I)

10 CONTINUE

C SAYA PILIH NORM-2. ANDA BOLEH PAKAI NORM YANG LAIN!

NORM = 0.0

DO 40 I=1,N

NORM = NORM + (X(I)-XO(I))*(X(I)-XO(I))

40 CONTINUE

NORM = SQRT(NORM)

WRITE(*,’(1X,A,I3)’) ’ITERASI KE-’, K WRITE(*,’(1X,A,F14.8)’) ’NORM-2 = ’, NORM

WRITE(*,’(1X,A,I3,A,F14.8)’) (’X(’,I,’) = ’, X(I),I=1,N) WRITE(*,*)

C LANGKAH 4

IF(NORM.LE.EPS) THEN

(73)

GOTO 400

END IF

C LANGKAH 5

K = K+1

C LANGKAH 6

DO 30 I=1,N

XO(I) = X(I)

30 CONTINUE

GOTO 100

C LANGKAH 7

200 CONTINUE

WRITE(*,9)

400 STOP

5 FORMAT(1X,I3)

6 FORMAT(1X,(6(1X,F14.8)))

7 FORMAT(1X,’KONVERGEN PADA ITERASI YANG KE- ’,I3,

*’ , NORM= ’,F14.8)

9 FORMAT(1X,’MELEBIHI BATAS MAKSIMUM ITERASI’)

END

(74)

(75)

Bab 7

Iterasi

Succesive-Over-Relaxation

✍Objektif :

Metode Iterasi Relaksasi (Relaxation method ) dinyatakan dengan rumus berikut:

x(_ik)= (1₋ω)x(_ik−1)+ ω aii

 bi−

i−1

X

j=1

aijx(_jk)− n

X

j=i+1

aijx(_jk−1)



 (7.1)

Untuk lebih jelasnya, marilah kita perhatikan contoh berikut, diketahui sistem persamaan linearAx=byaitu

4x1+ 3x2+ = 24 3x1+ 4x2−x3 = 30 −x2+ 4x3 = −24

memiliki solusi (3,4,₋5)t. Metode Gauss-Seidel dan Relaksasi denganω = 1,25 akan digu-nakan untuk menyelesaikan sistem persamaan linear di atas dengan x(0) = (1,1,1)t. Untuk

(76)

Tabel 7.1: Gauss-Seidel

k 0 1 2 3 4 5 6 7

x(₁k) 1 5,2500 3,1406 3,0879 3,0549 3,0343 3,0215 3,0134

x(₂k) 1 3,8125 3,8828 3,9267 3,9542 3,9714 3,9821 3,9888

x(₃k) 1 -5,0468 -5,0293 -5,0183 -5,0114 -5,0072 -5,0044 -5,0028

Tabel 7.2: Relaksasi denganω= 1,25

k 0 1 2 3 4 5 6 7

x(₁k) 1 6,3125 2,6223 3,1333 2,9570 3,0037 2,9963 3,0000

x(₂k) 1 3,5195 3,9585 4,0102 4,0075 4,0029 4,0009 4,0002

x(₃k) 1 -6,6501 -4,6004 -5,0967 -4,9735 -5,0057 -4,9983 -5,0003

setiap nilaik= 1,2,3, ..., persamaan Gauss-Seidelnya adalah

x(₁k) = ₋0,75x(₂k−1)+ 6

x₂(k) = ₋0,75x₁(k)+ 0,25x(₃k−1)+ 7,5 x(₃k) = 0,25x(₂k)₋6

Sedangkan persamaan untuk metode Relaksasi denganω= 1,25adalah

x₁(k) = ₋0,25x₁(k−1)₋0,9375x(₂k−1)+ 7,5

x(₂k) = ₋0,9375x(₁k)₋0,25x(₂k−1)+ 0,3125x(₃k−1)+ 9,375 x(₃k) = 0,3125x(₂k)₋0,25x(₃k−1)₋7,5

Tabel berikut ini menampilkan perhitungan dari masing-masing metode hingga iterasi ke-7. Dari kasus ini, bisa kita simpulkan bahwa iterasi Relaksasi memerlukan proses iterasi yang lebih singkat dibandingkan iterasi Gauss-Seidel. Jadi, pada kasus ini (dan juga secara umum), Relaksasi lebih efektif dibandingkan Gauss-Seidel. Pertanyaannya sekarang, bagaimana menen-tukan nilaiωyang optimum?

Metode Relaksasi dengan pilihan nilai ω yang berkisar antara 0 dan 1 disebut metode under-relaxation, dimana metode ini berguna agar sistem persamaan linear mencapai kon-disi konvergen walaupun sistem tersebut sulit mencapai konkon-disi konvergen dengan metode Gauss-Seidel. Sementara bilaωnilainya lebih besar dari angka 1, maka disebut metode succes-sive over-relaxation (SOR), yang mana metode ini berguna untuk mengakselerasi atau mem-percepat kondisi konvergen dibandingkan dengan Gauss-Seidel. Metode SOR ini juga sangat berguna untuk menyelesaikan sistem persamaan linear yang muncul dari persamaan diferensial-parsial tertentu.

Algoritma Iterasi Relaksasi