SKRIPSI Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika. Oleh :

(1)

NILAI EKSTREM LOKAL FUNGSI POLINOMIAL BERDERAJAT 5 YANG SIMETRIS MENGGUNAKAN METODE GOLDEN SECTION

SEARCH YANG DIKOMBINASIKAN DENGAN KONSEP ALJABAR DAN GEOMETRI

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika

Oleh :

Cresentia Carina Ardianti Ayuningtyas NIM : 131414039

PROGRAM STUDI PENDIDIKAN MATEMATIKA

JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

UNIVERSITAS SANATA DHARMA YOGYAKARTA

(2)

i

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika

Oleh :

Cresentia Carina Ardianti Ayuningtyas NIM : 131414039

PROGRAM STUDI PENDIDIKAN MATEMATIKA

JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

UNIVERSITAS SANATA DHARMA YOGYAKARTA

(3)

(4)

(5)

iv

HALAMAN PERSEMBAHAN

“A great discovery solves a great problem but there is a grain of discovery in the solution of any problem. Your problem may be modest, but if it challenges your curiosity and brings into play your inventive faculties, and if you solve it by own

means you may experience the tension and enjoy the triumph of discovery” George Polya

“Janganlah hendaknya kamu kuatir tentang apapun juga, tetapi nyatakanlah dalam segala hal keinginanmu kepada Allah dalam doa dan permohonan dengan

ucapan syukur.” Filipi 4:6

Karya ini kupersembahkan untuk :

Keluarga kecilku : Petrus Sunardi, Lucia Purwanti dan Ch. Lucky A. Barnabas Kresna R.

Sahabat seperjuangan : Fransiska Dian R., Rosalia Widi L., Paskalia K., Valentina Retno P., Reska D., Lusia Widya K.

Keluarga Van Lith Angkatan 20

(6)

v

PERNYATAAN KEASLIAN KARYA

Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini tidak memuat karya atau bagian karya orang lain, kecuali telah disebutkan dalam kutipan dan daftar pustaka, sebagaimana layaknya karya ilmiah.

Yogyakarta, 29 Mei 2017 Penulis

(7)

vi

LEMBAR PERNYATAAN PERSETUJUAN

PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIK Yang bertanda tangan di bawah ini saya mahasiswa Universitas Sanata Dharma : Nama : Cresentia Carina Ardianti Ayuningtyas

NIM : 131414039

Demi perkembangan ilmu pengetahuan saya memberikan kepada Perpustakaan Universitas Sanata Dharma karya ilmiah saya yang berjudul :

Dengan demikian, saya memberikan kepada Perpusatkaan Universitas Sanata Dharma hak untuk menyimpan, mengalihkan dalam bentuk media lain, mengolahnya dalam pangkalan data, mendistribusikan secara terbatas, dan mempublikasikannya di internet atau media lain untuk kepentingan akademik tanpa perlu meminta izin kepada saya atau memberikan royalti pada saya selama masih tetap mencantumkan nama saya sebagai penulis.

Demikian pernyataan ini yang saya buat dengan sebenarnya. Yogyakarta, 29 Mei 2017

Yang menyatakan

(8)

vii ABSTRAK

Cresentia Carina Ardianti Ayuningtyas, 2017. Nilai Ekstrem Lokal Fungsi Polinomial Berderajat 5 Yang Simetris Menggunakan Metode Golden Section Search Yang Dikombinasikan Dengan Konsep Aljabar Dan Geometri. Skripsi. Program Studi Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma, Yogyakarta.

Latar belakang dari penelitian ini adalah pengembangan dari penelitian terdahulu yang membahas tentang menentukan nilai ekstrem fungsi polinomial berderajat 5 tanpa menggunakan konsep turunan, tetapi menggunakan konsep aljabar dan geometri. Pada penelitian ini, metode yang digunakan untuk mencari nilai ekstrem lokal fungsi polinomial berderajat 5 adalah metode numerik yang dikombinasikan dengan konsep aljabar dan geometri. Objek yang diteliti adalah fungsi polinomial berderajat 5 yang simetris. Metode numerik yang digunakan adalah metode Golden Section Search.

Penelitian ini bertujuan untuk menentukan karakteristik fungsi polinomial berderajat 5 yang simetris, menentukan selang pada fungsi polinomial berderajat 5 yang simetris sehingga fungsi unimodal pada selang tersebut dan menentukan nilai ekstrem fungsi polinomial berderajat 5 yang simetris menggunakan metode Golden Section Search yang dikombinasikan dengan menggunakan konsep aljabar dan geometri. Langkah awal yang dilakukan dalam penelitian ini adalah menguji kesimetrisan fungsi polinomial berderajat 5, ( ) . Jika fungsi merupakan fungsi yang simetris maka proses dilanjutkan ke langkah selanjutnya. Fungsi merupakan fungsi yang simetris jika fungsi memiliki pusat simetri di

, dengan pusat simetri berupa titik simetri putar

( ( )). Langkah selanjutnya adalah melakukan translasi pada fungsi g dengan menggeser titik simetri putarnya ke O(0,0). Hasil translasi tersebut diperoleh suatu fungsi ganjil, yaitu fungsi .

Proses selanjutnya adalah menentukan pembuat nol dari fungsi dan menganalisis banyaknya nilai ekstrem yang dimiliki oleh fungsi berdasarkan banyaknya pembuat nol real dari fungsi . Hasil analisis tersebut menunjukkan ada 7 kasus berbeda yang menggambarkan kemungkinan dari nilai ekstrem lokal fungsi . Dari hasil analisis tersebut juga diperoleh selang sedemikian sehingga fungsi unimodal pada selang tersebut. Selang tersebut terbentuk dari dua pembuat nol real dari fungsi . Setelah diperoleh selang tersebut, nilai ekstrem lokal dari fungsi ditentukan dengan menggunakan metode Golden Section Search. Proses akhir dari penelitian ini adalah menentukan nilai ekstrem lokal dari fungsi dengan cara mentranslasikan kembali dari fungsi ke fungsi . Setiap proses yang dilakukan dalam penelitian ini disimulasikan menggunakan komputer dan dituliskan menjadi sebuah program yang diaplikasikan pada MATLAB.

Kata Kunci : Fungsi Polinomial Berderajat 5, Golden Section Search, Nilai Ekstrem, Polinomial, Unimodal.

(9)

viii ABSTRACT

Cresentia Carina Ardianti Ayuningtyas, 2017. Extreme Relative Value of Symmetric Fifth Degree Polynomial Function Use Golden Section Search Method which is Combined with Algebraic and Geometry Concept. Thesis. Mathematics Education Studi Program, Mathematics and Science Education Department, Faculty of Teacher and Traingin and Education, Sanata Dharma University, Yogyakarta.

The background of this research is the development from the previous research that discuss about extreme value of fifth degree polynomial function without derivative concepts, but with algebraic and geometry concepts. In this research, numerical method which is combined with algebraic and geometry concepts are used to determine extreme value of fifth degree polynomial function. The object of this research is symmetric fifth degree polynomial function. Golden Section Search method, one of numerical methods, is used in this research.

This research aims to determine characteristic of symmetric fifth degree polynomial function, determine interval such that symmetric fifth degree polynomial function is unimodal in that interval and determine extreme relative value of symmetric fifth degree polynomial function with Golden Section Search that is combined with algebraic and geometry concepts. The first step is to do the symmetry test of fifth degree polynomial function, ( ) . If is a symmetric function, then the process will be continued. Function g is symmetric if has symmetry center at

the center symmetry

of is rotational symmetry point ( ( )). The next step is to translate function by moving its rotational symmetry point to origin O(0,0). From the result of the translation, an odd function, which is called function , is obtained.

The next step is to determine the zeros of and analyzing how many has extreme relative value based on the zeros of which it has. The result of this analysis indicates that there are 7 different cases that illustrate the possibility of extreme relative value . Besides, the analysis’s result finds interval such that function is unimodal in this interval. The interval is formed of two zeros-real, which are adjacent, of . After the interval is found, extreme relative value of is determined by Golden Section Search method. The last process is to determine extreme relative value of by translating to . Every process in this research are simulated by computer and written into program that can be applied in MATLAB.

Keyword : Fifth Degree Polynomial Function, Golden Section Search, Extreme Value, Polynomial, Unimodal.

(10)

ix

KATA PENGANTAR

Puji dan syukur penulis haturkan kepada Tuhan Yang Maha Esa atas rahmat dan berkatNya, penulis dapat menyelesaikan skripsi dengan judul “Nilai Ekstrem Fungsi Polinomial Berderajat 5 yang Simetris Menggunakan Metode Golden Section Search yang Dikombinasikan dengan Konsep Aljabar dan Geometri” dengan baik. Skripsi ini disusun sebagai salah satu syarat untuk memperoleh gelar sarjana Pendidikan pada Program Studi Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma.

Banyak tantangan dan hambatan dalam proses penulisan skripsi ini, namun berkat dukungan, doa dan motivasi dari semua pihak, penulis dapat menyelesaikan skripsi ini. Pada kesempatan kali ini, penulis mengucapkan terimakasih kepada beberapa pihak, di antaranya :

1. Bapak Rohandi, Ph.D., selaku dekan Fakultas Keguruan dan Ilmu Pendidikan Universitas Sanata Dharma.

2. Bapak Dr. Hongki Julie, M.Si., selaku Ketua Program Studi Pendidikan Matematika Universitas Sanata Dharma.

3. Bapak Febi Sanjaya, M.Sc., selaku dosen pembimbing skripsi yang telah berkenan meluangkan waktu, tenaga serta pikiran untuk membimbing penulis sekaligus memberikan banyak masukan dan nasihat kepada penulis selama menyusun skripsi.

4. Bapak Beni Utomo, M.Sc., selaku dosen pembimbing akademik yang telah banyak membimbing, memberikan nasihat dan motivasi kepada penulis selama berlangsungnya perkuliahan di Universitas Sanata Dharma. 5. Bapak dan Ibu Dosen Program Studi Pendidikan Matematika yang telah

membimbing, mendidik dan memberi nasihat kepada penulis selama menuntut ilmu di Program Studi Pendidikan Matematika Universitas Sanata Dharma.

(11)

x

6. Seluruh staf sekretariat JPMIPA, Ibu Tari, Bapak Sugeng, Mas Arif dan Mas Made yang telah banyak membantu memberikan pelayanan kesekretariatan selama ini.

7. Kedua orangtuaku, Bapak Petrus Sunardi dan Ibu Lucia Purwanti, serta kakakku Christophorus Lucky Ardi Pratama, yang senantiasa memberikan motivasi, dukungan, semangat dan doa untuk penulis.

8. Teman-teman Pendidikan Matematika angkatan 2013, yang sudah berproses bersama selama empat tahun ini.

9. Semua pihak yang telah membantu penulis menyelesaikan skripsi ini baik secara langsung maupun tidak langsung yang tidak dapat penulis sebutkan satu persatu.

Penulis menyadari bahwa masih banyak kekurangan dalam penulisan skripsi ini. Oleh karena itu, penulis mengharapkan kritik dan saran yang membangun. Semoga tulisan ini dapat memberi manfaat dan wawasan kepada setiap pembaca.

Yogyakarta, 29 Mei 2017

(12)

xi DAFTAR ISI

Halaman

HALAMAN JUDUL ... i

HALAMAN PERSETUJUAN PEMBIMBING ... ii

HALAMAN PENGESAHAN ... iii

HALAMAN PERSEMBAHAN ... iv

HALAMAN KEASLIAN KARYA ... v

HALAMAN PERSETUJUAN PUBLIKASI ILMIAH ... vi

ABSTRAK ... vii

ABSTRACT ...viii

KATA PENGANTAR ... ix

DAFTAR ISI ... xi

DAFTAR SIMBOL ...xiv

DAFTAR GAMBAR ...xv

DAFTAR TABEL ... xviii

DAFTAR LAMPIRAN ... xix

BAB I PENDAHULUAN ...1 A. Latar Belakang ...1 B. Rumusan Masalah ...6 C. Pembatasan Masalah ...6 D. Batasan Istilah ...6 E. Tujuan Penelitian...8 F. Manfaat Penelitian...8

(13)

xii

G. Metode Penelitian ...9

H. Sistematika Penulisan ...10

BAB II LANDASAN TEORI ...12

A. Polinomial ...12

B. Fungsi Polinomial ...13

C. Pembuat Nol Fungsi Polinomial ...24

D. Diskiriminan ...37

E. Nilai Ekstrem Fungsi Polinomial ...39

F. Translasi ...43

G. Optimasi ...45

H. Golden Section ...47

I. Metode Golden Section Search ...50

J. Penelitian yang Relevan ...60

BAB III FUNGSI POLINOMIAL BERDERAJAT 5 ...64

A. Fungsi Polinomial Berderajat 5 ...64

B. Fungsi Polinomial Berderajat 5 yang Simetris ...69

C. Nilai Ekstrem Lokal Fungsi Polinomial Berderajat 5 Menggunakan Golden Section ...78

D. Proses Menentukan Nilai Ekstrem Lokal Fungsi Polinomial Berderajat 5 yang Simetris ...89

E. Uji Simetris Fungsi Polinomial Berderajat 5 ...95

(14)

xiii

BAB IV NILAI EKSTREM LOKAL FUNGSI POLINOMIAL

BERDERAJAT 5 YANG SIMETRIS ...99

A. Pembuat Nol dari Fungsi Polinomial ...99

B. Titik Ekstrem Lokal Fungsi Polinoimal Ditinjau dari Pembuat Nol Fungsi ...106

C. Nilai Ekstrem Lokal Fungsi Polinomial Menggunakan Metode Golden Section Search ...169

D. Nilai Ekstrem Fungsi Awal ...175

E. Analisis Kesalahan ...177 BAB V PENUTUP ...182 A. Kesimpulan...182 B. Saran ...188 DAFTAR PUSTAKA ...189 LAMPIRAN ...191

(15)

xiv

DAFTAR SIMBOL

: Himpunan semua bilangan real. : Himpunan semua bilangan kompleks. : Notasi tak hingga.

: Notasi bentuk ekuivalen atau bentuk biimplikasi. : Notasi implikasi.

̅ : , konjugat dari bilangan kompleks

∑ : Sigma atau notasi jumlahan suku-suku yang merupakan variabel berindeks atau suku-suku suatu deret.

⃗⃗⃗⃗⃗ : Vektor atau garis berarah dari titik A ke titik B.

̅̅̅̅ : Segmen garis yang menghubungkan titik A dan titik B. : Tanda akhir pembuktian.

(16)

xv

DAFTAR GAMBAR

Gambar 2.1 Grafik Fungsi Genap (Even Function) ... 16

Gambar 2.2 Grafik Fungsi Ganjil (Odd Function) ... 16

Gambar 2.3 Grafik Fungsi ( ) .... 17

Gambar 2.4 Grafik Fungsi ( ) ... 17

Gambar 2.5 (a) Fungsi Naik, (b) Fungsi Turun, (c) Fungsi Konstan ... 18

Gambar 2.6 Grafik Fungsi yang Mulus dan Kontinu (Smooth and Continous Curve)... 19

Gambar 2.7 Grafik Fungsi yang Tidak Kontinu ... 19

Gambar 2.8 Grafik Fungsi yang Tidak Mulus ... 20

Gambar 2.9 Sifat The End Behavior of Polynomials untuk bilangan ganjil . 23 Gambar 2.10 Sifat The End Behavior of Polynomials untuk bilangan genap 23 Gambar 2.11(a)Akar Ganda-Dua,(b)Akar Ganda-Tiga,(c)Akar Ganda-Empat 26 Gambar 2.12 Titik – Titik Puncak dari Fungsi Polinomial ... 39

Gambar 2.13 Nilai Ekstrem Lokal dan Nilai Ekstrem Global ... 41

Gambar 2.14 Pergeseran Grafik Fungsi secara Vertikal dan Horisontal ... 45

Gambar 2.15 Ilustrasi Golden Ratio ... 48

Gambar 2.16 Kondisi ketika ( ) ( ) ... 51

Gambar 2.19 (a) Kondisi ketika ( ) ( ), (b) Kondisi ketika ( ) ( ) ... 54

Gambar 2.20 Pereduksian Selang Metode Langsung Jika ( ) ( ) untuk Kasus Minimum ... 54

Gambar 2.21 Pereduksian Selang Metode Langsung Jika ( ) ( ) untuk Kasus Minimum ... 55

Gambar 2.22 Ilustrasi Pereduksian Selang Metode Langsung Jika ( ) ( ) untuk Kasus Minimum ... 55

Gambar 2.23 Ilustrasi Pereduksian Selang Metode Langsung Jika ( ) ( ) untuk Kasus Minimum ... 55

(17)

xvi

Gambar 2.24 Ilustrasi Pereduksian Selang Metode Golden Section Search

Jika ( ) ( ) untuk Kasus Minimum... 57

Gambar 2.25 Ilustrasi Pereduksian Selang Metode Golden Section Search Jika ( ) ( ) untuk Kasus Minimum... 57

Gambar 3.1 (a), (b), (c), (d) Berbagai Macam Bentuk Grafik Fungsi Polinomial Berderajat 5 ... 66

(e), (f), (g), (h) Berbagai Macam Bentuk Grafik Fungsi Polinomial Berderajat 5 ... 67

Gambar 3.2 Grafik Fungsi ( ) . 74

Gambar 3.3 Translasi Grafik Fungsi ... 75

Gambar 3.5 Translasi Grafik Fungsi ... 78

Gambar 3.7 Diagram Proses Menentukan Nilai Ekstrem Lokal Fungsi Polinomial Berderajat 5 yang Simetris untuk ... 93

Gambar 3.8 Diagram Proses Menentukan Nilai Ekstrem Lokal Fungsi Polinomial Berderajat 5 yang Simetris untuk ... 94

Gambar 4.1 Grafik Fungsi ( ) ( )( ) ... 107

Gambar 4.5 Kemungkinan Grafik Fungsi yang Memiliki 2 nilai Ekstrem Lokal pada [ √ ] ... 115

Gambar 4.8 Grafik Fungsi ( ) ( ) ... 130

(18)

xvii

Gambar 4.16 (a) Grafik Fungsi dan ... 152

(b) Pergerakan garis sebesar dan Titik Potongnya dengan Grafik Fungsi ... 153

Gambar 4.17 Kemungkinan bentuk grafik jika ada 2 titik potong antara dan ( ) ... 157

Gambar 4.18 Grafik fungsi dan ... 157

Gambar 4.19 Sumbu X (y=0) digeser ke bawah sebesar ... 159

Gambar 4.21 Kemungkinan bentuk grafik jika terdapat 3 titik potong dan ( ) ... 161

Gambar 4.23 Sumbu X (y=0) digeser ke bawah sebesar ... 163

Gambar 2.25 Ilustrasi kesalahan metode numerik karena kebergantungan nilai pada kasus 6 ... 179

Gambar 4.26 Ilustrasi keterbatasan iterasi dan kebergantungan nilai metode numerik pada kasus 6... 180

(19)

xviii

DAFTAR TABEL

Tabel 2.1 Penamaan Beberapa Fungsi Polinomial ... 13

Tabel 2.2 Sifat The End Behavior of Polynomials ... 22

Tabel 3.1 Hasil Iterasi Menentukan Nilai Minimum Lokal di ... 82

Tabel 3.2 Hasil Iterasi Menentukan Nilai Minimum Lokal di ... 84

Tabel 3.3 Hasil Iterasi Menentukan Nilai Maksimum Lokal di ... 87

Tabel 3.4 Hasil Iterasi Menentukan Nliai Maksimum Lokal di ... 89

Tabel 5.1 Kemungkinan Banyaknya Nilai Pembuat Nol Real dari Fungsi ....184

Tabel 5.2 Kemungkinan Banyaknya Nilai Ekstrem Lokal Fungsi Berdasarkan Pembuat Nol dari Fungsi ...185

(20)

xix

DAFTAR LAMPIRAN

1. Code Program MATLAB ... 192

2. Contoh Hasil Perhitungan MATLAB Kasus 1 ... 217

(21)

1 BAB I PENDAHULUAN A. Latar Belakang

Masalah optimasi merupakan permasalahan yang berkaitan dengan mencari nilai ekstrem dari suatu fungsi. Nilai ekstrem fungsi identik dengan nilai dari suatu variabel bebas yang memaksimumkan atau meminimumkan suatu fungsi. Konsep turunan sering digunakan untuk mencari nilai ekstrem dari sebuah fungsi, salah satunya adalah fungsi polinomial atau suku banyak. Pencarian nilai ekstrem dari fungsi polinomial menggunakan konsep turunan dapat dilakukan dengan mencari akar-akar persamaan dari turunan pertama fungsi polinomial.

Konsep turunan dapat mudah digunakan untuk mencari nilai ekstrem pada fungsi polinomial yang sederhana, seperti fungsi kuadrat dan fungsi kubik. Sebab, hasil turunan pertama dari fungsi kuadrat dan fungsi kubik dapat dengan mudah dicari akar-akar persamaannya. Masalah seringkali muncul apabila konsep turunan digunakan untuk mencari nilai ekstrem dari beberapa fungsi polinomial berderajat tinggi, seperti polinomial berderajat 4, 5, dan seterusnya. Permasalahan yang muncul adalah metode yang digunakan untuk mencari akar-akar persamaan dari turunan pertama fungsi polinomial berderajat tinggi secara analitik. Salah satu metode yang sering digunakan adalah metode Horner. Namun, metode Horner tidak dapat digunakan dengan mudah untuk mencari

(22)

seluruh akar-akar persamaan dari turunan pertama fungsi polinomial berderajat tinggi.

Berbagai penelitian muncul untuk menyelidiki metode yang dapat digunakan untuk mencari nilai ekstrem dari fungsi polinomial tanpa menggunakan konsep turunan. Taylor dan Hansen (2008) dalam artikel “Optimization Cubic Function without Calculus” menunjukkan hasil penelitian tentang pencarian nilai ekstrem pada fungsi polinomial berderajat 3 atau fungsi kubik tanpa menggunakan konsep turunan tetapi menggunakan konsep sederhana aljabar dan geometri. Penelitian tersebut menghasilkan suatu formula mencari nilai ekstrem fungsi polinomial berderajat 3, yang hasilnya sama dengan formula akhir jika menggunakan turunan.

Ayuningtyas, Setyarini dan Retnosari (2016) dalam artikel “Permasalahan Optimasi Fungsi Polinomial Berderajat Tinggi Tanpa Melibatkan Konsep Turunan”, mencoba mengembangkan penelitian dari Taylor dan Hansen, pada fungsi polinomial yang berorde lebih tinggi, yaitu fungsi polinomial berderajat 5. Penelitian yang dilakukan tetap menggunakan ide dasar yang sama yaitu melibatkan konsep sederhana aljabar dan geometri. Hasil penelitian pengembangan tersebut masih menunjukkan permasalahan dalam mencari nilai ekstrem fungsi polinomial berderajat 5 dengan mengunakan konsep aljabar dan geometri dan meninggalkan sistem persamaan yang tidak dapat diselesaikan secara eksak.

(23)

Permasalahan yang masih ditinggalkan dalam hasil penelitian Ayuningtyas, Setyarini dan Retnosari, melatarbelakangi penelitian ini untuk meninjau lebih jauh metode yang dapat digunakan dalam mencari nilai ekstrem fungsi polinomial berderajat 5 tanpa menggunakan konsep turunan. Pada penelitian ini penyelesaian dalam menentukan nilai ekstrem fungsi polinomial berderajat 5 menggunakan metode numerik, yaitu sebuah teknik penyelesaian secara sistematis dengan menggunakan operasi hitung atau aritmetika dan dilakukan secara iteratif baik manual atau dengan bantuan komputer. Metode numerik menggunakan pendekatan atau aproksimasi untuk mencari solusi dan sifatnya bersifat hampiran, yang artinya terdapat galat atau error.

Menurut Priswanto (2005), secara numeris terdapat beberapa metode yang dapat digunakan untuk menentukan nilai ekstrem dari fungsi non-linear satu variabel, yaitu metode Golden Section Search, metode Fibonacci, metode Biseksi dan metode Newton-Raphson. Metode Biseksi dan Newton-Raphson menggunakan teknik yang melibatkan turunan pertama dan kedua dari fungsi. Sedangkan, metode Golden Section Search dan metode Fibonacci menggunakan teknik evaluasi nilai fungsi dan penyempitan selang.

Jika ditinjau dari nilai awalan, metode Golden Section Search dan Fibonacci merupakan metode tertutup, dan metode Biseksi dan metode Newton-Raphson merupakan metode terbuka. Metode Golden Section Search dan metode Fibonacci keduanya tidak menggunakan konsep

(24)

turunan dalam menentukan nilai ekstrem dari fungsi non-linear satu variabel tanpa kendala. Kedua metode tersebut menggunakan penyempitan atau pereduksian selang awal yang diketahui. Namun, yang menjadi pembeda dari kedua metode tersebut adalah konstanta yang digunakan untuk melakukan eliminasi atau reduksi selang. Pada metode Golden Section Search, konstanta yang digunakan untuk mengeliminasi selang selalu tetap atau konstan untuk setiap iterasi. Sedangkan pada metode Fibonacci, konstanta yang digunakan untuk mengeliminasi selang berbeda untuk setiap iterasi. Konstanta yang digunakan pada metode Fibonacci menggunakan suku-suku barisan Fibonacci tertentu di setiap iterasi yang disesuaikan dengan formula pada algoritmanya.

Jika ditinjau dari penentuan konstanta, metode Golden Section Search lebih sederhana daripada metode Fibonacci, karena konstanta yang digunakan tetap untuk setiap iterasi. Pada metode Fibonacci, setiap iterasi konstanta bergantung pada suku-suku barisan Fibonacci tertentu, yang artinya diperlukan proses untuk mencari suku tertentu atau suku yang diminta di setiap iterasi. Oleh karena itu, peneliti memilih metode Golden Section Search sebagai metode yang tepat pada penelitian ini untuk mencari nilai ekstrem fungsi polinomial dengan satu variabel, sebab algoritma yang digunakan tidak menggunakan konsep turunan dan konstanta yang digunakan untuk mereduksi selang selalu konstan untuk setiap iterasi.

(25)

Tugas akhir ini akan mencoba untuk menggabungkan ide dasar pada penelitian-penelitian yang sudah ada dengan salah satu metode numerik, yaitu metode Golden Section Search. Metode Golden Section Search hanya dapat digunakan pada fungsi yang unimodal pada selang tertentu, yang artinya fungsi hanya memiliki satu maksimum atau minimum pada selang tersebut. Metode Golden Section Search merupakan metode tertutup (bracketing method), artinya perlu diketahui selang yang mempunyai nilai batas atas dan batas bawah sedemikian sehingga ada satu nilai ekstrem yang termuat dalam selang tersebut. Penggunaan metode Golden Section Search biasanya menggunakan selang yang sudah diketahui terlebih dahulu, yang menjamin bahwa fungsi bersifat unimodal pada selang tersebut. Namun, pada penelitian ini akan diteliti bagaimana mencari selang yang sedemikian sehingga fungsi, khususnya fungsi polinomial berderajat 5, bersifat unimodal pada selang tersebut. Penelitian ini akan difokuskan pada fungsi polinomial berderajat 5 yang bersifat simetris atau memiliki titik simetri putar (rotational symmetry).

Penggabungan kedua metode tersebut akan menjadi menarik untuk diteliti karena hasil algoritma dari kedua metode tersebut akan disimulasikan secara numeris menggunakan komputer dan dituangkan menjadi sebuah program yang dapat diaplikasikan pada software pemrograman seperti MATLAB.

(26)

B. Rumusan Masalah

Berdasarkan uraian di atas, peneliti dapat merumuskan masalah dalam penelitian ini adalah sebagai berikut.

1. Bagaimana karakteristik fungsi polinomial berderajat 5 yang simetris? 2. Bagaimana cara menentukan selang pada fungsi polinomial berderajat

5 yang simetris sehingga fungsi bersifat unimodal pada selang tersebut?

3. Bagaimana cara menentukan nilai ekstrem lokal fungsi polinomial berderajat 5 yang simetris dengan menggunakan Metode Golden Section Search yang dikombinasikan dengan menggunakan konsep aljabar dan geometri?

C. Pembatasan Masalah

Pembatasan masalah pada penelitian ini adalah fungsi polinomial yang digunakan dibatasi pada fungsi polinomal berderajat 5 dalam satu variabel yang mempunyai titik simetri putar (rotational symmetry) dan pencarian nilai ekstrem fungsi polinomial tanpa menggunakan konsep turunan.

D. Batasan Istilah

Berdasarkan latar belakang, untuk menghindari kesalahpahaman dalam memahami hasil penelitian ini, maka diperlukan batasan istilah sebagai berikut.

(27)

1. Nilai maksimum dari suatu fungsi pada himpunan adalah nilai fungsi terbesar yang dicapai pada keseluruhan himpunan , dimana adalah daerah asal dari .

2. Nilai minimum dari suatu fungsi pada himpunan adalah nilai fungsi terkecil yang dicapai pada keseluruhan himpunan , dimana adalah daerah asal dari .

3. Nilai maksimum lokal dari fungsi pada interval terbuka adalah nilai fungsi yang terbesar yang dicapai pada keseluruhan himpunan interval terbuka tersebut.

4. Nilai minimum lokal dari fungsi pada interval terbuka adalah nilai fungsi yang terbesar yang dicapai pada keseluruhan himpunan interval terbuka tersebut.

5. Nilai ekstrem global adalah nilai maksimum atau minimum dari sebuah fungsi.

6. Nilai ekstrem lokal adalah nilai maksimum atau minimum lokal dari sebuah fungsi.

7. Nilai ekstrem adalah nilai ekstrem global atau lokal dari sebuah fungsi.

8. Titik simetri putar (rotational symmetry point) adalah titik yang menjadi pusat simetri putar pada sebuah bangun atau kurva.

9. Fungsi bersifat unimodal pada suatu selang jika pada selang tersebut fungsi hanya memuat satu nilai maksimum atau minimum lokal.

(28)

E. Tujuan Penelitian

Penelitian ini bertujuan untuk :

1. Mengetahui karakteristik fungsi polinomial berderajat 5 yang simetris. 2. Menentukan selang pada fungsi polinomial berderajat 5 yang simetris

sehingga fungsi bersifat unimodal pada selang tersebut.

3. Menentukan algoritma dalam mencari nilai ekstrem fungsi polinomial berderajat 5 yang simetris dengan menggunakan Metode Golden Section Search yang dikombinasikan dengan menggunakan konsep aljabar dan geometri.

F. Manfaat Penelitian

Manfaat yang dapat diperoleh dari penelitian ini adalah : 1. Bagi Pembaca

Pembaca dapat menambah pengetahuan tentang karakteristik fungsi polinomial berderajat yang simetris dan metode Golden Section Search yang dimodifikasi untuk mencari nilai ekstrem fungsi polinomial berderajat 5 yang simetris tanpa menggunakan konsep turunan. Selain itu, pembaca dapat menggunakan algoritma dan program yang terdapat di tugas akhir ini untuk menentukan nilai ekstrem fungsi polinomial berderajat 5 yang simetris menggunakan MATLAB atau software yang sejenis.

(29)

2. Bagi Penulis

Penulis dapat menambah pengetahuan dan pengalaman dalam melakukan penelitian tentang metode Golden Section Search yang dimodifikasi untuk mencari nilai ekstrem fungsi polinomial berderajat 5 yang simetris tanpa menggunakan konsep turunan.

3. Bagi Universitas

Universitas dapat menambah hasil penelitian yang dapat digunakan untuk penelitian-penelitian selanjutnya yang memiliki kaitan dengan penelitian ini.

G. Metode Penelitian

Metode yang digunakan pada penelitian ini adalah metode studi literatur atau studi pustaka dan simulasi numeris dengan komputer. Metode studi pustaka yang dilakukan adalah dengan mempelajari buku, literatur, jurnal dan hasil penelitian yang berkaitan dengan metode Golden Section Search, optimasi fungsi polinomial berderajat 5 dan karakteristik fungsi polinomial berderajat 5. Buku, jurnal dan hasil penelitian tersebut berperan sebagai data sekaligus sumber data yang menjadi acuan dalam proses penelitian ini. Langkah-langkah yang dilakukan dalam penelitian ini adalah :

1. Mencari dan membaca berbagai referensi terkait topik nilai ekstrem fungsi polinomial, fungsi polinomial berderajat 5, metode Golden

(30)

Section Search melalui buku, jurnal ilmiah, penelitian yang relevan, dan data di internet.

2. Mempelajari konsep nilai ekstrem pada fungsi polinomial, fungsi polinomial berderajat 5, konsep dan algoritma metode Golden Section Search.

3. Mengeksplorasi pengetahuan dengan melakukan uji coba menggunakan metode Golden Section Search dalam mencari nilai ekstrem fungsi polinomial berderajat 5 dengan bantuan aplikasi Microsoft Excel, Geogebra dan Matlab.

4. Menyusun program metode Golden Section Search untuk proses optimasi fungsi polinomial berderajat 5 di aplikasi Matlab.

5. Menyusun seluruh materi dan hasil penelitian secara runtut agar mudah dipahami oleh pembaca.

H. Sistematika Penulisan

Bab pertama merupakan bagian pendahuluan. Bagian pendahuluan ini berisi mengenai latar belakang, rumusan masalah, pembatasan masalah, batasan istilah, tujuan, manfaat, metode penelitian dan sistematika penulisan.

Bab dua berisi penjelasan tentang definisi polinomial, fungsi polinomial satu variabel, akar-akar dari persamaan polinomial, diskriminan persamaan kuadrat, metode yang digunakan untuk menentukan akar-akar persamaan polinomial, nilai ekstrem pada fungsi

(31)

polinomial, definisi fungsi naik dan fungsi turun, definisi fungsi ganjil dan fungsi genap, definsi translasi, permasalahan optimasi dan metode Golden Section Search yang akan menjadi dasar teori dari penelitian ini. Selain itu, bab dua juga berisikan penelitian yang relevan terkait dengan penulisan skripsi ini.

Bab tiga berisi karakteristik fungsi polinomial berderajat 5 yang simetris dan gambaran secara umum tentang langkah-langkah dalam menentukan nilai ekstrem fungsi polinomial berderajat 5 yang simetris. Setiap langkah dalam menentukan nilai ekstrem dituangkan dalam program yang disimulasikan menggunakan software MATLAB. Pada bab tiga juga berisikan program yang telah disusun sesuai dengan langkah yang sedang dibahas.

Bab empat berisi pembahasan lebih lanjut tentang proses pencarian nilai ekstrem fungsi polinomial berderajat 5 yang simetris, yaitu khususnya tentang mencari selang pada fungsi polinomial yang simetris, sehingga fungsi bersifat unimodal pada selang tersebut. Setelah ditemukan selang yang membuat fungsi bersifat unimodal, proses menentukan nilai ekstrem dilanjutkan dengan menggunakan metode Golden Section Search. Bab empat juga berisikan program yang telah disusun yang disesuaikan dengan langkah atau proses yang sedang dibahas pada bab empat.

Bab lima yang merupakan bab terakhir dalam skripsi ini, berisikan kesimpulan hasil penelitian dan saran-saran yang dapat digunakan untuk penelitian selanjutnya.

(32)

12 BAB II

LANDASAN TEORI

Pada bab ini berisikan landasan teori yang digunakan dalam tugas akhir. Landasan teori yang digunakan meliputi polinomial, fungsi polinomial, akar-akar dari persamaan polinomial, diskriminan, titik ekstrem lokal pada fungsi polinomial, translasi, optimasi, Golden Section, Metode Golden Section dan penelitian yang relevan.

A. Polinomial

Aufmann dalam buku “College Algebra” menyatakan bahwa monomial adalah sebuah konstanta atau sebuah variabel atau hasil kali dari konstanta dan satu atau lebih variabel, dengan variabel yang memiliki eksponen bilangan bulat nonnegatif. Derajat dari monomial adalah jumlah eskponen pada variabel. Jumlahan berhingga dari bermacam-macam monomial disebut polinomial. Setiap monomial pada polinomial disebut suku dari polinomial.

Definisi 2.1 (Aufmann, 1990:26)

Bentuk umum dari polinomial satu variabel ( ) adalah :

dengan ( ) adalah konstanta yang merupakan bilangan real atau kompleks, dan adalah bilangan bulat nonnegatif.

Koefisien disebut sebagai leading coefficient dan disebut sebagai leading term. Dari definisi di atas, setiap polinomial dapat dinyatakan sebagai jumlahan berhingga dari suku-suku monomial yang

(33)

berbentuk dengan variabel yang dipangkatkan oleh bilangan bulat tidak negatif. Pangkat terbesar dari suku-suku di dalam polinomial adalah derajat dari polinomial.

E.J Barbeau (2003) menyatakan bahwa dalam kasus , suku banyak atau polinomial dikatakan polinomial berderajat dapat dituliskan . Berikut adalah penamaan beberapa fungsi polinomial berderajat tertentu menurut E.J. Barbeau.

Tabel 2.1 Penamaan Beberapa Fungsi Polinomial Degree of Polynomial Type of Polynomial

1 Linear 2 Quadratic 3 Cubic 4 Quartic 5 Quintic B. Fungsi Polinomial

Relasi f dari himpunan D ke himpunan R adalah fungsi jika dan hanya jika setiap anggota himpunan D memiliki tepat satu pasangan dengan anggota di R oleh relasi f. Himpunan D disebut domain dari f dan himpunan R yang menjadi bayangan dari anggota himpunan D disebut range dari f. Fungsi dilambangkan dengan : (Prayudi, 2006: 33)

(34)

Misal diketahui * ( ) + dan * ( ) + maka fungsi disebut fungsi real dan dapat dilambangkan dengan : (Clapham, 1990: 148)

Penyajian fungsi dapat berupa himpunan pasangan terurut, rumus fungsi, diagram panah atau grafik fungsi (Aufmann, 1990: 148).

Fungsi dapat diklasifikasikan menjadi fungsi ganjil (odd function), fungsi genap (even function), atau bukan keduanya.

Definisi 2.2 (Aufmann,190:150)

Fungsi adalah fungsi genap jika ( ) ( ) untuk setiap anggota domain .

Fungsi adalah fungsi ganjil jika ( ) ( ) untuk setiap anggota domain . Contoh 2.1 : 1. ( ) Diperhatikan bahwa : ( ) ( ) ( ) ( )

Fungsi memenuhi ( ) ( ), maka fungsi adalah fungsi genap.

(35)

2. ( ) Diperhatikan bahwa : ( ) ( ) ( ) ( ) ( ) ( )

Fungsi memenuhi ( ) ( ), maka fungsi adalah fungsi ganjil.

3. ( ) Diperhatikan bahwa :

( ) ( ) ( )

Pada bentuk di atas, fungsi tidak memenuhi bentuk ( ) ( ) dan ( ) ( ), maka fungsi bukan fungsi genap dan bukan fungsi genap.

Ciri geometris dari fungsi genap adalah grafik fungsinya simetris terhadap sumbu Y. Sumbu Y menjadi sumbu simetri dari grafik fungsi genap. Artinya, jika grafik fungsi telah diperoleh untuk maka grafik secara keseluruhan dapat digambarkan secara mudah dengan mencerminkan terhadap sumbu Y. Sedangkan, ciri geometris dari fungsi ganjil adalah grafik fungsinya simetris terhadap titik asal O(0,0). Titik O(0,0) merupakan titik simetri putar (rotational symmetry) dari grafik fungsi ganjil. Artinya, jika grafik fungsi telah diperoleh untuk maka

(36)

grafik secara keseluruhan dapat diperoleh dengan merotasikan sebesar dengan pusat rotasi titik O(0,0). (Stewart, 2009: 28)

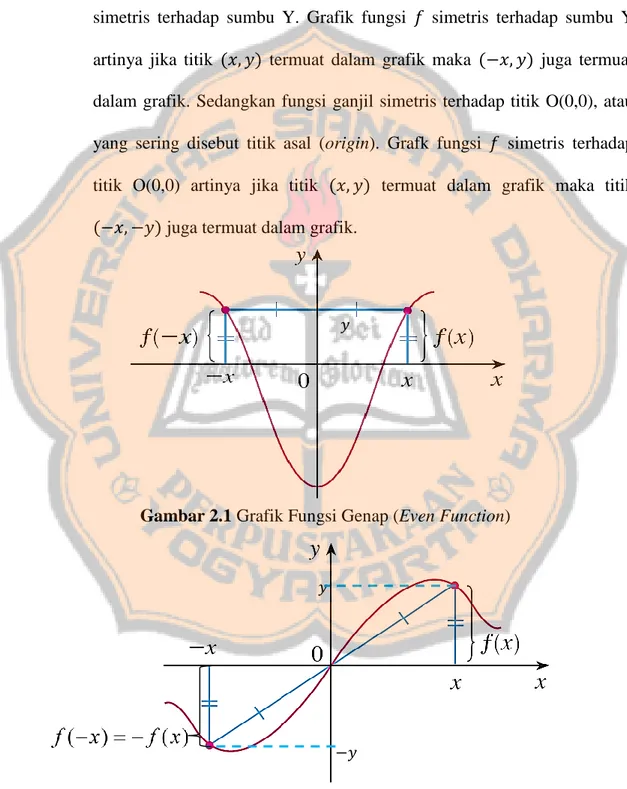
Menurut Carico (1984:123), jika dilihat secara grafik, fungsi genap simetris terhadap sumbu Y. Grafik fungsi simetris terhadap sumbu Y artinya jika titik ( ) termuat dalam grafik maka ( ) juga termuat dalam grafik. Sedangkan fungsi ganjil simetris terhadap titik O(0,0), atau yang sering disebut titik asal (origin). Grafk fungsi simetris terhadap titik O(0,0) artinya jika titik ( ) termuat dalam grafik maka titik ( ) juga termuat dalam grafik.

Gambar 2.1 Grafik Fungsi Genap (Even Function) 𝑦

Gambar 2.2 Grafik Fungsi Ganjil (Odd Function) Sumber : Calculus (Stewart, 2009:27)

𝑦

(37)

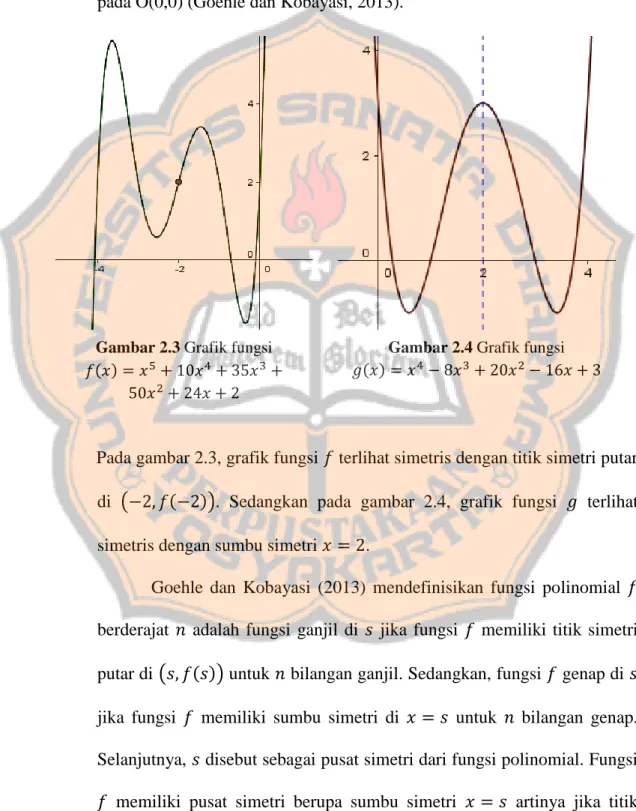
Pada beberapa grafik fungsi polinomial terlihat seperti fungsi genap tetapi sumbu simetrinya bukan sumbu Y. Ada pula beberapa grafik fungsi polinomial terlihat seperti fungsi ganjil tetapi titik simetrinya bukan pada O(0,0) (Goehle dan Kobayasi, 2013).

Pada gambar 2.3, grafik fungsi terlihat simetris dengan titik simetri putar di ( ( )). Sedangkan pada gambar 2.4, grafik fungsi terlihat simetris dengan sumbu simetri .

Goehle dan Kobayasi (2013) mendefinisikan fungsi polinomial berderajat adalah fungsi ganjil di jika fungsi memiliki titik simetri putar di ( ( )) untuk bilangan ganjil. Sedangkan, fungsi genap di jika fungsi memiliki sumbu simetri di untuk bilangan genap. Selanjutnya, disebut sebagai pusat simetri dari fungsi polinomial. Fungsi memiliki pusat simetri berupa sumbu simetri artinya jika titik

Gambar 2.4 Grafik fungsi 𝑔(𝑥) 𝑥 𝑥 𝑥 𝑥 Gambar 2.3 Grafik fungsi

𝑓(𝑥) 𝑥 𝑥 𝑥 𝑥 4𝑥

(38)

( ) termuat dalam grafik maka titik ( ) juga termuat dalam grafik. Sedangkan, fungsi memiliki pusat simetri berupa titik simetri putar ( ), dengan adalah nilai fungsi dari , artinya jika titik ( ) termuat dalam grafik maka titik ( ) juga termuat dalam grafik.

Grafik sebuah fungsi dapat berupa garis lurus ataupun kurva lengkung. Salah satu hal yang penting dalam membuat sketsa grafik fungsi adalah mengetahui fungsi naik atau fungsi turun atau fungsi konstan. Aufmann (1990:157) menjelaskan tentang fungsi naik (increasing function), fungsi turun (decreasing function) dan fungsi konstan (constant function) sebagai berikut :

Definisi 2.3 (Aufmann,1990:157)

Jika a dan b adalah anggota dalam interval I (baik interval tertutup ataupun terbuka) yang merupakan himpunan bagian dari domain fungsi , maka : (i) fungsi naik pada I jika ( ) ( ) untuk setiap

(ii) fungsi turun pada I jika ( ) ( ) untuk setiap

(iii) fungsi konstan pada I jika ( ) ( ) untuk setiap dan anggota I.

Gambar 2.5(a) Fungsi Naik

Gambar 2.5(b). Fungsi

(39)

Definisi 2.4 (Suryawan, 2016: 55)

Fungsi polinomial adalah sebuah fungsi P: dalam variabel yang berbentuk :

( )

dengan adalah konstanta, yang disebut koefisien polinomal, dan adalah bilangan bulat nonnegatif.

Domain atau daerah asal untuk semua fungsi polinomial real adalah . Fungsi polinomial merupakan fungsi yang terdefinisi dan kontinu untuk semua nilai (Stewart, 2009: 40). Selain itu, setiap fungsi polinomial memiliki grafik fungsi yang berbentuk kurva mulus dan kontinu (smooth continuous curves). Sebuah kurva mulus adalah kurva yang tidak memiliki ujung yang lancip. Sedangkan, kurva yang kontinu artinya kurva tidak memiliki lubang atau lompatan. (Swokowski dan Cole, 2004: 248)

Gambar 2.6 Grafik fungsi yang mulus dan kontinu (smooth continuous curve)

Gambar 2.7 Grafik fungsi yang tidak kontinu

(40)

Grafik fungsi polinomial berderajat 0 atau fungsi konstan berbentuk garis lurus horisontal. Sedangkan grafik fungsi polinomial berderajat 1 atau fungsi linear berbentuk garis lurus atau linear dengan kemiringan tidak nol. Grafik dari fungsi polinomial berderajat 2 atau fungsi kuadrat selalu berbentuk parabola (James Stewart, 2009: 40).

Definisi 2.5 (Swokowski dan Cole, 2004: 260)

Sebuah polinomial ( ) dibagi oleh polinomial ( ), dengan ( ) ( ) artinya dapat ditemukan polinomial ( ) dan ( ) sedemikian sehingga :

( ) ( ) ( ) ( )

dengan ( ) kurang dari ( ). ( ) disebut sebagai pembagi dan ( ) adalah sisa.

Definisi 2.5 sering disebut sebagai definisi dari algoritma pembagian pada polinomial atau division algorithm for polynomials.

Gambar 2.8 Grafik fungsi yang tidak mulus Sumber : courses.lumenlearning.com

(41)

Teorema 2.1 (Spitzbart & Bardell, 1958: 75)

Jika sebuah polinomial ( ) dibagi dengan , dengan bilangan sembarang hingga sisanya berupa konstanta, maka sisanya adalah ( ). Bukti :

Misalkan hasil bagi ( ) oleh ( ) adalah ( ) dan sisa pembagiannya adalah konstanta , akan ditunjukkan bahwa ( ) .

Berdasarkan definisi 2.3, maka bentuk fungsi polinomial dapat dituliskan menjadi :

( ) ( ) ( ) Untuk , maka :

( ) ( ) ( )

Teorema 2.1 terbukti. QED

Menurut Aufmann (1990), bentuk grafik dari fungsi polinomial dapat diperkirakan dengan leading term test atau sering disebut dengan sifat the end behavior, yaitu dengan mengetahui sejauh mana nilai fungsi bergerak naik atau turun dari kiri ke kanan. Jika diketahui fungsi polinomial berderajat , ( ) , maka disebut leading term dan disebut leading coefficient dari fungsi . Leading term test atau sifat dari the end behavior dapat memperkirakan nilai fungsi hanya dengan melihat leading term dan leading coefficient dari fungsi . Leading term adalah suku yang memuat

(42)

pangkat tertinggi dari fungsi polinomial , artinya mendominasi fungsi . Diperhatikan bahwa untuk dengan yang semakin besar, maka juga akan bertambah semakin besar. Oleh karena itu, grafik fungsi polinomial dengan sebagai leading term memiliki sifat sebagai berikut :

bilangan genap bilangan ganjil

Jika maka ( ) Jika maka ( ) Grafik fungsi semakin naik ke kiri dan semakin naik ke kanan (up to left and up to right).

Jika maka ( ) Jika maka ( ) Grafik fungsi semakin turun ke kiri dan semakin naik ke kanan (down to left and up to right).

Jika maka ( ) Jika maka ( ) Grafik fungsi semakin turun ke kiri dan semakin turun ke kanan (down to left and down to right).

Jika maka ( ) Jika maka ( ) Grafik fungsi semakin naik ke kiri dan semakin turun ke kanan (up to left and down to right). Tabel 2.2 Sifat The End Behavior of Polynomials (Aufmann, 1990)

(43)

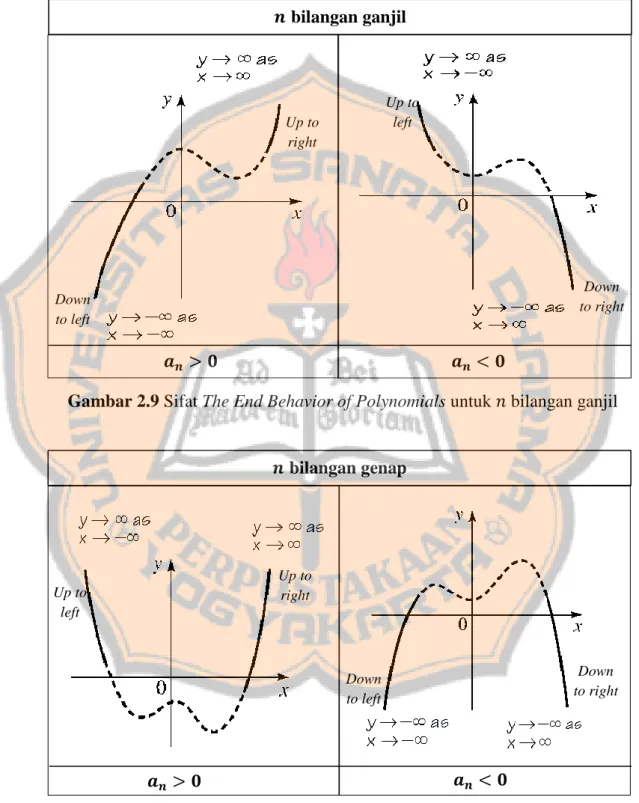
Berikut adalah gambar yang mengilustrasikan sifat the end behavior of polynomials :

Gambar 2.9 Sifat The End Behavior of Polynomials untuk 𝑛 bilangan ganjil 𝒂_𝒏 𝟎 Up to right Down to left Down to right Up to left 𝒂_𝒏 𝟎 𝒏 bilangan ganjil Up to right Up to left 𝒂𝒏 𝟎 Down to right Down to left 𝒂_𝒏 𝟎 𝒏 bilangan genap

(44)

C. Pembuat Nol Fungsi Polinomial

Pembuat nol dari fungsi polinomial disebut juga solusi atau akar dari persamaan polinomial ( ) . Menurut Departemen Pendidikan dan Kebudayaan (1995), persamaan polinomial adalah polinomial satu variabel atau lebih yang sama dengan 0. Bentuk umum dari persamaan polinomial satu variabel dalam dapat dituliskan :

dengan ( ) adalah konstanta yang merupakan bilangan real atau kompleks, dan adalah bilangan bulat nonnegatif.

Definisi 2.6 (Aufmaan,1990:225)

Jika ( ) adalah sebuah fungsi polinomial, maka nilai dari yang membuat ( ) bernilai 0 disebut pembuat nol dari ( ) atau akar-akar dari persamaan ( ) .

Teorema 2.2 (Spitzbart & Bardell, 1958:76)

Sebuah fungsi polinomial ( ) mempunyai faktor jika dan hanya jika ( ) .

Bukti :

1. Misal fungsi mempunyai faktor . Akan ditunjukkan ( ) . Berdasarkan asumsi bahwa adalah faktor dari fungsi dapat dituliskan :

( ) ( ) ( ) (2.1) untuk suatu polinomial ( ).

(45)

Misal R adalah sisa pembagian dari ( ) oleh , maka dari persamaan (2.1) diperoleh .

Berdasarakan teorema 2.1, jika fungsi dibagi oleh , maka sisa pembagiannya adalah ( ) Oleh karena itu, ( ) . (terbukti) 2. Misal ( ) . Akan ditunjukkan adalah faktor dari fungsi .

Asumsi ( ) , berdasarkan teorema 2.1 maka : ( ) ( ) ( )

( ) ( ) ( ) (2.2) untuk suatu polinomial ( ).

Dari persamaan (2.2) jelas bahwa ( ) adalah faktor dari fungsi polinomial .

Dari 1 dan 2, teorema 2.2 terbukti. QED

Pembuat nol dari fungsi polinomial dapat berupa bilangan yang kembar dan diulang untuk beberapa kali pembuat nol kembar atau disebut multiple zero. Sedangkan, akar-akar dari persamaan polinomial yang diulang untuk beberapa kali disebut akar-akar ganda atau multiple roots. Aufmann dalam buku “College Algebra” juga mengungkapkan definisi dari multiple zero of polynomial.

Definisi 2.7 (Aufmann, 1990:226)

Jika fungsi polinomial memiliki ( ) sebagai faktor untuk kali, maka disebut sebagai pembuat nol yang kembar sebanyak dari polinomial .

(46)

Sebagai contoh, misal diketahui ( ) ( )( )( )( )( )( 4). Pada fungsi polinomial P, untuk nilai adalah : 5 sebagai pembuat nol kembar-dua atau zero of multiplicity 2

-2 sebagai pembuat nol kembar-tiga atau zero of multiplicity 3

-4 sebagai pembuat nol tunggal atau zero of multiplicity 1 (simple zero) Chapra dan Canale (1989) menyatakan bahwa jika akar-akar dari persamaan polinomial diulang sebanyak kali, dengan adalah bilangan ganjil maka grafik fungsi polinomial akan memotong sumbu X di titik pembuat nol tersebut. Sedangkan untuk bilangan genap, maka grafik fungsi polinomial akan menyinggung sumbu X di titik pembuat nol tersebut.

Teorema 2.3 (Loveless, 2011)

Bilangan adalah pembuat nol dari fungsi polinomial ( ) berderajat ( ) jika dan hanya jika ( ) ( ) ( ) untuk suatu polinomial ( ) berderajat .

Sumber : Numerical Method for Engineers 6th Edition Gambar 2.11(a). Akar

ganda-dua

Gambar 2.11(b). Akar ganda-tiga

Gambar 2.11(c). Akar ganda-empat

(47)

Bukti :

Misal fungsi polinomial ( ) berderajat dengan .

(i) Asumsi ( ) ( ) ( ) untuk suatu polinomial ( ) berderajat . Akan ditunjukkan adalah pembuat nol dari fungsi .

( ) ( ) ( ) ( ) ( ) ( )

( ) (2.3)

Berdasarkan definisi 2.4, persamaan (2.3) menunjukkan bahwa adalah pembuat nol dari fungsi . (terbukti)

(ii) Asumsi adalah pembuat nol dari fungsi . Akan ditunjukkan ( ) ( ) ( ) untuk suatu polinomial ( ) berderajat .

( ) ,

( ) ∑

Berdasarkan definisi 2.4 dan asumsi adalah pembuat nol dari fungsi , maka ( ) . ( ) ( ) ( ) ( ) ∑ ∑ ∑ ( ) 2 4

(48)

Suku dengan dieliminasi karena ( ) ( ) .

Oleh karena itu, fungsi pada persamaan (2.4) dapat menjadi :

( ) ∑ ( )

Karena maka bentuk ( ) dapat difaktorkan menjadi : ( ) ( )( ) Misalkan ( ) ( _{) maka}

( ) ( ) ( ) (2.5) dengan ( ) adalah fungsi polinomial dengan derajat . Persamaan (2.5) disubstitusikan ke persamaan (2.4) menjadi :

( ) ∑ ( ) ( ) ( ) ∑ ( ) ( ) ( ) Perhatikan bahwa : ( ) ∑ ( ) ∑ ( ₎

Suku terjadi satu kali disaat dan . Jadi, ( ) adalah polinomial dengan derajat . (terbukti)

(49)

Teorema 2.4 (Meserve, 1959:139)

Setiap fungsi polinomial berderajat memiliki pembuat nol bilangan kompleks yang tidak harus berbeda.

Bukti :

Pembuktian teorema ini menggunakan kontradiksi. Kasus 1 :

Diketahui fungsi polinomial berderajat 0. Misal adalah pembuat nol dari fungsi .

Berdasarkan definisi 2.4 yaitu tentang definisi fungsi polinomial, fungsi polinomial merupakan fungsi konstan dengan konstanta bukan nol, sehigga fungsi dapat dituliskan dalam bentuk :

( ) ( ) ( ) dengan .

Diperhatikan dari bentuk fungsi bahwa untuk semua nilai , berlaku ( ) . Artinya fungsi tidak memiliki pembuat nol fungsi atau dengan kata lain fungsi memiliki 0 pembuat nol. Hal ini bersifat kontradiksi dengan asumsi yang dimiliki yaitu fungsi memiliki 1 pembuat nol yaitu .

Kasus 2 :

Misal diketahui fungsi polinomial ( ) berderajat , dan adalah pembuat nol dari ( ) yang berjumlah .

(50)

Berdasarkan teorema 2.1 dan 2.2, maka :

( ) ( ) ( ) untuk suatu polinomial ( ) yang derajatnya 1 kurangnya dari derajat ( ) dan ( ) mempunyai nilai pembuat nol, misal .

( ) ( )( ) ( ) untuk suatu polinomial ( ) yang derajatnya 2 kurangnya dari derajat ( ) dan ( ) mempunyai nilai pembuat nol, misal .

( ) ( )( )( ) ( ) untuk satu polinomial ( ) yang derajatnya 3 kurangnya dari derajat ( ) dan ( ) mempunyai nilai pembuat nol, misal .

. . .

( ) ( ) ( )( )( ) ( ) untuk suatu polinomial ( ) yang derajatnya kurangnya dari derajat ( ) dan

( ) mempunyai nilai pembuat nol, misal .

Jika ( ) maka ( ) . Oleh karena itu haruslah ( ) adalah fungsi konstan. Misal ( ) .

Asumsi yang sudah dibuat adalah masih ada pembuat nol fungsi yaitu

. juga merupakan pembuat nol dari ( ), maka : ( ) .

Persamaan tersebut dapat terjadi jika dan hanya jika , yang mengakibatkan ( ) . Hal ini kontradiksi dengan asumsi bahwa ( ) adalah polinomial berderajat .

(51)

Jadi, fungsi polinomial berderajat memiliki bilangan real pembuat nol

fungsi. Jadi, teorema 2.4 terbukti. QED

Teorema 2.5 (Aufmann, 1990:234)

Jika ( √ ) adalah pembuat nol dari fungsi polinomial ( ) dengan koefisien bilangan real, maka konjugatnya yaitu juga merupakan pembuat nol dari fungsi polinomial ( )

Bukti :

Misal adalah pembuat nol dari fungsi P atau ( ) . Akan ditunjukkan ̅ adalah pembuat nol juga atau ( ̅)

( ) (2.6) dengan ( ) adalah bilangan real.

Karena bilangan kompleks yang ada di ruas kiri sama dengan bilangan kompleks di ruas kanan pada persamaan (2.6), maka berlaku juga untuk konjugatnya.

̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ ̅

̅̅̅̅̅̅̅ ̅̅̅̅̅̅̅̅̅̅̅̅ ̅̅̅̅̅ ̅̅̅ (sifat ̅̅̅̅̅̅̅ ̅ ̅)

̅̅̅ ̅̅̅ ̅̅̅̅̅̅ ̅̅̅̅̅̅ ̅̅̅ ̅ ̅̅̅ (sifat ̅̅̅̅̅ ̅ ̅)

̅ ̅ ̅ (sifat ̅̅̅ ̅ dan konjugat dari bilangan real adalah bilangan itu sendiri)

̅ ̅ _̅ _(2.7)

Dari persamaan (2.7) dapat ditulis sebagai ( ̅) .

(52)

Teorema 2.6 (Loveless, 2011)

Setiap fungsi polinomial berderajat n memiliki paling banyak pembuat nol bilangan real.

Bukti :

Pembuktian teorema ini menggunakan induksi matematika.

Misalkan adalah fungsi polinomial berderajat dalam variabel . (i) Langkah Dasar :

Jika , maka fungsi adalah fungsi konstan. Berdasarkan definisi 2.4, maka fungsi dengan dapat dinyatakan dalam bentuk :

( ) ( ) ( ) dengan .

Jelas bahwa nilai ( ) untuk sembarang nilai , sehingga fungsi tidak mempunyai nilai pembuat nol. Jadi, untuk tidak ada nilai pembuat nol dari fungsi .

(ii) Diasumsikan benar untuk bahwa setiap polinomial berderajat memiliki paling banyak pembuat nol bilangan real untuk suatu bilangan bulat dengan .

(iii) Akan dibuktikan untuk berlaku fungsi polinomial berderajat mempunyai paling banyak pembuat nol bilangan real.

(53)

Misalkan fungsi berderajat . Jika fungsi f tidak memiliki pembuat nol, maka jelas 0 .

Jika fungsi memiliki paling tidak satu pembuat nol, misalkan a adalah pembuat nol dari fungsi f, maka berdasarkan teorema 2.3 dapat dituliskan

( ) ( ) ( )

dengan ( ) adalah suatu polinomial yang berderajat .

Berdasarkan asumsi untuk , artinya fungsi memiliki paling banyak pembuat nol bilangan real. Sedangkan, a adalah pembuat nol dari fungsi f.

Jadi, ( ) ( ) ( ) memiliki paling banyak pembuat nol bilangan real.

Dari (i),(ii),(iii) maka dapat disimpulkan untuk setiap polinomial berderajat memiliki paling banyak pembual nol bilangan real.

Teorema 2.6 terbukti. QED

Pembuat nol fungsi polinomial atau akar-akar dari persamaan polinomial dapat berupa bilangan kompleks atau bilangan real. Teorema 2.4 menunjukkan jika fungsi polinomial mempunyai akar kompleks, maka akar tersebut selalu berpasangan dengan konjugatnya, sehingga setiap fungsi polinomial memiliki akar-akar kompleks yang berpasangan. Pembuat nol real dapat menentukan apakah grafik fungsi polinomial memotong atau menyinggung sumbu X. Sedangkan pembuat nol yang

(54)

memuat bilangan imajiner tidak membuat grafik fungsi memotong dan meyinggung sumbu X. (Splitzbart dan Bardell, 1958:160).

Ada beberapa metode yang dapat digunakan untuk mencari pembuat nol dari fungsi polinomial atau akar-akar persamaan polinomial. Berdasarkan teorema 2.4, fungsi linear atau fungsi polinomial berderajat 1 memiliki 1 nilai pembuat nol real. Operasi aljabar sederhana dapat digunakan untuk menentukan akar dari fungsi linear.

Contoh 2.2 :

( ) Pembuat nol dari dapat ditentukan dengan cara :

( )

Fungsi kuadrat atau fungsi polinomial berderajat 2 memiliki 2 nilai pembuat nol. Metode yang dapat digunakan untuk menentukan akar-akar dari persamaan kuadrat adalah metode pemfaktoran, melengkapkan kuadrat sempurna atau metode abc (metode dengan formula fungsi kuadrat). Metode abc atau menggunakan formula kuadratik dapat diselesaikan dengan formula berikut. (Swokowski dan Cole, 2004: 84) Jika maka :

√

(55)

Contoh 2.3 :

( )

Penentuan pembuat nol dari dapat dilakukan dengan cara : 1. Metode Pemfaktoran

( ) ( )( )

atau 2. Metode Melengkapkan Kuadrat Sempurna

( ) 4 4 ( ) 4 √ 4 atau atau

(56)

3. Metode abc atau menggunakan formula kuadrat (Quadratic Formula) ( ) √ 4 ( ) √( ) 4( )( ) ( ) √ 4 √ atau atau

Pembuat nol dari fungsi polinomial berderajat 3 atau yang lebih tinggi lagi dapat ditentukan dengan metode Horner dan beberapa metode secara numerik. Metode Horner merupakan metode yang dapat digunakan untuk menentukan akar-akar fungsi polinomial secara analitis. Metode Horner menggunakan konsep pembagian fungsi polinomial dengan nilai-nilai yang diduga sebagai faktornya. Namun, tidak semua bentuk fungsi polinomial dapat diselesaikan dengan mudah oleh metode Horner. Oleh karena itu, ada beberapa metode yang dapat digunakan secara numerik untuk menentukan akar-akar dari fungsi polinomial.

(57)

D. Diskriminan

Persamaan kuadrat memiliki nilai diskriminan (discriminant). Nilai diskriminan menentukan banyaknya pembuat nol fungsi kuadrat yang real atau akar real dari persamaan kuadrat. Formula kuadrat (The Quadratic Formula) untuk menentukan akar-akar persamaan kuadrat berbentuk :

√ 4

Bentuk 4 disebut sebagai diskriminan dari formula kuadrat (Quadratic Formula). Diskriminan sering dilambangkan dengan notasi . (Swokowski dan Cole, 2004: 85)

Teorema 2.7 (Swokowski dan Cole, 2004: 85)

Diketahui persamaan kuadrat mempunyai diskriminan 4 .

(i) Jika , maka persamaan kuadrat memiliki 2 akar real yang berbeda.

(ii) Jika , maka persamaan kuadrat memiliki 2 akar real yang kembar, artinya persamaan kuadrat hanya memiliki 1 akar real.

(iii) Jika , maka persamaan kuadrat memiliki 2 akar kompoleks yang berbeda.

Bukti :

Dari persamaan (2.8) dan definisi diskriminan maka persamaan 2.8 dapat dituliskan menjadi :

√

(58)

(i) Misal , maka persamaan (2.9) menjadi : √ √ dan √ karena , maka √

diperoleh 2 nilai real yang berbeda. (terbukti) (ii) Misal , maka persamaan (2.9) menjadi :

√ dan dan

diperoleh 2 nilai yang sama, yaitu

. (terbukti)

(iii) Misal , maka persamaan (2.9) menjadi : √ karena , maka √ √( ) dan √( )

diperoleh 2 nilai x yang merupakan bilangan kompleks. (terbukti) Dari (i), (ii), (iii) maka teorema 2.7 terbukti. QED

Berdasarkan teorema 2.7 yang berkaitan dengan diskriminan, berakibat bahwa nilai diskriminan menentukan kedudukan akar-akar persamaan kuadrat terhadap sumbu X dalam grafik fungsi kuadrat.

Jika , maka grafik fungsi kuadrat memotong sumbu X di 2 titik. Jika , maka grafik fungsi kuadrat menyinggung sumbu X di 1 titik. Jika , maka grafik fungsi kuadrat tidak memotong sumbu X.

(59)

E. Nilai Ekstrem Fungsi Polinomial

Swokowski dan Cole 2004:249 dalam buku “Fundamentals of College Algebra” menyatakan bahwa meningkatnya derajat (degree) pada fungsi polinomial maka grafik fungsinya biasanya menjadi lebih rumit. Grafik fungsi polinomial berderajat tinggi berbentuk kurva mulus yang memiliki beberapa titik puncak (high points and low points), seperti titik P, Q, R dan S pada gambar 2.12. Keempat titik tersebut dapat disebut sebagai titik balik atau turning points pada grafik.

Setiap ordinat dari titik balik disebut nilai ekstrem lokal (extremum) dari fungsi polinomial. Pada setiap titik ekstrem lokal, fungsi mengalami perubahan dari fungsi naik menjadi fungsi turun, atau sebaliknya.

Gambar 2.12 Titik-Titik Puncak dari Fungsi Polinomial X Y

(60)

Teorema 2.8 (Swokowski dan Cole, 2004: 249)

Sebuah fungsi polinomial berderajat memiliki paling banyak titik balik.

Nilai ekstrem pada fungsi polinomial dapat berupa nilai maksimum atau nilai minimum. Nilai ekstrem juga terbagi menjadi nilai ekstrem global (absolut) atau lokal (relatif). Titik balik (turning points) pada fungsi polinomial sering disebut juga titik ekstrem lokal. (Carico, 1984: 117)

Definisi 2.8 (Stewart, 2009: 318)

Sebuah fungsi memiliki sebuah maksimum global atau ekstrem maksimum global di jika ( ) ( ) untuk semua dalam , dimana adalah daerah asal dari . Nilai maksimum dari adalah ( ). Begitu pula, fungsi memiliki sebuah minimum global atau ekstrem minimum global di jika ( ) ( ) untuk semua dalam D, dimana D adalah daerah asal dari . Nilai minimum dari adalah ( )

Definisi 2.9 (Stewart, 2009: 319)

Sebuah fungsi memiliki maksimum lokal atau ekstrem maksimum relatif di jika ( ) ( ) ketika dekat atau di selang terbuka yang memuat .

Begitu pula, memiliki minimum lokal atau ekstrem minimum relatif di jika ( ) ( ) ketika dekat atau di selang terbuka yang memuat .

(61)

Fungsi memiliki ekstrem global di c jika ( ) adalah nilai maksimum atau minimum global. Sedangkan, fungsi memiliki ekstrem lokal di jika ( ) adalah maksimum atau minimum lokal.

Pada gambar 2.12 menunjukkan bahwa di titik P dan R terdapat nilai maksimum lokal. Sedangkan di titik Q dan S terdapat nilai minimum lokal. Fungsi pada gambar 2.12, tidak memiliki nilai maksimum dan minimum global karena di kanan titik S, fungsi naik tanpa batas dan di kiri titik P, fungsi turun tanpa batas. Sedangkan, jika diperhatikan pada gambar 2.13, fungsi memiliki nilai maksimum lokal yang terletak di titik A dan C, dan memiliki nilai minimum lokal di titik B. Titik A merupakan titik maksimum lokal sekaligus titik maksimum global, karena pada titik A nilai fungsinya tertinggi untuk setiap pada domain fungsi. Fungsi pada gambar 2.13 tidak memiliki nilai minimum global karena di kiri titik A dan di kanan titik C, nilai fungsi turun tanpa batas.

(62)

Teorema 2.9

Diantara 2 nilai pembuat nol real dari fungsi polinomial atau 2 akar real persamaan polinomial terdapat minimal 1 titik balik.

Bukti :

Pembuktian dari teorema ini akan menggunakan kontradiksi.

Asumsikan diantara 2 nilai pembuat nol dari fungsi polinomial tidak ada titik balik.

Misal dan adalah pembuat nol dari fungsi polinomial dengan , artinya ( ) dan ( ) .

Dari asumsi yang dipunyai, fungsi tidak memiliki titik balik diantara dan , artinya tidak terjadi perubahan dari fungsi naik menjadi fungsi turun atau sebaliknya pada selang , -.

Kasus 1 : Fungsi naik pada selang , -.

Dari definisi fungsi naik, maka berlaku ( ) ( ) untuk setiap , - dengan .

dan merupakan anggota , - dan , karena fungsi naik pada , - maka berlaku ( ) ( ). Hal tersebut kontradiksi dengan fakta bahwa dan adalah pembuat nol dari fungsi , yang artinya ( ) ( ) . Oleh karena itu, memiliki minimal 1 titik balik.

Kasus 2 : Fungsi konstan pada selang , -.

Dari definisi fungsi konstan, maka berlaku ( ) ( ) untuk setiap , -.