Aplikasi metode Kuhn Tucker untuk menentukan portofolio optimal

(1)

i

APLIKASI METODE KUHN-TUCKER

UNTUK MENENTUKAN PORTOFOLIO OPTIMAL

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika

Oleh :

Nia Christie Novena. Lie

101414021

PROGRAM STUDI PENDIDIKAN MATEMATIKA

JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM

FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

UNIVERSITAS SANATA DHARMA

YOGYAKARTA

(2)

: rlelo rnfnleslc rtr?leJ

trIT'YNflAON flIISTUHJ YIN

TYIAIIIdO OITO.{OTUOd NYXIIJNflNflru XTIINN V

W

JTN-NTIE X UOOTfl W ISYXIAdV

ffiD

ll

l--v

'E*qqq*"4

(3)

en ?ue^oNepspqSqN

-@

sllnued

tIgZ requteseq gI

!rr1ef3o1

'rlelrry etfuq

a{qefq

eueuquEaqsa qa1snd.mgmp _{uup rrsdprDl}_rrrBIBp

usrynqesry qelaEuei( _[snca{trJel Eueroe,fta1uurtq nnp er{,w1luntrlsur _{sprt Iul s$rckes 6uef rsdpls e,llqBq s,(qnffftmscs ueguop uuqqer(uetu a(es

VAUIDT XVTTSWT NYVIYTArufl{

(4)

elT'uue^oN el$!n{J ?lN

@

'uerlepr(ueu Euea

tIgZ requrese61 _{8I ?re{efEo,t}

'efueueq-nueqes ueEuep pnq a(es rm uesla(ued uullpuep uuEuag

'snnuad _lauqesa,(Bs eunuu€ryryu"cueur dalel BurBIes u,t?s sp?dq nledor uu:llreqruew tmdneu efes psp ur4 stwureu npad eduul spuepe)p uuEuquedel _{n}unu1q etpatu nste pruelur rp efuuopsurylqndueru uep

sq?qJel ?.tuces e{uuueysnqusrpueu 'u1up uulq8uud {nruaq ur?lep a(uelole8ueu

'qq

epeu

_{{nlueq ul?pp}uulqSu8ueu treduu(ueu

{nlm

{grl

?uu?qc sl€u?S ss{sJe

lun

uaelqsndre4

"pdq

uu:llroqtueu e{us uepiluep ueEueg

TrtrtrJ.do

olaof,o.f,uod

N\'xflJ.Nuxtu,tr

xilNn

v

tx

)N-N

H

nx

fl ooJ.fl Ii[

IsY)uldv

,

: ppnpeq Euu.r( qep41e&q euusqg u1BrrBS ss1rsrelrun ueq4sndred sp€de{ w{uequau efes 'uunqepEued

nql

ue8uuqueryed rrueg

lz0vlvlOl

:

?^\srssqel\I roruoN

el'I '?ue oN epslnlS qN : €ru?N

: srru?qq s1uuss ss1$e _1unua\slsaqutu el(Bs _{'rur gelrreqrp}ueEuq epuqleq Euea

SII{Ifl (IlrTY NVCNIINfldDT

xnJ.Nn

Hwritlr valtY)t Nvffmflsufld

ttvvrY^Nutd

uvgr^Ifl'I

(5)

IS'ru'su,$Au!tr8/rarntrAl,{uug'q3

tS _A{'ouq.rlng

1S'IAI'su&Eulrro&rntrAl,tuug'q3 pd'S _'oilqpng,{puy snu!11acr"tr4tr .r(I uuEuua

spusl

durlEual BrtrBN

ffi

1eJg.& rynuetueru uel4u,turp ueq

?I0Z reqoqo g leEEuel eped I[n6ued

ql

uedep rp us{ueqeuodgp qe1el

IZO'I'IOI

elT'BtreaoN epsFqS BlN : qelo

TYntrIdO OITO.IOIUOd NVXnINgNgW

XOINfI

I AuNJN-NHNX

flOOIflI

[ ISYXITdV

ISdtDTS

NVHVSACNIId NY'\IV'IYH

g

uloEEuy

1 ulo88uy

slrqeqes

Bnlex

uBlEq"f

(6)

vi

Karya ini kupersembahkan untuk :

Tuhan Yesus Kristus

Papa dan Mama

Segenap keluarga

(7)

vii

So I say to you, ask and it will be given to you;

search, and you will find; knock, and the door

will be opened for you.

Jesus Christ

Everything is theoretically impossible,

until it is done.

Robert A. Heinlein

Let us always meet each other with smile, for

the smile is the beginning of love.

Mother Teresa

Start where you are. Use what you

have. Do what you can.

Arthur Ashe

…jika kamu punya pemimpi besar biarkan

orang lain melihat mimpimu.

(8)

viii

KATA PENGANTAR

Puji dan syukur penulis ucapkan terima kasih kepada Tuhan Yang Maha Esa karena atas berkat dan rahmat kasih-Nya penulis dapat menyelesaikan skripsi ini dengan judul “Aplikasi Metode Kuhn-Tucker Untuk Menentukan Portofolio

Optimal”. Skripsi ini disusun sebagai salah satu syarat untuk memperoleh gelar Sarjana Pendidikan di Program Studi S1 Pendidikan Matematika, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma.

Dalam menyelesaikan skripsi ini banyak hambatan-hambatan yang Penulis temukan, namun hambatan-hambatan tersebut dapat penulis hadapi dengan adanya bantuan dari berbagai pihak. Oleh karena itu, dalam kesempatan ini penulis ingin mengucapkan terimaksih kepada:

1. Rohandi, Ph.D. selaku Dekan Fakultas Keguruan dan Ilmu Pendidikan Universitas Sanata Dharma.

2. Dr. Marcellinus Andy Rudhito S.Pd selaku Ketua Jurusan Pendidikan Matematika Universitas Sanata Dharma.

3. Sutrisno, M.Sc selaku Dosen Pembimbing yang telah membimbing dan mengarahkan penulis dalam penyusunan skripsi ini.

4. Segenap Dosen Jurusan Pendidikan Matematika Universitas Sanata Dharma yang telah membagikan ilmunya selama penulis menjadi mahasiswa di Universitas Sanata Dharma.

(9)

ix

6. Untuk Boby Culius Ertanto yang telah memberikan semangat selama penulis menjalani perkuliahan.

7. Sahabat-sahabatku Robertus Indra Satria Permana, Susi Kurniasih, Natanael Jalung Liah, Just five of Us, danExtravaganza-cilex yang selalu memberi semangat dan motivasi yang luar biasa.

8. Rekan-rekan mahasiswa Pendidikan Matematika angkatan 2010 yang memberikan dukungan dan motivasi selama belajar di Universitas Sanata Dharma.

Penulis menyadari bahwa masih banyak kekurangan-kekurangan dalam penyusunan skrisi ini. Oleh karena itu, Penulis mohon maaf atas kekurangan tersebut. Semoga skripsi ini dapat berguna bagi kita semua, terutama bagi para mahasiswa prodi Pendidikan matematika. Kritik dan saran dari pembaca akan penulis terima dengan baik sebagai bahan evaluasi.

Yogyakarta, 3 Oktober 2014

(10)

x

DAFTAR ISI

HALAMAN JUDUL ... i

HALAMAN PERSETUJUAN DOSEN PEMBIMBING ... ii

LEMBAR PERNYATAAN KEASLIAN KARYA ... iii

LEMBAR PERSETUJUAN KARYA ILMIAH ... iv

HALAMAN PENGESAHAN ... v

HALAMAN PERSEMBAHAN ... vi

KATA PENGANTAR ... viii

DAFTAR ISI ... x

DAFTAR LAMBANG DAN SINGKATAN ... xii

DAFTAR GAMBAR ... xiii

DAFTAR TABEL ... xiv

ABSTRAK ... xv

ABSTRACT ... xvi

BAB I. PENDAHULUAN ... 1

1.1Latar Belakang Masalah ... 1

1.2Rumusan Masalah ... 3

1.3Tujuan Penelitian ... 3

1.4Manfaat Penelitian ... 4

1.5Batasan Masalah... 4

1.6Batasan Istilah ... 5

BAB II. DASAR TEORI ... 6

2.1Himpunan Konvek ... 6

2.2Bentuk Kuadratik ... 7

2.3Fungsi Konvek ... 9

2.4Titik Ekstrim ... 11

(11)

xi

2.6Statistik Multivariat ... 16

2.7Pasar Modal ... 19

2.8Saham ... 20

2.8.1. Pengertian Saham ... 20

2.8.2. Jenis-Jenis Saham ... 21

2.9Investasi ... 24

2.9.1. Pengertian Investasi ... 24

2.9.2. Resiko Investasi ... 24

2.10 Teori Portofolio ... 25

2.10.1.Pengertian Portofolio ... 25

2.10.2.Return dan resiko Portofolio ... 26

BAB III OPTIMASI KUADRATIK ... 35

3.1Pemrograman Kuadratik ... 35

3.2Pengali Lagrange ... 35

3.3Metode Kuhn-Tucker ... 36

BAB IV PEMBAHASAN ... 41

4.1.Pengumpulan Data ... 41

4.2.Perhitungan Return dan Resiko Individual ... 46

4.3.Perhitungan Return dan Resiko Portofolio ... 49

4.4.Bentuk Umum Optimasi Kuadratik Untuk Optimisasi Portofolio ... 52

4.5.Penyelesaian Optimasi Kuadratik Untuk Menentukan Portofolio Optimal ... 53

4.6.Portofolio Optimal ... 56

BAB V PENUTUP ... 60

4.7.Kesimpulan ... 60

4.8. Saran ... 60

(12)

xii

DAFTAR LAMBANG DAN SINGKATAN

: Himpunan semua bilangan real

n

(13)

xiii

DAFTAR GAMBAR

Gambar 2.1 Fungsi Konvek dan Bukan Fungsi Konvek ... 7

Gambar 2.2Grafik Konvek

f x

( )



x

2 ... 10

Gambar 2.3 Perintah Pada Matlab ... 40

Gambar 2.4 Output Matlab ... 40

Gambar 4.1 Halaman Awal Yahoo Finance ... 42

Gambar 4.2 Pencarian Data Saham PT Mandiri TBK ... 42

Gambar 4.3 Data Saham PT Mandiri TBK ... 43

Gambar 4.4 Historical Prices PT Mandiri TBK ... 43

Gambar 4.5 Periode Harga Saham ... 44

Gambar 4.6 Harga Saham PT Mandiri TBK ... 44

Gambar 4.7 Data Saham PT Mandiri TBK Pada Lembar Kerja Excel ... 44

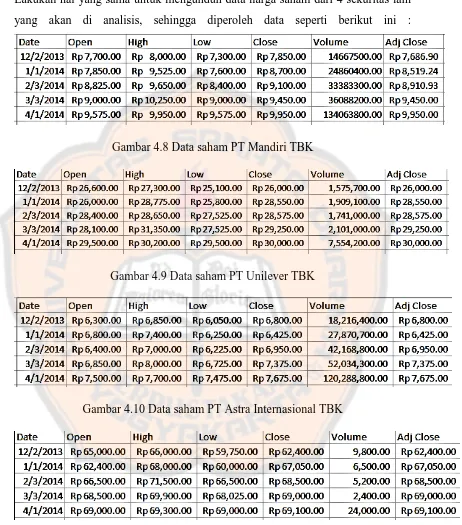
Gambar 4.8 Data Saham PT Mandiri TBK ... 45

Gambar 4.9 Data Saham PT UnileverTBK ... 45

Gambar 4.10 Data Saham PT Astra Internasional TBK ... 45

Gambar 4.11 Data Saham PT Sampoerna TBK ... 45

Gambar 4.12 Data Saham PT Indofood TBK ... 46

Gambar 4.13 Program Optimasi Portofolio ... 55

Gambar 4.14 Output Program Optimasi Portofolio ... 55

(14)

xiv

DAFTAR TABEL

Tabel 4.1 Return Individual Lima Perusahaan ... 47

Tabel 4.2 Nilai Return Ekspektasi ... 48

Tabel 4.3 Nilai Variansi ... 49

Tabel 4.4 Return Masing-Masing Sekuritas ... 51

Tabel 4.5 Solusi Optimasi Portofolio ... 56

(15)

xv

ABSTRAK

Christie Novena. Lie, Nia. 2014. Aplikasi Metode Kuhn-Tucker untuk

Menentukan Portofolio Optimal. Skripsi. Yogyakarta : Program Studi

Pendidikan Matematika, Jurusan Pendidikan Matematika Dan Ilmu

Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan,

Universitas Sanata Dharma.

Portofolio saham merupakan gabungan dari beberapa saham dari berbagai sekuritas. Masalah utama dalam pembentukan portofolio adalah bagaimana menentukan proporsi alokasi dana untuk masing-masing sekuritas pada portofolio tersebut sedemikian sehingga portofolio yang disusun menjadi sebuah portofolio yang optimal, dalam kasus ini, yaitu portofolio yang memberikan resiko paling kecil. Untuk mendapatkan portofolio yang optimal, digunakan metode optimasi kuadratik untuk meminimumkan resiko portofolio yang solusinya dicari dengan metode Kuhn-Tucker dan dapat diselesaikan menggunakan fungsi “quadprog”

pada software MATLAB. Berdasarkan hasil optimisasi yang diperoleh, didapatkan proporsi dana untuk masing-masing sekuritas dari lima sekuritas yang diteliti yaitu PT Mandiri TBK (BMRI) sebesar 21,92%, PT Unilever (UNVR) sebesar 15,56%, PT Astra Internasional (ASII) sebesar 14,46%, PT Hanjaya Mandala Sampoerna (HMSP) sebesar 27,88% dan PT Indofood CBP Sukses Makmur (ICBP) sebesar 20,18%. Proporsi alokasi dana tersebut akan memberikan portofolio yang optimal yaitu memberikan resiko paling kecil.

(16)

xvi

ABSTRACT

Christie Novena. Lie, Nia. 2014. Kuhn-Tucker Methods Application to

Determine Optimal Portofolio. Thesis. Yogyakarta : Mathematics

Education Study Program, Department of Mathematics Education and

Natural Science, Faculty of Teachers Training and Education, Sanata

Dharma University.

Stock portfolio is a combination of several stocks of various securities . The main problem in the formation of a portfolio is how to determine the proportion of funds allocated to each of the securities in the portfolio so that the portfolio compiled into an optimal portfolio , in this case , the portfolio which gives the smallest risk . To obtain the optimal portfolio , quadratic optimization method is used to minimize the risk of a portfolio whose solution sought by the Kuhn - Tucker method and can be solved using the " quadprog " in MATLAB software . Based on the optimization results obtained , the proportion of funds obtained for each of the five securities securities under study , namely PT Mandiri TBK ( BMRI ) amounted to 21.92 % , PT Unilever ( UNVR ) amounted to 15.56 % , PT Astra International ( ASII ) of 14.46 % , PT Hanjaya Mandala Sampoerna ( HMSP ) amounted to 27.88 % and PT Indofood CBP Sukses Makmur ( ICBP ) of 20.18 % . The proportion of the allocation of these funds will provide an optimal portfolio that gives the smallest risk

(17)

1

BAB I

PENDAHULUAN

1.1Latar Belakang Masalah

Metematika merupakan salah satu ilmu pengetahuan yang tidak dapat dilepaskan dari kehidupan sehari-hari. Dari kegiatan sehari-hari sangat mudah ditemukan matematika dalam kehidupan manusia, misalnya ketika akan berberlanja dipasar atau disupermarket. Selain itu, matematika juga sangat berkaitan erat dengan ilmu pengetahuan lainnya. Misalnya ekonomi, fisika, dan lain-lain.

Penerapan matematika yang sangat dekat dengan manusia adalah masalah optimasi. Contoh masalah optimasi dalam kehidupan manusia adalah bagaimana seseorang mampu menggunakan pendapatannnya untuk memenuhi kebutuhan hidupnya, dengan memperhatikan pendapatan yang terbatas dan memperhitungkan banyaknya kebutuhan yang harus dipenuhi. Atau dengan kata lain, manusia harus mampu meminimumkan pengeluaran sehingga pendapatan yang terbatas mampu memenuhi kebutuhannya.

(18)

2

terlebih dahulu saham-saham tersebut. Hal ini dimaksudkan agar dapat menentukan kualitas, prospek, dan tingkat resiko yang ada pada saham-saham tersebut.

Analisis dengan portofolio merupakan salah satu alternatif yang dapat dipilih dalam menganalisis saham-saham sebelum pada akhirnya memutuskan membeli saham tersebut. Didalam investasi, jika seorang investor hanya tergantung pada satu investasi saja, maka akan semakin banyak resiko yang harus ditanggung oleh investor tersebut. Dalam keputusan investasi harus selalu dingat bahwa, investasi yang dilakukan adalah untuk mendapatkan keuntungan dimasa datang.

Setelah melihat masalah diatas, maka penulis tertarik menganalisis permasalahan portofolio saham. Portofolio saham adalah kumpulan dari ebberapa saham. Dengan melihat portofolio sebagai alternatif untuk mengambil keputusan investasi bagi para calon investor terlebih dalam meminimalkan resiko. Hal ini sangat diperlukan bagi para calon investor sebagai pertimbangan dalam berinvestasi. Sehingga hal ini akan menjadi bahan untuk melakukan analisis saham.

Portofolio yang diharapakan bagi seorang investor adalah portofolio yang optimal. Portofolio yang optimal adalah portofolio yang mampu memberikan tingkat pengembalian yang terbesar dengantingkat resiko yang sudah pasti. Analisis portofolio optimal tersebut dapat dilakukan dengan berbagai cara, dalam penelitian kali ini penulis memilih untuk menyelesaikan masalah pembentukan portofolio saham tersebut dengan metode optimasi kuadratik yang solusinya akan dicari dengan metode Kuhn-Tucker. Dengan optimasi kuadratik akan diperoleh solusi yang dapat menentukan portofolio optimal dengan meminimumkan resiko. Dengan meminimumkan resiko diharapkan agar analisis yang dilakukan adalah analisi yang sederhana.

(19)

Lima perusahaan yang akan coba dianalisis adalah PT Mandiri TBK, PT Unilever TBK, PT Astra Internasional, PT Hanjaya Mandala Sampoerna, dan PT Indofood CBP Sukses Makmur. Untuk menganalisis portofolio saham ini, penulis akan mengunduh Historical Prices masing-masing perusahaan pada periode Desember 2013 sampai dengan April 2014. Data Historical Prices akan diunduh pada situs Yahoo Finance : http://finance.yahoo.com.

1.2Rumusan Masalah

Berdasarkan penjabaran latar belakang diatas, yang akan menjadi pokok permasalahan didalam penelitian ini dirumuskan sebagai berikut:

a) Bagaimana menyelesaikan masalah optimasi kuadratik dengan metode Kuhn-Tucker?

b) Bagaimana membentuk model matematika dari suatu portofolio agar mendapatkan nilai resiko yang minimum?

c) Bagaimana menentukan portofolio yang optimal menggunakan metode optimisasi kuadratik?

1.3Tujuan Penelitian

Sesuai dengan rumusan masalah diatas, maka tujuan penelitian ini adalah :

a) Mendapatkan solusi untuk menyelesaikan masalah optimasi kuadratik dengan metode Kuhn-Tucker.

b) Mendapatkan model matematika dari suatu portofolio agar mendapatkan nilai resiko yang minimum.

(20)

1.4Manfaat Penelitian

Manfaat utama dari penelitian ini adalah didapatkannnya model matematika dari suatu portofolio dan portofolio yang optimal dengan menggunakan metode optimisasi kuadratik. Selain itu, penelitian ini diharapkan dapat memberi manfaat antara lain untuk :

a) Bagi peneliti :

Penelitian ini diharapkan dapat menambah wawasan pengetahuan peneliti mengenai pasar modal terutama tentang optimisasi nilai resiko portofolio saham.

b) Bagi investor :

1) Dapat memberikan tambahan referensi masukan tentang manfaat portofolio dalam menentukan keputusan investasi dan memberikan pandangan untuk tidak hanya berinvestasi hanya pada satu jenis saham saja.

2) Membantu investor menentukan model yang tepat agar portofolio yang disusun sudah menghasilkan nilai resiko yang optimal.

c) Bagi pihak lain:

Penelitian ini diharapkan dapat menjadi tambahan ilmu pengetahuan yang dapat dijadikan referensi untuk penelitian lebih lanjut.

1.5Batasan Masalah

Agar dapat memfokuskan penelitian maka perlu diberi batasan, yaitu : a. Studi penelitian dilakukan pada saham bursa efek Indonesia.

Nilai-nilai saham pada bursa efek diambil dari Yahoo Finance (http://finance.yahoo.com/) pada periode Desember 2013 sampai dengan April 2014. Untuk itu diasumsikan bahwa perekonomian yang terjadi di Indonesia dalam keadaan normal dan semua data

(21)

b. Untuk mempermudah perhitungan manual hanya akan diambil 5 sektor saham, yakni PT Mandiri TBK (BMRI), PT Unilever (UNVR), PT Astra Internasional (ASII), PT Hanjaya Mandala Sampoerna (HMSP), dan PT Indofood CBP Sukses Makmur (ICBP).

c. Portofolio Optimal sederhana dengan menggunakan Historical Prices.

1.6Batasan Istilah

Beberapa batasan istilah yang digunakan dalam penelitian ini, yaitu : a. Portofolio saham

Portofolio saham adalah kumpulan dari beberapa saham. b. Portofolio optimal

Portofolio optimal adalah portofolio yang mampu memberikan resiko terkecil.

c. Return

Return adalah tingkat pengembalian (hasil yang diperoleh dari investasi)

d. Return individu

Return individu adalah return masing-masing sekuritas. e. Return ekspektasi

Return ekspektasi adalah return yang diharapkan akan diperoleh pada masa yang akan datang.

f. Return realisasi

Return realisasi adalah return yang sudah terjadi. g. Resiko

Resiko adalah penyimpangan nilai yang sudah terjadi dengan nilai ekspektasinya.

h. Rata-rata tertimbang

(22)

6

BAB II

DASAR TEORI

Untuk menyelesaikan masalah optimasi untuk menentukan portofolio yang optimal, dibutuhkan teori-teori optimasi yang mendukung. Beberapa teori yang digunakan untuk menyelesaikan optimisasi tersebut meliputi himpunan konvek, bentuk kuadratik, fungsi konvek, titik ekstrim, pengali lagrange, dan pemrograman kuadratik.

2.1Himpunan Konvek

Definisi berikut ini menjelaskan konsep tentang himpunan konvek.

Definisi 2.1. (Mital, K.V 1983). Sebuah himpunan K n disebut konvek jika kombinasi linier konvek dari dua titik di K termasuk di dalam K. Atau dengan

kata lain, K adalah himpunan konvek jika

x x

₁

,

₂

  

K

x K

dimana

1 2

(1

)

,0

1

x

 



x





x

 



.

Sebagai ilustrasi, suatu himpunan konvek _k  n_{. Dapat ditentukan}

sembarang titik p yang berada pada segmen garis yang menghubungkan sembarang dua titik yakni

p

₁ dan

p

₂, maka titik p yang berada diantara titik

1

(23)

Gambar 2.1 fungsi konvek dan bukan fungsi konvek

Pada gambar 2.1 dapat dilihat bahwa jika diambil sembarang 2 titik pada sebuah segmen garis maka kedua titik tersebut masih berada pada satu garis yang sama.

2.2Bentuk Kuadratik

Uraian berikut ini akan menjelaskan definisi dari bentuk kuadratik.

Suatu fungsi

f

:

n



yang berbentuk

2 2 2

11 1 22 2 nn n 12 1 2 13 1 3 23 2 3 ij

f(x) = c x + c x + ...+ c x + c x x + c x x + c x x + ...,c



R,i, j = 1,2,...n

disebut bentuk kuadratik didalam variabel

x ,x ,x ,...x

1 2 2 n. Jika

a

11

disubsitusikan kedalam

c

_ii dan

a + a

_ji _ij ke

c

_ij, maka akan didapat :

n n

2 2 2

11 1 22 2 nn n 12 1 2 21 2 1 ij i j

i= 1 j= 1

f(x) = a x + a x + ...+ a x + a x x + a x x + ...=



a x x = x'Ax. dengan

1 2

n

x x x =

x

           

,

11 1n

n1 nn

a … a

A=

a a

 

 

 

(24)

'

x Ax=



x1 x2 xn



11 1n

n1 nn

a … a

a a           1 2 n x x x             .

Selanjutnya, akan diberikan definisi yang menjelaskan sifat bentuk kuadratik apakah definit positif, semidefinit positif, definit negatif atau semidefinit negatif. Definisi ini akan digunakan untuk menentukan kekonvekan sebuah fungsi yang berbentuk kuadratik.

Definisi 2.2. (Mital, K.V 1983). Sebuah bentuk kuadratik x Ax' disebut definit positif jika x Ax' 0untuk semua x0. Disebut definit semidefinit positif jika

' 0

x Ax untuk semua x0 dan setidaknya ada satu vektor tidak nol yang membuat x Ax' 0. Definit negatif dan semidefinit negatif didefinisikan dengan membalik tanda ketidaksamaan pada definisi diatas.

Teorema 2.1. (Mital, K.V 1983). Misalkan nilai eigen dari matrik simetrik A

berordo nn, adalah

   

1

, , ,... ,

2 3 k

k



n

.

Maka bentuk kuadratik x Ax'

adalah:

(i) Definit positif

 



_j

0

untuk semua j;

(ii) Definit negatif

 



j

0

untuk semua j;

(iii) Semidefinit positif

 



j

0

;

(iv) Semidefinit positif

 



j

0

;

Contoh 2.1. Bentuk kuadratik f x

( ) 7



x₁2



10

x₂2



7

x₃2



4

x x_{1 2}



2

x x_{1 3}



4

x x_{2 3}

jika diubah kedalam bentuk umum bentuk kuadratik akan menjadi



1 2 3



( )

f x  x x x

7 2 1

2 10 2

1 2 7

(25)

Setelah diubah kedalam bentuk umum bentuk kuadratik, maka dapat diketahui matrik A dari bentuk tersebut. Matrik A untuk bentuk kuadrat diatas adalah

A =

7 2 1

2 10 2

1 2 7

   _ _         .

Dari matrik A ini akan ditentukan nilai eigen dari bentuk kuadrat

2 2 2

1 2 3 1 2 1 3 2 3

( ) 7

10

7

4

2

4

f x



x



x



x



x x



x x



x x .

7 2 1

2 10 2 0

1 2 7

          

Untuk mencari nilai eigen matriks diatas, terlebih dahulu akan dihitung determianan dari





IA



dengan metode Sarrus, sehingga diperoleh:

Det





IA



=





7



10 2

2 7



 

  - (-2)

2 2

1  7

 

 - 1

2 10

1 2



 



Det





IA



= 3 2

24 180 432 0

      atau

(





6) (

2



 

12) 0

Dari faktor diatas, didapat nilai eigen untuk bentuk kuadratik diatas adalah 6, 6, dan 12. Semua nilai eigen yang didapat bernilai positif, maka bentuk kuadratik

2 2 2

1 2 3 1 2 1 3 2 3

( ) 7

10

7

4

2

4

f x



x



x



x



x x



x x



x x adalah bentuk kuadratik yang definit positif.

2.3Fungsi konvek

Beberapa definisi dibawah ini akan menjelaskan tentang fungsi konvek beserta hubungannnya dengan himpunan konvek yang telah dijelaskan diatas.

Definisi 2.3. (Mital, K.V 1983). Andaikan n

x K  dimana K adalah

himpunan konveks. Fungsi f(x) dikatakan konveks jika untuk setiap dua titik

x

1

(26)

1 2 1 2

f((1 -



)x +



x )



(1 -



)f(x )+



f(x ),0

 



1

Gambar 2.2 Grafik Fungsi Konvek

f x

( )



x

2

Sebagai contoh, fungsi

f x

( )



x

2 adalah sebuah fungsi konvek. Hal ini dapat dilihat dari kombinasi liner konvek

(1 - )f(x )+



₁



f(x )

₂ yang digambarkan sebagai titik pada tali busur yang menghubungkan

f(x

₁

)



A

dan

2

f(x ) B



, serta



f(x )+

₁

(1





)

f(x ) C

₂



adalah titik yang menghubungkan

1

f(x )

dan

f(x )

₂ . Terlihat pada gambar bahwa kombinasi liner konvek

1 2

(1 - )f(x )+



f(x )

selalu berada diatas

f (1- )x + x

(



1



2

)

, hal ini

mengakibatkan nilai dari

f

((1





)

x + x ) (1- )f(x )+ f(x )

₁



₂





₁



₂ . Maka fungsi

f x

( )



x

2 adalah fungsi konvek.

Pada pembahasan diatas telah dijelaskan bagaimana sebuah sifat bentuk kuadratik yang memenuhi definit positif, semidefinit positif, definit negatif dan semidefinit negatif. Selanjutnya, teorema-teorema dibawah ini akan menjelaskan jika sebuah fungsi yang semidefinit positif adalah sebuah fungsi konvek.

Teorema 2.2. (Mital, K.V 1983). Diberikan n

x dan f(x) = x Ax' adalah sebuah bentuk kuadratik. Jika f(x) adalah semidefinit positif , maka f(x) adalah

(27)

Bukti :

Misal

x

₁ dan

x

₂ adalah dua titik pada n

dan

x

 

(1



)

x

₁





x

₂, 0 λ 1. Karena f x( )x Ax' adalah semidefinit positif, maka nilai x Ax' 0 untuk

semua n

x .

1 2

(1) ( )f x f x( ) f x( )  (1 )x Ax1' 1x Ax2 2 ((1 )x1x2) ' ((1A )x1x2) 1 1 2 2 1 1 1 2 1 1 2 (1 )x Ax' x Ax (x Ax' x A' x ' )(A x x x)

       

2 2

1 1 2 2 1 1 2 2 1 2

(1 ) 'x Ax x Ax (1 ) x Ax'  x Ax' 2 (1 ) 'x Ax

       

1 2 2 2 1 2

(1 )( 'x Ax x Ax' 2 'x Ax )  

   

1 2 1 2

(1 )(x x ) 'A(x x ) 0.  

    

Karena 0  1dan

x

1



x

2adalah vektor pada n

maka :

1 2

( ) (1- ) ( ) + ( )

f x 



f x



f x .

Karena nilai f x( ) (1- ) ( ) +



f x1



f x( )2 , maka fungsif(x) adalah fungsi konvek.

2.4Titik Ekstrim

Titik ektrim suatu fungsi dapat berupa titik maksimal/ minimal global atau maksimal/minimal lokal yang dijelaskan pada definisi berikut :

Definisi 2.4. (Mital, K. V 1983). Fungsi f(x) mempunyai titik minimal global

pada dalam n

jika untuk semua x dalam n, f(x) ≥ f(

. Untuk titik

maksimal global pertidaksamaannya bertanda sebaliknya.

Definisi berikut ini akan memberikan uraian tentang peminimum lokal dari suatu fungsi.

Definisi 2.5. (Mital, K.V, 1983). Fungsi f(x) mempunyai titik minimal lokal atau

relatif pada dalam n

jika terdapat � dipersekitaran dari , sedemikian

(28)

Dari definisi diatas, jelas terlihat bahwa nilai maksimum global akan lebih besar atau sama dengan nilai maksimum lokal. Sedangkan nilai minimum global akan lebih kecil atau sama dengan nilai minimum lokal.

Teorema dibawah ini akan menunjukan bahwa nilai minimum lokal dari sebuah fungsi konvek juga merupakan nilai minimum global fungsi tersebut.

Teorema 2.3. (Mital, K.V 1983). Andaikan n

K adalah himpunan konvek,

jika x K dan f(x) adalah fungsi konvek. Jika f(x) memiliki nilai minimum lokal,

maka nilai itu juga merupakan nilai minimum global. Jika f(x) memiliki nilai

minimum lokal dibeberapa titik, maka nilai minimum global dicapai oleh

kombinasi linier dari titik-titik tersebut.

Bukti :

Misalkan f(x) memiliki nilai minimum relatif di

x

₀, dengan

x

₁



K

. Untuk semua  > 0 maka dapat dipilih , 0  1, sehingga terdapat:

0 1

x= x + (1- )x



yang berada di sekitar  di

x

0. Dengan menggunakan

definisi relative minimum, didapat

0 0

f(x )



f(x )



f(x )

0



f( x + (1- )x )



0



1

0 1

f(x )+ (1 - )f(x )





{karena f(x) konvek}



(1- )f(x ) (1-



₀





)

f(x )

₁



f(x )

0



f(x )

1 , karena 1 positif

(29)

Jika terdapat titik

y

₀dimana minimum itu dicapai, maka:

f(x )= f(y )

₀ ₀ . Karena K adalah salah satu titik didalam K, maka jika berlaku di

x

₁ juga belaku pada

1

y

. Sehingga diperoleh

0 0 0

( )

( x

(1

) y )

f x



f



 



0 0 0

(x

(1

) (y )

(y )

f





 



0 0 0

( )

( x

(1

) y )

f x



f



 



.

Dari penjabaran diatas dapat dilihat bahwa, nilai minimum juga berlaku pada kombinasi linier konvek dari

x

0 dan

y

0. Sehingga himpunan titik dimana f(x)

minimum adalah himpunan minimum konvek dan merupakan kombinasi linier dari titik tersebut.

Selain beberapa teori yang telah dijabarkan diatas, dibutuhkan teori lain sebagai pendukung untuk menentukan portofolio optimal. Teori tersebut adalah teori tentang nilai harapan. Pada pembahasan mengenai resiko portofolio akan dicari nilai harapan dari masing-masing sekuritas dan nilai harapan portofolio, untuk itu akan dibahas terlebih dahulu tentang nilai harapan.

2.5Nilai Harapan

Definisi 2.6. (Abdus Salam, 1989). Misalkan bahwa suatu variabel random X

mempunyai distribusi diskrit dengan fungsi peluang dari X adalah f. Nilai

harapan dari X ditulis dengan lambang E(X). Nilai harapan dari x atau E(X)

adalah suatu jumlahan yang didefinisikan sebagai berikut :

( ) _x ( )

E X 



xf x (1.1)

( ) ( )

x x f x  



(1.2)

Definisi 2.7 (Abdus Salam, 1989) . Jika sebuah variabel random X mempunyai

(30)

Ekspektasi dari X ditulis dengan lambing E(X). Nilai Ekspektasi x atau E(X)

didefinisikan sebagai berikut:

( ) ( )

E x xf x dx









(1.3)

Teorema 2.4. (Abdus Salam, 1989): Jika YaXb, dimana a dan b adalah konstanta maka E Y( )aE(X)b.

Bukti :

( ) E(aX b) E Y  

(aX b f x dx) ( )











( ) ( )

a xf x dx b f x dx

 

 









(X) b aE

 

Definisi 2.8 (Abdus Salam, 1989). Misalkan X adalah sebuah variabel random

dengan Mean (lambang



)E X( ). Varian dari X ditulis Var X( )

,didefinisikan sebagai berikut :

Var X( )E



(X)



2 (1.4) Beberapa sifat varian :

1.

E X

(





)

2



E X

(

2

)





2 Bukti :

Dari definisi (1.1)diatas diketahui bahwa E X( ).

Maka :

2 2 2

(

)

(

2

)

E X







E X





X





2 2

(

) 2

( )

E X



E X









2 2

(

) 2

E X

 

(31)

2 2

( ) 2

E X

 







2 2

(

)

E X







2. Jika

X

₁ dan

X

₂ adalah variabel random bebas, maka

1 2 1 2

(

)

(

)

(

)

Var X



X



Var X



Var X

. Bukti:

Berdasarkan definisi (1.1) diatas bahwa E X( ), maka

E X

(

1

)





1 dan

2 2

(

)

E X





sehingga

E X

(

₁



X

₂

)

 

 

₁ ₂ . Maka :





2

1 2 1 2 1 2

( ) ( )

Var X X E X X   

2

1 1 2 2

(( ) ( ))

E X  X  

 _    _

2 2

1 1 2 2 1 1 2 2

( ) ( ) 2( )( )

E X  X  X  X  

 _       _

1 2 1 1 2 2

(

)

(

) 2 (

)(

)

Var X

E X



X









Karena

X

₁ dan

X

₂ bebas, maka :



E X

(

1





1

)(

X

2





2

)





E X

(

1





1

) E(

X

2





2

)



(E

X

1



1

)(E

X

2



2

)







1 1 2 2

(

   

)(

)

 



0



Karena



E X

(

1





1

)(

X

2





2

)





0

, maka

1 2 1 2

(

)

(

)

(

) 0

Var X



X



Var X



Var X



. Sehingga,

1 2 1 2

(

)

(

)

(

)

(32)

3.Varian dari X adalah konstan.

E X

(

2

)





2,2_{adalah konstan.}

Definisi 2.9. (Abdus Salam, 1989). Kovarian didefinisikan sebagai berikut:







1

( ) ( ) ( , )

N

xy i i

i

X E X Y E Y p x y







  (1.5)

dengan



xy adalah nilai kovarian antara dua peubah acak,

X

i adalah nilai

variabel acak X ke-i,

Y

_i adalah nilai variabel acak Y ke-i, p x y( , ) adalah

probabilitas terjadinya

X

_i dan

Y

_i, dan

n

adalah banyaknya kondisi masa depan i (1, 2, 3...N).

Kovarian antara dua peubah acak adalah suatu hubungan antara dua peubah acak tersebut. Misalnya Sekuritas A dan Sekuritas B. Nilai kovarian yang positif akan menunjukan nilai kedua sekuritas tersebut bergerak kea rah yang sama (jika sekuritas A meningkat maka sekuritas B akan meningkat, sebaliknya jika sekuritas A menurun maka sekuritas B akan menurun). Sedangkan nilai kovarian yang negatif akan menunjukan pergerakan kedua sekuritas yang bergerak berlawanan (jika nilai sekuritas A meningkat maka nilai sekuritas B menurun, sebaliknya jika niali sekuritas A menurun maka nilai sekuritas B akan meningkat).

2.6Statistika Multivariat

Pembahasan selanjutnya akan dibahas tentang statistika multivariat. Materi dalam teori ini akan membantu untuk membentuk matrik varian-kovarian yang digunakan untuk membentuk solusi dari optimasi kuadratik dalam pembentukan portofolio saham.

(33)

p variabel yakni x



( , , ,... )

x x x₁ ₂ ₃ xp dari sebanyak n individu ditulis sebagai

berikut :

11 12 1

21 22 2

1 2

p

n n np

x x x

X

x x x

              

Pada matrik data mltivariat, rata-rata masing variabel mean disajikan dalam bentuk vektor mean. Sebelum membahas hal ini akan dibahas beberapa pengertian khusus.

1. Matrik kolom atau vektor kolom adalah matrik yang terdiri dari satu kolom atau matrik berordo n1 . Matrik kolom dinyatakan dalam bentuk sebagai berikut :

1 2 n x x X x              .

2. Matrik baris atau vektor baris adalah matrik yang terdiri dari satu baris atau matrik yang berordo 1n . Matrik baris dinyatakan dalam bentuk sebagi berikut :

1 2 p

X  x x x _.

3. Vektor nol adalah vektor yang setiap elemennya adalah nol (bilangan nol). Contoh vektor nol adalah sebagai berikut :



0 0 0



atau

0 0 0             .

4. Vektor satuan atau vektor unit adalah vektor yang setiap

(34)



1 1 1



atau 1 1 1             .

Setelah membahas beberapa pengertian khusus selanjutnya akan dibahas vektor mean yang merupakan matrik yang menyajikan rata-rata dari masing-masing variabel. Bentuk vektor mean adalah sebagai berikut :

Misalkan suatu matrikX  x₁ x₂ x_p_maka vektor mean dari matrik X

tersebut adalah  ₁ ₂ _p_ atau matrik

1 1 1

x x x

X

x x x

             ,

maka vektor mean dari matrik tersebut adalah

1

1 1 1

1' '1

n

ij ij

i

x X X

n n n







  .

Pada data multivariate terdapat matrik varian kovarian. Matrik varian-kovarian adalah matrik gabungan dari variansi dari tiap variabel dan

kovariansi pada dua variabel yang berbeda. Matrik Varian-kovarian dilambangkan dengan  .

( ) '( )

E X



X



  



1 1 2 2

1 1 2 2 p p p p

X X

E X X X

X            _    _{ } _  __ __    __    __ _ __   

1 1 1 1 1 1 2 2 1 1

2 2 1 1 2 2 2 2 2 2

1 1 2 2

( )( ) ( )( ) .... ( )( )

p p p p

p p p p p p p p

X X X X X X

E

X X X X X X

(35)

2

1 12 1 2

21 12 2 2 1 2 ... ... ... p p

n n p

               _ _{ }        _ _{ }      2

1 12 1 2

1 2 2

2 1 2

p p

n n p

                        .

Dari matrik



diatas terlihat bahwa elemen utama dari matrik tersebut berisi nilai varian dari setiap variabel sedangkan elemen lain adalah nilai kovarian dari dua variable.

Sebagai pendukung teori matematika untuk menyelesaikan masalah pembentukan portofolio saham yang optimal diperlukan teori-teori dalam bidang ekonomi yang berhubungan dengan pembentikan portofolio. Beberapa teori dalam bidang ekonomi yang akan dijabarkan adalah pasar modal, saham, investasi, dan teori portofolio.

2.7Pasar Modal

(36)

Pasar modal (bursa efek) terbesar di Indonesia adalah Bursa Efek Jakarta (BEJ). Sekuritas yang diperjual belikan di BEJ adalah saham preferen

(preferren stock), saham biasa (common stock), hak (rights), dan obligasi konvertibel (convertible bonds). Selain BEJ bursa efek yang terbesar di Indonesia adalah Bursa Efek Surabaya (BES). BEJ menggunakan sebuah jaringan komputer untuk menangani transaksi yang terjadi di BEJ setiap harinya yang mencapai 3.800 transaksi, yakni dengan sistem otomatisasi bernama

Jakarta Automated Trading System (JATS). Sistem ini dioperasikan pertama kali pada tanggal 22 Mei 1995. Sistem JATS ini mampu menangani 50.000 transaksi setiap harinya. Sama halnya dengan sistem otomatisasi JATS yang digunakan di BEJ, di BES menerapkan Surabaya Market Information and Automated Remote Trading (S-MART). Sistem ini mulai dioperasikan pada tanggal 19 September 1996.

Untuk melindungi semua investor dipasar saham, pada tahun 1976 melalui Keputusan Presiden, departemen keuangan Indonesia mendirikan Badan Pelaksana Pasar Modal (BAPEPAM) yang bertujuan untuk melaksanakan kegiataan pasar modal. Dan pada tahun 1990 BAPEPAM diubah sebagai Badan Pengawas Pasar Modal yang hanya berfungsi sebagai pembuat regulasi (regulator), pengkoordinasi semua bursa-bursa pasar modal yang ada di Indonesia serta mengawasi jalannnya pasar modal.

2.8Saham

Berikut ini akan dijelaskan beberapa hal yang terkait dengan saham, yakni pengertian saham dan jenis-jenis saham.

2.8.1. Pengertian Saham

(37)

adalah surat berharga yang merupakan tanda kepemilikan seseorang terhadap suatu perusahan. Sedangkan, Bambang Riyanto (1995 : 250) menjelaskan Saham adalah tanda bukti peserta dalam suatu Perseroan Terbatas (PT). Bagi peserta PT tersebut, hasil yang diterima dari penjualan saham “akan tetap tertanam” didalam perusahan tersebut selama perusahan itu ada, meskipun pemegang saham itu bukanlah pemegang saham yang permanen, karena bisa saja saham tersebut dijual.

Dengan membeli saham pada suatu perusahan, berarti investor telah menginvestasikan dana dengan harapan akan mendapatkan keuntungan dari hasil penjualan kembali saham tersebut. Bentuk saham adalah secarik kertas yang menerangkan bahwa pemilik kertas tersebut adalah pemilik perusahan yang menerbitkan surat berharga tersebut dan porsi kepemilikan ditentukan oleh berapa besar dana yang ditanamkan dalam perusahan tersebut (Darmadji, 2001 : 5).

Dari definisi para ahli diatas, maka dapat disimpulkan bahwa Saham adalah surat berharga yang menunjukan bukti kepemilikan seseorang atau lembaga atas sebuah perusahaan yang sah secara hukum.

2.8.2. Jenis-Jenis Saham

Menurut Ahmad (2004) ada dua jenis saham, yakni : a. Berdasarkan Cara Peralihannya

Saham berdasarkan cara peralihannya dibedakan menjadi dua yakni Saham Atas Unjuk (Bearer Stocks) dan Saham Atas Nama (Registered stocks). Saham Atas Unjuk

(38)

berhak hadir dan mengeluarkan pendapat saat rapat pemegang saham. Sedangkan Saham Atas Nama (Registered stocks) adalah saham yang ditulis secara jelas siapa pemiliknya. Sehingga untuk mengalihkan saham tersebut harus melalui prosedur tertentu, yakni melalui dokumen peralihan kemudian nama pemilik baru akan dicatat dalam buku perusahan yang memuat nama pemegang saham. Karena didalam saham ini sudah ada nama pemiliknya, maka jika sertifikat saham ini hilang maka pemilik dapat meminta pergantian nama karena namanya sudah tercatat dalam buku perusahaan.

b. Berdasarkan Hak Tagihannnya

Saham jika dilihat berdasarkan Hak Tagihannnya dibedakan menjadi :

1. Saham Biasa (Common Stocks).

Saham biasa adalah surat biasa yang paling banyak dan paling luas diperdagangkan. Selain berhak mengeluarkan suara saat Rapat Umum Pemegang Saham (RUPS), pemilik saham biasa juga berhak mendapatkan laba (deviden) yang dihasilkan perusahaan serta mendapatkan keuntungan dari kenaikan modal (nilai) dari saham yang disebut capital gain. Menurut Siamat (2004:385), ciri-ciri saham biasa adalah sebagai berikut:

a) Dividen dibayarkan sepanjang perusahaan memperoleh laba.

b) Memiliki hak suara (one share one vote).

(39)

2. Saham Preferen (Preferren Stocks)

Saham Preferen (Preferren Stocks) adalah saham yang disertai dengan preferensi tertentu diatas saham biasa untuk hal pembagian deviden dan pembagian kekayaan saat perusahaan dibubarkan. Saham Preferen biasanya akan memberikan deviden yang tetap setiap tahunnya. Selain itu, Saham Preferen tidak memiliki hari jatuh (perpetuity) dan pemiliknya tidak mempunyai hakatas RUPS. Para pemegang Saham Preferen akan dijamin untuk mendapatkan deviden dalam jumlah yang tetap sebelum ada jumlah tertentu yang dibayarkan kepada pemegang saham biasa. Karena itu, pemegang Saham Preferen akan kehilangan haknya atas suara managemen perusahan dan atas pembagian laba diluar yang telah ditetapkan. Ciri-ciri Saham Preferen menurut Siamat (2004:385) adalah sebagai berikut:

a. Memiliki hak paling dahulu memperoleh deviden. b. Tidak memiliki hak suara.

c. Dapat mempengaruhi manajemen perusahaan terutama dalam pencalonan pengurus.

d. Memiliki hak pembayaran sebesar nilai nominal saham lebih dahulu setelah kreditur apabila perusahaan dilikuidasi.

c. Berdasarkan Kinerja Perdagangan

Jika dilihat dari kenerja perdagangannnya, saham dibagi menjadi:

(40)

2. Income Stock adalah saham yang membayar deviden melebihi jumlah rata-rata pendapatan.

3. Growth Stocks adalah saham yang dikeluarkan oleh perusahan yang laba dan pasarnya berkembang.

4. Speculative Stocks . Semua saham yang diperdagangkan merupakan saham spekulatif, karena saat membeli tidak ada kepastian keuntungan yang akan didapat tetapi memiliki kemungkinan penghasilan yang tinggi di masa yang akan datang meskipun belum pasti.

5. Counter Cylical Stocks adalah saham perusahaan yang keuntungan dipengaruhi oleh siklus usaha.

2.9Investasi

Berikut ini akan dijelaskan hal-hal yang berkaitan dengan investasi.

2.9.1. Pengertian Investasi

Menurut Mulyadi (1991 : 85), investasi adalah pengikat sumber-sumber jangka panjang untuk menghasilkan laba jangka panjang. Orang yang akan menginvestasikan dananya berharap untuk mendapatkan kembali dana yang telah diinvestasikannnya. Selain itu, Investasi juga disebut sebagai uang yang dipakai untuk menghasilkan uang (E.A Koetin, 1993 : 58). Melihat dari definisi pada ahli diatas, dapat dikatakan investasi adalah kegiatan yang dilakukan untuk memperoleh laba dengan cara menginvestasikan dana pada satu atau lebih aset selama periode tertentu.

2.9.2. Resiko Investasi

(41)

hasil yang sesungguhnya dengan hasil yang diharapkan menggambarkan resiko dari investasi tersebut.

Agus Sartono (1995 : 39), mengatakan bahwa resiko berarti kemungkinan tidak tercapainya keuntungan yang diharapkan atau kemungkinan return yang dihasilkan menyimpang dari return yang diharapkan, maka resiko akan semakin besar. Resiko ini dapat terjadi karena lesunya ekonomi akibat resesi, adanya persaingan dalam dunia usaha, terjadi inflasi sehingga daya beli menurun, naik turunnya tingkat bunga dan mata uang terhadap valuta asing, serta resiko yang terjadi akibat perubahan kebijakan pemerintah.

Menurut Francis Jack Clark (1976 : 318), terdapat dua macam resiko yakni resiko tidak sistematik dan sistematik. Resiko tidak sistematik adalah resiko yang dapat dihilangkan dengan diversifikasi sedangkan resiko yang sistematik merupakan resiko yang diakibatkan oleh pasar yang akan mempegaruhi semua perusahaan dan tidak dapat dihilangkan dengan diversifikasi seperti perang dan inflasi.

2.10 Teori Portofolio

Selanjutnya akan dijelaskan beberapa hal yang berhubungan dengan Teori Portofolio meliputi pengertian portofolio serta return dan resiko portofolio.

2.10.1. Pengertian Portofolio

(42)

2.10.2. Return dan Resiko Portofilo

a) Return Portofolio

Berdasarkan Jogiyanto (2007), untuk menghitung return realisasi dan return ekspektasi dari portofolio digunakan nilai rata-rata tertimbang return dari return-return seluruh sekuritas. Tetapi, nilai resiko portofolio tidak harus sama dengan nilai rata-rata tertimbang resiko-resiko seluruh sekuritas. Resiko portofolio bisa lebih kecil dari nilai rata-rata tertimbang resiko masing-masing sekuritas tunggal.

Berdasarkan Jogiyanto (2007:147), return Realisasi Portofolio (portfolio realized return) merupakan rata-rata tertimbang dari return-return realisasi masing-masing sekuritas tunggal dalam suatu portofolio. Secara matematis return realisasi portofolio dapat dirumuskan sebagai berikut:

1 ( . ) n

p i i

i

R k R





(1.6)

dengan Rpadalah return realisasi portofolio,

k

i adalah porsi

sekuritas ke-i terhadap seluruh sekuritas dalam portofolio,

R

_i adalah return realisasi dari sekuritas ke-i, dan n adalah banyaknya sekuritas.

Return Ekspektasi Portofolio (portfolio expected return) dalam Jogiyanto (2007 : 158) merupakan rata-rata tertimbang dari return-return ekspektasi masing-masing sekuritas tunggal dalam portofolio. Secara matematis return ekspektasi portofolio dirumuskan sebagai berikut:

1

( ) ( . ( )) n

p i i

i

E R k E R



(43)

denganE R

(

_p

)

adalah return ekspektasi portofolio,

k

_i adalah proporsi sekuritas i terhadap seluruh sekuritas dalam portofolio,

( )

_i

E R

adalah return ekspektasi dari sekuritas ke-i, dan n adalah banyaknya sekuritas.

Contoh 2.1. Suatu portofolio terdiri dari 3 macam sekuritas

dengan proporsi yang sama, yakni 1

3 bagian. Return ekspektasi

masa yang akan datang untuk masing-masing sekuritas adalah 15% untuk sekuritas pertama, 18% untuk sekuritas kedua, dan 21% untuk sekuritas ketiga. Maka besarnya return ekspektasi untuk portofolio tersebut adalah:

3

1

( _p) ( .E( ))_i _i i

E R k R





1 1 1

.15% .18% .21%

3 3 3

   18%.

Hal ini berarti, besarnya tingkat keuntungan yang diharapkan dari portofolio yang terdiri dari 3 macam sekuritas tersebut sebesar 18%.

b) Resiko Portofolio

(44)

portofolio, Jogiyanto (2007) mengawali dengan membahas portofolio dengan dua aktiva.

1) Portofolio dengan dua aktiva

Andaikan suatu portofolio memiliki dua aktiva, yaitu sekuritas A dan B. Proporsi masing-masing sekuritas didalam portofolio berturut-turut adalah a dan b ( b = 1 – a), return realisasi A sebesar RA dan return realisasi B sebesar RB, maka

return realisasi dari portofolio tersebut adalah :

.

. .

p A B

R



a R



b R (1.8)

Sedangkan return ekspektasi sebesar :

(

_P

)

( .

_A

)

( .

_B

).

E R



E a R



E b R

(1.9)

Nilai resiko salah satunya dapat diukur dengan menggunakan standar deviasi (standart deviation) atau varian (variance) yang merupakan kuadrat dari deviasi standart. Dengan menggunakan standar deviasi atau varian ini, resiko yang diukur adalah seberapa besar nilai setiap item (sekuritas) yang menyimpang dari rata-ratanya. Dengan demikian, resiko portofolio dapat dirumuskan sebagai :

2 2

var(Rp)p E R pE R( p) (1.10)

dengan

var(

R_p

)

adalah varian return portofolio, dan



_p2adalah besarnya kuadrat dari deviasi standart.

Dengan mensubsitusikan persamaan (1.7) kedalam persamaan (1.9)maka didapat :

2 var(R_p)_E R( _p E R( _p)_





2

( . _A . _B) ( . ( _a) . ( _B)

E a R b R a E R b E R

(45)





2

. _A . _B ( . _A) ( . _B)

E a R b R E a R E b R

   





2

. A . B . ( A) . ( B)

E a R b R a E R b E R

   





2

( . _A . ( _A)) ( . _B . ( _B))

E a R a E R b R b E R

   





2

.( _A ( _A)) .( _B ( _B))

E a R E R b R E R

   

2 2 2 2

[( .(

A

(

A

))

.(

B

(

B

))

E a R E R b R E R









2. . (

a b R

_A

E R

(

_A

)).(

R

_B

E R

(

_B

))]





2 2 2 2

.E[

_A

(

_A

)]

.E[

_B

(

_B

)]

a R E R b R E R









2. . . [

a b E R

_A

E R

(

_A

)).(

R

_B

E R

(

_B

))]





Sehingga diperoleh

2 2 2 2 2

var(

R_p

)





_p



a

.E[

R_A



E R

(

_A

)]



b

.E[

R_B



E R

(

_B

)]

+

2. . . [

a b E R

_A



E R

(

_A

)).(

R

_B



E R

(

_B

))]

. (1.11) Berdasarkan Jogiyanto (2007), kovarian (covariance) antara return saham A dan B ditulis sebagai Cov (RA, RB) atau

, A B R R



. Kovarian akan menunjukan hubungan pergerakan dari nilai return sekuritas A dan B. Nilai kovarian yang positif akan menunjukan nilai kedua sekuritas tersebut bergerak kearah yang sama (jika nilai sekuritas A meningkat, maka nilai sekuritas B

juga meningkat, demikian sebaliknya jika nilai sekuritas A

menurun maka nilai sekuritas B juga menurun). Sedangkan nilai kovarian yang negatif menunjukan nilai kedua sekuritas bergerak kearah yang berlainan (jika nilai sekuritas A

(46)

sekuritas A menurun nilai sekuritas B meningkat). Hal ini berarti kedua sekuritas tersebut saling mengkompensasi satu sama lain. Jika harga saham sekuritas A turun maka kekurangan dari sekuritas A tersebut ditutupi dengan kelebihan dari sekuritas B.

Demikian pula sebaliknya, jika harga saham B mengalami penurunan maka kekurangan dari harga saham sekuritas B

ditutupi dengan kelebihan dari sekuritas A. Nilai kovarian nol menunjukan bahwa nilai kedua sekuritas independen, yakni pergerakan nilai sekuritas tidak saling berhubungan (nilai sekuritas A tidak mempengaruhi nilai sekuritas B, demikian sebaliknya nilai sekuritas B tidak mempengaruhi nilai sekuritas

A). Nilai kovarian bergantung pada return-return ekspektasi dari sekuritas A dan B, dihitung dengan rumus berikut :



 



. 1

cov( . ) ( ) . ( ) .

n

A B RA RB Ai A Bi B i

i

R R



R E R R E R P



 



  (1.12)

dengan

cov(

R R

_A

. )

_B adalah kovarian return antara saham A dan saham B,

R

_Ai adalah return masa depan saham A kondisi ke-i,

Bi

R

adalah return masa depan saham A kondisi ke-i,

E R

(

_A

)

adalah return ekspektasi saham A,

E R

(

_B

)

adalah return ekspektasi saham B,

P

_i adalah probabilitas terjadinya masa depan untuk kondisi ke-i, n adalah banyaknya kondisi masa depan dari i i(1, 2, 3,... )n .

2) Portofolio dengan banyak aktiva

(47)

maka proporsi masing-masing sekuritas adalah , , , sedangkan besarnya varian untuk masing-masing sekuritas adalah � , � , � dan besarnya kovarian masing-masing sekuritas ( ke-1 dan ke-2) , (ke-2 dan ke-3), (ke-3 dan ke-1) adalah , , . Maka besarnya varian untuk ketiga sekuritas ini adalah

2 2 2 2 2 2 2

1 1 2 2 3 3

[ . . . ]

p w w w















1 2 12 1 3 13 2 3 23

2. . .

w w



2. . .

w w



2. . .

w w





= [proporsi varian] + [proporsi kovarian]. (1.13) Dengan demikian, resiko portofolio adalah jumlah dari proporsi varian dan kovarian masing-masing aktiva pada persamaan (1.13) dapat dituliskan kembali sebagai





11 12 13 1

2

1 2 3 21 22 23 2

31 32 33 3

p

w

w w w w

w                    _ _{  }         . Matrik

11 12 13 21 22 23

31 32 33

                  

dapat disebut sebagai matrik varian

kovarian untuk 3 aktiva. Berdasarkan materi pada subbab sebelumnya yakni pada subab 2.6 tentang matrik varian-kovaria, diagonal utama matrik ini yakni � , � , � berisi nilai varian masing-masing aktiva. Sedangkan bagian diluar diagonal ini merupakan kovarian yakni � , � , � . Matrik ini adalah matrik yang simetrik, karena bagian atas luar diagonal sama dengan bagian bawah luar diagonal.

Berdasarkan uraian diatas, maka untuk n-aktiva varian portofolio dapat dirumuskan sebagai

2 2 2 2 2 2 2 2 2

1 1 2 2 3 3

[ . . . ... . ]

p w w w wn n

(48)

1 2 12 1 3 13

[2. . .

w w



2. . .

w w



...





2 2 1 ( 1)

2. . .

w w_n



_n

... 2.

w_n_

. .

w_n



_n_ _n

]



 

(1.14)

atau dapat dituliskan sebagai

2 2 2

1 1 1

. . .

n n n

p i i i j ij

i i j

w w w

  

  









. (1.15)

Rumus diatas dapat dijabarkan kembali menjadi

2

1 1 1

. . . .

n n n

p i i ii i j i j ij

i i j

w w w w

   

  









Bagian pertama dan kedua dari rumus diatas dapat digabung menjadi :

2 1

. .

n n

p i j ij

i i j

w w

 

 





(1.16)

c) Menentukan Portofolio Yang Efisien

Berdasarkan Jogiyanto (2007), portofolio yang efisien (efficient portfolio) merupakan portofolio yang mampu memberikan return ekspektasi terbesar dengan resiko yang sudah tertentu atau memberikan resiko terkecil dengan return ekspektasi yang sudah tertentu. Portofolio yang efisien dapat ditentukan dengan memilih tingkat return ekspektasi yang tertentu dan meminimumkan resikonya atau menentukan resikonya dan kemudian memaksimumkan ekspektasinya.

(49)

menggunakan model ini pada Jogiyanto (2007), ada beberapa asumsi yang digunakan pada model ini , yaitu :

1. Waktu yang digunakan hanya satu periode. 2. Tidak ada biaya transaksi.

3. Preferensi investor hanya didasarkan pada return ekspektasi dan resiko dari portofolio.

4. Tidak ada pinjaman dan simpanan bebas resiko.

Asumsi yang menyatakan bahwa preferensi investor hanya didasarkan pada return ekspektasi dan resiko portofolio sebenarnya menganggap bahwa investor memiliki utility yang sama (pada dasarnya berbeda). Jika preferensi investor berbeda karena utility mereka berbeda maka optimal portofolio untuk tiap-tiap investor akan berbeda. Demikian juga jika tersedia pinjaman dan simpanan bebas resiko maka optimal portofolio akan berbeda juga.

Pada model Markowitz, titik optimal ditentukan dengan menggunakan metode penyelesaian optimasi. Fungsi obyektif yang digunakan adalah fungsi resiko portofolio berdasarkan metode Markowitz. Fungsi obyektif ini akan diminimalkan dengan menetapkan beberapa kendala. Kendala pertama adalah total proporsi yang diinvestasikan dimasing-masing aktiva. Untuk seluruh n aktiva adalah totalnya sama dengan 1 (dana yang diinvestasikan 100%). Misal _� adalah proporsi aktiva ke-i yang dke-ike-investaske-ikan dengan n aktiva, maka kendala pertama dapat dituliskan sebagai

1 1 n

i i

w

 



(50)

0,

1, 2,...

i

w

 

i

n

Kendala ketiga adalah jumlah rata-rata dari seluruh return masing-masing aktiva (�_� sama dengan return portofolio (�_� , yaitu

1 . n

i i p i

w R R

 



Sehingga bentuk optimasinya adalah

meminumumkan 2 2 2

1 1 1

. . .

n n n

p i i i j i j ij

i i j

w w w

   

  









= T. . w  w

dengan 1 2 n w w w w              dan 11 1 1 n m mn a a a a  _{ } _     . dengan kendala:  1 1 n i i w  





w

_i

0,

 

i

1, 2,...

n



1 . n

i i p i

w R R

 

(51)

35

BAB III

OPTIMASI KUADRATIK

3.1Pemrograman Kuadratik

Berdasarkan Mital (1987), pemrogaman kuadratik merupakan persoalan optimasi nonlinear berkendala dimana fungsi obyektifnya berbentuk kuadratik dan fungsi kendala berbentuk linier. Jika fungsi obyektif merupakan fungsi konveks maka masalah pemrograman kuadratik tersebut disebut pemrograman kuadratik konveks. Bentuk umum dari pemrograman kuadratis adalah sebagai berikut :

meminimumkan: f(x) = Px+ x'Ax

n n n

j j jk j k

j= 1 j= 1 k= 1

=



P x +



A x x (1.17)

dengan kendala A x beq



eq

,

x



0

Dengan x, P dan A dari bentuk kuadratik diatas didefinisikan sebagai berikut :

, , .

1 1

11 1n

2 2

n1 nn

n n

x P

a … a

x P

x = P = A=

a a

x P

    _ _

    _ _

     

   

3.2Pengali Lagrange

(52)

dipengaruhi oleh kondisi persyaratan atau kendala g(x,y) = 0 dan terdiri atas pembentukan fungsi penolong.

Langkah awal metode pengganda lagrange adalah dengan membentuk fungsi baru yakni F yang merupakan gabungan antara dua fungsi obyektif, fungsi kendala dan ditambah dengan sejumlah variabel pengganda (). Bentuk fungsi baru tersebut dapat ditulis sebagai berikut :

� , , � = , + � , (1.18) dengan syarat : ��

� = , �� = ,

�� = .

Lambang � (lambda) pada fungsi F, mewakili angka yang belum ditentukan besarnya dan nilainya tidak tergantung pada x dan y, yang disebut pengali (tak tentu) Lagrange.

3.3Kondisi Kuhn-Tucker

(53)

Syarat cukup :

2 2 2

2

1 1 2 1

2 2 2

2

2 1 2 2

2 2 2

2 1 2 ... ... ( ) ... n n i j

n n n

f f f

x x x x x

f f f

f

H x x x x x x

x x

f f f

x x x x x

             _{ }              

dengan x =

Solusi untuk pemrograman kuadratik dengan kendala persamaan diatas : meminimumkan: f(x) = Px+ x'Ax

n n n

j i jk j k

j= 1 j= 1 k= 1

=



P x +



A x x

dengan kendala A x b_eq



_eq

,

x



0

,

adalah dengan menentukan syarat perlu dan syarat cukup seperti berikut ini :

(A )

0 eq beq

L f

x x



x

 

 _{ } _

  

( eq eq) 0

L A b       0 x

Contoh 2.2 : Tentukan nilai minimum dari fungsi berikut ini :





1

1 2 2 1 0 ( ) 0 2 x f x x x

x

 

 _ __{ }

   

Ekstrim minimum jika H(x) definit positif Ekstrim maksimum jika H(x) definit negatif

(54)

dengan kendala : 1 2

2 1 4

4 1 6

x x     _       

     , x0 .

Solusi dari fungsi diatas akan diselesaikan secara manual dan bantuan Matlab. Dengan cara manual fungsi f x( ) dapat ditulis menjadi f x

( )

 

x12

2

x22.

Sedangkan fungsi kendala dapat ditulis manjadi : { + = 4 4 + = 6.

Dari fungsi obyektif dan fungsi kendala diatas dibentuk fungsi Lagrange :

2 2

1 2 1 1 2 2 1 2

( , )

2

(2

4)

(4

6)

L x



 

x x





x

  

x



x

 

x . (3.1)

Suku yang dengan variabel  untuk membentuk fungsi Lagrange diatas adalah fungsi kendala bukan fungsi obyektif. Karena terdapat dua buah kendala, maka diperlukan dua buah :

1 1 2 1 1 2

1

2 2 4 2( 2 ) 0

L

x x

x



       

 (3.2)

2 1 2

2

4 0

L x

x

 

    

 (3.3)

1 2

1

(2 4) 0

L x x



       (3.4) 1 2 2

(4 6) 0

L

x x



     

 (3.5)

Dari persamaan (3.4) dan (3.5) diperoleh

1 2 1 2

1 1 2

(2 4) 0

(4 6) 0

2 2 0

1 2 x x x x x x x      _{   }    

(55)

1 2 1 2 1 2

2 2 1 2 2 1 5

2(1) 2 4 0 2 4 6 1 2 4 6

4(2) 0 8 22 2 8

                     _              

Dengan bantuan sofware matematika, yakni Matlab diperoleh nilai

x

₁dan

x

₂ yang sama dengan hasil

x

₁dan

x

₂yang dicari dengan cara manual, yakni

x

₁



1

dan

x

2



2

. Untuk menyelesaikan fungsi diatas dengan matlab, fungsi tersebut

ditulis menjadi :

Meminimumkan :

f x

( )



x

T

. .x

 



T

.x

dengan kendala :

 Aeq. xbeq



x

_i



0

dengan : 1 0 0 2  _{ } _   , 0 0  _{  }    , 2 1 4 1 eq a b A c d     _ _{ } _

    , dan

4 6 eq r b s     _{   }     .

Dengan menggunakan Matlab, optimasi bentuk kuadratik diatas diselesaikan dengan menggunakan perintah berikut ini :

[x,sigma2min] = quadprog(sigma,α,[],[],Aeq,beq,lb,[])

dengan 0

0

lb   

(56)