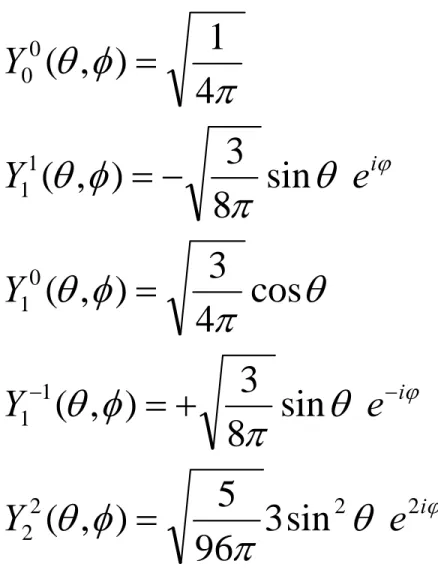3.Fungsi Legendre
3.1. Pengembangan fungsi Legendre
3.2. Sifat-sifat Fungsi Legendre
3.3. Legendre Asosiasi
3.4. Harmonik Sferis
3.1. Pengembangan Fungsi
Legendre
Fungsi Legendre dapat langsung dikembangkan dari basis fisika yakni elektrostatik:
1 0
4
1
r
q
πε
ϕ
=
r r1θ
q z=a zϕ
(3.1)2 / 1 2 2 0
)
cos
2
(
4
−−
+
=
θ
πε
ϕ
q
r
a
ar
Dalam koordinat polar r dan
θ
:Dapat diekspansikan dalam polinomial Pn:
∑
∞ =⎟
⎠
⎞
⎜
⎝
⎛
=
0 0)
(cos
4
n n nr
a
P
q
θ
πε
ϕ
Disini Pn adalah polinomial Legendre dan dapat didefinisikan:
1
|
|
,
)
(
)
2
1
(
)
,
(
0 2 / 1 2=
<
+
−
=
∑
∞ = −P
x
t
t
t
xt
x
t
g
n n ng(t,x) merupakan fungsi generator untuk polinomial Legendre (3.3)
(3.2)
∑
∞ = −=
−
+
−
0 2 2 2 2 / 1 2)
2
(
)
!
(
2
)!
2
(
)
2
1
(
n n nn
xt
t
n
t
xt
Fungsi generator dapat diekspansikan:
∑
∞ =−
−
=
0 2)
2
(
!
)!
2
(
!
)!
1
2
(
n nt
xt
n
n
nt
xt
)
2
(
−
2Ekspansi binomial dari menghasilkan deret dobel:
∑
∞∑
= = − −−
−
=
+
−
0 0 2 2 2 / 1 2)
2
(
)!
(
!
!
)
1
(
)
!
(
2
)!
2
(
)
2
1
(
n n k k k n k n nk
n
k
x
t
n
t
n
n
t
xt
∑∑
∞ = = + −−
−
=
0 0 2(
2
)
)!
(
!
!
2
)!
2
(
)
1
(
n n k k n k n n kx
t
k
n
k
n
n
(3.4) (3.5)∑ ∑
∞ = = − − −−
−
−
−
=
+
−
0 ] 2 / [ 0 2 2 2 2 / 1 2)
2
(
)!
2
(
)!
(
!
2
)!
2
2
(
)
1
(
)
2
1
(
n n k n k n k n kx
t
k
n
k
n
k
k
n
t
xt
Dapat diatur urutan sumasi:
(3.6) Bandingkan dengan (3.4) diperoleh:
∑
= −−
−
−
−
=
[ /2] 0 2)!
2
(
)!
(
!
2
)!
2
2
(
)
1
(
)
(
n k k n n k nx
k
n
k
n
k
k
n
x
P
(3.7)Dapat dievaluasi langsung beberapa Pn(x) untuk n kecil.
1
)
(
0x
=
P
x
x
P
1(
)
=
2
1
2
3
)
(
2 2x
= x
−
P
Kembali ke masalah elektrostatis, untuk kasus dipole:
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
2 1 01
1
4
r
r
q
πε
ϕ
r2 r r1θ
q z=a zϕ
-q z=-a⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
2 1 01
1
4
r
r
q
πε
ϕ
Diekspansikan sesuai cosinus, untuk (r>a) :
⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = − −1/2 2 1/2 2 0 cos 2 1 cos 2 1 4 r a r a r a r a q θ θ πε ϕ (3.8) (3.9) Jelas bahwa suku kedua serupa dengan pertama kecuali dengan mengganti a menjadi –a.
Gunakan (3.4) akan diperoleh:
⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ =
∑
∑
∞ = ∞ =0 0 0 ) 1 )( (cos ) (cos 4 n n n n n n n r a P r a P q θ θ πε ϕ (3.10)⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = (cos ) (cos ) .... 4 2 3 3 1 0 r a P r a P q θ θ πε ϕ
Suku pertama (dan suku paling dominan kalau r>>>a) adalah : 2 1 0 ) (cos 4 2 r P aq θ πε ϕ =
Yang merupakan potensial dipol listrik yang sudah biasa dikenal. Disini 2aq merupakan momen dipol.
(3.11)
Pelajari sendiri:
z
Multipol listrik linear
z
Polinomial Gegenbauer
∑
∞ = +=
−
+
−
21 0 2 / 1 2 / 1 2(
)
)!
(
)
2
1
(
2
n n m n m mt
x
T
m
t
xt
π
+ + + + -+ + -(3.13)Latihan
z
Kembangkan potensial listrik dari deretan
muatan yang membentuk kuadrupol:
z
Gunakan E = −∇ϕ untuk mendapatkan
komponen-komponen medan listrik sebuah
dipole listrik. Anggap
r>>>a.
-2q q
z=a z
q z=-a
3.2. Sifat-sifat Fungsi Legendre
Hubungan Rekursi dan Sifat-sifat Khusus
2 / 1 2
)
2
1
(
)
,
(
t
x
=
−
xt
+
t
−g
Seperti pada fungsi Bessel, fungsi generator pada polinomial Legendre dapat dimanfaatkan untuk mengembangkan
hubungan rekursi Turunkan terhadap t:
∑
∞ = −=
+
−
−
=
∂
∂
0 1 2 / 3 2(
)
)
2
1
(
)
,
(
n n nx
t
nP
t
xt
t
x
t
x
t
g
Dapat disusun menjadi:
0
)
(
)
(
)
(
)
2
1
(
0 0 1 2+
−
=
+
−
∑
∑
∞ = ∞ = − n n n n n nx
t
t
x
P
x
t
nP
t
xt
(3.14)Seterusnya (buktikan!):
)
(
)
(
)
1
(
)
(
)
1
2
(
n
+
xP
nx
=
n
+
P
n+1x
+
nP
n−1x
Inilah hubungan rekursi tiga suku seperti pada fungsi Bessel. Misal untuk n=1:
)
(
)
(
2
)
(
3
xP
1x
=
P
2x
+
P
0x
Dari hal ini:
)
1
3
(
)
(
21 2 2x
=
x
−
P
Nilai Pn(x) untuk orde n yang lebih tinggi secara iterasi. (3.15)
Polinomial Legendre
)
15
70
63
(
)
(
)
3
30
35
(
)
(
)
3
5
(
)
(
)
1
3
(
)
(
)
(
1
)
(
3 5 8 1 5 2 4 8 1 4 3 2 1 3 2 2 1 2 1 0x
x
x
x
P
x
x
x
P
x
x
x
P
x
x
P
x
x
P
x
P
+
−
=
+
−
=
−
=
−
=
=
=
Secara manual teknik menghitung polinomial
Legendre dapat membosankan. Namun dengan
komputer digital hal ini dapat mudah dilakukan:
)
1
/(
)]
(
)
(
[
)
(
)
(
2
)
(
1 1 1=
−
−−
−
−+
+x
xP
x
P
x
xP
x
P
x
n
P
n n n n n (3.16)Persamaan Diferensial
∑
∞ ==
+
−
=
∂
∂
0 2 / 3 2'
(
)
)
2
1
(
)
,
(
n n nx
t
P
t
xt
t
x
x
t
g
Sifat-sifat lain polinomial Legendre dapat diperoleh dengan diferensiasi fungsi generator:
0
)
(
)
(
'
)
2
1
(
0 0 2−
=
+
−
∑
∑
∞ = ∞ = n n n n n nx
t
t
P
x
t
P
t
xt
atau (3.17)dari hal ini:
)
(
)
(
'
2
)
(
'
)
(
'
1x
P
1x
xP
x
P
x
P
n++
n−=
n+
n (3.18)Diferensiasikan (3.15) terhadap x kemudian kalikan dua dan gabung dengan persamaan (3.18), didapat:
)
(
)
1
2
(
)
(
'
)
(
'
1x
P
1x
n
P
x
P
n+−
n−=
+
n (3.19)Gabungan (3.15) dan (3.19) menghasikan macam-macam relasi, diantaranya:
)
(
'
)
(
)
1
(
)
(
'
1x
n
P
x
xP
x
P
n+=
+
n+
n)
(
'
)
(
)
(
'
1x
nP
x
xP
x
P
n−=
−
n+
n)
(
)
(
)
(
'
)
1
(
−
x
2P
nx
=
nP
n−1x
−
nxP
nx
)
(
)
1
(
)
(
)
1
(
)
(
'
)
1
(
−
x
2P
nx
=
n
+
xP
nx
−
n
+
P
n+1x
(3.20) (3.21) (3.22) (3.23)Diferensiasikan (3.22) dan gunakan (3.21) untuk menghilangkan P’n-1(x) diperoleh p.d. orde-2:
0
)
(
)
1
(
)
(
'
2
)
(
"
)
1
(
−
x
2P
nx
−
xP
nx
+
n
n
+
P
nx
=
(3.24) Persamaan terakhir inilah yang disebut dengan persamaan diferensial Legendre.Dalam banyak kasus di Fisika, pers. Legendre sering juga dinyatakan dalam diferensiasi terhadap
θ
, dengan x = cosθ
0
)
(cos
)
1
(
)
(cos
sin
sin
1
+
+
=
⎟
⎠
⎞
⎜
⎝
⎛
θ
θ
θ
θ
θ
θ
nn
n
P
nd
dP
d
d
(3.25)∑
∞ = −=
+
−
=
0 2 / 1 2)
(
)
2
1
(
)
,
(
n n nx
t
P
t
xt
x
t
g
Kembali ke fungsi generator:
Untuk x=1, dapat dievaluasi:
∑
∞ = −=
−
=
+
−
=
0 2 / 1 21
1
)
2
1
(
)
1
,
(
n nt
t
t
t
t
g
Dapat disimpulkan:1
)
1
(
=
nP
Juga dapat dibuktikan dengan cara serupa:
n n
P
(
−
1
)
=
(
−
1
)
(3.26)
Bila x=0, maka dapat dievaluasi:
∑
∞ = −=
+
=
0 2 / 1 2)
0
(
)
1
(
)
0
,
(
n n nt
P
t
t
g
Sementara kita ketahui bahwa:
....
!
2
)
1
2
....(
3
.
1
)
1
(
....
1
)
1
(
+
2 −1/2=
−
21 2+
38 4+
+
−
n n−
t
2n+
n
n
t
t
t
Maka:0
)
0
(
!
)!
2
(
!
)!
1
2
(
)
1
(
!
2
)
1
2
....(
3
.
1
)
1
(
)
0
(
1 2 2=
−
−
=
−
−
=
+ n n n n nP
n
n
n
n
P
(3.28)Paritas
Dapat dibuktikan dengan mudah bahwa:
z
g(-t,-x) = g(t, x)
z
P
n(-
x) = (-1)
nP
n(
x)
(3.29) (3.30)
Latihan
z
Lihat Arfken
1. Tunjukkan bahwa
Petunjuk dalam koordinat polar sferis:
2. Tunjukkan bahwa:
Hasil ini bermanfaat untuk menghitung muatan
terinduksi pada bola metal oleh suatu muatan titik
q.
2 1 1 ) (cos ) 1 ( ) (cos + + + ⎥⎦ = − + ⎤ ⎢⎣ ⎡ ∂ ∂ n n n n r P n r P z θ θ θ θ θ ∂ ∂ − ∂ ∂ = ∂ ∂ r r z 1 sin cos
∑
∞ = + = + − − 0 2 / 3 2 2 ) ( ) 1 2 ( ) 2 1 ( 1 n n n x t P n t tx tOrtogonalitas Fungsi Legendre
Persamaan differensial Legendre (3.24):
dapat ditulis:
Kalikan dengan
P
m(
x) kemudian integrasi
dengan batas -1 sampai 1, didapat:
0
)
(
)
1
(
)
(
'
2
)
(
"
)
1
(
−
x
2P
nx
−
xP
nx
+
n
n
+
P
nx
=
0
)
(
)
1
(
)]
(
'
)
1
[(
−
x
2P
x
+
n
n
+
P
x
=
dx
d
n n∫
∫
− −+
−
+
=
=
⎭
⎬
⎫
⎩
⎨
⎧
−
−
−
1 1 1 1 2 2)
(
)
(
)]
1
(
)
1
(
[
)]
(
'
)
1
[(
)
(
)]
(
'
)
1
[(
)
(
dx
x
P
x
P
n
n
m
m
dx
x
P
x
dx
d
x
P
x
P
x
dx
d
x
P
m n m n n m (3.31) (3.32)Karena faktor (1-
x
2) maka suku sebelah kiri
=0, sehingga:
Untuk
m
≠
n, maka:
tampak ortogonalitas pada interval [-1,1].
Masih harus dihitung untuk
m=n, jelas
integral tidak sama dengan nol.
Bagaimana mencarinya?
0
)
(
)
(
)]
1
(
)
1
(
[
1 1=
+
−
+
∫
−dx
x
P
x
P
n
n
m
m
n m0
)
(
)
(
1 1=
∫
−dx
x
P
x
P
n m (3.33)Dari fungsi generator:
Integrasikan dari
x=-1 sampai 1, maka suku
bersilang akan menjadi nol, sehingga:
Misalkan
y = 1-2tx+t
2, didapat:
2 0 1 2)
(
)
2
1
(
⎟
⎠
⎞
⎜
⎝
⎛
=
+
−
∑
∞ = − n n nx
t
P
t
xt
[
]
∑ ∫
∫
∞ = − −=
+
−
0 1 1 2 2 1 1 2(
)
2
1
n n nP
x
dx
t
t
xt
dx
⎟
⎠
⎞
⎜
⎝
⎛
−
+
=
=
+
−
∫
∫
+ − −t
t
t
y
dy
t
t
xt
dx
t t1
1
ln
1
2
1
2
1
2 2 ) 1 ( ) 1 ( 1 1 2 (3.35) (3.34)Ekspansikan dalam deret pangkat:
Sehingga dapat disimpulkan (bandingkan 3.34
dan 3.36):
Jadi:
∑
∞ =+
=
⎟
⎠
⎞
⎜
⎝
⎛
−
+
0 21
2
2
1
1
ln
1
n nn
t
t
t
t
[
]
1
2
2
)
(
1 1 2+
=
∫
−n
dx
x
P
n (3.36) (3.37) n m n mn
dx
x
P
x
P
, 1 12
1
2
)
(
)
(
δ
+
=
∫
−Definisi alternatif untuk
polinomial Legendre
z
Pelajari sendiri formula Rodrigues
n n n n
x
dx
d
n
x
P
(
1
)
!
2
1
)
(
⎟
2−
⎠
⎞
⎜
⎝
⎛
=
(3.38)Latihan:
Contoh-contoh penggunaan di Fisika
1. Medan Gravitasi Bumi
Salah satu penggunaan deret Legendre adalah
untuk menjelaskan potensial gravitasi Bumi.
Dengan
R =radius equator = 6378,1
± 0,1 km
Dapat ditulis:
2 2/
km
001
,
0
494
,
62
s
R
GM
±
=
( )
⎟
⎠
⎞
⎜
⎝
⎛
−
=
∑
∞ = + 2 1)
(cos
)
,
(
n n n r R nP
a
r
R
R
GM
r
U
θ
θ
2. Bola dalam Medan Uniform
Problem: mencari potensial yang terdistorsi
karena ada bola konduktor dengan radius
r
0.z E
Potensial elektrostatik memenuhi pers.
Laplace:
0
2
=
∇ V
Gunakan metode separasi variabel (lihat. Fisika
Matematika II) pada koordinat polar sferis:
(Mengapa tidak ada ketergantungan
ϕ
?)
Bagaimana mencari koefisien
a
ndan
b
n?
Gunakan syarat batas kondisi fisis.
∑
∑
∞ = + ∞ =+
=
0 1 0)
(cos
)
(cos
n n n n n n n nr
P
b
P
r
a
V
θ
θ
Bila medan original (tak terdistorsi) adalah
E
0maka:
V(rÆ
∞)=− E
0z =
− E
0r cos
θ
= − E
0r P
1(cos
θ
)
Karena deret Legendre adalah unique maka
dapat disimpulkan:
a
n= 0, untuk
n>1
a
1= − E
0∑
∑
∞ = + ∞ =+
=
0 1 0)
(cos
)
(cos
n n n n n n n nr
P
b
P
r
a
V
θ
θ
Kita dapat memilih pada bola konduktor dan
bidang
θ
=
π
/2 potensial =0, sehingga:
Supaya hal ini bisa terjadi maka semua
koefisien
P
n(cos
θ
) harus nol.
a
0= b
0= 0
b
n= 0 untuk n
≥ 2
z E0
)
(cos
)
(cos
)
(
2 1 0 1 0 0 2 0 1 0 0 0 0=
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
+
+
=
=
∑
∞ = + n n n nr
P
b
P
r
E
r
b
r
b
a
r
r
V
θ
θ
Dan juga
b
1=
E
0r
03Potensial elektrostatik (di luar bola) menjadi:
Pada teori Medan Elektromagnetik, hasil yang
sama dapat dikerjakan dengan metode
bayangan (detail lihat Jackson).
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
−
=
+
−
=
3 3 0 1 0 2 3 0 0 1 01
)
(cos
)
(cos
)
(cos
r
r
rP
E
r
r
E
rP
E
V
θ
θ
θ
Sebagai informasi tambahan, kerapatan
muatan permukaan terinduksi dapat dihitung:
Momen dipole listrik terinduksi:
θ
ε
ε
σ
03
0 0cos
0E
r
V
r r=
∂
∂
−
=
= 0 0 3 04
r
E
P
=
π
ε
Pelajari sendiri
3.3. Fungsi Legendre Asosiasi
Fungsi Legendre Asosiasi dapat dikembangkan dari fungsi Legendre:
0
)
(
)
1
(
)
(
'
2
)
(
"
)
1
(
−
x
2P
nx
−
xP
nx
+
n
n
+
P
nx
=
Diturunkan sebanyak m kali akan diperoleh:0
)
1
)(
(
'
)
1
(
2
"
)
1
(
−
x
2u
−
x
m
+
u
+
n
−
m
n
+
m
+
u
=
Dengan:P
(x
)
dx
d
u
m n m≡
(3.39)Sekarang kalau kita ambil:
)
(
)
1
(
)
(
)
1
(
)
(
2 /2 2 /2P
x
dx
d
x
x
u
x
x
v
m n m m m=
−
−
=
(3.40)Masukkan ke (3.31) (latihan!!!) akan diperoleh:
0
1
)
1
(
'
2
"
)
1
(
2 2 2=
⎥
⎦
⎤
⎢
⎣
⎡
−
−
+
+
−
−
v
x
m
n
n
xv
v
x
Pers. (3.33) merupakan p.d. Legendre asosiasi yang akan kembali menjadi Legendre bila m=0.
Dalam koordinat polar, Legendre asosiasi menjadi:
(3.41)
0
sin
)
1
(
sin
sin
1
2 2=
⎥
⎦
⎤
⎢
⎣
⎡
−
+
+
⎟
⎠
⎞
⎜
⎝
⎛
v
m
n
n
d
dv
d
d
θ
θ
θ
θ
θ
(3.42)Solusi reguler, dilabelkan kembali Pm n(x) adalah:
)
(
)
1
(
)
(
)
(
2 /2P
x
dx
d
x
x
P
x
v
m n m m m n=
−
≡
Beberapa fungsi Legendre asosiasi:
θ
θ
θ
θ
θ
θ
θ
θ
θ
3 2 / 3 2 3 3 2 2 2 3 2 2 3 2 / 1 2 2 2 3 1 3 2 2 2 2 2 / 1 2 1 2 2 / 1 2 1 1sin
15
)
1
(
15
)
(
sin
cos
15
)
1
(
15
)
(
sin
)
1
cos
5
(
)
1
)(
1
5
(
)
(
sin
3
)
1
(
3
)
(
sin
cos
3
)
1
(
3
)
(
sin
)
1
(
)
(
=
−
=
=
−
=
−
=
−
−
=
=
−
=
=
−
=
=
−
=
x
x
P
x
x
x
P
x
x
x
P
x
x
P
x
x
x
P
x
x
P
(3.43)dan dihubungkan dengan:
)
(x
P
nmP
n−m(x
)
)
(
)!
(
)!
(
)
1
(
)
(
P
x
m
n
m
n
x
P
n m m nm+
−
−
=
−dan jelas bahwa:
)
(
)
(
0x
P
x
P
n=
nTerdapat juga fungsi generator untuk Legendre Asosiasi, namun amat sangat jarang digunakan di Fisika.
(3.44)
Hubungan Rekursi:
Karena ada dua indeks (n dan m) maka ada macam-macam variasi hubungan rekursi. Beberapa diantaranya dapat dilihat di Arfken. Misal: m n m n m n
m
n
P
m
n
P
xP
n
1
)
(
)
1(
1
)
12
(
+
=
+
−+
−
+
+ (3.46)Paritas Fungsi Legendre Asosiasi:
)
(
)
1
(
)
(
x
P
x
P
nm−
=
−
m+n nmOrtogonalitas Fungsi Legendre Asosiasi:
q p m q m p
m
q
m
q
q
dx
x
P
x
P
, 1 1(
)!
)!
(
1
2
2
)
(
)
(
δ
−
+
+
=
∫
−atau dalam koordinat polar:
q p m q m p
m
q
m
q
q
d
P
P
, 1 1(
)!
)!
(
1
2
2
sin
)
(cos
)
(cos
θ
θ
θ
θ
δ
−
+
+
=
∫
− (3.47) (3.48) (3.49)Contoh kasus di Fisika:
Medan induksi magnet dari loop arus
ϕ dλ x y z r θ I Potensial vektor:
r
Id
d
λ
π
μ
4
0=
A
Dari argumentasi simetri tampak bahwa A hanya
mempunyai komponen
ϕ
0 dan independen dariϕ
. A)
,
(
ˆ
0θ
ϕ
A
ϕr
=
A
(3.50) (3.51)Persamaan Maxwell:
,
J
H
=
×
∇
(
∂
D
/
∂
t
=
0
,
pada satuan MKS) Karena maka:μ
0H
=
B
=
∇
×
A
J
A
=
μ
0×
∇
×
∇
Disini J adalah rapat arus. Pada masalah ini nilai J adalah nol kecuali pada loop itu sendiri. Jadi untuk yang jauh dari loop:
0
)
,
(
ˆ
0=
×
∇
×
∇
ϕ
A
ϕr
θ
Dalam koordinat sferis:
⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ∂ ∂ − ∂ ∂ − ∂ ∂ − ∂ ∂ − = × ∇ × ∇ ˆ ( , ) ˆ 2 1 1 (cot ) 2 2 2 2 2 2 0 0 ϕ ϕ ϕ ϕ ϕ θ ϕ θ θ θ ϕ A r A r r A r r A r A = 0 (3.52) (3.53) (3.54) (3.55)
)
(
)
(
)
,
(
θ
θ
ϕr
=
R
r
Θ
A
Gunakan metode separasi variabel: Didapat
0
sin
)
1
(
cot
0
)
1
(
2
2 2 2 2 2 2=
Θ
−
Θ
+
+
Θ
+
Θ
=
+
−
+
θ
θ
θ
θ
d
n
n
d
d
d
R
n
n
dr
dR
r
dr
R
d
r
(3.56) (3.57)Persamaan yang kedua merupakan Legendre asosiasi dengan m=1
)
(cos
)
(
θ
=
P
n1θ
Θ
Konstanta separasi n(n+1) dipilih untuk membuat solusi ini well behaved.
Solusi trial R(r) = rα , didapat
α
= n, −n − 1. Solusi pertama divergen ketika r→∞. Sehingga solusi yang sesuai:)
(cos
)
(cos
1 1 1 1θ
θ
ϕ n n n n n n nP
r
a
c
P
r
b
A
+ +⎟
⎠
⎞
⎜
⎝
⎛
=
=
dan:∑
∞ = +⎟
⎠
⎞
⎜
⎝
⎛
=
1 1 1)
(cos
)
,
(
n n n nP
r
a
c
r
A
ϕθ
θ
Dari potensial vektor ini dapat dicari medan magnet (latihan!!) (3.59)
3.4. Harmonik Sferis
Dalam separasi variabel dari (a) pers. Laplace, (b) pers. gelombang klassik bergantung ruang, dan (c) pers. gelombang Schrodinger
untuk gaya sentral,
0
)
(
2 2+
=
∇
ψ
k
f
r
ψ
Ketergantungan angular datang sepenuhnya dari operator Laplacian adalah:
0
)
(
)
1
(
)
(
sin
)
(
sin
sin
)
(
2 2 2+
+
ΘΦ
=
Φ
Θ
+
⎟
⎠
⎞
⎜
⎝
⎛
Θ
Φ
ϕ
ϕ
ϕ
θ
θ
θ
θ
θ
θ
ϕ
n
n
d
d
d
d
d
d
(3.61) (3.62)2 2 2
)
(
)
(
1
m
d
d
−
=
Φ
Φ
ϕ
ϕ
ϕ
Ketergantungan azimutal: Dengan solusi: ϕ ϕϕ
e
ime
im,
)
(
=
−Φ
Yang memenuhi kondisi ortogonalitas:
2 1 2 1 , 2 0
2
m m im ime
d
e
ϕ
πδ
π ϕ ϕ=
∫
− (3.63) (3.64) (3.65)Dapat dibuktikan dengan argumentasi fisis (misal dalam
elektrostatik dan kuantum) bahwa m harus merupakan bilangan bulat (buktikan!)
ϕ
π
ϕ
e
im2
1
)
(
=
Φ
Pers. (3.56) menuntun kepada:
yang merupakan ortonormal (ortogonal dan ternormalisasi) terhadap sudut azimuth
ϕ
(3.66)
Ketergantungan pada Sudut:
Kita lihat kembali ortogonalitas fungsi Legendre Asosiasi pada pers. (3.48) atau (3.49). Kita dapat definisikan fungsi ortonormal dari
Legendre asosiasi, yakni:
)
(cos
)!
(
)!
(
2
1
2
)
(cos
θ
nmθ
m nP
m
n
m
n
n
+
−
+
=
P
(3.67)φ
θ
π
φ
θ
m im n m m nP
e
m
n
m
n
n
Y
(cos
)
)!
(
)!
(
4
1
2
)
1
(
)
,
(
2 / 1⎥
⎦
⎤
⎢
⎣
⎡
+
−
+
−
≡
Ketergantungan pada sudut dari solusi pers. (3.62) menjadi:
)
(
)
(cos
θ
Φ
ϕ
m nP
Hal terakhir disebut Harmonik sferis, yang dapat ditulis menjadi:
(3.68)
Disini dimasukkan suku fasa (-1)m untuk menyesuaikan dan memudahkan pada perhitungan real di banyak kasus Fisika.
ϕ ϕ ϕ
θ
π
φ
θ
θ
π
φ
θ
θ
π
φ
θ
θ
π
φ
θ
π
φ
θ
i i ie
Y
e
Y
Y
e
Y
Y
2 2 2 2 1 1 0 1 1 1 0 0sin
3
96
5
)
,
(
sin
8
3
)
,
(
cos
4
3
)
,
(
sin
8
3
)
,
(
4
1
)
,
(
=
+
=
=
−
=
=
− −Tabel beberapa Harmonik Sferis:
3.5. Operator Momentum Angular
Dalam Mekanika Kuantum, konsep momentum angular memegang peran yang sangat penting serupa dengan yang terjadi pada
Mekanika Klassik, disini momentum angular dihubungkan dengan torsi. Namun dalam Mekanika Kuantum kita mengeksplorasi
Hamiltonian klassik yang hanya tergantung pada momentum angular.
z x y L=r×p θ φ Posisi partikel R,θ,ϕ momentum p
Sekarang perhatikan sebuah partikel klassik yang bergerak dalam permukaan bola, partikel boleh kemana saja selama
tetap berada jarak konstan R dari pusat bola. Jadi variabel
Dalam kasus ini momentum selalu tegak lurus posisi:
p•r = 0
Vektor momentum angular klassik:
L = r×p
Sekarang kita lihat kuadrat dari momentun angular:
L2 = (r×p)• (r×p)
= (r•r)(p•p) − (r•p)(p•r) = r2p2 = R2p2
Tidak ada energi potensial pada masalah ini, hanya energi kinetik. Hamiltonian untuk gerakan ini:
dengan I merupakan momen inersia.
I
L
mR
L
m
p
H
2
2
2
2 2 2 2=
=
=
Definisi klassik untuk momentum angular L = r×p memberikan komponen: y z x
yp
zp
L
=
−
z x yzp
xp
L
=
−
x y zxp
yp
L
=
−
)
/
(
x
i
p
x= h
−
∂
∂
∇
−
= h
i
p
Operator momentum seperti biasanya ditulis:
h
Sekarang dapat kita evaluasi beberapa komutator: [Lx , z] = [ypz
−
zpy , z] = y [pz , z] = −i y[Lx , pz] = [ypz
−
zpy , pz] =−
[z, pz] py = −i py [Lx , x] = 0[Lx , px] = 0
dan masih banyak lagi komutator serupa.
h
i p
x, x] =
[ [y, py] = ih [z, pz] = ih Hubungan ini dapat diringkas:
* posisi dan momentum:
, juga dan
[x, py] = 0, juga [x, pz]=[y, px]=[y, pz]=[z, px]= [z, py]=0
x i L z z i L y y i L x y i L z x i L y z i L x L z L y L x y x z x z y z y x h h h h h h − = − = − = = = = = = = ] , [ ; ] , [ ; ] , [ ] , [ ; ] , [ ; ] , [ 0 ] , [ ] , [ ] , [ x y z z x y y z x y x z x z y z y x z z y y x x
p
i
L
p
p
i
L
p
p
i
L
p
p
i
L
p
p
i
L
p
p
i
L
p
L
p
L
p
L
p
h
h
h
h
h
h
−
=
−
=
−
=
=
=
=
=
=
=
]
,
[
;
]
,
[
;
]
,
[
]
,
[
;
]
,
[
;
]
,
[
0
]
,
[
]
,
[
]
,
[
x y z * posisi dan momentum angular:z y x z x x x z x x y x L i xp i yp i p L x p z L xp zp L L L h h h + = − = − = − =[ , ] [ , ] [ , ] ] , [ y x z x z y L i L L L i L L , ] = h dan [ , ] = h [
x,y,z
i,j,k
L
i
L
L
i,
j]
=
ijk kdengan
=
[
h
ε
1 2 3Sekarang kita gunakan komutator-komutator tersebut untuk menyelesaikan hubungan komutasi antar
komponen L. Misalnya:
Dengan mudah dapat dibuktikan juga:
Secara simbolik dapat ditulis:
ε
ijk adalah Levi civita yang bernilai +1 untuk permutasi genap/ siklis (123, 231, 312) dan−
1 untuk permutasi ganjil/ antisiklis (132, 321, 213), serta bernilai nol kalau ada indeks yang sama.2 2 2 2 z y x
L
L
L
+
+
=
L
]
,
[
]
,
[
]
,
[
L
2L
z=
L
2x+
L
2y+
L
2zL
z=
L
2x+
L
2yL
z y z y z y y x z x z x xL
L
L
L
L
L
L
L
L
L
L
L
[
,
]
+
[
,
]
+
[
,
]
+
[
,
]
=
0
=
+
+
−
−
=
i
h
L
xL
yi
h
L
yL
xi
h
L
yL
xi
h
L
xL
ySekarang kita lihat kuadrat dari momentum angular
Evaluasi komutator berikut:
Dapat dibuktikan juga berlaku untuk Lx dan Ly
0
]
,
Karena L2 berkomutasi dengan semua komponen
momentum angular, kita dapat temukan eigenstate simultan dari L2 dan salah satu komponen L.
Biasanya dipilih L2 dan L
z. Anggap harga eigen
masing-masing
λ
dan m :L2 |
λ
m〉 =λ
|λ
m〉 Lz |λ
m〉 = mħ |λ
m〉Dalam representasi (
θ
,ϕ
) fungsi eigen: 〈θ
,ϕ
|λ
m〉 =ψ
λm(θ
,ϕ
)Kita dapatkan:
〈
θ
,ϕ
| L2|λ
m〉 =λ
〈θ
,ϕ
|λ
m〉 〈θ
,ϕ
|Lz|λ
m〉 = mħ 〈θ
,ϕ
|λ
m〉Untuk menyelesaikan masalah ini, maka perlu menyatakan
L2 dan L
z dalam representasi (
θ
,ϕ
).Berikut akan dibuktikan bahwa representasi 〈
θ
,ϕ
|λ
m〉 atauψ
λm(θ
,ϕ
) adalah harmonik sferisY
λm(
θ
,
φ
)
L2 dan L z dalam representasi (
θ
,ϕ
):ϕ
∂
∂
−
= h
i
L
z ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ − = 2 2 22 2 sin 1 sin sin 1ϕ
θ
θ
θ
θ
θ
h L Tampak bahwa:)
,
(
)
,
(
θ
φ
lmθ
φ
m l zY
m
Y
L
=
h
)
,
(
)
1
(
)
,
(
2 2θ
φ
mθ
φ
l m ll
l
Y
Y
=
+
h
L
Pendekatan Operator Secara Umum
Sekarang kita tinjau metode operator, sebut saja
triplet operator momentum angular
J
x,
J
y,
J
zyang
tidak tergantung pada representasi. Ketiga
operator ini tidak terbatas pada
L
x,
L
y,
L
zyang
didefinisikan dari hubungan Klassik.
Hubungan komutasi:
[
J
x, J
y] =
iħJ
zx,y,z siklis
Kita definisikan:
J
2=
J
Maka, seperti sebelumnya:
[J
2,
J
i] = 0,
i= x, y atau z
Sekarang kita pilih eigenstate yang merupakan
eigenstate simultan untuk J
2dan
J
zdengan harga
eigen
λ
Jdan
mħ.
J
2|λ
Jm
〉 =
λ
J|
λ
Jm
〉
J
z|
λ
Jm
〉 = mħ |
λ
Jm
〉
Lalu kita definisikan operator non-hermitian:
J
+=
J
x+
iJ
yKomutasi dengan
J
zdapat dengan mudah
dievaluasi:
[
J
z,
J
+] =
ħJ
+; [
J
z,
J
−] = − ħJ
−[
J
+,
J
−] = 2
ħ J
zLebih lanjut dapat dibuktikan (latihan!)
J
+J
−= J
2− J
z2+
ħJ
zJ
−J
+= J
2− J
z2
− ħJ
zPengenalan pada
J
+,
J
−tidaklah begitu aneh,
karena serupa pada kasus operator tangga
naik/turun dalam osilator harmonis (akan dibahas
pada bab berikutnya)
Dari relasi komutasi, diperoleh
J
zJ
+=
J
+(
J
z+
ħ)
Sehingga:
J
zJ
+|
λ
Jm
〉= J
+(
J
z+
ħ) |λ
Jm
〉 = (m+1) ħ J
+|
λ
Jm
〉
Tampak bahwa
J
+|
λ
Jm
〉 merupakan eigenstate dari
J
zyang memiliki harga eigen (
m+1) ħ. Oleh karena
itu
J
+disebut sebagai operator tangga naik.
Hal serupa dapat dibuktikan
J
zJ
−|
λ
Jm
〉= (m−1) ħ J
−|
λ
Jm
〉
Jadi
J
−merupakan operator tangga turun.
Dapat ditulis:
J
+|
λ
Jm
〉= c
λ
Jm |λ
Jm+1
〉
J
−|
λ
Jm
〉= d
λ
Jm |λ
Jm
−1〉
Dengan
c dan d merupakan konstanta yang harus
dihitung.
Sebelum menghitung itu kita lihat bahwa nilai
m
punya batas bawah dan batas atas. Hal ini secara
mudah dibuktikan dengan kenyataan bahwa harga
ekspektasi
J
x2+
J
y2
tidak bisa negatif, atau:
0 ≤ 〈
λ
Jm|J
x2+
J
y2
|λ
Jm
〉 = 〈
λ
Jm|J
2−J
z2|λ
Jm
〉=
λ
J−(mħ)
2Jadi (
mħ)
2≤
λ
J
, artinya untuk nilai
λ
Jtertentu nilai
m
Di atas
m
maxtidak ada keadaan lagi, artinya:
J
+|
λ
Jm
max〉 = 0
dan juga
J
−J
+|
λ
Jm
max〉 = 0
atau
(J
2−
J
z2− ħJ
z) |
λ
Jm
max〉 = 0,
hal ini memberikan:
λ
J− m
max(
m
max+1)
ħ
2= 0
Hal serupa dari kenyataan tidak ada lagi keadaan
di bawah
m
min, maka
J
−|
λ
Jm
min〉 = 0, diperoleh:
Kedua persamaan digabung, diperoleh:
m
max(
m
max+1) =
m
min(
m
min−1)
Salah satu solusi persamaan ini:
m
min=
m
max+1,
hal ini tentu saja tidak mungkin. Solusi yang benar
adalah:
m
max= − m
minMisal
m
max=
j, maka
λ
J=
j(j +1) ħ
2Hasil terakhir ini sangat mirip dengan harga
eigen L
2yang dikerjakan (dengan susah payah!)
menggunakan cara diferensial.
Tetapi apakah J dan L sama persis? Ternyata
tidak, bahkan akan ada kejutan disini.
Nilai
j tidak boleh sembarang, hal ini terlihat:
m
max− m
min=
j
− (−j) = 2j
Karena
m
max− m
minselalu bulat positif atau
nol, maka 2
j demikian juga.
Artinya
j bisa bulat, nol atau setengah-bulat
(
half-integer).
Kondisi
j yang dapat mempunyai nilai
setengah-bulat ini agak mengejutkan karena berbeda
dengan
l dari L
2yang hanya boleh bernilai
bilangan bulat positif atau nol. Jadi tampak
bahwa J
2dan L
2sedikit berbeda.
Apakah fisisnya ada untuk kasus
j setengah bulat
(yang secara Klassik tidak ada analoginya)?
Ternyata ada yaitu untuk momentum angular spin.
Selanjutnya L disebut sebagai momentum angular
orbital, S disebut sebagai momentum angular
spin. Sedangkan momentum angular J merujuk ke
Sekarang kita evaluasi nilai konstanta
c dan d.
Keadaan |
λ
Jm
〉 kita tulis saja sebagai |jm〉.
Karena J
−=
J
++maka
〈jm| J
−J
+|
jm
〉 = 〈( J
+)
jm| J
+|
jm
〉 = |c
jm|
2Sementara
〈jm| J
−J
+|
jm
〉 = 〈jm| J
2− J
z2− ħJ
z|
jm
〉
=
j(j+1)ħ
2− m
2ħ
2−ħmħ
Jadi
c
jm=
ħ [j(j+1)
− m(m+1)]
½Evaluasi
J
+J
−pada |
jm
〉 akan menghasilkan
d
jm=
ħ [j(j+1)
− m(m−1)]
½Dapat diringkas untuk kedua operator tangga
> + + − + >= + | jm j( j 1) m(m 1) | jm 1 J h > − − − + >= − | jm j( j 1) m(m 1) | jm 1 J hPelajari Sendiri
z