MODEL OPTIMASI VEHICLE ROUTING PROBLEM DAN IMPLEMENTASINYA ISKANDAR

(1)

MODEL OPTIMASI VEHICLE ROUTING PROBLEM DAN

IMPLEMENTASINYA

ISKANDAR

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

BOGOR

2010

(2)

PERNYATAAN MENGENAI TESIS DAN

SUMBER INFORMASI

Dengan ini saya menyatakan bahwa tesis Model Optimasi Vehicle Routing Problem dan Implementasinya adalah karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Bogor, Juni 2010 Iskandar NIM G551070531

(3)

ABSTRACT

ISKANDAR. Optimization Model of Vehicle Routing Problem and Its Implementation. Supervised by AMRIL AMAN and FARIDA HANUM.

A class of distribution of commodities problem can be modeled mathematically as a combinatorial optimization in the form of application of graph theory, namely Vehicle Routing Problem (VRP). VRP is a generalization of Travelling Salesman Problem (TSP), which can be described as the problem of designing routes of vehicles from a depot to a set of customers that minimized the total travel distance of vehicles. The routes must be started and ended at the depot, visited each customer only once by exactly one vehicle. VRP can be extended further by associating capacity of the vehicles, this class of problem is called Capacitated Vehicle Routing Problem (CVRP). The aims of this research are to formulate the model for distribution of commodities as a CVRP and to implement it for the distribution problem of Serambi Indonesia news paper in the area of Banda Aceh. This problem is solved by branch and bound method using LINGO 8.0 software. The results show that, optimal routes are shorter than the existing routes.

Keywords: optimization, distribution, vehicle routing problem, branch and bound method, news paper

(4)

RINGKASAN

ISKANDAR. Model Optimasi Vehicle Routing Problem dan Implementasinya. Dibimbing oleh AMRIL AMAN dan FARIDA HANUM.

Masalah distribusi barang merupakan salah satu aspek penting yang perlu diperhatikan oleh setiap perusahaan. Hal ini berkaitan dengan masalah optimasi rute distribusi barang dari tempat produksi ke sejumlah konsumen. Keputusan tentang rute kendaraan dibuat untuk mengoptimalkan total jarak tempuh, waktu tempuh, jumlah kendaraan yang harus dioperasikan dan sumber daya lain yang tersedia supaya diperoleh keuntungan yang optimal sekaligus dapat mengurangi biaya logistik.

Secara matematis, masalah penentuan rute kendaraan dalam mendistribusikan barang dari tempat produksi yang disebut dengan depot ke sejumlah pelanggan yang tersebar di sejumlah tempat disebut dengan Vehicle Routing Problem (VRP). VRP bertujuan meminimumkan total jarak tempuh kendaraan sehingga dapat meminimumkan biaya logistik perusahaan dengan memperhatikan beberapa kendala atau batasan-batasan (1) setiap pelanggan dikunjungi tepat satu kali oleh satu kendaraan, (2) setiap rute berawal dan berakhir di depot, dan (3) total permintaan pelanggan dalam satu rute tidak melebihi kapasitas kendaraan. Salah satu variasi VRP adalah Capacitated Vehicle Routing Problem (CVRP) yaitu dengan menambahkan kendala kapasitas kendaraan yang identik, sehingga panjang rute kendaraan dibatasi oleh kapasitas angkut kendaraan yang digunakan.

Masalah penentuan rute kendaraan dalam mendistribusikan barang dapat dimodelkan sebagai integer linear programming (ILP). Model yang dibuat diharapkan dapat meminimumkan total jarak tempuh rute perjalanan kendaraan dan memenuhi kendala-kendala berikut: (1) setiap konsumen hanya dapat dikunjungi tepat satu kali oleh satu kendaraan, (2) total jumlah permintaan konsumen dalam satu rute tidak melebihi kapasitas kendaraan yang melayani rute tersebut, (3) setiap rute perjalanan kendaraan berawal dari depot, (4) setiap rute perjalanan kendaraan berakhir di depot, (5) kekontinuan rute, artinya setiap kendaraan yang mengunjungi suatu konsumen, setelah selesai melayani akan meninggalkan konsumen tersebut, (6) tidak terdapat subtour pada formulasi yang dibuat.

Penentuan solusi model dilakukan dengan metode branch and bound dengan bantuan software LINGO 8.0. Solusi yang diperoleh merupakan solusi optimal yang meminimumkan fungsi tujuan dan memenuhi semua kendala atau batasan-batasan yang dibuat.

Implementasi model dilakukan dengan cara menyimulasikan model pada data distribusi koran Serambi Indonesia pada depot percetakan Banda Aceh. Data-data yang digunakan adalah jarak antara depot dengan pelanggan dan jarak antar pelanggan, jumlah permintaan masing-masing pelanggan, jumlah kendaraan yang dioperasikan dan kapasitas masing-masing kendaraan. Penentuan rute distribusi koran Serambi Indonesia selama ini hanya berdasarkan pengalaman pengemudi, di mana pengemudi terlebih dahulu memilih rute yang terdekat dengan depot

(5)

percetakan sehingga total jarak yang ditempuh dari seluruh rute perjalanan belum tentu menghasilkan rute yang optimal.

Hasil yang diperoleh menunjukkan bahwa model yang dibuat menghasilkan rute distribusi koran Serambi Indonesia depot percetakan Banda Aceh dengan total jarak yang minimum. Hal tersebut dapat dilihat dari perbandingan antara rute optimal yang diperoleh dengan rute distribusi koran saat ini.

Kata kunci: optimasi, distribusi, masalah rute kendaraan, metode branch and bound, koran.

(6)

©Hak cipta milik IPB, tahun 2010

Hak cipta dilindungi Undang-Undang

1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya.

a. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik atau tinjauan suatu masalah.

b. Pengutipan tidak merugikan kepentingan yang wajar IPB.

2. Dilarang mengumumkan dan memperbanyak sebagian atau seluruh karya tulis dalam bentuk apapun tanpa izin IPB.

(7)

MODEL OPTIMASI VEHICLE ROUTING PROBLEM DAN

IMPLEMENTASINYA

ISKANDAR

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Program Studi Matematika Terapan

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

BOGOR

2010

(8)

(9)

Judul Tesis : Model Optimasi Vehicle Routing Problem dan Implementasinya Nama : Iskandar

NIM : G551070531

Disetujui Komisi Pembimbing

Dr. Ir.Amril Aman, M.Sc. Dra. Farida Hanum, M.Si.

Ketua Anggota

Diketahui

Ketua Program Studi Dekan Sekolah Pascasarjana Matematika Terapan

Dr. Ir. Endar H. Nugrahani, M.S. Prof. Dr. Ir. Khairil A. Notodiputro, M.S.

(10)

PRAKATA

Segala puji dan syukur penulis panjatkan ke hadirat Allah SWT yang telah memberikan segala rahmat dan karunia-Nya, sehingga penulis dapat menyelesaikan tesis yang berjudul “Model Optimasi Vehicle Routing Problem dan Implementasinya”. Penulis menyadari bahwa dalam penyusunan tesis ini masih banyak terdapat kekurangan, hal ini disebabkan karena pengetahuan yang dimiliki oleh penulis sangat terbatas.

Pada kesempatan ini penulis mengucapkan terima kasih yang sebesar-besarnya kepada:

1. Bapak Dr. Ir.Amril Aman, M.Sc. dan Ibu Dra. Farida Hanum, M.Si. selaku pembimbing, pendidik dan pengajar yang dengan penuh kesabaran memberikan bimbingan, arahan, nasihat serta motivasi kepada penulis.

2. Bapak Drs. Prapto Tri Supriyo, M.Kom. selaku penguji, pendidik dan pengajar yang telah memberikan saran dan kritikannya kepada penulis.

3. Departemen Agama RI yang telah memberikan beasiswa kepada penulis untuk melanjutkan pendidikan Sekolah Pascasarjana pada Institut Pertanian Bogor. 4. Ketua Departemen, ketua Program Studi dan seluruh staf pengajar, serta staf

administrasi Departemen Matematika yang turut membantu proses penyelesaian tesis ini.

5. Harian Serambi Indonesia Nanggroe Aceh Darussalam khususnya kepada Bapak Muhammad Jafar selaku manager sirkulasi dan Bapak Firdaus D, SE.Ak selaku manager umum yang telah berkenan memberikan data distribusi koran Serambi Indonesia yang digunakan dalam penelitian ini.

6. Kepala sekolah dan seluruh staf pengajar MTs Negeri Matangglumpang Dua Kabupaten Bireuen Nanggroe Aceh Darussalam yang turut mendoakan dan memotivasi penulis dalam menyelesaikan tesis ini.

7. Isteri tercinta Sufriana, S.Pd, anak tersayang Rifka Dara Febriana dan Alfarabi, Ayahanda M.Yusuf BB, Alm. Ibunda Zaimah, Ayah dan Ibu mertua, kakak, adik serta seluruh keluarga yang selalu mendoakan, memberikan semangat, dorongan dan memotivasi kepada penulis di setiap waktu dalam menyelesaikan tesis ini.

8. Bapak Djajuli dan keluarga di Bogor, yang telah memberikan bantuan, dukungan dan doa kepada penulis dalam penyelesaian tesis ini.

9. Seluruh teman-teman yang turut membantu dalam penyelesaian tesis ini. Penulis mendoakan semoga segala bantuan, bimbingan dan pengarahan yang diberikan mendapat ganjaran yang berlipat ganda dari Allah SWT, dan semoga tesis ini bermanfaat bagi kita semua. Amiin.

Bogor, Juni 2010 Iskandar

(11)

RIWAYAT HIDUP

Penulis dilahirkan di Bireuen Nanggroe Aceh Darussalam pada tanggal 30 Mei 1971 dari Ayah M.Yusuf dan Ibu (Almarhumah) Zaimah. Penulis adalah putra ke empat dari sepuluh bersaudara.

Tahun 1990 penulis lulus dari SMA Negeri 1 Bireuen NAD dan pada tahun yang sama lulus seleksi masuk pada Jurusan Matematika Fakultas Tarbiyah IAIN Ar-Raniry Banda Aceh dan lulus pada tahun 1996.

Pada tahun 1997 penulis diterima sebagai Pegawai Negeri Sipil dan bertugas sebagai guru Matematika di Madrasah Tsanawiyah Negeri Peudada sampai tahun 2005. Tahun 2005 penulis dimutasi ke Madrasah Tsanawiyah Negeri Matangglumpang Dua dan sampai sekarang masih bertugas di sekolah tersebut.

Pada tahun 2007 penulis mendapat kesempatan untuk melanjutkan pendidikan Program Magister pada program studi Matematika Terapan di Sekolah Pascasarjana Institut Pertanian Bogor melalui beasiswa dari Departemen Agama Republik Indonesia.

(12)

xi

Halaman

DAFTAR TABEL ... xii

DAFTAR GAMBAR ... xii

DAFTAR LAMPIRAN ... xii

I PENDAHULUAN ... 1 1.1 Latar Belakang ... 1 1.2 Tujuan Penelitian ... 3 1.3 Manfaat Penelitian ... 3 II TINJAUAN PUSTAKA ... 4 2.1 Graf ... 4 2.2 Linear Programming ... 4

2.2.1 Solusi Suatu Linear Programming ... 5

2.3 Integer Linear Programming ... 6

2.4 Metode Branch and Bound ... 7

2.5 Traveling Salesman Problem (TSP) ... 11

2.6 Vehicle Routing Problem (VRP) ... 13

2.7 Capacitated Vehicle Routing Problem (CVRP) ... 18

III ALUR PENELITIAN ... 22

3.1 Pendeskripsian dan Formulasi Masalah ... 22

3.2 Pemodelan ... 22

3.3 Penentuan Solusi Model ... 22

3.4 Implementasi Model ... 23

IV DESKRIPSI DAN PEMODELAN MASALAH VEHICLE ROUTING PROBLEM DISTRIBUSI KORAN ... 24

4.1 Data ... 24

4.2 Deskripsi Masalah ... 24

4.3 Formulasi Masalah ... 26

4.4 Model ... 27

V HASIL DAN PEMBAHASAN ... 30

5.1 Implementasi Model ... 30

5.2 Hasil Penentuan Rute Kendaraan ... 31

5.3 Perbandingan Rute Solusi Optimal dengan Rute Ini ... 35

VI SIMPULAN DAN SARAN ... 37

6.1 Simpulan ... 37

6.2 Saran ... 37

DAFTAR PUSTAKA ... 38

(13)

xii 1 Data agen pelanggan PT Harian Serambi Indonesia untuk percetakan di

Banda Aceh ... 27

2 Rute solusi optimal untuk kendaraan pertama ... 32

3 Rute solusi optimal untuk kendaraan kedua ... 32

4 Rute saat ini untuk kendaraan pertama ... 33

5 Rute saat ini untuk kendaraan kedua ... 34

6 Perbandingan rute solusi optimal dan rute saat ini berdasarkan muatan dan jarak tempuh kendaraan ... 35

DAFTAR GAMBAR

Halaman 1 Daerah fisibel LP ………..………. 9

2 Grafik ruang LP1 dan LP2 ………...………... 9

3 Pencabangan dengan metode branch and bound untuk menemukan sulosi IP ………..………..………..………. 11

4 Contoh penyelesaian TSP ……… ……… 12

5 Contoh penyelesaian VRP satu depot dengan 3 rute …..……….……… 13

6 Rute solusi optimal ………..……….. 33

7 Rute kendaraan saat ini ………..……… 35

8 Rute solusi optimal dan rute saat ini ………..…. 36

DAFTAR LAMPIRAN

Halaman 1 Pemecahan masalah pencabangan pada contoh dengan menggunakan software LINGO 8.0 ... 40

2 Matriks jarak antarlokasi ... 44

3 Program penyelesaian masalah penentuan rute kendaraan distribusi koran Serambi Indonesia depot percetakan Banda Aceh dengan menggunakan software LINGO 8.0 ... 45

4 Hasil solusi LINGO 8.0 masalah penentuan rute kendaraan distribusi koran Serambi Indonesia depot percetakan Banda Aceh ... 47

(14)

I PENDAHULUAN

1.1 Latar Belakang

Salah satu aspek penting yang harus diperhatikan oleh perusahaan dalam mendistribusikan barang hasil produksi adalah masalah penentuan rute kendaraan. Keputusan tentang rute kendaraan dibuat untuk mengoptimalkan jarak tempuh, biaya perjalanan, waktu tempuh, jumlah kendaraan yang harus dioperasikan dan sumber daya lain yang tersedia supaya diperoleh keuntungan yang optimal sekaligus dapat mengurangi biaya logistik.

Secara umum permasalahan optimasi pendistribusian produk dari suatu perusahaan ke beberapa agen atau pelanggan yang saling terpisah secara matematis termasuk dalam kelas permasalahan yang disebut Vehicle Routing Problem (VRP). VRP pertama kali diperkenalkan oleh Dantzig dan Ramser pada tahun 1959 yang berorientasi pada masalah optimasi kombinatorial yaitu optimasi yang melibatkan banyak variabel (peubah). Bentuk dasar VRP secara umum berkaitan dengan masalah penentuan suatu himpunan rute kendaraan (vehicle) yang melayani satu himpunan pelanggan yang diasosiasikan dengan node dengan demand atau permintaan yang diketahui dan rute yang menghubungkan depot dengan konsumen dan satu konsumen dengan konsumen yang lain dinamakan dengan arc (Toth & Vigo 2002). Dalam kehidupan sehari-hari banyak dijumpai terapan VRP antara lain pendistribusian barang hasil produksi oleh produsen ke konsumen, pengambilan surat dari kotak-kotak pos yang tersebar di seluruh kota, pengantaran dan penjemputan anak sekolah dengan bis sekolah dan lain-lain. VRP merupakan masalah penentuan rute kendaraan yang melayani beberapa pelanggan. Setiap kendaraan memiliki kapasitas angkut dan setiap pelanggan memiliki permintaan (demand). Tiap pelanggan dikunjungi tepat satu kali oleh satu kendaraan dan total demand tiap rute tidak boleh melebihi kapasitas angkut kendaraan. Dalam VRP sendiri dikenal pula istilah depot, tempat kendaraan harus berangkat dan kembali ke depot itu. Hal tersebut menyebabkan VRP sering disebut sebagai permasalahan m-TSP. VRP merupakan masalah optimasi kombinatorial dari dua masalah yaitu masalah penentuan rute atau Traveling Salesman Problem (TSP) dan masalah kapasitas atau Bin Packing Problem (BPP).

(15)

Kedua masalah tersebut termasuk dalam kategori NP-Hard Problem, yang berarti waktu komputasi yang digunakan akan semakin sulit dan lama seiring dengan meningkatnya ruang lingkup masalah. Tujuan yang ingin dicapai adalah meminimalkan total jarak tempuh dan meminimalkan jumlah kendaraan yang digunakan. VRP sendiri memiliki beberapa faktor penentu dalam implementasinya pada dunia nyata.

Formulasi VRP diharapkan dapat membentuk sejumlah rute yang dapat meminimumkan total jarak tempuh atau total biaya yang memenuhi batasan: (1) setiap rute harus dimulai dan berakhir di depot, (2) total permintaan pelanggan pada setiap rute tidak melebihi kapasitas kendaraan, (3) setiap pelanggan dikunjungi tepat satu kali oleh satu kendaraan. Berbagai jenis kendala yang dihadapi pada permasalahan VRP, dapat menghasilkan banyak variasi dari VRP itu sendiri antara lain: kendaraan yang digunakan dapat mempunyai kapasitas yang sama (homogen) atau tidak sama (heterogen), jika kapasitas semua kendaraan yang digunakan adalah sama, misalnya C maka VRP ini dinamakan Capacitated Vehicle Routing Problem (CVRP), kendaraan melakukan kegiatan pengantaran dan penjemputan sekaligus maka dikenal dengan masalah Vehicle Routing Problem with Pickup and Delivery (VRPDP), adanya selang waktu tertentu bagi konsumen untuk menerima pelayanan maka masalahnya menjadi Vehicle Routing Problem with Time Window (VRPTW) dan lain-lain.

Penentuan solusi optimal dari permasalahan VRP dapat diselesaikan dengan metode eksak yaitu metode branch and bound. Penelitian tentang VRP dengan metode ini antara lain dilakukan oleh Larsen (2001) dan Rich (1999). Untuk masalah dalam ruang lingkup yang besar dan kompleks, metode ini membutuhkan waktu yang relatif lama untuk menentukan solusi yang optimal karena metode tersebut mengakomodasi semua solusi yang mungkin dari suatu permasalahan, baru kemudian ditentukan solusi optimalnya. Penyelesaian masalah VRP dengan jumlah pelanggan yang berukuran besar dan kompleks dapat diselesaikan dengan metode pendekatan yaitu metode heuristik dan metaheuristik. Metode eksak menjamin solusi yang diperoleh merupakan solusi optimal sedangkan metode heuristik lebih menekankan pada perolehan solusi fisibel secara cepat dari segi waktu komputasi meskipun tidak menjamin solusi tersebut akan optimal.

(16)

Pada penelitian ini dibuat formulasi masalah pendistribusian barang ke dalam model optimasi Capacitated Vehicle Routing Problem (CVRP) dan di implimentasikan pada permasalahan distribusi koran dari pusat distribusi ke agen pelanggannya dengan menggunakan metode branch and bound dengan bantuan software LINGO 8.0.

1.2 Tujuan Penelitian

Berdasarkan latar belakang masalah di atas, maka tujuan penelitian ini adalah sebagai berikut:

1. memformulasikan masalah distribusi barang kedalam model CVRP, 2. mengimplementasikan model pada kasus distribusi koran harian

Serambi Indonesia dan menentukan solusinya dengan metode branch and bound.

1.3 Manfaat Penelitian

Penelitian ini diharapkan dapat memberikan informasi tentang model CVRP dan metode penyelesaiannya sehingga penerapannya dapat bermanfaat dalam kehidupan sehari-hari.

(17)

II TINJAUAN PUSTAKA

Untuk memahami permasalahan yang berhubungan dengan penentuan rute optimal kendaraan dalam mendistribusikan barang serta menentukan solusinya maka diperlukan beberapa konsep teori berikut:

2.1 Graf

Definisi 1 (Graf , Graf Berarah dan Graf Takberarah)

Suatu graf G adalah pasangan terurut (V,A) dengan V merupakan himpunan takkosong dan berhingga yang anggota-anggotanya disebut simpul (node/vertex) dan A merupakan himpunan berhingga garis yang menghubungkan simpul-simpul anggota V yang disebut dengan sisi (arc atau edge). Sisi yang menghubungkan simpul i dengan simpul j dinyatakan dengan {i,j}. Dalam suatu graf, jika sisi yang menghubungkan simpul-simpulnya berarah maka graf tersebut dinamakan graf berarah (directed graph/digraf). Jika semua sisi yang menghubungkan simpul-simpulnya tidak berarah maka dinamakan graf takberarah (undirected graph) (Foulds 1992).

2.2 Linear Programming

Linear programming (LP) atau pemrograman linear adalah suatu masalah optimasi yang memenuhi ketentuan-ketentuan:

1) tujuan dari masalah tersebut adalah untuk memaksimumkan atau meminimumkan suatu fungsi linear dari sejumlah variabel keputusan. Fungsi yang akan dimaksimumkan atau diminimumkan itu disebut fungsi objektif, 2) nilai-nilai variabel keputusannya harus memenuhi semua himpunan kendala;

setiap kendala harus berupa persamaan linear atau pertidaksamaan linear, 3) ada pembatasan tanda untuk setiap variabel. Untuk sembarang variabel ,

pembatasan tanda menentukan harus taknegatif atau tandanya tidak dibatasi. (Winston 2004)

(18)

Definisi 2 (Bentuk standar suatu LP)

Suatu linear programming didefinisikan mempunyai bentuk standar sebagai berikut:

Minimumkan terhadap

(2.1) dengan x dan c merupakan vektor yang berukuran n, vektor b berukuran m; sedangkan A merupakan matriks yang berukuran m × n yang disebut juga dengan matriks kendala.

( Nash & Sofer 1996) Model linear programming (LP) menyajikan bentuk matematis dari fungsi objektif dan pembatasnya yang berupa fungsi linear. Pada tulisan ini suatu linear programming (LP) memiliki bentuk standar sebagai berikut (Taha 2003):

dengan cj, aij dan bi merupakan konstanta yang nilainya diketahui.

2.2.1 Solusi Suatu Linear Programming (LP)

Untuk menyelesaikan suatu masalah linear programming (LP) agar diperoleh solusi yang optimum dapat dilakukan dengan banyak metode. Salah

(19)

satu metode yang paling umum digunakan adalah metode simpleks yang mulai dikembangkan oleh Dantzig tahun 1947. Metode ini merupakan metode iteratif untuk menyelesaikan masalah linear programming dalam bentuk standar.

Pada linear programming (2.1), vektor x yang memenuhi kendala Ax = b disebut sebagai solusi dari linear programming (2.1). Misalkan matriks A dapat dinyatakan sebagai A = (B N), dengan B adalah matriks berukuran m × m yang merupakan matriks yang elemennya berupa koefisien variabel basis dan N merupakan matriks yang elemennya berupa koefisien variabel nonbasis pada matriks kendala. Matriks B disebut matriks basis untuk linear programming.

2.3 Integer Linear Programming

Sebuah model pengoptimalan disebut model integer linear programming (ILP) atau disebut juga integer programming (IP) jika variabel-variabel keputusan yang digunakan berupa bilangan bulat (integer). Jika semua variabel keputusan harus berupa integer maka model tersebut dinamakan pure integer programming, tetapi jika hanya sebagian yang harus integer maka disebut mixed integer programming. Sedangkan integer programming yang semua variabelnya harus bernilai 0 atau 1 disebut 0-1 integer programming.

(Rardin 1998) Secara sederhana model linear programming (LP) dengan pembatas tambahan berupa variabelnya bernilai integer disebut sebagai integer programming (IP). Dalam tulisan ini suatu integer programming (IP) memiliki bentuk standar sebagai berikut:

(20)

Definisi 3 (Linear Programming Relaksasi)

Linear programming relaksasi dari suatu integer programming merupakan linear programming yang diperoleh dari integer programming tersebut dengan

menghilangkan kendala bilangan bulat atau kendala 0-1 pada variabelnya. (Winston 1995)

2.4 Metode Branch and Bound

Untuk memperoleh solusi optimal dari masalah integer programming dapat dipecahkan dengan metode branch and bound. Prinsip dasar dari metode branch and bound adalah memecah daerah fisibel dari masalah LP-relaksasi dengan cara membuat subproblem baru sehingga masalah IP dapat terpecahkan. Daerah fisibel suatu LP adalah daerah yang memuat titik-titik yang dapat memenuhi semua kendala linear masalah LP (Taha 2003).

Setiap subproblem diukur dengan tiga cara sebagai berikut:

1. Batas dari subproblem ≤ solusi optimum yang didapat saat ini (z*) 2. LP-relaksasi tidak memiliki solusi fisibel.

3. Solusi optimum dari LP-relaksasi berupa integer. Jika solusi ini lebih baik dari solusi optimum yang didapat sebelumnya maka solusi ini menjadi solusi optimum yang baru dan cara pertama digunakan kembali untuk semua subproblem dengan nilai z* baru yang lebih besar.

Adapun langkah-langkah metode branch and bound untuk masalah pemaksimuman, menurut Taha (2003) adalah sebagai berikut:

Ditetapkan batas bawah awal z = untuk nilai optimum dari fungsi objektif ILP dan tetapkan i = 0.

Langkah 1 (pem-fathom-an dan pembatasan)

Dipilih LPi sebagai subproblem untuk diteliti. Kemudian LPi diselesaikan

dan LPi di-fathom-kan jika memenuhi salah satu dari ketiga kondisi berikut:

1. Nilai optimum z dari LPi tidak dapat menghasilkan nilai objektif yang

lebih baik daripada batas bawah sekarang.

2. LPi menghasilkan solusi integer fisibel yang lebih baik daripada batas

bawah sekarang.

(21)

Dalam hal ini akan muncul dua kasus yaitu:

1. Jika LPi di-fathom-kan dan solusi yang diperoleh lebih baik daripada

batas bawah sekarang, maka batas bawah z diperbaharui. Jika semua subproblem di-fathom-kan maka proses dihentikan. ILP optimum dihubungkan dengan batas bawah sekarang, bila ada. Jika sebaliknya, dipilih i = i + 1, dan ulangi Langkah 1.

2. Jika LPi tidak di-fathom-kan, proses dilanjutkan ke Langkah 2 untuk

melakukan pencabangan pada LPi.

Langkah 2 (pencabangan)

Dipilih sebarang variabel xj yang nilai optimumnya adalah xj* yang tidak

memenuhi batasan integer dalam solusi LPi. Bidang [xj*] < xj < [xj*] + 1 (dengan

[v] sebagai integer terbesar yang ≤ v) dieliminasi dengan membuat dua subproblem LP yang sesuai dengan xj ≤ [xj*] dan xj ≥ [xj*] + 1. Kemudian

ditentukan i = i + 1 , dan kembali pada Langkah 1.

Untuk memudahkan pemahaman tentang metode branch and bound diberikan contoh sebagai berikut:

Contoh:

Misalkan diberikan masalah integer sebagai berikut:

Solusi optimum dari LP-relaksasi contoh tersebut (LP0) adalah z = 4.85,

x1 = 2.75, dan x2 = 2.1 (lihat Lampiran 1a). Daerah fisibel LP-relaksasi dari

masalah di atas dapat dilihat pada Gambar 1. Menurut metode branch and bound, karena solusi optimum LP-relaksasi tersebut tidak memenuhi syarat integer, maka harus dibuat subproblem baru. Dipilih sembarang variabel xi optimum yang tidak

memenuhi syarat integer, misalnya x1 = 2.75, sehingga bidang 2 < x1 < 3 bukan

daerah fisibel bagi masalah IP dan harus dipisahkan. Ruang LP0 semula diganti

dengan dua ruang LP yakni LP1 dan LP2 dengan ruang solusi yang didefinisikan

sebagai berikut:

(22)

- Ruang LP2= ruang LP0 + kendala (x1 ≥ 3)

Ruang solusi dari LP1 dan LP2 dapat dilihat pada Gambar 2.

Dari gambar di atas terlihat bahwa batasan baru LP1 dan LP2 tidak dapat

dipenuhi secara bersamaan, sehingga LP1 dan LP2 harus dibuat menjadi dua buah

LP yang berbeda. Kemudian masalah LP1 dan LP2 diselesaikan satu per satu.

Misalkan LP1 dipilih pertama kali untuk diselesaikan, sehingga permasalahannya

menjadi: 1 8 0 1 2 ₅ 6 • • • ₇ • • • • 3 2 0 • ₁ 2 ₃ ₄ ₅ ₆ ₇ -2 -1 • 3 2 3 -2 -1 • 1 8 4 • X1 X2 • • • LP2 LP1 5

Gambar 2 Grafik ruang LP1 dan LP2.

• • • • • • 1 • 4 • 4 • • X1 X2 • 5

Gambar 1 Daerah fisibel LP.

Solusi optimum LP0 z=4.85, x1=2.75, x2=2.1

•

(23)

Diperoleh solusi optimum untuk masalah LP di atas, yaitu z = 4.4 , x1 = 2,

dan x2 = 2.4 (lihat Lampiran 1b). Karena solusi optimum LP1 bukan solusi

optimum integer, maka LP1 tidak di-fathom-kan, sehingga dilakukan pencabangan

di LP1 menjadi 2 subproblem, yakni LP3 dan LP4. Ruang solusi LP3 dan LP4

didefinisikan sebagai berikut:

- Ruang LP3 = ruang LP0 + kendala (x1 ≤ 2) + kendala (x2 ≤ 2) = ruang LP1 +

kendala (x2 ≤ 2)

- Ruang LP4 = ruang LP0 + kendala (x1 ≤ 2) + kendala (x2 ≥ 3) = ruang LP1 +

kendala (x2 ≥ 3)

Solusi optimum dari LP3 adalah z = 4 dengan x1 = 2 dan x2 = 2 (lihat

Lampiran 1d). Karena solusi LP3 integer, maka LP3 di-fathom-kan. Nilai z = 4

sebagai calon batas bawah solusi optimum IP. Solusi optimum dari LP4 adalah z

= 3.5 dengan x1 = 0.5 dan x2 = 3 (lihat Lampiran 1e). Karena solusi LP4 (z = 3.5

dengan x1 = 0.5 dan x2 = 3) tidak memenuhi syarat integer maka semestinya LP4

tidak di-fathom-kan. Namun karena nilai z = 3.5 tidak lebih baik dari batas bawah sebelumnya (z = 4 dengan x1 = 2 dan x2 = 2) maka LP4 di-fathom-kan, sehingga

solusi LP4 bukan solusi optimum IP. Calon batas bawah untuk solusi optimum IP

adalah z = 4.

Selanjutnya diselesaikan LP2, dan dari penghitungan diperoleh solusi

optimum LP2 adalah z = 4.80 dengan x1 = 3 dan x2 = 1.8 (lihat Lampiran 1c).

Seperti yang diketahui bahwa dari penyelesaian LP0 sudah diperoleh nilai

optimum yaitu z = 4.85 artinya nilai z tidak mungkin akan lebih besar dari 4.85 dan tidak mungkin akan lebih baik dari calon batas bawah sebelumnya (z = 4). Karena semua variabel dari fungsi objektif pada LP3 telah memenuhi syarat

integer yaitu z = 4 dengan x1 = 2 dan x2 = 2 maka tidak mungkin LP2 akan

menghasilkan solusi integer yang lebih baik, sehingga LP2 di-fathom-kan dan

tidak perlu dilakukan pencabangan. Karena semua subproblem sudah di-fathom-kan, maka pencabangan berhenti, sehingga diperoleh solusi optimumnya dari penyelesaian LP3 yaitu z = 4 dengan x1 = 2 dan x2 = 2.

(24)

Penggunaan metode branch and bound untuk menyelesaikan masalah IP pada contoh di atas dapat dilihat pada Gambar 3. Penghitungan nilai-nilai variabel dilakukan dengan bantuan software LINGO 8.0.

2.5 Traveling Salesman Problem (TSP)

Traveling Salesman Problem (TSP) merupakan suatu masalah optimasi untuk mencari rute terpendek bagi seorang salesman yang menjajakan produknya dengan melakukan tour yang dimulai dari tempat asalnya menuju n kota tepat satu kali kemudian kembali ke tempat asalnya. Tujuannya adalah untuk meminimumkan biaya operasional salesman yang dikeluarkan oleh perusahaan. Rute kendaraan pada masalah TSP merupakan cycle Hamilton yaitu path tertutup yang memuat semua node pada graf yang mempresentasikan jaringan jalan yang menghubungkan tiap kota. Tujuannya adalah menentukan rute perjalanan yang fisibel sedemikian sehingga jarak tempuh yang melalui rute tersebut minimum.

Menurut Garfinkel dan Nemhauser (1972) secara matematis TSP dapat dinyatakan sebagai suatu graf berarah G=(V,A) dengan V={0,1, ..., n} menyatakan himpunan node yang menunjukkan lokasi kota dan A={(i, j) | i, j V, i ≠ j} merupakan himpunan sisi berarah (arc) yang menyatakan jalan penghubung tiap kota. Node 0 menyatakan kota asal/depot yang merupakan tempat seorang

x2 ≥ 3

Gambar 3 Pencabangan dengan metode branch and bound untuk menemukan solusi IP.

z = 4.85, x1 =2.75, dan x2 =2.1

z = 4.4, x1 =2, dan x2 =2.4 z = 4.8, x1 =3, dan x2 =1.8

z = 4, x1 =2, dan x2 =2

batas bawah (optimal)

z = 3.5, x1 =0.5, dan x2 =3 x1 ≥ 3 x1 ≤ 2 x2 ≤ 2 LP0 LP1 LP3 LP4 LP2

(25)

salesman memulai perjalanan. Misalkan adalah jarak tempuh (biaya perjalanan) dari kota i ke kota j dan jika variabel keputusannya adalah:

maka TSP dapat diformulasikan secara matematis sebagai berikut:

dengan kendala:

Persamaan (2.21) merupakan fungsi tujuannya yaitu meminimumkan total jarak tempuh (biaya perjalanan). Kendala (2.22) dan (2.23) menggambarkan bahwa salesman mendatangi dan meninggalkan setiap kota tepat satu kali, sedangkan kendala (2.24) memastikan bahwa tidak terdapat subrute dan kendala (2.25) menjamin bahwa xij merupakan integer biner.

Contoh solusi dari TSP dapat dilihat pada Gambar 4.

Depot

Kota Rute

(26)

2.6 Vehicle Routing Problem (VRP)

Kallehauge et al. (2001) mendefinisikan permasalahan m-TSP sebagai salah satu variasi dari TSP, di mana terdapat m salesman yang mengunjungi sejumlah kota dan tiap kota hanya dapat dikunjungi oleh tepat satu salesman saja. Tiap salesman berawal dari suatu depot dan pada akhir perjalanannya juga harus kembali ke depot tersebut.

Permasalahan m-TSP ini dikenal sebagai Vehicle Routing Problem (VRP). Jadi VRP berkaitan dengan penentuan rute optimal untuk permasalahan yang melibatkan lebih dari satu kendaraan (vehicle) dengan kapasitas tertentu untuk melayani sejumlah konsumen sesuai dengan permintaannya masing-masing. Dalam masalah VRP ini, setiap kota diasosiasikan sebagai lokasi konsumen dan tiap kendaraan yang digunakan untuk mengunjungi sejumlah konsumen memiliki kapasitas tertentu. Total jumlah permintaan pelanggan dalam suatu rute tidak melebihi kapasitas kendaraan yang ditugasi melayani rute tersebut dan setiap pelanggan dikunjungi hanya satu kali oleh satu kendaraan. Pada masalah VRP juga terdapat suatu depot di mana tiap kendaraan harus berangkat dan kembali ke depot itu. Permasalahan VRP bertujuan meminimalkan total jarak tempuh kendaraan atau total biaya dari setiap rute perjalanan, selain itu bisa juga bertujuan meminimalkan banyaknya kendaraan yang digunakan (m). Sebagai contoh, penyelesaian masalah VRP dengan satu depot ditunjukkan dalam gambar berikut:

Pelanggan

Rute

Gambar 5 Contoh penyelesaian VRP satu depot dengan 3 rute. Depot

(27)

Permasalahan VRP yang dituliskan oleh Toth and Vigo (2002) menjelaskan bahwa VRP adalah masalah penentuan rute kendaraan dalam mendistribusikan barang dari tempat produksi yang dinamakan depot ke konsumen dengan tujuan meminimumkankan total jarak tempuh kendaraan. Untuk mencapai tujuan tersebut perlu diperhatikan beberapa batasan yang harus dipenuhi yaitu setiap kendaraan yang akan mendistribusikan barang ke konsumen harus memulai rute perjalanan dari tempat produksi (depot), setiap pelanggan hanya boleh dilayani satu kali oleh satu kendaraan, setiap pelanggan mempunyai permintaan yang harus dipenuhi dan diasumsikan permintaaan tersebut sudah diketahui sebelumnya. Setiap kendaraan memiliki batasan kapasitas tertentu artinya setiap kendaraan akan melayani pelanggan sesuai dengan kapasitasnya. Selanjutnya juga harus dipenuhi bahwa tidak terdapat subrute untuk setiap kendaraan.

Menurut Toth and Vigo (2002), secara matematis VRP dapat dinyatakan sebagai suatu digraf G=(V, A) dengan V={0,1,..., n} adalah himpunan simpul yang menunjukkan lokasi pelanggan dan A={(i, j) | i, j V, i ≠ j} yaitu himpunan sisi berarah yang menyatakan jalan penghubung antarlokasi pelanggan. Simpul 0 menunjukkan depot, yaitu tempat menyimpan kendaraan yang digunakan untuk distribusi dan merupakan tempat dimulainya suatu rute kendaraan. Banyaknya kendaraan yang tersedia di depot adalah K dengan kapasitas kendaraan ke-k adalah Ck. Setiap pelanggan i memiliki permintaan sebanyak di.

Toth and Vigo (2002) memformulasikan VRP dalam bentuk pemrograman linear integer dengan tujuan meminimalkan total biaya atau total jarak tempuh dari rute perjalanan pendistribusian barang/jasa adalah sebagai berikut:

dengan kendala:

Kendala ini untuk memastikan bahwa setiap konsumen dikunjungi tepat satu kali oleh satu kendaraan.

(28)

Batasan tersebut untuk menjamin bahwa terdapat K kendaraan yang beroperasi yang memulai rute dari depot.

Batasan ini memastikan bahwa setiap konsumen akan dikunjungi oleh kendaraan yang sudah dijadwalkan untuk konsumen tersebut.

Kendala tersebut menjamin bahwa total permintaan konsumen dalam setiap rute tidak melebihi kapasitas kendaraan.

Kendala ini memastikan bahwa tidak terdapat subrute pada formulasi yang ada.

Batasan ini memastikan bahwa variabel keputusan merupakan integer biner.

Batasan ini menjamin variabel keputusan merupakan integer biner. Dengan variabel keputusan:

dengan:

V = himpunan node

A = himpunan sisi berarah (arc),

cij = jarak/biaya perjalanan dari konsumen i ke konsumen j di = jumlah permintaan konsumen i

Ck = kapasitas kendaraan ke- k

(29)

Permasalahan VRP yang dikemukakan oleh Kallehauge et al. (2001) adalah menyangkut masalah distribusi barang dari tempat produksi (depot) ke sejumlah konsumen yang tersebar di sejumlah tempat. Tujuannya adalah untuk meminimalkan total jarak tempuh (total biaya) dari rute perjalanan kendaraan dalam mendistribusikan barang. Rute yang dibentuk harus memenuhi batasan-batasan yaitu setiap pelanggan hanya dikunjungi satu kali oleh satu kendaraan, semua pelanggan harus dilayani sesuai dengan permintaannya masing-masing yang diketahui sebelumnya. Kendaraan yang digunakan adalah homogen dan memiliki batasan kapasitas tertentu sehingga rute yang dilalui tidak melebihi kapasitasnya. Setiap rute kendaraan berawal dari depot dan pada akhirnya juga harus kembali ke depot.

Secara matematis Kallehauge et al. (2001) mendefinisikan VRP sebagai suatu digraf G=(N,A), dengan N merupakan simpul yang terdiri atas gabungan himpunan pelanggan C dan depot. Himpunan C berupa simpul 1 sampai n sedangkan simpul depot adalah 0 dan n+1. A adalah himpunan sisi berarah yaitu penghubung antarsimpul yang merupakan jaringan jalan yang digunakan oleh kendaraan. Semua rute berawal dari simpul 0 dan berakhir di impul n+1. Himpunan kendaraan V merupakan kumpulan kendaraan yang homogen dengan kapasitas q. Setiap pelanggan atau simpul i untuk setiap i anggota C memiliki permintaan sebesar di, sehingga panjang rute yang dilalui oleh setiap kendaraan

dibatasi oleh kapasitas kendaraan. Setiap sisi (i,j) pada graf memiliki jarak tempuh cij yaitu jarak dari simpul i ke simpul j dan diasumsikan jarak tempuh cij=cji.

Tujuannya adalah menentukan himpunan rute dengan total jarak tempuh atau biaya perjalanan yang minimum dengan syarat setiap rute berawal di simpul 0 dan berakhir di simpul n+1, setiap pelanggan dilayani tepat satu kali oleh satu kendaraan dan memenuhi kendala kapasitas kendaraan. Kallehauge et al. (2001) memodelkan masalah VRP tersebut ke dalam model matematis sebagai berikut:

(30)

Batasan ini menjamin bahwa tiap pelanggan hanya dapat dikunjungi tepat satu kali oleh satu kendaraan.

Batasan tersebut untuk memastikan bahwa total jumlah permintaan pelanggan dalam satu rute tidak melebihi kapasitas kendaraan.

Batasan tersebut menjamin bahwa setiap kendaraan memulai rute perjalanan dari depot.

Batasan ini memastikan bahwa setiap kendaraan yang mengunjungi suatu pelanggan, setelah selesai melayani akan meninggalkan pelanggan tersebut.

Kendala tersebut memastikan bahwa setiap rute perjalanan kendaraan berakhir di depot.

Batasan variabel keputusan merupakan integer biner Dengan variabel keputusan:

dengan:

V = himpunan kendaraan dengan kapasitas yang identik C = himpunan konsumen/pelanggan

N = himpunan node/vertex (simpul), {0,1,...,n+1} A = himpunan sisi berarah (arc),

cij = jarak/biaya perjalanan dari konsumen i ke konsumen j di = total jumlah permintaan konsumen i

q = kapasitas kendaraan

Formulasi model matematis yang dibuat oleh Kallehauge et al. dan Toth &Vigo mempunyai tujuan yang sama yaitu meminimumkan total jarak

(31)

tempuh/biaya dari setiap rute perjalanan. Perbedaannya adalah Toth &Vigo hanya memperhitungkan biaya perjalanan untuk perjalanan awal dari depot, kemudian mengunjungi semua konsumen, tanpa memperhitungkan perjalanan kembali ke depot pada akhir perjalanan tersebut; sedangkan Kallehauge et al. memperhitungkan biaya perjalanan untuk perjalanan awal dari depot, kemudian mengunjungi semua konsumen dan perjalanan kembali ke depot.

2.7 Capacitated Vehicle Routing Problem (CVRP)

Capacitated Vehicle Routing Problem (CVRP) merupakan salah satu variasi dari masalah VRP dengan penambahan kendala kapasitas kendaraan yang identik. Setiap kendaraan yang melayani konsumen disyaratkan memiliki batasan kapasitas sehingga banyaknya konsumen yang dilayani oleh setiap kendaraan dalam satu rute bergantung pada kapasitas kendaraan. Permasalahan CVRP bertujuan meminimumkan total jarak tempuh rute perjalanan kendaraan dalam mendistribusikan barang dari tempat produksi yang dinamakan dengan depot ke sejumlah konsumen.

Menurut Kara et al. (2004) masalah CVRP adalah masalah pengoptimalan jarak tempuh perjalanan kendaraan dalam pendistribusian barang dari tempat poduksi (depot) ke sejumlah agen pelanggan sehingga menghasilkan rute dengan total jarak tempuh yang minimum. Penentuan rute kendaraan tersebut harus memperhatikan beberapa batasan yaitu setiap kendaraan harus memulai rute perjalanan dari depot dan setelah melayani sejumlah konsumen juga harus kembali ke depot. Setiap konsumen hanya dilayani tepat satu kali oleh satu kendaraan. Terdapat sejumlah kendaraan di depot dengan kapasitas yang identik yang digunakan untuk melayani konsumen. Kendaraan-kendaraan tersebut memiliki kapasitas tertentu sehingga panjang rute yang dilalui oleh setiap kendaraan dalam melayani setiap konsumen sesuai dengan kapasitasnya. Setiap rute kendaraan tidak memiliki subrute sehingga rute yang terbentuk adalah sebanyak kendaraan yang dioperasikan.

Kara et al. (2004) mendefinisikan Capacitated Vehicle Routing Problem (CVRP) sebagai suatu graf berarah G=(N,A) dengan adalah himpunan simpul (vertex), menyatakan depot yaitu tempat kendaraan memulai dan mengakhiri rute perjalanan dan menyatakan konsumen (C).

(32)

Sedangkan adalah himpunan sisi berarah (arc) yang merupakan himpunan sisi yang menghubungkan antarsimpul. Setiap simpul memiliki permintaan (demand) sebesar dengan adalah integer positif. Himpunan V={1,2,...,K} merupakan kumpulan kendaraan yang homogen dengan kapasitas yang identik yaitu Q, sehingga panjang setiap rute dibatasi oleh kapasitas kendaraan. Setiap arc memiliki jarak tempuh yaitu jarak dari simpul i ke simpul j. Jarak perjalanan ini diasumsikan simetrik yaitu dan . Permasalahan dari CVRP adalah menentukan himpunan dari K rute kendaraan yang memenuhi kondisi berikut: (1) setiap rute berawal dan berakhir di depot, (2) setiap konsumen harus dilayani tepat satu kali oleh satu kendaraan, (3) total permintaan konsumen dari setip rute tidak melebihi kapasitas kendaraan, dan (4) total jarak dari semua rute diminimumkan.

Permasalahan tersebut kemudian diformulasikan ke dalam model matematika dengan tujuan meminimumkan total jarak tempuh perjalanan kendaraan. Variabel adalah variabel keputusan yang bernilai 1 jika arc merupakan solusi dari masalah CVRP dan bernilai 0 jika bukan solusi, dan variabel merupakan integer yang dihubungkan dengan setiap konsumen . Variabel keputusan hanya akan terdefinisi jika . Adapun formulasinya adalah sebagai berikut:

dengan kendala

Batasan ini memastikan bahwa tiap pelanggan hanya dikunjungi tepat satu kali oleh satu kendaraan.

Batasan tersebut menjamin bahwa setiap rute perjalanan kendaraan berawal dari depot.

(33)

Batasan bahwa setiap rute perjalanan kendaraan berakhir di depot.

Batasan ini memastikan bahwa tidak terdapat subrute pada setiap rute yang terbentuk.

Variabel keputusan hanya akan terdefinisi jika Jika maka kendala (2.46)

tidak mengikat, sehingga dan Sedangkan jika maka kendala tersebut menunjukkan bahwa sehingga batasan subtour elimination terpenuhi.

Variabel keputusan merupakan integer biner

Variabel keputusannya adalah:

dengan:

V = {1,...,K} = himpunan kendaraan dengan kapasitas yang identik K = banyaknya kendaraan yang digunakan

N = himpunan node (simpul)

C = himpunan konsumen/pelanggan A = himpunan sisi berarah (arc),

cij = jarak/biaya perjalanan dari konsumen i ke konsumen j di = total jumlah permintaan konsumen i

= kapasitas kendaraan

uik = muatan kendaraan ke- k setelah mengunjungi konsumen ke- i

Formulasi model matematis CVRP Kara et al. (2004) tersebut pada intinya menekankan pada batasan subtour elimination yaitu mengeliminasi subtour supaya tidak terdapat subrute pada rute-rute yang terbentuk yang dikaitkan

(34)

dengan batasan kapasitas kendaraan. Variabel keputusan hanya akan terdefinisi jika jumlah permintaan konsumen i dan konsumen j tidak melebihi kapasitas kendaraan.

(35)

III ALUR PENELITIAN

Penelitian ini dibagi menjadi empat tahap yaitu (1) pendeskripsian dan formulasi masalah, (2) pemodelan, (3) penentuan solusi model, dan (4) implementasi model.

3.1 Pendeskripsian dan Formulasi Masalah

Tahap pertama dalam pemodelan adalah menentukan tujuan penentuan rute kendaraan dalam mendistribusikan barang. Secara umum tujuan masalah penentuan rute kendaraan dalam mendistribusikan barang adalah meminimumkan total jarak tempuh kendaraan dengan mempertimbangkan kapasitas kendaraan, jumlah permintaan setiap pelanggan dan jarak antarpelanggan.

Dalam masalah penentuan rute kendaraan ini, variabel keputusan akan dibatasi oleh beberapa batasan. Batasan tersebut terdiri atas beberapa batasan umum yang mencakup permasalahan penentuan rute kendaraan dalam mendistribusikan barang dari depot ke setiap pelanggannya.

3.2 Pemodelan

Setelah tahapan formulasi masalah, selanjutnya formulasi masalah tersebut dipresentasikan ke dalam model matematik. Model ini mendeskripsikan masalah menjadi suatu sistem persamaan atau pertidaksamaan atau ekspresi matematik lainnya. Masalah penetuan rute kendaraan dapat dimodelkan sebagai model Integer Linear Programming (ILP).

3.3 Penentuan Solusi Model

Penyelesaian model matematik yang sederhana dapat diselesaikan secara manual, namun untuk model matematik yang lebih kompleks menyangkut dengan masalah nyata akan membutuhkan bantuan komputer. Penentuan solusi model masalah rute kendaraan digunakan metode branch and bound dengan bantuan software LINGO 8.0. Selanjutnya solusi yang diperoleh merupakan solusi yang memenuhi semua batasan dan meminimumkan fungsi tujuan.

(36)

3.4 Implementasi Model

Implementasi model dilakukan dengan cara menyimulasikan model dengan menggunakan data pendistribusian koran harian Serambi Indonesia Nanggroe Aceh Darussalam depot percetakan Banda Aceh.

(37)

IV DESKRIPSI DAN PEMODELAN MASALAH VEHICLE

ROUTING PROBLEM DISTRIBUSI KORAN

4.1 Data

Data yang digunakan dalam penelitian ini adalah data kegiatan distribusi koran harian Serambi Indonesia Nanggroe Aceh Darussalam pada depot percetakan Banda Aceh. Data yang diambil adalah jarak antara depot dengan agen pelanggan dan jarak antaragen pelanggan yang dibuat dalam bentuk matriks jarak antarlokasi (Lampiran 2), jumlah permintaan untuk setiap agen pelanggan dan jumlah kendaraan yang digunakan.

Data diperoleh dari wawancara dengan pihak terkait dan pencatatan dari dokumen di kantor harian Serambi Indonesia Banda Aceh. Pengambilan data dilakukan pada bulan April 2009.

4.2 Deskripsi Masalah

Koran harian Serambi Indonesia merupakan salah satu harian pagi yang terbit tiap hari di Nanggroe Aceh Darussalam. Koran harian ini mulai diterbitkan pertama kali pada tanggal 17 Pebruari 1989 oleh PT Aceh Media Grafika yang merupakan induk perusahaan dari harian Serambi Indonesia. Pada saat didirikan, perusahaan ini hanya mempunyai satu buah percetakan yaitu percetakan di Banda Aceh yang melayani pengiriman koran ke seluruh Aceh bahkan sampai ke Sumatera Utara. Namun seiring dengan perkembangan dan persaingan bisnis surat kabar yang semakin ketat, maka pada bulan Juni tahun 2003 dioperasikan lagi sebuah percetakan di Lhokseumawe untuk melayani konsumen di wilayah timur Aceh dan terakhir pada bulan Maret 2007 dioperasikan lagi percetakan di Blang Pidie untuk melayani konsumen yang berada di wilayah barat dan selatan Aceh.

Penambahan percetakan ini dilakukan untuk memenuhi permintaan konsumen agar koran sampai ke tangan pembaca tepat pada waktunya. Terlebih lagi pada industri surat kabar yang mengharuskan produk bisa sampai ke pelanggan dengan tepat waktu, karena surat kabar merupakan produk yang menjual informasi tentang kejadian-kejadian yang terjadi di berbagai negara. Hal ini sangat penting karena mengingat media surat kabar memuat berita-berita yang

(38)

terbaru dan menarik sehingga kedatangan barang tepat waktu sangat diperlukan. Oleh karena itu kemampuan untuk mengelola jaringan distribusi dalam penyaluran hasil produksi saat ini merupakan salah satu komponen yang sangat penting agar semua permintaan pelanggan dapat terlayani dengan baik dan pada akhirnya keuntungan yang diperoleh akan optimal.

Masalah pendistribusian surat kabar Harian Serambi Indonesia ke seluruh agen pelanggan merupakan tanggung jawab bagian sirkulasi yang dikepalai oleh seorang manajer. Dalam pelaksanaan distribusi ini bagian sirkulasi didukung oleh 6 unit kendaraan roda empat yang tersebar pada masing-masing tempat percetakan sesuai dengan kebutuhannya dalam melayani konsumen. Di percetakan Banda Aceh terdapat 2 unit kendaraan, percetakan Lhokseumawe 2 unit kendaraan dan percetakan Blang Pidie mempunyai 2 unit kendaraan. Setiap kendaraan mempunyai kapasitas yang sama yaitu 10000 eksemplar koran.

Mengingat bisnis surat kabar ini ada hubungannya dengan waktu, maka kedatangan barang tepat waktu menjadi salah satu pilar utama pemasaran. Agar ketepatan waktu dapat dicapai maka koran yang telah dicetak sekitar pukul 02.00 pagi langsung didistribusikan kepada konsumen dengan menggunakan jalur yang terbagi dalam beberapa wilayah pengiriman sesuai dengan permintaan dan kapasitas kendaraan kecuali jika ada berita-berita penting yang harus ditunggu. Tujuan distribusi tersebut adalah untuk menjamin koran datang tepat waktu di lokasi konsumen yang berbeda, jumlah koran tidak berkurang atau tidak ada koran yang rusak, serta memudahkan agen pelanggan untuk mendapatkan koran sesuai dengan yang dipesan.

Penentuan rute kendaraan dalam mendistribusikan koran Serambi Indonesia ke setiap agen pelanggan, selama ini hanya berdasarkan pengalaman pengemudi. Untuk permasalahan rute, pengemudi terlebih dahulu memilih rute yang terdekat dengan depot/percetakan, sehingga total jarak yang ditempuh dari seluruh rute perjalanan belum tentu menghasilkan rute optimal. Oleh karena itu perlu dibuat suatu model matematis dalam pendistribusian koran Serambi Indonesia yang akan memberikan informasi mengenai urutan rute kendaraan, sehingga menghasilkan rute dengan total jarak yang minimum dengan mempertimbangkan kendala

(39)

kapasitas kendaraan, setiap rute berawal dan berakhir di depot dan setiap pelanggan dikunjungi tepat satu kali oleh satu kendaraan.

Pada penelitian ini sebagai data simulasi model diambil data distribusi koran Serambi Indonesia pada depot/percetakan Banda Aceh, karena pada dasarnya model itu berlaku untuk semua depot/percetakan, hanya saja perlu penyesuaian dengan data-data yang ada pada masing-masing depot/percetakan tersebut.

4.3 Formulasi Masalah

Fungsi tujuan dari model penentuan rute kendaraan dalam pendistribusian koran pada penelitian ini adalah meminimumkan total jarak tempuh dari rute perjalanan kendaraan dengan memperhatikan batasan-batasan (kendala-kendala) yang ada sehingga rute-rute yang terbentuk merupakan rute-rute dengan jarak yang minimum yang memenuhi semua kendala-kendala tersebut.

Adapun kendala-kendala yang dihadapi adalah:

1. Setiap konsumen hanya dapat dikunjungi tepat satu kali oleh satu kendaraan.

2. Total jumlah permintaan konsumen dalam satu rute tidak melebihi kapasitas kendaraan yang melayani rute tersebut.

3. Setiap rute perjalanan kendaraan berawal dari depot 4. Setiap rute perjalanan kendaraan berakhir di depot.

5. Kekontinuan rute, artinya setiap kendaraan yang mengunjungi suatu konsumen, setelah selesai melayani akan meninggalkan konsumen tersebut 6. Tidak terdapat subtour pada formulasi yang dibuat.

Untuk menyederhanakan masalah maka dalam penelitian ini digunakan asumsi-asumsi sebagai berikut:

1. Semua permintaan pelanggan dapat dipenuhi.

2. Jumlah permintaan pelanggan sudah diketahui sebelumnya.

3. Kendaraan yang digunakan mempunyai kapasitas yang sama yaitu 10000 eksemplar koran.

4. Kecepatan kendaraan konstan yaitu 60 km/jam.

5. Jarak antarlokasi adalah simetrik, artinya jarak dari konsumen i ke konsumen j sama dengan jarak dari konsumen j ke konsumen i.

(40)

Tabel 1 Data agen pelanggan PT Harian Serambi Indonesia untuk percetakan di Banda Aceh

No. Nama Pelanggan Jumlah Permintaan (Eksemplar)

0 PT. Harian Serambi Indonesia 0

1 Trimora Agency Banda Aceh 3950

2 Dadang Supriadi Lampriet 1480

3 Darussalam Post 1621

4 Azra Agency Krueng Raya 1892

5 Joni Sukandar Seutui 1175

6 Nila Agency Lhoknga 635

7 Montasik Raya Post Lambaro Kafee 655

8 Abrah Agency Sibreh 612

9 Makmu Beusaree Indrapuri 595

10 Barona Agency Seulimum 493

11 Saree Agency 250

12 Syahril Agency Padang Tiji 520

13 Mulyadi Agency Sigli 1850

14 Sunaryati Agency Beureunun 1610

15 M. Jafar Lueng Putu 325

16 Rusli Ismail Meureudu 367

17 Kios Waspada Ulee Glee 673

Total Permintaan 18703

4.4 Model

Tujuan dari model matematik penentuan rute kendaraan yang dibuat adalah meminimumkan total jarak tempuh kendaraan dalam mendistribusikan koran dari tempat percetakan ke sejumlah agen pelanggan yang tersebar di sejumlah tempat. Total jarak yang minimum dari rute-rute kendaraan dapat meminimumkan biaya dan dapat mengurangi biaya operasional namun tetap memenuhi ketentuan-ketentuan dari manajemen perusahaan.

Berdasarkan formulasi masalah penentuan rute pendistribusian koran di atas, maka secara matematis dapat dibuat dalam model berikut:

Misalkan didefinisikan:

(41)

K = banyaknya kendaraan yang digunakan N = himpunan simpul (node) = {0,1,...,17}

C = himpunan konsumen/pelanggan = {1,2,...,17} A = himpunan sisi berarah (arc) = {(i,j) | i,j ∈ N, i≠j}

= jarak dari konsumen i ke konsumen j = total jumlah permintaan konsumen i = kapasitas kendaraan = 10000 eksemplar

=muatan kendaraan ke-k setelah mengunjungi konsumen ke-i Variabel keputusan:

Fungsi tujuan dari permasalahan penentuan rute distribusi koran adalah meminimumkan total jarak tempuh/total biaya dari rute perjalanan.

Kendala-kendala:

1. Setiap konsumen hanya dapat dikunjungi tepat satu kali oleh satu kendaraan.

3. Setiap rute perjalanan kendaraan berawal dari depot.

(42)

5. Kekontinuan rute, artinya setiap kendaraan yang mengunjungi suatu konsumen, setelah selesai melayani akan meninggalkan konsumen tersebut

6. Tidak terdapat subtour pada semua rute.

Variabel keputusan hanya akan terdefinisi jika Jika maka kendala

tidak mengikat, sehingga dan Sedangkan jika maka kendala tersebut menunjukkan bahwa

sehingga batasan subtour elimination terpenuhi. 7. Variabel keputusan merupakan integer biner.

(43)

V HASIL DAN PEMBAHASAN

5.1 Implementasi Model

Model yang telah diperoleh kemudian diimplementasikan dengan cara menyimulasikan model. Simulasi tersebut menggunakan data jarak antarlokasi pelanggan, jumlah permintaan pelanggan, dan jumlah kendaraan yang digunakan PT Harian Serambi Indonesia pada percetakan (depot) Banda Aceh.

Rute kendaraan yang diharapkan adalah:

1. Setiap agen pelanggan hanya dikunjungi satu kali oleh satu kendaraan.

2. Setiap kendaraan melayani agen pelanggan sesuai dengan batasan kapasitasnya.

3. Setiap rute kendaraan berawal dari depot. 4. Setiap rute kendaraan berakhir di depot.

5. Setelah melayani agen pelanggan, kendaraan akan meninggalkan agen pelanggan tersebut.

6. Tidak terdapat subrute pada setiap rute yang ada.

Pemodelan dari permasalahan tersebut adalah sebagai berikut:

Fungsi tujuannya adalah meminimumkan total jarak tempuh dari rute perjalanan kendaraan.

dengan kendala-kendala:

1. Setiap konsumen dikunjungi tepat satu kali oleh satu kendaraan.

(44)

3. Setiap rute perjalanan kendaraan berawal dari depot.

4. Setiap rute perjalanan kendaraan berakhir di depot.

5. Kekontinuan rute, artinya setiap kendaraan yang mengunjungi suatu konsumen, setelah selesai melayani akan meninggalkan konsumen tersebut.

6. Tidak terdapat subtour pada semua rute

Variabel keputusan hanya akan terdefinisi jika Jika maka kendala

tidak mengikat, sehingga dan

Sedangkan jika maka kendala tersebut menunjukkan bahwa sehingga batasan subtour elimination terpenuhi.

7. Variabel keputusan merupakan integer biner.

5.2 Hasil Penentuan Rute Kendaraan

Setelah model matematik diformulasikan dengan bentuk integer linear programming maka selanjutnya diproses dengan menggunakan software LINGO 8.0 dengan metode branch and bound (lihat Lampiran 3), sehingga dihasilkan rute kendaraan untuk percetakan Banda Aceh yang dapat meminimumkan total jarak tempuh kendaraan dalam mendistribusikan koran setiap harinya. Rute kendaraan tersebut memberikan informasi tentang perbandingan rute kendaraan yang ada sekarang dengan rute yang dihasilkan dari pemodelan yang dibuat. Pada Tabel 2 dan Tabel 3 diberikan solusi optimal yang diperoleh dari masalah penentuan rute yang dibuat.

(45)

Tabel 2 Rute solusi optimal untuk kendaraan pertama

No. Nama pelanggan Jumlah permintaan

(Eksemplar)

5 Joni Sukandar Seutui 1175

9 Makmu Beusaree Indrapuri 595

11 Saree Agency 250

Tabel 3 Rute solusi optimal untuk kendaraan kedua

(Eksemplar)

4 Azra Agency Krueng Raya 1892

3 Darussalam Post 1621

1 Trimora Agency Banda Aceh 3950

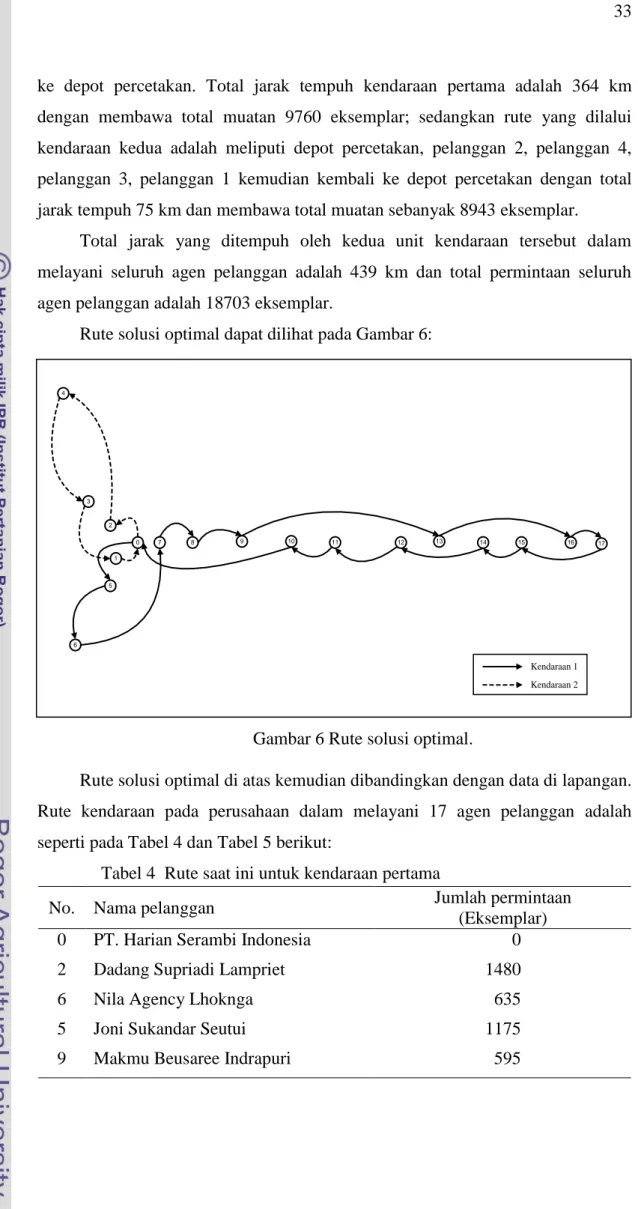
Berdasarkan kedua tabel di atas, dapat dijelaskan bahwa untuk melayani seluruh agen pelanggan sesuai dengan permintaannya masing-masing maka dibutuhkan dua unit kendaraan. Untuk kendaraan pertama, rute yang dilalui adalah berawal dari depot percetakan, pelanggan 5, pelanggan 6, pelanggan 7, pelanggan 8, pelanggan 9, pelanggan 13, pelanggan 16, pelanggan 17, pelanggan 15, pelanggan 14, pelanggan 12, pelanggan 11, pelanggan 10 kemudian kembali

(46)

ke depot percetakan. Total jarak tempuh kendaraan pertama adalah 364 km dengan membawa total muatan 9760 eksemplar; sedangkan rute yang dilalui kendaraan kedua adalah meliputi depot percetakan, pelanggan 2, pelanggan 4, pelanggan 3, pelanggan 1 kemudian kembali ke depot percetakan dengan total jarak tempuh 75 km dan membawa total muatan sebanyak 8943 eksemplar.

Total jarak yang ditempuh oleh kedua unit kendaraan tersebut dalam melayani seluruh agen pelanggan adalah 439 km dan total permintaan seluruh agen pelanggan adalah 18703 eksemplar.

Rute solusi optimal dapat dilihat pada Gambar 6:

4 11 10 14 15 16 17 9 12 13 8 7 0 5 1 2 3 6 Kendaraan 2 Kendaraan 1

Gambar 6 Rute solusi optimal.

Rute solusi optimal di atas kemudian dibandingkan dengan data di lapangan. Rute kendaraan pada perusahaan dalam melayani 17 agen pelanggan adalah seperti pada Tabel 4 dan Tabel 5 berikut:

Tabel 4 Rute saat ini untuk kendaraan pertama

(Eksemplar)

5 9

Joni Sukandar Seutui 1175

(47)

Tabel 4 Rute saat ini untuk kendaraan pertama (lanjutan)

(Eksemplar)

11 Saree Agency 250

Tabel 5 Rute saat ini untuk kendaraan kedua

(Eksemplar)

3 Darussalam Post 1621 4 Azra Agency Krueng Raya 1892 1 Trimora Agency Banda Aceh 3950

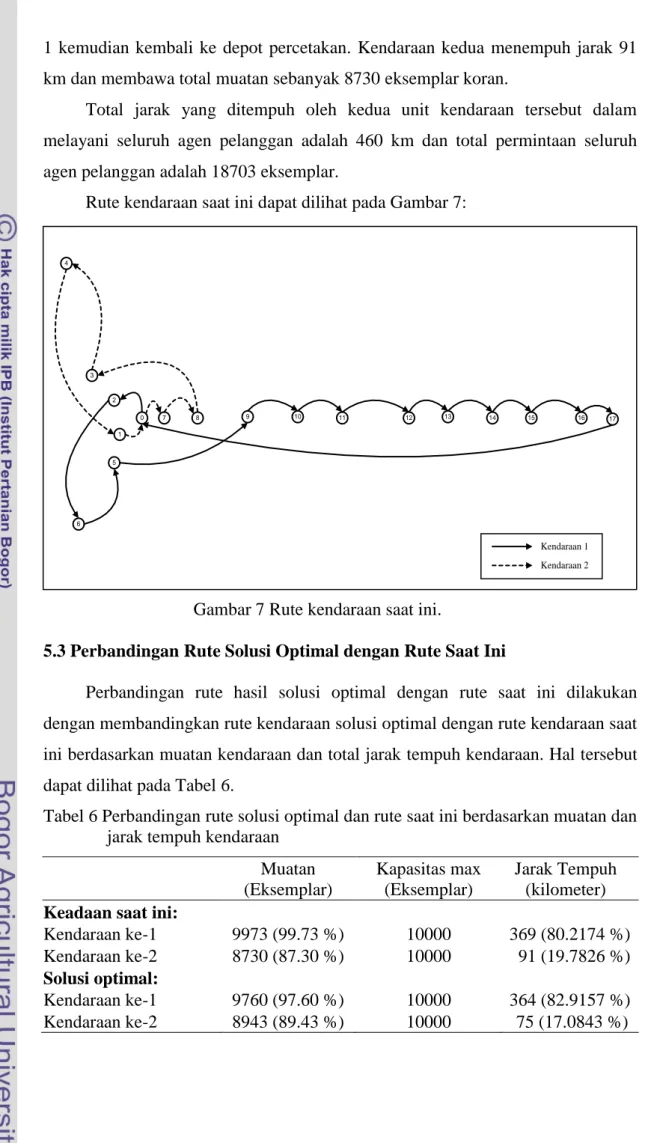
Tabel 4 dan Tabel 5 di atas memperlihatkan bahwa untuk melayani seluruh agen pelanggan sesuai dengan permintaannya masing-masing maka dibutuhkan dua unit kendaraan. Untuk kendaraan pertama, rute yang dilalui adalah berawal dari depot percetakan, pelanggan 2, pelanggan 6, pelanggan 5, pelanggan 9, pelanggan 10, pelanggan 11, pelanggan 12, pelanggan 13, pelanggan 14, pelanggan 15, pelanggan 16, pelanggan 17 lalu kembali ke depot percetakan dengan total jarak tempuh adalah 369 km dan membawa total muatan 9973 eksemplar koran, sedangkan rute yang dilalui kendaraan kedua adalah meliputi depot percetakan, pelanggan 7, pelanggan 8, pelanggan 3, pelanggan 4, pelanggan

(48)

1 kemudian kembali ke depot percetakan. Kendaraan kedua menempuh jarak 91 km dan membawa total muatan sebanyak 8730 eksemplar koran.

Total jarak yang ditempuh oleh kedua unit kendaraan tersebut dalam melayani seluruh agen pelanggan adalah 460 km dan total permintaan seluruh agen pelanggan adalah 18703 eksemplar.

Rute kendaraan saat ini dapat dilihat pada Gambar 7:

4 11 10 14 15 16 17 9 12 13 8 7 0 5 1 2 3 6 Kendaraan 2 Kendaraan 1

Gambar 7 Rute kendaraan saat ini.

5.3 Perbandingan Rute Solusi Optimal dengan Rute Saat Ini

Perbandingan rute hasil solusi optimal dengan rute saat ini dilakukan dengan membandingkan rute kendaraan solusi optimal dengan rute kendaraan saat ini berdasarkan muatan kendaraan dan total jarak tempuh kendaraan. Hal tersebut dapat dilihat pada Tabel 6.

Tabel 6 Perbandingan rute solusi optimal dan rute saat ini berdasarkan muatan dan jarak tempuh kendaraan

Muatan (Eksemplar) Kapasitas max (Eksemplar) Jarak Tempuh (kilometer)

Keadaan saat ini:

Kendaraan ke-1 9973 (99.73 %) 10000 369 (80.2174 %) Kendaraan ke-2 8730 (87.30 %) 10000 91 (19.7826 %)

Solusi optimal:

Kendaraan ke-1 9760 (97.60 %) 10000 364 (82.9157 %) Kendaraan ke-2 8943 (89.43 %) 10000 75 (17.0843 %)

(49)

Berdasarkan Tabel 6 dapat disimpulkan bahwa masing-masing rute kendaraan pada solusi optimal memiliki total jarak tempuh yang lebih pendek dibandingkan dengan total jarak tempuh rute kendaraan saat ini. Pada rute solusi optimal, total jarak tempuh untuk kedua kendaraan adalah 439 kilometer, sedangkan total jarak tempuh untuk kedua kendaraan saat ini adalah 460 kilometer, sehingga ada penghematan jarak tempuh 21 kilometer. Dengan kata lain, total jarak tempuh kendaraan pada solusi optimal adalah 95.4348 % dari total jarak tempuh kendaraan saat ini. Total muatan yang dibawa oleh kendaraan pertama pada solusi optimal lebih sedikit dari total muatan yang dibawa kendaraan pertama saat ini yaitu masing-masing 97.60 % dan 99.73 % dari total muatan kendaraan, sedangkan total muatan yang dibawa kendaraan kedua pada solusi optimal lebih banyak dari total muatan yang dibawa oleh kendaraan kedua saat ini yaitu masing-masing 89.43 % dan 87.30 % dari total muatan kendaraan.

Perbedaan antara rute kendaraan solusi optimal dengan rute kendaraan saat ini dapat dilihat pada Gambar 8.

4 11 10 14 15 16 17 9 12 13 8 7 0 5 1 2 3 6

Rute Optimal Kendaraan 2 Rute Optimal Kendaraan 1

Rute Saat ini Kendaraan 1 Rute Saat ini Kendaraan 2

Gambar 8 Rute solusi optimal dan rute saat ini.

Dari hasil perbandingan rute kendaraan solusi optimal dan rute kendaraan saat ini, perbedaan total jarak tempuh semua armada kendaraan dapat menjadi pertimbangan bagi PT Harian Serambi Indonesia untuk memilih rute kendaraan yang dipakai guna meminimalkan biaya distribusi koran.

(50)

VI SIMPULAN DAN SARAN

6.1 Simpulan

Berdasarkan hasil pembahasan yang didapatkan dalam penelitian ini, maka dapat dibuat beberapa simpulan:

1. Masalah distribusi barang dapat diformulasikan dalam model Capacitated Vehicle Routing Problem.

2. Pengembangan model penentuan rute kendaraan dalam mendistribusikan koran harian Serambi Indonesia menghasilkan total jarak tempuh yang lebih pendek daripada rute yang diterapkan saat ini. 3. Total jarak tempuh kendaraan dalam mendistribusikan koran dapat

menjadi pertimbangan bagi PT Harian Serambi Indonesia untuk memilih rute kendaraan yang dapat digunakan untuk efisiensi perusahaan.

6.2 Saran

1. Penelitian ini dapat dikembangkan untuk menyelesaikan masalah penentuan rute kendaraan dengan jumlah data yang lebih banyak.

2. Penelitian ini juga dapat dikembangkan untuk menyelesaikan masalah penentuan rute kendaraan dengan mempertimbangkan kendala waktu.