MA2082 BIOSTATISTIKA Orang Biologi Tidak Anti Statistika

Catatan Kuliah

MA2082 BIOSTATISTIKA

“Orang Biologi Tidak Anti Statistika”

disusun oleh

Khreshna I.A. Syuhada, MSc. PhD.

Kelompok Keilmuan STATISTIKA - FMIPA Institut Teknologi Bandung

Tentang MA2082 Biostatistika

A. Bentuk perkuliahan:

1. Tatap muka di kelas

2. Praktikum di Lab. Statistika dan Komputasi B. Jadwal kuliah:

1. Tatap muka di kelas:

• Senin; 11.45-13.00; R.9021 • Rabu; 9-10.15; R.9301

Catatan: Jadwal khusus untuk Minggu-1, Minggu-2 dan Ujian 2. Praktikum: dimulai Minggu-5

C. Silabus:

• Statistika deskriptif (1 minggu) • Peluang (1 minggu)

• Peubah acak dan distribusi (diskrit dan kontinu) (2 minggu) • Penaksiran (2 minggu)

• Uji hipotesis (1 sampel) untuk mean dan proporsi (2 minggu) • Uji hipotesis 2 sampel (1 minggu)

• Analisis variansi (1 minggu)

• Analisis data kategorikal (1 minggu) • Analisis regresi (1 minggu)

D. Buku teks:

Bernard Rosner, 2006, Fundamentals of Biostatistics, 6th ed. E. Penilaian: 1. Ujian 1,2,3 (80%) : 24 Agustus 2011 (20%), 12 Oktober 2011 (30%), 30 November 2011 (30%). 2. PR, Kuis (10%) 3. Praktikum (15%)

Matriks kegiatan perkuliahan

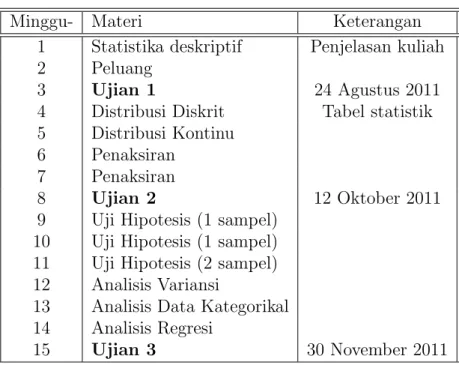
Table 1: Materi kuliah MA2082 Biostatistika. Minggu- Materi Keterangan

1 Statistika deskriptif Penjelasan kuliah 2 Peluang

3 Ujian 1 24 Agustus 2011

4 Distribusi Diskrit Tabel statistik 5 Distribusi Kontinu

6 Penaksiran 7 Penaksiran

8 Ujian 2 12 Oktober 2011

9 Uji Hipotesis (1 sampel) 10 Uji Hipotesis (1 sampel) 11 Uji Hipotesis (2 sampel) 12 Analisis Variansi

13 Analisis Data Kategorikal 14 Analisis Regresi

15 Ujian 3 30 November 2011

Daftar Isi

1 Statistika Deskriptif 1

1.1

Pendahuluan

. . . 1

1.2

Data, Jenis Data, Memahami Data

. . . 2

1.3

Ukuran Pusat/Lokasi dan Penyebaran

. . . 3

1.4

Mengamati Observasi Luar

. . . 5

1.5

Data Kelompok

. . . 6

1.6

Memahami Grafik

. . . 7

2 Peluang 1 2.1

Ilustrasi

. . . 1

2.2

Konsep Peluang

. . . 2

2.3

Peluang Bersyarat dan Teorema Bayes

. . . 3

3 Peubah Acak dan Distribusi 1 3.1

Ilustrasi

. . . 1

3.2

Peubah Acak Diskrit

. . . 2

3.3

Distribusi Diskrit

. . . 4

3.4

Peubah Acak dan Distribusi Kontinu

. . . 5

4 Penaksiran 1 4.1

Distribusi Normal

. . . 1

4.2

Penaksiran Titik dan Selang

. . . 4

4.3

Penaksiran untuk Distribusi Binomial

. . . 7

5 Uji Hipotesis 1 5.1

Konsep Uji Hipotesis

. . . 1

5.2

Uji Hipotesis Untuk Mean

. . . 3

5.3

Uji Hipotesis Untuk Proporsi

. . . 8

5.4

Selang Kepercayaan

. . . 10

6 Analisis Variansi 1 6.1

Konsep Anava (1 Arah)

. . . 1

6.2

Langkah-langkah UH

. . . 2

7 Analisis Data Kategorik 1 7.1

Ilustrasi

. . . 1 7.2

Uji Chi-Kuadrat

. . . 2 7.3

Uji Homogenitas

. . . 4 8 Analisis Regresi 1 8.1

Konsep “Relation”

. . . 1

8.2

Model Regresi Linier Sederhana

. . . 2

8.3

Penaksir Kuadrat Terkecil

. . . 3

8.4

Uji Hipotesis

. . . 4

8.5

Korelasi

. . . 5

BAB 1

Statistika Deskriptif

Silabus: Jenis data, ukuran pusat/lokasi, ukuran penyebaran, koefisien variasi, observasi luar, data kelompok, grafik

Tujuan:

1. Membedakan jenis data dan memahami data 2. Menghitung dan memaknai ukuran lokasi/pusat 3. Membedakan variansi dan koefisien variasi 4. Mengamati observasi luar

5. Memahami data kelompok 6. Membuat dan menafsirkan grafik

1.1

Pendahuluan

• Statistika dan Biostatistika: apa, untuk apa? • Statistik versus Statistika

• Manfaat BioStatistika

Statistika adalah ilmu yang digunakan untuk mengumpulkan, mengorganisasi, melakukan inferensi dan menafsirkan data. Secara singkat, statistika adalah ilmu/pekerjaan untuk meyimpulkan tentang suatu fenomena pada populasi menggunakan sampel.

1.2

Data, Jenis Data, Memahami Data

Data adalah hasil observasi tunggal (datum) yang didapat baik secara langsung (observasi/survey, praktikum) ataupun tidak langsung (buku, koran, internet) Jenis data:

• Nominal (jenis kelamin, golongan darah) • Ordinal (tingkat kecemasan, tingkat nyeri) • Rasio/interval (denyut nadi, tekanan darah)

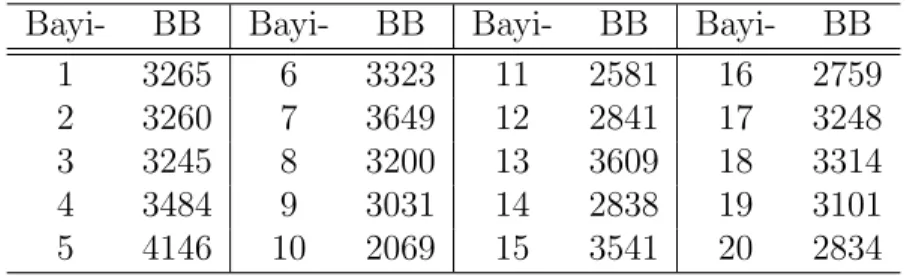
Contoh/ilustrasi dan interpretasi: 1. Berat badan bayi:

Table 1.1: Data sampel berat badan bayi (di AS) baru lahir. Bayi- BB Bayi- BB Bayi- BB Bayi- BB

1 3265 6 3323 11 2581 16 2759 2 3260 7 3649 12 2841 17 3248 3 3245 8 3200 13 3609 18 3314 4 3484 9 3031 14 2838 19 3101 5 4146 10 2069 15 3541 20 2834

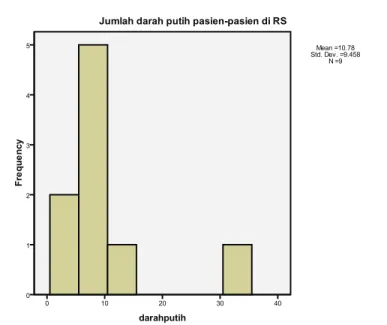
2. Jumlah darah putih (×1000) pasien-pasien di RS: 0 357889

1 02 2 3 5

3. Dapatkah anda mencari dan menafsirkan data berbentuk grafik? 4. Dapatkah anda mencari data yang bersifat kategorikal?

1.3

Ukuran Pusat/Lokasi dan Penyebaran

• Ukuran lokasi: Mean (aritmetik), Median, Modus • Ukuran Penyebaran: Jangkauan, Variansi, Kuartil • Variansi versus Koefisien Variasi

Misalkan data sampel adalah

x1, x2, . . . , xn,

dimana xi menyatakan titik sampel ke-i. Sampel diatas diperoleh dari

popu-lasi dan kita ingin melakukan inferensi untuk popupopu-lasi dengan memanfaatkan sampel. Langkah pertama adalah meringkas data untuk kemudian menghi-tung MEAN, MEDIAN dan MODUS (selanjutnya disebut ukuran lokasi atau pusat).

Mean (aritmetik) didefinisikan sebagai ¯ x = ∑n i=1 xi n Sifat-sifat mean

(a) Untuk suatu konstanta k,

n

∑

i=1

k xi =· · ·

(b) Jika yi = xi+ k maka ¯y = ¯x + k. Buktikan!

(c) Jika yi = k xi maka ¯y =· · · .

Median atau median sampel seringkali dikatakan sebagai nilai tengah. Den-gan demikian, menghitung median haruslah dilakukan pada data yang sudah diurutkan. Definisi median adalah

(a) Observasi ke-((n + 1)/2), (n ganjil), atau

Diskusi: Bagaimana (perbandingan) nilai mean dan median untuk data yang (i) simetrik, (ii) menceng ke kanan, (iii) menceng ke kiri?

Modus atau Mode adalah ukuran pusat yang menyatakan nilai observasi yang paling sering muncul. Menentukan modus dapat dilakukan pada data tanpa diurutkan (meskipun lebih mudah apabila diurutkan lebih dahulu).

LATIHAN:

Tentukan ukuran lokasi/pusat dari contoh data diatas.

Ukuran penyebaran menyatakan seberapa jauh data menyebar dari mean. Mis-alkan kita memiliki dua data sampel. Kedua sampel memiliki mean yang sama, namun memiliki penyebaran data yang berbeda. Beberapa ukuran penyebaran antara lain:

1. Jangkaun (Range):

R = xmaks− xmin

2. Variansi atau variansi sampel:

s2 =

∑n

i=1(xi− ¯x)2

n− 1

Catatan:

Deviasi standar atau simpangan baku adalah akar kuadrat dari variansi. 3. Kuantil atau persentil:

Sifat-sifat variansi:

Diketahui data sampel x1, . . . , xn memiliki variansi s2x. Jika data sampel

(a) yi = xi+ k,

(b) yi = k xi,

untuk suatu konstanta k, maka

s2_y = . . . LATIHAN:

Tentukan ukuran penyebaran dari contoh data diatas.

Variansi versus Koefisien Variasi

Kita dapat menghitung suatu ukuran yang mengaitkan ukuran penyebaran (deviasi standar) dengan ukuran lokasi (mean), yaitu koefisien variasi

(coeffi-cient of variation - CV):

CV = 100%× (s/¯x)

yang tidak dipengaruhi unit ukuran yang dipakai. CV bermanfaat untuk mem-bandingkan variabilitas beberapa sampel yang berbeda relatif terhadap nilai mean-nya. Dapat pula kita membanding CV dari beberapa variabel.

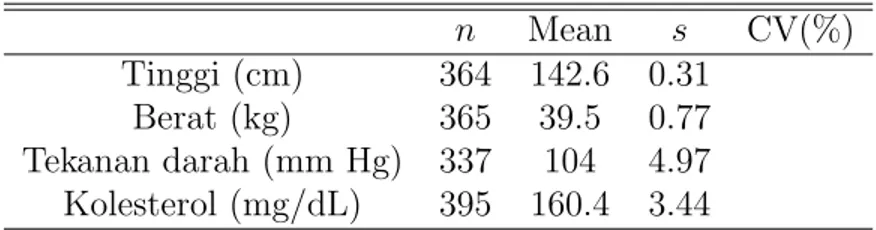
LATIHAN:

Table 1.2: Faktor risiko kardiovaskular pada anak.

n Mean s CV(%) Tinggi (cm) 364 142.6 0.31

Berat (kg) 365 39.5 0.77 Tekanan darah (mm Hg) 337 104 4.97 Kolesterol (mg/dL) 395 160.4 3.44

1.4

Mengamati Observasi Luar

Observasi luar atau outlier adalah nilai/observasi yang “menyimpang” dari nilai-nilai/observasi yang lain. Observasi luar dapat ditentukan/dihitung den-gan melihat apakah ada nilai/observasi yang LEBIH BESAR dari

K3+ 1.5 (K3− K1)

atau LEBIH KECIL dari

K1− 1.5 (K3− K1).

Dalam praktiknya, observasi luar dapat menyatakan sesuatu yang baik/jelek. Misalnya, seseorang dengan tingkat kecerdasan (IQ) yang sangat tinggi (jauh diatas rata-rata alias observasi luar) adalah baik. Seringkali observasi luar diabaikan dalam analisis data meskipun sesungguhnya cara ini tidaklah tepat. Mendeteksi observasi luar adalah sesuatu yang sangat menantang dalam statis-tika.

LATIHAN:

Adakah observasi luar pada contoh data diatas?

1.5

Data Kelompok

Pandang data sampel dengan 275 observasi. Ukuran sampel tersebut terlalu besar sehingga menampilkan data apa adanya menjadi tidak efisien. Dengan demikian, data sampel dapat dikelompokkan. Pengelompokan ini dapat pula terjadi (harus dilakukan) karena tingkat keakuratan data yang diambil tidak dapat diperoleh dengan baik.

Pengelompokan data memberikan masalah: Berapa banyak kelompok atau interval kelas (class intervals) yang ingin kita buat? Berapa lebar interval (interval width)? Salah satu formula yang bisa kita pakai adalah Formula Sturges, dimana banyaknya interval kelas adalah

k = 1 + (3.322× log₁₀n),

dimana n adalah besar sampel. Lebar intervalnya:

w = R/k,

dengan R adalah jangkauan.

Untuk contoh data sampel dengan 275 observasi, kita peroleh:

k ≈ 8, w = (63 − 18)/8 = 5.625

Dengan demikian, lebar kelas interval adalah 5 atau 10. Diketahui obervasi terkecil dan terbesar, berturut-turut, adalah 18 dan 63. Jadi, kelas interval yang bisa dibuat adalah:

10-19 20-29 30-39 40-49 50-59 60-69

1.6

Memahami Grafik

Beberapa tampilan visual (baca: grafik) untuk data adalah diagram bar/batang (bar chart), diagram batang dan daun (stem-and-leaf plot), histogram, box-plot. Contoh, kita pandang data jumlah darah putih pasien-pasien di RS:

Figure 1.1: Box-plot - Jumlah darah putih pasien.

BAB 2

Peluang

Silabus: Ruang sampel dan kejadian, konsep peluang, peluang bersyarat, Teo-rema Bayes.

Tujuan:

1. Mendefinisikan ruang sampel dan kejadian 2. Menghitung peluang suatu kejadian

3. Menghitung peluang bersyarat suatu kejadian

4. Memanfaatkan Teorema Bayes untuk menghitung peluang suatu keja-dian

2.1

Ilustrasi

Ilustrasi-1. Tanti baru saja mengikuti tes mata. Ia masih teringat beberapa huruf yang muncul: A-E-M-R-S. Kini, Tanti mencoba menyusun kata-kata yang mungkin dari huruf-huruf tersebut.

Ilustrasi-2. Hanin bermaksud menyumbangkan darahnya di suatu tempat donor. Hanin terlebih dahulu harus dicek golongan darahnya.

• Golongan darah yang mungkin untuk Hanin adalah...

• Rupanya Hanin tidak sendirian. Ada Hana dan Hanan disana yang

memiliki maksud yang sama dengan Hanin. Jika seorang diantara mereka dipilih secara acak menjadi pendonor, berapa peluang orang yang ter-pilih adalah Hana?

• Jika, diantara mereka bertiga, Hanan terpilih menjadi pendonor, berapa

peluang golongan darah Hanan adalah B?

Ilustrasi-3. Untuk keperluan praktikum di Lab, B dan G haruslah menda-patkan hewan (burung) percobaan. B dan G memutuskan untuk mendap-atkan itu dengan cara menembak. Pada waktu yang disepakati, B dan G secara bersamaan menembak sasaran tertentu. Peluang tembakan B menge-nai sasaran adalah 0.7 sedangkan peluang tembakan G (bebas dari tembakan B) mengenai sasaran adalah 0.4.

• Berapa peluang sebuah tembakan mengenai sasaran? • Berapa peluang sasaran tertembak?

Ilustrasi-4. “Ayahku meninggal waktu usiaku tiga tahun. Lalu Ibu kawin lagi. Dengan ayah tiriku, Ibu mendapat dua orang anak tiri dan melahirkan tiga orang anak. Ketika usiaku lima belas tahun, Ibu pun meninggal. Ayah tiriku kawin lagi dengan seorang janda yang sudah beranak dua. Ia melahirkan dua orang anak pula dengan ayah tiriku”

2.2

Konsep Peluang

Definisi:

Ruang sampel, S, adalah himpunan semua hasil mungkin dari suatu per-cobaan. Kejadian, E, adalah himpunan bagian dari ruang sampel. Peluang suatu kejadian, P (E), adalah rasio dari banyaknya titik kejadian dan ruang sampel, atau

P (E) = n(E)

n(S),

dimana n(E) dan n(S), berturut-turut, adalah banyaknya titik kejadian dan ruang sampel.

Sifat-sifat peluang:

1. 0≤ P (E) ≤ 1

2. P ({}) = 0 3. P (S) = 1

4. Untuk kejadian A dan B,

P (A∪ B) = P (A) + P (B) − P (A ∩ B)

5. Jika kejadian A dan B saling asing maka P (A∩ B) = 0 6. Kejadian A dan kejadian B dikatakan saling bebas jika

P (A∩ B) = P (A) P (B)

LATIHAN:

Kerjakan ilustrasi-ilustrasi diatas. SOLUSI:

1. Ilustrasi-1:

SERAM, M ERAS, SEM AR, RAM ES, ....

2. Ilustrasi-3:

Misalkan B kejadian B menembak sasaran Misalkan G kejadian G menembak sasaran

Misalkan T kejadian sebuah tembakan mengenai sasaran Misalkan S kejadian sasaran tertembak

P (T ) = P (G∩ Bc) + P (B∩ Gc)

= (0.4)(0.3) + (0.7)(0.6)

P (S) = 1− P (Gc∩ Bc)

= 1− (0.6)(0.3)

2.3

Peluang Bersyarat dan Teorema Bayes

Ilustrasi-1. Pandang Ilustrasi-3 diatas.

• Jika sebuah tembakan mengenai sasaran, berapa peluang bahwa itu

tem-bakan G?

• Berapa peluang bahwa, jika sasaran tertembak, kedua tembakan

menge-nai sasaran?

• Berapa peluang bahwa, jika sasaran tertembak, tembakan G mengenai

sasaran?

Ilustrasi-2. Seorang praktikan, Ega, tahu bahwa sebuah lembar kerja prak-tikum akan berada di salah satu dari tiga buah kotak surat lab yang ada. Misalkan pi adalah peluang bahwa Ega akan menemukan lembar kerja

prak-tikum setelah mengecek kotak surat lab i dengan cepat jika ternyata surat tersebut berada di kotak surat lab i, i = 1, 2, 3.

• Misalkan Ega mengecek kotak surat 1 tidak menemukan surat. Berapa

peluang hal itu akan terjadi?

• Jika diketahui Ega mengecek kotak surat 1 tidak menemukan surat,

be-rapa peluang bahwa surat itu ada di kotak surat 1?

Definisi:

Peluang kejadian A, apabila kejadian B telah terjadi, adalah peluang bersyarat

P (A|B) yaitu:

P (A|B) = P (A∩ B

P (B) ,

asalkan P (B) > 0. Jelas bahwa jika kejadian A dan B saling bebas maka

P (A|B) = P (A).

Peluang total:

P (B) = P (B|A)P (A) + P (B|Ac)P (Ac)

TEOREMA BAYES:

Misalkan {B1, B2, . . . , Bn} adalah partisi dari ruang sampel dan misalkan A

adalah kejadian yang terobservasi. Peluang kejadian Bj diberikan A adalah

P (Bj|A) =

P (A Bj)

P (A)

= ∑_nP (A|Bj) P (Bj)

LATIHAN:

1. Kerjakan ilustrasi-ilustrasi diatas

2. Tes darah di suatu laboratorium akan 95% efektif dalam mendeteksi suatu penyakit tertentu jika penyakit itu ada. Namun demikian, tes tersebut juga memberikan ’hasil positif yang salah’ pada 1% orang sehat yang dites. Jika 0.5% dari populasi mengidap penyakit tertentu tersebut, tentukan peluang bahwa seseorang menderita penyakit itu jika hasil tes positif?

SOLUSI:

1. Ilustrasi-1:

Misalkan B kejadian B menembak sasaran Misalkan G kejadian G menembak sasaran

Misalkan T kejadian sebuah tembakan mengenai sasaran Misalkan S kejadian sasaran tertembak

P (G|T ) = P (G∩ T ) P (T ) = P (G∩ B c₎ P (G∩ Bc_{) + P (B} ∩ Gc₎ = (0.4)(0.3) (0.4)(0.3) + (0.7)(0.6) P (G∩ B|S) = P (G∩ S) P (B ∩ S) P (S) = P (G)P (B) 1− P (Gc∩ Bc₎ = (0.4)(0.7) 1− (0.6)(0.3) P (G|S) = P (G∩ S) P (S) = P (G∩ S) 1− P (Gc∩ Bc₎ = 0.4 1− (0.6)(0.3)

2. Ilustrasi-2:

Misalkan Ki, i = 1, 2, 3 adalah kejadian lembar kerja praktikum berada

di kotak surat lab i. Misalkan T kejadian mengecek kotak surat lab 1 tidak mendapatkan lembar kerja praktikum. Peluang hal itu akan terjadi adalah

P (T ) = P (T|K1)P (K1) + P (T|K2)P (K2) + P (T|K3)P (K3)

= (1− p1)(1/3) + 1/3 + 1/3

Jika diketahui Ega mengecek kotak surat lab 1 dan tidak menemukan surat, maka peluang bahwa lembar kerja praktikum itu ada di kotak surat lab 1 adalah

P (K1|T ) =

P (T|K1)P (K1)

P (T|K1)P (K1) + P (T|K2)P (K2) + P (T|K3)P (K3)

= (1− p1)(1/3) (1− p1)(1/3) + 1/3 + 1/3

BAB 3

Peubah Acak dan Distribusi

Silabus: Konsep peubah acak, fungsi peluang (probability density function), fungsi distribusi (cumulative distribution function), mean dan variansi, dis-tribusi diskrit (binomial, Poisson, geometrik), disdis-tribusi kontinu (normal, ser-agam/uniform, eksponensial).

Tujuan:

1. Memahami definisi dan menentukan peubah acak (p.a)

2. Menghitung fungsi peluang (f.p) dan fungsi distribusi (f.d); f.p ke f.d; f.d ke f.p

3. Menghitung mean dan variansi

4. Mempelajari distribusi diskrit (binomial, Poisson) dan kontinu (normal, eksponensial)

5. Menghitung peluang suatu p.a dari distribusi diskrit atau kontinu

3.1

Ilustrasi

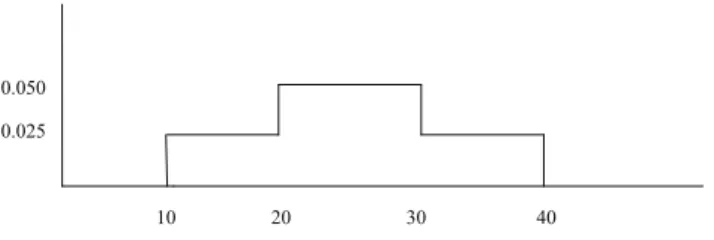
(Ilustrasi-1) Manajemen suatu klinik kesehatan mengetahui bahwa lima persen penelepon yang mendaftar untuk periksa dokter tidak akan datang ke klinik. Dengan alasan ini, manajemen tidak ragu untuk menerima pendaftaran se-banyak 52 orang, walaupun kapasitas klinik sebenarnya hanya untuk 50 orang. Berapa peluang setiap penelepon/pendaftar yang datang akan dilayani dokter? (Ilustrasi-2) Lama waktu (dalam menit) mahasiswa mengikuti praktikum di Lab adalah peubah acak dengan fungsi peluang tertentu. Tentukan peluang seorang mahasiswa mengikuti praktikum lebih dari 15 menit? antara 20 dan 35 menit?

0.050 0.025

10 20 30 40

Figure 3.1: Fungsi peluang lama waktu mahasiswa di Lab.

3.2

Peubah Acak Diskrit

Peubah Acak

• Peubah acak tidaklah “acak” dan bukanlah “peubah”

• Peubah acak adalah “fungsi” yang memetakan anggota S ke bilangan

real R P.A. Diskrit

Peubah acak X dikatakan diskrit jika terdapat barisan terhitung dari bilangan

{ai, i = 1, 2, . . .} sedemikian hingga P( ∪ i {X = ai} ) =∑ i P (X = ai) = 1 Catatan:

Sebuah peubah acak diskrit tidak selalu berasal ruang sampel diskrit.

FX disebut fungsi distribusi (diskrit) dari X jika terdapat barisan terhitung

{ai, i = 1, 2, . . .} dari bilangan real dan barisan {pi, i = 1, 2, . . .} dari bilangan

positif yang bersesuaian sedemikian hingga ∑ i pi = 1 dan FX(x) = ∑ pi

Jika diberikan himpunan terhitung {ai, i = 1, 2, . . .} dan bilangan positif

{pi, i = 1, 2, . . .} sdh

∑

i pi = 1, fungsi peluang pX(x) adalah

pX(x) = pi = P (X = ai),

dengan x = ai

Fungsi distribusi (kumulatif):

F (x) = P (X ≤ x)

Sifat-sifat:

(a) F fungsi tidak turun (b) limx→∞ F (x) = 1

(c) limx→−∞ F (x) = 0

(d) F fungsi kontinu kanan Catatan:

• P (a < X ≤ b) = F (b) − F (a) • P (X ≤ b) ̸= P (X < b) • P (X < b) = P( lim n→∞ { X ≤ b − 1 n }) = lim n→∞ P ( X ≤ b − 1 n ) = lim n→∞ F ( b− 1 n ) Contoh/Latihan:

1. Diketahui S = {00, 01, 10, 11}. Misalkan X peubah acak yang meny-atakan banyaknya “0”. Nilai yang mungkin dari X adalah..., dengan fungsi peluang dan fungsi distribusi...

2. Tentukan fungsi peluang dari fungsi distribusi berikut:

F (x) =          0, x <−3.1 3/5, −3.1 ≤ x < 0 7/10, 0≤ x < 1 1, 1≤ x

3. Diketahui fungsi peluang sebagai berikut: f (x) =                    p, x =−1.9 0.1, x =−0.1 0.3, x = 20p p, x = 3 4p, x = 4 0, yang lain Hitung P (−1.9 ≤ |X| ≤ 3), F (2), F (F (3.1))

3.3

Distribusi Diskrit

(Ilustrasi-1) Pasien di IGD adalah orang-orang yang dianggap dekat dengan kematian. Kesembuhan dari penyakit yang dideritanya bagi mereka adalah seperti mimpi. Untuk bisa bertahan hidup dari hari ke hari sudahlah meru-pakan mukjizat. Asumsikan bahwa setiap orang memiliki peluang yang sama untuk dapat bertahan hidup sampai hari esok sebesar α. Jika jumlah pasien IGD pada suatu hari adalah 5 orang, berapa peluang besok hanya akan ada 2 orang saja yang masih hidup?

(Ilustrasi-2) Banyaknya kecelakaan yang terjadi di tol setiap hari berdistribusi Poisson dengan parameter λ = 3. Berapa peluang tidak ada kecelakaan pada hari ini?

(Ilustrasi-3) Tiga mahasiswi dokter yang sedang melakukan residensi bertu-gas di kamar mayat. Untuk menentukan siapa yang akan masuk ke “ruan-gan idaman” tersebut pertama kali, mereka sepakat untuk mengundi den“ruan-gan melantunkan koin. Seseorang dengan hasil lantunan yang berbeda dengan yang lain akan menjadi orang pertama. Jika X menyatakan banyaknya lantu-nan koin yang harus dilakukan, tentukan P (X = 3).

Distribusi Binomial

Misalkan S ={sukses, gagal} adalah ruang sampel yang menotasikan ’sukses’ atau ’gagal’ dari suatu percobaan.

Definisikan X(sukses) = 1 dan X(gagal) = 0 dan

pX(1) = P (X = 1) = p

pX(0) = P (X = 0) = 1− p

dan jika X menyatakan banyaknya sukses yang diperoleh maka X dikatakan sebagai peubah acak Binomial dengan parameter (n, p), dimana

pX(k) = B(k; n, p) = Cknp

k_{(1− p)}n−k

Distribusi Poisson

Misalkan X peubah acak dengan fungsi peluang

pX(i) = e−λ

λi

i!

untuk i = 0, 1, 2, . . . dan λ > 0. X disebut peubah acak Poisson dengan pa-rameter λ.

Distribusi Geometrik

Misalkan percobaan-percobaan dilakukan hingga diperoleh sukses yang per-tama. Percobaan-percobaan tersebut saling bebas dan memiliki peluang suk-ses p. Misalkan X menyatakan banyaknya percobaan yang dilakukan untuk mendapatkan sukses pertama tersebut, maka X dikatakan peubah acak Ge-ometrik dengan parameter p. Fungsi peluangnya adalah

p(n) = P (X = n) = (1− p)n−1p,

untuk n = 1, 2, . . . dan p > 0.

3.4

Peubah Acak dan Distribusi Kontinu

(Ilustrasi) Riset bidang psikologi melibatkan pengukuran perilaku. Hasil-hasil pengukuran akan berbeda antara individu satu dengan yang lainnya. Namun demikian, sesungguhnya hasil-hasil tersebut dapat diprediksi sebagai kelom-pok individu. Salah satu pola umum pada hasil pengukuran (tentunya berupa angka) adalah bahwa kebanyakan pengukuran-pengukuran tersebut terkonsen-trasi di sekitar mean dari distribusi tersebut. Ada sedikit hasil pengukuran yang jauh dari mean. Apabila distribusi frekuensi digambarkan, akan tampak kurva berbentuk bel (bell-shaped curve) yang disebut DISTRIBUSI NOR-MAL.

P.A. Kontinu

Misalkan X peubah acak dan fungsi distribusinya FX dapat diturunkan. Fungsi

peluang fX adalah turunan dari fungsi distribusi,

fX(x) =

d

dxFX(x)

atau dengan kata lain

FX(x) =

∫ x −∞

fX(t) dt

Definisi: Jika X adalah peubah acak sedemikian hingga fungsi peluangnya ada (turunan dari fungsi distribusi) maka X dikatakan sebagai peubah acak kontinu. Catatan: 1 = FX(∞) = ∫ _∞ −∞ fX(t) dt P (a≤ X ≤ b) = FX(b)− FX(a) = ∫ b a fX(t) dt P (X = a) = ∫ a a fX(t) dt = 0 Distribusi Normal

Definisi: Peubah acak kontinu X adalah peubah acak Normal atau GAUSS dengan parameter µ dan σ2 _{jika fungsi peluang f}

X nya sbb: fX(x) = 1 √ 2 π σ exp(−(x − µ) 2 / 2 σ2), −∞ ≤ x ≤ ∞ Contoh/Latihan:

Ukuran ideal jumlah mahasiswa di kelas BioStat adalah 60 orang. Namun demikian, PS Biologi ITB mencatat bahwa biasanya hanya 30 persen maha-siswa saja dari total yang terdaftar yang benar-benar hadir dalam perkuliahan. Jika PS Biologi ITB memutuskan menerima 180 mahasiswa untuk kelas Bio-Stat, berapa peluang bahwa lebih dari 60 orang hadir di kelas?

Teorema Limit DeMoivre-Laplace

Jika Sn menyatakan ‘banyaknya sukses’ yang terjadi pada n percobaan

inde-penden, dengan peluang sukses adalah p, maka untuk setiap a < b,

P ( a≤ √Sn− np np(1− p) ≤ b ) → Φ(b) − Φ(a),

untuk n→ ∞. (pendekatan Normal untuk Binomial akan ‘baik’ jika np(1 − p) besar, np(1− p) ≥ 10)

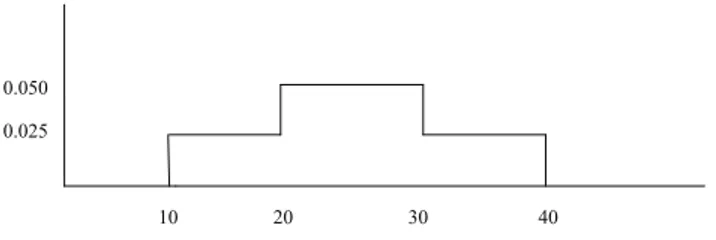
0.050 0.025

10 20 30 40

Figure 3.2: Fungsi peluang lama waktu mahasiswa di Lab.

Distribusi Uniform

Definisi: Peubah acak kontinu X dikatakan berdistrbusi seragam pada selang (a, b) jika fungsi peluang fX nya sbb:

fX(x) =

1

b− a, a≤ x ≤ b

Contoh/Latihan: Lama waktu (dalam menit) mahasiswa mengikuti praktikum di Lab adalah peubah acak dengan fungsi peluang tertentu. Tentukan peluang seorang mahasiswa mengikuti praktikum lebih dari 15 menit? antara 20 dan 35 menit?

Distribusi Gamma

Peubah acak Gamma: Misalkan percobaan Bernoulli diulang-ulang se-banyak n kali, maka se-banyaknya ‘sukses’ yang diperoleh adalah peubah acak berdistribusi Binomial dengan parameter n dan p, dimana p adalah peluang sukses. Jika kita memandang banyaknya percobaan Bernoulli yang dilakukan sampai diperoleh (dan termasuk) sukses ke-r, maka kita dapatkan peubah acak beristribusi Binomial negatif dengan parameter r dan p. Peubah acak Gamma adalah analogi dalam bentuk kontinu untuk peubah acak Binomial negatif. Dalam hal ini kita pandang peubah acak Binomial negatif ini sebagai waktu yang diberikan untuk sukses ke-r.

Definisi: Peubah acak kontinu X adalah peubah acak Gamma jika memiliki fungsi peluang f (x) = λ α Γ(α)x α−1_e−λx_{, x > 0}

dimana α dan λ adalah bilang real positif. Kita katakan X berdistribusi Gamma dengan parameter α dan λ; x∼ Gamma(α, λ).

Definisi Fungsi Gamma: Γ(t) = ∫ _∞ 0 xt−1e−xdx Catatan: Γ(t + 1) = t Γ(t), t > 0 Contoh/Latihan:

1. Tentukan fungsi peluang dari fungsi distribusi berikut:

F (x) =                0, x < 0 1 3 + x 5, 0≤ x < 1 3 5, 1≤ x < 2 9 10, 2≤ x < 3 1, x≥ 3

BAB 4

Penaksiran

Silabus: Distribusi normal, penaksiran parameter, penaksiran titik dan pe-naksiran selang, selang kepercayaan untuk mean dan proporsi.

Tujuan:

1. Mempelajari distribusi normal dan menghitung peluang suatu p.a berdis-tribusi normal standar

2. Memahami konsep penaksiran titik dan penaksiran selang 3. Menghitung selang kepercayaan untuk mean dan proporsi

4.1

Distribusi Normal

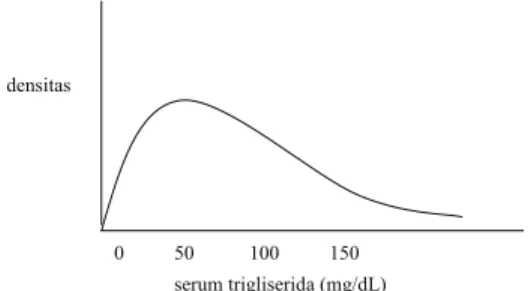
Perhatikan fungsi peluang dari X, p.a yang menyatakan kandungan serum trigliserida dalam tubuh. Distribusi peluangnya tidak simetri dan menceng ke kanan (skew to the right atau positively skewed) sbb (Gb 4.1):

densitas

0 50 100 150 serum trigliserida (mg/dL)

Figure 4.1: Fungsi peluang serum trigliserida 1

densitas 0 50 80 90 100 110 DBP 0.03 0.02 0.01 A B C

Figure 4.2: Fungsi peluang tekanan darah diatolik

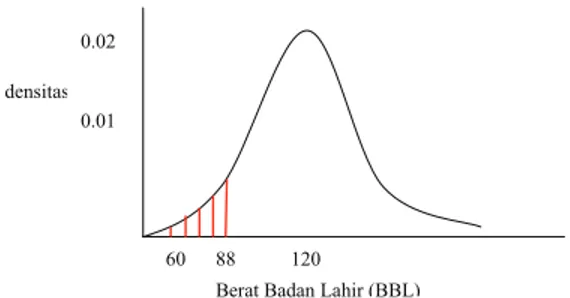
densitas

60 88 120 Berat Badan Lahir (BBL) 0.02

0.01

Figure 4.3: Fungsi peluang Berat Badan Lahir

Sedangkan fungsi peluang dari tekanan darah diatolik (DBP - diastolic blood

presure) pada laki-laki usia 35-44 tahun adalah seperti gambar berikut (Gb

4.2). Area A, B, C berturut-turut menyatakan peluang terjadinya hipertensi ringan, sedang dan berat. Umumnya DBP terjadi disekitar 80 mm Hg, dimana kemudian kemungkinannya berkurang seiring dengan berubahnya nilai DBP yang jauh dari 80.

Fungsi peluang dari peubah acak yang menyatakan Berat Badan Lahir berikut fungsi distribusinya saat BB-nya 88 atau P (X ≤ 88) (Gb 4.3). Area tersebut memiliki arti khusus dalam kebidanan atau obstetrics dimana 88 adalah nilai batas atau cutoff point yang digunakan untuk mengidentifikasi bayi BBLR.

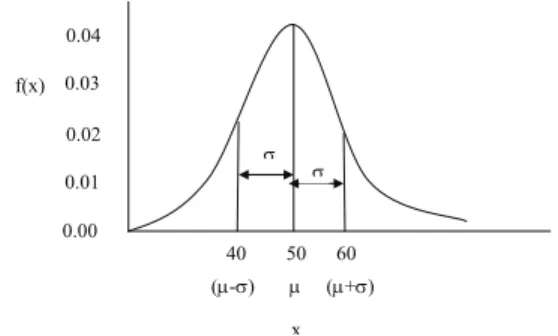
f(x) 40 50 60 ( - ) ( + ) x 0.04 0.03 0.02 0.01 0.00

Figure 4.4: Fungsi peluang dari distribusi normal

Definisi Distribusi Normal

Misalkan X peubah acak berdistribusi normal dengan parameter µ dan σ2_.

Fungsi peluangnya adalah

fX(x) = 1 √ 2 π σ exp ( − 1 2 σ2(x− µ) 2 ) , −∞ < x < ∞,

Notasi: X ∼ N(µ, σ2_{), dengan mean µ = E(X) dan variansi σ}2 _{= V ar(X).}

Contoh: fungsi peluang untuk distribusi normal dengan mean 50 dan variansi 100 (Gb 4.4).

Distribusi N (0, 1) adalah kasus khusus dari distribusi N (µ, σ2_{) dengan mean}

0 dan variansi 1. Distribusi ini disebut juga distribusi normal standar/baku (Gb 4.5). Sifatnya adalah simetrik disekitar 0. Sifat empirik yang penting dari distribusi normal baku adalah

P (−1 < X < 1) = 0.6827,

P (−1.96 < X < 1.96) = 0.95,

P (−2.576 < X < 2.576) = 0.99.

f(x) -2.58 -1.96 -1 0 1 1.96 2.58 ( ) x 0.04 0.03 0.02 0.01 0.00 68% area 95% area 99% area

Figure 4.5: Fungsi peluang dari distribusi normal standar Contoh/Latihan:

1. Diketahui Z ∼ N(0, 1). Tentukan nilai c dari persamaan peluang berikut: (a) P (Z > c) = 0

(b) P (|Z| ≤ c) = 0.25 (c) P (−c < Z < 2 c) = 0.68 (d) P (c ≤ Z < 0) = 0.324

2. Misalkan diameter pohon dari suatu spesies tertentu adalah peubah acak berdistribusi normal dengan mean 8 (inchi) dab deviasi standar 2 (inchi). Hitung peluang bahwa sebuah pohon memiliki diameter yang tak wajar yaitu lebih dari 12.

4.2

Penaksiran Titik dan Selang

Misalkan suatu populasi memiliki mean µ. Misalkan X1, X2, . . . , Xn

sam-pel acak dari populasi tersebut. Penaksir untuk µ (disebut penaksir samsam-pel) adalah ¯ X = 1 n n ∑ i=1 Xi, dengan sifat E( ¯X) = µ, V ar( ¯X) = σ2/n,

dimana deviasi standarnya adalah σ/√n yang disebut standard error of mean

variablitas mean sampel yang diperoleh dari sampel acak (berulang) berukuran

n dari populasi yang sama.

Teorema Limit Pusat

Misalkan X1, X2, . . . , Xn sampel acak dari populasi dengan mean µ dan

vari-ansi σ2_{. Maka, untuk n besar,}

¯

X ∼ N(µ, σ2/n),

meskipun distribusi populasinya tidak normal.

Contoh. Hitung peluang bahwa mean BBL dari sampel berukuran 10 akan berada diantara 98 dan 126 (diketahui data populasi: mean 112 dan deviasi standar 20.6). Solusi: P (98 < ¯X < 126) = Φ ( 126− 112 20.6/√10 ) − Φ ( 98− 112 20.6/√10 ) =· · ·

Perhatikan transformasi peubah acak:

Z = X¯ − µ

σ/√n,

dimana Z berdistribusi normal standar. Akibatnya, 95% nilai Z akan berada diantara -1.96 dan 1.96. Dengan kata lain, 95% mean sampel berada di selang

(

µ− 1.96 σ/√n , µ + 1.96 σ/√n

) Catatan:

Dalam praktiknya, nilai σ tidak diketahui dan harus ditaksir oleh deviasi stan-dar sampel s.

Distribusi t

Jika X1, X2, . . . , Xn sampel acak berdistribusi normal dengan mean µ dan

variansi σ2_{, maka}

¯

X− µ

S/√n ∼ tn−1,

berdistribusi t dengan derajat kebebasan (degrees of freedom) n− 1, dimana

P (td< td,u) = u.

Selang Kepercayaan untuk Mean

100%(1−α) selang kepercayaan (SK) atau confidence interval (CI) untuk mean dari distribusi normal dengan variansi tidak diketahui adalah

( ¯ x− t_{n−1,1−α/2}s/√n , ¯x + t_{n−1,1−α/2}s/√n ) atau dituliskan ¯ x± tn−1,1−α/2s/ √ n Contoh/Latihan

1. Tentukan persentil ke-5 (atas) atau persentil ke-95 dari distribusi t den-gan derajat kebebasan 23.

2. Hitung 95% selang kepercayaan untuk mean BBL berdasarkan sampel berukuran 10. Diketahui: ¯x = 116.9; s = 21.7.

Selang Kepercayaan untuk Mean - Sampel Besar

Nilai pendekatan 100%(1−α) selang kepercayaan (SK) atau confidence interval (CI) untuk mean dari distribusi normal (sampel besar) dengan variansi tidak diketahui adalah ( ¯ x− z1−α/2s/ √ n , ¯x + z1−α/2s/ √ n ) dengan ukuran sampel n > 200.

Catatan:

Panjang SK dipengaruhi oleh nilai n, s, dan α. Jika:

n membesar, maka panjang SK... s membesar, maka panjang SK... α mengecil, maka panjang SK...

Contoh/Latihan

1. Hitung 95% dan 99% selang kepercayaan untuk mean temperatur berdasarkan sampel berukuran 10 dan 100. Diketahui: ¯x = 97.2; s = 0.189.

4.3

Penaksiran untuk Distribusi Binomial

Misalkan Xi p.a Bernoulli dengan peluang “sukses” p. Kita dapat menghitung

E(Xi) = p, V ar(Xi) = p(1− p).

Untuk sejumlah n p.a Bernoulli, X = ∑n_i=1 Xi, kita dapatkan p.a Binomial

dengan E(X) =· · · dan V ar(X) = · · · .

Pandang X p.a Binomial dengan parameter n dan p. Penaksir untuk p adalah ˆ

p atau proporsi sampel, yaitu

ˆ p = 1 n n ∑ i=1 Xi = X/n, dengan E(ˆp) =· · · , V ar(ˆp) = · · ·

Untuk n besar, berdasarkan TLP, maka ˆp berdistribusi normal dengan mean

p dan variansi p(1− p)/n. Dengan demikian, 100%(1 − α) selang kepercayaan

untuk p adalah ( ˆ p− z1−α/2 √ ˆ p(1− ˆp)/n , ˆp + z1−α/2 √ ˆ p(1− ˆp)/n ) Contoh/Latihan:

1. Tentukan 95% SK untuk proporsi penderita kanker pada 10000 wanita berusia 50-54 tahun, dimana diketahui 400 diantaranya menderita kanker. 2. Lakukan perhitungan diatas untuk α = 0.01 dan sampel berukuran n =

1000.

BAB 5

Uji Hipotesis

Silabus: Konsep uji hipotesis, kesalahan tipe 1 dan 2, uji hipotesis untuk mean (1 dan 2 sampel), uji hipotesis untuk proporsi (1 dan 2 sampel), uji hipotesis 2 sampel berpasangan.

Tujuan:

1. Mempelajari konsep uji hipotesis

2. Memahami dan menghitung kesalahan tipe 1 dan 2 3. Melakukan uji hipotesis untuk mean

4. Melakukan uji hipotesis untuk proporsi

5. Membedakan uji hipotesis 2 sampel independen dan berpasangan

5.1

Konsep Uji Hipotesis

Uji hipotesis (UH) adalah bagian dari statistika inferensi. UH bertujuan un-tuk mengambil kesimpulan secara statistik (signifikan) dari hipotesis-hipotesis yang diberikan. Kesimpulan tersebut didasarkan pada tingkat signifikansi α (yang sesungguhnya adalah tingkat kesalahan tipe I).

Tahap-tahap dalam pelaksanaan UH adalah

1. Membuat (menyatakan) hipotesis nol, H0, dan hipotesis alternatif, Ha

atau H1,

3. Menentukan statistik uji (test statistic),

4. Menentukan daerah kritis (critical region) atau daerah penolakan/penerimaan, 5. Menghitung statistik uji dengan data sampel

6. Mengambil kesimpulan: “menolak atau gagal menolak H0”

Contoh:

1. Ini cerita tentang kematian karena kanker yang diduga dimulai dari radiasi nuklir. Diketahui terjadi 13 kematian pada pekerja di suatu proyek nuklir, dimana 5 kematian diantaranya disebabkan oleh kanker. Berdasarkan data statistik, pihak otoritas kesehatan mengklaim bahwa sekitar 20% kematian disebabkan oleh kanker. Benarkah klaim pihak otoritas kesehatan?

2. Misalkan X p.a menyatakan tinggi tubuh suatu jenis binatang air. Dike-tahui X berdistribusi normal dengan mean µ. Akan diuji

H0 : µ = 3 vs H1 : µ > 3

dengan menggunakan data sampel 6 binatang air terpilih acak dengan mean 3.763 dan deviasi standar 0.724. Apakah kesimpulan yang diambil dari uji hipotesis tersebut?

Kesalahan Tipe-1 dan Tipe-2

Kesalahan-kesalahan dalam UH dibagi atas:

- kesalahan tipe-1 atau α, yaitu kesalahan “menolak H0 yang benar, atau

P (menolak H0| H0benar)

- kesalahan tipe-2 atau β, yaitu kesalahan “menerima H0 yang salah, atau

P (menerima H0| H0salah)

Catatan:

• Tidak ada hubungan antara α dan β • 1 − β adalah kuasa atau power dari UH

Kaitan antara pengambilan kesimpulan dan kesalahan dapat dilihat dalam tabel berikut:

Table 5.1: Pengambilan kesimpulan dan tipe kesalahan.

H0 benar H0 salah

H0 gagal ditolak keputusan benar β

H0 ditolak α keputusan benar

Dua jenis uji hipotesis nol vs hipotesis alternatif: 1. Uji hipotesis 2-sisi atau two-sided:

H0 : µ = µ0 vs H1 : µ ̸= µ0

2. Uji hipotesis 1-sisi atau one-sided:

H0 : µ = µ0 vs H1 : µ > µ0

atau

H0 : µ = µ0 vs H1 : µ < µ0

5.2

Uji Hipotesis Untuk Mean

Uji hipotesis pada 1-sampel

Uji hipotesis untuk mean populasi dapat dilakukan pada kasus (i) pengam-bilan sampel berasal dari populasi yang berdistribusi normal dengan variansi diketahui atau tidak diketahui, (ii) pengambilan sampel berasal dari populasi yang tidak berdistribusi normal.

Seorang peneliti tertarik untuk menguji mean umur orang-orang dari suatu populasi: apakah mean umur orang-orang dari populasi tersebut berbeda dari 30 tahun? (apakah mean umur orang-orang tersebut 30 tahun?). Untuk itu, diambil sampel sebanyak 10 orang dan dihitung bahwa ¯x = 27. Asumsikan

data berasal dari distribusi normal dengan σ2 _{= 20. Tahapan UH-nya adalah}

1. Hipotesis:

2. Tingkat signifikansi: α = 0.05 3. Statistik uji:

Z = X¯ − µ0

σ/√n ∼ N(0, 1)

4. Daerah kritis:

Tolak H0 jika z ≥ 1.96 atau z ≤ −1.96

5. Perhitungan:

z = √27− 30

20/10 =−2.12 6. Kesimpulan:

Tolak H0, karena z ≤ −1.96. Dengan kata lain, mean umur suatu

pop-ulasi bukanlah 30 tahun atau berbeda dari 30 tahun.

Pengambilan kesimpulan dapat pula dilakukan dengan menghitung p-value, yaitu nilai α terkecil untuk menolak H0. Dengan kata lain “tolak H0 jika

p-value lebih kecil dari α”. Pada contoh diatas, nilai p-value adalah

p− value = P (Z ≤ z) + P (Z ≥ z) = 2 × P (Z ≤ −2.12) = 0.034.

Jadi, karena 0.034 < 0.05 maka H0 ditolak.

Contoh/Latihan:

Lakukan UH untuk soal diatas. Pertanyaan yang diajukan adalah “apakah mean umur populasi kurang dari 30 tahun?”. Gunakan tingkat signifikansi

α = 0.01. Bagaimana jika n = 20 dan ¯x = 27?

Bagaimana jika σ tidak diketahui?

Gunakan statistik uji:

T = x¯− µ0

s/√n ∼ tn−1.

Contoh: Castillo dan Lilioja meneliti suatu teknik untuk mengukur indeks massa tubuh atau BMI. Mereka ingin menguji apakah mean BMI suatu pop-ulasi bukanlah 35. Dilakukan perhitungan pada 14 orang dewasa (laki-laki) dan diperoleh ¯x = 30.5 dan s = 10.64. Tahapan UH-nya adalah

1. Hipotesis:

H0 : µ = 35, Ha: µ ̸= 35

2. Tingkat signifikansi: α = 0.05 3. Statistik uji:

T = X¯ − µ0

s/√n ∼ tn−1

4. Daerah kritis:

Tolak H0 jika t≥ 2.16 atau t ≤ −2.16

5. Perhitungan:

t = 30.5− 35

10.64/√14 =−1.58 6. Kesimpulan:

H0 gagal ditolak (dengan kata lain, diterima), karena −2.16 ≤ t ≤ 2.16

atau bukan dalam daerah penolakan. Tidak ada alasan untuk men-dukung klaim bahwa mean BMI bukanlah 35.

Contoh/Latihan: Lakukan pengambilan kesimpulan pada masalah BMI den-gan menggunakan p-value. Bagaimana menurut anda? Manakah yang lebih mudah dilakukan? (dibandingkan dengan menentukan z atau t pada tabel)

Bagaimana UH dilakukan pada mean populasi yang tidak berdis-tribusi normal?

Ambil sampel cukup besar! Contoh: PR.

Uji hipotesis pada 2-sampel

Uji hipotesis untuk mean populasi dapat dilakukan dengan maksud untuk menguji adanya perbedaan antara mean 2 populasi.

Seorang ahli pertanian meyakini bahwa butir jagung yang lebih besar dapat diperoleh jika menggunakan Zat B, daripada Zat A, dalam memberantas tikus perusak. Untuk itu, sang ahli memberikan Zat A dan B pada 80 bagian la-han pertanian (masing-masing Zat diberikan ke 40 bagian lala-han). Hasil yang diperoleh adalah:

Zat A:

109,98,103,97,101,102,91,106, 101,98,88,105,100,95,98,98, 97,94,108,102,105,100,113,101

89,99,102,104, 110,95,91,99, 100,104,106,101,96,109,95,96 Zat B: 105,113,106,110,104,122,102,107, 109,111,117,111,102,117,109,107, 110,111,99,103,111,101,103,111, 118,99,107,110,114,109,109,128, 109,112,119,108,114,109,106,109.

Benarkah klaim ahli pertanian tersebut? Tahapan UH-nya adalah

1. Hipotesis: H0 : µ1 = µ2, Ha: µ1 < µ2 atau H0 : µD = 0, Ha : µD < 0, dimana µD = µ1− µ2. 2. Tingkat signifikansi: α = 0.05 3. Statistik uji: T = ( ¯X1 − ¯X2)− 0 sp √ 1/n1+ 1/n2 ∼ tn1+n2−2,

jika diasumsikan σ1 = σ2, dimana

s2_p = (n1− 1)s 2 1+ (n2− 1)s22 n1+ n2− 2 , atau T = √( ¯X1− ¯X2)− 0 s2 1/n1+ s22/n2 , jika diasumsikan σ1 ̸= σ2 4. Daerah kritis:

Tolak H0 jika t < t78,0.05=−1.662, atau

Tolak H0 jika t < t78,0.05=−1.662

5. Perhitungan:

n1 = 40, ¯x1 = 100.15, s1 = 5.73

n2 = 40, ¯x2 = 109.53, s2 = 6.06

t =−7.11

6. Kesimpulan:

Tolak H0, karena t = −7.11 < −1.662. Dengan kata lain, data

men-dukung klaim ahli pertanian tersebut.

Catatan:

• Uji mean untuk 2 sampel mengasumsikan bahwa data berasal dari

dis-tribusi normal

• Uji mean 2 sampel dengan asumsi σ1 = σ2 akan valid jika ukuran

sam-pelnya besar

Uji hipotesis pada 2-sampel Berpasangan

Uji hipotesis untuk mean diatas dilakukan pada 2 mean yang saling bebas atau independen. Uji untuk mean dapat pula dilakukan pada 2 sampel yang berpasangan.

Sebuah studi dimaksudkan untuk melihat apakah merokok dapat menurunkan kadar “platelet” dalam darah. Sebelas sampel darah diambil dari 11 orang SE-BELUM dan SESUDAH orang-orang tersebut merokok. Data yang diperoleh dalah prosentase maksimum platelet:

Apakah data sampel mendukung tujuan studi tersebut? Tahapan UH-nya adalah

1. Hipotesis: H0 : µD = µ1− µ2 = 0, Ha : µD > 0 2. Tingkat signifikansi: α = 0.05 3. Statistik uji: T = ¯ D− µD0 s /√n ∼ tn−1

Table 5.2: Kadar platelet sebelum dan sesudah merokok. Sebelum Sesudah D=Beda=Seb-Ses

27 25 2 29 25 4 37 27 10 56 44 12 46 30 16 82 67 15 80 53 27 57 53 4 61 52 9 59 60 -1 43 28 15 4. Daerah kritis:

Tolak H0 jika t > t10,0.95= 1.812, atau

5. Perhitungan:

nD = 11, ¯D = 10.27, sD = 7.98,

t = 4.27

6. Kesimpulan:

Tolak H0, karena t > 1.812. Dengan kata lain, kadar platelet dalam

darah menurun akibat merokok.

5.3

Uji Hipotesis Untuk Proporsi

Pandang 2 proporsi populasi, p1 dan p2. Kita ingin membandingkan, misalnya,

apakah proporsi p1 yang menyatakan proporsi wanita yang bekerja di bidang

ilmu hayati BERBEDA dengan proporsi p2 yaitu proporsi wanita yang bekerja

di bidang teknik. Misalkan

• X1 banyaknya “sukses” dari sampel berukuran n1 dari populasi 1

• X2 banyaknya “sukses” dari sampel berukuran n2 dari populasi 2

• X1 ∼ B(n1, p1) dan X2 ∼ B(n2, p2)

• Penaksir proporsinya adalah

ˆ

p1 = X1/n1, ˆp2 = X2/n2

Bagaimana kita melakukan uji hipotesis untuk persoalan diatas? Tahapan UH-nya adalah

1. Hipotesis: H0 : δ = p1 − p2 = 0, Ha : δ̸= 0 2. Tingkat signifikansi: α = 0.05 3. Statistik uji: Z = ˆ δ− 0 s.e(ˆδ) ∼ N(0, 1), dimana ˆ δ = ˆp1− ˆp2, dan s.e(ˆδ) = √ ˆ p1(1− ˆp1) n1 +pˆ2(1− ˆp2) n2 ,

jika diasumsikan bahwa p1 ̸= p2, ATAU

s.e(ˆδ) = √ ˆ p(1− ˆp) n1 +p(1ˆ − ˆp) n2 ,

jika diasumsikan bahwa p1 = p2, yaitu

ˆ

p = X1+ X2

n1+ n2

4. Daerah kritis:

Tolak H0 jika z ≤ zα/2, atau z ≥ z1−α/2

5. Perhitungan 6. Kesimpulan

Contoh/Latihan. Dalam sebuah studi, akan diuji keefektifan suatu perlakuan terhadap “aphid infestation”. Sampel tumbuhan yang diambil acak berukuran 100 diambil dan diberikan perlakuan tersebut. Sampel lain berukuran 100 tidak diberi perlakuan. Ditemukan bahwa 35 tumbuhan yang diberi perlakuan dan 85 tumbuhan yang tidak diberi perlakuan “infested with aphids”. Apakah data mendukung klaim bahwa perlakuan efektif? Gunakan α = 0.001.

Solusi: 1. Hipotesis: H0 : δ = p1 − p2 = 0, Ha : δ < 0 2. Tingkat signifikansi: α = 0.001 3. Statistik uji: Z = ˆ δ− 0 s.e(ˆδ) ∼ N(0, 1), dimana ˆ δ = ˆp1− ˆp2, dan s.e(ˆδ) = √ ˆ p1(1− ˆp1) n1 +pˆ2(1− ˆp2) n2 , 4. Daerah kritis: Tolak H0 jika z ≤ zα =−3.09 5. Perhitungan: ˆ p1 = 35/100, ˆp2 = 80/100, ˆδ =−0.45, s.e(ˆδ) = 0.06225, z =−7.23 6. Kesimpulan:

Tolak H0karena z =−7.23 < −3.09. Dengan kata lain, data mendukung

klaim bahwa perlakuan efektif untuk mengendalikan “aphids”.

5.4

Selang Kepercayaan

PELAJARI selang kepercayaan dalam kaitannya dengan Uji Hipotesis!

BAB 6

Analisis Variansi

Silabus: Konsep uji hipotesis untuk mean lebih dari 2 sampel, asumsi dalam analisis variansi, distribusi F.

Tujuan:

1. Memahami dan menggunakan uji mean lebih dari 2 sampel 2. Mempelajari asumsi dalam analisis variansi

3. Menggunakan distribusi F

6.1

Konsep Anava (1 Arah)

Uji hipotesis (UH) untuk mean pada 2 sampel/grup dapat dilanjutkan (ex-tended) ke lebih dari 2 sampel, sebut k sampel dengan ukuran sampel ni, i =

1, 2, . . . , k. Teknik atau metode untuk melakukan UH tersebut adalah “ANAL-ISIS VARIANSI” (1 arah). Perhatikan bahwa ukuran sampel tidak harus sama.

Catatan:

Jika k = 2 maka dapat kita lakukan uji t dua sisi dan menggunakan deviasi standar “pooled”

Asumsi yang digunakan adalah:

• Data saling bebas (independen) • Data berasal dari distribusi normal

6.2

Langkah-langkah UH

Langkah-langkah dalam analisis variansi: 1. Hipotesis: H0 : µ1 = µ2 =· · · = µk H1 : 2. Tingkat signifikansi: α 3. Statistik uji: F = BSS/(k− 1) W SS/(n− k) ∼ Fk−1,n−k, dimana BSS =∑ ni(¯yi − ¯y)2, T SS =∑(yi− ¯y)2, W SS = T SS− BSS 4. Daerah kritis:

Tolak H0 jika Fhit ≥ Fk−1,n−k(1− α)

atau

Tolak H0 jika Fhit ≥ Fk−1,n−k(α)

5. Perhitungan. 6. Kesimpulan.

6.3

Contoh

Sebuah percobaan dilakukan untuk membandingkan 3 perlakuan Diet. Vari-abel responnya adalah “weight gain” pada suatu periode. Hasil percobaannya adalah sbb:

• Diet 1: 8,16,9

• Diet 2: 9,16,21,18,11

• Diet 3: 15,10,17,6

Ujilah pada tingkat α = 0.05 bahwa “expected weight gain” untuk 3 perlakuan tersebut tidak sama.

Solusi: 1. Hipotesis: H0 : µ1 = µ2 = µ3, H1 : H0salah 2. α = 0.05 3. Statistik uji: Fhit ∼ F2,9,0.95 atau Fhit ∼ F2,9,0.05 4. Daerah kritis:

Tolak H0 jika Fhit ≥ 4.26

5. Perhitungan: ¯

y = 13, BSS = 36, W SS = 210 Fhit = 0.7714

6. Kesimpulan:

Contoh/Latihan:

1. Data berikut menyatakan waktu kesembuhan (jam) yang diakibatkan tiga merek obat sakit kepala yang berlainan yang diberikan pada 25 penderita demam.

Obat A: 5,4,8,6,3,3,5,2 Obat B: 9,7,8,6,9,3,7,4,1 Obat C: 7,6,9,4,7,2,3,4

Apakah data mendukung klaim bahwa obat A lebih efektif menyem-buhkan sakit kepala dibandingkan obat B? Gunakan α = 0.10.

2. Seorang mahasiswa melakukan studi tentang ketertarikan orang terhadap perkuliahan ’Pengantar Lingkungan’, ’Mikrobiologi’ atau ’Bistatistika’ dan memberikan penilaian seberapa tertarik terhadap perkuliahan tsb (skala 1-10). Didapat data sbb:

Peng. Lingk. MikroBio BioStat

7 9 3

6 10 5

8 6 2

4 7 7

6 7 3

Apakah ada perbedaan rata-rata penilaian ketiga perkuliahan tsb (Gu-nakan α = 0.05)? Jawablah dengan uji hipotesis dan lengkapi tabel ANOVA berikut: Sumber variasi JK d.k RK F Perlakuan Galat Total 14 Catatan: F0.01(2, 12) = 6.93, F0.01(12, 2) = 99.42, F0.05(2, 12) = 3.89, F0.05(12, 2) = 19.41.

BAB 7

Analisis Data Kategorik

Silabus: Data kategorik, konsep association dan relation, uji kebebasan, uji homogenitas, distribusi χ2.

Tujuan:

1. Menggunakan data kategorik dalam analisis statistik 2. Memahami konsep “hubungan”

3. Mempelajari dan menggunakan uji kebebasan 4. Mempelajari dan menggunakan uji homogenitas 5. Menggunakan distribusi χ2

7.1

Ilustrasi

(Ilustrasi-1) The chronic heart condition angina pectoris menyebabkan nyeri pada dada secara periodik. Suatu studi ingin melihat ke-efektif-an Timolol dalam mencegah angina attack. Untuk keperluan itu, sejumlah pasien diberi

Timolol atau Placebo.

Angina-free Not angina-free

Timolol 44 116

(Ilustrasi-2) Yayasan Kanker Indonesia memberikan klaim “Merokok menye-babkan sakit jantung”. Setujukah anda dengan klaim itu? Bagaimana anda melakukan analisis statistik untuk menjawab klaim YKI?

Data Kategorik

Jelaskan pengertian data kategorik?

Bagaimana kita melakukan analisis data kategorik?

7.2

Uji Chi-Kuadrat

Uji χ2 Notasi: Kolom 1 Kolom 2 Baris 1 O11 O12 Baris 2 O21 O22

dimana Oij menyatakan banyak observasi di baris ke-i dan kolom ke-j.

Langkah-langkah UH: 1. Hipotesis:

H0 : Tidak ada perbedaan dalam perlakuan ... dan ...

2. Tingkat signifikansi: α 3. Statistik uji: χ2 =∑ (O − E) 2 E ∼ χ 2 (b−1)(k−1), dimana Eij =

(Total baris ke-i)× (Total kolom ke-j) Total

4. Daerah kritis:

Tolak H0 jika χ2hit ≥ χ

2 1(α)

5. Perhitungan:

Oij, Eij, χ2hit

6. Kesimpulan.

Untuk persoalan perlakuan Timolol dan Placebo diatas, maka langkah-langkah UH-nya adalah

1. Hipotesis:

H0 : Tidak ada perbedaan dalam perlakuan Timolol dan Placebo

2. Tingkat signifikansi: α = 0.05 3. Statistik uji: χ2 =∑ (O − E) 2 E ∼ χ 2 (2−1)(2−1), dimana Eij =

(Total baris ke-i)× (Total kolom ke-j)

Total , i, j = 1, 2 4. Daerah kritis:

Tolak H0 jika χ2hit ≥ χ21(0.05) = 3.84

5. Perhitungan: Kolom 1 Kolom 2 Baris 1 44(32.83) 116(127.17) 160 Baris 2 19(30.17) 128(116.83) 147 63 244 307 χ2 hit = 9.978 6. Kesimpulan: Tolak H0 karena χ21 = 9.978≥ 3.84.

Nilai χ2_:

• Tidak akan bernilai negatif

• Bernilai (dekat) ke NOL jika “O” dekat dengan “E” • Bernilai POSITIF (besar) jika “O” jauh dari “E”

Uji kebebasan?

H0 : Perlakuan “Timolol dan Placebo” SALING BEBAS dengan Angina

At-tack.

Contoh/Latihan:

Dalam suatu percobaan klinik, 99 pasien TB diberi perlakuan “PAS, Strepto-mycin, dan Kombinasi”. Setelah waktu tertentu, sampel “sputum” dianalisis menggunakan “smear test” dan “culture test”.

+ Smear -Smear, +Culture -Smear, -Culture

PAS 56 30 13

Streptomycin 46 18 20

Komb 37 18 35

7.3

Uji Homogenitas

Uji homogenitas?

BAB 8

Analisis Regresi

Silabus: Peubah bebas dan terikat, konsep relation, model regresi linier, pe-naksir kuadrat terkecil, uji koefisien, koefisien determinasi, korelasi.

Tujuan:

1. Mempelajari peubah bebas dan terikat serta konsep relation

2. Memodelkan peubah bebas dan terikat yang linier terhadap parameter 3. Menurunkan rumus penaksir kuadrat terkecil

4. Melakukan uji hipotesis untuk koefisien regresi

5. Menghitung dan menafsirkan koefisien determinasi dan korelasi

8.1

Konsep “Relation”

Hubungan antara peubah-peubah dapat berupa hubungan yang memiliki se-bab dan akibat (kausalitas). Peubah yang menjadi sese-bab adalah “peubah be-bas” atau prediktor. Sedangkan peubah yang menjadi akibat adalah “peubah terikat” atau respon.

Contoh:

• Hubungan antara umur dan tekanan darah

• Hubungan antara tingkat kebisingan dan stres pada bayi yang dirawat • Hubungan antara hasil TPA dan keberhasilan mahasiswa keperawatan

Diskusi:

• Dapatkah anda menenetukan peubah bebas dan terikat dari persoalan

diatas?

• Apakah hubungan diatas berlaku satu arah? dua arah?

• Adakah syarat utama untuk jenis data pada hubungan diatas?

8.2

Model Regresi Linier Sederhana

Hubungan dua peubah, prediktor dan respon, dapat dianalisis dengan ter-lebih dahulu menggambarkan garis lurus atau linier. Selanjutnya, plot dari data/observasi pada garis lurus tadi dapat membawa kita mencari model yang tepat. Kita ketahui bahwa persamaan garis lurus dapat dibangun dan dapat memiliki “slope” bernilai positif atau negatif.

Model regresi linier sederhana:

Y = α + β X + ε,

dimana

• Y peubah terikat atau respon • X peubah bebas atau prediktor

• ε adalah galat yang diasumsikan berdistribusi normal dengan mean nol

dan variansi σ2

• α intercept • β slope

Catatan:

- Nilai (sebenarnya) dari α, β, σ2 _{umumnya tidak diketahui}

- Data atau observasi: (x1, y1), . . . , (xn, yn) digunakan untuk menaksir

param-eter tersebut

Hubungan dua peubah yang dibangun dalam model regresi akan berhubun-gan POSITIF jika memiliki slope bernilai positif. Denberhubun-gan kata lain, “jika X

membesar maka nilai Y akan membesar”. Atau, sebagai contoh, “jika tingkat kebisingan makin tinggi maka stres bayi di ruang rawat akan meningkat”. Diskusi:

Dapatkah anda menggambarkan hubungan NEGATIF pada model regresi? Berikan contoh.

8.3

Penaksir Kuadrat Terkecil

Parameter regresi (α, β, σ2) dapat ditaksir dengan metode KUADRAT TERKE-CIL atau Least Square dari observasi sebagai berikut:

ˆ β = Sxy Sxx , ˆα = ¯y− ˆβ ¯x, dimana Sxy = ∑ x y− n ¯x ¯y dan Sxx = ∑ x2− n ¯x2

Dengan demikian, penaksir model regresi atau garis regresi atau persamaan regresinya adalah

ˆ

y = ˆα + ˆβ x,

yang meminimumkan jumlah kuadrat galat (galat = jarak antara nilai yi

den-gan garis regresi)

Ilustrasi: Tingkat kebisingan ruang rawat (termasuk alat-alat dan personal) menyebabkan tingginya tingkat stres bayi yang dirawat. Data yang diperoleh sbb:

Observasi ke- Tgkt Bising (X) Tgkt Stres (Y )

1 1 5 2 3 6 3 8 10 4 2 4 5 7 8 6 8 9 7 4 5

Persamaan garis regresinya adalah: ˆ

y = 3.28 + 0.728 x

Dari persamaan diatas, kita ketahui bahwa ˆβ > 0. Artinya garis regresi

memi-liki slope positif, yaitu y akan membesar apabila x membesar.

Sebagian orang berpendapat bahwa persamaan garis regresi dapat digunakan untuk PREDIKSI nilai y, jika diberikan nilai x tertentu. Hal ini tidak benar karena persamaan regresi hanya dapat memberikan nilai y jika diberikan nilai

x pada domainnya saja, bukan untuk PREDIKSI ke depan.

8.4

Uji Hipotesis

Setelah persamaan regresi diperoleh, kita akan menguji apakah koefisen regresi, yaitu α dan β, sama dengan NOL atau tidak. Apabila β = 0 maka kita dapat mengatakan bahwa “X tidak mempengaruhi Y ”. Sebab, berapapun nilai x, akan diperoleh nilai y yang sama.

Untuk keperluan uji hipotesis diatas, langkah-langkahnya sbb: 1. Hipotesis: H0 : β = 0, H1 : β > 0, atau H0 : β = 0, H1 : β < 0, atau H0 : β = 0, H1 : β ̸= 0 2. Tingkat signifikansi α 3. Statistik uji: T = ˆ β− β0 s.e( ˆβ) ∼ tn−2 4. Daerah kritis:

Tolak H0 jika t > tn−2(1− α), atau...

5. Perhitungan. 6. Kesimpulan.

Contoh/Latihan:

Lakukan uji hipotesis untuk β pada ilustrasi kebisingan pada tingkat stres. Koefisien Determinasi

Kita dapat menghitung koefisien determinasi, r2_{, pada analisis regresi,}

r2 = S

2

xy

SxxSyy

yang menyatakan prosentase banyaknya variasi dalam nilai y yang dijelaskan oleh nilai x. Nilai r2 yang diharapkan adalah nilai yang tinggi, kira-kira lebih dari 80%.

Catatan:

• 0 ≤ r2 _{≤ 1}

• Jika r2 _{= 1 maka seluruh titik sampel berada di garis lurus (untuk slope}

positif atau negatif)

• Jika r2 _{= 0 maka tidak ada hubungan linier antara X dan Y}

8.5

Korelasi