Penentuan Durasi Nyala Lampu Lalu Lintas Berdasarkan Panjang Antrian Kendaraan Menggunakan Metode Backpropagation

(1)

Fakultas Ilmu Komputer

Universitas Brawijaya

2948

Penentuan Durasi Nyala Lampu Lalu Lintas Berdasarkan Panjang Antrian

Kendaraan Menggunakan Metode

Backpropagation

Shibron Arby Azizy1_{, Imam Cholissodin}2_{, Edy Santoso}3

Program Studi Teknik Informatika, Fakultas Ilmu Komputer, Universitas Brawijaya Email: 1_{[email protected],}2_{[email protected],}3_{[email protected]}

Abstrak

Lalu lintas merupakan salah satu lokasi dimana orang-orang menghabiskan waktunya. Saat ini dengan pertumbuhan kendaraan yang semakin pesat membuat kondisi lalu lintas di Indonesia semakin padat setiap harinya. Salah satu cara untuk menguraikan kepadatan lalu lintas adalah dengan adanya lampu lalu lintas. Namun, kinerja lampu lalu lintas saat ini dirasa kurang optimal dikarenakan penentuan durasi waktu lalu lintas yang masih statis berdasarkan waktu tertentu. Maka dari itu dibutuhkan suatu sistem yang dapat menentukan waktu, sehingga waktu pada lampu lalu lintas dapat lebih dinamis berdasarkan kondisi lalu lintas. Penelitian ini mengunakan metode backpropagation untuk menentukan durasi nyala lampu lalu lintas berdasarkan panjang antrian kendaraan. Hasil dari pengujian data latih didapatkah bahwa fungsi aktivasi yang cocok adalah fungsi Linear dengan a = 3, iterasi yang optimal didapatkan ketika iterasi 10, jumlah node pada hidden layer yang optimal adalah 2, dan nilai learningrate yang optimal adalah 0,02. Hasil evaluasi yang diperoleh ketika memproses data uji menggunakan fungsi aktivasi, jumlah iterasi, jumlah node pada hidden layer, dan nilai learning rate yang optimal menghasilkan nilai RMSE sebesar 0,0888978841028.

Kata kunci: lalu lintas, lampu lalu lintas, penentuan, backpropagation, RMSE Abstract

Traffic is one location where people spend a lot of time. Currently with the rapid growth of vehicles makes conditions in Indonesia is getting crowded every day. One way to solve this problem is with traffic lights. However, the current traffic light performance is considered less than optimal. Therefore required a system that can determine the time, so the time at the traffic light can be more dynamic based on traffic conditions. This research uses backpropagation method to determine the duration of traffic lights based on queue lenght of vehicle. The result of the trained data test obtained is the Linear function with a = 3, the optimal iteration obtained at iteration 10, the optimal number of nodes in the hidden layer is 2, and the optimal value of learning rate is 0,02. The evaluation result when processing the test data using the optimal activation function, the optimal number of iterations, the optimal number of nodes in the hidden layer, and the optimal learning rate yields RMSE value of 0,0888978841028.

Keywords: tarffic, traffic light, determining, backpropagation, RMSE.

1. PENDAHULUAN

Lalu lintas adalah hal penting dalam kehidupan bermasyarakat. Lalu lintas dan kendaraan umum merupakan salah satu kunci pertumbuhan ekonomi. Tetapi lalu lintas memiliki banyak permasalahan yang terjadi, mulai dari permasalahan yang biasa saja seperti jalanan rusak sampai masalah besar seperti kecelakaan yang menyebabkan korban jiwa. Di Indonesia, lalu lintas memiliki permasalahan lama yang masih belum terselesaikan, yaitu

(2)

Indonesia semakin padat. Salah satu cara untuk mengurai kepadatan lalu lintas adalah dengan adanya lampu lalu lintas. Namun dalam beberapa kondisi, lampu lalu lintas kurang efisien untuk menangani masalah tersebut.

Kondisi ini menjadi motivasi utama diadakannya penelitian mengenai Sistem Pengaturan Lampu Lalu Lintas Terdistribusi (SPLLLT). Lalu lintas yang ada saat ini hanya berorientasi terhadap waktu dan ditidak menyesuakan kondisi lalu lintas. SPLLLT diharapkan dapat menjadi bentuk evolusi dari lampu lalu lintas yang ada saat ini. Maka dari itu dibutuhkan suatu sistem yang dapat menentukan waktu sehingga waktu pada lampu lalu lintas dapat lebih dinamis berdasarkan kondisi lalu lintas. Sistem ini akan dapat memecah kepadatan lalu lintas dengan lebih efisien. Jadi ketika volume kendaraan tinggi, maka selisih waktu antara lampu merah dan lampu hijau akan dibuat dekat, begitupun sebaliknya.

Pada penelitian Wicaksana et al. (2014), dijelaskan tentang metode neuro fuzzy untuk pengambilan keputusan pada kasus pemindahan lalu lintas. Metode gabungan dari jaringan syaraf tiruan dan logika fuzzy ini berhasilkan melewatkan 97.07% dari jumlah kendaraan yang sedang mengantri pada lampu lalu lintas. Metode jaringan syaraf tiruan yang digunakan adalah Levenberg-Marquardt Backpropagation. Dan pada penelitian Royani et al. (2013), dijelaskan metode Fuzzy Neural Network (FNN) dan Algoritme Genetika untuk mengatur lampu lalu lintas. Pada peneltian ini, diterapkan metode FNN pada kontrol sinyal dan Algoritme Genetika untuk proses pembelajarannya. Sedangkan penelitian Yohannes et al. (2015), dijelakan secara lengkap urutan penggunaan metode Bakpropagation untuk penentuan upah minimum kota. Parameter yang menentukan adalah tingkat inflasi. Jadi upah minimum kota ditentukan berdasarkan tingkat inflasi yang ada. Penelitian ini memiliki nilai Root Mean Square Error sebesar 0.0728.

Dengan melihat penelitian-penelitian tersebut, maka penulis berniat menggunakan algoritme backpropagation pada penelitian ini. Backpropagation merupakan salah satu algoritme jaringan syaraf tiruan yang digunakan untuk kasus prediksi dan penentuan. Jaringan syaraf tiruan sendiri merupakan metode yang diadaptasi dari jaringan syaraf manusia pada dunia nyata. Pada arsitekturnya terdapat banyak neuron yang saling terhubung dan membentuk janringan. Setiap neuron yang terhubung

memiliki bobot. Bobot inilah yang akan perbarui pada proses pembelajaran backpropagation. Pada penelitian ini algoritme backpropagation digunakan untuk menentukan durasi nyala lampu lalu lintas berdasarkan panjang antrian kendaraan dan harapannya penelitian ini mendapatkan hasil yang optimal.

2. BACKPROPAGATION

Backpropagation merupakan salah satu metode pembelajaran dalam jaringan syaraf tiruan. Proses pembelajaran dalam backpropagation dilakukan dengan penyesuaian bobot-bobot (w) dengan arah mundur berdasarkan nilai error dalam proses pembelajaran. Backpropagation biasanya digunakan dalam kasus-kasus yang membutuhkan prediksi dan penentuan didalam penyelesaiannya.

Proses pertama sebelum masuk ke algoritme backpropagation adalah proses normalisasi. Proses ini digunakan untuk menyetarakan range nilai pada setiap fitur menjadi antara 0 sampai dengan 1. Proses normalisasi penting dilakukan agar salah satu fitur yang memiliki tipe nilai yang tinggi tidak menjadi dominan dan juga sebaliknya. Rumus normalisasi dapat dilihat pada persamaan berikut:

𝑥′_{= (0.8 ×} 𝑥−𝑚𝑖𝑛

𝑚𝑎𝑥−𝑚𝑖𝑛) + 0.1 (1)

Keterangan :

x

= data

x’

= data hasil normalisasi

min value

= nilai minimum

max value

= nilai maksimum

Fungsi aktivasi digunakan untuk

mengaktifkan

node

berdasarkan

hasil

perhitungan sinyal-sinyal

input

. Fungsi

aktivasi yang digunakan adalah fungsi

ReLU

. Rumus fungsi aktivasi :

𝑦 = 𝑚𝑎𝑥(0, 𝑥) , 𝑥 ≥ 0

(2)

𝑦 = 0, 𝑥 < 0

(3)

Keterangan :

x

= hasil perhitungan sinyal – sinyal

input

y

= fungsi untuk mengaktivasi nilai

x

Backpropagation memiliki 3 proses

utama,

yaitu

proses

Feedforward

,

(3)

bagian proses didalamnya. Pertama proses

penghitungan

output

pada semua node

hidden layer

z

j (

j

=1,...,m) berdasarkan

inputan

x

i (

i

=1,..., n).

𝑧_𝑛𝑒𝑡

𝑘

= ∑

𝑛𝑖=1

𝑥

𝑖

× 𝑣

𝑘𝑖

(4)

𝑧

𝑘

= 𝑚𝑎𝑥 (0, 𝑧_𝑛𝑒𝑡

𝑘

)

(5)

Keterangan :

z_net

k = net

hidden

unit

k

x

i

= nilai aktivasi dari unit

x

i

v

kj

= nilai bobot sambungan dari

x

ij ke

unit

z

k

Kedua adalah menghitung output

pada semua

node output layer

y

k (

k

=1,...,n)

berdasarkan

output

pada

hidden

layer

(

z

j)

yang didapatkan pada proses sebelumnya.

𝑦_𝑛𝑒𝑡

𝑘

= ∑

𝑚𝑗=1

𝑧

𝑗

× 𝑤

𝑘𝑗

(6)

𝑦

𝑘

= 𝑚𝑎𝑥 (0, 𝑦_𝑛𝑒𝑡

𝑘

)

(7)

Keterangan :

y_net

k = net

output

unit

k

z

j

= nilai aktivasi dari unit

z

j

w

kj

= nilai bobot sambungan dari

z

ij ke

unit

y

k

Setelah proses

feedforward

selesai,

proses

selanjutnnya

adalah

proses

backpropagation

. Sama seperti proses

feedforward

, proses

backpropagation

dibagi

menjadi beberapa bagian, yang pertama

yaitu hitung

error

δk (k=1,...,n) pada

output

layer

terlebih dahulu berdasarkan output

sistem y

k

dan output target t

k

(k=1,...,m).

𝛿

𝑘

= 𝑦

𝑘

(1 − 𝑦

𝑘

)(𝑡

𝑘

− 𝑦

𝑘

)

(8)

Keterangan:

δk

: Nilai error ouput layer

k

y

k

: Nilai

output

k

sistem

t

k

: Nilai

output

k

target

Kedua adalah menghitung

error

δh

(

k

=1,...,n) pada semua

node hidden layer

berdasarkan

error

pada

output

layer

(

δk)

yang didapatkan pada proses sebelumnya.

𝛿

𝑗

= 𝑧

𝑘

(1 − 𝑧

𝑘

)(∑

𝑘∈𝑜𝑢𝑡𝑝𝑢𝑡

𝑤

ℎ,𝑘

𝛿

𝑘

)

(9)

Keterangan:

δ

j

: Nilai

error hidden layer j

z

k

: Nilai

output hidden layer

k

w

j,k

: Nilai bobot penghubung

hidden

layer

j

dan

output layer

k

δ

k

: Nilai

error ouput layer

k

yang

terhubung dengan

hidden layer

Setelah proses

backpropagation

selesai,

proses selanjutnnya adalah proses

weight

updating

. Proses ini akan mengupdate bobot

w

berdasarkan hasil

error

δ

yang diperoleh

pada proses sebelumnya. Sama seperti

proses

backpropagation

, proses

weight

updating

dibagi menjadi beberapa bagian,

yang pertama yaitu menghitung

update

bobot penghubung

input layer

dengan

hidden layer

(

v

).

𝑣′

𝑗𝑖

= 𝑣

𝑗𝑖

+ (𝛼 × 𝛿

𝑗

× 𝑥

𝑖

)

(10)

Kedua adalah menghitung

update

bobot

penghubung

hidden layer

dengan

output

layer

(

w

).

𝑤′

𝑘𝑗

= 𝑤

𝑘𝑗

+ (𝛼 × 𝛿

𝑘

× 𝑧

𝑗

)

(11)

Untuk

iterasi

beriktnya,

lakukan

penghitungan persamaan 1-11 sebanyak

iterasi dan jumlah data yang sudah

ditentukan.

Untuk menghitung

error

digunakan

fungsi

RMSE

. Rumus untuk RMSE

𝑅𝑀𝑆𝐸 = √

∑𝑛𝑖=1𝑑𝑖2

𝑛

(12)

Dimana:

RMSE

: Nilai RMSE

d

i

: Selisih

output

sistem pada data ke-i

dengan

output

target pada data ke-i

n

: Jumlah Data

Karena pada awal proses ada proses

normalisasi data, untuk mengembalikan

range

nilainya

maka

perlu

proses

denormalisasi data.

𝑥

′′

₌

(𝑚𝑎𝑥−𝑚𝑖𝑛)×(𝑥′−0,1)

0.8

+ 𝑚𝑖𝑛

(13)

Keterangan:

𝑥′′

:

Nilai denormalisasi

3. METODE

(4)

Sukarno-hatta dan jalan Coklat, Kelurahan Lowokwaru, Kota Malang. Adapun data antrian kendaraan dapat dilihat pada Tabel 1.

Tabel 1 Data Panjang Antrian Kendaraan

No Utara

(x1)

Timur (x2)

Selatan (x3)

Barat (x4)

1 75 20 55 20

2 50 35 27 17

3 33 15 35 28

4 28 12 45 7

... ... ... ... ...

72 48 56 80 55

73 20 5 57 5

74 33 75 42 15

75 80 75 35 11

Sebelum diproses lebih lanjut, data perlu dinormalisasi terlebih dahulu menggunakan Persamaan 1. Ini dilakukan untuk meyetarakan range semua data pada rentang 0 sampai dengan 1. Hasil normalisasi data dapat dilihat pada Tabel 2.

Tabel 2 Normalisasi Data Panjang Antrian Kendaraan

No Utara

(x1)

Timur (x2)

Selatan (x3)

Barat (x4)

1 0,600 0,233 0,467 0,329

2 0,433 0,333 0,280 0,294

3 0,320 0,200 0,333 0,420

4 0,287 0,180 0,400 0,180

... ... ... ... ...

72 0,420 0,473 0,633 0,729

73 0,233 0,133 0,480 0,157

74 0,320 0,600 0,380 0,271

75 0,633 0,600 0,333 0,226

Setelah data dinormalisasi kemudian lakukan proses feedforward dengan menghitung nilai keluaran pada hidden layer (z) dengan menggunakan Persamaan 4. Penelitian ini menggunkan 2 node pada hidden layer. Hasil penghitungan hidden layer bisa dilihat pada Tabel 3.

Tabel 3 Output Hidden Layer

Nilai output masing – masing node

z_net1 z_net2

0,337 0,277

Setelah output didapatkan, dilakukan perhitungan menggunakan fungsi aktivasi ReLu seperti pada Persamaan 2 atau 5. Hasil

perhitungan dapat dilihat pada Tabel 4. Tabel 4 Hasil Fungsi Aktivasi ReLU

z1 z2

0,583 0,569

Kemudian lanjut perhitungan output pada output layer menggunakan persamaan 6. Karena output yang dibutuhkan 4, maka penelitian ini menggunakan outpt layer sebanyak 4 Hasil perhitungan dapat dilihat pada Tabel 5.

Tabel 5 Output Pada Output Layer

y_net1 y_net1 y_net1 y_net1

0,383 0,388 0,35 0,265

Setelah output didapatkan, dilakukan perhitungan menggunakan fungsi aktivasi ReLu seperti pada Persamaan 2 atau 7. Hasil perhitungan dapat dilihat pada Tabel 6.

Tabel 6 Hasil Fungsi Aktivasi ReLU

y1 y1 y1 y1

0,383 0,388 0,35 0,265

Setelah proses feedforward selesai, dilanjutkan ke proses backpropagation untuk menghitung error. Pertama hitung error pada output layer (δk) menggunakan Persamaan 8. Hasil perhitungan dapat dilihat pada Tabel 7.

Tabel 7 Perhitungan erroroutput layer

Nilai error output layer

δ1 δ2 δ3 δ4

-0,059 -0,046 -0,033 -0,04

Kemudian lanjut perhitungan error pada hidden layer (δ1) menggunakan persamaan 9. Hasil perhitungan dapat dilihat pada Tabel 8.

Tabel 8 Perhitungan errorhidden layer

Nilai error pada hidden layer

δ 1 δ 2

0,2 0,187

Setelah proses backpropagation selesai, dilanjutkan ke proses weight updating. Proses ini menggunakan Persamaan 10 dan 11. Hasil perhitungan dapat dilihat pada Tabel 9 dan Tabel 10.

Tabel 9 Bobot Awal

w111 w112 w121 w122

0,210 0,200 0,300 0,150

w131 w132 w141 w142

0,330 0,420 0,400 0,250

w211 w212 w213 w214

0,230 0,440 0,120 0,130

(5)

0,390 0,180 0,450 0,300

Tabel 10 Bobot Hasil Weight Update

w111 w112 w121 w122 Proses diatas akan terus diulang sebanyak data yang digunakan dan sebanyak iterasi yang ditetukan diawal.

4. HASIL PENGUJIAN

Sub-bab ini membahas hasil dan pengujian program untuk penentuan durasi nyala lampu lalu lintas dengan menggunakan metode Backpropagation.Pengujian terdiri dari pengujian fungsi aktivasi, pengujian jumlah iterasi, pengujian jumlah node pada hidden layer, dan pengujian nilai learning rate. Setiap nilai yang dihasilkan dari keempat pengujian akan digunakanuntuk memproses data uji untuk menghasilkan nilai evaluasi yang optimal.

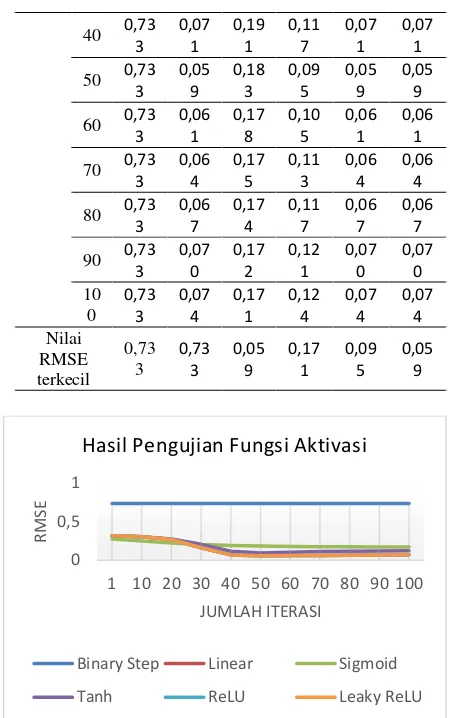
Pengujian fungsi aktivasi digunakan untuk menentukan fungsi aktivasi yang cocok pada permasalahan ini. Macam-macam fungsi aktivasi yang diuji adalah Binary Step, Linear, Sigmoid, Tanh, ReLU, dan Leaky ReLU. Berdasarkan artikel yang ditulis oleh Surmenok (2017), nilai a pada fungsi linear yang digunakan sebesar 1 dan nilai a pada fungsi Leaky ReLU sebesar 0,01. Tabel 11 dan Gambar 1 menunjukan hasil dari pengujian fungsi aktivasi.

Tabel 11 Hasil Pengujian Fungsi Aktivasi

Fungsi Aktivasi

Gambar 1 Grafik Pengujian Fungsi Aktivasi

Berdasarkan grafik pengujian fungsi aktivasi yang ditunjukan pada Gambar 1 dan Tabel 11 dapat diketahui bahwa nilai RMSE terkecil didapatkan dengan menggunakan fungsi aktivasi linear, ReLU, dan Leaky ReLU dengan nilai 0,059. Ini dikarenakan karakteristik keluaran data yang nilainya tidak mungkin lebih kecil atau sama dengan 0 dan penggunaan konstanta a = 1, sehingga hasil dari penggunaan ketiga fungsi aktivasi tersebut sama. Karena hasilnya sama, maka fungsi aktivasi yang akan digunakan adalah fungsi linear karena fungsi tersebut masih ada kemungkinan menghasilkan error yang lebih kecil dengan inisialisasi konstanta a yang tepat. Ini dikarenkan konstanta a pada fungsi linear juga berpengaruh terhadap perbaikan error (Gupta, 2018).

Karena Menggunakan fungsi aktivasi Linear maka perlu adanya pengujian tambahan yaitu pengujian konstanta a yang ada pada fungsi linear. Konstanta a berpengaruh terhadap perbaikan error sehingga perlu dicari nilai a

Hasil Pengujian Fungsi Aktivasi

Binary Step Linear Sigmoid

(6)

Tabel 12 Hasil Pengujian Konstanta a

Jumlah Iterasi

Nilai RMSE

Konstanta a (Fungsi Aktivasi = Linear,

learningrate = 0,02, dan jumlah node

hidden = 2)

1 2 3 4 5

1 0,316 0,298 0,264 0,215 0,153

10 0,305 0,157 0,056 0,061 0,062

20 0,268 0,057 0,063 0,071 0,078

30 0,164 0,062 0,073 0,084 0,095

40 0,071 0,069 0,083 0,097 0,109

50 0,059 0,075 0,093 0,109 0,122

60 0,061 0,082 0,103 0,120 0,134

70 0,064 0,089 0,111 0,129 0,146

80 0,067 0,095 0,119 0,139 0,157

90 0,070 0,102 0,127 0,148 0,168

100 0,074 0,107 0,134 0,158 0,179

Nilai RMSE Terkecil

0,059 0,057 0,056 0,061 0,062

Gambar 2 Grafik Pengujian Konstanta a Berdasarkan hasil pengujian yang ditunjukan pada Gambar 2 dan Tabel 12 dapat dilihat bahwa nilai a yang menghasilkan error terkecil adalah 3. Nilai a lebih dari 3 cenderung menghasilkan error lebih besar dikarenakan perbaikan error yang melampaui batas minimum perbaikan sehingga error semakin besar, sedangkan jika nilai a lebih kecil dari 3 juga akan menghasilkan error yang lebih besar dikarenakan perbaikan error yang terlalu kecil mengakibatkan error yang terlambat menuju optimal (Surmenok, 2017).

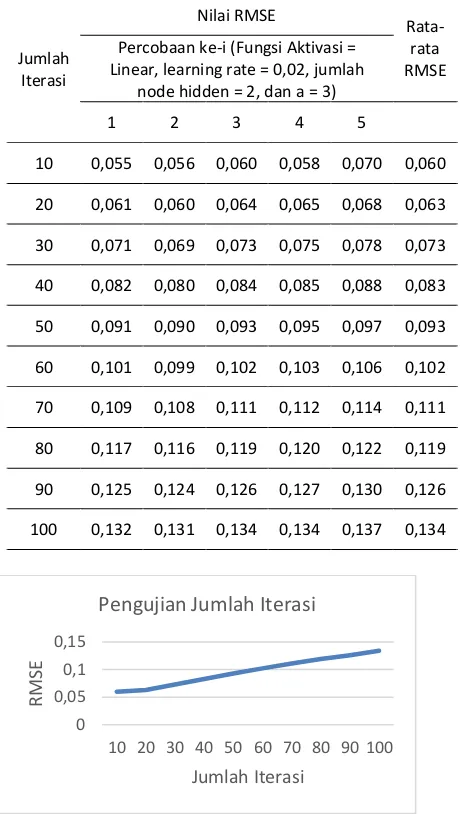
Pengujian jumlah iterasi dilakukan untuk mengetahui berapa jumlah iterasi yang optimal untuk mendapatkan nilai error terkecil pada penelitian ini. Jumlah iterasi yang diuji yaitu 10,

20, 30, 40, 50, 60, 70, 80, 90, dan 100. Setiap 1 nilai yang diuji akan dilakukan 5 kali percobaan. Tabel 13 Hasil Pengujian Jumlah Iterasi

Jumlah Iterasi

Nilai RMSE

Rata-rata RMSE Percobaan ke-i (Fungsi Aktivasi =

Linear, learning rate = 0,02, jumlah node hidden = 2, dan a = 3)

1 2 3 4 5

10 0,055 0,056 0,060 0,058 0,070 0,060

20 0,061 0,060 0,064 0,065 0,068 0,063

30 0,071 0,069 0,073 0,075 0,078 0,073

40 0,082 0,080 0,084 0,085 0,088 0,083

50 0,091 0,090 0,093 0,095 0,097 0,093

60 0,101 0,099 0,102 0,103 0,106 0,102

70 0,109 0,108 0,111 0,112 0,114 0,111

80 0,117 0,116 0,119 0,120 0,122 0,119

90 0,125 0,124 0,126 0,127 0,130 0,126

100 0,132 0,131 0,134 0,134 0,137 0,134

Gambar 3 Grafik Pengujian Jumlah Iterasi

Berdasarkan grafik pengujian jumlah iterasi yang ditunukan pada Gambar 3 dan Tabel 13 dapat dilihat bahwa nilai rata-rata RMSE terkecil didapatkan ketika iterasi = 10 yaitu sebesar 0,06. Pada Gambar 3 terlihat grafik yang konsisten menanjak setelah iterasi ke 10. Hal ini dikarenakan pada iterasi ke 10, nilai error sudah mencapai titik optimal sehingga perbaikan pada iterasi berikutnya menyebabkan error yang lebih buruk. Menurut Sharma (2017), jika suatu parameter terlalu besar maka akan menyebabkan cost atau error semakin buruk. Sehingga pada proses pengujian berikutnya akan digunakan iterasi sebanyak 10.

Pengujian jumlah node pada hidden layer dilakukan untuk mengetahui berapa jumlah node yang optimal pada hidden layer untuk mendapatkan nilai error terkecil pada penelitian 0,05

0,055 0,06 0,065

1 2 3 4 5

RMSE

Nilai Konstanta a

Hasil Pengujian Konstanta a

0 0,05 0,1 0,15

10 20 30 40 50 60 70 80 90 100

RMSE

Jumlah Iterasi

(7)

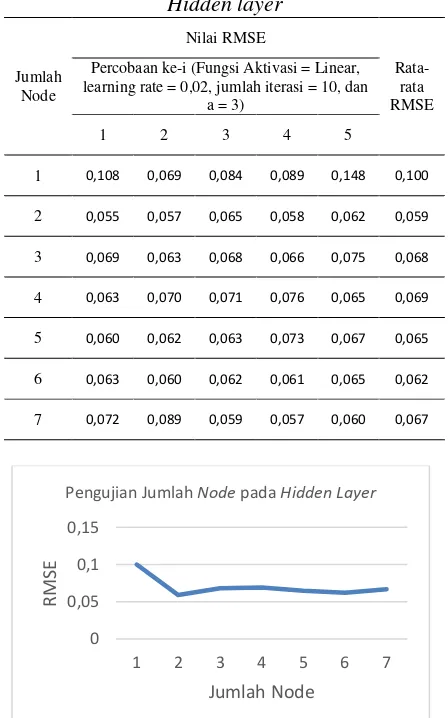
ini. Menurut Heaton (2005) jumlah nodehidden layer yang baik adalah 2/3 dari jumlah input ditambah dengan jumlah output. Karena jumlah input adalah 4 dan jumlah output adalah 4 maka menurut Heaton jumlah node pada hidden layer adalah 6 sampai dengan 7 buah node. Sehingga jumlah node yang akan diuji yaitu sebesar 1, 2, 3, 4, 5, 6, dan 7.

Tabel 14 Hasil Pengujian Jumlah Node Pada Hidden layer

Jumlah Node

Nilai RMSE

Rata-rata RMSE Percobaan ke-i (Fungsi Aktivasi = Linear,

learning rate = 0,02, jumlah iterasi = 10, dan a = 3)

1 2 3 4 5

1 0,108 0,069 0,084 0,089 0,148 0,100

2 0,055 0,057 0,065 0,058 0,062 0,059

3 0,069 0,063 0,068 0,066 0,075 0,068

4 0,063 0,070 0,071 0,076 0,065 0,069

5 0,060 0,062 0,063 0,073 0,067 0,065

6 0,063 0,060 0,062 0,061 0,065 0,062

7 0,072 0,089 0,059 0,057 0,060 0,067

Gambar 4 Grafik Pengujian Jumlah Node pada Hidden Layer

Berdasarkan grafik pengujian jumlah

node

pada

hidden layer

yang ditunjukkan

pada Gambar 4 dan Tabel 14 dapat dilihat

bahwa pada jumlah

node

sebanyak 2

memiliki nilai rata-rata

RMSE

yang terkecil

dengan nilai

error

0,059. Sedangkan jumlah

node

sebanyak 1 memiliki nilai

RMSE

yang

berbeda dan jauh lebih besar dari yang

lainnya dikarenakan kurangnya variasi.

Selain itu, jika jumlah node kurang dari 2

akan terjadi kondisi

underfitting

, yaitu

kondisi dimana jaringan tidak dapat dapat

memepelajari pola yang ada dengan baik

yang mengakibatkan kurang baiknya hasil

peramalan. Tetapi ketika jumlah node terlalu

banyak

maka

akan

terjadi

kondisi

overfitting,

yaitu kondisi dimana jaringan

kehilangan kemampuan dalam generalisasi

dan mempelajari pola-pola yang diuji.

Sehingga untuk proses selanjutnya akan

digunakan jumlah

node

pada

hidden layer

sebanyak 2.

Pengujian nilai

learning rate

dilakukan

untuk mengetahui berapa nilai

learning rate

yang optimal untuk mendapatkan nilai

error

terkecil pada penelitian ini. Nilai

learning

rate

yang digunakan yaitu 0,01; 0,02; 0,03;

0,04; 0,05; 0,06; 0,07; 0,08; 0,09; dan 0,1.

Setiap 1 nilai yang diuji akan dilakukan 5

kali percobaan.

Tabel 15 Hasil Pengujian Nilai Learning Rate

Nilai Learning

Rate

Nilai RMSE

Rata-rata RMSE Percobaan ke-i (Fungsi Aktivasi = Linear, jumlah iterasi = 10, jumlah Node Hidden = 2, dan a = 3)

1 2 3 4 5

0,01 0,0925 0,0689 0,0975 0,0873 0,0838 0,0860

0,02 0,0597 0,0674 0,0603 0,0599 0,0586 0,0612

0,03 0,0641 0,0630 0,0623 0,0591 0,0599 0,0617

0,04 0,0650 0,0686 0,0604 0,0636 0,0626 0,0640

0,05 0,0679 0,0712 0,0696 0,0743 0,0675 0,0701

0,06 0,0709 0,0675 0,0692 0,0700 0,0692 0,0694

0,07 0,0722 0,0704 0,0723 0,0732 0,0693 0,0715

0,08 0,0820 0,0842 0,0849 0,0813 0,0824 0,0830

0,09 0,0915 0,0910 0,0930 0,0896 0,0932 0,0917

0,1 0,1019 0,0974 0,0930 0,0999 0,0999 0,0984

Gambar 5 Grafik Pengujian Nilai Learning Rate

0 0,05 0,1 0,15

1 2 3 4 5 6 7

RMSE

Jumlah Node

Pengujian Jumlah Nodepada Hidden Layer

0 0,05 0,1 0,15

0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,1

RMSE

Nilai Learning Rate

(8)

Berdasarkan grafik pengujian nilai learning rate yang ditunjukkan pada Gambar 5 dan Tabel 15 dapat dilihat bahwa learning rate dengan nilai 0,02 memiliki nilai rata-rata RMSE yang paling kecil dengan nilai 0, 0612. Nilai learning rate lebih dari 0,02 cenderung menghasilkan error lebih besar dikarenakan perbaikan error yang melampaui batas minimum perbaikan sehingga error semakin besar, sedangkan jika nilai learning rate lebih kecil dari 0,02 juga akan menghasilkan error yang lebih besar dikarenakan perbaikan error yang terlalu kecil mengakibatkan error yang terlambat menuju optimal (Surmenok, 2017). Sehingga pada penelitian ini didapatkan nilai learning rate paling optimal sebesar 0,02.

Setelah semua pengujian dilakukan mulai dari pengujian fungsi aktivasi, pengujian jumlah iterasi, pengujian jumlah node pada hidden layer, dan pengujian nilai learning rate, selanjutnya dilakukan pemrosesan data uji mengggunakan nilai-nilai hasil pengujian. Fungsi aktivasi yang digunakan adalah fungsi Linear dengan a = 3, jumlah iterasi yanng digunakan adalah 10, jumlah hiddenlayer adalah 1, jumlah node pada hiddenlayer adalah 2, dan nilai learningrate sebesar 0,02.

Tabel 16 Hasil Proses Data Uji

Masukan Keluaran

X1 X2 X3 X4 Y1 Y2 Y3 Y3

50 55 40 15 16 16 25 19

60 35 40 15 16 16 24 19

95 23 65 25 21 23 33 27

90 25 70 29 21 24 34 28

80 35 60 25 20 22 32 25

40 75 37 15 16 17 25 20

48 56 80 55 24 27 38 32

20 5 57 5 12 10 18 12

33 75 42 15 16 17 25 20

80 75 35 11 19 20 29 23

Dari hasil pengujian data uji pada Tabel 16

diperoleh nilai RMSE sebesar

0,0888978841028. Penghitungan dilakukan

menggunakan Persamaan 12.

5. KESIMPULAN DAN SARAN

Dari hasil penelitian didapatkan bahwa metode Backpropagation dapat digunakan untuk menentukan durasi nyala lampu lalu lintas bedasarkan panjang antrian kendaraan dengan nilai RMSE sebesar

0,0888978841028

. Penelitian selanjutnya dapat menambahkan input dan juga menggunakan tambahan algoritma lain seperti algoritma optimasi

sehingga output bisa lebih baik. Selain itu, penggunkaan sensor berbasis citra bisa digunakan untuk membuat penelitian ini real-time.

6. REFERENSI

Badan Pusat Statisik. (2014). Perkembangan Jumlah Kendaraan Bermotor Menurut Jenis tahun 1987-2013. Dipetik Mei 29,

2017, dari

https://www.bps.go.id/linkTabelStatis/v iew/id/1413

Badan Pusat Statistik. (2016). Panjang Jalan Menurut Jenis Permukaan,1957-2015 (Km). Dipetik Mei 29, 2017, dari https://www.bps.go.id/linkTableDinami s/view/id/820

Barnston, A. G. (1992). Correspondance Among the Correlation, RMSE, and Heidke Foreecast Verification Measure; Refinement of the Heidke Score. Climate Analysis Center, NMC/NWS/NOAA, Washington, D.C., VII, 699-709.

G, E. A., Djakfar, L., & Wicaksono, A. (2014). Manajemen Lalu Lintas Pada Simpang Borobudur Kota Malang. JTIIK, VIII, 169.

Gupta, D. (2018, January 3). Fundamentals of Deep Learning – Activation Functions and When to Use Them? Diambil kembali dari Analytics Vidhya: https://www.analyticsvidhya.com/blog/ 2017/10/fundamentals-deep-learning-activation-functions-when-to-use-them/ Gutierrez, D. D. (2015). Machine Learning And

Data Science (1st ed.).

Jauhari, D., Himawan, A., & Dewi, C. (2016). Prediksi Distribusi Air PDAM Menggunakan Metode Jaringan Syaraf Tiruan Backpropagation Di PDAM Kota Malang. III.

Kusmagi, M. A. (2010). Selamat Berkendara Di Jalan Raya (Vol. 1). Jakarta.

Panchal, G., Ganatra, A., Kosta, Y. P., & Panchal, D. (2011). Behaviour Analysis of Multilayer Perceptrons with Multiple Hidden Neurons and Hidden Layers. International Journal of Computer Theory and Engineering, 3(2), 1-6. Royani, T., Haddadnia, J., & Alipoor, M. (2013).

(9)

International Journal of Computer and Electrical Engineering, V(1), 142-146. SB, D. (2011). Budaya Tertib Lalu Lintas (Vol.

I). Jakarta.

Sharma, A. (2017). Understanding Activation Functions in Deep Learning. Dipetik

Januari 14, 2018, dari

https://www.learnopencv.com/understa nding-activation-functions-in-deep-learning/

Sharma, S. (2017). Towards Data Science. Dipetik January 4, 2018, dari https://towardsdatascience.com/epoch-

vs-iterations-vs-batch-size-4dfb9c7ce9c9

Sivanandam, S. N., Sumathi, S., & Deepa, S. N. (2006). Introduction to Neura Network Using Matlab 6.0 (Vol. II). New Delhi. Smith, L. N. (2017). Cyclical Learning Rates for

Training Neural Networks. Cornell University Library, 6, 1-10.

Surmenok, P. (2017). Towards Data Science. Dipetik Januari 13, 2018, dari https://towardsdatascience.com/estimati ng-optimal-learning-rate-for-a-deep-neural-network-ce32f2556ce0

Wicaksana, M. D., Azizie, F. A., Amirullah, I., & Nurtanio, I. (2014). Sistem Pengambilan Keputusan Waktu Perpindahan Lampu Lalu Lintas Menggunakan Metode Neuro-Fuzzy Pada Sistem Tranportasi Cerdas. 1-8. Yohannes, E., Mahmudy, W. F., & Rahmi, A.