PEMODELAN PENDERITA DEMAM BERDARAH DENGUE (DBD) DI KABUPATEN GRESIK MENGGUNAKAN ARIMA DAN REGRESI
NONPARAMETRIK KERNEL SKRIPSI
Disusun Oleh
LAILATUL FITRIYAH NIM. H72215016
PROGRAM STUDI MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI UNIVERSITAS ISLAM NEGERI SUNAN AMPEL
SURABAYA 2019
ABSTRAK
PEMODELAN PENDERITA DEMAM BERDARAH DENGUE (DBD) DI KABUPATEN GRESIK MENGGUNAKAN ARIMA DAN REGRESI
NONPARAMETRIK KERNEL
Penyakit DBD merupakan salah satu masalah utama dalam bidang kesehatan karena dapat menyerang semua golongan umur dan akan menyebabkan kematian, khususnya pada anak-anak. Penyebaran virus DBD disebabkan oleh virus dengue yang ditularkan melalui gigitan nyamuk Aedes Aegypti. Penyebaran dengue dipengaruhi oleh faktor iklim seperti curah hujan, suhu dan kelembaban. Metode ARIMA merupakan salah satu model yang menggunakan data time series berdasarkan pada data variabel yang diamati. Metode regresi nonparametrik kernel merupakan salah satu metode yang digunakan untuk memperkirakan ekspektasi dengan menggunakan fungsi kernel. Penelitian ini bertujuan untuk membandingan hasil model dari metode ARIMA dan regresi nonparametrik kernel Gaussian pada data penderita DBD periode Januari 2013-Desember 2018. Berdasarkan hasil analisis yang diperoleh untuk metode ARIMA diperoleh nilai MSE sebesar287,9809 dan nilai R-squared sebesar 0,659. Sedangkan untuk metode regresi nonparametrik kernel Gaussian diperoleh nilai MSE sebesar 69,1173 dan R-squared sebesar 0,9034. Berdasarkan hasil analisis yang diperoleh, metode terbaik dalam pemodelan penderita DBD yaitu metode regresi nonparametrik kernel dengan estimator Shibata diperoleh nilai bandwidth optimal sebesar 1,05 dan menggunakan fungsi kernel Gaussian.
Kata kunci : demam berdarah dengue (DBD), ARIMA, regresi nonparametrik kernel, estimator shibata, bandwidth, fungsi gaussian
ABSTRACT
MODELING OF DENGUE HEMORRHAGIC FEVER (DHF) SUFFERERS IN GRESIK DISTRICT USING ARIMA AND NONPARAMETRIC
REGRESSION OF KERNEL
DHF is one of the main isuue in the health, it can attack all age groups and also caused of the death, especially for children. The dengue virus is transmitted through the bite of Aedes Aegypti. Climatic factors become the main caused of the dengue virus, such as rainfall, temperatue, and humidity. ARIMA method is one model that used time series data based on the observed variable data. Meanwhile, the nonparametric kernel regression method is the methods that used to estimate the expectation by using the kernel function. This study aims to compare the model results of the ARIMA method and Gaussian kernel nonparametric regression through DHF’s sufferer data since the January 2013 until December 2018. Based on the analysis, ARIMA method obtained an MSE value of 287.9809 and R-squared value of 0.659.Whereas the Gaussian kernel nonparametric regression method obtained an MSE value of 69.1173 and an R-squared of 0.9034. Based on the results, the best method in modeling DHF sufferers is nonparametric kernel regression method by using Shibata estimator obtained an optimal bandwidth value of 1.05 and using the Gaussian kernel function.
Keywords : dengue hemorrhagic fever (DHF), ARIMA, kernel nonparametric regression, shibata estimator, bandwidth, gaussian function
DAFTAR ISI
ABSTRAK ... iii
ABSTRACT ... iv
DAFTAR ISI ... v
DAFTAR TABEL ... vii
DAFTAR GAMBAR ... viii
DAFTAR LAMPIRAN ... ix BAB I PENDAHULUAN ... 1 1.1 Latar Belakang ... 1 1.2 Rumusan Masalah ... 8 1.3 Tujuan ... 9 1.4 Manfaat ... 9 1.5 Batasan Masalah ... 10
BAB II KAJIAN PUSTAKA ... 11
2.1 Demam Berdarah Dengue ... 11
2.1.1 Diagnosa Klinis ... 12
2.1.2 Fase Demam Berdarah ... 13
2.2 Peramalan ... 14
2.3 Time Series ... 15
2.4 Stasioneritas ... 17
2.5 ACFdan PACF ... 20
2.5.1 ACF (Autocorrelation Function) ... 20
2.5.2 PACF (Partial Autocorrelation Function)... 22
2.6 White Noise ... 23
2.7 ARIMA (Autoregressive Integrated Moving Average) ... 24
2.7.1 Model AR (Model Autoregressive) ... 25
2.7.4 Model ARIMA (Autoregressive Integrated Moving Average) ... 27
2.8 Regresi Nonparametrik ... 28
BAB III METODE PENELITIAN ... 40
3.1 Jenis Penelitian ... 40
3.2 Jenis dan Sumber Data ... 40
3.3Teknis Analisis Data ... 40
BAB IV HASIL DAN PEMBAHASAN ... 48
4.1 Pemodelan ARIMA ... 48
4.2 Pemodelan Regresi Nonparametrik Kernel... 53
4.2.1 Pemilihan Bandwidth Optimum Dengan Estimator Shibata ... 54
4.2.2 Pembentukan Model Regresi Nonparametrik Kernel ... 55
4.3 Hasil Perbandingan Model Menggunakan ARIMA dan Regresi Nonparametrik Kernel ... 57
BAB V PENUTUP ... 61
5.1 Simpulan ... 61
5.2 Saran ... 61
DAFTAR TABEL
Tabel 2.1 Transformasi Box-cox... 18
Tabel 4.1 Model Statistik ARIMA (8, 1, 8) ... 47
Tabel 4.2 Estimasi Parameter Model ARIMA (8, 1, 8) ... 48
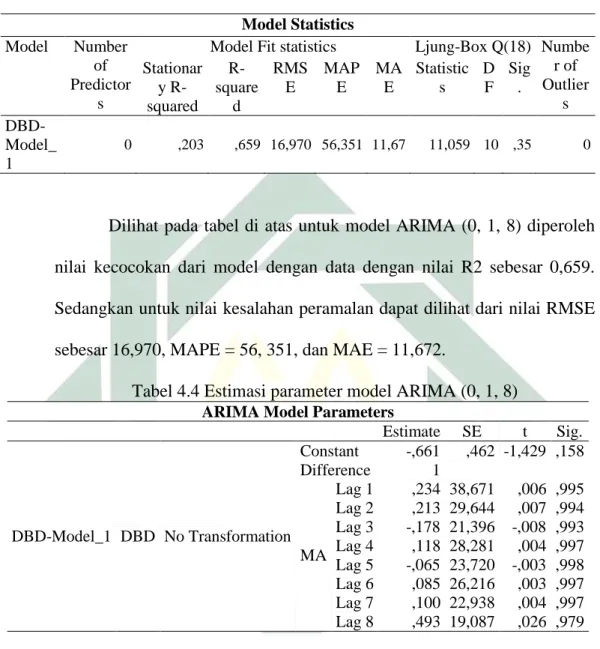
Tabel 4.3 Model Statistik ARIMA (0, 1, 8) ... 50
Tabel 4.4 Estimasi Parameter Model ARIMA (0, 1, 8) ... 51
Tabel 4.5 Model Statistik Model ARIMA (8, 1, 0) ... 53
Tabel 4.6 Estimasi Parameter Model ARIMA (8, 1, 0) ... 53
Tabel 4.7 Hasil Perbandingan Model ARIMA ... 55
Tabel 4.8 Hasil Nilai Bandwidth dengan Estimator Shibata... 56
DAFTAR GAMBAR
Gambar 3.1 Diagram Alir Penelitian ... 42
Gambar 4.1 Plot Time Series Sebelum Differencing ... 43
Gambar 4.2 Plot ACF dan PACF Sebelum Differencing ... 44
Gambar 4.3 Plot Time Series Sesudah Differencing ... 45
Gambar 4.4 Plot ACF dan PACF Differencing 1. ... 46
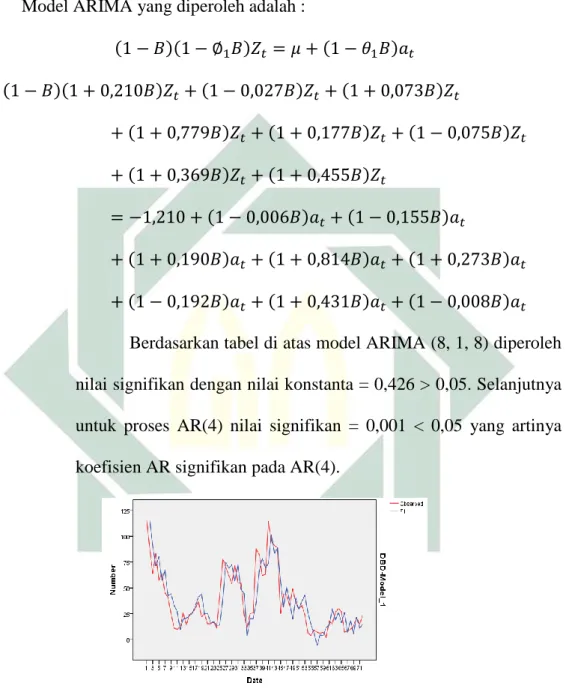
Gambar 4.5 Time Series ARIMA (8, 1, 8) ... 46
Gambar 4.6 Time Series ARIMA (0, 1, 8) ... 48
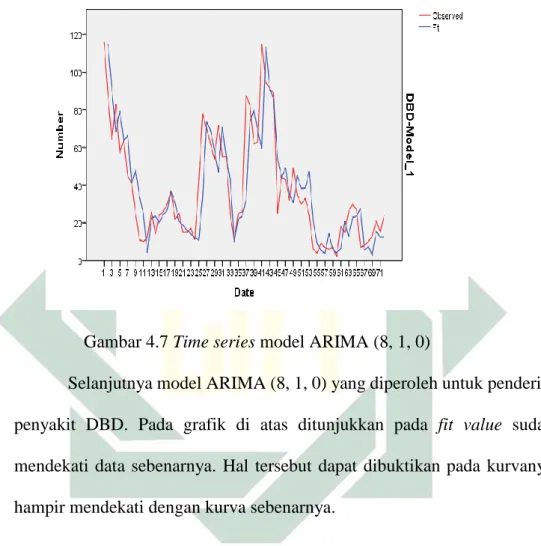
Gambar 4.7 Time Series ARIMA (8, 1, 0) ... 50
Gambar 4.8 Plot Antara Bandwidth dengan Shibata ... 54
Gambar 4.9 Plot Estimasi Metode ARIMA (0, 1, 8) ... 57
DAFTAR LAMPIRAN
Lampiran 1 Data
Lampiran 2 Program Mencari Nilai Bandwidth Optimal dengan Estimator Shibata
Lampiran 3 Program Regresi Nonparametrik Kernel SSE, MSE dan R2 Lampiran 4 Hasil Perbandingan Data Aktual dengan Menggunakan Metode
BAB I PENDAHULUAN 1.1 Latar Belakang
Tingkat dari curah hujan dan kelembaban yang tinggi merupakan salah satu faktor yang dapat mengakibatkan sumber penyakit berkembang lebih cepat. Pada saat musim hujan dapat menimbulkan banyak penyakit. Penyakit yang menjadi perhatian utama adalah penyakit Demam Berdarah Dengue (DBD). DBD adalah penyakit yang ditemukan di sebagian besar wilayah tropis dan subtropis, terutama Asia Tenggara, termasuk Indonesia. DBD merupakan salah satu masalah utama di sektor kesehatan karena dapat menyerang semua kelompok umur dan akan menyebabkan kematian, terutama pada anak-anak. Penyebab dari virus dengue dapat menyebabkan penyebaran virus DBD yang dapat ditularkan dari gigitan nyamuk Aedes Aegypti. Penyakit DBD tidak bisa dipandang remeh, harus ada penanggulangan yang serius sehingga jumlah kasus bisa ditekan. Penyakit DBD masih menjadi masalah di sektor kesehatan baik di daerah perkotaan maupun pedesaan. Berdasarkan pernyataan dari badan kesehatan WHO, DBD adalah masalah kesehatan bagi orang-orang di Indonesia di daerah tropis di garis khatulistiwa yang memungkinkan perkembangbiakan nyamuk aedes aegypti yang termasuk vektor dari virus dengue.
Beberapa faktor yang dapat mempengaruhi penyebaran dengue seperti suhu, kelembaban dan curah hujan. Nyamuk aedes aegypti dapat
2
bertahan hidup dalam jangka waktu yang lama dengan suhu antara 28℃ -32℃. Dengan faktor kepadatan penduduk dapat mempengaruhi tingginya angka kejadian penyakit DBD, semakin banyak penduduk maka peluang untuk tergigit nyamuk oleh jenis nyamuk aedes aegypti akan lebih tinggi(Suryani, 2018). Data DBD juga memuat variasi musiman, yakni akan naik atau turun pada periode waktu tertentu. Maka sangat penting untuk meneliti kejadian DBD menggunakan metode yang tepat sesuai dengan karakteristik yang ada.
Kasus Demam Berdarah Dengue (DBD) pada tahun 2017 yang terjadi di Indonesia sebanyak 68.407 kasus mengalami penurunan yang signifikan dari tahun 2016 yang berjumlah 204.171 kasus penderita penyakit DBD. Jumlah kasus DBD yang tertinggi di pulau jawa yaitu terdapat di tiga provinsi antara lain, Jawa Barat berjumlah 10.016 kasus, Jawa Timur dengan jumlah 7.838 kasus dan di Jawa Tengah sebanyak 7.400 kasus. Sedangkan untuk jumlah kasus terendah terjadi di provisnsi Maluku Utara sebanyak 37 kasus(Indrayani & Wahyudi, 2017).
Kasus penderita penyakit DBD yang terjadi di Kabupaten Gresik pada tahun 2017 sebanyak 49 kasus, pada tahun 2018 menurun hanya terjadi 18 kasus dan pada tahun 2019 mengalami peningkatan kembali pada bulan Januari terdapat 33 kasus. Penderita DBD memiliki kriteria trombosit dari World Health Organization (WHO) kurang dari 100. Penderita yang positif DBD termasuk dari semua usia, anak-anak dan juga dewasa(Puspitowati,
3
Terdapat banyak faktor yang dapat menyebabkan penyakit, begitu juga dengan penyakit demam berdarah. Faktor-faktor tersebut berasal dari individu sendiri maupun dari lingkungan. Faktor yang dapat memicu terjadinya penyakit demam berdarah adalah faktor dari lingkungan termasuk perubahan suhu, curah hujan dan kelembaban udara yang dapat mengakibatkan nyamuk lebih sering bertelur dan virus dengue berkembang biak dengan cepat.
Pentingnya kesehatan adalah modal utama dalam kehidupan manusia sehingga Rasulullah SAW menganjurkan upaya untuk menyembuhkan penyakit melalui pengobatan meskipun yang memberi kesembuhan adalah Allah SWT. Sebagaimana Firman Allah dalam Al-Qur’an Surah Ash-Shu’ara’ ayat 78-82 sebagai berikut :
ِنيِدۡهَي َوُهَف ِنَِقَلَخ يِ ذلَّٱ
٧٨
ِينِق ۡسَيَو ِنُِمِع ۡطُي َوُه يِ
لَّٱَو
ذ
٧٩
ِينِف ۡشَي َوُهَف ُت ۡضِرَم ا
َذوَإِ
٨٠
ِينِيۡ ُيُ ذمُث ِنُِتيِمُي يِ
لَّٱَو
ذ
٨١
ٓيِطَخ ِلِ َرِفۡغَي ن
َ
أ ُعَم ۡط
َ
أ ٓيِ
لَّٱَو
ذ
َٔ ٔ
ِنيِدلٱ َمۡوَي ِتِ
٨٢
Artinya :(yaitu Tuhan) yang telah menciptakan aku, maka Dialah yang menunjuki aku. Dan Tuhanku yang Dia memberi makan dan minum kepadaku. Dan apabila aku sakit Dialah yang menyembuhkan aku. Dan yang akan mematikan aku kemudian akan menghidupkan aku (kembali). Dan yang amat kuinginkan akan mengampuni kesalahanku pada hari kiamat.
4
segala penyakit diturunkan Allah kepada hambaNya selalu disertai dengan obatnya dan Allah akan mengampuni segala dosa-dosanya. Hal tersebut merupakan sebuah kenikmatan yang diberikan oleh Allah yang wajib disyukuri. Dan sebaiknya jika melakukan upaya pencegahan suatu penyakit sebelum datangnya penyakit, karena kesehatan yang diberikan Allah adalah mahal harganya. Salah satu pepatah Arab mengatakan bahwa mencegah lebih baik dari pada pengobatan.
Untuk mengantisipasi kenaikan banyak kasus penyakit demam berdarah, Menteri Kesehatan dan Dinas Kesehatan telah mengeluarkan berbagai aturan dan kebijakan. Salah satu aturannya adalah melaksanakan Pemberantasan Sarang Nyamuk (PSN) melalui pemberdayaan masyarakat yang dikenal dengan pemberantasan dengan 3M (Mengubur, Menutup, dan Menguras). Tetapi dengan berbagai upaya yang telah dilakukan belum memberikan hasil yang optimal terhadap pemberantasan sarang nyamuk sehingga penanganan kasus dari penyakit DBD masih terlambat.
Data demam berdarah merupakan data berkala, yaitu data yang disajikan dalam kurun waktu tertentu. Data berkala erat kaitannya dengan prediksi atau peramalan. Salah satu upaya preventif kasus DBD adalah dengan melakukan pemodelan data penyebaran penyakit. Suatu teknik yang digunakan untuk memperkirakan atau memprediksi peristiwa pada masa yang akan datang dengan memperhatikan peristiwa pada masa lampau dan sekarang dapat disebut dengan prediksi atau peramalan. Dengan dilakukan
5
prediksi atau peramalan ini dapat membantu untuk mengoptimalkan upaya pencegahan sejak dini agar keterlambatan tidak akan terjadi lagi.
Metode time series merupakan salah satu metode permalan yang bersifat objektif. Metode yang tepat digunakan untuk melakukan prediksi pada masa yang akan datang terhadap peristiwa dengan nilai historis pada masa lalu dan sekarang adalah metode time series. Metode time series juga menunjukkan hasil yang kontinu pada variabel yang diperoleh berdasarkan rentang waktu yang sama(Achmanda, 2018).
Peramalan DBD telah banyak dilakukan di berbagai kota atau daerah dengan menggunakan beberapa metode peramalan. Lina Zakiyah (2018) melakukan peramalan jumlah penderita penyakit DBD di kota Surabaya menggunakan perbandingan metode ARIMA dan metode INGARCH. Berdasarkan penelitian tersebut metode ARIMA memang sesuai untuk data time series yang ditampilkan pada penelitian suatu prediksi atau peramalan. Pada penelitian sebelumnya oleh Gunawan, dkk (2018) yaitu peramalan jumlah penderita DBD di kota Denpasar menggunakan Model Fungsi Transfer Multivariat adalah salah satu metode dari time series yang cocok pada penelitian suatu prediksi atau peramalan.
Para peneliti juga banyak yang menggunakan metode regresi nonparametrik kernel untuk mendapatkan hasil yang optimal dari suatu penelitian yang dilakukan. Anisa Ika Indrayanti (2014) melakukan penelitian mengenai estimator kernel cosinus dan kernel gaussian dalam model regresi nonparametrik pada data butterfly diagram siklus aktivitas
6
matahari ke-23 pada studi kasus BPD lapan watukosek, yaitu dengan melakukan perbandingan antara estimator kernel gaussian dan cosinus yang menunjukkan bahwa model terbaik adalah dengan menggunakan estimator kernel gaussian dengan nilai bandwidth 0,1 dan nilai MSE sebesar 3,67. Begitu juga pada penelitian yang dilakukan oleh Tri Ayuningtyas (2018) mengenai regresi nonparametrik kernel Nadaraya Watson dalam data time series pada studi kasus indeks harga saham gabungan terhadap kurs, inflasi dan tingkat suku bunga periode Januari 2015-Maret 2018 yang menghasilkan nilai bandwidth optimal sebesar 305,1946 dan nilai MAPE sebesar 5,4%. Penelitian yang dilakukan oleh Anisa Ika Indrayanti (2014) menunjukkan bahwa hasil yang terbaik adalah menggunakan fungsi kernel Gaussian.
Model Autoregressive Integrated Moving Average (ARIMA) merupakan model untuk meramalkan satu variabel (univariat). Model ARIMA merupakan salah satu metode yang telah dikembangkan oleh George Box dan Gwilym Jenkins yang disebut dengan metode ARIMA Box-Jenkins. Model ARIMA merupakan gabungan dari model Autoregressive (AR) dan Moving Average (MA). Secara umum model ARIMA dituliskan dengan notasi ARIMA (p, d, q ). Untuk mendapatkan model ARIMA maka akan dilakukan tiga tahap pemodelan yaitu identifikasi, penaksiran dan pengujian(Pankratz, 1991).
7
Menurut John E Hanke dkk (2000), metode runtun waktu Box-Jenkins atau metode ARIMA adalah salah satu metode yang dapat digunakan untuk mecari suatu pola data yang sesuai dengan beberapa sekelompok data. Metode ARIMA digunakan untuk melakukan permalan dengan waktu jangka pendek yang akurat, sedangkan untuk peramalan dengan waktu jangka panjang akan mendapatkan ketepatan hasil peramalan yang kurang baik(Aziz, Sayuti, & Mustakim, 2017).
Selain metode ARIMA, analisis hubungan antara sepasang variabel atau lebih dapat juga dianalisis menggunakan analisis regresi. Analisis regresi merupakan salah satu cara statistik yang dapat digunakan untuk mengetahui hubungan antara sepasang variabel atau lebih. Dalam regresi terdapat dua pendekatan yang digunakan yaitu pendekatan parametrik dan nonparametrik. Pendekatan parametrik digunakan jika model fungsi diketahui berdasarkan teori atau masa lalu. Sedangkan pendekatan nonparametrik digunakan jika tidak ada asumsi bentuk kurva atau fungsi regresi. Dalam regresi nonparametrik terdapat beberapa pendekatan yang dapat digunakan antara lain histogram, kernel, spline, dan lain-lain(Hardle, 1990).
Dalam pendekatan kernel bentuk estimasinya dipengaruhi oleh fungsi kernel 𝐾 dan bandwidth ℎ. Bandwidth ℎ adalah salah satu parameter penghalus yang digunakan untuk memeriksa kemulusan dari kurva estimasi. Penggunaan regresi nonparametrik dapat digunakan pada beberapa jenis data salah satunya adalah data time series, karena data time series sering
8
fluktuatif dan galatnya diasumsikan saling berkorelasi(Astuti, Srinadi, & Susilawati, 2018).
Berdasarkan analisis di atas dengan melihat perkembangan kasus penderita penyakit DBD di kabupaten Gresik belum pernah dilakukan permalan jumlah penderita penyakit DBD. Maka perlu dilakukan suatu pemodelan menjadi langkah preventif untuk membuat kebijakan pencegahan terjadinya peningkatan jumlah penderita penyakit DBD. Oleh karena itu dalam penelitian ini akan dilakukan pemodelan jumlah kasus penderita penyakit DBD di Kabupaten Gresik dengan menggunakan perbandingan antara model ARIMA dan regresi nonparametrik kernel.
1.2 Rumusan Masalah
Berdasarkan latar belakang di atas, maka dapat diambil pokok permasalahan sebagai berikut :
a. Bagaimana model ARIMA untuk jumlah kasus penyakit DBD di Kabupaten Gresik ?
b. Bagaimana model regresi nonparametrik kernel jumlah kasus penyakit DBD di Kabupaten Gresik ?
c. Bagaimaana perbandingan model jumlah kasus penyakit DBD menggunakan ARIMA dengan regresi nonparamterik kernel di Kabupaten Gresik ?
9
1.3 Tujuan
Berdasarkan rumusan masalah di atas, maka tujuan yang ingin dicapai pada penelitian ini adalah :
a. Mengetahui model ARIMA untuk jumlah kasus penyakit DBD di Kabupaten Gresik.
b. Mengetahui model regresi nonparametrik kernel jumlah kasus penyakit DBD di Kabupaten Gresik.
c. Mengetaahui perbandingan model jumlah kasus penyakit DBD menggunakan ARIMA dengan regresi nonparamterik kernel di Kabupaten Gresik.
1.4 Manfaat
Dalam penelitian ini diharapkan memberikan manfaat sebagai berikut : a. Dapat menambah wawasan dan memahami tentang model ARIMA dan
regresi nonparametrik kernel dalam memprediksi jumlah kasus Demam Berdarah Dengue (DBD) di Kaupaten Gresik
b. Dapat memberikan informasi mengenai model jumlah kasus penyakit DBD di Kabupaten Gresik dengan menggunakan model ARIMA dan regresi nonparametrik kernel.
c. Dapat dijadikan acuan dalam membuat pemodelan sebaran data kasus penyakit DBD di Kabupaten Gresik.
10
1.5 Batasan Masalah
Agar suatu penelitian dapat terarah, maka penulis membuat batasan masalah sebagai berikut :
a. Data yang digunakan dalam penelitian ini adalah data bulanan dari tahun 2013-2018 jumlah penderita penyakit DBD di Kabupaten Gresik. b. Metode yang digunakan dalam penelitian ini adalah model ARIMA dan
BAB II KAJIAN PUSTAKA 2.1 Demam Berdarah Dengue
Demam Berdarah Dengue (DBD) adalah salah satu penyakit yang disebabkan oleh virus dengue. Dengue merupakan virus yang ditularkan melalui nyamuk Aedes yaitu nyamuk yang paling cepat berkembang, di dunia ini banyak orang yang terinfeksi setiap tahunnya. Virus dengue ditemukan di kawasan tropik dan subtropik, untuk kawasan Indonesia dengan cuaca tropis yang sesuai untuk pertumbuhan hewan dan tumbuhan serta tempat berkembangnya berbagai macam penyakit, seperti nyamuk yang banyak menularkan pada masalah kesehatan.
Demam Berdarah Dengue (DBD) atau Dengue Haemorrhagic Fever (DHF) merupakan salah satu masalah kesehatan yang disebabkan oleh nyamuk spesies Aedes aegypti dan Aedes albopictus menjdi nyamuk penular (vektor) primer dan nyamuk spesies Aedes polynesiensi, Aedes scutellaris serta Aedes niveus sebagai vektor sekunder(Indrayani & Wahyudi, 2017).
Demam Berdarah Dengue (DBD) adalah salah satu masalah kesehatan warga negara di Indonesia dimana jumlah penderitanya semakin bertambah dan penyebarannya juga semakin luas. Penyakit DBD merupakan masalah kesehatan masyarakat yang menular dan pada
12
umumnya menyerang usia anak-anak umur kurang dari 15 tahun dan juga dapat menyerang pada orang dewasa(Widoyono, 2005).
Seseorang yang terkena penyakit DBD ditandai dengan demam secara mendadak antara 2 sampai dengan 7 hari tanpa faktor yang jelas, kondisi tubuh lemah disertai dengan tanda pendarahan pada kulit berbentuk bintik pendarahan (petechie), lebam (echymosis), ruam (purpura) dan kadang-kadang mimisan(Indrawan, 2001).
2.1.1 Diagnosa Klinis
Berdasarkan jenis gejala yang ditimbulkan infeksi virus dengue dapat dikelompokkan menjadi 3, yaitu(Indonesia, 2010):
a. Demam Dengue (DD)
Demam Dengue (DD) memberikan gejala infeksi yang berbeda pada golongan umur tertentu. Gejala pada bayi adalah demam disertai dengan munculnya ruam. Gejala pada orang dewasa adalah sakit kepala, demam tinggi, nyeri di belakang mata, mual dan muntah, dan muncul ruam. Penyakit ini disertai dengan menurunnya keping darah (trombosit) dan sel darah putih (leukosit)(Sitio, 2008).
b. Demam Berdarah Dengue (DBD)
Demam Berdarah Dengue (DBD) menimbulkan gejala yang hampir sama pada gejala Demam Dengue (DD). Namun pada kasus DBD terjadi pendarahan yang hebat, pelebaran hati lebih
13
dari 2 cm, dan kenaikan hematokrit dengan penurunan jumlah trombosit yang cepat.
c. Dengue Shock Syndrome (DSS)
Pada kasus ini terjadi apabila seseorang terserang virus dengue untuk yang kedua kalinya. Gejala pada kasus ini adalah nadi berdenyut cepat, kulit dingin dan lembab, gelisah, dan terjadi kebocoran cairan di luar pembuluh darah. DSS merupakan infeksi virus dengue terparah yang dapat mengakibatkan kematian.
2.1.2 Fase Demam Berdarah
Setelah terinfeksi virus dengue pada penderita penyakit demam berdarah akan mengalami 3 fase, yaitu(Indonesia, 2010) :
a. Fase Febris
Pada fase ini panas mendadak tinggi selama 2 sampai dengan 7 hari disertai muka kemerahan, sakit kepala, dan sakit di seluruh tubuh.
b. Fase Kritis
Pada fase ini terjadi penurunan suhu tubuh, kerusakan pada pembuluh darah, dan timbulnya kebocoran plasma yang berproses selama 24 sampai 48 jam pada hari ke 3 sampai 7 hari. Pada fase kritis dapat terjadi shock akibat dari tanda fase kritis tersebut.
14
c. Fase Pemulihan
Setelah melewati pada fase ke dua yaitu fase kristis terjadi pengembalian cairan secara perlahan pada 48 sampai 72 jam setelahnya. Pada fase pemulihan ini keadaan penderita penyakit demam berdarah mulai membaik.
2.2 Peramalan
Peramalan (forecasting) adalah suatu sistem yang digunakan untuk meramalkan atau memprediksi suatu hal, peristiwa atau kejadian pada masa yang akan datang dengan memperhatikan data yang signifikan pada masa lampau dan sekarang. Metode peramalan dibagi menjadi dua yaitu metode yaitu kualitatif dan kuantitatif. Metode kualitatif bersifat subjektif karena hanya menggunakan suatu anggapan dari para ahli dan hasilnya sesuai dengan peneliti. Sedangkan metode kuantitatif bersifat objektif dan data bersumber pada masa lampau(Pramana & Anggraeni, 2016).
Dalam kehidupan segala sesuatu tidak ada yang pasti, maka dari itu dilakukan strategi melalui peramalan atau prediksi untuk memeperkirakan segala sesuatu yang tidak pasti tersebut. Prediksi dalam ilmu Matematika hanya dapat meminimumkan akibat dari ketidakpastian dengan meminimalisir kesalahan suatu prediksi yang dapat dilihatdari nilai Mean Square Error (MSE), Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE) dan lain sebagainya. Jika salah satu dari nilai kesalahan tersebut semakin kecil maka semakin baik nilai hasil peramalan
15
2.3 Time Series
Data berkala atau time series merupakan data yang dikumpulkan dari waktu ke waktu untuk mengilustrasikan suatu kemajuan atau kecondongan suatu peristiwa atau kejadian dan pada dasarnya jarak atau interval dari waktu ke waktu yaitu sama(Boediono & Wayan, 2004). Time series digunakan untuk memperoleh gambaran dari suatu keadaan atau sifat variabel di waktu yang lampau untuk peramalan dari nilai variabel pada masa yang akan datang.
Adapun komponen-komponen pada data berkala atau time series adalah(Hanke & Wichers, 2005):
a. Gerakan Horizontal
Geraka horizontal merupakan pergerakan data yang berfluktuasi di sekitar nilai konstan atau rata-rata yang membentuk garis horizontal yang disebut dengan data stasioner.
b. Gerakan Trend
Pola pada gerakan trend ini adalah jika suatu data bergerak pada jangka waktu tertentu dan cenderung menuju ke satu arah balik naik atau turun.
16
c. Gerakan musiman
Gerakan musiman adalah gerakan yang berulang-ulang secara teratur selama kurang lebih satu tahun, misalnya pola yang berulang setiap minggu, setiap bulan, atau kuartal. Pada kuartal terjadi setiap empat bulan.
Menurut Boediono& Wayan (2004), komponen rangkaian waktu dibagi menjadi empat jenis, yakni:
a. Gerakan jangka panjang (long time movement)
Gerakan jangka panjang adalah suatu gerakan yang menunjukkan arah perkembangan secara umum deret berkala yang meliputi jangka waktu yang panjang. Pada umumnya jangka waktu yang digunakan adalah sepuluh tahun lebih. Ciri-ciri dari gerakan jangka panjang adalah menunjukkan variasi sekuler yang menyerupai garis lurus yang disebut dengan garis arah (trend line).
b. Gerakan musiman (seasonal variation)
Gerakan musiman ini mempunya ciri-ciri pola tetap dari waktu ke waktu dengan jangka waktu tertentu. Gerakan musiman terjadi akibat karena adanya peristiwa-peristiwa tertentu.
c. Gerakan melingkar (siklis)
Gerakan melingkar merupakan variasi rangkaian waktu yang menunjukkan gerakan berayun pada sekitar arah atau kurva arah. Lingkaran atau siklik bersifat berkala atau tidak.
17
d. Gerakan acak (random)
Gerakan acak merupakan rangkaian waktu yang menunjukkan gerakan yang tak teratur yang dapat disebabkan oleh beberapa faktor di luar dugaan, seperti wabah, gempa bumi dan lain sebagainya.
2.4 Stasioneritas
Stasioneritas adalah suatu bentuk dimana tidak ada perubahan rata-rata (mean) dan varians dari waktu ke waktu atau keduanya selalu konstan (tidak terjadi pertumbuhan atau penurunan) pada setiap waktu. Data stasioner merupakan data dimana rata-rata nilai pada suatu data tidak ada perubahan pada waktu, dengan kata lain fluktuasi data berada di sekitar nilai rata-rata dan varians yang konstan.
Para peniliti mengamati pola pada plot data digunakan untuk memutuskan data yang diperoleh stasioner atau nonstasioner. Jika plot data deret berkala cenderung konstan yaitu tidak terdapat kenaikan atau penurunan maka data sudah dikatakan stasioner.
Terdapat cara yang dapat dilakukan untuk mengatasi ketidakstasioneran. Ketidakstasioneran data terbagi menjadi dua, yaitu data tidak stasioner dalam rata-rata dan data tidak stasioner dalam varian. Apabila data tidak stasioner dalam rata-rata dapat dilakukan pembedaan (differencing) yaitu penyelisihan data atau pengurangan data tertentu dengan data sebelumnya dengan berurutan. Jika differencing ordo satu masih belum meghasilkan data yang stasioner maka akan dilanjut
18
differencing pada ordo kedua, dan seterusnya sehingga diperoleh data yang stasioner.
Notasi yang digunakan dalam metode pembeda (differencing) adalah operator shift mundur (backward shift) yang disimbolkan dengan huruf 𝐵 dengan penerapan sebagai berikut :
𝐵𝑋𝑡= 𝑋𝑡−1 (2.1)
Notasi 𝐵 yang dipasangkan dengan 𝑋𝑡 digunakan untuk menggeser data satu periode ke belakang dan jika dua penerapan 𝐵 dengan 𝑋𝑡 untuk menggeser data dua periode ke belakang sebagai berikut :
𝐵(𝐵𝑋𝑡) = 𝐵2𝑋
𝑡 = 𝑋𝑡−2 (2.2)
Ketika salah satu data deret berkala tidak stasioner, maka data tersebut dapat dibuat mendekati data stasioner dengan cara melakukan differencing pertama dari deret data dengan persamaan :
Differencing pertama:
𝑋′𝑡 = 𝑋𝑡− 𝑋𝑡−1 (2.3)
Mengaplikasikan operator shift mundur sehingga persamaan dapat ditulis kembali menjadi :
𝑋′𝑡 = 𝑋𝑡− 𝐵𝑋𝑡= (1 − 𝐵) 𝑋𝑡 (2.4)
Differencing pertama dinyatakan dengan (1 − 𝐵) serupa dengan differencing kedua yang dapat dihitung menggunakan persamaan sebagai berikut :
19 Differencing kedua: 𝑋"𝑡= 𝑋′𝑡− 𝑋′𝑡−1 = (𝑋𝑡− 𝑋𝑡−1) − (𝑋𝑡−1− 𝑋𝑡−2) = (𝑋𝑡− 2𝑋𝑡−1+ 𝑋𝑡−2) (2.5) = (1 − 2𝐵 + 𝐵2)𝑋 𝑡 = (1 − 𝐵2)𝑋𝑡
Differencing kedua diberi notasi (1 − 𝐵2)
Tujuan dari menghitung differencing adalah untuk memperoleh data stasioner secara umum ketika ditemukan differencing pada orde ke-n untuk memperoleh data stasioner dapat ditulis sebagai berikut :
𝑋𝑡𝑛 = (1 − 𝐵)𝑛𝑋
𝑡 (2.6)
Untuk menstasionerkan data dalm bentuk varian dapat dilakukan dengan proses transformasi, secara umum dapat dilakukan dengan power transformation (𝜆) yaitu : 𝑇(𝑋𝑡) = { 𝑋𝑡𝜆−1 𝜆 , 𝜆 ≠ 0 ln 𝑋𝑡, 𝜆 = 0 (2.7)
Dengan (𝜆) adalah parameter transformasi dan 𝑇(𝑋𝑡) merupakan fungsi transformasi terhadap 𝑋𝑡. Berikut merupakan nilai dari 𝜆 beserta transformasinya(Makridakis, Wheelwright, & McGee, 1999) :
20
Tabel 2.1 Transformasi Box-Cox Nilai 𝝀 Transformasi -1 1 𝑋𝑡 -0,5 1 √𝑋𝑡 0 ln 𝑋𝑡 0,5 √𝑋𝑡 1 𝑋𝑡 (Stasioner) 2.5 ACFdan PACF
2.5.1 ACF (Autocorrelation Function)
Suatu proses (𝑋𝑡) yang stasioner mempunyai rata-rata konstan
𝐸(𝑋𝑡) = 𝜇 dan varian konstan 𝑉𝑎𝑟(𝑋𝑡) = 𝐸(𝑋𝑡− 𝜇)2 = 𝜎2. Kovarian
antar 𝑋𝑡 dan 𝑋𝑡+𝑘 adalah
𝛾𝑘 = 𝐶𝑜𝑣(𝑋𝑡, 𝑋𝑡+𝑘) = 𝐸(𝑋𝑡− 𝜇)(𝑋𝑡+𝑘− 𝜇). (2.8)
Autokorelasi (ACF) adalah korelasi atau hubungan antara data pengamatan pada suatu deret yang berkala. Untuk menghitung koefisien autokorelasi lag-k (𝜌𝑘) antara variabel 𝑋𝑡 dan 𝑋𝑡+𝑘 pada suatu populasi yaitu
𝜌𝑘 = 𝑐𝑜𝑣(𝑋𝑡 ,𝑋𝑡+𝑘)
√𝑣𝑎𝑟(𝑋𝑡)√𝑣𝑎𝑟(𝑋𝑡+𝑘) (2.9)
Keterangan :
Var(𝑋𝑡) = Var(𝑋𝑡+𝑘) = 𝛾0, 𝛾𝑘 dinamakan fungsi autokovarian
21
Pada koefisein autokorelasi 𝜌𝑘 tidak diketahui dan diperkirakan dengan (𝑟𝑘) yang merupakan koefisien korelasi pada sampel dengan rumus : 𝑟𝑘 = ∑𝑛−𝑘𝑡=1(𝑥𝑡−𝑥̅)(𝑥𝑡+𝑘−𝑥̅) ∑𝑛𝑡=1(𝑥𝑡−𝑥̅)2 (2.10) Keterangan : 𝑟𝑘 = koefisien korelasi
𝑥𝑡 = nilai variabel X pada periode t
𝑥𝑡+𝑘 = nilai variabel X pada periode t+k
𝑥̅ = nilai rata-rata variabel X
Untuk mengetahui apakah koefisien autokorelasi yang diperoleh signifikan atau tidak signifikan maka perlu dilakukan pengujian dengan hipotesis
𝐻0: 𝜌𝑘= 0 (koefisien autokorelasi tidak signifikan)
𝐻1: 𝜌𝑘 ≠ 0 (koefisien autokorelasi signifikan) Uji statistik yang digunakan adalah :
𝑡 = 𝑟𝑘
𝑆𝐸(𝑟𝑘) (2.11)
𝑆𝐸(𝑟𝑘) = √1+2 ∑𝑘−1𝑡=1𝑟𝑖2
𝑛 (2.12)
Keterangan :
𝑆𝐸(𝑟𝑘) = standar error untuk autokorelasi pada lag ke-k
𝑟𝑖 = autokorelasi pada lag ke-i
22
Kriteria keputusan 𝐻0 ditolak jika 𝑡𝛼 2,𝑛−1
< 𝑡 < −𝑡𝛼 2,𝑛−1
2.5.2 PACF (Partial Autocorrelation Function)
Autokorelasi parsial adalah nilai keeratan hubungan antara variabel
𝑋𝑡 dan 𝑋𝑡+𝑘 setelah hubungan linear dengan variabel 𝑋𝑡+1 , 𝑋𝑡+2 ... 𝑋𝑡+𝑘
dihilangkan sehingga fungsi autokorelasi parsial dapat dirumuskan
𝛷𝑘𝑘 = 𝐶𝑜𝑟𝑟(𝑋𝑡, 𝑋𝑡+𝑘|𝑋𝑡+1, … , 𝑋𝑡+𝑘−1 ) (2.13)
Koefisien autokorelasi parsial digunakan untuk menaksir derajat hubungan antara nilai-nilai sekarang dengan nilai-nilai sebelumnya dengan pengaruh nilai variabel time lag yang lain dianggap konstan.
Autokorelasi parsial diperoleh melalui model regresi dimana variabel dependent 𝑋𝑡+𝑘 dari proses stasioner pada lag k, sehingga variabel
𝑋𝑡+𝑘−1, 𝑋𝑡+𝑘−2, … , 𝑋𝑡 dapat ditulis sebagai berikut :
𝑋𝑡+𝑘 = 𝛷𝑘1𝑋𝑡+𝑘−1+ 𝛷𝑘2𝑋𝑡+𝑘−2+ ⋯ + 𝛷𝑘𝑖𝑋𝑡+1+ 𝜀𝑡+𝑘 (2.14) Keterangan :
𝛷𝑘𝑖 = parameter regresi ke-i
𝜀𝑡+𝑘 = residual normal yang tidak berkorelasi dengan 𝑋𝑡+𝑘−𝑗 untuk 𝑗 ≥ 1, maka diperoleh fungsi autokorelasi sebagai berikut :
𝜌𝑗 = 𝛷𝑘1𝜌𝑗+ 𝛷𝑘2𝜌𝑗−2+ ⋯ + 𝛷𝑘𝑘𝜌𝑗−𝑘 (2.15)
Untuk j = 1, 2, ..., k sehingga diperoleh persamaan
𝜌1 = 𝛷𝑘1𝜌0+ 𝛷𝑘2𝜌1+ ⋯ + 𝛷𝑘𝑘𝜌𝑘−1
𝜌2 = 𝛷𝑘1𝜌1 + 𝛷𝑘2𝜌0+ ⋯ + 𝛷𝑘𝑘𝜌𝑘−2
23
2.6 White Noise
White noise adalah suatu barisan dari variabel acak yang berdiri sendiri dan berdistribusi normal. White noise mempunyai keadaan stasioneritas yang lebih erat dimana nilai autokovarian harus nol(Prahesti, Puspita, & Agustina, 2016). Data deret berkala mengalami proses white noise jika autokorelasi antara deret 𝑋𝑡 dan 𝑋𝑡+𝑘 untuk semua lag k yang mendekati nol, nilai antara lag pada deret tidak berkorelasi satu sama lain.
Proses {𝑎𝑡} disebut suatu proses white noise jika {𝑎𝑡} merupakan barisan variabel acak yang tidak berkorelasi dari suatu distribusi dengan rata-rata konstan E(𝑎𝑡) = 𝜇0 yang biasa diasumsikan dengan nol, varians konsta Var(𝑎𝑡) = 𝜎𝛼2 dan 𝛾
𝑘 = Cov(𝑎𝑡, 𝑎𝑡+𝑘) = 0 untuk semua k ≠ 0. Oleh karena itu suatu proses white noise {𝑎𝑡} adalah stasioner dengan fungsi autokovarian. 𝛾𝑘 = {𝜎𝑎 2, 𝑘 = 0 0, 𝑘 ≠ 0 (2.16) Fungsi autokorelasi 𝜌𝑘 = {1, 𝑘 = 00, 𝑘 ≠ 0 (2.17)
Fungsi autokorelasi parsial
𝛷𝑘𝑘 = {1, 𝑘 = 00, 𝑘 ≠ 0 (2.18)
Untuk mengetahui apakah suatu deret memenuhi suatu proses white noise maka dilakukan uji hipotesis berikut :
24
Menggunakan uji statistik Ljung-Box atau Box Pierce
𝑄 = 𝑛(𝑛 + 2) ∑ 𝑟2𝑘
𝑛−𝑘 𝑚
𝑘−1 (2.19)
Keterangan :
n = banyaknya observasi dalam deret berkala k = lag waktu
m = banyaknya lag yang diuji
𝑟𝑘 = koefisien autokorelasi pada periode ke-k
Jika autokorelasi dihitung dari proses white noise maka uji statistik Q berdistribusi 𝑋2 dengan derajat bebas m, sedangkan untuk residual model peramalan uji statistik Q berdistribusi 𝑋2 dengan derajat bebas m dikurangi banyaknya parameter yang diestimasi dalam model. Untuk pengambilan keputusan jika 𝐻0 ditolak adalah 𝑄 ≥ 𝑋2
𝛼,𝑑𝑓. 2.7 ARIMA (Autoregressive Integrated Moving Average)
ARIMA merupakan salah satu model peramalan time series yang hanya bersumber pada data variabel yang akan diamati. ARIMA memiliki sifat fleksibel dan tingkat akurasi peramalan yang cukup tinggi(Putri & Anggraeni, 2018). Model ARIMA merupakan model yang mengabaikan suatu variabel independen dalam melakukan prediksi. Model ARIMA mengaplikasikan data pada masa lampau dan sekarang dari variabel dependen untuk membuat prediksi dalam jangka waktu pendek yang akurat. Tujuan model ARIMA adalah untuk mendefinisikan pada hubungan statistik yang baik antara variabel yang diprediksi dan variabel pada masa lampau sehingga peramlan dapat
25
Model ARIMA pada umumnya (Box-Jenkins) dapat dirumuskan dengan notasi ARIMA (p,d,q) dalam bentuk ini dapat dijelaskan bahwa notasi p menunjukkan orde / derajat Autoregressive (AR), d menunjukkan orde / derajat Differencing (pembedaan) dan q menunjukkan orde / derajat Moving Average (MA)(Hendrawan, 2012).
2.7.1 Model AR (Model Autoregressive)
Model Autoregressive adalah salah satu model yang menggambarkan variabel dependen dan dipengaruhi oleh variabel dependen itu sendiri pada periode dan waktu sebelumnya. Secara umum untuk model Autoregressive dengan ordo AR (p) atau model ARIMA (p,0,0) dinyatakan sebagai berikut(Box, Jenkins, & Reinsel, 2008) :
𝑍𝑡 = ∅1𝑍𝑡−1+ ∅2𝑍𝑡−2+ ⋯ + ∅𝑝𝑍𝑡−𝑝+ 𝑎𝑡 (2.20)
Keterangan :
∅𝑝 = parameter autoregressive ke-p
𝑍𝑡−𝑝 = independen variabel
𝑎𝑡 = white noise nilai kesalahan pada saat t
Variabel independen merupakan variabel yang sejenis pada periode t terakhir, sedangkan 𝑎𝑡 adalah nilai error atau unit residual yang merupakan gangguan acak yang tidak dapat dijelaskan oleh model. Perhitungan autoregressive dapat dilakukan dalam beberapa proses sebagai berikut :
26
b. Menentukan nilai orde p (menetukan panjang persamaan yang terbentuk)
c. Mengestimasi nilai koefisien autoregressive∅1, ∅2, … , ∅𝑝
Setelah mendapatkan model yang sesuai, maka model dapat digunakan sebagai prediksi atau nilai ramal pada masa yang akan datang.
2.7.2 Model MA (Moving Average)
Model moving average (MA) dengan orde q dapat dinotasikan dengan MA(q) atau ARIMA (0,0,q) dengan bentuk umum dapat dinotasikan sebagai berikut(Box, Jenkins, & Reinsel, 2008) :
𝑍𝑡 = 𝑎𝑡− 𝜃1𝑎𝑡−1− 𝜃2𝑎𝑡−2− ⋯ − 𝜃𝑞𝑎𝑡−𝑞 (2.21)
Keterangan :
𝜃𝑞 = parameter moving average ke - q
𝑎𝑡−1, 𝑎𝑡−2, … , 𝑎𝑡−𝑞 = selisih nilai aktual dengan nilai prakiraan
Persamaan model di atas adalah nilai 𝑍𝑡 tergantung pada nilai yang sebelumnya dari pada nilai variabel itu sendiri. Untuk melakukan pendekatan antara proses autoregressive (AR) dan moving average (MA) diperlukan pengukuran autokorelasi nilai berturut-turut dari 𝑍𝑡, sedangkan untuk model moving average mengukur autokorelasi antara nilai error atau nilai residualnya.
27
2.7.3 Model ARMA (Autoregressive Moving Average)
Model ARMA merupakan penggabungan dari model autoregressive (AR) dan model moving average (MA) dengan orde ARMA (p,q). Persamaan ARMA gabungan dari model AR dan MA dapat dinotasikan dalam bentuk umum sebagai berikut(Box, Jenkins, & Reinsel, 2008) :
𝑍𝑡 = ∅1𝑍𝑡−1+ ∅2𝑍𝑡−2+ ⋯ + ∅𝑝𝑍𝑡−𝑝+ 𝑎𝑡− 𝜃1𝑎𝑡−1− 𝜃2𝑎𝑡−2−
⋯ − 𝜃𝑞𝑎𝑡−𝑞 (2.22)
2.7.4 Model ARIMA (Autoregressive Integrated Moving Average)
Model ARIMA disebut dengan runtut waktu Box-Jenkins. Model ARIMA dapat digunakan untuk asumsi jangka pendek, sedangkan untuk asumsi jangka panjang ketepatan asumsinya kurang baik. Model ARIMA merupakan gabungan dari dua model yaitu model autoregressive (AR) yang diintegrasikan dengan model moving average (MA). Pada umumnya model ARIMA dapat dinotasikan dengan (p,d,q), denga p adalah derajat proses AR, d adalah orde pembedaan dan q adalah derajat proses MA(Nachrowi & Usman, 2006).
Model umum dari autoregressive orde p, integrate orde d, dan moving average orde q yang menjadi satu sehingga terbentuk ARIMA (p,d,q) yang merupakan hasil penggabungan antara proses stasioner dengan proses nonstasioner yang telah distasionerkan. Bentuk umum model ARIMA (p, d, q) adalah(Ekananda, 2014):
28 Keterangan : 𝜇 = konstanta (1 − 𝐵) = pembedaan pertama (1 − ∅1𝐵)𝑍𝑡 = koefisien model AR (1 − 𝜃1𝐵)𝛼𝑡 = koefisien model MA 2.8 Regresi Nonparametrik
Regresi nonparametrik dapat digunakan pada data yang mempunyai distribusi normal ataupun tidak berdistribusi normal. Regresi nonparametrik pertamakali diperkenalkan oleh Francis Galtom pada tahun 1885. Pendekatan nonparametrik merupakan pendekatan regresi yang sesuai untuk pola yang tidak diketahui bentuknya, dan tidak terdapat pengalaman informasi masa lalu mengenai pola data
Estimasi juga dapat dilakukan berdasarkan pada pendekatan yang tidak terikat dengan asumsi bentuk kurva regresi khusus yang memberikan fleksibilitas yang lebih besar. Kurva regresi yang sesuai, maka pendekatan ini dinamakan dengan pendekatan nonparametrik.
Regresi nonparametrik merupakan metode regresi untuk memahami pola hubungan antara variabel terikat y dan variabel bebas x. Regresi nonparametrik tidak membutuhkan asumsi mengenai bentuk kurva regresi, oleh karena itu regresi nonparametrik bersifat fleksibel terhadap perubahan pola data. Secara umum hubungan variabel dapat dinyatakan sebagai 𝑌𝑖 = 𝑚(𝑋𝑖) + 𝜀𝑖, 𝑖 =
29
diketahui disebut dengan fungsi regresi atau kurva regresi. Fungsi regresi hanya diasumsikan dalam suatu ruang fungsi yang berdimensi tidak hingga. Kemudian estimasi 𝑚(𝑋𝑖) dapat dilakukan berdasarkan data pengamatan dengan teknik penghalus tertentu.
Terdapat beberapa teknik penghalus dalam regresi nonparametrik yaitu histogram, estimasi kernel, estimasi spline, deret fourier, dan k-NN.
2.8.1 Fungsi Kernel
Model pendekatan nonparametrik yang umum digunakan adalah estimator kernel. Hal ini disebabkan estimator kernel mempunyai beberapa kelebihan yaitu estimator kernel mempunyai bentuk yang fleksibel dan mudah disesuaikan dan estimator kernel mempunyai rata-rata kekonvergenan yang relatif cepat.
Beberapa jenis fungsi kernel sebagai berikut : a. Kernel Gaussian : 𝐾(𝑢) = 1 √2𝜋exp (− 1 2𝑢 2)𝐼 (−∞,∞)(𝑢) b. Kernel Kudrat : 𝐾(𝑢) =15 8 (1 − 4𝑢 2)2𝐼 [−0,5 ;0,5](𝑢) c. Kernel Segitiga : 𝐾(𝑢) = (1 − |𝑢|)𝐼[−1,1](𝑢) d. Kernel Epanechnikov : 𝐾(𝑢) =3 4(1 − 𝑢 2)𝐼 [−1,1](𝑢) e. Kernel Uniform : 𝐾(𝑢) =1 2𝐼[−1,1](𝑢)
Secara umum untuk fungsi kernel pada dimensi satu dapat didefinisikan sebagai berikut :
𝐾ℎ(𝑢) = 1
ℎ𝐾 ( 𝑢
30
Fungsi kernel 𝐾 merupakan fungsi yang kontinu, terbatas, simetrik, dan terintegral ke satu, ∫−∞∞ 𝐾(𝑢)𝑑𝑢 = 1.
Jika suatu fungsi kernel memenuhi syarat berikut :
a. ∫−∞∞ 𝐾(𝑢)𝑑𝑢 = 1 b. ∫−∞∞ 𝑢𝐾(𝑢)𝑑𝑢 = 0 c. ∫∞ 𝑢2𝐾(𝑢)𝑑𝑢 ≠ 0 −∞ d. ∫∞ 𝐾(𝑢2)𝑑𝑢 −∞ < ∞
Maka fungsi kernel 𝐾 termasuk fungsi berordo 2.
2.8.2 Estimasi Densitas Kernel
Estimator densitas kernel merupakan salah satu pengembangan dari estimator histogram. Estimator densitas kernel adalah metode pendekatan dengan fungsi kernel terhadap fungsi densitas yang belum diketahui. Pemulusan pada densitas kernel bergantung dari fungsi kernel dan nilai bandwidth. Estimator densitas kernel dengan fungsi 𝑓̂(𝑥) adalah (Zulfikar, 2008): 𝑓̂(𝑥)𝑑𝑥 =1 𝑛∑ 𝐾ℎ(𝑥𝑖 − 𝑥) 𝑛 𝑖=1 𝑓̂(𝑥)𝑑𝑥 = 1 𝑛ℎ∑ 𝐾 ( 𝑥𝑖−𝑥 ℎ ) 𝑛 𝑖=1 (2.25)
Dengan 𝐾 adalah fungsi kernel yang kontinu dan spesifik yang memenuhi persamaan ∫ 𝐾(𝑥)𝑑𝑥 = 1. Selanjutnya ℎ adalah nilai bandwidth dengan bilangan positif. Beberapa asumsi kernel yang harus dipenuhi adalah sebagai berikut (Reyes, Fernandez, & Cao, 2014):
31
a. 𝐾(𝑥) ≥ 0, untuk semua 𝑥
b. 𝐾(𝑥) bersifat simetris, 𝐾(−𝑥) = 𝐾(𝑥), untuk semua 𝑥
c. ∫ 𝐾(𝑥)𝑑𝑥 = 1
d. ∫ 𝑥𝐾(𝑥)𝑑𝑥 = 0
e. ∫ 𝑥2𝐾(𝑥)𝑑𝑥 = 𝜇2𝐾 ≠ 0 dengan 𝜇2𝐾 momen kedua tertentu
f. ∫[𝐾(𝑥)]2𝑑𝑥 = ∫ 𝐾2(𝑥)𝑑𝑥 = ‖𝐾‖22 = 𝐸[𝐾2(𝑥)] = 𝑅(𝐾)
2.8.3 Regresi Nonparametrik Kernel
Regresi nonparametrik kernel dengan menggunakan pendekatan linear konstan menggunakan sampel random (𝑥𝑖, 𝑦𝑖), 𝑖 = 1, 2, 3, … , 𝑛. Estimasi kurva 𝑦̂ = 𝑚̂ (𝑥) diperoleh dengan meminimumkan :
∑𝑛 𝜀𝑖2
𝑖=1 𝐾ℎ(𝑥 − 𝑋𝑖) = ∑𝑛𝑖=1{𝑦𝑖− [𝛿0+ 𝛿1(𝑥 − 𝑋𝑖) + ⋯ + 𝛿𝑝(𝑥 −
𝑋𝑖)𝑝]}2𝐾
ℎ(𝑥 − 𝑋𝑖)
Dimana 𝐾 adalah fungsi kernel dan ℎ disebut bandwidth(Hafiyusholeh, 2006).
2.9 Estimasi Bias
Pada estimator densitas kernel fungsi 𝑓̂(𝑥) merupakan estimator yang tak bias dari suatu fungsi densitas 𝑓(𝑥). Jika fungsi 𝑓̂(𝑥) adalah estimator densitas kernel dari suatu fungsi densitas 𝑓(𝑥) pada titik 𝑥𝜖𝑅 dan 𝑋𝑖 berdistribusi ekuivalen dengan fungsi densitas 𝑓(𝑥), maka untuk estimasi bias adalah(Apriani, 2015):
32 𝐸[𝑓̂(𝑥)] = 𝐸 [1 𝑛ℎ∑ 𝐾 ( 𝑋𝑖− 𝑥 ℎ ) 𝑛 𝑖=1 ] 𝐸[𝑓̂(𝑥)] = 1 𝑛ℎ∑ 𝐸 [𝐾 ( 𝑋𝑖− 𝑥 ℎ )] 𝑛 𝑖=1 𝐸[𝑓̂(𝑥)] =1 ℎ𝐸 [𝐾 ( 𝑋𝑖 − 𝑥 ℎ )] 𝐸[𝑓̂(𝑥)] =1 ℎ∫ 𝐾 ( 𝑦 − 𝑥 ℎ ) 𝑓(𝑦)𝑑𝑦 Misalkan 𝑠 =𝑦−𝑥
ℎ maka 𝑑𝑦 = ℎ𝑑𝑠, sehingga didapatkan :
𝐸[𝑓̂(𝑥)] =1
ℎ∫ 𝐾(𝑠)𝑓(𝑥 + 𝑠ℎ)ℎ𝑑𝑠
𝐸[𝑓̂(𝑥)] = ∫ 𝐾(𝑠)𝑓(𝑥 + 𝑠ℎ)𝑑𝑠
Dengan mengaplikasikan suatu pendekatan ekspansi taylor dari fungsi𝑓(𝑥 + 𝑠ℎ) dan nilai 𝑠ℎ = 0 ketika ℎ → 0 sehingga untuk setiap kernel pada orde ke-𝑣 dapat menggunakan kaidah sebagai berikut (Saputra & Listyani, 2016): 𝑓(𝑥 + 𝑠ℎ) = 𝑓(𝑥) + 𝑓′(𝑥)𝑠ℎ + 1 2!𝑓 ′′(𝑥)ℎ2𝑠2+ 1 2!𝑓 ′′′(𝑥)ℎ3𝑠3+ ⋯ + 1 𝑣!𝑓 𝑣(𝑥)ℎ𝑣𝑠𝑣+ 𝑜(ℎ𝑣)
Dengan 𝑜(ℎ𝑣) adalah sisa dari orde yang lebih rendah dari ℎ𝑣 ketika ℎ → 0
sehingga ekspansi taylor orde 2 untuk fungsi𝑓(𝑥 + 𝑠ℎ) adalah :
𝑓(𝑥 + 𝑠ℎ) = 𝑓(𝑥) + 𝑓′(𝑥)𝑠ℎ + 1
2!𝑓
′′(𝑥)ℎ2𝑠2+ 𝑜(ℎ𝑣)
33 𝐸[𝑓̂(𝑥)] = ∫ 𝐾(𝑠) [𝑓(𝑥) + 𝑓′(𝑥)ℎ𝑠 +1 2𝑓 ′′(𝑥)ℎ2𝑠2+ 𝑜(ℎ2)] 𝑑𝑠 𝐸[𝑓̂(𝑥)] = 𝑓(𝑥) ∫ 𝐾(𝑠)𝑑𝑠 + 𝑓′(𝑥)ℎ ∫ 𝑠𝐾(𝑠)𝑑𝑠 +1 2𝑓 ′′(𝑥)ℎ2∫ 𝑠2𝐾(𝑠)𝑑𝑠 + 𝑜(ℎ2) ∫ 𝐾(𝑠)𝑑𝑠 𝐸[𝑓̂(𝑥)] = 𝑓(𝑥)(1) + 𝑓′(𝑥)ℎ(0) +1 2𝑓 ′′(𝑥)ℎ2∫ 𝑠2𝐾(𝑠)𝑑𝑠 + 𝑜(ℎ2)(1) 𝐸[𝑓̂(𝑥)] = 𝑓(𝑥) +1 2𝑓 ′′(𝑥)ℎ2𝜇 2(𝐾) + 𝑜(ℎ2) (2.26)
Kemudian menghitung nilai bias dan variansi dari fungsi 𝑓̂(𝑥), yaitu (Yuniarti & Hartati, 2017): a. Bias dari 𝑓̂(𝑥) 𝐵𝑖𝑎𝑠 𝑓̂(𝑥) = 𝐸[𝑓̂(𝑥)] − 𝑓(𝑥) 𝐵𝑖𝑎𝑠 𝑓̂(𝑥) = 𝑓(𝑥) +1 2𝑓 ′′(𝑥)ℎ2𝜇 2(𝐾) + 𝑜(ℎ2) − 𝑓(𝑥) 𝐵𝑖𝑎𝑠 𝑓̂(𝑥) =1 2𝑓 ′′(𝑥)ℎ2𝜇 2(𝐾) + 𝑜(ℎ2) (2.27) b. Variansi dari 𝑓̂(𝑥)
Untuk menghitung variansi dari 𝑓̂(𝑥) dapat menggunakan pendekatan taylor orde 1.
𝑉𝑎𝑟 (𝑓̂(𝑥)) = 1 𝑛2𝑉𝑎𝑟(∑ 𝐾(𝑋𝑖− 𝑥) 𝑛 𝑖=1 ) 𝑉𝑎𝑟 (𝑓̂(𝑥)) = 1 𝑛2∑ 𝑉𝑎𝑟(𝐾(𝑋𝑖 − 𝑥)) 𝑛 𝑖=1 𝑉𝑎𝑟 (𝑓̂(𝑥)) = 1 𝑛𝑉𝑎𝑟(𝐾(𝑋𝑖 − 𝑥)) 𝑉𝑎𝑟 (𝑓̂(𝑥)) = 1 𝑛{𝐸[𝐾 2(𝑋 𝑖− 𝑥)] − (𝐸[𝐾(𝑋𝑖 − 𝑥)])2} 𝑉𝑎𝑟 (𝑓̂(𝑥)) = 1 𝑛{ 1 ℎ2∫ 𝐾 2(𝑦−𝑥 ℎ ) 𝑓(𝑦)𝑑𝑦 − (𝑓(𝑥) + 𝑜(ℎ)) 2 }
34
Mensubstitusikan 𝑠 =𝑦−𝑥
ℎ maka 𝑑𝑦 = ℎ𝑑𝑠, sehingga diperoleh :
𝑉𝑎𝑟 (𝑓̂(𝑥)) = 1 𝑛ℎ2∫ 𝐾 2(𝑠)𝑓(𝑥 + 𝑠ℎ)ℎ𝑑𝑠 −1 𝑛(𝑓(𝑥) + 𝑜(ℎ)) 2 𝑉𝑎𝑟 (𝑓̂(𝑥)) = 1 𝑛ℎ∫ 𝐾 2(𝑠)𝑑𝑠𝑓(𝑥 + 𝑠ℎ) −1 𝑛(𝑓(𝑥) + 𝑜(ℎ)) 2 𝑉𝑎𝑟 (𝑓̂(𝑥)) = 1 𝑛ℎ𝑅(𝐾)𝑓(𝑥) + 𝑜(ℎ) − 1 𝑛(𝑓(𝑥) + 𝑜(ℎ)) 2 𝑉𝑎𝑟 (𝑓̂(𝑥)) = 1 𝑛ℎ𝑅(𝐾)𝑓(𝑥) + 𝑜 1 𝑛ℎ (2.28) 2.10 Estimator Shibata
Estimator untuk regresi non parametrik kernel dengan menggunakan pemilihan bandwidth shibata dengan mendefinisikan fungsi loss.
Definisi fungsi loss
𝐿(ℎ) = 𝑛−1∑𝑛𝑗=1[𝑚(𝑋𝑗) − 𝑚̂ℎ(𝑋𝑗)]2 (2.29)
Nilai rata-rata dari fungsi loss adalah 𝑅(ℎ) = 𝐸[𝐿(ℎ)] yang disebut dengan Risk. 𝑅(ℎ) = 𝐸 (𝑛−1∑ [𝑚(𝑋 𝑗) − 𝑚̂ℎ(𝑋𝑗)] 2 𝑛 𝑗=1 ) (2.30)
Fungsi 𝑅(ℎ) atau 𝐿(ℎ) merupakan kriteria yang digunakan untuk mengukur kebaikan estimator. Nilai terkecil dari kriteria adalah suatu indikasi dari estimator yang terbaik. Perhitungan lain yang berhubungan dengan 𝑅(ℎ) adalah salah satu prediksi risk yang disebut dengan prediksi mean square error yang berhubungan dengan 𝑅(ℎ) yaitu :
𝑝(ℎ) = 𝜎2+ 𝑅(ℎ) (2.31)
35
meminimumkan 𝑝(ℎ) juga akan meminimumkan 𝑅(ℎ). Sehingga untuk mengestimasi nilai 𝑝(ℎ) adalah dengan mean square error.
𝑀𝑆𝐸(ℎ) = 𝑛−1∑ (𝑌
𝑗− 𝑚̂ℎ(𝑋𝑗)) 2 𝑛
𝑗=1 (2.32)
Nilai 𝑀𝑆𝐸(ℎ) merupakan nilai estimator yang bias terhadap nilai
𝑝(ℎ), untuk membuktikan bahwa nilai 𝑀𝑆𝐸(ℎ) bias terhadap nilai 𝑝(ℎ)
dapat dilihat pada uraian berikut :
𝑀𝑆𝐸(ℎ) = 𝑛−1∑ (𝑌 𝑗− 𝑚̂ℎ(𝑋𝑗)) 2 𝑛 𝑗=1 = 𝑛−1∑𝑛𝑗=1[𝑌𝑗2 + 𝑚̂ℎ2(𝑋𝑗) − 2 (𝑌𝑗𝑚̂ℎ(𝑋𝑗))] Dengan memperhatikan nilai 𝑌𝑗 = 𝑚(𝑋𝑗) + 𝜀𝑗, maka :
𝑀𝑆𝐸(ℎ) = 𝑛−1∑ [(𝑚(𝑋 𝑗) + 𝜀𝑗) 2 + 𝑚̂ℎ2(𝑋𝑗) − 2 (𝑚(𝑋𝑗)) + 𝑛 𝑗=1 𝜀𝑗𝑚̂ℎ(𝑋𝑗)] = 𝑛−1∑𝑛𝑗=1[𝑚2(𝑋𝑗) + 𝜀𝑗2+ 2𝑚(𝑋𝑗)𝜀𝑗+ 𝑚̂ℎ2(𝑋𝑗) − 2 (𝑚(𝑋𝑗)𝑚̂ℎ(𝑋𝑗) + 𝜀𝑗𝑚̂ℎ(𝑋𝑗))] = 𝑛−1∑𝑛𝑗=1[𝑚2(𝑋𝑗) + 𝜀𝑗2+ 2𝑚(𝑋𝑗)𝜀𝑗+ 𝑚̂ℎ2(𝑋𝑗) + (−2𝑚(𝑋𝑗)𝑚̂ℎ(𝑋𝑗) − 2𝜀𝑗𝑚̂ℎ(𝑋𝑗))] = 𝑛−1∑𝑛𝑗=1[𝜀𝑗2+ 𝑚2(𝑋𝑗) + 𝑚̂ℎ2(𝑋𝑗) − 2𝑚(𝑋𝑗)𝑚̂ℎ(𝑋𝑗) − 2𝜀𝑗𝑚̂ℎ(𝑋𝑗) + 2𝑚(𝑋𝑗)𝜀𝑗] = 𝑛−1∑ [𝜀 𝑗2+ 𝑚2(𝑋𝑗) + 𝑚̂ℎ2(𝑋𝑗) − 2𝑚(𝑋𝑗)𝑚̂ℎ(𝑋𝑗) − 2𝜀𝑗𝑚̂ℎ(𝑋𝑗) − 𝑛 𝑗=1 𝑚(𝑋𝑗)] (2.33)
36 𝐿(ℎ) = 𝑛−1∑ [𝑚(𝑋𝑗) − 𝑚̂ℎ(𝑋𝑗)] 2 𝑛 𝑗=1 = 𝑛−1∑[𝑚2(𝑋 𝑗) + 𝑚̂ℎ2(𝑋𝑗) − 2𝑚(𝑋𝑗)𝑚̂ℎ(𝑋𝑗)] 𝑛 𝑗=1
Maka persamaan (2.33) menjadi :
𝑀𝑆𝐸(ℎ) = 𝑛−1∑𝑗=1𝑛 𝜀𝑗2+ 𝐿(ℎ) − 2𝑛−1∑𝑗=1𝑛 𝜀𝑗(𝑚̂ℎ(𝑋𝑗)) − 𝑚(𝑋𝑗) Dengan melihat bahwa nilai error 𝜀𝑗 adalah nilai ekspektasi nol dan variansi 𝜎2 maka : 𝐸[𝑀𝑆𝐸(ℎ)] = 𝑛−1∑ 𝐸(𝜀 𝑗2) + 𝐸(𝐿(ℎ)) − 2𝑛−1𝐸 𝑛 𝑗=1 (∑𝑛𝑗=1𝜀𝑗(𝑚̂ℎ(𝑋𝑗)) − 𝑚(𝑋𝑗)) = 𝜎2+ 𝑅(ℎ) + 𝐸𝐶 𝑙𝑛 (2.34) Dengan nilai 𝐸𝐶𝑙𝑛= −2𝑛−1𝐸 (∑𝑛𝑗=1𝜀𝑗(𝑚̂ℎ(𝑋𝑗)) − 𝑚(𝑋𝑗)) (2.35)
Untuk estimator kernel shibata untuk 𝑚̂ℎ(𝑥) dari fungsi regresi adalah :
𝑚̂ℎ(𝑥) = 𝑛−1∑ 𝑊ℎ𝑖(𝑥)𝑌𝑖 𝑛 𝑖=1 Dimana : 𝑊ℎ𝑖(𝑥) =∑ 𝐾 ( 𝑋𝑖− 𝑥 ℎ ) 𝑛 𝑖=1 ∑𝑛𝑖=1𝐾 (𝑋𝑖ℎ− 𝑥)
Sehingga dapat diperoleh persamaan untuk estimator shibata dari fungsi regresi adalah(Hafiyusholeh, 2006) :
37
2.11 Pemilihan Bandwidth Optimum
Pada regresi kernel yang menjadi masalah utama adalah pada pemilihan bandwidth yang digunakan untuk menyeimbangkan nilai antara bias dan varians dari fungsi tersebut. Jika nilai bandwidth kecil maka kurva yang dihasilkan kurang mulus tetapi memiliki bias kecil. Sedangkan jika nilai bandwidth besar maka kurva yang dihasilkan terlalu mulus sehingga memiliki bias besar dan varians rendah.
Untuk menghasilkan kurva yang optimal maka dapat dilakukan pemulusan kurva dengan menggunakan bandwidth yang paling optimal. Pemilihan bandwidth optimal dengan menggunakan estimasi shibata.
2.12 Evaluasi Ketepatan Model 2.12.1 Koefisien Determinasi
Koefisien determinasi digunakan untuk mengetahui seberapa besar keterlibatan antara variabel independen terhadap variabel dependennya, sehingga untuk mendapatkan nilai koefisien determinasi dapat dihitung dengan persmaan berikut :
𝑅2 = 𝐽𝐾𝑅 𝐽𝐾𝑇 = 𝐽𝐾𝑅 𝐽𝐾𝑅+𝐽𝐾𝐺 (2.45) Keterangan : 𝐽𝐾𝑅 (𝐽𝑢𝑚𝑙𝑎ℎ 𝐾𝑢𝑎𝑑𝑟𝑎𝑡 𝑃𝑒𝑟𝑙𝑎𝑘𝑢𝑎𝑛) = ∑𝑛𝑖=1(𝑦̂1− 𝑦̅)2 𝐽𝐾𝐺 (𝐽𝑢𝑚𝑙𝑎ℎ 𝐾𝑢𝑎𝑑𝑟𝑎𝑡 𝐺𝑎𝑙𝑎𝑡) = ∑𝑛𝑖=1(𝑦𝑖− 𝑦̂1)2 𝐽𝐾𝑇 (𝐽𝑢𝑚𝑙𝑎ℎ 𝐾𝑢𝑎𝑑𝑟𝑎𝑡 𝑇𝑜𝑡𝑎𝑙) = 𝐽𝐾𝑅 + 𝐽𝐾𝐺
38
𝑅2 = koefisien determinasi
𝑦𝑖 = data aktual subjek ke-𝑖 𝑦̂1 = hasil estimasi subjek ke-𝑖 𝑦̅ = rat-rata data aktual
Nilai koefisien determinasi berada di titik interval 0 sampai dengan 1. Apabila nilai koefisien determinasi semakin mendekati 1, maka model yang dihasilkan semakin baik. Akan tetapi jika sebaliknya, apabila nilai koefisien determinasi semakin mendekati 0, maka model yang dihasilkan kurang baik(Nanda, Suparti, & Hoyyi, 2016).
2.12.2 MSE (Mean Square Error)
Untuk melihat seberapa besar nilai kegalatan dari suatu estimator dapat dilihat dari nilai MSE (Mean Square Error). Jika semakin kecil nilai MSE maka semakin baik hasil atau model yang diperoleh. Persamaan yang digunakan untuk menghitung nilai MSE adalah (Sungkawa & Megasari, 2011):
𝑀𝑆𝐸 =∑𝑛𝑖=1𝑒𝑖2 𝑛 → 𝑅𝑀𝑆𝐸 = √ ∑𝑛𝑖=1𝑒𝑖2 𝑛 𝑀𝑆𝐸 =∑𝑛𝑖=1(𝑋𝑖−𝐹𝑖)2 𝑛 (2.46) Keterangan :
𝑒𝑖 = (𝑋𝑖− 𝐹𝑖) = kesalahan pada periode ke-i
39
BAB III
METODE PENELITIAN 3.1 Jenis Penelitian
Penelitian ini merupakan jenis penelitian kuantitatif karena data yang digunakan berupa data yang bersifat kuantitatif yaitu menggunakan data berupa data numerik. Penelitian kuantitatif merupakan suatu penelitian yang informasi dan data yang dikelola menggunakan statistik.
3.2 Jenis dan Sumber Data
Data yang digunakan pada penelitian ini adalah data sekunder yaitu berupa data dari Dinas Kesehatan Kabupaten Gresik. Jenis datanya adalah data runtun waktu (time series) karena secara kronologis data tersebut disusun berdasarkan waktu yang digunakan untuk melihat perubahan dalam rentan waktu tertentu. Data yang digunakan dalam penelitian ini adalah data jumlah penderita penyakit Demam Berdarah Dengue (DBD) periode Januari 2013 hingga Desember 2018.
3.3Teknis Analisis Data
Setelah data yang diperlukan telah terkumpul, maka untuk tahapan selanjutnya adalah menganalisis data tersebut. Teknis analisis data adalah langkah-langkah penyelesaian analisis data hingga selesai yang akan digambarkan dengan diagram alir penelitian pada gambar Gambar 3.1.
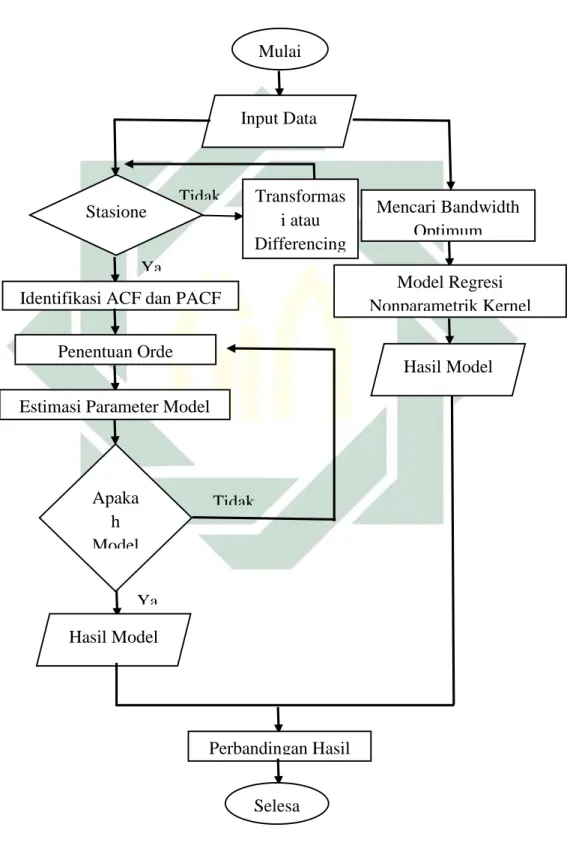
Berdasarkan Gambar 3.1 maka dapat dijelaskan untuk analisis data dalam penelitian ini sebagai berikut:
a. Analisis data penderita penyakit DBD yaitu dengan menentukan apakah sebuah data time series bersifat stasioner yang nilai rata-rata tidak bergeser pada sepanjang waktu. Apabila data tidak stasioner, maka konversi data harus dilakukan agar menjadi stasioner dengan menggunakan metode transformasi atau differencing.
b. Setelah data time series sudah stasioner, maka langkah selanjutnya adalah menentukan model yang akan digunakan. Penentuan model dilakukan dengan cara identifikasi ACF dan PACF. ACF digunakan untuk mengukur korelasi antara pengamatan dengan lag ke-k, sedangkan PACF digunakan untuk mengukur korelasi antara pengamatan dengan lag ke-k dan dengan mengontrol korelasi antara dua pengamatan dengan lag kurang dari k. c. Langkah selanjutnya adalah menguji autokorelasi nilai residual untuk
memenuhi syarat dalam menentukan model ARIMA, yaitu dengan syarat ketentuan adalah residual yang white noise dan berdistribusi normal. d. Setelah menghasilkan suatu model dari ARIMA maka langkah selanjutnya
adalah melakukan estimasi parameter model dalam ARIMA. Estimasi parameter merupakan perhitungan yang dilakukan untuk mendapatkan nilai parameter suatu model yaitu dengan menghitung dari model Autoregressive (AR), model Moving Average (MA), dan model Autoregressive Moving Average (ARMA).
e. Langkah selanjutnya adalah menguji model apakah model sudah baik untuk digunakan. Untuk melihat model yang baik dapat dilihat dari nilai residualnya. Jika nilai residualnya white noise, maka model dapat dikatakan baik dan apabila nilai residualnya tidak white noise maka model dapat dikatakan tidak baik.
Salah satu cara untuk melihat white noise dapat diuji melalui korelogram ACF dan PACF dari residual. Apabila nilai ACF dan PACF tidak signifikan, hal ini mengindikasikan residual white noise artinya model sudah sesuai. Jika model tidak sesuai maka dilakukan kembali dalam pembentukan orde ARIMA.
f. Setelah semua tahap terlewati maka akan didapat model dari ARIMA. Langkah selanjutnya adalah membandingkan antara dua model yaitu hasil model ARIMA dan hasil model dari regresi nonparametrik kernel.
g. Untuk regresi nonparametrik kernel, langkah awal adalah menentukan nilai bandwidth optimum dengan menggunakan estimator Shibata.
h. Melakukan pemodelan penderita penyakit DBD menggunakan fungsi kernel Gaussian.
i. Membandingkan hasil dari kedua model yaitu model ARIMA dan model regresi nonparametrik kernel dengan fungsi kernel Gaussian dengan menghitung nilai MSE.
j. Menghasilkan model yang paling optimal dalam pemodelan penderita DBD di kabupaten Gresik.
Adapun diagram alir penelitian ini dapat disajikan pada Gambar 3.1 sebagai berikut :
Gambar 3.1 Diagram Alir Penelitian
ARIMA Regresi Nonparametrik Mulai Input Data Mencari Bandwidth Optimum Stasione r Transformas i atau Differencing Model Regresi Nonparametrik Kernel Identifikasi ACF dan PACF
Penentuan Orde Estimasi Parameter Model
Apaka h Model Hasil Model Hasil Model Perbandingan Hasil Selesa Tidak Ya Ya Tidak
BAB IV
HASIL DAN PEMBAHASAN
Hasil dan pembahasan dari penelitian ini adalah pemodelan penyakit DBD di Kabupaten Gresik pada periode Januari 2013 sampai dengan periode Desember 2018 dengan menggunakan metode ARIMA dan regresi nonparametrik kernel.
4.1 Pemodelan ARIMA
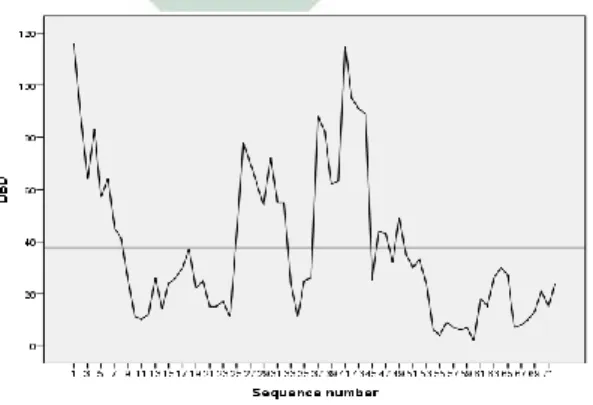
Pada tahap pertama akan dilakukan analisis data untuk membentuk model ARIMA dan untuk langkah selanjutnya akan dilakukan identifikasi stasioneritas data tersebut. Stasioneritas sebuah data merupakan syarat dari pembentukan model analisis time series dan merupakan langkah pertama yang dilakukan untuk membentuk model ARIMA. Data dikatakan stasioner apabila tidak ada perubahan yang fluktuatif yaitu data yang tidak terlalu naik dan tidak terlalu turun. Jika data tidak stasioner maka dilakukan differencing. Untuk mengidentifikasi data dapat dilakukan dengan melihat hasil dari plot data time series dimana data stasioner tidak terlalu fluktuatif dan stasioner terhadap mean dan varians.
45
Plot time series sebelum differencing data menunjukkan belum mempunyai pola yang teratur, sehingga data tersebut belum dikatakan stasioner dalam mean. Sehingga perlu dilakukan differencing.
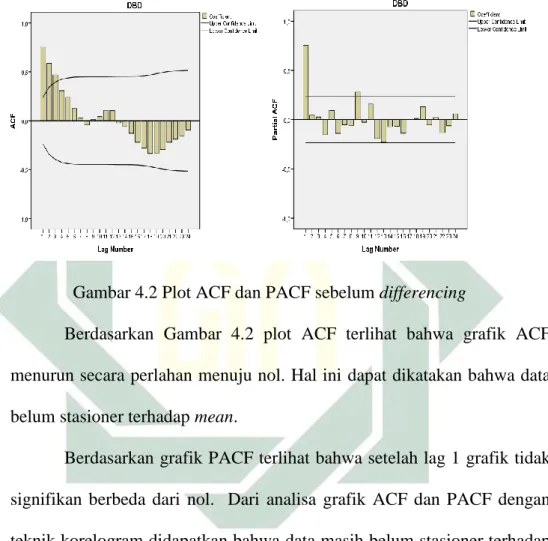
Gambar 4.2 Plot ACF dan PACF sebelum differencing
Berdasarkan Gambar 4.2 plot ACF terlihat bahwa grafik ACF menurun secara perlahan menuju nol. Hal ini dapat dikatakan bahwa data belum stasioner terhadap mean.
Berdasarkan grafik PACF terlihat bahwa setelah lag 1 grafik tidak signifikan berbeda dari nol. Dari analisa grafik ACF dan PACF dengan teknik korelogram didapatkan bahwa data masih belum stasioner terhadap varians sehingga transformasi yang dilakukan agar data stasioner adalah dengan differencing.
46
Gambar 4.3 Plot time series sesudah differencing 1
Setelah dilakukan differencing pertama menunjukkan bahwa data telah stasioner. Hal tersebut dilihat dari plot rata-rata yang terlalu fluktuatif dan berada disekitar nilai tengah dan trend sudah mendekati sumbu horizontal.
Selanjutnya akan dilakukan uji korelogram dengan fungsi autokorelasi (ACF) yaitu dengan melihat plot antara 𝜌𝑘 dan 𝑘 (lag). Uji korelogram sebagaimana pada Gambar 4.3 menurun dengan cepat seiring dengan meningkatnya nilai 𝑘, maka dapat disimpulkan data sudah stasioner. Setelah data stasioner maka akan dilakukan identifikasi model ARIMA dengan cara uji signifikan parameter.
47
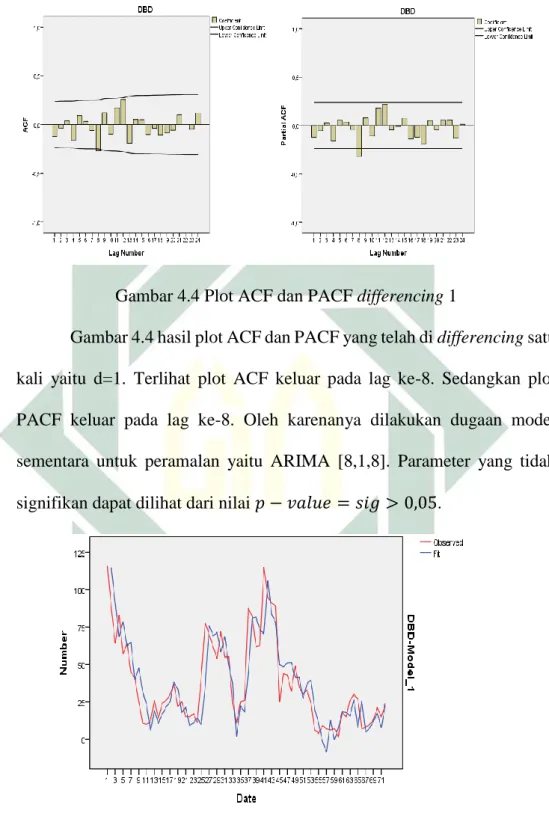
Gambar 4.4 Plot ACF dan PACF differencing 1
Gambar 4.4 hasil plot ACF dan PACF yang telah di differencing satu kali yaitu d=1. Terlihat plot ACF keluar pada lag ke-8. Sedangkan plot PACF keluar pada lag ke-8. Oleh karenanya dilakukan dugaan model sementara untuk peramalan yaitu ARIMA [8,1,8]. Parameter yang tidak signifikan dapat dilihat dari nilai 𝑝 − 𝑣𝑎𝑙𝑢𝑒 = 𝑠𝑖𝑔 > 0,05.
48
Untuk model ARIMA (8, 1, 8) diperoleh model penderita penyakit DBD terlihat pada fit value sudah mendekati data sebenarnya. Hal tersebut dapat dilihat pada gambar bahwa kurvanya hampir mendekati kurva data sebelumnya.
Tabel 4.1 Model Statistik ARIMA (8, 1, 8)
Model Statistics
Model Number
of Predictor
s
Model Fit statistics Ljung-Box Q(18) Numbe
r of Outlier s Stationar y R-squared R-square d RMS E MAP E MA E Statistic s D F Sig . DBD-Model_ 1 0 ,291 ,697 17,153 51,558 11,21 5,107 2 ,08 0
Pada tabel di atas untuk model ARIMA (8, 1, 8) diperoleh nilai kecocokan dari model dengan data pada nilai R2 sebesar 0,697. Sedangkan untuk nilai kesalahan peramalan dapat dilihat dari nilai RMSE = 17,153, MAPE = 51,558, dan MAE = 11,209.
Tabel 4.2 Estimasi Parameter Model ARIMA (8, 1, 8) ARIMA Model Parameters
Estimate SE t Sig. DBD-Model_1 DBD No Transformation Constant -1,210 1,509 -,802 ,426 AR Lag 1 -,210 ,289 -,725 ,472 Lag 2 ,027 ,256 ,105 ,917 Lag 3 -,073 ,235 -,311 ,757 Lag 4 -,779 ,230 -3,381 ,001 Lag 5 -,177 ,237 -,746 ,459 Lag 6 ,075 ,225 ,334 ,740 Lag 7 -,369 ,219 -1,684 ,098 Lag 8 -,455 ,234 -1,947 ,057 Difference 1 MA Lag 1 ,006 11,634 ,001 1,000 Lag 2 ,155 2,980 ,052 ,959 Lag 3 -,190 9,895 -,019 ,985 Lag 4 -,814 13,045 -,062 ,950 Lag 5 -,273 3,659 -,075 ,941 Lag 6 ,192 3,434 ,056 ,956