Analisis Rangkaian Listrik
Di Kawasan
s
Sudaryatno Sudirham
1
Pengantar
Kita telah melihat bahwa analisis di kawasan fasor lebih sederhana dibandingkan dengan analisis di kawasan waktu
karena tidak melibatkan persamaan diferensial melainkan persamaan-persamaan aljabar biasa. Akan tetapi analisis tersebut terbatas hanya untuk sinyal sinus dalam keadaan
mantap.
Berikut ini kita akan mempelajari analisis rangkaian di kawasan s, yang dapat kita terapkan pada rangkaian dengan
sinyal sinus maupun bukan sinus, keadaan mantap maupun keadaan peralihan.
2
Isi
1. Transformasi Laplace
2. Analisis Menggunakan Transformasi Laplace 3. Fungsi Jaringan
4. Tanggapan Frekuensi Rangkaian Orde-1 5. Tanggapan Frekuensi Rangkaian Orde-2
3
Transformasi Laplace
4
Perhitungan rangkaian akan memberikan kepada kita hasil yang juga merupakan fungsis. Jika kita perlu mengetahui hasil perhitungan dalam fungsitkita dapat mencari transformasi balik dari pernyataan bentuk gelombang sinyal
dari kawasan ske kawasan t. Pada langkah awal kita akan berusaha memahami
transformasi Laplace beserta sifat-sifatnya.
Melalui transformasi Laplace ini, berbagai bentuk gelombang sinyal di kawasan waktu yang dinyatakan sebagai fungsit,
dapat ditransformasikan ke kawasan smenjadi fungsis.
Jika sinyal diyatakan sebagai fungsis, makapernyataan elemen rangkaian pun harus disesuaikan dan penyesuaian ini
membawa kita pada konsep impedansi di kawasans.
5
Dalam pelajaran Analisis di Kawasans, kita akan melakukan transformasi pernyataan fungsi dari kawasan t ke kawasan s melalui Transformasi Laplace, yang secara matematis didefinisikan sebagai
suatu integral
∫
∞ −= 0 ()
)
(s fte stdt
F
Fungsi waktu s adalah peubah kompleks:
s = σ+ jω
Batas bawah integrasi adalah nol yang berarti bahwa kita hanya meninjau sinyal-sinyal kausal
Transformasi Laplace
Dalam pelajaran Analisis Rangkaian di kawasan fasor, kita melakukan transformasi fungsi sinus (fungsit) ke dalam bentuk fasor melalui
relasi Euler.
Sebelum membahas Taransformasi Laplace lebih lanjut, kita akan mencoba memahami proses apa yang terjadi dalam transformasi ini.
Kita lihat bentuk yang ada di dalam tanda integral, yaitu
t j t t j
st fte fte e
e t
f() − = ()−(σ+ω) = () −σ −ω
Fungsi waktu Eksponensial
kompleks Meredam jika σ> 0f(t) bentuk sinusoidal
t t e−jωt=cosω−sinω
7 Jadi perkalianf(t) dengan faktor eksponensial kompleks
menjadikanf(t) berbentuksinusoidal teredam.
Sehingga integral dari 0 sampai∞mempunyai nilai limit, dan bukan bernilai tak hingga.
Kita lihat sekarang Transformasi Laplace
t t t j t j
t t j t j t j t j t j
e t
e e e
e e e e e te
σ −
σ − ω − ω − ω − ω
σ − ω − ω − ω − ω ω + σ −
ω − ω =
+ =
+ = ω
) cos(
2
2 cos
0 ) ( ) ( ) ( 0
0 0
0 0
) sin (cos )
(
t t Ae e Ae Ae
Ae−st= −σ+jωt= −σt −jωt= −σt ω− ω
) sin (cos
( )
) ( ) (
t t Ae
e Ae Ae
e Ae
at t j t a t j a st at
ω − ω =
= =
+ σ −
ω − + σ − ω + + σ − − −
∫
∞ −= 0 ()
)
(s fte stdt
F
Bentuk gelombang sinyal yang kita hadapi dalam rangkaian listrik tersusun dari tiga bentuk gelombang dasar yaitu:
(1) anak tangga, (2) eksponensial, dan (3) sinusoidal
) ( ) (t Aut f =
) ( ) (t e ut f = −at
) ( cos ) (t A tut
f = ω
sinus teredam (1)
(2)
(3)
8 Jadi semua bentuk gelombang yang kita temui dalam rangkaian listrik, setelah dikalikan dengan e−stdan kemudian diintegrasi dari
0 sampai∞akan kita peroleh F(s) yang memiliki nilai limit.
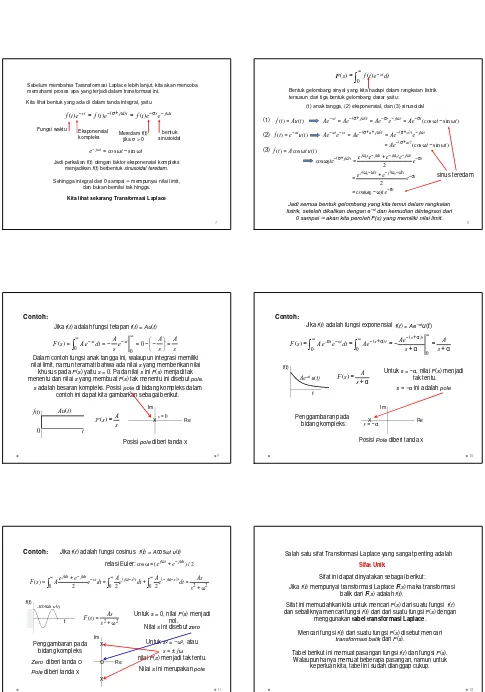
Contoh:
Jikaf(t) adalah fungsi tetapanf(t) = Au(t)
s A s A e
s A dt e A s
F st st =
− − = − =
=
∫
∞ − − ∞ 0) (
0 0
Dalam contoh fungsi anak tangga ini, walaupun integrasi memiliki nilai limit, namun teramati bahwa ada nilaisyang memberikan nilai khusus padaF(s) yaitus= 0. Pada nilaisiniF(s) menjadi tak menentu dan nilaisyang membuatF(s) tak menentu ini disebutpole.
s A s
F()= Re
Im
0 = s X
Posisipole diberi tandaX s adalah besaran kompleks. Posisipole di bidang kompleks dalam
contoh ini dapat kita gambarkan sebagai berikut.
f(t)
0
Au(t)
t
9
f(t) = Ae−αtu(t) Jika f(t) adalah fungsi exponensial
α + = α + − = =
=
∞ α + − ∞ − +α
∞ α −
∫
∫
sAs Ae Ae
dt e e A s F
t s t s st
t
-0 ) (
0 ) ( 0
) (
Contoh:
α + =
s A s F()
t f(t)
Ae-atu(t)
Untuks= −α, nilaiF(s) menjadi tak tentu. s = −αini adalahpole
Re Im
α − = sX
PosisiPole diberi tandaX Penggambaran pada
bidang kompleks:
10
Contoh: Jika f(t) adalah fungsi cosinus f(t) = Acosωt u(t) relasi Euler:cosω=(ejωt+e−jωt)/2
2 2 ) ( 0 ) ( 0
0 2 2 2
) (
ω + = +
= +
=
∫
∞ ω −ω −∫
∞ ω−∫
∞ −ω− sAs dt e A dt e A dt e e e A s
F st j st j st
t j t j
2 2 ) (
ω + =
s As s F
t f(t)
Acosωt u(t)
Untuks= 0, nilaiF(s) menjadi nol. Nilais ini disebutzero
Untuks2= −ω2, atau
nilaiF(s) menjadi tak tentu. Nilais ini merupakanpole
ω ± = j s Penggambaran pada
bidang kompleks Zero diberi tandaO Polediberi tandaX
Re Im
X
X O
11
Salah satu sifat Transformasi Laplace yang sangat penting adalah Sifat Unik
Sifat ini dapat dinyatakan sebagai berikut: Jika f(t) mempunyai transformasi Laplace F(s) maka transformasi
balik dari F(s) adalah f(t).
Sifat ini memudahkan kita untuk mencari F(s) dari suatu fungsi f(t) dan sebaliknya mencari fungsi f(t) dari dari suatu fungsi F(s) dengan
menggunakan tabel transformasi Laplace.
Mencari fungsi f(t) dari suatu fungsi F(s) disebut mencari transformasi balikdari F(s).
Tabel berikut ini memuat pasangan fungsi f(t) dan fungsi F(s). Walaupun hanya memuat beberapa pasangan, namun untuk
keperluan kita, tabel ini sudah dianggap cukup.
ramp teredam : [ t e−at]u(t)
ramp : [ t ]u(t) sinus tergeser : [sin (ωt + θ)]u(t) cosinus tergeser : [cos (ωt + θ)]u(t) sinus teredam : [e−atsin ωt]u(t) cosinus teredam : [e−atcos ωt]u(t)
sinus : [sin ωt]u(t) cosinus : [cos ωt]u(t) eksponensial : [e−at]u(t) anak tangga : u(t)
1
impuls : δ(t)
Pernyataan Sinyal di Kawasan s
L[f(t)] =F(s) Pernyataan Sinyal di Kawasan t
f(t)
s 1
a s+
1
2 2+ω
s s
2 2+ω ω s
(+)2+ω2 + a s
a s
(+ )2+ω2 ω a s
2 2
sin cos
ω +
θ ω − θ s s
2 2
cos sin
ω +
θ ω + θ s s
2
1 s
( )2
1 a s+
Tabel Transformasi Laplace
13
Sifat Unik
Sifat ini dapat dinyatakan sebagai berikut: Jika f(t) mempunyai transformasi Laplace F(s) maka
transformasi balik dari F(s) adalah f(t).
Dengan kata lain
Jika pernyataan di kawasan ssuatu bentuk gelombang v(t) adalah V(s), maka pernyataan di kawasan t suatu bentuk
gelombang V(s) adalah v(t).
14
Sifat-Sifat Transformasi Laplace
Sifat Linier
Karena transformasi Laplace adalah sebuah integral, maka ia bersifat linier.
Transformasi Laplace dari jumlah beberapa fungsi t adalah jumlah dari transformasi masing-masing fungsi.
Jika f(t)=A1f1(t)+A2f2(t) maka transformasi Laplace-nya adalah
[
]
) ( ) (
) ( ) (
) ( ) ( ) (
2 2 1 1
02 2 01 1 0 11 22
s A s A
dt t f A dt t f A
dt e t f A t f A
s st
F F F
+ =
+ =
+ =
∫
∫
∫
∞ ∞
∞ −
dengan F1(s) dan F2(s) adalah transformasi Laplace
dari f1(t) danf2(t). Bukti:
15
Fungsi yang merupakan integrasi suatu fungsi t
) ( ) (
0f1xdx
t f =
∫
tMisalkan maka
dt t f s e dx x f s e dt e dx x f s
st t
st st t
∫
∫
∫ ∫
∞ −∞ − ∞
−
− −
− = =
0 1 0 01 0 0
1() () ()
) ( F
bernilai nol untuk t = ∞karena e−st= 0 pada t→∞, bernilai nol untuk t = 0 karena integral yang di dalam tanda kurung akan bernilai nol (intervalnya nol).
s s dt e t f s dt t f s e
s st
st ()
) ( 1 ) ( )
( 1
0 1 0
1
F
F = =
− −
=
∫
∫
∞ − ∞ −
Jika , maka transformasi Laplacenya adalah
s s s) ()
( F
F =
) ( ) (
0f1xdx
t f =
∫
tBukti:
16
Fungsi yang merupakan diferensiasi suatu fungsi
Misalkan dt
t df t
f()= 1() maka
[
]
∫
∫
∞ − = − ∞− ∞ − −=
0 1 0 1 0
1() () ()( )
)
( e dt f te ft se dt
dt t df
s st st st
F
bernilai nol untuk t = ∞karena e−st= 0 untuk t→ ∞ bernilai −f(0) untuk t= 0.
) 0 ( ) ( ) 0 ( ) ( ) (
1 1 0
1 s f te dt f s s f dt
t
df = st − = −
∫
∞ − FL
Jika
maka transformasi Laplacenya adalah dt
t df t f()= 1()
)
0
(
)
(
)
(
s
=
s
F
1s
−
f
1F
Bukti:
Ini adalah nilaif1(t) padat= 0
17
Translasi di Kawasant
Jika transformasi Laplace dari f(t) adalah F(s), maka transformasi Laplace dari f(t−a)u(t−a) untuk a> 0
adalah e−asF(s).
Translasi di Kawasans
Jika transformasi Laplace dari f(t) adalah F(s) , maka transformasi Laplace dari e−αtf(t)
adalah F(s+ α).
Pen-skalaan (scaling)
Jika transformasi Laplace dari f(t) adalah F(s) , maka untuk a > 0 transformasi dari f(at) adalah
a s F a 1
Nilai Awal dan Nilai Akhir
0
0
) ( lim ) ( lim : akhir Nilai
) ( lim ) ( lim : awal Nilai
→ ∞ →
∞ → + →
= =
s t
s t
s s t f
s s t f
F F
19
konvolusi : nilai akhir : nilai awal : penskalaan : translasi dis: translasi di t:
A1F1(s) + A2F2(s) linier : A1f1(t) + A2f2(t)
diferensiasi : integrasi :
A1F1(s) + A2F2(s) linier : A1f1(t) + A2f2(t)
Pernyataan F(s) =L[f(t)] Pernyataan f(t)
∫
t dx x f0 () s
s) (
F
dt t df()
) 0 ( ) (s−f − sF
2 2 ()
dt t f
d s2F(s)−sf(0−)−f′(0−)
3 3()
dt t f d
) 0 ( ) 0 (
) 0 ( ) ( 2 3
− −
−
′′ − −
− f sf
f s s s F
[f(t−a)]u(t−a) e−asF(s) )
(t f
e−at F(s+a)
) (at
f
a s aF 1
0
) ( lim
+ →
t
t f
) ( lim
∞ →
s
s sF
) ( lim
∞ →
t
t f
0
) ( lim
→
s
s sF
dx x t f x f
t ) ( ) (
01 2−
∫
F1(s F)2(s)Tabel Sifat-Sifat Transformasi Laplace
20
21
Transformasi Laplace
Diagram
pole – zero
Transformasi Balik
CONTOH: Carilah transformasi Laplace dari bentuk gelombang berikut:
) ( 3 ) ( c).
; ) ( ) 10 sin( 5 ) ( b).
; ) ( ) 10 cos( 5 ) ( a).
2 3 2 1
t u e t v
t u t t v
t u t t v
t − = = =
Mencari Transformasi Laplace
2 3 ) ( ) ( 3 )
( 3
2
3 = − → = +
s s t u e t
v t V
a) Dari tabel transformasi Laplace: f(t) = [cos ωt]u(t) () 2 2 ω + =
s s s F Penyelesaian:
100 5 ) 10 ( 5 ) ( ) ( ) 10 cos( 5 )
( 1 2 2 2
1 = → = + = +
s s s
s s t u t t
v V
b) Dari tabel transformasi Laplace: f(t) = [sin ωt]u(t) () 2+ω2
ω =
s s F
100 s
50 ) 10 (
10 5 ) ( ) ( ) 10 sin( 5 )
( 2 2 2 2
2 + = +
× = → =
s s t u t t
v V
c) Dari tabel transformasi Laplace: f(t) = [e−at]u(t)
a s s F
+ = 1 ) (
22
CONTOH: Gambarkan diagram pole-zero dari
s s s
s A s s
s c). () 5
24 , 3 ) 2 (
) 2 ( ) ( b). 1 2 ) (
a). 2 =
+ +
+ = +
= F F
F
Mencari Diagram pole-zero
8 , 1 2 di pole ) 8 , 1 ( 24 , 3 ) 2 (
0 24 , 3 ) 2
( 2
j s j
s s
± − = → ± = − = +
= + +
Re Im
Re Im
+j1,8 −2
−j1,8 a). Fungsi ini mempunyai pole di s= −1
tanpa zero tertentu.
b). Fungsi ini mempunyai zero di s= −2 Sedangkanpoledapat dicari dari
c). Fungsi ini tidak mempunyai zero tertentu sedangkan pole terletak di titik asal, s = 0 + j0.
Re Im
× −1
23
Transformasi balik adalah mencari f(t) dari suatu F(s) yang diketahui.
Mencari Transformasi Balik
Akan tetapi pada umumnya F(s) berupa rasio polinomial yang bentuknya tidak sesederhana dan tidak selalu ada pasangannya
seperti dalam tabel. Untuk mengatasi hal itu, F(s) kita uraikan menjadi suatu penjumlahan dari bentuk-bentuk yang ada dalam
tabel, sehingga kita akan memperoleh f(t) sebagai jumlah dari transformasi balik setiap uraian.
Hal ini dimungkinkan oleh sifat linier dari transformasi Laplace Jika F(s) yang ingin dicari transformasi baliknya ada dalam tabel transformasi Laplace yang kita punyai, pekerjaan kita
cukup mudah.
Bentuk Umum F(s) ) ( ) )( ( ) ( ) )( ( ) ( 2 1 2 1 n m p s p s p s z s z s z s K s − − − − − − = L L F
Jika ada pole-pole yang bernilai sama kita katakan bahwa F(s) mempunyai pole ganda.
Dalam bentuk umum ini jumlah pole lebih besar dari jumlah zero, Jadi indeksn> m
Bentuk umum fungsis adalah
Jika F(s) memiliki pole yang semuanya berbeda, pi≠pjuntuk i≠j ,
dikatakan bahwa F(s) mempunyai pole sederhana.
Jika ada pole yang berupa bilangan kompleks kita katakan bahwa F(s) mempunyai pole kompleks.
25
Fungsi Dengan Pole Sederhana
t p n t p t p n
e
k
e
k
e
k
t
f
=
1+
2+
L
+
2 1
)
(
) ( ) ( ) ( ) ( ) )( ( ) ( ) )( ( ) ( 2 2 1 1 2 1 2 1 n n n m p s k p s k p s k p s p s p s z s z s z s K s − + + − + − = − − − − − − = L L L FF(s) merupakan kombinasi linier dari beberapa fungsi sederhana. k1, k2,…..kndi sebut residu.
Jika semua residu sudah dapat ditentukan, maka
Bagaimana cara menentukan residu ? Apabila F(s) hanya mempunyai pole sederhana, maka ia dapat diuraikan sebagai berikut
26
Jika kita kalikan kedua ruas dengan (s −p1), faktor (s−p1) hilang dari ruas kiri, dan ruas kanan menjadi k1ditambah suku-suku lain yang
semuanya mengandung faktor (s−p1).
k2diperoleh dengan mengakalikan kedua ruas dengan (s −p2) kemudian substitusikan s = p2, dst. Jika kemudian kita substitusikan s = p1maka semua suku di
ruas kanan bernilai nol kecuali k1
1 1 2 1 1 2 1 1 1 ) ( ) ( ) ( ) )( ( k p p p p z p z p z p K n m = − − − − − L L
Cara menentukan residu:
) ( ) ( ) ( ) ( ) )( ( ) ( ) )( ( ) ( 2 2 1 1 2 1 2 1 n n n m p s k p s k p s k p s p s p s z s z s z s K s − + + − + − = − − − − − − = L L L F ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) )( ( 1 2 1 2 1 1 1 2 2 1 n n n m p s p s k p s p s k p s p s k p s p s z s z s z s K − − + + − − + − − = − − − − − L L L
Dengan demikian kita perolehk1
27
CONTOH:Carilah f(t) dari fungsi transformasi berikut.
) 3 )( 1 ( 4 ) ( = + + s s s F 3 2 1 2 ) ( + − + + = s s s F ) 1 (+
×s ( 3) 3( 1)
4 2
1+ + + =
+ s s
k k s
1
masukkan s=− 2
) 3 1 ( 4 1= = + − k ) 3 (+
×s 2
1 ( 3) 1 ) 1 ( 4 k s s k s+ = + + +
3
masukkan s=− 2
) 1 3 (
4 2=− = + − k t t e e t
f()=2−−2−3 3 1 ) 3 )( 1 ( 4 )
( 1 2
+ + + = + + = s k s k s s s F 28 ) 3 )( 1 ( ) 2 ( 4 ) ( + + + = s s s s F
CONTOH:Carilah f(t) dari fungsi transformasi berikut.
3 1 ) 3 )( 1 ( ) 2 ( 4 )
( 1 2
+ + + = + + + = s k s k s s s s F ) 1 (+
×s ( 3) 3( 1) )
2 (
4 2
1+ + + = + + s s k k s s 1
masukkan s=− 2
) 3 1 ( ) 2 1 ( 4 1= = + − + − k ) 3 (+
×s 2
1 ( 3) 1 ) 1 ( ) 2 ( 4 k s s k s
s + +
+ = + +
3
masukkan s=− 2
) 1 3 ( ) 2 3 ( 4 2= = + − + − k 3 2 1 2 ) ( = + + + s s s
F t t
e e t
f()=2−+2−3
29 ) 4 )( 1 ( ) 2 ( 6 ) ( = + ++ s s s s s F
CONTOH:Carilah f(t) dari fungsi transformasi berikut.
4 1 ) 4 )( 1 ( ) 2 ( 6 )
( 1 2 3
+ + + + = + + + = s k s k s k s s s s s F s
× ( 1)( 4) 1 4
) 2 (
6 2 3
1+ + + + = + + + s s k s s k k s s s
masukkans= 0 3
) 4 0 )( 1 0 ( ) 2 0 ( 6 1= = + + + k ) 1 ( 4 ) 1 ( ) 4 ( ) 2 ( 6 3 2 1 + + + + + = + + s s k k s s k s s s ) 1 (+ ×s
masukkans= −4
2 ) 4 1 ( 1 ) 2 1 ( 6
2=− = + − − + − k ) 4 ( +
×s 6(( 21)) 1( 4) s21(s 4) k3 k s s k s s
s + +
+ + + = + + 1 ) 1 4 ( 4 ) 2 4 ( 6
3=− = + − − + − k 4 1 1 2 3 ) ( = +−+ + −+ s s s s
F t t
e e t
f()=3−2−−1−4 masukkans= −1
Dalam formulasi gejala fisika, fungsi F(s) merupakan rasio polinomial dengan koefisien riil. Jika F(s) mempunyai pole kompleks yang berbentuk p= −α+ jβ, maka ia juga harus mempunyai pole lain yang
berbentuk p* = −α −jβ; sebab jika tidak maka koefisien polinomial tersebut tidak akan riil.
Jadi untuk sinyal yang secara fisik kita temui, pole kompleks dari F(s) haruslah terjadi secara berpasangan konjugat.
L L+ +α− β+ +α+ β+
= j s k j s k
s) *
(
F
Residu k dan k* juga merupakan residu konjugat sebab F(s) adalah fungsi rasional dengan koefisien rasional. Residu ini dapat kita cari dengan cara yang sama seperti mencari residu pada uraian fungsi
dengan pole sederhana.
Fungsi Dengan Pole Kompleks
Oleh karena itu uraian F(s) harus mengandung dua suku yang berbentuk
31
Transformasi balik dari dua suku dengan pole kompleks
L L+ +α−β+ +α+β+
= j s k j s k
s) *
(
F
L
L+ β+θ+
= 2 −αcos( )
)
(t ke t
f ) cos( 2 2 2 * ) ( ) ( ) ( )) ( ( )) ( ( ) ( ) ( ) ( ) ( θ + β = + = + = + = + = α − θ + β − θ + β α − θ + β + α − θ + β − α − β + α − θ − β − α − θ β + α − β − α − t t j t j t t j t j t j j t j j t j t j k e k e e e k e k e k e e k e e k e k ke t f adalah 32
CONTOH: Carilah transformasi balik dari
) 8 4 ( 8 ) ( 2 + + = s s s s F 2 2 2 32 16 4 j s=− ± − =− ± Memberikan pole
sederhana di s = 0
memberi pole kompleks 2 2 2 2 ) 8 4 ( 8 )
( 1 2 2
2 s j
k j s k s k s s s s + + + − + + = + + = ∗ F 2 2 8 8 8 ) 2 2 ( 8 ) 2 2 ( ) 8 4 ( 8 ) 4 / 3 ( 2 2 2 2 2 2 π + − = + − = = − − = + + = − + × + + = → j j s j s e j j s s j s s s s k ) 4 / 3 ( 2 2
2 − π
∗= →k ej
[
]
() 2 cos(2 3/4)2 2 ) ( 2 2 2 2 ) ( 2 ) 2 4 / 3 ( ) 2 4 / 3 ( 2 ) 2 2 ( ) 4 / 3 ( ) 2 2 ( ) 4 / 3 ( π + + = + + = + + = − + π − + π − + − π − − − π t e t u e e e t u e e e e t u f(t) t t j t j t t j j t j j 1 8 8 ) 8 4 ( 8 0 2
1= + + × = =
→ = s s s s s k 33
Pada kondisi tertentu, F(s) dapat mempunyai pole ganda. Penguraian F(s) yang demikian ini dilakukan dengan “memecah” faktor yang mengandung pole ganda dengan tujuan untuk mendapatkan bentuk fungsi dengan pole sederhana yang dapat diuraikan seperti contoh sebelumnya.
2 2 1 1 ) )( ( ) ( ) ( p s p s z s K s − − − = F pole ganda − − − − = ) )( ( ) ( 1 ) ( 2 1 1
2 s p s p
z s K p s s F pole sederhana ) ( ) ( 2 2 1 1 p s k p s k − + −
Fungsi Dengan Pole Ganda
34 Uraikan menjadi: 2 2 2 21 2 1 2 2 1 1
2 ( )( ) ( )
1 ) ( p s k p s p s k p s k p s k p s s − + − − = − + − − = F 2 2 2 2 12 1 11 ) ( ) ( p s k p s k p s k s − + − + − = F t p t p t p te k e k e k t
f 1 2 2
2 12 11 ) ( = + + 35 Maka: sehingga:
CONTOH: Tentukan transformasi balik dari fungsi: 2 ) 2 )( 1 ( ) ( + + = s s s s F 2 ) 1 ( 1 ) 2 ( 2 1 ) 2 ( 1 ) 2 )( 1 ( ) 2 ( 1 ) 2 )( 1 ( ) ( 2 2 1 1 2 1 2 = + = → − = + = → + + + + = + + + = + + = − = − = s s s s k s s k s k s k s s s s s s s s s F 2 12 11 2 ) 2 ( 2 2 1 ) 2 ( 2 ) 2 )( 1 ( 1 2 2 1 1 ) 2 ( 1 ) ( + + + + + = + + + + − = + + + − + = ⇒ s s k s k s s s s s s s F 1 1 1 1 2 1 2 12 1
11= −+ =− → = −+ = → − = − = s s s k s k ) 2 ( 2 2 1 1 1 ) ( 2 + + + + + − = ⇒ s s s s
F t t t
te e e t
f()=−−+−2 +2 −2
Analisis Rangkaian Listrik
Menggunakan
Transformasi Laplace
37
Kita mengetahui hubungan tergangan-arus di kawasan waktu pada elemen-elemenR, L, danC adalah
∫
=
=
=
=
dt
i
C
v
dt
dv
C
i
dt
di
L
v
Ri
v
c C C C
L L
R R
1
atau
Dengan melihat tabel sifat-sifat transformasi Laplace, kita akan memperoleh hubungan tegangan-arus elemen-elemen di kawasanssebagai berikut:
38
Hubungan Tegangan-Arus Elemen
di Kawasan s
Resistor: VR(s)=RIR(s)
Induktor: VL(s)=sLIL(s)−LiL(0)
Kapasitor:
s v sC
s
s C C
C()= ()+ (0)
I V
Kondisi awal Kondisi awal adalah kondisi elemen
sesaat sebelum peninjauan.
39
Konsep Impedansi di Kawasan
s
Impedansi di kawasan s adalah rasio tegangan terhadap arus di kawasan s dengan kondisi awal nol
sC s C
s Z sL s L
s Z R s s
Z C
C L L R R
R 1
) (
) ( ; ) (
) ( ; ) (
)
( = = = = =
=
I V I
V I
V
Dengan konsep impedansi ini maka hubungan tegangan-arus untuk resistor, induktor, dan kapasitor menjadi sederhana.
) ( 1 ; (s) ) ( ; (s) )
( s
sC sL
s R
s R L L C C
R I V I V I
V = = =
Admitansi, adalahY = 1/Z
sC Y sL Y R
YR= L= ; C= 1 ; 1
40
Representasi Elemen di Kawasan s
R IR (s)
+
VR(s)
−
− + sL
LiL(0)
+
VL (s)
− IL (s)
+ − +
VC (s)
− IC (s)
s vC(0) Representasi dengan Menggunakan Sumber Tegangan
ElemenR, L, danC di kawasans,jika harus memperhitungkan adanya simpanan energi awal pada elemen, dapat dinyatakan dengan meggunakan sumber tegangan atau sumber arus.
Kondisi awal )
( ) (s R Rs
R I
V = VL(s)=sLIL(s)−LiL(0)
s v sC
s
s C C
C()= ()+ (0)
I V
41
Jika Kondisi awal = 0
R IR (s)
+
VR(s)
−
sL +
VL (s)
−
IL (s) +
VC (s)
− IC (s)
) ( ) (s R Rs
R I
V = VL(s)=sLIL(s)
sC s
s C
C
) ( )
( I
V =
Jika simpanan energi awal adalah nol, maka sumber tegangan tidak perlu digambarkan.
R IR (s)
+
VR(s)
−
IL (s)
+
VL (s)
− sL
s
iL(0) CvC(0)
IC (s)
+
VC (s)
− sC
1
) ( ) (s R Rs
R I
V =
− =
s i s sL
s L
L L
) 0 ( ) ( )
( I
V C() 1
(
C(s) CvC(0))
sCs= I +
V
Representasi dengan Menggunakan Sumber Arus
Kondisi awal Jika Kondisi awal = 0
R IR (s)
+
VR(s)
−
sL +
VL (s)
−
IL (s) +
VC (s)
− IC (s)
) ( ) (s R Rs
R I
V = VL(s)=sLIL(s)
sC s
s C
C
) ( )
( I
V =
43
Transformasi Rangkaian
Representasi elemen dapat kita gunakan untuk mentransformasi rangkaian ke kawasan s. Dalam melakukan transformasi rangkaian perlu kita perhatikan juga apakah rangkaian yang kita transformasikan
mengandung simpanan energi awal atau tidak. Jika tidak ada simpanan energi awal, maka sumber
tegangan ataupun sumber arus pada representasi elemen tidak perlu kita gambarkan.
44
Saklar S pada rangkaian berikut telah lama ada di posisi 1. Pada t= 0 saklar dipindahkan ke posisi 2 sehingga rangkaian RLC seri terhubung ke sumber tegangan 2e−3tV. Transformasikan rangkaian ke kawasan suntuk t > 0.
1/2 F 1 H 3 Ω 2e−3tV
+ vC
− S
1
2 + − + − 8 V
s 3 +
− +
− +
VC(s)
− 3
2 + s
s 2
s 8
tegangan awal kapasitor = 8/s
tegangan kapasitor CONTOH:
Saklar S telah lama ada di posisi 1 dan sumber 8 V membuat rangkaian memiliki
kondisi awal, yaitu
vC0= 8 V dan iL0= 0
arus awal induktor = 0
Transfor-masi
Kondisi awal akan nol jika rangkaiannnya adalah sepeti berikut
45
1
1/2 F 1 H 3 Ω 2e−3tV
+ vC
− S
2 + −
Saklar S telah lama ada di posisi 1 dan tak ada sumber tegangan,
maka kondisi awal = 0
vC0= 0 V dan iL0= 0
s 3 + −
+
VC(s)
− 3
2 +
s s
2
Transfor-masi
tegangan kapasitor arus awal induktor = 0
tegangan awal kapasitor = 0
46
Hukum arus Kirchhoff (HAK) dan hukum tegangan Kirchhoff (HTK) berlaku di kawasan s
∑
== n
k kt i 1
0 ) (
0 ) ( )
( )
(
1 1 0
0 1
= =
=
∑
∑ ∫
∫ ∑
= =
∞ −
∞ −
=
n
k k n
k
st k st n
k
kt e dt i te dt s
i I
0 ) ( 1
∑
== n
k kt v
0
)
(
)
(
)
(
1 1 0
0 1
=
=
=
∑
∑ ∫
∫ ∑
= =
∞ −
∞ −
=
n
k k n
k
st k st
n
k
k
t
e
dt
v
t
e
dt
s
v
V
HAK di Kawasant :
HAK di Kawasans
HTK di Kawasant :
HTK di Kawasans 47
Hukum Kirchhoff
Pembagi Tegangan dan Pembagi Arus
∑
∑
== k ekivparalel k
seri
ekiv Z Y Y
Z ;
) ( )
( ; ) ( )
(
s Z
Z s s Y
Y
s total
seri ekiv
k k total paralel ekiv
k
k I V V
I = =
CONTOH: Carilah VC(s) pada rangkaian impedansi seri RLC berikut ini
) ( ) 2 )( 1 (
2 ) ( 2 3 2 ) ( 2 3
/ 2 ) (
2 s s s s s
s s
s s
s
s in in in
R V V V
V
+ + = + + = + + =
s 3 + −
+
VC(s)
− Vin (s)
s 2
MisalkanVin(s) = 10/s 2 1 ) 2 )( 1 ( 20 )
( 1 2 3
+ + + + = + + = s k s k s k s s s s C V
Inilah tanggapan rangkaian RLCseri denganR = 3Ω, L= 1H, C= 0,5 F
dan sinyal masukan anak tangga dengan amplitudo 10 V. t t C C e e t v s s s s 2 10 20 10 ) ( 2 10 1 20 10 ) ( − −+ − = ⇒ + + + − + = ⇒V 10 ) 1 ( 20 ; 20 ) 2 ( 20 ; 10 ) 2 )( 1 ( 20 2 3 1 2 0 1 = + = − = + = = + + = → − = − = = s s s s s k s s k s s k s 3 + − +
VC(s)
− Vin (s)
s 2
49
Prinsip Proporsionalitas
The image part with relationship ID rId4 was not found in the file.
Ks
Y(s)
X(s)
sL R +
− 1/sC
Vin (s)
) ( 1 ) ( ) / 1 ( )
( 2 s
RCs LCs RCs s sC sL R R
s in in
R V V
V + + = + + = CONTOH:
Hubungan linier antara masukan dan keluaran
50
Teorema Rangkaian
Prinsip Superposisi ⋅ ⋅ ⋅ + + + = () () () )( 1 1 2 2 3 3
os KsX s KsX s KsX s
Y
Ks
Yo(s)
X1(s)
X2(s)
Ks1
Y1(s) = Ks1X1(s) X1(s)
Ks2
Y2(s) = Ks2X2(s) X2(s) ) ( ) ( )
( 1 1 2 2
os KsX s KsX s
Y = +
Keluaran rangkaian yang mempunyai beberapa masukan adalah jumlah keluaran dari setiap masukan sendainya
masukan-masukan itu bekerja sendiri-sendiri
51
Teorema Thévenin dan Norton
) ( ) ( 1 ) ( ) ( ) ( ; ) ( ) ( ) ( s s Y Z Z s s s Z s s s N T N T T T hs N T N ht T I V V I I I V V = = = = = =
CONTOH: Carilah rangkaian ekivalen Thevenin dari rangkaian impedansi berikut ini.
+ − B E B A N R sC 1 2 2+ω
s
s ( 1/ )( )
/ ) / 1 ( / 1 ) ( ) ( 2 2 2
2+ω = + +ω
+ = = s RC s RC s s s sC R sC s s ht T V V ) / 1 ( 1 / 1 / ) / 1 ( || RC s C sC R sC R RC R
ZT= = + = +
+ − B E B A N ZT T V
Tegangan Thévenin Arus Norton
Impedansi Thévenin
52
Metoda Unit Output
CONTOH: Dengan menggunakan metoda unit output, carilah V2(s) pada rangkaian impedansi di bawah ini
sL
R 1/sC
I1(s)
+
V2(s) −
IC (s) IR (s)
IL (s)
2 2 2 ) ( ) ( ) ( / 1 1 ) ( 1 ) ( ) ( 1 ) ( : Misalkan LCs sC sL s sC s s sC sC s s s s L C L C C = × = → = = → = = → = = → = V I I I V V V ) ( 1 ) ( ) ( 1 ) ( 1 1 1 ) ( ) ( ) ( 1 ) ( 1 ) ( ) ( ) ( 1 2 1 2 2 * 1 2 2 * 1 2 2 s RCs LCs R s K s RCs LCs R s I K R RCs LCs sC R LCs s s s R LCs s LCs s s s s s L R R C L R I I V I I I I V V V + + = = ⇒ + + = = ⇒ + + = + + = + = ⇒ + = → + = + = → 53
Metoda Metoda Analisis
Metoda Superposisi
CONTOH: Dengan menggunakan metoda superposisi, carilah tegangan induktor vo(t) pada rangkaian berikut ini.
+
− Bsinβt
Au(t) R L + vo − R + − R sL + Vo1 − R s A + − R sL + Vo − R s A 2 2+β
β s B R sL + Vo2 − R 2 2+β
β s B L R s A A sL R L s A sL R RLs R sL R RLs s sL R RLs ZL R
θ − − θ β − = − = β + = → +β = θ β + = β − = β − + = → β + − = β + = → β − + β + + + β + + = + = ⇒ j j j s L R s e L R k L R e L R j L R j s L R s s k L R L R s s k j s k j s k L R s k RB L R s A s s s 2 2 3 1 2 2 2 2 2 2 / 2 2 1 3 2 1 o2 o1 o 4 ) / ( 1 / 2 tan , 4 ) / ( 1 2 / 1 ) )( 2 / ( ) 2 / ( ) 2 / ( ) ( 2 / 2 2 / 2 / ) ( ) ( )
( V V
V
(
)
+ β + + β + − β + = ⇒ θ − β θ − β − − − ) ( ) ( 2 2 2 2 2 2 o 4 ) / ( 1 ) 2 / ( ) 2 / ( 2 2 ) ( t j t j t L R t L R e e L R e L R L R RB e A t v ) cos( 4 ) / ( 4 2 ) ( 2 2 2 2 2 2o β−θ
β + β + β + β − =
⇒ − t
L R RB e L R B R A t v t L R L R s A s 2 / 2 / ) (
o1 = +
⇒V ) )( 2 / ( 2 )
( 2 2
o2 β + + β = s L R s s RB s V 55
Metoda Reduksi Rangkaian
CONTOH:Dengan menggunakan metoda reduksi rangkaian carilah tegangan induktor vo(t) pada rangkaian berikut ini
+ − R sL + Vo − R s A 2 2+β β s B Rs L + Vo − R 2 2+β
β s
B sR
A
R/2sL +Vo
− sR A s B + β + β 2 2 R/2 sL + Vo − + − + β + β sR A s B R 2 2 2 + β + β × + = sR A s B R R sL sL s 2 2 o() /2 2
V ) )( 2 / ( ) 2 / ( 2 / 2 / ) ( 2 2
o + +β
β + + = s L R s s RB L R s A s V 56
Metoda Rangkaian Ekivalen Thévenin
CONTOH:Cari tegangan induktor dengan menggunakan rangkaian ekivalen Thévenin.
+ − R sL + Vo − R s A 2 2+β β s B + − R R s A 2 2+β β s B 2 2 2 2 2 / 2 / 2 1 ) ( ) ( β + β + = β + β × × + × + = = s RB s A s B R s A R R R s s ht T V V 2 R ZT= + − ZT sL + Vo − VT ) )( 2 / ( ) 2 / ( 2 / 2 / 2 / 2 / 2 / ) ( ) ( 2 2 2 2 o β + + β + + = β + β + + = + = s L R s s RB L R s A s RB s A R sL sL s Z sL sL s T T V V 57
Metoda Tegangan Simpul
+ − R sL + Vo − R s A 2 2+β β s
B
CONTOH: Cari tegangan induktor dengan menggunakan metoda tegangan simpul.
0 1 1 1 1 ) ( 2 2 o − − +ββ =
+ + s B s A R sL R R s V ) )( 2 / ( ) 2 / ( 2 / 2 / 2 ) ( atau 2 ) ( 2 2 2 2 o 2 2 o β + + β + + = β + β + + = β + β + = + s L R s s RB L R s A s B Rs A R Ls RLs s s B Rs A RLs R Ls s V V 58
Metoda Arus Mesh
CONTOH: Pada rangkaian berikut ini tidak terdapat simpanan energi awal. Gunakan metoda arus mesh untuk menghitung i(t)
+
− 10kΩ
10mH
1µF 10 u(t)
i(t) 10kΩ
+
− 10
4 10 4 0.01s I(s)
IA IB
s s) 10 ( 1 = V s 6 10
(
)
0 10 ) ( 10 10 10 ) ( 0 10 ) ( 10 01 . 0 ) ( 10 4 6 4 4 4 4 = × − + + = × − + + − s s s s s s s A B B A I I I I(
2 10)
() ) ( 2 s s s s B A II = +
59
(
)(
)
) )( ( 10 10 10 02 , 0 10 10 10 10 2 02 , 0 10 ) ( ) ( 0 10 ) ( ) ( 10 2 10 01 . 0 10 6 4 2 4 6 4 2 4 2 4 β − α − = + + = − + + × + = = ⇒ = × − + + + − ⇒ s s s s s s s s s s s s s s s s B B B I I I I[
]
mAFungsi Jaringan
61
Bahasan kita berikut ini adalah
mengenai Fungsi Jaringan
Fungsi Jaringan merupakan fungsisyang merupakan karakteristik rangkaian dalam menghadapi adanya suatu masukan ataupun memberikan relasi antara masukan dan keluaran.
Pengertian Dan Macam Fungsi Jaringan. Peran Fungsi Alih.
Hubungan Bertingkat Kaidah Rantai
Bahasan akan mencakup
62
Fungsi Jaringan
Prinsip proporsionalitas berlaku di kawasan s. Faktor proporsionalitas yang menghubungkan keluaran dan
masukan berupa fungsi rasional dalam s dan disebut fungsi jaringan (network function).
) ( Masukan Sinyal
) ( Nol Status Tanggapan Jaringan
Fungsi
s s =
Definisi ini mengandung dua pembatasan, yaitu a) kondisi awal harus noldan
b) sistem hanya mempunyai satu masukan
63
Pengertian dan Macam Fungsi Jaringan
Fungsi jaringan yang sering kita hadapi ada dua bentuk, yaitu fungsi masukan (driving-point function) dan
fungsi alih (transfer function) Fungsi masukan adalah perbandingan antara tanggapan di suatu gerbang (port) dengan masukan di gerbang yang sama. Fungsi alih adalah perbandingan antara tanggapan di suatu gerbang dengan masukan pada gerbang yang berbeda.
64
Fungsi Masukan
) (
) ( ) ( ; ) (
) ( ) (
s s s Y s s s Z
V I I
V =
=
impedansi masukan admitansi masukan
Fungsi Alih
) (
) ( ) ( : Alih Impedansi
; ) (
) ( ) ( : Alih Admitansi
) (
) ( ) ( : Arus Alih Fungsi
; ) (
) ( ) ( : Tegangan Alih Fungsi
o o
o o
s s s T
s s s T
s s s T
s s s T
in Z
in Y
in I
in V
I V V
I I I
V V
= =
= =
65
CONTOH: Carilah impedansi masukan yang dilihat oleh sumber pada rangkaian-rangkaian berikut ini
RCs R Z
R RCs Cs R Y
Cs RCs Cs R Z
in in in
+ =
⇒
+ = + =
+ = + =
1
1 1 b).
; 1 1 a). a).
R + − Vs(s)
R Is(s)
b).
Cs 1
Cs 1
Carilah fungsi alih rangkaian-rangkaian berikut CONTOH:
a). R
+
Vin(s)
−
+ Vo(s)
− R
Iin(s)
b). Io(s)
sRC sC R R s s s T RCs Cs R Cs s s s T in I in V + = + = = + = + = = 1 1 / 1 / 1 ) ( ) ( ) ( b). ; 1 1 / 1 / 1 ) ( ) ( ) ( a). o o I I V V 67
Tentukan impedansi masukan dan fungsi alih rangkaian di bawah ini CONTOH: R1 R2 L C + vin − + vo − Transformasi
ke kawasan s R1 R2
Ls
1/Cs + Vin(s)
−
+ Vo (s)
−
(
) (
)
1 ) ( ) )( 1 ( / 1 ) )( / 1 ( || / 1 2 1 2 2 1 2 1 2 1 2 1 + + + + + = + + + + + = + + = Cs R R LCs R Ls Cs R Ls R Cs R R Ls Cs R R Ls Cs R Zin 2 2 o ) ( ) ( ) ( R Ls R s s s T inV = = +
V V
68
CONTOH:
Tentukan impedansi masukan dan
fungsi alih rangkaian di samping ini −
+ R2 + vin − + vo − R1
C1 C2
Transformasi rangkaian ke kawasan s
−
+
R2
+ Vin(s)
−
+ Vo(s)
− R1
1/C1s 1/C2s
(
)
1 / 1 / / 1 || 1 1 1 1 1 1 1 11 = + = +
= s C R R s C R s C R s C R Zin 1 1 1 1 ) / 1 ( || ) / 1 ( || ) ( ) ( ) ( 2 2 1 1 1 2 1 1 1 2 2 2 1 1 2 2 1 2 o + + − = + × + − = − = − = = s C R s C R R R R s C R s C R R s C R s C R Z Z s s s T in V V V 69 CONTOH: 1MΩ 1µF
µvx
A + vs − + vx − + vo 1MΩ
1µF +−
106 106/s
µVx
A +
Vx
− + Vo(s) 106
106/s +− +
Vs(s)
−
Persamaan tegangan untuk simpul A:
(
)
0 10 10 10 10 10 10 6 6 6 6 6 6 = µ − − − + + − − − − − − x x in A s s V V V V 1 ) 3 ( 1 ) 1 2 2 ( atau 0 ) 2 )( 1 ( ) 1 ( 1 1 / 10 10 / 10 : sedangkan 2 2 6 6 6 + µ − + = ⇒ = µ − − + + + = µ − − − + + ⇒ + = → + = + = s s s s s s s s s s s s s in x in x x x in x x A A A x V V V V V V V V V V V V V s s s s s s s T s x s V 1 ) 3 ( ) ( ) ( ) ( ) ( )
( o 2
+ µ − + µ = µ = = V V V V Fungsi alih :
70
Peran Fungsi Alih
Dengan pengertian fungsi alih, keluaran dari suatu rangkaian di kawasan sdapat dituliskan sebagai
. kawasan di nol) status (tanggapan keluaran : ) ( kawasan di masukan sinyal pernyataan : ) ( alih fungsi adalah ) ( dengan ; ) ( ) ( ) ( s s s s s T s s T s Y X X Y = 0 1 1 1 0 1 1 1 ) ( ) ( ) ( a s a s a s a b s b s b s b s a s b s T n n n n m m m m + + ⋅⋅ ⋅⋅ ⋅ + + + ⋅⋅ ⋅⋅ ⋅ + = = − − − − ) ( ) )( ( ) ( ) )( ( ) ( 2 1 2 1 n m p s p s p s z s z s z s K s T − ⋅⋅ ⋅⋅ ⋅ − − − ⋅⋅ ⋅⋅ ⋅ − − =
Fungsi alihT(s) akan memberikan zero di z1…. zm pole di p1…. pn. T(s) pada umumnya
berbentuk rasio polinom
Rasio polinom ini dapat dituliskan:
71
Pole dan zero yang berasal dari T(s) disebut pole alami dan zero alami, karena mereka ditentukan semata-mata oleh parameter
rangkaian dan bukan oleh sinyal masukan;
Poledanzeroyang berasal dari X(s) disebut pole paksa dan zero paksakarena mereka ditentukan oleh fungsi pemaksa (masukan). Poledan zerodapat mempunyai nilai riil ataupun kompleks konjugat karena koefisien dari b(s) dan a(s) adalah riil.
Sementara itu sinyal masukan X(s) juga mungkin mengandung zerodan polesendiri. Oleh karena itu sinyal keluaran Y(s) akan mengandung pole dan zero yang dapat
berasal dari T(s) ataupun X(s).
CONTOH:
106 106/s
µVx
A +
Vx
− + Vo(s) 106
106/s +− +
Vs(s)
−
Jikavin= cos2t u(t) , carilah pole dan zerosinyal keluaran Vo(s) untuk µ= 0,5
4 )
( 2
+ =
s s s in
V
Fungsi alih :
s s s s s TV
1 5 , 2 5 , 0 1 ) 3 ( )
( 2 2
+ + = + µ − +
µ =
) 2 )( 2 ( ) 5 , 0 )( 2 (
5 , 0
4 1 5 , 2 5 , 0 ) ( ) ( )
( 2 2
o
j s j s
s s
s
s s
s s s s T s V in
− + + + =
+ + + =
= V
V
Pole dan zero adalah :
riil alami : 5 . 0
riil alami : 2
pole s
pole s
− =
− =
imajiner paksa : 2
imaginer paksa : 2
riil paksa satu : 0
pole j s
pole j s
zero s
+ =
− = =
73
Rangkaian Dengan Masukan Sinyal Impuls
Impuls dinyatakan dengan x(t) = δ(t). Pernyataan sinyal ini di kawasan s adalah X(s) = 1
) ( 1 ) ( ) ( ) ( ) (
os TsXs Ts Hs
V = = × =
Vo(s) yang diperoleh dengan X(s) = 1 ini disebut H(s)
agar tidak rancu dengan T(s).
Karena X(s) = 1 tidak memberikan
polepaksa, makaH(s) hanya akan mengandung polealami.
Keluaran di kawasan t, vo(t) = h(t),
diperoleh dengan transformasi balik H(s). Bentuk gelombang h(t) terkait dengan pole
yang dikandung oleh H(s). Pole riil akan memberikan komponen eksponensial pada
h(t); polekompleks konjugat (dengan bagian riil negatif ) akan memberikan komponen sinus teredam pada h(t).
Pole-poleyang lain akan memberikan bentuk-bentuk h(t) tertentu yang akan kita
lihat melalui contoh berikut.
74
Jika sinyal masukan pada rangkaian dalam contoh-3.5 adalah vin= δ(t) ,
carilah pole dan zero sinyal keluaran untuk nilai µ= 0,5 ; 1 ; 2 ; 3 ; 4, 5. CONTOH:
106 106/s
µVx
A +
Vx
− + Vo(s) 106
106/s +− +
Vs(s) −
1 ) 3 ( ) (
2+ −µ +
µ =
s s s TV Dengan masukan vin= δ(t)
berarti Vin(s) = 1, maka
keluaran rangkaian adalah :
1 ) 3 ( )
( 2
+ µ − +
µ =
s s s H
5 , 0 dan 2 di riil dua 5 0 2
5 0 1 5 2
5 0 ) ( 5 , 0
2+ + = + + ⇒ =− =− =
⇒ =
µ pole s s
) , )(s (s
,
s , s
, s
H
1 di riil dua ) 1 (
5 , 0 1 2 1 ) ( 1
2
2+ + = + ⇒ =−
= ⇒ =
µ pole s
s s s s H
2 / 3 5 , 0 di kompleks dua ) 2 / 3 5 , 0 )( 2 / 3 5 , 0 (
2 1
2 ) ( 2
2 s s j s j pole s j
s
s ⇒ =− ±
+ + − + = + + = ⇒ =
µ H
1 di imajiner dua ) 1 )( 1 (
3 1 3 ) ( 3
2 s j s j pole s j s
s ⇒ =±
− + = + = ⇒ =
µ H
2 / 3 5 , 0 di kompleks dua ) 2 / 3 5 , 0 )( 2 / 3 5 , 0 (
4 1
4 ) ( 4
2 s s j s j pole s j
s
s ⇒ = ±
+ − − − = + − = ⇒ =
µ H
1 di riil dua ) 1 (
5 1 2 5 ) ( 5
2
2− + = − ⇒ =
= ⇒ =
µ pole s
s s s s H
75
Contoh ini memperlihatkan bagaimana fungsi alih menentukan bentuk gelombang sinyal keluaran melalui pole-poleyang dikandungnya. Berbagai macam poletersebut akan memberikan h(t) dengan perilaku
sebagai berikut.
µ= 0,5 : dua poleriil negatif tidak sama besar; sinyal keluaran sangat teredam. µ= 1 : dua poleriil negatif sama besar ; sinyal keluaran teredam kritis. µ= 2 : dua polekompleks konjugat dengan bagian riil negatif ; sinyal keluaran
kurang teredam, berbentuk sinus teredam.
µ= 3 : dua poleimaginer; sinyal keluaran berupa sinus tidak teredam. µ= 4 : dua polekompleks konjugat dengan bagian riil positif ; sinyal keluaran
tidak teredam, berbentuk sinus dengan amplitudo makin besar. µ= 5 : dua poleriil posistif sama besar; sinyal keluaran eksponensial dengan
eksponen positif; sinyal makin besar dengan berjalannya t.
76
Posisi poledan bentuk gelombang keluaran
77
Rangkaian Dengan Masukan Sinyal Anak Tangga
Transformasi sinyal masukan yang berbentuk gelombang anak tangga x(t) = u(t) adalah X(s) = 1/s. Jika fungsi alih adalah T(s) maka sinyal keluaran adalah
s s T s s T
s) () () ()
( = X =
Y
Tanggapan terhadap sinyal anak tangga ini dapat kita sebut
s s s
s T s) () ()
( H
G = =
Karena H(s) hanya mengandung polealami, maka dengan melihat bentuk G(s) kita segera mengetahui bahwa tanggapan terhadap sinyal anak tangga di kawasan s akan mengandung satu polepaksa disamping pole-polealami.
Polepaksa ini terletak di s= 0 + j0 (lihat gambar)
1 2 )
( 2
+ + =
s s s TV
s j s j s s s s s
) 2 / 3 5 , 0 )( 2 / 3 5 , 0 (
2 1
) 1 (
2 )
( 2
+ + − + = + + =
G
Denganµ= 2 fungsi alihnya adalah
Dengan sinyal masukan X(s) = 1/s, tanggapan rangkaian adalah CONTOH:
Jika µ= 2 dan sinyal masukan berupa sinyal anak tangga, carilah pole danzero sinyal keluaran dalam rangkaian contoh-3.7,
Dari sini kita peroleh :
0 0 di paksa satu : 0
negatif riil bagian dengan
konjugat kompleks dua : 2 / 3 5 , 0
j pole
s
pole j
s
+ =
± − =
79
CONTOH: R1 +
Vin
− 1/Cs +
Vo
− R2
Ls +
Vo − +
Vin
−
1 1 / 1 / 1 ) (
1 1 1 =R+ Cs=RCs+
Cs s TV
Ls R
R s TV = +
2 2 2()
R1 +
Vin
− 1/Cs R2
Ls +V
o −
+ + + +
+ +
=
+ + +
+ + +
+ + =
+ +
+ +
=
) ( ) (
/ 1
) ( / 1 / 1
) ( / 1
) ( || / 1
) ( || / 1 ) (
2 1 2 2
2 2
2
1 2 2 2 2 2
2
1 2
2 2
2
R R s C R L LCs
Ls R Ls R
R
R Ls R Cs
Ls R Cs Ls R Cs
Ls R Cs Ls R
R
R Ls R Cs
Ls R Cs Ls R
R s TV
Hubungan Bertingkat
dan
Dua Rangkaian dihubungkan
80
Fungsi alih dari rangkaian yang diperoleh dengan menghubungkan kedua rangkaian secara bertingkat tidak serta merta merupakan perkalian fungsi alih
masing-masing.
Hal ini disebabkan terjadinya pembebanan rangkaian pertama oleh rangkaian kedua pada waktu mereka dihubungkan. Untuk mengatasi hal ini kita dapat
menambahkan rangkaian penyangga di antara kedua rangkaian sehingga rangkaian menjadi seperti di bawah ini.
R1 +
Vin − 1/Cs
R2
Ls +
Vo
−
+
−