RANDITA GUSTIAN PUTRI
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
BOGOR 2013
PENYELESAIAN MASALAH ROTASI ALIRAN FLUIDA
KENTAL VON KARMAN MENGGUNAKAN
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudul Penyelesaian Masalah Rotasi Aliran Fluida Kental Von Karman Menggunakan Metode Homotopi adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
Bogor, Juli 2013
Randita Gustian Putri
ABSTRAK
RANDITA GUSTIAN PUTRI. Penyelesaian Masalah Rotasi Aliran Fluida Kental Von Karman Menggunakan Metode Homotopi. Dibimbing oleh JAHARUDDIN dan ALI KUSNANTO.
Persamaan Von Karman merupakan persamaan yang menjelaskan tentang aliran fluida kental yang disebabkan oleh cakram yang berputar terus-menerus. Dengan menganggap aliran tunak dan laminar, aliran fluida kental tak-termampatkan dinyatakan dalam persamaan Von Karman dengan suatu kecepatan sudut dan kecepatan dalam arah vertikal sebagai peubah tak bebasnya. Persamaan Von Karman ini merupakan persamaan taklinear yang diselesaikan menggunakan metode homotopi. Penggunaan metode homotopi dilakukan dengan mendefinisikan fungsi homotopi yang memerlukan parameter bantu untuk mengontrol daerah kekonvergenan penyelesaian. Penyelesaian yang dihasilkan merupakan suatu rumus rekursif dengan suatu hampiran awal yang diberikan. Menggunakan software berbasis fungsional diperoleh penyelesaian berupa besaran komponen kecepatan yang konvergen ke suatu nilai.
Kata kunci: persamaan Von Karman, metode homotopi, masalah taklinear, komponen kecepatan
ABSTRACT
RANDITA GUSTIAN PUTRI. Problem Solving of Von Karman Rotation Viscous Fluid Flow Using Homotopy Method. Supervised by JAHARUDDIN and ALI KUSNANTO.
Von Karman equation is an equation that describes fluid viscous flow induced by infinite disk rotation. By assuming steady flow and laminar, viscous incompressible fluid flow is represented in Von Karman equation by an angular velocity and the vertical direction velocity as the independent variables. Von Karman equation is a nonlinear problem that is solved using the homotopy method. The use of homotopy method is done by defining an homotopy function that requires auxiliary parameters to control the convergent region of the solution. The solution is a recursive formula with given initial conditions. Using software based-functional shows that velocity components converge to a value.
Keywords: Von Karman equation, homotopy method, nonlinear problem, velocity components
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada
Departemen Matematika
RANDITA GUSTIAN PUTRI
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PEGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
BOGOR 2013
PENYELESAIAN MASALAH ROTASI ALIRAN FLUIDA
KENTAL VON KARMAN MENGGUNAKAN
Judul Skripsi: Penyelesaian Masalah Rotasi Aliran Fluida Kental Von Karman Menggunakan Metode Homotopi
Nama : Randita Gustian Putri NllY1 : G54090020
Disetujui oleh
Dr J aharuddin, MS Drs Ali Kusnanto, MSi
Pembimbing I Pembimbing II
Judul Skripsi : Penyelesaian Masalah Rotasi Aliran Fluida Kental Von Karman Menggunakan Metode Homotopi
Nama : Randita Gustian Putri
NIM : G54090020
Disetujui oleh
Dr Jaharuddin, MS Pembimbing I
Drs Ali Kusnanto, MSi Pembimbing II
Diketahui oleh
Dr Berlian Setiawaty, MS Ketua Departemen
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah SWT atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih ialah rotasi fluida, dengan judul Penyelesaian Masalah Rotasi Aliran Fluida Kental Von Karman Menggunakan Metode Homotopi.
Terima kasih penulis ucapkan kepada Bapak Ranu dan Ibu Sri Lestari selaku orang tua atas doa dan dukungannya, serta Bapak Dr Jaharuddin, MS dan Drs Ali Kusnanto, MSi selaku pembimbing atas semua ilmu, motivasi, dan bantuannya selama penulisan karya ilmiah ini. Di samping itu, penulis ucapkan terima kasih kepada Ibu Elis Khatizah, MSi selaku dosen penguji atas saran dan kritik dalam penulisan karya ilmiah ini. Ungkapan terima kasih juga disampaikan kepada seluruh dosen Departemen Matematika yang telah memberikan ilmu kepada penulis, seluruh staf Departemen Matematika, teman-teman B06 TPB IPB angkatan 2009, mahasiwa Matematika angkatan 46, teman-teman kost Pondok Dinar, mahasiswa S2 IPB angkatan 2012, serta mahasiswa Matematika angkatan 43 sampai angkatan 45, atas segala kasih sayang dan doanya.
Semoga karya ilmiah ini bermanfaat.
Bogor, Juli 2013
DAFTAR ISI
DAFTAR GAMBAR vi DAFTAR LAMPIRAN vi PENDAHULUAN 1 Latar Belakang 1 Perumusan Masalah 2 Tujuan Penelitian 2 TINJAUAN PUSTAKA 2Persamaan Kontinuitas Fluida 2
Persamaan Navier Stokes 3
Metode Homotopi 4
HASIL DAN PEMBAHASAN 5
Aplikasi Metode 6
Studi Kasus 12
SIMPULAN DAN SARAN 15
Simpulan 15
Saran 16
DAFTAR PUSTAKA 16
LAMPIRAN 17
DAFTAR GAMBAR
1 Kurva terhadap h 13
2 Grafik fungsi w terhadap dengan h = -0.5 dan = 0.26167 14 3 Grafik fungsi g terhadap dengan h = -0.5 dan = 0.26167 15
DAFTAR LAMPIRAN
1 Penurunan Persamaan (58) dan (59) 17
2 Penurunan Persamaan (62) dan (63) 19
3 Penurunan Persamaan (68) dan (69) 21
PENDAHULUAN
Latar Belakang
Rotasi aliran fluida kental Von Karman merupakan masalah yang terkenal dalam mekanika fluida. Salah satu aplikasinya adalah rotasi bahan bakar pesawat ruang angkasa yang diluncurkan oleh NASA. Rotasi aliran fluida kental Von Karman digunakan untuk menganalisis karakteristik bahan bakar pesawat ruang angkasa yang mudah terbakar dalam keadaan sedikit gravitasi. Penelitian ini didasarkan pada laju aliran bahan bakar dan kecepatan rotasi bahan bakar. Kecepatan rotasi bahan bakar sangat memengaruhi timbulnya percikan api pada media bahan bakar. Aliran Von Karman mengontrol besaran kecepatan rotasi agar bahan bakar tidak menimbulkan percikan api yang dapat memengaruhi media bahan bakar (Williams dan Nayagam 2002). Secara umum, persamaan Von Karman menjelaskan tentang aliran fluida kental yang disebabkan oleh cakram yang berputar terus-menerus. Dengan menganggap aliran tunak dan laminar, aliran fluida kental tak-termampatkan ini berputar terus-menerus di atas cakram dengan suatu kecepatan sudut. Persamaan gerak dari fluida ini dinyatakan dalam persamaan kontinuitas dan persamaan Navier-Stokes dengan suatu kondisi batas tertentu. Von Karman mengubah persamaan diferensial parsial pada persamaan kontinuitas dan persamaan Navier-Stokes menjadi persamaan diferensial biasa menggunakan suatu transformasi (Liao 2004). Banyak penelitian yang telah menerapkan rotasi aliran fuida kental Von Karman. Di antaranya adalah efek kondisi batas magnetik pada dinamo (Gissinger et al. 2008), model turbulen dengan aliran Von Karman (Poncet dan Schiestel 2008), dan induksi rotasi aliran Von Karman dengan feromagnetik (Verchille et al. 2010).
Pada umumnya, persamaan rotasi aliran fluida kental Von Karman merupakan persamaan taklinear yang masih sulit untuk ditemukan penyelesaiannya. Beberapa peneliti telah menggunakan pendekatan numerik atau kombinasi analitik dan numerik untuk menyelesaikan masalah tersebut, diantaranya metode pendekatan numerik untuk menyelesaikan persamaan Von Karman (Benton 1966) dan metode homotopi tetapi dengan pendekatan deret polynomial (El-Nahhas 2007). Salah satu metode yang memberikan pendekatan penyelesaian analitik secara eksplisit dari persamaan taklinear adalah metode homotopi. Dalam metode ini, didefinisikan suatu operator linear dan operator taklinear yang didasarkan pada bentuk taklinear masalah tersebut. Kemudian didefinisikan fungsi homotopi dengan penambahan beberapa parameter. Penyelesaian masalah taklinear dengan menggunakan metode homotopi dimisalkan dalam bentuk deret.
Di dalam karya ilmiah ini, dibahas penyelesaian masalah rotasi aliran fluida kental menggunakan metode homotopi. Menggunakan software berbasis fungsional akan ditentukan penyelesaian berupa komponen kecepatan dalam sistem koordinat silinder.
2
Perumusan Masalah
Persamaaan kontinuitas dan persamaan Navier-Stokes pada rotasi aliran fluida kental Von Karman merupakan persamaan taklinear yang dinyatakan dalam sistem koordinat silinder. Penggunaan transformasi memunculkan suatu parameter yang akan ditentukan dalam penyelesaian persamaan Von Karman, sehingga masalah penyelesaian persamaan Von Karman menjadi kompleks. Metode homotopi digunakan untuk menyelesaikan masalah tersebut, dengan mendefinisikan suatu fungsi homotopi yang didasarkan pada persamaan Von Karman.
Tujuan Penelitian
Berdasarkan latar belakang di atas, maka tujuan penelitian adalah
a Mengkonstruksi ulang penurunan persamaan kontinuitas dan persamaan Navier-Stokes dalam sistem koordinat silinder yang merupakan persamaan Von Karman (Streeter dan Wiley 1985).
b Menggunakan metode homotopi untuk menyelesaikan persamaan Von Karman.
c Menggambarkan grafik penyelesaian persamaan Von Karman dengan
software berbasis fungsional, kemudian memberikan tafsiran terhadap
hasil-hasil tersebut.
TINJAUAN PUSTAKA
Persamaan Kontinuitas Fluida
Persamaan kontinuitas diturunkan berdasarkan pada kesetimbangan massa.
Kesetimbangan massa menyatakan bahwa perubahan massa rata-rata merupakan selisih antara massa rata-rata yang masuk dan massa rata-rata yang keluar (Streeter dan Wiley 1985). Dengan demikian, persamaan kontinuitas dapat dituliskan dalam bentuk
̅
dengan rapat massa fluida, dan ̅ vektor kecepatan, serta t waktu. Jika fluida memiliki sifat tak termampatkan, maka diperoleh suatu bentuk khusus dari persamaan (1) yaitu: ̅ atau dengan ̅ ( ) dimana u, dan masing-masing merupakan komponen kecepatan dalam arah x, y, dan z. Karena elemen volume yang dilalui fluida dapat berbentuk sebarang, maka dapat diturunkan pula persamaan kontinuitas pada
3 sistem koordinat silinder. Sistem koordinat silinder dinyatakan dalam bentuk pasangan terurut (r,,z) dengan dan . Jika aturan rantai
digunakan, maka diperoleh persamaan berikut
[ o in) ]
[ in o ]
Jika persamaan (3) dan (4) disubstitusikan ke dalam persamaan (2), maka diperoleh
( ) ( ) dengan
o in
in o
masing-masing merupakan kecepatan dalam arah r, dalam arah sudut , dan Vz
kecepatan dalam arah sumbu-z.
Persamaan Navier-Stokes
Persamaan Navier-Stokes diturunkan berdasarkan persamaan gerak pada fluida. Persamaan gerak ini berpadanan dengan kekekalan momentum yang menyatakan bahwa rata perubahan momentum merupakan selisih antara rata-rata momentum yang masuk dengan rata-rata-rata-rata momentum yang keluar kemudian dijumlahkan dengan jumlah gaya-gaya yang terjadi pada sistem.
Penurunan persamaan Navier-Stokes dilakukan dengan asumsi-asumsi sebagai berikut:
1 Fluida memiliki koefisien kekentalan (viskositas) yang konstan. 2 Fluida memiliki sifat tak termampatkan.
3 Kecepatan aliran fluida pada suatu titik tidak bergantung terhadap waktu (tunak).
4 Aliran fluida bersifat kontinu dan tidak saling berpotongan (laminar). 5 Gaya gravitasi diabaikan.
Berdasarkan asumsi, persamaaan Navier-Stokes dituliskan dalam persamaan vektor (Streeter dan Wiley 1985) berikut:
̅
̅
dengan , p, dan masing-masing merupakan rapat massa fluida, tekanan fluida,
dan koefisien kekentalan. Asumsikan kecepatan aliran fluida bersifat tunak, sehingga ̅ tidak bergantung pada t. Bentuk ̅ adalah turunan vektor ̅ terhadap t sehingga diperoleh persamaan berikut :
[ ] [ ] [ ] [ ]
4 [ ] [ ]
Elemen volume yang dilalui fluida dapat berbentuk sebarang. Oleh karena itu, dapat diturunkan pula persamaan gerak untuk elemen volume yang berbentuk silinder. Penurunan ini diperoleh dengan transformasi dari sistem koordinat siku-siku ke sistem koordinat silinder. Selanjutnya, dengan menggunakan persamaan kontinuitas pada persamaan (5), maka diperoleh persamaan Navier-Stokes pada sistem koordinat silinder berikut:
[ ] [ ] [ ] Metode Homotopi
Berikut ini diberikan ilustrasi konsep metode homotopi. Misalkan diberikan persamaan diferensial berikut:
dengan N operator turunan, t variabel bebas dan u(t) fungsi yang akan ditentukan. Selanjutnya, didefinisikan pula suatu operator L yang memenuhi
L[ f ] = 0, bila f = 0. (12)
Misalkan u0(t) merupakan pendekatan awal dari penyelesaian persamaan (11) dan
q [0,1] suatu parameter. Didefinisikan suatu fungsi H sebagai berikut:
H[;q] = (1 - q) L[-u0(t)] + qN[]. (13) Berdasarkan persamaan (13), untuk q = 0 dan q = 1 masing-masing memberikan persamaan berikut:
H[(t;0);q] = L[(t;0) - u0(t)] dan
H[(t;1);q] = N[(t;1)].
Menurut persamaan (11) sampai (13) diperoleh bahwa fungsi (t;0)=u0(t) dan
(t;1)=u(t) masing-masing merupakan penyelesaian dari persamaan
H[(t;0);0] = 0 dan H[(t;1);1] = 0.
Dengan demikian peningkatan nilai q dari 0 sampai 1 menyatakan perubahan nilai
H[;q] dari L[ - u0(t)] ke N[]. Dalam topologi hal ini disebut deformasi.
Perluasan metode homotopi lebih lanjut dapat dituliskan dalam bentuk persamaan deformasi orde nol berikut :
( ) ,( ) ( )- ( ) ,( )- dengan ( ) adalah pendekatan awal, h dan B(t) masing-masing merupakan parameter bantu dan fungsi bantu. Jika q = 0 dan q = 1, maka dari persamaan (14) akan diperoleh ( ) dan ,( )- .
Selanjutnya, karena parameter q bernilai dari 0 sampai 1, maka ( ) memetakan dari penduga awal ke penyelesaian eksak u(t). Dengan menggunakan konsep deret Taylor, ( ) dapat diuraikan menjadi
5 ( ) ∑ dimana ( ) ( ) |
Kemudian dengan menurunkan persamaan (14) terhadap q hingga n kali serta mengevaluasi pada q = 0 dan dibagi dengan n! akan diperoleh bentuk persamaan orde ke-n berikut:
[ ( ) ( )] ( ) , ⃗ - dengan , ⃗ - ( ) ( ) | ( ) { Untuk q = 1, maka persamaan (15) menjadi
( ) ∑
Hasil ini menunjukkan adanya hubungan antara penyelesaian eksak dengan pendekatan awal dan , n = … yang akan ditentukan. Penyele aian pendekatan , n = 1,2, … diperoleh dari per amaan ) dengan terlebih dahulu menentukan operator linear L. Pemilihan operator L perlu memperhatikan validitas dari metode homotopi.
HASIL DAN PEMBAHASAN
Tinjau persamaan kontinuitas dan persamaan Navier-Stokes dalam sistem koordinat silinder pada persamaan (8) sampai (10) dengan kondisi batas diberikan sebagai berikut :
ketika
ketika dengan kecepatan sudut sepanjang sumbu-z.
Selanjutnya, didefinisikan variabel
( ) ⁄
dan transformasi berikut
( ) ( ) ( ) ⁄
Jika transformasi pada persamaan (19) sampai (23) digunakan, maka persamaan (5), (8), (9), dan (10) menjadi persamaan diferensial biasa berikut:
6
() () - () () (
() () () () ()
() () () ()
() () Kondisi batas pada persamaan (17) dan (18) menjadi
Berdasarkan persamaan (27) diperoleh
() () Jika persamaan (29) disubstitusikan ke dalam persamaan (24) dan (25), maka diperoleh persamaan berikut:
() () () () () ()
() () () () ()
dan kondisi batas (28) menjadi
Perhatikan bahwa pada kondisi batas (32) tidak diketahui kondisi batas untuk . Oleh karena itu, didefinisikan
( ) serta menggunakan transformasi
() dan
dengan merupakan parameter. Jika per amaan 33) dan (34) digunakan, maka persamaan (30) dan (31) menjadi
() , ()- ( ) () () ()
() , ()- () () ()
dan kondisi batas (32) menjadi
Dalam karya ilmiah ini akan dibahas penyelesaian persamaan (35) dan (36) dengan kondisi batas (37) menggunakan metode homotopi.
Aplikasi Metode
Berikut ini akan dibahas penggunaan metode homotopi yang telah diuraikan sebelumnya. Misalkan penyelesaian dari masalah nilai batas persamaan (35) dan (36) menggunakan fungsi basis berupa fungsi eksponensial. Pemisalan ini berdasarkan pada penyelesaian bentuk homogen persamaan (35) dan (36) yang berbentuk eksponensial. Himpunan basisnya sebagai berikut:
*e p | + Penyelesaian persamaan (35) dan (36) dapat dinyatakan dalam bentuk:
() ∑ ( ) () ∑ ( )
7 dengan dan adalah koefisien deret yang akan ditentukan. Selanjutnya, jika merupakan parameter bantu, maka berdasarkan persamaan (38) dan (39) dipilih pendekatan awal dari dan sebagai berikut:
e p e p e p ,e p e p - Berikut ini akan ditentukan penyelesaian dari masalah kondisi batas (35) dan (36) menggunakan pendekatan metode homotopi. Dalam metode homotopi ini, suatu operator linear dipilih berdasarkan persamaan (35) dan (36), yaitu
( ) ( )
Berdasarkan operator dan diperoleh
e p e p e p dan
e p e p dimana dan merupakan koefisien. Kemudian dari persamaan (35) dan (36) didefinisikan operator taklinear sebagai berikut:
, ( ) ( ) ( ) ( )- ( ) ( ) ( ) ( ) ( ), ( )- ( ) ( ) ( ) ( ) [ ( ) ] ( ) dan , ( ) ( ) ( ) ( )- ( ) ( ) ( ), ( ( ) ( ) ( ) ( )
dengan q [0,1] merupakan suatu parameter, dan adalah fungsi yang bergantung pada dan q, dan fungsi yang bergantung pada q. Didefinisikan fungsi homotopi H sebagai berikut:
dan
dengan dan merupakan dua parameter bantu yang taknol, dan adalah dua fungsi bantu yang tak nol.
Selanjutnya, misalkan fungsi dan adalah penyelesaian dari persamaan berikut:
dan
8
Berdasarkan persamaan (48) dan (49), persamaan (50) dan (51) dapat dituliskan sebagai berikut:
dengan kondisi batas dari persamaan (37) menjadi
( ) ( ) ( ) | ( ) | dan Berdasarkan persamaan (52) dan (53), untuk q = 0 diperoleh
yang masing-masing merupakan pendekatan awal dari dan . Kemudian ketika q = 1, , diperoleh
Pemilihan pendekatan awal pada persamaan (40) dan (41) menjamin adanya fungsi dan yang dapat diturunkan hingga n kali terhadap q. Jika fungsi diturunkan terhadap q hingga n kali di q = 0 kemudian dibagi n!, maka diperoleh
()
|
Karena () pada persamaan (54) adalah tunggal, maka memiliki penyajian deret Taylor di q = 0, yaitu berbentuk:
( ) ∑ ( ) | atau ( ) () ∑ ()
Selanjutnya, untuk q = 1 diperoleh
( ) () ∑ ()
Karena , maka diperoleh
() () ∑ (
)
Jika fungsi diturunkan terrhadap q hingga n kali di q = 0, kemudian dibagi dengan n!, maka diperoleh
()
( )
| Karena () pada persamaan (55) adalah tunggal, maka memiliki penyajian deret Taylor di q = 0, yaitu berbentuk:
( ) ∑
( )
|
9 atau
∑ () .
Selanjutnya, untuk q = 1 diperoleh
( ) ∑ ()
Karena , maka diperoleh
∑
.
Jika fungsi diturunkan terhadap q hingga n kali di q = 0, kemudian dibagi dengan n!, maka diperoleh
( )
| Karena pada persamaan (56) adalah tunggal, maka memiliki penyajian deret Taylor di q = 0, yaitu berbentuk:
∑ ( ) | atau ∑
Selanjutnya, untuk q = 1 diperoleh
∑ Karena , maka diperoleh
∑
Jika fungsi diturunkan terhadap q hingga n kali di q = 0, kemudian dibagi dengan n!, maka diperoleh adalah
( )
| Karena pada persamaan (57) adalah tunggal, maka memiliki penyajian deret Taylor di q = 0, yaitu berbentuk:
∑ ( ) | atau ∑ Selanjutnya, untuk q = 1 diperoleh
10
∑ Karena , maka diperoleh
∑
Hasil ini menunjukkan adanya hubungan antara penyelesaian eksak dari persamaan (35) dan (36) dengan pendekatan awal , , serta
dan , n … yang akan ditentukan. Per amaan untuk menentukan
dan diperoleh jika kedua ruas dari persamaan (52) dan (53) diturunkan terhadap q hingga n kali dan dievaluasi pada q = 0 kemudian dibagi n!, maka akan diperoleh persamaan berikut:
[ ] ⃗ ⃗ )
[ ] ⃗ ⃗ dengan kondisi batas
dimana ⃗ ⃗ ) ( ) | dan ⃗ ⃗ ) ( ) | Penurunan persamaan (58) dan (59) diberikan pada lampiran 1.
Jika persamaan (46) dan (47) masing-masing disubstitusikan ke persamaan (60) dan (61), maka diperoleh bentuk dan sebagai berikut:
⃗ ⃗ ) ∑[ ] ∑ [∑ ] ∑ [∑ ] ∑ dan ⃗ ⃗ ) ∑[ ] ∑ ∑ 0 1 dengan
11 ∑ ∑ ∑ ∑
Penurunan persamaan (62) dan (63) diberikan pada lampiran 2.
Terdapat empat besaran yang akan ditentukan yaitu , , - , dan
- , sedangkan hanya terdapat dua persamaan untuk dan . Dengan demikian dibutuhkan dua persamaan tambahan untuk menentukan - , dan - .
Berdasarkan persamaan (39), (58) dan (59) dapat dipilih fungsi bantu
dan berikut:
() e p( ) () e p( ) dengan dan bilangan bulat. Misalkan dipilih
dan sehingga dari persamaan (64) dan (65) dipilih fungsi bantu sebagai berikut
dan Selanjutnya untuk penyederhanaan dipilih
Berdasarkan persamaan (40) dan (41), dan dapat dimisalkan dalam bentuk ⃗ ⃗ ∑ ( ) e p ⃗ ⃗ ∑ ( ) e p dimana ( ) dan ( ) merupakan koefisien yang tidak bergantung pada . Ada dua cara untuk menentukan dan dari persamaan (66) dan (67). Cara pertama yaitu dengan membuat ( ) dan ( ) menjadi nol, sehingga diperoleh
( ) dan Penyelesaian persamaan (68) memberikan
Kemudian cara kedua, yaitu dengan membuat ( ) dan ( ) . Sehingga, diperoleh persamaan berikut
( ) Penyelesaian persamaan (69) memberikan
| | ⁄ dan (| |) ⁄ Penurunan persamaan (68) dan (69) diberikan pada lampiran 3.
Cara pertama hanya menemukan hubungan dan sehingga digunakan cara kedua. Berdasarkan cara kedua ini digunakan untuk menentukan - , dan - dari persamaan berikut:
12
( ⃗ ) dan ( ⃗ )
dengan . ⃗ - - / dan . ⃗ - - / adalah koefisien dari persamaan ⃗ ⃗ ∑ ( ⃗ ) e p ⃗ ⃗ ∑ ( ⃗ ) e p Berdasarkan persamaan (70) dan (71), dan dapat dimisalkan dalam bentuk : ∑ e p ∑ e p
dengan dan merupakan koefisien yang akan ditentukan. Dari persamaan (58) dan (59) dan berdasarkan persamaan (72) dan (73), maka penyelesaian persamaan (35) dan (36) untuk orde ke-m dapat dinyatakan sebagai berikut:
() ∑ ∑ ( ) () ∑ ∑ e p( ) dengan ∑ dan ∑ .
Dengan demikian dan untuk orde ke-m pada persamaan (30) dan (31) sebagai berikut () [ ∑ ∑ e p( ) ] () ∑ ∑ e p( ) Studi Kasus
Pada bagian ini akan dibahas suatu studi kasus penyelesaian persamaan Von Karman dengan menggunakan metode homotopi. Berdasarkan uraian pada
13 bagian aplikasi metode, berikut ini prosedur untuk menentukan penyelesaian dari persamaan Von Karman (30) dan (31):
1 Misalkan diberikan pendekatan awal (40) dan (41) untuk suatu .
2 Menentukan penyelesaian pendekatan untuk orde ke-m dari persamaan Von Karman (30) dan (31) dilakukan sebagai berikut:
i Menentukan n n- ⃗ n- ⃗ n- n- dan n n- ⃗ n- ⃗ n- n- pada persamaan (62) dan (63).
ii Menentukan dan dari persamaan (70) dan (71) dengan = = (| - |) ⁄ .
iii Menentukan dan ) dari persamaan (72) dan (73) dengan
an,k dan bn,k diperoleh dari persamaan (58) dan (59).
3 Menentukan penyelesaian persamaan Von Karman (30) dan (31) dari persamaan (74) dan (75).
Berdasarkan Gambar 1, jika = 0, maka nilai mencapai kekonvergenan untuk h pada selang -1/5 h 0. Jika = 1/4 maka nilai mencapai kekonvergenan untuk h pada selang -3/5 h 0. Selanjutnya jika = 0.26167 diperoleh selang h yang lebih besar untuk mencapai yang konvergen. Oleh karena itu, dalam penelitian ini dipilih = 0.26167 dan h = -0.5 dalam menentukan penyelesaian persamaan (30) dan (31). Berdasarkan persamaan (62) dan (63) dengan pendekatan awal (40) dan (41) diperoleh
() . e p( ) . e p( ) . e p( ) . e p( ) () . e p( ) . e p( ) . e p( ) () . e p( ) . e p( ) . e p( ) . e p( ) . e p( ) . e p( ) () . e p( ) . e p( ) . e p( ) . e p( ) . e p( ) . e p( )
Penyelesaian persamaan (35), (36), dan (37) dengan metode homotopi adalah Gambar 1 Kurva terhadap h
: = 0 : = 0.25 ─── : = 0.26167
14
() () () () () () () () () () () () () ()
dengan (), (), (), (), (), (), (), dan () diberikan pada Lampiran 4.
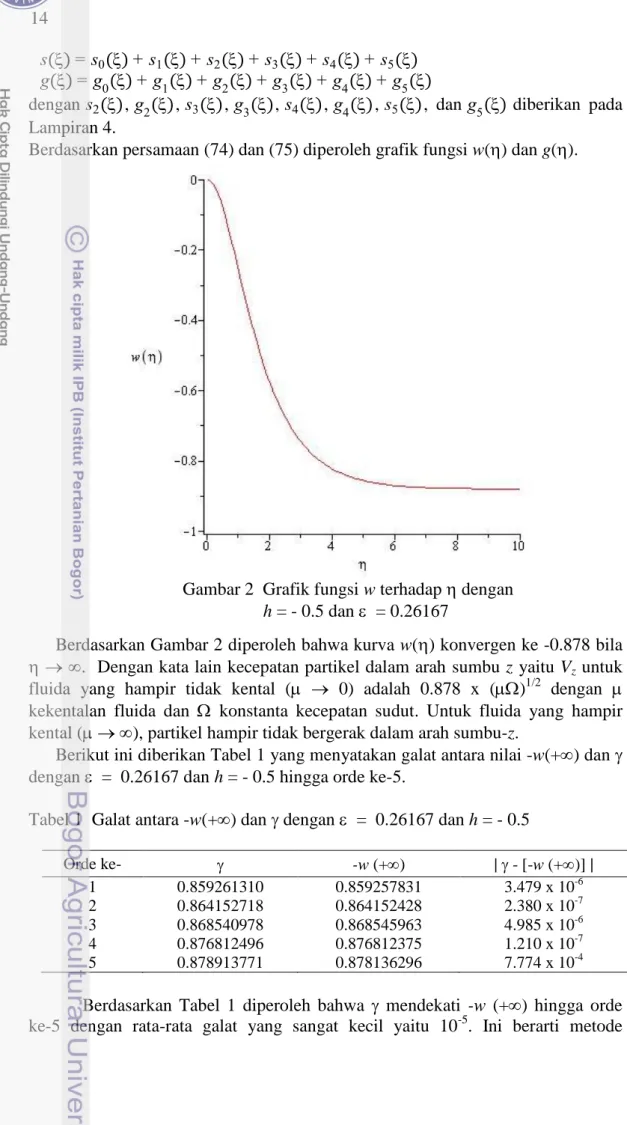
Berdasarkan persamaan (74) dan (75) diperoleh grafik fungsi w() dan g().
Berdasarkan Gambar 2 diperoleh bahwa kurva w() konvergen ke -0.878 bila
. Dengan kata lain kecepatan partikel dalam arah sumbu z yaitu Vz untuk
fluida yang hampir tidak kental ( 0) adalah 0.878 x ( )1/2 dengan kekentalan fluida dan konstanta kecepatan sudut. Untuk fluida yang hampir
kental ( ), partikel hampir tidak bergerak dalam arah sumbu-z.
Berikut ini diberikan Tabel 1 yang menyatakan galat antara nilai -w(+) dan dengan = 0.26167 dan h = - 0.5 hingga orde ke-5.
Tabel 1 Galat antara -w(+) dan dengan = 0.26167 dan h = - 0.5
Orde ke- -w (+) | - [-w (+)] | 1 0.859261310 0.859257831 3.479 x 10-6 2 0.864152718 0.864152428 2.380 x 10-7 3 0.868540978 0.868545963 4.985 x 10-6 4 0.876812496 0.876812375 1.210 x 10-7 5 0.878913771 0.878136296 7.774 x 10-4
Berdasarkan Tabel 1 diperoleh bahwa mendekati -w (+) hingga orde ke-5 dengan rata-rata galat yang sangat kecil yaitu 10-5. Ini berarti metode
Gambar 2 Grafik fungsi w terhadap dengan
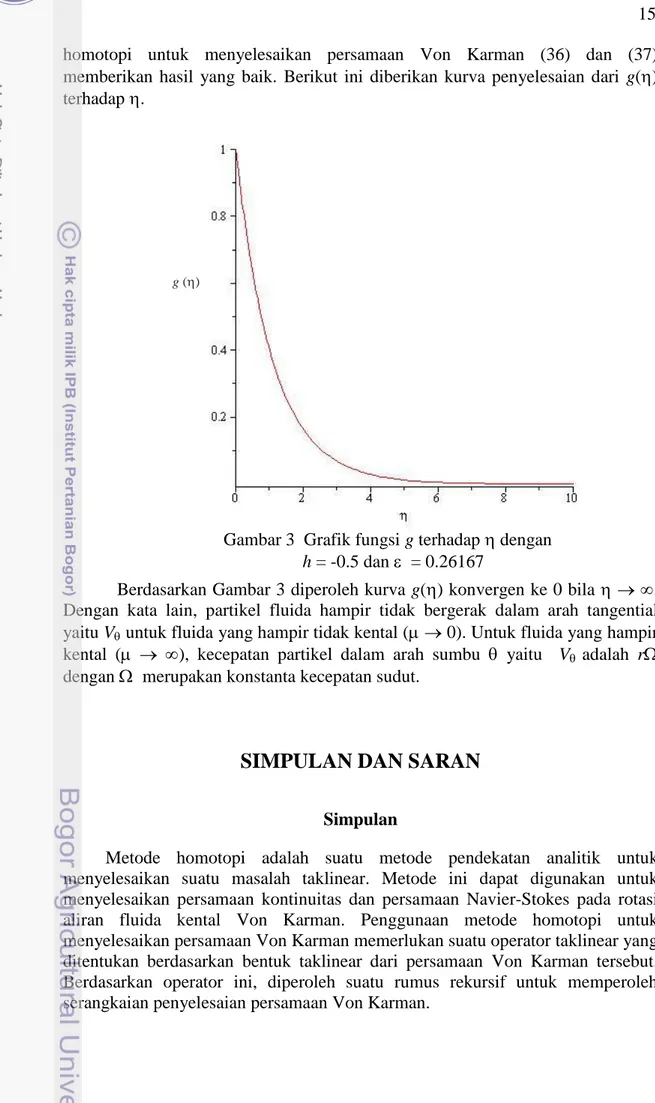
15 homotopi untuk menyelesaikan persamaan Von Karman (36) dan (37) memberikan hasil yang baik. Berikut ini diberikan kurva penyelesaian dari g() terhadap .
Berdasarkan Gambar 3 diperoleh kurva g() konvergen ke 0 bila . Dengan kata lain, partikel fluida hampir tidak bergerak dalam arah tangential yaitu V untuk fluida yang hampir tidak kental ( 0). Untuk fluida yang hampir kental ( ), kecepatan partikel dalam arah sumbu yaitu V adalah r dengan merupakan konstanta kecepatan sudut.
SIMPULAN DAN SARAN
Simpulan
Metode homotopi adalah suatu metode pendekatan analitik untuk menyelesaikan suatu masalah taklinear. Metode ini dapat digunakan untuk menyelesaikan persamaan kontinuitas dan persamaan Navier-Stokes pada rotasi aliran fluida kental Von Karman. Penggunaan metode homotopi untuk menyelesaikan persamaan Von Karman memerlukan suatu operator taklinear yang ditentukan berdasarkan bentuk taklinear dari persamaan Von Karman tersebut. Berdasarkan operator ini, diperoleh suatu rumus rekursif untuk memperoleh serangkaian penyelesaian persamaan Von Karman.
Gambar 3 Grafik fungsi g terhadap dengan
h = -0.5 dan = 0.26167 g ()
16
Penyelesaian hampiran persamaan Von Karman merupakan kombinasi linear dari rangkaian penyelesaian tersebut. Semakin tinggi orde yang digunakan, maka semakin mendekati penyelesaian eksak dari persamaan Von Karman.
Dalam penelitian ini, diperoleh penyelesaian masalah berupa besaran komponen kecepatan sudut dan komponen kecepatan dalam arah sumbu-z dari masalah Von Karman. Untuk fluida yang kental, partikel fluida bergerak dengan kecepatan sudut sebesar r tetapi partikel fluida tidak bergerak dalam arah sumbu-z. Untuk fluida yang tak kental, partikel fluida tidak bergerak dalam arah sudut , tetapi partikel fluida bergerak dengan kecepatan dalam arah sumbu-z sebesar 0.878 x ( )1/2. Pemilihan parameter h dan menentukan kekonvergenan dari penyelesaian tersebut.
Saran
Dalam karya ilmiah ini digunakan beberapa asumsi untuk memperoleh pendekatan penyelesaian analitik dari masalah Von Karman. Perlu adanya penelitian lanjutan untuk masalah Von Karman bila beberapa asumsi tidak digunakan.
DAFTAR PUSTAKA
Benton ER. 1966. On the flow due to a rotating disk. J.Fluid Mech. 24:781-800. Doi: http://dx.doi.org/10.1017/S002211206001009.
El-Nahhas A. 2007. Analytic approximations for Von Karman swirling flow. Sci. 44(3):181-187.
Gissinger C, Iskakov A, Fauve S, Purmy E. 2008. Effect of magnetic boundary condition on the dynamo threshold of Von Karman swirling flow. Europhysics
Letter. Doi:10.1209/0295-5075/82/29001.
Liao. 2004. Beyond Perturbation : Introduction to The Homotopy Analysis
Method. New York (US) : Boca Raton.
Poncet S, Schiestel R, Manchaux R. 2008. Turbulence modelling of the Von Karman flow: viscous and inertial stirrings. Internal Journal of Heat and Fluid
Flow. 29(1):62-74. Doi: 10.1016/j.ijheatfluidflow.2007.05.005.
Streeter VL, Wiley EB. 1985. Mekanika Fluida Jilid 1. Prijono A, penerjemah. Jakarta(ID) : Penerbit Erlangga. Terjemahan dari : Fluid Mechanics, Ed ke-8. Temam R. 1977. Navier-Stokes Equation : Theory and Numerical Analysis. New
York (US) : North-Holland Publishing Company.
Verchille G, Pilhon N, Bourgoin M, Odier P, Pinton JF. 2010. Induction in Von Karman flow driven by ferromagnetic impellers. Phys. Doi: 10.1088.1367-2630/12/3/033006.
Williams FA, Nayagam V. 2002. Dynamics of diffusion flames in Von Karman swirling flow studied. Microgravity Research NASA[Internet]. California, San
Diego. [diunduh Mei 2012]. Tersedia pada:
17 Lampiran 1 Penurunan Persamaan (58) dan (59)
Tinjau persamaan (59) dan (60) berikut:
atau
, ( ) ()- , ( ) ()- [ ( ) ()] [ ( ) ()] Turunan pertama terhadap q dari kedua ruas persamaan (59) dan (60) masing-masing sebagai berikut:
, ( ) ( , ( ) ()- , ( ) ( () ( ) () [ ( ) ()] [ ( ) ()] [ ( ) ()] Turunan kedua , ( ) ( , ( ) ( , ( ) ( () , ( ) ( ) ( ) ( () , ( ) ( ) ( ) ( [ ( ) ()] [ ( ) ()] [ ( ) ()]
Dengan langkah yang sama, turunan ke – n terhadap q adalah
, ( ) ( , ( ) ( , ( ) ( () , ( ) ( ) ( ) ( () , ( ) ( ) ( ) ( [ ( ) ()] [ ( ) ()] [ ( ) ()]
18
Untuk q = 0 dan kedua ruas dikalikan dengan diperoleh
[ ⃗ ⃗ ) 0 ⃗ ⃗ / dengan { } ⃗ { } () | () | ⃗ ⃗ ) ( ) | ⃗ ⃗ ) ( ) | dan {
19 Lampiran 2 Penurunan Persamaan (62) dan (63)
Tinjau persamaan (60) berikut: ⃗ ⃗ ) ( ) | Untuk n = 1, diperoleh ⃗ ⃗ ) ( ) ( ) ( ) ( ) ( ) ( )
Karena dan maka diperoleh ⃗ ⃗ ( ) Untuk n = 2, diperoleh ⃗ ⃗ ( Secara umum untuk n … diperoleh
⃗ ⃗ ) ∑[ ] ∑ [∑ ] ∑ [∑ ] ∑ dimana ∑ ∑ ∑ ∑ Selanjutnya, tinjau persamaan (61) berikut:
⃗ ⃗ ) ( ) | Untuk n = 1, diperoleh ( ⃗ ⃗ ) () , ()- () () () Untuk n = 2, diperoleh
20
( ⃗ ⃗ )
Secara umum untuk n … diperoleh
⃗ ⃗ ) ∑[ ] ∑ ∑ 0 1
21 Lampiran 3 Penurunan Persamaan (68) dan (69)
Berdasarkan persamaan (62) dan (63), maka untuk n = 1 diperoleh
⃗ ⃗ ( )
⃗ ⃗ sehingga, persamaan (66) dan (67) dapat diuraikan sebagai berikut
[- ] e p (- ) [ - - - - - e p e p , -e p ( )e p ( )e p ( )e p ( )e p [ ] e p ( ) – – e p e p ( ) e p ( ) e p ( ) e p
Oleh karena itu, diperoleh konstanta berikut ( ) ( ) ( ) ( ) ( ) ( ) – ( )
Jika ( ) dan ( ) , maka mengakibatkan atau
( ) ( ) Jika dua persamaan di atas diselesaikan, maka diperoleh
Jika ( ) dan ( ) maka mengakibatkan
atau
– atau
( ) Jika dua persamaan diatas diselesaiakan, maka diperoleh
(| |) (| |)
22
Lampiran 4 Nilai , s(), dan g()
Berdasarkan persamaan (62) dan (70), diperoleh konstanta dan . Jika dan diperoleh Kemudian, bila diperoleh parameter = 0.26167. Jika dan , diperoleh
( ) , √ √ √ -
Dengan cara yang sama diperoleh
–
– ) Selanjutnya untuk mendapatkan solusi s() dan g() digunakan parameter = 0.26167 dan h = -0.5.
Berdasarkan persamaan (58) dan (70), untuk n = 1 diperoleh 0 1 ⃗ ⃗ dengan 0 - 1 dan ⃗ ⃗ sebagai berikut
0 1 ( ) ( )
⃗ ⃗ ( ) ( ) ( ) ( ) ( ) ( ) ( ) Sehingga diperoleh ( ) dan sebagai berikut
( ) . (- ) - . (- ) . (- ) - . (- )
Berdasarkan persamaan (59) dan (71), untuk n = 1 diperoleh [ ] ⃗ ⃗ dengan [ - ] dan ⃗ ⃗ sebagai berikut
[ ] ( ) ( ) ( ) ⃗ ⃗ . ( ) . ( )
sehingga diperoleh
( ) . ( ) . ( ) . ( ) Dengan cara yang sama diperoleh
() . ( ) . ( ) . ( ) . ( ) . ( ) . ( ) () . ( ) . ( ) . ( ) . ( ) . ( ) . ( ) . () . ( ) . ( ) . ( ) . ( ) . ( ) . ( ) () . ( ) . ( ) . ( ) . ( ) . ( ) . () . ( ) . ( ) ( )
23 . ( ) . ( ) . ( ) . e p . e p () . ( ) . ( ) . ( ) . e p . e p . e p . e p . e p . () . ( ) . ( ) . ( ) . e p . e p . e p . e p - - . e p - - . e p - ( ) . ( ) . ( ) . ( ) . e p . e p . e p . e p . e p .
24
RIWAYAT HIDUP
Penulis dilahirkan di Ponorogo tanggal 15 Agustus 1991 sebagai anak pertama dari 2 bersaudara dari pasangan Ranu dan Sri Lestari. Pendidikan formal yang ditempuh penulis yaitu di SDN Ujung Menteng 01 Pagi lulus pada tahun 2003, SMP Negeri 193 Jakarta Timur lulus pada tahun 2006, SMA Negeri 89 Jakarta lulus pada tahun 2009 dan pada tahun yang sama penulis di terima di Institut Pertanian Bogor melalui jalur USMI di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.
Selama menuntut ilmu di IPB, penulis berkecimpung dalam kepanitiaan berbagai acara di antaranya adalah Matematika Ria 2011 sebagai staf kesekretariatan, Matematika Ria 2012 sebagai dtaf kesekretariatan, dan IPB Mathamatics Challenges 2012 (IMC) sebagai ketua divisi kesekretariatan. Penulis mendapat beasiswa Peningkatan Prestasi Akademik (PPA) periode 2010-2013. Selain itu, penulis juga pernah menjadi asisten dosen untuk mata kuliah Metode Statistik dan Kalkulus III serta menjadi pengajar bimbel di sekitar kampus.