DIKTAT METODE NUMERIK - eprints3

Metode Numerik

i

M ETOD E N UM ERI K

D isusun

ole h

I r . Su dia di, M .M .A.E.

I r . Riz a n i Te gu h , M T

SEKOLAH TI N GGI M AN AJEM EN I N FORM ATI KA D AN KOM PU TER

GLOBAL I N FORM ATI KA– M D P

Metode Numerik

i

KATA PENGANTAR

Per t ama-t ama penulis mengucapkan puji dan syukur kehadir at Tuhan Yang Maha Kuasa atas segala limpahan r ahmat Nya, hingga Diktat Metode Numer ik ini dapat diselesaikan. Mudah-mudahan diktat ini dapat membantu mahasisw a STMIK Global Infor mat ika MDP dan AMIK MDP dalam mengikuti mat a kuliah Metode Numer ik maupun mat a kuliah yang ber kaitan.

Penulis mengucapkan ter imakasih dan menyampaikan penghar agaan yang set inggi-tingginya pada Ketua STMIK Global Infor mat ika MDP dan Dir ekt ur AMIK MDP yang selalu member ikan dor ongan baik pada penulis maupun pada r ekan-r ekan dosen lainnya untuk menyusun mat er i kuliah, baik dalam bentuk diktat atau buku. Dor ongan ter sebut telah menambah semangat penulis dalam menyelesaikan tulisan ini. Ucapan ter imakasih juga penulis sampaikan pada r ekan-r ekan dosen yang telah membantu penulis dalam menyelesaikan diktat ini. Mudahan-mudahan dengan adanya dor ongan dan dukungan yang diber ikan pada penulis akan dapat dihasilkan diktat lain dalam w akt u singkat .

Meskipun telah ber hasil dit er bitkan, penulis menyadar i bahw a diktat ini masih sangat seder hana dan tentu masih banyak kekur angan dan kelemahannya. Oleh kar ena itu penulis menghar apkan sar an dan kr itik yang membangun dar i pembaca sekalian, sehingga dapat dihasilkan diktat yang lebih baik pada masa yang akan datang. Sar an, kr itik dan kor eksi dapat disampaikan pada alamat ,

sudiadi@stmik-mdp.net atau r izani@mdp.ac.id

Akhir nya penulis mengucapkan selamat belajar kepada selur uh mahasisw a STMIK Global Infor mat ika MDP. Mudahan-mudahan sukses selalu menyer t ai saudar a-saudar a.

Palembang, 6 Apr il 2015 Penulis,

Metode Numerik

iii

Metode Numerik

1 BAB I PENDAHULUAN

1.1 Definisi

Metode numer ik adalah teknik untuk menyelesaikan per masalahan-per masalahan yang difor mulasikan secar a mat ematis dengan menggunakan oper asi hitungan (arithmatic) yaitu oper asi t ambah, kur ang, kali, dan bagi.

Alasan pemakaian met ode numer ik adalah banyak per masalahan mat ematis tidak dapat diselesaikan dengan met ode analit ik. Jika ter dapat penyelesaian secar a analit ik, mungkin pr oses penyelesaiannya sangat r umit, sehingga tidak effisien.

Contoh 1.1

a) Menentukan akar -akar polynomial

30,2 x7 + 1,25 x5 – 100 x4 + 15 x3 – 64 x2 – x + 31 = 0 b) Menentukan akar -akar per samaan

b) Menentukan akar -akar per samaan

1.2 Per bedaan Metode Analitik dan Metode Numer ik

Per bedaan antar a met ode analit ik dan met ode numer ic dapat dijelaskan sebagai ber ikut .

a. Solusi dar i met ode numer ik selalu ber bentuk angka. Sedangkan pada met ode analit ik biasanya dalam bentuk fungsi mat emat ik yang selanjut nya dapat dievaluasi untuk menghasilkan nilai dalam bentuk angka at au numer ik.

b. Solusi dar i met ode numer ik menghasilkan solusi hampir an. Sedangkan met ode analitik menghasilkan solusi sejati.

1.3 Hampir an dan Galat

Metode Numerik

2 Contoh 1.2

Tentukan solusi dar i integr asi-t entu ber ikut dengan menggunakan met ode numer ik.

Penyelesaian

Sebelum menentukan solusi menggunakan metode numer ik, per t ama-t ama kita tentukan solusi dengan met ode analit ik untuk mendapatkan nilai sejati.

Solusi dengan metode numer ik.

Kita t elah mengetahui bahw a pr oses int egr asi f (x) dar i x = a sampai x = b mer upakan luas bidang yang dibatasi oleh f (x), sumbu x, gar is x= a, dan gar is x= b.

Untuk mencar i luas bidang yang dimaksud, kita bagi bidang menjadi beber apa tr apesium, seper t i gambar ber ikut .

Gambar 1.1 Metode Tr apesium

f (x) = –x2 + 2x + 3

f (x)

x –1 0 1/2 1 3/2 2 3

a b c d Solusi analitik dalam bentuk fungsi matematik

Nilai numerik didapat dengan mengevaqluasi fungsi

Metode Numerik

3 Luas bidang yang akan dicar i = a + b + c + d

Solusi hampir an = a + b + c + d

= 27/ 16 + 31/ 16 + 31/ 16 + 27/ 16 = 116/ 16 = 29/ 4

Galat = solusi sejati – solusi hampir an = 22/ 3 – 29/ 4 = 1/ 12

Metode Numerik

4 BAB II

ATURAN PEMBULATAN DAN ANGKA BENA

2.1 Angkan Bena (Significan Figure)

Angka bena, disebut juga sebagai angka penting atau angka signifikan adalah jumlah angka yang digunakan sebagai bat as minimal tingkat keyakinan. Angka bena ter dir i dar i angka past i dan angka taksir an. Angka taksir an ter let ak pada akhir angka signifikan.

Contoh 2.1

Pada bilangan 27,63; angka 3 adalah angka taksir an 2.2 Atur an-atur an tentang angka bena

a) Setiap angka yang bukan nol pada suat u bilangan adalah angka bena

Contoh 2.2

Bilangan 14,256 adalah bilangan yang ter dir i dar i 5 angka bena. Bilangan 43,12375 adalah bi langan yang ter dir i dar i 7 angka bena.

b) Setiap angka nol yang t er let ak di antar a angka-angka bukan nol adalah angka bena.

Contoh 2.3

Bilangan 7000,2003 adalah bilangan yang t er dir i dar i 9 angka.

c) Setiap angka nol yang t er let ak di antar a angka-angka bukan nol adalah angka bena.

Contoh 2.4

Bilangan 7000,2003 adalah bilangan yang t er dir i dar i 9 angka bena.

d) Angka nol yang ter let ak di belakang angka bukan nol yang ter akhir dan di belakang tanda desimal adalah angka bena.

Contoh 2.5

Bilangan 23,50000 adalah bi langan yang ter dir i dar i 7 angka bena. Bilangan 278,300 adalah bilangan yang ter dir i dar i 6 angka bena. Contoh 2.6

Ber dasar kan atur an c dan d, maka

Bilangan 270,0090 memiliki 7 angka bena. Bilangan 0,0090 memiliki 2 angka bena. Bilangan 0,001360 memiliki 4 angka bena.

Metode Numerik

5 Contoh 2.7

Bilangan 3500000 mer upakan bilangan dengan 2 angka bena.

f) Angka nol yang ter let ak di depan angka bukan nol yang per t ama bukan mer upakan angka bena.

Contoh 2.8

Bilangan 0,0000352 mer upakan bilangan dengan 3 angka bena. Bilangan 0,1764 mer upakan bilangan dengan 4 angka bena. Bilangan 0,0000012 mer upakan bilangan dengan 2 angka bena.

g) Semua angka nol yang t er let ak di belakang angka bukan nol yang t er akhir , dan ter let ak di depan t anda desimal mer upakan angka bena.

Contoh 2.9

Bilangan 7000, mer upakan bilangan dengan 5 angka bena.

h) Untuk menunjukkan jumlah angka bena, kita dapat member i t anda pada angka yang mer upakan bat as angka bena dengan gar is baw ah, gar is at as, at au cetak tebal. Contoh 2.10

1256 adalah bilangan yang mempunyai 4 angka signifikan 1256 adalah bilangan yang mempunyai 3 angka signifikan

Per hatikanlah bahw a angka 0 bisa menjadi angka bena atau bukan. Misal pada bilangan 0.001360; tiga buah angka nol per t ama bukan angka bena, sedangkan 0 yang ter akhir adalah angka bena. Pengukur an dilakukan sampai ketelit ian 4 digit.

2.3 Penulisan angka bena dalam notasi ilmiah

Jumlah angka bena akan ter lihat dengan past i bila bilangan dit ulis dalam notaasi ilmiah (scientific notation) . Misalnya t etapan dalam kimia dan fisika at au ukur an jar ak dalam ast r onomi.

Contoh 2.11

a) 4,3123 x 101 memi liki 5 angka signifikan b) 1,764 x 10-1 memiliki 4 angka signifikan c) 1,2 x 10-6 memiliki 2 angka signifikan d) 2,78300 x 102 memiliki 6 angka signifikan e) 9,0 x 10-3 memiliki 2 angka signifikan

g) 6,02 x 1023 ( bilangan Avogadr o) memiliki 24 angka signifikan i) 1,5 x 107 memiliki 8 angka signifikan ( jar ak bumi -matahar i)

Metode Numerik

6

notasi ilmiah, maka bilangan 0,7 x 103; 12 x 107; dan bilangan –23,4 x 107 t idak ter masuk notasi ilmiah kar ena nilai a tidak memenuhi 1 |a|< 10.

Contoh 2.12

Bilangan 17500000 jika dit ulis dalam notasi ilmiah menjadi 1,75 x 107

Bilangan –0,0000000187 jika ditulis dalam notasi ilmiah menjadi –0,87 x 10–8 Bilangan 900000000000 jika ditulis dalam notasi ilmiah menjadi 9 x 1012. 2.4 Aturan Pembulatan

Pembulatan suatu bilangan ber ar t i menyimpan angka bena dan membuang bukan angka bena dengan mengikuti at ur an-at ur an ber ikut:

a) Tandai bilangan yang ter masuk angka signifikan dan angka t idak signifikan.

Contoh 2.12

Empat angka bena dar i bilangan 16,7321 adalah

b) Jika digit per tama dar i bukan angka bena lebih besar dar i 5, maka digit ter akhir dar i angka bena dit ambah 1. Selanjutnya buang bukan angka bena.

Contoh 2.13

Jika bilangan 23,472 dibulatkan menjadi t iga angka signifikan, maka dit ulis menjadi 23,5

c) Jika digit per t ama dar i bukan angka bena lebih kecil dar i 5, maka buang bukan angka bena.

Contoh 2.14

Jika bilangan 23,674 dibulatkan menjadi empat angka signifikan, maka dit ulis menjadi 23,67

d) Jika digit per t ama dar i bilangan bukan angka bena sama dengan 5, maka:

-Jika digit t er akhir dar i angka signifikan ganjil, maka digit ter akhir angka signifikan dit ambah 1. Selanjut nya buang angka t idak signifikan.

Contoh 2.15

Jika bilangan 37,759 dibulatkan menjadi t iga angka bena, maka dit ulis menjadi 37,8

-Jika digit t er akhir dar i angka bena mer upakan bilangan genap genap, maka buang bukan angka bena.

Contoh 2.16

Jika bilangan 79,859 dibulatkan menjadi t iga angka bena, maka dit ulis menjadi 79,8

2.5 Atur an-atur an pada Oper asi Ar itmatika Angka Bena 2.5.1 Penjumlahan dan pengur angan

Metode Numerik

7

" Hasil penjumlahan atau pengurangan hanya boleh mempunyai angka dibelakang koma sebanyak angka di belakang koma yang paling sedikit pada bilangan-bilangan yang dilakukan operasi penjumlahan atau pengurangan".

Contoh 2.17

2,34 + 0,345 = 2,685 (dibulatkan menjadi 2,68) 34,31 + 2,165 = 36,475 (dibulatkan menjadi 36,48) 40,55 + 3,1 + 10,222 = 53,872 (dibulatkan menjadi 53,9) 14,2294 – 2,37 = 11,8594 (dibulatkan menjadi 11,86)

2.5.2 Perkalian dan pembagian:

" Hasil perkalian atau pembagian hanya boleh mempunyai angka bena sebanyak bilangan dengan angka bena paling sedikit".

Contoh 2.18

(32,1 × 1,234) ÷ 1,2 = 33,0095

Bilangan yang mempunyai angka signifikan paling sedikit adalah 1,2 (2 angka signifikan).

Jadi hasil perkalian dan pembagian di atas dibulatkan menjadi 33 (2 angka signifikan).

Contoh 2.19

Metode Numerik

8

Contoh 2.20 Selesaikan

[15,2 x (2,8 x 10–4 )] + [(8,456 x 10–4) 0,177] [4,256 x 10–3 ] + [4,7774011… x 10–3]

Bulatkan besaran-besaran di dalam kurung [4,3 x 10–3 ] + [4,78 x 10–3]

9,08 x 10–3 Bulatkan 9,1 x 10–3

Metode Numerik

9 BAB III

HAMPIRAN DAN GALAT

3.1 Definisi

Hampir an, pendekat an atau apr oksimasi (approximation) didefinisikan sebagai nilai yang mendekat i solusi sejati (exact solution) . Galat atau kesalahan (error) sebenar nya ( ) didefinisikan sebagai selisih solusi sejati (x0) dengan solusi hampir an (x),

= x0 – x ( 3.1)

Galat atau kesalahan (error) r elatif sebenar nya ( r) didefinisikan sebagai per bandingan

antar a kesalahan sebenar nya ( ) dengan solusi sejati (x0) ,

Contoh 3.1

Misal hasil pengukur an panjang sebuah jembatan dan paku masing-masing adalah 9.999 dan 9 cm. Jika ukur an panjang sebenar nya adalah 10.000 dan dan 10 cm, tentukan:

a) Kesalahan sebenar nya

b) Kesalahan r elatif untuk setiap kasus Penyelesaian

a) Kesalahan sebenar nya ( ) pada pengukur an jembat an,

= 10.000 – 9.999 = 1 cm

Kesalahan sebenar nya ( ) pada pengukur an paku,

= 10 – 9 = 1 cm

b) Kesalahan r elatif sebenar nya ( r) pada pengukur an jembat an adalah

Kesalahan r elatif sebenar nya ( r) pada pengukur an jembat an adalah

Walaupun kedua pengukur an mempunyai kesalahan yang sama, yaitu 1 cm, tapi kesalahan r elatif sebenar nya jauh lebih kecil pada pengukur an jembatan. Ar t inya pengukur an yang dilakukan pada jembat an jauh lebih baik dibandingkan pengukur an yang dilakukan pada paku.

Metode Numerik

10

Akan tetapi kita tetap masih menghadapi kendala, kar ena nilai kesalahan ( ) sebenar nya membut uhkan infor masi tentang solui sejati (x0) . Oleh kar ena it u kita

hitung nilai kesalahan r elatif hampir an dengan membandingkan antar a selisih it er asi sekar ang dengan iter asi sebelumnya t er hadap nilai it er asi sekar ang, yaitu

Bat as t oler ansi kesalahan ( s) dit entukan oleh jumlah angka bena yang akan kita

gunakan. Hubungan antar a t oler ansi kesalahan ( s) dan angka signifikan (n) adalah, s = ( 0,5 x 102– n) % ( 3.5)

Pada w akt u melakukan komputasi, nilai kesalahan yang ter jadi mungkin ber nilai negatif. Akan tetapi biasanya kita tidak memper t imbangkan apakah hasilnya positif atau negatif, tapi lebih memper hat ikan har ga absolutnya, apakah masih lebih besar atau sudah lebih kecil dar i bat as t oler ansi kesalahan ( s) . Jika har ga abolut kesalahan

r elat if hampir an ( r h) lebih kecil dar i bat as t oler ansi kesalahan ( s) at au

| r h| < s ( 3.6)

maka komputasi selesai.

3.2 Jenis-jenis Galat

Fakt or -fakt or yang menyebabkan kesalahan pada metode numer ik antar a lain: a) Kesalahan kar ena baw aan data (inherent error)

b) Kesalahan kar ena pembulatan (round-off error) c) Kesalahan kar ena pemot ongan (truncation error) 3.2.1 Kesalahan kar ena baw aan data (inherent error)

Kesalahan baw aan data mer upakan kesalahan dar i nilai data. Misal kekelir uan dalam menyalin data, salah membaca skala atau kesalahan kar ena kur angnya penger t ian mengenai hukum-hukum fisik dar i data yang diukur .

3.2.2 Kesalahan kar ena pembulatan (round-off error)

Kesalahan kar ena pembulatan (round-off error) ter jadi kar ena tidak kita memper hitungkan beber apa angka ter akhir dar i suatu bilangan; ar t inya solusi hampir an digunakan untuk menggantikan solusi sejati ( eksak) .

Contoh 3.2

Tulis bilangan ber ikut menjadi t iga angka bena. Penyelesaian

8632574 dapat dibulatkan menjadi 8630000 3,1415926 dapat dibulatkan menjadi 3,14 3.2.3 Kesalahan kar ena pemotongan (truncation error)

Metode Numerik

11 Der et Taylor dan Der et McClaur in

Misal f, dan semua tur unannya, yaitu f , f , …, f (n) kontinu pada selang [a, b]. Jika x0 [a, b], maka untuk nilai-nilai x di sekitar x0 dan x [a, b], f(x) dapat

diper luas ( diekspansi) ke dalam der et Taylor ,

Jika dimisalkan x – x0 = h, maka

Untuk alasan pr aktis, pr oses komputasi dilakukan sampai pada suku ke n saja. Ar t inya ada bagian atau beber apa suku sisanya yang dipot ong dan tidak dimasukkan ke dalam pr oses komputasi. Suku-suku yang diabaikan ter sebut dikenal sebagai Residu; dan mer upakan galat kar ena pemot ongan. Jika faktor r esidu dimasukkan ke dalam der et Taylor , maka per samaan ( 1.1) menjadi,

Rn(x) adalah Residu, dan mer upakan besar galat yang timbul akibat pemot ongan.

Rn(x) dihitung dengan r umus,

Kar ena nilai c yang tepat tidak diketahui, maka kita per lu menghitung nilai maksimum |Rn| untuk menghitung besar nya galat, yait u

Contoh 3.3

Tentukan nilai hampir an dar i ln (0,60) sampai or de ke 4 di sekitar titik x0 = 1 dan

ber ikan nilai galat hampir an maksimum!

Penyelesaian

f (x) = ln x f (1) = 0

f (x) = 1/x f (1) = 1

f (x) = –1/x2 f (1) = –1

f (x) = 2/x3 f (1) = 2

f (4)(x) = –6/x4 f (4)(1) = –6

Metode Numerik

12

Galat pemotongan maksimum

Contoh 3.4

Tentukan hampiran fungsi f (x) = cos x sampai suku orde ke 6 di sekitar x0 = 0.

Penyelesaian

Metode Numerik

13 f(x) = cos x f(0)= 1

f (x) = –sinx f (0) = 0

f (x) = –cosx f (x) = –1

f (x) = sin x f (x) = 0

f (4)(x) = cos x f (4)(x) = 1

f (5)(x) = –sin x f (5)(x) = 0

f (6)(x) = –cos x f (6)(x) = –1

f (7)(x) = sin x f (7)((x) = 0

f (8)(x) = cos x f (8)(x) = 1

f (9)(x) = –sin x f (9)(x) = 0

f (10)(x) = –cos x f (10)(x) = –1

Hampiran fungsi f (x) = cos x sampai suku orde ke 6 di sekitar x0 = 0 adalah

Hampiran cos( /4) sampai suku orde ke 6 di sekitar x0 = 0 adalah

Latihan

Metode Numerik

14 BAB IV

SOLUSI PERSAMAAN DAN SISTEM PERSAMAAN NON-LINIER

4.1 Akar -akar Per samaan Non-Linier

Dalam bidang Sains dan Rekayasa kit a ser ing memer lukan untuk mencar i akar -akar ( solusi) dar i suatu per samaan. Jika per samaan dalam bentuk seder hana, kit a dengan mudah dapat menentukan akar -akar nya. Akan tetapi banyak per samaan yang mempunyai bentuk non-linier yang sulit atau bahkan belum ada penyelesaiannya, seper t i yang dijelaskan pada bab 1, maka kita tidak bisa menentukan solusi sejati (exact solution) . Dengan met ode numer ik kit a dapat menentukan akar -akar per samaan secar a pendekat an, atau hampir an, atau apr oksimasi (approximation) .

4.2 Metode Penyelesaian Persamaan Non-Linier

Secar a gar is besar , met ode yang digunakan untuk menentukan akar -akar atau penyelesaian per samaan non-linier dikelompokkan menjadi met ode, yaitu met ode ter t utup dan ter buka.

4.2.1 Metode Tert utup atau Metode Pengur ung (Bracketing Method)

Metode Ter t utup disebut juga Metode Pengur ung (bracketing method) adalah met ode yang mencar i akar at au akar -akar di dalam selang [a, b]. Metode t er t utup ter dir i dar i beber apa jenis, yaitu met ode gr afis, met ode bagi dua (bisection), dan met ode posisi salah (regula falsi) .

a) Metode Gr afis

Metode gr afis adalah met ode yang seder hana unt uk memper oleh hampir an nilai x unt uk fungsi f(x) = 0 atau tit ik di mana gr afik fungsi memotong sb. x. Misal ter dapat fungsi f(x) = x3 – x2 – 4x – 1. Lalu kita gambar kan gr afik fungsi ter sebut pada koor dinat Kar tesius ( lihat gambar ber ikut) .

Dar i gambar ter sebut kita dapat memper kir akan nilai dar i akar -akar per samaan, yaitu x1 = ( –1,4) , x2 = ( –0,3) , dan x3 = ( 2,7) .

y

O x

Metode Numerik

15

Metode Numerik

16

Metode bagi dua disebut juga pemot ongan biner (binary chopping) , met ode pembagian dua (interval halving) , atau met ode Bolzano adalah met ode suatu jenis pencar ian nilai hampir an secar a inkr emental dengan car a membagi inter val menjadi dua bagian.

Pr insip met ode bagi dua adalah mengur ung akar fungsi pada int er val [xi, xf] .

Selanjut nya inter val ter sebut ter us mener us dibagi dua hingga sekecil mungkin, sehingga nilai hampir an yang dicar i dapat ditentukan dengan tingkat akur asi t er tent u.

Algor itma adalah sebagai ber ikut :

1. Taksir batas baw ah (xi) dan bat as at as (xf ) dengan syar at f (xi) . f (xf) < 0

2. Hit ung nilai hampir an akar dengan r umus, xr = (xi + xf)/2

Metode Numerik

17

Jika f (xi). f (xr) > 0, maka xi = xr. Lanjutkan ke langkah 4

Jika f (xi). f (xr) = 0, maka akar = xr. St op.

4. Hit ung nilai hampir an akar yang bar u dengan r umus pada langkah 2. Ingat, nilai xi dan/ atau xf adalah nilai bar u yang didapat dar i langkah 3.

5. Jika nilai akar telah mencapai tingkat akur asi yang telah dit entukan, stop komputasi. Jika tidak kembali ke langkah 3.

Gambar 4.4

Gr afik dar i Algor it ma Metode Bagi Dua

Nilai xr dicar i dengan r umus

Jumlah lelar an atau iter asi R untuk menjamin nilai solusi hampir an memiliki galat kur ang dar i bat as t oler ansi kesalahan rh adalah

Metode Numerik

18

Nilai hampir an akar didapat dengan r umus, xr = (xi + xf)/2 = ( 0 + 1) / 2 = 0,5

Metode Numerik

19

c) Metode Regula Falsi (False Posisition Method)

Istilah Regula Falsi - ber asal dar i bahasa latin - atau Metode Posisi Palsu (False Posisition Method) t er masuk met ode ter t utup atau met ode pengur ung. Per bedaannya dengan met ode bagi dua adalah pada car a menentukan nilai akar . Per samaannya adalah nilai akar yang dicar i dikur ung oleh inter val ter tutup [xi, xf ].

Pada metode posisi palsu digunakan gar is lur us yang menghubungkan titik koor dinat (xi, f (xi)) dan (xf, f (xf)). Per potongan gar is yang dibuat dengan

sumbu x menghasilkan t aksir an nilai akar yang dicar i. Algor itma adalah sebagai ber ikut :

Metode Numerik

20

Lanjut kan dengan it er asi kedua dengan menggunakan maka xi= 0,15919 dan xf = 1

f (xi ) = f( 0,15919) = 1 .1 7 2 5 3 6 4 dan f (xf) = f( 1) = 0,0009119

Metode Numerik

21 4.2.2 Metode Ter buka

Metode ter buka adalah met ode yang menggunakan sat u, atau dua tebakan aw al yang tidak per lu mengur ung akar . Metode ter buka t er dir i dar i beber apa jenis, yaitu met ode It er asi Tit ik Tet ap, met ode New ton-Raphson, dan met ode Secant. a) Metode It er asi Titik Tetap

Metode Numerik

22

Metode Numerik

24

Gambar 4.8 Konvergen dan berosilasi

Gambar 4.9 Divergen dan berosilasi

x7

x1 x3 x5 x9x10 x8 x6 x4 x2 x0

0

y

x y= x

x= g(x)

x0

x4

x1

x5x3 x2

y

0 x

Metode Numerik

25

Gambar 4.10 Divergen dan monoton

Kriteria konvergensi metode iterasi titik tetap

Telah diketahui sebelumnya bahwa untuk menentukan akar atau akar-akar dari suatu

fungsi suatu persamaan maka harus ditetapkan f (x) = 0 sedemikian rupa sehingga

x = g(x). Selanjutnya dilakukan langkah iterasi dengan menggunakan nilai hampiran

xr +1 = g(xr) (4.4)

Solusi sejati

s = g(s) (4.5)

Persamaan (4.4) – (4.5) didapat

xr + 1 – s= g(xr ) – g(s) (4.6)

sebuah fungsi f (x) dan turunan pertamanya kontinu pada selang tertutup [a, b], maka

terdapat sekurang-kurangnya satu harga dari x = dalam selang tersebut yang

dilalui oleh sebuah garis yang sejajar garis yang menghubungkan s dan x.

Selanjutnya substituis pers. (4.6) ke (4.8) didapat,

xr + 1 – s= (xr – s)g( ) (4.9)

Karena xr – s = r , maka

r + 1 = r g( ) (4.10)

s x0 x1 x2

x = g(x)

x y

0

Metode Numerik

26

Jika |g( )| > 1 mungkin divergen untuk salah satu akar, tapi konvergen untuk akar

lainnya.

Jika g( ) positif, kesalahan akan positif hingga iterasi monoton (Gbr 4.7 dan 4.10).

Jika g( ) negatif, kesalahan akan berosilasi hingga iterasi monoton (Gbr. 4.8 dan 4.9).

Latihan

Dari fungsi f (x) = –0,874x2 + 1,75x + 2,627, tentukan

a) Semua kemungkinan prosedur iterasi titik tetap dari f(x) = 0

b) Tentukan akar atau akar-akar dari fungsi tersebut!

b) Metode New ton-Raphson

Metode ini juga ter masuk met ode ter buka seper t i halnya met ode it er asi t it ik tetap.

Rumus yang digunakan pada metode New ton-Raphson dapat dit ur unkan secar a gr afis maupun per luasan der et Taylor .

Penurunan r umus iterasi Newton-Raphson secar a grafis

Metode Numerik

27 Sehingga iter asi Newton-Raphson didapat

Penur unan rumus iter asi Newton-Raphson dengan per luasan der et Taylor Per luasan der et Taylor dapat dinyat akan sebagai,

Sebagai langkah untuk menghitung solusi hampir an, kita dapat mengabaikan suku-suku setelah tur unan per t ama. Sehingga der et Taylor dapat dit ulis menjadi,

Pada saat kur va memot ong sumbu x, maka f(xi +1) = 0.

( = per samaan 4.12)

Contoh 4.6

Tentukan solusi hampir an akar dar i fungsi f (x) = e–x –xdengan menggunakan met ode New ton-Raphson. Gunakan tebakan aw al x0 = 0 dan s = 0,00000005

Penyelesaian

f (x) = e–x –x f(0) = 1 – 0 = 1

f (x) = –e–x – 1 f (0) = –1 – 1 = –2

f (x) = e–x –x f(0,5) = e–0,5 – 0,5 = 0,10653

f (x) = –e–x – 1 f (0,5) = –e–0,5 – 1 = –1,60653

Metode Numerik

28

r xr f(xi) f'(xi) erh

0 0 1 -2 -

1 0 .5 0 0 0 0 0 0 0 .1 0 6 5 3 0 7 -1 .6 0 6 5 3 0 7 1 .0 0 0 0 0 0 0

2 0 .5 6 6 3 1 1 0 0 .0 0 1 3 0 4 5 -1 .5 6 7 6 1 5 5 0 .1 1 7 0 9 2 9

3 0 .5 6 7 1 4 3 2 0 .0 0 0 0 0 0 2 -1 .5 6 7 1 4 3 4 0 .0 0 1 4 6 7 3

4 0 .5 6 7 1 4 3 3 0 .0 0 0 0 0 0 0 -1 .5 6 7 1 4 3 3 0 .0 0 0 0 0 0 2

Kriter ia Konvergensi Metode Newton-Raphson Pr osedur iter asi metode ter buka xi +1 = g(xi)

Selanjut nya didapat

Kar ena syar at cukup konver gen , maka met ode New ton-Raphson

Latihan

Tentukan solusi hampir an akar dar i fungsi f (x) = x3 – 6x2 + 11x – 6 dengan menggunakan met ode New ton-Raphson.

Gunakan tebakan aw al x0 = 4 dan s = 0,000005

c) Metode Secant

Metode iter asi Secant mer upakan met ode yang dihasilkan dar i modifikasi dar i met ode New ton-Raphson dengan car a mengganti f (x) pada per samaan ( 4.12) dengan bentuk yang mendekat i seper ti pada gambar ber ikut .

Metode Numerik

29

Gambar 4.12

Iterasi Metode Secant secara grafis

Subst it usi per samaan ( 4.15) ke ( 4.12) didapat

Contoh 4.7

Tentukan solusi hampir an akar dar i fungsi f (x) = e–x – 3x2dengan

menggunakan met ode Secant. Gunakan tebakan aw al x0 = 0,5 dan x1 = 1 ser t a

s = 0,00000005

Penyelesaian

f (xi – 1 ) = f (x0) = f(0,5) = e–0,5 – 3(0,5)2 = –0,14347

f (xi) = f (x1) = f (1) = e–1 – 3(12)= –2,6321

Hasil it er asi dapat dilihat pada tabel ber ikut.

s x

0

f(xi)

f(x)

f(xi–1)

xi

xi-1

Metode Numerik

30

Metode penyelesian sistem per samaan non-linier ter dir i dar i met ode iter asi tit ik t etap dan met ode New ton-Raphson. Bentuk umum sist em per samaan non-linier adalah sebagai ber ikut .

Metode iter asi t itik tetap seper ti pada per samaan ( 4.24) disebut met ode Jacobi. Untuk meningkatkan kecepatan konver gensi, maka nilai hampir an var iabel yang didapat langsung digunakan untuk mentukan nilai hampir an var iabel selanjut nya.

Sehingga per samaan ( 4.24) menjadi

Metode iter asi titik t etap seper t i pada per samaan ( 4.24) disebut met ode Seidel. Conton 4.9

Selesaikan sist em per samaan non-linier ber ikut dengan met ode it er asi Seidel.

f1(x, y) = x2 –xy – 10 = 0

f2(x, y) = y + 3xy2 – 57 = 0

Metode Numerik

31 Penyelesaian

Prosedur iter asi titik tetap

r xr yr rhx(%) rhy(%)

0 1 4 - -

1 2 .2 5 0 0 0 -5 1 .0 0 0 0 0 5 5 .5 5 5 5 6 1 0 7 .8 4 3 1

2 -0 .0 9 6 8 1 8 1 2 .4 3 7 5 0 2 4 2 4 .0 5 1 1 0 6 .2 7 7 4

3 0 .0 1 2 3 0 -2 4 2 9 3 .2 8 0 3 2 8 8 7 .2 8 8 9 1 0 3 .3 4 4 3

4 -0 .0 0 0 4 1 7 2 8 8 4 4 .3 8 8 8 0 3 0 8 7 .4 1 5 1 0 3 .3 3 3 1

5 0 .0 0 0 0 1 -2 1 8 6 5 2 7 4 .2 9 3 5 2 3 1 0 0 .1 4 4 1 0 3 .3 3 3 3

6 0 .0 0 0 0 0 6 5 5 9 5 8 2 8 5 .7 9 3 3 4 3 0 9 9 .9 9 2 1 0 3 .3 3 3 3

Ter nyat a hasil iter asi diver gen Pr osedur iter asi t itik t etap lainnya

Latihan

Selesaikan sistem persamaan non-linier berikut dengan metode iterasi Seidel.

f1(x, y) = x + x2y – 3 = 0

f2(x, y) = y2 + xy – 5 = 0

Gunakan s = 0,000005 dan tebakan awal x0 = 2dan y0 = 1

4.3.2 Metode Newton-Raphson

Metode Numerik

32 Contoh 4.10

Selesaikan sist em per samaan non-linier ber ikut dengan met ode it er asi New ton-Raphson.

f1(x, y) = u = x2 + xy – 10 = 0

f2(x, y) = v = y + 3xy2 – 57 = 0

Gunakan s = 0,000005 dan t ebakan aw al x0 = 1dan y0 = 4

Penyelesaian

u0 = x02 + x0y0 – 10 = 12 + (1)(4) – 10 = –5

v0 = y0 + 3x0y02 – 57 = 4 + (3)(1)(42) – 57 = –5

Dar i per samaan ( 4.26)

Dar i per samaan ( 4.27)

Nilai x dan y selanjut nya dit r unjukkan pada tabel ber ikut .

r xr yr ur vr |erhx| |erhy|

0 1 4 -5 -5

1 2 .2 7 4 5 1 1 .6 9 6 0 7 8 -0 .9 6 8 8 6 0 -3 5 .6 7 4 8 0 .5 6 0 3 4 5 1 .3 5 8 3 8 2

2 3 .0 7 1 4 8 1 2 .2 5 0 9 5 0 6 .3 4 7 7 4 9 -8 .0 6 1 5 3 0 .2 5 9 4 7 5 0 .2 4 6 5 0 5

3 2 .2 8 1 2 2 0 2 .6 4 2 1 9 2 1 .2 3 1 3 8 8 -6 .5 8 0 9 9 0 .3 4 6 4 2 0 0 .1 4 8 0 7 5

Metode Numerik

33

5 2 .0 5 7 7 1 6 2 .9 2 7 5 5 7 0 .2 5 8 2 7 6 -1 .1 6 4 9 3 0 .0 4 0 6 8 2 0 .0 3 4 1 1 8

6 2 .0 2 3 2 3 4 2 .9 7 0 8 6 2 0 .1 0 4 2 2 5 -0 .4 5 7 8 2 0 .0 1 7 0 4 3 0 .0 1 4 5 7 7

7 2 .0 0 9 0 1 4 2 .9 8 8 7 1 0 0 .0 4 0 4 9 7 -0 .1 7 5 4 3 0 .0 0 7 0 7 8 0 .0 0 5 9 7 2

8 2 .0 0 3 4 3 5 2 .9 9 5 7 0 2 0 .0 1 5 4 4 7 -0 .0 6 6 4 3 0 .0 0 2 7 8 5 0 .0 0 2 3 3 4

9 2 .0 0 1 2 9 8 2 .9 9 8 3 7 7 0 .0 0 5 8 3 9 -0 .0 2 5 0 3 0 .0 0 1 0 6 8 0 .0 0 0 8 9 2

1 0 2 .0 0 0 4 8 9 2 .9 9 9 3 8 9 0 .0 0 2 1 9 9 -0 .0 0 9 4 1 0 .0 0 0 4 0 5 0 .0 0 0 3 3 7

1 1 2 .0 0 0 1 8 4 2 .9 9 9 7 7 0 .0 0 0 8 2 7 -0 .0 0 3 5 4 0 .0 0 0 1 5 2 0 .0 0 0 1 2 7

1 2 2 .0 0 0 0 6 9 2 .9 9 9 9 1 4 0 .0 0 0 3 1 1 -0 .0 0 1 3 3 5 .7 3 E-0 5 4 .7 8 E-0 5

1 3 2 .0 0 0 0 2 6 2 .9 9 9 9 6 8 0 .0 0 0 1 1 7 -0 .0 0 0 5 0 2 .1 5 E-0 5 1 .8 E-0 5

1 4 2 .0 0 0 0 1 2 .9 9 9 9 8 8 4 .3 8 E-0 5 -0 .0 0 0 1 9 8 .0 9 E-0 6 6 .7 5 E-0 6

1 5 2 .0 0 0 0 0 4 2 .9 9 9 9 9 5 1 .6 5 E-0 5 -7 E-0 5 3 .0 4 E-0 6 2 .5 3 E-0 6

Latihan

Selesaikan sist em per samaan non-linier ber ikut dengan met ode it er asi New ton-Raphson.

f1(x, y) = x + x2y – 3 = 0

f2(x, y) = y2 + xy – 5 = 0

Metode Numerik

34 BAB V

SISTEM PERSAMAAN LINIER

5.1 Solusi Sistem Per samaan Linier

Kita telah mengenal penyelesaian sist em per samaan linier , seper t i eliminasi Gauss, Gauss-Jor dan, atau met ode balikan mat r iks. Metode-met ode ter sebut ter masuk met ode langsung. Pada bab ini akan dibahas met ode t ak langsung atau disebut juga metode it er asi.

Metode iter asi yang akan dibahas adalah met ode it er asi Jacobi , dan Gauss-Seidel. Pada met ode Jacobi, nilai hampir an dikor eksi secar a ser entak. Ar t inya nilai hampir an mengacu pada nilai hampir an sebelumnya. Sedangkan pada met ode Gauss-Seidel, nilai hampir an dihit ung ber dasar kan nilai hampir an ter bar u at au ter akhir .

Misal t er dapat sist em per samaan linier , a11x1 + a12x2 + … + a1nxn = b1

a21x1 + a22x2 + … + a2nxn = b2

a31x1 + a32x2 + … + a3nxn = b3 (5.1)

. . . an1x1 + an2x2 + … + annxn = bn

Jika sistem per samaan linier ter sebut ditulis dalam bentuk mat r iks, maka

Sehingga Ax = b (5.3)

Hal yang per lu diper hat ikan adalah selur uh elemen A 0. Jika ada elemen A = 0, maka lakukan per t ukar an bar is.

Metode Numerik

35

maka matr iks A dapat ditulis dalam bentuk A = D + L + U ( 5.4)

Substitusi persamaan (5.4) ke (5.3) didapat, (D + L + U)x = b (5.5)

5.2 Metode Iter asi Jacobi

Metode it er asi Jacobi adalah metode it er asi yang menghitung nilai hampir an sekar ang atau ter bar u dengan mengacu pada nilai hampir an sebelumnya.

Dar i per samaan ( 5.4) didapat Dx + (L + U)x = b

Dx = b – (L + U)x x = D–1b – D–1(L + U)x

x(k +1)= D–1b – D–1(L + U)x(k) ( 5.6)

Metode Numerik

36 5.3 Metode Iter asi Gauss-Seidel

Metode it er asi Gauss-Seidel adalah met ode it er asi yang menghitung nilai hampir an sekar ang dengan mengacu pada nilai hampir an ter bar u.

Kar ena A = D + L + U, maka dar i per s. ( 5.3) didapat

(D + L + U)x= b atau Dx + Lx + Ux = b

Sehingga Dx = b – Lx – Ux

x = D–1b – D–1Lx – D–1Ux

x(k +1) = D–1b – D–1Lx(k +1)– D–1Ux(k) ( 5.8)

5.4 Konver gensi Iter asi Gauss-Seidel dan Jacobi

Syar at cukup agar iter asi konver gen, maka sist em per samaan linier har us mempunyai bentuk dominan secar a diagonal. Dalam bentuk mat r iks, A har us mer upakan matr iks dominan secar a diagonal.

Dalam bentuk per t aksamaan,

Contoh 5.1

Selesaikan sist em per samaan linier ber ikut dengan menggunakan it er asi Jacobi dan Gauss-Seidel!

4x1 + 2x2 + x3 = 15

x1 + 5x2 – x3 = 7

x1 + x2 + 8x3 = 12

Metode Numerik

37 Penyelesaian

Nilai aw al x1(0) = 0, x2(0) = 0, x3(0) = 0

Metode Iterasi Jacobi Iterasi pertama

It er asi ke dua

Iterasi ke tiga

Hasil it er asi selanjut nya ditabelkan.

Hasil Per hit ungan ( Metode It er asi Jacobi)

k x1 x2 x3 1 2 3

0 0.00000 0.00000 0.00000 - - -

1 3.75000 1.40000 1.50000 1.00000 1.00000 1.00000

2 2.67500 0.95000 0.85625 0.40187 0.473684 0.75182

11 2.99999 1.00000 1.00000 8.82E-06 3.14E-07 9.19E-06

Metode Numerik

38

Metode Iterasi Gauss-Seidel Iterasi pertama

Iterasi kedua

Iterasi ketiga

Hasil it er asi selanjut nya ditabelkan.

Hasil Per hit ungan ( Metode It er asi Jacobi)

k x1 x2 x3 1 2 3

0 0 0 0 - - -

1 3,75000 0,65000 0,95000 1,00000 1,00000 1,00000

2 3,18750 0,95250 0,9825 0,176471 0,317585 0,033079

3 3,02812 0,99088 0,997625 0,052632 0,038728 0,015161

4 3,00516 0,99849 0,999544 0,007643 0,00763 0,00192

5 3,00087 0,99974 0,999925 0,001429 0,001242 0,000381

6 3,00015 0,99996 0,999987 0,000239 0,000219 6,21E-05

7 3,00003 0,99999 0,999998 4,17E-05 3,75E-05 1,1E-05

8 3,00000 1,00000 1,00000 7,16E-06 6,49E-06 1,87E-06

Metode Numerik

39 BAB VII

DIFFERENSIASI NUMERIK

7.1 Pendahuluan

Rumus hampir an tur unan dapat dihasilkan dengan car a melakukan differ ensiasi polinomial yang dihasilkan dar i pr oses pencocokan kur va (curve fitting) atau dengan menggunakan met ode selisih New ton-Gr egor y.

7.2 Polinomial Pencocokan Kur va

Pr oses pencocokan kur va menghasilkan sebuah poli nomial yang mempunyai bentuk,

pn(x) = a0 + a1x + a2x2 + a3x3 + …

( 7.1)

Untuk mencar i tur unan dar i pn(x), kit a dapat secar a langsung melakukan differ ensiasi

per samaan ( 7.1) Tur unan per t ama

Tur unan kedua

Contoh 7.1

Dar i tabel ber ikut tentukan nilai f ( 4) dengan menggunakan polinom der ajat 3.

xi 3 4 6 7,5

f(xi) 1047,248 1162,174 1278,663 1396,578

Penyelesaian

Metode Numerik

40 7.3 Metode Selisih Newton-Gregory

7.3.1 Polinomial Selisih-Maju

Untuk menentukan hampiran turunan pertama, tinjau polinom selisih-maju pada bab 6.

Tur unan per t ama

Tur unan kedua

Jika x = x0 , maka dar i per samaan ( 7.5) didapat

Metode Numerik

41 Sedangkan tur unan ke dua menjadi

Contoh 7.2

Dar i tabel ber ikut tentukan nilai f (3,4) dan f (3,4) dengan menggunakan metode selisih-maju.

x1 3,4 3,5 3,6 3,7

f(x1) 0,294118 0,285714 0,277778 0,270270

Penyelesaian

i x f(x) f 2f 3f

0 3,4 0,294118

–0,008404

1 3,5 0,294118 0,000468

–0,007936 –0,00004

2 3,6 0,277778 0,000428

–0,007508

3 3,7 0,270270

h = x1 – x0 = 3,5 – 3,4 = 0,1

Karena 3,4 = x0, maka

Kar ena s = 0, maka f (3,4) dan f (3,4) dicar i dengan per samaan ( 7.9) dan ( 7.10)

Contoh 7.3

Dar i contoh soal 7.2 tentukan nilai f (3,7) dan f (3,7) dengan menggunakan metode selisih-maju.

Metode Numerik

42

i x f(x) f 2f 3f

0 3,4 0,294118

–0,008404

1 3,5 0,294118 0,000468

–0,007936 –0,00004

2 3,6 0,277778 0,000428

–0,007508

3 3,7 0,270270

h = x1 – x0 = 3,5 – 3,4 = 0,1

Kar ena 3,7 = x3, maka

Dar i per samaan ( 7.7) dan ( 7.8) didapat

7.3.2 Polinomial Selisih-Mundur

Untuk menentukan hampir an tur unan per t ama, tinjau polinom selisih-mundur yang t elah dibahas pada bab 6.

Metode Numerik

43 Tur unan per t ama

Tur unan kedua

Sehingga tur unan per tama menjadi

Sedangkan tur unan ke dua menjadi

Contoh 7.4

Dar i tabel ber ikut tentukan nilai f(3,4) dan f (3,4) dengan menggunakan met ode selisih-mundur .

x1 3,4 3,5 3,6 3,7

f(x1) 0,294118 0,285714 0,277778 0,270270

Penyelesaian

i x f(x) f 2f 3f

–3 3,4 0,294118

–0,008404

–2 3,5 0,294118 0,000468

–0,007936 –0,00004

–1 3,6 0,277778 0,000428

–0,007508

0 3,7 0,270270

h

=

x

0

–

x

–1

= 3,7 – 3,6 = 0,1

Metode Numerik

44 Dar i per samaan ( 7.12) dan ( 7.13)

Tugas

Dar i tabel ber ikut tentukan nilai f (3,52) dan f (3,52) dengan menggunakan met ode selisih-maju dan met ode selisih-mundur .

x1 3,4 3,5 3,6 3,7

Metode Numerik

45 BAB VIII INTEGRASI NUMERIK

8.1 Pendahuluan

Integr asi numer ik adalah pr oses mencar i hampir an luas bidang yang dibatasi oleh f (x)

dan sumbu x pada selang ter tutup [a, b]. Jika f(x) dihampir i dengan polinomial pn(x),

maka int egr asi numer ik dit ulis dalam bent uk,

Pr oses pencar ian nilai hampir an I dilakukan jika:

a. Fungsi f(x), disebut int r egr an, mempunyai bentuk yang sulit untuk dilakukan pr oses integr asi.

b. Nilai x dan f (x) hanya dalam bentuk t abel diskr it .

Gambar 8.1 Gambar 8.2

Luas bidang yang dibatasi f(x) Hampiran luas bidang yang dibatasi pn(x)

Pr oses menentukan nilai hampir an integr asi numer ik dilakukan dengan beber apa car a atau met ode, yait u met ode manual, pencocokan polinomial, atur an tr apesium, at ur an titik t engah, atur an Simpson, int egr asi Romber g, ser ta Kuadr at ur Gauss.

y

f (x)

x

O a _b

f (x)

x y

pn(x)

Metode Numerik

46 8.1 Metode Manual

Pr oses int egr asi numer ik secar a manual adalah menentukan luas bidang dengan car a menggambar per segi-per segi yang ber ada di baw ah gr afik f(x). Jumlah per segi yang ber ada di baw ah gr afik dikalikan dengan luas masing-masing per segi mer upakan luas bidang yang dibatasinya, seper t i yang dit unjukkan pada Gambar 8.3.

Gambar 8.3

Hampir an luas bi dang metode manual

8.2 Polinomial Pencocokan Kur va

Jika ter dapat sebuah fungsi f (x) yang sulit untuk dilakukan pr oses int egr asi, seperti

atau data yang menyajikan nilai f (x) untuk nilai xter t entu, seper t i tabel ber ikut ,

x 1 2 3 4 5

f(x) 2,1722 2,7638 4,4899 7,3912 12,1832

maka f(x) dapat dihampir i dengan pn(x) seper t i per samaan ber ikut ,

pn(x) = a0 + a1x + a1x2 + … ( 8.3)

Contoh 8.1

b y

f (x)

x

O a

Metode Numerik

47 Penyelesaian

x 1 2 3 4

f(x) 2,1722 2,7638 4,4899 7,3912

f (x) = a0 + a1 x + a2 x2 + a3 x3

a0 + a1 + a2 + a3 = 2,1722

a0 + 2a1 + 4a2 + 8a3 = 2,7638

a0 + 3a1 + 9a2 + 27a3 = 4,4899

a0 + 4a1 + 16a2 + 64a3 = 7,3912

Didapat

f (x) = 2,6744 – 1,0355x + 0,5266x2+ 0,0068x3

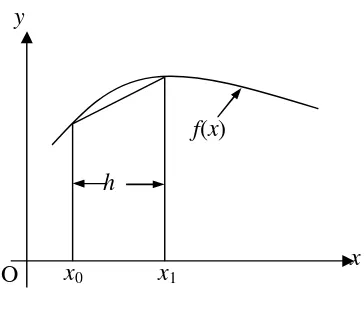
8.3 Atur an Tr apesium

Metode Numerik

48

Luas satu pias trapesium adalah

Par amet er inter polasi s dicar i dengan per samaan,

s = (x – x0)/h atau x = x0 + sh ( 8.5)

Sehingga, dx = h ds ( 8.6)

Subst it usi per samaan ( 8.6) - ( 8.8) ke ( 8.4) didapat

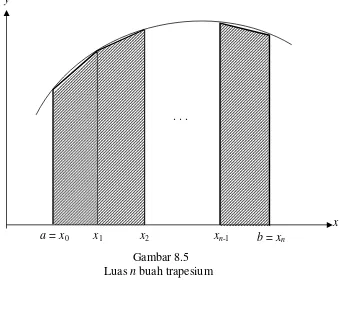
Jika selang t er tutup [a, b] dibagi menjadi n buah bidang, maka luas hampir an f(x)

ditunjukkan pada ber ikut

h

x

0

x

1

O

x

f

(

x

)

y

Metode Numerik

49

n

= (

x

n

–

x

0

)/

h

(8.9)

Luas selur uh bidang untuk jar ak h yang sama adalah

Luas selur uh bidang untuk jar ak h yang tidak sama

Contoh 8.2 Dar i table ber ikut

x

n-1

a

=

x

0

x

1

x

2

b

=

x

n

Gambar 8.5

Luas

n

buah trapesium

. . .

Metode Numerik

50

x

f

(

x

)

x

f

(

x

)

x

f

(

x

)

0,4 5,1600 1,2 3,1067 2,0 5,0000

0,6 3,6933 1,4 3,3886 2,2 5,7491

0,8 3,1400 1,6 3,8100 2,4 6,5933

1,0 3,0000 1,8 4,3511 2,6 7,5092

Penyelesaian

Dar i tabel didapat f (x0) = 5,1600

2 f (x1) = 2(3,6933) = 7,3866 ; 2 f (x2) = 2(3,1400) = 6,2800

2 f (x3) = 2(3,0000) = 6,0000 ; 2 f (x4) = 2(3,1067) = 6,2034

2 f (x5) = 2(3,3886) = 6,7772 ; 2 f (x6) = 2(3,8100) = 7,6200

2 f (x7) = 2(4,3511) = 8,7022 ; f (x8) = 5,0000

8.4 At ur an Titik Tengah

Gambar ber ikut adalah sebuah per segi panjang dar i x = x0 sampai x = x1 dan titik

Metode Numerik

51

Gambar 8.6 At ur an titik tengah

Gambar 8.7

nbuah per segi panjang dengan panjang masing-masing f (xn + h/2)

x

3

x

1

x

2

x

n-1

b

=

x

_n

a

=

x

0

x

y

b

=

x

1

x

1/2

a

=

x

0

x

y

h

Metode Numerik

52 Luas n buah t it ik tengah adalah

Per samaan ( 8.12) adalah hampir an integr asi f(x) menggunakan met ode t itik tengah Contoh 8.3

Dar i tabel ber ikut ,

x

f

(

x

)

x

f

(

x

)

x

f

(

x

)

0,4

5,1600

1,0

3,0000

1,6

3,8100

0,6

3,6933

1,2

3,1067

1,8

4,3511

0,8

3,1400

1,4

3,3886

2,0

5,0000

Penyelesaian

n

= 8 ;

x

n

=

x

8

=

2,0

;

x

0

=

0,4

Dar i per samaan ( 8.5) didapat

h

= (

x

n

–

x

0

)/

n =

( 2,0 – 0,4) / 8 = 0,2

Dar i tabel didapat:

f

(

x

0

+

h

/2) =

f

(0,4+0,1) =

f

(0,5) = 4,4266

f

(

x

1

+

h

/2) =

f

(0,6+0,1) =

f

(0,7) = 3,4166

f

(

x

2

+

h

/2) =

f

(0,8+0,1) =

f

(0,9) = 3,0700

f

(

x

3

+

h

/2) =

f

(1,0+0,1) =

f

(1,1) = 3,0534

f

(

x

4

+

h

/2) =

f

(1,2+0,1) =

f

(1,3) = 3,2476

f

(

x

5

+

h

/2) =

f

(1,4+0,1) =

f

(1,5) = 3,5993

f

(

x

6

+

h

/2) =

f

(1,6+0,1) =

f

(1,7) = 4,0806

Metode Numerik

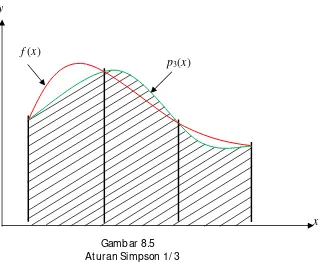
53 8.5 Atur an Simpson 1/ 3

Atur an simpson 1/ 3 adalah atur an yang mencocokkan polinomial der ajat 2 pada tiga titik data diskr it yang mempunyai jar ak yang sama.

Gambar 8.4 Atur an Simpson 1/ 3

Dar i per samaan ( 8.5)

s

= (

x

–

x

0

)/

h

atau

x

=

x

0

+ sh

Sehingga

Untuk x

=

x

0

,

maka s

= 0

Untuk x

=

x

2

,

maka s

= 2

x

1

= 2

h

x

1

=

h

x

0

= 0

p

2

(

x

)

f

(

x

)

Metode Numerik

54 atau dapat dit ulis dalam bentuk

Contoh 8.4

dengan menggunakan met ode:

a.

Tr apesium

b.

Tit ik t engah

c.

Simpson 1/ 3

Bandingkan hasil masing-masing met ode dengan solusi sejatinya. Penyelesaian

Solusi sejati

a.

Metode Tr apesium

n

= (

x

n

–

x

0

)/

h =

(1 – 0) / 0,1 = 10

Metode Numerik

55

0

0

0,5000

6

0,6

0,6154

1

0,1

0,5238

7

0,7

0,6296

2

0,2

0,5454

8

0,8

0,6428

3

0,3

0,5652

9

0,9

0,6552

4

0,4

0,5833

10

1,0

0,6666

5

0,5

0,6000

0,59438

b.

Metode Titik Tengah

f

(

x

0

+

h

/2) =

f

(0,0+0,05) =

f

(0,05) = 0,5122

f

(

x

1

+

h

/2) =

f

(0,1+0,05) =

f

(0,15) = 0,5348

f

(

x

2

+

h

/2) =

f

(0,2+0,05) =

f

(0,25) = 0,5556

f

(

x

3

+

h

/2) =

f

(0,3+0,05) =

f

(0,35) = 0,5744

f

(

x

4

+

h

/2) =

f

(0,4+0,05) =

f

(0,45) = 0,5918

f

(

x

5

+

h

/2) =

f

(0,5+0,05) =

f

(0,55) = 0,6078

f

(

x

6

+

h

/2) =

f

(0,6+0,05) =

f

(0,65) = 0,6226

f

(

x

7

+

h

/2) =

f

(0,7+0,05) =

f

(0,75) = 0,6364

f

(

x

8

+

h

/2) =

f

(0,8+0,05) =

f

(0,85) = 0,6491

f

(

x

9

+

h

/2) =

f

(0,9+0,05) =

f

(0,95) = 0,6610

c.

Metode Simpson 1/ 3

Metode Numerik

56

i

x

f

(

x

)

i

x

f

(

x

)

0

0

0,5000

6

0,6

0,6154

1

0,1

0,5238

7

0,7

0,6296

2

0,2

0,5454

8

0,8

0,6428

3

0,3

0,5652

9

0,9

0,6552

4

0,4

0,5833

10

1,0

0,6666

5

0,5

0,6000

Kesimpulan

Solusi sejati

Metode

Trapesium

Titik Tengah

Simpson 1/3

0,59453

0,59438

0,59459

0,59452

Metode Simpson adalah met ode yang paling mendekat i solusi sejat i.

8.6 Atur an Simpson 3/ 8

Atur an simpson 3/ 8 adalah atur an yang mencocokkan polinomial der ajat 3 pada empat titik data diskr it yang mempunyai jar ak yang sama.

Dar i Gambar 8.5 didapat

Dar i per samaan ( 8.5)

s

= (

x

–

x

0

)/

h

atau

x

=

x

0

+ sh

Dar i per samaan ( 8.5)

Metode Numerik

57 Gambar 8.5 At ur an Simpson 1/ 3

Sehingga

Untuk x

=

x

0

,

didapat s

= 0

Untuk x

=

x

2

,

didapat s

= 2

atau dapat dit ulis dalam bentuk

p

3

(

x

)

f

(

x

)

Metode Numerik

58 Contoh 8.5

Bandingkan hasilnya dengan met ode Tr apesium, Titik Tengah, Simpson 1/ 3, dan solusi Sejati.

Penyelesaian

h

= (

x

n

–

x

0

)/

n =

(1 – 0) / 9 = 0,11111

i

x

i

f

i

2

f

i

3

f

i

0 0 ,0 0 0 0 0 0 ,5

1 0 ,1 1 1 1 1 1 ,5 7 8 9 4 7 3 6 8

2 0 ,2 2 2 2 2 1 ,6 5

3 0 ,3 3 3 3 3 1 ,1 4 2 8 5 7 1 4 3

4 0 ,4 4 4 4 4 1 ,7 7 2 7 2 7 2 7 3

5 0 ,5 5 5 5 6 1 ,8 2 6 0 8 6 9 5 7

6 0 ,6 6 6 6 7 1 ,2 5

7 0 ,7 7 7 7 8 1 ,9 2

8 0 ,8 8 8 8 9 1 ,9 6 1 5 3 8 4 6 2

9 1 ,0 0 0 0 0 0 ,6 6 6 6 6 6 6 6 7

= 1,16666

= 2,39286

= 10,70931

Hasil per hitungan dar i contoh 8.4 dan 8.5 didapat

Solusi sejati

Metode

Trapesium

Titik Tengah

Simpson 1/3

Simpson 3/8

0,59453

0,59438

0,59459

0,59452

0,59454

Metode Numerik

59

Suat u data ser ing mempunyai jar ak yang ber beda pada sebagian tit ik, sedangkan sebagian titik lainnya sama. Sebetulnya kita dapat menggunakan atur an tr apesium, khususnya per samaan ( 8.11) . Akan tetapi jika kita ingin meningkat kan tingkat ket elit ian, maka kombinasi penggunaan met ode t r apesium, Simpson 1/ 3, dan Simpson 3/ 8 menjadi pilihan yang lebih baik dar i pada menggunakan met ode t r apesium secar a keselur uhan.

Atur an kombinasinya adalah sebagai ber ikut :

-Untuk selang ber ur ut an mempunyai jar ak yang sama dan ber jumlah genap, gunakan atur an Simpson.

-Untuk selang ber ur ut an mempunyai jar ak sama dan ber jumlah kelipatan tiga, gunakan atur an Simpson 3/ 8.

Gambar 8.6 Atur an Gabungan

8.8 Metode Newton-Cotes

Bentuk umum dar i met ode New ton-Cotes dit unjukkan pada per samaan ber ikut .

O

y

x

h

1

h

1

h

1

h

1

h

2

h

2

h

2

h

3

h

3

x

0

x

1

x

2

x

3

x

4

x

5

x

6

x

7

x

8

x

9

Simpson 1/3 Simpson 3/8

Metode Numerik

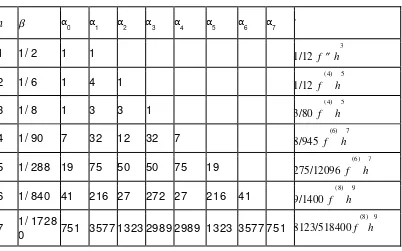
60

Tabel 8.1 adalah tujuh dar i 10 r umus New ton-Cotes. Rumus 1 sampai 4 masing-masing didapat dengan atur an t r apesium, Simpson 1/ 3, Simpson 3/ 8, dan Boole. Rumus 5 dan set er usnya didapat dengan menggunakan polinom inter polasi selisih maju der ajat 4, 5, dan set er usnya.

Contoh 8.6

Metode Numerik

61

x

2

f

2

2

f

1

4

f

0

f

2

3

f

1

x

3

f

3

2

f

2

f

3

x

4

f

4

= 4

f

0

+ 8

f

0

+ 20/3 2

f

0

+ 8/3 3

f

0

+42/135 4

f

0

f

0

=

f

1

–

f

0

2

f

0

=

f

1

–

f

0

=

(

f

2

–

f

1

) – (

f

1

–

f

0

) =

f

2

– 2

f

1

+

f

0

3

f

0

=

2

f

1

– 2

f

0

= (

f

3

– 2

f

2

+

f

1

) – (

f

2

– 2

f

1

+

f

0

)

=

f

3

– 3

f

2

+ 3

f

1

–

f

0

4

f

0

=

3

f

1

– 3

f

0

= (

f

4

– 3

f

3

+ 3

f

2

–

f

1

) – (

f

3

– 3

f

2

+ 3

f

1

–

f

0

)

=

f

4

– 4

f

3

+ 6

f

2

– 4

f

1

+

f

0

Sehingga

I

= 4

f

0

+ 8

f

0

+ 20/3 2

f

0

+ 8/3 3

f

0

+ 42/135 4

f

0

= 4

f

0

+ 8(

f

1

–

f

0

) + 20/3(

f

2

– 2

f

1

+

f

0

)+8/3(

f

3

–3

f

2

+ 3

f

1

–

f

0

) +42/135 (

f

4

– 4

f

3

+ 6

f

2

–

4

f

1

+

f

0

)

= 4

f

0

+ 8

f

1

– 8

f

0

+ 20/3

f

2

– 40/3

f

1

+ 20/3

f

0

+ 8/3

f

3

– 8

f

2

+ 8

f

1

– 8/3

f

0

+ 42/135

f

4

–168/135

f

3

+ 252/135

f

2

–168/135

f

1

+ 42/135

f

0

= 42/135

f

0

+192/135

f

1

+ 72/135

f

2

+ 192/135

f

3

+ 42/135

f

4

= 14/45

f

0

+64/45

f

1

+ 24/45

f

2

+ 64/45

f

3

+ 14/45

f

4

= 28/90

f

0

+ 128/90

f

1

+ 48/90

f

2

+ 128/90

f

3

+ 28/90

f

4

Metode Numerik

62

Didapat nilai n

= 4, = 1/90,

0

= 7,

1

= 32,

2

= 12,

3

= 32,

4

= 7, sesuai yang

tertera pada Tabel 8.1

8.9 Kuadratur

Gauss

Hasil integrasi sejati

f

(

x

) dari titik

a

sampai titik

b

adalah

Hasil integr asi sejati ditunjukkan pada Gambar 8.7a. Jika integr asi diselesaikan dengan menggunakan met ode tr apesium, maka

seper t i yang dit unjukkan pada Gambar 8.7b. Galat pada met ode tr apesium dapat diper kecil dengan menggunakan met ode Kuadr at ur Gauss.

(

a) (

b)

Gambar 8.7

Jika kaidah tr apesium diter apkan pada fungsi konstan atau fungsi linier , dan dit ulis dalam bentuk koefisien tak t entu, maka akan menghasilkan nilai sejati dalam bentuk

x

b

f

(

x

)

a

a

b

Metode Numerik

63

Per samaan ( 8.12) adalah r umus

Gauss-Legendre

2 tit ik dan dapat digener alisir menjadi r umus

Gauss-Legendre untuk

n

titik seper ti yang ditunjukkan pada per samaan ( 8.13) .

Gabungkan per samaan ( 810) dengan ( 8.13) didapat

Selanjut nya lakukan tr ansfor masi bidang x ke bidang t. Dar i Gambar 8.8

Didapat

(a) (

b)

Gambar 8.8

Tr ansfor masi bidang x ke bidang t

Maka per samaan ( 8.16) menjadi x

=

mt

+

c

(8.18)

b

a

x

1

x

2

x

f

(

x

)

x

F

(

t

)

Metode Numerik

64

dan

dx = m dt

(8.19)

Dar i per samaan ( 8.18) , didapat f

(

x

) =

f

(

mt

+

c

)

Definisikan

F

(

t

) =

f

(

mt

+

c

) =

f

(

x

)

(8.20)

Subst it usi per samaan ( 8.15) – ( 8.20) ke per samaan ( 8.14) , didapat

Dar i per samaan ( 8.21) didapat

Per samaan ( 8.23 a) sampai ( 8.23d)

Metode Numerik

66

= 0,4 (1.

F

(–0,577350269) + 1.

F

(0,577350269))

= 0,4 (

F

(–0,577350269) +

F

(0,577350269))

BAB IX

PERSAMAAN DIFFERENSIAL BIASA

9.1 Jenis-jenis Per saman Differ ensial

Metode Numerik

67

Solusi numer ik yang akan dibahas hanya mencakup Per saman Differ ensial Biasa ( PDB) Or de Per t ama.

Metode Euler dibedakan menjadi 3 bentuk, yait u: - Metode Euler Maju (

Forward)

- Metode Euler Mundur (

Backward)

- Metode Euler yang Dimodifikasi (

Modified)

- Met ode Euler Langkah Maju (

Forward)