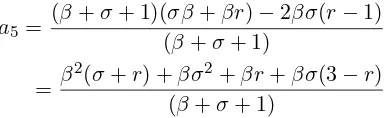Konstruksi Fungsi Lyapunov Untuk Menentukan Kestabilan Pada Sistem Lorenz - ITS Repository

TUGAS AKHIR - SM0141501

KONSTRUKSI FUNGSI LYAPUNOV UNTUK

MENENTUKAN KESTABILAN SISTEM LORENZ

RENI SUNDARI

NRP 1213 100 098

Dosen Pembimbing:

Prof.Dr.Erna Apriliani,M.Si

JURUSAN MATEMATIKA

Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Teknologi Sepuluh Nopember

FINAL PROJECT - SM141501

A CONSTRUCTION OF LYAPUNOV FUNCTION

FOR DETERMINING STABILITY LORENZ

SYSTEM

RENI SUNDARI

NRP 1213 100 098

Supervisors:

Prof.Dr.Erna Apriliani,M.Si

DEPARTMENT OF MATHEMATICS

LEMBAR PENGESAHAN

KONSTRUKSI FUNGSI LYAPUNOV UNTUK

MENENTUKAN KESTABILAN SISTEM

LORENZ

A CONSTRUCTION OF LYAPUNOV

FUNCTION FOR DETERMINING

STABILITY LORENZ SYSTEM

Diajukan Untuk Memenuhi Salah Satu Syarat

Untuk Memperoleh Gelar Sarjana Sains

pada

Bidang Studi Matematika Terapan

Program Studi S-1 Jurusan Matematika

Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Teknologi Sepuluh Nopember Surabaya

Oleh:

RENI SUNDARI

NRP. 1213 100 098

Menyetujui,

Dosen Pembimbing II,

Dosen Pembimbing I,

Prof.Dr.Erna Apriliani,M.Si

NIP.

NIP. 19660414 199102 2 001

Mengetahui,

Ketua Jurusan Matematika

FMIPA ITS

Prof. Dr. Erna Apriliani, M.Si

NIP. 19660414 199102 2 001

KONSTRUKSI FUNGSI LYAPUNOV UNTUK

MENENTUKAN KESTABILAN SISTEM

LORENZ

Nama Mahasiswa

:

RENI SUNDARI

NRP

:

1213 100 098

Jurusan

:

Matematika FMIPA-ITS

Pembimbing

:

Prof.Dr.Erna Apriliani,M.Si

Abstrak

Fungsi

Lyapunov

adalah

salah

satu

fungsi

yang

dikonstruksi

untuk

memeriksa

kestabilan

global

dari

suatu sistem non linier.

Pada penelitian ini digunakan

metode

Variabel

Gradien,

Kravoskii

dan

Energi

Casimir

dalam

mengkonstruksi

fungsi

Lyapunov.

Berdasarkan hasil perhitungan dn simulasi yang dilakukan

menggunakan

metode

variabel

gradien

dan

metode

Energi Casimir diperoleh fungsi Lyapunov untuk sistem

Lorenz

pada

semua

titik

kesetimbangan.Sedangkan

metode

Kravoskii

belum

menghasilkan

fungsi

Lyapuno

untuk

sistem

Lorenz

pada

semua

titik

kesetimbangan.

Kata-kunci:

Fungsi

Lyapunov,Metode

Variabel

Gradien,Metode Krasovkii, Metode

Energi-Casimir, Sistem Lorenz

.

A CONSTRUCTION OF LYAPUNOV

FUNCTION FOR DETERMINING STABILITY

LORENZ SYSTEM

Name

:

RENI SUNDARI

NRP

:

1213 100 098

Department

:

Mathematics FMIPA-ITS

Supervisor

:

Prof.Dr.Erna Apriliani,M.Si

Abstract

Lyapunov function is a function that is constructed to

examine the global stability of a system of non linear. Research

on Variable Gradient method is used, Kravoskii and energy

Casimir in constructing Lyapunov function.

Based on the

results of the calculations are performed using simulated dn

method of variable gradient method and Casimir Energy

retrieved Lyapunov function for a system of Lorenz on all

point of equilibrium. While the Kravoskii method is not yet

generating function Lyapunov for all points on the Lorenz

system equilibrium.

Keywords:

Lyapunov

Function,Variabel

Gradien

method,Krasovkii

Method,

Energy-Casimir

Method, Lorenz System

KATA PENGANTAR

Assalamu’alaikum Wr. Wb.

Alhamdulillaahirobbil’aalamiin, segala puji dan syukur

penulis panjatkan ke hadirat Allah SWT yang telah

memberikan limpahan rahmat, taufik serta hidayah-Nya,

sehingga penulis dapat menyelesaikan Tugas Akhir yang

berjudul

”KONSTRUKSI FUNGSI LYAPUNOV UNTUK

MENENTUKAN KESTABILAN PADA SISTEM

LORENZ”

sebagai salah satu syarat kelulusan Program Sarjana Jurusan

Matematika FMIPA Institut Teknologi Sepuluh Nopember

(ITS) Surabaya.

Tugas Akhir ini dapat terselesaikan dengan baik berkat

bantuan dan dukungan dari berbagai pihak. Oleh karena itu,

penulis menyampaikan ucapan terima kasih dan penghargaan

kepada:

1. Bapak Dr.

Imam Mukhlash,

S.Si,

MT selaku

Ketua Jurusan Matematika ITS yang telah memberikan

dukungan dan motivasi selama perkuliahan hingga

terselesaikannya Tugas Akhir ini.

2. Ibu Prof.Erna Apriliani,M.Si selaku dosen pembimbing

atas segala bimbingan dan motivasinya kepada penulis

sehingga dapat terselesaikan dengan baik.

3. Bapak dan Ibu dosen penguji atas semua saran dan

masukan yang telah diberikan.

4. Bapak Drs. Iis Herisman, M.Si selaku koordinator Tugas

Akhir.

5. Ibu Dian Winda selaku dosen wali yang telah

memberikan

arahan

akademik

selama

penulis

menempuh pendidikan di Jurusan Matematika FMIPA

ITS.

6. Bapak dan Ibu dosen serta para staf Jurusan

Matematika ITS yang tidak dapat penulis sebutkan

satu-persatu.

Penulis juga menyadari bahwa dalam pengerjaan ini

masih terdapat kekurangan. Oleh sebab itu, kritik dan saran

yang bersifat membangun sangat penulis harapkan demi

kesempurnaan Tugas Akhir ini. Akhirnya, penulis berharap

semoga penulisan ini dapat bermanfaat bagi banyak pihak.

Surabaya, 05 Januari 2017

Penulis

DAFTAR ISI

DAFTAR GAMBAR

DAFTAR TABEL

DAFTAR LAMPIRAN

LAMPIRAN A Listing Program ...

41

LAMPIRAN B Biodata Penulis ...

41

BAB I

PENDAHULUAN

Pada bab ini diuraikan tentang latar belakang yang

mendasari penulisan tugas akhir.

Di dalamnya mencakup

identifikasi

permasalahan,

beberapa

informasi

tentang

penelitian terdahulu yang berhubungan dengan topik tugas

akhir. Uraian ini bersifat umum yang menjelaskan secara

ringkas hal-hal yang akan dilakukan pada penyelesaian

tugas akhir. Dari informasi tersebut kemudian dirumuskan

permasalahan yang akan dibahas, tujuan, batasan masalah,

manfaat, dan kontribusi penelitian dari tugas akhir ini.

1.1

Latar Belakang

Matematika

merupakan

disiplin

ilmu

yang

dapat

diterapkan dalam berbagai ilmu pengetahuan dan dapat

memberikan interpretasi solusi analitis yang lebih rinci.

Permasalahan-permasalahan nyata dapat diselesaikan dengan

metode teoritis dan matematis setelah melalui tahap-tahap

pemodelan matematika. Suatu model matematika dikatakan

baik apabila mampu memberikan gambaran objeknya dengan

cukup jelas atau secara luas mampu menggambarkan keadaan

yang sesungguhnya, sehingga tujuan dari penyusunan model

tercapai.

Permasalahan yang terjadi dalam kehidupan sehari-hari

kebanyakan merupakan sistem dinamik.

Sistem dinamik

yaitu suatu sistem persamaan yang dipengaruhi oleh

perubahan gerak dan waktu.

Salah satu kajian penting

dalam permasalahan sistem dinamik yakni bagaimana

keadaan sistem, apakah sistem tersebut merupakan sistem

2

yang stabil atau tak stabil.

Aleksander

Mikhailovich

Lyapunov

dalam

tesisnya

yang berjudul

A general task about the stability of motion

mengembangkan dua metode untuk menganalisis kestabilan

dari suatu kesetimbangan, yang dikenal dengan metode

Lyapunov langsung (The Second Method of Lyapunov

)

dan metode Lyapunov tak langsung (First Method).

Hal

yang unik dari metode Lyapunov langsung bahwa untuk

menyelesaikan permasalahan kestabilan sistem, yang perlu

diketahui adalah bentuk persamaan diferensial sistemnya

atau bentuk fisisnya bukan solusinya [1].

Metode

Lyapunov

pertama

hanya

digunakan

mendapatkan kestabilan lokal (hanya disekitar titik yang

diselidiki) tidak mendapatkan kestabilan global dari sistem

dinamik nonlinier. Sedangkan untuk mendapatkan kestabilan

global digunakan metode Lyapunov langsung. Penyelesian

kestabilan sistem dinamik dengan metode Lyapunov langsung

mensyaratkan suatu fungsi, yang disebut sebagai fungsi

Lyapunov.

Yaitu fungsi skalar yang memenuhi beberapa

syarat diantaranya jika ada sebuah fungsi definit positif

sedemikian sehingga turunan dari yaitu semidefinit negatif

[1].

Metode Lyapunov langsung banyak diterapkan untuk

menganalisis kestabilan baik sistem linier maupun sistem

nonlinier, sistem

time-invariant

dan juga sistem

time-varrying.

3

1.2

Rumusan Masalah

Berdasarkan

uraian

di

atas,

permasalahan

yang

diselesaikan dalam Tugas Akhir ini adalah:

a. Bagaimana pembentukan fungsi Lyapunov dengan

menggunakan

metode

variabel

gradien,

metode

Krasovskii dan metode Energi-Casimir pada sistem

Lorenz?

b. Bagaimana analisa kestabilan dari masing-masing fungsi

Lyapunov yang dihasilkan dari metode variabel gradien,

metode Krasovskii dan metode Energi-Casimir pada

sistem Lorenz?

1.3

Batasan Masalah

Penelitian ini menjelaskan tentang penentuan kestabilan

dari sistem Lorenz menggunakan metode variabel gradien,

metode

Krasovskii

dan

metode

Energi-Casimir

yang

merupakan pengembangan dari analisis kestabilan dengan

menggunakan fungsi Lyapunov pada sistem persamaan

diferensial tak linier. Selanjutnya dilakukan simulasi dengan

Matlab 2010. Berdasarkan rumusan masalah di atas, batasan

masalah dari Tugas Akhir ini adalah: sigma (rasio viskositas

terhadap konduktivitas termal) sama dengan 10, beta

(perbandingan luas dan ketebalan lapisan) sama dengan

8₃

.

1.4

Tujuan

Berdasarkan rumusan masalah di atas, tujuan dari

penelitian yang diusulkan ini adalah

a. Mendapatkan fungsi Lyapunov dengan menggunakan

metode variabel gradien, metode Krasovskii dan metode

Energi-Casimir pada sistem Lorenz.

4

variabel gradien, metode Krasovskii dan metode

Energi-Casimir pada sistem Lorenz.

1.5

Manfaat

Adapun manfaat Tugas Akhir ini adalah sebagai berikut :

a. Sebagai salah satu referensi bagi peneliti selanjutnya

yang berkaitan dengan analisis kestabilan sistem Lorenz.

b. Memberikan gambaran tahap pengkonstruksi fungsi

Lyapunov pada sistem nonlinier sebagai contoh sistem

Lorenz.

c. Sebagai salah satu kontribusi untuk pengembangan

ilmu pengetahuan pada Matematika Terapan di bidang

sistem dinamik.

1.6

Sistematika Penulisan

Penulisan disusun dalam lima bab, yaitu:

1. BAB I PENDAHULUAN

Bab ini berisi tentang gambaran umum dari penulisan

yang meliputi latar belakang, rumusan masalah, batasan

masalah, tujuan, manfaat, dan sistematika penulisan.

2. BAB II TINJAUAN PUSTAKA

Bab ini membahas landasan teori yang mendasari

penulisan Tugas Akhir.

Didalamnya mencakup

penelitian terdahulu, sistem Lorenz, metode Variabel

Gradien, metode Kravoskii, dan metode Energi Casimir.

3. BAB III METODE PENELITIAN

5

4. BAB IV ANALISIS DAN PEMBAHASAN

Pada bab ini akan dijelaskan secara detail mengenai

pembentukan fungsi Lyapunov dengan menggunakan

tiga metode yaitu metode Variabel gradien, metode

Kravoskii, dan metode Energi Casimir beserta analisis

kestabilan dari masing-masing metode.

5. BAB V PENUTUP

BAB II

TINJAUAN PUSTAKA

Bab ini membahas landasan teori yang mendasari

penulisan Tugas Akhir.

Didalamnya mencakup penelitian

terdahulu, pembentukan fungsi Lyapunov menggunakan

metode Variabel gradien, metode Krasovkii, dan metode

Energi Casimir beserta analisis kestabilan pada

masing-masing metode.

2.1

Penelitian Terdahulu

Penelitian yang berkaitan dengan fungsi Lyapunov dan

sistem Lorenz banyak dilakukan oleh peneliti. Pada tahun

2012, Aldila Sakinah Putri melakukan penelitian yang

berjudul Metode Lyapunov untuk menentukan kestabilan

system persamaan Lorenz.

Dalam penelitiannya untuk

menentukan kestabilan digunakan dua macam metode

Lyapunov yaitu metode Lyapunov pertama dan metode

Lyapunov kedua. Hasil dari penelitian tersebut yaitu dengan

menggunakan metode Lyapunov pertama didapatkan tiga

titik kesetimbangan.

Dan analisa kestabilan pada titik

kesetimbangan, untuk 0

< r <

1 merupakan stabil asimtotik

dengan titik kesetimbangan yang berbentuk node.

Untuk

r

= 1 merupakan stabil dengan titik kesetimbangan yang

berbentuk spiral node. Untuk

r >

470

/

19 merupakan tidak

stabil dengan titik kesetimbangan yang berbentuk spiral

saddle point dengan index 2 sedangkan untuk

r

= 470

/

19

belum dapat ditentukan kestabilannya. Sedangkan metode

Lyapunov kedua dihasilkan turunan parsial fungsi Lyapunov

yang bernilai definit negatif[2].

8

Sedangkan

penelitian

tentang

menentukan

fungsi

Lyapunov dengan menggunakan metode yang berbeda

dengan metode yang digunakan oleh Aldila Sakinah. Dalam

Tesis yang berjudul Konstruksi Fungsi Lyapunov pada Model

Epidemi SIRS oleh Bulqis Nebulla (2016) menghasilkan

bahwa metode variabel gradien dan metode Energi-Casimir

dapat digunakan untuk mengkonstruksi fungsi Lyapunov pada

titik kesetimbangan bebas dan kesetimbangan endemi dan

system yang dihasilkan stabil sedangkan metode Krasovskii

belum dapat dikonstruksi fungsi Lyapunov[3].

Pada Tugas Akhir ini akan dibahas tentang konstruksi

fungsi Lyapunov untuk menentukan kestabilan sistem Lorenz.

2.2

Sistem Lorenz

Sistem Lorenz dikembangkan pada tahun 1963 oleh

Edward Lorenz sebagai model matematika sederhana untuk

konveksi atmosfer, persamaan Lorenz merupakan persamaan

nonlinier tiga dimensi yang terdiri dari sistem deterministik.

Pada awalnya sebagai pendekatan persamaan tertentu yang

mencirikan aliran subjek cair dangkal untuk pendinginan dan

pemanasan secara universal dari atas dan bawah.Model ini

kemudian membentuk system persamaan differensial biasa

sesuai dinamika fluida: sebagai berikut:[4]



9

(rasio viskositas tehadap konduktivitas termal),

r

(perbedaan

temperature antara bagian atas dan bagian bawah lapisan),

dan

β

(perbandingan luas dan ketebalan lapisan).

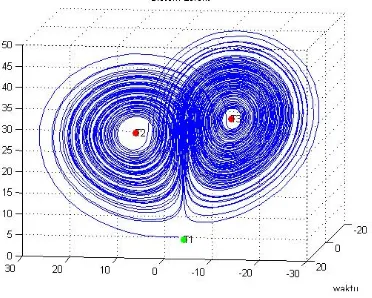
Mengingat nilai parameter tertentu, persamaan Lorenz

juga dikenal menghasilkan solusi kacau. Kekacauan digunakan

untuk mendefinisikan suatu sistem dimana perubahan

parameter kecil pada kondisi awal menghasilkan pengaruh

besar dalam hasil, atau dikenal sebagai efek kupu-kupu.

Solusi kacau membentuk strange attractor (penarik Lorenz).

Sebuah partikel dengan kondisi awal dalam penarik tersebut

bergerak di dalamnya. Namun gerakan yang sebenarnya dari

partikel tampaknya acak.

Oleh karena itu, sistem Lorenz

adalah sistem deterministik tetapi tidak dapat diprediksi.

Sebenarnya sistem yang dimodelkan oleh persamaan Lorenz

dapat juga menghasilkan solusi yang tidak kacau. Dengan

memberikan kombinasi parameter yang tepat, sejumlah orbit

stabil menuju titik tetap tertentu, berhingga maupun tak

hingga.

2.3

Kestabilan dan Titik Kesetimbangan

Setiap sistem memiliki keadaan setimbang yang

berbeda-beda.

Keadaan setimbang suatu sistem dapat terjadi

pada suatu titik yang disebut titik kesetimbangan.

Titik

kesetimbangan adalah suatu titik saat sistem tidak mengalami

perubahan sepanjang waktu. Sebuah titik

x

e

∈

R

n

adalah

sebuah titik kesetimbangan dari sistem persamaan diferensial

˙

x

=

f

(

x

) jika memenuhi

f

(

x

e

) = 0 .[5]

Kestabilan disekitar titik setimbang

x

e

dapat ditentukan

dengan memperhatikan nilai-nilai eigen yang diperoleh

persamaan karakteristik.

Secara umum, kestabilan titik

kesetimbangan mempunyai sifat sebagai berikut:

10

adalah bagian realnya negatif.

•

Tidak stabil, jika paling sedikit terdapat satu nilai eigen

yang didapatkan berupa bagian realnya positif.

Fungsi Lyapunov

Fungsi Lyapunov adalah suatu fungsi yang memenuhi tiga

pernyataan berikut ini.

Definisi 2.1[6]

Diberikan fungsi

V

:

D

_→

R

dan

x

e

∈ D

,titik kesetimbangan sistem persamaan diferensial

nonlinier.Fungsi

V

disebut fungsi Lyapunov jika memenuhi

pernyataan berikut:

•

1. Fungsi

V

kontinu dan mempunyai turunan parsial

pertama yang kontinu pada

_D

.

•

2. Fungsi

V

(

x

)

>

0 untuk

x

_{∈ D}

dengan

x

₆

=

x

e

dan

V

(

x

e

) = 0 dengan

x

=

x

e

(dengan titik kesetimbangan

x

e

merupakan titik minimum global).

•

3. Fungsi

V

(

˙

x

)

_≤

0 untuk setiap

x

_{∈ D}

Terdapat beberapa tipe kestabilan yang sesuai dengan solusi

nol

x

(

t

)

_≡

0 dari sistem nonlinear yang bergantung pada

waktu.

Definisi 2.2[6]

a. Solusi nol

x

(

t

)

_≡

0 pada sistem nonlinear yang

bergantung pada waktu adalah stabil Lyapunov jika

sebarang

ε >

0, terdapat

δ

=

δ

ε

>

0 sedemikian

sehingga jika

_k

x

(0)

_k

=

δ

, maka

_k

x

(

t

)

_k

< ε, t

_≥

0.

b. Solusi nol

x

(

t

)

_≡

0 pada sistem nonlinear yang

bergantung pada waktu adalah stabil asymptotis lokal

jika solusi nol stabil Lyapunov dan terdapat

δ

1

>

0 sedemikan sehingga jika

_k

x

(0)

_k

<

δ

1

,

maka

11

c. Solusi nol

x

(

t

)

_≡

0 pada sistem nonlinear yang

bergantung pada waktu adalah stabil asymptotis global

jika solusi nol stabil Lyapunov dan untuk semua

x

(0)

_∈

R

n

maka lim

t→∞

x

(

t

) = 0.

d. Solusi nol

x

(

t

)

_≡

0 pada sistem nonlinear yang

bergantung pada waktu adalah tidak stabil jika solusi

nol bukan stabil Lyapunov.

Teorema 2.1 [6]

Diberikan sistem

x

˙

=

f

(

x

)

dan

x

e

adalah titik kesetimbangan

dari sistem tersebut yang memenuhi

f

(

x

e

) = 0.

Jika terdapat

fungsi kontinu dimana fungsi

V

:

R

n

→

R

sedemikian sehingga

a.

V

(

x

e

) = 0

b.

V

(

x

)

>

0 untuk semua

x

₆

=

x

e

c. ˙

V

(

x

)

<

0 untuk semua

x

₆

=

x

e

d. jika

_k

x

_{k → ∞}

maka

V

(

x

)

_{→ ∞}

Maka

x

e

adalah stabil asymptotis global.

2.3.1

Konstruksi Fungsi Lyapunov

Konstruksi fungsi Lyapunov dapat dilakukan dengan

secara langsung yaitu dengan menggunakan beberapa

metode.

Berikut metode-metode untuk mengkonstruksi

fungsi Lyapunov, yaitu [6]:

2.3.2

Metode Variabel Gradien

Diberikan

V

:

_{D →}

_R

adalah fungsi diferensial kontinu

dan

g

(

x

) =

∂V

∂x T

12

Kemudian, mengkonstruksi

g

(

x

) sedemikian sehingga

g

(

x

)

adalah gradien dari fungsi definit positif dan

V

˙

(

x

) =

g

T

₍

_x

₎

_f

₍

_x

₎

_<

₀

_{, x}

_{∈ D}

_{, x}

₆

_{= 0. Fungsi}

_V

₍

_x

_{) bisa dihitung}

Fungsi

g

:

R

n

→

R

n

adalah vektor gradien nilai skalar fungsi

V

:

_R

n

_→

R

n

jika hanya jika

∂g

i

Pertama-pertama

harus

memenuhi

sebagai

berikut:

13

differensial sedemikian sehingga

f

(0) = 0.

Maka untuk

setiap

x

_∈

R

n

terdapat

α

_∈

[0

,

1] sedemikian sehingga

g

T

₍

_x

₎

_f

₍

_x

_{) =}

_g

T

₍

_x

₎

∂f ∂x

(

αx

)

x

Teorema 2.2 Teorema Krasovkii

Diberikan

x

(

t

) = 0

adalah titik kesetimbangan untuk sistem dinamika non linier

˙

x

(

t

) =

f

(

x

(

t

))

, x

(0) =

x

0

, t

≥

0

(2.5)

Dimana

f

:

_{D →}

R

n

adalah diferensial kontinu dan

_D

adalah

himpunan buka dengan 0

_{∈ D}

. Diasumsikan terdapat matrik

definit positif

P

_∈

R

nxn

dan

R

_∈

R

nxn

sedemikian sehingga

[

∂f

∂x

(

x

)]

T

_P

₊

_P

_[

∂f

∂x

(

x

)]

≥ −

R, x

∈ D

, x

6

= 0

(2.6)

Maka solusi nol

x

(

t

)

=

0 pada persamaan adalah

kesetimbangan tunggal stabil asymptotis dengan fungsi

lyapunov

V

(

x

) =

f

T

₍

_x

₎

_{P f}

₍

_x

_{). Jika}

_{D ≡}

_R

n

_{, maka solusi nol}

x

(

t

) = 0 pada persamaan adalah ketimbangan tunggal stabil

asymptotis global.

2.3.4

Metode Energi-Casimir

Pada metode ini memanfaatkan keberadaan invarian

dinamika atau pergerakan integral yang disebut fungsi

Casimir dari sistem dinamika nonlinier.

Diberikan fungsi

C

:

_{D →}

R

dan didefinisikan

Teorema 2.3

(Teorema Energi-Casimir) dengan menganggap

sistem dinamika nonlinier dimana

f

:

_{D →}

R

n

adalah lipschitz

kontinu pada

_D

. Diberikan

x

e

∈ D

adalah titik kesetimbangan

14

fungsi Casimir. Diasumsikan bahwa vektor

_C

′

i

(

x

e

)

, i

= 2

, , r

terdapat

α

_≥

0 sedemikian sehingga

E

′′

(

x

e

) +

α

Kemudian, solusi kesetimbangan

x

(

t

)

_≡

x

e

dari sistem

dinamika nonlinier adalah stabil lyapunov dengan fungsi

lyapunov

Khususnya andaikan dapat dikonstruksi suatu fungsi

H

:

D →

R

sedemikian sehingga ˙

H

(

x

) = 0 sepanjang lintasan

dari sistem dinamika nonlinier. Jika

_C

1

, . . . ,

C

r

adalah fungi

Casimir maka

∂

∂t

[

H

+

E

(

C

1

, . . . ,

C

r

)]

x

(

t

) = 0

(2.10)

Untuk setiap fungsi

E

:

R

r

→

R

. Oleh karena itu, walaupun

jika

H

tidak definit positif saat titik kesetimbangan

x

e

∈ D

fungsi

V

(

x

) =

H

(

x

) +

E

(

_C

1

(

x

)

, ..,

C

r

(

x

)) dapat dibuat definit

k

r

v

r

= 0 mempunyai paling tidak satu penyelesaian, yaitu

k

1

= 0

, k

2

= 0

, . . . , k

r

= 0. Jika ini adalah satu-satunya

15

2.3.6

Definit Positif dan Negatif

Sifat definit positif dan negatif sebuah fungsi maupun

matriks sangatlah penting saat mengkonstruksi fungsi

Lyapunov. Sebuah fungsi

V

:

_{D →}

R

dan

x

_{∈ D}

dikatakan

[8]:

1. Positif jika

V

(

x

)

>

0 untuk semua

x

₆

= 0 dan

V

(0) = 0

2. Semi positif jika

V

(

x

)

_≥

0 untuk semua

x

3. Negatif jika

V

(

x

)

<

0 untuk semua

x

0 dan

V

(

x

) = 0

4. Semidefinit negatif jika

V

(

x

)

_≥

0 untuk semua

x

Dan sebuah matrik

P

_∈

R

nxn

dikatakan:

1. Definit positif (

P >

0) jika

x

′

P x >

0 untuk semua

x

₆

= 0

2. Semidefinit positif (

P

_≥

0) jika

x

′

P x

_≥

0 untuk semua

x

3. Definit negatif (

P <

0) jika

x

′

P x <

0 untuk semua

x

₆

= 0

4. Semidefinit negatif jika (

P

₆

= 0) jika

x

′

P x

_≥

0 untuk

BAB III

METODE PENELITIAN

Bab ini menjelaskan langkah-langkah yang digunakan

dalam penyelesaian masalah pada Tugas Akhir. Disamping

itu, dijelaskan pula prosedur dan proses pelaksanaan tiap-tiap

langkah yang dilakukan dalam menyelesaikan Tugas Akhir.

3.1

Tahapan Penelitian

a. Studi Literatur

Tahap ini dikaji teori-teori yang berkaitan dengan

penelitian tentang mengkonstruksi fungsi Lyapunov

pada sistem nonlinier dengan menggunakan beberapa

metode. Diantaranya metode variabel gradien, metode

Krasovskii, dan Energi-Casimir.

b. Mencari kestabilan lokal

Pada tahap ini dianalisis kestabilan lokal dengan

pelinieran dan analisis kestabilan berdasarkan

nilai-nilai eigen. Metode yang digunakan untuk mengubah

system nonlinier ke sistem linier adalah metode

Jacobian dan dihasilkan matrik Jacobi.

Selanjutnya

titik kesetimbangan yang telah didapatkan dimasukkan

kedalam matrik Jacobi dan dihasilkan nilai eigen-nilai

eigen yang selanjutnya dianalisis kestabilannya.

c. Mengkonstruksi fungsi Lyapunov

Tahap ini dilakukan konstruksi fungsi Lyapunov dengan

beberapa metode.

Metode yang digunakan sebagai

berikut:

1.

Metode variabel gradien

Pada tahap ini yang

18

dilakukan adalah membangun gradien fungsi Lyapunov

yang ingin dicari.

Selanjutnya dicari nilai

a

ij

yang

memenuhi proposisi 2.1. kemudian dimasukkan nilai

a

ij

yang diperoleh kedalam gradient fungsi Lyapunov tadi.

Kemudian mencari fungsi Lyapunov dan diuji kevalidan

fungsi Lyapunov.

2. Metode Krasovkii

Pada tahap ini yang dilakukan

adalah mencari matriks Jacobi system.

Kemudian

memasukkan nilai titik kesetimbangan dan parameter.

Lalu mencari nilai dari matrik

P

dan matrik

R

harus

definit negatif. Kemudian menghitung fungsi Lyapunov.

Setelah didapatkanfungsi Lyapunov, kemudian diuji

kevalidan fungsi Lyapunov.

3.

Metode Energi-Casimir

Pada tahap ini yang

dilakukan adalah memisalkan fungsi energi casimir

yang memenuhi asumsi, kemudian mencari nilai matrik

E

. Kemudian menghitung fungsi Lyapunov dan diuji

kevalidan fungsi Lyapunov.

d. Menganalisis kestabilan global

Setelah didapatkan fungsi Lyapunov dari

masing-masing metode selanjutnya hasilnya diuji kestabilan

dengan dilihat kedefinitan dan turunannya dilihat

kedefinitannya.

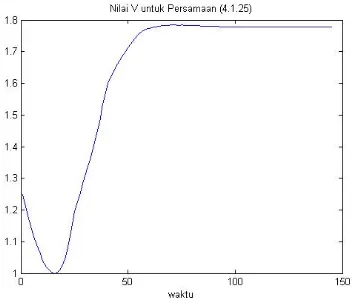
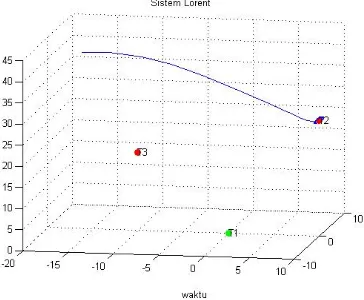
e. Membuat simulasi

Fungsi Lyapunov yang telah didapatkan selanjutnya

dilakukan simulasi dengan menggunakan Matlab.

f. Analisis Hasil dan Kesimpulan

BAB IV

ANALISIS DAN PEMBAHASAN

Pada bab ini dijelaskan tentang titik kesetimbangan,

analisis

kestabilan

sistem,

menganalisis

kestabilan

menggunakan metode dan membandingkan fungsi Lyapunov

menggunakan metode variabel gradien, metode Kravoskii dan

metode Energi-Casimir.

4.1

Sistem Non Linier

Sistem non linier yang digunakan pada pembahasan ini

adalah sistem Lorenz.

Pada sistem Lorenz seperti pada

Persamaan (2.1) akan dilakukan konstruksi fungsi Lyapunov

dengan menggunakan metode Variabel Gradien, metode

Krasovkii, dan metode Energi-Casimir.

4.2

Titik Kesetimbangan

Untuk mendapatkan titik kesetimbangan dari sistem

(2.1)yaitu

f

1

(

x, y, z

) =

dxdt

,

f

2

(

x, y, z

) =

dy

dt

, dan

f

3

(

x, y, z

) =

dz

dt

dengan (

x, y, z

)

∈

R

3

merupakan titik kesetimbangan dari

sistem (2.1), dapat diperoleh jika

dx

sehingga sistem persamaan (2.1) menjadi

σ

(

y

₋

x

) = 0

(4.1)

x

(

r

₋

z

)

₋

y

) = 0

(4.2)

xy

₋

βz

= 0

(4.3)

Dari persamaan (4.1) didapatkan

y

=

x

, dengan

σ

adalah

konstanta.

Jika

y

=

x

= 0, maka didapatkan

z

= 0 ,

dengan mengsubstitusikannya pada persamaan (4.3), dengan

20

β

adalah konstanta. Jika

y

=

x

₆

= 0, maka persamaan (4.2)

diperoleh

x

=

x

(

r

₋

z

)

(4.4)

Jika

x

₆

= 0, maka pandang persamaan (4.4) dibagikan

x

sehingga diperoleh 1 = 1(

r

₋

z

)

z

=

r

₋

1 Substitusikan

z

=

r

₋

1 pada persamaan

(4.3), diperoleh

x

2

₌

_bz

₌

_b

₍

_r

₋

_{1) Sehingga diperoleh}

x

=

_±

p

(

b

(

r

₋

1)) . Jika b diambil bilangan positif, maka

diperoleh

r

₋

1

>

0 atau

r >

1.Jika

r >

1 maka terdapat dua

titik kesetimbangan yaitu (

p

(

b

(

r

₋

1))

,

p

(

b

(

r

₋

1))

, r

₋

1)

dan (

₋

p

(

b

(

r

₋

1))

,

₋

p

(

b

(

r

₋

1))

, r

₋

1), sedangkan

r <

1

terdapat satu titik kesetimbangan yaitu pada titik (0

,

0

,

0).

4.3

Kestabilan Lokal

Sistem persamaan (2.1) merupakan sistem nonlinier.

Kestabilan dari sistem persaman nonlinier sulit dianalisis,

sehingga untuk memudahkan menganalisis, sistem tersebut

diubah menjadi sistem linier. Metode yang digunakan untuk

mengubah sistem nonlinier menjadi sistem linier adalah

metode matrik Jacobi. Diketahui bahwa

f

1

(

x, y, z

) =

σ

(

y

−

x

)

f

2

(

x, y, z

) =

x

(

r

−

z

)

−

y

f

3

(

x, y, z

) =

xy

−

βz

Matrik Jacobi yang dibentuk dari sistem diatas adalah

J

=

21

Karena

β

,

σ

dan

r

adalah konstanta positif, maka

akar-akar persamaan karakteristik yang diperoleh adalah

λ

1

=

−

β,λ

2,3

=

−

1₂

(

σ

+1)

±

1₂

p

(

σ

2

₋

_{(2 + 4}

_r

₎

_σ

_+1).

Untuk

r <

1, kondisi didalam akar kuadrat kurang dari

(

σ

₋

1)

2

_{, menjadikan}

_{λ <}

_{0 sehingga nilai eigen bernilai}

negatif dan riil. Oleh karena itu, titik kesetimbangan pada

titik (0

,

0

,

0) bersifat stabil.

Kemudian titik kesetimbangan

T

2

= (

X

∗

, Y

∗

, Z

∗

) =

(

p

β

(

r

₋

1)

,

p

β

(

r

₋

1)

, r

₋

1) disubstitusikan ke dalam

persamaan (4.3.1), sehingga diperoleh matriks

22

Tabel 4.1: Tabel Routh-Hurwitz

λ

3

a

1

a

3

λ

2

a

2

a

4

λ

a

5

0

λ

0

_a

6

0

Nilai eigen matriks diperoleh dari

det

(

λ

_{I − J}

) = 0, maka

det





λ

+

σ

₋

σ

0

−

1

λ

+1

p

β

(

r

₋

1)

−

p

β

(

r

₋

1)

₋

p

β

(

r

₋

1)

λ

+

β





= 0

(

λ

+

σ

)((

λ

+1)(

λ

+

β

) +

β

(

r

₋

1)) +

σ

(

λ

(

β

(

r

₋

1))

₋

(

λ

+

β

) = 0

(

λ

3

) + (

β

+

σ

+ 1)

λ

2

+ (

σβ

+

βr

)

λ

+ 2

βσ

(

r

₋

1) = 0

Selanjutnya, analisis kestabilan pada persamaan diatas

dapat diperoleh dengan menggunakan tabel 4.1

Routh-Hurwitz. Misalkan

a

1

λ

3

+

a

2

λ

2

+

a

3

λ

+

a

4

= 0 maka

a

1

= 1;

a

2

= (

β

+

σ

+ 1);

a

3

= (

σβ

+

βr

);

a

4

= 2

βσ

(

r

−

1);

Agar sistem stabil, maka semua suku kolom pertama pada

tabel haruslah bertanda sama maka

a

2

,

a

5

,

a

6

haruslah

bernilai positif. Selanjutnya dihitung nilai

a

5

dengan rumus

a

5

=

a2a3a−2a1a4

,

a

6

=

a

4

a

5

=

(

β

+

σ

+ 1)(

σβ

+

βr

)

₋

2

βσ

(

r

₋

1)

(

β

+

σ

+ 1)

=

β

2

₍

_σ

₊

_r

_{) +}

_βσ

2

₊

_βr

₊

_βσ

₍₃

₋

_r

₎

23

Nilai

a

5

bernilai positif jika

r <

σ(σ+β+3)σ−β−1

dengan

r

bernilai

positif ketika

σ > β

+ 1. Selanjutnya dicari nilai

a

6

, yaitu

a

6

=

a

4

= 2

βσ

(

r

−

1)

Untuk

a

6

akan bernilai positif jika

r >

1.

Sehingga

untuk mendapatkan semua nilai bernilai positif jika 1

<

r <

σ(σ+bβ+3)_σ−β−₁

, maka dua titik kesetimbangan

T

2,3

=

4.4

Konstruksi Fungsi Lyapunov

Selanjutnya akan dicari kestabilan global titik setimbang

dari sistem Lorenz.

Metode yang digunakan untuk

menganalisis kestabilan global yaitu metode Lyapunov.

Metode ini mengsyaratkan untuk mengkonstruksi sebuah

fungsi yang dapat menganalisis sifat sistem, yang disebut

fungsi Lyapunov.

4.4.1

Metode Variabel Gradien

Metode variabel gradien adalah salah satu metode

yang digunakan untuk membentuk fungsi Lyapunov.Metode

ini membantu pengkonstruksian fungsi Lyapunov secara

sistematis dan terstruktur tetapi terdapat kesulitan dalam

mengevaluasi fungsi Lyapunov.

Langkah-langkah untuk

mendapatkan fungsi fungsi Lyapunov dari sistem sebagai

berikut:

24

Dengan

_∇

V

i

=

P

n_j=1

h

ij

x

j

, i

= 1

, . . . , n, h

ij

adalah

sebuah konstanta dan

x

j

dalah variabel suatu sistem,

yang memenuhi kondisi curl yaitu

_∂x∂2V

i∂xj

=

∇Vi

∂xj

=

∇Vj

∂xi

2. Variabel gradien fungsi Lyapunov

_∇

V

digunakan untuk

mencari ˙

V

, dimana ˙

V

= (

_∇

V

)

T

_X

_˙

_.

3. Fungsi Lyapunov dapat dihitung dengan integral

V

(

x

) =

Z

x

0

∇

V

(

x

)d

x

Dengan menggunakan metode variabel gradien.

Diberikan sistem persamaan (2.1) sehingga dimisalkan

∇

V

(

x

) =

Selanjutnya mencari nilai

h

ij

yang memenuhi kondisi curl dan

turunan dari fungsi Lyapunov bernilai negatif. Maka turunan

dari fungsi Lyapunov adalah

25

Agar memenuhi kondisi curl yaitu

_∂x∂2V

i∂xj

=

Berdasarkan hasil diatas, maka pemilihan

h

ij

yang memenuhi

kondisi curl yaitu

h

ij

=

h

ji

. Sehingga persamaan menjadi

˙

Agar ˙

V

adalah fungsi negatif, maka dipilih semua didalam

kurung pada persamaan (4.7) adalah positif, adalah

•

h

11

σ

−

h

12

r

+

h

12

z

−

h

13

y >

0

26

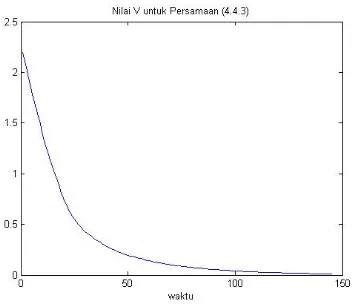
Fungsi Lyapunov diperoleh dengan

27

Dari persamaan (4.8) diperoleh

V

(

X

0

_{, Y}

0

_{, Z}

0

_{) = 0. Turunan}

untuk fungsi Lyapunov (4.8) pada titik kesetimbangan titik

nol adalah

Selanjutnya untuk mengecek turunan

V

diatas adalah negatif,

maka dimasukkan ke dalam program.

Titik kesetimbangan pada dua titik yang lain

Fungsi Lyapunov dengan menggunakan metode Variabel

Gradien telah diperoleh pada persamaan (4.8).

Fungsi

Lyapunov (4.9) dapat dimodifikasi dengan memasukkan titik

kesetimbangan yanga lain yaitu

T

2,3

= (

X

∗

, Y

∗

, Z

∗

) =

(

_±

p

β

(

r

₋

1)

,

_±

p

β

(

r

₋

1)

, r

₋

1) dengan 1

< r <

σ(σ+β+3)_σ−β−₁

sehingga diperoleh fungsi Lyapunov , yaitu

V

=

1

Dimana persamaan diatas didapatkan

V >

0 untuk

x

=

x

∗

,

y

=

y

∗

, dan

z

=

z

∗

serta

V

(

T

2

) = 0 dan

V

(

T

3

) = 0. Turunan

fungsi Lyapunov pada titik kesetimbangan ini adalah

28

Maka diperoleh ˙

V

(

T

2,3

) = 0,karena persamaan (4.11) tidak

terlihat bahwa ˙

V <

0 untuk semua

X

,

Y

, dan

Z

. Selanjutnya,

untuk mengecek turunan dari adalah negatif, maka dicek

dengan memasukkan ke program.

4.4.2

Metode Krasovkii

Berdasarkan teorema 2.2, maka langkah pertama untuk

mengkonstruksi fungsi Lyapunov adalah mendapatkan matrik

Jacobi dari sistem (2.1), yaitu

J

=





−

σ

σ

0

r

₋

z

₋

1

₋

x

y

x

₋

β





(4.12)

Titik kesetimbangan pada titik asal yaitu

T

1

=

(

X

0

_{, Y}

0

_{, Z}

0

_{) = (0}

_,

₀

_,

_{0) disubstitusikan pada matriks J,}

sehingga diperoleh matriks

J

(

T

1

) =





−

σ

σ

0

r

₋

1

0

0

0

₋

β





(4.13)

29

Berdasarkan

metode

Krasovkii,

kondisi

titik

kesetimbangan menjadi stabil asymptotis pada

F

(

x

) =

J

T

P

+

P

_J

+

R

= 0 atau

_J

T

P

+

P

_J

=

₋

R

, dengan

R

adalah matriks identitas. Nilai

P

ij

dapat diperoleh dengan

30

(tanpa tahun) adalah sebagai berikut

σ

= 10 ,

β

=

8₃

. Dengan

bantuan program Matlab maka diperoleh

P

=

31

Selanjutnya turunan

V

adalah

˙

dengan memasukkan

T

1

pada persaman(4.15) diperoleh

˙

V

(

T

1

) = 0. Selanjutnya untuk mengecek turunan

V

diatas

adalah negatif, maka dimasukkan ke dalam program.

Titik kesetimbangan pada dua titik yang lain

Dua titik kesetimbangan yaitu

T

2

= (

X

∗

, Y

∗

, Z

∗

) =

(

_±

p

β

(

r

₋

1)

,

_±

p

β

(

r

₋

1)

, r

₋

1) dengan 1

< r <

σ(σ+β+3)_σ−β−1

disubstitusikan pada matriks

_J

, sehingga diperoleh matriks

J

(

T

2

) =

33

Kondisi titik kesetimbangan menjadi stabil asymptotis

pada

F

(

x

) =

_J

T

_P

₊

_P

_J

₊

_R

_{= 0 atau}

_J

T

_P

₊

_P

_J

₌

₋

_R

_,

dengan

R

adalah matriks identitas, maka

R

11

=

−

2

σP

11

+

P

21

+

P

12

+

c

(

P

31

+

P

13

) =

−

1

R

12

=

−

σP

12

+

P

22

+

cP

32

+

σP

11

−

P

12

+

cP

13

= 0

R

13

=

−

σP

13

+

P

23

+

cP

33

−

cP

12

−

βP

13

= 0

R

21

=

P

11

−

(1 +

σ

)

P

21

+ (

P

31

+

P

23

) +

P

22

= 0

R

22

=

P

12

−

P

22

+

cP

32

+

σP

21

−

P

22

+

cP

23

=

−

1

R

23

=

P

13

−

P

23

+

cP

33

+

−

cP

22

−

βP

23

= 0

R

31

=

−

2

cP

21

−

(

σ

+

β

)

P

31

+

P

32

+

cP

33

= 0

R

32

=

−

cP

22

−

βP

32

+

σP

31

−

P

32

+

cP

33

= 0

R

33

=

−

cP

23

−

βP

33

−

cP

32

−

βP

33

=

−

1

Nilai

P

ij

dapat diperoleh dengan memasukkan nilai

parameter yang diperoleh dari O.Knill adalah sebagai berikut

σ

= 10 ,

β

= 8

/

3 dan 1

< r <

σ(σ+β+3_σ−β−₁

= 24

.

7. Diambil

r

= 24 dan dengan program Matlab maka diperoleh

P

=





P

11

P

12

P

13

P

21

P

22

P

23

P

31

P

32

P

33





=





0

,

1346 0

,

2943

0

.

0050

0

.

0448

0

.

4694

₋

0

.

2792

0

.

1676

0

.

1766

0

,

3381





34

35

Karena hasil yang terlihat belum terlihat bahwa ˙

V

adalah

negatif. Selanjutnya untuk mengecek turunan diatas adalah

negatif, maka dimasukkan ke dalam program.

Titik kesetimbangan

T

3

= (

−

Langkah yang kedua yaitu mendapatkan matrik P

memenuhi persamaan (2.6).

Misalkan

R

=

J

T

_P

₊

_{P J}

36

37

dengan

R

adalah matriks identitas, maka

R

11

=

−

2

σP

11

+

P

21

+

P

12

+

c

(

P

31

+

P

13

) =

−

1

R

12

=

−

σP

12

+

P

22

+

cP

32

+

σP

11

−

P

12

+

cP

13

= 0

R

13

=

−

σP

13

+

P

23

+

cP

33

−

cP

12

−

βP

13

= 0

R

21

=

σP

11

−

(1 +

σ

)

P

21

+ (

P

31

+

P

23

) +

P

22

= 0

R

22

=

σP

12

−

P

22

+

cP

32

+

σP

21

−

P

22

+

cP

23

=

−

1

R

23

=

σP

13

−

P

23

+

cP

33

+

−

cP

22

−

βP

23

= 0

R

31

=

−

2

cP

21

−

(

σ

+

β

)

P

31

+

P

32

+

cP

33

= 0

R

32

=

−

cP

22

−

βP

32

+

σP

31

−

P

32

+

cP

33

= 0

R

33

=

−

cP

23

−

βP

33

−

cP

32

−

βP

33

=

−

1

dimana

c

=

₋

p

β

(

r

₋

1).

Nilai

P

ij

dapat diperoleh dengan memasukkan nilai

parameter yang diperoleh dari O.Knill adalah sebagai berikut

σ

= 10 ,

β

= 8

/

3 dan 1

< r <

σ(σ+β+3_σ−β−1

= 24

.

7.Diambil

r

= 24

dan dengan program Matlab maka diperoleh

P

=





P

11

P

12

P

13

P

21

P

22

P

23

P

31

P

32

P

33





=





−

5

,

6421

₋

15

,

1891

₋

0

,

6584

0

,

3580

₋

27

,

2288

₋

23

,

1679

11

,

9840

11

,

3115

₋

17

,

2225





38

39

Karena hasil yang terlihat belum terlihat bahwa ˙

V

adalah

negatif.

Selanjutnya untuk mengecek turunan dari diatas

adalah negatif dengan dimasukkan ke dalam program.

4.4.3

Metode Energi-Casimir

Pada metode Energi-Casimir, langkah yang digunakan

untuk mengkonstruksi fungsi Lyapunov pada sistem (2.1)

adalah sebagai berikut: Terdapat konstanta Lipschitz

k

(

t

)

yang memenuhi

_k

f

(

x

1

(

t

)

, t

)

−

f

(

x

2

(

t

)

, t

)

k ≤

k

(

t

)

k

x

1

−

x

2

k

40

dx

dt

=

f

(

x

(

t

)

, t

)

dy

dt

=

f

(

y

(

t

)

, t

)

dz

dt

=

f

(

z

(

t

)

, t

)

Misalkan terdapat vektor

x

= (

x

1

, x

2

)

, y

= (

y

1

, y

2

),

dan

z

= (

z

1

, z

2

).

Selanjutnya akan dicari nilai

k

(

t

) yang

merupakan konstanta Lipschitz yang memenuhi

k

f

(

x

1

(

t

)

, t

)

−

f

(

x

2

(

t

)

, t

)

k ≤

k

(

t

)

k

x

1

−

x

2

k

dengan

k

f

(

x

1

(

t

)

, t

)

−

f

(

x

2

(

t

)

, t

k

=

k





a

11

a

21

a

31





k

Berdasarkan sistem persamaan (2.1) dapat dibentuk

sebagai berikut

•

a

11

=

σ

(

y

1

−

x

1

)

−

σ

(

y

2

−

x

2

) =

σ

(

y

1

−

y

2

)

−

σ

(

x

1

−

x

2

)

Misalkan

σ

(

y

1

−

y

2

) =

δ

1

(

t

)(

x

1

−

x

2

) maka

a

11

= (

δ

1

(

t

)

−

σ

)(

x

1

−

x

2

) Maka didapatkan

|

a

11

|

=

|

(

δ

1

(

t

)

−

σ

)(

x

1

−

x

2

)

| ≤ |

(

δ

1

(

t

)

−

σ

)

||

(

x

1

−

x

2

)

|

(4.22)

•

a

21

=

rx

1

−

y

1

−

x

1

z

1

−

(

rx

2

−

y

2

−

x

2

z

2

) =

r

(

x

1

−

x

2

)

−

(

y

1

−

y

2

)

−

(

x

1

z

1

−

x

2

z

2

) Misalkan

r

(

x

1

−

x

2

) =

δ

2

(

t

)(

y

1

−

y

2

)

dan (

x

1

z

1

−

x

2

z

2

) =

δ

3

(

t

)(

y

1

−

y

2

) Maka

a

21

= (

δ

2

(

t

)

−

1

−

δ

3

(

t

))(

y

1

−

y

2

)

Sehingga didapatkan

|

a

21

|

=

|

(

δ

2

(

t

)

−

1

−

δ

3

(

t

))(

y

1

−

y

2

)

| ≤ |

(

δ

2

(

t

)

−

1

−

δ

3

(

t

))

||

(

y

1

−

y

2

)

|

41

Selanjutnya persamaan (4.22), (4.23) dan (4.24) dapat

dituliskan sebagai berikut

Maka sistem memenuhi kondisi Lipschitz.

Misalkan fungsi casimir dengan syarat

C

_i′

(

x

e

) adalah bebas

linier. Pada sistem (2.1) dengan titik kesetimbangan memiliki

variabel berjumlah 3, maka

n

= 3. Karena itu, fungsi Casimir

yang dimisalkan ada dua. Misalkan

C

1

=

(x)

2

bebas linier. Langkah selanjutnya adalah menghitung

E

(

x

)

,

42

Yang memenuhi syarat

E

′

(

x

e

) = 0 dan

x

T

E

Selanjutnya dengan memilih sebarang

µ

1

dan

µ

2

adalah

43

Karena telah memenuhi asumsi pada langkah selanjutnya

akan dibuktikan bahwa

Maka fungsi Lyapunov pada titik kesetimbangan

T

1

= (0

,

0

,

0)

44

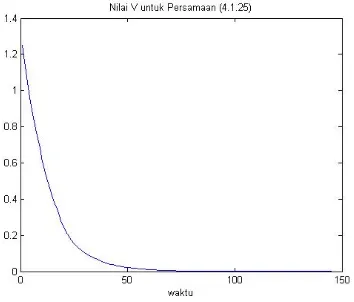
Fungsi Lyapunov (4.25) adalah definit positif, karena

V

(

x

)

>

0 untuk semua

x, y, z

serta

V

(

T

1

) = 0.

Turunan dari

Titik kesetimbangan pada dua titik yang lain

Berdasarkan

langkah

yang

telah

dijabarkan

pada

sebelumnya. Selanjutnya dicari fungsi Lyapunov untuk dua

titik kesetimbangan yang lain yaitu

T

2,3

= (

X

∗

, Y

∗

, Z

∗

) =

(

_±

p

β

(

r

₋

1)

,

_±

p

β

(

r

₋

1)

, r

₋

1) dengan 1

< r <

σ(σ+β+3)_σ−β−₁

Pada sistem (2.1) dengan titik kesetimbangan

T

2,3

memiliki

variabel berjumlah 3, maka

n

= 3.

Karena itu, fungsi

Casimir yang dimisalkan ada dua. Misalkan

C

1

=

b(y)

2

untuk menguji bahwa vektor

C

₁′

dan

C

₂′

adalah bebas linier.

Misalkan

S

=

C

₁′

, C

₂′

adalah bebas linier jika

k

1

C

Didapatkan

k

1

=

k

2

= 0 yang merupakan satu-satunya

45

Yang memenuhi syarat

E

′

(

x

e

) = 0 dan

x

T

E

Selanjutnya dengan memilih sebarang

µ

1

dan

µ

2

adalah

46

Karena telah memenuhi asumsi pada langkah selanjutnya

akan dibuktikan bahwa

Dipilih

α

= 1 sehingga

E

′′

(

x

e

) +

α

Maka

fungsi

Lyapunov

pada

titik

kesetimbangan

47

Fungsi Lyapunov (4.28) adalah definit positif, karena

V

(

x

)

>

0 untuk semua

x, y, z

serta

V

(

T

2

) = 0 dan

V

(

T

3

) = 0

. Turunan dari persamaan (4.28) adalah

˙

48

4.5

Simulasi

Pada Subbab ini akan dibahas cara mendapatkan

sousi numerik dari sistem persamaan Lorenz dan hasil

simulasi numerik.

Hal ini bertujuan untuk memudahkan

dalam menganalisis sistem dan mengetahui perilaku sistem.

Penyelesaian numerik yang digunakan adalah metode

Runge-kutta orde 4 dan 5 dalam Software Matlab(R2010a).

4.5.1

Pada titik kesetimbangan nol

Nilai parameter yang digunakan dalam simulasi diperoleh

dari O.knill(tanpa tahun) adalah

σ

= 10,

β

=

8₃

dengan

kondisi awal (

X, Y, Z

) = (1

,

1

,

1).

Hasil simulasi yang

diperoleh adalah sebagai berikut

Gambar 4.1: Grafik sistem Lorenz dengan r=0.5

49

Gambar 4.2: Grafik sistem Lorenz dengan r=24

Berdasarkan gambar 4.2 terlihat bahwa titik awal di sekitar

titik kesetimbangan (0,0,0) dan

r

= 24. Pergerakan garis

membentuk angka delapan yang dikenal ”Lorenzt Attractor”

dan sistem bersifat tidak stabil.

50

membentuk angka delapan yang dikenal ”Lorenzt Attractor”

dan sistem bersifat tidak stabil.

Hasil penyelesaian dari fungsi Lyapunov yang dikontruksi

menggunakan variabel gradien beserta turunannya.

Gambar 4.4: Grafik Fungsi Lyapunov

51

Berdasarkan gambar 4.4 dan 4.5, terlihat bahwa fungsi

Lyapunov (4.8) semua berada pada nilai positif dan bergerak

menuju nol. Dan turunan dari persamaan(4.9) dimana semua

nilai berada pada bagian negatif dan bergerak menuju titik

nol.Hal ini menunjukkan bahwa Fungsi Lyapunov dapat

dikonstruksi dengan metode Variabel gradien untuk sistem

Lorenz pada titik kesetimbangan nol dengan parameter

r

= 0

.

5

<

1. Sistem Lorenz pada titik kesetimbangan nol

bersifat stabil jika

r

_≤

1.

Gambar 4.6: Grafik Fungsi Lyapunov

52

Gambar 4.7: Grafik Turunan Fungsi Lyapunov

Gambar 4.8: Grafik Fungsi Lyapunov

Berdasarkan gambar 4.8, terlihat bahwa pada r=1.5 tidak

berlaku fungsi Lyapunov yang dikonstruksi karena nilai tidak

bergerak menuju titik nol.

53

Gambar 4.9: Grafik Fungsi Lyapunov

Gambar 4.10: Grafik Turunan Fungsi Lyapunov

54

juga.Hal ini menunjukkan bahwa Fungsi Lyapunov tidak

dapat dikonstruksi dengan metode Kravoskii untuk sistem

Lorenz pada titik kesetimbangan nol dengan parameter

r

=

0

.

5

<

1.

Berikut hasil penyelesaian dari fungsi Lyapunov dengan

metode Energi-Casimir beserta turunannya.

Gambar 4.11: Grafik Fungsi Lyapunov