Informasi Dokumen
- Penulis:
- Sudianto Manullang
- Andri Kristianto S.
- Tri Andri Hutapea
- Lasker Pangarapan Sinaga
- Bornok Sinaga
- Mangaratua Marianus S.
- Pardomuan N. J. M. Sinambela
- Pengajar:
- Agung Lukito
- Muhammad Darwis M.
- Turmudi
- Nanang Priatna
- Sekolah: Kementerian Pendidikan dan Kebudayaan
- Mata Pelajaran: Matematika
- Topik: Kelas 11 SMA Matematika Siswa 2017
- Tipe: buku
- Tahun: 2017
- Kota: Jakarta
Ringkasan Dokumen
I. INDUKSI MATEMATIKA
Bab ini membahas induksi matematika, sebuah metode pembuktian yang penting dalam matematika. Melalui induksi, siswa diharapkan dapat memahami dan menjelaskan metode pembuktian pernyataan matematis, serta menerapkannya dalam berbagai konteks. Induksi matematika terdiri dari dua langkah utama: langkah awal dan langkah induksi. Pada langkah awal, kita menunjukkan bahwa pernyataan benar untuk nilai dasar, sedangkan pada langkah induksi, kita menunjukkan bahwa jika pernyataan benar untuk suatu nilai k, maka juga benar untuk nilai k+1. Dengan cara ini, kita dapat membuktikan kebenaran pernyataan untuk semua bilangan asli.
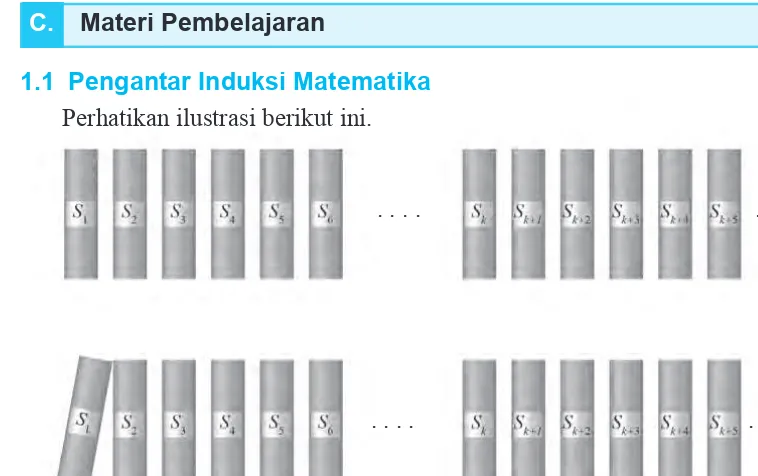
1.1 Pengantar Induksi Matematika
Pengantar ini memberikan ilustrasi tentang bagaimana induksi matematika berfungsi, menggunakan contoh visual dari objek yang jatuh. Konsep ini membantu siswa memahami bahwa jika satu pernyataan benar, maka pernyataan yang lebih umum juga benar. Dengan memanfaatkan kelompok belajar, siswa didorong untuk mengajukan dan mendiskusikan masalah kontekstual yang relevan, sehingga mereka dapat menemukan prinsip-prinsip matematika secara mandiri.
1.2 Prinsip Induksi Matematika
Prinsip ini menjelaskan langkah-langkah yang diperlukan untuk membuktikan pernyataan matematis menggunakan induksi. Dalam hal ini, siswa belajar bahwa untuk membuktikan P(n) benar, langkah awal harus menunjukkan kebenaran untuk n=1, dan langkah induksi harus menunjukkan bahwa P(k) benar mengarah pada P(k+1) juga benar. Dengan memahami prinsip ini, siswa dapat menerapkan induksi matematika untuk berbagai situasi.
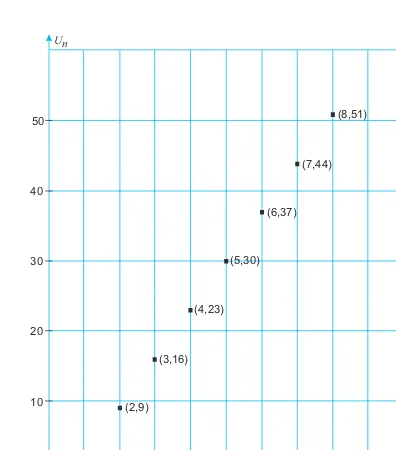
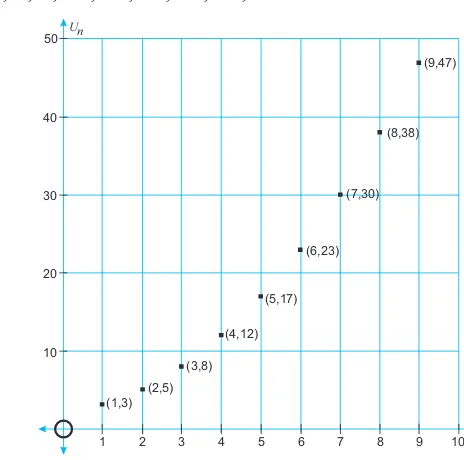
1.3 Bentuk-Bentuk Penerapan Induksi Matematika
Dalam bagian ini, siswa diajarkan berbagai penerapan induksi matematika, termasuk dalam barisan bilangan, keterbagian, dan ketidaksamaan. Siswa diberi contoh konkret dan masalah yang harus mereka selesaikan menggunakan prinsip induksi. Ini mencakup penerapan pada barisan bilangan dan pembuktian sifat keterbagian menggunakan induksi untuk menunjukkan bahwa suatu pernyataan berlaku untuk semua bilangan alami.
II. PROGRAM LINEAR
Bab ini membahas program linear, yang merupakan alat penting dalam memecahkan masalah optimasi di berbagai bidang. Siswa belajar tentang konsep kendala, fungsi objektif, dan cara menyelesaikan masalah yang melibatkan dua variabel. Melalui pembelajaran ini, siswa diharapkan dapat menganalisis dan menyelesaikan masalah kontekstual yang berkaitan dengan program linear, serta memahami cara menggambarkan solusi secara geometris.
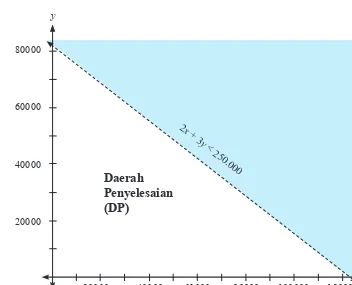
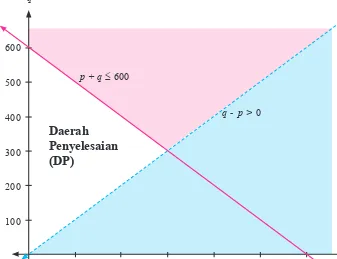
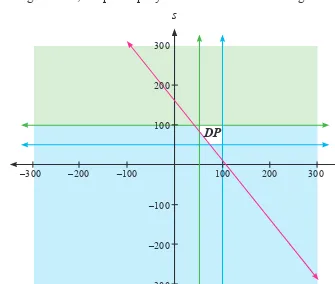
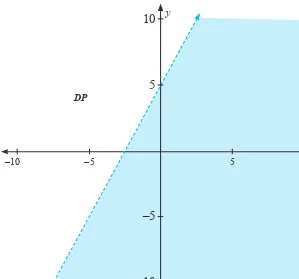
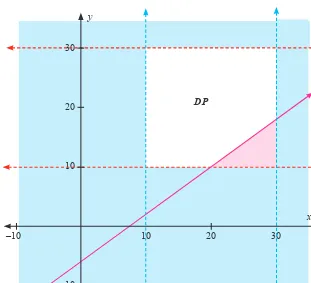
2.1 Pertidaksamaan Linear Dua Variabel
Bagian ini menjelaskan konsep pertidaksamaan linear dua variabel dan penerapannya dalam kehidupan sehari-hari. Siswa diajarkan untuk memodelkan situasi nyata menggunakan pertidaksamaan dan menemukan himpunan solusi. Melalui contoh, siswa belajar bagaimana menginterpretasikan hasil dalam konteks yang lebih luas dan memahami pentingnya batasan dalam pengambilan keputusan.
2.2 Program Linear
Di sini, siswa diperkenalkan pada masalah program linear dan metode penyelesaiannya. Mereka belajar tentang fungsi objektif dan bagaimana menentukan nilai maksimum atau minimum dalam konteks masalah nyata. Pembelajaran ini mendorong siswa untuk berpikir kritis dan kreatif dalam memecahkan masalah, serta menunjukkan tanggung jawab dalam analisis dan keputusan yang diambil.