DESAIN DAN ANALISIS ALGORITMA KOMPUTASI MATRIKS YANG MENGANDUNG MATRIKS TOEPLITZ DENGAN FFT
THEO PRATAMA NRP 5114 100 029 Dosen Pembimbing 1
Rully Soelaiman, S.Kom., M.Kom. Dosen Pembimbing 2
Ir. F.X. Arunanto, M.Sc. DEPARTEMEN INFORMATIKA
Fakultas Teknologi Informasi dan Komunikasi Institut Teknologi Sepuluh Nopember
DESAIN DAN ANALISIS ALGORITMA KOMPUTASI MATRIKS YANG MENGANDUNG MATRIKS TOEPLITZ DENGAN FFT
THEO PRATAMA NRP 5114 100 029 Dosen Pembimbing 1
Rully Soelaiman, S.Kom., M.Kom. Dosen Pembimbing 2
Ir. F.X. Arunanto, M.Sc. DEPARTEMEN INFORMATIKA
Fakultas Teknologi Informasi dan Komunikasi Institut Teknologi Sepuluh Nopember
DESIGN AND ANALYSIS OF MATRIX COMPUTATION ALGORITHM CONTAINING TOEPLITZ MATRIX STRUCTURE WITH FFT
THEO PRATAMA NRP 5114 100 029 Supervisor 1
Rully Soelaiman, S.Kom., M.Kom. Supervisor 2
Ir. F.X. Arunanto, M.Sc. INFORMATICS DEPARTMENT
Faculty of Information Technology Institut Teknologi Sepuluh Nopember Surabaya, 2018
DENGAN FFT
Nama : THEO PRATAMA
NRP : 5114 100 029
Departemen : Departemen Informatika FTIF-ITS Pembimbing I : Rully Soelaiman, S.Kom., M.Kom. Pembimbing II : Ir. F.X. Arunanto, M.Sc.
Abstrak
Diberikan suatu konfigurasi warna kucing melingkar sepanjang N dan banyaknya putaran komunikasi barisan kucing sebanyak K. Untuk setiap komunikasi, kucing-kucing tersebut berubah warna. Transformasi perubahan warna ini dimodelkan menjadi suatu matriks transformasi sebesar N × N tetapi banyaknya pemangkatan yaitu K mencapai 109 dan besarnya matriks transformasi mencapai 50000 sehingga algoritma perkalian secara umum dengan kompleksitasO(N3) dan pemangkatan matriks pada umumnya kurang cepat untuk menyelesaikan permasalahan ini. Pada permasalahan ini juga terdapat sifat khusus dimana matriks transformasi ini memiliki submatriks berjenis Matriks Toeplitz dan jika matriks ini dilakukan perkalian, matriks ini selalu konsisten menghasilkan matriks dengan struktur yang serupa.
Pada tugas akhir ini akan dirancang penyelesaian masalah dengan melakukan pemodelan masalah seperti yang sudah dijelaskan pada paragraf pertama. Matriks transformasi yang terbentuk akan dilakukan perkalian menggunakan konvolusi, Fast Fourier Transform, dan pemangkatan secara modular dalam penyelesaiannya.
Solusi yang dikembangkan berjalan dengan kompleksitas waktu O(N log N log K), dimana N merupakan besarnya matriks transformasi dan K merupakan besarnya pemangkatan
matriks. Solusi ini berhasil melakukan komputasi matriks dengan substruktur Matriks Toeplitz dengan sangat cepat dibandingkan dengan perkalian dan pemangkatan matriks secara umum.
Kata Kunci: konvolusi, Matriks Toeplitz, matriks transformasi, FFT
STRUCTURE WITH FFT
Name : THEO PRATAMA
NRP : 5114 100 029
Major : Informatics Department Faculty of IT-ITS Supervisor I : Rully Soelaiman, S.Kom., M.Kom. Supervisor II : Ir. F.X. Arunanto, M.Sc.
Abstract
Given a set configuration of cat’s color in circular line with length N and K which K is the amount of circular communication from the line of cats. For each communication, the color of cat will be transformed into a certain color. Transformation of these color will be modeled into a transformation matrix with size N × N and the amount of power K. K has upper bound constraint 109 and the the size of matrix will be as huge as 50000 so the naive algorithm with complexity O(N3) and general matrix exponentiation don’t fast enough to solve this problem. For problem, there is a specific behavior which is this matrix has a Toeplitz Matrix as a sub-matrix and if this matrix is multiplied together, this matrix will be consistent producing a matrix with same structure.
In this final project the writer will design and analyze a solution to solve the problem that stated in first paragraph. The transformation matrix will multiplied with convolution, Fast Fourier Transform, and modular exponent for the computation.
The developed solution run with complexity timeO(N log N log K) which N is a size of transformation matrix and K is size of the power of matrix. The solution show very fast performance than general matrix multiplication and exponentiation.
Keywords: convolution, Toeplitz Matrix, transformation matrix, FFT
Puji syukur penulis panjatkan kepada Tuhan Yang Maha Esa atas pimpinan, penyertaan, dan karunia-Nya sehingga penulis dapat menyelesaikan Tugas Akhir yang berjudul :
DESAIN DAN ANALISIS ALGORITMA KOMPUTASI MATRIKS YANG MENGANDUNG MATRIKS TOEPLITZ
DENGAN FFT
Penelitian Tugas Akhir ini dilakukan untuk memenuhi salah satu syarat meraih gelar Sarjana di Jurusan Teknik Informatika Fakultas Teknologi Informasi Institut Teknologi Sepuluh Nopember. Dengan selesainya Tugas Akhir ini diharapkan apa yang telah dikerjakan penulis dapat memberikan manfaat bagi perkembangan ilmu pengetahuan terutama di bidang teknologi informasi serta bagi diri penulis sendiri selaku peneliti.
Penulis mengucapkan terima kasih kepada semua pihak yang telah memberikan dukungan baik secara langsung maupun tidak langsung selama penulis mengerjakan Tugas Akhir maupun selama menempuh masa studi antara lain:
• Kedua orang tua dan keluarga penulis yang selalu mendoakan dan memberikan dukungan pada setiap langkah yang penulis lakukan dan dukungan selama pengerjaan Tugas Akhir. • Bapak Rully Soelaiman, S.Kom., M.Kom. selaku Dosen
Pembimbing yang telah banyak meluangkan waktu untuk memberikan ilmu, nasihat, motivasi, pandangan dan bimbingan kepada penulis baik selama penulis menempuh masa kuliah maupun selama pengerjaan Tugas Akhir ini.
• Bapak Ir. F.X. Arunanto, M.Sc. selaku dosen pembimbing yang telah memberikan ilmu dan masukan kepada penulis. • Teman-teman, Kakak-kakak dan Adik-adik administrator
Laboratorium Pemrograman 2 yang telah menjadi bagian keluarga penulis di Departemen Informatika ITS.
• Seluruh tenaga pengajar, asisten dosen, dan karyawan Departemen Informatika ITS yang telah memberikan ilmu dan waktunya demi berlangsungnya kegiatan belajar mengajar di Departemen Informatika ITS.
• Seluruh anggota competitive programming yang telah memberikan motivasi dalam belajar, ilmu, dan pengalaman kepada penulis.
• Seluruh teman penulis di Departemen Informatika ITS yang telah memberikan dukungan dan semangat kepada penulis selama penulis menyelesaikan Tugas Akhir ini.
• Pihak Bidikmisi yang telah membantu penulis agar dapat berkuliah di Departemen Informatika ITS dengan adanya dukungan finansial dan moral.
• Seluruh pihak-pihak lain yang tidak dapat disebutkan disini yang telah membantu selama berkuliah di Departemen Informatika ITS.
Penulis mohon maaf apabila masih ada kekurangan pada Tugas Akhir ini. Penulis juga mengharapkan kritik dan saran yang membangun untuk pembelajaran dan perbaikan di kemudian hari. Semoga melalui Tugas Akhir ini penulis dapat memberikan kontribusi dan manfaat yang sebaik-baiknya.
Surabaya, Januari 2018
SAMPUL . . . . i
LEMBAR PENGESAHAN . . . . viii
ABSTRAK . . . . ix
ABSTRACT . . . . xi
KATA PENGANTAR . . . . xiii
DAFTAR ISI . . . . xv
DAFTAR TABEL . . . . xix
DAFTAR GAMBAR . . . xxiii
DAFTAR KODE SUMBER . . . xxvii
BAB I PENDAHULUAN . . . . 1 1.1 Latar Belakang . . . 1 1.2 Rumusan Masalah . . . 3 1.3 Batasan Masalah . . . 3 1.4 Tujuan . . . 4 1.5 Manfaat . . . 4 1.6 Metodologi . . . 4 1.7 Sistematika Penulisan . . . 5
BAB II DASAR TEORI . . . 7
2.1 Deskripsi Permasalahan . . . 7
2.2 Deskripsi Permasalahan Versi Mudah (COLORCAT ) 8 2.3 Deskripsi Permasalahan Versi Sulit (BLCATS) . . 10
2.4 Deskripsi Umum . . . 11
2.4.1 Matriks Toeplitz . . . 11
2.4.2 Matriks Transformasi . . . 12
2.4.3 Pemangkatan Modular . . . 12
2.4.4 Transformasi Fourier Diskrit . . . 12
2.4.5 Inversi Transformasi Fourier Diskrit . . . . 13
2.4.6 Transformasi Fourier Cepat . . . 13
2.4.7 Roots of Unity . . . 15
2.4.8 Konvolusi . . . 16
2.4.9 Polinomial . . . 17
2.4.10 Optimasi FFT untuk Komputasi Bilangan Real . . . 17
2.4.11 Representasi Titik Polinomial . . . 17
2.4.12 Perkalian Polinomial dengan FFT . . . 18
2.5 Strategi Penyelesaian Permasalahan BLCATS . . . 19
2.5.1 Pendefinisan Transformasi dari Masalah dan Pengkodean Konfigurasi . . . 20
2.5.2 Perumusan Transformasi . . . 22
2.5.3 Pembangkitan Matriks Transformasi . . . . 29
2.5.4 Struktur Matriks Toeplitz dalam Matriks Transformasi . . . 33
2.5.5 Konvolusi pada Perkalian Matriks Transformasi . . . 35
2.5.6 Pemangkatan dan Perkalian Akhir Matriks Transformasi . . . 43
BAB III DESAIN . . . . 45
3.1 Desain Umum Sistem . . . 45
3.2 Desain Class Bilangan Kompleks (cpx) . . . . 45
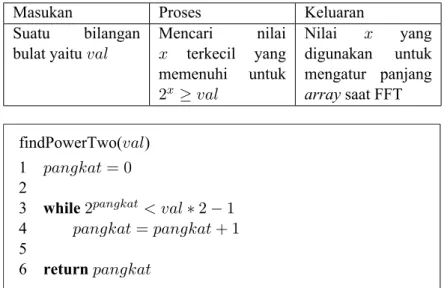
3.3 Desain Fungsi Mencari Nilai Pangkat Dua Terdekat (f indP owerT wo) . . . . 47
3.4 Desain Class Fourier Transform (F F T ) . . . . 47
3.5 Desain Class Matriks yang Memiliki Submatriks Matriks Toeplitz (SpecialM atrix) . . . . 55
3.6 Desain Fungsi Pembangkitan Matriks Transformasi (generateT ransf ormationM atrix) 56 3.7 Desain Fungsi Pemangkatan Matriks (exponent) . 58 3.8 Desain Fungsi Pengkodean Warna Menjadi Angka (encodeColor) . . . . 58
3.9 Desain Fungsi Solve . . . 65
BAB IV IMPLEMENTASI . . . . 69
4.2 Rancangan Data . . . 69
4.2.1 Data Masukan . . . 70
4.2.2 Data Keluaran . . . 70
4.3 Implementasi Algoritma . . . 70
4.3.1 Header yang Diperlukan . . . . 70
4.3.2 Pre-Processor . . . 71
4.3.3 Variabel Global . . . 72
4.3.4 Implementasi Fungsi Main . . . 72
4.3.5 Implementasi Fungsi FindPowerTwo . . . 74
4.3.6 Implementasi Class cpx . . . 75
4.3.7 Implementasi Class FFT . . . 76
4.3.8 Implementasi Class SpecialMatrix . . . 84
4.3.9 Implementasi Fungsi GenerateTransformationMatrix . . . 94
4.3.10 Implementasi Fungsi Exponent . . . 97
4.3.11 Implementasi Fungsi Solve . . . 98
4.3.12 Implementasi Fungsi EncodeColor . . . 101
BAB V UJI COBA DAN EVALUASI . . . 103
5.1 Lingkungan Uji Coba . . . 103
5.2 Uji Coba Kebenaran . . . 104
5.3 Uji Coba Kinerja . . . 105
BAB VI KESIMPULAN . . . 107
6.1 Kesimpulan . . . 107
6.2 Saran . . . 108
DAFTAR PUSTAKA . . . 109
Lampiran A HASIL UJI COBA PADA SITUS SPOJ SEBANYAK 12 KALI . . . 111
Lampiran B MATRIKS TRANSFORMASI YANG TERBENTUK UNTUK N = 2 hingga N = 15 . . . 113
Lampiran C TABEL UJI COBA PEFORMA
PERKALIAN MATRIKS DENGAN
ALGORITMA NAIVE UNTUK N = 10
HINGGA N = 1000 . . . 121
Lampiran D TABEL UJI COBA PEFORMA
PERKALIAN MATRIKS DENGAN FFT
UNTUK N = 10 HINGGA N = 1000 . . . 127 BIODATA PENULIS . . . 133
Tabel 2.1 Contoh Konfigurasi Warna Kucing Setelah K Putaran . . . 9 Tabel 2.2 Contoh Transformasi Warna Kucing untuk
Satu Putaran Secara Bertahap . . . 9 Tabel 2.3 Pengkodean Warna untuk Barisan Kucing
⟨GRGRG⟩ . . . 21 Tabel 2.4 Hasil Transformasi untuk Semua
Kemungkinan x dan y untuk f (x, y) . . . . . 21 Tabel 2.5 Tabel Konvolusi Hasil Pre-Komputasi . . . . 41 Tabel 2.6 Tabel Hasil Perkalian dalam Representasi Satu
Baris dan Dua Kolom Awal . . . 43 Tabel 3.1 Masukan, Proses, dan Keluaran Fungsi
Mencari Nilai Pangkat Dua Terdekat . . . 48 Tabel 3.2 Masukan, Proses, dan Keluaran Fungsi Init
Class FFT . . . 50 Tabel 3.3 Masukan, Proses, dan Keluaran Fungsi Init
Class FFT . . . 52 Tabel 3.4 Masukan, Proses, dan Keluaran Fungsi
Transform Class FFT . . . 52 Tabel 3.5 Masukan, Proses, dan Keluaran Fungsi
MassFFT Class FFT . . . 52 Tabel 3.6 Masukan, Proses, dan Keluaran Fungsi
Pembangkitan Matriks Transformasi Class FFT 58 Tabel 3.7 Masukan, Proses, dan Keluaran Fungsi
Pemangkatan Matriks Transformasi . . . 64 Tabel 3.8 Masukan, Proses, dan Keluaran Fungsi Encode
Color . . . 65 Tabel 4.1 Penjelasan Variabel Global . . . 72 Tabel 4.2 Penjelasan Variabel Fungsi main (1) . . . 73
Tabel 4.3 Penjelasan Variabel Fungsi main (2) . . . 74 Tabel 4.4 Penjelasan Variabel Fungsi findPowerTwo . . 75 Tabel 4.5 Penjelasan Variabel Atribut Class cpx . . . 76 Tabel 4.6 Penjelasan Variabel Atribut Class FFT . . . . 77 Tabel 4.7 Penjelasan Variabel Fungsi bitReverse Class FFT 79 Tabel 4.8 Penjelasan Variabel Fungsi transform Class FFT 80 Tabel 4.9 Penjelasan Variabel Fungsi MassFFT Class
FFT (1) . . . 81 Tabel 4.10 Penjelasan Variabel Fungsi MassFFT Class
FFT (2) . . . 82 Tabel 4.11 Penjelasan Variabel Fungsi MassIFFT Class FFT 83 Tabel 4.12 Penjelasan Variabel Atribut Class SpecialMatrix 85 Tabel 4.13 Penjelasan Variabel Fungsi Operator * Class
SpecialMatrix (1) . . . 90 Tabel 4.14 Penjelasan Variabel Fungsi Operator * Class
SpecialMatrix (2) . . . 91 Tabel 4.15 Penjelasan Variabel Fungsi Operator * Class
SpecialMatrix (3) . . . 92 Tabel 4.16 Penjelasan Variabel Fungsi Operator * Class
SpecialMatrix (4) . . . 93 Tabel 4.17 Penjelasan Variabel Fungsi Operator * Class
SpecialMatrix (5) . . . 94
Tabel 4.18 Penjelasan Variabel Fungsi
GenerateTransformationMatrix (1) . . . 96
Tabel 4.19 Penjelasan Variabel Fungsi
GenerateTransformationMatrix (2) . . . 97 Tabel 4.20 Penjelasan Variabel Fungsi Exponent . . . 98 Tabel 4.21 Penjelasan Variabel Fungsi Solve . . . 101 Tabel 4.22 Penjelasan Variabel Fungsi EncodeColor . . . 102 Tabel 5.1 Kecepatan Maksimal, Minimal, dan Rata-Rata
dari Hasil Uji Coba Pengumpulan 12 Kali pada Situs Pengujian Daring Spoj . . . 104
Tabel C.1 Uji Coba Peforma Perkalian Matriks dengan Algoritma Naive (1) . . . 121 Tabel C.2 Uji Coba Peforma Perkalian Matriks dengan
Algoritma Naive (2) . . . 122 Tabel C.3 Uji Coba Peforma Perkalian Matriks dengan
Algoritma Naive (3) . . . 123 Tabel C.4 Uji Coba Peforma Perkalian Matriks dengan
Algoritma Naive (4) . . . 124 Tabel C.5 Uji Coba Peforma Perkalian Matriks dengan
Algoritma Naive (5) . . . 125 Tabel D.1 Uji Coba Peforma Perkalian Matriks dengan
FFT (1) . . . 127 Tabel D.2 Uji Coba Peforma Perkalian Matriks dengan
FFT (2) . . . 128 Tabel D.3 Uji Coba Peforma Perkalian Matriks dengan
FFT (3) . . . 129 Tabel D.4 Uji Coba Peforma Perkalian Matriks dengan
FFT (4) . . . 130 Tabel D.5 Uji Coba Peforma Perkalian Matriks dengan
Gambar 2.1 Ilustrasi Struktur Matriks Toeplitz . . . 11 Gambar 2.2 Properti Roots of Unity pada FFT . . . . 16 Gambar 2.3 Ilustrasi Perkalian dengan FFT pada
Polinomial . . . 19 Gambar 2.4 Bagian Matriks Toeplitz pada Matriks
Transformasi . . . 40 Gambar 3.1 Pseudocode Fungsi Main . . . . 46 Gambar 3.2 Pseudocode Class Bilangan Kompleks cpx (1) 46 Gambar 3.3 Pseudocode Class Bilangan Kompleks cpx (2) 47 Gambar 3.4 Pseudocode Fungsi Pencari Pangkat Dua
Terdekat . . . 48 Gambar 3.5 Pseudocode Class FFT . . . . 50 Gambar 3.6 Pseudocode Fungsi Init Class FFT . . . 51 Gambar 3.7 Pseudocode Fungsi bitReverse Class FFT . . 51 Gambar 3.8 Pseudocode Fungsi Transform Class FFT . . 53 Gambar 3.9 Pseudocode Fungsi MassFFT Class FFT (1) 53 Gambar 3.10 Pseudocode Fungsi MassFFT Class FFT (2) 54 Gambar 3.11 Pseudocode Fungsi MassIFFT Class FFT (1) 54 Gambar 3.12 Pseudocode Fungsi MassIFFT Class FFT (2) 55 Gambar 3.13 Pseudocode Class SpecialMatrix . . . . 57 Gambar 3.14 Pseudocode Fungsi Constructor (1) Class
SpecialMatrix . . . 57 Gambar 3.15 Pseudocode Fungsi Constructor (2) Class
SpecialMatrix . . . 58 Gambar 3.16 Pseudocode Fungsi Override Operator *
Class SpecialMatrix (1) . . . 59 Gambar 3.17 Pseudocode Fungsi Override Operator *
Class SpecialMatrix (2) . . . 60
Gambar 3.18 Pseudocode Fungsi Override Operator * Class SpecialMatrix (3) . . . 61 Gambar 3.19 Pseudocode Fungsi Pembangkitan Matriks
Transformasi (1) . . . 62 Gambar 3.20 Pseudocode Fungsi Pembangkitan Matriks
Transformasi (2) . . . 63 Gambar 3.21 Pseudocode Fungsi Pemangkatan Matriks
Transformasi . . . 64 Gambar 3.22 Pseudocode Fungsi Encode Color . . . . 65 Gambar 3.23 Pseudocode Fungsi Solve (1) . . . . 66 Gambar 3.24 Pseudocode Fungsi Solve (2) . . . . 67 Gambar 5.1 Hasil Umpan Balik Solusi pada Daring SPOJ
dengan Waktu Terendah . . . 104 Gambar 5.2 Perbandingan Kinerja Perkalian Matriks, A
Perkalian dengan FFT dan B Perkalian dengan Algoritma Naive . . . 106 Gambar 5.3 Perbandingan Kinerja A dengan Optimasi
dan B Tanpa Optimasi massF F T untuk K = 109 . . . 106 Gambar A.1 Hasil Pengumpulan Kode Sumber Sebanyak
12 Kali . . . 111 Gambar B.1 Matriks Transformasi untuk N = 2 . . . 113 Gambar B.2 Matriks Transformasi untuk N = 3 . . . 113 Gambar B.3 Matriks Transformasi untuk N = 4 . . . 113 Gambar B.4 Matriks Transformasi untuk N = 5 . . . 114 Gambar B.5 Matriks Transformasi untuk N = 6 . . . 114 Gambar B.6 Matriks Transformasi untuk N = 7 . . . 114 Gambar B.7 Matriks Transformasi untuk N = 8 . . . 115 Gambar B.8 Matriks Transformasi untuk N = 9 . . . 115 Gambar B.9 Matriks Transformasi untuk N = 10 . . . . 116 Gambar B.10 Matriks Transformasi untuk N = 11 . . . . 116 Gambar B.11 Matriks Transformasi untuk N = 12 . . . . 117 Gambar B.12 Matriks Transformasi untuk N = 13 . . . . 117
Gambar B.13 Matriks Transformasi untuk N = 14 . . . . 118 Gambar B.14 Matriks Transformasi untuk N = 15 . . . . 119
Kode Sumber 4.1 Header yang diperlukan . . . . 71 Kode Sumber 4.2 Pre-processor yang diperlukan . . . 71 Kode Sumber 4.3 Variabel global yang diperlukan . . . . 72 Kode Sumber 4.4 Variabel global FFT dideklarasikan
setelah definisi Class FFT . . . 72 Kode Sumber 4.5 Fungsi main (1) . . . 72 Kode Sumber 4.6 Fungsi main (2) . . . 73 Kode Sumber 4.7 Fungsi findPowerTwo . . . 74 Kode Sumber 4.8 Deklarasi Class cpx (1) . . . 75 Kode Sumber 4.9 Deklarasi Class cpx (2) . . . 76 Kode Sumber 4.10 Deklarasi Class FFT (1) . . . 76 Kode Sumber 4.11 Deklarasi Class FFT (2) . . . 77 Kode Sumber 4.12 Deklarasi Fungsi Init Class FFT (1) . . 77 Kode Sumber 4.13 Deklarasi Fungsi Init Class FFT (2) . . 78 Kode Sumber 4.14 Deklarasi Fungsi BitReverse Class FFT 78 Kode Sumber 4.15 Deklarasi Fungsi Transform Class FFT
(1) . . . 79 Kode Sumber 4.16 Deklarasi Fungsi Transform Class FFT
(2) . . . 80 Kode Sumber 4.17 Deklarasi Fungsi MassFFT Class FFT (1) 80 Kode Sumber 4.18 Deklarasi Fungsi MassFFT Class FFT (2) 81 Kode Sumber 4.19 Deklarasi Fungsi MassIFFT Class FFT 83 Kode Sumber 4.20 Deklarasi Class SpecialMatrix (1) . . . 84 Kode Sumber 4.21 Deklarasi Class SpecialMatrix (2) . . . 85 Kode Sumber 4.22 Deklarasi Fungsi Constructor (1) Class
SpecialMatrix . . . 86 Kode Sumber 4.23 Deklarasi Fungsi Constructor (2) Class
SpecialMatrix . . . 86
Kode Sumber 4.24 Deklarasi Fungsi Operator * Class SpecialMatrix (1) . . . 87 Kode Sumber 4.25 Deklarasi Fungsi Operator * Class
SpecialMatrix (2) . . . 88 Kode Sumber 4.26 Deklarasi Fungsi Operator * Class
SpecialMatrix (3) . . . 89 Kode Sumber 4.27 Deklarasi Fungsi Operator * Class
SpecialMatrix (4) . . . 89 Kode Sumber 4.28 Fungsi GenerateTransformationMatrix
(1) . . . 94 Kode Sumber 4.29 Fungsi GenerateTransformationMatrix
(2) . . . 95 Kode Sumber 4.30 Fungsi GenerateTransformationMatrix
(3) . . . 96 Kode Sumber 4.31 Fungsi Exponent (1) . . . 97 Kode Sumber 4.32 Fungsi Exponent (2) . . . 98 Kode Sumber 4.33 Fungsi Solve (1) . . . 99 Kode Sumber 4.34 Fungsi Solve (2) . . . 100 Kode Sumber 4.35 Fungsi Solve (3) . . . 101 Kode Sumber 4.36 Fungsi EncodeColor (1) . . . 101 Kode Sumber 4.37 Fungsi EncodeColor (2) . . . 102
Pada bab ini akan dijelaskan latar belakang, rumusan masalah, batasan masalah, tujuan, metodologi dan sistematika penulisan Tugas Akhir.
1.1 Latar Belakang
Matriks Toeplitz adalah suatu struktur matriks spesial dimana diagonalnya sama dengan penurunan dari kiri ke kanan bersifat konstan. Pekalian suatu matriks non Toeplitz memiliki kompleksitas O(N3) [1]. Pada Matriks Toeplitz murni, perkalian dari Matriks Toeplitz dapat diturunkan kompleksitasnya dengan membawa perhitungan Matriks Toeplitz ke dalam bentuk frekuensi, di mana perkalian dari Matriks Toeplitz dapat menggunakan prinsip perkalian polinomial dengan Fast Fourier Transform menjadi O(N log N) [2]. Penulis mencoba mengaplikasikan algoritma ini agar dapat digunakan untuk matriks lain yang memiliki submatriks Matriks Toeplitz, tidak hanya Matriks Toeplitz murni.
Aplikasi dari penggunaan komputasi Matriks Toeplitz salah satunya adalah penyelesaian dari permasalahan yang terdapat pada daring SPOJ Klasik 24370 berjudul “Magical Colourful Cats (Hard)”1yang pada tahapan komputasinya ternyata perlu dilakukan
pemodelan masalah kedalam bentuk matriks transformasi yang membutuhkan komputasi pemangkatan matriks yang memiliki submatriks Matriks Toeplitz dengan dimensi yang besar dengan cepat. Latar belakang dari permasalahan ini mengangkat permasalahan untuk melakukan perhitungan N kucing dengan
1www.spoj.com/problems/BLCATS 1
N merupakan bilangan bulat antara 1 sampai 50000 dengan konfigurasi N buah simbol yang merepresentasikan suatu warna kucing dari V0 hingga VN−1 setelah K putaran transformasi
dengan K merupakan bilangan bulat antara 1 hingga 109. Suatu warna kucing Vi disimbolkan dengan salah satu dari
⟨R, W, G⟩. Suatu simbol Vi mod N akan bertransformasi dengan
simbol V(i+1) mod N dan seterusnya hingga simbol VN−1 akan
bertransformasi dengan V0 yang merupakan makna dari satu
putaran siklis transformasi. Untuk setiap simbol warna kucing Vi mod N bertransformasi dengan simbol warna kucing Vi+1
mod N membuat simbol warna kucing Vi mod N dan Vi+1
mod N ini berubah menjadi suatu simbol warna yang belum muncul dari kedua simbol kucing tersebut, tetapi apabila kedua simbol warna kucing ini memiliki simbol yang sama maka tidak terjadi perubahan simbol.
Penulis akan mencoba menyelesaikan permasalahan ini dengan melakukan pemodelan transformasi pada permasalahan menjadi bentuk persamaan aljabar linear berupa matriks transformasi. Penulis menemukan bahwa matriks transformasi ini sangat besar dan tidak dapat di selesaikan dengan algoritma sederhana. Selain itu, setelah diteliti oleh penulis, matriks transformasi ini mengandung suatu struktur submatriks Matriks Toeplitz. Penulis akan mencoba untuk melakukan komputasi matriks transformasi ini secara efisien dengan suatu pendekatan yang lain.
Hasil tugas akhir ini diharapkan dapat menentukan algoritma dan struktur data yang tepat untuk dapat menyelesaikan permasalahan di atas dengan optimal dan diharapkan dapat memberikan kontribusi pada perkembangan ilmu pengetahuan dan teknologi informasi.
1.2 Rumusan Masalah
Rumusan masalah yang diangkat dalam Tugas Akhir ini adalah sebagai berikut:
1. Bagaimana menganalisis dan menentukan algoritma dan struktur data yang tepat dalam menyelesaikan permasalahan pemodelan dan komputasi matriks transformasi perhitungan konfigurasi N simbol setelah K putaran transformasi? 2. Bagaimana mengimplementasi algoritma dan struktur
data yang digunakan dalam menyelesaikan permasalahan pemodelan dan komputasi matriks transformasi perhitungan konfigurasi N simbol setelah K putaran transformasi? 3. Bagaimana hasil dari kinerja algoritma dan struktur data yang
digunakan dalam menyelesaikan permasalahan pemodelan dan komputasi matriks transformasi perhitungan konfigurasi N simbol setelah K putaran transformasi?
1.3 Batasan Masalah
Permasalahan yang dibahas pada Tugas Akhir ini memiliki beberapa batasan, yaitu sebagai berikut:
1. Implementasi algoritma menggunakan bahasa pemrograman C++.
2. Uji coba kebenaran dilakukan dengan uji submission ke situs penilaian daring SPOJ.
3. Batas maksimum jumlah simbol warna kucing (N ) adalah 50000 kucing.
4. Batas maksimum jumlah putaran transformasi (K) adalah 109 putaran.
5. Dataset yang digunakan untuk pengujian kinerja algoritma adalah dataset pada permasalahan 24370 berjudul Magical Colourful Cats (Hard).
1.4 Tujuan
Tujuan dari Tugas Akhir ini adalah sebagai berikut:
1. Melakukan analisis dan desain algoritma untuk menyelesaikan permasalahan pemodelan dan komputasi matriks transformasi perhitungan konfigurasi N simbol setelah K putaran transformasi siklis.
2. Mengevaluasi hasil dari kinerja algoritma untuk menyelesaikan permasalahan pemodelan dan komputasi matriks transformasi perhitungan konfigurasi N simbol setelah K putaran transformasi siklis.
1.5 Manfaat
Tugas akhir ini diharapkan dapat membantu menyelesaikan permasalahan komputasi perhitungan konfigurasi N simbol untuk K putaran transformasi siklis khususnya dalam pemodelan permasalahan dan komputasi matriks dengan submatriks Matriks Toeplitz.
1.6 Metodologi
Metodologi yang digunakan dalam pengerjaan Tugas Akhir ini adalah sebagai berikut:
1. Penyusunan proposal Tugas Akhir
Pada tahap ini dilakukan penyusunan proposal Tugas Akhir yang berisi permasalahan dan gagasan solusi yang akan diteliti pada permasalahan klasik SPOJ 24730 Magical Colorful Cats (Hard).
2. Studi literatur
Pada tahap ini dilakukan pencarian informasi dan studi literatur mengenai pengetahuan atau metode yang dapat digunakan dalam penyelesaian masalah. Informasi
didapatkan dari materi-materi yang berhubungan dengan algoritma yang digunakan untuk penyelesaian permasalahan ini, materi-materi tersebut didapatkan dari buku, jurnal, maupun internet.
3. Desain
Pada tahap ini dilakukan desain rancangan algoritma yang digunakan dalam solusi untuk pemecahan permasalahan klasik SPOJ 24730 Magical Colorful Cats (Hard).
4. Implementasi perangkat lunak
Pada tahap ini dilakukan implementasi atau realiasi dari rancangan desain algoritma yang telah dibangun pada tahap desain ke dalam bentuk program.
5. Uji coba dan evaluasi
Pada tahap ini dilakukan uji coba kebenaran implementasi. Pengujian kebenaran dilakukan pada sistem penilaian daring SPOJ sesuai dengan masalah yang dikerjakan untuk diuji apakah luaran dari program telah sesuai.
6. Penyusunan buku Tugas Akhir
Pada tahap ini dilakukan penyusunan buku Tugas Akhir yang berisi dokumentasi hasil pengerjaan Tugas Akhir.
1.7 Sistematika Penulisan
Berikut adalah sistematika penulisan buku Tugas Akhir ini: 1. BABI: PENDAHULUAN
Bab ini berisi latar belakang, rumusan masalah, batasan masalah, tujuan, metodologi dan sistematika penulisan Tugas Akhir.
2. BAB II: DASAR TEORI
Bab ini berisi dasar teori mengenai permasalahan dan algoritma penyelesaian yang digunakan dalam Tugas Akhir 3. BAB III: DESAIN
digunakan dalam penyelesaian permasalahan. 4. BAB IV: IMPLEMENTASI
Bab ini berisi implementasi berdasarkan desain algortima yang telah dilakukan pada tahap desain.
5. BAB V: UJI COBA DAN EVALUASI
Bab ini berisi uji coba dan evaluasi dari hasil implementasi yang telah dilakukan pada tahap implementasi.
6. BAB VI: KESIMPULAN
Bab ini berisi kesimpulan yang didapat dari hasil uji coba yang telah dilakukan.
Pada bab ini akan dijelaskan mengenai dasar teori yang menjadi dasar pengerjaan Tugas Akhir ini.
2.1 Deskripsi Permasalahan
Diberikan N simbol yang menyatakan urutan warna suatu kucing dari posisi 1 sampai N dengan konfigurasi dari N simbol tersebut dinyatakan dalam vektor ⃗V =⟨V0, V1, Vi, . . . , VN−1⟩ dengan 0 ≤
i < N dan Vi ∈ {R, G, W }. Simbol R, G, dan W menyatakan
warna dari kucing yaitu merah, hijau, dan putih.
Kucing-kucing tersebut berada dalam barisan yang tersusun secara melingkar dan mereka akan berkomunikasi ke kucing tepat di sebelah kanannya. Kucing Vi akan berkomunikasi dengan kucing
V(i+1) mod N dan seterusnya hingga kucing terakhir yaitu VN−1
akan berkomunikasi dengan VN mod N.
Untuk kucing Vi yang melakukan komunikasi dengan kucing
V(i+1) mod N, kedua kucing ini akan mengalami perubahan warna. Warna kucing Vi dan V(i+1) mod N akan berubah warna menjadi
suatu warna yang belum muncul dari kedua kucing tersebut apabila warna dari kedua kucing tersebut berbeda, jika warna dari kedua kucing tersebut sama maka tidak akan terjadi perubahan warna. Secara matematis perubahan warna ini dapat diformulasikan menjadi persamaan 2.1.
Vi= V(i+1) mod N = {R, G, W }
−{Vi, V(i+1) mod N} , jika
Vi ̸= V(i+1) mod N V(i+1) mod N , jika
Vi = V(i+1) mod N
(2.1) Kucing-kucing tersebut akan melakukan komunikasi sebanyak K putaran. Komunikasi telah mengalami satu putaran komunikasi jika kucing V0 berkomunikasi dengan V1, Vi telah berkomunikasi
dengan Vi+1, hingga VN−1 berkomunikasi kembali dengan V0.
Diberikan N konfigurasi warna kucing dan K merupakan jumlah putaran komunikasi yang dilakukan. Tentukan konfigurasi akhir warna kucing-kucing tersebut.
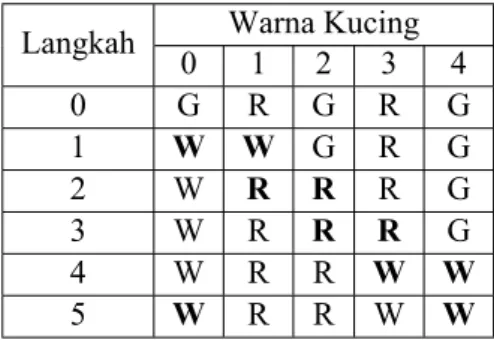
Sebagai contoh, Tabel 2.1 merupakan contoh untuk K = 4 dan N = 5 dengan konfigurasi awal kelima kucing tersebut adalah ⟨GRGRG⟩. Pada setiap putarannya, kucing akan saling berkomunikasi ke kucing sebelah kanannya hingga kembali ke posisi awal yaitu kucing ke-0. Tabel 2.2 menunjukkan perubahan warna kucing untuk satu putaran dari konfigurasi ⟨GRGRG⟩ secara bertahap. Dari Tabel 2.2 terlihat bahwa transformasi untuk satu putaran dari kucing dengan konfigurasi ⟨GRGRG⟩ adalah ⟨W RRW W ⟩. Maka untuk konfigurasi akhir dari kucing yang telah mengalami K = 4 putaran dapat dilihat dari Tabel 2.1 adalah ⟨W W W GW ⟩.
2.2 Deskripsi Permasalahan Versi Mudah
(COLORCAT)
Besarnya batasan permasalahan ini yaitu K = 30000 dan N = 20000 dengan batas waktu 1 detik untuk setiap kasus uji. Cara mencari konfigurasi akhir dengan teknik brute force tidak memadai jika tanpa optimisasi. Optimisasi dapat dilakukan dengan cara
Tabel 2.1 Contoh Konfigurasi Warna Kucing Setelah K Putaran K Warna Kucing ke-i
0 1 2 3 4 0 G R G R G 1 W R R W W 2 R W W W R 3 R R G W R 4 W W W G W
Tabel 2.2 Contoh Transformasi Warna Kucing untuk Satu Putaran Secara Bertahap
Langkah Warna Kucing
0 1 2 3 4 0 G R G R G 1 W W G R G 2 W R R R G 3 W R R R G 4 W R R W W 5 W R R W W
melakukan kompresi dari besarnya N menjadi N′ sehingga solusi brute force nantinya memiliki kompleksitas akhir O(N′ × K). Tantangan dari solusi ini adalah pada bagian kompresi besarnya N agar kompleksitas akhir kurang dari 108 untuk lolos dari time limit exceeded. Untuk melakukan kompresi, penulis menggunakan metode memoisasi dengan pre-komputasi seluruh kemungkinan transformasi untuk suatu partisi barisan kucing sepanjang L. Untuk jumlah partisi dengan dengan jumlah kucing adalah N menjadi beberapa bagian sepanjang L adalah N′ = N /L sehingga nantinya brute force dilakukan terhadap hasil kompresi kedalam partisi-partisi ini. Solusi permasalahan dari versi mudah tidak menjadi bahasan dalam tugas akhir ini.
2.3 Deskripsi Permasalahan Versi Sulit (BLCATS)
Besarnya batasan permasalahan ini yaitu K = 109dan N = 50000
dengan batas waktu 5-10 detik untuk setiap kasus uji. Cara mencari konfigurasi akhir dengan menggunakan teknik brute force maupun optimized brute force dengan teknik kompresi dan pre-komputasi seperti permasalahan versi mudah tentu sangat tidak memadai. Melalui riset ini, penulis menemukan bahwa transformasi ini dapat dimodelkan dalam suatu matriks transformasi yang disimbolkan dengan M t. Permasalahan ini dapat dibawa ke dalam bentuk persamaan matematis ⃗V′ = ⃗V × MtK dengan ⃗V merupakan konfigurasi awal dari warna kucing sejumlah N , ⃗V′ merupakan konfigurasi akhir dari kucing setelah mengalami K putaran dan M t merupakan matriks transformasi dari permasalahan ini. Permasalahan sebenarnya muncul ketika melakukan penyelesaian
⃗
V′ = ⃗V × MtKdengan pemangkatan dari M t itu sendiri memiliki dimensi yang besar yaitu M t dapat berdimensi N×N dan besarnya pemangkatan yaitu K = 109.
Penulis menemukan bahwa matriks transformasi M t dari permasalahan merupakan suatu matriks khusus. Matriks tersebut
TN = T0,0 T0,1 . T0,N−2 T0,N−1 T1,0 . . . T0,N−2 . . . . . TN−2,0 . . . T0,1 TN−1,0 TN−2,0 . T1,0 T0,0
Gambar 2.1 Ilustrasi Struktur Matriks Toeplitz
memiliki dimensi N × N dengan submatriks Mt pada bagian diagonal kanan bawah dengan dimensi N − 1 × N − 1 memenuhi struktur Matriks Toeplitz sehingga dapat dikatakan matriks M t merupakan matriks yang memiliki submatriks berjenis Matriks Toeplitz khususnya pada bagian diagonal kanan bawah. Matriks ini juga memiliki sifat khusus yang setelah dilakukan perkalian pada setiap tahapannya selalu menghasilkan matriks berjenis Matriks Toeplitz secara konsisten.
2.4 Deskripsi Umum
Pada subbab ini akan dijelaskan mengenai deskripsi-deskripsi umum yang terdapat pada tugas akhir ini.
2.4.1 Matriks Toeplitz
Matriks Toeplitz merupakan suatu matriks yang hasil penurunan diagonal dari kiri ke kanan adalah sama. Jika TN merupakan
Matriks Toeplitz dengan dimensi N×N dan Ti,jmerupakan elemen
dari matriks T pada posisi i, j maka Ti,j = Ti+1,j+1dengan 0 ≤
i, j < N . Gambar 2.1 merupakan gambaran dari struktur suatu Matriks Toeplitz yang memiliki dimensi N× N.
2.4.2 Matriks Transformasi
Matriks transformasi secara umum merupakan matriks yang dilihat sebagai transformasi yang memetakan x padaRnke dalam y pada Rm[3]. Pada kasus permasalahan ini matriks transformasi M
takan
memetakan ⃗V ke dalam konfigurasi akhir ⃗V′ untuk satu putaran komunikasi dan dinyatakan sebagai Mt : ⃗V → ⃗V′. Jika ⃗V
memiliki dimensi N maka ⃗V′ memiliki dimensi N juga sehingga Mt:RN → RN untuk dimensi Mtadalah N× N [3].
2.4.3 Pemangkatan Modular
Pemangkatan modular merupakan teknik untuk memangkatkan suatu bilangan x pangkat y dalam modulus p atau dinyatakan dalam xy mod p. Pemangkatan modular ini memiliki kompleksitas O(log N) dengan cara merubah bilangan pemangkat yaitu y menjadi basis biner lalu dilakukan perkalian bertahap [4].
2.4.4 Transformasi Fourier Diskrit
Transformasi fourier diskrit merupakan transformasi dari deret x0, x1, x2, . . . , xN−1 menjadi deret bilangan
kompleks X0, X1, X2, . . . , XN−1 dinyatakan sebagai
Xk =
∑N−1
n=0 xne−i2πkn/N. Transformasi Fourier digunakan
dalam melakukan analisa dari kejadian berulang. Transformasi Fourier melakukan transformasi domain waktu ke domain frekuensi [2].
Transformasi Fourier Diskrit ini digunakan dalam melakukan transformasi polinomial dari representasi koefisien menjadi representasi titik agar dapat dilakukan perkalian dengan cepat. Perkalian polinomial dalam representasi koefisien adalah O(N2) sedangkan pada representasi titik hanya membutuhkan O(N ).
2.4.5 Inversi Transformasi Fourier Diskrit
Inversi Transformasi Fourier Diskrit merupakan transformasi yang mengembalikan hasil dari transformasi fourier pada domain frekuensi menjadi domain waktu kembali [2]. Inversi dari Transformasi Fourier dinyatakan sebagai xk=
∑N−1
n=0 Xnei2πkn/N.
Inversi Transformasi Fourier Diskrit ini akan mengembalikan deret bilangan kompleks pada domain frekuensi menjadi domain waktu kembali. Pada perkalian polinomial, inversi dari Transformasi Fourier dilakukan untuk merubah representasi titik dari polinomial setelah dilakukan perkalian secara O(N) menjadi bentuk polinomial dengan representasi koefisien kembali [5].
2.4.6 Transformasi Fourier Cepat
Transformasi Fourier Cepat merupakan algoritma untuk melakukan Transformasi Fourier Diskrit secara cepat yang ditemukan oleh Cooley-Tukey. Transformasi Fourier Cepat atau biasa disebut dengan FFT (Fast Fourier Transform) [6]. FFT memungkinkan proses Transformasi Fourier berjalan dengan kompleksitas O(N log N).
Transformasi Fourier Cepat memiliki dua pendekatan dalam memecah masalah menjadi sub-masalah. Salah satunya adalah desimasi terhadap waktu dan desimasi terhadap frekuensi. Pada desimasi terhadap waktu, pemecahan masalah didasari atas memecah permasalahan menjadi dua yaitu deret sampel saat waktu ganjil dan saat waktu genap. Pada desimasi terhadap frekuensi, pemecahan masalah didasari atas memecah permasalahan menjadi dua yaitu deret waktu setengah awal dan setengah akhir [2]. Berikut adalah FFT dengan desimasi terhadap waktu yang membutuhkan pengurutan secara bit reverse terlebih dahulu untuk
mendapatkan hasil FFT secara berurut.
Xk= N∑−1
n=0
xne−i2πkn/N, k = 0, 1, 2, . . . , N− 1. (2.2)
Pada persamaan 2.2, e−i2πkn/Nsama dengan Nthroot of unity ke-k yaitu ωknN maka dapat ditulis menjadi seperti persamaan 2.3.
Xk = N∑−1
n=0
xnωNkn, k = 0, 1, 2, . . . , N− 1. (2.3)
Dengan menggunakan desimasi waktu, maka persamaan dapat dipecah menjadi dua bagian yaitu bagian sampel dengan waktu ganjil dan genap menjadi persamaan 2.4.
Xk= N 2−1 ∑ n=0 x2nωk(2n)N +ωrN N 2−1 ∑ n=0 x2n+1ωNk(2n), k = 0, 1, 2, . . . , N−1. (2.4) Menggunakan identitas ωN /2 = ωN2 maka 2.4 dapat diubah menjadi
persamaan 2.5. Xk = N 2−1 ∑ n=0 x2nωknN 2 + ωNr N 2−1 ∑ n=0 x2n+1ωknN 2 , k = 0, 1, 2, . . . , N− 1. (2.5) Maka dapat dilihat penjumlahan dari persamaan 2.5 merupakan DFT dari ukuran N /2, bagian pertama melibatkan himpunan suku ganjil{x2n|n = 0, 1, . . . , N/2 − 1}, dan bagian kedua melibatkan
nyatakan yn = x2n dan zn = x2n+1 maka didapatkan hasil pada 2.6 dan 2.7. Yk= N 2−1 ∑ n=0 ynωNkn, k = 0, 1, 2, . . . , N /2− 1. (2.6) Zk= N 2−1 ∑ n=0 znωNkn, k = 0, 1, 2, . . . , N /2− 1. (2.7)
Ketika persamaan 2.6 dan 2.7 diselesaikan secara rekursif maka akan didapatkan bahwa setengah suku awal adalah sama seperti yang ditunjukkan pada 2.8.
Xk = Yk+ ωNkZk, k = 0, 1, 2, . . . , N /2− 1. (2.8) Dengan menggunakan ω N 2+k N = −ωNk dan ω N 2 N 2 = 1, maka sisa setengah suku akhir adalah sesuai persamaan pada 2.9.
Xk+N
2 = Yk− ω k
NZk, k = 0, 1, 2, . . . , N /2− 1. (2.9)
Proses komputasi dari persamaan 2.8 dan 2.9 merupakan operasi yang disebut dengan operasi kupu-kupu Cooley Tukey [6].
2.4.7 Roots of Unity
Roots of unity adalah n bilangan kompleks yang memenuhi zn= 1. Untuk Transformasi Fourier Xk =
∑N−1
n=0 xne−i2πkn/N, ωN ≡
e−i2π/Nsehingga Xk=
∑N−1
n=0 xnωNkndengan ωN merupakan Nth
roots of unity. Pencarian e−i2π/N juga dapat diselesaikan dengan persamaan trigonometri eix = ei(−2π/N) = cos(−2π/N) + i
ωNN = 1 ωNN +k = ωk
N
ωNN /2=−1 ωNN /2+k=−ωNk
Gambar 2.2 Properti Roots of Unity pada FFT
sin(−2π/N) [2]. Roots of unity ini menjadi pilihan titik-titik yang dijadikan dasar pada evaluasi polinomial [2].
Beberapa properti penting dari pemilihan titik pada FFT didasari oleh roots of unity adalah seperti pada Gambar 2.2.
2.4.8 Konvolusi
Konvolusi secara umum merupakan operasi matematika yang menerima suatu fungsi f (x) dan g(x) untuk menghasilkan fungsi ketiga yang fungsi ketiga ini merupakan integral dari perkalian titik dari kedua fungsi dengan fungsi f (x) akan digeser di atas fungsi g(x) dan dinyatakan dengan f ∗ g [2]. Secara diskrit, konvolusi dapat dinyatakan sebagai persamaan 2.10.
c[k] =
n+k
∑
n=0
a[k]b[k− n] (2.10)
Konvolusi pada domain waktu ekuivalen dengan perkalian dikawasan frekuensi dan konvolusi pada domain frekuensi ekuivalen dengan perkalian pada domain waktu [Bracewell, 1965].
2.4.9 Polinomial
Polinomial merupakan pernyataan matematika yang menyatakan jumlahan dari beberapa perkalian dari sebuah variabel konstan dengan koefisiennya [3]. Secara umum polinomial dinyatakan seperti persamaan 2.11. fN(x) = N ∑ i=0 aixi (2.11)
Pangkat tertinggi dari variabel x dari fungsi f (x) disebut dengan orde atau derajat dari polinomial. Sebuah polinomial f (x) dengan orde a dan g(x) dengan orde b jika dilakukan perkalian maka akan menghasilkan h(x) dengan orde a + b.
2.4.10 Optimasi FFT untuk Komputasi Bilangan Real Optimasi pada FFT untuk bilangan real adalah dengan memanfaatkan bagian bilangan imajiner dari FFT. Dua perhitungan dapat dijadikan satu proses FFT dengan cara menyisipkan fungsi kedua kedalam bagian imajiner fungsi pertama. Setelah dilakukan komputasi FFT, selanjutnya adalah ekstraksi hasil, dikarenakan pada tahap ini hasil dari FFT kedua fungsi tersebut bercampur. Optimasi ini memberikan kenaikan peforma untuk komputasi yang membutuhkan banyak perhitungan FFT sekaligus, terutama dalam perkalian polinomial dengan koeifisien dari polinomial berupa bilangan real tanpa imajiner [5].
2.4.11 Representasi Titik Polinomial
Suatu polinomial f (x) dapat direpresentasikan sebagai suatu himpunan pasangan (x, y) dengan y = f (x) untuk suatu x merupakan suatu bilangan sembarang. Pada representasi titik, polinomial dapat dikembalikan kebentuk representasi koefisien
dengan cara melakukan interpolasi terhadap titik-titik pasangan (x, y) pada suatu himpunan titik f (x).
Untuk suatu polinomial dengan representasi koefisien dapat diubah kedalam representasi titiknya dengan cara melakukan Transformasi Fourier dari f (x). Transformasi Fourier akan menghasilkan suatu himpunan hasil pasangan (x, y = f (x)) dengan x merupakan roots of unity.
f (x) = {(x0, y0), (x1, y1), (xi, yi), . . . , (xN, yN)} dengan i =
0, 1, 2, . . . , N dan xi = ωNi dan ωiN merupakan bilangan roots of
unity ke-i dari Nthroots of unity.
Hasil dari representasi titik Transformasi Fourier dapat dikembalikan kedalam representasi koefisiennya dengan cara melakukan Inversi Transformasi Fourier [2].
2.4.12 Perkalian Polinomial dengan FFT
Perkalian polinomial AN(x) dengan BN(x) dengan FFT dilakukan
dengan langkah-langkah berikut ini :
1. Preproses Melakukan penambahan nilai 0 pada polinomial AN(x) apabila polinomial tidak memiliki orde hasil pangkat
dua.
2. Preproses Melakukan penambahan nilai 0 pada polinomial BN(x) apabila polinomial tidak memiliki orde hasil pangkat
dua.
3. Evaluasi FFT Melakukan evaluasi FFT dari polinomial AN(x) dengan FFT pada 2N + 1 roots of unity.
4. Evaluasi FFT Melakukan evaluasi FFT dari polinomial BN(x) dengan FFT pada 2N + 1 roots of unity.
5. Perkalian Titik Melakukan perkalian titik dari CN(x) =
Gambar 2.3 Ilustrasi Perkalian dengan FFT pada Polinomial
6. Inversi FFT Melakukan interpolasi titik dari CN(x)
pada 2N + 1 titik untuk mendapatkan polinomial dalam representasi koefisien kembali.
Ilustrasi 2.3 merupakan gambaran dari bagaimana FFT dapat melakukan perkalian polinomial yang sebelumnya memiliki kompleksitas O(N2) menjadi O(N log N) dengan membawa polinomial ke representasi titiknya untuk dilakukan perkalian titik [2].
2.5 Strategi Penyelesaian Permasalahan BLCATS
Pada subbab ini akan dipaparkan mengenai strategi penyelesaian masalah klasik pada daring SPOJ dengan kode BLCATS. Secara singkat, strategi penyelesaian masalah dari BLCATS terbagi menjadi tujuh bagian besar yaitu :
1. Pendefinisian transformasi dari masalah dan pengkodean konfigurasi.
2. Perumusan transformasi.
4. Analisis struktur Matriks Toeplitz dalam matriks transformasi.
5. Konvolusi pada perkalian matriks transformasi. 6. Pemangkatan dan perkalian akhir matriks transformasi. Sebagai contoh, pada subbab ini akan digunakan contoh untuk melakukan pencarian konfigurasi akhir untuk barisan kucing sepanjang N = 5, putaran komunikasi sebanyak K = 4, dan konfigurasi warna dari kucing pada barisan adalah {GRGRG}.
Titik utama dari tugas akhir ini adalah cara memodelkan dan melakukan komputasi dari perkalian matriks transformasi yang ukuran dari matriks ini besarnya mencapai 50000 × 50000 agar dapat dilakukan dengan cepat.
2.5.1 Pendefinisan Transformasi dari Masalah dan Pengkodean Konfigurasi
Pada permasalahan klasik SPOJ 24730 Magical Colorful Cats (Hard), jawaban akhir merupakan konfigurasi dari kucing yang dikodekan dalam {R, G, W } setelah mengalami komunikasi sebanyak K putaran komunikasi. Komunikasi dari kucing didefinisikan dengan persamaan 2.1.
Untuk dapat dilakukan perhitungan, warna dari kucing akan dikodekan dengan angka dengan R = 0, G = 1, dan W = 2. Tabel 2.3 adalah tabel konfigurasi warna dari contoh permasalahan setelah dilakukan pengkodean.
Apabila transformasi dinyatakan dengan fungsi f (x, y) = ax + by dengan x = Vi dan y = V(i+1) mod N, maka hasil dari f (x, y) berada pada rentang{0, 1, 2}. Tabel 2.4 merupakan daftar kemungkinan dari semua konfigurasi x dan y terhadap hasil f (x, y) dengan 0≤ x, y ≤ 2.
Tabel 2.3 Pengkodean Warna untuk Barisan Kucing⟨GRGRG⟩ Posisi Warna 1 1 (G) 2 0 (R) 3 1 (G) 4 0 (R) 5 1 (G)
Tabel 2.4 Hasil Transformasi untuk Semua Kemungkinan x dan y untuk f (x, y) x y f (x, y) 0 0 0 0 1 2 0 2 1 1 0 2 1 1 1 1 2 0 2 0 1 2 1 0 2 2 2
Mengambil sampel pada Tabel 2.4 pada saat nilai x = 0 dan y = 1 akan didapatkan hasil pada persamaan 2.12 dan 2.13, untuk sampel saat nilai x = 1 dan y = 0 akan didapatkan hasil seperti pada persamaan 2.14 dan 2.15.
0a + 1b≡ 2 (mod 3) (2.12)
1a + 0b≡ 2 (mod 3) (2.14)
a≡ 2 (mod 3) (2.15)
Dari persamaan 2.13 dan 2.15 didapatkan bahwa f (x, y) dapat dinyatakan dengan rumus pada 2.16.
f (x, y) = (2x + 2y) mod 3 (2.16) 2.5.2 Perumusan Transformasi
Sebagai pendahuluan, untuk N = 2 dengan konfigurasi awal ⃗
V2 = ⟨V0, V1⟩, warna akhir dari setiap anggota dari ⃗V2 adalah V0 = V1 = 2(2V0+ 2V1) + 2(2V0+ 2V1) mod 3. Hal ini terjadi
karena kucing mengalami transformasi sebanyak dua kali yaitu saat V0 bertransformasi dengan V1 dan saat V1 bertransformasi dengan V0. Transformasi dari kedua kucing tersebut dapat dirumuskan
dengan persamaan di bawah ini.
V0 = V1= (2V0+ 2V1) mod 3 (2.17)
Setelah kucing V0 dan V1 berubah warna menjadi (2V0 + 2V1)
mod 3 maka selanjutnya kucing V1 akan bertransformasi dengan V0 kembali. Transformasi antara V1 dan V0 dinyatakan dengan
persamaan 2.18 dan dengan menyerdehanakan persamaan maka didapatkan seperti pada persamaan 2.19 dan 2.20.
V1= V0 = (8V0+ 8V1) mod 3 (2.19)
V1= V0 = (2V0+ 2V1) mod 3 (2.20)
Matriks transformasi M tN merupakan matriks transformasi untuk
N kucing, oleh sebab itu jika hasil dari persamaan 2.20 diubah menjadi vektor kolom penyusun matriks, didapatkan M t2 seperti
pada persamaan 2.21. M t2 = [ 2 2 2 2 ] (2.21) Pencarian konfigurasi warna akhir dari barisan melingkar kucing sepanjang dua dengan konfigurasi awal disimbolkan dengan ⃗V2
untuk satu putaran didapatkan dengan perhitungan 2.22. ⃗
V2′ = ⃗V2M t2 (2.22)
Apabila transformasi terjadi sebanyak K kali putaran, maka konfigurasi akhirnya didapat dengan cara memangkatkan matriks transformasi sebanyak K kali seperti yang ditunjukkan 2.23.
⃗
V2′= ⃗V2M tK2 (2.23)
Matriks transformasi yang ditemukan dalam permasalahan untuk N = 2 tidak dapat digunakan untuk sembarang nilai N . Matriks transformasi untuk suatu barisan melingkar kucing sepanjang N bersifat unik.
2.5.2.1 Contoh Transformasi untuk N = 3 dengan Konfigurasi Awal adalah ⃗V3=⟨V0, V1, V2⟩
Transformasi antara V0 dengan V1 didapat dari hasil pada kasus
sebelumnya yang ditunjukkan pada persamaan 2.17 sehingga tidak diperlukan perhitungan ulang. Jika pada kasus pencarian matriks transformasi untuk N = 2 transformasi berhenti pada V1 lalu V1
akan bertransformasi dengan V0, maka untuk N = 3 transformasi
akan berlanjut ke V2. Transformasi antara V1 dan V2 ditunjukkan
pada persamaan 2.24 dan 2.25.
V1 = V2= (2V1+ 2V2) mod 3 (2.24)
V1= V2 = (2(2V0+ 2V1) + 2V2) mod 3 (2.25)
Perlu diketahui, karena V1 sebelumnya telah bertransformasi
dengan V0 maka nilai V1 sudah berubah menjadi (2V0 + 2V1)
mod 3.
V1 = V2 = (4V0+ 4V1+ 2V2) mod 3 (2.26)
V1 = V2 = (1V0+ 1V1+ 2V2) mod 3 (2.27)
Langkah terakhir dari transformasi adalah transformasi antara kucing terakhir dengan kucing pada posisi pertama yaitu transformasi antara VN−1 dengan V0. Nilai pada V0 sebelumnya
sudah berubah menjadi (2V0 + 2V1) mod 3 dan nilai V2 telah
berubah menjadi (1V0 + 1V1 + 2V2) mod 3 maka nilai dari V0
ini.
V2 = V0 = (2(1V0+ 1V1+ 2V2) + 2(2V0+ 2V1)) mod 3 (2.28)
V2 = V0= (6V0+ 6V1+ 4V2) mod 3 (2.29)
V2 = V0= (0V0+ 0V1+ 1V2) mod 3 (2.30)
Jika kita kumpulkan semua persamaannya dari 2.24 hingga 2.30 maka didapatkan rumus untuk masing-masing Vi dengan 0 ≤ i <
N ditunjukkan di bawah ini.
V0 = (0V0+ 0V1+ 1V2) mod 3 (2.31)
V1 = (1V0+ 1V1+ 2V2) mod 3 (2.32)
V2 = (0V0+ 0V1+ 1V2) mod 3 (2.33)
Jika persamaan pada 2.31, 2.32, dan 2.33 dijadikan vektor kolom penyusun matriks transformasi, maka didapatkan matriks M t3pada
2.34. M t3 = 00 11 00 1 2 1 (2.34)
Sama seperti saat jumlah N = 2, konfigurasi akhir dari barisan kucing melingkar dengan konfigurasi awal ⃗V3 setelah mengalami
K putaran dapat dinyatakan dengan persamaan 2.35. ⃗
V3′ = ⃗V3M tK3 (2.35)
Untuk mencari matriks transformasi pada barisan kucing sepanjang N dapat dilakukan dengan cara seperti yang sudah dijelaskan di atas. Pencarian persamaan ini kurang aplikatif dalam komputer sehingga perlu cara lain untuk mencari matriks transformasi ini dengan cara yang lebih efisien agar dapat dibangkitkan oleh program secara otomatis.
2.5.2.2 Contoh Pencarian Konfigurasi Akhir untuk N = 5 dengan Konfigurasi Awal Kucing V5 =⟨G, R, G, R, G⟩ Setelah K = 4 Putaran.
Perlu diketahui, persamaan V0 bertransformasi dengan V1 sama
dengan persamaan 2.27 dan untuk V1 bertransformasi dengan V2
sama dengan persamaan 2.33. Persamaan untuk transformasi kucing V2 dengan V3 ditunjukkan pada persamaan di bawah
ini.
V2 = V3= (2V2+ 2V3) mod 3 (2.36)
V2 = V3= (2(1V0+ 1V1+ 2V2) + 2V3) mod 3 (2.37)
V2 = V3 = (2V 0 + 2V1+ 1V2+ 2V3) mod 3 (2.38)
Persamaan untuk transformasi kucing V3 dengan V4 ditunjukkan
pada persamaan berikut.
V3= V4 = (2(2V 0 + 2V1+ 1V2+ 2V3) + 2V4) mod 3 (2.40)
V3 = V4= (1V 0 + 1V1+ 2V2+ 1V3+ 2V4) mod 3 (2.41)
Persamaan untuk transformasi terakhir yaitu kucing V4 dengan V0
ditunjukkan pada persamaan di bawah ini.
V4= V0 = (2V4+ 2V0) mod 3 (2.42)
V4= V0 = (2(1V 0+1V1+2V2+1V3+2V4)+2(2V0+2V1)) mod 3
(2.43)
V4= V0 = (0V0+ 0V1+ 1V2+ 2V3+ 1V4) mod 3 (2.44)
Jika dilihat pada persamaan 2.30, 2.38, 2.41, dan 2.44, rumus untuk mencari masing-masing Vi dengan 0 ≤ i < N adalah sebagai
berikut.
V0 = (0V0+ 0V1+ 1V2+ 2V3+ 1V4) mod 3 (2.45)
V1 = (1V0+ 1V1+ 2V2) mod 3 (2.46)
V2= (2V 0 + 2V1+ 1V2+ 2V3) mod 3 (2.47)
V4= (0V0+ 0V1+ 1V2+ 2V3+ 1V4) mod 3 (2.49)
Persamaan 2.45 hingga 2.49 diubah menjadi vektor kolom penyusun matriks transformasi M t5 sehingga didapatkan matriks
seperti pada persamaan 2.50.
M t5 = 0 1 2 1 0 0 1 2 1 0 1 2 1 2 1 2 0 2 1 2 1 0 0 2 1 (2.50)
Perhitungan pencarian konfigurasi akhir ditunjukkan di bawah ini. ⃗ V5′ = ⃗V5M tK5 mod 3 (2.51) ⃗ V5′=[1 0 1 0 1] 0 1 2 1 0 0 1 2 1 0 1 2 1 2 1 2 0 2 1 2 1 0 0 2 1 4 mod 3 (2.52) ⃗ V5′ =[1 0 1 0 1] 2 1 0 2 2 2 1 0 2 2 2 2 1 0 2 0 1 2 1 0 1 2 1 2 1 mod 3 (2.53) ⃗ V5′ =[2 2 2 1 2] (2.54)
Dengan mengkodekan bentuk angka menjadi bentuk kode warna kembali maka didapatkan hasil akhir seperti pada persamaan 2.55.
⃗
V5′ =[W W W G W] (2.55)
Hasil dari 2.49 merupakan konfigurasi akhir dari ⃗V5 =⟨GRGRG⟩
setelah mengalami transformasi sebanyak empat kali putaran. Pada tahap ini, perlu diketahui bahwa permasalahan sudah dapat diselesaikan tetapi komputasi pemangkatan matriks ini tergolong berat jika dengan batasan permasalahan yaitu N = 50000 dan K = 109. Diperlukan adanya cara lain untuk melakukan komputasi matriks ini.
2.5.3 Pembangkitan Matriks Transformasi
Jika transformasi Vi adalah transformasi setelah mengalami
komunikasi dari tetangganya yaitu Vi−1 dan Vi+1 untuk 0 <
i < N − 1 dapat dinyatakan sebagai transformasi bagian tengah yang disimbolkan dengan V midi dan transformasi VN−1
dengan V0 dinyatakan sebagai transformasi bagian akhir yang
disimbolkan V endN maka matriks transformasi M tN dapat
disusun dari kumpulan vektor kolom yang ditunjukkan pada persamaan 2.56.
M tN = [V endN, V mid1, V mid2, V midi, . . . , V midN−2, V endN]
(2.56) Dengan menyatakan V midi = (2V midi−1 + 2Vi+1) mod 3
dapat dilakukan generalisasi seperti pada persamaan 2.57.
V midi= (2i+1V0+ 2i+1V1+
i
∑
j=1
2i−j+1Vj+1) mod 3 (2.57)
Hasil modulo tiga dari persamaan 2.57 dapat dicari melalui fakta di bawah ini.
2i≡ 2 (mod 3), i ∈ 2N + 1, i > 0 (2.58)
2i≡ 1 (mod 3), i ∈ 2N, i > 0 (2.59) Persamaan 2.57 dapat disederhanakan menjadi persamaan saat i bilangan ganjil dan i bilangan genap. Saat i merupakan bilangan ganjil dimisalkan dengan o maka V midomenjadi seperti pesamaan
2.60.
V mido= (1V0+1V1+(2V2+1V2+2V3+1V4+· · ·+2Vo+1)) mod 3
(2.60) Saat i merupakan bilangan genap dimisalkan dengan e maka V mide
menjadi seperti pada persamaan 2.61.
V mide= (2V0+2V1+(1V2+2V2+1V3+2V4+· · ·+2Ve+1)) mod 3
(2.61) Dengan persamaan 2.60 dan 2.61 maka dilihat bahwa untuk i bilangan ganjil, koefisien dari V0dan V1memiliki nilai 1 dan untuk V2 hingga VN−1 nilai koefisien akan bergantian secara berseling
memiliki nilai 2 dan untuk V2 hingga VN−1 nilai koefisien akan
bergantian secara berseling antara 1 dan 2.
Seperti yang dijelaskan sebelumnya, V endN merupakan
transformasi akhir yaitu transformasi dari VN−1 dengan V0
maka V endN memiliki rumus seperti yang ditunjukkan pada
persamaan 2.62.
V endN = (2V midN−2+ 4V0+ 4V1) mod 3 (2.62)
Dengan melihat V endN membutuhkan perhitungan V midN−2
maka permasalahan dapat kita pecah menjadi permasalahan saat N merupakan bilangan ganjil dan saat N merupakan bilangan genap.
Untuk V endN dengan N merupakan bilangan genap dimisalkan
dengan ne maka persamaan V endne menjadi seperti pada
persamaan 2.63.
V endne= (5V0+5V1+(2V2+1V2+2V3+1V4+· · ·+1Vne−1)) mod 3
(2.63) Untuk V endN dengan N merupakan bilangan ganjil yang
dimisalkan dengan no maka persamaan V endno menjadi seperti
pada persamaan 2.64.
V endno = (6V0+6V1+(1V2+2V2+1V3+2V4+· · ·+1Vno−1)) mod 3
(2.64) Dengan menggunakan persamaan 2.65 dan 2.66 maka persamaan 2.63 menjadi 2.67 dan persamaan 2.64 menjadi 2.68.
6≡ 0 (mod 3) (2.66)
V endne= (2V0+2V1+(2V2+1V2+2V3+1V4+· · ·+1Vne−1)) mod 3
(2.67)
V endno= (0V0+0V1+(1V2+2V2+1V3+2V4+· · ·+1Vno−1)) mod 3
(2.68) Dengan melihat persamaan 2.67 dan 2.68 dapat ditarik kesimpulan bahwa untuk N merupakan bilangan genap, koefisien dari V0dan V1
memiliki nilai 2 dan untuk N merupakan bilangan ganjil, koefisien dari V0 dan V1 memiliki nilai 0. Koefisien dari V2 hingga VN−1
akan bergantian secara berseling antara 2 dan 1 untuk N bilangan genap dan berseling antara 1 dan 2 untuk N bilangan ganjil. Dengan mengaplikasikan penjelasan di atas maka untuk melakukan pembangkitan matriks transformasi sesuai contoh permasalahan dengan N = 5 adalah sebagai berikut :
1. Matriks transformasi yang ingin dibangkitkan adalah M t5,
karena dalam kasus ini N = 5.
2. M t5dibangun oleh vektor-vektor kolom penyusunnya yaitu
[V end5, V mid1, V mid2, V mid3, V end5].
3. N bernilai ganjil sehingga V end5 = [0, 0, 1, 2, 1] dengan
menggunakan persamaan pada 2.68.
4. Untuk nilai i ganjil pada V midi adalah V mid1 =
[1, 1, 2, 0, 0] dan V mid3 = [1, 1, 2, 1, 2] dengan
menggunakan persamaan 2.60.
5. Untuk nilai i genap pada V midi adalah V mid2 =
[2, 2, 1, 2, 0] dengan menggunakan persamaan 2.61.
6. Dengan menggabungkan nilai V mid dan V end maka didapatkan matriks sesuai dengan 2.50. Sudah terbukti bahwa
cara pembangkitan dapat mencari matriks transformasi dengan benar.
Contoh matriks transformasi untuk N = 2 hingga N = 15 dapat dilihat pada lampiran B. Dengan menggunakan observasi akan terlihat pola dari matriks sesuai dengan penjelasan di atas.
2.5.4 Struktur Matriks Toeplitz dalam Matriks Transformasi
Matriks transformasi M tN merupakan matriks yang dibangun oleh
vektor kolom dari persamaan V end dan V mid sesuai dengan persamaan 2.56. Dengan Ta,b merupakan elemen pada matriks
M tN pada baris a kolom b dengan 0≤ a, b < N, maka koefisien
Vj pada V midi dan V endN untuk 0 ≤ j < N akan membangun
nilai pada Tj,i. Dengan memasukkan persamaan 2.56 dan 2.57 pada
vektor kolom matriks untuk kolom 1 . . . N − 1 maka didapatkan persamaan di bawah ini.
V mido= (1V0+ 1V1+ o+1 ∑ j=2 Tj−1,o−1Vj) mod 3 (2.69) V mide= (2V0+ 2V1+ e+1 ∑ j=2 Tj−1,e−1Vj) mod 3 (2.70)
Persamaan 2.70 adalah persamaan V mid dengan e merupakan simbol saat i bernilai genap sedangkan 2.69 adalah persamaan Vmid dengan o merupakan simbol saat i bernilai ganjil. V mide
merupakan kombinasi linear dari vektor kolom ke e pada matriks M tN dengan e = 2, 4, 6, 8, . . . dan V mido merupakan kombinasi
linear dari vektor kolom ke o pada matriks M tN dengan o =
1, 3, 5, 7, . . . . Kolom terakhir pada matriks M tN dibangun oleh
matriks akan menjadi persamaan 2.71 dan 2.72. V endno = (0V0+ 0V1+ no+1∑ j=2 Tj−1,no−1Vj) mod 3 (2.71) V endne= (2V0+ 2V1+ ne+1∑ j=2 Tj−1,ne−1Vj) mod 3 (2.72)
Pada persamaan 2.69 hingga 2.72 didapatkan kesimpulan bahwa M tN untuk N bernilai ganjil dan N bernilai genap memiliki pola
yang berbeda. Maka persamaan sebelumnya pada 2.56 dapat diubah menjadi seperti pada persamaan 2.73.
Persamaan pada 2.73 merupakan bentuk umum dari matriks transformasi M tN. Untuk kolom ke 2 ≤ j < N − 1 pada suku
ke-j dengan 2 ≤ i < N memenuhi struktur Matriks Toeplitz karena Ti,j = T i + 1, j + 1 untuk 2 ≤ i, j < N. Bagian pada
Matriks Toeplitz yaitu bagian dari Ti,j untuk 2 < i, j < N − 1
tidak perlu dituliskan ulang dikarenakan nilai dari Ti,j dapat dicari
dengan menggunakan persamaan yang ditunjukkan pada persamaan 2.73.
Jadi, dalam pembangkitan matriks transformasi M tN dapat
dilakukan dengan melihat nilai dari N dan posisi kolom dan baris saat pembangkitan menunjukkan nilai genap atau ganjil. Matriks Toeplitz juga ditemukan pada matriks transformasi ini, sehingga kita tidak perlu melakukan pembangkitan seluruh N × N dari matriks M tN melainkan hanya membutuhkan dua baris
dan dua kolom awal saja untuk mempercepat pembangkitan dan pemangkatan nantinya. Walaupun begitu, karena baris pertama dan kedua dari matriks selalu bernilai sama untuk N berapapun, maka
dapat dituliskan salah satu barisnya saja. M tN = [V endno,
V mido, V mide, . . . , V mide,
V endno] , untuk N bernilai
ganjil, no = N ,
o = 1, 3, 5, . . . , N − 3, dan e = 2, 4, 6, . . . , N− 2 [V endne,
V mido, V mide, . . . , V mido,
V endne] , untuk N bernilai
genap, ne = N ,
o = 1, 3, 5, . . . , N − 2, dan e = 2, 4, 6, . . . , N− 3
(2.73) 2.5.5 Konvolusi pada Perkalian Matriks Transformasi Perkalian pada matriks transformasi M tN dapat dibentuk menjadi
suatu konvolusi dikarenakan terdapat properti dari Matriks Toeplitz. Pada bagian sebelumnya telah dijelaskan bahwa matriks M tN ini
akan berbentuk dua baris awal dan dua kolom awal saja dengan baris pertama dan kedua selalu bernilai sama. Hasil perkalian ini nantinya juga akan berbentuk dua baris dan dua kolom awalnya saja dikarenakan telah mewakili matriks keseluruhan.
Baris pertama dan kedua setelah dilakukan perkalian bernilai sama sehingga dapat dituliskan rowi yaitu nilai baris pada kolom ke i
seperti pada persamaan 2.74.
rowi = N∑−1
j=0
Perkalian dilakukan dalam matriks yang sudah dikodekan dalam dua baris dan dua kolom awal dari matriks dengan baris pertama dan kedua bernilai sama sehingga dengan menyatakan rowAi sebagai
baris pertama dengan kedua matriks A pada kolom i, rowBisebagai
baris pertama dan kedua matriks B pada kolom i, colA0i sebagai
kolom pertama pada matriks A pada baris ke-i, colA1i sebagai
kolom kedua pada matriks A pada baris ke-i. colB0isebagai kolom
pertama pada matriks B pada baris ke-i, dan colB1isebagai kolom
kedua pada matriks B pada baris ke-i persamaan pada 2.74 dapat dituliskan menjadi seperti pada persamaan 2.75.
rowi= rowA0rowBi+ i+1
∑
k=0
rowAkrowBi+1−k− rowA0rowBi+i
− rowAi+1rowB0
+
N∑−1
k=i−1
rowAkcolB1N−1−k− rowAi−1colB10 − rowAicolB11 (mod 3), untuk i>0
(2.75) Serupa dengan penjabaran di atas, jika col0i dan col1i merupakan
kolom pertama dan kedua dari matriks hasil perkalian, maka didapatkan persamaan 2.76 dan 2.77.
col0i = N∑−1 j=0 Ai,jBj,0 (mod 3) (2.76) col1i = N∑−1 j=0 Ai,jBj,1 (mod 3) (2.77)
Dengan merubah bentuk persamaan 2.76 dan 2.77 menggunakan representasi dua baris dan dua kolom awal, maka didapatkan persamaan 2.78 dan 2.79.
col0i = colA0icolB00
+
i+1
∑
k=0
colA1kcolB0i+1−k − colA1i+1colB00 − colA10colB0i+1
+
N∑−1
k=i−1
rowAkcolB0N−1−k− rowA1colB0i
− rowA0colB0i−1 (mod 3), untuk i>0
(2.78) col1i = colA0icolB10
+
i+1
∑
k=0
colA1kcolB1i+1−k − colA1i+1colB10 − colA10colB1i+1
+
N∑−1 k=i−1
rowAkcolB1N−1−k− rowA1colB1i
− rowA0colB1i−1 (mod 3), untuk i>0
(2.79) Pada persamaan 2.75, 2.78, dan 2.79, bagian dari persamaan yang mengandung notasi zigma adalah konvolusi yang dapat dinyatakan sebagai A⊛ B(i) yaitu konvolusi dari A dan B pada nilai berorde i yang dapat dinyatakan sebagai sebagai berikut ini.
i+1
∑
k=0