Kalkulus Variasi
Pendahuluan, Model Matematika, Keterkontrolan
Toni Bakhtiar
Departemen Matematika IPB
Outline
Beberapa contoh masalah kontrol optimum Rumusan masalah kontrol optimum
1 Model matematika 2 Persamaan state 3 Fungsi kendala
Reachability, controllability, observability Sistem kendali
Masalah Inventori-Produksi
Sumber: Sethi & Thompson (2006) Fungsional objektif: min P Z T 0 h(I ˆI)2 2 + c(P Pˆ)2 2 e rt dt. Fungsi kendala: ˙I(t) = P(t) D(t), I(0) = I0,dengan I tingkat inventori, P tingkat produksi, D tingkat permintaan, ˆI tingkat inventori yang ingin dicapai, ˆP tingkat produksi yang ingin dicapai, dan e rt faktor diskon.
Masalah: menentukan tingkat produksi P =P(t) sedemikian sehingga meminimumkan biaya-biaya penalti akibat tidak terpenuhinya target dalam inventori dan produksi.
Masalah Pemasaran melalui Iklan
Sumber: Sethi & Thompson (2006) Fungsional objektif: max c Z ∞ 0 (π(G) c(t))e rt dt. Fungsi kendala: ˙ G(t) = c(t) δG(t), G(0) = G0,
dengan π tingkat penerimaan (revenue) yang merupakan fungsi dari citra perusahaan (goodwill ) G , c biaya produksi (iklan), dan δ laju depresiasi. Masalah: menentukan besarnya biaya yang dikeluarkan untuk iklan c =c(t)sedemikian sehingga memaksimumkan tingkat keuntungan.
Masalah Pemeliharaan dan Pemanenan Ikan
Sumber: Sydsæter et al. (2008) Fungsional objektif: max u x(T)P(T , x(T))e rT Z T 0 cx(t)u(t)e rt dt . Fungsi kendala: ˙x(t) = x(t)g(t, u(t)), x(0) = x0,
dengan x(t)berat ikan pada saat t, P(t, x) harga ikan dengan berat x pada saat t, u(t) banyaknya pakan ikan yang digunakan, dan c >0 biaya pakan ikan.
Masalah: menentukan banyaknya pakan ikan yang digunakan u =u(t) sedemikian sehingga memaksimumkan keuntungan.
Masalah Energi dan Kualitas Lingkungan
Sumber: Chiang (1992) Fungsional objektif: max E Z T 0 U(C(E), P(E))dt. Fungsi kendala: ˙S(t) = E(t), S(0) = S0, S(T) 0,dengan U fungsi utilitas yang bergantung pada konsumsi energi C(E)dan polusi P(E), E laju penggunaan energi (BBM), dan S persediaan energi (BBM).
Masalah: menentukan laju penggunaan energi (BBM) E =E(t) sedemikian sehingga memaksimumkan utilitas.
Masalah Kebijakan Antipolusi
Sumber: Chiang (1992) Fungsional objektif: max E Z T 0 U(C(E), P) dt. Fungsi kendala: ˙S(t) = A(t) E(t), ˙P(t) = αE(t) βA(t) δP(t), S(0) = S0, S(T) 0, P(0) = P0, P(T) 0,dengan U fungsi utilitas yang bergantung pada konsumsi energi C(E)dan tingkat polusi P, E laju penggunaan energi (BBM), A aktivitas antipolusi, dan S persediaan energi (BBM).
Masalah: menentukan laju penggunaan energi (BBM) E =E(t) sedemikian sehingga memaksimumkan utilitas.
Perumusan Masalah Kontrol Optimum
Masalah kontrol optimum adalah masalah menentukan peubah kontrol yang dapat mengendalikan suatu proses sedemikian sehingga memenuhi beberapa kendala …sik dan dalam waktu yang sama mengoptimumkan kriteria tertentu.
Masalah kontrol optimum dapat diselesaikan melalui dua pendekatan:
1 program dinamik (Bellman, 1957) 2 prinsip maksimum (Pontryagin, 1962)
Dalam kuliah ini akan dibahas penyelesaian masalah kontrol optimum melalui pendekatan prinsip maksimum.
Pendekatan prinsip maksimum banyak menggunakan teknik dalam kalkulus variasi.
Dalam kuliah ini, kalkulus variasi merupakan bahan UTS dan kontrol optimum, sebagai penerapan kalkulus variasi, merupakan bahan UAS.
Model Matematika
Perumusan masalah kontrol optimum membutuhkan: Model matematika dari proses yang akan dikendalikan. Fungsi kendala.
Spesi…kasi dari kriteria yang akan dioptimumkan (fungsional objektif). Model matematika dari suatu proses umumnya dinyatakan dalam bentuk persamaan state (berupa persamaan diferensial):
˙x(t) =g(x(t), u(t), t), dengan x(t) = 0 B B B @ x1(t) x2(t) .. . xn(t) 1 C C C A, u(t) = 0 B B B @ u1(t) u2(t) .. . um(t) 1 C C C A, g(x, u, t) = 0 B B B @ g1(x, u, t) g2(x, u, t) .. . gn(x, u, t) 1 C C C A. x(t) disebut sebagai vektor peubah state dan u(t)disebut sebagai vektor peubah kontrol
Model Matematika
Klasi…kasi model:nonlinear dan time-varying (non-autonomous atau takmandiri): ˙x(t) =g(x(t), u(t), t).
nonlinear dan time-invariant (autonomous atau mandiri): ˙x(t) =g(x(t), u(t)).
linear dan time-varying :
˙x(t) =A(t)x(t) +B(t)u(t). linear dan time-invariant:
Model Matematika
Analisis model taklinear ˙x =g(x, u)biasanya dilakukan melalui model linear padanannya (linearized model ) yang berbentuk ˙x =Ax +Bu, dengan A merupakan matriks Jacobi yang dievaluasi di sekitar titik tetapnya: A= 2 6 4 ∂g1 ∂x1 ∂g1 ∂xn .. . . .. ... ∂gn ∂x1 ∂gn ∂xn 3 7 5 x=¯x .
Model Matematika
Example
Sebuah mobil berjalan lurus meninggalkan titik asal. Jarak mobil dari titik asal pada saat t dinyatakan sebagai s(t). Mobil diasumsikan dapat dikendalikan melalui percepatan (menginjak pedal gas) atau perlambatan (menginjak pedal rem) yang dinyatakan sebagai
¨s(t) =a(t) +b(t),
Persamaan State
Example (Lanjutan)
Dapat dide…niskan vektor peubah state dan vektor peubah kontrol: x(t) = x1(t) x2(t) = s(t) ˙s(t) , u(t) = u1(t) u2(t) = a(t) b(t) . Diperoleh ˙x1 =x2 dan ˙x2 =u1+u2, sehingga dalam notasi matriks
diperoleh model matematika ˙x(t) = 0 1
0 0 x(t) +
0 0
Fungsi Kendala
Example (Lanjutan)
Jika mobil mulai berjalan dari titik asal pada saat t0 dan berhenti di titik e
pada saat tf, maka diperoleh kendala
x1(t0) = 0, x1(tf) =e,
x2(t0) = 0, x2(tf) =0.
Dalam notasi matriks, x(t0) =
0
0 , x(tf) = e 0 .
Jika ada syarat tambahan bahwa mobil tidak boleh mundur, berputar, atau berbelok maka harus ada kendala tambahan
Fungsi Kendala
Example (Lanjutan)
Maksimum percepatan ialah M1 dan maksimum perlambatan ialah M2
(admissible control ):
0 u1(t) M1,
M2 u2(t) 0.
Banyaknya BBM mula-mula G liter dan diasumsikan tidak ada pengisian BBM di tengah jalan yang dilewati:
Z tf
t0
[k1u1(t) +k2x2(t)]dt G .
Diinginkan mobil tiba di titik e secepat mungkin: min J =tf t0 =
Z tf
t0 dt.
Example (Ringkasan)
Masalah kontrol optimum (multivariabel, state terbatas, input terbatas, kendala integral): min J := Z tf t0 dt dengan kendala: ˙x1=x2, ˙x2=u1+u2, x1(t0) =0, x1(tf) =e, x2(t0) =0, x2(tf) =0, 0 x1(t) e, 0 x2, 0 u1(t) M1, M2 u2(t) 0, Z tf t0 [k1u1(t) +k2x2(t)]dt G .
Masalah Kontrol Optimum
Untuk selanjutnya, kriteria (fungsional objektif) diasumsikan berbentuk J =S(x(tf), tf) +
Z tf
t0
f(x(t), u(t), t)dt. Fungsi S disebut sebagai scrap value atau salvage value.
Masalah kontrol optimum adalah masalah menentukan admissible control u (t)yang dapat mengendalikan sistem dinamik
˙x(t) =g(x(t), u(t), t),
sedemikian sehingga mampu mengikuti admissible trajectory x (t)dalam interval waktu [t0, tf] dan mengoptimumkan fungsional objektif
J =S(x(tf), tf) +
Z tf
t0
f(x(t), u(t), t)dt. u (t)disebut kontrol optimum dan x (t)trajektori optimum.
Reachability
Diberikan sistem dinamik (proses):
˙x(t) =g(x(t), u(t), t),
De…nition
State z dikatakan reachable (dapat dicapai) pada waktu T dari sebarang state y jika 9u 2Ω(u)sedemikian sehingga
x(t0) = y ,
Controllability
Diberikan sistem dinamik (proses):
˙x(t) =g(x(t), u(t), t),
De…nition
Sistem dinamik dikatakan controllable (terkontrol) jika sebarang state z reachable (dapat dicapai) dari sebarang state y .
Observability
Diberikan sistem dinamik (proses):
˙x(t) = g(x(t), u(t), t), x(t0) =x0,
w(t) = h(x(t)) ! observasi (pengamatan, pengukuran)
De…nition
Sistem dinamik dikatakan observable (dapat diobservasi) jika berdasarkan u, w , dan [t0, tf], kondisi awal x0 dapat ditentukan.
Controllability
Example
Adakah u sehingga sistem berikut terkontrol?
˙x =x+u, x(t0) =x0, x(T) =xT.
Jawab: Sistem di atas dikatakan terkontrol jika dapat ditemukan fungsi kendali u(t)sedemikian sehingga membawa sistem dari titik(t0, x0)
menuju titik (T , xT)dengan x0, xT, t06=T sebarang. Akan dicari u dalam
bentuk paling sederhana, yaitu u(t) =k (konstan). Diperoleh ˙x =x+k , dx x+k =dt , Z dx x+k = Z dt , x(t) =Cet k.
Example (Lanjutan)
Dari nilai awal dan nilai akhir diperoleh sistem persamaan: x(t0) =x0 , Cet k =x0,
x(T) =xT , CeT k =xT,
sehingga diperoleh solusi:
C = x0 xT et0 eT, k = x0 xT et0 eTe t0 x 0 =: u(t). ) Sistem terkontrol.
Controllability
Example
Tentukan kendali konstan u(t) =k sehingga sistem berikut terkontrol: ¨x = ˙x+2x+u,
x(0) = 0, x(1) = 1, ˙x(0) = 0.
Solution
Dengan mensubstitusikan u(t) =k diperoleh PD orde dua
¨x ˙x 2x=k. Penyelesaian dari persamaan karakteristik r2 r 2=0 ialah r =2 dan r = 1, sehingga diperoleh solusi homogen
xh(t) =C1e2t+C2e t. Jika xp merupakan solusi partikular maka
2xp =k atau xp(t) = 12k, sehingga solusi umum PD ialah
x(t) =C1e2t+C2e t 12k.
Syarat batas x(0) =0 dan ˙x(0) =0 memberikan C1+C2 12k =0, 2C1 C2 =0,
sehingga didapatkan 3C1 = 12k atau C1 = 16k dan C2 = 13k. Solusi umum
PD menjadi x(t) = 16ke2t+13ke t 12k. Dari syarat batas x(1) =1 diperoleh k = 1 1 6e2+ 1 3e 1 1 2 =: u(t).
Problem
Adakah u sehingga sistem berikut terkontrol?
˙x =x+ut, x(t0) =x0, x(T) =xT.
Problem
Adakah u sehingga sistem berikut terkontrol?
Teorema Keterkontrolan
Diberikan sistem dinamik linear dan time-invariant: ˙x =Ax+Bu dengan A berukuran n n.
Theorem
Sistem dinamik di atas controllable (terkontrol) jika dan hanya jika controllability matrix
M = [B AB A2B . . . An 1B]
berpangkat penuh, yaitu rank(M) =n. Bukti: lihat, misalnya, Ogata (1997), hal. 737.
Teorema di atas hanya menjamin keterkontrolan sistem tetapi tidak memberikan fungsi input u yang dapat mengontrol sistem.
Example
Dari sistem ˙x =x+u diperoleh A=1 dan B =1 sehingga M = (1))rank(M) =1 (penuh).
Example
Untuk sistem
¨x = ˙x+2x+u, misalkan x1 =x dan x2 = ˙x, sehingga diperoleh
˙x1 = ˙x =x2,
˙x2 = ¨x = ˙x+2x+u = x2+2x1+u.
Dalam notasi matriks: ˙x1 ˙x2 = 0 1 2 1 x1 x2 + 0 1 u.
Example (Lanjutan) Sistem: ˙x = 0 1 2 1 A x+ 0 1 B u. Controlability matrix: M = 0 1 1 1 )rank(M) =2 (penuh)
Example Sistem ˙x = 2 4 a1 0 0 0 a2 0 0 0 a3 3 5 x+ 2 4 1 1 1 3 5 u terkontrol karena untuk ai 6=0 diperoleh
M = 2 4 1 a1 a21 1 a2 a22 1 a3 a23 3 5)rank(M) =3.
Example Sistem ˙x = 2 4 a1 0 0 0 a2 0 0 0 a3 3 5 x+ 2 4 0 1 1 3 5 u tidak terkontrol (uncontrolable) karena
M = 2 4 0 0 0 1 a2 a22 1 a3 a23 3 5)rank(M) =2.
Problem
Periksa keterkontrolan sistem-sistem berikut:
˙x = 2 4 1 1 0 0 1 0 0 0 2 3 5 x+ 2 4 0 1 1 3 5 u. ˙x = a b 0 c x+ 1 0 u.
Sistem Kendali (Control System)
Sistem: susunan, himpunan, atau kumpulan benda (komponen …sik) yang saling berhubungan dan saling memengaruhi sebagai sebuah kesatuan. Contoh: sistem pengatur suhu, sistem kesetimbangan tubuh, sistem perekonomian, dsb.
Kendali: pengendali (control ), pengatur (regulator ).
Sistem kendali: susunan beberapa komponen …sik yang saling terhubung sedemikian sehingga dapat
mengatur/mengendalikan/memerintah diri sendiri atau sistem lain. Bagian-bagian sistem kendali:
1 Sistem (proses, plant)
2 Input: rangsangan, tindakan, perintah (biasanya dari luar) kepada
sistem agar melakukan sesuatu.
3 Output: respon dari sistem akibat input.
4 Disturbance input (noisy, exogeneous input): angin, gelombang, sinar
Ktesibios (Yunani, 300 SM): Float valve regulator
1 Sistem: proses penampungan air (on-o¤ control, bang-bang control ) 2 Input: ketinggian air
Berdasarkan cara pengendalian (control action), sistem dibedakan atas:
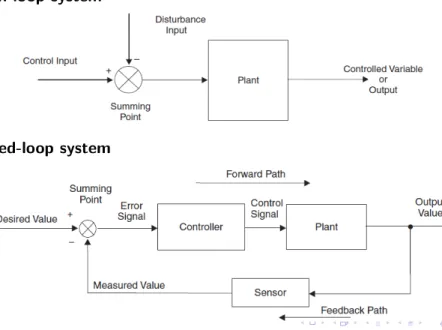
1 Open-loop system: sistem yang tidak mempertimbangkan output
dalam proses selanjutnya. Contoh: mesin cuci, AC, microwave, lampu lalu-lintas.
lebih sederhana, lebih murah, kurang presisi selalu stabil
2 Closed-loop system: sistem yang menggunakan output sebagai
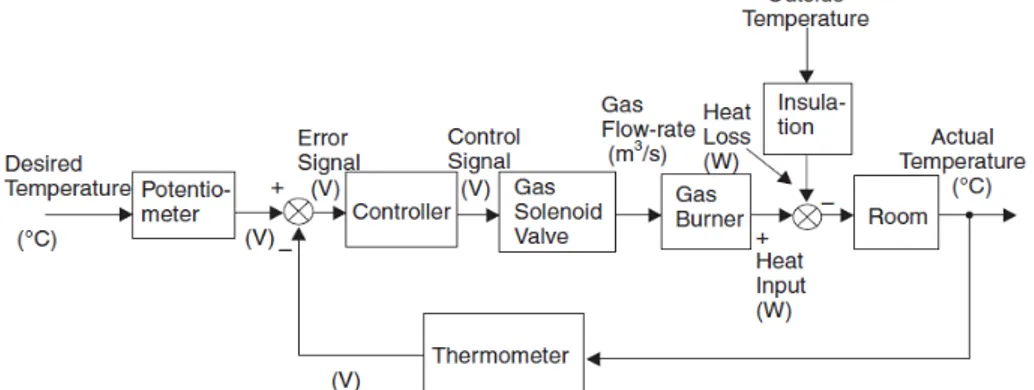
umpanbalik (feedback) dalam proses selanjutnya. Contoh: katup Ktesibios, autopilot, AC automatik, dsb.
lebih rumit, butuh sensor untuk mencatat output (karena itu lebih mahal), lebih presisi
Diagram Blok
Open-loop systemSistem Pengendali Kapal dengan Autopilot
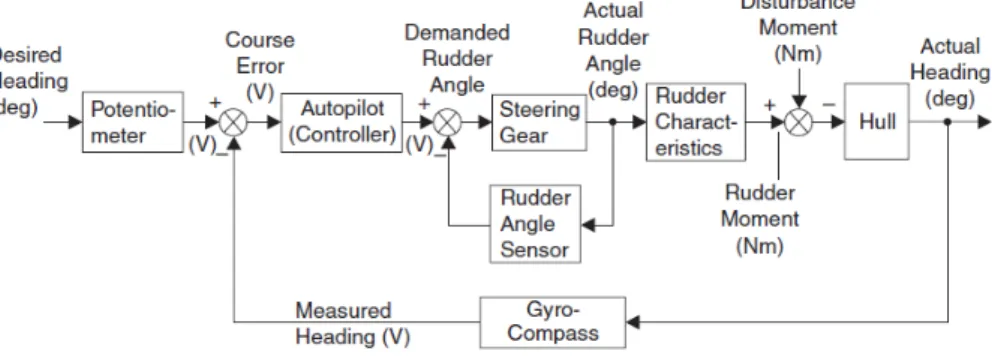
Autopilot didesain untuk menjaga arah kapal (heading ) terhadap berbagai gangguan seperti angin (wind ), arus (current), dan gelombang (waves). Arah kapal diukur dengan gyro-compass dan dicocokkan dengan arah yang dikehendaki. Autopilot kemudian menghitung sudut kemudi (rudder ) yang dibutuhkan dan mengirim sinyal ke gir kendali (steering gear ). Sudut kemudi aktual diukur dengan sensor dan dibandingkan dengan sudut yang dibutuhkan. Beda sudut dan beda arah dijadikan umpanbalik (feedback).
Sistem Pengendali Kecepatan
Kecepatan mobil diukur menggunakan sensor (speedometer ) dan
dibandingkan dengan kecepatan yang diinginkan (reference speed, di jalan tol 80-100 km/jam) dalam blok "Compute". Berdasarkan perbedaan kecepatan aktual dan yang diinginkan, pedal gas/rem/kopling diinjak untuk mengubah gaya yang dikenakan pada mobil melalui mesin, sistem transmisi, dan roda.
Fungsi Transfer
Misalkan sistem dinamik suatu proses dinyatakan dalam persamaan diferensial orde-2 berikut:
a ¨x(t) +b ˙x(t) +cx(t) =Ku(t), x(0) =0, ˙x(0) =0, dengan x peubah state, u peubah kontrol, dan a, b, c, K
konstanta-konstanta.
Transformasi Laplace persamaan di atas memberikan: as2X(s) +bsX(s) +cX(s) =KU(s) ,X(s) = K
as2+bs+cU(s)
Fungsi transfer P(s)merupakan fungsi yang menghubungkan input dan output, yaitu
P(s):= K
Fungsi Transfer
Dalam bentuk diagram blok:
U(s) ! K
as2+bs+c !X(s)
Beberapa fungsi yang lazim dijadikan input:
Fungsi u(t) U(s) Impulse u(t) = ∞ ; t =0 0 ; t 6=0 U(s) =e s Step u(t) = C ; t 0 0 ; t <0 U(s) = C s Ramp u(t) = Ct ; t 0 0 ; t <0 U(s) = C s2 Parabolic u(t) = Ct 2 ; t 0 0 ; t <0 U(s) = 2C s3