Informasi Dokumen
- Penulis:
- Arif Wibisono, S.Pd, M.Kom
- Sekolah: Universitas
- Mata Pelajaran: Pendidikan Teknologi Informasi
- Topik: Teknik Digital
- Tipe: buku
- Tahun: 2017
- Kota: Semarang
Ringkasan Dokumen
I. PENGENALAN KONSEP DIGITAL
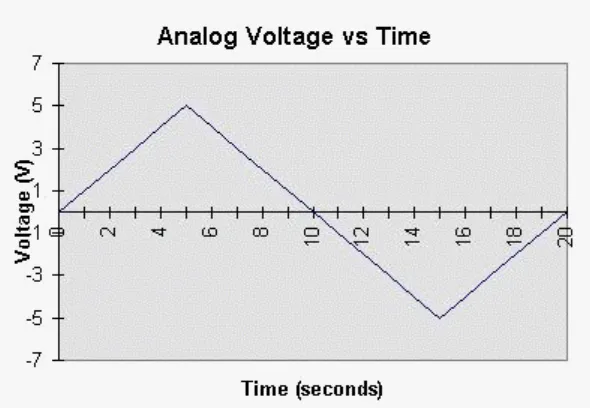
Bab ini membahas dasar-dasar konsep digital, termasuk representasi bilangan dalam bentuk analog dan digital. Representasi analog menunjukkan perubahan kuantitas secara kontinu, sementara representasi digital menggunakan simbol diskrit (digit) untuk menyatakan nilai. Kelebihan dan keterbatasan sistem digital juga diuraikan, dengan penekanan pada kemudahan desain, penyimpanan informasi, dan ketelitian. Namun, sistem digital memerlukan konversi dari analog ke digital dan sebaliknya, yang merupakan langkah penting dalam penerapannya.
1.1. Representasi Bilangan
Representasi bilangan dibagi menjadi dua kategori: analog dan digital. Pada representasi analog, perubahan kuantitas terjadi secara bertahap, sedangkan pada representasi digital, perubahan terjadi dalam langkah-langkah diskrit. Contoh analog termasuk speedometer mobil, sedangkan contoh digital adalah jam digital. Pemahaman tentang perbedaan ini penting untuk memahami sistem digital.
1.2. Kelebihan Dan Keterbatasan Sistem Digital
Sistem digital memiliki beberapa kelebihan seperti kemudahan desain, penyimpanan informasi yang lebih baik, dan ketelitian yang tinggi. Namun, keterbatasan utama adalah kebutuhan untuk mengkonversi sinyal analog menjadi digital dan sebaliknya, yang memerlukan perangkat tambahan seperti ADC dan DAC. Ini menunjukkan kompleksitas dalam penerapan sistem digital dalam kondisi nyata.
1.3. Sistem Bilangan Digital
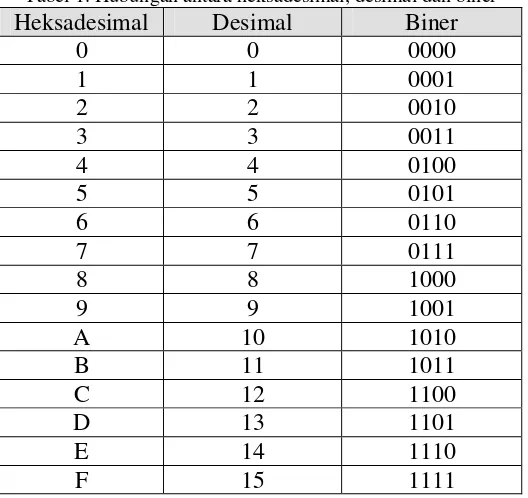
Sistem bilangan digital mencakup desimal, biner, oktal, dan heksadesimal. Sistem biner adalah yang paling umum digunakan dalam teknologi digital karena hanya memiliki dua simbol, yaitu 0 dan 1. Pemahaman tentang sistem bilangan ini penting untuk menganalisis dan mendesain rangkaian digital. Setiap sistem memiliki karakteristik dan aplikasi yang berbeda dalam konteks digital.
II. SISTEM BILANGAN DAN KODE
Bab ini membahas konversi antara berbagai sistem bilangan dan kode yang digunakan dalam sistem digital. Penekanan diberikan pada konversi antara biner dan desimal, serta operasi aritmetika seperti penjumlahan dan pengurangan dalam sistem biner. Kode BCD dan kode heksadesimal juga dijelaskan, menunjukkan pentingnya pengkodean dalam representasi data.
2.1. Konversi Biner ke Desimal
Konversi biner ke desimal dilakukan dengan menjumlahkan bobot dari bit yang bernilai 1. Ini adalah proses yang fundamental dalam memahami bagaimana data biner dapat diterjemahkan ke dalam format yang lebih mudah dipahami, yaitu desimal. Contoh diberikan untuk memperjelas langkah-langkah konversi ini.
2.2. Konversi Desimal ke Biner
Konversi dari desimal ke biner dapat dilakukan dengan metode pembagian berturut-turut dengan 2. Proses ini memungkinkan representasi bilangan desimal dalam bentuk biner, yang merupakan dasar dari pengolahan data digital. Contoh konversi disertakan untuk memperjelas metode ini.
2.3. Penjumlahan Biner
Penjumlahan biner dilakukan dengan cara yang mirip dengan penjumlahan desimal, tetapi dengan lebih sedikit kasus yang perlu dipertimbangkan. Ini menunjukkan kesederhanaan sistem biner dan pentingnya operasi ini dalam pengolahan data. Contoh penjumlahan biner disertakan untuk ilustrasi.
III. RANGKAIAN LOGIKA
Bab ini menjelaskan tentang rangkaian logika digital yang beroperasi berdasarkan prinsip aljabar Boolean. Operasi dasar seperti AND, OR, dan NOT dijelaskan dengan penggunaan tabel kebenaran untuk menggambarkan hubungan antara input dan output. Pemahaman tentang rangkaian logika sangat penting dalam desain sistem digital.
3.1. Konstanta dan Variable Boolean
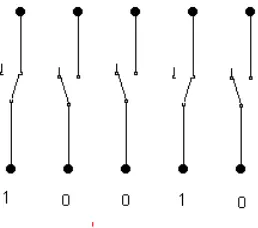
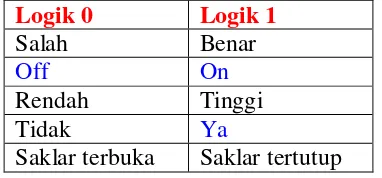
Aljabar Boolean menggunakan dua nilai, 0 dan 1, untuk merepresentasikan keadaan logika. Ini memudahkan analisis dan desain rangkaian logika karena tidak ada nilai pecahan atau negatif. Prinsip dasar ini menjadi fondasi dalam pengembangan sistem digital.
3.2. Operasi-Operasi Logika Boolean
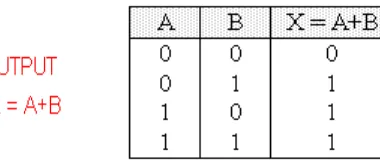
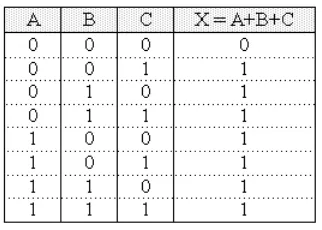
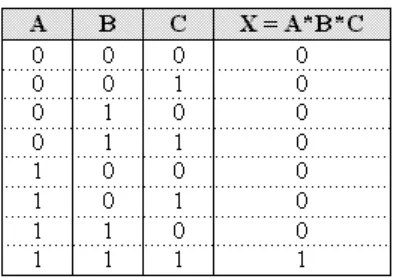
Operasi dasar dalam aljabar Boolean terdiri dari penjumlahan logika (OR), perkalian logika (AND), dan komplementasi (NOT). Tabel kebenaran digunakan untuk menggambarkan hasil dari operasi-operasi ini berdasarkan kombinasi input. Ini membantu dalam memahami bagaimana rangkaian logika berfungsi.
Referensi Dokumen
- TEKNIK DIGITAL teori dan aplikasi ( Depari, G. )